इस पेज पर मेट्रिक की ग्लॉसरी के शब्द शामिल हैं. ग्लॉसरी में मौजूद सभी शब्दों के लिए, यहां क्लिक करें.
A
सटीक
सही कैटगरी के अनुमान की संख्या को अनुमान की कुल संख्या से भाग देने पर. यानी:
उदाहरण के लिए, अगर किसी मॉडल ने 40 सही और 10 गलत अनुमानों का अनुमान लगाया है, तो उसका सटीक अनुमान:
बाइनरी क्लासिफ़िकेशन, सही अनुमान और गलत अनुमान की अलग-अलग कैटगरी के लिए खास नाम उपलब्ध कराता है. इसलिए, बाइनरी क्लासिफ़िकेशन के लिए सटीक होने का फ़ॉर्मूला इस तरह है:
कहां:
- TP, ट्रू पॉज़िटिव (सही अनुमान) की संख्या है.
- TN, ट्रू नेगेटिव (सही अनुमान) की संख्या है.
- FP, फ़ॉल्स पॉज़िटिव (गलत अनुमान) की संख्या है.
- FN, फ़ॉल्स निगेटिव (गलत अनुमान) की संख्या है.
सटीक होने की तुलना, प्रिसिज़न और रीकॉल से करें.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: सटीक, रीकॉल, सटीक जानकारी, और इससे जुड़ी मेट्रिक देखें.
पीआर कर्व के नीचे का एरिया
पीआर एयूसी (पीआर कर्व के नीचे का हिस्सा) देखें.
आरओसी कर्व के नीचे का क्षेत्र
AUC (कर्व के नीचे का हिस्सा) देखें.
AUC (आरओसी कर्व के नीचे का हिस्सा)
0.0 से 1.0 के बीच की संख्या, बाइनरी क्लासिफ़िकेशन मॉडल की, पॉज़िटिव क्लास को नेगेटिव क्लास से अलग करने की क्षमता को दिखाती है. AUC जितना 1.0 के करीब होगा, मॉडल की क्लास को एक-दूसरे से अलग करने की क्षमता उतनी ही बेहतर होगी.
उदाहरण के लिए, यहां दी गई इमेज में एक ऐसा क्लासिफ़िकेशन मॉडल दिखाया गया है जो पॉज़िटिव क्लास (हरे रंग के ओवल) को नेगेटिव क्लास (बैंगनी रंग के रेक्टैंगल) से पूरी तरह से अलग करता है. इस असली से ज़्यादा बेहतर मॉडल का AUC 1.0 है:

इसके उलट, नीचे दी गई इमेज में क्लासिफ़िकेशन मॉडल के नतीजे दिखाए गए हैं. इस मॉडल ने रैंडम नतीजे जनरेट किए हैं. इस मॉडल का AUC 0.5 है:

हां, पिछले मॉडल का AUC 0.0 नहीं, बल्कि 0.5 है.
ज़्यादातर मॉडल, इन दोनों चरम स्थितियों के बीच में होते हैं. उदाहरण के लिए, यहां दिया गया मॉडल, सकारात्मक और नकारात्मक नतीजों को कुछ हद तक अलग करता है. इसलिए, इसका AUC 0.5 से 1.0 के बीच है:

AUC, क्लासिफ़िकेशन थ्रेशोल्ड के लिए सेट की गई किसी भी वैल्यू को अनदेखा करता है. इसके बजाय, एयूसी, कैटगरी में बांटने की सभी संभावित सीमाओं को ध्यान में रखता है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: आरओसी और AUC देखें.
k पर औसत प्रीसिज़न
किसी एक प्रॉम्प्ट पर मॉडल की परफ़ॉर्मेंस की खास जानकारी देने वाली मेट्रिक. यह रैंक वाले नतीजे जनरेट करती है, जैसे कि किताब के सुझावों की नंबर वाली सूची. k पर औसत सटीक नतीजा, हर काम के नतीजे के लिए, k पर सटीक नतीजा वैल्यू का औसत होता है. इसलिए, k पर औसत सटीक नतीजों का फ़ॉर्मूला यह है:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
कहां:
- \(n\) , सूची में मौजूद काम के आइटम की संख्या है.
k पर रीकॉल करें के साथ तुलना करें.
B
आधारभूत
यह एक ऐसा मॉडल है जिसका इस्तेमाल, किसी दूसरे मॉडल (आम तौर पर, ज़्यादा जटिल मॉडल) की परफ़ॉर्मेंस की तुलना करने के लिए, रेफ़रंस पॉइंट के तौर पर किया जाता है. उदाहरण के लिए, लॉजिस्टिक रिग्रेशन मॉडल, डीप मॉडल के लिए अच्छे बेसलाइन के तौर पर काम कर सकता है.
किसी खास समस्या के लिए, बेसलाइन से मॉडल डेवलपर को यह तय करने में मदद मिलती है कि नए मॉडल को कम से कम कितनी परफ़ॉर्मेंस हासिल करनी चाहिए, ताकि वह काम का हो सके.
C
लागत
नुकसान का समानार्थी शब्द.
काउंटरफ़ैक्टुअल फ़ेयरनेस
यह एक निष्पक्षता मेट्रिक है. इससे यह पता चलता है कि क्लासिफ़िकेशन मॉडल, एक व्यक्ति के लिए वही नतीजा देता है जो एक या उससे ज़्यादा संवेदनशील एट्रिब्यूट को छोड़कर, पहले व्यक्ति के लिए देता है. किसी मॉडल में भेदभाव के संभावित सोर्स को दिखाने के लिए, क्लासिफ़िकेशन मॉडल के लिए, काउंटरफ़ैक्टुअल फ़ेयरनेस का आकलन करना एक तरीका है.
ज़्यादा जानकारी के लिए, इनमें से कोई एक लेख पढ़ें:
- मशीन लर्निंग क्रैश कोर्स में, फ़ेयरनेस: काउंटरफ़ैक्टुअल फ़ेयरनेस के बारे में जानकारी.
- जब दुनियाएं आपस में टकरती हैं: निष्पक्षता के लिए, अलग-अलग काउंटरफ़ैक्टुअल अनुमान को शामिल करना
क्रॉस-एन्ट्रॉपी
मल्टी-क्लास क्लासिफ़िकेशन की समस्याओं के लिए, लॉग लॉस का सामान्यीकरण. क्रॉस-एन्ट्रापी, दो संभाव्यता डिस्ट्रिब्यूशन के बीच के अंतर को मेज़र करता है. perplexity भी देखें.
क्यूमुलेटिव डिस्ट्रिब्यूशन फ़ंक्शन (सीडीएफ़)
ऐसा फ़ंक्शन जो टारगेट वैल्यू से कम या उसके बराबर सैंपल की फ़्रीक्वेंसी तय करता है. उदाहरण के लिए, लगातार वैल्यू के सामान्य डिस्ट्रिब्यूशन पर विचार करें. सीडीएफ़ से पता चलता है कि करीब 50% सैंपल, माध्य से कम या उसके बराबर होने चाहिए. साथ ही, करीब 84% सैंपल, माध्य से एक स्टैंडर्ड डिविएशन कम या उसके बराबर होने चाहिए.
D
डेमोग्राफ़िक पैरिटी
निष्पक्षता मेट्रिक, जो तब पूरी होती है, जब किसी मॉडल के क्लासिफ़िकेशन के नतीजे, किसी दिए गए संवेदनशील एट्रिब्यूट पर निर्भर न हों.
उदाहरण के लिए, अगर लिलिपुटियन और ब्रॉबडिंगनियन, दोनों ही ग्लब्बडबड्रीब यूनिवर्सिटी में आवेदन करते हैं, तो डेमोग्राफ़ी के हिसाब से बराबरी तब हासिल होती है, जब लिलिपुटियन और ब्रॉबडिंगनियन, दोनों के लिए स्वीकार किए गए लोगों का प्रतिशत एक जैसा हो. भले ही, एक ग्रुप औसतन दूसरे ग्रुप से ज़्यादा योग्य हो.
समान संभावना और समान अवसर के साथ तुलना करें. इनमें, संवेदनशील एट्रिब्यूट के आधार पर, एग्रीगेट में कैटगरी के नतीजों को दिखाने की अनुमति होती है. हालांकि, कुछ खास ग्राउंड ट्रूथ लेबल के लिए, कैटगरी के नतीजों को संवेदनशील एट्रिब्यूट के आधार पर दिखाने की अनुमति नहीं होती. डेमोग्राफ़ी के हिसाब से बराबरी के लिए ऑप्टिमाइज़ करते समय, फ़ायदे और नुकसान को एक्सप्लोर करने वाले विज़ुअलाइज़ेशन के लिए, "स्मार्ट मशीन लर्निंग की मदद से, भेदभाव को रोकना" देखें.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में निष्पक्षता: डेमोग्राफ़िक के हिसाब से बराबरी देखें.
E
मशीन से चलने वाले वाहन की दूरी (ईएमडी)
दो डिस्ट्रिब्यूशन की तुलना करने का तरीका. मशीन की दूरी जितनी कम होगी, डिस्ट्रिब्यूशन उतने ही मिलते-जुलते होंगे.
दूरी में बदलाव करना
इससे पता चलता है कि दो टेक्स्ट स्ट्रिंग एक-दूसरे से कितनी मिलती-जुलती हैं. मशीन लर्निंग में, बदलाव की दूरी इन वजहों से काम की होती है:
- बदलाव की दूरी का हिसाब लगाना आसान है.
- बदलाव की दूरी की सुविधा, दो ऐसी स्ट्रिंग की तुलना कर सकती है जो एक-दूसरे से मिलती-जुलती हों.
- बदलाव की दूरी से यह पता चलता है कि अलग-अलग स्ट्रिंग, किसी दी गई स्ट्रिंग से कितनी मिलती-जुलती हैं.
बदलाव की दूरी की कई परिभाषाएं हैं. हर परिभाषा में अलग-अलग स्ट्रिंग ऑपरेशन का इस्तेमाल किया जाता है. उदाहरण के लिए, लेवेंश्टाइन दूरी देखें.
अनुभवजन्य क्यूमुलेटिव डिस्ट्रिब्यूशन फ़ंक्शन (eCDF या EDF)
क्यूमुलेटिव डिस्ट्रिब्यूशन फ़ंक्शन, जो किसी असल डेटासेट के एम्पिरिकल मेज़रमेंट पर आधारित होता है. x-ऐक्सिस पर किसी भी बिंदु पर फ़ंक्शन की वैल्यू, डेटासेट में मौजूद उन ऑब्ज़र्वेशन का हिस्सा होती है जो तय की गई वैल्यू से कम या उसके बराबर होते हैं.
एन्ट्रॉपी
जानकारी के सिद्धांत में, किसी संभावना के बंटवारे के अनुमानित होने के बारे में जानकारी दी गई है. इसके अलावा, एन्ट्रोपी को इस तरह भी परिभाषित किया जाता है कि हर उदाहरण में कितनी जानकारी होती है. जब किसी रैंडम वैरिएबल की सभी वैल्यू एक जैसी होती हैं, तो डिस्ट्रिब्यूशन में सबसे ज़्यादा एन्ट्रापी होती है.
"0" और "1" जैसी दो संभावित वैल्यू वाले सेट का एन्ट्रापी (उदाहरण के लिए, बाइनरी क्लासिफ़िकेशन समस्या में लेबल) का यह फ़ॉर्मूला है:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
कहां:
- H एन्ट्रॉपी है.
- p, "1" उदाहरणों का अंश है.
- q, "0" उदाहरणों का फ़्रैक्शन है. ध्यान दें कि q = (1 - p)
- आम तौर पर, लॉग को लॉग2 कहा जाता है. इस मामले में, एन्ट्रापी की इकाई बिट होती है.
उदाहरण के लिए, मान लें कि:
- 100 उदाहरणों में वैल्यू "1" है
- 300 उदाहरणों में वैल्यू "0" है
इसलिए, एंट्रॉपी की वैल्यू यह है:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 0.81 बिट प्रति उदाहरण
पूरी तरह से बैलेंस किए गए सेट (उदाहरण के लिए, 200 "0" और 200 "1") के लिए, हर उदाहरण में 1.0 बिट का एन्ट्रापी होगा. किसी सेट के असंतुलित होने पर, उसका एन्ट्रापी 0.0 की ओर बढ़ता है.
फ़ैसला लेने वाले ट्री में, एन्ट्रापी से जानकारी हासिल करने में मदद मिलती है. इससे स्प्लिटर को, क्लासिफ़िकेशन के फ़ैसला लेने वाले ट्री के बढ़ने के दौरान शर्तें चुनने में मदद मिलती है.
एन्ट्रॉपी की तुलना इनसे करें:
- गिनाई इंप्यूरिटी
- क्रॉस-एंट्रॉपी लॉस फ़ंक्शन
एन्ट्रोपी को अक्सर शैनन का एन्ट्रोपी कहा जाता है.
ज़्यादा जानकारी के लिए, डिसीज़न फ़ॉरेस्ट कोर्स में संख्यात्मक सुविधाओं के साथ बाइनरी क्लासिफ़िकेशन के लिए एग्ज़ैक्ट स्प्लिटर देखें.
समान अवसर
फ़ेयरनेस मेट्रिक, जिससे यह पता चलता है कि कोई मॉडल, संवेदनशील एट्रिब्यूट की सभी वैल्यू के लिए, मनचाहा नतीजा बराबर अच्छी तरह से अनुमान लगा रहा है या नहीं. दूसरे शब्दों में, अगर किसी मॉडल के लिए पॉज़िटिव क्लास का नतीजा पाना ज़रूरी है, तो सभी ग्रुप के लिए ट्रू पॉज़िटिव रेट एक जैसा होना चाहिए.
सभी को बराबर अवसर मिलना, समान संभावनाओं से जुड़ा है. इसके लिए ज़रूरी है कि सभी ग्रुप के लिए, सही पॉज़िटिव रेट और फ़ॉल्स पॉज़िटिव रेट, दोनों एक जैसे हों.
मान लें कि Glubbdubdrib University, Lilliputians और Brobdingnagians दोनों को, गणित के एक कठिन प्रोग्राम में शामिल करती है. लिलिपुटियन के माध्यमिक स्कूलों में, गणित की कक्षाओं के लिए बेहतर पाठ्यक्रम उपलब्ध कराया जाता है. ज़्यादातर छात्र-छात्राएं, यूनिवर्सिटी प्रोग्राम के लिए ज़रूरी शर्तें पूरी करते हैं. ब्रॉबडिंगन के सेकंडरी स्कूलों में, मैथ की क्लास नहीं दी जाती हैं. इस वजह से, वहां के बहुत कम छात्र-छात्राएं मैथ में पास हो पाते हैं. "प्रवेश दिया गया" लेबल के लिए, सभी को समान अवसर मिलते हैं. यह बात तब लागू होती है, जब किसी देश (लिलिपुटियन या ब्रॉबडिंगनागियन) के लिए, ज़रूरी शर्तें पूरी करने वाले सभी छात्र-छात्राओं को समान रूप से प्रवेश दिया जाए. भले ही, वे लिलिपुटियन हों या ब्रॉबडिंगनागियन.
उदाहरण के लिए, मान लें कि 100 Lilliputians और 100 Brobdingnagians ने Glubbdubdrib University में आवेदन किया है और दाखिले के फ़ैसले इस तरह किए गए हैं:
टेबल 1. लिलिपुटियन आवेदक (90% क्वालिफ़ाई हैं)
| क्वालिफ़ाई हुई | अयोग्य | |
|---|---|---|
| स्वीकार किया गया | 45 | 3 |
| अस्वीकार किया गया | 45 | 7 |
| कुल | 90 | 10 |
|
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं का प्रतिशत: 45/90 = 50% शर्तें पूरी न करने वाले छात्र-छात्राओं का प्रतिशत: 7/10 = 70% लिलिपुटियन छात्र-छात्राओं का कुल प्रतिशत: (45+3)/100 = 48% |
||
टेबल 2. Brobdingnagian आवेदक (10% क्वालिफ़ाई हैं):
| क्वालिफ़ाई हुई | अयोग्य | |
|---|---|---|
| स्वीकार किया गया | 5 | 9 |
| अस्वीकार किया गया | 5 | 81 |
| कुल | 10 | 90 |
|
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं का प्रतिशत: 5/10 = 50% शर्तें पूरी न करने वाले छात्र-छात्राओं का प्रतिशत: 81/90 = 90% ब्रॉबडिंगनागियन छात्र-छात्राओं का कुल प्रतिशत: (5+9)/100 = 14% |
||
ऊपर दिए गए उदाहरणों से पता चलता है कि ज़रूरी शर्तें पूरी करने वाले सभी छात्र-छात्राओं को बराबर अवसर मिलते हैं. ऐसा इसलिए है, क्योंकि ज़रूरी शर्तें पूरी करने वाले Lilliputians और Brobdingnagians, दोनों के लिए 50% संभावना होती है कि उन्हें स्वीकार किया जाए.
सभी को समान अवसर मिलना ज़रूरी है. हालांकि, निष्पक्षता की इन दो मेट्रिक के लिए ज़रूरी शर्तें पूरी नहीं की गई हैं:
- डेमोग्राफ़िक पैरिटी: Lilliputians और Brobdingnagians को यूनिवर्सिटी में अलग-अलग दरों पर स्वीकार किया जाता है; 48% Lilliputians छात्र-छात्राओं को स्वीकार किया जाता है, लेकिन सिर्फ़ 14% Brobdingnagian छात्र-छात्राओं को स्वीकार किया जाता है.
- समान संभावनाएं: ज़रूरी शर्तें पूरी करने वाले लिलिपुटियन और ब्रॉबडिंगनागियन, दोनों छात्र-छात्राओं को स्वीकार किए जाने की संभावना एक जैसी होती है. हालांकि, यह शर्त पूरी नहीं होती कि ज़रूरी शर्तें पूरी न करने वाले लिलिपुटियन और ब्रॉबडिंगनागियन, दोनों छात्र-छात्राओं को अस्वीकार किए जाने की संभावना एक जैसी होती है. अमान्य आवेदनों को अस्वीकार करने की दर, लिलिपुटियन के लिए 70% है, जबकि ब्रॉबडिंगनागियन के लिए यह दर 90% है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में निष्पक्षता: सभी के लिए बराबर अवसर देखें.
बराबर ऑड
यह मेट्रिक यह आकलन करती है कि कोई मॉडल, संवेदनशील एट्रिब्यूट की सभी वैल्यू के लिए, नतीजों का अनुमान एक जैसा अच्छी तरह से लगा रहा है या नहीं. यह मेट्रिक, पॉज़िटिव क्लास और नेगेटिव क्लास, दोनों के लिए यह आकलन करती है. दूसरे शब्दों में, सभी ग्रुप के लिए ट्रू पॉज़िटिव रेट और फ़ॉल्स नेगेटिव रेट, दोनों एक जैसे होने चाहिए.
सभी के लिए बराबर संभावनाएं, सभी के लिए बराबर अवसर से जुड़ी है. यह सिर्फ़ किसी एक क्लास (पॉज़िटिव या नेगेटिव) के लिए, गड़बड़ी की दरों पर फ़ोकस करती है.
उदाहरण के लिए, मान लें कि Glubbdubdrib University ने गणित के एक कठिन प्रोग्राम में, Lilliputians और Brobdingnagians, दोनों को स्वीकार किया है. लिलिपुटियन के सेकंडरी स्कूलों में, मैथ की कक्षाओं का बेहतर पाठ्यक्रम उपलब्ध कराया जाता है. साथ ही, ज़्यादातर छात्र-छात्राएं यूनिवर्सिटी प्रोग्राम के लिए ज़रूरी शर्तें पूरी करते हैं. ब्रॉबडिंगन के सेकंडरी स्कूलों में, गणित की क्लास नहीं होतीं. इस वजह से, वहां के बहुत कम छात्र-छात्राएं क्वालीफ़ाई कर पाते हैं. समान अवसरों की शर्त तब पूरी होती है, जब कोई भी आवेदक, चाहे वह छोटा हो या बड़ा, ज़रूरी शर्तें पूरी करता हो, तो उसे प्रोग्राम में शामिल होने की उतनी ही संभावना होती है जितनी किसी दूसरे आवेदक को. इसके अलावा, अगर कोई आवेदक ज़रूरी शर्तें पूरी नहीं करता है, तो उसे प्रोग्राम में शामिल होने की उतनी ही संभावना होती है जितनी किसी दूसरे आवेदक को.
मान लें कि 100 लिलिपुटियन और 100 ब्रॉबडिंगनागियन, ग्लब्बडब्रिब यूनिवर्सिटी में आवेदन करते हैं. साथ ही, दाखिले के फ़ैसले इस तरह लिए जाते हैं:
टेबल 3. लिलिपुटियन आवेदक (90% क्वालिफ़ाई हैं)
| क्वालिफ़ाई हुई | अयोग्य | |
|---|---|---|
| स्वीकार किया गया | 45 | 2 |
| अस्वीकार किया गया | 45 | 8 |
| कुल | 90 | 10 |
|
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं का प्रतिशत: 45/90 = 50% शर्तें पूरी न करने वाले छात्र-छात्राओं का प्रतिशत: 8/10 = 80% लिलिपुटियन छात्र-छात्राओं का कुल प्रतिशत: (45+2)/100 = 47% |
||
टेबल 4. Brobdingnagian आवेदक (10% क्वालिफ़ाई हैं):
| क्वालिफ़ाई हुई | अयोग्य | |
|---|---|---|
| स्वीकार किया गया | 5 | 18 |
| अस्वीकार किया गया | 5 | 72 |
| कुल | 10 | 90 |
|
ज़रूरी शर्तें पूरी करने वाले छात्र-छात्राओं का प्रतिशत: 5/10 = 50% शर्तें पूरी न करने वाले छात्र-छात्राओं का प्रतिशत: 72/90 = 80% ब्रॉबडिंगनागियन छात्र-छात्राओं का कुल प्रतिशत: (5+18)/100 = 23% |
||
यहां सभी के लिए संभावनाएं बराबर हैं, क्योंकि ज़रूरी शर्तें पूरी करने वाले Lilliputian और Brobdingnagian, दोनों के लिए 50% संभावना है कि उन्हें स्वीकार किया जाए. साथ ही, ज़रूरी शर्तें पूरी न करने वाले Lilliputian और Brobdingnagian, दोनों के लिए 80% संभावना है कि उन्हें अस्वीकार किया जाए.
"सुपरवाइज़्ड लर्निंग में अवसर की समानता" में, बराबर संभावनाओं को आधिकारिक तौर पर इस तरह से परिभाषित किया गया है: "अगर Ŷ और A, Y के आधार पर स्वतंत्र हैं, तो प्रिडिक्टर Ŷ, सुरक्षित एट्रिब्यूट A और नतीजे Y के लिए बराबर संभावनाओं को पूरा करता है."
evals
इसका इस्तेमाल मुख्य रूप से एलएलएम के आकलन के लिए किया जाता है. मोटे तौर पर, evals, इवैलुएशन के किसी भी फ़ॉर्म का छोटा नाम है.
आकलन
किसी मॉडल की क्वालिटी को मेज़र करने या अलग-अलग मॉडल की तुलना करने की प्रोसेस.
सुपरवाइज़्ड मशीन लर्निंग मॉडल का आकलन करने के लिए, आम तौर पर पुष्टि करने वाले सेट और टेस्ट सेट के आधार पर इसका आकलन किया जाता है. एलएलएम का आकलन करने के लिए, आम तौर पर क्वालिटी और सुरक्षा से जुड़े बड़े आकलन किए जाते हैं.
F
F1
बाइनरी क्लासिफ़िकेशन वाली "रोल-अप" मेट्रिक, जो प्रिसिज़न और रीकॉल, दोनों पर निर्भर करती है. यहां फ़ॉर्मूला दिया गया है:
निष्पक्षता मेट्रिक
"निष्पक्षता" की गणितीय परिभाषा, जिसे मेज़र किया जा सकता है. आम तौर पर इस्तेमाल होने वाली निष्पक्षता मेट्रिक में ये शामिल हैं:
निष्पक्षता की कई मेट्रिक एक-दूसरे के साथ काम नहीं करतीं. निष्पक्षता की मेट्रिक के साथ काम न करने की समस्या देखें.
फ़ॉल्स निगेटिव (FN)
ऐसा उदाहरण जिसमें मॉडल ने गलती से नेगेटिव क्लास का अनुमान लगाया है. उदाहरण के लिए, मॉडल का अनुमान है कि कोई ईमेल मैसेज स्पैम नहीं है (नेगेटिव क्लास), लेकिन वह ईमेल मैसेज असल में स्पैम है.
फ़ॉल्स निगेटिव रेट
असल पॉज़िटिव उदाहरणों का अनुपात, जिनके लिए मॉडल ने गलती से नेगेटिव क्लास का अनुमान लगाया. गलत नतीजे मिलने की दर का हिसाब लगाने के लिए, यह फ़ॉर्मूला इस्तेमाल करें:
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में थ्रेशोल्ड और कॉन्फ़्यूज़न मैट्रिक देखें.
फ़ॉल्स पॉज़िटिव (FP)
ऐसा उदाहरण जिसमें मॉडल ने गलती से पॉज़िटिव क्लास का अनुमान लगाया है. उदाहरण के लिए, मॉडल का अनुमान है कि कोई ईमेल मैसेज स्पैम (पॉज़िटिव क्लास) है, लेकिन वह ईमेल मैसेज वाकई स्पैम नहीं है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में थ्रेशोल्ड और कॉन्फ़्यूज़न मैट्रिक देखें.
फ़ॉल्स पॉज़िटिव रेट (एफ़पीआर)
असल नेगेटिव उदाहरणों का अनुपात, जिनके लिए मॉडल ने गलत तरीके से पॉज़िटिव क्लास का अनुमान लगाया. नीचे दिए गए फ़ॉर्मूला से, गलत नतीजे मिलने की दर का हिसाब लगाया जाता है:
फ़ॉल्स पॉज़िटिव रेट, आरओसी कर्व में एक्स-ऐक्सिस होता है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: आरओसी और AUC देखें.
सुविधाओं की अहमियत
वैरिएबल की अहमियत का दूसरा नाम.
सफलता का अनुपात
एमएल मॉडल के जनरेट किए गए टेक्स्ट का आकलन करने वाली मेट्रिक. सफलता का अनुपात, जनरेट किए गए "सफल" टेक्स्ट आउटपुट की संख्या को जनरेट किए गए टेक्स्ट आउटपुट की कुल संख्या से भाग देने पर मिलता है. उदाहरण के लिए, अगर किसी बड़े लैंग्वेज मॉडल ने कोड के 10 ब्लॉक जनरेट किए, जिनमें से पांच सही थे, तो सही ब्लॉक का अनुपात 50% होगा.
हालांकि, आंकड़ों के लिए फ़्रैक्शन ऑफ़ सक्सेस का इस्तेमाल आम तौर पर किया जाता है, लेकिन एआई में यह मेट्रिक मुख्य रूप से ऐसे टास्क को मेज़र करने के लिए काम की होती है जिनकी पुष्टि की जा सकती है. जैसे, कोड जनरेशन या गणित की समस्याएं.
G
gini impurity
एन्ट्रापी जैसी मेट्रिक. स्प्लिटर, गिनी इंप्यूरिटी या एन्ट्रापी से मिली वैल्यू का इस्तेमाल करते हैं. इससे, फ़ैसला लेने वाले पेड़ों के लिए, अलग-अलग कैटगरी बनाने की शर्तें तय की जाती हैं. जानकारी हासिल करना, एन्ट्रापी से मिलता है. गिनिन इंप्यूरिटी से मिली मेट्रिक के लिए, दुनिया भर में स्वीकार किया गया कोई समान शब्द नहीं है. हालांकि, नाम न होने के बावजूद यह मेट्रिक, जानकारी हासिल करने के लिए उतनी ही ज़रूरी है.
Gini impurity को gini index या सिर्फ़ gini भी कहा जाता है.
H
हिंज का टूटना
क्लासिफ़िकेशन के लिए, लॉस फ़ंक्शन का परिवार. इसे हर ट्रेनिंग उदाहरण से, फ़ैसले की सीमा को जितना हो सके उतना दूर खोजने के लिए डिज़ाइन किया गया है. इससे, उदाहरणों और सीमा के बीच का मार्जिन बढ़ जाता है. KSVMs, हिंज लॉस (या इससे जुड़े फ़ंक्शन, जैसे कि स्क्वेयर्ड हिंज लॉस) का इस्तेमाल करते हैं. बाइनरी क्लासिफ़िकेशन के लिए, हिंज लॉस फ़ंक्शन को इस तरह से परिभाषित किया गया है:
यहां y सही लेबल है, जो -1 या +1 हो सकता है. साथ ही, y', क्लासिफ़िकेशन मॉडल का रॉ आउटपुट है:
इसलिए, हिंग लॉस बनाम (y * y') का प्लॉट कुछ ऐसा दिखता है:

I
निष्पक्षता मेट्रिक के साथ काम न करना
यह विचार कि निष्पक्षता के कुछ सिद्धांत एक-दूसरे के साथ काम नहीं करते और एक साथ लागू नहीं किए जा सकते. इसलिए, सभी एमएल समस्याओं पर लागू होने वाली, निष्पक्षता को मेज़र करने वाली कोई एक मेट्रिक नहीं है.
ऐसा लग सकता है कि यह बात हतोत्साहित करने वाली है, लेकिन निष्पक्षता मेट्रिक के साथ काम न करने का मतलब यह नहीं है कि निष्पक्षता को बढ़ावा देने की कोशिशें बेकार हैं. इसके बजाय, यह सुझाव दिया गया है कि किसी एआई मॉडल की समस्या के हिसाब से, निष्पक्षता को परिभाषित किया जाना चाहिए. ऐसा, इसके इस्तेमाल के उदाहरणों से होने वाले नुकसान को रोकने के मकसद से किया जाना चाहिए.
फ़ेयरनेस मेट्रिक के साथ काम न करने के बारे में ज़्यादा जानने के लिए, "फ़ेयरनेस (अ)संभव है" लेख पढ़ें.
निष्पक्षता
निष्पक्षता मेट्रिक, जो यह जांच करती है कि मिलते-जुलते लोगों को एक जैसा दर्जा दिया गया है या नहीं. उदाहरण के लिए, Brobdingnagian Academy यह पक्का करके, सभी को एक जैसा मौका देना चाहती है कि एक जैसे ग्रेड और स्टैंडर्ड टेस्ट के स्कोर वाले दो छात्र-छात्राओं को, दाखिला पाने की बराबर संभावना हो.
ध्यान दें कि किसी व्यक्ति के लिए निष्पक्षता का आकलन, इस बात पर पूरी तरह से निर्भर करता है कि आपने "मिलती-जुलती" (इस मामले में, ग्रेड और टेस्ट के स्कोर) को कैसे तय किया है. अगर मिलती-जुलती मेट्रिक में अहम जानकारी (जैसे, छात्र के सिलेबस की कठिनाई) मौजूद नहीं है, तो निष्पक्षता से जुड़ी नई समस्याएं पैदा हो सकती हैं.
किसी व्यक्ति के लिए निजता बनाए रखने के बारे में ज़्यादा जानने के लिए, "जानकारी के ज़रिए निजता बनाए रखना" लेख पढ़ें.
जानकारी हासिल करना
फ़ैसला फ़ॉरेस्ट में, किसी नोड के एन्ट्रापी और उसके चाइल्ड नोड के एन्ट्रापी के वज़ीदार (उदाहरणों की संख्या के हिसाब से) योग के बीच का अंतर. किसी नोड का एन्ट्रापी, उस नोड में मौजूद उदाहरणों का एन्ट्रापी होता है.
उदाहरण के लिए, एन्ट्रापी की ये वैल्यू देखें:
- पैरंट नोड की एन्ट्रॉपी = 0.6
- काम के 16 उदाहरणों वाले एक चाइल्ड नोड का एन्ट्रापी = 0.2
- काम के 24 उदाहरणों वाले किसी दूसरे चाइल्ड नोड का एन्ट्रापी = 0.1
इसलिए, 40% उदाहरण एक चाइल्ड नोड में और 60% उदाहरण दूसरे चाइल्ड नोड में हैं. इसलिए:
- चाइल्ड नोड की वेटेड एन्ट्रॉपी का कुल योग = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
इसलिए, आपको यह जानकारी मिलेगी:
- जानकारी का फ़ायदा = पैरंट नोड की एन्ट्रॉपी - चाइल्ड नोड की वेटेड एन्ट्रॉपी का योग
- जानकारी का फ़ायदा = 0.6 - 0.14 = 0.46
ज़्यादातर स्प्लिटर, ऐसी शर्तें तय करते हैं जिनसे ज़्यादा से ज़्यादा जानकारी हासिल की जा सके.
इंटर-रेटर एग्रीमेंट
यह मेज़र करता है कि कोई टास्क करते समय, रेटिंग देने वाले लोग कितनी बार एक-दूसरे से सहमत होते हैं. अगर रेटर आपसे सहमत नहीं हैं, तो हो सकता है कि टास्क के निर्देशों को बेहतर बनाने की ज़रूरत हो. इसे कभी-कभी एनोटेट करने वाले लोगों के बीच सहमति या रेटिंग देने वाले लोगों के बीच भरोसे का स्तर भी कहा जाता है. कोहेन का कप्पा भी देखें. यह, रेटिंग देने वाले अलग-अलग लोगों के बीच सहमति का सबसे लोकप्रिय मेज़रमेंट है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में कैटगरी वाला डेटा: आम समस्याएं देखें.
L
L1 लॉस
लॉस फ़ंक्शन, जो असल लेबल वैल्यू और मॉडल की अनुमानित वैल्यू के बीच के अंतर की एब्सोल्यूट वैल्यू का हिसाब लगाता है. उदाहरण के लिए, यहां पांच उदाहरणों वाले बैच के लिए, L1 लॉस का हिसाब लगाया गया है:
| उदाहरण की असल वैल्यू | मॉडल की अनुमानित वैल्यू | डेल्टा की ऐब्सलूट वैल्यू |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 लॉस | ||
L2 लॉस की तुलना में, L1 लॉस, आउटलायर के लिए कम संवेदनशील होता है.
कुल गड़बड़ी का औसत, हर उदाहरण के लिए L1 का औसत नुकसान होता है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लीनियर रिग्रेशन: लॉस देखें.
L2 लॉस
लॉस फ़ंक्शन, जो असल लेबल वैल्यू और मॉडल की अनुमानित वैल्यू के बीच के अंतर का स्क्वेयर कैलकुलेट करता है. उदाहरण के लिए, यहां पांच उदाहरणों के बैच के लिए, L2 लॉस का हिसाब लगाया गया है:
| उदाहरण की असल वैल्यू | मॉडल की अनुमानित वैल्यू | डेल्टा का स्क्वेयर |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 हार | ||
स्क्वेयर करने की वजह से, L2 लॉस, आउटलायर के असर को बढ़ा देता है. इसका मतलब है कि L2 लॉस, L1 लॉस के मुकाबले खराब अनुमानों पर ज़्यादा तेज़ी से प्रतिक्रिया करता है. उदाहरण के लिए, पिछले बैच के लिए L1 लॉस, 16 के बजाय 8 होगा. ध्यान दें कि 16 में से 9 आउटलायर, एक ही डेटा पॉइंट के हैं.
रिएगर्सन मॉडल आम तौर पर, लॉस फ़ंक्शन के तौर पर L2 लॉस का इस्तेमाल करते हैं.
वर्ग में गड़बड़ी का माध्य, हर उदाहरण के लिए L2 का औसत नुकसान होता है. स्क्वेयर्ड लॉस, L2 लॉस का दूसरा नाम है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लॉजिस्टिक रिग्रेशन: लॉस और रेगुलराइज़ेशन देखें.
एलएलएम के आकलन (evals)
लार्ज लैंग्वेज मॉडल (एलएलएम) की परफ़ॉर्मेंस का आकलन करने के लिए, मेट्रिक और मानदंडों का सेट. खास जानकारी के तौर पर, एलएलएम के आकलन:
- शोधकर्ताओं को उन क्षेत्रों की पहचान करने में मदद करना जहां एलएलएम में सुधार की ज़रूरत है.
- ये अलग-अलग एलएलएम की तुलना करने और किसी खास टास्क के लिए सबसे अच्छे एलएलएम की पहचान करने में मदद करते हैं.
- यह पक्का करने में मदद मिलती है कि एलएलएम का इस्तेमाल सुरक्षित और सही तरीके से किया जा रहा है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लार्ज लैंग्वेज मॉडल (एलएलएम) देखें.
हार
सुपरवाइज़्ड मॉडल की ट्रेनिंग के दौरान, यह मेज़र किया जाता है कि मॉडल का अनुमान, उसके लेबल से कितना अलग है.
लॉस फ़ंक्शन, लॉस का हिसाब लगाता है.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में लीनियर रिग्रेशन: लॉस देखें.
लॉस फ़ंक्शन
ट्रेनिंग या जांच के दौरान, एक ऐसा गणितीय फ़ंक्शन जो उदाहरणों के बैच पर नुकसान का हिसाब लगाता है. लॉस फ़ंक्शन, अच्छे अनुमान लगाने वाले मॉडल के लिए कम लॉस दिखाता है. वहीं, खराब अनुमान लगाने वाले मॉडल के लिए ज़्यादा लॉस दिखाता है.
आम तौर पर, ट्रेनिंग का लक्ष्य, लॉस फ़ंक्शन से मिलने वाले लॉस को कम करना होता है.
कई तरह के लॉस फ़ंक्शन मौजूद हैं. जिस तरह का मॉडल बनाया जा रहा है उसके लिए सही लॉस फ़ंक्शन चुनें. उदाहरण के लिए:
- L2 लॉस (या वर्ग में गड़बड़ी का माध्य) लीनियर रिग्रेशन के लिए लॉस फ़ंक्शन है.
- लॉग लॉस, लॉजिस्टिक रिग्रेशन के लिए लॉस फ़ंक्शन है.
M
कुल गड़बड़ी का मध्यमान (एमएई)
L1 लॉस का इस्तेमाल करने पर, हर उदाहरण के लिए औसत लॉस. कुल गड़बड़ी का मध्यमान इस तरह से कैलकुलेट करें:
- किसी बैच के लिए L1 लॉस का हिसाब लगाएं.
- L1 लॉस को बैच में मौजूद उदाहरणों की संख्या से भाग दें.
उदाहरण के लिए, पांच उदाहरणों के इस बैच पर L1 लॉस का हिसाब लगाएं:
| उदाहरण की असल वैल्यू | मॉडल की अनुमानित वैल्यू | नुकसान (असल और अनुमानित वैल्यू के बीच का अंतर) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 लॉस | ||
इसलिए, L1 लॉस 8 है और उदाहरणों की संख्या 5 है. इसलिए, कुल गड़बड़ी का मध्यमान यह है:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
कुल गड़बड़ी के औसत की तुलना वर्ग में गड़बड़ी का माध्य और रूट मीन स्क्वेयर की गड़बड़ी से करें.
k पर औसत सटीक अनुमान (mAP@k)
पुष्टि करने वाले डेटासेट में, सभी k पर औसत सटीक नतीजे के स्कोर का आंकड़ों के हिसाब से औसत. k पर औसत सटीकता का एक इस्तेमाल, सुझाव देने वाले सिस्टम से जनरेट किए गए सुझावों की क्वालिटी का आकलन करना है.
"औसत" वाक्यांश का इस्तेमाल करना ज़रूरी नहीं है, लेकिन मेट्रिक का नाम सही है. आखिरकार, यह मेट्रिक कई k पर औसत सटीक वैल्यू का औसत ढूंढती है.
मीन स्क्वेयर एरर (एमएसई)
L2 लॉस का इस्तेमाल करने पर, हर उदाहरण के लिए औसत लॉस. मीन स्क्वेयर एरर का हिसाब इस तरह लगाया जाता है:
- किसी बैच के लिए L2 लॉस का हिसाब लगाएं.
- L2 लॉस को बैच में मौजूद उदाहरणों की संख्या से भाग दें.
उदाहरण के लिए, पांच उदाहरणों के इस बैच पर लागू होने वाले लॉस पर विचार करें:
| वास्तविक मान | मॉडल का अनुमान | हार मिली | स्क्वेयर्ड लॉस |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L2 हार | |||
इसलिए, मीन स्क्वेयर एरर यह है:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
मीन स्क्वेयर्ड एरर, ट्रेनिंग के लिए एक लोकप्रिय ऑप्टिमाइज़र है. यह खास तौर पर लीनियर रिग्रेशन के लिए इस्तेमाल किया जाता है.
मीन स्क्वेयर एरर की तुलना, कुल गड़बड़ी का मध्यमान और रूट मीन स्क्वेयर एरर से करें.
TensorFlow Playground, लॉस वैल्यू का हिसाब लगाने के लिए, मीन स्क्वेयर्ड एरर का इस्तेमाल करता है.
मीट्रिक
ऐसा आंकड़ा जिसमें आपकी दिलचस्पी है.
मकसद एक ऐसी मेट्रिक है जिसे मशीन लर्निंग सिस्टम ऑप्टिमाइज़ करने की कोशिश करता है.
Metrics API (tf.metrics)
मॉडल का आकलन करने के लिए TensorFlow API. उदाहरण के लिए, tf.metrics.accuracy
से यह पता चलता है कि किसी मॉडल के अनुमान, लेबल से कितनी बार मेल खाते हैं.
मिनीमैक्स लॉस
जनरेट किए गए डेटा और रीयल डेटा के डिस्ट्रिब्यूशन के बीच क्रॉस-एन्ट्रोपी के आधार पर, जनरेटिव अडवर्सेरी नेटवर्क के लिए लॉस फ़ंक्शन.
जनरेटिव ऐडवर्सरी नेटवर्क के बारे में बताने के लिए, पहले पेपर में मिनिमैक्स लॉस का इस्तेमाल किया गया है.
ज़्यादा जानकारी के लिए, जनरेटिव ऐडवर्सरी नेटवर्क कोर्स में लॉस फ़ंक्शन देखें.
मॉडल की क्षमता
मॉडल, ऐसी समस्याओं को कितनी आसानी से हल कर सकता है. मॉडल जितनी ज़्यादा मुश्किल समस्याओं को हल कर सकता है उसकी क्षमता उतनी ही ज़्यादा होती है. आम तौर पर, मॉडल के पैरामीटर की संख्या बढ़ने पर, मॉडल की क्षमता भी बढ़ती है. क्लासिफ़िकेशन मॉडल की क्षमता की आधिकारिक परिभाषा के लिए, वीसी डाइमेंशन देखें.
नहीं
नेगेटिव क्लास
बाइनरी क्लासिफ़िकेशन में, एक क्लास को पॉज़िटिव और दूसरी क्लास को नेगेटिव कहा जाता है. पॉज़िटिव क्लास वह चीज़ या इवेंट है जिसकी जांच मॉडल कर रहा है और नेगेटिव क्लास दूसरी संभावना है. उदाहरण के लिए:
- किसी मेडिकल टेस्ट में नेगेटिव क्लास, "ट्यूमर नहीं" हो सकती है.
- किसी ईमेल के क्लासिफ़िकेशन मॉडल में नेगेटिव क्लास, "स्पैम नहीं है" हो सकती है.
पॉज़िटिव क्लास के साथ तुलना करें.
O
कैंपेन का मकसद
वह मेट्रिक जिसे आपका एल्गोरिदम ऑप्टिमाइज़ करने की कोशिश कर रहा है.
मकसद फ़ंक्शन
गणित का वह फ़ॉर्मूला या मेट्रिक जिसे मॉडल ऑप्टिमाइज़ करना चाहता है. उदाहरण के लिए, लीनियर रिग्रेशन के लिए मकसद फ़ंक्शन आम तौर पर मायन स्क्वेयर्ड लॉस होता है. इसलिए, किसी रेखीय रिग्रेशन मॉडल को ट्रेनिंग देते समय, ट्रेनिंग का मकसद मीन स्क्वेयर्ड लॉस को कम करना होता है.
कुछ मामलों में, मकसद फ़ंक्शन को ज़्यादा से ज़्यादा बढ़ाना होता है. उदाहरण के लिए, अगर मकसद का फ़ंक्शन सटीक होना है, तो लक्ष्य सटीक जानकारी को बढ़ाना है.
नुकसान भी देखें.
P
k पर पास (pass@k)
लार्ज लैंग्वेज मॉडल से जनरेट किए गए कोड (उदाहरण के लिए, Python) की क्वालिटी का पता लगाने वाली मेट्रिक. ज़्यादा जानकारी के लिए, k पर पास होने का मतलब है कि k जनरेट किए गए कोड ब्लॉक में से कम से कम एक कोड ब्लॉक, अपनी सभी यूनिट टेस्ट पास करेगा.
लार्ज लैंग्वेज मॉडल, अक्सर प्रोग्रामिंग से जुड़ी मुश्किल समस्याओं के लिए अच्छा कोड जनरेट करने में परेशानी महसूस करते हैं. सॉफ़्टवेयर इंजीनियर, एक ही समस्या के लिए कई (k) समाधान जनरेट करने के लिए, लार्ज लैंग्वेज मॉडल को निर्देश देते हैं. इसके बाद, सॉफ़्टवेयर इंजीनियर यूनिट टेस्ट के हिसाब से, हर समाधान की जांच करते हैं. k पर पास होने की गिनती, यूनिट टेस्ट के नतीजों पर निर्भर करती है:
- अगर उनमें से एक या उससे ज़्यादा समाधान यूनिट टेस्ट पास करते हैं, तो एलएलएम कोड जनरेशन चैलेंज को पास कर लेता है.
- अगर कोई भी समाधान यूनिट टेस्ट पास नहीं करता है, तो एलएलएम उस कोड जनरेशन चैलेंज को पूरा नहीं कर पाता.
k पर पास करने का फ़ॉर्मूला इस तरह है:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
आम तौर पर, k की ज़्यादा वैल्यू से k स्कोर में ज़्यादा पास मिलते हैं. हालांकि, k की ज़्यादा वैल्यू के लिए, ज़्यादा बड़े लैंग्वेज मॉडल और यूनिट टेस्टिंग के संसाधनों की ज़रूरत होती है.
प्रदर्शन
अलग-अलग मतलब के लिए इस्तेमाल किया जाने वाला शब्द:
- सॉफ़्टवेयर इंजीनियरिंग में इसका स्टैंडर्ड मतलब. जैसे: यह सॉफ़्टवेयर कितना तेज़ (या बेहतर) तरीके से काम करता है?
- मशीन लर्निंग में इसका मतलब. यहां परफ़ॉर्मेंस से इस सवाल का जवाब मिलता है: यह मॉडल कितना सही है? इसका मतलब है कि मॉडल के अनुमान कितने अच्छे हैं?
पर्म्यूटेशन वैरिएबल की अहमियत
वैरिएबल की अहमियत का एक टाइप, जो फ़ीचर की वैल्यू को बदलने के बाद, मॉडल के अनुमान में हुई गड़बड़ी का आकलन करता है. वैरिएशन के क्रम में बदलाव करने की अहमियत, मॉडल पर निर्भर नहीं करती.
perplexity
इससे यह पता चलता है कि मॉडल अपना टास्क कितनी अच्छी तरह पूरा कर रहा है. उदाहरण के लिए, मान लें कि आपका टास्क यह है कि किसी उपयोगकर्ता के फ़ोन कीबोर्ड पर टाइप किए जा रहे शब्द के पहले कुछ अक्षर पढ़े जाएं और उस शब्द को पूरा करने के लिए, संभावित शब्दों की सूची दी जाए. इस टास्क के लिए, पेरप्लेक्सिटी, P, अनुमानित तौर पर उन अनुमानों की संख्या होती है जिन्हें आपको अपनी सूची में शामिल करना होता है, ताकि उसमें वह असली शब्द शामिल हो जिसे उपयोगकर्ता टाइप करने की कोशिश कर रहा है.
पेरप्लेक्सिटी, क्रॉस-एन्ट्रापी से इस तरह जुड़ी है:
पॉज़िटिव क्लास
वह क्लास जिसकी जांच की जा रही है.
उदाहरण के लिए, कैंसर मॉडल में पॉज़िटिव क्लास "ट्यूमर" हो सकती है. ईमेल के कैटगरी मॉडल में, पॉज़िटिव क्लास "स्पैम" हो सकती है.
नेगेटिव क्लास के साथ कंट्रास्ट करें.
पीआर AUC (पीआर कर्व के अंदर का हिस्सा)
इंटरपोलेशन किए गए प्रिसिज़न-रीकॉल कर्व के नीचे का एरिया. इसे क्लासिफ़िकेशन थ्रेशोल्ड की अलग-अलग वैल्यू के लिए, (रीकॉल, प्रिसिज़न) पॉइंट प्लॉट करके पाया जाता है.
प्रीसिज़न
क्लासिफ़िकेशन मॉडल के लिए एक मेट्रिक, जो इस सवाल का जवाब देती है:
जब मॉडल ने पॉज़िटिव क्लास का अनुमान लगाया, तो कितने प्रतिशत अनुमान सही थे?
यहां फ़ॉर्मूला दिया गया है:
कहां:
- 'सही मायनों में पॉज़िटिव' का मतलब है कि मॉडल ने पॉज़िटिव क्लास का सही अनुमान लगाया.
- फ़ॉल्स पॉज़िटिव का मतलब है कि मॉडल ने गलती से पॉज़िटिव क्लास का अनुमान लगाया है.
उदाहरण के लिए, मान लें कि किसी मॉडल ने 200 पॉज़िटिव अनुमान लगाए. इन 200 पॉज़िटिव अनुमानों में से:
- 150 ट्रू पॉज़िटिव थे.
- इनमें से 50 फ़ॉल्स पॉज़िटिव थे.
इस मामले में:
सटीक और रीकॉल के साथ कंट्रास्ट करें.
ज़्यादा जानकारी के लिए, मशीन लर्निंग क्रैश कोर्स में क्लासिफ़िकेशन: सटीक, रीकॉल, सटीक जानकारी, और इससे जुड़ी मेट्रिक देखें.
k पर सटीक (precision@k)
आइटम की रैंक वाली सूची का आकलन करने वाली मेट्रिक. k पर सटीक नतीजे, सूची में पहले k आइटम में से "काम के" आइटम के हिस्से की पहचान करते हैं. यानी:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
k की वैल्यू, लिस्ट में मौजूद आइटम की संख्या से कम या उसके बराबर होनी चाहिए. ध्यान दें कि लौटाई गई सूची की लंबाई, हिसाब लगाने का हिस्सा नहीं है.
काम का होना या न होना, अक्सर व्यक्तिगत राय पर निर्भर करता है. विश्लेषक भी अक्सर इस बात पर सहमत नहीं होते कि कौनसे आइटम काम के हैं.
इसके साथ तुलना करें:
प्रीसिज़न-रीकॉल कर्व
अलग-अलग क्लासिफ़िकेशन थ्रेशोल्ड पर, प्रिसिज़न बनाम रीकॉल का कर्व.
अनुमान में पक्षपात
यह वैल्यू बताती है कि डेटासेट में अनुमान का औसत, लेबल के औसत से कितना अलग है.
इसे मशीन लर्निंग मॉडल में मौजूद बायस या नैतिकता और निष्पक्षता में बायस के साथ न जोड़ें.
अनुमानित पैरिटी
यह एक निष्पक्षता मेट्रिक है. इससे यह पता चलता है कि किसी क्लासिफ़ायर के लिए, सटीक रेट, सबग्रुप के लिए एक जैसे हैं या नहीं.
उदाहरण के लिए, कॉलेज में दाखिला पाने का अनुमान लगाने वाला मॉडल, देश के हिसाब से अनुमानित समानता को पूरा करेगा. ऐसा तब होगा, जब लिलिपुटियन और ब्रॉबडिंगनियन के लिए, सटीक अनुमान लगाने की दर एक जैसी हो.
अनुमानित किराया बराबरी को कभी-कभी किराया बराबरी का अनुमान भी कहा जाता है.
अनुमानित समानता के बारे में ज़्यादा जानकारी के लिए, "निष्पक्षता की परिभाषाएं बताई गई हैं" (सेक्शन 3.2.1) देखें.
किराये की अनुमानित समानता
प्रेडिकटिव पैरिटी का दूसरा नाम.
प्रोबैबिलिटी डेंसिटी फ़ंक्शन
यह फ़ंक्शन, किसी खास वैल्यू वाले डेटा सैंपल की फ़्रीक्वेंसी की पहचान करता है. जब किसी डेटासेट की वैल्यू, लगातार फ़्लोटिंग-पॉइंट वाली संख्याएं होती हैं, तो एग्ज़ैक्ट मैच बहुत कम होते हैं. हालांकि, वैल्यू x से वैल्यू y तक, प्रोबैबिलिटी डेंसिटी फ़ंक्शन को इंटिग्रेट करने पर, x और y के बीच डेटा सैंपल की अनुमानित फ़्रीक्वेंसी मिलती है.
उदाहरण के लिए, मान लें कि किसी नॉर्मल डिस्ट्रिब्यूशन का औसत 200 और स्टैंडर्ड डिवीऐशन 30 है. 211.4 से 218.7 की रेंज में आने वाले डेटा सैंपल की अनुमानित फ़्रीक्वेंसी तय करने के लिए, 211.4 से 218.7 के बीच के सामान्य डिस्ट्रिब्यूशन के लिए, प्रायिकता घनत्व फ़ंक्शन को इंटिग्रेट किया जा सकता है.
R
रीकॉल
क्लासिफ़िकेशन मॉडल के लिए एक मेट्रिक, जो इस सवाल का जवाब देती है:
जब ग्राउंड ट्रूथ पॉज़िटिव क्लास था, तो मॉडल ने कितने प्रतिशत अनुमानों की सही तरीके से पहचान पॉज़िटिव क्लास के तौर पर की?
यहां फ़ॉर्मूला दिया गया है:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
कहां:
- 'सही मायनों में पॉज़िटिव' का मतलब है कि मॉडल ने पॉज़िटिव क्लास का सही अनुमान लगाया.
- फ़ॉल्स नेगेटिव का मतलब है कि मॉडल ने नेगेटिव क्लास का अनुमान गलती से लगाया है.
उदाहरण के लिए, मान लें कि आपके मॉडल ने उन उदाहरणों के लिए 200 अनुमान लगाए जिनके लिए ज़मीनी सच्चाई पॉज़िटिव क्लास थी. इन 200 अनुमानों में से:
- इनमें से 180 ट्रू पॉज़िटिव थे.
- 20 फ़ॉल्स निगेटिव थे.
इस मामले में:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
ज़्यादा जानकारी के लिए, क्लासिफ़िकेशन: सटीक जानकारी, रीकॉल, सटीक जानकारी, और इससे जुड़ी मेट्रिक देखें.
k पर रीकॉल (recall@k)
आइटम की रैंक वाली सूची दिखाने वाले सिस्टम का आकलन करने वाली मेट्रिक. k पर रीकॉल, सूची में मौजूद काम के आइटम की कुल संख्या में से, पहले k आइटम में मौजूद काम के आइटम के हिस्से की पहचान करता है.
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
k पर सटीक के साथ कंट्रास्ट करें.
आरओसी (रिसीवर ऑपरेटिंग चैरेक्टरिस्टिक) कर्व
बाइनरी क्लासिफ़िकेशन में, अलग-अलग क्लासिफ़िकेशन थ्रेशोल्ड के लिए, ट्रू पॉज़िटिव रेट बनाम फ़ॉल्स पॉज़िटिव रेट का ग्राफ़.
आरओसी कर्व के आकार से पता चलता है कि बाइनरी क्लासिफ़िकेशन मॉडल, पॉज़िटिव क्लास को नेगेटिव क्लास से अलग करने में कितना कारगर है. उदाहरण के लिए, मान लें कि कोई बाइनरी क्लासिफ़िकेशन मॉडल, सभी नेगेटिव क्लास को सभी पॉज़िटिव क्लास से पूरी तरह से अलग करता है:

पिछले मॉडल का आरओसी कर्व कुछ ऐसा दिखता है:
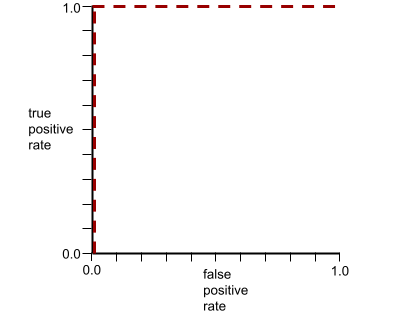
इसके उलट, नीचे दी गई इमेज में किसी खराब मॉडल के लिए, लॉजिस्टिक रिग्रेशन की रॉ वैल्यू का ग्राफ़ दिखाया गया है. यह मॉडल, नेगेटिव क्लास को पॉज़िटिव क्लास से अलग नहीं कर सकता:

इस मॉडल के लिए आरओसी कर्व इस तरह दिखता है:

वहीं, असल दुनिया में, ज़्यादातर बाइनरी क्लासिफ़िकेशन मॉडल, सकारात्मक और नकारात्मक कैटगरी को कुछ हद तक अलग करते हैं. हालांकि, आम तौर पर ऐसा पूरी तरह से नहीं होता. इसलिए, एक सामान्य आरओसी कर्व इन दोनों चरम स्थितियों के बीच होता है:

आरओसी कर्व पर (0.0,1.0) के सबसे करीब मौजूद पॉइंट से, सैद्धांतिक तौर पर, कैटगरी तय करने के लिए सही थ्रेशोल्ड का पता चलता है. हालांकि, असल दुनिया की कई अन्य समस्याएं, क्लासिफ़िकेशन के लिए सही थ्रेशोल्ड चुनने पर असर डालती हैं. उदाहरण के लिए, शायद गलत नतीजे मिलने से, गलत तरीके से सही नतीजे मिलने से ज़्यादा परेशानी होती है.
AUC नाम की अंकों वाली मेट्रिक, आरओसी कर्व को एक फ़्लोटिंग-पॉइंट वैल्यू में बताती है.
रूट मीन स्क्वेयर्ड एरर (RMSE)
मीन स्क्वेयर्ड एरर का वर्गमूल.
आरओयूजीई (गिसटिंग इवैलुएशन के लिए रीकॉल-ओरिएंटेड अंडरस्टडी)
मेट्रिक का एक फ़ैमिली, जो अपने-आप खास जानकारी देने और मशीन से अनुवाद करने वाले मॉडल का आकलन करता है. ROUGE मेट्रिक से यह पता चलता है कि रेफ़रंस टेक्स्ट, एमएल मॉडल के जनरेट किए गए टेक्स्ट से कितना ओवरलैप होता है. ROUGE परिवार के हर सदस्य के मेज़रमेंट अलग-अलग तरीके से ओवरलैप होते हैं. ROUGE के ज़्यादा स्कोर से पता चलता है कि रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट के बीच, कम स्कोर के मुकाबले ज़्यादा समानता है.
आम तौर पर, ROUGE प्रोग्राम में शामिल हर सदस्य के लिए ये मेट्रिक जनरेट होती हैं:
- स्पष्टता
- रीकॉल
- F1
ज़्यादा जानकारी और उदाहरणों के लिए, यहां जाएं:
ROUGE-L
ROUGE फ़ैमिली का एक सदस्य, जो रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में, सबसे लंबे कॉमन सबसिक्वेंस की लंबाई पर फ़ोकस करता है. नीचे दिए गए फ़ॉर्मूले, ROUGE-L के लिए रीकॉल और प्रिसिज़न का हिसाब लगाते हैं:
इसके बाद, F1 का इस्तेमाल करके, ROUGE-L रिकॉल और ROUGE-L प्रिसिज़न को एक ही मेट्रिक में रोल अप किया जा सकता है:
ROUGE-L, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में मौजूद किसी भी नई लाइन को अनदेखा करता है. इसलिए, सबसे लंबा कॉमन सबसीक्वेंस एक से ज़्यादा वाक्यों में हो सकता है. जब रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में कई वाक्य होते हैं, तो आम तौर पर ROUGE-Lsum नाम का ROUGE-L का वैरिएशन एक बेहतर मेट्रिक होती है. ROUGE-Lsum, किसी पैसेज में मौजूद हर वाक्य के लिए सबसे लंबा सामान्य सबसिक्वेंस तय करता है. इसके बाद, उन सबसे लंबे सामान्य सबसिक्वेंस का औसत निकालता है.
ROUGE-N
ROUGE फ़ैमिली में मौजूद मेट्रिक का एक सेट, जो रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में, किसी खास साइज़ के शेयर किए गए N-gram की तुलना करता है. उदाहरण के लिए:
- ROUGE-1, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में शेयर किए गए टोकन की संख्या को मेज़र करता है.
- ROUGE-2, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में, शेयर किए गए बिग्राम (2-ग्राम) की संख्या को मेज़र करता है.
- ROUGE-3, रेफ़रंस टेक्स्ट और जनरेट किए गए टेक्स्ट में, शेयर किए गए ट्राइग्राम (3-ग्राम) की संख्या को मेज़र करता है.
ROUGE-N फ़ैमिली के किसी भी सदस्य के लिए, ROUGE-N रीकॉल और ROUGE-N प्रिसिज़न का हिसाब लगाने के लिए, नीचे दिए गए फ़ॉर्मूले का इस्तेमाल किया जा सकता है:
इसके बाद, F1 का इस्तेमाल करके, ROUGE-N रिकॉल और ROUGE-N प्रिसिज़न को एक ही मेट्रिक में रोल अप किया जा सकता है:
ROUGE-S
ROUGE-N का एक ऐसा वर्शन जिसमें स्किप-ग्राम मैचिंग की सुविधा होती है. इसका मतलब है कि ROUGE-N सिर्फ़ उन N-ग्रैम की गिनती करता है जो एग्ज़ैक्ट मैच करते हैं. हालांकि, ROUGE-S एक या उससे ज़्यादा शब्दों से अलग किए गए N-ग्रैम की भी गिनती करता है. उदाहरण के लिए, आप नीचे दिया गया तरीका अपना सकते हैं:
- रेफ़रंस टेक्स्ट: सफ़ेद बादल
- जनरेट किया गया टेक्स्ट: सफ़ेद रंग के बादल
ROUGE-N का हिसाब लगाते समय, दो ग्राम वाला सफ़ेद बादल, सफ़ेद बादल से मेल नहीं खाता. हालांकि, ROUGE-S का हिसाब लगाते समय, सफ़ेद बादल और सफ़ेद बादल एक जैसे माने जाते हैं.
R-squared
रिग्रेशन मेट्रिक, यह बताती है कि किसी लेबल में, किसी एक फ़ीचर या फ़ीचर सेट की वजह से कितना बदलाव हुआ है. आर-स्क्वेयर, 0 और 1 के बीच की वैल्यू होती है. इसका मतलब इस तरह समझा जा सकता है:
- R-स्क्वेयर के 0 होने का मतलब है कि किसी लेबल का कोई भी वैरिएशन, फ़ीचर सेट की वजह से नहीं है.
- R-squared का 1 होना, इस बात का संकेत है कि किसी लेबल का सारा वैरिएशन, फ़ीचर सेट की वजह से है.
- 0 से 1 के बीच का आर-स्क्वेयर यह दिखाता है कि किसी खास सुविधा या सुविधाओं के सेट से, लेबल के वैरिएशन का अनुमान किस हद तक लगाया जा सकता है. उदाहरण के लिए, R-स्क्वेयर के 0.10 होने का मतलब है कि लेबल में वैरिएंस का 10 प्रतिशत, फ़ीचर सेट की वजह से है. R-स्क्वेयर के 0.20 होने का मतलब है कि 20 प्रतिशत, फ़ीचर सेट की वजह से है.
आर-स्क्वेयर, मॉडल की अनुमानित वैल्यू और ग्राउंड ट्रूथ के बीच के पियरसन कोरिलेशन कोएफ़िशिएंट का स्क्वेयर होता है.
S
स्कोरिंग
सुझाव देने वाले सिस्टम का वह हिस्सा जो कैन्डिडेट जनरेशन फ़ेज़ से जनरेट किए गए हर आइटम के लिए वैल्यू या रैंकिंग देता है.
मिलते-जुलते कॉन्टेंट का पता लगाने के लिए मेज़र
क्लस्टरिंग एल्गोरिदम में, इस मेट्रिक का इस्तेमाल करके यह तय किया जाता है कि दो उदाहरण कितने मिलते-जुलते हैं.
कम जानकारी होना
किसी वेक्टर या मैट्रिक्स में शून्य (या शून्य) पर सेट किए गए एलिमेंट की संख्या को उस वेक्टर या मैट्रिक्स में मौजूद एंट्री की कुल संख्या से divide किया जाता है. उदाहरण के लिए, 100 एलिमेंट वाले मैट्रिक्स पर विचार करें, जिसमें 98 सेल में शून्य है. डेटा के कम होने का हिसाब इस तरह लगाया जाता है:
फ़ीचर स्पैर्सिटी का मतलब, फ़ीचर वेक्टर की स्पैर्सिटी से है; मॉडल स्पैर्सिटी का मतलब, मॉडल वेट की स्पैर्सिटी से है.
स्क्वेयर्ड हिंज लॉस
हिंग लॉस का वर्ग. स्क्वेयर्ड हिंज लॉस, सामान्य हिंज लॉस की तुलना में आउटलायर को ज़्यादा सख्ती से दंडित करता है.
स्क्वेयर्ड लॉस
L2 लॉस के लिए समानार्थी शब्द.
T
टेस्ट लॉस
मेट्रिक, जो टेस्ट सेट के मुकाबले मॉडल के लॉस को दिखाती है. मॉडल बनाते समय, आम तौर पर टेस्ट में शामिल डेटा का नुकसान कम करने की कोशिश की जाती है. इसकी वजह यह है कि कम टेस्ट लॉस, कम ट्रेनिंग लॉस या कम पुष्टि करने के लिए इस्तेमाल होने वाले लॉस की तुलना में, क्वालिटी का बेहतर सिग्नल होता है.
टेस्ट लॉस और ट्रेनिंग लॉस या पुष्टि करने के दौरान होने वाले लॉस के बीच का बड़ा अंतर, कभी-कभी यह बताता है कि आपको रेगुलराइज़ेशन रेट बढ़ाना होगा.
टॉप-k सटीक
जनरेट की गई सूचियों की पहली k पोज़िशन में, "टारगेट लेबल" दिखने की संख्या का प्रतिशत. ये सूचियां, आपके हिसाब से सुझाव हो सकती हैं या सॉफ़्टमैक्स के हिसाब से क्रम में लगाए गए आइटम की सूची हो सकती हैं.
टॉप-k सटीक जानकारी को k पर सटीक जानकारी भी कहा जाता है.
बुरा बर्ताव
कॉन्टेंट में बुरे बर्ताव, धमकी या आपत्तिजनक कॉन्टेंट किस हद तक है. मशीन लर्निंग के कई मॉडल, आपत्तिजनक कॉन्टेंट की पहचान कर सकते हैं और उसका आकलन कर सकते हैं. इनमें से ज़्यादातर मॉडल, कई पैरामीटर के आधार पर नुकसान पहुंचाने वाले कॉन्टेंट की पहचान करते हैं. जैसे, अपशब्दों के इस्तेमाल का लेवल और धमकी देने वाली भाषा का लेवल.
ट्रेनिंग में हुई कमी
यह एक मेट्रिक है, जो किसी खास ट्रेनिंग के दौरान मॉडल के लॉस को दिखाती है. उदाहरण के लिए, मान लें कि लॉस फ़ंक्शन मीन स्क्वेयर्ड गड़बड़ी है. शायद 10वें आइटरेशन के लिए ट्रेनिंग लॉस (मीन स्क्वेयर्ड एरर) 2.2 है और 100वें आइटरेशन के लिए ट्रेनिंग लॉस 1.9 है.
लॉस कर्व, ट्रेनिंग लॉस को दोहराव की संख्या के मुकाबले प्लॉट करता है. लॉस कर्व से, ट्रेनिंग के बारे में ये अहम जानकारी मिलती है:
- नीचे की ओर ढलान का मतलब है कि मॉडल की परफ़ॉर्मेंस बेहतर हो रही है.
- ऊपर की ओर बढ़ने का मतलब है कि मॉडल की परफ़ॉर्मेंस खराब हो रही है.
- सपाट ढलान का मतलब है कि मॉडल कंसीवर्जेंस तक पहुंच गया है.
उदाहरण के लिए, यहां दिया गया लॉस कर्व, कुछ हद तक आदर्श है. इसमें यह दिखाया गया है:
- शुरुआती दोहरावों के दौरान, डाउनवर्ड स्लोप का ज़्यादा होना. इससे पता चलता है कि मॉडल में तेज़ी से सुधार हो रहा है.
- ट्रेनिंग के आखिर तक धीरे-धीरे सपाट (लेकिन अब भी नीचे की ओर) स्लोप, जिसका मतलब है कि शुरुआती दोहरावों के मुकाबले, मॉडल में अब भी धीमी रफ़्तार से सुधार हो रहा है.
- ट्रेनिंग के आखिर में, प्लैटफ़ॉर्म के ढलान में कोई बदलाव नहीं होता. इससे पता चलता है कि मॉडल के एलिमेंट एक-दूसरे से मिल गए हैं.

ट्रेनिंग लॉस अहम है, लेकिन जनरलाइज़ेशन भी देखें.
खतरे को सही आंकना (TN)
एक उदाहरण, जिसमें मॉडल ने नेगेटिव क्लास का सही अनुमान लगाया है. उदाहरण के लिए, मॉडल यह अनुमान लगाता है कि कोई ईमेल मैसेज स्पैम नहीं है और वह ईमेल मैसेज वाकई स्पैम नहीं है.
ट्रू पॉज़िटिव (TP)
एक उदाहरण, जिसमें मॉडल ने पॉज़िटिव क्लास का सही अनुमान लगाया है. उदाहरण के लिए, मॉडल यह अनुमान लगाता है कि कोई ईमेल मैसेज स्पैम है और वह ईमेल मैसेज वाकई स्पैम है.
ट्रू पॉज़िटिव रेट (टीपीआर)
रिवॉल्कर का समानार्थी शब्द. यानी:
आरओसी कर्व में, असल पॉज़िटिव रेट, y-ऐक्सिस होता है.
V
वैलिडेशन लॉस
यह एक मेट्रिक है, जो ट्रेनिंग के किसी खास इटरेशन के दौरान, पुष्टि करने वाले सेट पर मॉडल के लॉस को दिखाती है.
जनरलाइज़ेशन कर्व भी देखें.
वैरिएबल की अहमियत
स्कोर का एक सेट, जो मॉडल के लिए हर फ़ीचर की अहमियत दिखाता है.
उदाहरण के लिए, एक फ़ैसला लेने वाले ट्री का इस्तेमाल करके, घर की कीमत का अनुमान लगाया जा सकता है. मान लें कि यह फ़ैसला लेने वाला ट्री, तीन सुविधाओं का इस्तेमाल करता है: साइज़, उम्र, और स्टाइल. अगर तीन सुविधाओं के लिए वैरिएबल की अहमियत का सेट, {size=5.8, age=2.5, style=4.7} के तौर पर कैलकुलेट किया जाता है, तो डिसीज़न ट्री के लिए साइज़, उम्र या स्टाइल से ज़्यादा अहम है.
वैरिएबल की अहमियत बताने वाली अलग-अलग मेट्रिक मौजूद हैं. इनसे एआई विशेषज्ञों को मॉडल के अलग-अलग पहलुओं के बारे में जानकारी मिल सकती है.
W
वासरस्टीन लॉस
जनरेटिव अडवर्सेरी नेटवर्क में आम तौर पर इस्तेमाल किया जाने वाला लॉस फ़ंक्शन. यह जनरेट किए गए डेटा और असल डेटा के डिस्ट्रिब्यूशन के बीच ईअर्थ मूवर की दूरी पर आधारित होता है.


