Modulo circunferencia

Módulo de autoaprendizaje:
Paralelogramos y Circunferencia
•Alumnos: -Jorge Martínez
-Claudio Vargas
-Felipe Vargas

Hola:
Con este modulo queremos que
aprendaz de un manera poco
tradicional lo relacionado con la
circunferencia y los
paralelogramos.
Ren y Stimpy te acompañaran durante
el tiempo que uses el módulo, Ren
es poco tolerante pero stimpy es
más relajado.
Lo único que te podemos decir es que
pongas bastante atención a las
propiedades para que puededas
resolver todos los problemas que te
plantearemos.
Buena surte….

Circunferencia:
Definición de Circunferencia:
Una circunferencia es un conjunto
infinito de puntos que están a igual
distancia de un punto llamado centro
de la circunferencia.
Ox
Punto O = centro de
la circunferencia

Elementos de la circunferencia
A
L1 = Recta Tangente de la circunferencia
B
D O
E
C
AB = Diámetro de la circunferencia
L1
L2
Ox = Centro de circunferencia
x
OA = OB = OC = Radio de la circunferencia.
DE = Cuerda de la Circunferencia
L2 = Recta secante de la circunferencia

Área y Perímetro de la circunferencia
a) Área : Es la superficie que la circunferencia cubre
r A = p . r 2
b) Perímetro: es la medida del contorno de la circunferencia
r
P = 2 . p . r
O x
O x

Ángulos y Arcos en la circunferencia
a) Ángulo formado por dos radios:
O
A
a
B
Relación entre el
ángulo y el arco:
a = AB
A este ángulo se le llama también ángulo
central
x

b) Ángulo formado por dos cuerdas:
b Relación entre el ángulo y el arco:
O
A
C
b = AC
2
B
x
A este ángulo se le llama también ángulo inscrito

c) Los dos ángulos anteriores en una misma circunferencia:
A
b Relación entre los dos ángulos:
C
a = 2b
B
O x a

d) Varios ángulos inscritos formando el mismo arco:
b Relación entre los ángulos:
O
A
C
a = b = d
B
a
d x

e) Ángulo formado por dos cuerdas:
Medida del ángulo a :
a = AD + BC
2
a
A
D
B
C
O x

f) Ángulo formado por dos secantes:
O
a = AC - BD
2
A
B
C
D
a P
x

g) Ángulo formado por dos tangentes:
C D
O
a = ACB - ADB
2
a
A
B
P
x

h) Ángulo formado por una cuerda y una tangente:
O
a = AB
2
a
A
B
x
A este ángulo se le llama también ángulo semi inscrito

i) Ángulos que forma una semicircunferencia:
O x Medida del ángulo a :
a = 90°
A a
C
B

j) Ángulo formado por una secante y una tangente:
O
a = AC - AB
2
A
B
C
a P
x

k) Arcos formados por rectas paralelas que cortan la circunferencia:
O Relación entre arcos:
AB = CD
A
D
B
C
x

l) Ángulos opuestos de un cuadrilátero inscrito:
O
Relación entre ángulos:
a + b = 180°
A
D
B
C
a
x b

Ejercicios:
Ejemplo:
O X 46°
Hallar:
y
B
a
Ð = 112
°
Ð x
=
?
ÐBAC
A
C
A C
B
x
y
Según la propiedad a= 2b, se
puede invertir la propiedd para
hallar en este caso b que es igual a
= 46
= 23°
2
2
Aplica las propiedades:
B)34
A)45
O x

Ejercicios:
= °
72
?
?
a
=
=
x
y
?
= 140
°
BDC
y
Ð =
C
A
x a
B y
A
y
0x
B D
C
A)x=80;y=55
B)x=90;y=144
A) 40 B)70
O x

Ejercicios:
x
Ð = 75
°
y
=
?
y
Ð = 115
°
Ð x
=
?
A D
B
C
C
B
0x x y
A
0x
A)90 B)20
a)245 B)65
y
x
60

Ejercicios:
x
Ð = 61
°
y
=
?
x
Ð = 40
°
Ð y
=
?
A
C
B
y
x
E
A
C
D
y
B
200°
B)132
A)120 B)80
O x
O x
A)119
x
241º

Ejercicios:
A
?
=
?
x
=
y
?
=
?
x
=
y
A
D
x y 65°
C
O x
B
B
C
D 2x y
3x+10°
A)x=65;y=57,5
B)x=40;y=68,5
A)x=34;y=68
O x B)x=56;y=85

Segmentos en la circunferencia
1er Teorema: los dos segmentos tangentes a una circunferencia
desde un punto exterior son congruentes y determinan ángulos
iguales con el segmento que une el punto exterior al centro.
O x
A
B
P
AP , BP segmentos tangentes:
AP = BP , ÐOPA = ÐOPB

2do Teorema: si se trazan dos rectas secantes desde un punto
exterior a una circunferencia, entonces:
A
B
P
AP . BP = PD . PC
C
D
O x

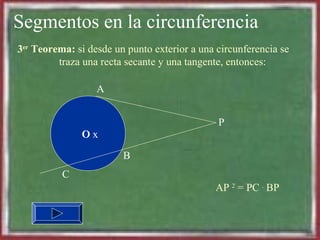
3er Teorema: si desde un punto exterior a una circunferencia se
traza una recta secante y una tangente, entonces:
O
A
P
AP 2 = PC . BP
B
C
x

4to Teorema: si se trazan dos cuerdas que se cortan dentro de la
circunferencia, entonces:
A
D
E
O x
C B AE . BE = CE . DE

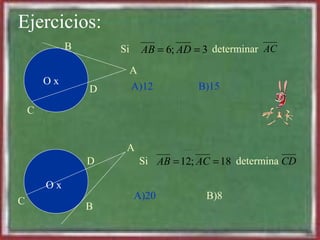
Ejercicios:
B A
C
D
Si A P = 6 ; B P = 1 5 y PC =8 Determinar PD
P
En este caso hay que aplicar el
teorema 2 . Si tú lo aplicas bien
te tendría que resultar 11.2
Si B P = 5 y P C = 2 0 determinar AP A
B
C
P
A)20 B)10
O x
O x

Ejercicios:
EB = 2× AE;CD =15 AE
Si D E = 5 ; determinar
OE = 8 AB
A
B
C
D
E
Si O D = 1 0 y determinar
C
E ÐAEC = 90°
A B
D
A)5 B)10
A) 6 B)12
O x
O x

Ejercicios:
Si A B = 6 ; A D = 3 determinar AC
A
B
C
D
Si A B = 1 2 ; A C = 1 8 determina C D
A
D
C B
A)12 B)15
A)20 B)8
O x
O x

Ejercicios:
Si A D = D B ; E C = 1 4 ; A E = 4 determinar AD
A
B
C
D
E
A)36 B)6
O x
Si B P = 1 5 ; A B = ( B P : 3 ) 2 determinar PT
T
O x A)8.6 B)10
B A
P

Paralelogramos:
Definición de paralelogramo:
Un paralelogramo es un cuadrilátero que tiene dos
pares de lados paralelos. Se pueden clasificar en:
• Rectángulos: tienen los cuatro ángulos rectos,
pero dos pares de lados iguales.
• Rombos: tienen los cuatro lados iguales.
• Romboides: No tienen lados ni ángulos iguales.

Paralelogramos:
CCuuaaddrraaddoo Lados iguales Ángulos
iguales
Diagonales se
bisecan y son
perpendicular
es entre si.
RReeccttáánngguulloo Lados
peralelos
iguales
Ángulos
rectos
Sus
diagonales se
bisecan.
RRoommbboo Lados iguales Águlos
oblicuos
Sus
diagonales se
bisecan y son
perpendicular
es entre si.
RRoommbbooiiddee Lados iguales Ángulos
obicuos
Sus
diagonales se
bisecan.
Los ángulos
interno y
opuestos son
congruentes;
como los
ángulos
internos no
puestos son
suplementarios.

Ejemplos de Paralelogramos:
Rectangulo:
2 pares de lados
iguales y todos sus
angulos son rectos
(90°)
b
a a
b

Ejercicios
Hallar las variables:
Perímetro: 40 Aquí hay que recordar que tiene todos sus
20
B C
2x
A D
lados iguales, asi es que 2x=20
Por lo que resulta que x es igual a 10
B C
E
A D
Rombo Perímetro: 40
DE = 15, BE = 3a , AC =6a, EC = 3a

A
B C
D
2x
3x-7
20
x
B C
D
A
Hallar x e y:
Perímetro = 86
Perímetro: 40
36
43
y3

A
B
B C
A
C
D
D
BAC x
Ð = -
CAD x
4 5
Ð = +
2 15
Hallar x:
2x+10 4x-30
Trapecio
y
Nota: los ángulos
adyacentes de lados
paralelos suman 180°.

Esperamos que hayas
aprendido lo que se te
presentó, y que lo
puedas utilizar enel
futuro.
Ren y Stimpy…
…Fin del módulo…

¡NO! ¿en qué piensas idiota?
Bueno, ya que le vamos a
hacer, házlo otra vez.
¡¡Déjalo!!
Es solo un niño.
Una pista:
X se obtiene con la propiedad
b): del ángulo formado por dos
cuerdas.

Mmm…Parece que
haz aprendido algo
Pero te falta mucho.
¡Que bien eres muy
inteligente¡
¡¡Eres super¡¡

¡¡Como es que eres
tan tonto!!, eso es
BÁSICO.
Dale otra
oportunidad po’.
No seas malito
Observa bien. Pista: la
cuerda AB divide a la
circunferencia en dos partes
iguales

Esó, muy bien.
Me haz
sorprendido, creí
que eras mas tonto.
Muy bien hecho
amiguito,
demuestra que eres
un matemático.
Se resolvía observando que Y vale
144 y que X vale 90 por ser ángulo
inscrito compartiendo cuerdas con el
ángulo central Ð B O C que vale 180.

Me arrepiento de lo dicho
anteriormente. ¿Cómo
puede haber gente tan
incompetente?
No le hagas caso ,
sé que pudes
lograrlo, confío
en ti.
Pista: usa la propiedad h):
ángulo formado por una
cuerda y una tangente.
a = AB
2

Pon atencion para que sepas como
resolver otro parecido. Eres un genio,
¡¡MAESTRO!!
Se resolvía dividiendo 80:2, ya que se
formaba un triángulo isósceles donde cada
ángulo basal vale 70 y el ángulo del
vertice 40. En la circunferencia 2
segmentos valen 140 faltando 80 para
completar 360, a los 80 se le aplicaba la
propiedad nombrada en la pista.

Pista: x = 75º, y es un
ángulo formado por
dos cuerdas. Usa esa
propiedad.
No puede ser
tan dificil!!
Piensa un
poco
más…

Que bien uno
bueno!!!
Así se hace,
vamos
mejorando…
Se resolvía dándose cuenta que x
formaba un arco que vale 60º + y.
Además, x = 75º, por lo que el arco
debe ser el doble de 75º, o sea
150º, y 150º – 60º = 90º.

Eso no fue muy
inteligente… Es un simple
ejercicio…piensa…
Pista: y = 115º, por lo que
su arco es 230º. El total de
la circunferencia es 360º

Parece que es tu dia
de suerte…
Demuestra lo
que puedes
hacer…
Se resolvía restando 230º
a 360º, quedando el arco
del ángulo x. Lo que
queda, que es 130º, se
divide por 2 y da 65º, que
es la medida de x.

Eres un caso
perdido…
Coloca más
atención a lo
que haces…
Pista: te dan el valor del ángulo
y el de uno de los arcos.
Reemplaza los valores en la
fórmula del teorema.

Se resuelve al
reemplazar los valores
del ángulo x y del arco
que vale 241º. Al hacer
la operación debiera
dar 119º.
Me haz
sorprendido…
Muy bien sigue
así…

Pista: usa el
Ja ja fallaste…
teorema del ángulo
formado por dos
rectas tangentes.
Mira bien el
ejercicio…

Que sorpresa…
Se resolvía restando el doble
del ángulo a 200º, y así sale
que y = 120º.
piensa..
Eres brillante

Pista: el semiperímetro de
una circunferencia mide
180º.
No!!! ¡Como eres
tan tonto?
Con calma…

Pista: el semiperímetro de
una circunferencia mide
180º.
Más aprende mi
tortuga…
No grites que
menos piensa…

Bajo presión
trabajas mejor.
Eres muy
bieno para
esto
Se resolvía haciendo
3x+10+2x=180º. De ahí
se saca que x=34º.
Posteriormente se iguala
3x+10+y=180º, pero ya
se sabe el valor de x.

¿sabes usar lo
que tienes arriba
del cuello?
Pista: la cuerda BD
divide a la
circunferencia en dos
partes iguales..
No le
hagascaso

Te felicito,
primera y última
Se resolvía restando 180º - 65º=
115º, que es el arco que forma y.
Posteriormente se divide ese valor
por 2, y sale el ángulo y.
vez…
Muy bien…

5 . 20 = x2. Se
resuelve y se obtiene
x = 10º.
Si sabes usar la
cabeza,
disculpa…
Ren está celoso,
el no sabe…

No sabes JA JA
JA JA JA…
Confío en ti
piensa un poco…
Pista: usa el teorema Nº3.

No era tan
dificil, tubiste
suerte…
5 . 10 = 2x . x
Tu representas el
magis
ignaciano…

No puede ser
tan dificil!! Eres muy
Pista: usa el
teorema 3.
bieno para
esto

Pon atencion para que sepas como
resolver otro parecido. Eres un genio,
¡¡MAESTRO!!
Se resolvía haciendo 18 . 2 = x2.
De ahí se saca que x = 6.

Eso no fue muy
inteligente…
Pista: OD es radio, y es igual a
OC, que vale 10.
Con calma…

Parece que es tu dia
de suerte…
Así se hace,
vamos
mejorando…
Se resolvía haciendo 62 = 3 . (x+3).
Ahí sale que x = 9.
El lado entonces vale 12

Pista: Usa el teorema 3,
reemplaza los valores que
ya te dan.
No puede ser
tan dificil!!
Dale otra
oportunidad po’.
No seas malito

Si sabes usar la
El valor de x se hallaba al
resolver la ecuación que
resulta al reemplazar los
valores en el teorema 3,
quedando 122 = 18 . x .
cabeza,
disculpa…
Muy bien sigue
así…

Dale otra
oportunidad po’.
No seas malito
No sabes JA JA
JA JA JA…
Pista: reemplaza los valores
que te dan en el teorema 3.

Se resolvía al hacer
18 . 4 = 2x . x . De ahí
se obtiene que x es
igual a 6.
Si sabes usar la
cabeza,
disculpa…
Muy bien sigue
así…

Pista: reemplaza los valores en
el teorema 2.
Dale otra
oportunidad po’.
No seas malito
No sabes JA JA
JA JA JA…

Tu representas el
magis
ignaciano…
Bajo presión
trabajas mejor.
Se resolvía haciendo 15 . 5 = x2.
De ahí se obtiene que x = 8,6.

Pista: reemplaza los valores dados
en el teorema 3.
No puede ser
tan dificil!!
Mira bien el
ejercicio…

Modulo circunferencia

Más contenido relacionado

La actualidad más candente (8)

Similar a Modulo circunferencia (20)

Último (20)

Modulo circunferencia

Notas del editor