COMP.FUNCIONES REALES DE VARIABLE REAL (1).pptx

Solución
Considere las funciones 𝑓 y 𝑔 definidas por
Halle el rango de la función 𝑔 ∘ 𝑓.
𝑓 𝑥 = −𝑥2
− 2𝑥 − 2, −2 < 𝑥 < 1 , 𝑔 𝑥 = 𝑥2
+ 5𝑥 +
31
4
Podemos expresar las funciones de la
manera siguiente
𝐷𝑜𝑚 𝑔 ∘ 𝑓 = 𝑥 ∈ 𝑅 ∶ 𝑥 ∈ 𝐷𝑜𝑚(𝑓) ∧ 𝑓(𝑥) ∈ 𝐷𝑜𝑚(𝑔)
𝑓 𝑥 = − 𝑥 + 1 2
− 1, −2 < 𝑥 < 1
𝑔 𝑥 = 𝑥 +
5
2
2
+
6
4
𝐷𝑜𝑚(𝑔 ∘ 𝑓) = 𝑥 ∈ 𝑅 ∶ 𝑥 ∈ −2,1 ∧ − 𝑥 + 1 2
− 1, ∈ R
𝐷𝑜𝑚(𝑔 ∘ 𝑓) = −2,1
Luego tenemos que 𝑔 ∘ 𝑓 𝑥 = 𝑔 𝑓 𝑥
= 𝑓(𝑥) +
5
2
2
+
6
4
Hallaremos la variación de 𝑓(𝑥).
• −2 < 𝑥 < 1
⇒ −1 < 𝑥 + 1 < 2
⇒ 0 ≤ 𝑥 + 1 2 < 4
⇒ −5 < − 𝑥 + 1 2
− 1 ≤ −1
⇒ −5 < 𝑓(𝑥) ≤ −1
Luego
• −
5
2
< 𝑓 𝑥 +
5
2
≤
3
2
⇒ 0 ≤ 𝑓(𝑥) +
5
2
2
<
25
4
⇒
3
2
≤ 𝑓(𝑥) +
5
2
2
+
6
4
<
31
4
Así, el 𝑅𝑎𝑛(𝑔 ∘ 𝑓) =
3
2
,31
4

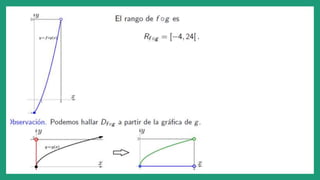
otra forma
Tenemos 𝒇(𝒙) = −(𝒙 + 𝟏)𝟐
− 𝟏; −𝟐 < 𝒙 < 𝟏.
Graficando tenemos
Luego el 𝑅𝑎𝑛𝑓 = ] − 5; −1], el cual será ahora el
dominio de la función 𝑔 𝑥 = 𝑥 +
5
2
2
+
6
4
Graficamos la función 𝑔 𝑥 = 𝑥 +
5
2
2
+
6
4
Así, el 𝑅𝑎𝑛(𝑔 ∘ 𝑓) =
3
2
,31
4

PREGUNTA 2
Solución
Dadas las funciones 𝑓 y 𝑔 definidas por
𝑓(𝑥) = 𝑥 + |𝑥| − 2, −4 < 𝑥 < 3
𝑔 𝑥 =
𝑥2 + 2𝑥 − 3 −1 ≤ 𝑥 ≤ 0
2 + 𝑥 𝑥 ≥ 0
Halle 𝑒𝑙 𝑑ominio y la regla de correspondencia de 𝑓 ∘ 𝑔
Consideremos
𝐷𝑜𝑚(𝑓 ∘ 𝑔) = 𝐷𝑜𝑚(𝑓 ∘ 𝑔1) ∪ 𝐷𝑜𝑚(𝑓 ∘ 𝑔2).
𝑓(𝑥) = 𝑥 + |𝑥| − 2, −4 < 𝑥 < 3
𝑔 𝑥 =
𝑔1 𝑥 = 𝑥2 + 2𝑥 − 3 −1 ≤ 𝑥 ≤ 0
𝑔2 𝑥 = 2 + 𝑥 𝑥 ≥ 0
𝐷𝑜𝑚(𝑓 ∘ 𝑔1) = {𝑥 ∈ 𝐷𝑜𝑚𝑔1 ∧ 𝑔1(𝑥) ∈ 𝐷𝑜𝑚𝑓 }
𝑥 ∈ [−1; 0[ ∧ 𝑥 + 1 2 − 4 ∈ ] − 4; 3[
𝑥 ∈ [−1; 0[ ∧ −4 < 𝑥 + 1 2
−4 < 3
𝑥 ∈ [−1; 0[ ∧ 0 < 𝑥 + 1 2
< 7
𝑥 ∈ [−1; 0[ ∧ 𝑥 + 1 2 −7 < 0
𝑥 ∈ [−1; 0[ ∧ 𝑥 + 1 − 7 𝑥 + 1 + 7 < 0
𝑥 ∈ [−1; 0[ ∧ 𝑥 ∈ −1 − 7, −1 + 7
𝑥 ∈ −1,0
𝐷𝑜𝑚(𝑓 ∘ 𝑔1) = −1,0
𝑓 ∘ 𝑔1 𝑥 = 𝑓 𝑔1 𝑥 = 𝑓 𝑥2
+ 2𝑥 − 3
= 𝑥2
+ 2𝑥 − 3 + |𝑥2
+ 2𝑥 − 3| − 2
= − 2

PREGUNTA 2
(𝑓 ∘ 𝑔) 𝑥 =
−2 −1 < 𝑥 < 0
2 + 2 𝑥 0 ≤ 𝑥 < 1
𝐷𝑜𝑚(𝑓 ∘ 𝑔2) = {𝑥 ∈ 𝐷𝑜𝑚𝑔2 ∧ 𝑔2(𝑥) ∈ 𝐷𝑜𝑚 (𝑓 )}
𝑥 ∈ [ 0, +∞[ ∧ 2 + 𝑥 ∈ ] − 4; 3[
𝑥 ∈ [ 0, +∞[ ∧ −4 < 2 + 𝑥 < 3
𝑓 ∘ 𝑔2 𝑥 = 𝑓 𝑔2 𝑥 = 𝑓 2 + 𝑥
= 2 + 𝑥 + 2 + 𝑥 − 2
𝑥 ∈ [ 0, +∞[ ∧ −6 < 𝑥 < 1
𝑥 ∈ [ 0, +∞[ ∧ 0 ≤ 𝑥 < 1
𝑥 ∈ [0,1[
𝐷𝑜𝑚 𝑓 ∘ 𝑔2 = [0,1[
= 2 + 2 𝑥

Dadas las funciones:
Dadas las funciones:
solución
Luego:

ECUACIONES PARAMÉTRICAS
se denominan Ecuaciones Paramétricas.
Si 𝑓 𝑦 𝑔 son funciones continuas de 𝑡 en un intervalo 𝑡0, 𝑡1 donde t es llamado
parámetro. Entonces las ecuaciones :
𝐶:
𝑥 = 𝑓(𝑡)
𝑦 = 𝑔(𝑡)
, 𝑡 ∈ 𝑡0, 𝑡1
Al conjunto de puntos (𝑥, 𝑦) que se obtiene cuando 𝑡 varía sobre el intervalo
𝑡0, 𝑡1 , se le llama la gráfica de las ecuaciones paramétricas.
A las ecuaciones paramétricas y a la gráfica, juntas, es a lo que se le llama una
curva plana, que se denota por C.

𝐶:
𝑥 = 𝑡3 − 4𝑡
𝑦 = 𝑡2 − 4
, 𝑡 ∈ −2,2
Podemos suprimir 𝑡 porque
Bosqueje la grafica de la curva definida por las ecuaciones paramétricas:
Solución
𝑡 𝑥 𝑦
−2 0 0
−1 3 −3
0 0 −4
1 −3 −3
2 0 0
𝑥 = ± 𝑦 + 4
3
− 4 ± 𝑦 + 4
Dando algunos valores a la variable 𝑡
obtenemos los pares ordenados que permiten
ver el sentido del recorrido de la curva.
Al despejar la variable 𝑡 de la expresión
𝑦 = 𝑡2
− 4,
es decir, 𝑡 = ± 𝑦 + 4 y reemplazando
este valor en 𝑥 = 𝑡3 − 4𝑡 se tiene la
relación en coordenadas cartesianas:

Considere las siguientes curvas con ecuaciones paramétrica
𝐶:
𝑥(𝑡) = 1 + 𝑙𝑜𝑔2𝑡
𝑦(𝑡) = 16𝑡−2 + 2
, 𝑡 ∈ 1, +∞
I. Obtenga la ecuación cartesiana de la curva C:
II. Grafique la curva C indicando su orientación o recorrido.
Solución
𝑥 = 1 + 𝑙𝑜𝑔2𝑡 → 𝑥 − 1 = 𝑙𝑜𝑔2𝑡 → 𝑡 = 2𝑥−1
Remplazando obtenemos
𝑦 = 16 2𝑥−1 −2 + 2
𝑦 = 2−2𝑥+6
+ 2

𝐶:
𝑥 𝑡 = 3 − 4𝑠𝑒𝑛(𝑡)
𝑦 𝑡 = −3 + 4cos(𝑡)
, 0 ≤ 𝑡 ≤
𝜋
2
solución

𝐶: 3𝑥2 + 6𝑦2 = 18 ,
Halle la ecuación paramétrica de la curva dada en coordenadas cartesianas
Para determinar la ecuación paramétrica dividimos ambos miembros de
la igualdad entre 18
Solución
𝐶:
𝑥2
6
+
𝑦2
3
= 1
𝐶:
𝑥
6
2
+
𝑦
3
2
= 1,

𝐶:
𝑥(𝑡) = 1 + 5𝑠𝑒𝑛𝑡
𝑦 𝑡 = 2 + 15𝑐𝑜𝑠𝑡
, 𝜋 ≤ 𝑡 ≤ 2𝜋
Solución
𝑥 − 1
5
= 𝑠𝑒𝑛𝑡
𝑥 − 2
15
= 𝑐𝑜𝑠𝑡
𝑥 − 1
5
2
= 𝑠𝑒𝑛2
𝑡
𝑦 − 2
15
2
= 𝑐𝑜𝑠2
𝑡
𝑥 − 1
5
2
+
𝑦 − 2
15
2
= 1
𝑥 − 1
5
2
+
𝑦 − 1
15
2
= 1

𝐶:
𝑥 𝑡 = 𝑡2 + 2𝑡 + 2
𝑦(𝑡) = 𝑡2 + 2𝑡 + 2 2 , −2 ≤ 𝑡 ≤ 0

COMP.FUNCIONES REALES DE VARIABLE REAL (1).pptx

Más contenido relacionado

Similar a COMP.FUNCIONES REALES DE VARIABLE REAL (1).pptx (20)

Último (20)

COMP.FUNCIONES REALES DE VARIABLE REAL (1).pptx