OLIMPIADA 2022 COMUNIDAD VALENCIANA. EJERCICIO DIÉDRICO PASO A PASO.pdf
2 recomendaciones3,487 vistas
El documento presenta los pasos para resolver un ejercicio de diédrico que consiste en dibujar las proyecciones de un cubo apoyado en un plano. Primero se determina la intersección entre dos planos y se abaten las rectas de intersección y un punto. Luego se dibuja el cuadrado de la cara del cubo apoyada en uno de los planos. Finalmente, se obtienen las proyecciones horizontales y verticales del cubo estudiando su visibilidad.
OLIMPIADA 2022 COMUNIDAD VALENCIANA. EJERCICIO DIÉDRICO PASO A PASO.pdf
- 1. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ c o t a s´ x A´´ s” E”1 s”1 x1 x2 E” E´ E´ F” G” H” E” G” H” F” Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA Resolución paso a paso
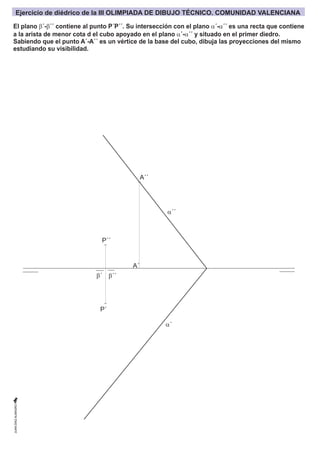
- 2. b´ A´´ P´´ P´ a´´ a´ b´´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA A´
- 3. b´ A´´ h´´ f´´ f´ P´´ P´ a´´ a´ b´´ 1. En primer lugar, vamos a sacar la intersección entre el plano b (que contiene a la línea de tierra y al punto P) y el plano a. Para ello, comenzamos por hacer las rectas horizontal (h) y frontal (f) del plano a, que pasan por P y pertenecen por tanto a los planos b y a . h´ A´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 4. b´ I´´ A´´ h´´ f´´ f´ P´´ P´ a´´ a´ b´´ 1. En primer lugar, vamos a sacar la intersección entre el plano b (que contiene a la línea de tierra y al punto P) y el plano a. El punto I de intersección de las rectas f y h pertenecerá a la recta de intersección r entre a y b I´ h´ A´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 5. b´ I´´ A´´ h´´ f´´ f´ P´´ P´ a´´ a´ b´´ 1. En primer lugar, vamos a sacar la intersección entre el plano b (que contiene a la línea de tierra y al punto P) y el plano a. Al ser b un plano que contiene a la línea de tierra, sabemos que las proyecciones r´y r´´ de la recta intersección de b y a se van a cortar en la LT, en el mismo punto que se cortan a´y a´´. Como tenemos el punto I y sabemos lo anterior, sólo hay que unir I con a´y a´´ en la LT. I´ h´ r´ r´´ A´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 6. b´ I´´ r´´ I´ I0 A´´ h´´ f´´ h´ f´ P´´ P´ a´´ a´ b´´ 2. Una vez tenemos la recta r intersección de a-b, vamos a abatir la recta intersección y el punto A Para abatir la recta intersección r, basta con abatir el punto de intersección I y tendremos la recta abatida, r0. cota c o t a r0 r´ A´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 7. b´ I´´ r´´ I´ I0 A´´ A0 h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 2. Una vez tenemos la recta r intersección de a-b, vamos a abatir la recta intersección y el punto A Abatimos el plano a sobre el plano horizontal a partir del punto A. c o t a r0 r´ A´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 8. b´ I´´ r´´ r0 I´ I0 A´´ A0 B0 C0 D0 h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´´ b´´ 3. Sabemos que en la recta intersección r se encuentra la arista de menor cota de la cara del cubo apoyada en a. También sabemos que el punto A es otro vértice de la misma cara. c o t a r´ Como tenemos la r abatida y el punto A también abatido, el siguiente paso es dibujar abatido el cuadrado del cubo que apoya en a, es decir, dibujar el cuadrado en verdadera magnitud. A´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 9. b´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 D0 h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 4. Teniendo la cara ABCD abatida, podemos obtener la PROYECCIÓN HORIZONTAL. c o t a Para otener la arista C´D´, basta con trazar perpendiculares desde C0 y D0 a la charnela a´, hasta cortar en r´. A´ C´ D´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
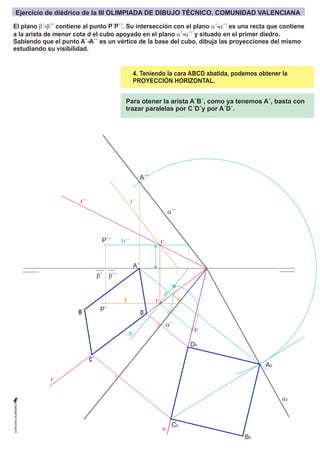
- 10. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 D0 h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 4. Teniendo la cara ABCD abatida, podemos obtener la PROYECCIÓN HORIZONTAL. c o t a Para otener la arista A´B´, como ya tenemos A´, basta con trazar paralelas por C´D´y por A´D´. C´ D´ B´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
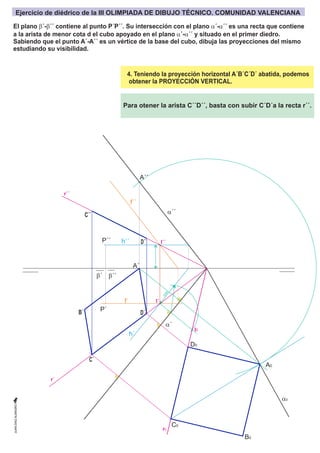
- 11. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 C´ C´´ D0 D´ D´´ B´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 4. Teniendo la proyección horizontal A´B´C´D´ abatida, podemos obtener la PROYECCIÓN VERTICAL. c o t a Para otener la arista C´´D´´, basta con subir C´D´a la recta r´´. El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 12. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 4. Teniendo la proyección horizontal A´B´C´D´ abatida, podemos obtener la PROYECCIÓN VERTICAL. c o t a Para otener el resto de la proyección vertical, lo hacemos por paralelas, como en la proyección horizontal. A´´ B´´ es paralela a C´´ D´´, y A´´ D´´ es paralela a C´´ B´´. El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 13. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 5. Para obtener la cara superior del cubo podemos hacer una perpendicular en cualquiera de los vértices de la cara inferior respecto al plano a, por ejemplo en la A. Dicha perpendicular será una recta oblícua, por tanto no podemos poner la medida de la arista en verdadera magnitud. Para ello, podemos aplicar un GIRO: c o t a Trazamos por A la recta perpendicular s al plano a. s” s´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 14. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 5. Para obtener la cara superior del cubo podemos hacer una perpendicular en cualquiera de los vértices de la cara inferior respecto al plano a, por ejemplo en la A. Dicha perpendicular será una recta oblícua, por tanto no podemos poner la medida de la arista en verdadera magnitud. Para ello, podemos aplicar un GIRO: c o t a Giramos la recta s, que es oblícua, convirtiéndola en frontal, a partir del punto arbitrario x. s” s”1 s” girada a frontal (en verdadera magnitud) x x1 x2 s´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 15. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 5. Para obtener la cara superior del cubo podemos hacer una perpendicular en cualquiera de los vértices de la cara inferior respecto al plano a, por ejemplo en la A. Dicha perpendicular será una recta oblícua, por tanto no podemos poner la medida de la arista en verdadera magnitud. Para ello, podemos aplicar un GIRO: c o t a Colocamos, sobre la proyección vertical girada de s (s”1) la medida en verdadera magnitud del lado del cuadrado s” lado del cuadrado x E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 s´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 16. b´ A´ I´´ r´´ r´ r0 I´ I0 A´´ A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 5. Para obtener la cara superior del cubo podemos hacer una perpendicular en cualquiera de los vértices de la cara inferior respecto al plano a, por ejemplo en la A. Dicha perpendicular será una recta oblícua, por tanto no podemos poner la medida de la arista en verdadera magnitud. Para ello, podemos aplicar un GIRO: c o t a Mediante Thales, llevamos la medida en verdadera magnitud del lado del cuadrado A”-E”1, a la recta s”. Así, tendremos colocada proyección vertical de la arista AE en su sitio. x s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 s´ E” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 17. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 6. Una vez tenemos el punto E”, podemos sacar el resto de aristas de la proyección vertical por paralelas a la arista AE y al resto de aristas de la cara inferior. c o t a x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 s´ E” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 18. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 7. A partir del punto E”, podemos obtener E´sobre s´. c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” E´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 19. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 8. A partir del punto E´, podemos obtener el resto de proyecciones horizontales de los vértices que faltan mediante paralelas, como en la proyección vertical. c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” G” H” F” E´ El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA F” G” H”
- 20. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 8. A partir del punto E´, podemos obtener el resto de proyecciones horizontales de los vértices que faltan mediante paralelas, como en la proyección vertical. c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” E´ F” G” H” E” G” H” F” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 21. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 9. Ahora sólo falta resolver el problema de la VISIBILIDAD. ¿Qué aristas serán continuas y cuales serán discontinuas. c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” E´ E´ F” G” H” E” G” H” F” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA PROYECCIÓN HORIZONTAL: Como la cara ABCD es la que está apoyada en el plano a, la cara EFGH estará encima y será visible, por tanto las aristas A´D´, D´C´y D´F´serán discontinuas.
- 22. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ 9. Ahora sólo falta resolver el problema de la VISIBILIDAD. ¿Qué aristas serán continuas y cuales serán disco c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” E´ PROYECCIÓN VERTICAL: Como la cara ABCD es la que está apoyada en el plano a, la cara EFGH estará encima y será visible, por tanto las aristas A´B´, A´D´y A´E´serán discontinuas. E´ F” G” H” E” G” H” F” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 23. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” E´ E´ F” G” H” E” G” H” F” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA
- 24. b´ A´ I´´ r´´ r´ r0 I´ I0 A0 B0 C0 C´ C´´ D0 D´ D´´ B´ B´´ h´´ f´´ h´ f´ P´´ P´ a´´ a0 a´ b´´ c o t a s´ x A´´ s” lado del cuadrado E”1 s”1 s” girada a frontal (en verdadera magnitud) x1 x2 E” E´ E´ F” G” H” E” G” H” F” El plano b´-b´´ contiene al punto P´P´´. Su intersección con el plano a´-a´´ es una recta que contiene a la arista de menor cota d el cubo apoyado en el plano a´-a´´ y situado en el primer diedro. Sabiendo que el punto A´-A´´ es un vértice de la base del cubo, dibuja las proyecciones del mismo estudiando su visibilidad. Ejercicio de diédrico de la III OLIMPIADA DE DIBUJO TÉCNICO. COMUNIDAD VALENCIANA