![1.2 Métodos pictóricos y tabulares en la estadística descriptiva 23
¿Cuáles son algunas características interesantes de este
histograma? ¿Cuál es un valor de diferencia típico? ¿Apro-
ximadamente qué proporción de los competidores corren la
última distancia más rápido que la primera?
23. En un estudio de ruptura de la urdimbre durante el tejido de
telas (Technometrics, 1982: 63), se sometieron a prueba 100
muestras de hilo. Se determinó el número de ciclos de es-
fuerzo hasta ruptura para cada muestra de hilo y se obtuvie-
ron los datos siguientes:
86 146 251 653 98 249 400 292 131 169
175 176 76 264 15 364 195 262 88 264
157 220 42 321 180 198 38 20 61 121
282 224 149 180 325 250 196 90 229 166
38 337 65 151 341 40 40 135 597 246
211 180 93 315 353 571 124 279 81 186
497 182 423 185 229 400 338 290 398 71
246 185 188 568 55 55 61 244 20 284
393 396 203 829 239 236 286 194 277 143
198 264 105 203 124 137 135 350 193 188
a. Construya un histograma de frecuencia relativa basado
en los intervalos de clase 0-100, 100-200, . . . y co-
mente sobre las características del histograma.
b. Construya un histograma basado en los siguientes inter-
valos de clase: 0-50, 50-100, 100-150, 150-200,
200-300, 300-400, 400-500, 500-600 y 600-900.
c. Si las especificaciones de tejido requieren una resistencia
a la ruptura de por lo menos 100 ciclos, ¿qué proporción
de los especímenes de hilos en esta muestra sería consi-
derada satisfactoria?
24. El conjunto de datos adjuntos consiste en observaciones de
resistencia al esfuerzo cortante (lb) de soldaduras de puntos
ultrasónicas aplicadas en un cierto tipo de lámina alclad.
Construya un histograma de frecuencia relativa basado en
diez clases de ancho igual con límites 4000, 4200, . . . [El
histograma concordará con el que aparece en (“Comparison
of Properties of Joints Prepared by Ultrasonic Welding and
Other Means”, J. of Aircraft, 1983: 552-556).] Comente so-
bre sus características.
5434 4948 4521 4570 4990 5702 5241
5112 5015 4659 4806 4637 5670 4381
4820 5043 4886 4599 5288 5299 4848
5378 5260 5055 5828 5218 4859 4780
5027 5008 4609 4772 5133 5095 4618
4848 5089 5518 5333 5164 5342 5069
4755 4925 5001 4803 4951 5679 5256
5207 5621 4918 5138 4786 4500 5461
5049 4974 4592 4173 5296 4965 5170
4740 5173 4568 5653 5078 4900 4968
5248 5245 4723 5275 5419 5205 4452
5227 5555 5388 5498 4681 5076 4774
4931 4493 5309 5582 4308 4823 4417
5364 5640 5069 5188 5764 5273 5042
5189 4986
25. Una transformación de valores de datos por medio de alguna
función matemática, tal como o 1/x a menudo produce
un conjunto de números que tienen “mejores” propiedades
estadísticas que los datos originales. En particular, puede ser
posible encontrar una función para la cual el histograma de
valores transformados es más simétrico (o, incluso mejor,
más parecido a una curva en forma de campana) que los datos
originales. Por ejemplo, el artículo (“Time Lapse Cinemato-
graphicAnalysis of Beryllium-Lung Fibroblast Interactions”,
Environ. Research, 1983: 34-43) reportó los resultados de ex-
perimentos diseñados para estudiar el comportamiento de
ciertas células individuales que habían estado expuestas a be-
rilio. Una importante característica de dichas células indivi-
duales es su tiempo de interdivisión (IDT, por sus siglas en
inglés). Se determinaron tiempos de interdivisión de un gran
número de células tanto en condiciones expuestas (tratamien-
to) como no expuestas (control). Los autores del artículo uti-
lizaron una transformación logarítmica, es decir, valor
transformado log(valor original). Considere los siguientes
tiempos de interdivisión representativos.
IDT log10(IDT) IDT log10(IDT) IDT log10(IDT)
28.1 1.45 60.1 1.78 21.0 1.32
31.2 1.49 23.7 1.37 22.3 1.35
13.7 1.14 18.6 1.27 15.5 1.19
46.0 1.66 21.4 1.33 36.3 1.56
25.8 1.41 26.6 1.42 19.1 1.28
16.8 1.23 26.2 1.42 38.4 1.58
34.8 1.54 32.0 1.51 72.8 1.86
62.3 1.79 43.5 1.64 48.9 1.69
28.0 1.45 17.4 1.24 21.4 1.33
17.9 1.25 38.8 1.59 20.7 1.32
19.5 1.29 30.6 1.49 57.3 1.76
21.1 1.32 55.6 1.75 40.9 1.61
31.9 1.50 25.5 1.41
28.9 1.46 52.1 1.72
Use los intervalos de clase 10–20, 20–30, . . . para cons-
truir un histograma de los datos originales. Use los intervalos
1.1–1.2, 1.2–1.3, . . . para hacer lo mismo con los datos
transformados. ¿Cuál es el efecto de la transformación?
26. En la actualidad se está utilizando la difracción retrodisper-
sada de electrones en el estudio de fenómenos de fractura.
La siguiente información sobre ángulo de desorientación
(grados) se extrajo del artículo (“Observations on the Face-
ted Initiation Site in the Dwell-Fatigue Tested Ti-6242
Alloy: Crystallographic Orientation and Size Effects”, Me-
tallurgical and Materials Trans., 2006: 1507-1518).
Clase: 0–5 5–10 10–15 15–20
Frec. rel.: 0.177 0.166 0.175 0.136
Clase: 20–30 30–40 40–60 60–90
Frec. rel.: 0.194 0.078 0.044 0.030
a. ¿Es verdad que más de 50% de los ángulos muestreados
son más pequeños que 15°, como se afirma en el artículo?
b. ¿Qué proporción de los ángulos muestreados son por lo
menos de 30°?
c. ¿Aproximadamente qué proporción de los ángulos son
de entre 10° y 25°?
d. Construya un histograma y comente sobre cualquier ca-
racterística interesante.
2x
c1_p001-045.qxd 3/12/08 2:31 AM Page 23](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-41-320.jpg)
![El riesgo de desarrollar deficiencia de hierro es especialmente alto durante el embarazo. El
problema con la detección de tal deficiencia es que algunos métodos para determinar el es-
tado del hierro pueden ser afectados por el estado de gravidez mismo. Considérense las si-
guientes observaciones ordenadas de concentración de receptores de transferrina de una
muestra de mujeres con evidencia de laboratorio de anemia por deficiencia de hierro eviden-
te (“Serum Transferrin Receptor for the Detection of Iron Deficiency in Pregnancy”, Amer.
J. of Clinical Nutrition, 1991: 1077-1081):
7.6 8.3 9.3 9.4 9.4 9.7 10.4 11.5 11.9 15.2 16.2 20.4
Como n 12 es par, el n/2 los valores sexto y séptimo ordenados deben ser promedia-
dos:
Note que si la observación más grande, 20.4, no hubiera aparecido en la muestra, la media-
na muestral resultante de las n 11 observaciones habría sido el valor medio 9.7 [el (n + 1)/2
sexto valor ordenado]. La media muestral es , la cual es
un tanto más grande que la mediana debido a los valores apartados 15.2, 16.2 y 20.4. ■
Los datos del ejemplo 1.13 ilustran una importante propiedad de en contraste con .
La mediana muestral es muy insensible a los valores apartados. Si, por ejemplo, las dos xi
más grandes se incrementan desde 16.2 y 20.4 hasta 26.2 y 30.4, respectivamente, no se
vería afectada. Por lo tanto, en el tratamiento de valores apartados, y no son extremos
opuestos de un espectro.
Debido a que los valores grandes presentes en la muestra del ejemplo 1.13 afectan
a más que , con esos datos. Aunque tanto como ubican el centro de un con-
junto de datos, en general no serán iguales porque se enfocan en aspectos diferentes de la
muestra.
Análogo a como valor medio de la muestra es un valor medio de la población, la
mediana poblacional, denotada por . Como con y , se puede pensar en utilizar la me-
diana muestral para hacer una inferencia sobre . En el ejemplo 1.13, se podría utilizar
10.05 como estimación de la concentración de la mediana en toda la población de
la cual se tomó la muestra. A menudo se utiliza una mediana para describir ingresos o sala-
rios (debido a que no es influida en gran medida por unos pocos salarios grandes). Si el sa-
lario mediano de una muestra de ingenieros fuera 66 416 dólares se podría utilizar
como base para concluir que el salario mediano de todos los ingenieros es de más de 60 000
dólares.
x
|
x
|
m
|
x
|
x
m
|
x
|
x
|
x
x
x
|
x
|
x
x
|
x
x
|
x
x
|
xi/n 5 139.3/12 5 11.61
x 5
x
| 5
9.7 1 10.4
2
5 10.05
1.3 Medidas de ubicación 27
Ejemplo 1.13
DEFINICIÓN La mediana muestral se obtiene ordenando primero las n observaciones de la más
pequeña a la más grande (con cualesquiera valores repetidos incluidos de modo que
cada observación muestral aparezca en la lista ordenada). Entonces,
El valor
medio único
si n es
impar
El promedio
de los dos
valores promedio de
n
2
n-ésimo
y
n
2
1
n-ésimo
valores ordenados
medios si n
es par
x
|
¨
«
«
«
«
©
«
«
«
«
ª
n
2
1
n-ésimo
valor ordenado
c1_p001-045.qxd 3/12/08 2:31 AM Page 27](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-45-320.jpg)
![30 CAPÍTULO 1 Generalidades y estadística descriptiva
dos es igual a la relación entre y y entre y m. En particular, subsecuentemente se utili-
zará x/n para hacer inferencias sobre p. Si, por ejemplo, una muestra de 100 propietarios de
automóviles reveló que 22 tenían su automóvil desde por lo menos 5 años atrás, en tal caso se
podría utilizar 22/100 0.22 como estimación puntual de la proporción de todos los propie-
tarios que tenían su automóvil desde por lo menos 5 años atrás. Se estudiarán las propiedades
de x/n como una estimación de p para ver cómo se puede utilizar x/n para responder otras pre-
guntas inferenciales. Con k categorías (k 2), se pueden utilizar las k proporciones muestra-
les para responder preguntas sobre las proporciones de población p1, . . . , pk.
x
m
|
x
|
EJERCICIOS Sección 1.3 (33-43)
33. El artículo (“The Pedaling Technique of Elite Endurance
Cyclists”, Inst. J. of Sport Biomechanics, 1991: 29-53) re-
portó los datos adjuntos sobre potencia de una sola pierna
sometida a una alta carga de trabajo.
244 191 160 187 180 176 174
205 211 183 211 180 194 200
a. Calcule e interprete la media y la mediana muestral.
b. Suponga que la primera observación hubiera sido 204 en
lugar de 244. ¿Cómo cambiarían la media y la mediana?
c. Calcule una media recortada eliminando las observacio-
nes muestrales más pequeñas y más grandes. ¿Cuál es el
porcentaje de recorte correspondiente?
d. El artículo también reportó valores de potencia de una
sola pierna con carga de trabajo baja. La media muestral
de n 13 observaciones fue x
119.8 (en realidad
119.7692) y la 14a.observación, algo así como un valor ex-
tremo, fue 159. ¿Cuál es el valor de x
de toda la muestra?
34. La exposición a productos microbianos, especialmente en-
dotoxina, puede tener un impacto en la vulnerabilidad a
enfermedades alérgicas. El artículo (“Dust Sampling Methods
for Endotoxin-An Essential, But Underestimated Issue”,
Indoor Air, 2006: 20-27) consideró temas asociados con la
determinación de concentración de endotoxina. Los siguien-
tes datos sobre concentración (EU/mg) en polvo asentado
de una muestra de hogares urbanos y otra de casas campes-
tres fueron amablemente suministrados por los autores del
artículo citado.
U: 6.0 5.0 11.0 33.0 4.0 5.0 80.0 18.0 35.0 17.0 23.0
C: 4.0 14.0 11.0 9.0 9.0 8.0 4.0 20.0 5.0 8.9 21.0
9.2 3.0 2.0 0.3
a. Determine la media muestral de cada muestra. ¿Cómo se
comparan?
b. Determine la mediana muestral de cada muestra. ¿Cómo
se comparan? ¿Por qué es la mediana de la muestra ur-
bana tan diferente de la media de dicha muestra?
c. Calcule la media recortada de cada muestra eliminando
la observación más pequeña y más grande. ¿Cuáles son
los porcentajes de recorte correspondientes? ¿Cómo se
comparan los valores de estas medias recortadas a las
medias y medianas correspondientes?
35. La presión de inyección mínima (lb/pulg2
) de especímenes
moldeados por inyección de fécula de maíz se determinó
con ocho especímenes diferentes (la presión más alta co-
rresponde a una mayor dificultad de procesamiento) y se
obtuvieron las siguientes observaciones (tomadas de “Ther-
moplastic Starch Blends with Polyethylene-Co-Vinyl Alco-
hol: Processability and Physical Properties”, Polymer Engr.
and Science, 1994: 17-23):
15.0 13.0 18.0 14.5 12.0 11.0 8.9 8.0
a. Determine los valores de la media muestral, la mediana
muestral y la media 12.5% recortada y compare estos
valores.
b. ¿En cuánto se podría incrementar la observación de la
muestra más pequeña, actualmente 8.0, sin afectar el va-
lor de la mediana muestral?
c. Suponga que desea los valores de la media y la mediana
muestrales cuando las observaciones están expresadas en
kilogramos por pulgada cuadrada (kg/pulg2
) en lugar de
lb/pulg2
. ¿Es necesario volver a expresar cada observación
en kg/pulg2
o se pueden utilizar los valores calculados en
el inciso a) directamente? [Sugerencia: 1 kg 2.2 lb.]
36. Una muestra de 26 trabajadores de plataforma petrolera ma-
rina tomaron parte en un ejercicio de escape y se obtuvieron
los datos adjuntos de tiempo (s) para completar el escape
(“Oxygen Consumption and Ventilation During Escape from
an Offshore Platform”, Ergonomics, 1997: 281-292):
389 356 359 363 375 424 325 394 402
373 373 370 364 366 364 325 339 393
392 369 374 359 356 403 334 397
a. Construya una gráfica de tallo y hojas de los datos. ¿Có-
mo sugiere la gráfica que la media y mediana muestra-
les se comparen?
b. Calcule los valores de la media y mediana muestrales
[Sugerencia: xi 9638.]
c. ¿En cuánto se podría incrementar el tiempo más largo,
actualmente de 424, sin afectar el valor de la mediana
muestral? ¿En cuánto se podría disminuir este valor sin
afectar el valor de la mediana muestral?
d. ¿Cuáles son los valores de x
y cuando las observacio-
nes se reexpresan en minutos?
37. El artículo (“Snow Cover and Temperature Relationships in
North America and Eurasia”, J. Climate and Applied Me-
teorology, 1983: 460-469) utilizó técnicas estadísticas para
relacionar la cantidad de cobertura de nieve sobre cada
x
|
c1_p001-045.qxd 3/12/08 2:31 AM Page 30](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-48-320.jpg)
![El reporte de una medida de centro da sólo información parcial sobre un conjunto o distri-
bución de datos. Diferentes muestras o poblaciones pueden tener medidas idénticas de cen-
tro y aún diferir entre sí en otras importantes maneras. La figura 1.17 muestra gráficas de
puntos de tres muestras con las mismas media y mediana, aunque el grado de dispersión en
1.4 Medidas de variabilidad 31
continente para promediar la temperatura continental. Los
datos allí presentados incluyeron las siguientes diez obser-
vaciones de la cobertura de nieve en octubre en Eurasia du-
rante los años 1970-1979 (en millones de km2
):
6.5 12.0 14.9 10.0 10.7 7.9 21.9 12.5 14.5 9.2
¿Qué reportaría como valor representativo, o típico de co-
bertura de nieve en octubre durante este periodo y qué mo-
tivaría su elección?
38. Los valores de presión sanguínea a menudo se reportan a
los 5 mmHg más cercanos (100, 105, 110, etc.). Suponga
que los valores de presión sanguínea reales de nueve indivi-
duos seleccionados al azar son
118.6 127.4 138.4 130.0 113.7 122.0 108.3
131.5 133.2
a. ¿Cuál es la mediana de los valores de presión sanguínea
reportados?
b. Suponga que la presión sanguínea del segundo indivi-
duo es 127.6 en lugar de 127.4 (un pequeño cambio en
un solo valor). ¿Cómo afecta esto a la mediana de los va-
lores reportados? ¿Qué dice esto sobre la sensibilidad de
la mediana al redondeo o agrupamiento en los datos?
39. La propagación de grietas provocadas por fatiga en varias
partes de un avión ha sido el tema de extensos estudios en
años recientes. Los datos adjuntos se componen de vidas de
propagación (horas de vuelo/104
) para alcanzar un tamaño
de agrietamiento dado en orificios para sujetadores utiliza-
dos en aviones militares (“Statistical Crack Propagation in
Fastener Holes ander Spectrum Loading”, J. Aircraft, 1983:
1028-1032):
0.736 0.863 0.865 0.913 0.915 0.937 0.983 1.007
1.011 1.064 1.109 1.132 1.140 1.153 1.253 1.394
a. Calcule y compare los valores de la media y mediana
muestrales.
b. ¿En cuánto se podría disminuir la observación muestral
más grande sin afectar el valor de la mediana?
40. Calcule la mediana muestral, media 25% recortada, media
10% recortada y media muestral de los datos de duración
dados en el ejercicio 27 y compare estas medidas.
41. Se eligió una muestra de n 10 automóviles y cada uno se
sometió a una prueba de choque a 5 mph. Denotando un ca-
rro sin daños visibles por S (por éxito) y un carro con daños
por F, los resultados fueron los siguientes:
S S F S S S F F S S
a. ¿Cuál es el valor de la proporción muestral de éxitos
x/n?
b. Reemplace cada S con 1 y cada F con 0. Acto seguido
calcule x
de esta muestra numéricamente codificada.
¿Cómo se compara x
con x/n?
c. Suponga que se decide incluir 15 carros más en el expe-
rimento. ¿Cuántos de éstos tendrían que ser S para dar
x/n 0.80 para toda la muestra de 25 carros?
42. a. Si se agrega una constante c a cada xi en una muestra y
se obtiene yi xi c, ¿cómo se relacionan la media
y mediana muestrales de las yi con la media y mediana
muestrales de las xi? Verifique sus conjeturas.
b. Si cada xi se multiplica por una constante c y se obtiene
yi cxi, responda la pregunta del inciso a). De nuevo,
verifique sus conjeturas.
43. Un experimento para estudiar la duración (en horas) de
un cierto tipo de componente implicaba poner diez
componentes en operación y observarlos durante 100 ho-
ras. Ocho de ellos fallaron durante dicho periodo y se re-
gistraron las duraciones. Denote las duraciones de dos
componentes que continuaron funcionando después
de 100 horas por 100. Las observaciones muestrales re-
sultantes fueron:
48 79 100 35 92 86 57 100 17 29
¿Cuáles de las medidas del centro discutidas en esta sección
pueden ser calculadas y cuáles son los valores de dichas
medidas? [Nota: Se dice que los datos obtenidos con este
experimento están “censurados a la derecha”.]
1.4 Medidas de variabilidad
Figura 1.17 Muestras con medidas idénticas de centro pero diferentes cantidades de variabilidad.
30 40
* * * * * * * * *
50 60 70
1:
2:
3:
c1_p001-045.qxd 3/12/08 2:31 AM Page 31](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-49-320.jpg)
![programa de computadora S-Plus. La caja sin cáncer aparece alargada en comparación con
la caja con cáncer (fs 18 vs. fs 11) y las posiciones de las líneas medianas en las dos ca-
jas muestran más asimetría en la mitad media de la muestra sin cáncer que la muestra con
cáncer. Los valores apartados están representados por segmentos de línea horizontales y no
hay distinción entre los valores apartados moderados y extremos. ■
1.4 Medidas de variabilidad 39
EJERCICIOS Sección 1.4 (44-61)
44. El artículo (“Oxygen Consumption During Fire Suppres-
sion: Error of Heart Rate Estimation”, Ergonomics, 1991:
1469-1474) reportó los siguientes datos sobre consumo de
oxígeno (ml/kg/min) para una muestra de diez bomberos
que realizaron un simulacro de supresión de incendio.
29.5 49.3 30.6 28.2 28.0 26.3 33.9 29.4 23.5 31.6
Calcule lo siguiente:
a. El rango muestral.
b. La varianza muestral s2
a partir de la definición (es de-
cir, calculando primero las desviaciones y luego eleván-
dolas al cuadrado, etcétera).
c. La desviación estándar muestral.
d. s2
utilizando el método más corto.
45. Se determinó el valor del módulo deYoung (GPa) de placas
fundidas compuestas de ciertos sustratos intermetálicos y se
obtuvieron las siguientes observaciones muestrales
(“Strength and Modulus of a Molybdenum-Coated Ti-
25A1-10Nb-3U-1Mo Intermetallic”, J. of Materials Engr.
and Performance, 1997: 46-50):
116.4 115.9 114.6 115.2 115.8
a. Calcule x
y las desviaciones de la media.
b. Use las desviaciones calculadas en el inciso a) para
obtener la varianza muestral y la desviación estándar
muestral.
c. Calcule s2
utilizando la fórmula para el numerador Sxx.
d. Reste 100 de cada observación para obtener una mues-
tra de valores transformados. Ahora calcule la varianza
muestral de estos valores transformados y compárela
con s2
de los datos originales.
46. Las observaciones adjuntas de viscosidad estabilizada (cP)
realizadas en probetas de un cierto grado de asfalto con
18% de caucho agregado se tomaron del artículo (“Visco-
sity Characteristics of Rubber-Modified Asphalts”, J. of
Materials in Civil Engr. 1996: 153-156):
2781 2900 3013 2856 2888
a. ¿Cuáles son los valores de la media y mediana mues-
trales?
b. Calcule la varianza muestral por medio de la fórmula de
cálculo. [Sugerencia: Primero reste un número conve-
niente de cada observación.]
47. Calcule e interprete los valores de la mediana muestral, la
media muestral y la desviación estándar muestral de las si-
guientes observaciones de resistencia a la fractura (MPa,
leídas en una gráfica que aparece en el artículo (“Heat-Re-
sistant Active Brazing of Silicon Nitride: Mechanical Eva-
luation of Braze Joints”, Welding J., agosto de 1997):
87 93 96 98 105 114 128 131 142 168
48. El ejercicio 34 presentó los siguientes datos sobre concentra-
ción de endotoxina en polvo asentado, obtenidos con una
muestra de casas urbanas y una muestra de casas campestres:
U: 6.0 5.0 11.0 33.0 4.0 5.0 80.0 18.0 35.0 17.0 23.0
C: 4.0 14.0 11.0 9.0 9.0 8.0 4.0 20.0 5.0 8.9 21.0
9.2 3.0 2.0 0.3
a. Determine el valor de la desviación estándar muestral de
cada muestra, interprete estos valores y luego contraste
la variabilidad en las dos muestras. [Sugerencia: xi
237.0 para la muestra urbana y 128.4 para la muestra
campestre y x2
i 10 079 para la muestra urbana y
1617.94 para la muestra campestre.]
b. Calcule la dispersión de los cuartos de cada muestra y
compare. ¿Transmiten el mismo mensaje las dispersio-
nes de los cuartos sobre la variabilidad que las desvia-
ciones estándar? Explique.
c. Los autores del artículo citado también proporcionan
concentraciones de endotoxina en el polvo presente en
bolsas captadoras de polvo:
U: 34.0 49.0 13.0 33.0 24.0 24.0 35.0 104.0 34.0 40.0 38.0 1.0
C: 2.0 64.0 6.0 17.0 35.0 11.0 17.0 13.0 5.0 27.0 23.0
28.0 10.0 13.0 0.2
Construya una gráfica de caja comparativa (como se hizo en
el artículo citado) y compare y contraste las cuatro muestras.
49. Un estudio de la relación entre edad y varias funciones vi-
suales (tales como agudeza y percepción de profundidad)
reportó las siguientes observaciones de área de la lámina es-
clerótica (mm2
) de las cabezas del nervio óptico humano
(“Morphometry of Nerve Fiber Bundle Pores in the Optic
Nerve Head of the Human”, Experimental Eye Research,
1988: 559-568):
2.75 2.62 2.74 3.85 2.34 2.74 3.93 4.21 3.88
4.33 3.46 4.52 2.43 3.65 2.78 3.56 3.01
a. Calcule xi y x2
i .
b. Use los valores calculados en el inciso a) para calcular la
varianza muestral s2
y luego la desviación estándar mues-
tral s.
50. En 1997, una mujer demandó a un fabricante de teclados de
computadora y lo acusó de que sus repetitivas lesiones por
esfuerzo eran provocadas por el teclado (Genessy . Digital
c1_p001-045.qxd 3/12/08 2:31 AM Page 39](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-57-320.jpg)
![Ejercicios suplementarios 43
68. a. ¿Con qué valor de c es mínima la cantidad (xi c)2
?
[Sugerencia: Tome la derivada con respecto a c, iguale a
0 y resuelva.]
b. Utilizando el resultado del inciso a), ¿cuál de las dos
cantidades (xi x
)2
y (xi )2
será más pequeña
que la otra (suponiendo que x
)?
69. a. Sean a y b constantes y sea yi axi b con i 1, 2, . . . ,
n. ¿Cuáles son las relaciones entre x
y y
y entre y ?
b. Una muestra de temperaturas para iniciar una cierta
reacción química dio un promedio muestral (°C) de 87.3
y una desviación estándar muestral de 1.04. ¿Cuáles son
el promedio muestral y la desviación estándar medidos
en °F? [Sugerencia: F
9
5 C 32.]
70. El elevado consumo de energía durante el ejercicio continúa
después de que termina la sesión de entrenamiento. Debido
a que las calorías quemadas por ejercicio contribuyen a la
pérdida de peso y tienen otras consecuencias, es importante
entender el proceso. El artículo (“Effect of Weight Training
Exercise and Treadmill Exercise on Post-Exercise Oxygen
Consumption”, Medicine and Science in Sports and Exerci-
se, 1998: 518-522) reportó los datos adjuntos tomados de un
estudio en el cual se midió el consumo de oxígeno (litros) de
forma continua durante 30 minutos de cada uno de 15 suje-
tos tanto después de un entrenamiento con pesas como des-
pués de una sesión de ejercicio en una caminadora.
Sujeto 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15
Peso (x) 14.6 14.4 19.5 24.3 16.3 22.1
23.0 18.7 19.0 17.0 19.1 19.6
23.2 18.5 15.9
Caminadora (y) 11.3 5.3 9.1 15.2 10.1 19.6
20.8 10.3 10.3 2.6 16.6 22.4
23.6 12.6 4.4
a. Construya una gráfica de caja comparativa de las obser-
vaciones del ejercicio con pesas y la caminadora y co-
mente sobre lo que ve.
b. Debido a que estos datos aparecen en pares (x, y), con
mediciones de x y y de la misma variable en dos condi-
ciones distintas, es natural enfocarse en las diferencias
que existen en ellos: d1 x1 – y1, . . . , dn xn – yn.
Construya una gráfica de caja de las diferencias mues-
trales. ¿Qué sugiere la gráfica?
71. La siguiente es una descripción dada por MINITAB de los
datos de resistencia dados en el ejercicio 13.
Med. Desv. Media
Resistencia N Media Mediana rec. est. SE
variable 153 135.39 135.40 135.41 4.59 0.37
Resistencia Mínima Máxima Q1 Q3
variable 122.20 147.70 132.95 138.25
a. Comente sobre cualesquiera características interesantes
(los cuartiles y los cuartos son virtualmente idénticos en
este caso).
b. Construya una gráfica de caja de los datos basada en los
cuartiles y comente sobre lo que ve.
72. Los desórdenes y síntomas de ansiedad con frecuencia pue-
den ser tratados exitosamente con benzodiazepina. Se sabe
que los animales expuestos a estrés exhiben una disminu-
ción de la ligadura de receptor de benzodiazepina en la cor-
teza frontal. El artículo (“Decreased Benzodiazepine
Receptor Binding in Prefrontal Cortex in Combat-Related
Posttraumatic Stress Disorder”, Amer. J. of Psychiatry.
2000: 1120-1126) describió el primer estudio de ligadura
de receptor de benzodiazepina en individuos que sufren de
PTSD. Los datos anexos sobre una medición de ligadura a
receptor (volumen de distribución ajustado) se leyeron en
una gráfica que aparece en el artículo.
PTSD: 10, 20, 25, 28, 31, 35, 37, 38, 38, 39, 39,
42, 46
Saludables: 23, 39, 40, 41, 43, 47, 51, 58, 63, 66, 67,
69, 72
Use varios métodos de este capítulo para describir y resu-
mir los datos.
73. El artículo (“Can We Really Walk Straight?, Amer. J. of
Physical Anthropology, 1992: 19-27) reportó sobre un ex-
perimento en el cual a cada uno de 20 hombres saludables
se les pidió que caminarán en línea recta como fuera posi-
ble hacia un punto a 60 m de distancia a velocidad normal.
Considérense las siguientes observaciones de cadencia (nú-
mero de pasos por segundo):
0.95 0.85 0.92 .95 0.93 0.86 1.00 0.92 0.85 0.81
0.78 0.93 0.93 1.05 0.93 1.06 1.06 0.96 0.81 0.96
Use los métodos desarrollados en este capítulo para resumir
los datos; incluya una interpretación o discusión en los ca-
sos en que sea apropiado. [Nota: El autor del artículo utili-
zó un análisis estadístico un tanto complejo para concluir
que las personas no pueden caminar en línea recta y sugirió
varias explicaciones para esto.]
74. La moda de un conjunto de datos numéricos es el valor que
ocurre con más frecuencia en el conjunto.
a. Determine la moda de los datos de cadencia dados en el
ejercicio 73.
b. Para una muestra categórica, ¿cómo definiría la catego-
ría modal?
75. Se seleccionaron especímenes de tres tipos diferentes de ca-
ble y se determinó el límite de fatiga (Mpa) de cada espéci-
men y se obtuvieron los datos adjuntos.
Tipo 1 350 350 350 358 370 370 370 371
371 372 372 384 391 391 392
Tipo 2 350 354 359 363 365 368 369 371
373 374 376 380 383 388 392
Tipo 3 350 361 362 364 364 365 366 371
377 377 377 379 380 380 392
a. Construya una gráfica de caja comparativa y comente
sobre las similitudes y diferencias.
b. Construya un diagrama de caja comparativo (una gráfi-
ca de puntos de cada muestra con una escala común).
Comente sobre las similitudes y diferencias.
c. ¿Da la gráfica de caja comparativa del inciso a) una eva-
luación informativa de similitudes y diferencias? Expli-
que su razonamiento.
sy
2
sx
2
c1_p001-045.qxd 3/12/08 2:31 AM Page 43](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-61-320.jpg)
![44 CAPÍTULO 1 Generalidades y estadística descriptiva
76. Las tres medidas de centro introducidas en este capítulo son
las media, la mediana y la media recortada. Dos medidas de
centro adicionales que de vez en cuando se utilizan son el
rango medio, el cual es el promedio de las observaciones
más pequeñas y más grandes y el cuarto medio, el cual es el
promedio de los dos cuartos. ¿Cuál de estas medidas de
centro son resistentes a los efectos de los valores apartados
y cuáles no? Explique su razonamiento.
77. Considere los siguientes datos sobre el tiempo de repara-
ción activo (horas) de una muestra de n 46 receptores de
comunicaciones aerotransportados:
0.2 0.3 0.5 0.5 0.5 0.6 0.6 0.7 0.7 0.7 0.8 0.8
0.8 1.0 1.0 1.0 1.0 1.1 1.3 1.5 1.5 1.5 1.5 2.0
2.0 2.2 2.5 2.7 3.0 3.0 3.3 3.3 4.0 4.0 4.5 4.7
5.0 5.4 5.4 7.0 7.5 8.8 9.0 10.3 22.0 24.5
Construya lo siguiente:
a. Una gráfica de tallo y hojas en la cual los dos valores
más grandes se muestran por separado en la fila HI.
b. Un histograma basado en seis intervalos de clase con 0
como el límite inferior del primer intervalo y anchos de
intervalo de 2, 2, 2, 4, 10 y 10, respectivamente.
78. Considere una muestra x1, x2, . . . , xn y suponga que los va-
lores de , s2
y s han sido calculados.
a. Sea yi xi con i 1, . . . , n. ¿Cómo se comparan
los valores de s2
y s de las yi con los valores correspon-
dientes de las xi? Explique.
b. Sea zi (xi )/s con i 1, . . . , n. ¿Cuáles son los va-
lores de la varianza muestral y la desviación estándar
muestral de las zi?
79. Si y denotan la media y la varianza de la muestra
x1, . . . , xn y si y denotan estas cantidades cuando
se agrega una observación adicional xn1 a la muestra.
a. Demuestre cómo se puede calcular con y .
b. Demuestre que
de modo que pueda ser calculada con xn1, , y .
c. Suponga que una muestra de 15 torzales de hilo para te-
las dio por resultado un alargamiento del hilo mediano
muestral de 12.58 mm y una desviación estándar mues-
tral de 0.512 mm. ¿Cuáles son los valores de la media
muestral y la desviación estándar muestral de las 16 ob-
servaciones de alargamiento?
80. Las distancias de recorrido de rutas de autobuses de cual-
quier sistema de tránsito particular por lo general varían de
una ruta a otra. El artículo (“Planning of City Bus Routes”,
J. of the Institution of Engineers, 1995: 211-215) da la si-
guiente información sobre las distancias (km) de un sistema
particular.
Distancia 6–8 8–10 10–12 12–14 14–16
Frecuencia 6 23 30 35 32
Distancia 16–18 18–20 20–22 22–24 24–26
Frecuencia 48 42 40 28 27
Distancia 26–28 28–30 30–35 35–40 40–45
Frecuencia 26 14 27 11 2
a. Trace un histograma correspondiente a estas frecuencias.
b. ¿Qué proporción de estas distancias de ruta son menores
que 20? ¿Qué proporción de estas rutas tienen distancias
de recorrido de por lo menos 30?
c. ¿Aproximadamente cuál es el valor de 90o
percentil de
la distribución de distancia de recorrido de las rutas?
d. ¿Aproximadamente cuál es la distancia de recorrido de
ruta mediana?
81. Un estudio realizado para investigar la distribución de tiem-
po de frenado total (tiempo de reacción más tiempo de mo-
vimiento de acelerador a freno, en ms) durante condiciones
de manejo reales a 60 km/h da la siguiente información
sobre la distribución de los tiempos (“A Field Study on
Braking Response during Driving”, Ergonomics, 1995:
1903-1910):
media 535 mediana 500 moda 500
Desv. estd. 96 mínima 220 máxima 925
5o
percentil 400 10o
percentil 430
90o
percentil 640 95o
percentil 720
¿Qué puede concluir sobre la forma de un histograma de es-
tos datos? Explique su razonamiento.
82. Los datos muestrales x1, x2, . . . , xn en ocasiones represen-
tan una serie de tiempo, donde xt el valor observado de
una variable de respuesta x en el tiempo t. A menudo la se-
rie observada muestra una gran cantidad de variación alea-
toria, lo que dificulta estudiar el comportamiento a largo
plazo. En tales situaciones, es deseable producir una ver-
sión alisada de la serie. Una técnica para hacerlo implica el
alisamiento o atenuación exponencial. Se elige el valor de
una constante de alisamiento (0 1). Luego con
valor alisado o atenuado en el tiempo t se hace con
t 2, 3, . . . , n, .
a. Considere la siguiente serie de tiempo en la cual xt
temperatura (°F) del efluente en una planta de tratamien-
to de aguas negras en el día t: 47, 54, 53, 50, 46, 46, 47,
50, 51, 50, 46, 52, 50, 50. Trace cada xt contra t en un
sistema de coordenadas de dos dimensiones (una gráfi-
ca de tiempo-serie). ¿Parece haber algún patrón?
b. Calcule las con 0.1. Repita con 0.5. ¿Qué
valor de da una serie más atenuada?
c. Sustituya en el miembro de
la derecha de la expresión para , acto seguido sustituya
en función de xt2, y , y así sucesivamente. ¿De
cuántos de los valores x1, xt1, . . . , x1 depende ? ¿Qué
le sucede al coeficiente de xtk conforme k se incrementa?
d. Remítase al inciso c). Si t es grande, ¿qué tan sensible es
a la inicialización ? Explique.
[Nota: Una referencia pertinente es el artículo “Simple Sta-
tistics for Interpreting Environmental Data”, Water Pollu-
tion Control Fed. J., 1981: 167-175.]
83. Considere las observaciones numéricas x1, . . . , xn. Con fre-
cuencia interesa saber si las xi están (por lo menos en forma
aproximada) simétricamente distribuidas en torno al mismo
valor. Si n es por lo menos grande de manera moderada, el
grado de simetría puede ser valorado con una gráfica de ta-
llo y hojas o un histograma. Sin embargo, si n no es muy
grande, las gráficas mencionadas no son informativas en
x1 5 x1
xt
xt
xt23
xt22
xt
xt21 5 axt21 1 s1 2 adxt22
xt
xt
xt 5 axt 1 s1 2 adxt21
x1 5 x1
xt
s2
n
xn
s2
n11
ns2
n11 5 sn 2 1ds2
n 1
n
n 1 1
sxn11 2 xnd2
xn11
xn
xn11
s2
n11
xn11
s2
n
xn
x
x
x
c1_p001-045.qxd 3/12/08 2:31 AM Page 44](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-62-320.jpg)
![Las operaciones de unión e intersección pueden ser ampliadas a más de dos eventos. Para
tres eventos cualesquiera A, B y C, el evento A B C es el conjunto de resultados contenidos
en por lo menos uno de los tres eventos, mientras que A B C es el conjunto de resulta-
dos contenidos en los tres eventos. Se dice que los eventos dados A1, A2, A3, . . . , son mutuamen-
te excluyentes (disjuntos por pares) si ninguno de dos eventos tienen resultados en común.
Con diagramas de Venn se obtiene una representación pictórica de eventos y manipula-
ciones con eventos. Para construir un diagrama de Venn, se traza un rectángulo cuyo interior
representará el espacio muestral S. En tal caso cualquier evento A se representa como el inte-
rior de una curva cerrada (a menudo un círculo) contenido en S. La figura 2.1 muestra ejem-
plos de diagramas de Venn.
50 CAPÍTULO 2 Probabilidad
Figura 2.1 Diagramas de Venn.
A B
a) Diagrama de Venn
de los eventos A y B
A B
e) Eventos mutuamente
excluyentes
A B
c) La región sombreada
es A B
A
d) La región sombreada
es A'
A B
b) La región sombreada
es A B
1. Cuatro universidades, 1, 2, 3 y 4, están participando en un
torneo de básquetbol. En la primera ronda, 1 jugará con 2 y
3 jugará con 4. Acto seguido los ganadores jugarán por el
campeonato y los dos perdedores también jugarán. Un po-
sible resultado puede ser denotado por 1324 (1 derrota a 2
y 3 derrota a 4 en los juegos de la primera ronda y luego 1
derrota a 3 y 2 derrota a 4).
a. Enumere todos los resultados en S.
b. Que A denote el evento en que 1 gana el torneo. Enume-
re los resultados en A.
c. Que B denote el evento en que 2 gana el juego de cam-
peonato. Enumere los resultados en B.
d. ¿Cuáles son los resultados en A B y en A B? ¿Cuá-
les son los resultados en A?
2. Suponga que un vehículo que toma una salida particular de
una autopista puede virar a la derecha (R), virar a la izquier-
da (L) o continuar de frente (S). Observe la dirección de cada
uno de tres vehículos sucesivos.
a. Elabore una lista de todos los resultados en el evento A
en que los tres vehículos van en la misma dirección.
b. Elabore una lista de todos los resultados en el evento B
en que los tres vehículos toman direcciones diferentes.
c. Elabore una lista de todos los resultados en el evento C
en que exactamente dos de los tres vehículos dan vuelta
a la derecha.
d. Elabore una lista de todos los resultados en el evento D
en que dos vehículos van en la misma dirección.
e. Enumere los resultados en D, C D y C D.
3. Tres componentes están conectados para formar un sistema
como se muestra en el diagrama adjunto. Como los compo-
nentes del subsistema 2-3 están conectados en paralelo, di-
cho subsistema funcionará si por lo menos uno de los dos
componentes individuales funciona. Para que todo el siste-
ma funcione, el componente 1 debe funcionar y por lo tan-
to el subsistema 2-3 debe hacerlo.
El experimento consiste en determinar la condición de cada
componente [E (éxito) para un componente que funciona y
F (falla) para un componente que no funciona].
a. ¿Qué resultados están contenidos en el evento A en que
exactamente dos de los tres componentes funcionan?
b. ¿Qué resultados están contenidos en el evento B en
que por lo menos dos de los componentes funcionan?
c. ¿Qué resultados están contenidos en el evento C en que
el sistema funciona?
d. Ponga en lista los resultados en C, A C, A C, B
C y B C.
4. Cada muestra de cuatro hipotecas residenciales está clasi-
ficada como tasa fija (F ) o tasa variable (V ).
a. ¿Cuáles son los 16 resultados en S?
b. ¿Qué resultados están en el evento en que exactamente
tres de las hipotecas seleccionadas son de tasa fija?
c. ¿Qué resultados están en el evento en que las cuatro hi-
potecas son del mismo tipo?
d. ¿Qué resultados están en el evento en que a lo sumo una
de las cuatro es una hipoteca de tasa variable?
e. ¿Cuál es la unión de eventos en los incisos c) y d) y cuál
es la intersección de estos dos eventos?
f. ¿Cuáles son la unión e intersección de los dos eventos en
los incisos b) y c)?
5. Una familia compuesta de tres personas, A, B y C, pertene-
ce a una clínica médica que siempre tiene disponible un
doctor en cada una de las estaciones 1, 2 y 3. Durante cier-
ta semana, cada miembro de la familia visita la clínica una
vez y es asignado al azar a una estación. El experimento
consiste en registrar la estación para cada miembro. Un
EJERCICIOS Sección 2.1 (1-10)
2
1
3
c2_p046-085.qxd 3/12/08 3:58 AM Page 50](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-68-320.jpg)
![probabilidad de que ocurra A deberá ser no negativa. El espacio muestral es por definición el
evento que debe ocurrir cuando se realiza el experimento (S contiene todos los posibles re-
sultados), así se dice el axioma 2 que es la máxima probabilidad posible de 1 está asignada
a S. El tercer axioma formaliza la idea que si se desea la probabilidad de que ocurra al me-
nos uno de varios eventos, y no ocurran dos al mismo tiempo, entonces la probabilidad de
que por lo menos uno ocurra es la suma de las probabilidades de los eventos individuales.
Comprobación Primero considérese el conjunto infinito
Como , los eventos en este conjunto son disjuntos y Ai . El tercer axioma
da entonces
Esto puede suceder sólo si P() 0.
Ahora supóngase que A1, A2, . . . , Ak son eventos disjuntos y anéxense a éstos el con-
junto finito De nuevo si se invoca el tercer axioma.
como se deseaba. ■
Considere lanzar una tachuela al aire. Cuando se detiene en el suelo, o su punta estará ha-
cia arriba (el resultado U) o hacia abajo (el resultado D). El espacio muestral de este even-
to es por consiguiente S {U, D}. Los axiomas especifican P(S) 1, por lo que la
asignación de probabilidad se completará determinando P(U) y P(D). Como U y D están
desarticulados y su unión S, la siguiente proposición implica que
1 P(S ) P(U) P(D)
Se desprende que P(D) 1 P(U). Una posible asignación de probabilidades es P(U)
0.5, P(D) 0.5, mientras que otra posible asignación es P(U ) 0.75, P(D) 0.25. De
hecho, si p representa cualquier número fijo entre 0 y 1, P(U) p, P(D) 1 p es una
asignación compatible con los axiomas. ■
Regresemos al experimento del ejemplo 2.4, en el cual se prueban las baterías que salen de la
línea de ensamble una por una hasta que se encuentra una con el voltaje dentro de los límites
prescritos. Los eventos simples son E1 {E}, E2 {FE}, E3 {FFE}, E4 {FFFE}, . . . .
Suponga que la probabilidad de que cualquier batería resulte satisfactoria es de 0.99. Entonces
se puede demostrar que P(E1) 0.99, P(E2) (0.01)(0.99), P(E3) (0.01)2
(0.99), . . . es una
asignación de probabilidades a los eventos simples que satisface los axiomas. En particular, co-
mo los Ei son disjuntos y S E1 E2 E3 . . . , debe ser el caso de que
1 P(S ) P(E1) P(E2) P(E3) . . .
0.99[1 0.01 (0.01)2
(0.01)3
. . .]
Aquí se utilizó la fórmula para la suma de una serie geométrica:
a 1 ar 1 ar2
1 ar3
1 c 5
a
1 2 r
Pa ´
k
i51
Aib 5 Pa ´
`
i51
Aib 5 g
`
i51
PsAid 5 g
k
i51
PsAid
Ak11 5 [, Ak12 5 [, Ak13 5 [, . . . .
Ps[d 5 g Ps[d
A1 5 [, A2 5 [, A3 5 [, . . . .
52 CAPÍTULO 2 Probabilidad
PROPOSICIÓN P() 0 donde es el evento nulo (el evento que no contiene resultados en abso-
luto). Esto a su vez implica que la propiedad contenida en el axioma 3 es válida para
un conjunto finito de eventos.
Ejemplo 2.11
Ejemplo 2.12
c2_p046-085.qxd 3/12/08 3:58 AM Page 52](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-70-320.jpg)
![complemento “menos que . . .” (en algunos problemas es más fácil trabajar con “más
que. . .” que con “cuando . . .”). Cuando se tenga dificultad al calcular P(A) directamente,
habrá que pensar en determinar P(A).
Esto se debe a que 1 P(A) P(A) P(A) puesto que P(A) 0.
Cuando los eventos A y B son mutuamente excluyentes, P(A B) P(A) P(B).
Para eventos que no son mutuamente excluyentes, la adición de P(A ) y P(B) da por resul-
tado un “doble conteo” de los resultados en la intersección. El siguiente resultado muestra
cómo corregir esto.
Comprobación Obsérvese primero que A B puede ser descompuesto en dos eventos
excluyentes, A y B A; la última es la parte B que queda afuera de A. Además, B por sí
mismo es la unión de los dos eventos excluyentes A B y A B, por lo tanto P(B)
P(A B) + P(A B). Por lo tanto
P(A B) P(A) P(B A) P(A) [P(B) P(A B)]
P(A) P(B) P(A B)
En cierto suburbio residencial, 60% de las familias se suscriben al periódico en una ciudad
cercana, 80% lo hacen al periódico local y 50% de todas las familias a ambos periódicos. Si
se elige una familia al azar, ¿cuál es la probabilidad de que se suscriba a (1) por lo menos a
uno de los dos periódicos y (2) exactamente a uno de los dos periódicos?
Con A {se suscribe al periódico metropolitano} y B {se suscribe al periódico lo-
cal}, la información dada implica que P(A) 0.6, P(B) 0.8 y P(A B) 0.5. La pro-
posición precedente ahora lleva a
P(se suscribe a por lo menos uno de los dos periódicos)
P(A B) P(A) P(B) P(A B) 0.6 0.8 0.5 0.9
El evento en que una familia se suscribe a sólo el periódico local se escribe como A B
[(no metropolitano) y local]. Ahora la figura 2.4 implica que
0.9 P(A B) P(A) P(A B) 0.6 P(A B)
a partir de la cual P(A B) 0.3. Asimismo P(A B) P(A B) P(B) 0.1. Todo
esto se ilustra en la figura 2.5, donde se ve que
P(exactamente uno) P(A B) P(A B) 0.1 0.3 0.4
2.2 Axiomas, interpretaciones y propiedades de probabilidad 55
PROPOSICIÓN Para cualquier evento A, P(A) 1.
PROPOSICIÓN Para dos eventos cualesquiera A y B.
P(A B) P(A) P(B) P(A B)
Ejemplo 2.14
Figura 2.4 Representación de A B como una unión de eventos excluyentes. ■
A B
c2_p046-085.qxd 3/12/08 3:58 AM Page 55](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-73-320.jpg)
![Resultados igualmente probables
En muchos experimentos compuestos de N resultados, es razonable asignar probabilidades
iguales a los N eventos simples. Éstos incluyen ejemplos tan obvios como lanzar al aire una
moneda o un dado imparciales una o dos veces (o cualquier número fijo de veces) o selec-
cionar una o varias cartas de un mazo bien barajado de 52 cartas. Con p P(Ei) por cada i,
1
N
i1
P(Ei)
N
i1
p p N por lo tanto p
Es decir, si existen N resultados igualmente probables, la probabilidad de cada uno es 1/N.
Ahora considérese un evento A, con N(A) como el número de resultados contenidos
en A. Entonces
P(A)
Ei en A
P(Ei)
Ei en A
Por lo tanto, cuando los resultados son igualmente probables, el cálculo de probabili-
dades se reduce a contar: determinar tanto el número de resultados N(A) en A como el nú-
mero de resultados N en S y formar su relación.
Cuando dos dados se lanzan por separado, existen N 36 resultados (elimine la primera
fila y la primera columna de la tabla del ejemplo 2.3). Si ambos dados son imparciales, los
36 resultados son igualmente probables, por lo tanto P(Ei) 3
1
6. Entonces el evento A
{suma de dos números 7} consta de seis resultados (1, 6), (2, 5), (3, 4), (4, 3), (5, 2) y
(6, 1), por lo tanto
P(A) ■
1
6
6
36
N(A)
N
N(A)
N
1
N
1
N
2.2 Axiomas, interpretaciones y propiedades de probabilidad 57
Ejemplo 2.16
11. Una compañía de fondos de inversión mutua ofrece a sus
clientes varios fondos diferentes: un fondo de mercado de
dinero, tres fondos de bonos (a corto, intermedio y a largo
plazos), dos fondos de acciones (de moderado y alto riesgo)
y un fondo balanceado. Entre los clientes que poseen accio-
nes en un solo fondo, los porcentajes de clientes en los di-
ferentes fondos son como sigue:
Mercado de dinero 20% Acciones de alto riesgo 18%
Bonos a corto plazo 15% Acciones de riesgo
Bonos a plazo moderado 25%
intermedio 10% Balanceadas 7%
Bonos a largo plazo 5%
Se selecciona al azar un cliente que posee acciones en sólo
un fondo.
a. ¿Cuál es la probabilidad de que el individuo selecciona-
do posea acciones en el fondo balanceado?
b. ¿Cuál es la probabilidad de que el individuo posea ac-
ciones en un fondo de bonos?
c. ¿Cuál es la probabilidad de que el individuo selecciona-
do no posea acciones en un fondo de acciones?
12. Considere seleccionar al azar un estudiante en cierta univer-
sidad y que A denote el evento en que el individuo seleccio-
nado tenga una tarjeta de crédito Visa y que B sea el evento
análogo para la tarjeta MasterCard. Suponga que P(A)
0.5, P(B) 0.4 y P(A B) 0.25.
a. Calcule la probabilidad de que el individuo seleccionado
tenga por lo menos uno de los dos tipos de tarjetas (es de-
cir, la probabilidad del evento A B).
b. ¿Cuál es la probabilidad de que el individuo seleccionado
no tenga ningún tipo de tarjeta?
c. Describa, en función de A y B, el evento de que el estudian-
te seleccionado tenga una tarjeta Visa pero no una Master-
Card y luego calcule la probabilidad de este evento.
13. Una firma consultora de computación presentó propuestas en
tres proyectos. Sea Ai {proyecto otorgado i}, con i 1, 2,
3 y suponga que P(A1) 0.22, P(A2) 0.25, P(A3) 0.28,
P(A1 A2) 0.11, P(A1 A3) 0.05, P(A2 A3) 0.07,
P(A1 A2 A3) 0.01. Exprese en palabras cada uno de
los siguientes eventos y calcule la probabilidad de cada uno:
a. A1 A2
b. A
1 A
2 [ Sugerencia: (A1 A2) A
1 A
2]
c. A1 A2 A3 d. A
1 A
2 A
3
e. A
1 A
2 A3 f. (A
1 A
2) A3
14. Una compañía de electricidad ofrece una tarifa de consumo
mínimo a cualquier usuario cuyo consumo de electricidad
EJERCICIOS Sección 2.2 (11-28)
c2_p046-085.qxd 3/12/08 3:58 AM Page 57](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-75-320.jpg)
![Cuando los diversos resultados de un experimento son igualmente probables (la misma pro-
babilidad es asignada a cada evento simple), la tarea de calcular probabilidades se reduce a
contar. Sea N el número de resultados en un espacio muestral y N(A) el número de resulta-
dos contenidos en un evento A.
P(A) (2.1)
N(A)
N
2.3 Técnicas de conteo 59
La probabilidad de que tenga que detenerse en la primera
señal es 0.4, el problema análogo para la segunda señal es
0.5 y la probabilidad de que tenga que detenerse en por lo
menos una de las dos señales es 0.6. ¿Cuál es la probabili-
dad de que tenga que detenerse
a. En ambas señales?
b. En la primera señal pero no en la segunda?
c. En exactamente una señal?
23. Las computadoras de seis miembros del cuerpo de profeso-
res en cierto departamento tienen que ser reemplazadas.
Dos de ellos seleccionaron computadoras portátiles y los
otros cuatro escogieron computadoras de escritorio. Su-
ponga que sólo dos de las configuraciones pueden ser rea-
lizadas en un día particular y las dos computadoras que van
a ser configuradas se seleccionan al azar de entre las seis
(lo que implica 15 resultados igualmente probables; si las
computadoras se numeran 1, 2, . . . , 6 entonces un resultado
se compone de las computadoras 1 y 2, otro de las compu-
tadoras 1 y 3, y así sucesivamente).
a. ¿Cuál es la probabilidad de que las dos configuraciones
seleccionadas sean computadoras portátiles?
b. ¿Cuál es la probabilidad de que ambas configuraciones se-
leccionadas sean computadoras de escritorio?
c. ¿Cuál es la probabilidad de que por lo menos una configu-
ración seleccionada sea una computadora de escritorio?
d. ¿Cuál es la probabilidad de que por lo menos una compu-
tadora de cada tipo sea elegida para configurarla?
24. Demuestre que si un evento A está contenido en otro even-
to B (es decir, A es un subconjunto de B), entonces P(A)
P(B). [Sugerencia: Con los eventos A y B, A y B A son
eventos excluyentes y B A (B A), como se ve en el
diagrama de Venn.] Para los eventos A y B, ¿qué implica es-
to sobre la relación entre P(A B), P(A) y P(A B)?
25. Las tres opciones principales en un tipo de carro nuevo son
una transmisión automática (A), un quemacocos (B) y un
estéreo con reproductor de discos compactos (C). Si 70% de
todos los compradores solicitan A, 80% solicitan B, 75% so-
licitan C, 85% solicitan A o B, 90% solicitan A o C, 95%
solicitan B o C y 98% solicitan A o B o C, calcule las proba-
bilidades de los siguientes eventos. [Sugerencia: “A o B” es
el evento en que por lo menos una de las dos opciones es so-
licitada; trate de trazar un diagrama de Venn y rotule todas
las regiones.]
a. El siguiente comprador solicitará por lo menos una de
las tres opciones.
b. El siguiente comprador no seleccionará ninguna de las
tres opciones.
c. El siguiente comprador solicitará sólo una transmisión
automática y ninguna otra de las otras dos opciones.
d. El siguiente comprador seleccionará exactamente una de
estas tres opciones.
26. Un sistema puede experimentar tres tipos diferentes de
defectos. Sea Ai (i 1, 2, 3) el evento en que el sistema tie-
ne un defecto de tipo i. Suponga que
P(A1) 0.12 P(A2) 0.07 P(A3) 0.05
P(A1 A2) 0.13 P(A1 A3) 0.14
P(A2 A3) 0.10 P(A1 A2 A3) 0.01
a. ¿Cuál es la probabilidad de que el sistema no tenga un
defecto de tipo 1?
b. ¿Cuál es la probabilidad de que el sistema tenga tanto
defectos de tipo 1 como de tipo 2?
c. ¿Cuál es la probabilidad de que el sistema tenga tanto
defectos de tipo 1 como de tipo 2 pero no de tipo 3?
d. ¿Cuál es la probabilidad de que el sistema tenga a lo su-
mo dos de estos defectos?
27. Un departamento académico con cinco miembros del cuerpo
de profesores, Anderson, Box, Cox, Cramer y Fisher, debe
seleccionar dos de ellos para que participen en un comité de
revisión de personal. Como el trabajo requerirá mucho tiem-
po, ninguno está ansioso de participar, por lo que se decidió
que el representante será elegido introduciendo cinco trozos
de papel en una caja, revolviéndolos y seleccionando dos.
a. ¿Cuál es la probabilidad de que tanto Anderson como
Box serán seleccionados? [Sugerencia: Nombre los re-
sultados igualmente probables.]
b. ¿Cuál es la probabilidad de que por lo menos uno de los
dos miembros cuyo nombre comienza con C sea selec-
cionado?
c. Si los cinco miembros del cuerpo de profesores han dado
clase durante 3, 6, 7, 10 y 14 años, respectivamente, en la
universidad, ¿cuál es la probabilidad de que los dos repre-
sentantes seleccionados acumulen por lo menos 15 años
de experiencia académica en la universidad?
28. En el ejercicio 5, suponga que cualquier individuo que en-
tre a la clínica tiene las mismas probabilidades de ser asig-
nado a cualquiera de las tres estaciones independientemente
de adónde hayan sido asignados otros individuos.
¿Cuál es la probabilidad de que
a. Los tres miembros de una familia sean asignados a la
misma estación?
b. A lo sumo dos miembros de la familia sean asignados a
la misma estación?
c. Cada miembro de la familia sea asignado a una estación
diferente?
2.3 Técnicas de conteo
c2_p046-085.qxd 3/12/08 3:58 AM Page 59](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-77-320.jpg)
![el número de combinaciones; el segundo es más grande que el primero por un factor de 3!
puesto que así es como cada combinación puede ser ordenada.
Generalizando la línea de razonamiento anterior se obtiene una relación simple entre
el número de permutaciones y el número de combinaciones que produce una expresión con-
cisa para la última cantidad.
Nótese que (n
n) 1 y (n
0) 1 puesto que hay sólo una forma de seleccionar un conjunto
de (todos) n elementos o de ningún elemento y (n
1) n puesto que existen n subconjun-
tos de tamaño 1.
Una mano de bridge se compone de 13 cartas seleccionadas de entre un mazo de 52 cartas
sin importar el orden. Existen (5
1
2
3) 52!/13!39! manos de bridge diferentes, lo que asciende a
aproximadamente 635 000 millones. Como existen 13 cartas de cada palo, el número de ma-
nos compuestas por completo de tréboles y/o espadas (nada de cartas rojas) es (2
1
6
3)
26!/13!13! 10400600. Una de estas manos (2
1
6
3)se compone por completo de espadas y una
se compone por completo de tréboles, por lo tanto existen [(2
1
6
3) 2] manos compuestas por
completo de tréboles y espadas con ambos palos representados en la mano. Supóngase que
una mano de bridge repartida de un mazo bien barajado (es decir, 13 cartas se seleccionan
al azar de entre 52 posibilidades) y si
A {la mano se compone por completo de espadas y tréboles con ambos palos re-
presentados}
B {la mano se compone de exactamente dos palos}
Los N (5
1
2
3) posibles resultados son igualmente probables, por lo tanto
P(A) 0.0000164
Como existen (4
2) 6 combinaciones compuestas de dos palos, de las cuales espadas y tré-
boles es una de esas combinaciones,
P(B) 0.0000983
Es decir, una mano compuesta por completo de cartas de exactamente dos de los cuatro pa-
los ocurrirá aproximadamente una vez por cada 100 000 manos. Si juega bridge sólo una
vez al mes, es probable que nunca le repartan semejante mano. ■
El almacén de una universidad recibió 25 impresoras, de las cuales 10 son impresoras láser
y 15 son modelos de inyección de tinta. Si 6 de estas 25 se seleccionan al azar para que las
revise un técnico particular, ¿cuál es la probabilidad de que exactamente 3 de las seleccio-
nadas sean impresoras láser (de modo que las otras 3 sean de inyección de tinta)?
Sea D3 {exactamente 3 de las 6 seleccionadas son impresoras de inyección de tin-
ta}. Suponiendo que cualquier conjunto particular de 6 impresoras es tan probable de ser ele-
gido como cualquier otro conjunto de 6, se tienen resultados igualmente probables, por lo
tanto P(D3) N(D3)/N, donde N es el número de formas de elegir 6 impresoras de entre las
25 y N(D3) es el número de formas de elegir 3 impresoras láser y 3 de inyección de tinta. Por
lo tanto N (2
6
5
). Para obtener N(D3), primero se piensa en elegir 3 de las 15 impresoras de
inyección de tinta y luego 3 de las impresoras láser. Existen (1
3
5
) formas de elegir las 3 im-
presoras de inyección de tinta y (1
3
0
) formas de elegir las 3 impresoras láser; N(D3) es ahora
6
2
1
6
3 2
5
1
2
3
2
1
6
3 2
5
1
2
3
N(A)
N
64 CAPÍTULO 2 Probabilidad
PROPOSICIÓN
n!
k!(n k)!
Pk,n
k!
n
k
Ejemplo 2.22
Ejemplo 2.23
c2_p046-085.qxd 3/12/08 3:59 AM Page 64](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-82-320.jpg)
![el producto de estos dos números (visualícese un diagrama de árbol, en realidad aquí se está
utilizando el argumento de la regla de producto), por lo tanto
P(D3) 0.3083
Sea D4 {exactamente 4 de las 6 impresoras seleccionadas son impresoras de inyección de
tinta} y defínanse D5 y D6 del mismo modo. Entonces la probabilidad de seleccionar por lo
menos 3 impresoras de inyección de tinta es
P(D3 D4 D5 D6) P(D3) P(D4) P(D5) P(D6)
0.8530
■
1
6
5
1
0
0
2
6
5
1
5
5
1
1
0
2
6
5
1
4
5
1
2
0
2
6
5
1
3
5
1
3
0
2
6
5
3
1
!1
5
2
!
!
3
1
!
0
7
!
!
6
2
!1
5
9
!
!
1
3
5
1
3
0
2
6
5
N(D3)
N
2.3 Técnicas de conteo 65
29. Con fecha de abril de 2006, aproximadamente 50 millones
de nombres de dominio web.com fueron registrados (p. ej.,
yahoo.com).
a. ¿Cuántos nombres de dominio compuestos de exacta-
mente dos letras pueden ser formados? ¿Cuántos nom-
bres de dominio de dos letras existen si como caracteres
se permiten dígitos y números? [Nota: Una longitud de
carácter de tres o más ahora es obligatoria.]
b. ¿Cuántos nombres de dominio existen compuestos de
tres letras en secuencia? ¿Cuántos de esta longitud exis-
ten si se permiten letras o dígitos? [Nota: En la actuali-
dad todos están utilizados.]
c. Responda las preguntas hechas en b) para secuencias de
cuatro caracteres.
d. Con fecha de abril de 2006, 97 786 de las secuencias de
cuatro caracteres utilizando letras o dígitos aún no ha-
bían sido reclamadas. Si se elige un nombre de cuatro
caracteres al azar, ¿cuál es la probabilidad de que ya ten-
ga dueño?
30. Un amigo mío va a ofrecer una fiesta. Sus existencias actua-
les de vino incluyen 8 botellas de zinfandel, 10 de merlot y
12 de cabernet (él sólo bebe vino tinto), todos de diferentes
fábricas vinícolas.
a. Si desea servir 3 botellas de zinfandel y el orden de servi-
cio es importante, ¿cuántas formas existen de hacerlo?
b. Si 6 botellas de vino tienen que ser seleccionadas al azar
de las 30 para servirse, ¿cuántas formas existen de ha-
cerlo?
c. Si se seleccionan al azar 6 botellas, ¿cuántas formas
existen de obtener dos botellas de cada variedad?
d. Si se seleccionan 6 botellas al azar, ¿cuál es la probabili-
dad de que el resultado sea dos botellas de cada variedad?
e. Si se eligen 6 botellas al azar, ¿cuál es la probabilidad de
que todas ellas sean de la misma variedad.
31. a. Beethoven escribió 9 sinfonías y Mozart 27 conciertos
para piano. Si el locutor de una estación de radio de una
universidad desea tocar primero una sinfonía de Beetho-
ven y luego un concierto de Mozart, ¿de cuántas mane-
ras puede hacerlo?
b. El gerente de la estación decide que en cada noche sucesi-
va (7 días a la semana), se tocará una sinfonía de Beetho-
ven, seguida por un concierto para piano de Mozart,
seguido por un cuarteto de cuerdas de Schubert (de los
cuales existen 15). ¿Durante aproximadamente cuántos
años se podría continuar con esta política antes de que
exactamente el mismo programa se repitiera?
32. Una tienda de equipos de sonido está ofreciendo un precio
especial en un juego completo de componentes (receptor,
reproductor de discos compactos, altavoces, casetera). Al
comprador se le ofrece una opción de fabricante por ca-
da componente.
Receptor: Kenwood, Onkyo, Pioneer, Sony, Sherwood
Reproductor de discos compactos: Onkyo, Pioneer, Sony,
Technics
Altavoces: Boston, Infinity, Polk
Casetera: Onkyo, Sony, Teac, Technics
Un tablero de distribución en la tienda permite al cliente co-
nectar cualquier selección de componentes (compuesta de
uno de cada tipo). Use las reglas de producto para respon-
der las siguientes preguntas.
a. ¿De cuántas maneras puede ser seleccionado un compo-
nente de cada tipo?
b. ¿De cuántas maneras pueden ser seleccionados los com-
ponentes si tanto el receptor como el reproductor de dis-
cos compactos tienen que ser Sony?
EJERCICIOS Sección 2.3 (29-44)
c2_p046-085.qxd 3/12/08 3:59 AM Page 65](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-83-320.jpg)
![La primera etapa del problema implica un cliente que selecciona una de las tres mar-
cas de reproductor de DVD. Sea Ai {marca i adquirida}, con i 1, 2 y 3. Entonces P(A1
0.50, P(A2) 0.30 y P(A3) 0.20. Una vez que se selecciona una marca de reproductor
de DVD, la segunda etapa implica observar si el reproductor de DVD seleccionado necesita
reparación dentro de garantía. Con B {necesita reparación} y B {no necesita repara-
ción}, la información dada implica que P(B | A1) 0.25, P(B | A2) 0.20 y P(B | A3) 0.10.
El diagrama de árbol que representa esta situación experimental se muestra en la fi-
gura 2.10. Las ramas iniciales corresponden a marcas diferentes de reproductores de DVD;
hay dos ramas de segunda generación que emanan de la punta de cada rama inicial, una pa-
ra “necesita reparación” y la otra para “no necesita reparación”. La probabilidad de que
P(Ai) aparezca en la rama i-ésima inicial, en tanto que las probabilidades condicionales
P(B | Ai) y P(B | Ai) aparecen en las ramas de segunda generación. A la derecha de cada ra-
ma de segunda generación correspondiente a la ocurrencia de B, se muestra el producto de
probabilidades en las ramas que conducen hacia fuera de dicho punto. Ésta es simplemente
la regla de multiplicación en acción. La respuesta a la pregunta planteada en 1 es por lo tan-
to P(A1 B) P(B°A1) P(A1) 0.125. La respuesta a la pregunta 2 es
P(B) P[(marca 1 y reparación) o (marca 2 y reparación) o (marca 3 y reparación)]
P(A1 B) P(A2 B) P(A3 B)
0.125 0.060 0.020 0.205
Finalmente,
P(A1°B) 0.61
P(A2°B) 0.29
y
P(A3°B) 1 P(A1°B) P(A2°B) 0.10
0.060
0.205
P(A2 B)
P(B)
0.125
0.205
P(A1 B)
P(B)
2.4 Probabilidad condicional 71
Figura 2.10 Diagrama de árbol para el ejemplo 2.29.
Marca 2
M
arca 1
M
arca 3
P(A
3 )
0.20
P(A1
)
0.50
P(A2) 0.30
P(B A2) 0.20
Reparación
P(B' A2) 0.80
Ninguna reparación
P(B A3) 0.10
Reparación
P(B' A3) 0.90
Ninguna reparación
P(B' A1) 0.75
Ninguna reparación
P(B A1) 0.25
Reparación
P(B A3) P(A3) P(B A3) 0.020
P(B A2) P(A2) P(B A2) 0.060
P(B A1) P(A1) P(B A1) 0.125
P(B) 0.205
c2_p046-085.qxd 3/12/08 3:59 AM Page 71](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-89-320.jpg)
![2.4 Probabilidad condicional 75
51. Una caja contiene seis pelotas rojas y cuatro verdes y una se-
gunda caja contiene siete pelotas rojas y tres verdes. Se selec-
ciona una pelota al azar de la primera caja y se le coloca en
la segunda caja. Luego se selecciona al azar una pelota de la
segunda caja y se le coloca en la primera caja.
a. ¿Cuál es la probabilidad de que se seleccione una pelo-
ta roja de la primera caja y de que se seleccione una pe-
lota roja de la segunda caja?
b. Al final del proceso de selección, ¿cuál es la probabilidad
de que los números de pelotas rojas y verdes que hay en
la primera caja sean idénticas a los números iniciales?
52. Un sistema se compone de bombas idénticas, #1 y #2. Si
una falla, el sistema seguirá operando. Sin embargo, debido
al esfuerzo adicional, ahora es más probable que la bom-
ba restante falle de lo que era originalmente. Es decir,
r P(#2 falla | #1 falla) P(#2 falla) q. Si por lo menos
una bomba falla alrededor del final de su vida útil en 7% de
todos los sistemas y ambas bombas fallan durante dicho pe-
riodo en sólo 1%, ¿cuál es la probabilidad de que la bomba
#1 falle durante su vida útil de diseño?
53. Un taller repara tanto componentes de audio como de vi-
deo. Sea A el evento en que el siguiente componente traído
a reparación es un componente de audio y sea B el evento
en que el siguiente componente es un reproductor de discos
compactos (así que el evento B está contenido en A). Su-
ponga que P(A) 0.6 y P(B) 0.05. ¿Cuál es P(B | A)?
54. En el ejercicio 13, Ai {proyecto otorgado i}, con i 1, 2, 3.
Use las probabilidades dadas allí para calcular las siguien-
tes probabilidades y explique en palabras el significado de
cada una.
a. P(A2°A1) b. P(A2 A3°A1) c. P(A2 A3°A1)
d. P(A1 A2 A3°A1 A2 A3).
55. Las garrapatas de venados pueden ser portadoras de la en-
fermedad de Lyme o de la Erhlichiosis granulocítica huma-
na (HGE, por sus siglas en inglés). Con base en un estudio
reciente, suponga que 16% de todas las garrapatas en cierto
lugar portan la enfermedad de Lyme, 10% portan HGE y
10% de las garrapatas que portan por lo menos una de estas
enfermedades en realidad portan las dos. Si determina que
una garrapata seleccionada al azar ha sido portadora de
HGE, ¿cuál es la probabilidad de que la garrapata seleccio-
nada también porte la enfermedad de Lyme?
56. Para los eventos A y B con P(B) 0, demuestre que P(A | B)
P(A | B) 1.
57. Si P(B | A) P(B), demuestre que P(B|A) P(B). [Suge-
rencia: Sume P(B | A) a ambos lados de la desigualdad da-
da y luego utilice el resultado del ejercicio 56.]
58. Demuestre que para tres eventos cualesquiera A, B y C con
P(C) 0, P(A B | C) P(A | C) P(B | C) – P(A B | C).
59. En una gasolinería, 40% de los clientes utilizan gasolina re-
gular (A1), 35% usan gasolina plus (A2) y 25% utilizan pre-
mium (A3). De los clientes que utilizan gasolina regular, sólo
30% llenan sus tanques (evento B). De los clientes que utili-
zan plus, 60% llenan sus tanques, mientras que los que uti-
lizan premium, 50% llenan sus tanques.
a. ¿Cuál es la probabilidad de que el siguiente cliente pida
gasolina plus y llene el tanque (A2 B)?
b. ¿Cuál es la probabilidad de que el siguiente cliente lle-
ne el tanque?
c. Si el siguiente cliente llena el tanque, ¿cuál es la proba-
bilidad que pida gasolina regular? ¿Plus? ¿Premium?
60. El 70% de las aeronaves ligeras que desaparecen en vuelo
en cierto país son posteriormente localizadas. De las aero-
naves que son localizadas, 60% cuentan con un localizador
de emergencia, mientras que 90% de las aeronaves no locali-
zadas no cuentan con dicho localizador. Suponga que una
aeronave ligera ha desaparecido.
a. Si tiene un localizador de emergencia, ¿cuál es la proba-
bilidad de que no sea localizada?
b. Si no tiene un localizador de emergencia, ¿cuál es la
probabilidad de que sea localizada?
61. Componentes de cierto tipo son enviados a un distribuidor en
lotes de diez. Suponga que 50% de dichos lotes no contie-
nen componentes defectuosos, 30% contienen un componente
defectuoso y 20% contienen dos componentes defectuosos.
Se seleccionan al azar dos componentes de un lote y se
prueban. ¿Cuáles son las probabilidades asociadas con 0, 1
y 2 componentes defectuosos que están en el lote en cada
una de las siguientes condiciones?
a. Ningún componente probado está defectuoso.
b. Uno de los dos componentes probados está defectuoso.
[Sugerencia: Trace un diagrama de árbol con tres ramas
de primera generación correspondientes a los tres tipos
diferentes de lotes.]
62. Una compañía que fabrica cámaras de video produce un mo-
delo básico y un modelo de lujo. Durante el año pasado,
40% de las cámaras vendidas fueron del modelo básico. De
aquellos que compraron el modelo básico, 30% adquirieron
una garantía ampliada, en tanto que 50% de los que compra-
ron el modelo de lujo también lo hicieron. Si sabe que un
comprador seleccionado al azar tiene una garantía ampliada,
¿qué tan probable es que él o ella tengan un modelo básico?
63. Para los clientes que compran un refrigerador en una tienda
de aparatos domésticos, sea A el evento en que el refrigera-
dor fue fabricado en EU, B el evento en que el refrigerador
contaba con una máquina de hacer hielos y C el evento en
que el cliente adquirió una garantía ampliada. Las probabi-
lidades pertinentes son
P(A) 0.75 P(B°A) 0.9 P(B°A) 0.8
P(C°A B) 0.8 P(C°A B) 0.6
P(C°A B) 0.7 P(C°A B) 0.3
a. Construya un diagrama de árbol compuesto de ramas de
primera, segunda y tercera generaciones y anote el even-
to y la probabilidad apropiada junto a cada rama.
b. Calcule P(A B C).
c. Calcule P(B C).
d. Calcule P(C).
e. Calcule P(A | B C), la probabilidad de la compra de un
refrigerador fabricado en EU dado que también se adquirie-
ron una máquina de hacer hielos y una garantía ampliada.
64. En el ejemplo 2.30, suponga que la tasa de incidencia de la
enfermedad es de 1 en 25 y no de 1 en 1000. ¿Cuál es en-
tonces la probabilidad de un resultado de prueba positivo?
Dado que el resultado de prueba es positivo, ¿cuál es la pro-
babilidad de que el individuo tenga la enfermedad? Dado un
resultado de prueba negativo, ¿cuál es la probabilidad de
que el individuo no tenga la enfermedad?
c2_p046-085.qxd 3/12/08 3:59 AM Page 75](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-93-320.jpg)
![La definición de probabilidad condicional permite revisar la probabilidad P(A) originalmente
asignada a A cuando después se informa que otro evento B ha ocurrido; la nueva probabilidad
de A es P(A | B). En los ejemplos, con frecuencia fue el caso de que P(A | B) difería de la pro-
babilidad no condicional P(A), lo que indica que la información “B ha ocurrido” cambia la
probabilidad de que ocurra A. A menudo la probabilidad de que ocurra o haya ocurrido A no se
ve afectada por el conocimiento de que B ha ocurrido, así que P(A | B) P(A). Es entonces
76 CAPÍTULO 2 Probabilidad
2.5 Independencia
65. En una gran universidad, en la búsqueda que nunca termina
de un libro de texto satisfactorio, el Departamento de Estadís-
tica probó un texto diferente durante cada uno de los últimos
tres trimestres. Durante el trimestre de otoño, 500 estudiantes
utilizaron el texto del profesor Mean; durante el trimestre de
invierno, 300 estudiantes usaron el texto del profesor Median
y durante el trimestre de primavera, 200 estudiantes utiliza-
ron el texto del profesor Mode. Una encuesta realizada al fi-
nal de cada trimestre mostró que 200 estudiantes se sintieron
satisfechos con el libro de Mean, 150 con el libro de Median
y 160 con el libro de Mode. Si se selecciona al azar un estu-
diante que cursó estadística durante uno de estos trimestres y
admite haber estado satisfecho con el texto, ¿es probable que
el estudiante haya utilizado el libro de Mean, Median o Mo-
de? ¿Quién es el autor menos probable? [Sugerencia: Trace
un diagrama de árbol o use el teorema de Bayes.]
66. Considere la siguiente información sobre vacacionistas (ba-
sada en parte en una encuesta reciente de Travelocity): 40%
revisan su correo electrónico de trabajo, 30% utilizan un te-
léfono celular para permanecer en contacto con su trabajo,
25% trajeron una computadora portátil consigo, 23% revisan
su correo electrónico de trabajo y utilizan un teléfono celular
para permanecer en contacto y 51% ni revisan su correo elec-
trónico de trabajo ni utilizan un teléfono celular para per-
manecer en contacto ni trajeron consigo una computadora
portátil. Además, 88 de cada 100 que traen una computado-
ra portátil también revisan su correo electrónico de trabajo y
70 de cada 100 que utilizan un teléfono celular para perma-
necer en contacto también traen una computadora portátil.
a. ¿Cuál es la probabilidad de que un vacacionista selec-
cionado al azar que revisa su correo electrónico de tra-
bajo también utilice un teléfono celular para permanecer
en contacto.
b. ¿Cuál es la probabilidad de que alguien que trae una
computadora portátil también utilice un teléfono celular
para permanecer en contacto.
c. Si el vacacionista seleccionado al azar revisó su correo
electrónico de trabajo y trajo una computadora portátil,
¿cuál es la probabilidad de que él o ella utilice un telé-
fono celular para permanecer en contacto?
67. Ha habido una gran controversia durante los últimos años
con respecto a qué tipos de vigilancia son apropiados para
impedir el terrorismo. Suponga que un sistema de vigilancia
particular tiene 99% de probabilidades de identificar correc-
tamente a un futuro terrorista y 99.9% de probabilidades de
identificar correctamente a alguien que no es un futuro terro-
rista. Si existen 1000 futuros terroristas en una población de
300 millones y se selecciona al azar uno de estos 300 millones,
examinado por el sistema e identificado como futuro terro-
rista, ¿cuál es la probabilidad de él o ella que sean futuros te-
rroristas? ¿Le inquieta el valor de esta probabilidad sobre el
uso del sistema de vigilancia? Explique.
68. Una amiga que vive en Los Ángeles hace viajes frecuentes
de consultoría a Washington, D.C.; 50% del tiempo viaja en
la línea aérea #1, 30% del tiempo en la aerolínea #2 y el
20% restante en la aerolínea #3. Los vuelos de la aerolínea
#1 llegan demorados a D.C. 30% del tiempo y 10% del
tiempo llegan demorados a L.A. Para la aerolínea #2, estos
porcentajes son 25% y 20%, en tanto que para la aerolínea
#3 los porcentajes son 40% y 25%. Si se sabe que en un via-
je particular ella llegó demorada a exactamente uno de los
destinos, ¿cuáles son las probabilidades posteriores de haber
volado en las aerolíneas #1, #2 y #3? Suponga que la proba-
bilidad de arribar con demora a L.A. no se ve afectada por lo
que suceda en el vuelo a D.C. [Sugerencia: Desde la punta de
cada rama de primera generación en un diagrama de árbol,
trace tres ramas de segunda generación identificadas, respec-
tivamente, como, 0 demorado, 1 demorado y 2 demorado.]
69. En el ejercicio 59, considere la siguiente información adi-
cional sobre el uso de tarjetas de crédito:
El 70% de todos los clientes que utilizan gasolina regular y
que llenan el tanque usan una tarjeta de crédito.
El 50% de todos los clientes que utilizan gasolina regular
y que no llenan el tanque usan una tarjeta de crédito.
El 60% de todos los clientes que llenan el tanque con gaso-
lina plus usan una tarjeta de crédito.
El 50% de todos los clientes que utilizan gasolina plus y
que no llenan el tanque usan una tarjeta de crédito.
El 50% de todos los clientes que utilizan gasolina premium
y que llenan el tanque usan una tarjeta de crédito.
El 40% de todos los clientes que utilizan gasolina premium y
que no llenan el tanque usan una tarjeta de crédito.
Calcule la probabilidad de cada uno de los siguientes even-
tos para el siguiente cliente que llegue (un diagrama de ár-
bol podría ayudar).
a. {Plus, tanque lleno y tarjeta de crédito}
b. {Premium, tanque no lleno y tarjeta de crédito}
c. {Premium y tarjeta de crédito}
d. {Tanque lleno y tarjeta de crédito}
e. {Tarjeta de crédito}
f. Si el siguiente cliente utiliza una tarjeta de crédito, ¿cuál
es la probabilidad de que pida premium?
c2_p046-085.qxd 3/12/08 3:59 AM Page 76](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-94-320.jpg)
![Independencia de más de dos eventos
La noción de independencia de dos eventos puede ser ampliada a conjuntos de más de dos
eventos. Aunque es posible ampliar la definición para dos eventos independientes trabajan-
do en función de probabilidades condicionales y no condicionales, es más directo y menos
tedioso seguir las líneas de la última proposición.
Parafraseando la definición, los eventos son mutuamente independientes si la probabili-
dad de la intersección de cualquier subconjunto de “n”-elementos, es igual al producto de las
probabilidades individuales. Al utilizar la propiedad de multiplicación para más de dos eventos
independientes, es legítimo reemplazar una o más de las Ai por su complemento (p. ej., si A1,
A2 y A3 son eventos independientes, también lo son A1
, A2
y A3
). Como fue el caso con dos even-
tos, con frecuencia se especifica al principio de un problema la independencia de ciertos
eventos. La probabilidad de una intersección puede entonces ser calculada vía multiplicación.
El artículo “Reliability Evaluation of Solar Photovoltaic Arrays” (Solar Energy, 2002:
129–141) presenta varias configuraciones de redes fotovoltaicas solares compuestas de celdas
solares de silicio cristalino. Considérese primero el sistema ilustrado en la figura 2.14(a).
Existen dos subsistemas conectados en paralelo y cada uno contiene tres celdas. Para que el
sistema funcione, por lo menos uno de los dos subsistemas en paralelo debe funcionar. Den-
tro de cada subsistema, las tres celdas están conectadas en serie, así que un subsistema fun-
cionará sólo si todas sus celdas funcionan. Considere un valor de duración particular t0 y
suponga que desea determinar la probabilidad de que la duración del sistema exceda de t0.
Sea Ai el evento en que la duración de la celda i excede de t0 (i 1, 2, . . . , 6). Se supone
que las Ai son eventos independientes (ya sea que cualquier celda particular que dure más
de t0 horas no tenga ningún efecto en sí o no cualquier otra celda lo hace) y que P(Ai) 0.9
por cada i puesto que las celdas son idénticas. Entonces
P(la duración del
sistema excede de t0) P[(A1 A2 A3) (A4 A5 A6)]
P(A1 A2 A3) P(A4 A5 A6)
P [(A1 A2 A3) (A4 A5 A6)]
(0.9)(0.9)(0.9) (0.9)(0.9)(0.9) (0.9)(0.9)(0.9)(0.9)(0.9)(0.9) 0.927
Alternativamente,
P(la duración del sistema excede de t0) 1 P(ambas duraciones del subsistema son t0)
1 [P(la duración del subsistema es t0)]2
1 [1 P(la duración del subsistema es t0)]2
1 [1 (0.9)3
]2
0.927
2.5 Independencia 79
Ejemplo 2.35
Figura 2.14 Configuración del sistema para el ejemplo 2.35: (a) en serie-paralelo;
(b) vinculado en cruz total.
1 2 3
4 5 6
1 2 3
4 5 6
(a) (b)
DEFINICIÓN Los eventos A1, . . . , An son mutuamente independientes si por cada k (k 2,
3, . . . , n) y cada subconjunto de índices i1, i2, . . . , ik,
P(Ai1
Ai2
. . . Aik
) P(Ai1
) P(Ai2
) . . . P(Aik
).
c2_p046-085.qxd 3/12/08 3:59 AM Page 79](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-97-320.jpg)
![80 CAPÍTULO 2 Probabilidad
Considérese a continuación el sistema vinculado en cruz mostrado en la figura 2.14(b), ob-
tenido a partir de la red conectada en serie-paralelo mediante la conexión de enlaces a tra-
vés de cada columna de uniones. Ahora bien, el sistema falla en cuanto toda una columna
falla y la duración del sistema excede de t0 sólo si la duración de cada columna lo hace. Pa-
ra esta configuración,
P(la duración del sistema
es de por lo menos t0) [P(la duración de la columna excede de t0)]3
[1 P(duración de la columna t0)]3
[1 P(la duración de ambas celdas en una columna es t0)]3
[1 (1 0.9)2
]3
0.970 ■
70. Reconsidere el escenario de la tarjeta de crédito del ejercicio
47 (sección 2.4) y demuestre que A y B son dependientes uti-
lizando primero la definición de independencia y luego ve-
rificando que la propiedad de multiplicación no prevalece.
71. Una compañía de exploración petrolera en la actualidad tie-
ne dos proyectos activos, uno enAsia y el otro en Europa. Sea
A el evento en que el proyecto asiático tiene éxito y B el even-
to en que el proyecto europeo tiene éxito. Suponga que A y B
son eventos independientes con P(A) 0.4 y P(B) 0.7.
a. Si el proyecto asiático no tiene éxito, ¿cuál es la proba-
bilidad de que el europeo también fracase? Explique su
razonamiento.
b. ¿Cuál es la probabilidad de que por lo menos uno de los
dos proyectos tenga éxito?
c. Dado que por lo menos uno de los dos proyectos tiene
éxito, ¿cuál es la probabilidad de que sólo el proyecto
asiático tenga éxito?
72. En el ejercicio 13, ¿es cualquier Ai independiente de cual-
quier otro Aj? Responda utilizando la propiedad de multipli-
cación para eventos independientes.
73. Si A y B son eventos independientes, demuestre que A y B
también son independientes. [Sugerencia: Primero establez-
ca una relación entre P(A B), P(B) y P(A B).]
74. Suponga que las proporciones de fenotipos sanguíneos en
una población son las siguientes:
A B AB O
0.42 0.10 0.04 0.44
Suponiendo que los fenotipos de dos individuos selecciona-
dos al azar son independientes uno de otro, ¿cuál es la pro-
babilidad de que ambos fenotipos sean O? ¿Cuál es la
probabilidad de que los fenotipos de dos individuos selec-
cionados al azar coincidan?
75. Una de las suposiciones que sustentan la teoría de las gráfi-
cas de control (véase el capítulo 16) es que los puntos dibu-
jados consecutivamente son independientes entre sí. Cada
punto puede señalar que un proceso de producción está fun-
cionando correctamente o que existe algún funcionamiento
defectuoso. Aun cuando un proceso esté funcionando de
manera correcta, existe una pequeña probabilidad de que un
punto particular señalará un problema con el proceso. Supon-
ga que esta probabilidad es de 0.05. ¿Cuál es la probabilidad
de que por lo menos uno de 10 puntos sucesivos indique un
problema cuando de hecho el proceso está operando correc-
tamente? Responda está pregunta para 25 puntos sucesivos.
76. La probabilidad de que un calificador se equivoque al mar-
car cualquier pregunta particular de un examen de opciones
múltiples es de 0.1. Si existen diez preguntas y éstas se mar-
can en forma independiente, ¿cuál es la probabilidad de que
no se cometan errores? ¿Que por lo menos se cometa un
error? Si existen n preguntas y la probabilidad de un error
de marcado es p en lugar de 0.1, dé expresiones para estas
dos probabilidades.
77. La costura de un avión requiere 25 remaches. La costura
tendrá que ser retrabajada si alguno de los remaches está
defectuoso. Suponga que los remaches están defectuosos
independientemente uno de otro, cada uno con la misma
probabilidad.
a. Si 20% de todas las costuras tienen que ser retrabajadas,
¿cuál es la probabilidad de que un remache esté defec-
tuoso?
b. ¿Qué tan pequeña deberá ser la probabilidad de un re-
mache defectuoso para garantizar que sólo 10% de las
costuras tienen que ser retrabajadas?
78. Una caldera tiene cinco válvulas de alivio idénticas. La pro-
babilidad de que cualquier válvula particular se abra en un
momento de demanda es de 0.95. Suponiendo que operan
independientemente, calcule P(por lo menos una válvula se
abre) y P(por lo menos una válvula no se abre).
79. Dos bombas conectadas en paralelo fallan independiente-
mente una de otra en cualquier día dado. La probabilidad de
que falle sólo la bomba más vieja es de 0.10 y la probabili-
dad de que sólo la bomba más nueva falle es de 0.05. ¿Cuál
es la probabilidad de que el sistema de bombeo falle en
cualquier día dado (lo que sucede si ambas bombas fallan)?
80. Considere el sistema de componentes conectados como en
la figura adjunta. Los componentes 1 y 2 están conectados
en paralelo, de modo que el subsistema trabaja si y sólo si
EJERCICIOS Sección 2.5 (70-89)
c2_p046-085.qxd 3/12/08 3:59 AM Page 80](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-98-320.jpg)
![2.5 Independencia 81
1 o 2 trabaja; como 3 y 4 están conectados en serie, qué sub-
sistema trabaja si y sólo si 3 y 4 trabajan. Si los componen-
tes funcionan independientemente uno de otro y P(el
componente trabaja) 0.9, calcule P(el sistema trabaja).
81. Remítase otra vez al sistema en serie-paralelo introducido
en el ejemplo 2.35 y suponga que existen sólo dos celdas en
lugar de tres en cada subsistema en paralelo [en la figura
2.14(a), elimine las celdas 3 y 6 y renumere las celdas 4 y
5 como 3 y 4]. Utilizando P(Ai) 0.9, es fácil ver que la
probabilidad de que la duración del sistema exceda de t0 es
de 0.9639. ¿A qué valor tendría que cambiar 0.9 para incre-
mentar la duración del sistema de 0.9639 a 0.99? [Sugeren-
cia: Sea P(Ai) p, exprese la confiabilidad del sistema en
función de p, luego haga x p2
.]
82. Considere lanzar en forma independiente dos dados impar-
ciales, uno rojo y otro verde. Sea A el evento en que el da-
do rojo muestra 3 puntos, B el evento en que el dado verde
muestra 4 puntos y C el evento en que el número total de
puntos que muestran los dos dados es 7. ¿Son estos eventos
independientes por pares (es decir, ¿son A y B eventos inde-
pendientes, son A y C independientes y son B y C indepen-
dientes? ¿Son los tres eventos mutuamente independientes?
83. Los componentes enviados a un distribuidor son revisados
en cuanto a defectos por dos inspectores diferentes (cada
componente es revisado por ambos inspectores). El primero
detecta 90% de todos los defectuosos que están presentes y
el segundo hace lo mismo. Por lo menos un inspector no de-
tecta un defecto en 20% de todos los componentes defectuo-
sos. ¿Cuál es la probabilidad de que ocurra lo siguiente?
a. ¿Un componente defectuoso será detectado sólo por el
primer inspector? ¿Por exactamente uno de los dos ins-
pectores?
b. ¿Los tres componentes defectuosos en un lote no son
detectados por ambos inspectores (suponiendo que las
inspecciones de los diferentes componentes son inde-
pendientes unas de otras)?
84. El 70% de todos los vehículos examinados en un centro de ve-
rificación de emisiones pasan la inspección. Suponiendo que
vehículos sucesivos pasan o fallan independientemente uno de
otro, calcule las siguientes probabilidades:
a. P(los tres vehículos siguientes inspeccionados pasan).
b. P(por lo menos uno de los tres vehículos siguientes pasa).
c. P(exactamente uno de los tres vehículos siguientes pasa).
d. P(cuando mucho uno de los tres vehículos siguientes
inspeccionados pasa).
e. Dado que por lo menos uno de los tres vehículos si-
guientes pasa la inspección, ¿cuál es la probabilidad de
que los tres pasen (una probabilidad condicional)?
85. Un inspector de control de calidad verifica artículos recién
producidos en busca de fallas. El inspector examina un
artículo en busca de fallas en una serie de observaciones in-
dependientes, cada una de duración fija. Dado que en reali-
dad está presente una imperfección, sea p la probabilidad de
que la imperfección sea detectada durante cualquier obser-
vación (este modelo se discute en “Human Performance in
Sampling Inspection”, Human Factors, 1979: 99–105).
a. Suponiendo que un artículo tiene una imperfección, ¿cuál
es la probabilidad de que sea detectada al final de la se-
gunda observación (una vez que una imperfección ha si-
do detectada, la secuencia de observaciones termina)?
b. Dé una expresión para la probabilidad de que una imper-
fección sea detectada al final de la n-ésima observación.
c. Si cuando en tres observaciones no ha sido detectada una
imperfección, el artículo es aprobado, ¿cuál es la probabi-
lidad de que un artículo imperfecto pase la inspección?
d. Suponga que 10% de todos los artículos contienen una
imperfección [P(artículo seleccionado al azar muestra
una imperfección) 0.1]. Con la suposición del inciso
c), ¿cuál es la probabilidad de que un artículo seleccio-
nado al azar pase la inspección (pasará automáticamen-
te si no tiene imperfección, pero también podría pasar si
tiene una imperfección)?
e. Dado que un artículo ha pasado la inspección (sin imper-
fecciones en tres observaciones), ¿cuál es la probabilidad
de que sí tenga una imperfección? Calcule para p 0.5.
86. a. Una compañía maderera acaba de recibir un lote de
10 000 tablas de 2 4. Suponga que 20% de estas tablas
(2 000) en realidad están demasiado tiernas o verdes para
ser utilizadas en construcción de primera calidad. Se eli-
gen dos tablas al azar, una después de la otra. Sea A
{la primera tabla está verde} y B {la segunda tabla es-
tá verde}. Calcule P(A), P(B) y P(A B) (un diagrama
de árbol podría ayudar). ¿Son A y B independientes?
b. Con A y B independientes y P(A) P(B) 0.2, ¿cuál
es P(A B)? ¿Cuánta diferencia existe entre esta res-
puesta y P(A B) en el inciso a)? Para propósitos de
cálculo P(A B), ¿se puede suponer que A y B del in-
ciso a) son independientes para obtener en esencia la
probabilidad correcta?
c. Suponga que un lote consta de 10 tablas, de las cuales
dos están verdes. ¿Produce ahora la suposición de inde-
pendencia aproximadamente la respuesta correcta para
P(A B)? ¿Cuál es la diferencia crítica entre la situación
en este caso y la del inciso a)? ¿Cuándo piensa que una
suposición de independencia sería válida al obtener
una respuesta aproximadamente correcta a P(A B)?
87. Remítase a las suposiciones manifestadas en el ejercicio 80
y responda la pregunta planteada allí para el sistema de la
figura adjunta. ¿Cómo cambiaría la probabilidad si ésta fue-
ra un subsistema conectado en paralelo al subsistema ilus-
trado en la figura 2.14(a)?
88. El profesor Stan der Deviation puede tomar una de las rutas
en el trayecto del trabajo a su casa. En la primera ruta, hay
2
1
5
3
6
7
4
2
1
3 4
c2_p046-085.qxd 3/12/08 3:59 AM Page 81](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-99-320.jpg)
![82 CAPÍTULO 2 Probabilidad
cuatro cruces de ferrocarril. La probabilidad de que sea de-
tenido por un tren en cualquiera de los cruces es 0.1 y los
trenes operan independientemente en los cuatro cruces. La
otra ruta es más larga pero sólo hay dos cruces, indepen-
dientes uno de otro, con la misma posibilidad de que sea de-
tenido por un tren al igual que en la primera ruta. En un día
particular, el profesor Deviation tiene una reunión progra-
mada en casa durante cierto tiempo. Cualquiera ruta que to-
me, calcula que llegará tarde si es detenido por los trenes en
por lo menos la mitad de los cruces encontrados.
a. ¿Cuál ruta deberá tomar para reducir al mínimo la pro-
babilidad de llegar tarde a la reunión?
b. Si lanza al aire una moneda imparcial para decidir que ru-
ta tomar y llega tarde, ¿cuál es la probabilidad de que
tomó la ruta de los cuatro cruces?
89. Suponga que se colocan etiquetas idénticas en las dos ore-
jas de un zorro. El zorro es dejado en libertad durante un
tiempo. Considere los dos eventos C1 {se pierde la eti-
queta de la oreja izquierda} y C2 {se pierde la etiqueta de
la oreja derecha}. Sea P(C1) P(C2) y suponga que
C1 y C2 son eventos independientes. Derive una expresión
(que implique ) para la probabilidad de que exactamente
una etiqueta se pierda dado que cuando mucho una se pier-
de (“Ear Tag Loss in Red Foxes”, J. Wildlife Mgmt., 1976:
164–167). [Sugerencia: Trace un diagrama de árbol en el
cual las dos ramas iniciales se refieren a si la etiqueta de la
oreja izquierda se pierde.]
90. Una pequeña compañía manufacturera iniciará un turno de no-
che. Hay 20 mecánicos empleados por la compañía.
a. Si una cuadrilla nocturna se compone de 3 mecánicos,
¿cuántas cuadrillas diferentes son posibles?
b. Si los mecánicos están clasificados 1, 2, . . . , 20 en or-
den de competencia, ¿cuántas de estas cuadrillas no in-
cluirían al mejor mecánico?
c. ¿Cuántas de las cuadrillas tendrían por lo menos 1 de los
10 mejores mecánicos?
d. Si se selecciona al azar una de estas cuadrillas para que
trabajen una noche particular, ¿cuál es la probabilidad
de que el mejor mecánico no trabaje esa noche?
91. Una fábrica utiliza tres líneas de producción para fabricar
latas de cierto tipo. La tabla adjunta da porcentajes de latas
que no cumplen con las especificaciones, categorizadas por
tipo de incumplimiento de las especificaciones, para cada
una de las tres líneas durante un periodo particular.
Línea 1 Línea 2 Línea 3
Manchas 15 12 20
Grietas 50 44 40
Problema con la argolla
de apertura 21 28 24
Defecto superficial 10 8 15
Otros 4 8 2
Durante este periodo, la línea 1 produjo 500 latas fuera de
especificación, la 2 produjo 400 latas como esas y la 3 fue
responsable de 600 latas fuera de especificación. Suponga
que se selecciona al azar una de estas 1500 latas.
a. ¿Cuál es la probabilidad de que la lata la produjo la lí-
nea 1? ¿Cuál es la probabilidad de que la razón del in-
cumplimiento de la especificación es una grieta?
b. Si la lata seleccionada provino de la línea 1, ¿cuál es la
probabilidad de que tenía una mancha?
c. Dado que la lata seleccionada mostró un defecto superfi-
cial, ¿cuál es la probabilidad de que provino de la línea 1?
92. Un empleado de la oficina de inscripciones en una univer-
sidad en este momento tiene diez formas en su escritorio en
espera de ser procesadas. Seis de éstas son peticiones de ba-
ja y las otras cuatro son solicitudes de sustitución de curso.
a. Si selecciona al azar seis de estas formas para dárselas a
un subordinado, ¿cuál es la probabilidad de que sólo uno
de los dos tipos permanezca en su escritorio?
b. Suponga que tiene tiempo para procesar sólo cuatro de
estas formas antes de salir del trabajo. Si estas cuatro se
seleccionan al azar una por una, ¿cuál es la probabilidad
de que cada forma subsiguiente sea de un tipo diferente de
su predecesora?
93. Un satélite está programado para ser lanzado desde Cabo Ca-
ñaveral en Florida y otro lanzamiento está programado para
la Base de la Fuerza Aérea Vandenberg en California. Sea A
el evento en que el lanzamiento en Vandenberg se hace a la
hora programada y B el evento en que el lanzamiento en Ca-
bo Cañaveral se hace a la hora programada. Si A y B son
eventos independientes con P(A) P(B) y P(A B) 0.626,
P(A B) 0.144, determine los valores de P(A) y P(B).
94. Un transmisor envía un mensaje utilizando un código bina-
rio, esto es, una secuencia de ceros y unos. Cada bit trans-
mitido (0 o 1) debe pasar a través de tres relevadores para
llegar al receptor. En cada relevador, la probabilidad es 0.20
de que el bit enviado será diferente del bit recibido (una in-
versión). Suponga que los relevadores operan independien-
temente uno de otro.
Transmisor A Relevador 1 A Relevador 2 A Relevador 3
A Receptor
a. Si el transmisor envía un 1, ¿cuál es la probabilidad de
que los tres relevadores envíen un 1?
b. Si el transmisor envía un 1, ¿cuál es la probabilidad de
que el receptor reciba un 1? [Sugerencia: Los ocho re-
sultados experimentales pueden ser mostrados en un
diagrama de árbol con tres ramas de generación, una por
cada relevador.]
c. Suponga que 70% de todos los bits enviados por el
transmisor son 1. Si el receptor recibe un 1, ¿cuál es la
probabilidad de que un 1 fue enviado?
95. El individuo A tiene un círculo de cinco amigos cercanos
(B, C, D, E y F). A escuchó cierto rumor originado fuera del
círculo e invitó a sus cinco amigos a una fiesta para contar-
les el rumor. Para empezar, A escoge a uno de los cinco al
EJERCICIOS SUPLEMENTARIOS (90-114)
c2_p046-085.qxd 3/12/08 3:59 AM Page 82](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-100-320.jpg)
![Ejercicios suplementarios 83
azar y se lo cuenta. Dicho individuo escoge entonces
al azar a uno de los cuatro individuos restantes y repite el
rumor. Después, de aquellos que ya oyeron el rumor uno se
lo cuenta a otro nuevo individuo y así hasta que todos oyen
el rumor.
a. ¿Cuál es la probabilidad de que el rumor se repita en el
orden B, C, D, E y F?
b. ¿Cuál es la probabilidad de que F sea la tercera perso-
na en la reunión a quien se cuenta el rumor?
c. ¿Cuál es la probabilidad de que F sea la última persona
en oír el rumor?
96. Remítase al ejercicio 95. Si en cada etapa la persona que
actualmente “oyó” el rumor no sabe quién ya lo oyó y se-
lecciona el siguiente receptor al azar de entre todos los cin-
co probables individuos, ¿cuál es la probabilidad de que F
aún no haya escuchado el rumor después de que el rumor
haya sido contado diez veces en la reunión?
97. Un ingeniero químico está interesado en determinar si cierta
impureza está presente en un producto. Un experimento tie-
ne una probabilidad de 0.80 de detectarla si está presente. La
probabilidad de no detectarla si está ausente es de 0.90.
Las probabilidades previas de que la impureza esté presen-
te o ausente son de 0.40 y 0.60, respectivamente. Tres expe-
rimentos distintos producen sólo dos detecciones. ¿Cuál es
la probabilidad posterior de que la impureza esté presente?
98. A cada concursante en un programa de preguntas se le pi-
de que especifique una de seis posibles categorías de entre
las cuales se le hará una pregunta. Suponga P(el concur-
sante escoge la categoría i)
1
6 y concursantes sucesivos
escogen sus categorías independientemente uno de otro. Si
participan tres concursantes en cada programa y los tres en
un programa particular seleccionan diferentes categorías,
¿cuál es la probabilidad de que exactamente uno seleccio-
ne la categoría 1?
99. Los sujetadores roscados utilizados en la fabricación de
aviones son levemente doblados para que queden bien
apretados y no se aflojen durante vibraciones. Suponga
que 95% de todos los sujetadores pasan una inspección ini-
cial. De 5% que fallan, 20% están tan seriamente defectuo-
sos que deben ser desechados. Los sujetadores restantes son
enviados a una operación de redoblado, donde 40% no
pueden ser recuperados y son desechados. El otro 60% de
estos sujetadores son corregidos por el proceso de redobla-
do y posteriormente pasan la inspección.
a. ¿Cuál es la probabilidad de que un sujetador que acaba
de llegar seleccionado al azar pase la inspección inicial-
mente o después del redoblado?
b. Dado que un sujetador pasó la inspección, ¿cuál es la
probabilidad de que apruebe la inspección inicial y de
que no necesite redoblado?
100. Un porcentaje de todos los individuos en una población
son portadores de una enfermedad particular. Una prue-
ba de diagnóstico para esta enfermedad tiene una tasa de
detección de 90% para portadores y de 5% para no porta-
dores. Suponga que la prueba se aplica independientemen-
te a dos muestras de sangre diferentes del mismo individuo
seleccionado al azar.
a. ¿Cuál es la probabilidad de que ambas pruebas den el
mismo resultado?
b. Si ambas pruebas son positivas, ¿cuál es la probabilidad
de que el individuo seleccionado sea un portador?
101. Un sistema consta de dos componentes. La probabilidad de
que el segundo componente funcione de manera satisfacto-
ria durante su duración de diseño es de 0.9, la probabilidad
de que por lo menos uno de los dos componentes lo haga
es de 0.96 y la probabilidad de que ambos componentes lo
hagan es de 0.75. Dado que el primer componente funciona
de manera satisfactoria durante toda su duración de diseño,
¿cuál es la probabilidad de que el segundo también lo haga?
102. Cierta compañía envía 40% de sus paquetes de correspon-
dencia nocturna vía un servicio de correo Express E1. De
estos paquetes, 2% llegan después del tiempo de entrega
garantizado (sea L el evento “entrega demorada”). Si se
selecciona al azar un registro de correspondencia nocturna
del archivo de la compañía, ¿cuál es la probabilidad de que
el paquete se fue vía E1 y llegó demorado?
103. Remítase al ejercicio 102. Suponga que 50% de los paque-
tes nocturnos se envían vía servicio de correo Express E2 y
el 10% restante se envía por E3. De los paquetes enviados
vía E2, sólo 1% llegan demorados, en tanto que 5% de los
paquetes manejados por E3 llegan demorados.
a. ¿Cuál es la probabilidad de que un paquete selecciona-
do al azar llegue demorado?
b. Si un paquete seleccionado al azar llegó a tiempo, ¿cuál
es la probabilidad de que no fue mandado vía E1?
104. Una compañía utiliza tres líneas de ensamble diferentes: A1,
A2 y A3, para fabricar un componente particular. De los fa-
bricados por la línea A1, 5% tienen que ser retrabajados para
corregir un defecto, mientras que 8% de los componentes de
A2 tienen que ser retrabajados y 10% de los componentes
de A3 tienen que ser retrabajados. Suponga que 50% de to-
dos los componentes los produce la línea A1, 30% la línea A2
y 20% la línea A3. Si un componente seleccionado al azar
tiene que ser retrabajado, ¿cuál es la probabilidad de que
provenga de la línea A1? ¿De la línea A2? ¿De la línea A3?
105. Desechando la posibilidad de cumplir años el 29 de febre-
ro, suponga que es igualmente probable que un individuo
seleccionado al azar haya nacido en cualquiera de los de-
más 365 días.
a. Si se seleccionan al azar diez personas, ¿cuál es la pro-
babilidad que tendrán diferentes cumpleaños? ¿De que
por lo menos dos tengan el mismo cumpleaños?
b. Si k reemplaza a diez en el inciso a), ¿cuál es la k más
pequeña para la cual existe por lo menos una probabili-
dad de 50-50 de que dos o más personas tengan el mis-
mo cumpleaños?
c. Si seleccionan diez personas al azar, ¿cuál es la proba-
bilidad de que por los menos dos tengan el mismo cum-
pleaños o por lo menos dos tengan los mismos tres
últimos dígitos de sus números del Seguro Social? [No-
ta: El artículo “Methods for Studying Coincidences” (F.
Mosteller y P. Diaconis, J. Amer. Stat. Assoc., 1989:
853–861) discute problemas de este tipo.]
106. Un método utilizado para distinguir entre rocas graníticas
(G) y basálticas (B) es examinar una parte del espectro infra-
rrojo de la energía solar reflejada por la superficie de la ro-
ca. Sean R1, R2 y R3 intensidades espectrales medidas a tres
c2_p046-085.qxd 3/12/08 3:59 AM Page 83](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-101-320.jpg)
![84 CAPÍTULO 2 Probabilidad
longitudes de onda diferentes, en general, para granito R1
R2 R3, en tanto que para basalto R3 R1 R2. Cuando se
hacen mediciones a distancia (mediante un avión), varios or-
denamientos de Ri pueden presentarse ya sea que la roca sea
basalto o granito. Vuelos sobre regiones de composición co-
nocida han arrojado la siguiente información:
Granito Basalto
R1 R2 R3 60% 10%
R1 R3 R2 25% 20%
R3 R1 R2 15% 70%
Suponga que para una roca seleccionada al azar en cierta
región P(granito) 0.25 y P(basalto) 0.75.
a. Demuestre que P(granito | R1 R2 R3) P(basalto |
R1 R2 R3). Si las mediciones dieron R1 R2 R3,
¿clasificaría la roca como granito o como basalto?
b. Si las mediciones dieron R1 R3 R2, ¿cómo clasifi-
caría la roca? Responda la misma pregunta para R3
R1 R2.
c. Con las reglas de clasificación indicadas en los incisos
a) y b) cuando se seleccione una roca de esta región,
¿cuál es la probabilidad de una clasificación errónea?
[Sugerencia: G podría ser clasificada como B o B como
G y P(B) y P(G) son conocidas.]
d. Si P(granito p en lugar de 0.25, ¿existen valores de p
(aparte de 1) para los cuales una roca siempre sería cla-
sificada como granito?
107. A un sujeto se le permite una secuencia de vistazos para de-
tectar un objetivo. Sea Gi {el objetivo es detectado en el
vistazo i-ésimo}, con pi P(Gi). Suponga que los Gi son
eventos independientes y escriba una expresión para la pro-
babilidad de que el objetivo haya sido detectado al final del
vistazo n-ésimo. [Nota: Este modelo se discute en “Predicting
Aircraft Detectability”, Human Factors, 1979: 277–291.]
108. En un juego de béisbol de Ligas menores, el lanzador del
equipo A lanza un “strike” 50% del tiempo y una bola 50%
del tiempo; los lanzamientos sucesivos son independientes
unos de otros y el lanzador nunca golpea a un bateador. Sa-
biendo esto, el “mánager” del equipo B ha instruido al pri-
mer bateador que no le batee a nada. Calcule la probabilidad
de que:
a. El bateador reciba base por bolas en el cuarto lanza-
miento.
b. El bateador reciba base por bolas en el sexto lanza-
miento (por lo que dos de los primeros cinco deben ser
“strikes”), por medio de un argumento de conteo o un
diagrama de árbol.
c. El bateador recibe base por bolas.
d. El primer bateador en el orden al bat anota mientras no
hay ningún “out” (suponiendo que cada bateador utili-
za la estrategia de no batearle a nada).
109. Cuatro ingenieros, A, B, C y D han sido citados para entre-
vistas de trabajo a las 10 A.M., el viernes 13 de enero, en
Random Sampling, Inc. El gerente de personal ha progra-
mado a los cuatro para las oficinas de entrevistas 1, 2, 3 y
4, respectivamente. Sin embargo, el secretario del gerente
no está enterado de esto, por lo que los asigna a las oficinas
de un modo completamente aleatorio (¡Qué más!) ¿Cuál es
la probabilidad de que
a. Los cuatro terminen en las oficinas correctas?
b. Ninguno de los cuatro termine en la oficina correcta?
110. Una aerolínea particular opera vuelos a las 10 A.M., de
Chicago a Nueva York, Atlanta y Los Ángeles. Sea A el
evento en que el vuelo a Nueva York está lleno y defina
los eventos B y C en forma análoga para los otros dos vuelos.
Suponga que P(A) 0.6, P(B) 0.5, P(C) 0.4 y los tres
eventos son independientes. ¿Cuál es la probabilidad de que
a. Los tres vuelos estén llenos? Que por lo menos uno no
esté lleno?
b. Sólo el vuelo a Nueva York esté lleno? Que exactamen-
te uno de los tres vuelos esté lleno?
111. Un gerente de personal va a entrevistar cuatro candidatos
para un puesto. Éstos están clasificados como 1, 2, 3 y 4 en
orden de preferencia y serán entrevistados en orden aleato-
rio. Sin embargo, al final de cada entrevista, el gerente sa-
brá sólo cómo se compara el candidato actual con los
candidatos previamente entrevistados. Por ejemplo, el or-
den de entrevista 3, 4, 1, 2 no genera información después de
la primera entrevista, muestra que el segundo candidato es
peor que el primero y que el tercero es mejor que los pri-
meros dos. Sin embargo, el orden 3, 4, 2, 1 generaría la
misma información después de cada una de las primeras
tres entrevistas. El gerente desea contratar al mejor candi-
dato pero debe tomar una decisión irrevocable de contratar-
lo o no contratarlo después de cada entrevista. Considere la
siguiente estrategia: Rechazar automáticamente a los pri-
meros s candidatos y luego contratar al primer candidato
subsiguiente que resulte mejor entre los que ya fueron en-
trevistados (si tal candidato no aparece, el último entrevis-
tado es el contratado).
Por ejemplo, con s 2, el orden 3, 4, 1, 2 permitiría con-
tratar al mejor, en tanto que el orden 3, 1, 2, 4 no. De los cua-
tro posibles valores de s (0, 1, 2 y 3), ¿cuál incrementa al
máximo a P(el mejor es contratado)? [Sugerencia: los 24 or-
denamientos de entrevista igualmente probables: s 0 signi-
fica que el primer candidato es automáticamente contratado.]
112. Considere cuatro eventos independientes A1, A2, A3 y A4 y
sea pi P(Ai) con i 1, 2, 3, 4. Exprese la probabilidad
de que por lo menos uno de estos eventos ocurra en fun-
ción de las pi y haga lo mismo para la probabilidad de que
por lo menos dos de los eventos ocurran.
113. Una caja contiene los siguientes cuatro papelitos y cada
uno tiene exactamente las mismas dimensiones: (1) gana el
premio 1; (2) gana el premio 2; (3) gana el premio 3; (4)
ganan los premios 1, 2 y 3. Se selecciona un papelito al
azar. Sea A1 {gana el premio 1}, A2 {gana el premio
2} y A3 {gana el premio 3}. Demuestre que A1 y A2 son
independientes, que A1 y A3 son independientes y que A2 y
A3 también son independientes (esta es una independencia
por pares). Sin embargo, demuestre que P(A1 A2 A3)
P(A1) P(A2) · P(A3), así que los tres eventos no son mu-
tuamente independientes.
114. Demuestre que si A1, A2 y A3 son eventos independientes,
entonces P(A1 | A2 A3) P(A1).
c2_p046-085.qxd 3/12/08 3:59 AM Page 84](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-102-320.jpg)
![(Monte Whitney) y el valor más pequeño posible es 282 (Valle de la Muerte). El conjun-
to de todos los valores posibles de Y es el conjunto de todos los números en el intervalo en-
tre 282 y 14 494, es decir,
{y: y es un número, 282 y 14 494}
y existe un número infinito de números en este intervalo. ■
Dos tipos de variables aleatorias
En la sección 1.2, se distinguió entre los datos que resultan de observaciones de una varia-
ble de conteo y los datos obtenidos observando valores de una variable de medición. Una
distinción un poco más formal caracteriza dos tipos diferentes de variables aleatorias.
3.1 Variables aleatorias 89
DEFINICIÓN Una variable aleatoria discreta es una variable aleatoria cuyos valores posibles o
constituyen un conjunto finito o bien pueden ser puestos en lista en una secuencia in-
finita en la cual existe un primer elemento, un segundo elemento, y así sucesivamen-
te (“contablemente” infinita).
Una variable aleatoria es continua si ambas de las siguientes condiciones aplican:
1. Su conjunto de valores posibles se compone de o todos los números que hay en un
solo intervalo sobre la línea de numeración (posiblemente de extensión infinita, es
decir, desde hasta ) o todos los números en una unión excluyente de dichos
intervalos (p. ej., [0, 10] [20, 30]).
2. Ningún valor posible de la variable aleatoria tiene probabilidad positiva, esto es,
P(X c) 0 con cualquier valor posible de c.
Aunque cualquier intervalo sobre la línea de numeración contiene un número infinito de nú-
meros, se puede demostrar que no existe ninguna forma de crear una lista infinita de todos
estos valores, existen sólo demasiados de ellos. La segunda condición que describe una va-
riable aleatoria continua es tal vez contraintuitiva, puesto que parecería que implica una pro-
babilidad total de cero con todos los valores posibles. Pero en el capítulo 4 se verá que los
intervalos de valores tienen probabilidad positiva; la probabilidad de un intervalo se reduci-
rá a cero a medida que su ancho tienda a cero.
Todas las variables aleatorias de los ejemplos 3.1-3.4 son discretas. Como otro ejemplo, su-
ponga que se eligen al azar parejas de casados y que a cada persona se le hace una prueba de
sangre hasta encontrar un esposo y esposa con el mismo factor Rh. Con X el núme-
ro de pruebas de sangre que serán realizadas, los posibles valores de X son D {2, 4, 6, 8, . . .}.
Como los posibles valores se dieron en secuencia, X es una variable aleatoria discreta. ■
Para estudiar las propiedades básicas de las variables aleatorias discretas, sólo se re-
quieren las herramientas de matemáticas discretas: sumas y diferencias. El estudio de varia-
bles continuas requiere las matemáticas continuas del cálculo: integrales y derivadas.
Ejemplo 3.6
EJERCICIOS Sección 3.1 (1-10)
1. Una viga de concreto puede fallar o por esfuerzo cortante (S)
o flexión (F). Suponga que se seleccionan al azar tres vigas
que fallaron y que se determina el tipo de falla de cada una.
Sea X el número de vigas entre las tres seleccionadas que
fallaron por cortante. Ponga en lista cada resultado en el es-
pacio muestral junto con el valor asociado de X.
2. Dé tres ejemplos de variables aleatorias de Bernoulli (apar-
te de los que aparecen en el texto).
3. Con el experimento del ejemplo 3.3, defina dos variables
aleatorias más y mencione los valores posibles de cada una.
4. Sea X el número de dígitos no cero en un código postal
seleccionado al azar. ¿Cuáles son los posibles valores de X?
Dé tres posibles resultados y sus valores X asociados.
5. Si el espacio muestral S es un conjunto infinito, ¿implica es-
to necesariamente que cualquier variable aleatoria X definida
c3_p086-129.qxd 3/12/08 4:01 AM Page 89](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-107-320.jpg)
![Como F es una constante entre enteros positivos
F(x) { 0 x 1
1 (1 p)[x]
x 1
(3.5)
donde [x] es el entero más grande x (p. ej., [2.7] 2). Así pues, si p 0.51 como el ejem-
plo de los nacimientos, entonces la probabilidad de tener que examinar cuando mucho cinco
nacimientos para ver el primer niño es F(5) 1 (0.49)5
1 0.0282 0.9718, mien-
tras que F(10) 1.0000. Esta función de distribución acumulativa se ilustra en la figura 3.6.
3.2 Distribuciones de probabilidad para variables aleatorias discretas 97
En los ejemplos presentados hasta ahora, la función de distribución acumulativa se de-
rivó de la función masa de probabilidad. Este proceso puede ser invertido para obtener la
función masa de probabilidad de la función de distribución acumulativa siempre que
ésta esté disponible. Por ejemplo, considérese otra vez la variable aleatoria del ejemplo 3.7
(el número de bombas en servicio en una gasolinería); los valores posibles de X son 0,
1, . . . , 6. Entonces
p(3) P(X 3)
[p(0) p(1) p(2) p(3)] [p(0) p(1) p(2)]
P(X 3) P(X 2)
F(3) F(2)
Más generalmente, la probabilidad de que X quede dentro de un intervalo especificado es
fácil de obtener a partir de la función de distribución acumulativa. Por ejemplo,
P(2 X 4) p(2) p(3) p(4)
[p(0) . . . p(4)] [p(0) p(1)]
P(X 4) P(X 1)
F(4) F(1)
Obsérvese que P(2 X 4) F(4) F(2). Esto es porque el valor 2 de X está incluido
en 2 X 4, así que no se desea restar su probabilidad. Sin embargo, P(2 X 4)
F(4) F(2) porque X 2 no está incluido en el intervalo 2 X 4.
x
F(x)
1
0 1 2 3 4 5 50 51
Figura 3.6 Gráfica de F(x) del ejemplo 3.14. ■
PROPOSICIÓN Para dos números cualesquiera a y b con a b.
P(a X b) F(b) F(a )
donde “a” representa el valor posible de X más grande que es estrictamente menor
que a. En particular, si los únicos valores posibles son enteros y si a y b son enteros,
entonces
P(a X b) P(X a o a 1 o . . . o b)
F(b) F(a 1)
Con a b se obtiene P(X a) F(a) F(a 1) en este caso.
c3_p086-129.qxd 3/12/08 4:01 AM Page 97](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-115-320.jpg)
![La razón para restar F(a) en lugar de F(a) es que se desea incluir P(X a);
F(b) F(a) da P(a X b). Esta proposición se utilizará extensamente cuando se calcu-
len las probabilidades binomial y de Poisson en las secciones 3.4 y 3.6.
Sea X el número de días de ausencia por enfermedad tomados por un empleado seleccio-
nado al azar de una gran compañía durante un año particular. Si el número máximo de días
de ausencia por enfermedad permisibles al año es de 14, los valores posibles de X son
0, 1, . . . , 14. Con F(0) 0.58, F(1) 0.72, F(2) 0.76, F(3) 0.81, F(4) 0.88 y
F(5) 0.94,
P(2 X 5) P(X 2, 3, 4 o 5) F(5) F(1) 0.22
y
P(X 3) F(3) F(2) 0.05 ■
98 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
Ejemplo 3.15
EJERCICIOS Sección 3.2 (11-28)
11. En un taller de servicio automotriz especializado en afinacio-
nes se sabe que 45% de todas las afinaciones se realizan en
automóviles de cuatro cilindros, 40% en automóviles de seis
cilindros y 15% en automóviles de ocho cilindros. Sea X el
número de cilindros en el siguiente carro que va a ser afinado.
a. ¿Cuál es la función masa de probabilidad de X?
b. Trace tanto una gráfica lineal como un histograma de
probabilidad de la función masa de probabilidad del
inciso a).
c. ¿Cuál es la probabilidad de que el siguiente carro afinado
sea de por lo menos seis cilindros? ¿Más de seis cilin-
dros?
12. Las líneas aéreas en ocasiones venden boletos de más. Su-
ponga que para un avión de 50 asientos, 55 pasajeros tienen
boletos. Defina la variable aleatoria Y como el número de
pasajeros con boletos que en realidad aparecen para el vue-
lo. La función masa de probabilidad de Y aparece en la tabla
adjunta.
a. ¿Cuál es la probabilidad de que el vuelo acomodará a to-
dos los pasajeros con boleto que aparecieron?
b. ¿Cuál es la probabilidad de que no todos los pasajeros
con boleto que aparecieron puedan ser acomodados?
c. Si usted es la primera persona en la lista de espera (lo que
significa que será el primero en abordar el avión si hay
boletos disponibles después de que todos los pasajeros
con boleto hayan sido acomodados), ¿cuál es la probabi-
lidad de que podrá tomar el vuelo? ¿Cuál es esta proba-
bilidad si usted es la tercera persona en la lista de espera?
13. Una empresa de ventas en línea dispone de seis líneas telefó-
nicas. Sea X el número de líneas en uso en un tiempo espe-
cificado. Suponga que la función masa de probabilidad de X
es la que se da en la tabla adjunta.
Calcule la probabilidad de cada uno de los siguientes eventos.
a. {cuando mucho tres líneas están en uso}
b. {menos de tres líneas están en uso}
c. {por lo menos tres líneas están en uso}
d. {entre dos y cinco líneas, inclusive, están en uso}
e. {entre dos y cuatro líneas, inclusive, no están en uso
f. {por lo menos cuatro líneas no están en uso}
14. El departamento de planeación de un condado requiere que
un contratista presente uno, dos, tres, cuatro o cinco formas
(según la naturaleza del proyecto) para solicitar un permiso
de construcción. Sea Y número de formas requeridas del
siguiente solicitante. Se sabe que la probabilidad de que se
requieran y formas es proporcional a y, es decir, p(y) ky
con y 1, . . . , 5.
a. ¿Cuál es el valor de k? [Sugerencia: 5
y1 p(y) 1.]
b. ¿Cuál es la probabilidad de que cuando mucho se requie-
ran tres formas?
c. ¿Cuál es la probabilidad de que se requieran entre dos y
cuatro formas (inclusive)?
d. ¿Podría ser p(y) y2
/50 con y 1, . . . , 5 la función
masa de probabilidad de Y?
15. Muchos fabricantes cuentan con programas de control de ca-
lidad que incluyen la inspección de los materiales recibidos
en busca de defectos. Suponga que un fabricante de compu-
tadoras recibe tarjetas madre en lotes de cinco. Se seleccio-
nan dos tarjetas de cada lote para inspeccionarlas. Se pueden
representar los posibles resultados del proceso de selección
por pares. Por ejemplo, el par (1, 2) representa la selec-
ción de las tarjetas 1 y 2 para inspección.
a. Mencione los diez posibles resultados diferentes.
b. Suponga que las tarjetas 1 y 2 son las únicas tarjetas de-
fectuosas en un lote de cinco. Dos tarjetas tienen que ser
seleccionadas al azar. Defina X como el número de tarje-
tas defectuosas observadas entre las inspeccionadas. En-
cuentre la distribución de probabilidad de X.
c. Sea F(x) la función de distribución acumulativa de X. Pri-
mero determine F(0) P(X 0), F(1) y F(2); luego ob-
tenga F(x) para todas las demás x.
16. Algunas partes de California son particularmente propensas
a los temblores. Suponga que en un área metropolitana, 30%
de todos los propietarios de casa están asegurados contra da-
ños provocados por terremotos. Se seleccionan al azar cuatro
y 45 46 47 48 49 50 51 52 53 54 55
p(y) 0.05 0.10 0.12 0.14 0.25 0.17 0.06 0.05 0.03 0.02 0.01
x 0 1 2 3 4 5 6
p(x) 0.10 0.15 0.20 0.25 0.20 0.06 0.04
c3_p086-129.qxd 3/12/08 4:01 AM Page 98](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-116-320.jpg)
![propietarios de casa, sea X el número entre los cuatro que es-
tán asegurados contra terremotos.
a. Encuentre la distribución de probabilidad de X [Sugeren-
cia: Sea S un propietario de casa asegurado y F uno no
asegurado. Entonces un posible resultado es SFSS, con
probabilidad (0.3)(0.7)(0.3)(0.3) y el valor 3 de X asocia-
do. Existen otros 15 resultados.]
b. Trace el histograma de probabilidad correspondiente.
c. ¿Cuál es el valor más probable de X?
d. ¿Cuál es la probabilidad de que por lo menos dos de los
cuatro seleccionados estén asegurados contra terremotos?
17. El voltaje de una batería nueva puede ser aceptable (A) o
inaceptable (U). Una linterna requiere dos baterías, así que
las baterías serán independientemente seleccionadas y pro-
badas hasta encontrar dos aceptables. Suponga que 90% de
todas las baterías tienen voltajes aceptables. Sea Y el núme-
ro de baterías que deben ser probadas.
a. ¿Cuál es p(2), es decir P(Y 2)?
b. ¿Cuál es p(3)? [Sugerencia: Existen dos resultados dife-
rentes que producen Y 3.]
c. Para tener Y 5, ¿qué debe ser cierto de la quinta bate-
ría seleccionada? Mencione los cuatro resultados con los
cuales Y 5 y luego determine p(5).
d. Use el patrón de sus respuestas en los incisos a)–c)
para obtener una fórmula general para p(y).
18. Dos dados de seis caras son lanzados al aire en forma inde-
pendiente. Sea M el máximo de los dos lanzamientos (por
lo tanto M(1, 5) 5, M(3, 3) 3, etcétera).
a. ¿Cuál es la función masa de probabilidad de M? [Suge-
rencia: Primero determine p(1), luego p(2), y así sucesi-
vamente.]
b. Determine la función de distribución acumulativa de M y
dibújela.
19. Una biblioteca se suscribe a dos revistas de noticias semana-
les, cada una de las cuales se supone que llega en el correo
de los miércoles. En realidad, cada una puede llegar el miér-
coles, jueves, viernes o sábado. Suponga que las dos llegan
independientemente una de otra y para cada una P(mié)
0.3, P(jue) 0.4, P(vie) 0.2 y P(sáb) 0.1. Sea Y el
número de días después del miércoles que pasan para que am-
bas revistas lleguen (por lo tanto los posibles valores de Y son
0, 1, 2 o 3). Calcule la función masa de probabilidad de
Y [Sugerencia: Hay 16 posibles resultados: Y(M, M) 0,
Y(V, J) 2, y así sucesivamente.]
20. Tres parejas y dos individuos solteros han sido invitados a un
seminario de inversión y han aceptado asistir. Suponga que
la probabilidad de que cualquier pareja o individuo particular
llegue tarde es de 0.4 (una pareja viajará en el mismo ve-
hículo, así que ambos llegarán a tiempo o bien ambos llega-
rán tarde). Suponga que diferentes parejas e individuos llegan
puntuales o tarde independientemente unos de otros. Sea X
el número de personas que llegan tarde al seminario.
a. Determine la función masa de probabilidad de X. [Suge-
rencia: Designe las tres parejas #1, #2 y #3 y los dos in-
dividuos #4 y #5.]
b. Obtenga la función de distribución acumulativa de X y
úsela para calcular P(2 X 6).
21. Suponga que lee los números de este año del NewYork Times y
que anota cada número que aparece en un artículo de noticias:
el ingreso de un oficial ejecutivo en jefe, el número de cajas de
vino producidas por una compañía vinícola, la contribución ca-
ritativa total de un político durante el año fiscal previo, la edad
de una celebridad y así sucesivamente. Ahora enfóquese en el
primer dígito de cada número, el cual podría ser 1, 2, . . . , 8
o 9. Su primer pensamiento podría ser que el primer dígito X
de un número seleccionado al azar sería igualmente probable
que fuera una de las nueve posibilidades (una distribución
uniforme discreta). Sin embargo, mucha evidencia empírica así
como también algunos argumentos teóricos, sugieren una dis-
tribución de probabilidad alternativa llamada ley de Benford:
p(x) P(el primer dígito es x) log10 (1 1/x) x 1, 2, . . . , 9
a. Calcule las probabilidades individuales y compare con la
distribución uniforme discreta correspondiente.
b. Obtenga la función de distribución acumulativa de X.
c. Utilizando la función de distribución acumulativa, ¿cuál
es la probabilidad de que el primer dígito sea cuando mu-
cho 3? ¿Por lo menos 5?
[Nota: La ley de Benford es la base de algunos procedimien-
tos de auditoría utilizados para detectar fraudes en reportes fi-
nancieros, por ejemplo, por el Servicio de Ingresos Internos.]
22. Remítase al ejercicio 13 y calcule y trace la gráfica de la fun-
ción de distribución acumulativa F(x). Luego utilícela para
calcular las probabilidades de los eventos dados en los inci-
sos a)–d) de dicho problema.
23. Una organización de protección al consumidor que habitual-
mente evalúa automóviles nuevos reporta el número de
defectos importantes encontrados en cada carro examinado.
Sea X el número de defectos importantes en un carro selec-
cionado al azar de cierto tipo. La función de distribución
acumulativa de X es la siguiente:
¨ 0 x 0
«0.06 0 x 1
«0.19 1 x 2
F(x)
©0.39 2 x 3
« 0.67 3 x 4
«0.92 4 x 5
«0.97 5 x 6
ª 1 6 x
Calcule las siguientes probabilidades directamente con la
función de probabilidad acumulativa:
a. p(2), es decir, P(X 2) b. P(X 3)
c. P(2 X 5) d. P(2 X 5)
24. Una compañía de seguros ofrece a sus asegurados varias opcio-
nes diferentes de pago de primas. Para un asegurado seleccio-
nado al azar, sea X el número de meses entre pagos sucesivos.
La función de distribución acumulativa es la siguiente:
¨ 0 x 1
«0.30 1 x 3
F(x)
©
0.40 3 x 4
0.45 4 x 6
«0.60 6 x 12
ª 1 12 x
3.2 Distribuciones de probabilidad para variables aleatorias discretas 99
c3_p086-129.qxd 3/12/08 4:01 AM Page 99](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-117-320.jpg)
![a. ¿Cuál es la función de masa de probabilidad de X?
b. Con sólo la función de distribución acumulativa, calcule
P(3 X 6) y P(4 X).
25. En el ejemplo 3.12, sea Y el número de niñas nacidas antes
de que termine el experimento. Con p P(B) y 1 – p P(G),
¿cuál es la función masa de probabilidad de Y? [Sugerencia:
Primero ponga en lista los posibles valores de Y, inicie con
el más pequeño y continúe hasta que encuentre una fórmu-
la general.]
26. Alvie Singer vive en 0 en el diagrama adjunto y sus cuatro
amigos viven en A, B, C y D. Un día Alvie decide visitarlos,
así que lanza al aire una moneda imparcial dos veces para
decidir a cuál de los cuatro visitar. Una vez que está en la
casa de uno de sus amigos, o regresará a su casa o bien pro-
seguirá a una de las dos casas adyacentes (tales como 0, A o
C, cuando está en B) con cada una de las tres posibilidades
cuya probabilidad es
1
3. De este modo, Alvie continúa visi-
tando a sus amigos hasta que regresa a casa.
a. Sea X el número de veces que Alvie visita a un amigo.
Obtenga la función masa de probabilidad de X.
b. Sea Y el número de segmentos de línea recta que Alvie
recorre (incluidos los que conducen a o que parten de 0).
¿Cuál es la función masa de probabilidad de Y?
c. Suponga que sus amigas viven en A y C y sus amigos en
B y D. Si Z el número de visitas a amigas, ¿cuál es la
función masa de probabilidad de Z?
27. Después de que todos los estudiantes salieron del salón de
clases, un profesor de estadística nota que cuatro ejemplares
del texto se quedaron debajo de los escritorios. Al principio
de la siguiente clase, el profesor distribuye los cuatro libros
al azar a cada uno de los cuatro estudiantes (1, 2, 3 y 4) que
dicen haber dejado los libros. Un posible resultado es que 1
reciba el libro de 2, que 2 reciba el libro de 4 y que 3 reciba
su propio libro y que 4 reciba el libro de 1. Este resultado
puede ser abreviado como (2, 4, 3, 1).
a. Mencione los otros 23 posibles resultados.
b. Si X es el número de estudiantes que reciben su propio li-
bro, determine la función masa de probabilidad de X.
28. Demuestre que la función de distribución acumulativa de
F(x) es una función no decreciente; es decir, x1 x2 im-
plica que F(x1) F(x2). ¿En qué condición será F(x1)
F(x2)?
100 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
B
C
A
D
0
Considérese una universidad que tiene 15 000 estudiantes y sea X el número de cursos en
los cuales está inscrito un estudiante seleccionado al azar. La función de masa de probabi-
lidad de X se determina como sigue. Como p(1) 0.01, se sabe que (0.01) (15000) 150
de los estudiantes están inscritos en un curso y asimismo con los demás valores de x.
(3.6)
El número promedio de cursos por estudiante o el valor promedio de X en la población
se obtiene al calcular el número total de cursos tomados por todos los estudiantes y al dividir
entre el número total de estudiantes. Como cada uno de los 150 estudiantes está tomando un
curso, estos 150 contribuyen con 150 cursos al total. Asimismo, 450 estudiantes contribuyen
con 2(450) cursos, y así sucesivamente. El valor promedio de la población de X es entonces
4.57 (3.7)
Como 150/15 000 0.01 p(1), 450/15000 0.03 p(2), y así sucesivamente, una ex-
presión alterna para (3.7) es
1 p(1) 2 p(2) . . . 7 p(7) (3.8)
La expresión (3.8) muestra que para calcular el valor promedio de la población de X,
sólo se necesitan los valores posibles de X junto con las probabilidades (proporciones). En
particular, el tamaño de la población no viene al caso en tanto la función masa de probabi-
lidad esté dada por (3.6). El valor promedio o medio de X es entonces el promedio ponde-
rado de los posibles valores 1, . . . , 7, donde las ponderaciones son las probabilidades de
esos valores.
1(150) 2(450) 3(1950) . . . 7(300)
15000
3.3 Valores esperados
x 1 2 3 4 5 6 7
p(x) 0.01 0.03 0.13 0.25 0.39 0.17 0.02
Número de inscrito 150 450 1950 3750 5850 2550 300
c3_p086-129.qxd 3/12/08 4:01 AM Page 100](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-118-320.jpg)
![Valor esperado de una función
A menudo interesará el valor esperado de alguna función h(X) en lugar de X propiamente
dicha.
Suponga que una librería adquiere diez ejemplares de un libro a $6.00 cada uno para ven-
derlos a $12.00 en el entendimiento de que al final de un periodo de 3 meses cualquier
ejemplar no vendido puede ser compensado por $2.00. Si X el número de ejemplares ven-
didos, entonces el ingreso neto h(X) 12X 2(10 X) 60 10X 40. ■
El siguiente ejemplo sugiere una forma fácil de calcular el valor esperado de h(X).
Sea X el número de cilindros del motor del siguiente carro que va a ser afinado en cierto
taller. El costo de una afinación está relacionado con X mediante h(X) 20 3X 0.5X2
.
Como X es una variable aleatoria, también lo es h(X); denote esta última variable aleatoria
por Y. Las funciones de masa de probabilidad de X y Y son las siguientes:
3.3 Valores esperados 103
Ejemplo 3.21
Ejemplo 3.22
x 4 6 8 y 40 56 76
p(x) 0.5 0.3 0.2 p(y) 0.5 0.3 0.2
Con D* denotando posibles valores de Y,
E(Y) E[h(X)]
D*
y p(y) (3.11)
(40)(0.5) (56)(0.3) (76)(0.2)
h(4) (0.5) h(6) (0.3) h(8) (0.2)
D
h(x) p(x)
De acuerdo con la ecuación (3.11), no fue necesario determinar la función masa de proba-
bilidad de Y para obtener E(Y); en su lugar, el valor esperado deseado es un promedio pon-
derado de los posibles valores de h(x) (y no de x). ■
Esto es, E[h(X)] se calcula del mismo modo que E(X), excepto que h(x) sustituye a x.
Una tienda de computadoras adquirió tres computadoras de un tipo a $500 cada una. Las
venderá a $1000 cada una. El fabricante se comprometió a readquirir cualquier computado-
ra que no se haya vendido después de un periodo especificado a $200 cada una. Sea X el nú-
mero de computadoras vendidas y suponga que p(0) 0.1, p(1) 0.2, p(2) 0.3 y
p(3) 0.4. Con h(X) denotando la utilidad asociada con la venta de X unidades, la informa-
ción dada implica que h(X) ingreso costo 1000X 200(3 X) 1500 800X 900.
La utilidad esperada es entonces
E[h(X)] h(0) p(0) h(1) p(1) h(2) p(2) h(3) p(3)
( 900)(0.1) ( 100)(0.2) (700)(0.3) (1500)(0.4)
$700 ■
PROPOSICIÓN Si la variable aleatoria X tiene un conjunto de posibles valores D y una función
masa de probabilidad p(x), entonces el valor esperado de cualquier función h(X), de-
notada por E[h(X)] o h(X), se calcula con
E[h(X)]
D
h(x) p(x)
Ejemplo 3.23
c3_p086-129.qxd 3/12/08 4:01 AM Page 103](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-121-320.jpg)
![Reglas de valor esperado
La función de interés h(X) con bastante frecuencia es una función lineal aX b. En este
caso, E[h(X)] es fácil de calcular a partir de E(X).
104 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
PROPOSICIÓN E(aX b) a E(X) b
(O, con notación alternativa, aX b X b.)
Parafraseando, el valor esperado de una función lineal es igual a la función lineal eva-
luada con el valor esperado E(X). Como h(X) en el ejemplo 3.23 es lineal y E(X) 2,
E[h(X)] 800(2) 900 $700, como antes.
Comprobación
E(aX b)
D
(ax b) p(x) a
D
x p(x) b
D
p(x)
aE(X) b ■
Dos casos especiales de proposición producen dos reglas importantes de valor espe-
rado.
1. Con cualquier constante a, E(aX) a E(X) (considérese b 0). (3.12)
2. Con cualquier constante b, E(X b) E(X) b (considérese a 1).
La multiplicación de X por una constante cambia la unidad de medición (de dólares a
centavos, donde a 100, pulgadas a centímetros, donde a 2.54, etc.). La regla 1 dice que
el valor esperado en las nuevas unidades es igual al valor esperado en las viejas unidades
multiplicado por el factor de conversión a. Asimismo, si se agrega una constante b a cada
valor posible de X, entonces el valor esperado se desplazará en esa misma cantidad cons-
tante.
Varianza de X
El valor esperado de X describe dónde está centrada la distribución de probabilidad. Utili-
zando la analogía física de colocar una masa puntual p(x) en el valor x sobre un eje unidi-
mensional, si el eje estuviera entonces soportado por un fulcro colocado en , el eje no
tendería a ladearse. Esto se ilustra para dos distribuciones diferentes en la figura 3.7.
p(x)
0.5
1 2 3
(a )
5
p(x)
0.5
1 2 3 5 6 7 8
(b )
Figura 3.7 Dos distribuciones de probabilidad diferentes con 4.
Aunque ambas distribuciones ilustradas en la figura 3.7 tienen el mismo centro , la
distribución de la figura 3.7(b) tiene una mayor dispersión o variabilidad que la de la figu-
ra 3.7(a). Se utilizará la varianza de X para evaluar la cantidad de variabilidad en (la distri-
bución de) X, del mismo modo que se utilizó s2
en el capítulo 1 para medir la variabilidad
en una muestra.
c3_p086-129.qxd 3/12/08 4:01 AM Page 104](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-122-320.jpg)
![La cantidad h(X) (X – )2
es la desviación al cuadrado de X con respecto a su me-
dia y 2
es la desviación al cuadrado esperada, es decir, el promedio ponderado de desvia-
ciones al cuadrado, donde las ponderaciones son probabilidades de la distribución. Si la
mayor parte de la distribución de probabilidad está cerca de , entonces 2
será relativamen-
te pequeña. Sin embargo, existen valores x alejados de que tienen una gran p(x), en ese
caso 2
será bastante grande.
Si X es el número de cilindros del siguiente carro que va a ser afinado en un taller de servi-
cio, con la función masa de probabilidad dada en el ejemplo 3.22 [p(4) 0.5, p(6) 0.3,
p(8) 0.2, a partir de la cual 5.4], entonces
V(X) 2
8
x4
(x 5.4)2
p(x)
(4 5.4)2
(0.5) (6 5.4)2
(0.3) (8 5.4)2
(0.2) 2.44
La desviación estándar de X es 2
.4
4
1.562. ■
Cuando la función masa de probabilidad p(x) especifica un modelo matemático
para la distribución de los valores de la población, tanto 2
como miden la dispersión de
los valores en la población; 2
es la varianza de la población y es su desviación estándar.
Fórmula abreviada para 2
El número de operaciones aritméticas necesarias para calcular 2
pueden reducirse si se uti-
liza una fórmula de cálculo alternativa.
3.3 Valores esperados 105
DEFINICIÓN Sea p(x) la función masa de probabilidad de X y su valor esperado. En ese caso la
varianza de X, denotada por V(X) o 2
X o simplemente 2
, es
V(X)
D
(x )2
p(x) E[(X )2
]
La desviación estándar (DE) de X es
X
2
X
PROPOSICIÓN V(X) 2
D
x2
p(x)
2
E(X2
) [E(X)]2
Al utilizar esta fórmula, E(X2
) se calcula primero sin ninguna sustracción; acto seguido E(X)
se calcula, se eleva al cuadrado y se resta (una vez) de E(X2
).
La función masa de probabilidad del número de cilindros X del siguiente carro que va a ser
afinado en un taller se dio en el ejemplo 3.24 como p(4) 0.5, p(6) 0.3 y p(8) 0.2,
a partir de las cuales 5.4 y
E(X2
) (42
)(0.5) (62
)(0.3) (82
)(0.2) 31.6
Por lo tanto 2
31.6 (5.4)2
2.44 en el ejemplo 3.24. ■
Ejemplo 3.24
Ejemplo 3.25
c3_p086-129.qxd 3/12/08 4:01 AM Page 105](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-123-320.jpg)
![Comprobación de la fórmula abreviada
Expándase (x )2
en la definición de 2
para obtener x2
2x 2
y luego lleve a
cada uno de los tres términos:
2
D
x2
p(x) 2
D
x p(x) 2
D
p(x)
E(X2
) 2 2
E(X2
) 2
■
Reglas de varianza
La varianza de h(X) es el valor esperado de la diferencia al cuadrado entre h(X) y su valor
esperado:
V[h(X)] 2
h (X)
D
{h(x) E[h(X)]}2
p(x) (3.13)
Cuando h(X) aX b, una función lineal
h(x) E[h(X)] ax b (a b) a(x )
Sustituyendo esto en la ecuación (3.13) se obtiene una relación simple entre V[h(X)] y V(X):
106 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
El valor absoluto es necesario porque a podría ser negativa, no obstante una desviación es-
tándar no puede serlo. Casi siempre la multiplicación por a corresponde a un cambio de la
unidad de medición (p. ej., kg a lb o dólares a euros). De acuerdo con la primera relación
en (3.14), la desviación estándar en la nueva unidad es la desviación estándar original mul-
tiplicada por el factor de conversión. La segunda relación dice que la adición o sustracción
de una constante no impacta la variabilidad; simplemente desplaza la distribución a la dere-
cha o izquierda.
En el problema de ventas de computadoras del ejemplo 3.23, E(X) 2 y
E(X2
) (0)2
(0.1) (1)2
(0.2) (2)2
(0.3) (3)2
(0.4) 5
así que V(X) 5 (2)2
1. La función de utilidad h(X) 800X 900 tiene entonces la
varianza (800)2
· V(X) (640 000)(1) 640 000 y la desviación estándar 800. ■
29. La función masa de probabilidad de X el número de de-
fectos importantes en un aparato eléctrico de un tipo selec-
cionado al azar es
Calcule lo siguiente:
a. E(X).
b. V(X) directamente a partir de la definición.
c. La desviación estándar de X.
d. V(X) por medio de la fórmula abreviada.
30. Se selecciona al azar un individuo que tiene asegurado su au-
tomóvil con una compañía. Sea Y el número de infracciones
de tránsito por las que el individuo fue citado durante los úl-
timos 3 años. La función masa de probabilidad de Y es
PROPOSICIÓN
En particular,
(3.14)
saX 5 |a| ? sX, sX1b 5 sX
VsaX 1 bd 5 s2
aX1b 5 a2
? s2
X and saX1b 5 |a| ? sx
Ejemplo 3.26
EJERCICIOS Sección 3.3 (29-45)
x 0 1 2 3 4
p(x) 0.08 0.15 0.45 0.27 0.05
y 0 1 2 3
p(y) 0.60 0.25 0.10 0.05
c3_p086-129.qxd 3/12/08 4:01 AM Page 106](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-124-320.jpg)
![a. Calcule E(Y).
b. Suponga que un individuo con Y infracciones incurre en
un recargo de $100Y2
. Calcule la cantidad esperada del
recargo.
31. Remítase al ejercicio 12 y calcule V(Y) y Y. Determine en-
tonces la probabilidad de que Y esté dentro de una desvia-
ción estándar de 1 de su valor medio.
32. Un distribuidor de enseres para el hogar vende tres mode-
los de congeladores verticales de 13.5, 15.9 y 19.1 pies cú-
bicos de espacio de almacenamiento, respectivamente. Sea
X la cantidad de espacio de almacenamiento adquirido
por el siguiente cliente que compre un congelador. Suponga
que X tiene la función masa de probabilidad
a. Calcule E(X), E(X2
) y V(X).
b. Si el precio de un congelador de X pies cúbicos de capa-
cidad es 25X 8.5, ¿cuál es el precio esperado pagado
por el siguiente cliente que compre un congelador?
c. ¿Cuál es la varianza del precio 25X 8.5 pagado por el
siguiente cliente?
d. Suponga que aunque la capacidad nominal de un conge-
lador X, la real es h(X) X 0.01X2
. ¿Cuál es la capa-
cidad real esperada del congelador adquirido por el
siguiente cliente?
33. Sea X una variable aleatoria de Bernoulli con función
masa de probabilidad como en el ejemplo 3.18.
a. Calcule E(X2
).
b. Demuestre que V(X) p(1 p).
c. Calcule E(X79
).
34. Suponga que el número de plantas de un tipo particular en-
contradas en una región particular (llamada cuadrante por
ecologistas) en cierta área geográfica es una variable aleato-
ria X con función masa de probabilidad
p(x) {c/x3
x 1, 2, 3, . . .
0 de lo contrario
¿Es E(X) finita? Justifique su respuesta (ésta es otra distribu-
ción que los estadísticos llamarían de cola gruesa).
35. Un pequeño mercado ordena ejemplares de cierta revista
para su exhibidor de revistas cada semana. Sea X deman-
da de la revista, con función masa de probabilidad
Suponga que el propietario de la tienda paga $1.00 por cada
ejemplar de la revista y el precio para los consumidores es
de $2.00. Si las revistas que se quedan al final de la semana
no tienen valor de recuperación, ¿es mejor ordenar tres o
cuatro ejemplares de la revista? [Sugerencia: Tanto para tres
o cuatro ejemplares ordenados, exprese un ingreso neto
como una función de la demanda X y luego calcule el ingre-
so esperado.]
36. Sea X el daño incurrido (en dólares) en un tipo de accidente
durante un año dado. Valores posibles de X son 0, 1000,
5000 y 10000 dólares con probabilidades de 0.8, 0.1, 0.08,
y 0.02, respectivamente. Una compañía particular ofrece una
póliza con deducible de $500. Si la compañía desea que su
utilidad esperada sea de $100, ¿qué cantidad de prima debe-
rá cobrar?
37. Los n candidatos para un trabajo fueron clasificados como
1, 2, 3, . . . , n. Sea X el rango de un candidato seleccio-
nado al azar, de modo que X tenga la función masa de pro-
babilidad
p(x) {1/n x 1, 2, 3, . . . , n
0 de lo contrario
(ésta se llama distribución uniforme discreta). Calcule E(X)
y V(X) por medio de la fórmula abreviada. [Sugerencia: La
suma de los primeros n enteros positivos es n(n 1)/2,
mientras que la suma de sus cuadrados es n(n 1)(2n 1) /6.]
38. Sea X el resultado cuando un dado imparcial es lanzado
una vez. Si antes de lanzar el dado le ofrecen o (1/3.5) dóla-
res o h(X) 1/X dólares, ¿aceptaría la suma garantizada o
jugaría? [Nota: Generalmente no es cierto que 1(E/X)
E(1/X).]
39. Una compañía de productos químicos en la actualidad tiene
en existencia 100 lb de un producto químico, el cual se ven-
de a sus clientes en lotes de 5 lb. Sea X el número de lo-
tes solicitados por un cliente seleccionado al azar y suponga
que X tiene la función masa de probabilidad
Calcule E(X) y V(X). Calcule enseguida el número esperado
de libras que quedan una vez que se envía el pedido del si-
guiente cliente y la varianza del número de libras sobrantes.
[Sugerencia: El número de libras que quedan es una función
lineal de X.]
40. a. Trace una gráfica lineal de la función masa de probabi-
lidad de X en el ejercicio 35. Enseguida determine la
función masa de probabilidad de X y trace su gráfica li-
neal. Con base en estas dos figuras, ¿qué se puede decir
sobre V(X) y V(X)?
b. Use la proposición que implica V(aX b) para estable-
cer una relación general entre V(X) y V(X).
41. Use la definición en la expresión (3.13) para comprobar que
V(aX b) a2
2
X. [Sugerencia: Con h(X) aX b,
E[h(X)] a b, donde E(X).]
42. Suponga E(X) 5 y E[X(X 1)] 27.5. ¿Cuál es
a. E(X2
)? [Sugerencia: E[X(X 1)] E(X2
X] E(X2
)
E(X)]?
b. V(X)?
c. La relación general entre las cantidades E(X), E[X(X) 1)]
y V(X)?
43. Escriba una regla general para E(X c), donde c es una
constante. ¿Qué sucede cuando hace c , el valor espera-
do de X?
44. Un resultado llamado desigualdad de Chebyshev establece
que para cualquier distribución de probabilidad de una
3.3 Valores esperados 107
x 13.5 15.9 19.1
p(x) 0.2 0.5 0.3
x 1 2 3 4 5 6
p(x) 1
1
5 1
2
5 1
3
5 1
4
5 1
3
5 1
2
5
x 1 2 3 4
p(x) 0.2 0.4 0.3 0.1
c3_p086-129.qxd 3/12/08 4:01 AM Page 107](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-125-320.jpg)
![a. Determine P(X 2).
b. Determine P(X 5).
c. Determine P(1 X 4).
d. ¿Cuál es la probabilidad que ninguna de estas 25 tarjetas
esté defectuosa?
e. Calcule el valor esperado y la desviación estándar X.
49. Una compañía que produce cristales finos sabe por expe-
riencia que 10% de sus copas de mesa tienen imperfecciones
cosméticas y deben ser clasificadas como “de segunda”.
a. Entre seis copas seleccionadas al azar, ¿qué tan probable
es que sólo una sea de segunda?
b. Entre seis copas seleccionadas al azar, ¿qué tan probable es
que por lo menos dos sean de segunda?
c. Si las copas se examinan una por una, ¿cuál es la proba-
bilidad de cuando mucho cinco deban ser seleccionadas
para encontrar cuatro que no sean de segunda?
50. Se utiliza un número telefónico particular para recibir tanto lla-
madas de voz como faxes. Suponga que 25% de las llamadas
entrantes son faxes y considere una muestra de 25 llamadas en-
trantes. ¿Cuál es la probabilidad de que
a. Cuando mucho 6 de las llamadas sean un fax?
b. Exactamente 6 de las llamadas sean un fax?
c. Por lo menos 6 de las llamadas sean un fax?
d. Más de 6 de las llamadas sean un fax?
51. Remítase al ejercicio previo.
a. ¿Cuál es el número esperado de llamadas entre las 25 que
impliquen un fax?
b. ¿Cuál es la desviación estándar del número entre las 25
llamadas que implican un fax?
c. ¿Cuál es la probabilidad de que el número de llamadas
entre las 25 que implican una transmisión de fax so-
brepase el número esperado por más de 2 desviaciones
estándar?
52. Suponga que 30% de todos los estudiantes que tienen que
comprar un texto para un curso particular desean un ejem-
plar nuevo (¡los exitosos!), mientras que el otro 70% desea
comprar un ejemplar usado. Considere seleccionar 25 com-
pradores al azar.
a. ¿Cuáles son el valor medio y la desviación estándar del
número que desea un ejemplar nuevo del libro?
b. ¿Cuál es la probabilidad de que el número que desea
ejemplares nuevos esté a más de dos desviaciones están-
dar del valor medio?
c. La librería tiene 15 ejemplares nuevos y 15 usados en exis-
tencia. Si 25 personas llegan una por una a comprar el tex-
to, ¿cuál es la probabilidad de las 25 que obtengan el tipo
de libro que desean de las existencias actuales? [Sugeren-
cia: Sea X el número que desea un ejemplar nuevo.
¿Con qué valores de X obtendrán las 15 lo que desean?]
d. Suponga que los ejemplares nuevos cuestan $100 y los
usados $70. Suponga que la librería en la actualidad tie-
ne 50 ejemplares nuevos y 50 usados. ¿Cuál es el valor
esperado del ingreso total por la venta de los siguientes
25 ejemplares comprados? Asegúrese de indicar qué re-
gla de valor esperado está utilizando. [Sugerencia: Sea
h(X) el ingreso cuando X de los 25 compradores de-
sean ejemplares nuevos. Exprese esto como una función
lineal.]
53. El ejercicio 30 (sección 3.3) dio la función masa de proba-
bilidad de Y, el número de citaciones de tránsito de un indi-
viduo seleccionado al azar asegurado por una compañía
particular. ¿Cuál es la probabilidad de que entre 15 indivi-
duos seleccionados al azar
a. por lo menos 10 no tengan citaciones?
b. menos de la mitad tengan por lo menos una citación?
c. el número que tengan por lo menos una citación esté en-
tre 5 y 10, inclusive?*
54. Un tipo particular de raqueta de tenis viene en tamaño me-
diano y en tamaño extragrande. El 60% de todos los clientes
en una tienda desean la versión extragrande.
a. Entre diez clientes seleccionados al azar que desean este
tipo de raqueta, ¿cuál es la probabilidad de que por lo
menos seis deseen la versión extragrande?
b. Entre diez clientes seleccionados al azar, ¿cuál es la proba-
bilidad de que el número que desea la versión extragrande
esté dentro de una desviación estándar del valor medio?
c. La tienda dispone actualmente de siete raquetas de cada
versión. ¿Cuál es la probabilidad de que los siguientes
diez clientes que desean esta raqueta puedan obtener la
versión que desean de las existencias actuales?
55. El 20% de todos los teléfonos de cierto tipo son llevados a
servicio mientras se encuentran dentro de la garantía. De és-
tos, 60% puede ser reparado, mientras el 40% restante debe
ser reemplazado con unidades nuevas. Si una compañía ad-
quiere diez de estos teléfonos, ¿cuál es la probabilidad de
que exactamente dos sean reemplazados bajo garantía?
56. La Junta de Educación reporta que 2% de los dos millones
de estudiantes de preparatoria que toman el SAT cada año
reciben un trato especial a causa de discapacidades documen-
tadas (Los Angeles Times, 16 de julio de 2002). Considere
una muestra aleatoria de 25 estudiantes que recientemente
presentaron el examen.
a. ¿Cuál es la probabilidad de que exactamente 1 reciba un
trato especial?
b. ¿Cuál es la posibilidad de que por lo menos 1 reciba
un trato especial?
c. ¿Cuál es la probabilidad de que por lo menos 2 reciban
un trato especial?
d. ¿Cuál es la probabilidad de que el número entre los 25
que recibieron un trato especial esté dentro de 2 desvia-
ciones estándar del número que esperaría reciba un trato
especial?
e. Suponga que a un estudiante que no recibe un trato espe-
cial se le permiten 3 horas para el examen, mientras que
a un estudiante que recibió un trato especial se le permi-
ten 4.5 horas. ¿Qué tiempo promedio piensa que le sería
permitido a los 25 estudiantes seleccionados?
57. Suponga que 90% de todas las baterías de cierto proveedor
tienen voltajes aceptables. Un tipo de linterna requiere que
las dos baterías sean tipo D y la linterna funcionará sólo
si sus dos baterías tienen voltajes aceptables. Entre diez lin-
ternas seleccionadas al azar, ¿cuál es la probabilidad de que
por lo menos nueve funcionarán? ¿Qué suposiciones hizo
para responder la pregunta planteada?
114 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
*
“Entre a y b, inclusive” equivale a (a X b).
c3_p086-129.qxd 3/12/08 4:01 AM Page 114](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-132-320.jpg)
![58. Un distribuidor recibe un lote muy grande de componentes.
El lote sólo puede ser caracterizado como aceptable si la
proporción de componentes defectuosos es cuando mucho
de 10. El distribuidor decide seleccionar 10 componentes al
azar y aceptar el lote sólo si el número de componentes de-
fectuosos presentes en la muestra es cuando mucho de 2.
a. ¿Cuál es la probabilidad de que el lote será aceptado
cuando la proporción real de componentes defectuosos es
de 0.01?, 0.05? 0.10? 0.20? 0.25?
b. Sea p la proporción real de componentes defectuosos
presentes en el lote. Una gráfica de P(se acepta el lote) en
función de p y con p sobre el eje horizontal y P(se acep-
ta el lote) sobre el eje vertical, se llama curva caracterís-
tica de operación del plan de muestreo de aceptación.
Use los resultados del inciso a) para trazar esta curva con
0 p 1.
c. Repita los incisos a) y b) con “1” reemplazando a “2” en
el plan de muestreo de aceptación.
d. Repita los incisos a) y b) con “15” reemplazando a “10”
en el plan de muestreo de aceptación.
e. ¿Cuál de estos planes de muestreo, el del inciso a), c) o
d) parece más satisfactorio y por qué?
59. Un reglamento que requiere que se instale un detector de
humo en todas las casas previamente construidas ha estado
en vigor en una ciudad particular durante 1 año. Al departa-
mento de bomberos le preocupa que muchas casas perma-
nezcan sin detectores. Sea p la proporción verdadera de
las casas que tienen detectores y suponga que se inspeccio-
na una muestra aleatoria de 25 casas. Si ésta indica marca-
damente que menos de 80% de todas las casas tienen un
detector, el departamento de bomberos lanzará una campaña
para la puesta en ejecución de un programa de inspección
obligatorio. Debido a lo caro del programa, el departamento
prefiere no requerir tales inspecciones a menos que una evi-
dencia muestral indique que se requieren. Sea X el número
de casas con detectores entre las 25 muestreadas. Considere
rechazar el requerimiento de que p 0.8 si x 15.
a. ¿Cuál es la probabilidad de que el requerimiento sea re-
chazado cuando el valor real de p es 0.8?
b. ¿Cuál es la probabilidad de no rechazar el requerimiento
cuando p 0.7? ¿Cuándo p 0.6?
c. ¿Cómo cambian las “probabilidades de error” de los inci-
sos a) y b) si el valor 15 en la regla de decisión es reem-
plazado por 14?
60. Un puente de cuota cobra $1.00 por cada automóvil de uso
particular y $2.50 por cualquier otro vehículo. Suponga que
durante el día 60% son vehículos de uso particular. Si 25
vehículos cruzan el puente durante un periodo determinado
del día, ¿cuál es la expectativa de ingresos resultantes en el
día? [Sugerencia: Exprese X número de automóviles de
uso particular; cuando el ingreso por concepto de cuota h(X)
es una función lineal de X].
61. Un estudiante que está tratando de escribir un ensayo para
un curso tiene la opción de dos temas, A y B. Si selecciona
el tema A, el estudiante pedirá dos libros mediante préstamo
interbiblioteca, mientras que si selecciona el tema B, el es-
tudiante pedirá cuatro libros. El estudiante cree que un buen
ensayo necesita recibir y utilizar por lo menos la mitad de
los libros pedidos para uno u otro tema seleccionado. Si la
probabilidad de que un libro pedido mediante préstamo inter-
biblioteca llegue a tiempo es de 0.9 y los libros llegan inde-
pendientemente uno de otro, ¿qué tema deberá seleccionar el
estudiante para incrementar al máximo la probabilidad de es-
cribir un buen ensayo? ¿Qué pasa si la probabilidad de que lle-
guen los libros es de sólo 0.5 en lugar de 0.9?
62. a. Con n fijo, ¿hay valores de p(0 p 1) para los cuales
V(X) 0? Explique por qué esto es así.
b. ¿Con qué valor de p se incrementa al máximo V(X)? [Su-
gerencia: Trace la gráfica de V(X) en función de p o bien
tome una derivada.]
63. a. Demuestre que b(x; n, 1 p) b(n x; n, p).
b. Demuestre que B(x; n, 1 p) 1 B(n x 1; n, p).
[Sugerencia: Cuando mucho x éxitos (S) equivalen a por
lo menos (n x) fracasos (F).]
c. ¿Qué implican los incisos a) y b) sobre la necesidad de
incluir valores de p más grandes que 0.5 en la tabla A.1
del apéndice?
64. Demuestre que E(X) np cuando X es una variable aleatoria
binomial [Sugerencia: Primero exprese E(X) como una suma
con límite inferior x 1. Luego saque a np como factor, sea
y x 1 de modo que la suma sea de y 0 a y n 1
y demuestre que la suma es igual a 1.]
65. Los clientes en una gasolinería pagan con tarjeta de crédi-
to (A), tarjeta de débito (B) o efectivo (C). Suponga qué
clientes sucesivos toman decisiones independientes con
P(A) 0.5, P(B) 0.2 y P(C) 0.3.
a. Entre los siguientes 100 clientes, ¿cuáles son la media y
varianza del número que paga con tarjeta de débito? Ex-
plique su razonamiento.
b. Conteste el inciso a) para el número entre 100 que no pa-
gan con efectivo.
66. Una limusina de aeropuerto puede transportar hasta cuatro
pasajeros en cualquier viaje. La compañía aceptará un máxi-
mo de seis reservaciones para un viaje y un pasajero debe te-
ner una reservación. Según registros previos, 20% de los que
reservan no se presentan para el viaje. Responda las siguien-
tes preguntas, suponiendo independencia en los casos en que
sea apropiado.
a. Si se hacen seis reservaciones, ¿cuál es la probabilidad de
que por lo menos un individuo con reservación no pueda
ser acomodado en el viaje?
b. Si se hacen seis reservaciones, ¿cuál es el número espe-
rado de lugares disponibles cuando la limusina parte?
c. Suponga que la distribución de probabilidad del número
de reservaciones hechas se da en la tabla adjunta.
Sea X el número de pasajeros en un viaje seleccionado al
azar. Obtenga la función masa de probabilidad de X.
67. Remítase a la desigualdad de Chebyshev dada en el ejercicio
44. Calcule P(°X ° k) con k 2 y k 3 cuando
X Bin (20, 0.5) y compare con el límite superior corres-
pondiente. Repita para X Bin(20, 0.75).
3.4 Distribución de probabilidad binomial 115
Número de reservaciones 3 4 5 6
Probabilidad 0.1 0.2 0.3 0.4
c3_p086-129.qxd 3/12/08 4:01 AM Page 115](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-133-320.jpg)
![Sea X el número de criaturas de un tipo particular capturadas en una trampa durante un
periodo determinado. Suponga que X tiene una distribución de Poisson con 4.5, así que
en promedio las trampas contendrán 4.5 criaturas [El artículo “Dispersal Dynamics of the
Bivalve Gemma Gemma in a Patchy Environment (Ecological Monographs, 1995: 1–20) su-
giere este modelo: el molusco bivalvo Gemma gemma es una pequeña almeja.] La probabi-
lidad de que una trampa contenga exactamente cinco criaturas es
P(X 5) 0.1708
La probabilidad de que una trampa contenga cuando mucho cinco criaturas es
P(X 5)
5
x0
e 4.5
1 4.5 . . .
0.7029 ■
La distribución de Poisson como límite
La siguiente proposición proporciona el razonamiento para utilizar la distribución de Pois-
son en muchas situaciones.
(4.5)5
5!
(4.5)2
2!
e 4.5
(4.5)x
x!
e 4.5
(4.5)5
5!
122 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
Ejemplo 3.39
De acuerdo con esta proposición, en cualquier experimento binomial en el cual n es
grande y p es pequeña, b(x; n, p) p(x; ), donde np. Como regla empírica, esta apro-
ximación puede ser aplicada con seguridad si n 50 y np 5.
Si un editor de libros no técnicos hace todo lo posible porque sus libros estén libres de erro-
res tipográficos, de modo que la probabilidad de que cualquier página dada contenga por lo
menos uno de esos errores es de 0.005 y los errores son independientes de una página a otra,
¿cuál es la probabilidad de que una de sus novelas de 400 páginas contenga exactamente una
página con errores? ¿Cuándo mucho tres páginas con errores?
Con S denotando una página que contiene por lo menos un error y F una página libre
de errores, el número X de páginas que contienen por lo menos un error es una variable alea-
toria binomial con n 400 y p 0.005, así que np 2. Se desea
P(X 1) b(1; 400, 0.005) p(1; 2) 0.270671
El valor binomial es b(1; 400, 0.005) 0.270669, así que la aproximación es muy buena.
Asimismo
P(X 3)
3
x0
p(x, 2)
3
x0
e 2
0.135335 0.270671 0.270671 0.180447
0.8571
y éste de nuevo se aproxima bastante al valor binomial P(X 3) 0.8576. ■
La tabla 3.2 muestra la distribución de Poisson con 3 junto con las tres distribu-
ciones binomiales con np 3 y la figura 3.8 (generada por S-Plus) ilustra una gráfica de la
distribución de Poisson junto con las dos primeras distribuciones binomiales. La aproxima-
ción es de uso limitado con n 30, pero desde luego la precisión es mejor con n 100 y
mucho mejor con n 300.
2x
x!
e 2
(2)1
1!
PROPOSICIÓN Suponga que en la función masa de probabilidad binomial b(x; n, p), si n A y
p A 0 de tal modo que np tienda a un valor 0. Entonces b(x; n, p) A p(x; ).
Ejemplo 3.40
c3_p086-129.qxd 3/12/08 4:01 AM Page 122](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-140-320.jpg)
![Proceso de Poisson
Una aplicación muy importante de la distribución de Poisson surge en conexión con la ocu-
rrencia de eventos de algún tipo en el transcurso del tiempo. Eventos de interés podrían ser
visitas a un sitio web particular, pulsos de alguna clase registrados por un contador, mensa-
jes de correo electrónico enviados a una dirección particular, accidentes en una instalación
industrial o lluvias de rayos cósmicos observados por astrónomos en un observatorio par-
ticular. Se hace la siguiente suposición sobre la forma en que los eventos de interés ocurren:
1. Existe un parámetro 0 de tal modo que durante cualquier intervalo de tiempo corto
t, la probabilidad de que ocurra exactamente un evento es t o(t).*
2. La probabilidad de que ocurra más de un evento durante t es o(t) [la que junto con
la suposición 1, implica que la probabilidad de cero eventos durante t es 1
t o(t)].
3. El número de eventos ocurridos durante este intervalo de tiempo t es independiente del
número ocurrido antes de este intervalo de tiempo.
Informalmente, la suposición 1 dice que durante un corto intervalo de tiempo, la probabili-
dad de que ocurra un solo evento es aproximadamente proporcional a la duración del inter-
valo de tiempo, donde es la constante de proporcionalidad. Ahora sea Pk(t) la probabilidad
de que k eventos serán observados durante cualquier intervalo de tiempo particular de dura-
ción t.
124 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
PROPOSICIÓN Pk(t) et
(t)k
/k!, de modo que el número de eventos durante un intervalo de
tiempo de duración t es una variable de Poisson con parámetro t. El número es-
perado de eventos durante cualquier intervalo de tiempo es entonces t, así que el nú-
mero esperado durante un intervalo de tiempo unitario es .
La ocurrencia de eventos en el transcurso del tiempo como se describió se llama proceso de
Poisson; el parámetro especifica el ritmo del proceso.
Suponga que llegan pulsos a un contador a un ritmo promedio de seis por minuto, así que
6. Para determinar la probabilidad de que en un intervalo de 0.5 min se reciba por lo
menos un pulso, obsérvese que el número de pulsos en ese intervalo tiene una distribución
de Poisson con parámetro t 6(0.5) 3 (se utiliza 0.5 min porque está expresada co-
mo ritmo por minuto). Entonces con X el número de pulsos recibidos en el intervalo de
30 segundos,
P(1 X) 1 P(X 0) 1 0.950 ■
En lugar de observar eventos en el transcurso del tiempo, considere observar eventos
de algún tipo que ocurren en una región de dos o tres dimensiones. Por ejemplo, se podría
seleccionar un mapa de una región R de un bosque, ir a dicha región y contar el número de
árboles. Cada árbol representaría un evento que ocurre en un punto particular del espacio.
Conforme a suposiciones similares a 1–3, se puede demostrar que el número de eventos que
ocurren en una región R tiene una distribución de Poisson con parámetro a(R), donde
a(R) es el área de R. La cantidad es el número esperado de eventos por unidad de área o
volumen.
e 3
(3)0
0!
Ejemplo 3.42
*
Una cantidad es o(t) (léase “o minúscula de delta t”) si, a medida que t tiende a cero, también lo hace o(t)/t.
Es decir, o(t) es incluso más insignificante (tiende a 0 más rápido) que t mismo. La cantidad (t)2
tiene esta pro-
piedad, pero sen(t) no.
c3_p086-129.qxd 3/12/08 4:01 AM Page 124](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-142-320.jpg)
![94. Considere un mazo compuesto de siete cartas, marcadas 1,
2, . . . , 7. Se seleccionan al azar tres de estas cartas. Defina
una variable aleatoria W como W la suma de los números
resultantes y calcule la función masa de probabilidad de W.
Calcule entonces y 2
. [Sugerencia: Considere los resul-
tados sin orden, de modo que (1, 3, 7) y (3, 1, 7) no son re-
sultados diferentes. Entonces existen 35 resultados y pueden
ser puestos en lista. (Este tipo de variable aleatoria en reali-
dad se presenta en conexión con una prueba de hipótesis lla-
mada prueba de suma de filas de Wilcoxon, en la cual hay
una muestra x y una muestra y y W es la suma de las filas de
x en la muestra combinada.)]
95. Después de barajar un mazo de 52 cartas, un tallador repar-
te 5. Sea X el número de palos representados en la mano
de 5 cartas.
a. Demuestre que la función masa de probabilidad de X es
[Sugerencia: p(1) 4P(todas son espadas), p(2) 6P(sólo
espadas y corazones con por lo menos una de cada palo) y
p(4) 4P(2 espadas una de cada otro palo).]
b. Calcule , 2
y .
96. La variable aleatoria binomial negativa X se definió como el nú-
mero de fallas (F) que preceden al r-ésimo éxito (S). Sea Y
el número de ensayos necesarios para obtener el r-ésimo éxito
(S). Del mismo modo en que fue derivada la función masa de
probabilidad, derive la función masa de probabilidad de Y.
97. De todos los clientes que adquieren abrepuertas de cochera
automáticas, 75% adquieren el modelo de transmisión por
cadena. Sea X el número entre los siguientes 15 compra-
dores que seleccionan el modelo de transmisión por cadena.
a. ¿Cuál es la función masa de probabilidad de X?
b. Calcule P(X 10).
c. Calcule P(6 X 10).
d. Calcule y 2
.
e. Si la tienda actualmente tiene en existencia 10 modelos
de transmisión por cadena y 8 modelos de transmisión
por flecha, ¿cuál es la probabilidad de que las solicitudes
de estos 15 clientes puedan ser satisfechas con las exis-
tencias actuales?
98. Un amigo recientemente planeó un viaje de campamento.
Tenía dos linternas, una que requería una sola batería de 6 V
y otra que utilizaba dos baterías de tamaño D. Antes había
empacado dos baterías de 6 V y cuatro tamaño D en su
“camper”. Suponga que la probabilidad de que cualquier ba-
tería particular funcione es p y que las baterías funcionan o
fallan independientemente una de otra. Nuestro amigo desea
llevar sólo una linterna. ¿Con qué valores de p deberá llevar
la linterna de 6 V?
99. Un sistema k de n es uno que funcionará si y sólo si por lo
menos k de los n componentes individuales en el sistema
funcionan. Si los componentes individuales funcionan inde-
pendientemente uno de otro, cada uno con probabilidad de
0.9, ¿cuál es la probabilidad de que un sistema 3 de 5 fun-
cione?
90. Si X tiene una distribución de Poisson con parámetro . De-
muestre que E(X) derivada directamente de la defini-
ción de valor esperado. [Sugerencia: El primer término en la
suma es igual a 0 y luego x puede ser eliminada. Ahora sa-
que como factor a y demuestre que la suma es uno.]
91. Suponga que hay árboles distribuidos en un bosque de
acuerdo con un proceso de Poisson bidimensional con pará-
metro , el número esperado de árboles por acre es de 80.
a. ¿Cuál es la probabilidad de que en un terreno de un cuar-
to de acre, haya cuando mucho 16 árboles?
b. Si el bosque abarca 85 000 acres, ¿cuál es el número es-
perado de árboles en el bosque?
c. Suponga que selecciona un punto en el bosque y constru-
ye un círculo de 0.1 milla de radio. Sea X el número de
árboles dentro de esa región circular. ¿Cuál es la función
masa de probabilidad de X? [Sugerencia: 1 milla cuadra-
da 640 acres.]
92. A una estación de inspección de equipo vehicular llegan au-
tomóviles de acuerdo con un proceso de Poisson con razón
10 por hora. Suponga que un vehículo que llega con
probabilidad de 0.5 no tendrá violaciones de equipo.
a. ¿Cuál es la probabilidad de que exactamente diez lleguen
durante la hora y que los diez no tengan violaciones?
b. Con cualquier y 10 fija, ¿cuál es la probabilidad de que
y automóviles lleguen durante la hora, diez de los cuales
no tengan violaciones?
c. ¿Cuál es la probabilidad de que lleguen diez carros “sin
violaciones” durante la siguiente hora? [Sugerencia: Sume
la probabilidades en el inciso b) desde y 10 hasta .]
93. a. En un proceso de Poisson, ¿qué tiene que suceder tanto en
el intervalo de tiempo (0, t) como en el intervalo (t, t
t) de modo que no ocurran eventos en todo el intervalo
(0, t t)? Use esto y las suposiciones 1–3 para escribir
una relación entre P0(t t) y P0(t).
b. Use el resultado del inciso a) para escribir una expresión
para la diferencia P0(t t) P0(t). Divida entonces en-
tre t y permita que t A 0 para obtener una ecuación
que implique (d/dt)P0(t), la derivada de P0(t) con respec-
to a t.
c. Verifique que P0(t) et
satisface la ecuación del in-
ciso b).
d. Se puede demostrar de manera similar a los incisos a) y
b) que Pk(t)s debe satisfacer el sistema de ecuaciones di-
ferenciales
Pk(t) Pk1(t) Pk(t)
k 1, 2, 3, . . .
Verifique que Pk(t) e t
(t)k
/k! satisface el sistema. (En
realidad esta es la única solución.)
d
dt
126 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
EJERCICIOS SUPLEMENTARIOS (94-122)
x 1 2 3 4
p(x) 0.002 0.146 0.588 0.264
c3_p086-129.qxd 3/12/08 4:01 AM Page 126](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-144-320.jpg)
![100. Un fabricante de baterías para linternas desea controlar la
calidad de sus productos rechazando cualquier lote en el
que la proporción de baterías que tienen un voltaje inacep-
table parezca ser demasiado alto. Con esta finalidad, de
cada lote de 10 000 baterías, se seleccionaron y probarán
25. Si por lo menos 5 de estas generan un voltaje inacepta-
ble, todo el lote será rechazado. ¿Cuál es la probabilidad de
que un lote será rechazado si
a. 5% de las baterías en el lote tienen voltajes inaceptables?
b. 10% de las baterías en el lote tienen voltajes inacepta-
bles?
c. 20% de las baterías en el lote tienen voltajes inacepta-
bles?
d. ¿Qué les sucedería a las probabilidades en los incisos
a)–c) si el número de rechazo crítico se incrementara de
5 a 6?
101. De las personas que pasan a través de un detector de meta-
les en un aeropuerto, el 0.5% lo activan; sea X el núme-
ro entre un grupo de 500 seleccionado al azar que activan
el detector.
a. ¿Cuál es la función masa de probabilidad (aproximada)
de X?
b. Calcule P(X 5).
c. Calcule P(5 X).
102. Una firma consultora educativa está tratando de decidir si
los estudiantes de preparatoria que nunca antes han utiliza-
do una calculadora de mano pueden resolver cierto tipo de
problema más fácilmente con una calculadora que utiliza
lógica polaca inversa o una que no utiliza esta lógica. Se
selecciona una muestra de 25 estudiantes y se les permite
practicar con ambas calculadoras. Luego a cada estudiante
se le pide que resuelva un problema con la calculadora po-
laca inversa y un problema similar con la otra. Sea p
P(S), donde S indica que un estudiante resolvió el proble-
ma más rápido con la lógica polaca inversa que sin ella y
sea X número de éxitos.
a. Si p 0.5, ¿cuál es P(7 X 18)?
b. Si p 0.8, ¿cuál es P(7 X 18)?
c. Si la pretensión de que p 0.5 tiene que ser rechazada
cuando X 7 o X 18, ¿cuál es la probabilidad de re-
chazar la pretensión cuando en realidad es correcta?
d. Si la decisión de rechazar la pretensión p 0.5 se hace
como en el inciso c), ¿cuál es la probabilidad de que la
pretensión no sea rechazada cuando p 0.6? ¿Cuándo
p 0.8?
e. ¿Qué regla de decisión escogería para rechazar la pre-
tensión de que p 0.5 si desea que la probabilidad en
el inciso c) sea cuando mucho de 0.01?
103. Considere una enfermedad cuya presencia puede ser iden-
tificada por medio de un análisis de sangre. Sea p la proba-
bilidad de que un individuo seleccionado al azar tenga la
enfermedad. Suponga se seleccionan independientemente
n individuos para analizarlos. Una forma de proceder es
analizar cada una de las n muestras de sangre. Un proce-
dimiento potencialmente más económico, de análisis en
grupo se introdujo durante la Segunda Guerra Mundial pa-
ra identificar hombres sifilíticos entre los reclutas. En pri-
mer lugar, se toma una parte de cada muestra de sangre, se
combinan estos especímenes y se realiza un solo análisis.
Si ninguno tiene la enfermedad, el resultado será negativo
y sólo se requiere un análisis. Si por lo menos un individuo
está enfermo, el análisis de la muestra combinada dará un
resultado positivo, en cuyo caso se realizan los análisis de
los n individuos. Si p 0.1 y n 3, ¿cuál es el número es-
perado de análisis si se utiliza este procedimiento? ¿Cuál
es el número esperado cuando n 5? [El artículo “Ran-
dom Multiple-Access Communication and Group Testing”
(IEEE Trans. on Commun., 1984: 769–774) aplicó estas
ideas a un sistema de comunicación en el cual la dicotomía
fue usuario ocioso/activo en lugar de enfermo/no enfermo.]
104. Sea p1 la probabilidad de que cualquier símbolo de código
particular sea erróneamente transmitido a través de un
sistema de comunicación. Suponga que en diferentes sím-
bolos, ocurren errores de manera independiente uno de
otro. Suponga también que con probabilidad p2 un símbo-
lo erróneo es corregido al ser recibido. Sea X el número de
símbolos correctos en un bloque de mensaje compuesto
de n símbolos (una vez que el proceso de corrección ha ter-
minado). ¿Cuál es la distribución de probabilidad de X?
105. El comprador de una unidad generadora de potencia requie-
re de arranques consecutivos exitosos antes de aceptar la uni-
dad. Suponga que los resultados de arranques individuales
son independientes entre sí. Sea p la probabilidad de que
cualquier arranque particular sea exitoso. La variable aleato-
ria de interés es X el número de arranques que deben ha-
cerse antes de la aceptación. Dé la función masa de
probabilidad de X en el caso c 2. Si p 0.9, ¿cuál es P(X
8)? [Sugerencia: Con x 5, exprese p(x) “recursivamen-
te” en términos de la función masa de probabilidad evalua-
da con los valores más pequeños x 3, x 4, . . . , 2.]
(Este problema fue sugerido del artículo “Evaluation of a
Start-Up Demonstration Test”, J. Quality Technology,
1983: 103–106.)
106. Una aerolínea ha desarrollado un plan para un club de via-
jeros ejecutivos sobre la premisa de que 10% de sus clien-
tes actuales calificarían para membresía.
a. Suponiendo la validez de esta premisa, entre 25 clientes
actuales seleccionados al azar, ¿cuál es la probabilidad
de que entre 2 y 6 (inclusive) califiquen para membresía?
b. De nuevo suponiendo la validez de la premisa, ¿cuál es
el número esperado de clientes que califican y la desvia-
ción estándar del número que califica en una muestra
aleatoria de 100 clientes actuales?
c. Sea X el número en una muestra al azar de 25 clientes
actuales que califican para membresía. Considere recha-
zar la premisa de la compañía a favor de la pretensión
de que p 0.10 si x 7. ¿Cuál es la probabilidad de
que la premisa de la compañía sea rechazada cuando en
realidad es válida?
d. Remítase a la regla de decisión introducida en el inciso
c). ¿Cuál es la probabilidad de que la premisa de la
compañía no sea rechazada aun cuando p 0.20 (es de-
cir, 20% califican)?
107. 40% de las semillas de mazorcas de maíz (maíz moderno)
portan sólo una espiga y el 60% restante portan dos espigas.
Una semilla con una espiga producirá una mazorca con es-
pigas únicas 29% del tiempo, en tanto que una semilla con
dos espigas producirán una mazorca con espigas únicas
26% del tiempo. Considere seleccionar al azar diez semillas.
Ejercicios suplementarios 127
c3_p086-129.qxd 3/12/08 4:01 AM Page 127](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-145-320.jpg)
![a. ¿Cuál es la probabilidad de que exactamente cinco de es-
tas semillas porten una sola espiga y de que produzcan
una mazorca con una sola espiga?
b. ¿Cuál es la probabilidad de que exactamente cinco de
estas mazorcas producidas por estas semillas tengan es-
pigas únicas? ¿Cuál es la probabilidad de que cuando
mucho cinco mazorcas tengan espigas únicas?
108. Un juicio terminó con el jurado en desacuerdo porque ocho
de sus miembros estuvieron a favor de un veredicto de cul-
pabilidad y los otros cuatro estuvieron a favor de la abso-
lución. Si los jurados salen de la sala en orden aleatorio y
cada uno de los primeros cuatro que salen de la sala es aco-
sado por un reportero para entrevistarlo, ¿cuál es la función
masa de probabilidad de X el número de jurados a favor
de la absolución entre los entrevistados? ¿Cuántos de los
que están a favor de la absolución espera que sean entrevis-
tados?
109. Un servicio de reservaciones emplea cinco operadores de
información que reciben solicitudes de información inde-
pendientemente uno de otro, cada uno de acuerdo con un
proceso de Poisson con razón 2 por minuto.
a. ¿Cuál es la probabilidad de que durante un periodo de
un min dado, el primer operador no reciba solicitudes?
b. ¿Cuál es la probabilidad de que durante un periodo de
un min dado, exactamente cuatro de los cinco operado-
res no reciban solicitudes?
c. Escriba una expresión para la probabilidad de que du-
rante un periodo de un min dado, todos los operadores
reciban exactamente el mismo número de solicitudes.
110. En un gran campo se distribuyen al azar las langostas de
acuerdo con una distribución de Poisson con parámetro
2 por yarda cuadrada. ¿Qué tan grande deberá ser el
radio R de una región de muestreo circular para que la pro-
babilidad de hallar por lo menos una en la región sea igual
a 0.99?
111. Un puesto de periódicos ha pedido cinco ejemplares de
cierto número de una revista de fotografía. Sea X el nú-
mero de individuos que vienen a comprar esta revista. Si X
tiene una distribución de Poisson con parámetro 4,
¿cuál es el número esperado de ejemplares que serán ven-
didos?
112. Los individuos A y B comienzan a jugar una secuencia de
partidas de ajedrez. Sea S {A gana un juego} y suponga
que los resultados de juegos sucesivos son independientes
con P(S) p y P(F) 1 p (nunca empatan). Jugarán
hasta que uno de ellos gane diez juegos. Sea X el núme-
ro de partidas jugadas (con posibles valores 10, 11, . . . ,
19).
a. Con x 10, 11, . . . , 19, obtenga una expresión para
p(x) P(X x).
b. Si un empate es posible, con p P(S), q P(F), 1
p q P(empate), ¿cuáles son los posibles valores de
X? ¿Cuál es P(20 X)? [Sugerencia: P(20 X) 1
P(X 20).]
113. Un análisis para detectar la presencia de una enfermedad
tiene una probabilidad de 0.20 de dar un resultado falso po-
sitivo (lo que indica que un individuo tiene la enfermedad
cuando éste no es el caso) y una probabilidad de 0.10 de
dar un resultado falso negativo. Suponga que diez individuos
son analizados, cinco de los cuales tienen la enfermedad y
cinco de los cuales no. Sea X el número de lecturas posi-
tivas que resultan.
a. ¿Tiene X una distribución binomial? Explique su razo-
namiento.
b. ¿Cuál es la probabilidad de que exactamente tres de
diez resultados sean positivos?
114. La función masa de probabilidad binomial negativa gene-
ralizada está dada por
nb(x; r, p) k(r, x) pr
(1 p)x
x 0, 1, 2, . . .
Sea X el número de plantas de cierta especie encontrada en
una región particular y tenga esta distribución con p 0.3 y
r 2.5. ¿Cuál es P(X 4)? ¿Cuál es la probabilidad de
que por lo menos se encuentre una planta?
115. Defina una función p(x; , ) mediante
p(x; , )
{ e
e
x 0, 1, 2, . . .
0 de lo contrario
a. Demuestre que p(x; , ) satisface las dos condiciones
necesarias para especificar una función masa de proba-
bilidad. [Nota: Si una firma emplea dos mecanógrafos,
uno de los cuales comete errores tipográficos a razón de
por página y el otro a razón de por página y cada
uno ellos realiza la mitad del trabajo de mecanografía
de la firma, entonces p(x; , ) es la función masa de
probabilidad de X el número de errores en una pági-
na escogida al azar.]
b. Si el primer mecanógrafo (razón ) teclea 60% de todas
las páginas, ¿cuál es la función masa de probabilidad de
X del inciso a)?
c. ¿Cuál es E(X) para p(x; , ) dada por la expresión mos-
trada?
d. ¿Cuál es 2
para p(x; , ) dada por esta expresión?
116. La moda de una variable aleatoria discreta X con función
masa de probabilidad p(x) es ese valor x*
con el cual p(x)
alcanza su valor más grande (el valor x más probable).
a. Sea X Bin(n, p). Considerando la razón b(x 1; n,
p)/b(x; n, p), demuestre que b(x; n, p) se incrementa con
x en tanto x np (1 p). Concluya que el modo x*
es el entero que satisface (n 1)p 1 x*
(n 1)p.
b. Demuestre que si X tiene una distribución de Poisson
con parámetro , la moda es el entero más grande me-
nor que . Si es un entero, demuestre que tanto 1
como son modas.
117. Un disco duro de computadora tiene diez pistas concéntri-
cas, numeradas 1, 2, . . . , 10 desde la más externa hasta la
más interna y un solo brazo de acceso. Sea pi la proba-
bilidad de que cualquier solicitud particular de datos hará
que el brazo se vaya a la pista i (i 1, . . . , 10. Supon-
ga que las pistas accesadas en búsquedas sucesivas son in-
dependientes. Sea X el número de pistas sobre las cuales
pasa el brazo de acceso durante dos solicitudes sucesivas
(excluida la pista que el brazo acaba de dejar, así que los
x
x!
1
2
x
x!
1
2
128 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad
c3_p086-129.qxd 3/12/08 4:01 AM Page 128](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-146-320.jpg)
![valores posibles son x 0, 1, . . . , 9). Calcule la función
masa de probabilidad de X [Sugerencia: P(el brazo
está ahora sobre la pista i y X j) P(X j°el
brazo está ahora sobre i) pi. Una vez que se escribe la
probabilidad condicional en función de p1, . . . , p10, me-
diante la ley de la probabilidad total, se obtiene la probabi-
lidad deseada sumando a lo largo de i.]
118. Si X es una variable aleatoria hipergeométrica demuestre
directamente con la definición que E(X) nM/N (conside-
re sólo el caso n M). [Sugerencia: Saque como factor a
nM/N de la suma para E(X) y demuestre que los términos
adentro de la suma son de la forma h(y; n 1, M 1,
N 1) donde y x 1.]
119. Use el hecho de que
todos x
(x )2
p(x)
x:°x° k
(x )2
p(x)
para comprobar la desigualdad de Chebyshev dada en el
ejercicio 44.
120. El proceso de Poisson simple de la sección 3.6 está carac-
terizado por una razón constante a la cual los eventos ocu-
rren por unidad de tiempo. Una generalización de esto es
suponer que la probabilidad de que ocurra exactamente un
evento en el intervalo [t, t t] es (t) t o(t). Se
puede demostrar entonces que el número de eventos que
ocurren durante un intervalo [t1, t2] tiene una distribución
de Poisson con parámetro
t2
t1
(t) dt
La ocurrencia de eventos en el transcurso del tiempo en esta
situación se llama proceso de Poisson no homogéneo. El
artículo “Inference Based on Retrospective Ascertain-
ment”, J. Amer. Stat. Assoc., 1989: 360–372, considera la
función de intensidad
(t) eabt
en su forma apropiada para eventos que implican la trans-
misión VIH (el virus del SIDA) vía transfusiones sanguí-
neas. Suponga que a 2 y b 0.6 (cercanos a los valores
sugeridos en el artículo), con el tiempo en años.
a. ¿Cuál es el número esperado de eventos en el intervalo
[0, 4?]? ¿En [2, 6]?
b. ¿Cuál es la probabilidad de que cuando mucho ocurran
15 eventos en el intervalo [0, 0.9907]?
121. Considere un conjunto de A1, . . . , Ak de eventos mutua-
mente excluyentes y exhaustivos y una variable aleatoria X
cuya distribución depende de cuál de los eventos Ai ocurra
(p. ej., un viajero abonado podría seleccionar una de tres
rutas posibles de su casa al trabajo, con X como el tiempo
de recorrido). Sea E(X°Ai) el valor esperado de X dado que
el evento Ai ocurre. Entonces se puede demostrar que E(X)
E (X°Ai) P(Ai) el promedio ponderado de las “expec-
tativas condicionales” individuales donde las ponderacio-
nes son las probabilidades de la división de eventos.
a. La duración esperada de una llamada de voz a un núme-
ro telefónico particular es de 3 minutos, mientras que la
duración esperada de una llamada de datos a ese mismo
número es de 1 minuto. Si 75% de las llamadas son de
voz, ¿cuál es la duración esperada de la siguiente lla-
mada?
b. Una pastelería vende tres diferentes tipos de galletas
con briznas de chocolate. El número de briznas de cho-
colate en un tipo de galleta tiene una distribución de
Poisson con parámetro i i 1 (i 1, 2, 3). Si 20%
de todos los clientes que compran una galleta con briz-
nas de chocolate selecciona el primer tipo, 50% elige el
segundo tipo y el 30% restante opta por el tercer tipo,
¿cuál es el número esperado de briznas en una galleta
comprada por el siguiente cliente?
122. Considere una fuente de comunicaciones que transmite pa-
quetes que contienen lenguaje digitalizado. Después de cada
transmisión, el receptor envía un mensaje que indica si
la transmisión fue exitosa o no. Si una transmisión no es
exitosa, el paquete es reenviado. Suponga que el paquete de
voz puede ser transmitido un máximo de 10 veces. Supo-
niendo que los resultados de transmisiones sucesivas son
independientes una de otra y que la probabilidad de que
cualquier transmisión particular sea exitosa es p, determine
la función masa de probabilidad de la variable aleatoria
X el número de veces que un paquete es transmitido.
Luego obtenga una expresión para el número de veces es-
perado que un paquete es transmitido.
?
Ejercicios suplementarios 129
Bibliografía
Johnson, Norman, Samuel Kotz y Adrienne Kemp. Discrete Uni-
variate Distributions. Wiley, Nueva York, 1972. Una enciclo-
pedia de información sobre distribuciones discretas.
Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models
and Applications (2a. ed.), Macmillan, Nueva York, 1994.
Contiene una discusión a fondo tanto de las propiedades gene-
rales de distribuciones discretas y continuas como los resulta-
dos para distribuciones específicas.
Ross, Sheldon, Introduction to Probability Models (7a. ed.), Aca-
demic Press, Nueva York, 2003. Una fuente de material sobre
el proceso de Poisson y generalizaciones y una amena intro-
ducción a otros temas de probabilidad aplicada.
c3_p086-129.qxd 3/12/08 4:01 AM Page 129](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-147-320.jpg)
![Una variable aleatoria (va) discreta es una cuyos valores posibles o constituyen un conjun-
to finito o bien pueden ser puestos en lista en una secuencia infinita (una lista en la cual exis-
te un primer elemento, un segundo elemento, etc.). Una variable aleatoria cuyo conjunto de
valores posibles es un intervalo completo de números no es discreta.
Recuérdese de acuerdo con el capítulo 3 que una variable aleatoria X es continua si
1) sus valores posibles comprenden un solo intervalo sobre la línea de numeración (para al-
guna A B, cualquier número x entre A y B es un valor posible) o una unión de intervalos
disjuntos y 2) P(X c) 0 para cualquier número c que sea un valor posible de X.
En el estudio de la ecología de un lago, se mide la profundidad en lugares seleccionados,
entonces X la profundidad en ese lugar es una variable aleatoria continua. En este caso A
es la profundidad mínima en la región muestreada y B es la profundidad máxima. ■
Si se selecciona al azar un compuesto químico y se determina su pH X, entonces X es una
variable aleatoria continua porque cualquier valor pH entre 0 y 14 es posible. Si se conoce
más sobre el compuesto seleccionado para su análisis, entonces el conjunto de posibles va-
lores podría ser un subintervalo de [0, 14], tal como 5.5 x 6.5 pero X seguiría siendo
continua. ■
Sea X la cantidad de tiempo que un cliente seleccionado al azar pasa esperando que le cor-
ten el pelo antes de que comience su corte de pelo. El primer pensamiento podría ser que X
es una variable aleatoria continua, puesto que se requiere medirla para determinar su valor.
Sin embargo, existen clientes suficientemente afortunados que no tienen que esperar antes
de sentarse en el sillón del peluquero. Así que el caso debe ser P(X 0) 0. Condicional
en cuanto a los sillones vacíos, aun cuando, el tiempo de espera será continuo puesto que X
podría asumir entonces cualquier valor entre un tiempo mínimo posible A y un tiempo má-
ximo posible B. Esta variable aleatoria no es ni puramente discreta ni puramente continua
sino que es una mezcla de los dos tipos. ■
Se podría argumentar que aunque en principio las variables tales como altura, peso y
temperatura son continuas, en la práctica las limitaciones de los instrumentos de medición
nos restringen a un mundo discreto (aunque en ocasiones muy finamente subdividido). Sin
embargo, los modelos continuos a menudo representan muy bien de forma aproximada si-
tuaciones del mundo real y con frecuencia es más fácil trabajar con matemáticas continuas
(el cálculo) que con matemáticas de variables discretas y distribuciones.
Distribuciones de probabilidad de variables continuas
Supóngase que la variable X de interés es la profundidad de un lago en un punto sobre la su-
perficie seleccionado al azar. Sea M la profundidad máxima (en metros), así que cual-
quier número en el intervalo [0, M] es un valor posible de X. Si se “discretiza” X midiendo
la profundidad al metro más cercano, entonces los valores posibles son enteros no negativos
menores que o iguales a M. La distribución discreta resultante de profundidad se ilustra con
un histograma de probabilidad. Si se traza el histograma de modo que el área del rectángu-
lo sobre cualquier entero posible k sea la proporción del lago cuya profundidad es (al me-
tro más cercano) k, entonces el área total de todos los rectángulos es 1. En la figura 4.1a)
aparece un posible histograma.
Si se mide la profundidad con mucho más precisión y se utiliza el mismo eje de me-
dición de la figura 4.1a), cada rectángulo en el histograma de probabilidad resultante es mu-
cho más angosto, aun cuando el área total de todos los rectángulos sigue siendo 1. En la
4.1 Funciones de densidad de probabilidad 131
4.1 Funciones de densidad de probabilidad
Ejemplo 4.1
Ejemplo 4.2
Ejemplo 4.3
c4_p130-183.qxd 3/12/08 4:04 AM Page 131](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-149-320.jpg)
![figura 4.1b) se ilustra un posible histograma; tiene una apariencia mucho más regular que el
histograma de la figura 4.1a). Si se continúa de esta manera midiendo la profundidad más y
más finamente, la secuencia resultante de histogramas se aproxima a una curva más regular,
tal como la ilustrada en la figura 4.1c). Como en cada histograma el área total de todos los
rectángulos es igual a 1, el área total bajo la curva regular también es 1. La probabilidad de
que la profundidad en un punto seleccionado al azar se encuentre entre a y b es simplemen-
te el área bajo la curva regular entre a y b. Es de manera exacta una curva regular del tipo
ilustrado en la figura 4.1c) la que especifica un distribución de probabilidad continua.
Para que f(x) sea una función de densidad de probabilidad legítima, debe satisfacer las
dos siguientes condiciones:
1. f(x) 0 con todas las x
2.
f(x) dx área bajo la curva f(x)
1
La dirección de una imperfección con respecto a una línea de referencia sobre un objeto circu-
lar tal como un neumático, un rotor de freno o un volante está, en general, sujeta a incertidum-
bre. Considérese la línea de referencia que conecta el vástago de la válvula de un neumático con
su punto central y sea X el ángulo medido en el sentido de las manecillas del reloj con respecto
a la ubicación de una imperfección. Una posible función de densidad de probabilidad de X es
f(x) 3
1
60 0 x 360
0 de lo contrario
132 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
DEFINICIÓN Sea X una variable aleatoria continua. Entonces, una distribución de probabilidad o
función de densidad de probabilidad (fdp) de X es una función f(x) tal que para dos
números cualesquiera a y b con a b,
P(a X b)
b
a
f(x) dx
Es decir, la probabilidad de que X asuma un valor en el intervalo [a, b] es el área so-
bre este intervalo y bajo la gráfica de la función de densidad, como se ilustra en la fi-
gura 4.2. La gráfica de f(x) a menudo se conoce como curva de densidad.
Figura 4.1 a) Histograma de probabilidad de profundidad medida al metro más cercano; b) histograma
de probabilidad de profundidad medida al centímetro más cercano; c) un límite de una secuencia de histo-
gramas discretos.
a) b) c)
0 M 0 M 0 M
Figura 4.2 P(a X b) el área debajo de la curva de densidad entre a y b.
a b
x
Ejemplo 4.4
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 132](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-150-320.jpg)
![La función de densidad de probabilidad aparece dibujada en la figura 4.3. Claramente f(x)
0. El área bajo la curva de densidad es simplemente el área de un rectángulo (altura)
(base) (3
1
60)(360) 1. La probabilidad de que el ángulo esté entre 90° y 180° es
P(90 X 180)
180
90
dx
°
x180
x90
0.25
La probabilidad de que el ángulo de ocurrencia esté dentro de 90° de la línea de referencia
es
P(0 X 90) P(270 X 360) 0.25 0.25 0.50
1
4
x
360
1
360
Como siempre que 0 a b 360 en el ejemplo 4.4, P(a X b) depende sólo del an-
cho b a del intervalo, se dice que X tiene una distribución uniforme.
La gráfica de cualquier función de densidad de probabilidad uniforme es como la de la fi-
gura 4.3 excepto que el intervalo de densidad positiva es [A, B] en lugar de [0, 360].
En el caso discreto, una función masa de probabilidad indica cómo estan distribuidas
pequeñas “manchas” de masa de probabilidad de varias magnitudes a lo largo del eje de
medición. En el caso continuo, la densidad de probabilidad está “dispersa” en forma conti-
nua a lo largo del intervalo de posibles valores. Cuando la densidad está dispersa uniforme-
mente a lo largo del intervalo, se obtiene una función de densidad de probabilidad uniforme
como en la figura 4.3.
Cuando X es una variable aleatoria discreta, a cada valor posible se le asigna una pro-
babilidad positiva. Esto no es cierto en el caso de una variable aleatoria continua (es decir,
se satisface la segunda condición de la definición) porque el área bajo una curva de densi-
dad situada sobre cualquier valor único es cero:
c
c
c e
c e
El hecho de que P(X c) 0 cuando X es continua tiene una importante consecuen-
cia práctica: La probabilidad de que X quede en algún intervalo entre a y b no depende de
si el límite inferior a o el límite superior b está incluido en el cálculo de probabilidad
P(a X b) P(a X b) P(a X b) P(a X b) (4.1)
fsxddx 5 0
fsxddx 5 lim
eS0
PsX 5 cd 5
4.1 Funciones de densidad de probabilidad 133
DEFINICIÓN Se dice que una variable aleatoria continua X tiene una distribución uniforme en el
intervalo [A, B] si la función de densidad de probabilidad de X es
f(x; A, B) B
1
A
A x B
0 de lo contrario
Figura 4.3 Función de densidad de probabilidad del ejemplo 4.4. ■
Área sombreada P(90 X 180)
x
1
360
f(x)
0 360
x
f(x)
360
270
180
90
Ï
Ì
Ó
´
c4_p130-183.qxd 3/12/08 4:04 AM Page 133](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-151-320.jpg)
![Exactamente como en el caso discreto, a menudo es útil pensar en la población de interés
como compuesta de valores X en lugar de individuos u objetos. La función de densidad de pro-
babilidad es entonces un modelo de la distribución de valores en esta población numérica y con
base en este modelo se pueden calcular varias características de la población (tal como la media).
4.1 Funciones de densidad de probabilidad 135
EJERCICIOS Sección 4.1 (1-10)
1. Sea X la cantidad de tiempo durante la cual un libro puesto
en reserva durante dos horas en la biblioteca de una univer-
sidad es solicitado en préstamo por un estudiante seleccio-
nado y suponga que X tiene la función de densidad
f(x)
0.5x 0 x 2
0 de lo contrario
Calcule las siguientes probabilidades:
a. P(X 1)
b. P(0.5 X 1.5)
c. P(1.5 X)
2. Suponga que la temperatura de reacción X (en °C) en cier-
to proceso químico tiene una distribución uniforme con
A 5 y B 5.
a. Calcule P(X 0).
b. Calcule P( 2.5 X 2.5).
c. Calcule P( 2 X 3).
d. Para que k satisfaga 5 k k 4 5, calcule
P(k X k 4).
3. El error implicado al hacer una medición es una variable
aleatoria continua X con función de densidad de probabilidad
f(x)
0.09375(4 x2
) 2 x 2
0 de lo contrario
a. Bosqueje la gráfica de f(x).
b. Calcule P(X 0).
c. Calcule P( 1 X 1).
d. Calcule P(X 0.5 o X 0.5).
4. Sea X el esfuerzo vibratorio (lb/pulg2
) en el aspa de una tur-
bina de viento a una velocidad del viento particular en un
túnel aerodinámico. El artículo “Blade Fatigue Life Assess-
ment with Application to VAWTS” (J. Solar Energy Engr.
1982: 107-111) propone la distribución Rayleigh, con fun-
ción de densidad de probabilidad
f(x; )
x
2
e x
2
/(2
2
)
x 0
0 de lo contrario
como modelo de la distribución X.
a. Verifique que f(x; ) es una función de densidad de pro-
babilidad legítima.
b. Suponga que 100 (un valor sugerido por una gráfica
en el artículo). ¿Cuál es la probabilidad de que X es cuan-
do mucho de 200? ¿Menos de 200? ¿Por lo menos de 200?
c. ¿Cuál es la probabilidad de que X esté entre 100 y 200
(de nuevo con 100)?
d. Dé una expresión para P(X x).
5. Un profesor universitario nunca termina su disertación an-
tes del final de la hora y siempre termina dentro de 2 minu-
tos después de la hora. Sea X el tiempo que transcurre
entre el final de la hora y el final de la disertación y supon-
ga que la función de densidad de probabilidad de X es
f(x)
kx2
0 x 2
0 de lo contrario
a. Determine el valor de k y trace la curva de densidad co-
rrespondiente. [Sugerencia: El área total bajo la gráfica
de f(x) es 1.]
b. ¿Cuál es la probabilidad de que la disertación termine
dentro de un minuto del final de la hora?
c. ¿Cuál es la probabilidad de que la disertación continúe
después de la hora durante entre 60 y 90 segundos.
d. ¿Cuál es la probabilidad de que la disertación continúe
durante por lo menos 90 segundos después del final de
la hora?
6. El peso de lectura real de una pastilla de estéreo ajustado a
3 gramos en un tocadiscos particular puede ser considerado
como una variable aleatoria continua X con función de den-
sidad de probabilidad
f(x)
k[1 (x 3)2
] 2 x 4
0 de lo contrario
a. Trace la gráfica de f(x).
b. Determine el valor de k.
c. ¿Cuál es la probabilidad de que el peso real de lectura
sea mayor que el peso prescrito?
d. ¿Cuál es la probabilidad de que el peso real de lectura
esté dentro de 0.25 gramos del peso prescrito?
e. ¿Cuál es la probabilidad de que el peso real difiera del
peso prescrito por más de 0.5 gramos?
7. Se cree que el tiempo X (min) para que un ayudante de la-
boratorio prepare el equipo para cierto experimento tiene
una distribución uniforme con A 25 y B 35.
a. Determine la función de densidad de probabilidad de X
y trace la curva de densidad de correspondiente.
b. ¿Cuál es la probabilidad de que el tiempo de preparación
exceda de 33 min?
c. ¿Cuál es la probabilidad de que el tiempo de preparación
esté dentro de dos min del tiempo medio? [Sugerencia:
Identifique en la gráfica de f(x).]
d. Con cualquier a de modo que 25 a a 2 35,
¿cuál es la probabilidad de que el tiempo de preparación
esté entre a y a 2 min?
8. Para ir al trabajo, primero tengo que tomar un camión cerca
de mi casa y luego tomar un segundo camión. Si el tiempo de
espera (en minutos) en cada parada tiene una distribución
uniforme con A 0 y B 5, entonces se puede demostrar
que el tiempo de espera total Y tiene la función de densidad
de probabilidad
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 135](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-153-320.jpg)
![Sea X el espesor de una cierta lámina de metal con distribución uniforme en [A, B]. La fun-
ción de densidad se muestra en la figura 4.6. Con x A, F(x) 0, como no hay área bajo
la gráfica de la función de densidad a la izquierda de la x. Con x B, F(x) 1, puesto que
toda el área está acumulada a la izquierda de la x. Finalmente con A x B,
F(x)
x
f(y) dy
x
A B
1
A
dy
B
1
A
y
°
°
°
yx
yA
B
x
A
A
La función de distribución acumulativa completa es
0 x A
F(x)
B
x
A
A
A x B
1 x B
La gráfica de esta función de distribución acumulativa aparece en la figura 4.7.
Utilización de F(x) para calcular probabilidades
La importancia de la función de distribución acumulativa en este caso, lo mismo que para va-
riables aleatorias discretas, es que las probabilidades de varios intervalos pueden ser calculadas
con una fórmula o una tabla de F(x).
4.2 Funciones de distribución acumulativa y valores esperados 137
PROPOSICIÓN Sea X una variable aleatoria continua con función de densidad de probabilidad f(x) y
función de distribución acumulativa F(x). Entonces con cualquier número a,
P(X a) 1 F(a)
y para dos números cualesquiera a y b con a b.
P(a X b) F(b) F(a)
Ejemplo 4.6
Figura 4.6 Función de densidad de probabilidad de una distribución uniforme.
f(x)
1
BA
A B
1
BA
A B
x x
Área sombreada F(x)
Figura 4.7 Función de distribución acumulativa de una distribución uniforme. ■
F(x)
A B x
1
Ï
ÌÓ
c4_p130-183.qxd 3/12/08 4:04 AM Page 137](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-155-320.jpg)
![Valores esperados
Para una variable aleatoria discreta X, E(X) se obtuvo sumando x p(x) a lo largo de posibles
valores de X. Aquí se reemplaza la suma con la integración y la función masa de probabilidad
por la función de densidad de probabilidad para obtener un promedio ponderado continuo.
La función de densidad de probabilidad de las ventas semanales de grava X fue
f(x)
3
2
(1 x2
) 0 x 1
0 de lo contrario
por lo tanto
E(X)
x f(x) dx
1
0
x
3
2
(1 x2
) dx
3
2
1
0
(x x3
) dx
3
2
x
2
2
x
4
4
°
°
°
x1
x0
3
8
■
Cuando la función de densidad de probabilidad f(x) especifica un modelo para la dis-
tribución de valores en una población numérica, entonces es la media de la población, la
cual es la medida más frecuentemente utilizada de la ubicación o centro de la población.
Con frecuencia se desea calcular el valor esperado de alguna función h(X) de la varia-
ble aleatoria X. Si se piensa en h(X) como una nueva variable aleatoria Y, se utilizan técni-
cas de estadística matemática para derivar la función de densidad de probabilidad de Y y
E(Y) se calcula a partir de la definición. Afortunadamente, como en el caso discreto, existe
una forma más fácil de calcular E[h(X)].
Dos especies compiten en una región por el control de una cantidad limitada de un cierto re-
curso. Sea X la proporción del recurso controlado por la especie 1 y suponga que la fun-
ción de densidad de probabilidad de X es
f(x)
1 0 x 1
0 de lo contrario
la cual es una distribución uniforme en [0, 1]. (En su libro Ecological Diversity, E. C. Pielou
llama a esto el modelo del “palo roto” para la asignación de recursos, puesto que es análogo
4.2 Funciones de distribución acumulativa y valores esperados 141
Ejemplo 4.11
DEFINICIÓN El valor esperado o valor medio de una variable aleatoria continua X con función de
densidad de probabilidad f(x) es
X E(X)
x f(x) dx
PROPOSICIÓN Si X es una variable aleatoria continua con función de densidad de probabilidad f(x)
y h(X) es cualquier función de X, entonces
E[h(X)] h(X)
h(x) f(x) dx
Ejemplo 4.10
(continuación
del ejemplo
4.9)
Ï
Ì
Ó
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 141](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-159-320.jpg)
![142 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
a la ruptura de un palo en un lugar seleccionado al azar.) Entonces la especie que controla
la mayor parte de este recurso controla la cantidad
h(X) máx(X, 1 X)
1 X si 0 X
1
2
X si
1
2
X 1
La cantidad esperada controlada por la especie que controla la mayor parte es entonces
E[h(X)]
máx(x, 1 x) f(x) dx
1
0
máx(x, 1 x) 1 dx
1/2
0
(1 x) 1 dx
1
1/2
x 1 dx
3
4
■
Para h(X) una función lineal, E[h(X)] E(aX b) aE(X) b.
En el caso discreto, la varianza de X se definió como la desviación al cuadrado esperada con
respecto a y se calculó por medio de suma. En este caso de nuevo la integración reempla-
za a la suma.
La varianza y la desviación estándar dan medidas cuantitativas de cuánta dispersión hay
en la distribución o población de valores x. La forma más fácil de calcular 2
es utilizar una
fórmula abreviada.
Para X ventas semanales de grava, se calcula E(X)
3
8. Como
E(X2
)
x2
f(x) dx
1
0
x2
3
2
(1 x2
) dx
1
0
3
2
(x2
x4
) dx
1
5
V(X)
1
5
3
8
2
3
1
2
9
0
0.059 y X 0.244 ■
Cuando h(X) aX b, el valor esperado y la varianza de h(X) satisfacen las mismas pro-
piedades que en el caso discreto: E[h(X)] a b y V[h(X)] a2
2
.
Ï
Ì
Ó
DEFINICIÓN La varianza de una variable aleatoria continua X con función de densidad de proba-
bilidad f(x) y valor medio es
2
X V(X)
(x )2
f(x) dx E[(X )2
]
La desviación estándar (DE) de X es X V
(X
)
.
PROPOSICIÓN V(X) E(X2
) [E(X)]2
EJERCICIOS Sección 4.2 (11-27)
11. La función de distribución acumulativa del tiempo de prés-
tamo X como se describe en el ejercicio 1 es
x 0
F(x)
x
4
2
0 x 2
1 2 x
Use ésta para calcular lo siguiente:
a. P(X 1)
b. P(0.5 X 1)
c. P(X 0.5)
d. El tiempo de préstamo medio ˜
[resolver 0.5 F( ˜
)]
e. F(x) para obtener la función de densidad f(x)
Ï
ÌÓ
Ejemplo 4.12
(continuación
del ejemplo
4.10)
c4_p130-183.qxd 3/12/08 4:04 AM Page 142](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-160-320.jpg)
![4.2 Funciones de distribución acumulativa y valores esperados 143
f. E(X)
g. V(X) y X
h. Si al prestatario se le cobra una cantidad h(X) X2
cuan-
do el tiempo de préstamo es X, calcule el cobro esperado
E[h(X)].
12. La función de distribución acumulativa de X ( error de
medición) del ejercicio 3 es
0 x 2
F(x)
1
2
3
3
2 4x
x
3
3
2 x 2
1 2 x
a. Calcule P(X 0).
b. Calcule P(1 X 1).
c. Calcule P(0.5 X).
d. Verifique que f(x) está dada en el ejercicio 3 obteniendo
F’(x).
e. Verifique que ˜
0.
13. El ejemplo 4.5 introdujo el concepto de intervalo de tiempo
en el flujo de tránsito y propuso una distribución particular
para X el intervalo de tiempo entre dos carros consecuti-
vos seleccionados al azar (s). Suponga que en un entorno de
tránsito diferente, la distribución del intervalo de tiempo
tiene la forma
f(x)
k
x4
x 1
0 x 1
a. Determine el valor de k con el cual f(x) es una función de
densidad de probabilidad legítima.
b. Obtenga la función de distribución acumulativa.
c. Use la función de distribución acumulativa de (b) para
determinar la probabilidad de que el intervalo de tiempo
exceda de 2 segundos y también la probabilidad de que
el intervalo esté entre 2 y 3 segundos.
d. Obtenga un valor medio del intervalo de tiempo y su
desviación estándar.
e. ¿Cuál es la probabilidad de que el intervalo de tiempo
quede dentro de una desviación estándar del valor medio?
14. El artículo “Modeling Sediment and Water Column Interac-
tions for Hidrophobic Pollutants” (Water Research, 1984:
1169-1174) sugiere la distribución uniforme en el intervalo
7.5, 20) como modelo de profundidad (cm) de la capa de
bioturbación en sedimento en una región.
a. ¿Cuáles son la media y la varianza de la profundidad?
b. ¿Cuál es la función de distribución acumulativa de la
profundidad?
c. ¿Cuál es la probabilidad de que la profundidad observa-
da sea cuando mucho de 10? ¿Entre 10 y 15?
d. ¿Cuál es la probabilidad de que la profundidad observa-
da esté dentro de una desviación estándar del valor me-
dio? ¿Dentro de dos desviaciones estándar?
15. Sea X la cantidad de espacio ocupado por un artículo colo-
cado en un contenedor de un pie3
. La función de densidad
de probabilidad de X es
f(x)
90x8
(1 x) 0 x 1
0 de lo contrario
a. Dibuje la función de densidad de probabilidad. Luego
obtenga la función de distribución acumulativa de X y
dibújela.
b. ¿Cuál es P(X 0.5) [es decir, F(0.5)]?
c. Con la función de distribución acumulativa de (a), ¿cuál
es P(0.25 X 0.5)? ¿Cuál es P(0.25 X 0.5)?
d. ¿Cuál es el 75o
percentil de la distribución?
e. Calcule E(X) y X.
f. ¿Cuál es la probabilidad de que X esté a más de una des-
viación estándar de su valor medio?
16. Responda los incisos a)-f) del ejercicio 15 con X tiempo
de disertación después de la hora dado en el ejercicio 5.
17. Si la distribución de X en el intervalo [A, B] es uniforme.
a. Obtenga una expresión para el (100p)o
percentil.
b. Calcule E(X), V(X) y X.
c. Con n, un entero positivo, calcule E(Xn
).
18. Sea X el voltaje a la salida de un micrófono y suponga que
X tiene una distribución uniforme en el intervalo de 1 a 1.
El voltaje es procesado por un “limitador duro” con valores
de corte de 0.5 y 0.5, de modo que la salida del limitador
es una variable aleatoria Y relacionada con X por Y X si
|X| 0.5, Y 0.5 si X 5 y Y 0.5 si X 0.5.
a. ¿Cuál es P(Y 0.5)?
b. Obtenga la función de distribución acumulativa de Y y
dibújela.
19. Sea X una variable aleatoria continua con función de distri-
bución acumulativa
0 x 0
F(x)
4
x
1 ln
4
x 0 x 4
1 x 4
[Este tipo de función de distribución acumulativa es sugeri-
do en el artículo “Variabilitiy in Measured Bedload-Trans-
port Rates” (Water Resources Bull., 1985: 39-48) como
modelo de cierta variable hidrológica.] Determinar:
a. P(X 1)
b. P(1 X 3)
c. La función de densidad de probabilidad de X
20. Considere la función de densidad de probabilidad del tiem-
po de espera total Y de dos camiones
2
1
5
y 0 y 5
f(y) 2
5
2
1
5
y 5 y 10
0 de lo contrario
introducida en el ejercicio 8.
a. Calcule y trace la función de distribución acumulativa
de Y. [Sugerencia: Considere por separado 0 y 5 y
5 y 10 al calcular F(y). Una gráfica de la función
de densidad de probabilidad debe ser útil.]
b. Obtenga una expresión para el (100p)o
percentil. [Sugeren-
cia: Considere por separado 0 p 0.5 y 0.5 p 1.]
c. Calcule E(Y) y V(Y). ¿Cómo se comparan estos valores
con el tiempo de espera probable y la varianza de un
solo camión cuando el tiempo está uniformemente dis-
tribuido en [0, 5]?
21. Un ecólogo desea marcar una región de muestreo circular
de 10 m de radio. Sin embargo, el radio de la región resul-
tante en realidad es una variable aleatoria R con función de
densidad de probabilidad
Ï
ÌÓ
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 143](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-161-320.jpg)
![144 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
La distribución normal es la más importante en toda la probabilidad y estadística. Muchas po-
blaciones numéricas tienen distribuciones que pueden ser representadas muy fielmente por
una curva normal apropiada. Los ejemplos incluyen estaturas, pesos y otras características fí-
sicas (el famoso artículo Biométrica 1903 “On the Laws of Inheritance in Man” discutió mu-
chos ejemplos de esta clase), errores de medición en experimentos científicos, mediciones
antropométricas en fósiles, tiempos de reacción en experimentos psicológicos, mediciones de
inteligencia y aptitud, calificaciones en varios exámenes y numerosas medidas e indicadores
económicos. Incluso cuando la distribución subyacente es discreta, la curva normal a menu-
do da una excelente aproximación. Además, aun cuando las variables individuales no estén
¿Cuál es el área esperada de la región circular resultante?
22. La demanda semanal de gas propano (en miles de galones)
de una instalación particular es una variable aleatoria X con
función de densidad de probabilidad
f(x)
21
x
1
2 1 x 2
0 de lo contrario
a. Calcule la función de distribución acumulativa de X.
b. Obtenga una expresión para el (100p)o
percentil. ¿Cuál
es el valor de ˜
?
c. Calcule E(X) y V(X).
d. Si 1500 galones están en existencia al principio de la se-
mana y no se espera ningún nuevo suministro durante
la semana, ¿cuántos de los 1500 galones se espera que
queden al final de la semana? [Sugerencia: Sea h(x)
cantidad que queda cuando la demanda es x.]
23. Si la temperatura a la cual cierto compuesto se funde es una
variable aleatoria con valor medio de 120°C y desviación es-
tándar de 2°C, ¿cuáles son la temperatura media y la desvia-
ción estándar medidas en °F? [Sugerencia: °F 1.8°C 32.]
24. La función de densidad de probabilidad de Pareto de X es
f(x; k, )
k
x
k1
k
x
0 x
introducida en el ejercicio 10.
a. Si k 1, calcule E(X).
b. ¿Qué se puede decir sobre E(X) si k 1?
c. Si k 2, demuestre que V(X) k 2
(k 1)2
(k 2)1
.
d. Si k 2, ¿qué se puede decir sobre V(X)?
e. ¿Qué condiciones en cuanto a k son necesarias para ga-
rantizar que E(Xn
) es finito?
25. Sea X la temperatura en °C a la cual ocurre una reacción quí-
mica y sea Y la temperatura en °F (así que Y 1.8X 32).
a. Si la mediana de la distribución X es ˜
, demuestre que
1.8 ˜
32 es la mediana de la distribución Y.
b. ¿Cómo está relacionado el 90o
percentil de la distribu-
ción Y con el 90o
de la distribución X? Verifique su con-
jetura.
c. Más generalmente, si Y aX b, ¿cómo está relacio-
nado cualquier percentil de la distribución Y con el per-
centil correspondiente de la distribución X?
26. Sea X los gastos médicos totales (en miles de dólares) in-
curridos por un individuo particular durante un año dado.
Aunque X es una variable aleatoria discreta, suponga que
su distribución es bastante bien aproximada por una distri-
bución continua con función de densidad de probabilidad
f(x) k(1 x/2.5)7
con x 0.
a. ¿Cuál es el valor de k?
b. Dibuje la función de densidad de probabilidad de X.
c. ¿Cuáles son el valor esperado y la desviación estándar
de los gastos médicos totales?
d. Un individuo está cubierto por un plan de aseguramiento
que le impone una provisión deducible de $500 (así que
los primeros $500 de gastos son pagados por el individuo).
Luego el plan pagará 80% de cualquier gasto adicional que
exceda de $500 y el pago máximo por parte del individuo
(incluida la cantidad deducible) es de $2500. Sea Y la can-
tidad de gastos médicos de este individuo pagados por la
compañía de seguros. ¿Cuál es el valor esperado de Y?
[Sugerencia: Primero indague qué valor de X correspon-
de al gasto máximo que sale del bolsillo de $2500. Lue-
go escriba una expresión para Y como una función de X
(la cual implique varios precios diferentes) y calcule el
valor esperado de la función.]
27. Cuando se lanza un dardo a un blanco circular, considere la
ubicación del punto de aterrizaje respecto al centro. Sea X
el ángulo en grados medido con respecto a la horizontal
y suponga que X está uniformemente distribuida en [0, 360].
Defina Y como la variable transformada Y h(X)
(2/360)X , por lo tanto, Y es el ángulo medido en ra-
dianes y Y está entre y . Obtenga E(Y) y y obteniendo
primero E(X) y X y luego utilizando el hecho de que h(X)
es una función lineal de X.
f(r)
3
4
[1 (10 r)2
] 9 r 11
0 de lo contrario
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
4.3 Distribución normal
c4_p130-183.qxd 3/12/08 4:04 AM Page 144](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-162-320.jpg)
![156 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
a. Una probeta es aceptable sólo si su dureza oscila entre
67 y 75, ¿cuál es la probabilidad de que una probeta se-
leccionada al azar tenga una dureza aceptable?
b. Si el rango de dureza aceptable es (70 c, 70 c), ¿con
qué valor de c tendría 95% de todas las probetas una du-
reza aceptable?
c. Si el rango de dureza aceptable es como el del inciso a)
y la dureza de cada una de diez probetas seleccionadas
al azar se determina de forma independiente, ¿cuál es el
valor esperado de probetas aceptables entre las diez?
d. ¿Cuál es la probabilidad de que cuando mucho ocho de
diez probetas independientemente seleccionadas tengan
una dureza de menos de 73.84? [Sugerencia: Y el nú-
mero de entre las diez probetas con dureza de menos de
73.84 es una variable binomial; ¿cuál es p?]
47. La distribución de peso de paquetes enviados de cierta ma-
nera es normal con valor medio de 12 lb y desviación están-
dar de 3.5 lb. El servicio de paquetería desea establecer
un valor de peso c más allá del cual habrá un cargo extra.
¿Qué valor de c es tal que 99% de todos los paquetes estén
por lo menos 1 lb por debajo del peso de cargo extra?
48. Suponga que la tabla A.3 del apéndice contiene (z) sólo
para z 0. Explique cómo aún así podría calcular
a. P( 1.72 Z 0.55)
b. P( 1.72 Z 0.55)
¿Es necesario tabular (z) para z negativo? ¿Qué propiedad
de la curva normal estándar justifica su respuesta?
49. Considere los bebés nacidos en el rango “normal” de 37-43
semanas de gestación. Datos extensos sustentan la suposi-
ción de que el peso de nacimiento de estos bebés nacidos en
Estados Unidos está normalmente distribuido con media de
3432 g y desviación estándar de 482 g. [El artículo “Are Ba-
bies Normal?” (The American Statistician (1999): 298-302)
analizó datos de un año particular; con una selección sensi-
ble de intervalos de clase, un histograma no parecía del todo
normal pero después de una investigación se determinó que
esto se debía a que en algunos hospitales medían el peso en
gramos, en otros lo medían a la onza más cercana y luego lo
convertían en gramos. Una selección modificada de interva-
los de clase que permitía esto produjo un histograma que era
descrito muy bien por una distribución normal.]
a. ¿Cuál es la probabilidad de que el peso de nacimiento de
un bebé seleccionado al azar de este tipo exceda de 4000
gramos? ¿Esté entre 3000 y 4000 gramos?
b. ¿Cuál es la probabilidad de que el peso de nacimiento de
un bebé seleccionado al azar de este tipo sea de menos
de 2000 gramos o de más de 5000 gramos?
c. ¿Cuál es la probabilidad de que el peso de nacimiento
de un bebé seleccionado al azar de este tipo exceda de
7 libras?
d. ¿Cómo caracterizaría el 0.1% más extremo de todos los
pesos de nacimiento?
e. Si X es una variable aleatoria con una distribución nor-
mal y a es una constante numérica (a 0), entonces
Y aX también tiene una distribución normal. Use esto
para determinar la distribución de pesos de nacimiento
expresados en libras (forma, media y desviación están-
dar) y luego calcule otra vez la probabilidad del inciso c)
¿Cómo se compara ésta con su respuesta previa?
50. En respuesta a preocupaciones sobre el contenido nutricional
de las comidas rápidas. McDonald’s ha anunciado que utili-
zará un nuevo aceite de cocinar para sus papas a la francesa
que reducirá sustancialmente los niveles de ácidos grasos e
incrementará la cantidad de grasa poliinsaturada más benéfi-
ca. La compañía afirma que 97 de 100 personas no son capa-
ces de detectar una diferencia de sabor entre los nuevos y los
viejos aceites. Suponiendo que esta cifra es correcta (como
proporción de largo plazo) ¿cuál es la probabilidad aproxi-
mada de que en una muestra aleatoria de 1000 individuos que
han comprado papas a la francesa en McDonald’s:
a. ¿Por lo menos 40 puedan notar la diferencia de sabor en-
tre los dos aceites?
b. Cuando mucho 5% pueda notar la diferencia de sabor
entre los dos aceites?
51. La desigualdad de Chebyshev (véase el ejercicio 44 del
capítulo 3), es válida para distribuciones continuas y dis-
cretas. Estipula que para cualquier número k que satisfaga
k 1, P(°X ° k) 1/k2
(véase el ejercicio 44 en
el capítulo 3 para una interpretación). Obtenga esta proba-
bilidad en el caso de una distribución normal con k 1, 2,
3 y compare con el límite superior.
52. Sea X el número de defectos en un carrete de cinta magné-
tica de 100 m (una variable de valor entero). Suponga que
X tiene aproximadamente una distribución normal con
25 y 5. Use la corrección por continuidad para calcu-
lar la probabilidad de que el número de defectos sea:
a. Entre 20 y 30, inclusive.
b. Cuando mucho 30. Menos de 30.
53. Si X tiene una distribución binomial con parámetros n 25 y
p, calcule cada una de las siguientes probabilidades mediante
la aproximación normal (con la corrección por continuidad)
en los casos p 0.5, 0.6, y 0.8 y compare con las probabili-
dades exactas calculadas con la tabla A.1 del apéndice.
a. P(15 X 20)
b. P(X 15)
c. P(20 X)
54. Suponga que 10% de todas las flechas de acero producidas
por medio de un proceso no cumplen con las especificacio-
nes pero pueden ser retrabajadas (en lugar de ser desecha-
das). Considere una muestra aleatoria de 200 flechas y sea
X el número entre éstas que no cumplen con las especifica-
ciones y pueden ser retrabajadas. ¿Cuál es la probabilidad
aproximada de que X sea
a. Cuando mucho 30?
b. Menos que 30?
c. Entre 15 y 25 (inclusive)?
55. Suponga que sólo 75% de todos los conductores en un esta-
do usan con regularidad el cinturón de seguridad. Se selec-
ciona una muestra aleatoria de 500 conductores. ¿Cuál es la
probabilidad de que
a. Entre 360 y 400 (inclusive) de los conductores en la
muestra usen con regularidad el cinturón de seguridad?
b. Menos de 400 de aquellos en la muestra usen con regu-
laridad el cinturón de seguridad?
c4_p130-183.qxd 3/12/08 4:04 AM Page 156](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-174-320.jpg)
![56. Demuestre que la relación entre un percentil normal gene-
ral y el percentil z correspondiente es como se estipuló en
esta sección.
57. a. Demuestre que si X tiene una distribución normal con
parámetros y , entonces Y aX b (una función li-
neal de X) también tiene una distribución normal. ¿Cuá-
les son los parámetros de la distribución de Y [es decir,
E(Y) y V(Y)]? [Sugerencia: Escriba la función de distri-
bución acumulativa de Y, P(Y y), como una integral
que implique la función de densidad de probabilidad de
X y luego derive con respecto a y para obtener la función
de densidad de probabilidad de Y.]
b. Si cuando se mide en °C, la temperatura está normal-
mente distribuida con media de 115 y desviación están-
dar de dos, ¿qué se puede decir sobre la distribución de
temperatura medida en °F?
58. No existe una fórmula exacta para función de distribución
acumulativa normal estándar (z), aunque se han publicado
varias aproximaciones en artículos. La siguiente se tomó de
“Approximations for Hand Calculators Using Small Integer
Coefficients” (Mathematics of Computation, 1977: 214-
222). Con 0 z 5.5,
P(Z z) 1 (z)
0.5 exp
El error relativo de esta aproximación es de menos de 0.042%.
Úsela para calcular aproximaciones a las siguientes probabi-
lidades y compare siempre que sea posible con las probabili-
dades obtenidas con la tabla A.3 del apéndice.
a. P(Z 1) b. P(Z 3)
c. P( 4 Z 4) d. P(Z 5)
(83z 351)z 562
703/z 165
4.4 Distribuciones exponencial y gama 157
La curva de densidad correspondiente a cualquier distribución normal tiene forma de campa-
na y por consiguiente es simétrica. Existen muchas situaciones prácticas en las cuales la va-
riable de interés para un investigador podría tener una distribución asimétrica. Una familia de
distribuciones que tiene esta propiedad es la familia gama. Primero se considera un caso es-
pecial, la distribución exponencial y luego se le generaliza más adelante en esta sección.
Distribución exponencial
La familia de distribuciones exponenciales proporciona modelos de probabilidad que son
muy utilizados en disciplinas de ingeniería y ciencias.
4.4 Distribuciones exponencial y gama
Algunas fuentes escriben la función de densidad de probabilidad exponencial en la forma
(1/b)ex/b
, de modo que 1/. El valor esperado de una variable aleatoria exponencial-
mente distribuida X es
E(X)
0
x ex
dx
Para obtener este valor esperado se requiere integrar por partes. La varianza de X se calcula
utilizando el hecho de que V(X) E(X2
) [E(X)]2
. La determinación de E(X2
) requiere inte-
grar por partes dos veces en sucesión. Los resultados de estas integraciones son los siguientes:
Tanto la media como la desviación estándar de la distribución exponencial son iguales a 1/.
En la figura 4.26 aparecen algunas gráficas de varias funciones de densidad de probabilidad
exponenciales.
m 5
1
l
s2
5
1
l2
DEFINICIÓN Se dice que X tiene una distribución exponencial con parámetro ( 0) si la fun-
ción de densidad de probabilidad de X es
f(x; )
elx
x 0
0 de lo contrario (4.5)
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 157](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-175-320.jpg)
![158 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
0.5
1
2
x
2
0.5
1
f(x; )
Figura 4.26 Curvas de densidad exponencial.
La función de densidad de probabilidad exponencial es fácil de integrar para obtener la fun-
ción de densidad acumulativa.
Suponga que el tiempo de respuesta X en una terminal de computadora en línea (el tiempo
transcurrido entre el final de la consulta de un usuario y el inicio de la respuesta del siste-
ma a dicha consulta) tiene una distribución exponencial con tiempo de respuesta esperado
de 5 s. Entonces E(X) 1/ 5, por lo tanto 0.2. La probabilidad de que el tiempo de
respuesta sea cuando mucho de 10 s es
P(X 10) F(10; 0.2) 1 e(0.2)(10)
1 e2
1 0.135 0.865
La probabilidad de que el tiempo de respuesta sea de entre 5 y 10 s es
P(5 X 10) F(10; 0.2) F(5; 0.2)
(1 e2
) (1 e1
) 0.233 ■
La distribución exponencial se utiliza con frecuencia como modelo de la distribución
de tiempos entre la ocurrencia de eventos sucesivos, tales como clientes que llegan a una
instalación de servicio o llamadas que entran a un conmutador. La razón de esto es que la
distribución exponencial está estrechamente relacionada con el proceso de Poisson discuti-
do en el capítulo 3.
Aunque una comprobación completa queda fuera del alcance de este libro, el resultado es
fácil de verificar para el tiempo X1 hasta que ocurre el primer evento:
P(X1 t) 1 P(X1 t) 1 P[ningún evento en (0, t)]
1
et
0
!
(t)0
1 et
la cual es exactamente la función de distribución acumulativa de la distribución exponencial.
Ï
Ì
Ó
Ejemplo 4.21
PROPOSICIÓN Suponga que el número de eventos que ocurren en cualquier intervalo de tiempo de
duración t tiene una distribución de Poisson con parámetro t (donde , la razón del
proceso de eventos, es el número esperado de eventos que ocurren en una unidad de
tiempo) y que los números de ocurrencias en intervalos no traslapantes son indepen-
dientes uno de otro. Entonces la distribución del tiempo transcurrido entre la ocu-
rrencia de dos eventos sucesivos es exponencial con parámetro .
F(x; )
0 x 0
1 ex
x 0
c4_p130-183.qxd 3/12/08 4:04 AM Page 158](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-176-320.jpg)
![Suponga que se reciben llamadas durante las 24 horas en una “línea de emergencia para pre-
vención del suicidio” de acuerdo con un proceso de Poisson a razón 0.5 llamadas por
día. Entonces el número de días X entre llamadas sucesivas tiene una distribución exponen-
cial con valor de parámetro 0.5, así que la probabilidad de que transcurran más de dos días
entre llamadas es
P(X 2) 1 P(X 2) 1 F(2; 0.5) e(0.5)(2)
0.368
El tiempo esperado entre llamadas sucesivas es 1/0.5 2 días. ■
Otra aplicación importante de la distribución exponencial es modelar la distribución
de la duración de un componente. Una razón parcial de la popularidad de tales aplicaciones
es la propiedad de “ falta de memoria o amnesia” de la distribución exponencial. Supon-
ga que la duración de un componente está exponencialmente distribuida con parámetro .
Después de poner el componente en servicio, se deja que pase un periodo de t0 horas y lue-
go se ve si el componente sigue trabajando; ¿cuál es ahora la probabilidad de que dure por
lo menos t horas más? En símbolos, se desea P(X t t0°X t0). Por la definición de pro-
babilidad condicional,
P(X t t0°X t0)
Pero el evento X t0 en el numerador es redundante, puesto que ambos eventos pueden ocu-
rrir si y sólo si X t t0. Por consiguiente,
P(X t t0°X t0)
P(
P
X
(X
t
t0)
t0)
et
Esta probabilidad condicional es idéntica a la probabilidad original P(X t) de que el com-
ponente dure t horas. Por lo tanto, la distribución de duración adicional es exactamente la
misma que la distribución original de duración, así que en cada punto en el tiempo el com-
ponente no muestra ningún efecto de desgaste. En otras palabras, la distribución de la dura-
ción restante es independiente de la antigüedad actual.
Aunque la propiedad de amnesia se justifica por lo menos en forma aproximada en
muchos problemas aplicados, en otras situaciones los componentes se deterioran con el
tiempo o de vez en cuando mejoran con él (por lo menos hasta cierto punto). Las distribu-
ciones gama, Weibull y lognormales proporcionan modelos de duración más generales (las
últimas dos se discuten en la siguiente sección).
La función gama
Para definir la familia de distribuciones gama, primero se tiene que introducir una función
que desempeña un importante papel en muchas ramas de las matemáticas.
1 F(t t0; )
1 F(t0; )
P[(X t t0) (X t0)]
P(X t0)
4.4 Distribuciones exponencial y gama 159
Ejemplo 4.22
Las propiedades más importantes de la función gama son las siguientes:
1. Con cualquier 1, () ( 1) ( 1) [vía integración por partes].
2. Con cualquier entero positivo, n, (n) (n 1)!
3.
1
2
.
DEFINICIÓN Con 0, la función gama () se define como
()
0
x1
ex
dx (4.6)
c4_p130-183.qxd 3/12/08 4:04 AM Page 159](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-177-320.jpg)
![se llama función gama incompleta [en ocasiones la función gama incompleta se refiere a
la expresión (4.9) sin el denominador () en el integrando]. Existen tablas extensas de F(x; )
disponibles; en la tabla A.4 del apéndice se presenta una pequeña tabulación para 1,
2, . . . , 10 y x 1, 2, . . . , 15.
Suponga que el tiempo de reacción X de un individuo seleccionado al azar a un estímulo tie-
ne una distribución gama estándar con 2. Como
P(a X b) F(b) F(a)
cuando X es continua,
P(3 X 5) F(5; 2) F(3; 2) 0.960 0.801 0.159
La probabilidad de que el tiempo de reacción sea de más de 4 s es
P(X 4) 1 P(X 4) 1 F(4; 2) 1 0.908 0.092 ■
La función gama incompleta también se utiliza para calcular probabilidades que im-
plican distribuciones gama no estándar. Estas probabilidades también se obtienen casi ins-
tantáneamente con varios paquetes de software.
Suponga que el tiempo de sobrevivencia de un ratón macho seleccionado al azar expuesto a
240 rads de radiación gama tiene una distribución gama con 8 y 15. (Datos en Sur-
vival Distributions: Reliability Applications in the Biomedical Services, de A. J. Gross y
V. Clark, sugiere 8.5 y 13.3.) El tiempo de sobrevivencia esperado es E(X)
(8)(15) 120 semanas, en tanto que V(X) (8)(15)2
1800 y X 1
8
0
0
42.43
semanas. La probabilidad de que un ratón sobreviva entre 60 y 120 semanas es
P(60 X 120) P(X 120) P(X 60)
F(120/15; 8) F(60/15; 8)
F(8; 8) F(4; 8) 0.547 0.051 0.496
La probabilidad de que un ratón sobreviva por lo menos 30 semanas es
P(X 30) 1 P(X 30) 1 P(X 30)
1 F(30/15; 8) 0.999 ■
Distribución ji cuadrada
La distribución ji cuadrada es importante porque es la base de varios procedimientos de in-
ferencia estadística. El papel central desempeñado por la distribución ji cuadrada en infe-
rencia se deriva de su relación con distribuciones normales (véase el ejercicio 71). Se
discutirá esta distribución con más detalle en capítulos posteriores.
4.4 Distribuciones exponencial y gama 161
Ejemplo 4.23
Ejemplo 4.24
PROPOSICIÓN Si X tiene una distribución gama con parámetros y entonces con cualquier x 0,
la función de distribución acumulativa de X es
P(X x) F(x; , ) F
x
;
donde F(; ) es la función gama incompleta.
c4_p130-183.qxd 3/12/08 4:04 AM Page 161](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-179-320.jpg)
![162 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
DEFINICIÓN Sea un entero positivo. Se dice entonces que una variable aleatoria X tiene una dis-
tribución ji cuadrada con parámetro si la función de densidad de probabilidad de
X es la densidad gama con /2 y 2. La función de densidad de probabilidad
de una variable aleatoria ji cuadrada es por lo tanto
f(x; ) 2 /2
1
( /2)
x( /2)1
ex/2
x 0 (4.10)
0 x 0
El parámetro se llama número de grados de libertad (gl) de X. A menudo se uti-
liza el símbolo 2
en lugar de “ji cuadrada”.
EJERCICIOS Sección 4.4 (59-71)
59. Sea X el tiempo entre dos llegadas sucesivas a la ventanilla
de autopago de un banco local. Si X tiene una distribución ex-
ponencial con 1 (la cual es idéntica a una distribución
gama estándar con 1), calcule lo siguiente:
a. El tiempo esperado entre dos llegadas sucesivas.
b. La desviación estándar del tiempo entre dos llegadas su-
cesivas.
c. P(X 4)
d. P(2 X 5)
60. Sea X la distancia (m) que un animal recorre desde el sitio de
su nacimiento hasta el primer territorio vacante que encuen-
tra. Suponga que ratas canguro con etiqueta en la cola, X tie-
ne una distribución exponencial con parámetro 0.01386
(como lo sugiere el artículo “Competition and Dispersal from
Multiple Nests”, Ecology, 1997: 873-883).
a. ¿Cuál es la probabilidad de que la distancia sea cuando
mucho de 100 m? ¿Cuándo mucho de 200? ¿Entre 100
y 200 m?
b. ¿Cuál es la probabilidad de que la distancia exceda la
distancia media por más de dos desviaciones estándar?
c. ¿Cuál es el valor de la distancia mediana?
61. La amplia experiencia con ventiladores de un tipo utiliza-
dos en motores diesel ha sugerido que la distribución ex-
ponencial proporciona un buen modelo del tiempo hasta
la falla. Suponga que el tiempo medio hasta la falla es de
25 000 horas. ¿Cuál es la probabilidad de que
a. Un ventilador seleccionado al azar dure por lo menos
20 000 horas? ¿Cuándo mucho 30 000 horas? ¿Entre
20 000 y 30 000 horas?
b. ¿Exceda la duración de un ventilador el valor medio por
más de dos desviaciones estándar? ¿Más de tres desvia-
ciones estándar?
62. El artículo “Microwave Observations of Daily Antarctic Sea-
Ice Edge Expansion and Contribution Rates” (IEEE Geosci.
and Remote Sensing Letters, 2006: 54-58) establece que “la
distribución del avance/retroceso diarios del hielo marino con
respecto a cada sensor es similar y es aproximadamente una
exponencial doble”. La distribución exponencial doble pro-
puesta tiene una función de densidad f(x) 0.5e|x|
para
x . La desviación estándar se da como 40.9 km.
a. ¿Cuál es el valor del parámetro ?
b. ¿Cuál es la probabilidad de que la extensión del cambio
del hielo marino esté dentro de una desviación estándar del
valor medio?
63. Un consumidor está tratando de decidir entre dos planes de
llamadas de larga distancia. El primero aplica una sola tari-
fa de 10¢ por minuto, en tanto que el segundo cobra una ta-
rifa de 99¢ por llamadas hasta de 20 minutos y luego 10¢
por cada minuto adicional que exceda de 20 (suponga que
las llamadas que duran un número no entero de minutos son
cobradas proporcionalmente a un cargo por minuto entero).
Suponga que la distribución de duración de llamadas del
consumidor es exponencial con parámetro .
a. Explique intuitivamente cómo la selección del plan de llama-
das deberá depender de cuál sea la duración de las llamadas.
b. ¿Cuál plan es mejor si la duración esperada de las llama-
das es de 10 minutos? ¿Y de 15 minutos? [Sugerencia:
Sea h1(x) el costo del primer plan cuando la duración
de las llamadas es de x minutos y sea h2(x) la función de
costo del segundo plan. Dé expresiones para estas dos
funciones de costo y luego determine el costo esperado
de cada plan.]
64. Evalúe lo siguiente:
a. (6) b. (5/2)
c. F(4; 5) (la función gama incompleta)
d. F(5; 4) e. F(0; 4)
65. Si X tiene una distribución gama estándar con 7 evalúe
lo siguiente:
a. P(X 5) b. P(X 5) c. P(X 8)
d. P(3 X 8) e. P(3 X 8)
f. P(X 4 o X 6)
66. Suponga que el tiempo empleado por un estudiante seleccio-
nado al azar que utiliza una terminal conectada a un sistema
de computadoras de tiempo compartido tiene una distribu-
ción gama con media de 20 min y varianza de 80 min2
.
a. ¿Cuáles son los valores de y ?
b. ¿Cuál es la probabilidad de que un estudiante utilice la
terminal durante cuando mucho 24 min?
c. ¿Cuál es la probabilidad de que un estudiante utilice la
terminal durante entre 20 y 40 min?
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 162](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-180-320.jpg)
![Las familias de distribuciones normal, gama (incluida la exponencial) y uniforme propor-
cionan una amplia variedad de modelos de probabilidad de variables continuas, pero exis-
ten muchas situaciones prácticas en las cuales ningún miembro de estas familias se adapta
bien a un conjunto de datos observados. Los estadísticos y otros investigadores han desarro-
llado otras familias de distribuciones que a menudo son apropiadas en la práctica.
Distribución Weibull
El físico sueco Waloddi Weibull introdujo la familia de distribuciones Weibull en 1939; su
artículo de 1951 “A Statistical Distribution Function of Wide Applicability” (J. Applied Me-
chanics, vol. 18: 293-297) discute varias aplicaciones.
4.5 Otras distribuciones continuas 163
67. Suponga que cuando un transistor de cierto tipo se somete
a una prueba de duración acelerada, la duración X (en sema-
nas) tiene una distribución gama acelerada con media de 24
semanas y desviación estándar de 12 semanas.
a. ¿Cuál es la probabilidad de que un transistor dure entre
12 y 24 semanas?
b. ¿Cuál es la probabilidad de que un transistor dure cuan-
do mucho 24 semanas? ¿Es la mediana de la distribu-
ción de duración menor que 24? ¿Por qué si o por qué
no?
c. ¿Cuál es el 99o
percentil de la distribución de duración?
d. Suponga que la prueba termina en realidad después de t
semanas. ¿Qué valor de t es tal que sólo el 0.5% de todos
los transistores continuarán funcionando al término de la
prueba?
68. El caso especial de la distribución gama en la cual es un
entero positivo n se llama distribución Erlang. Si se reem-
plaza por 1/ en la expresión (4.8), la función de densi-
dad de probabilidad Erlang es
f(x; , n)
(
(
n
x
)n
1
1
e
)
!
x
x 0
0 x 0
Se puede demostrar que si los tiempos entre eventos sucesi-
vos son independientes, cada uno con distribución exponen-
cial con parámetro , entonces el tiempo total que transcurre
antes de que ocurran los siguientes n eventos tiene una fun-
ción de densidad de probabilidad f(x; , n).
a. ¿Cuál es el valor esperado de X? Si el tiempo (en minu-
tos) entre llegadas de clientes sucesivos está exponen-
cialmente distribuido con 0.5, ¿cuánto tiempo se
puede esperar que transcurra antes de que llegue el déci-
mo cliente?
b. Si el tiempo entre llegadas de clientes está exponencial-
mente distribuido con 0.5, ¿cuál es la probabilidad
de que el décimo cliente (después del que acaba de lle-
gar) llegue dentro de los siguientes 30 min?
c. El evento {X t} ocurre si y sólo si ocurren n eventos
en el siguiente t. Use el hecho de que el número de even-
tos que ocurren en un intervalo de duración t tiene una
distribución de Poisson con parámetro t para escribir
una expresión (que implique probabilidades de Poisson)
para la función de distribución acumulativa de Erlang
F(t; , n) P(X t).
69. Un sistema consta de cinco componentes idénticos conecta-
dos en serie como se muestra:
En cuanto un componente falla, todo el sistema lo hace. Su-
ponga que cada componente tiene una duración que está ex-
ponencialmente distribuida con 0.01 y que los
componentes fallan de manera independiente uno de otro.
Defina los eventos Ai {el componente i-ésimo dura por lo
menos t horas}, i 1, . . . , 5, de modo que los Ai son even-
tos independientes. Sea X el tiempo al cual el sistema fa-
lla, es decir, la duración más corta (mínima) entre los cinco
componentes.
a. ¿A qué evento equivale el evento {X t} que implique
A1, . . . , A5?
b. Utilizando la independencia de los eventos Ai, calcule
P(X t). Luego obtenga F(t) P(X t) y la función
de densidad de probabilidad de X. ¿Qué tipo de distribu-
ción tiene X?
c. Suponga que existen n componentes y cada uno tiene
una duración exponencial con parámetro . ¿Qué tipo de
distribución tiene X?
70. Si X tiene una distribución exponencial con parámetro ,
derive una expresión general para el (100p)o
percentil de la
distribución. Luego especifique cómo obtener la mediana.
71. a. ¿A qué evento equivale el evento {X2
y} que implique
a X misma?
b. Si X tiene una distribución normal estándar, use el inciso
a) para escribir la integral que es igual a P(X2
y). Lue-
go derive con respecto a y para obtener la función de den-
sidad de probabilidad de X2
[el cuadrado de una variable
N(0, 1)]. Por último, demuestre que X2
tiene una
distribución ji cuadrada con 1 grados de libertad
[véase (4.10)]. [Sugerencia: Use la siguiente identidad.]
d
d
y
b(y)
a(y)
f(x) dx f[b(y)] b(y) f[a(y)] a(y)
1 2 3 4 5
Ï
Ì
Ó
Ï
Ì
Ó
Ï
Ì
Ó
4.5 Otras distribuciones continuas
c4_p130-183.qxd 3/12/08 4:04 AM Page 163](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-181-320.jpg)
![En situaciones prácticas, un modelo de Weibull puede ser razonable excepto que el
valor de X más pequeño posible puede ser algún valor que no se supone sea cero (esto
también se aplicaría a un modelo gama). La cantidad puede entonces ser considerada co-
mo un tercer parámetro de la distribución, lo cual es lo que Weibull hizo en su trabajo ori-
ginal. Con, por ejemplo, 3, todas las curvas que aparecen en la figura 4.28 se
desplazarían 3 unidades a la derecha. Esto equivale a decir que X tiene la función de
densidad de probabilidad (4.11) de modo que la función de distribución acumulativa de X
se obtiene reemplazando x en (4.12) por x .
Sea X la pérdida de peso por corrosión de una pequeña placa de aleación de magnesio
cuadrada sumergida durante 7 días en una solución inhibida acuosa al 20% de MgBr2. Su-
ponga que la pérdida de peso mínima posible es 3 y que el exceso X 3 sobre esta
mínima tiene una distribución Weibull con 2 y 4. (Este ejemplo se consideró en
“Practical Applications of the Weibull Distribution”, Industrial Quality Control, agosto de
1964: 71-78; los valores de y se consideraron como 1.8 y 3.67, respectivamente, aun
cuando en el artículo se utilizó una selección de parámetros un poco diferente.) La función
de distribución acumulativa de X es entonces
0 x 3
F(x; , , ) F(x; 2, 4, 3)
1 e[(x3)/4]
2
x 3
4.5 Otras distribuciones continuas 165
Ejemplo 4.26
0.5
1
0 5 10
f(x)
2
0
4
6
8
0.5
0 1.0 1.5 2.0 2.5
f(x)
x
x
a = 2, b = 1
a = 2, b = 0.5
a = 1, b = 1 (exponencial)
a = 10, b = 2
a = 10, b = 1
a = 10, b = 0.5
Figura 4.28 Curvas de densidad Weibull.
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:04 AM Page 165](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-183-320.jpg)
![166 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
Por consiguiente,
P(X 3.5) 1 F(3.5; 2, 4, 3) e0.0156
0.985
y
P(7 X 9) 1 e2.25
(1 e1
) 0.895 0.632 0.263 ■
Distribución lognormal
Hay que tener cuidado aquí; los parámetros y no son la media y la desviación estándar
de X sino de ln(X). Se puede demostrar que la media y varianza de X son
E(X) e
2
/2
V(X) e2
2
(e
2
1)
En el capítulo 5, se presenta una justificación teórica para esta distribución en cone-
xión con el Teorema del Límite Central, pero como con cualesquiera otras distribuciones, se
puede utilizar la lognormal como modelo incluso en la ausencia de semejante justificación.
La figura 4.29 ilustra gráficas de la función de densidad de probabilidad lognormal; aunque
una curva normal es simétrica, una curva lognormal tiene una asimetría positiva.
Como el ln(X) tiene una distribución normal, la función de distribución acumulativa
de X puede ser expresada en términos de la función de distribución acumulativa (z) de una
variable aleatoria normal estándar Z.
DEFINICIÓN Se dice que una variable aleatoria no negativa X tiene una distribución lognormal si
la variable aleatoria Y ln(X) tiene una distribución normal. La función de densidad
de probabilidad resultante de una variable aleatoria lognormal cuando el ln(X) está
normalmente distribuido con parámetros y es
f(x; , ) 2
1
x
e[ln(x)]
2
/(2
2
)
x 0
0 x 0
F(x; , ) P(X x) P[ln(X) ln(x)]
PZ
ln(x)
ln(x)
, x 0 (4.13)
Ï
ÌÓ
0.05
0
0.10
0.15
0.20
0.25
0 5 10 15 20 25
f(x)
x
m = 1, s = 1
m = 3, s = 1
m = 3, s = √3
Figura 4.29 Curvas de densidad lognormal.
c4_p130-183.qxd 3/12/08 4:04 AM Page 166](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-184-320.jpg)
![La distribución lognormal se utiliza con frecuencia como modelo de varias propiedades de
materiales. El artículo “Reliability of Wood Joist Floor Systems with Creep” (J. of Structu-
ral Engr., 1995: 946-954) sugiere que la distribución lognormal con 0.375 y 0.25
es un modelo factible de X el módulo de elasticidad (MDE, en 106
lb/pulg2
) de sistemas
de piso de viguetas de madera de pino grado #2. La media y varianza del módulo de elasti-
cidad son
E(X) e0.375 (0.25)
2
/2
e0.40625
1.50
V(X) e0.8125
(e0.0625
1) 0.1453
La probabilidad de que el módulo de elasticidad esté entre uno y dos es
P(1 X 2) P(ln(1) ln(X) ln(2))
P(0 ln(X) 0.693)
P
Z
(1.27) ( 1.50) 0.8312
¿Qué valor de c es tal que sólo el 1% de todos los sistemas tienen un módulo de elasticidad
que excede c? Se desea el valor de c con el cual
0.99 P(X c) P
Z
con la cual (ln(c) 0.375)/0.25 2.33 y c 2.605. Por lo tanto, 2.605 es el 99o
percentil
de la distribución del módulo de elasticidad. ■
Distribución beta
Todas las familias de distribuciones continuas estudiadas hasta ahora, excepto la distribu-
ción uniforme, tienen densidad positiva a lo largo de un intervalo infinito (aunque por lo ge-
neral la función de densidad se reduce con rapidez a cero más allá de unas cuantas
desviaciones estándar de la media). La distribución beta proporciona densidad positiva sólo
para X en un intervalo de longitud finita.
In(c) 0.375
0.25
0.693 0.375
0.25
0 0.375
0.25
La figura 4.30 ilustra varias funciones de densidad de probabilidad beta estándar. Las gráfi-
cas de la función de densidad de probabilidad son similares, excepto que están desplazadas
y luego alargadas o comprimidas para ajustarse al intervalo [A, B]. A menos que y sean
enteros, la integración de la función de densidad de probabilidad para calcular probabilida-
des es difícil. Se deberá utilizar una tabla de la función beta incompleta o un programa de
computadora apropiado. La media y varianza de X son
A (B A)
2
(B A)2
( )2
( 1)
4.5 Otras distribuciones continuas 167
DEFINICIÓN Se dice que una variable aleatoria X tiene una distribución beta con parámetros ,
(ambos positivos), A y B si la función de densidad de probabilidad de X es
f(x; , , A, B) B
1
A
(
(
)
(
)
) B
x
A
A
1
B
B
A
x
1
A x B
0 de lo contrario
El caso A 0, B 1 da la distribución beta estándar.
Ejemplo 4.27
Ï
ÌÓ
c4_p130-183.qxd 3/12/08 4:04 AM Page 167](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-185-320.jpg)
![4.5 Otras distribuciones continuas 169
a. ¿Cuál es la probabilidad de que la duración de un espé-
cimen sea cuando mucho de 250? ¿De menos de 250?
¿De más de 300?
b. ¿Cuál es la probabilidad de que la duración de un espé-
cimen esté entre 100 y 250?
c. ¿Qué valor es tal que exactamente 50% de todos los es-
pecímenes tengan duraciones que sobrepasen ese valor?
74. Sea X el tiempo (en 101
semanas) desde el envío de un
producto defectuoso hasta que el cliente lo devuelve. Supon-
ga que el tiempo de devolución mínimo es 3.5 y que el
excedente X 3.5 sobre el mínimo tiene una distribución de
Weibull con parámetros 2 y 1.5 (véase el artículo
Industrial Quality Control, citado en el ejemplo 4.26).
a. ¿Cuál es la función de distribución acumulativa de X?
b. ¿Cuáles son el tiempo de devolución esperado y la va-
rianza del tiempo de devolución? [Sugerencia: Primero
obtenga E(X 3.5) y V(X 3.5).]
c. Calcule P(X 5).
d. Calcule P(5 X 8).
75. Si X tiene una distribución de Weibull con la función de den-
sidad de probabilidad de la expresión (4.11), verifique que
(1 1/). [Sugerencia: En la integral para E(X)
cambie la variable y (x/)
, de modo que x y1/
.]
76. a. En el ejercicio 72, ¿cuál es la duración mediana de los
tubos? [Sugerencia: Use la expresión (4.12).]
b. En el ejercicio 74, ¿cuál es el tiempo de devolución
mediano?
c. Si X tiene una distribución de Weibull con la función de
distribución acumulativa de la expresión (4.12), obtenga
una expresión general para el percentil (100p)o
de la dis-
tribución.
d. En el ejercicio 74, la compañía desea negarse a aceptar
devoluciones después de t semanas. ¿Para qué valor de t
sólo el 10% de todas las devoluciones serán rechazadas?
77. Los autores del artículo del cual se extrajeron los datos en
el ejercicio 1.27 sugirieron que un modelo de probabilidad
razonable de la duración de las brocas era una distribución
lognormal con 4.5 y 0.8.
a. ¿Cuáles son el valor medio y la desviación estándar de
la duración?
b. ¿Cuál es la probabilidad de que la duración sea cuando
mucho de 100?
c. ¿Cuál es la probabilidad de que la duración sea por lo
menos de 200? ¿De más de 200?
78. El artículo “On Assessing the Accuracy of Offshore Wind
Turbine Reliability-Based Design Loads from the Environ-
mental Contour Method” (Intl. J. of Offshore and Polar
Engr., 2005: 132-140) propone la distribución de Weibull
con 1.817 y 0.863 como modelo de una altura (m)
de olas significativa durante una hora en un sitio.
a. ¿Cuál es la probabilidad de que la altura de las olas sea
cuando mucho de 0.5 m?
b. ¿Cuál es la probabilidad de que la altura de las olas ex-
ceda su valor medio por más de una desviación estándar?
c. ¿Cuál es la mediana de la distribución de la altura de las
olas?
d. Para 0 p 1, dé una expresión general para el percen-
til (100p)o
de la distribución de altura de olas.
79. Sea X la potencia mediana por hora (en decibeles) de se-
ñales de radio transmitidas entre dos ciudades. Los autores
del artículo “Families of Distributions for Hourly Median
Power and Instantaneous Power of Received Radio Sig-
nals” (J. Research National Bureau of Standards, vol. 67D,
1963: 753-762) argumentan que la distribución lognormal
proporciona un modelo de probabilidad razonable para X.
Si los valores de parámetros son 3.5 y 1.2, calcu-
le lo siguiente:
a. El valor medio y la desviación estándar de la potencia
recibida.
b. La probabilidad de que la potencia recibida esté entre 50
y 250 dB.
c. La probabilidad de que X sea menor que su valor medio.
¿Por qué esta probabilidad no es de 0.5?
80. a. Use la ecuación (4.13) para escribir una fórmula para la
mediana
~ de la distribución lognormal. ¿Cuál es la me-
diana de la distribución de potencia del ejercicio 79?
b. Recordando que z es la notación para el percentil
100(1 ) de la distribución normal estándar, escriba
una expresión para el percentil 100(1 ) de la distri-
bución lognormal. En el ejercicio 79, ¿qué valor exce-
derá la potencia recibida sólo 5% del tiempo?
81. Una justificación teórica basada en el mecanismo de falla
de cierto material sustenta la suposición de que la resisten-
cia dúctil X de un material tiene una distribución lognormal.
Suponga que los parámetros son 5 y 0.1.
a. Calcule E(X) y V(X).
b. Calcule P(X 125).
c. Calcule P(110 X 125).
d. ¿Cuál es el valor de la resistencia dúctil mediana?
e. Si diez muestras diferentes de un acero de aleación de es-
te tipo se sometieran a una prueba de resistencia, ¿cuántas
esperaría que tengan una resistencia de por lo menos 125?
f. Si 5% de los valores de resistencia más pequeños fueran
inaceptables, ¿cuál sería la resistencia mínima aceptable?
82. El artículo “The Statistics of Phytotoxic Air Pollutants” (J.
Royal Stat. Soc., 1989:183-198) sugiere la distribución
lognormal como modelo de la concentración de SO2 sobre
un cierto bosque. Suponga que los valores de parámetro
son 1.9 y 0.9.
a. ¿Cuáles son el valor medio y la desviación estándar de
la concentración?
b. ¿Cuál es la probabilidad de que la concentración sea
cuando mucho de 10? ¿De entre 5 y 10?
83. ¿Qué condición en relación con y es necesaria para que
la función de densidad de probabilidad beta estándar sea si-
métrica?
84. Suponga que la proporción X de área en un cuadrado selec-
cionado al azar que está cubierto por cierta planta tiene una
distribución beta estándar con 5 y 2.
a. Calcule E(X) y V(X).
b. Calcule P(X 0.2).
c. Calcule P(0.2 X 0.4).
d. ¿Cuál es la proporción esperada de la región de mues-
treo no cubierta por la planta?
85. Si X tiene una densidad beta estándar con parámetros y .
a. Verifique la fórmula para E(X) dada en la sección.
b. Calcule E[(1 X)m
]. Si X representa la proporción de
una sustancia compuesta de un ingrediente particular,
¿cuál es la proporción esperada que no se compone de
ese ingrediente?
c4_p130-183.qxd 3/12/08 4:04 AM Page 169](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-187-320.jpg)
![observaciones más grandes). Esto conduce a la siguiente definición general de percentiles
muestrales.
Una vez que se han calculado los valores porcentuales 100(i 0.5)/n(i 1, 2, . . . ,
n), se pueden obtener los percentiles muestrales correspondientes a porcentajes intermedios
mediante interpolación lineal. Por ejemplo, si n 10, los porcentajes correspondientes a las
observaciones muestrales ordenadas son 100(1 0.5)/10 5%, 100(2 0.5)/10 15%,
25%, . . . , y 100(10 0.5)/10 95%. El 10o
percentil está entonces a la mitad entre el
5o
percentil (observación muestral más pequeña) y el 15o
(segunda observación más pe-
queña). Para los propósitos, en este caso, tal interpolación no es necesaria porque una grá-
fica de probabilidad se basa sólo en los porcentajes 100(i 0.5)/n correspondientes a las n
observaciones muestrales.
Gráfica de probabilidad
Supóngase ahora que para los porcentajes 100(i 0.5)/n(i 1, . . . , n) se determinan los
percentiles de una distribución de población especificada cuya factibilidad está siendo in-
vestigada. Si la muestra en realidad se seleccionó de la distribución especificada, los per-
centiles muestrales (observaciones muestrales ordenadas) deberán estar razonablemente
próximos a los percentiles de distribución de población correspondientes. Es decir, con i
1, 2, . . . , n deberá haber una razonable concordancia entre la i-ésima observación muestral
más pequeña y el [100(i 0.5)/n]o
percentil de la distribución especificada. Considérense
los (percentil poblacional, percentil muestral) pares, es decir, los pares
,
con i 1, . . . , n. Cada uno de esos pares se dibuja como un punto en un sistema de coor-
denadas bidimensional. Si los percentiles muestrales se acercan a los percentiles de distri-
bución de población correspondientes, el primer número en cada par será aproximadamente
igual al segundo número. Los puntos dibujados se quedarán entonces cerca de una línea a
45°. Desviaciones sustanciales de los puntos dibujados con respecto a una línea a 45° hacen
dudar de la suposición de que la distribución considerada es la correcta.
Un experimentador conoce el valor de cierta constante física. El experimentador realiza n 10
mediciones independientes de este valor por medio de un dispositivo de medición particu-
lar y anota los errores de medición resultantes (error valor observado valor verdade-
ro). Estas observaciones aparecen en la tabla adjunta.
Porcentaje 5 15 25 35 45
Percentil z 1.645 1.037 0.675 0.385 0.126
Observación muestral 1.91 1.25 0.75 0.53 0.20
Porcentaje 55 65 75 85 95
Percentil z 0.126 0.385 0.675 1.037 1.645
Observación muestral 0.35 0.72 0.87 1.40 1.56
i-ésima observación
muestral más pequeña
[100(i 0.5)/n]o
percentil
de la distribución
4.6 Gráficas de probabilidad 171
DEFINICIÓN Se ordenan las n observaciones muestrales de la más pequeña a la más grande. Enton-
ces la observación i-ésima más pequeña en la lista se considera que es el [100(i
0.5)/n]o
percentil muestral.
Ejemplo 4.29
c4_p130-183.qxd 3/12/08 4:05 AM Page 171](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-189-320.jpg)
![(los puntos a la extrema izquierda de la gráfica están bien por arriba de la línea a 45°). Asimis-
mo, las dos observaciones muestrales más grandes son mucho más pequeñas que los percen-
tiles z asociados. Esta gráfica indica que la distribución normal estándar no sería una opción
factible del modelo de probabilidad que dio lugar a estos errores de medición observados. ■
A un investigador en general no le interesa saber con exactitud si una distribución de
probabilidad especificada, tal como la distribución normal estándar (normal con 0 y
1) o la distribución exponencial con 0.1, es un modelo factible de la distribución de
población de la cual se seleccionó la muestra. En cambio, la cuestión es si algún miembro
de una familia de distribuciones de probabilidad especifica un modelo factible, la familia de
distribuciones normales, la familia de distribuciones exponenciales, la familia de distribu-
ciones Weibull, y así sucesivamente. Los valores de los parámetros de una distribución casi
nunca se especifican al principio. Si la familia de distribuciones Weibull se considera como
modelo de datos de duración, ¿existen algunos valores de los parámetros y con los cuales
la distribución de Weibull correspondiente se adapta bien a los datos? Afortunadamente, casi
siempre es el caso de que sólo una gráfica de probabilidad bastará para evaluar la factibilidad
de una familia completa. Si la gráfica se desvía sustancialmente de una línea recta, ningún
miembro de la familia es factible. Cuando la gráfica es bastante recta, se requiere más tra-
bajo para estimar valores de los parámetros que generen la distribución más razonable del
tipo especificado.
Habrá que enfocarse en una gráfica para verificar la normalidad. Tal gráfica es útil en
trabajo aplicado porque muchos procedimientos estadísticos formales dan inferencias pre-
cisas sólo cuando la distribución de población es por lo menos aproximadamente normal.
Estos procedimientos en general no deben ser utilizados si la gráfica de probabilidad nor-
mal muestra un alejamiento muy pronunciado de la linealidad. La clave para construir una
gráfica de probabilidad normal que comprenda varios elementos es la relación entre los per-
centiles (z) normales estándares y aquellos de cualquier otra distribución normal:
( percentil z correspondiente)
Considérese primero el caso, 0. Si cada observación es exactamente igual al percentil
normal correspondiente con algún valor de , los pares ( [percentil z], observación) que-
dan sobre una línea a 45°, cuya pendientes es 1. Esto implica que los pares (percentil z, ob-
servación) quedan sobre una línea que pasa por (0, 0) (es decir, una con intercepción y
en 0) pero con pendiente en lugar de 1. El efecto del valor no cero de es simplemente
cambiar la intercepción y de 0 a .
percentil de una
distribución normal (, )
La muestra adjunta compuesta de n 20 observaciones de voltaje de ruptura dieléctrica
de un pedazo de resina epóxica apareció en el artículo “Maximum Likelihood Estimation
in the 3-Parameter Weibull Distribution” (IEEE Trans. on Dielectrics and Elec. Insul.,
4.6 Gráficas de probabilidad 173
Una gráfica de los n pares
([100(i 0.5)/n]o
percentil z, observación i-ésima más pequeña)
en un sistema de coordenadas bidimensional se llama gráfica de probabilidad nor-
mal. Si las observaciones muestrales se extraen en realidad de una distribución
normal con valor medio y desviación estándar , los puntos deberán quedar cerca
de una línea recta con pendiente e intercepción en . Así pues, una gráfica en la
cual los puntos quedan cerca de alguna línea recta sugiere que la suposición de una
distribución de población normal es factible.
Ejemplo 4.30
c4_p130-183.qxd 3/12/08 4:05 AM Page 173](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-191-320.jpg)
![Una distribución de población no normal a menudo puede ser colocada en una de las
siguientes tres categorías:
1. Es simétrica y tiene “colas más livianas” que una distribución normal; es decir la curva
de densidad declina con más rapidez en la cola de lo que lo hace una curva normal.
2. Es simétrica y con colas pesadas en comparación con una distribución normal.
3. Es asimétrica.
Una distribución uniforme es de cola liviana, puesto que su función de densidad se reduce a
cero afuera de un intervalo finito. La función de densidad f(x) 1/[(1 x2
)] en x
es de cola pesada, puesto que 1/(1 x2
) declina mucho menos rápidamente que ex2/2
. Las dis-
tribuciones lognormal y Weibull se encuentran entre aquellas que son asimétricas. Cuando
los puntos en una gráfica de probabilidad normal no se adhieren a una línea recta, la confi-
guración con frecuencia sugerirá que la distribución de la población se encuentra en una ca-
tegoría particular de estas tres categorías.
Cuando la distribución de la cual se selecciona la muestra es de cola liviana, las ob-
servaciones más grandes y más pequeñas en general no son tan extremas como podría espe-
rarse de una muestra aleatoria normal. Visualícese una línea recta trazada a través de la parte
media de la gráfica; los puntos a la extrema derecha tienden a estar debajo de la línea (va-
lor observado el percentil z) en tanto que los puntos a la extrema izquierda de la gráfica
tienden a quedar sobre la línea recta (valor observado percentil z). El resultado es una
configuración en forma de S del tipo ilustrado en la figura 4.32.
Una muestra tomada de una distribución de cola pesada también tiende a producir una
gráfica en forma de S. Sin embargo, en contraste con el caso de cola liviana, el extremo iz-
quierdo de la gráfica se curva hacia abajo (observado percentil z), como se muestra en la
figura 4.35a). Si la distribución subyacente es positivamente asimétrica (una cola izquierda
corta y una cola derecha larga), las observaciones muestrales más pequeñas serán más gran-
des que las esperadas con una muestra normal y también lo serán las observaciones más
grandes. En este caso, los puntos en ambos extremos de la gráfica quedarán sobre una línea
recta que pasa por la parte media, que produce una configuración curvada, como se ilustra
en la figura 4.35b). Una muestra tomada de una distribución lognormal casi siempre produ-
cirá la configuración mencionada. Una gráfica de (percentil z, ln(x)) pares deberán parecer-
se entonces a una línea recta.
4.6 Gráficas de probabilidad 175
Observación
Percentil z
a)
Observación
Percentil z
b)
Figura 4.35 Gráficas de probabilidad que sugieren una distribución no normal: a) una gráfica compatible con
una distribución de cola pesada; b) una gráfica compatible con una distribución positivamente asimétrica.
c4_p130-183.qxd 3/12/08 4:05 AM Page 175](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-193-320.jpg)
![Aun cuando la distribución de la población sea normal, los percentiles muestrales no
coincidirán exactamente con los teóricos debido a la variabilidad del muestreo. ¿Qué tanto
pueden desviarse los puntos de la gráfica de probabilidad de un patrón de línea recta antes
de que la suposición de normalidad ya no sea factible? Esta no es una pregunta fácil de res-
ponder. En general, es más probable que una pequeña muestra de una distribución normal
produzca una gráfica con un patrón no lineal que una grande. El libro Fitting Equations to
Data (véase la bibliografía del capítulo 13) presenta los resultados de un estudio de simulación
en el cual se seleccionaron numerosas muestras de diferentes tamaños de distribuciones nor-
males. Los autores concluyeron que en general varía mucho la apariencia de la gráfica de
probabilidad con tamaños de muestra de menos de 30 y sólo con tamaños de muestra mu-
cho más grandes en general predomina el patrón lineal. Cuando una gráfica está basada en
un pequeño tamaño de muestra, sólo un alejamiento muy sustancial de la linealidad se de-
berá considerar como evidencia concluyente de no normalidad. Un comentario similar se
aplica a gráficas de probabilidad para comprobar la factibilidad de otros tipos de distribu-
ciones.
Más allá de la normalidad
Considérese una familia de distribuciones de probabilidad que implica dos parámetros 1 y
2 y sea F(x; 1, 2) la función de distribución acumulativa correspondiente. La familia de dis-
tribuciones normales es una de esas familias, con 1 , 2 y F(x; , ) [(x )/].
Otro ejemplo es la familia Weibull, con 1 , 2 y
F(x; , ) 1 e(x/)
Otra familia más de este tipo es la familia gama, para la cual la función de distribución
acumulativa es una integral que implica la función gama incompleta que no puede ser ex-
presada en cualquier forma más simple.
Se dice que los parámetros 1 y 2 son parámetros de ubicación y escala, respecti-
vamente, si F(x; 1, 2) es una función de (x 1)/ 2. Los parámetros y de la familia
normal son los parámetros de ubicación y escala, respectivamente. Al cambiar la curva de
densidad acampanada se desplaza a la derecha o izquierda y al cambiar se alarga o com-
prime la escala de medición (la escala sobre el eje horizontal cuando se dibuja la función de
densidad). La función de distribución acumulativa da otro ejemplo
F(x; 1, 2) 1 ee(x
1
)/
2 x
Se dice que una variable aleatoria con esta función de distribución acumulativa tiene una
distribución de valor extremo. Se utiliza en aplicaciones que implican la duración de un
componente y la resistencia de un material.
Aunque la forma de la función de distribución acumulativa de valor extremo a prime-
ra vista pudiera sugerir que 1 es el punto de simetría de la función de densidad y por ende
la media y la mediana, éste no es el caso. En cambio, P(X 1) F( 1; 1, 2) 1 e1
0.632, y la función de densidad f(x; 1, 2) F(x; 1, 2) es negativamente asimétrica (una
larga cola inferior). Asimismo, el parámetro de escala 2 no es la desviación estándar (
1 0.5772 2 y 1.283 2). Sin embargo, al cambiar el valor de 1 cambia la ubicación
de la curva de densidad, mientras que al cambiar 2 cambia la escala del eje de medición.
El parámetro de la distribución de Weibull es un parámetro de escala, pero no es un
parámetro de ubicación. El parámetro en general se conoce como parámetro de forma.
Un comentario similar es pertinente para los parámetros y de la distribución gama. En
la forma usual, la función de densidad de cualquier miembro de o la distribución gama o Wei-
bull es positiva con x 0 y cero de lo contrario. Un parámetro de ubicación puede ser in-
troducido como tercer parámetro (se hizo esto para la distribución de Weibull) para
desplazar la función de densidad de modo que sea positiva si x y cero de lo contrario.
176 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
c4_p130-183.qxd 3/12/08 4:05 AM Page 176](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-194-320.jpg)
![Cuando la familia considerada tiene sólo parámetros de ubicación y escala, el tema de
si cualquier miembro de la familia es una distribución de población factible puede ser abor-
dado vía una gráfica de probabilidad única de fácil construcción. Primero se obtienen los
percentiles de la distribución estándar, una con 1 0 y 2 1, con los porcentajes
100 (i 0.5)/n (i 1, . . . , n). Los n pares (percentil estandarizado, observación) dan los
puntos en la gráfica. Esto es exactamente lo que se hizo para obtener una gráfica de proba-
bilidad normal ómnibus. Un tanto sorprendentemente, esta metodología puede ser aplicada
para dar una gráfica de probabilidad Weibull ómnibus. El resultado clave es que X tiene una
distribución de Weibull con parámetro de forma y parámetro de escala , entonces la va-
riable transformada ln(X) tiene una distribución de valor extremo con parámetro de ubica-
ción 1 ln() y parámetro de escala 1/. Así pues una gráfica de los pares (percentil
estandarizado de valor extremo, ln(x)) que muestre un fuerte patrón lineal apoya la selec-
ción de la distribución de Weibull como modelo de una población.
Las observaciones adjuntas son de la duración (en horas) del aislamiento de aparatos eléc-
tricos cuando la aceleración del esfuerzo térmico y eléctrico se mantuvo fijo a valores par-
ticulares (“On the Estimation of Life of Power Apparatus Insulation Under Combined
Electrical and Thermal Stress”, IEEE Trans. on Electrical Insulation, 1985: 70-78). Una
gráfica de probabilidad de Weibull necesita calcular primero los percentiles 5o
, 15o
, . . . , y
95o
de la distribución de valor extremo estándar. El (100p)o
percentil (p) satisface
p F( (p)) 1 ee (p)
de donde (p) ln[ln(1 p)].
Percentil 2.97 1.82 1.25 0.84 0.51
x 282 501 741 851 1072
ln(x) 5.64 6.22 6.61 6.75 6.98
Percentil 0.23 0.05 0.33 0.64 1.10
x 1122 1202 1585 1905 2138
ln(x) 7.02 7.09 7.37 7.55 7.67
Los pares (2.97, 5.64), (1.82, 6.22), . . . , (1.10, 7.67) se dibujan como puntos en la fi-
gura 4.36. La forma recta de la gráfica hacia la derecha argumenta firmemente a favor del
uso de la distribución de Weibull como modelo de duración de aislamiento, una conclusión
también alcanzada por el autor del citado artículo.
4.6 Gráficas de probabilidad 177
Ejemplo 4.31
3
5
8
7
6
2 1 0 1
ln(x)
Percentil
Figura 4.36 Gráfica de probabilidad Weibull de los datos de duración del aislamiento. ■
c4_p130-183.qxd 3/12/08 4:05 AM Page 177](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-195-320.jpg)
![Ejercicios suplementarios 179
EJERCICIOS SUPLEMENTARIOS (98-128)
98. Sea X el tiempo que una cabeza de lectura/escritura re-
quiere para localizar un registro deseado en un dispositivo
de memoria de disco de computadora una vez que la cabe-
za se ha colocado sobre la pista correcta. Si los discos giran
una vez cada 25 milisegundos, una suposición razonable es
que X está uniformemente distribuida en el intervalo [0, 25].
a. Calcule P(10 X 20).
b. Calcule P(X 10).
c. Obtenga la función de distribución acumulativa F(X).
d. Calcule E(X) y X.
99. Una barra de 12 pulg que está sujeta por ambos extremos se
somete a una cantidad creciente de esfuerzo hasta que
se rompe. Sea Y la distancia del extremo izquierdo al
punto donde ocurre la ruptura. Suponga que Y tiene la fun-
ción de densidad de probabilidad
f(y) 2
1
4y1
1
y
2 0 y 12
0 de lo contrario
Calcule lo siguiente:
a. La función de densidad de probabilidad de Y y dibújela.
b. P(Y 4), P(Y 6) y P(4 Y 6)
c. E(Y), E(Y2
) y V(Y).
d. La probabilidad de que el punto de ruptura ocurra a más
de 2 pulg del punto de ruptura esperado.
e. La longitud esperada del segmento más corto cuando
ocurre la ruptura.
100. Sea X el tiempo hasta la falla (en años) de cierto compo-
nente hidráulico. Suponga que la función de densidad de
probabilidad de X es f(x) 32/(x 4)3
con x 0.
a. Verifique que f(x) es una función de densidad de proba-
bilidad legítima.
b. Determine la función de distribución acumulativa.
c. Use el resultado del inciso b) para calcular la probabi-
lidad de que el tiempo hasta la falla esté entre dos y cin-
co años.
d. ¿Cuál el tiempo esperado hasta la falla?
e. Si el componente tiene un valor de recuperación igual a
100/(4 x) cuando su tiempo para la falla es x, ¿cuál
es el valor de recuperación esperado?
101. El tiempo X para la terminación de cierta tarea tiene una
función de distribución acumulativa F(x) dada por
0 x 0
x
3
3
0 x 1
1
1
2
7
3
x
7
4
3
4
x 1 x
7
3
1 x
7
3
a. Obtenga la función de densidad de probabilidad f(x) y
trace su gráfica.
b. Calcule P(0.5 X 2).
c. Calcule E(X).
93. Construya una gráfica de probabilidad que le permita evaluar
la factibilidad de la distribución lognormal como modelo de
los datos de cantidad de lluvia del ejercicio 83 (capítulo 1).
94. Las observaciones adjuntas son valores de precipitación du-
rante marzo a lo largo de un periodo de 30 años en Minnea-
polis-St. Paul.
a. Construya e interprete una gráfica de probabilidad nor-
mal con este conjunto de datos.
b. Calcule la raíz cuadrada de cada valor y luego constru-
ya una gráfica de probabilidad normal basada en estos
datos transformados. ¿Parece factible que la raíz cuadra-
da de la precipitación esté normalmente distribuida?
c. Repita el inciso b) después de transformar por medio de
raíces cúbicas.
95. Use un paquete de software estadístico para construir una grá-
fica de probabilidad normal de los datos de resistencia última
a la tensión dados en el ejercicio 13 del capítulo 1 y comente.
96. Sean y1, y2, . . . , yn, las observaciones muestrales ordenadas
(con y1 como la más pequeña y yn como la más grande). Una
verificación sugerida de normalidad es dibujar los pares
(1
((i 0.5)/n), yi). Suponga que se cree que las observa-
ciones provienen de una distribución con media 0 y sean
w1, . . . , wn los valores absolutos ordenados de las xi. Una
gráfica medio normal es una gráfica de probabilidad de las
wi. Más específicamente, como P(°Z° w) P(w
w) 2(w) 1, una gráfica medio normal es una grá-
fica de los pares (1
{[(i 0.5)/n 1]/2}, wi) La virtud
de esta gráfica es que los valores apartados pequeños o
grandes en la muestra original ahora aparecerán sólo en el
extremo superior de la gráfica y no en ambos extremos.
Construya una gráfica medio normal con la siguiente
muestra de errores de medición y comente: 3.78, 1.27,
1.44, 0.39, 12.38, 43.40, 1.15, 3.96, 2.34, 30.84.
97. Las siguientes observaciones de tiempo de falla (miles de
horas) se obtuvieron con una prueba de duración acelerada
de 16 chips de circuitos integrados de un tipo:
Use los percentiles correspondientes de la distribución
exponencial con 1 para construir una gráfica de pro-
babilidad. Luego explique por qué la gráfica valora la facti-
bilidad de la muestra habiendo sido generada con cualquier
distribución exponencial.
0.77 1.20 3.00 1.62 2.81 2.48
1.74 0.47 3.09 1.31 1.87 0.96
0.81 1.43 1.51 0.32 1.18 1.89
1.20 3.37 2.10 0.59 1.35 0.90
1.95 2.20 0.52 0.81 4.75 2.05
82.8 11.6 359.5 502.5 307.8 179.7
242.0 26.5 244.8 304.3 379.1 212.6
229.9 558.9 366.7 204.6
Ï
Ì
Ó
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:05 AM Page 179](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-197-320.jpg)
![180 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
102. Se sabe que el voltaje de ruptura de un diodo seleccionado
al azar de cierto tipo está normalmente distribuido con va-
lor medio de 40 V y desviación estándar de 1.5 V.
a. ¿Cuál es la probabilidad de que el voltaje de un solo
diodo esté entre 39 y 42?
b. ¿Qué valor es tal que sólo 15% de todos los diodos ten-
gan voltajes que excedan ese valor?
c. Si se seleccionan cuatro diodos independientemente,
¿cuál es la probabilidad de que por lo menos uno tenga
un voltaje de más de 42?
103. El artículo “Computer Assisted Net Weight Control” (Qua-
lity Progress, 1983: 22-25) sugiere una distribución normal
con media de 137.2 oz y desviación estándar de 1.6 oz del
contenido de frascos de cierto tipo. El contenido declarado
fue de 135 oz.
a. ¿Cuál es la probabilidad de que un solo frasco conten-
ga más que el contenido declarado?
b. Entre diez frascos seleccionados al azar, ¿cuál es la pro-
babilidad de que por lo menos ocho contengan más del
contenido declarado?
c. Suponiendo que la media permanece en 137.2, ¿a qué
valor se tendría que cambiar la desviación estándar de
modo que 95% de todos los frascos contengan más que
el contenido declarado?
104. Cuando tarjetas de circuito utilizadas en la fabricación de
reproductores de discos compactos se someten a prueba,
el porcentaje de tarjetas defectuosas es de 5%. Suponga
que se recibió un lote de 250 tarjetas y que la condición
de cualquier tarjeta particular es independiente de las
demás.
a. ¿Cuál es la probabilidad aproximada de que por lo
menos 10% de las tarjetas en el lote sean defectuosas?
b. ¿Cuál es la probabilidad aproximada de que haya exac-
tamente 10 defectuosas en el lote?
105. El artículo “Characterization of Room Temperature Dam-
ping in Aluminum-Indium Alloys” (Metallurgical Trans.
1993: 1611-1619) sugiere que el tamaño de grano de ma-
triz A1 (m) de una aleación compuesta de 2% de indio
podría ser modelado con una distribución normal con valor
medio de 96 y desviación estándar de 14.
a. ¿Cuál es la probabilidad de que el tamaño de grano ex-
ceda de 100?
b. ¿Cuál es la probabilidad de que el tamaño de grano esté
entre 50 y 80?
c. ¿Qué intervalo (a, b) incluye 90% central de todos los
tamaños de grano (de modo que 5% esté por debajo de
a y 5% por encima de b)?
106. El tiempo de reacción (en segundos) a un estímulo es una
variable aleatoria continua con función de densidad de pro-
babilidad
f(x)
3
2
x
1
2
1 x 3
0 de lo contrario
a. Obtenga la función de distribución acumulativa.
b. ¿Cuál es la probabilidad de que el tiempo de reacción
sea cuando mucho de 2.5 s? ¿De entre 1.5 y 2.5 s?
c. Calcule el tiempo de reacción esperado.
d. Calcule la desviación estándar del tiempo de reacción.
e. Si un individuo requiere más de 1.5 s para reaccionar a
una luz que se enciende y permanece encendida hasta que
transcurre un segundo más o hasta que la persona reaccio-
na (lo que suceda primero). Determine la cantidad de
tiempo esperado de que la luz permanezca encendida.
[Sugerencia: Sea h(X) el tiempo que la luz está encen-
dida como una función del tiempo de reacción X.]
107. Sea X la temperatura a la cual ocurre una reacción química.
Suponga que X tiene una función de densidad de probabilidad
f(x)
1
9
(4 x2
) 1 x 2
0 de lo contrario
a. Trace la gráfica de f(x).
b. Determine la función de distribución acumulativa y
dibújela.
c. ¿Es cero la temperatura mediana a la cual ocurre la
reacción? Si no, ¿es la temperatura mediana menor o
mayor que cero?
d. Suponga que esta reacción es independientemente reali-
zada una vez en cada uno de diez laboratorios diferentes
y que la función de densidad de probabilidad del tiempo
de reacción en cada laboratorio es como se da. Sea Y
el número entre los diez laboratorios en los cuales la
temperatura excede de uno. ¿Qué clase de distribución
tiene Y? (Dé el nombre y valores de los parámetros.)
108. El artículo “Determination of the MTF of Positive Photore-
sists Using the Monte Carlo Method” (Photographic Sci.
and Engr., 1983: 254-260) propone la distribución exponen-
cial con parámetro 0.93 como modelo de la distribución
de una longitud de trayectoria libre de fotones (m) en cier-
tas circunstancias. Suponga que éste es el modelo correcto.
a. ¿Cuál es la longitud de trayectoria esperada y cuál es su
desviación estándar?
b. ¿Cuál es la probabilidad de que la longitud de trayecto-
ria exceda de 3.0? ¿Cuál es la probabilidad de que la
longitud de trayectoria esté entre 1.0 y 3.0?
c. ¿Qué valor es excedido por sólo 10% de todas las lon-
gitudes de trayectoria?
109. El artículo “The Prediction of Corrosion by Statistical
Analysis of Corrosion Profiles” (Corrosion Science, 1985:
305-315) sugiere la siguiente función de distribución acumu-
lativa de la profundidad X de la picadura más profunda en
un experimento que implica la exposición de acero al man-
ganeso de carbono a agua de mar acidificada.
F(x; , ) ee(x)/
x
Los autores proponen los valores 150 y 90. Su-
ponga que éste es el modelo correcto.
a. ¿Cuál es la probabilidad de que la profundidad de la pi-
cadura más profunda sea cuando mucho de 150?
¿Cuándo mucho 300? ¿De entre 150 y 300?
b. ¿Por debajo de qué valor será observada la profundidad de
la picadura máxima en 90% de todos los experimentos?
c. ¿Cuál es la función de densidad de X?
d. Se puede demostrar que la función de densidad es unimo-
dal (una sola cresta). ¿Por encima de qué valor sobre el eje
de medición ocurre esta cresta? (Este valor es el modo.)
e. Se puede demostrar que E(X) 0.5772 . ¿Cuál
es la media de los valores dados de y y cómo se
Ï
Ì
Ó
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:05 AM Page 180](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-198-320.jpg)
![Ejercicios suplementarios 181
compara con la mediana y el modo? Trace la gráfica de
la función de densidad. [Nota: Ésta se conoce como
distribución de valor extremo más grande.]
110. Un componente tiene una duración X exponencialmente
distribuida con parámetro .
a. Si el costo de operación por unidad de tiempo es c,
¿cuál es el costo esperado de operación de este compo-
nente durante el tiempo que dura?
b. En lugar de un coeficiente de costos constante como en
el inciso a), suponga que el coeficiente de costos es
c(1 0.5eax
) con a 0, de modo que el costo por uni-
dad de tiempo es menor que c cuando el componente es
nuevo y se vuelve más caro a medida que el componen-
te envejece. Ahora calcule el costo de operación espe-
rado durante la duración del componente.
111. La moda de una distribución continua es el valor x*
que in-
crementa al máximo f(x).
a. ¿Cuál es la moda de una distribución normal con pará-
metros y ?
b. ¿Tiene una sola moda la distribución uniforme con pa-
rámetros A y B? ¿Por qué sí o por qué no?
c. ¿Cuál es la moda de una distribución exponencial con
parámetro ? (Trace una gráfica.)
d. Si X tiene una distribución gama con parámetros y y
1, halle la moda [Sugerencia: ln[f(x)] se incremen-
tará al máximo si y sólo si f(x) es, y puede ser más sim-
ple considerar la derivada de ln[f(x)].
e. ¿Cuál es la moda de una distribución ji cuadrada con
grados de libertad?
112. El artículo “Error Distribution in Navigation” (J. Institute of
Navigation, 1971: 429-442) sugiere que una distribución
exponencial reproduce con más o menos precisión a una
distribución de frecuencia de errores positivos (magnitudes
de errores). Sea X el error de posición lateral (millas náu-
ticas), el cual puede ser positivo o negativo. Suponga que la
función de densidad de probabilidad de X es
f(x) (0.1)e .2°x°
x
a. Trace una gráfica de f(x) y compruebe que f(x) es una
función de densidad de probabilidad legítima (demues-
tre que se integra a 1).
b. Obtenga la función de distribución acumulativa de X y
trácela.
c. Calcule P(X 0), P(X 2), P( 1 X 2), y la pro-
babilidad de cometer un error de más de dos millas.
113. En algunos sistemas, un cliente es asignado a una o dos pres-
tadoras de servicios. Si el tiempo para que el cliente sea aten-
dido por la prestadora de servicios i tiene una distribución
exponencial con parámetro i (i 1, 2) y p es la proporción de
todos los clientes atendidos por la prestadora de servicios 1,
entonces la función de densidad de probabilidad de X el
tiempo para ser atendido de un cliente seleccionado al azar es
f(x; 1, 2, p)
p1e1
x
(1 p)2e2
x
x 0
0 de lo contrario
Ésta a menudo se llama distribución hiperexponencial o ex-
ponencial combinada. Esta distribución también se propone
como modelo de la cantidad de lluvia en “Modeling Mon-
soon Affected Rainfall of Pakistan by Point Processes” (J.
Water Resources Planning and Mgmnt., 1992: 671-688).
a. Verifique que f(x; 1, 2, p) es una función de densidad
de probabilidad.
b. ¿Cuál es la función de distribución acumulativa F(x; 1,
2, p)?
c. Si f(x; 1, 2, p) es la función de densidad de probabili-
dad de X, ¿cuál es E(X)?
d. Utilizando el hecho de que E(X2
) 2/2
cuando X tiene
una distribución exponencial con parámetro , calcule
E(X2
) cuando X tiene la función de densidad de proba-
bilidad f(x; 1, 2, p). Luego calcule V(X).
e. El coeficiente de variación de una variable aleatoria (o dis-
tribución) es CV /. ¿Cuál es CV para una variable
aleatoria exponencial? ¿Qué puede decir sobre el valor de
CV cuando X tiene una distribución hiperexponencial?
f. ¿Cuál es el CV de una distribución Erlang con paráme-
tros y n como se definen en el ejercicio 68? [Nota: En
trabajo aplicado, el CV muestral se utiliza para decidir
cuál de las tres distribuciones podría ser apropiada.]
114. Suponga que en un estado particular se permite que las per-
sonas físicas que presentan su declaración de impuestos de-
tallen sus deducciones sólo si el total de las deducciones
detalladas es por lo menos de $5000. Sea X (en miles de dó-
lares) el total de deducciones detalladas en un formulario
seleccionado al azar. Suponga que X tiene la función de
densidad de probabilidad
f(x; )
k/x
x 5
0 de lo contrario
a. Encuentre el valor de k. ¿Qué restricción en es necesaria?
b. ¿Cuál es la función de distribución acumulativa de X?
c. ¿Cuál es la deducción total esperada en un formulario
seleccionado al azar? ¿Qué restricción en es necesa-
ria para que E(X) sea finita?
d. Demuestre que ln(X/5) tiene una distribución exponen-
cial con parámetro 1.
115. Sea Ii la corriente de entrada a un transistor e I0 la corrien-
te de salida. En ese caso la ganancia de corriente es pro-
porcional a ln(I0/Ii). Suponga que la constante de
proporcionalidad es 1 (lo que conduce a seleccionar una
unidad de medición particular), así que la ganancia de co-
rriente X ln(I0/Ii). Suponga que X está normalmente
distribuida con 1 y 0.05.
a. ¿Qué tipo de distribución tiene la razón I0/Ii?
b. ¿Cuál es la probabilidad de que la corriente de salida
sea más de dos veces la corriente de entrada?
c. ¿Cuáles son el valor esperado y la varianza de la razón
de corriente de salida a corriente de entrada?
116. El artículo “Response of SiCf/Si3N4 Composites Under
Static and Cyclic Loading-An Experimental and Statistical
Analysis” (J. of Engr. Materials and Technology, 1997:
186-193) sugiere que la resistencia a la tensión (MPa) de
compuestos en condiciones especificadas puede ser mode-
lada por una distribución de Weibull con 9 y 180.
a. Trace una gráfica de la función de densidad.
b. ¿Cuál es la probabilidad de que la resistencia de un es-
pécimen seleccionado al azar exceda de 175? ¿Sea de
entre 150 y 175?
c. Si se seleccionan al azar dos especímenes y sus resistencias
son independientes entre sí, ¿cuál es la probabilidad de que
por lo menos uno tenga una resistencia entre 150 y 175?
Ï
Ì
Ó
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:05 AM Page 181](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-199-320.jpg)
![182 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad
d. ¿Qué valor de resistencia separa al 10% de todos los es-
pecímenes más débiles del 90% restante?
117. Si Z tiene una distribución normal estándar, defina una
nueva variable aleatoria Y como Y Z . Demuestre
que Y tiene una distribución normal con parámetros y .
[Sugerencia: Y y si y sólo si Z ? Use ésta para definir
la función de distribución acumulativa de Y y luego derí-
vela con respecto a y.]
118. a. Suponga que la duración X de un componente, medida
en horas, tiene una distribución gama con parámetros
y . Sea Y la duración medida en minutos. Deduzca
la función de densidad de probabilidad de Y. [Sugerencia:
Y y si y sólo si X y/60. Use esto para obtener la fun-
ción de distribución acumulativa de Y y luego derívela pa-
ra obtener la función de densidad de probabilidad.]
b. Si X tiene una distribución gama con parámetros y ,
¿cuál es la distribución de probabilidad de Y cX?
119. En los ejercicios 111 y 112, así como también en muchas
otras situaciones, se tiene la función de densidad de proba-
bilidad f(x) de X y se desea conocer la función de densidad
de probabilidad de Y h(X). Suponga que h() es una fun-
ción invertible, de modo que y h(x) se resuelve para x a
fin de obtener x k(y). Entonces se puede demostrar que
la función de densidad de probabilidad de Y es
g(y) f [k(y)] °k(y)°
a. Si X tiene una distribución uniforme con A 0 y B 1,
derive la función de densidad de probabilidad de Y
ln(X).
b. Resuelva el ejercicio 117, utilizando este resultado.
c. Resuelva el ejercicio 118(b), utilizando este resultado.
120. Basado en los datos del experimento de lanzamiento de dar-
do, el artículo “Shooting Darts” (Chance, verano de 1997:
16-19) propuso que los errores horizontales y verticales al
apuntar a un blanco deben ser independientes unos de
otros, cada uno con una distribución normal con media 0 y
varianza 2
. Se puede demostrar entonces que la distancia
V del blanco al punto de aterrizaje es
f(v) ev2/22
v 0
a. ¿De qué familia introducida en este capítulo es esta
función de densidad de probabilidad?
b. Si 20 mm (cerca del valor sugerido por el artículo),
¿Cuál es la probabilidad de que un dardo aterrice dentro
de 25 mm (aproximadamente una pulg) del blanco?
121. El artículo “Three Sisters Give Birth on the Same Day”
(Chance, primavera de 2001, 23-25) utilizó el hecho de que
tres hermanas de Utah dieron a luz el 11 de marzo de 1998
como base para plantear algunas preguntas interesantes con
respecto a coincidencias de fechas de nacimiento.
a. No haciendo caso del año bisiesto y suponiendo que los
otros 365 días son igualmente probables, ¿cuál es la
probabilidad de que tres nacimientos seleccionados al
azar ocurran el 11 de marzo? Asegúrese de indicar qué,
si las hay, suposiciones adicionales está haciendo.
b. Con las suposiciones utilizadas en el inciso a), ¿cuál es
la probabilidad de que tres nacimientos seleccionados
al azar ocurran el mismo día?
c. El autor sugirió, basado en datos extensos, que el tiempo
de gestación (tiempo entre la concepción y el nacimiento)
podía ser modelado como si tuviera una distribución
normal con valor medio de 280 días y desviación están-
dar de 19.88 días. Las fechas esperadas para las tres her-
manas de Utah fueron el 15 de marzo, el 1 de abril y el
4 de abril, respectivamente. Suponiendo que las tres fe-
chas esperadas están en la media de la distribución,
¿cuál es la probabilidad de que los nacimientos ocurrie-
ran el 11 de marzo? [Sugerencia: La desviación de la fe-
cha de nacimiento con respecto a la fecha esperada está
normalmente distribuida con media 0.]
d. Explique cómo utilizaría la información del inciso c)
para calcular la probabilidad de una fecha de nacimien-
to común.
122. Sea X la duración de un componente, con f(x) y F(x) la fun-
ción de densidad de probabilidad y la función de distribución
acumulativa de X. La probabilidad de que el componente fa-
lle en el intervalo (x, x x) es aproximadamente f(x) x.
La probabilidad condicional de que falle en (x, x x) dado
que ha durado por lo menos x es f(x) x/[1 F(x)]. Divi-
diendo ésta entre x se produce la función de coeficiente
de falla:
r(x)
1
f(x
F
)
(x)
Una función de coeficiente de falla creciente indica que la
probabilidad de que los componentes viejos se desgasten
es cada vez más grande, mientras que un coeficiente de falla
decreciente evidencia una confiabilidad cada vez más
grande con la edad. En la práctica, a menudo se supone una
falla “en forma de tina de baño”.
a. Si X está exponencialmente distribuida, ¿cuál es r(x)?
b. Si X tiene una distribución de Weibull con parámetros
y , ¿cuál es r(x)? ¿Con qué valores de parámetros se
incrementará r(x)? ¿Con qué valores de parámetro de-
crecerá r(x) con x?
c. Como r(x)(d/dx)ln[1F(x)], ln[1F(x)] r(x)
dx. Suponga
r(x)
1
x
0 x
0 de lo contrario
de modo que si un componente dura horas, durará por
siempre (si bien parece irrazonable, este modelo puede
ser utilizado para estudiar el “desgaste inicial”). ¿Cuá-
les son la función de distribución acumulativa y la fun-
ción de densidad de probabilidad de X?
123. Sea que U tenga una distribución uniforme en el intervalo
[0, 1]. Entonces los valores observados que tienen esta dis-
tribución se obtienen con un generador de números aleato-
rios de computadora. Sea X (1/)ln(1 U).
a. Demuestre que X tiene una distribución exponencial
con parámetro . [Sugerencia: La función de distribu-
ción acumulativa de X es F(x) P(X x); X x equi-
vale a U ?]
b. ¿Cómo utilizaría el inciso a) y un generador de números
aleatorios para obtener valores observados derivados de
una distribución exponencial con parámetro 10?
124. Considere una variable aleatoria con media y desviación
estándar y sea g(X) una función especificada de X. La
aproximación de la serie de Taylor de primer grado a g(X)
en la cercanía de es
g(X) g() g() (X )
v
2
Ï
Ì
Ó
c4_p130-183.qxd 3/12/08 4:05 AM Page 182](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-200-320.jpg)
![Bibliografía 183
El miembro del lado derecho de esta ecuación es una función
lineal de X. Si la distribución de X está concentrada en un in-
tervalo a lo largo del cual g() es aproximadamente lineal
[p. ej., x
es aproximadamente lineal en (1, 2)], entonces la
ecuación produce aproximaciones a E(g(X)) y V(g(X)).
a. Dé expresiones para estas aproximaciones. [Sugeren-
cia: Use reglas de valor esperado y varianza de una fun-
ción lineal aX b.]
b. Si el voltaje a través de un medio se mantiene fijo
pero la corriente I es aleatoria, entonces la resistencia
también será una variable aleatoria relacionada con I
por R v/I. Si I 20 y I 0.5, calcule aproxima-
ciones a R y R.
125. Una función g(x) es convexa si la cuerda que conecta dos
puntos cualesquiera de su gráfica quedan sobre ésta. Cuan-
do g(x) es derivable, una condición equivalente es que pa-
ra cada x, la línea tangente en x queda por completo sobre
o debajo de la gráfica. (Véanse las figuras a continuación.)
¿Cómo se compara g() g(E(X)) con E(g(X))? [Sugeren-
cia: La ecuación de la línea tangente en x es y
g() g() (x ). Use la condición de convexidad,
sustituya x por X y considere los valores esperados. Nota:
A menos que g(x) sea lineal, la desigualdad resultante (por
lo general llamada desigualdad de Jensen) es estricta ( en
lugar de ); es válida tanto con variables aleatorias conti-
nuas como discretas.]
126. Si X tiene una distribución de Weibull con parámetros
2 y , demuestre que Y 2X2
/2
tiene una distribución ji
cuadrada con 2. [Sugerencia: La función de distribución
acumulativa de Y es P(Y y); exprese esta probabilidad en
la forma P(X g(y)), use el hecho de que X tiene una fun-
ción de distribución acumulativa de la forma de la expresión
(4.12) y derive con respecto a y para obtener la función de
densidad de probabilidad de Y.]
127. El registro crediticio de un individuo es un número calcu-
lado basado en el historial crediticio de dicho individuo el
cual ayuda a un prestamista a determinar cuánto se le pue-
de prestar o qué límite de crédito debe ser establecido
para una tarjeta de crédito. Un artículo en los Los Angeles
Times presentó datos que sugerían que una distribución
beta con parámetros A 150 y B 850, 8, 2 pro-
porcionaría una aproximación razonable a la distribución
de registros de crédito estadounidenses [Nota: Los regis-
tros de crédito son valores enteros].
a. Sea X un registro estadounidense de crédito selecciona-
do al azar. ¿Cuáles son el valor medio y la desviación
estándar de esta variable aleatoria? ¿Cuál es la probabi-
lidad de que X esté dentro de una desviación estándar
de su valor medio?
b. ¿Cuál es la probabilidad aproximada de que un registro
seleccionado al azar excederá de 750 (lo que los presta-
mistas consideran un muy buen registro)?
128. Sea V el volumen de lluvia y W el volumen de escurrimien-
to (ambos en mm). De acuerdo con el artículo “Runoff
Quality Analysis of Urban Catchments with Analytical
Probability Models” (J. of Water Resource Planning and
Management, 2006: 4-14), el volumen de escurrimiento
será 0 si V d y será k(V d) si V vd. Aquí d es el
volumen de almacenamiento en una depresión (una cons-
tante) y k (también una constante) es el coeficiente de es-
currimiento. El artículo citado propone una distribución
exponencial con parámetro para V.
a. Obtenga una expresión para la función de distribución
acumulativa de W. [Nota: W no es ni puramente conti-
nua ni puramente discreta; en cambio tiene una distri-
bución “combinada” con un componente discreto en 0
y es continua con valores w 0.]
b. ¿Cuál es la función de densidad de probabilidad de W
con w 0? Úsela para obtener una expresión para el
valor esperado de volumen de escurrimiento.
Línea
tangente
x
Bibliografía
Bury, Kart, Statistical Distributions in Engineering, Cambridge
Univ. Press, Cambridge, Inglaterra, 1999. Un estudio informa-
tivo y fácil de leer de distribuciones y sus propiedades.
Johnson, Norman, Samuel Kotz y N. Balakrishnan Continuous
Univariate Distributions, vols. 1-2, Wiley, Nueva York, 1994.
Estos dos volúmenes presentan un estudio exhaustivo de va-
rias distribuciones continuas.
Nelson, Wayne, Applied Life Data Analysis, Wiley, Nueva York,
1982. Presenta amplia discusión de distribuciones y métodos
que se utilizan en el análisis de datos de vida útil.
Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models
and Applications (2a. ed.), Macmillan, NuevaYork, 1994. Una
buena cobertura de las propiedades generales y distribuciones
específicas.
c4_p130-183.qxd 3/12/08 4:05 AM Page 183](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-201-320.jpg)
![Existen muchas situaciones experimentales en las cuales más de una variable aleatoria será
de interés para un investigador. Primero se consideran las distribuciones de probabilidad
conjunta para dos variables aleatorias discretas, enseguida para dos variables continuas y
por último para más de dos variables.
Dos variables aleatorias discretas
La función masa de probabilidad (fmp) de una sola variable aleatoria discreta X especifica
cuánta masa de probabilidad está colocada en cada valor posible de X. La función masa de
probabilidad conjunta de dos variables aleatorias discretas X y Y describe cuánta masa de pro-
babilidad se coloca en cada par posible de valores (x, y).
Una gran agencia de seguros presta servicios a numerosos clientes que han adquirido tanto
una póliza de propietario de casa como una póliza de automóvil en la agencia. Por cada tipo
de póliza, se debe especificar una cantidad deducible. Para una póliza de automóvil, las
opciones son $100 y $250, mientras que para la póliza de propietario de casa, las opciones
son 0, $100 y $200. Suponga que se selecciona al azar un individuo con ambos tipos de póli-
za de los archivos de la agencia. Sea X la cantidad deducible sobre la póliza de auto y Y
la cantidad deducible sobre la póliza de propietario de casa. Los posibles pares (X, Y) son
entonces (100, 0), (100, 100), (100, 200), (250, 0), (250, 100) y (250, 200); la función masa
de probabilidad conjunta especifica la probabilidad asociada con cada uno de estos pares,
con cualquier otro par tiene probabilidad cero. Suponga que la tabla de probabilidad con-
junta siguiente da la función masa de probabilidad conjunta:
y
p(x, y)
| 0 100 200
x
100 | 0.20 0.10 0.20
250 | 0.05 0.15 0.30
Entonces p(100, 100) P(X 100 y Y 100) P($100 deducible sobre ambas pólizas)
0.10. La probabilidad P(Y 100) se calcula sumando las probabilidades de todos los
pares (x, y) para los cuales y 100:
P(Y 100) p(100, 100) p(250, 100) p(100, 200) p(250, 200)
0.75 ■
5.1 Variables aleatorias conjuntamente distribuidas 185
5.1 Variables aleatorias conjuntamente distribuidas
Ejemplo 5.1
DEFINICIÓN Sean X y Y dos variables aleatorias discretas definidas en el espacio muestral S de un
experimento. La función masa de probabilidad conjunta p(x, y) se define para cada
par de números (x, y) como
p(x, y) P(X x y Y y)
Debe cumplirse que p(x, y) 0 y
x
y
p(x, y) 1.
Ahora sea A cualquier conjunto compuesto de pares de valores (x, y) (p. ej., A {(x, y):
x y 5} o {(x, y): máx(x, y) 3}). Entonces la probabilidad P[(X, Y) A] se obtiene
sumando la función masa de probabilidad conjunta incluidos todos los pares en A:
P[(X, Y) A]
(x, y)
A
p(x, y)
c5_p184-226.qxd 3/12/08 4:07 AM Page 185](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-203-320.jpg)
![La función masa de probabilidad de una de las variables sola se obtiene sumando p(x,
y) con los valores de la otra variable. El resultado se llama función masa de probabilidad
marginal cuando los valores p(x, y) aparecen en una tabla rectangular, las sumas son totales
marginales (filas o columnas).
Así pues para obtener la función masa de probabilidad marginal de X evaluada en, por ejem-
plo, x 100, las probabilidades p(100, y) se suman con todos los valores posibles de y. Si se
hace esto por cada valor posible de X se obtiene la función masa de probabilidad marginal
de X sola (sin referencia a Y). Con las funciones masa de probabilidad marginal, se pueden
calcular las probabilidades de eventos que implican sólo X o sólo Y.
Los valores posibles de X son x 100 y x 250, por lo que si se calculan los totales en las
filas de la tabla de probabilidad conjunta se obtiene
pX(100) p(100, 0) p(100, 100) p(100, 200) 0.50
y
pX(250) p(250, 0) p(250, 100) p(250, 200) 0.50
La función masa de probabilidad marginal de X es entonces
pX(x) {0.5 x 100, 250
0 de lo contrario
Asimismo, la función masa de probabilidad marginal de Y se obtiene con los totales de las
columnas como
¨0.25 y 0, 100
pY(y) ©0.50 y 200
ª0 de lo contrario
Por lo tanto, P(Y 100) pY(100) pY(200) 0.75 como antes. ■
Dos variables aleatorias continuas
La probabilidad de que el valor observado de una variable aleatoria continua X esté en un
conjunto unidimensional A (tal como un intervalo) se obtiene integrando la función de den-
sidad de probabilidad f(x) a lo largo del conjunto A. Asimismo, la probabilidad de que el par
(X, Y) de variables aleatorias continuas quede en un conjunto A en dos dimensiones (tal como
un rectángulo) se obtiene integrando una función llamada función de densidad conjunta.
186 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
DEFINICIÓN Las funciones masa de probabilidad marginal de X y de Y, denotadas por pX(x) y
pY(y), respectivamente, están dadas por
pX(x)
y
p(x, y) pY(y)
x
p(x, y)
DEFINICIÓN Sean X y Y variables aleatorias continuas. Una función de densidad de probabili-
dad conjunta f(x, y) de estas dos variables es una función que satisface f(x, y) 0
y
f(x, y) dx dy 1. Entonces para cualquier conjunto A en dos dimensiones
P[(X, Y) A]
A
f(x, y) dx dy
En particular, si A es el rectángulo {(x, y): a x b, c y d}, entonces
P[(X, Y) A] P(a X b, c Y d)
b
a
d
c
f(x, y) dy dx
Ejemplo 5.2
(continuación
del ejemplo
5.1)
c5_p184-226.qxd 3/12/08 4:07 AM Page 186](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-204-320.jpg)
![Se puede considerar que f(x, y) especifica una superficie situada a una altura f(x, y)
sobre el punto (x, y) en un sistema de coordenadas tridimensional. Entonces P[(X, Y) A]
es el volumen debajo de esta superficie y sobre la región A, similar al área bajo una curva en
el caso unidimensional. Esto se ilustra en la figura 5.1.
Un banco dispone tanto de una ventanilla para automovilistas como de una ventanilla nor-
mal. En un día seleccionado al azar, sea X la proporción de tiempo que la ventanilla
para automovilistas está en uso (por lo menos un cliente está siendo atendido o está esperan-
do ser atendido) y Y la proporción del tiempo que la ventanilla normal está en uso. Entonces
el conjunto de valores posibles de (X, Y) es el rectángulo D {(x, y): 0 x 1, 0 y 1}.
Suponga que la función de densidad de probabilidad conjunta de (X, Y ) está dada por
f(x, y)
{ (x y2
) 0 x 1, 0 y 1
0 de lo contrario
Para verificar que ésta es una función de densidad de probabilidad legítima, obsérvese que
f(x, y) 0 y
f(x, y) dx dy
1
0
1
0
6
5
(x y2
) dx dy
1
0
1
0
6
5
x dx dy
1
0
1
0
6
5
y2
dx dy
1
0
6
5
x dx
1
0
6
5
y2
dy
1
6
0
1
6
5
1
La probabilidad de que ninguna ventanilla esté ocupada más de un cuarto del tiempo es
P0 X
1
4
, 0 Y
1
4
1/4
0
1/4
0
6
5
(x y2
) dx dy
6
5
1/4
0
1/4
0
x dx dy
6
5
1/4
0
1/4
0
y2
dx dy
2
6
0
x
2
2
°
x1/4
x0
2
6
0
y
3
3
°
y1/4
y0
6
7
40
.0109 ■
Como con las funciones masa de probabilidad conjunta, con la función de densidad de
probabilidad conjunta de X y Y, se puede calcular cada una de las dos funciones de densi-
dad marginal.
6
5
5.1 Variables aleatorias conjuntamente distribuidas 187
Figura 5.1 P(X, Y) A volumen bajo la superficie de densidad sobre A.
f(x, y) y
x
A Rectángulo
sombreado
Superficie f(x, y)
Ejemplo 5.3
c5_p184-226.qxd 3/12/08 4:07 AM Page 187](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-205-320.jpg)
![Con cualquier x fija, f (x, y) se incrementa con y; con y fija, f (x, y) se incrementa con x. Esto
es apropiado porque las palabras de lujo implican que la mayor parte de la lata deberá estar
compuesta de almendras y nueces de acajú en lugar de cacahuates, así que la función de
densidad deberá ser grande cerca del límite superior y pequeña cerca del origen. La super-
ficie determinada por f(x, y) se inclina hacia arriba desde cero a medida que (x, y) se alejan
de uno u otro eje.
Claramente, f(x, y) 0. Para verificar la segunda condición sobre una función de den-
sidad de probabilidad conjunta, recuérdese que una integral doble se calcula como una inte-
gral iterada manteniendo una variable fija (tal como x en la figura 5.2), integrando con los
valores de la otra variable localizados a lo largo de la línea recta que pasa a través de la
variable fija y finalmente integrando todos los valores posibles de la variable fija. Así pues
f(x, y) dy dx
D
f(x, y) dy dx
1
0
1x
0
24xy dy dx
1
0
24x
y
2
2
°
y1x
y0
dx
1
0
12x(1 x)2
dx 1
Para calcular la probabilidad de que los dos tipos de nueces conformen cuando mucho 50%
de la lata, Sea A {(x, y): 0 x 1, 0 y 1, y x y 0.5}, como se muestra en la
figura 5.3. Entonces
P((X, Y) A)
A
f(x, y) dx dy
0.5
0
0.5x
0
24xy dy dx 0.0625
La función de densidad de probabilidad marginal de las almendras se obtiene manteniendo
X fija en x e integrando la función de densidad de probabilidad conjunta f(x, y) a lo largo de
la línea vertical que pasa por x:
fX(x)
f(x, y) dy {
1x
0
24xy dy 12x(1 x)2
0 x 1
0 de lo contrario
Por simetría de f(x, y) y la región D, la función de densidad de probabilidad marginal de Y
se obtiene reemplazando x y X en fX(x) por y y Y, respectivamente. ■
Variables aleatorias independientes
En muchas situaciones, la información sobre el valor observado de una de las dos variables
X y Y da información sobre el valor de la otra variable. En el ejemplo 5.1, la probabilidad
marginal de X con x 250 fue de 0.5, como lo fue la probabilidad de que X 100. Sin
embargo, si se sabe que el individuo seleccionado tuvo Y 0, entonces X 100 es cuatro
veces más probable que X 250. Por lo tanto, existe dependencia entre las dos variables.
5.1 Variables aleatorias conjuntamente distribuidas 189
Figura 5.3 Calcule de P[(X, Y) A] para el ejemplo 5.5.
x 1
1
x
y
0
.
5
x
y
1
A Región sombreada
y 0.5 x
c5_p184-226.qxd 3/12/08 4:07 AM Page 189](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-207-320.jpg)
![Más de dos variables aleatorias
Para modelar el comportamiento conjunto de más de dos variables aleatorias, se amplía el
concepto de una distribución conjunta de dos variables.
En un experimento binomial, cada ensayo podría dar por resultado uno de sólo dos
posibles resultados. Considérese ahora un experimento compuesto de n ensayos indepen-
dientes e idénticos, en los que cada ensayo puede dar uno cualquiera de r posibles resulta-
dos. Sea p1 P(resultado i en cualquier ensayo particular) y defínanse las variables
aleatorias como Xi el número de ensayos que dan el resultado i(i 1, . . . , r). Tal expe-
rimento se llama experimento multinomial y la función masa de probabilidad conjunta de
X1, . . . , Xr se llama distribución multinomial. Utilizando un argumento de conteo análo-
go al utilizado al derivar la distribución binomial, la función masa de probabilidad conjun-
ta de X1, . . . , Xr, se puede demostrar que es
p(x1, . . . , xr)
{ p1
x1 . . . pxr
r xi 0, 1, 2, . . . , con x1 . . . xr n
0 de lo contrario
El caso r 2 da la distribución binomial, con X1 número de éxitos y X2 n X1
número de fallas.
Si se determina el alelo de cada una de diez secciones de un chícharo obtenidas indepen-
dientemente y p1 P(AA), p2 P(Aa), p3 P(aa), X1 número de AA, X2 número de
Aa y X3 número de aa, entonces la función masa de probabilidad multinomial para estas
Xi es
p(x1, x2, x3) px1
1 px2
2 px3
3 xi 0, 1, . . . y x1 x2 x3 10
con p1 p3 0.25, p2 0.5.
P(X1 2, X2 5, X3 3) p(2, 5, 3)
(0.25)2
(0.5)5
(0.25)3
0.0769 ■
Cuando se utiliza cierto método para recolectar un volumen fijo de muestras de roca en una
región, existen cuatro tipos de roca. Sean X1, X2 y X3 la proporción por volumen de los tipos
de roca 1, 2 y 3 en una muestra aleatoriamente seleccionada (la proporción del tipo de roca
4 es 1 X1 X2 X3, de modo que una variable X4 sería redundante). Si la función de
densidad de probabilidad conjunta de X1, X2, X3 es
f(x1, x2, x3)
kx1x2(1 x3) 0 x1 1, 0 x2 1, 0 x3 1, x1 x2 x3 1
0 de lo contrario
10!
2! 5! 3!
10!
(x1!)(x2!)(x3!)
n!
(x1!)(x2!) . . . (xr!)
5.1 Variables aleatorias conjuntamente distribuidas 191
DEFINICIÓN Si X1, X2, . . . , Xn son variables aleatorias discretas, la función masa de probabilidad
conjunta de las variables es la función
p(x1, x2, . . . , xn) P(X1 x1, X2 x2, . . . , Xn xn)
Si las variables son continuas, la función de densidad de probabilidad conjunta de
X1, . . . , Xn es la función f(x1, x2, . . . , xn) de modo que para n intervalos cualesquiera
[a1, b1], . . . , [an, bn],
P(a1 X1 b1, . . . , an Xn bn)
b1
a1
. . .
bn
an
f(x1, . . . , xn) dxn . . . dx1
Ejemplo 5.9
Ejemplo 5.10
c5_p184-226.qxd 3/12/08 4:07 AM Page 191](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-209-320.jpg)
![194 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
EJERCICIOS Sección 5.1 (1-21)
1. Una gasolinería cuenta tanto con islas de autoservicio como de
servicio completo. En cada isla, hay una sola bomba de gaso-
lina sin plomo regular con dos mangueras. Sea X el número de
mangueras utilizadas en la isla de autoservicio y en un tiempo
particular y sea Y el número de mangueras en uso en la isla de
servicio completo en ese tiempo. La función masa de probabi-
lidad conjunta de X y Y aparece en la tabla adjunta.
p(x, y)
| 0 2
0 | 0.10 0.04 0.02
x 1 | 0.08 0.20 0.06
2 | 0.06 0.14 0.30
a. ¿Cuál es P(X 1 y Y 1)?
b. Calcule P(X 1 y Y 1).
c. Describa el evento (X 0 y Y 0) y calcule su proba-
bilidad.
d. Calcule la función masa de probabilidad marginal de X
y Y. Utilizando pX(x), ¿cuál es P(X 1)?
e. ¿Son X y Y variables aleatorias independientes? Explique.
2. Cuando un automóvil es detenido por una patrulla de segu-
ridad, cada uno de los neumáticos es revisado en cuanto a
desgaste y cada uno de los faros es revisado para ver si está
apropiadamente alineado. Sean X el número de faros que
necesitan ajuste y Y el número de neumáticos defectuosos.
a. Si X y Y son independientes con pX(0) 0.5, pX(1) 0.3,
pX(2) 0.2 y pY(0) 0.6, pY(1) 0.1, pY(2) pY(3)
0.05, pY(4) 0.2, muestre la función masa de probabi-
lidad conjunta de (X, Y) en una tabla de probabilidad
conjunta.
b. Calcule P(X 1 y Y 1) con la tabla de probabilidad
conjunta y verifique que es igual al producto P(X 1)
P(Y 1).
c. ¿Cuál es P(X Y 0) (la probabilidad de ninguna vio-
lación)?
d. Calcule P(X Y 1).
3. Un supermercado cuenta tanto con una caja rápida como
con una superrápida. Sea X1 el número de clientes formados
en la caja rápida a una hora particular del día y sea X2 el
número de clientes formados en la caja superrápida a la
misma hora. Suponga que la función masa de probabilidad
de X1 y X2 es la que aparece en la tabla adjunta.
x2
| 0 1 2 3
0 | 0.08 0.07 0.04 0.00
1 | 0.06 0.15 0.05 0.04
x1 2 | 0.05 0.04 0.10 0.06
3 | 0.00 0.03 0.04 0.07
4 | 0.00 0.01 0.05 0.06
a. ¿Cuál es P(X1 1, X2 1), es decir, la probabilidad de
que haya exactamente un cliente en cada caja?
b. ¿Cuál es P(X1 X2), es decir, la probabilidad de que los
números de clientes en las dos cajas sean idénticos?
c. Sea A el evento en que hay por lo menos dos clientes
más en una caja que en la otra. Exprese A en función de
X1 y X2 y calcule la probabilidad de este evento.
d. ¿Cuál es la probabilidad de que el número total de clien-
tes en las dos líneas sea exactamente cuatro? ¿Por lo
menos cuatro?
4. Regrese a la situación descrita en el ejercicio 3.
a. Determine la función masa de probabilidad marginal de
X1 y enseguida calcule el número esperado de clientes
formados en la caja rápida.
b. Determine la función masa de probabilidad marginal
de X2.
c. Por inspección de las probabilidades P(X1 4), P(X2 0)
y P(X1 4, X2 0), ¿son X1 y X2 variables aleatorias
independientes? Explique.
5. El número de clientes que esperan en el servicio de envoltu-
ra de regalos en una tienda de departamentos es una variable
aleatoria X con valores posibles 0, 1, 2, 3, 4 y probabilidades
correspondientes 0.1, 0.2, 0.3, 0.25, 0.15. Un cliente selec-
cionado al azar tendrá 1, 2 ó 3 paquetes para envoltura con
probabilidades de 0.6, 0.3 y 0.1, respectivamente. Sea Y el
número total de paquetes que van a ser envueltos para los
clientes que esperan formados en la fila (suponga que el
número de paquetes entregado por un cliente es indepen-
diente del número entregado por cualquier otro cliente).
a. Determine P(X 3, Y 3), es decir, p(3, 3).
b. Determine p(4, 11)
6. Sea X el número de cámaras digitales Canon vendidas
durante una semana particular por una tienda. La función
masa de probabilidad de X es
x
| 0 1 2 3 4
pX(x) | 0.1 0.2 0.3 0.25 0.15
El 60% de todos los clientes que compran estas cámaras
también compran una garantía extendida. Sea Y el número
de compradores durante esta semana que compran una
garantía extendida.
a. ¿Cuál es P(X 4, Y 2)? [Sugerencia: Esta probabili-
dad es igual a P(Y 2|X 4) P(X 4); ahora piense
en las cuatro compras como cuatro ensayos de un expe-
rimento binomial, con el éxito en un ensayo correspon-
diente a comprar una garantía extendida.]
b. Calcule P(X Y).
c. Determine la función masa de probabilidad conjunta de
X y Y y luego la función masa de probabilidad marginal
de Y.
7. La distribución de probabilidad conjunta del número X de
carros y el número Y de autobuses por ciclo de señal en un
carril de vuelta a la izquierda propuesto se muestra en la
tabla de probabilidad conjunta anexa.
p(x, y)
| 0 2
0 | 0.025 0.015 0.010
1 | 0.050 0.030 0.020
2 | 0.125 0.075 0.050
x 3 | 0.150 0.090 0.060
4 | 0.100 0.060 0.040
5 | 0.050 0.030 0.020
y
1
y
1
c5_p184-226.qxd 3/12/08 4:07 AM Page 194](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-212-320.jpg)
![5.1 Variables aleatorias conjuntamente distribuidas 195
a. ¿Cuál es la probabilidad de que haya exactamente un
carro y exactamente un autobús durante un ciclo?
b. ¿Cuál es la probabilidad de que haya cuando mucho
un carro y cuando mucho un autobús durante un ciclo?
c. ¿Cuál es la probabilidad de que haya exactamente un
carro durante un ciclo? ¿Exactamente un autobús?
d. Suponga que el carril de vuelta a la izquierda tiene una
capacidad de cinco carros y un autobús que equivale a
tres carros. ¿Cuál es la probabilidad de un exceso de
vehículos durante un ciclo?
e. ¿Son X y Y variables aleatorias independientes? Explique.
8. Un almacén cuenta con 30 componentes de un tipo, de los cua-
les 8 fueron surtidos por el proveedor 1, 10 por el proveedor 2
y 12 por el proveedor 3. Seis de éstos tienen que ser seleccio-
nados al azar para un ensamble particular. Sea X el número
de componentes del proveedor 1 seleccionados, Y el núme-
ro de componentes del proveedor 2 seleccionados y que p(x, y)
denote la función masa de probabilidad conjunta de X y Y.
a. ¿Cuál es p(3, 2)? [Sugerencia: La probabilidad de que
cada muestra de tamaño 6 sea seleccionada es igual. Por
consiguiente, p(3, 2) (número de resultados con X 3
y Y 2)/(el número total de resultados). Ahora use la
regla de producto de conteo para obtener el numerador y
denominador.]
b. Utilizando la lógica del inciso a), obtenga p(x, y). (Esto
puede ser considerado como un muestreo con distribu-
ción hipergeométrica multivariante sin reemplazo de una
población finita compuesta de más de dos categorías.)
9. Se supone que cada neumático delantero de un tipo particu-
lar de vehículo está inflado a una presión de 26 lb/pulg2
.
Suponga que la presión de aire real en cada neumático es una
variable aleatoria: X para el neumático derecho y Y para el
izquierdo con función de densidad de probabilidad conjunta
f(x, y) {K(x2
y2
) 20 x 30, 20 y 30
0 de lo contrario
a. ¿Cuál es el valor de K?
b. ¿Cuál es la probabilidad de que ambos neumáticos estén
inflados a menos presión?
c. ¿Cuál es la probabilidad de que la diferencia en la pre-
sión del aire entre los dos neumáticos sea de cuando
mucho 2 lb/pulg2
?
d. Determine la distribución (marginal) de la presión del
aire en el neumático derecho.
e. ¿Son X y Y variables aleatorias independientes?
10. Annie y Alvie acordaron encontrarse entre las 5:00 P.M. y las
6:00 P.M. para cenar en un restaurante local de comida salu-
dable. Sea X la hora de llegada de Annie y Y la hora de
llegada de Alvie. Suponga que X y Y son independientes con
cada una distribuida uniformemente en el intervalo [5, 6].
a. ¿Cuál es la función de densidad de probabilidad conjun-
ta de X y Y?
b. ¿Cuál es la probabilidad de que ambos lleguen entre las
5:15 y las 5:45?
c. Si el primero en llegar espera sólo 10 min antes de irse a
comer a otra parte, ¿cuál es la probabilidad de que cenen
en el restaurante de comida saludable? [Sugerencia: El
evento de interés es A {(x, y):°x y°
1
6}.]
11. Dos profesores acaban de entregar los exámenes finales
para su copia. Sea X el número de errores tipográficos en el
examen del primer profesor y Y el número de tales errores
en el segundo examen. Suponga que X tiene una distribución
de Poisson con parámetro , que Y tiene una distribución de
Poisson con parámetro y que X y Y son independientes.
a. ¿Cuál es la función masa de probabilidad conjunta de X
y Y?
b. ¿Cuál es la probabilidad de que se cometa cuando
mucho un error en ambos exámenes combinados?
c. Obtenga una expresión general para la probabilidad de que
el número total de errores en los dos exámenes sea m (don-
de m es un entero no negativo). [Sugerencia: A {(x, y):
x y m} {(m, 0), (m 1, 1), . . . , (1, m 1),
(0, m)}. Ahora sume la función masa de probabilidad con-
junta a lo largo de (x, y) A y use el teorema binomial, el
cual dice que
m
k0
ak
bmk
(a b)m
con cualquier a, b.]
12. Dos componentes de una minicomputadora tienen la
siguiente función de densidad de probabilidad conjunta de
sus vidas útiles X y Y:
f(x, y) {xex(1y)
x 0 y y 0
0 de lo contrario
a. ¿Cuál es la probabilidad de que la vida útil X del primer
componente exceda de 3?
b. ¿Cuáles son las funciones de densidad de probabilidad
marginal de X y Y? ¿Son las dos vidas útiles indepen-
dientes? Explique.
c. ¿Cuál es la probabilidad de que la vida útil de por lo
menos un componente exceda de 3?
13. Tiene dos focos para una lámpara particular. Sea X la
vida útil del primer foco y Y la vida útil del segundo
(ambas en miles de horas). Suponga que X y Y son inde-
pendientes y que cada una tiene una distribución exponen-
cial con parámetro 1.
a. ¿Cuál es la función de densidad de probabilidad conjun-
ta de X y Y?
b. ¿Cuál es la probabilidad de que cada foco dure cuando
mucho 1000 horas (es decir, X 1 y Y 1)?
c. ¿Cuál es la probabilidad de que la vida útil total de los
dos focos sea cuando mucho de 2? [Sugerencia: Trace
una figura de la región A {(x, y): x 0, y 0, x
y 2} antes de integrar.]
d. ¿Cuál es la probabilidad de que la vida útil total esté
entre 1 y 2?
14. Suponga que tiene diez focos y que la vida útil de cada uno
es independiente de la de los demás y que la distribución de
cada vida útil es exponencial con parámetro .
a. ¿Cuál es la probabilidad de que los diez focos fallen
antes del tiempo t?
b. ¿Cuál es la probabilidad de que exactamente k de los
diez focos fallen antes del tiempo t?
c. Suponga que nueve de los focos tienen vidas útiles
exponencialmente distribuidas con parámetro y que el
foco restante tiene una vida útil que está exponencial-
mente distribuida con parámetro (fue hecho por otro
fabricante). ¿Cuál es la probabilidad de que exactamen-
te cinco de los diez focos fallen antes del tiempo t?
m
k
c5_p184-226.qxd 3/12/08 4:07 AM Page 195](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-213-320.jpg)
![Previamente se vio que cualquier función h(X) de una sola variable aleatoria X es por sí
misma una variable aleatoria. Sin embargo, para calcular E[h(X)], no fue necesario obtener
la distribución de probabilidad de h(X); en cambio, E[h(X)] se calculó como un promedio
ponderado de valores de h(x), donde la función de ponderación fue la función masa de pro-
babilidad p(x) o la función de densidad de probabilidad f(x) de X. Se obtiene un resultado
similar para una función h(X, Y) de dos variables aleatorias conjuntamente distribuidas.
196 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
15. Considere un sistema compuesto de tres componentes como
se ilustra. El sistema continuará funcionando en tanto el pri-
mer componente funcione y o el componente 2 o el compo-
nente 3 funcione. Sean X1, X2 y X3 las vidas útiles de los
componentes 1, 2 y 3, respectivamente. Suponga que las Xi
son independientes una de otra y que cada Xi tiene una dis-
tribución exponencial con parámetro .
a. Sea Y la vida útil del sistema. Obtenga la función de dis-
tribución acumulativa de Y y derívela para obtener la
función de densidad de probabilidad. [Sugerencia:
F(y) P(Y y); exprese el evento {Y y} en función
de uniones y/o intersecciones de los tres eventos {X1 y},
{X2 y} y {X3 y}.]
b. Calcule la vida útil esperada del sistema.
16. a. Con f(x1, x2, x3) del ejemplo 5.10, calcule la función de
densidad marginal conjunta de X1 y X3 (integrando
para x2).
b. ¿Cuál es la probabilidad de que las rocas de tipos 1 y 3
constituyan cuando mucho 50% de la muestra? [Suge-
rencia: Use el resultado del inciso a).]
c. Calcule la función de densidad de probabilidad marginal
de X1 [Sugerencia: Use el resultado del inciso a).]
17. Un ecólogo desea seleccionar un punto adentro de una región
de muestreo circular de acuerdo con una distribución unifor-
me (en la práctica esto podría hacerse seleccionando primero
una dirección y luego una distancia a partir del centro en esa
dirección). Sea X la coordenada x del punto seleccionado
y Y la coordenada y del punto seleccionado. Si el círculo
tiene su centro en (0, 0) y su radio es R, entonces la función
de densidad de probabilidad conjunta de X y Y es
f(x, y)
{
1
R2
x2
y2
R2
0 de lo contrario
a. ¿Cuál es la probabilidad de que el punto seleccionado
quede dentro de R/2 del centro de la región circular?
[Sugerencia: Trace una figura de la región de densidad
positiva D. Como f(x, y) es constante en D, el cálculo de
probabilidad se reduce al cálculo de un área.]
b. ¿Cuál es la probabilidad de que tanto X como Y difieran
de 0 por cuando mucho R/2?
c. Responda el inciso b) con R/2
reemplazando a R/2.
d. ¿Cuál es la función de densidad de probabilidad margi-
nal de X? ¿De Y? ¿Son X y Y independientes?
18. Remítase al ejercicio 1 y responda las siguientes preguntas:
a. Dado que X 1, determine la función masa de probabi-
lidad condicional de Y, es decir, pY°X (0°1), pY°X (1°1) y
pY°X (2°1).
b. Dado que dos mangueras están en uso en la isla de auto-
servicio, ¿cuál es la función masa de probabilidad con-
dicional del número de mangueras en uso en la isla de
servicio completo?
c. Use el resultado del inciso b) para calcular la probabili-
dad condicional P(Y 1|X 2).
d. Dado que dos mangueras están en uso en la isla de
servicio completo, ¿Cuál es la función masa de probabi-
lidad condicional del número en uso en la isla de auto-
servicio?
19. La función de densidad de probabilidad conjunta de las pre-
siones de los neumáticos delanteros derecho e izquierdo se
da en el ejercicio 9.
a. Determine la función de densidad de probabilidad con-
dicional de Y dado que X x y la función de densidad
de probabilidad condicional de X dado que Y y.
b. Si la presión del neumático derecho es de 22 lb/pulg2
,
¿cuál es la probabilidad de que la presión del neumático
izquierdo sea de por lo menos 25 lb/pulg2
? Compare con
P(Y 25).
c. Si la presión del neumático derecho es de 22 lb/pulg2
,
¿cuál es la presión esperada en el neumático izquierdo y
cuál es la desviación estándar de la presión en este neu-
mático?
20. Sean X1, X2, X3, X4, X5 y X6 los números de lunetas MM
azules, cafés, verdes, naranjas, rojas y amarillas, respectiva-
mente, en una muestra de tamaño n. Entonces estas Xi tie-
nen una distribución multinomial. De acuerdo con el sitio
web de MM, las proporciones de colores son p1 0.24,
p2 0.13, p3 0.16, p4 0.20, p5 0.13 y p6 0.14.
a. Si n 12, ¿cuál es la probabilidad de que haya exacta-
mente dos lunetas MM de cada color?
b. Con n 20, ¿cuál es la probabilidad de que haya cuan-
do mucho cinco lunetas naranjas? [Sugerencia: Consi-
dere la luneta naranja como un éxito y cualquier otro
color como falla.]
c. En una muestra de 20 lunetas MM, ¿cuál es la proba-
bilidad de que el número de lunetas azules, verdes o
naranjas sea por lo menos 10?
21. Sean X1, X2 y X3 las vidas útiles de los componentes 1, 2 y
3 en un sistema de tres componentes.
a. ¿Cómo definiría la función de densidad de probabilidad
condicional de X3 dado que X1 x1 y X2 x2?
b. ¿Cómo definiría la función de densidad de probabilidad
conjunta condicional de X2 y X3 dado que X1 x1?
1
3
2
5.2 Valores esperados, covarianza y correlación
c5_p184-226.qxd 3/12/08 4:07 AM Page 196](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-214-320.jpg)
![5.2 Valores esperados, covarianza y correlación 197
Cinco amigos compraron boletos para un concierto. Si los boletos son para asientos 1-5 en
una fila particular y los boletos se distribuyen al azar entre los cinco, ¿cuál es el número
esperado de asientos que separen a cualquiera dos de los cinco? Sean X y Y los números de
asiento del primer y segundo individuos, respectivamente. Los pares posibles (X, Y) son
(1, 2), (1, 3), . . . , (5, 4) y la función masa de probabilidad conjunta de (X, Y) es
p(x, y)
{2
1
0
x 1, . . . , 5; y 1, . . . , 5; x y
0 de lo contrario
El número de asientos que separan a los dos individuos es h(X, Y) |X Y| 1. La tabla
adjunta da h(x, y) para cada par posible (x, y).
h(x, y)
| 1 2 4 5
1 | — 0 1 2 3
2 | 0 — 0 1 2
y 3 | 1 0 — 0 1
4 | 2 1 0 — 0
5 | 3 2 1 0 —
Por lo tanto
E[h(X, Y)]
(x, y)
h(x, y) p(x, y)
5
x1
5
y1
(°x y° 1) 1 ■
x y
En el ejemplo 5.5, la función de densidad de probabilidad conjunta de la cantidad X de
almendras y la cantidad de nueces de acajú en una lata de una lb de nueces fue
f(x, y) {24xy 0 x 1, 0 y 1, x y 1
0 de lo contrario
Si una lb de almendras le cuesta a la compañía $1.00, una lb de nuez de acajú le cuesta $1.50
y una lb de cacahuates le cuesta $0.50, entonces el costo total del contenido de una lata es
h(X, Y) (1)X (1.5)Y (0.5)(1 X Y) 0.5 0.5X Y
(puesto que 1 X Y del peso se compone de cacahuates). El costo esperado total es
E[h(X, Y)]
h(x, y) f(x, y) dx dy
1
0
1x
0
(0.5 0.5x y) 24xy dy dx $1.10 ■
El método de calcular el valor esperado de una función h(X1, . . . , Xn) de n variables
aleatorias es similar al de dos variables aleatorias. Si las Xi son discretas, E[h(X1, . . . , Xn)]
es una suma de n dimensiones; si las Xi son continuas, es una integral de n dimensiones.
1
20
x
3
PROPOSICIÓN Sean X y Y variables aleatorias conjuntamente distribuidas con función masa de pro-
babilidad p(x, y) o función de densidad de probabilidad f (x, y) ya sea que las varia-
bles sean discretas o continuas. Entonces el valor esperado de una función h(X, Y)
denotada por E[h(X, Y)] o h(X, Y) está dada por
E[h(X, Y)]
x
y
h(x, y) p(x, y) Si X y Y son discretas
{'
'
'
'
h(x, y) f(x, y) dx dy Si X y Y son continuas
Ejemplo 5.13
Ejemplo 5.14
c5_p184-226.qxd 3/12/08 4:07 AM Page 197](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-215-320.jpg)
![198 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
Covarianza
Cuando dos variables aleatorias X y Y no son independientes, con frecuencia es de interés
valorar qué tan fuerte están relacionadas una con otra.
Es decir, como X X y Y Y son las desviaciones de las dos variables con respecto a
sus valores medios, la covarianza es el producto esperado de las desviaciones. Obsérvese
que Cov(X, X) E[(X X)2
] V(X).
La exposición razonada para la definición es como sigue. Suponga que X y Y tienen
una fuerte relación positiva entre ellas, lo que significa que los valores grandes de X tienden a
ocurrir con valores grandes de Y y los valores pequeños de X con los valores pequeños de
Y. Entonces la mayor parte de la masa o densidad de probabilidad estará asociada con (x
X) y (y Y) o ambos positivos (tanto X como Y sobre sus respectivas medias) o ambos
negativos, así que el producto (x X)(y Y) tenderá a ser positivo. Por tanto con una
fuerte relación positiva, Cov(X, Y) deberá ser bastante positiva. Con una fuerte relación
negativa los signos de (x X) y (y Y) tenderán a ser opuestos, lo que da un producto nega-
tivo. Por tanto con una fuerte relación negativa, Cov(X, Y) deberá ser bastante negativa. Si
X y Y no están fuertemente relacionadas, los productos positivo y negativo tenderán a eli-
minarse entre sí, lo que da una covarianza de cerca de 0. La figura 5.4 ilustra las diferentes
posibilidades. La covarianza depende tanto del conjunto de pares posibles como de las pro-
babilidades. En la figura 5.4, las probabilidades podrían ser cambiadas sin que se altere el
conjunto de pares posibles y esto podría cambiar drásticamente el valor de Cov(X, Y).
Las funciones masa de probabilidad conjunta y marginal de X cantidad deducible sobre
una póliza de automóvil y Y cantidad deducible sobre póliza de propietario de casa en el
ejemplo 5.1 fueron
p(x, y)
| 0 200 x
| 100 250 y
| 0 100 200
x
100 | 0.20 0.10 0.20 pX(x) | 0.5 0.5 pY(y) | 0.25 0.25 0.5
250 | 0.05 0.15 0.30
y
100
DEFINICIÓN La covarianza entre dos variables aleatorias X y Y es
Cov(X, Y) E[(X X)(Y Y)]
x
y
(x X)(y Y)p(x, y) X, Y discretas
{
(x X)(y Y)f(x, y) dx dy X, Y continuas
Ejemplo 5.15
Figura 5.4 p(x, y) 1/10 de cada uno de los diez pares correspondientes a los puntos indicados; a) cova-
rianza positiva; b) covarianza negativa; c) covarianza cerca de cero.
X
c)
X
b)
Y
Y
y
Y
X
a)
x
y
x
y
x
c5_p184-226.qxd 3/12/08 4:07 AM Page 198](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-216-320.jpg)
![202 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
En el capítulo 1, x1, x2, . . . , xn denotaron las observaciones en una sola muestra. Considérese
seleccionar dos muestras diferentes de tamaño n de la misma distribución de población. Las
xi en la segunda muestra virtualmente siempre diferirán por lo menos un poco de aquellas en
la primera muestra. Por ejemplo, una primera muestra de n 3 carros de un tipo particular
podría producir eficiencias de combustible x1 30.7, x2 29.4, x3 31.1, mientras que
una segunda muestra puede dar x1 28.8, x2 30.0 y x3 31.1. Antes de obtener datos,
existe incertidumbre sobre el valor de cada xi. Debido a esta incertidumbre, antes de que los
datos estén disponibles, cada observación se considera como una variable aleatoria y la
muestra se denota por X1, X2, . . . , Xn (letras mayúsculas para variables aleatorias).
Esta variación en los valores observados implica a su vez que el valor de cualquier
función de las observaciones muestrales, tal como la media muestral, la desviación estándar
muestral o la dispersión de los cuartos muestrales, también varía de una muestra a otra. Es
decir, antes de obtener x1, . . . , xn, existe incertidumbre en cuanto al valor de x
, el valor de
s, y así sucesivamente.
Suponga que la resistencia del material de un especimen seleccionado al azar de un tipo
particular tiene una distribución Weibull con valores de parámetro 2 (forma) y 5
número de asiento de A y Y el número de asiento de B.
Si A envía un mensaje escrito alrededor de la mesa a B en
la dirección en la cual están más cerca, ¿cuántos individuos
(incluidos A y B) esperarían manipular el mensaje?
25. Un topógrafo desea delimitar una región cuadrada con L de
lado. Sin embargo, debido a un error de medición, delimita
en cambio un rectángulo en el cual los lados norte-sur son
de longitud X y los lados este-oeste son de longitud Y.
Suponga que X y Y son independientes y que cada uno está
uniformemente distribuido en el intervalo [L A, L A]
(donde 0 A L). ¿Cuál es el área esperada del rectángu-
lo resultante?
26. Considere un pequeño transbordador que puede transportar
carros y autobuses. La cuota para carros es de $3 y para
autobuses es de $10. Sean X y Y el número de carros y auto-
buses, respectivamente, transportados en un solo viaje.
Suponga que la distribución conjunta de X y Y aparece en la
tabla del ejercicio 7. Calcule el ingreso esperado en un solo
viaje.
27. Annie y Alvie quedaron de encontrarse para desayunar
entre el mediodía (0:00 M.) y 1:00 P.M. Denote la hora de
llegada de Annie por X, y la de Alvie por Y y suponga que
X y Y son independientes con funciones de densidad de pro-
babilidad
fX(x) {3x2
0 x 1
0 de lo contrario
fY(y) {2y 0 y 1
0 de lo contrario
¿Cuál es la cantidad esperada de tiempo que el que llega
primero debe esperar a la otra persona? [Sugerencia: h(X,
Y) |X Y|.]
28. Demuestre que si X y Y son variables aleatorias indepen-
dientes, entonces E(XY) E(X) E(Y). Luego aplique esto
en el ejercicio 25. [Sugerencia: Considere el caso continuo
con f(x, y) fX(x) fY(y).]
29. Calcule el coeficiente de correlación , de X y Y del ejem-
plo 5.16 (ya se calculó la covarianza).
30. a. Calcule la covarianza de X y Y en el ejercicio 22.
b. Calcule para X y Y en el mismo ejercicio.
31. a. Calcule la covarianza entre X y Y en el ejercicio 9.
b. Calcule el coeficiente de correlación para X y Y.
32. Reconsidere las vidas útiles de los componentes de mini-
computadoras X y Y como se describe en el ejercicio 12.
Determine E(XY). ¿Qué se puede decir sobre Cov(X, Y) y ?
33. Use el resultado del ejercicio 28 para demostrar que cuan-
do X y Y son independientes Cov(X, Y) Corr(X, Y) 0.
34. a. Recordando la definición de 2
para una sola variable
aleatoria X, escriba una fórmula que sería apropiada para
calcular la varianza de una función h(X, Y) de dos varia-
bles aleatorias. [Sugerencia: Recuerde que la varianza es
simplemente un valor especial esperado.]
b. Use esta fórmula para calcular la varianza de la califica-
ción anotada h(X, Y) [ máx(X, Y)] en el inciso b) del
ejercicio 22.
35. a. Use las reglas de valor esperado para demostrar que
Cov(aX b, cY d) ac Cov(X, Y).
b. Use el inciso a) junto con las reglas de varianza y desvia-
ción estándar para demostrar que Corr(aX b, cY d)
Corr(X, Y) cuando a y c tienen el mismo signo.
c. ¿Qué sucede si a y c tienen signos opuestos?
36. Demuestre que si Y aX b (a 0), entonces Corr(X, Y)
1 o 1. ¿En que condiciones será 1?
Ejemplo 5.19
5.3 Estadísticos y sus distribuciones
c5_p184-226.qxd 3/12/08 4:08 AM Page 202](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-220-320.jpg)
![con el otro método. La siguiente definición describe un método de muestreo encontrado a
menudo (por lo menos aproximadamente) en la práctica.
Las condiciones 1 y 2 pueden ser parafraseadas diciendo que las Xi son independientes e
idénticamente distribuidas (iid). Si el muestreo se realiza con reemplazo o de una población
infinita (conceptual), las condiciones 1 y 2 se satisfacen con exactitud. Estas condiciones
serán aproximadamente satisfechas si el muestreo se realiza sin reemplazo, aunque el tama-
ño de la muestra sea mucho más pequeño que el tamaño de la población N. En la práctica,
si n/N 0.05 (cuando mucho 5% de la población se muestrea), se puede proceder como si
las Xi formarán una muestra aleatoria. La virtud de este método de muestreo es que la dis-
tribución de probabilidad de cualquier estadístico es más fácil de obtener que con cualquier
otro método de muestreo.
Existen dos métodos generales de obtener información sobre una distribución de
muestreo estadístico. Uno implica cálculos basados en reglas de probabilidad y el otro
implica realizar un experimento de simulación.
Derivación de una distribución de muestreo
Se pueden utilizar reglas de probabilidad para obtener la distribución de un estadístico siem-
pre que sea una función “bastante simple” de las Xi y o existen relativamente pocos valores
X diferentes en la población o bien la distribución de la población tiene una forma “accesi-
ble”. Los dos ejemplos siguientes ilustran tales situaciones.
Un gran centro de servicio automotriz cobra $40, $45 y $50 por la afinación de carros de
cuatro, seis y ocho cilindros, respectivamente. Si 20% de sus afinaciones se realizan en
carros de cuatro cilindros, 30% en carros de seis cilindros y 50% en carros de ocho cilin-
dros, entonces la distribución de probabilidad de los ingresos por una afinación selecciona-
da al azar está dada por
x
| 40 45 50
p(x) | 0.2 0.3 0.5 con 46.5, 2
15.25
(5.2)
Suponga que en un día particular sólo se realizan dos trabajos de servicio que implican afi-
naciones. Sea X1 el ingreso por la primera afinación y X2 el ingreso por la segunda.
Suponga que X1 y X2 son independientes, cada una con la distribución de probabilidad mos-
trada en (5.2) [de modo que X1 y X2 constituyen una muestra aleatoria de la distribución
(5.2)]. La tabla 5.2 pone en lista pares posibles (x1, x2), la probabilidad de cada uno [calcu-
lado por medio de (5.2) y la suposición de independencia] y los valores x
y s2
resultantes.
Ahora para obtener la distribución de probabilidad de X
, el ingreso promedio muestral por
afinación, se debe considerar cada valor posible de x
y calcular su probabilidad. Por ejem-
plo, x
45 ocurre tres veces en la tabla con probabilidades 0.10, 0.09 y 0.10, por lo tanto
pX
(45) P(X
45) 0.10 0.09 0.10 0.29
Asimismo
pS2(50) P(S2
50) P(X1 40, X2 50 o X1 50, X2 40)
0.10 0.10 0.20
5.3 Estadísticos y sus distribuciones 205
DEFINICIÓN Se dice que las variables aleatorias X1, X2, . . . , Xn forman una muestra aleatoria sim-
ple de tamaño n si
1. Las Xi son variables aleatorias independientes.
2. Cada Xi tiene la misma distribución de probabilidad.
Ejemplo 5.20
c5_p184-226.qxd 3/12/08 4:08 AM Page 205](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-223-320.jpg)
![Es decir, la distribución de muestreo X
tiene su centro en la media de la población y la
distribución de muestreo S2
está centrada en la varianza de la población 2
.
Si se hubieran realizado cuatro afinaciones en el día de interés, el ingreso promedio
muestral X
estaría basado en una muestra aleatoria de cuatro Xi, cada una con la distribución
(5.2). Con más cálculos se obtiene la función masa de probabilidad de X
con n 4 como
x
| 40 41.25 42.5 43.75 45 46.25 47.5 48.75 50
pX
(x
) | 0.0016 0.0096 0.0376 0.0936 0.1761 0.2340 0.2350 0.1500 0.0625
De acuerdo con esta, X
46.50 y
2
X
3.8125 2
/4. La figura 5.8 es un histogra-
ma de probabilidad de esta función masa de probabilidad.
El ejemplo 5.20 sugiere que el cálculo de pX
(x
) y pS
2(s2
) puede ser tedioso. Si la distri-
bución original (5.2) hubiera permitido más de tres valores posibles, 40, 45 y 50, entonces
incluso con n 2 los cálculos hubieran sido más complicados. El ejemplo también sugiere,
sin embargo, que existen algunas relaciones generales entre E(X
), V(X
), E(S2
), y la media
y la varianza 2
de la distribución original. Éstas se formulan en la siguiente sección. Ahora
considérese un ejemplo en el cual la muestra aleatoria se extrae de una distribución continua.
Tiempo de servicio para un tipo de transacción bancaria es una variable aleatoria con dis-
tribución exponencial y parámetro . Suponga que X1 y X2 son tiempos de servicio para dos
clientes diferentes, supuestos independientes entre sí. Considere el tiempo de servicio total
To X1 X2 para los dos clientes, también un estadístico. La función de distribución acumu-
lativa de To con t 0,
FT0
(t) P(X1 X2 t) f(x1, x2) dx1 dx2
{(x1, x2):x1x2t}
t
0
tx1
0
ex1
ex2
dx2 dx1
t
0
[ex1
et
] dx1
1 et
tet
La región de integración se ilustra en la figura 5.9.
5.3 Estadísticos y sus distribuciones 207
Figura 5.8 Histograma de probabilidad de X
basado en el n 4 en el ejemplo 5.20. ■
40 42.5 45 47.5 50
Figura 5.9 Región de integración para obtener la función de distribución acumulativa de To
en el ejemplo 5.21.
x1
x2
x1
x1
x2
t
(x1, t x1)
Ejemplo 5.21
c5_p184-226.qxd 3/12/08 4:08 AM Page 207](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-225-320.jpg)
![208 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
La función de densidad de probabilidad de To se obtiene derivando FTo
(t):
fT0
(t) {2
tet
t 0
0 t 0
(5.5)
Esta es una función de densidad de probabilidad gama ( 2 y 1/). La función de
densidad de probabilidad de X
To/2 se obtiene a partir de la relación {X
x
} si y sólo si
{To 2x
} como
fX
(x
) {42
x
e 2x
x
0
0 x
0
(5.6)
La media y la varianza de la distribución exponencial subyacente son 1/ y 2
1/2
.
Con las expresiones (5.5) y (5.6) se puede verificar que E(X
) 1/, V(X
) 1/(22
), E(To)
2/, y V(To) 2/2
. Estos resultados sugieren de nuevo algunas relaciones generales entre
medias y varianzas de X
, To y la distribución subyacente. ■
Experimentos de simulación
El segundo método de obtener información sobre distribución de muestreo estadístico es
realizar un experimento de simulación. Este método casi siempre se utiliza cuando la obtención
vía reglas de probabilidad es demasiado difícil o complicada de realizar. Tal experimento vir-
tualmente siempre se realiza con la ayuda de una computadora. Las siguientes características
de un experimento deben ser especificadas:
1. El estadístico de interés (X
, S, una media recortada particular, etcétera).
2. La distribución de la población (normal con 100 y 15, uniforme con límite
inferior A 5 y superior B 10, etcétera).
3. El tamaño de muestra n(p. ej., n 10 o n 50).
4. El número de réplicas k (p. ej., k 500).
Luego se utiliza una computadora para obtener k diferentes muestras aleatorias, cada una de
tamaño n, de la distribución de población designada. Para cada una de las muestras, calcu-
le el valor del estadístico y construya un histograma de los k valores calculados. Este histo-
grama da la distribución de muestreo aproximada del estadístico. Mientras más grande es el
valor de k, mejor tenderá a ser la aproximación (la distribución de muestreo real emerge a
medida que k A ). En la práctica k 500 o 1000 casi siempre es suficiente si el estadís-
tico es “bastante simple”.
La distribución de la población del primer estudio de simulación es normal con 8.25 y
0.75, como se ilustra en la figura 5.10. [El artículo “Platelet Size in Myocardial
Infarction” (British Med. J., 1983: 449-451) sugiere esta distribución de volumen de pla-
quetas en individuos sin historial clínico de problemas de corazón serios.]
Ejemplo 5.22
Figura 5.10 Distribución normal, con 8.25 y 0.75.
6.00 6.75 7.50 9.00 9.75 10.50
8.25
¨
©
ª
0.75
c5_p184-226.qxd 3/12/08 4:08 AM Page 208](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-226-320.jpg)
![210 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
El aspecto final del histograma es su dispersión uno con respecto al otro. Mientras
más pequeño es el valor de n, más grande es la extensión hacia la cual la distribución se
esparce con respecto al valor medio. Por eso los histogramas con n 20 y n 30 están
basados en intervalos de clase más angostos que aquellos de los dos tamaños de muestra
más pequeños. Con los tamaños de muestra más grandes, la mayoría de los valores x
están
bastante cerca de 8.25. Este es el efecto de promediar. Cuando n es pequeño, un valor x
inusual puede dar por resultado un valor x
alejado del centro. Con un tamaño de muestra
grande, cualesquiera valores x inusuales, cuando se promedian con los demás valores
muestrales, seguirá tendiendo a producir un valor x
próximo a . Si se combinan estas
ideas se obtiene un resultado muy apegado a su intuición: X
basado en n grande tiende a
acercarse más a que X
basado en n pequeño. ■
Considere un experimento de simulación en el cual la distribución de la población es bastan-
te asimétrica. La figura 5.12 muestra la curva de densidad de las vidas útiles de un tipo de
control electrónico [ésta es en realidad una distribución lognormal con E(ln(X)) 3 y
V(ln(X)) 0.16]. De nueva cuenta el estadístico de interés es la media muestral X
. El experi-
mento utilizó 500 réplicas y consideró los mismos cuatro tamaños de muestra que en el ejem-
plo 5.22. Los histogramas resultantes junto con una curva de probabilidad normal generada
por MINITAB con los 500 x
valores basados en n 30 se muestran en la figura 5.13.
A diferencia del caso normal, estos histogramas difieren en cuanto a forma. En particular,
se vuelven progresivamente menos asimétricos a medida que el tamaño de muestra n se
incrementa. El promedio de los 500 x
valores con los cuatro tamaños de muestra diferentes
se aproximan bastante al valor medio de la distribución de la población. Si cada histograma se
hubiera basado en una secuencia interminable de valores x
en lugar de sólo 500, los cuatro
habrían tenido su centro en exactamente 21.7584. Por tanto los valores diferentes de n cam-
bian la forma mas no el centro de la distribución de muestreo de X
. La comparación de los
cuatro histogramas en la figura 5.13 también muestra que conforme n se incrementa, la dis-
persión de los histogramas decrece. El incremento de n produce un mayor grado de con-
centración en torno al valor medio de la población y hace que el histograma se vea más
como una curva normal. El histograma de la figura 5.13d) y la curva de probabilidad nor-
mal en la figura 5.13e) proporcionan una evidencia convincente de que un tamaño de mues-
tra de n 30 es suficiente para superar la asimetría de la distribución de la población y para
producir una distribución de muestreo X
aproximadamente normal.
Ejemplo 5.23
Figura 5.12 Curva de densidad del experimento de simulación del ejemplo 5.23 [E(X) 21.7584,
V(X) 82.1449].
0 25 50 75
0.01
0.02
0.03
0.04
0.05
x
f(x)
c5_p184-226.qxd 3/12/08 4:08 AM Page 210](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-228-320.jpg)
![212 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
EJERCICIOS Sección 5.3 (37-45)
37. Una marca particular de jabón para lavadora de platos se
vende en tres tamaños: 25 oz, 40 oz y 65 oz. El 20% de to-
dos los compradores seleccionan la caja de 25 oz, 50% se-
leccionan una caja de 40 oz y el 30% restante seleccionan
la caja de 65 oz. Sean X1 y X2 los tamaños de paquete selec-
cionados por dos compradores independientemente seleccio-
nados.
a. Determine la distribución de muestreo de X
, calcule
E(X
), y compare con .
b. Determine la distribución de muestreo de la varianza
muestral S2
, calcule E(S2
) y compare con 2
.
38. Hay dos semáforos en mi camino al trabajo. Sea X1 el
número de semáforos en los cuales me tengo que detener y
suponga que la distribución X1 es como sigue:
x1
| 0 1 2 1.1, 2
0.49
p(x1) | 0.2 0.5 0.3
Sea X2 el número de semáforos en los cuales me tengo que
detener camino a casa; X2 es independiente de X1. Suponga
que X2 tiene la misma distribución que X1, de modo que X1,
X2 es una muestra aleatoria de tamaño n 2.
a. Sea To X1 X2, y determine la distribución de proba-
bilidad de To.
b. Calcule To
. ¿Cómo se relaciona con , la media de la
población?
c. Calcule 2
To
. ¿Cómo se relaciona con 2
, la varianza de
la población?
39. Se sabe que 80% de todos los discos de almacenamiento
extraíbles funcionan satisfactoriamente durante el periodo
de garantía (son “éxitos”). Suponga que se seleccionan al
azar n 10 unidades de disco. Sea X el número de éxi-
tos en la muestra. El estadístico X/n es la proporción de la
muestra (fracción) de éxitos. Obtenga la distribución mues-
tral de este estadístico. [Sugerencia: Un posible valor de X/n
es 0.3, correspondiente a X 3. ¿Cuál es la probabilidad de
este valor (qué clase de variable aleatoria es X)?]
40. Una caja contiene diez sobres sellados numerados 1, . . . ,
10. Los primeros cinco no contienen dinero, cada uno de los
siguientes tres contiene $5 y hay un billete de $10 en cada
uno de los últimos dos. Se selecciona un tamaño de mues-
tra de 3 con reemplazo (así que se tiene una muestra alea-
toria) y se obtiene la cantidad más grande en cualquiera de
los sobres seleccionados. Si X1, X2 y X3 denotan las canti-
dades en los sobres seleccionados, el estadístico de interés
es M el máximo de X1, X2 y X3.
a. Obtenga la distribución de probabilidad de este estadís-
tico.
b. Describa cómo realizaría un experimento de simulación
para comparar las distribuciones de M con varios tama-
ños de muestra. ¿Cómo piensa que cambiaría la distri-
bución a medida que n se incrementa?
41. Sea X el número de paquetes enviados por un cliente selec-
cionado al azar vía una compañía de paquetería y mensaje-
ría. Suponga que la distribución de X es como sigue:
x
| 1 2 3 4
p(x) | 0.4 0.3 0.2 0.1
a. Considere una muestra aleatoria de tamaño n 2 (dos
clientes) y sea X
el número medio muestral de paquetes
enviados. Obtenga la distribución de probabilidad de X
.
b. Remítase al inciso a) y calcule P(X
2.5).
c. De nuevo considere una muestra aleatoria de tamaño
n 2, pero ahora enfóquese en el estadístico R el ran-
go muestral (diferencia entre los valores más grande y
más pequeño en la muestra). Obtenga la distribución de
R. [Sugerencia: Calcule el valor de R por cada resultado
y use las probabilidades del inciso a).]
d. Si se selecciona una muestra aleatoria de tamaño n 4,
¿Cuál es P(X
1.5)? [Sugerencia: No tiene que dar
todos los resultados posibles, sólo aquellos para los cua-
les x
1.5.]
42. Una compañía mantiene tres oficinas en una región, cada
una manejada por dos empleados. Información concernien-
te a salarios anuales (miles de dólares) es la siguiente:
Oficina 1 1 2 2 3 3
Empleado 1 2 3 4 5 6
Salario 29.7 33.6 30.2 33.6 25.8 29.7
a. Suponga que dos de estos empleados se seleccionan al
azar de entre los seis (sin reemplazo). Determine la dis-
tribución del salario medio muestral X
.
b. Suponga que se selecciona al azar una de las tres ofici-
nas. Sean X1 y X2 los salarios de los dos empleados.
Determine la distribución muestral de X
.
c. ¿Cómo se compara E(X
) de los incisos a) y b) con el
salario medio de la población ?
43. Suponga que la cantidad de líquido despachado por una
máquina está uniformemente distribuida con límite inferior
A 8 oz y límite superior B 10 oz. Describa cómo rea-
lizaría experimentos de simulación para comparar la distri-
bución de la (muestra) dispersión de los cuartos con
tamaños de muestra n 5, 10, 20 y 30.
44. Realice un experimento con un programa de computadora
estadístico u otro programa para estudiar la distribución
muestral de X
cuando la distribución de la población es
Weibull con 2 y 5, como en el ejemplo 5.19.
Considere los cuatro tamaños de muestra n 5, 10, 20 y 30
y en cada caso utilice 500 réplicas. ¿Con cuál de estos
tamaños de muestra la distribución muestral X
parece ser
aproximadamente normal?
45. Realice un experimento de simulación con un programa de
computadora estadístico u otro programa para estudiar
la distribución muestral de X
cuando la distribución de la
población es lognormal con E(ln(X)) 3 y V(ln(X)) 1.
Considere los cuatro tamaños de muestra n 10, 20, 30 y
50 y en cada caso utilice 500 réplicas. ¿Con cuál de estos
tamaños de muestra la distribución muestral X
parece ser
aproximadamente normal?
c5_p184-226.qxd 3/12/08 4:08 AM Page 212](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-230-320.jpg)
![Una dificultad práctica al aplicar el teorema del límite central es saber cuándo n es
suficientemente grande. El problema es que la precisión de la aproximación con una n
particular depende de la forma de la distribución subyacente original que está siendo
muestreada. Si la distribución subyacente tiende a una curva de densidad normal, entonces
la aproximación será buena incluso con n pequeña, mientras que si está lejos de ser normal,
entonces se requerirá una n grande.
Existen distribuciones de población para las cuales una n de 40 o 50 no son suficientes, pero
tales distribuciones rara vez se encuentran en la práctica. Por otra parte, la regla empírica a
menudo es conservadora; para muchas distribuciones de población, una n mucho menor que
30 serían suficientes. Por ejemplo, en el caso de una distribución de población uniforme, el
teorema del límite central da una buena aproximación con n 12.
Otras aplicaciones del teorema del límite central
El teorema del límite central puede ser utilizado para justificar la aproximación normal a
la distribución binomial discutida en el capítulo 4. Recuérdese que una variable binomial X
es el número de éxitos en una experiencia binomial compuesta de n ensayos independien-
tes con éxitos/fallas y p P(S) para cualquier ensayo particular. Defínanse nuevas varia-
bles aleatorias X1, X2, . . . , Xn como
Xi {1 Si el i-ésimo ensayo produce un éxito
(i 1, . . . , n)
0 Si el i-ésimo ensayo produce una falla
Como los ensayos son independientes y P(S) es constante de un ensayo a otro, las Xi son
idénticas (una muestra aleatoria de una distribución de Bernoulli). El teorema del límite cen-
tral implica entonces que si n es suficientemente grande, tanto la suma como el promedio
de las Xi tienen distribuciones normales de manera aproximada. Cuando se suman las Xi, se
agrega un 1 por cada S (éxito) que ocurra y un 0 por cada F (falla), por tanto X1 · · · Xn
X. La media muestral de las Xi es X/n, la proporción muestral de éxitos. Es decir, tanto X
como X/n son aproximadamente normales cuando n es grande. El tamaño de muestra nece-
sario para esta aproximación depende del valor de p: Cuando p se acerca a 0.5, la distribu-
ción de cada Xi es razonablemente simétrica (véase la figura 5.17), mientras que la
distribución es bastante asimétrica cuando p se acerca a 0 o 1. Utilizando la aproximación
sólo si tanto np 10 como a n(1 p) 10 garantiza que n es suficientemente grande para
superar cualquier asimetría en la distribución de Bernoulli subyacente.
Recuérdese por la sección 4.5 que X tiene una distribución lognormal si ln(X) tiene
una distribución normal.
5.4 Distribución de la media muestral 217
Figura 5.17 Dos distribuciones de Bernoulli: a) p 5 4 (razonablemente simétrica); b) p 5 1 (muy
asimétrica).
0 1
a)
0 1
b)
Regla empírica
Si n 30, se puede utiliza el teorema del límite central.
PROPOSICIÓN Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución para la cual sólo valo-
res positivos son posibles [P(Xi 0) 1]. Entonces si n es suficientemente grande,
el producto Y X1X2 · · · · · Xn tiene aproximadamente una distribución lognormal.
c5_p184-226.qxd 3/12/08 4:08 AM Page 217](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-235-320.jpg)
![218 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
Para verificar esto, obsérvese que
ln(Y) ln(X1) ln(X2) . . . ln(Xn)
Como ln(Y) es una suma de variables aleatorias independientes y distribuidas de manera
idéntica [las ln(Xi)], es aproximadamente normal cuando n es grande, así que Y tiene apro-
ximadamente una distribución lognormal. Como ejemplo de la aplicabilidad de este resul-
tado, Bury (Statistical Models in Applied Science, Wiley, p. 590) argumenta que el proceso
de daños en el flujo plástico y en la propagación de grietas es un proceso multiplicativo, de
modo que las variables tales como porcentaje de alargamiento y resistencia a la ruptura tie-
nen aproximadamente distribuciones lognormales.
EJERCICIOS Sección 5.4 (46-57)
46. El diámetro interno de un anillo de pistón seleccionado al
azar es una variable aleatoria con valor medio de 12 cm y
desviación estándar de 0.04 cm.
a. Si X
es el diámetro medio en una muestra aleatoria de
n 16 anillos, ¿dónde está centrada la distribución muestral
de X
y cuál es la desviación estándar de la distribución X
?
b. Responda las preguntas planteadas en el inciso a) con un
tamaño de muestra de n 64 anillos.
c. ¿Con cuál de las dos muestras aleatorias, la del inciso a)
o la del inciso b), es más probable que X
esté dentro de
0.01 cm de 12 cm? Explique su razonamiento.
47. Remítase al ejercicio 46. Suponga que el diámetro de la dis-
tribución es normal.
a. Calcule P(11.99 X
12.01) cuando n 16.
b. ¿Qué tan probable es que el diámetro medio muestral
exceda de 12.01 cuando n 25?
48. Sean X1, X2, . . . , X100 los pesos netos reales de 100 sacos
de 50 lb de fertilizante seleccionados al azar.
a. Si el peso esperado de cada saco es de 50 lb y la varian-
za es uno, calcule P(49.9 X
50.1) (aproximada-
mente) por medio del teorema del límite central.
b. Si el peso esperado es de 49.8 lb en lugar de 50 lb de
modo que en promedio los sacos están menos llenos,
calcule P(49.9 X
50.1).
49. Hay 40 estudiantes en una clase de estadística elemental.
Basado en años de experiencia, el instructor sabe que el
tiempo requerido para calificar un primer examen seleccio-
nado al azar es una variable aleatoria con un valor esperado
de seis min y una desviación estándar de seis min.
a. Si los tiempos de calificación son independientes y el
instructor comienza a calificar a las 6:50 p.m. y califica
en forma continua, ¿cuál es la probabilidad (aproxima-
da) de que termine de calificar antes de que se inicie el
programa de noticias de las 11:00 p.m.?
b. Si el reporte de deportes se inicia a la 11:10, ¿cuál es
la probabilidad de que se pierda una parte del reporte
si se espera hasta que termine de calificar antes de
prender la TV?
50. La resistencia a la ruptura de un remache tiene un valor
medio de 10 000 lb/pulg2
y una desviación estándar de 500
lb/pulg2
.
a. ¿Cuál es la probabilidad de que la resistencia a la ruptu-
ra media de una muestra aleatoria de 40 remaches sea de
entre 9900 y 10 200?
b. Si el tamaño de muestra hubiera sido de 15 y no de 40,
¿se podría calcular la probabilidad solicitada en el inci-
so a) con la información dada?
51. El tiempo requerido por un solicitante seleccionado al azar
de una hipoteca para llenar un formulario tiene una distri-
bución normal con valor medio de 10 min y desviación
estándar de dos min. Si cinco individuos llenan un formula-
rio en un día y seis en otro, ¿cuál es la probabilidad de que
la cantidad promedio muestral de tiempo requerido cada día
sea cuando mucho de 11 min?
52. La vida útil de un tipo de batería está normalmente distribuida
con valor medio de 10 horas y desviación estándar de una hora.
Hay cuatro baterías en un paquete. ¿Qué valor de vida útil es
tal que la vida útil total de todas las baterías contenidas en un
paquete exceda de ese valor en sólo 5% de todos los paquetes?
53. Se sabe que la dureza Rockwell de “pernos” de un tipo tie-
ne un valor medio de 50 y una desviación estándar de 1.2.
a. Si la distribución es normal, ¿cuál es la probabilidad de
que la dureza media de una muestra aleatoria de 9 per-
nos sea por lo menos de 51?
b. ¿Cuál es la probabilidad (aproximada) de que la dureza
media de una muestra aleatoria de 40 pernos sea por lo
menos de 51?
54. Suponga que la densidad de un sedimento (g/cm) de un
espécimen seleccionado al azar de cierta región está nor-
malmente distribuida con media de 2.65 y desviación están-
dar de 0.85 (sugerida en “Modeling Sediment and Water
Column Interactions for Hydrophobic Pollutants”, Water
Research, 1984: 1169-1174).
a. Si se selecciona una muestra aleatoria de 25 especíme-
nes, ¿cuál es la probabilidad de que la densidad del sedi-
mento promedio muestral sea cuando mucho de 3.00?
¿De entre 2.65 y 3.00?
b. ¿Qué tan grande debe ser un tamaño de muestra para
garantizar que la primera probabilidad en el inciso a) sea
por lo menos de 0.99?
55. El número de infracciones de estacionamiento aplicadas en
una ciudad en cualquier día de la semana dado tiene una
distribución de Poisson con parámetro 50. ¿Cuál es la
probabilidad aproximada de que
a. entre 35 y 70 infracciones sean aplicadas en un día par-
ticular? [Sugerencia: Cuando es grande, una variable
aleatoria de Poisson tiene aproximadamente una distri-
bución normal.]
c5_p184-226.qxd 3/12/08 4:08 AM Page 218](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-236-320.jpg)
![220 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
Las comprobaciones se dan al final de la sección. Un parafraseo de (5.8) es que el valor espe-
rado de una combinación lineal es la misma combinación lineal de los valores esperados, por
ejemplo, E(2X1 5X2) 21 52. El resultado (5.9) en la proposición 2 es un caso especial
de (5.11) en la proposición 3; cuando las Xi son independientes, Cov(Xi, Xj) 0 con i j
e igual a V(Xi) con i j (esta simplificación en realidad ocurre cuando las Xi no están correla-
cionadas, una condición más débil que la de independencia). Especializando al caso de una
muestra aleatoria (Xi idénticamente distribuidas) con ai 1/n con cada i da E(X
) y V(X
)
2
/n, como se discutió en la sección 5.4. Un comentario similar se aplica a las reglas para To.
Una gasolinería vende tres grados de gasolina; regular, extra y súper. Éstas se venden a
$21.20, $21.35 y $21.50 por galón, respectivamente. Sean X1, X2 y X3 las cantidades (galo-
nes) de estas gasolinas compradas en un día particular. Suponga que las Xi son indepen-
dientes con 1 1000, 2 500, 3 300, 1 100, 2 80, y 3 50. El ingreso por
las ventas es Y 21.2X1 21.35X2 21.5X3 y
E(Y) 21.21 21.352 21.53 $4125
V(Y) (21.2)2
2
1 (21.35)2
2
2 (21.5)2
2
3 104 025
Y 10402
5
$322.53 ■
Diferencia entre dos variables aleatorias
Un caso especial importante de una combinación lineal se presenta con n 2, a1 1 y
a2 1:
Y a1X1 a2X2 X1 X2
Entonces se tiene el siguiente corolario de la proposición.
El valor esperado de una diferencia es la diferencia de los dos valores esperados, pero la
varianza de una diferencia entre dos variables independientes es la suma, no la diferencia,
de las dos varianzas. Existe tanta variabilidad en X1 X2 como en X1 X2 [escribiendo
X1 X2 X1 (1)X2, (1)X2 tiene la misma cantidad de variabilidad que X2].
Una compañía automotriz equipa un modelo particular con un motor de seis cilindros o un
motor de cuatro cilindros. Sean X1 y X2 eficiencias de combustible de carros de seis y cua-
tro cilindros seleccionados en forma independiente al azar, respectivamente. Con 1 22,
2 26, 1 1.2 y 2 1.5,
E(X1 X2) 1 2 22 26 4
V(X1 X2) 2
1 2
2 (1.2)2
(1.5)2
3.69
X1X2
3
.6
9
1.92
Si se cambia la notación de modo que X1 se refiera al carro de cuatro cilindros, entonces
E(X1 X2) 4, pero la varianza de la diferencia sigue siendo de 3.69. ■
El caso de variables aleatorias normales
Cuando las Xi forman una muestra aleatoria de una distribución normal, X
y To están normal-
mente distribuidas. He aquí un resultado más general con respecto a combinaciones lineales.
Ejemplo 5.28
Ejemplo 5.29
COROLARIO E(X1 X2) E(X1) E(X2) y, si X1 y X2 son independientes, V(X1 X2)
V(X1) V(X2).
c5_p184-226.qxd 3/12/08 4:08 AM Page 220](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-238-320.jpg)
![El ingreso total por la venta de los tres grados de gasolina en un día particular fue Y 21.2X1
21.35X2 21.5X3, y se calculó Y 4125 y (suponiendo independencia) Y 322.53. Si las
Xi están normalmente distribuidas, la probabilidad de que el ingreso sea de más de 4500 es
P(Y 4500) P
Z
P(Z 1.16) 1 (1.16) 0.1230 ■
El teorema del límite central también puede ser generalizado para aplicarlo a ciertas combina-
ciones lineales. En general, si n es grande y no es probable que algún término individual con-
tribuya demasiado al valor total, entonces Y tiene aproximadamente una distribución normal.
Comprobaciones en el caso n 2
En cuanto al resultado por lo concerniente a los valores esperados, suponga que X1 y X2 son
continuas con función de densidad de probabilidad conjunta f(x1, x2). Entonces
E(a1X1 a2X2)
(a1x1 a2x2)f(x1, x2) dx1 dx2
a1
x1 f(x1, x2) dx2 dx1
a2
x2 f(x1, x2) dx1 dx2
a1
x1 fX1
(x1) dx1 a2
x2 fX2
(x2) dx2
a1E(X1) a2E(X2)
La suma reemplaza a la integración en el caso discreto. El argumento en cuanto a la varian-
za resultante no requiere especificar si la variable es discreta o continua. Recordando que
V(Y) E[(Y Y)2
],
V(a1X1 a2X2) E{[a1X1 a2X2 (a11 a22)]2
}
E{a2
1(X1 1)2
a2
2(X2 2)2
2a1a2(X1 1)(X2 2)}
La expresión adentro de las llaves es una combinación lineal de las variables Y1 (X1 1)2
,
Y2 (X2 2)2
y Y3 (X1 1)(X2 2), así que si se acarrea la operación E a través de
los tres términos se obtiene a2
1V(X1) a2
2V(X2) 2a1a2 Cov(X1, X2) como se requiere. ■
4500 4125
322.53
5.5 Distribución de una combinación lineal 221
PROPOSICIÓN Si X1, X2, . . . , Xn son variables aleatorias independientes normalmente distribuidas
(con quizá diferentes medias y/o varianzas), entonces cualquier combinación lineal de
las Xi también tiene una distribución normal. En particular, la diferencia X1 X2 entre
dos variables independientes normalmente distribuidas también está distribuida en
forma normal.
Ejemplo 5.30
(continuación
del ejemplo
5.28)
EJERCICIOS Sección 5.5 (58-74)
58. Una compañía naviera maneja contenedores en tres dife-
rentes tamaños: (1) 27 pies3
(3 3 3), (2) 125 pies3
y (3)
512 pies3
. Sea Xi (i 1, 2, 3) el número de contenedores de
tipo i embarcados durante una semana dada. Con i E(Xi)
y 2
i V(Xi), suponga que los valores medios y las desvia-
ciones estándar son como sigue:
1 200 2 250 3 100
1 10 2 12 3 8
c5_p184-226.qxd 3/12/08 4:08 AM Page 221](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-239-320.jpg)
![222 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
a. Suponiendo que X1, X2, X3 son independientes, calcule el
valor esperado y la varianza del volumen total embarca-
do [Sugerencia: Volumen 27X1 125X2 512X3.]
b. ¿Serían sus cálculos necesariamente correctos si las Xi
no fueran independientes? Explique.
59. Si X1, X2 y X3 representan los tiempos necesarios para rea-
lizar tres tareas de reparación sucesivas en cierto taller de
servicio. Suponga que son variables aleatorias normales
independientes con valores esperados 1, 2 y 3 y varian-
zas 2
1, 2
2 y 2
3, respectivamente.
a. Si 2 3 60 y 2
1 2
2 2
3 15, calcule
P(X1 X2 X3 200). ¿Cuál es P(150 X1 X2
X3 200)?
b. Con las i y i dadas en el inciso a), calcule P(55 X
)
y P(58 X
62).
c. Con las i y i dadas en el inciso a), calcule P(10
X1 0.5X2 0.5X3 5).
d. Si 1 40, 2 50, 3 60, 2
1 10, 2
2 12, y
2
3 14, calcule P(X1 X2 X3 160) y P(X1
X2 2 X3).
60. Cinco automóviles del mismo tipo tienen que realizar un
viaje de 300 millas. Los primeros dos utilizarán una marca
económica de gasolina y los otros tres una marca de renom-
bre. Sean X1, X2, X3, X4 y X5 las eficiencias de combustible
observadas (mpg) de los cinco carros. Suponga que estas
variables son independientes y normalmente distribuidas
con 1 2 20, 3 4 5 21 y 2
4 con la mar-
ca económica y 3.5 con la marca de renombre. Defina una
variable aleatoria Y como
Y
de modo que Y mide la diferencia de eficiencia entre la
gasolina económica y la de renombre. Calcule P(0 Y) y
P(1 Y 1). [Sugerencia: Y a1X1 . . . a5X5, con
a1 2
1
, . . . , a5
1
3.]
61. El ejercicio 26 introdujo variables aleatorias X y Y, el núme-
ro de carros y autobuses, respectivamente, transportados
por un transbordador en un solo viaje. La función masa de
probabilidad conjunta de X y Y se da en la tabla del ejerci-
cio 7. Es fácil verificar que X y Y son independientes.
a. Calcule el valor esperado, la varianza y la desviación
estándar del número total de vehículos en un solo viaje.
b. Si a cada carro se le cobran $3 y a cada autobús $10,
calcule el valor esperado, la varianza y la desviación
estándar del ingreso resultante de un solo viaje.
62. Un fabricante de un cierto componente requiere tres opera-
ciones de maquinado diferentes. El tiempo de maquinado de
cada operación tiene una distribución normal y los tres tiem-
pos son independientes entre sí. Los valores medios son 15,
30 y 20 min, respectivamente y las desviaciones estándar
son 1, 2 y 1.5 min respectivamente. ¿Cuál es la probabilidad
de que se requiera cuando mucho una hora de tiempo de
maquinado para producir un componente seleccionado al azar?
63. Remítase al ejercicio 3.
a. Calcule la covarianza entre X1 el número de clientes
en la caja rápida y X2 el número de clientes en la caja
súperrápida.
b. Calcule V(X1 X2). ¿Cómo se compara con V(X1)
V(X2)?
64. Suponga que el tiempo de espera para un autobús en la maña-
na está uniformemente distribuido en [0, 8], mientras que el
tiempo de espera en la noche está uniformemente distribuido
en [0, 10] independiente del tiempo de espera en la mañana.
a. Si toma el autobús en la mañana y en la noche durante
una semana, ¿cuál es su tiempo de espera total espera-
do? [Sugerencia: Defina las variables aleatorias X1, . . . ,
X10 y use una regla de valor esperado.]
b. ¿Cuál es la varianza de su tiempo de espera total?
c. ¿Cuáles son el valor esperado y la varianza de la dife-
rencia entre los tiempos de espera en la mañana y en la
noche en un día dado?
d. ¿Cuáles son el valor esperado y la varianza de la diferencia
entre el tiempo de espera total en la mañana y el tiempo de
espera total en la noche durante una semana particular?
65. Suponga que cuando el pH de cierto compuesto químico es
5.00, el pH medido por un estudiante de química de primer
año seleccionado al azar es una variable aleatoria con media
de 5.00 y desviación estándar de 0.2. Un gran lote del com-
puesto se subdivide y a cada estudiante se le da una mues-
tra en un laboratorio matutino y a cada estudiante en un
laboratorio vespertino. Sea X
el pH promedio determina-
do por los estudiantes matutinos y Y
el pH promedio
determinado por los estudiantes vespertinos.
a. Si el pH es una variable normal y hay 25 estudiantes
en cada laboratorio, calcule P(0.1 X
Y
0.1).
[Sugerencia: X
Y
es una combinación lineal de varia-
bles normales, así que está normalmente distribuida.
Calcule X
Y
y X
Y
.]
b. Si hay 36 estudiantes en cada laboratorio, pero las deter-
minaciones del pH no se suponen normales, calcule
(aproximadamente) P(0.1 X
Y
0.1).
66. Si se aplican dos cargas a una viga en voladizo como se
muestra en la figura adjunta, el momento de flexión en 0
debido a las cargas es a1X1 a2X2.
a. Suponga que X1 y X2 son variables independientes con
medias de 2 y 4 klb, respectivamente y desviación
estándar de 0.5 y 1.0 klb, respectivamente. Si a1 5
pies y a2 10 pies, ¿cuál es el momento de flexión
esperado y cuál es la desviación estándar del momento
de flexión?
b. Si X1 y X2 están normalmente distribuidas, ¿cuál es la
probabilidad de que el momento de flexión sea de más
de 75 klb-pie?
c. Suponga que las posiciones de las dos cargas son varia-
bles aleatorias. Denotándolas por A1 y A2, suponga que
estas variables tienen medias de 5 y 10 pies, respectiva-
mente, que cada una tiene una desviación estándar de
0.5 y que todas las Ai y Xi son independientes entre sí.
¿Cuál es el momento esperado ahora?
d. En la situación del inciso c), ¿cuál es la varianza del
momento de flexión?
X1 X2
a1 a2
0
X3 X4 X5
3
X1 X2
2
c5_p184-226.qxd 3/12/08 4:08 AM Page 222](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-240-320.jpg)
![5.5 Distribución de una combinación lineal 223
e. Si la situación es como se describe en el inciso a) excep-
to que Corr(X1, X2) 0.5 (de modo que las dos cargas
no sean independientes), ¿cuál es la varianza del mo-
mento de flexión?
67. Un tramo de tubería de PVC tiene que ser insertado en otro
tramo. La longitud del primer tramo está normalmente dis-
tribuido con valor medio de 20 pulg y desviación estándar
de 0.5 pulg. El segundo tramo es una variable aleatoria nor-
mal con media y desviación estándar de 15 pulg y 0.4 pulg,
respectivamente. La cantidad de traslape está normalmente
distribuido con valor medio de una pulg y desviación están-
dar de 0.1 pulg. Suponiendo que los tramos y cantidad de
traslape son independientes entre sí, ¿cuál es la probabili-
dad de que la longitud total después de la inserción esté
entre 34.5 pulg y 35 pulg?
68. Dos aviones vuelan en la misma dirección en dos corredo-
res adyacentes. En el instante t 0, el primer avión está a
10 km adelante del segundo. Suponga que la velocidad del
primero (km/h) está normalmente distribuida con media de
520 y desviación estándar de 10 y que la velocidad del
segundo también está normalmente distribuida con media y
desviación estándar de 500 y 10, respectivamente.
a. ¿Cuál es la probabilidad de que después de 2 horas de
vuelo, el segundo avión no haya alcanzado al primer
avión?
b. Determine la probabilidad de que los aviones estén
separados cuando mucho 10 km después de 2 horas.
69. Tres carreteras diferentes entroncan en una autopista particu-
lar. Suponga que durante un tiempo fijo, el número de
carros que llegan por cada carretera a la autopista es una
variable aleatoria, con valor esperado y desviación estándar
como se dan en la tabla
| Carretera 1 Carretera 2 Carretera 3
Valor esperado | 800 1000 600
Desviación estándar | 16 25 18
a. ¿Cuál es el número de carros total esperado que entran
a la autopista en este punto durante el periodo?
[Sugerencia: Sea Xi el número de la carretera i.]
b. ¿Cuál es la varianza del número total de carros que
entran? ¿Ha hecho suposiciones sobre la relación entre
los números de carros en las diferentes carreteras?
c. Con Xi denotando el número de carros que entran de la
carretera i durante el periodo, suponga que Cov(X1,
X2) 80, Cov(X1, X3) 90 y Cov(X2, X3) 100 (de
modo que las tres corrientes de tráfico no son indepen-
dientes). Calcule el número total esperado de los carros
que entran y la desviación estándar del total.
70. Considere una muestra aleatoria de tamaño n tomada de una
distribución continua con mediana 0 de modo que la proba-
bilidad de cualquier observación sea positiva de 0.5. Ha-
ciendo caso omiso de los signos de las observaciones,
clasifíquelas desde la más pequeña a la más grande en valor
absoluto y sea W la suma de las filas de las observacio-
nes con signos positivos. Por ejemplo, si las observaciones
son 0.3, 0.7, 2.1 y 2.5, entonces las filas de obser-
vaciones positivas son 2 y 3, de modo que W 5. En el
capítulo 15, W se llamará estadístico de filas con signo de
Wilcoxon. W puede representarse como sigue:
W 1 Y1 2 Y2 3 Y3 . . . n Yn
n
i1
i Yi
donde las Yi son variables aleatorias independientes de
Bernoulli, cada una con p 0.5(Yi 1 corresponde a la
observación con fila i positiva).
a. Determine E(Yi) y luego E(W) utilizando la ecuación
para W. [Sugerencia: Los primeros n enteros positivos
suman n(n 1)/2.]
b. Determine V(Yi) y luego V(W). [Sugerencia: La suma de
los cuadrados de los primeros n enteros positivos puede
expresarse como n(n 1)(2n 1)/6.]
71. En el ejercicio 66, el peso de viga contribuye al momento
de flexión. Suponga que la viga es de espesor y densidad
uniformes, de modo que la carga resultante esté uniforme-
mente distribuida en la viga. Si el peso de ésta es aleatorio,
la carga resultante a consecuencia del peso también es alea-
toria; denote esta carga por W(klb-pies).
a. Si la viga es de 12 pies de largo, W tiene una media de
1.5 y una desviación estándar de 0.25 y las cargas fijas
son como se describen en el inciso a) del ejercicio 66,
¿cuáles son el valor esperado y la varianza del momen-
to de flexión? [Sugerencia: Si la carga originada por la
viga fuera w klb-pies, la contribución al momento de fle-
xión sería w 12
0
x dx.]
b. Si las tres variables (X1, X2 y W) están normalmente dis-
tribuidas, ¿cuál es la probabilidad de que el momento de
flexión será cuando mucho de 200 klb-pies?
72. Tengo tres encargos que atender en el edificio de administra-
ción. Sea Xi el tiempo que requiere el i-ésimo encargo
(i 1, 2, 3) y sea X4 el tiempo total en minutos que me pa-
so caminando hasta y desde el edificio y entre cada encargo.
Suponga que las Xi son independientes y normalmente distri-
buidas con las siguientes medias y desviaciones estándar
1 15, 1 4, 2 5, 2 1, 3 8, 3 2, 4 12,
4 3. Pienso salir de mi oficina precisamente a las 10:00
a.m. y deseo pegar una nota en la puerta que diga “Regreso al-
rededor de las t a.m.”. ¿Qué hora debo escribir si deseo que la
probabilidad de mi llegada después de t sea de 0.01?
73. Suponga que la resistencia a la tensión de acero tipo A es
de 105 klb2
y que la desviación estándar de la resistencia a
la tensión es de 8 klb2
. Para acero tipo B, suponga que la
resistencia a la tensión esperada y la desviación estándar de
la resistencia a la tensión son de 100 klb2
y 6 klb2
, respec-
tivamente. Sea X
la resistencia a la tensión promedio de
una muestra aleatoria de 40 especímenes tipo A y sea Y
la resistencia a la tensión promedio de una muestra aleato-
ria de 35 especímenes tipo B.
a. ¿Cuál es la distribución aproximada de X
? ¿De Y
?
b. ¿Cuál es la distribución aproximada de X
Y
? Justifi-
que su respuesta.
c. Calcule (aproximadamente) P(1 X
Y
1).
d. Calcule P(X
Y
10). Si en realidad observó X
Y
10, dudaría que 1 2 5?
c5_p184-226.qxd 3/12/08 4:08 AM Page 223](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-241-320.jpg)
![224 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
74. En un área de suelo arenoso se plantaron 50 árboles
pequeños de un cierto tipo y otros 50 se plantaron en un
área de suelo arcilloso. Sea X el número de árboles
plantados en suelo arenoso que sobreviven un año y Y el
número de árboles plantados en suelo arcilloso que sobre-
viven un año. Si la probabilidad de que un árbol plantado
en suelo arenoso sobreviva un año es de 0.7 y la probabili-
dad de sobrevivencia de un año en suelo arcilloso es de 0.6,
calcule una aproximación a P(5 X Y 5) (no se
moleste con la corrección de continuidad).
75. Un restaurante sirve tres comidas que cuestan $12, $15 y
$20. Para una pareja seleccionada al azar que está comien-
do en este restaurante, sea X el costo de la comida del
hombre y Y el costo de la comida de la mujer. La función
masa de probabilidad conjunta de X y Y se da en la siguien-
te tabla:
y
p(x, y)
| 12 15 20
12 | 0.05 0.05 0.10
x 15 | 0.05 0.10 0.35
20 | 0 0.20 0.10
a. Calcule las funciones masa de probabilidad marginal de
X y Y.
b. ¿Cuál es la probabilidad de que las comidas del hombre
y la mujer cuesten cuando mucho $15 cada una?
c. ¿Son X y Y independientes? Justifique su respuesta.
d. ¿Cuál es el costo total esperado de la comida de las dos
personas?
e. Suponga que cuando una pareja abre las galletas de la
fortuna al final de la comida, encuentran el mensaje
“Recibirá como reembolso la diferencia entre el costo de
la comida más cara y la menos cara que eligió”. ¿Cuánto
espera reembolsar el restaurante?
76. En una estimación de costos, el costo total de un proyecto
es la suma de los costos de las tareas componentes. Cada
uno de estos costos es una variable aleatoria con distribución
de probabilidad. Se acostumbra obtener información sobre
la distribución de costos total sumando las características
de las distribuciones de costo de componente individuales;
esto se conoce como procedimiento de “despliegue”. Por
ejemplo, E(X1 . . . Xn) E(X1) . . . E(Xn), así que
el procedimiento de despliegue es válido para costo medio.
Suponga que hay dos tareas componentes y que X1 y X2 son
variables aleatorias independientes normalmente distribui-
das. ¿Es válido el procedimiento de despliegue para el 75º
percentil? Es decir, ¿Es el 75º percentil de la distribución de
X1 X2 el mismo que la suma de los 75º percentiles de las
dos distribuciones individuales? Si no, ¿cuál es la relación
entre el percentil de la suma y la suma de los percentiles?
¿Con qué percentiles es válido el procedimiento de desplie-
gue en este caso?
77. Una tienda de comida saludable vende dos marcas diferen-
tes de un tipo de grano. Sea X la cantidad (lb) de la mar-
ca A disponible y Y la cantidad de la marca B, disponible.
Suponga que la función de densidad de probabilidad con-
junta de X y Y es
f(x, y) {kxy x 0, y 0, 20 x y 30
0 de lo contrario
a. Trace la región de densidad positiva y determine el valor
de k.
b. ¿Son X y Y independientes? Responda obteniendo pri-
mero la función de densidad de probabilidad marginal
de cada variable.
c. Calcule P(X Y 25).
d. ¿Cuál es la cantidad total esperada de este grano dis-
ponible?
e. Calcule Cov(X, Y) y Corr(X, Y).
f. ¿Cuál es la varianza de la cantidad total de grano
disponible?
78. Sean X1, X2, . . . , Xn variables aleatorias que denotan n pos-
turas independientes para un artículo que está a la venta.
Suponga que cada Xi está uniformemente distribuida en el
intervalo [100, 200]. Si el vendedor se lo vende al postor más
alto, ¿cuánto puede esperar ganar en la venta? [Sugerencia:
Sea Y máx(X1, X2, . . . , Xn). Primero halle FY(y) observan-
do que Y y si y sólo si cada Xi es y. Luego obtenga la
función de densidad de probabilidad y E(Y).]
79. Suponga que para un individuo, la ingesta de calorías en el
desayuno es una variable aleatoria con valor esperado de
500 y desviación estándar de 50, la ingesta de calorías en el
almuerzo es aleatoria con valor esperado de 900 y desvia-
ción estándar de 100 y la ingesta de calorías en la comida
es una variable aleatoria con valor esperado de 2000 y des-
viación estándar de 180. Suponiendo que las ingestas en las
diferentes comidas son independientes entre sí, ¿cuál es la
probabilidad de que la ingesta de calorías promedio por día
durante el siguiente año (365 días) sea cuando mucho de
3500? [Sugerencia: Sean Xi, Yi y Zi las tres ingestas de calo-
rías en el día i. Entonces la ingesta total es (Xi Yi Zi).]
80. El peso medio del equipaje documentado por un pasajero de
clase turista seleccionado al azar que vuela entre dos ciuda-
des en cierta aerolínea es de 40 lb y la desviación estándar
es de 10 lb. La media y la desviación estándar de un pasa-
jero de clase de negocios son 30 lb y 6 lb, respectivamente.
a. Si hay 12 pasajeros de clase de negocios y 50 de clase
turista en un vuelo particular, ¿cuáles son el valor espe-
rado y la desviación estándar del peso total del equipaje?
b. Si los pesos individuales de los equipajes son variables
aleatorias independientes normalmente distribuidas,
¿cuál es la probabilidad de que el peso total del equipa-
je sea cuando mucho de 2500 lb?
81. Se ha visto que si E(X1) E(X2) . . . E(Xn) ,
entonces E(X1 . . . Xn) n. En algunas aplicacio-
nes, el número de Xi considerado no es un número fijo n
sino una variable aleatoria N. Por ejemplo, sea N el
número de componentes que son traídos a un taller de repa-
ración en un día particular y sea Xi el tiempo de reparación
EJERCICIOS SUPLEMENTARIOS (75-95)
c5_p184-226.qxd 3/12/08 4:08 AM Page 224](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-242-320.jpg)
![Ejercicios suplementarios 225
del i-ésimo componente, entonces el tiempo de reparación
total es X1 X2 . . . XN, la suma de un número aleato-
rio de variables aleatorias. Cuando N es independiente de
las Xi se puede demostrar que
E(X1 . . . XN) E(N)
a. Si el número de componentes traídos en un día particu-
lar es 10 y el tiempo de reparación esperado de un com-
ponente seleccionado al azar es de 40 min, ¿cuál es el
tiempo de reparación total de componentes entregados
en cualquier día particular?
b. Suponga que componentes de un tipo llegan para ser repa-
rados de acuerdo en un proceso de Poisson a razón de cin-
co por hora. El número esperado de defectos por
componente es de 3.5. ¿Cuál es el valor esperado del
número total de defectos en componentes traídos a repara-
ción durante un periodo de cuatro horas? Asegúrese de
indicar cómo su respuesta se deriva del resultado general
que se acaba de dar.
82. Suponga que la proporción de votantes rurales en un estado
que favorecen a un candidato particular es de 0.45 y que la
proporción de votantes suburbanos y urbanos que favorecen
al candidato es de 0.60. Si se obtiene una muestra de 200
votantes rurales y 300 votantes suburbanos y urbanos, ¿cuál
es la probabilidad aproximada de que por lo menos 250
de estos votantes favorezcan a este candidato?
83. Sea el pH verdadero de un compuesto químico. Se reali-
zará una secuencia de n determinaciones de pH muestrales
independientes. Suponga que cada pH muestra es una varia-
ble aleatoria con valor esperado y desviación estándar de
0.1. ¿Cuántas determinaciones se requieren si se desea que
la probabilidad de que el promedio muestral esté dentro
de 0.02 de pH verdadero sea por lo menos de 0.95? ¿Qué
teorema justifica su cálculo de probabilidad?
84. Si la cantidad de refresco que consumo en cualquier día dado
es independiente del consumo en cualquier otro día y está
normalmente distribuido con 13 oz y 2 y en este
momento tengo dos paquetes de seis botellas de 16 oz, ¿cuál
es la probabilidad de que todavía tenga algo de refresco
al cabo de 2 semanas (14 días)?
85. Remítase al ejercicio 58 y suponga que las Xi son indepen-
dientes entre sí y que cada una tiene una distribución nor-
mal. ¿Cuál es la probabilidad de que el volumen total
embarcado sea cuando mucho de 100 000 pies3
?
86. Un estudiante tiene una clase que se supone termina a las
9:00 a.m. y otra que se supone comienza a las 9:10 a.m. Su-
ponga que el tiempo real de terminación de la clase de las
9:00 a.m. es una variable aleatoria normalmente distribuida
X1 con media de 9:02 y desviación estándar de 1.5 min y que
la hora de inicio de la siguiente clase también es una varia-
ble aleatoria normalmente distribuida X2 con media de 9:10
y desviación estándar de un min. Suponga que el tiempo ne-
cesario para ir de un salón de clases al otro es una variable
aleatoria normalmente distribuida X3 con media de
seis min y desviación estándar de un min. ¿Cuál es la proba-
bilidad de que el estudiante llegue a la segunda clase antes
de que comience? (Suponga independencia de X1, X2 y X3,
la cual es razonable si el estudiante no presta atención a la
hora de terminación de la primera clase.)
87. a. Use la fórmula general de la varianza de una combinación
lineal para escribir una expresión para V(aX Y). Luego
si a Y/X, y demuestre que 1. [Sugerencia: La
varianza siempre es 0 y Cov(X, Y) X Y .]
b. Considerando que V(aX Y), concluya que 1.
c. Use el hecho de que V(W) 0 sólo si W es una cons-
tante para demostrar que 1 sólo si Y aX b.
88. Suponga que una calificación oral X y una calificación
cuantitativa Y de un individuo seleccionado al azar en un
examen de aptitud aplicado a nivel nacionalmente tienen
una función de densidad de probabilidad conjunta
f(x, y)
{
2
5
(2x 3y) 0 x 1, 0 y 1
0 de lo contrario
Se le pide que haga una predicción t de la calificación total
X Y del individuo. El error de predicción es la media del
error al cuadrado E[(X Y t)2
]. ¿Qué valor de t reduce al
mínimo el error de predicción?
89. a. Que Xi tenga una distribución ji cuadrada con parámetro
1 (véase la sección 4.4) y que X2 sea independiente de
X1 y que tenga una distribución ji cuadrada con paráme-
tro 2. Use la técnica del ejemplo 5.21 para demostrar
que X1 X2 tiene una distribución ji cuadrada con pará-
metro 1 2.
b. En el ejercicio 71 del capítulo 4, se le pidió que demos-
trara que si Z es una variable normal estándar, entonces
Z2
tiene una distribución ji cuadrada con 1. Sean Z1,
Z2, . . . , Zn n variables aleatorias normales estándar.
¿Cuál es la distribución de Z2
1 . . . Z2
n? Justifique su
respuesta.
c. Sean X1, . . . , Xn una muestra aleatoria de una distribu-
ción normal con media y varianza 2
. ¿Cuál es la dis-
tribución de la suma Y n
i1 [(Xi )/]2
? Justifique
su respuesta.
90. a. Demuestre que Cov(X, Y Z) Cov(X, Y) Cov(X, Z).
b. Sean X1 y X2 calificaciones cuantitativas y orales en un
examen de aptitud y sean Y1 y Y2 calificaciones corres-
pondientes en otro examen. Si Cov(X1, Y1) 5, Cov(X1,
Y2) 1, Cov(X2, Y1) 2 y Cov(X2, Y2) 8, ¿cuál es la
covarianza entre las dos calificaciones totales X1 X2 y
Y1 Y2?
91. Se selecciona al azar y se pesa dos veces un espécimen de roca
de un área particular. Sea W el peso real y X1 y X2 los dos pesos
medidos. Entonces X1 W E1 y X2 W E2, donde E1 y
E2 son los dos errores de medición. Suponga que los Ei son
independientes entre sí y de W y que V(E1) V(E2) 2
E.
a. Exprese , el coeficiente de correlación entre los dos
pesos medidos X1 y X2 en función de 2
W, la varianza
del peso real y 2
x , la varianza del peso medido.
b. Calcule cuando W 1 kg y E 0.01 kg.
92. Sea A el porcentaje de un constituyente en un espécimen de
roca seleccionado al azar y sea B el porcentaje de un segundo
constituyente en ese mismo espécimen. Suponga que D y E
son errores de medición al determinar los valores de A y B de
modo que los valores medidos sea X A D y Y B E,
respectivamente. Suponga que los errores de medición son
independientes entre sí y de los valores reales.
c5_p184-226.qxd 3/12/08 4:08 AM Page 225](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-243-320.jpg)
![226 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias
a. Demuestre que
Corr(X, Y) Corr(A, B) C
o
rr
(X
1,
X
2)
C
o
rr
(Y
1,
Y
2)
donde X1 y X2 son mediciones replicadas del valor de A
y Y1 y Y2 se definen análogamente con respecto a B.
¿Qué efecto tiene la presencia del error de medición en
la correlación?
b. ¿Cuál es valor máximo de Corr(X, Y) cuando Corr(X1,
X2) 0.8100 y Corr(Y1, Y2) 0.9025? ¿Es esto per-
turbador?
93. Sean X1, . . . , Xn variables aleatorias independientes con
valores medios 1, . . . , n y varianzas 2
1, . . . , 2
n.
Considere una función h(x1, . . . , xn) y úsela para definir una
nueva variable aleatoria Y h(X1, . . . , Xn). En condiciones
un tanto generales en cuanto a la función h, si las i son
pequeñas con respecto a las i correspondientes se puede
demostrar que E(Y) h(1, . . . , n) y
V(Y)
2
2
1 . . .
2
2
n
donde cada derivada parcial se evalúa en (x1, . . . , xn)
(1, . . . , n). Suponga tres resistores con resistencias
X1, X2, X3 conectadas en paralelo a través de una batería con
voltaje X4. Luego, según la ley de Ohm, la corriente es
Y X4 X
1
1
X
1
2
X
1
3
Sea 1 10 ohms, 1 1.0 ohms, 2 15 ohms, 2 1.0
ohms, 3 20 ohms, 3 1.5 ohms, 4 120 V, 4 4.0 V.
Calcule el valor esperado aproximado y la desviación están-
dar de la corriente (sugerido por “Random Samplings”,
CHEMTECH, 1984: 696-697).
94. Una aproximación más precisa a E[h(X1, . . . , Xn)] en el
ejercicio 93 es
h(1, . . . , n)
1
2
2
1 . . .
1
2
2
n
Calcule esto con Y h(X1, X2, X3, X4) dada en el ejercicio
93 y compárela con el primer término h(1, . . . , n).
95. Sean X y Y variables aleatorias normales estándar indepen-
dientes y defina una nueva variable aleatoria como U 0.6X
0.8Y.
a. Determine Corr(X, U).
b. ¿Cómo modificaría U para obtener Corr(X, U) con
un valor especificado de ?
,2
h
,x2
n
,2
h
,x2
1
,h
,xn
,h
,x1
Bibliografía
Devore, Jay y Kenneth Berk, Modern Mathematical Statistics
with Applications, Thomson-Brooks/Cole, Belmont, CA,
2007. Una exposición un poco más complicada de temas de
probabilidad que en el presente libro.
Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models
and Applications (2a. ed.). Macmillan, Nueva York, 1994.
Contiene una cuidadosa y amplia exposición de distribuciones
conjuntas, reglas de probabilidad y teoremas de límites.
c5_p184-226.qxd 3/12/08 4:08 AM Page 226](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-244-320.jpg)
![6.1 Algunos conceptos generales de estimación puntual 229
Ejemplo 6.1
Ejemplo 6.2
muestral X
”. La proposición “la estimación puntual de es 5.77” se escribe concisamente
como ˆ
5.77. Obsérvese que cuando se escribe ˆ 72.5, no hay ninguna indicación
de cómo se obtuvo esta estimación puntual (qué estadístico se utilizó). Se recomienda repor-
tar tanto el estimador como la estimación resultante.
Un fabricante automotriz ha producido un nuevo tipo de defensa, la que se presume absor-
be impactos con menos daño que las defensas previas. El fabricante ha utilizado esta defen-
sa en una secuencia de 25 choques controlados con un muro, cada uno a 10 mph, utilizando
uno de sus modelos de carro compacto. Sea X el número de choques que no provocaron
daños visibles al automóvil. El parámetro que tiene que ser estimado es p la proporción
de todos los choques que no provocaron daños [alternativamente, p P(ningún daño en un
choque)]. Si se observa que X es x 15, el estimador y estimación más razonables son
estimador p̂
X
n
estimación
n
x
1
2
5
5
0.60 ■
Si por cada parámetro de interés hubiera sólo un estimador puntual razonable, no
habría mucho para la estimación puntual. En la mayoría de los problemas, sin embargo, habrá
más de un estimador razonable.
Reconsidere las 20 observaciones adjuntas de voltaje de ruptura dieléctrica de piezas de
resina epóxica introducidas por primera vez en el ejemplo 4.30 (sección 4.6).
24.46 25.61 26.25 26.42 26.66 27.15 27.31 27.54 27.74 27.94
27.98 28.04 28.28 28.49 28.50 28.87 29.11 29.13 29.50 30.88
El patrón en la gráfica de probabilidad normal dado allí es bastante recto, así que ahora se
supone que la distribución de voltaje de ruptura es normal con valor medio . Como las dis-
tribuciones normales son simétricas, también es la vida útil mediana de la distribución. Se
supone entonces que las observaciones dadas son el resultado de una muestra aleatoria X1,
X2, . . . , X20 de esta distribución normal. Considere los siguientes estimadores y las estima-
ciones resultantes de :
a. Estimador X
, estimación x
xi /n 555.86/20 27.793
b. Estimador , estimación (27.94 27.98)/2 27.960
c. Estimador [mín(Xi) máx(Xi)]/2 el promedio de las dos vidas útiles extremas, esti-
mación [mín(xi) máx(xi)]/2 (24.46 30.88)/2 27.670
d. Estimador X
tr(10), la media 10% recortada (desechar el 10% más pequeño y más gran-
de de la muestra y luego promediar).
estimación x
tr(10)
27.838
Cada uno de los estimadores a) al d) utiliza una medición diferente del centro de la mues-
tra para estimar . ¿Cuál de las estimaciones se acerca más al valor verdadero? No se puede
responder esta pregunta sin conocer el valor verdadero. Una pregunta que se puede hacer es:
“¿Cuál estimador, cuando se utiliza en otras muestras de Xi, tiende a producir estimaciones
cercanas al valor verdadero? En breve se considerará este tipo de pregunta. ■
555.86 24.46 25.61 29.50 30.88
16
x
|
X
|
c6_p227-253.qxd 3/12/08 4:12 AM Page 229](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-247-320.jpg)
![En el futuro inmediato habrá un creciente interés por desarrollar aleaciones de Mg de bajo
costo para varios procesos de fundición. Es por consiguiente importante contar con formas
prácticas de determinar varias propiedades mecánicas de esas aleaciones. El artículo “On
the Development of a New Approach for the Determination of Yield Strength in Mg-based
Alloys” (Light Metal Age, octubre de 1998: 50-53) propuso un método ultrasónico para este
propósito. Considere la siguiente muestra de observaciones de módulo elástico (GPa) de
especímenes de aleación AZ91D tomados de un proceso de fundición a troquel:
44.2 43.9 44.7 44.2 44.0 43.8 44.6 43.1
Suponga que estas observaciones son el resultado de una muestra aleatoria X1, . . . , X8 toma-
da de la distribución de población de módulos elásticos en semejantes circunstancias. Se
desea estimar la varianza de la población 2
. Un estimador natural es la varianza muestral:
ˆ
2
S2
(
n
Xi
1
X
)2
La estimación correspondiente es
ˆ
2
s2
0.25125 0.251
La estimación de sería entonces ˆ
s 0
.
2
5
1
2
5
0.501.
Si se utiliza el divisor n en lugar de n 1 se obtendría un estimador alternativo (es
decir, la desviación al cuadrado promedio):
ˆ
2
estimación
1.75
8
875
0.220
En breve se indicará por qué muchos estadísticos prefieren S2
al estimador con divisor n. ■
En el mejor de todos los mundos posibles, se podría hallar un estimador ˆ con el cual
ˆ siempre. Sin embargo, ˆ es una función de las Xi muestrales, así que es una variable
aleatoria. Con algunas muestras, ˆ dará un valor más grande que , mientras que con otras
muestras ˆ subestimará . Si se escribe
ˆ error de estimación
entonces un estimador preciso sería uno que produzca errores de estimación pequeños, así
que los valores estimados se aproximarán al valor verdadero.
Una forma sensible de cuantificar la idea de ˆ cercano a es considerar el error al
cuadrado (ˆ )2
. Con algunas muestras, ˆ se acercará bastante a y el error al cuadrado
se aproximará a 0. Otras muestras pueden dar valores de ˆ alejados de , correspondientes
a errores al cuadrado muy grandes. Una medida general de precisión es el error cuadrático
medio ECM E[(ˆ )2
]. Si un primer estimador tiene una media del error al cuadrado
más pequeña que un segundo, es natural decir que el primer estimador es el mejor. Sin
embargo, el error cuadrático medio en general dependerá del valor de . Lo que a menudo
sucede es que un estimador tendrá una media del error al cuadrado más pequeña con algu-
nos valores de y una media del error al cuadrado más grande con otros valores. En gene-
ral no es posible determinar un estimador con el error cuadrático medio mínimo.
Una forma de librarse de este dilema es limitar la atención sólo en estimadores que
tengan una propiedad deseable específica y luego determinar el mejor estimador en este
grupo limitado. Una propiedad popular de esta clase en la comunidad estadística es el inses-
gamiento.
(Xi X
)2
n
15533.79 (352.5)2
/8
7
x2
i (xi)2
/8
7
X2
i (Xi)2
/n
n 1
230 CAPÍTULO 6 Estimación puntual
Ejemplo 6.3
c6_p227-253.qxd 3/12/08 4:12 AM Page 230](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-248-320.jpg)
![Suponga que X, el tiempo de reacción a un estímulo, tiene una distribución uniforme en el
intervalo desde 0 hasta un límite superior desconocido (por tanto la función de densidad
de X es rectangular con altura 1/ en el intervalo 0 x ). Se desea estimar con base
en una muestra aleatoria X1, X2, . . . , Xn de los tiempos de reacción. Como es el tiempo
más grande posible en toda la población de tiempos de reacción, considere como un primer
estimador el tiempo de reacción muestral más grande ˆ
1 máx(X1, . . . , Xn). Si n 5 y
x1 4.2, x2 1.7, x3 2.4, x4 3.9, x5 1.3, la estimación puntual de es ˆ
1 máx(4.2,
1.7, 2.4, 3.9, 1.3) 4.2.
El insesgamiento implica que algunas muestras darán estimaciones que exceden y
otras que darán estimaciones más pequeñas que , de lo contrario posiblemente no podría
ser el centro (punto de equilibrio) de la distribución de ˆ
1. Sin embargo, el estimador pro-
puesto nunca sobrestimará (el valor muestral más grande no puede exceder el valor de la
población más grande) y subestimará a menos que el valor muestral más grande sea igual
a . Este argumento intuitivo demuestra que ˆ
1 es un estimador sesgado. Más precisamente,
se puede demostrar (véase el ejercicio 32) que
E(ˆ
1)
n
n
1
como
n
n
1
1
n /(n 1) /(n 1) da el sesgo de ˆ
1, el cual tiende a 0 a medida que n se hace
grande.
Es fácil modificar ˆ
1 para obtener un estimador insesgado de . Considere el estimador
ˆ
2
n
n
1
máx(X1, . . . , Xn)
Utilizando este estimador en los datos se obtiene la estimación (6/5)(4.2) 5.04. El hecho
de que (n 1)/n 1 implica que ˆ
2 sobrestimará con algunas muestras y subestimará
otras. El valor medio de este estimador es
E(ˆ
2) E
n
n
1
máx(X1, . . . , Xn)
n
n
1
E[máx(X1, . . . , Xn)]
n
n
1
n
n
1
Si ˆ
2 se utiliza repetidamente en diferentes muestras para estimar , algunas estimaciones
serán demasiado grandes y otras demasiado pequeñas, pero a la larga no habrá ninguna ten-
dencia simétrica a subestimar o sobreestimar . ■
232 CAPÍTULO 6 Estimación puntual
Ejemplo 6.4
Principio de estimación insesgada
Cuando se elige entre varios estimadores diferentes de , se elige uno insesgado.
PROPOSICIÓN Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución con media y varian-
za 2
. Entonces el estimador
ˆ
2
S2
es un estimador insesgado de 2
.
(Xi X
)2
n 1
De acuerdo con este principio, el estimador insesgado ˆ
2 en el ejemplo 6.4 deberá ser
preferido al estimador sesgado ˆ
1. Considérese ahora el problema de estimar 2
.
c6_p227-253.qxd 3/12/08 4:12 AM Page 232](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-250-320.jpg)
![Comprobación Para cualquier variable aleatoria Y, V(Y) E(Y2
) [E(Y)]2
, por lo tanto
E(Y2
) V(Y) [E(Y)]2
. Aplicando esto a
S2
n
1
1 X2
i
se obtiene
E(S2
)
n
1
1
E(X2
i )
1
n
E[(Xi)2
]
n
1
1
(2
2
)
1
n
{V(Xi) [E(Xi)]2
}
n
1
1
n2
n2
1
n
n2
1
n
(n)2
n
1
1
{n2
2
} 2
(como se desea) ■
El estimador que utiliza el divisor n se expresa como (n 1)S2
/n, por lo tanto
E
n
n
1
E(S2
)
n
n
1
2
Este estimador es por consiguiente sesgado. El sesgo es (n 1)2
/n 2
2
/n. Como
el sesgo es negativo, el estimador con divisor n tiende a subestimar 2
y por eso muchos
estadísticos prefieren el divisor n 1 (aunque cuando n es grande, el sesgo es pequeño y
hay poca diferencia entre los dos).
Aun cuando S2
es insesgado para 2
, S es un estimador sesgado de (su sesgo
es pequeño a menos que n sea bastante pequeño). Sin embargo, existen otras buenas
razones para utilizar S como estimador, en especial cuando la distribución de la población
es normal. Éstas se volverán más aparentes cuando se discutan los intervalos de confianza
y la prueba de hipótesis en los siguientes capítulos.
En el ejemplo 6.2, se propusieron varios estimadores diferentes de la media de una
distribución normal. Si hubiera un estimador insesgado único para , el problema de esti-
mación se resolvería utilizando dicho estimador. Desafortunadamente, éste no es el caso.
(n 1)S2
n
(Xi)2
n
6.1 Algunos conceptos generales de estimación puntual 233
PROPOSICIÓN Si X1, X2, . . . , Xn es una variable aleatoria tomada de una distribución con media ,
entonces X
es un estimador insesgado de . Si además la distribución es continua y
simétrica, entonces y cualquier media recortada también son estimadores insesga-
dos de .
X
|
El hecho de que X
sea insesgado es simplemente un replanteamiento de una de las reglas de
valor esperado: E(X
) con cada valor posible de (para distribuciones discretas y con-
tinuas). El insesgamiento de los demás estimadores es más difícil de verificar.
El siguiente ejemplo introduce otra situación en la cual existen varios estimadores
insesgados para un parámetro particular.
En ciertas circunstancias contaminantes, orgánicos se adhieren con facilidad a las superfi-
cies de obleas y deterioran los dispositivos de fabricación de semiconductores. El artículo
“Ceramic Chemical Filter for Removal of Organic Contaminants” (J. of the Institute of
Environmental Sciences and Technology, 2003: 59-65) discutió una alternativa reciente-
mente desarrollada de filtros de carbón convencionales para eliminar contaminación
molecular transportada por el aire en aplicaciones de cuartos limpios. Un aspecto de la
investigación del desempeño de filtros implicó estudiar cómo se relaciona la concentración
de contaminantes en aire con la concentración en las superficies de obleas después de una
Ejemplo 6.5
c6_p227-253.qxd 3/12/08 4:12 AM Page 233](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-251-320.jpg)
![6.1 Algunos conceptos generales de estimación puntual 235
Tanto en el ejemplo anterior como en la situación que implica estimar una media de pobla-
ción normal, el principio de insesgamiento (prefiere un estimador insesgado a uno sesgado)
no puede ser invocado para seleccionar un estimador. Lo que ahora se requiere es un crite-
rio para elegir entre estimadores insesgados.
Estimadores con varianza mínima
Supóngase que ˆ
1 y ˆ
2 son dos estimadores de insesgados. Entonces, aunque la distribu-
ción de cada estimador esté centrada en el valor verdadero de , las dispersiones de las dis-
tribuciones en torno al valor verdadero pueden ser diferentes.
La figura 6.3 ilustra las funciones de densidad de probabilidad de los dos estimadores
insesgados, donde ˆ1 tiene una varianza más pequeña que ˆ
2. Entonces es más probable que ˆ
1
produzca una estimación próxima al valor verdadero que ˆ
2. El estimador insesgado con
varianza mínima es, en cierto sentido, el que tiene más probabilidades entre todos los esti-
madores insesgados de producir una estimación cercana al verdadero .
En el ejemplo 6.5, supóngase que cada Yi está normalmente distribuida con media xi y va-
rianza 2
(la suposición de varianza constante). Entonces se puede demostrar que el tercer
estimador ˆ
xi Yi /x2
i no sólo tiene una varianza más pequeña que cualquiera de los
otros dos estimadores insesgados, sino que de hecho es el estimador insesgado con varian-
za mínima, tiene una varianza más pequeña que cualquier otro estimador insesgado de .
En el ejemplo 6.4 se argumentó que cuando X1, . . . , Xn es una variable aleatoria tomada de
una distribución uniforme en el intervalo [0, ], el estimador
ˆ
1
n
n
1
máx(X1, . . . , Xn)
es insesgado para (previamente este estimador se denotó por ˆ
2 ). Este no es el único esti-
mador insesgado de . El valor esperado de una variable aleatoria uniformemente distribuida
es simplemente el punto medio del intervalo de densidad positiva, por lo tanto E(Xi) /2. Es-
to implica que E(X
) /2, a partir de la cual E(2X
) . Es decir, el estimador 2 2X
es in-
sesgado para .
Si X está uniformemente distribuida en el intervalo A, B, en ese caso V(X) 2
(B A)2
/12. Así pues, en esta situación, V(Xi) 2
/12, V(X
) 2
/n 2
/(12n) y
V(ˆ
2) V(2X
) 4V(X
) 2
/(3n). Se pueden utilizar los resultados del ejercicio 32 para
Principio de estimación insesgada con varianza mínima
Entre todos los estimadores de insesgados, se selecciona el de varianza mínima. El
ˆ resultante se llama estimador insesgado con varianza mínima (EIVM) de .
Ejemplo 6.6
Función de densidad de probabilidad de 2
^
Función de densidad de probabilidad de 1
^
Figura 6.3 Gráficas de las funciones de densidad de probabilidad de dos estimadores
insesgados diferentes.
c6_p227-253.qxd 3/12/08 4:12 AM Page 235](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-253-320.jpg)
![236 CAPÍTULO 6 Estimación puntual
demostrar que V(ˆ
1) 2
/[n(n 2)]. El estimador ˆ
1 tiene una varianza más pequeña que
ˆ
2 si 3n n(n 2), es decir, si 0 n2
n n(n 1). En tanto n 1, V(ˆ
1) V(ˆ
2), así
que ˆ
1 es mejor estimador que ˆ
2. Se pueden utilizar métodos más avanzados para demos-
trar que ˆ
1 es el estimador insesgado con varianza mínima de , cualquier otro estimador
insesgado de tiene una varianza que excede 2
/[n(n 2)]. ■
Uno de los triunfos de la estadística matemática ha sido el desarrollo de una metodo-
logía para identificar el estimador insesgado con varianza mínima en una amplia variedad
de situaciones. El resultado más importante de este tipo para nuestros propósitos tiene que
ver con la estimación de la media de una distribución normal.
Siempre que exista la seguridad de que la población que se está muestreando es normal, el
resultado dice que X
debería usarse para estimar . Entonces, en el ejemplo 6.2 la estima-
ción sería x
27.793.
En algunas situaciones, es posible obtener un estimador con sesgo pequeño que se
preferiría al mejor estimador insesgado. Esto se ilustra en la figura 6.4. Sin embargo, los
estimadores insesgados con varianza mínima a menudo son más fáciles de obtener que el
tipo de estimador sesgado cuya distribución se ilustra.
TEOREMA Sean X1, . . . , Xn una muestra aleatoria tomada de una distribución normal con pará-
metros y . Entonces el estimador ˆ
X
es el estimador insesgado con varianza
mínima para .
^
Función de densidad de probabilidad
de 2, el estimador insesgado con varianza mínima
Función de densidad de probabilidad
de 1, un estimador sesgado
^
Figura 6.4 Un estimador sesgado que es preferible al estimador insesgado con varianza mínima.
Algunas complicaciones
El último teorema no dice que al estimar la media de una población, se deberá utilizar el
estimador X
independientemente de la distribución que se está muestreando.
Suponga que se desea estimar la conductividad térmica de un material. Con técnicas de
medición estándar, se obtendrá una muestra aleatoria X1, . . . , Xn de n mediciones de con-
ductividad térmica. Suponga que la distribución de la población es un miembro de una de
las siguientes tres familias:
f(x) e(x)2
/(2 2
)
' x ' (6.1)
f(x)
[1 (
1
x )2
]
' x ' (6.2)
f(x)
{2
1
c
c x c
(6.3)
0 de lo contrario
1
2
2
Ejemplo 6.7
c6_p227-253.qxd 3/12/08 4:12 AM Page 236](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-254-320.jpg)
![Como los n componentes duran hasta Y1, n 1 duran una cantidad de tiempo adicional
Y2 Y1 adicional y n 2, duran una cantidad de tiempo Y3 Y2 adicional, y así sucesiva-
mente, otra expresión para Tr es
Tr nY1 (n 1)(Y2 Y1) (n 2)(Y3 Y2)
(n r 1)(Yr Yr1)
Pero Y1 es el mínimo de n variables exponenciales, por tanto E(Y1) 1/(n). Asimismo,
Y2 Y1 es la más pequeña de las n 1 vidas útiles restantes, cada exponencial con
parámetro (según la propiedad de amnesia), así que E(Y2 Y1) 1/[(n 1)].
Continuando, E(Yi1 Yi) 1/[(n i)], así que
E(Tr ) nE(Y1) (n 1)E(Y2 Y1) (n r 1)E(Yr Yr 1)
n
n
1
(n 1)
(n
1
1)
(n r 1)
(n r
1
1)
r
Por consiguiente, E(Tr /r) (1/r)E(Tr ) (1/r) (r/) 1/ como se dijo.
Como un ejemplo, supónganse que se prueban 20 componentes y r 10. Entonces
si los primeros diez tiempos de falla son 11, 15, 29, 33, 35, 40, 47, 55, 58 y 72, la estima-
ción de es
ˆ
111.5
La ventaja del experimento con censura es que termina más rápido que el experimen-
to sin censura. Sin embargo, se puede demostrar que V(Tr/r) 1/(2
r), la cual es más gran-
de que 1/(2
n), la varianza de X
en el experimento sin censura. ■
Reporte de una estimación puntual: el error estándar
Además de reportar el valor de una estimación puntual, se debe dar alguna indicación de su
precisión. La medición usual de precisión es el error estándar del estimador usado.
11 15 72 (10)(72)
10
238 CAPÍTULO 6 Estimación puntual
Ejemplo 6.9
(continuación
del ejemplo
6.2)
Suponiendo que el voltaje de ruptura está normalmente distribuido, ˆ
X
es la mejor esti-
mación de . Si se sabe que el valor de es 1.5, el error estándar de X
es X
/n
1.5/2
0
0.335. Si, como casi siempre es el caso, el valor de es desconocido, la esti-
mación ˆ
s 1.462 se sustituye en X
para obtener el error estándar estimado ˆ
X
sX
s/n
1.462/2
0
0.327. ■
El error estándar de p̂ X/n es
p̂ V
(X
/n
)
V
n
(X
2
)
n
n
p
2
q
p
n
q
Como p y q 1 p son desconocidas (¿de otro modo por qué estimar?), se sustituye p̂
x/n y q̂ 1 x/n en p̂ para obtener el error estándar estimado ˆ
p̂ p̂
q̂/
n
DEFINICIÓN El error estándar de un estimador ˆ es su desviación estándar ˆ V
(ˆ
)
. Si el error
estándar implica parámetros desconocidos cuyos valores pueden ser estimados, la
sustitución de estas estimaciones en ˆ da el error estándar estimado (desviación
estándar estimada) del estimador. El error estándar estimado puede ser denotado o por
ˆ
ˆ (el ^ sobre recalca que ˆ está siendo estimada) o por sˆ.
Ejemplo 6.10
(continuación
del ejemplo
6.1)
c6_p227-253.qxd 3/12/08 4:13 AM Page 238](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-256-320.jpg)
![* 0.02153 y la desviación estándar muestral de estas 100 estimaciones es sˆ
0.0091.
La estimación bootstrap del error estándar de ˆ
. Un histograma de los 100 ˆ
*
i resultó un tan-
to positivamente asimétrico lo que sugiere que la distribución muestral de ˆ
también tiene
esta propiedad. ■
En ocasiones un investigador desea estimar una característica poblacional sin suponer
que la distribución de la población pertenece a una familia paramétrica particular. Una ins-
tancia de esto ocurrió en el ejemplo 6.7, cuando una media 10% recortada fue propuesta
para estimar el centro de la distribución de la población simétrica. Los datos del ejemplo
6.2 dieron ˆ x
rec(10) 27.838 pero ahora no hay ninguna f(x; ) supuesta, por consiguiente
¿cómo se puede obtener una muestra bootstrap? La respuesta es considerar la muestra como
que constituye la población (las n 20 observaciones en el ejemplo 6.2) y considerar B
muestras diferentes, cada una de tamaño n, con reemplazo de esta población. El libro de
Bradley Efron y Robert Tibshirani o el de John Rice incluidos en la bibliografía del capítu-
lo proporcionan más información.
240 CAPÍTULO 6 Estimación puntual
EJERCICIOS Sección 6.1 (1-19)
1. Los datos adjuntos sobre resistencia a la flexión (MPa) de
vigas de concreto de un tipo se introdujeron en el ejemplo 1.2.
5.9 7.2 7.3 6.3 8.1 6.8 7.0
7.6 6.8 6.5 7.0 6.3 7.9 9.0
8.2 8.7 7.8 9.7 7.4 7.7 9.7
7.8 7.7 11.6 11.3 11.8 10.7
a. Calcule una estimación puntual del valor medio de resis-
tencia de la población conceptual de todas las vigas
fabricadas de esta manera y diga qué estimador utilizó:
[Sugerencia: xi 219.8.]
b. Calcule una estimación puntual del valor de resistencia
que separa el 50% más débil de dichas vigas del 50%
más resistente y diga qué estimador se utilizó.
c. Calcule e interprete una estimación puntual de la des-
viación estándar de la población . ¿Qué estimador uti-
lizó? [Sugerencia: x2
i 1860.94.]
d. Calcule una estimación puntual de la proporción de las
vigas cuya resistencia a la flexión exceda de 10 MPa.
[Sugerencia: Considere una observación como “éxito” si
excede de 10.]
e. Calcule una estimación puntual del coeficiente de varia-
ción de la población / y diga qué estimador utilizó.
2. Una muestra de 20 estudiantes que recientemente tomaron un
curso de estadística elemental arrojó la siguiente información
sobre la marca de calculadora que poseían. (T Texas
Instruments, H Hewlett Packard, C Casio, S Sharp):
T T H T C T T S C H
S S T H C T T T H T
a. Estime la proporción verdadera de los estudiantes que
poseen una calculadora Texas Instruments.
b. De los 10 estudiantes que poseían una calculadora TI, 4
tenían calculadoras con graficación. Estime la propor-
ción de estudiantes que no poseen una calculadora con
graficación TI.
3. Considere la siguiente muestra de observaciones sobre
espesor de recubrimiento de pintura de baja viscosidad
(“Achieving a Target Value for a Manufacturing Process: A
Case Study”, J. of Quality Technology, 1992: 22-26):
0.83 0.88 0.88 1.04 1.09 1.12 1.29 1.31
1.48 1.49 1.59 1.62 1.65 1.71 1.76 1.83
Suponga que la distribución del espesor de recubrimiento es
normal (una gráfica de probabilidad normal soporta fuerte-
mente esta suposición).
a. Calcule la estimación puntual de la mediana del espesor
de recubrimiento y diga qué estimador utilizó.
b. Calcule una estimación puntual de la mediana de la dis-
tribución del espesor de recubrimiento y diga qué esti-
mador utilizó.
c. Calcule la estimación puntual del valor que separa el
10% más grande de todos los valores de la distribución
del espesor del 90% restante y diga qué estimador utili-
zó. [Sugerencia: Exprese lo que está tratando de estimar
en función de y .]
d. Estime P(X 1.5), es decir, la proporción de todos los
valores de espesor menores que 1.5 [Sugerencia: Si
conociera los valores de y podría calcular esta pro-
babilidad. Estos valores no están disponibles, pero pue-
den ser estimados.]
e. ¿Cuál es el error estándar estimado del estimador que
utilizó en el inciso b)?
4. El artículo del cual se extrajeron los datos en el ejercicio 1
también dio las observaciones de resistencias adjuntas de
cilindros:
6.1 5.8 7.8 7.1 7.2 9.2 6.6 8.3 7.0 8.3
7.8 8.1 7.4 8.5 8.9 9.8 9.7 14.1 12.6 11.2
c6_p227-253.qxd 3/12/08 4:13 AM Page 240](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-258-320.jpg)
![Antes de obtener los datos, denote las resistencias de vigas
mediante X1, . . . , Xm y Y1, . . . , Yn las resistencias de cilindros.
Suponga que las Xi constituyen una muestra aleatoria de
una distribución con media 1 y desviación estándar 1 y
que las Yi forman una muestra aleatoria (independiente de
las Xi) de otra distribución con media 2 y desviación están-
dar 2.
a. Use las reglas de valor esperado para demostrar que
X
Y
es un estimador insesgado de 1 2. Calcule la
estimación con los datos dados.
b. Use las reglas de varianza del capítulo 5 para obtener
una expresión para la varianza y desviación estándar
(error estándar) del estimador del inciso a) y luego calcule
el error estándar estimado.
c. Calcule una estimación puntual de la razón 1/2 de las
dos desviaciones estándar.
d. Suponga que se seleccionan al azar una sola viga y un
solo cilindro. Calcule una estimación puntual de la va-
rianza de la diferencia X Y entre la resistencia de las
vigas y la resistencia de los cilindros.
5. Como ejemplo de una situación en la que varios estadísti-
cos diferentes podrían ser razonablemente utilizados para
calcular una estimación puntual, considere una población
de N facturas. Asociado con cada factura se encuentra su
“valor en libros”, la cantidad anotada de dicha factura. Sea
T el valor en libros total, una cantidad conocida. Algunos de
estos valores en libros son erróneos. Se realizará una audito-
ría seleccionando al azar n facturas y determinando el valor
auditado (correcto) para cada una. Suponga que la muestra da
los siguientes resultados (en dólares).
Sea
Y
valor en libros medio muestral
X
valor auditado medio muestral
D
error medio muestral
Proponga tres estadísticos diferentes para estimar el valor
total (correcto) auditado: uno que implique exactamente N y
X
, otro que implique T, N y D
y el último que implique T
y X
/Y
. Si N 5000 y T 1761300, calcule las tres estima-
ciones puntuales correspondientes. (El artículo “Statistical
Models and Analysis in Auditing”, Statistical Science, 1989:
2-33, discute propiedades de estos tres estimadores.)
6. Considere las observaciones adjuntas sobre el flujo de una
corriente de agua (miles de acres-pies) registradas en una esta-
ción en Colorado durante el periodo del 1 de abril al 31 de
agosto durante 31 años (tomadas de un artículo que apareció
en el volumen 1974 de Water Resources Research).
127.96 210.07 203.24 108.91 178.21
285.37 100.85 89.59 185.36 126.94
200.19 66.24 247.11 299.87 109.64
125.86 114.79 109.11 330.33 85.54
117.64 302.74 280.55 145.11 95.36
204.91 311.13 150.58 262.09 477.08
94.33
Una gráfica de probabilidad apropiada soporta el uso de la
distribución lognormal (véase la sección 4.5) como modelo
razonable de flujo de corriente de agua.
a. Calcule los parámetros de la distribución [Sugerencia:
Recuerde que X tiene una distribución lognormal con
parámetros y 2
si ln(X) está normalmente distribuida
con media y varianza 2
.]
b. Use las estimaciones del inciso a) para calcular una esti-
mación del valor esperado del flujo de corriente de agua
[Sugerencia: ¿Cuál es E(X)?]
7. a. Se selecciona una muestra de 10 casas en un área particu-
lar, cada una de las cuales se calienta con gas natural y se
determina la cantidad de gas (termias) utilizada por cada
casa durante el mes de enero. Las observaciones resultan-
tes son 103, 156, 118, 89, 125, 147, 122, 109, 138, 99. Sea
el consumo de gas promedio durante enero de todas las
casas del área. Calcule una estimación puntual de .
b. Suponga que hay 10 000 casas en esta área que utilizan
gas natural para calefacción. Sea la cantidad total de gas
consumido por todas estas casas durante enero. Calcule
con los datos del inciso a). ¿Qué estimador utilizó para
calcular su estimación?
c. Use los datos del inciso a) para estimar p, la proporción
de todas las casas que usaron por lo menos 100 termias.
d. Proporcione una estimación puntual de la mediana de la
población usada (el valor intermedio en la población de
todas las casas) basada en la muestra del inciso a). ¿Qué
estimador utilizó?
8. En una muestra aleatoria de 80 componentes de un tipo, se
encontraron 12 defectuosos.
a. Dé una estimación puntual de la proporción de todos los
componentes que no están defectuosos.
b. Se tiene que construir un sistema seleccionando al azar
dos de estos componentes y conectándolos en serie,
como se muestra a continuación.
La conexión en serie implica que el sistema funcionará siem-
pre y cuando ningún componente esté defectuoso (es decir,
ambos componentes funcionan apropiadamente). Estime la
proporción de todos los sistemas que funcionan de manera
apropiada. [Sugerencia: Si p denota la probabilidad de que el
componente funcione apropiadamente, ¿cómo puede ser
expresada P(el sistema funciona) en función de p?]
9. Se examina cada uno de 150 artículos recién fabricados y se
anota el número de rayones por artículo (se supone que los
artículos están libres de rayones) y se obtienen los siguien-
tes datos:
6.1 Algunos conceptos generales de estimación puntual 241
Factura
1 2 3 4 5
Valor en libros 300 720 526 200 127
Valor auditado 300 520 526 200 157
Error 0 200 0 0 30
c6_p227-253.qxd 3/12/08 4:13 AM Page 241](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-259-320.jpg)
![Sea X el número de rayones en un artículo seleccionado
al azar y suponga que X tiene una distribución de Poisson
con parámetro .
a. Determine un estimador insesgado de y calcule la esti-
mación de los datos. [Sugerencia: E(X) para una
distribución Poisson de X, por lo tanto E(X
) ?]
b. ¿Cuál es la desviación estándar (error estándar) de su
estimador? Calcule el error estándar estimado.
[Sugerencia: 2
X con distribución de Poisson de X.]
10. Con una larga varilla de longitud , va a trazar una curva
cuadrada en la cual la longitud de cada lado es . Por con-
siguiente el área de la curva será 2
. Sin embargo, no cono-
ce el valor de así que decide hacer n mediciones
independientes X1, X2, . . . , Xn de la longitud. Suponga que
cada Xi tiene una media (mediciones insesgadas) y
varianza 2
.
a. Demuestre que X
2
no es un estimador insesgado de 2
.
[Sugerencia: Con cualquier variable aleatoria Y, E(Y2
)
V(Y) [E(Y)]2
. Aplique ésta con Y X
.]
b. ¿Con qué valor de k es el estimador X
2
kS2
insesgado
para 2
? [Sugerencia: Calcule E(X
2
kS2
).]
11. De n1 fumadores seleccionados al azar, X1 fuman cigarrillos
con filtro, mientras que de n2 fumadoras seleccionadas al
azar, X2 fuman cigarrillos con filtro. Sean p1 y p2 las proba-
bilidades de que un varón y una mujer seleccionados al
azar, fumen, respectivamente, cigarrillos con filtro.
a. Demuestre que (X1/n1) (X2/n2) es un estimador inses-
gado de p1 p2. [Sugerencia: E(Xi) ni pi con i 1, 2.]
b. ¿Cuál es el error estándar del estimador en el inciso a)?
c. ¿Cómo utilizaría los valores observados x1 y x2 para esti-
mar el error estándar de su estimador?
d. Si n1 n2 200, x1 127 y x2 176, use el estimador
del inciso a) para obtener una estimación de p1 p2.
e. Use el resultado del inciso c) y los datos del inciso d)
para estimar el error estándar del estimador.
12. Suponga que un tipo de fertilizante rinde 1 por acre con
varianza 2
, mientras que el rendimiento esperado de un
segundo tipo de fertilizante es 2, con la misma varianza 2
.
Sean S2
1 y S2
2 las varianzas muestrales de rendimientos basa-
das en tamaños muestrales n1 y n2, respectivamente, de los
dos fertilizantes. Demuestre que el estimador combinado es
ˆ
2
es un estimador insesgado de 2
.
13. Considere una muestra aleatoria de X1, . . . , Xn de la fun-
ción de densidad de probabilidad
f(x; ) 0.5(1 x) 1 x 1
donde 1 1 (esta distribución se presenta en la física
de partículas. Demuestre que ˆ 3X
es un estimador inses-
gado de . [Sugerencia: Primero determine E(X) E(X
).]
14. Una muestra de n aviones de combate Pandemonium cap-
turados tienen los números de serie x1, x2, x3, . . . , xn. La
CIA sabe que los aviones fueron numerados consecutivamen-
te en la fábrica comenzando con y terminando con , por lo
que el número total de aviones fabricados es 1
(p. ej., si 17 y 29, entonces 29 17 1 13
aviones con números de serie 17, 18, 19, . . . , 28, 29 fueron
fabricados). Sin embargo, la CIA no conoce los valores de
y . Un estadístico de la CIA sugiere utilizar el estimador
máx(Xi) mín(Xi) 1 para estimar el número total de
aviones fabricados.
a. Si n 5, x1 237, x2 375, x3 202, x4 525 y
x5 418, ¿cuál es la estimación correspondiente?
b. ¿En qué condiciones de la muestra será el valor de la esti-
mación exactamente igual al número total verdadero de
aviones? ¿Alguna vez será más grande la estimación que
el total verdadero? ¿Piensa que el estimador es insesgado
para estimar 1? Explique en una o dos oraciones.
15. Si X1, X2, . . . , Xn representan una muestra aleatoria toma-
da de una distribución de Rayleigh con función de densidad
de probabilidad
f(x; )
x
e x2/(2 )
x 0
a. Se puede demostrar que E(X2
) 2 . Use este hecho
para construir un estimador insesgado de basado en
X2
i (y use reglas de valor esperado para demostrar que
es insesgado).
b. Calcule a partir de las siguientes n 10 observacio-
nes de esfuerzo vibratorio de un aspa de turbina en con-
diciones específicas:
16.88 10.23 4.59 6.66 13.68
14.23 19.87 9.40 6.51 10.95
16. Suponga que el crecimiento promedio verdadero de un tipo
de planta durante un periodo de un año es idéntico al de un
segundo tipo, aunque la varianza del crecimiento del primer
tipo es 2
, en tanto que para el segundo tipo, la varianza es
42
. Sean X1, . . . , Xm, m observaciones de crecimiento inde-
pendientes del primer tipo [por consiguiente E(Xi) , V(Xi)
2
] y sean Y1, . . . , Yn, n observaciones de crecimiento
independientes del segundo tipo [E(Yi) , V(Yi) 42
].
a. Demuestre que con cualquier entre 0 y 1, el estimador
ˆ
X
(1 )Y
es insesgado para .
b. Con m y n fijas, calcule V( ˆ
) y luego determine el valor de
que reduzca al mínimo V( ˆ
). [Sugerencia: Derive V( ˆ
)
con respecto a .]
17. En el capítulo tres, se definió una variable aleatoria bino-
mial negativa como el número de fallas que ocurren antes
del r-ésimo éxito en una secuencia de ensayos con éxitos y
fallas independientes e idénticos. La función masa de pro-
babilidad (fmp) de X es
nb(x; r, p)
{ pr
(1 p)x
x 0, 1, 2, . . .
0 de lo contrario
x r 1
x
(n1 1)S2
1 (n2 1)S2
2
n1 n2 2
242 CAPÍTULO 6 Estimación puntual
Número de
rayones
por artículo 0 1 2 3 4 5 6 7
Frecuencia
observada 18 37 42 30 13 7 2 1
c6_p227-253.qxd 3/12/08 4:13 AM Page 242](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-260-320.jpg)
![a. Suponga que r 2. Demuestre que
p̂ (r 1)/(X r 1)
es un estimador insesgado de p. [Sugerencia: Escriba
E(p̂) y elimine x r 1 dentro de la suma.]
b. Un reportero desea entrevistar a cinco individuos que
apoyan a un candidato y comienza preguntándoles si (S)
o no (F) apoyan al candidato. Si la secuencia de res-
puestas es SFFSFFFSSS estiman p la proporción ver-
dadera que apoya al candidato.
18. Sean X1, X2, . . . , Xn una muestra aleatoria de una función
de densidad de probabilidad f(x) simétrica con respecto a
, de modo que sea un estimador insesgado de . Si n es
grande, se puede demostrar que V( ) 1/(4n[ f()]2
).
a. Compara V( ) con V(X
X
) cuando la distribución subya-
cente es normal.
b. Cuando la función de densidad de probabilidad subya-
cente es Cauchy (véase el ejemplo 6.7), V(X
) por lo
tanto X
es un estimador terrible. ¿Cuál es V( ) en este
caso cuando n es grande?
19. Una investigadora desea estimar la proporción de estudian-
tes en una universidad que han violado el código de honor.
Habiendo obtenido una muestra aleatoria de n estudiantes,
se da cuenta que si a cada uno le pregunta “¿Has violado el
código de honor?” probablemente recibirá algunas respues-
tas faltas de veracidad. Considere el siguiente esquema,
conocido de técnica de respuesta aleatorizada. La investi-
gadora forma un mazo de 100 cartas de las cuales 50 son de
tipo I y 50 de tipo II.
Tipo I: ¿Has violado el código de honor (sí o no)?
Tipo II: ¿Es el último dígito de su número telefónico un 0,
1 o 2 (sí o no)?
A cada estudiante en la muestra aleatoria se le pide que
baraje el mazo, que saque una carta y que responda la pre-
gunta con sinceridad. A causa de la pregunta irrelevante en
las cartas de tipo II, una respuesta sí ya no estigmatiza a
quien contesta, así que se supone que éste es sincero. Sea p
la proporción de violadores del código de honor (es decir, la
probabilidad de que un estudiante seleccionado al azar sea
un violador) y sea P(respuesta sí). Entonces y p están
relacionados por 0.5p (0.5)(0.3).
a. Sea Y el número de respuestas sí, por consiguiente Y
Bin(n, ). Por tanto Y/n es un estimador insesgado de .
Obtenga un estimador de p basado en Y. Si n 80 y
y 20, ¿cuál es su estimación? [Sugerencia: Resuelva
0.5p 1.5 para p y luego sustituya Y/n en lugar de .]
b. Use el hecho de que E(Y/n) para demostrar que su
estimador p̂ es insesgado.
c. Si hubiera 70 cartas de tipo I y 30 de tipo II, ¿cuál sería
su estimador para p?
X
|
X
|
X
|
X
|
6.2 Métodos de estimación puntual 243
La definición de insesgamiento no indica en general cómo se pueden obtener los estimadores
insesgados. A continuación se discuten dos métodos “constructivos” para obtener estimado-
res puntuales: el método de momentos y el método de máxima verosimilitud. Por constructi-
vo se quiere dar a entender que la definición general de cada tipo de estimador sugiere
explícitamente cómo obtener el estimador en cualquier problema específico. Aun cuando se
prefieren los estimadores de máxima verosimilitud a los de momento debido a ciertas propie-
dades de eficiencia, a menudo requieren significativamente más cálculo que los estimadores
de momento. En ocasiones es el caso que estos métodos dan estimadores insesgados.
El método de momentos
La idea básica de este método es poder igualar ciertas características muestrales, tales como
la media, a los valores esperados de la población correspondiente. Luego resolviendo estas
ecuaciones con valores de parámetros conocidos se obtienen los estimadores.
DEFINICIÓN Si X1, . . . , Xn constituyen una muestra aleatoria proveniente de una función masa de
probabilidad o de una función de densidad de probabilidad f(x). Con k 1, 2,
3, . . . el k-ésimo momento de la población o el k-ésimo momento de la distribu-
ción f(x), es E(Xk
). El k-ésimo momento muestral es (1/n)n
i1Xk
i.
Por consiguiente el primer momento de la población es E(X) y el primer momento
muestral es Xi/n X
. Los segundos momentos de la población y muestral son E(X2
) y
X2
i/n, respectivamente. Los momentos de la población serán funciones de cualquier pará-
metro desconocido 1, 2, . . .
6.2 Métodos de estimación puntual
c6_p227-253.qxd 3/12/08 4:13 AM Page 243](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-261-320.jpg)
![6.2 Métodos de estimación puntual 245
E(X2
) V(X) [E(X)]2
r(1 p)(r rp 1)/p2
. Si se iguala E(X) a X
y E(X2
) a
(1/n)X2
i a la larga se obtiene
p̂
(1/n)X
X
2
i X
2 r̂
Como ilustración, Reep, Pollard y Benjamin (“Skill and Chance in Ball Games”, J.
Royal Stat. Soc., 1971: 623-629) consideran la distribución binomial negativa como modelo
del número de goles por juego anotados por los equipos de la Liga Nacional de Jockey.
Los datos de 1966-1967 son los siguientes (420 juegos):
Goles 0 1 2 3 4 5 6 7 8 9 10
Frecuencia 29 71 82 89 65 45 24 7 4 1 3
Entonces,
x
xi /420 [(0)(29) (1)(71) (10)(3)]/420 2.98
y
x2
i /420 [(0)2
(29) (1)2
(71) (10)2
(3)]/420 12.40
Por consiguiente,
p̂
12.40
2
.98
(2.98)2
0.85 r̂ 16.5
Aunque r por definición debe ser positivo, el denominador de r̂ podría ser negativo, lo que
indica que la distribución binomial negativa no es apropiada (o que el estimador de momen-
to es defectuoso). ■
Estimación de máxima verosimilitud
El método de máxima probabilidad lo introdujo por primera vez R. A. Fisher, genetista y
estadístico en la década de 1920. La mayoría de los estadísticos recomiendan este método,
por lo menos cuando el tamaño de muestra es grande, puesto que los estimadores resultantes
tienen ciertas propiedades de eficiencia deseables (véase la proposición en la página 249).
Se obtuvo una muestra de diez cascos de ciclista nuevos fabricados por una compañía. Al
probarlos, se encontró que el primero, el tercero y el décimo estaban agrietados, en tanto que
los demás no. Sea p P(casco agrietado) y defina X1, . . . , X10 como Xi 1 si el i-ésimo
casco está agrietado y cero de lo contrario. En ese caso las xi son 1, 0, 1, 0, 0, 0, 0, 0, 0, 1,
así que la función masa de probabilidad conjunta de la muestra es
f(x1, x2, . . . , x10; p) p(1 p)p p p3
(1 p)7
(6.4)
Ahora se hace la pregunta, “¿Con qué valor de p es más probable que la muestra observada
haya ocurrido?” Es decir, se desea encontrar el valor de p que incrementa al máximo la fun-
ción masa de probabilidad (6.4) o, en forma equivalente, que incrementa al máximo el loga-
ritmo natural de (6.4).*
Como
ln[f(x1, . . . , x10; p)] 3 ln(p) 7 ln(1 p) (6.5)
(2.98)2
12.40 (2.98)2
2.98
X
2
(1/n)X2
i X
2
X
Ejemplo 6.15
* Como ln[g(x)] es una función monotónica de g(x), determinar x para incrementar al máximo ln[g(x)] equivale a
incrementar al máximo g(x). En estadística, si se toma el logaritmo con frecuencia, un producto cambia a una
suma, con la cual es más fácil trabajar.
c6_p227-253.qxd 3/12/08 4:13 AM Page 245](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-263-320.jpg)
![la cual es una función derivable de p, igualando la derivada de (6.5) a cero se obtiene el valor
maximizante†
d
d
p
ln[f(x1, . . . , x10; p)]
3
p
1
7
p
0 ‰ p
1
3
0
n
x
donde x es el número de éxitos observados (cascos agrietados). La estimación de p ahora
es p̂ 1
3
0. Se llama estimación de máxima verosimilitud porque para x1, . . . , x10 estable-
cido, es el valor del parámetro que maximiza la probabilidad (función masa de probabili-
dad conjunta) de la muestra observada.
Obsérvese que si sólo se hubiera dicho que entre los diez cascos había tres agrietados,
la ecuación (6.4) sería reemplazada por la función masa de probabilidad binomial
(10
3 )p3
(1 p)7
, la cual también se incrementa al máximo con p̂ 1
3
0. ■
La función de verosimilitud dice qué tan probable es que la muestra observada sea una
función de los posibles valores de parámetro. Al incrementarse al máximo la probabilidad
se obtienen los valores de parámetro con los que la muestra observada es más probable que
haya sido generada, es decir, los valores de parámetro que “más concuerdan” con los datos
observados.
Suponga que X1, X2, . . . , Xn es una muestra aleatoria de una distribución exponencial con
parámetro . Debido a la independencia, la función de verosimilitud es un producto de las
funciones de densidad de probabilidad individuales:
f(x1, . . . , xn; ) (ex1) (exn) n
exi
El ln(verosimilitud) es
ln[f(x1, . . . , xn; )] n ln() xi
Si se iguala (d/d)[ln(verosimilitud)] a cero se obtiene n/ xi 0, o n/xi 1/x
.
Por consiguiente el estimador de máxima verosimilitud es ˆ
1/X
; es idéntico al método de
estimador de momentos [pero no es un estimador insesgado, puesto que E(1/X
) 1/E(X
)]. ■
†
Esta conclusión requiere que se verifique la segunda derivada, pero se omiten los detalles.
246 CAPÍTULO 6 Estimación puntual
DEFINICIÓN Que X1, X2, . . . , Xn tengan una función masa de probabilidad o una función de den-
sidad de probabilidad
f(x1, x2, . . . , xn; 1, . . . , m) (6.6)
donde los parámetros 1, . . . , m tienen valores desconocidos. Cuando x1, . . . , xn son
los valores muestrales observados y (6.6) se considera como una función de 1, . . . , m,
se llama función de verosimilitud. Las estimaciones de máxima verosimilitud (emv)
ˆ
1, . . . , ˆ
m son aquellos valores de las i que incrementan al máximo la función de pro-
babilidad, de modo que
f(x1, . . . , xn; ˆ
1, . . . , ˆ
m) f(x1, . . . , xn; 1, . . . , m) con todos los 1, . . . , m
Cuando se sustituyen las Xi en lugar de las xi, se obtienen los estimadores de máxi-
ma verosimilitud.
Ejemplo 6.16
c6_p227-253.qxd 3/12/08 4:13 AM Page 246](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-264-320.jpg)
![Sean X1, . . . , Xn una muestra aleatoria de una distribución normal. La función de probabi-
lidad es
f(x1, . . . , xn; , 2
)
2
1
2
e(x1)2/(2 2)
2
1
2
e(xn)2/(2 2)
2
1
2
n/2
e(xi)2/(2 2)
por consiguiente
ln[ f(x1, . . . , xn; , 2
)]
n
2
ln(22
)
2
1
2
(xi )2
Para determinar los valores maximizantes de y 2
, se deben tomar las derivadas parciales
de ln( f) con respecto a y 2
, igualarlas a cero y resolver las dos ecuaciones resultantes.
Omitiendo los detalles, los estimadores de máxima probabilidad resultantes son
ˆ
X
ˆ
2
(Xi
n
X
)2
El estimador de máxima verosimilitud de 2
no es el estimador insesgado, por consiguien-
te dos principios diferentes de estimación (insesgamiento y máxima verosimilitud) dan dos
estimadores diferentes. ■
En el capítulo 3, se analizó el uso de la distribución de Poisson para modelar el número de
“eventos” que ocurren en una región bidimensional. Suponga que cuando el área de la
región R que se está muestreando es a(R), el número X de eventos que ocurren en R tiene
una distribución de Poisson con parámetro a(R) (donde es el número esperado de even-
tos por unidad de área) y que las regiones no traslapantes dan X independientes.
Suponga que un ecólogo selecciona n regiones no traslapantes R1, . . . , Rn y cuenta el
número de plantas de una especie en cada región. La función masa de probabilidad conjun-
ta es entonces
p(x1, . . . , xn; )
el ln(verosimilitud) es
ln[p(x1, . . . , xn; )] xi ln[a(Ri)] ln() xi a(Ri) ln(xi!)
Con d/d ln(p) e igualándola a cero da
xi
a(Ri) 0
por consiguiente
a(
x
R
i
i)
El estimador de máxima verosimilitud es entonces ˆ
Xi/a(Ri). Ésta es razonablemen-
te intituitiva porque es la densidad verdadera (plantas por unidad de área), mientras que ˆ
es la densidad muestral puesto que a(Ri) es tan sólo el área total muestreada. Como
E(Xi) a(Ri), el estimador es insesgado.
En ocasiones se utiliza un procedimiento de muestreo alternativo. En lugar de fijar las
regiones que van a ser muestreadas, el ecólogo seleccionará n puntos en toda la región de
[a(R1)]x1 [a(Rn)]xn xi ea(Ri)
x1! xn!
[ a(Rn)]xnea(Rn)
xn!
[ a(R1)]x1ea(R1)
x1!
6.2 Métodos de estimación puntual 247
Ejemplo 6.17
Ejemplo 6.18
c6_p227-253.qxd 3/12/08 4:13 AM Page 247](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-265-320.jpg)
![interés y sea yi la distancia del i-ésimo punto a la planta más cercana. La función de dis-
tribución acumulativa de Y distancia a la planta más cercana es
FY(y) P(Y y) 1 P(Y y) 1 P
1
ey2
0
(
!
y2
)0
1 ey2
Al tomar la derivada de FY (y) con respecto a y proporciona
fY(y; ) {2yey2
y 0
0 de lo contrario
Si ahora se forma la probabilidad fY(y1; ) fY(yn; ), derive ln(verosimilitud), y así
sucesivamente, el estimador de máxima verosimilitud resultante es
ˆ
n
Y2
i
la que también es una densidad muestral. Se puede demostrar que un ambiente ralo (peque-
ño ), el método de distancia es en cierto sentido mejor, en tanto que en un ambiente den-
so, el primer método de muestreo es mejor. ■
Sean X1, . . . , Xn una muestra aleatoria de una función de densidad de probabilidad Weibull
f(x; , )
{
x1
e(x/)
x 0
0 de lo contrario
Si se escribe la verosimilitud y el ln(verosimilitud) y luego con (,/,)[ln( f)] 0 y
(,/,)[ln(f)] 0 se obtienen las ecuaciones
x
i
x
ln
i
(xi)
ln
n
(xi)
1
n
x
i
1/
Estas dos ecuaciones no pueden ser resueltas explícitamente para obtener fórmulas generales
de los estimadores de máxima verosimilitud ˆ
y ˆ
. En su lugar, por cada muestra x1, . . . , xn,
las ecuaciones deben ser resueltas con un procedimiento numérico iterativo. Incluso los esti-
madores de momento de y son un tanto complicados (véase el ejercicio 21). ■
Estimación de funciones de parámetros
En el ejemplo 6.17, se obtuvo el estimador de máxima verosimilitud de 2
cuando la distri-
bución subyacente es normal. El estimador de máxima verosimilitud de
2
, como
el de muchos otros estimadores de máxima verosimilitud, es fácil de derivar con la siguien-
te proposición.
número de plantas observadas
área total muestreada
ninguna planta en
un círculo de radio y
248 CAPÍTULO 6 Estimación puntual
Ejemplo 6.19
PROPOSICIÓN El principio de invarianza
Sean ˆ
1, ˆ
2, . . . , ˆ
m los estimadores de máxima verosimilitud de los parámetros
1, 2, . . . , m. Entonces el estimador de máxima verosimilitud de cualquier función
h( 1, 2, . . . , m) de estos parámetros es la función h(ˆ
1, ˆ
2, . . . , ˆ
m) de los estimado-
res de máxima verosimilitud.
c6_p227-253.qxd 3/12/08 4:13 AM Page 248](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-266-320.jpg)
![En el caso normal, los estimadores de máxima verosimilitud de y 2
son ˆ
X
y ˆ
2
(Xi X
)2
/n. Para obtener el estimador de máxima verosimilitud de la función h(, 2
)
2
, sustituya los estimadores de máxima verosimilitud en la función.
ˆ
ˆ
2
1
n
(Xi X
)2
1/2
el estimador de máxima verosimilitud de no es la desviación estándar muestral S y se
aproximan bastante cuando n es bastante pequeño. ■
El valor medio de una variable aleatoria X que tiene una distribución Weibull es
(1 1/)
El estimador de máxima verosimilitud de es por consiguiente ˆ
ˆ
(1 1/ˆ
), donde ˆ
y ˆ
son los estimadores de máxima verosimilitud de y . En particular X
no es el esti-
mador de máxima verosimilitud de , aunque es un estimador insesgado. Por lo menos con
n grande, ˆ
es un mejor estimador que X
■
Comportamiento con muestra grande del estimador
de máxima verosimilitud
Aunque el principio de la estimación de máxima verosimilitud tiene un considerable atrac-
tivo intuitivo, la siguiente proposición proporciona razones adicionales fundamentales para
el uso de estimadores de máxima verosimilitud.
Debido a este resultado y al hecho de que las técnicas basadas en el cálculo casi siempre
pueden ser utilizadas para derivar los estimadores de máxima verosimilitud (aunque a veces
se requieren métodos numéricos, tales como el método de Newton), la estimación de máxima
verosimilitud es la técnica de estimación más ampliamente utilizada entre los estadísticos.
Muchos de los estimadores utilizados en lo que resta del libro son estimadores de máxima
verosimilitud. La obtención de un estimador de máxima verosimilitud, sin embargo, requie-
re que se especifique la distribución subyacente.
Algunas complicaciones
En ocasiones no se puede utilizar el cálculo para obtener estimadores de máxima verosimilitud.
Suponga que mi tiempo de espera de un autobús está uniformemente distribuido en [0, ] y
que se observaron los resultados x1, . . . , xn de una muestra aleatoria tomada de esta distri-
bución. Como f(x; ) 1/ con 0 x , y 0 de lo contrario,
f(x1, . . . , xn; )
1
n
0 x1 , . . . , 0 xn
0 de lo contrario
En tanto máx(xi) , la verosimilitud es 1/ n
, la cual es positiva, pero en cuanto
máx(xi), la verosimilitud se reduce a 0. Esto se ilustra en la figura 6.5. El cálculo no fun-
ciona porque el máximo de la probabilidad ocurre en un punto de discontinuidad.
6.2 Métodos de estimación puntual 249
Ejemplo 6.22
PROPOSICIÓN En condiciones muy generales en relación con la distribución conjunta de la muestra,
cuando el tamaño de la muestra n es grande, el estimador de máxima verosimilitud
de cualquier parámetro es aproximadamente insesgado [E(ˆ) ] y su varianza es
casi tan pequeña como la que puede ser lograda por cualquier estimador. Expresado
de otra manera, el estimador de máxima verosimilitud ˆ es aproximadamente el esti-
mador insesgado con varianza mínima de .
Ejemplo 6.20
(continuación
del ejemplo
6.17)
Ejemplo 6.21
(continuación
del ejemplo
6.19)
c6_p227-253.qxd 3/12/08 4:13 AM Page 249](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-267-320.jpg)
![pero la figura indica que ˆ máx(Xi). Por consiguiente si mis tiempos de espera son 2.3,
3.7, 1.5, 0.4 y 3.2, entonces el estimador de máxima verosimilitud es ˆ 3.7. ■
Un método que a menudo se utiliza para estimar el tamaño de una población de vida sil-
vestre implica realizar un experimento de captura/recaptura. En este experimento, se captu-
ra una muestra inicial de M animales, y cada uno se éstos se etiqueta y luego son regresados
a la población. Tras de permitir un tiempo suficiente para que los individuos etiquetados
se mezclen con la población, se captura otra muestra de tamaño n. Con X el número de
animales etiquetados en la segunda muestra, el objetivo es utilizar las x observadas para esti-
mar la población de tamaño N.
El parámetro de interés es N, el cual asume sólo valores enteros, así que incluso
después de determinar la función de verosimilitud (función masa de probabilidad de X en
este caso), el uso del cálculo para obtener N presentaría dificultades. Si se considera un éxi-
to la recaptura de un animal previamente etiquetado, entonces el muestreo es sin reemplazo
de una población que contiene M éxitos y N M fallas, de modo que X es una variable alea-
toria hipergeométrica y la función de probabilidad es
p(x; N) h(x; n, M, N)
La naturaleza de valor entero de N, dificultaría tomar la derivada de p(x; N). Sin embargo,
si se considera la razón de p(x; N) a p(x; N 1), se tiene
Esta razón es más grande que 1 si y sólo si N Mn/x. El valor de N con el cual p(x; N) se
incrementa al máximo es por consiguiente el entero más grande menor que Mn/x. Si se uti-
liza la notación matemática estándar [r] para el entero más grande menor que o igual a r, el
estimador de máxima probabilidad de N es N̂ [Mn/x]. Como ilustración, si M 200 peces
se sacan del lago y etiquetan, posteriormente n 100 son recapturados y entre los 100 hay
x 11 etiquetados, en ese caso N̂ [(200)(100)/11] [1818.18] 1818. La estimación
es en realidad un tanto intuitiva; x/n es la proporción de la muestra recapturada etiquetada,
mientras que M/N es la proporción de toda la población etiquetada. La estimación se obtiene
igualando estas dos proporciones (estimando una proporción poblacional mediante una pro-
porción muestral). ■
Supóngase que X1, X2, . . . , Xn es una muestra aleatoria de una función de densidad
de probabilidad f(x; ) simétrica con respecto a aunque el investigador no está seguro de
la forma de la función f. Es entonces deseable utilizar un estimador ˆ robusto, es decir,
uno que funcione bien con una amplia variedad de funciones de densidad de probabilidad
(N M) (N n)
N(N M n x)
p(x; N)
p(x; N 1)
M
x N
n
x
M
N
n
250 CAPÍTULO 6 Estimación puntual
máx(xi)
Probabilidad
Figura 6.5 Función de probabilidad del ejemplo 6.22.
Ejemplo 6.23
c6_p227-253.qxd 3/12/08 4:13 AM Page 250](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-268-320.jpg)
![subyacentes. Un estimador como ése es una media recortada. En años recientes, los esta-
dísticos han propuesto otro tipo de estimador, llamado estimador M, basado en una genera-
lización de la estimación de máxima verosimilitud. En lugar de incrementar al máximo el
logaritmo de la probabilidad ln[ f(x; )] para una f específica, se incrementa al máximo
(xi; ). Se selecciona la “función objetivo” para que dé un estimador con buenas pro-
piedades de robustez. El libro de David Hoaglin y colaboradores (véase la bibliografía) con-
tiene una buena exposición de esta materia.
6.2 Métodos de estimación puntual 251
EJERCICIOS Sección 6.2 (20-30)
20. Se selecciona una muestra aleatoria de n cascos para ciclis-
tas fabricados por una compañía. Sea X el número entre
los n que están agrietados y sea p P(agrietado). Suponga
que sólo se observa X, en lugar de la secuencia de S y F.
a. Obtenga el estimador de máxima verosimilitud de p. Si
n 20 y x 3, ¿cuál es la estimación?
b. ¿Es insesgado el estimador del inciso a)?
c. Si n 20 y x 3, ¿cuál es el estimador de máxima
verosimilitud de la probabilidad (1 p)5
de que ningu-
no de los siguientes cinco cascos esté agrietado?
21. Si X tiene una distribución de Weibull con parámetros y
, entonces
E(X) (1 1/)
V(X) 2
{(1 2/) [(1 1/)]2
}
a. Basado en una muestra aleatoria X1, . . . , Xn, escriba
ecuaciones para el método de estimadores de momentos
y . Demuestre que, una vez que se obtiene la estima-
ción de , la estimación de se puede hallar en una
tabla de la función gama y que la estimación de es la
solución de una ecuación complicada que implica la fun-
ción gama.
b. Si n 20, x
28.0 y x2
i 16 500, calcule las esti-
maciones. [Sugerencia: [(1.2)]2
/(1.4) 0.95.]
22. Sea X la proporción de tiempo destinado que un estudiante
seleccionado al azar pasa resolviendo cierta prueba de apti-
tud. Suponga que la función de densidad de probabilidad de
X es
f(x; )
( 1)x 0 x 1
0 de lo contrario
donde 1 . Una muestra aleatoria de diez estudiantes
produce los datos x1 0.92, x2 0.79, x3 0.90, x4 0.65,
x5 0.86, x6 0.47, x7 0.73, x8 0.97, x9 0.94,
x10 0.77.
a. Use el método de momentos para obtener un estimador
de y luego calcule la estimación con estos datos.
b. Obtenga el estimador de máxima verosimilitud de y
luego calcule la estimación con los datos dados.
23. Dos sistemas de computadoras diferentes son monitoreados
durante un total de n semanas. Sea Xi el número de descom-
posturas del primer sistema durante la i-ésima semana y
suponga que las Xi son independientes y que se extraen de
una distribución de Poisson con parámetro 1. Asimismo,
sea Yi el número de descomposturas del segundo sistema du-
rante la semana i-ésima y suponga independencia con cada
Yi extraída de una distribución de Poisson con parámetro 2.
Derive los estimadores de máxima verosimilitud de 1, 2 y
1 2. [Sugerencia: Utilizando independencia, escriba la
función masa de probabilidad conjunta de las Xi y Yi juntas.]
24. Remítase al ejercicio 20. En lugar de seleccionar n 20
cascos para examinarlos, suponga que se examinan en suce-
sión hasta que se encuentran r 3 agrietados. Si el vigési-
mo percentil casco es el tercer agrietado (de modo que el
número de cascos examinados que no están agrietados sea
x 17), ¿cuál es el estimador de máxima verosimilitud de
p? ¿Es ésta la misma estimación del ejercicio 20? ¿Por qué
sí o por qué no? ¿Es la misma que la estimación calculada
con el estimador insesgado del ejercicio 17?
25. Se determina la resistencia al esfuerzo cortante de soldadu-
ras de puntos de prueba y se obtienen los siguientes datos
(lb/pulg2
):
392 376 401 367 389 362 409 415 358 375
a. Suponiendo que la resistencia al esfuerzo cortante está
normalmente distribuida, estime la resistencia al esfuer-
zo cortante promedio verdadera y la desviación estándar
de la resistencia al esfuerzo cortante utilizando el méto-
do de máxima verosimilitud.
b. De nuevo suponiendo una distribución normal, calcule
el valor de resistencia por debajo del cual 95% de todas
las soldaduras tendrán sus resistencias. [Sugerencia:
¿Cuál es el percentil 95 en función de y ? Utilice
ahora el principio de invarianza.]
26. Remítase al ejercicio 25. Suponga que decide examinar otra
soldadura de puntos de prueba. Sea X resistencia al esfuer-
zo cortante de la soldadura. Use los datos dados para obtener
el estimador de máxima verosimilitud de P(X 400).
[Sugerencia: P(X 400) ((400 )/).]
27. Sean X1, . . . , Xn una muestra aleatoria de una distribución
gama con parámetros y .
a. Derive las ecuaciones cuya solución da los estimadores
de máxima verosimilitud de y . ¿Piensa que pueden
ser resueltos explícitamente?
b. Demuestre que el estimador de máxima verosimilitud de
es ˆ
X
.
28. Si X1, X2, . . . , Xn representan una muestra aleatoria de la
distribución Rayleigh con función densidad dada en el ejer-
cicio 15. Determine:
a. El estimador de máxima verosimilitud de y luego cal-
cule la estimación con los datos de esfuerzo de vibración
dados en ese ejercicio. ¿Es este estimador el mismo que
el estimador insesgado del ejercicio 15?
c6_p227-253.qxd 3/12/08 4:13 AM Page 251](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-269-320.jpg)
![b. El estimador de máxima verosimilitud de la mediana de
la distribución del esfuerzo de vibración. [Sugerencia:
Exprese primero la mediana en función de .]
29. Considere la muestra aleatoria X1, X2, . . . , Xn de la función
de densidad de probabilidad exponencial desplazada
f(x; , ) {e(x )
x
0 de lo contrario
Con 0 da la función de densidad de probabilidad de la dis-
tribución exponencial previamente considerada (con densidad
positiva a la derecha de cero). Un ejemplo de la distribución
exponencial desplazada apareció en el ejemplo 4.5, en el
cual la variable de interés fue el tiempo entre vehículos en
el flujo de tráfico y 0.5 fue el tiempo entre vehículos
máximo posible.
a. Obtenga los estimadores de máxima verosimilitud de y .
b. Si n 10 observaciones de tiempo entre vehículos son
realizadas y se obtienen los siguientes resultados 3.11,
0.64, 2.55, 2.20, 5.44, 3.42, 10.39, 8.93, 17.82 y 1.30,
calcule las estimaciones de y .
30. En los instantes t 0, 20 componentes idénticos son puestos
a prueba. La distribución de vida útil de cada uno es expo-
nencial con parámetro . El experimentador deja la instala-
ción de prueba sin monitorear. A su regreso 24 horas más
tarde, el experimentador termina de inmediato la prueba des-
pués de notar que y 15 de los 20 componentes aún están en
operación (así que 5 han fallado). Derive el estimador de
máxima verosimilitud de . [Sugerencia: Sea Y el número
que sobreviven 24 horas. En ese caso Y Bin(n, p). ¿Cuál es
el estimador de máxima verosimilitud de p? Observe ahora
que p P(Xi 24), donde Xi está exponencialmente distri-
buida. Esto relaciona con p, de modo que el primero puede
ser estimado una vez que lo ha sido el segundo.]
252 CAPÍTULO 6 Estimación puntual
EJERCICIOS SUPLEMENTARIOS (31-38)
31. Se dice que un estimador ˆ es consistente si con cualquier
0, P(°ˆ ° ) A 0 a medida que n A . Es decir,
ˆ es consistente, si, a medida que el tamaño de muestra se
hace más grande, es menos y menos probable que ˆ se ale-
je más que del valor verdadero de . Demuestre que X
es
un estimador consistente de cuando 2
mediante la
desigualdad de Chebyshev del ejercicio 44 del capítulo 3.
[Sugerencia: La desigualdad puede ser reescrita en la forma
P(°Y Y° ) 2
Y /
Ahora identifique Y con X
.]
32. a. Sean X1, . . . , Xn una muestra aleatoria de una distribu-
ción uniforme en [0, ]. Entonces el estimador de máxi-
ma verosimilitud de es ˆ Y máx(Xi). Use el
hecho de que Y y si y sólo si cada Xi y para obtener
la función de distribución acumulativa de Y. Luego
demuestre que la función de densidad de probabilidad
de Y máx(Xi) es
fY(y)
{
nyn
n
1
0 y
0 de lo contrario
b. Use el resultado del inciso a) para demostrar que el esti-
mador de máxima verosimilitud es sesgado pero que
(n 1)máx(Xi)/n es insesgado.
33. En el instante t 0, hay un individuo vivo en una población.
Un proceso de nacimientos puro se desarrolla entonces
como sigue. El tiempo hasta que ocurre el primer nacimien-
to está exponencialmente distribuido con parámetro .
Después del primer nacimiento, hay dos individuos vivos. El
tiempo hasta que el primero da a luz otra vez es exponencial
con parámetro y del mismo modo para el segundo indivi-
duo. Por consiguiente, el tiempo hasta el siguiente naci-
miento es el mínimo de dos variables () exponenciales, el
cual es exponencial con parámetro 2. Asimismo, una vez
que el segundo nacimiento ha ocurrido, hay tres individuos
vivos, de modo que el tiempo hasta el siguiente nacimiento
es una variable aleatoria exponencial con parámetro 3 y así
sucesivamente (aquí se está utilizando la propiedad de
amnesia de la distribución exponencial). Suponga que se
observa el proceso hasta que el sexto nacimiento ha ocurri-
do y los tiempos hasta los nacimientos sucesivos son 25.2,
41.7, 51.2, 55.5, 59.5, 61.8 (con los cuales deberá calcular
los tiempos entre nacimientos sucesivos). Obtenga el esti-
mador de máxima verosimilitud de . [Sugerencia: La vero-
similitud es un producto de términos exponenciales.]
34. El error cuadrático medio de un estimador ˆ es ECM(ˆ)
E(ˆ )2
. Si ˆ es insesgado, entonces ECM(ˆ) V(ˆ), pero
en general ECM(ˆ) V(ˆ) (sesgo)2
. Considere el estima-
dor ˆ
2
KS2
, donde S2
varianza muestral. ¿Qué valor
de K reduce al mínimo el error cuadrático medio de este
estimador cuando la distribución de la población es normal?
[Sugerencia: Se puede demostrar que
E[(S2
)2
] (n 1) 4
/(n 1)
En general, es difícil determinar ˆ para reducir al mínimo
el ECM(ˆ), por lo cual se buscan sólo estimadores insesga-
dos y reducir al mínimo V(ˆ).]
35. Sean X1, . . . , Xn una muestra aleatoria de una función de
densidad de probabilidad simétrica con respecto a . Un
estimador de que se ha visto que funciona bien con una
amplia variedad de distribuciones subyacentes es el estima-
dor de Hodges-Lehmann. Para definirla, primero calcule
para cada i j y cada j 1, 2, . . . , n el promedio por pares
X
i,j (Xi Xj)/2. Entonces el estimador es la media-
na de las X
i,j . Calcule el valor de esta estimación con los
datos del ejercicio 44 del capítulo 1. [Sugerencia:
Construya una tabla con las xi en el margen izquierdo y en
la parte superior. Luego calcule los promedios en y sobre la
diagonal.]
36. Cuando la distribución de la población es normal, se puede
utilizar la mediana estadística {°X1 °, . . . , °Xn °}
X
|
X
|
c6_p227-253.qxd 3/12/08 4:13 AM Page 252](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-270-320.jpg)
![/0.6745 para estimar . Este estimador es más resistente a los
efectos de los valores apartados (observaciones alejadas del
grueso de los datos) que es la desviación estándar muestral.
Calcule tanto la estimación puntual correspondiente como s
de los datos del ejemplo 6.2.
37. Cuando la desviación estándar muestral S está basada en
una muestra aleatoria de una distribución de población nor-
mal, se puede demostrar que
E(S) 2
/(
n
1
)
(n/2)/((n 1)/2)
Use ésta para obtener un estimador insesgado de de la
forma cS. ¿Cuál es c cuando n 20?
38. Cada uno de n especímenes tiene que ser pesado dos veces en
la misma báscula. Sean Xi y Yi los dos pesos observados del
i-ésimo espécimen. Suponga que Xi y Yi son independientes
uno de otro, cada uno normalmente distribuido con valor me-
dio i (el peso verdadero del espécimen i) y varianza 2
.
a. Demuestre que el estimador de máxima verosimilitud de
2
es ˆ
2
(Xi Yi)2
/(4n). [Sugerencia: Si z
(z1
z2)/2, entonces (zi z
)2
(z1 z2)2
/2.]
b. ¿Es el estimador de máxima verosimilitud ˆ
2
un estima-
dor insesgado de 2
? Determine una estimador insesga-
do de 2
. [Sugerencia: Con cualquier variable aleatoria
Z, E(Z2
) V(Z) [E(Z)]2
. Aplique ésta a Z Xi Yi.]
Bibliografía 253
DeGroot, Morris y Mark Schervish, Probability and Statistics (3a.
ed.), Addison-Wesley, Boston, MA, 2002. Incluye una excelen-
te discusión tanto de propiedades generales como de métodos
de estimación puntual; de particular interés son los ejemplos
que muestran cómo los principios y métodos generales pueden
dar estimadores insatisfactorios en situaciones particulares.
Devore, Jay y Kenneth Berk, Modern Mathematical Statistics with
Applications. Thomson-Brooks/Cole, Belmont, CA, 2007. La
exposición es un poco más completa y compleja que la de este
libro.
Efron, Bradley y Robert Tibshirani, An Introduction to the
Bootstrap, Chapman and Hall, Nueva York, 1993. La Biblia
del bootstrap.
Hoaglin, David, Frederick Mosteller y John Turkey, Understan-
ding Robust and Exploratory Data Analysis, Wiley, Nueva
York, 1983. Contiene varios buenos capítulos sobre estimación
puntual robusta, incluido uno sobre estimación M.
How, Robert y Allen Craig, Introduction to Mathematical
Statistics (5a. ed.), Prentice-Hall, Englewood Cliffs, NJ, 1995.
Una buena discusión de insesgadez.
Rice, John, Mathematical Statistics and Data Analysis (3a. ed.),
Thomson-Brooks/Cole, Belmont, CA, 2007. Una agradable
mezcla de teoría y datos estadísticos.
Bibliografía
c6_p227-253.qxd 3/12/08 4:13 AM Page 253](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-271-320.jpg)
![262 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra
EJERCICIOS Sección 7.1 (1-11)
1. Considere una distribución de población normal con el va-
lor de conocido.
a. ¿Cuál es el nivel de confianza para el intervalo x
!
2.81/n
?
b. ¿Cuál es el nivel de confianza para el intervalo x
!
1.44/n
?
c. ¿Qué valor de z/2 en la fórmula de intervalo de confian-
za (7.5) da un nivel de confianza de 99.7%?
d. Responda la pregunta hecha en el inciso c) para un nivel
de confianza de 75%.
2. Cada uno de los siguientes intervalos es un intervalo de
confianza para frecuencia de resonancia promedio ver-
dadera (Hz) (es decir, media de la población) para todas las
raquetas de tenis de un tipo:
(114.4, 115.6) (114.1, 115.9)
a. ¿Cuál es el valor de la frecuencia de resonancia media
muestral?
b. Ambos intervalos se calcularon con los mismos datos
muestrales. El nivel de confianza para uno de estos inter-
valos es de 90% y para el otro es de 99%. ¿Cuál de los
intervalos tiene el nivel de confianza de 90% y por qué?
3. Suponga que se selecciona una muestra de 50 botellas de una
marca particular de jarabe para la tos y se determina el conte-
nido de alcohol. Sea el contenido promedio de alcohol de la
población de todas las botellas de la marca estudiada. Supon-
ga que el intervalo de confianza de 95% resultante es (7.8, 9.4).
a. ¿Habría resultado un intervalo de confianza de 90% calcu-
lado con esta muestra más angosto o más ancho que el
intervalo dado? Explique su razonamiento.
b. Considere la siguiente proposición: Existe 95% de pro-
babilidades de que el esté entre 7.8 y 9.4. ¿Es correc-
ta esta proposición? ¿Por qué sí o por qué no?
c. Considere la siguiente proposición: Se puede estar total-
mente confiado de que 95% de todas las botellas de este
tipo de jarabe para la tos tienen un contenido de alcohol
entre 7.8 y 9.4. ¿Es correcta esta proposición? ¿Por qué
sí o por qué no?
d. Considere la siguiente proposición: Si el proceso de se-
lección de una muestra de tamaño 50 y de cálculo del in-
tervalo de 95% correspondiente se repite 100 veces, 95
de los intervalos resultantes incluirán . ¿Es correcta
esta proposición? ¿Por qué sí o por qué no?
4. Se desea un intervalo de confianza para la pérdida por car-
ga parásita promedio verdadera (watts) de cierto tipo de
motor de inducción cuando la corriente a través de la línea
se mantiene a 10 amps a una velocidad de 1500 rpm. Su-
ponga que la pérdida por carga parásita está normalmente
distribuida con 3.0.
a. Calcule un intervalo de confianza para de 95% cuando
n 25 y x
58.3.
b. Calcule un intervalo de confianza para de 95% cuando
n 100 y x
58.3.
c. Calcule un intervalo de confianza para de 99% cuando
n 100 y x
58.3.
d. Calcule un intervalo de confianza para de 82% cuando
n 100 y x
58.3.
e. ¿Qué tan grande debe ser n si el ancho del intervalo de
99% para tiene que ser 1.0?
5. Suponga que la porosidad al helio (en porcentaje) de muestras
de carbón tomadas de cualquier costura particular está normal-
mente distribuida con desviación estándar verdadera de 0.75.
a. Calcule un intervalo de confianza de 95% para la poro-
sidad promedio verdadera de una costura si la porosidad
promedio en 20 especímenes de la costura fue de 4.85.
b. Calcule un intervalo de confianza de 98% para la poro-
sidad promedio verdadera de otra costura basada en 16
especímenes con porosidad promedio muestral de 4.56.
c. ¿Qué tan grande debe ser un tamaño de muestra si el an-
cho del intervalo de 95% tiene que ser de 0.40?
d. ¿Qué tan grande debe ser un tamaño de muestra para
calcular la porosidad promedio verdadera dentro de 0.2
con confianza de 99%?
6. Con base en pruebas extensas, se sabe que el punto de ceden-
cia de un tipo particular de varilla de refuerzo de acero suave
está normalmente distribuido con 100. La composición
de la varilla se modificó un poco, pero no se cree que la mo-
dificación haya afectado o la normalidad o el valor de .
a. Suponiendo que éste tiene que ser el caso, si una mues-
tra de 25 varillas modificadas dio por resultado un pun-
to de cedencia promedio muestral de 8439 lb, calcule un
intervalo de confianza de 90% para el punto de cedencia
promedio verdadero de la varilla modificada.
b. ¿Cómo modificaría el intervalo del inciso a) para obte-
ner un nivel de confianza de 92%?
7. ¿En cuánto se debe incrementar el tamaño de muestra n si
el ancho del intervalo de confianza (7.5) tiene que ser redu-
cido a la mitad? Si el tamaño de muestra n se incrementa
por un factor de 25, ¿qué efecto tendrá en el ancho del in-
tervalo? Justifique sus aseveraciones.
8. Sea 1 0, 2 0, con 1 2 . Entonces
Pz1
z2 1
a. Use esta ecuación para obtener una expresión más gene-
ral para un intervalo de confianza de 100(1 )% para
del cual el intervalo (7.5) es un caso especial.
b. Sea 0.05 y 1 /4, 2 3/4. ¿Da por resultado
esto un intervalo más angosto o más ancho que el inter-
valo (7.5)?
9. a. En las mismas condiciones que aquellas que conducen
al intervalo (7.5), P[(X
)/(/n
) 1.645] 0.95.
Use esta expresión para obtener un intervalo unilateral
para de ancho infinito y que proporcione un límite de
confianza inferior para . ¿Cuál es el intervalo para los
datos del ejercicio 5(a)?
b. Generalice el resultado del inciso a) para obtener un lí-
mite inferior con nivel de confianza de 100(1 )%.
X
/n
c7_p225-283.qxd 3/12/08 4:15 AM Page 262](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-280-320.jpg)
![7.2 Intervalos de confianza de muestra grande para una media y proporción de población 263
Se supuso en el intervalo de confianza para dado en la sección previa que la distribución
de la población es normal con el valor de conocido. A continuación se presenta un inter-
valo de confianza de muestra grande cuya validez no requiere estas suposiciones. Después
de demostrar cómo conduce el argumento a este intervalo se aplica en forma extensa para
producir otros intervalos de muestra grande y habrá que enfocarse en un intervalo
para una proporción de población p.
Intervalo de muestra grande para
Sean X1, X2, . . . , Xn una muestra aleatoria de una población con media y desviación es-
tándar . Siempre que n es grande, el teorema del límite central implica que X
tiene de ma-
nera aproximada una distribución normal cualquiera que sea la naturaleza de la distribución
de la población. Se deduce entonces que Z (X
)/(/n
) tiene aproximadamente una
distribución estándar normal, de modo que
P
z/2 z/2 1
Un argumento paralelo al dado en la sección 7.1 da x
! z/2 /n
como intervalo de
confianza de muestra grande para con un nivel de confianza de aproximadamente
100(1 )%. Es decir, cuando n es grande, el intervalo de confianza para dado antes
permanece válido cualquiera que sea la distribución de la población, siempre que el califi-
cador esté insertado “aproximadamente” enfrente del nivel de confianza.
Una dificultad práctica con este desarrollo es que el cálculo del intervalo de confian-
za requiere el valor de , el cual rara vez es conocido. Considérese la variable estandariza-
da (X
)/(S/n
), en la cual la desviación estándar muestral S ha sido reemplazada a .
Previamente había aleatoriedad sólo en el numerador de Z gracias a X
. En la nueva variable
estandarizada, tanto X
como S cambian de valor de una muestra a otra. Así que aparente-
mente la distribución de la nueva variable deberá estar más dispersa que la curva z para re-
flejar la variación extra en el denominador. Esto en realidad es cierto cuando n es pequeño.
Sin embargo, con n grande la sustitución de S en lugar de agrega un poco de variabilidad
extra, así que esta variable también tiene una distribución normal estándar. La manipulación
de la variable en la proposición de probabilidad, como en el caso de conocida, da un in-
tervalo de confianza de muestra grande general para .
X
/n
c. ¿Cuál es un intervalo análogo al del inciso b) que pro-
porcione un límite superior para ? Calcule este interva-
lo de 99% para los datos del ejercicio 4(a).
10. Una muestra aleatoria de n 15 bombas térmicas de cierto ti-
po produjo las siguientes observaciones de vida útil (en años):
2.0 1.3 6.0 1.9 5.1 0.4 1.0 5.3
15.7 0.7 4.8 0.9 12.2 5.3 0.6
a. Suponga que la distribución de la vida útil es exponen-
cial y use un argumento paralelo al del ejemplo 7.5 para
obtener un intervalo de confianza de 95% para la vida
útil esperada (promedio verdadero).
b. ¿Cómo debería modificarse el intervalo del inciso a) para
obtener un nivel de confianza de 99%?
c. ¿Cuál es un intervalo de confianza de 95% para la des-
viación estándar de la distribución de la vida útil? [Suge-
rencia: ¿Cuál es la desviación estándar de una variable
aleatoria exponencial?]
11. Considere los siguientes 1000 intervalos de confianza de
95% para que un consultor estadístico obtendrá para va-
rios clientes. Suponga que se seleccionan independiente-
mente uno de otro los conjuntos de datos en los cuales están
basados los intervalos. ¿Cuántos de estos 1000 intervalos
espera que capturen el valor correspondiente de ? ¿Cuál es
la probabilidad de que entre 940 y 960 de estos intervalos
contengan el valor correspondiente de ? [Sugerencia: Sea
Y el número entre los 1000 intervalos que contienen .
¿Qué clase de variable aleatoria es Y?]
7.2 Intervalos de confianza de muestra grande
para una media y proporción de población
c7_p225-283.qxd 3/12/08 4:15 AM Page 263](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-281-320.jpg)
![Desafortunadamente, la selección del tamaño de muestra para que dé un ancho de in-
tervalo deseado no es simple en este caso como lo fue en el caso de conocida. Por eso el
ancho de (7.8) es 2z/2s/n
. Como el valor de s no está disponible antes de que los datos
hayan sido recopilados, el ancho del intervalo no puede ser determinado tan sólo con la se-
lección de n. La única opción de un investigador que desea especificar el ancho deseado es
hacer una suposición instruida a qué valor de s podría ser. Siendo conservador y suponien-
do un valor más grande de s, se seleccionará un n más grande de lo necesario. El investiga-
dor puede ser capaz de especificar un valor razonablemente preciso del rango de población
(la diferencia entre los valores más grande y más pequeño). Entonces si la distribución de
la población no es demasiado asimétrica, si se divide el rango entre 4 se obtiene un valor
aproximado de lo que s podría ser.
Remítase al ejemplo 7.6 sobre voltaje de ruptura. Suponga que el investigador cree que vir-
tualmente todos los valores en la población se encuentran entre 40 y 70. Entonces (70 –
40)/4 7.5 da un valor razonable para s. El tamaño de muestra apropiado para estimar el
voltaje de ruptura promedio verdadero a dentro de 1 kV con nivel de confianza de 95%, es
decir, para que el intervalo de confianza de 95% tenga un ancho de 2 kV, es
n [(1.96)(7.5)/1]2
217 ■
Un intervalo de confianza de muestra grande general
Los intervalos de muestra grande x
! z/2 /n
y x
! z/2 s/n
son casos especiales de un
intervalo de confianza de muestra grande general para un parámetro . Suponga que ˆ es un es-
timador que satisface las siguientes propiedades: 1) Tiene aproximadamente una distribución
normal; 2) es insesgado (por lo menos aproximadamente); y 3) una expresión para ˆ, la des-
viación estándar de ˆ, está disponible. Por ejemplo, en el caso , ˆ
X
es un estimador
insesgado cuya distribución es aproximadamente normal cuando n es grande y
ˆ X
/n
. Estandarizando ˆ se obtiene la variable aleatoria Z (ˆ )/ˆ, la cual tiene aproxima-
damente una distribución normal estándar. Esto justifica la proposición de probabilidad
Pz/2 z/2 1 (7.9)
Suponga, primero, que ˆ parámetros desconocidos (p. ej., conocida en el caso ).
Entonces si se reemplaza cada en (7.9) por se obtiene ˆ ! z/2 ˆ, por consiguiente
los límites de confianza inferior y superior son ˆ z/2 ˆ y ˆ z/2 ˆ, respectivamente.
Suponga ahora que ˆ no implica pero sí implica por lo menos otro parámetro desconoci-
do. Sea sˆ la estimación de ˆ obtenido utilizando estimaciones en lugar de los parámetros
desconocidos (p. ej., s/n
estima /n
). En condiciones generales (esencialmente que sˆ
se aproxime a ˆ con la mayoría de las muestras), un intervalo de confianza válido es ˆ !
z/2 sˆ. El intervalo muestral grande x
! z/2 s/n
es un ejemplo.
Por último, suponga que ˆ no implica el desconocido. Este es el caso, por ejemplo,
cuando p, una proporción de población. Entonces (ˆ )/ˆ z/2 puede ser difícil de
resolver. Con frecuencia se puede obtener una solución aproximada reemplazando en ˆ
por su estimación ˆ. Esto da una desviación estándar estimada sˆ y el intervalo correspon-
diente es de nuevo ˆ ! z/2 sˆ.
Un intervalo de confianza para una proporción
de población
Sea p la proporción de “éxitos” en una población, donde éxito identifica a un individuo u
objeto que tiene una propiedad específica (p. ej., individuos que se graduaron en una uni-
versidad, computadoras que no requieren servicio de garantía, etc.). Una variable aleatoria
de n individuos que tiene que ser seleccionada y X es el número de éxitos en la muestra.
ˆ
ˆ
7.2 Intervalos de confianza de muestra grande para una media y proporción de población 265
Ejemplo 7.7
c7_p225-283.qxd 3/12/08 4:15 AM Page 265](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-283-320.jpg)
![El artículo “Repeatability and Reproducibility for Pass/Fail Data” (J. of Testing and Eval.,
1997: 151-153) reportó que en n 48 ensayos en un laboratorio particular, 16 dieron por
resultado la ignición de un tipo particular de sustrato por un cigarrillo encendido. Sea p la
proporción a largo plazo de tales ensayos que producirían ignición. Una estimación puntual
de p es p̂ 16/48 0.333. Un intervalo de confianza para p con un nivel de confianza de
aproximadamente 95% es
0.373
1
!
.08
0.139
(0.217, 0.474)
El intervalo tradicional es
0.333 ! 1.96 (0
.3
3
3
)(
0
.6
6
7
)/
4
8
0.333 ! 0.133 (0.200, 0.466)
Estos dos intervalos concordarían mucho más si el tamaño de muestra fuera sustancialmen-
te más grande. ■
Si se iguala al ancho del intervalo de confianza para p al ancho preespecificado w se
obtiene una ecuación cuadrática para el tamaño de muestra n necesario para dar un interva-
lo con un grado de precisión deseado. Si se suprime el subíndice en z/2, la solución es
n (7.12)
Omitiendo los términos en el numerador que implican w2
se obtiene
n
Esta última expresión es lo que resulta de igualar el ancho del intervalo tradicional a w.
Estas fórmulas desafortunadamente implican la p̂ desconocida. El método más con-
servador es aprovechar el hecho de que p̂q̂ [ p̂(1 p̂)] es un máximo cuando p̂ 0.5.
Por consiguiente si se utiliza p̂ q̂ 0.5 en (7.12), el ancho será cuando mucho w hacien-
do caso omiso de que el valor de p̂ resulte de la muestra. De manera alternativa, si el inves-
tigador cree de manera firme, basado en información previa, que p p0 0.5, en ese caso
se utiliza p0 en lugar de p̂. Un comentario similar es válido cuando p p0 0.5.
El ancho del intervalo de confianza de 95% en el ejemplo 7.8 es 0.257. El valor de n nece-
sario para garantizar un ancho de 0.10 independientemente del valor de p̂ es
4z2
p̂q̂
w2
2z2
p̂q̂ z2
w2
! 4
z4
p̂q̂
(p̂q̂
w
2
)
w
2
z
4
w2
0.333 (1.96)2
/96 ! 1.96(0
.3
3
3
)(
0
.6
6
7
)/
4
8
(
1
.9
6
)2
/9
2
1
6
1 (1.96)2
/48
Por consiguiente se deberá utilizar un tamaño de muestra de 381. La expresión para n basa-
da en el intervalo de confianza tradicional da un valor un poco más grande de 385. ■
Intervalos de confianza unilaterales
(límites de confianza)
Los intervalos de confianza discutidos hasta ahora dan tanto un límite de confianza inferior
como uno superior para el parámetro que se está estimando. En algunas circunstancias, es
posible que un investigador desee sólo uno de estos dos tipos de límites. Por ejemplo, es po-
sible que un psicólogo desee calcular un límite de confianza superior de 95% para el tiempo
7.2 Intervalos de confianza de muestra grande para una media y proporción de población 267
Ejemplo 7.8
Ejemplo 7.9
n 380.3
2(1.96)2
(0.25) (1.96)2
(0.01) ! 4
(1
.9
6
)4
(0
.2
5
)(
0
.2
5
0
.0
1
)
(
0
.0
1
)(
1
.9
6
)4
0.01
c7_p225-283.qxd 3/12/08 4:15 AM Page 267](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-285-320.jpg)
![270 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra
El intervalo de confianza para presentado en la sección 7.2 es válido siempre que n es
grande. El intervalo resultante puede ser utilizado cualquiera que sea la naturaleza de la dis-
tribución de la población. El teorema del límite central no puede ser invocado, sin embargo,
cuando n es pequeña. En este caso, una forma de proceder es hacer una suposición específi-
ca sobre la forma de la distribución de la población y luego obtener un intervalo de confian-
za adecuado a esa suposición. Por ejemplo, se podría desarrollar un intervalo de confianza
para , cuando una distribución gama describe la población, otro para el caso de una pobla-
ción Weibull, y así sucesivamente. Estadísticos en realidad han realizado este programa para
varias familias distribucionales diferentes. Como la distribución normal es más frecuente-
mente apropiada como modelo de una población que cualquier otro tipo de distribución, la
atención aquí se concentrará en un intervalo de confianza para esta situación.
El resultado clave que sustenta el intervalo de la sección 7.2 fue que con n grande, la
variable aleatoria Z (X
)/(S/n
) tiene aproximadamente una distribución normal es-
tándar. Cuando n es pequeño, no es probable que S se aproxime a , de modo que la varia-
bilidad de la distribución de Z surge la aleatoriedad tanto en el numerador como en el
denominador. Esto implica que la distribución de probabilidad de (X
)/(S/n
) se dis-
persará más que la distribución normal estándar. El resultado en el cual están basadas las in-
ferencias introduce una nueva familia de distribuciones de probabilidad llamada familia de
distribuciones t.
Propiedades de distribuciones t
Antes de aplicar este teorema, se impone una discusión de propiedades de distribuciones t.
Aunque la variable de interés sigue siendo (X
)/(S/n
), ahora se denota por T para re-
calcar que no tiene una distribución normal estándar cuando n es pequeña. Recuérdese que
tiene aproximadamente una distribución normal estándar.
Ahora prosiga como en la derivación del intervalo para p
haciendo una proposición de probabilidad (con probabili-
dad de 1 ) y resolviendo las desigualdades resultantes
para (véase el argumento exactamente después de (7.10)).]
Número de
ausencias 0 1 2 3 4 5 6 7 8 9 10
Frecuencia 1 4 8 10 8 7 5 3 2 1 1
27. Reconsidere el intervalo de confianza (7.10) para p y enfó-
quese en un nivel de confianza de 95%. Demuestre que los
límites de confianza concuerdan bastante bien con los del
intervalo tradicional (7.11) una vez que dos éxitos y dos
fallas se anexaron a la muestra [es decir, (7.11) basado en
x 2 éxitos (S) en n 4 ensayos]. [Sugerencia: 1.96 2.
Nota: Agresti y Coull demostraron que este ajuste del inter-
valo tradicional también tiene un nivel de confianza próxi-
mo al nivel nominal.]
7.3 Intervalos basados en una distribución
de población normal
SUPOSICIÓN La población de interés es normal, de modo que X1, . . . , Xn constituyen una muestra
aleatoria tomada de una distribución normal con y desconocidas.
TEOREMA Cuando X
es la media de una muestra aleatoria de tamaño n tomada de una distribu-
ción normal con media , la variable aleatoria
T (7.13)
tiene una distribución de probabilidad llamada distribución t con n – 1 grados de li-
bertad (gl).
X
S/n
c7_p225-283.qxd 3/12/08 4:15 AM Page 270](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-288-320.jpg)
![280 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra
Los datos adjuntos sobre voltaje de ruptura de circuitos eléctricamente sobrecargados se to-
maron de un diagrama de probabilidad normal que apareció en el artículo “Damage of Fle-
xible Printed Wiring Boards Associated with Lightning-Induced Voltage Surges”, (IEEE
Transactions on Components, Hybrids, and Manuf. Tech., 1985: 214-220). La linealidad del
diagrama apoyó de manera firme la suposición de que el voltaje de ruptura está aproxima-
damente distribuido en forma normal.
1470 1510 1690 1740 1900 2000 2030 2100 2190
2200 2290 2380 2390 2480 2500 2580 2700
Sea 2
la varianza de la distribución del voltaje de ruptura. El valor calculado de la varian-
za muestral es s2
137 324.3, la estimación puntual de 2
. Con grados de libertad n
1 16, un intervalo de confianza de 95% requiere 2
0.975,16
6.908 y 2
0.025,16
28.845. El
intervalo es
,
(76 172.3, 318 064.4)
Tomando la raíz cuadrada de cada punto extremo se obtiene (276.0, 564.0) como el intervalo
de confianza de 95% para . Estos intervalos son bastante anchos, lo que refleja la variabilidad
sustancial del voltaje de ruptura en combinación con un tamaño de muestra pequeño. ■
Los intervalos de confianza para 2
y cuando la distribución de la población no es
normal pueden ser difíciles de obtener, incluso cuando el tamaño de muestra es grande. En
esos casos, consulte a un estadístico conocedor.
16(137 324.3)
6.908
16(137 324.3)
28.845
EJERCICIOS Sección 7.4 (42-46)
42. Determine los valores de las siguientes cantidades:
a. 2
0.1,15 b. 2
0.1,25
c. 2
0.01,25 d. 2
0.005,25
e. 2
0.99,25 f. 2
0.995,25
43. Determine lo siguiente:
a. El 95o
percentil de la distribución ji cuadrada con
10.
b. El 5o
percentil de la distribución ji cuadrada con
10.
c. P(10.98 2
36.78), donde 2
es una variable alea-
toria ji cuadrada con 22.
d. P(2
14.611 o 2
37.652), donde 2
es una variable
aleatoria ji cuadrada con 25.
44. Se determinó la cantidad de expansión lateral (mils) con
una muestra de n 9 soldaduras de arco de gas metálico de
energía pulsante utilizadas en tanques de almacenamiento
de buques LNG. La desviación estándar muestral resultan-
te fue s 2.81 mils. Suponiendo normalidad, obtenga un
intervalo de confianza de 95% para 2
y para .
45. Se hicieron las siguientes observaciones de tenacidad a la
fractura de una placa base de acero maraging con 18% de
níquel [“Fracture Testing of Weldments”, ASTM Special
Publ. No. 381, 1965: 328-356 (en k/pulg
—
pu
—
lg., dadas en
orden creciente)]:
69.5 71.9 72.6 73.1 73.3 73.5 75.5 75.7
75.8 76.1 76.2 76.2 77.0 77.9 78.1 79.6
79.7 79.9 80.1 82.2 83.7 93.7
Calcule un intervalo de confianza de 99% para la desvia-
ción estándar de la distribución de la tenacidad a la fractu-
ra. ¿Es válido este intervalo cualquiera que sea la naturaleza
de la distribución? Explique.
46. Los resultados de una prueba de turbiedad de Wagner reali-
zada con 15 muestras de arena de prueba Ottawa estándar
(en microamperes)
26.7 25.8 24.0 24.9 26.4 25.9 24.4 21.7
24.1 25.9 27.3 26.9 27.3 24.8 23.6
a. ¿Es factible que esta muestra fuera seleccionada de una
distribución de población normal?
b. Calcule un límite de confianza superior con nivel de
confianza de 95% para la desviación estándar de turbiedad
de la población.
Ejemplo 7.15
c7_p225-283.qxd 3/12/08 4:15 AM Page 280](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-298-320.jpg)
![Ejercicios suplementarios 281
47. El ejemplo 1.10 introdujo las observaciones adjuntas sobre
fuerza de adhesión.
11.5 12.1 9.9 9.3 7.8 6.2 6.6 7.0
13.4 17.1 9.3 5.6 5.7 5.4 5.2 5.1
4.9 10.7 15.2 8.5 4.2 4.0 3.9 3.8
3.6 3.4 20.6 25.5 13.8 12.6 13.1 8.9
8.2 10.7 14.2 7.6 5.2 5.5 5.1 5.0
5.2 4.8 4.1 3.8 3.7 3.6 3.6 3.6
a. Calcule la fuerza de adhesión promedio verdadera de
una manera que dé información sobre precisión y con-
fiabilidad. [Sugerencia: xi 387.8 y x2
i 4247.08.]
b. Calcule un intervalo de confianza de 95% para la pro-
porción de todas las adhesiones cuyos valores de fuerza
excederían de 10.
48. Un triatlón incluye natación, ciclismo y carrera a pie y es
uno de los eventos deportivos amateurs más extenuantes.
El artículo “Cardiovascular and Thermal Response of
Triathlon Performance” (Medicine and Science in Sports
and Exercise, 1988: 385-389) reporta sobre un estudio de
investigación de nueve triatletas varones. Se registró el rit-
mo cardiaco máximo (pulsaciones/min) durante la actua-
ción de cada uno de los tres eventos. Para natacion, la media
y la desviación estándar muestrales fueron 188.0 y 7.2,
respectivamente. Suponiendo que la distribución de ritmo
cardiaco es (de manera aproximada) normal, construya un
intervalo de confianza de 98% para el ritmo cardiaco medio
verdadero de triatletas mientras nadan.
49. Para cada uno de los 18 núcleos de depósitos de carbonato
humedecidos con aceite, la cantidad de saturación de gas re-
sidual después de la inyección de un solvente se midió en la
corriente de agua de salida. Las observaciones, en porcen-
taje de volumen de poros, fueron
23.5 31.5 34.0 46.7 45.6 32.5
41.4 37.2 42.5 46.9 51.5 36.4
44.5 35.7 33.5 39.3 22.0 51.2
(Véase “Relative Permeability Studies of Gas-Water Flow
Following Solvent Injection in Carbonate Rocks”, Soc. Pe-
troleum Engineers J., 1976: 23-30.)
a. Construya una gráfica de caja de estos datos y comente
sobre cualquier característica interesante.
b. ¿Es factible que la muestra fuera seleccionada de una
distribución de población normal?
c. Calcule un intervalo de confianza de 98% para la canti-
dad promedio verdadera de saturación de gas residual.
50. Un artículo publicado en un periódico reporta que se utilizó
una muestra de tamaño 5 como base para calcular un inter-
valo de confianza de 95% para la frecuencia natural (Hz)
promedio verdadera de vigas deslaminadas de cierto tipo.
El intervalo resultante fue (229.764, 233.504). Usted decide
que un nivel de confianza de 99% es más apropiado que el
de 95% utilizado. ¿Cuáles son los límites del intervalo de
99% [Sugerencia: Use el centro del intervalo y su ancho
para determinar x
y s.]
51. El gerente financiero de una gran cadena de tiendas depar-
tamentales seleccionó una muestra aleatoria de 200 de sus
clientes que pagan con tarjeta de crédito y encontró que 136
habían incurrido en pago de intereses durante el año previo
a causa de saldos vencidos.
a. Calcule un intervalo de confianza de 90% para la pro-
porción verdadera de clientes de tarjeta de crédito que
incurrieron en pago de intereses durante el año previo.
b. Si el ancho deseado del intervalo de 90% es de 0.05, ¿qué
tamaño de muestra se requiere para garantizar esto?
c. ¿Especifica el límite superior del intervalo del inciso a)
un límite de confianza superior de 90% para la propor-
ción que se está estimando? Explique.
52. La alta concentración del elemento tóxico arsénico es de-
masiado común en el agua subterránea. El artículo “Evalua-
tion of Treatment Systems for the Removal of Arsenic from
Groundwater” (Practice Periodical of Hazardous, Toxic,
and Radioactive Waste Magmt., 2005: 152-157) reportó que
para una muestra de n 5 especímenes de agua seleccio-
nada para tratamiento por coagulación, la concentración de
arsénico media muestral fue de 24.3 g/l, y la desviación
estándar muestral fue de 4.1. Los autores del artículo citado
utilizaron métodos basados en t para analizar sus datos, así
que venturosamente tuvieron razón al creer que la distribu-
ción de concentración de arsénico era normal.
a. Calcule e interprete un intervalo de confianza de 95%
para concentración de arsénico verdadera en todos los
especímenes de agua.
b. Calcule un límite de confianza superior de 90% para la
desviación estándar de la distribución de la concentra-
ción de arsénico.
c. Pronostique la concentración de arsénico de un solo es-
pécimen de agua de modo que dé información sobre pre-
cisión y confiabilidad.
53. La infestación con pulgones de árboles frutales puede ser
controlada rociando un pesticida o mediante la inundación
con mariquitas. En un área particular, se seleccionan cuatro
diferentes arboledas de árboles frutales para experimenta-
ción. Las primeras tres arboledas se rocían con los pestici-
das 1, 2 y 3, respectivamente y la cuarta se trata con
mariquitas con los siguientes resultados de cosecha:
ni x
i
Número de (Medida de
Tratamiento árboles áridos/árbol) si
1 100 10.5 1.5
2 90 10.0 1.3
3 100 10.1 1.8
4 120 10.7 1.6
Sea i la cosecha promedio verdadera (medida de áridos/
árbol) después de recibir el i-ésimo tratamiento. En ese caso
1
3
(1 2 3) 4
mide la diferencia de las cosechas promedio verdaderas entre
el tratamiento con pesticidas y el tratamiento con mariquitas.
EJERCICIOS SUPLEMENTARIOS (47–62)
c7_p225-283.qxd 3/12/08 4:15 AM Page 281](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-299-320.jpg)
![282 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra
Cuando n1, n2 y n3 son grandes, el estimador ˆ obtenido al
reemplazar cada i con X
i es aproximadamente normal. Use
esto para obtener un intervalo de confianza muestral grande
de 100(1 )% y calcule el intervalo de 95% con los da-
tos dados.
54. Es importante que las máscaras utilizadas por bomberos
sean capaces de soportar altas temperaturas porque los
bomberos comúnmente trabajan en temperaturas de 200-
500°F. En una prueba de un tipo de máscara, a 11 de 55
máscaras se les desprendió la mica a 250°. Construya un in-
tervalo de confianza de 90% para la proporción de másca-
ras verdadera de este tipo cuya mica se desprendería a 250°.
55. Un fabricante de libros de texto universitarios está interesado
en investigar la resistencia de las encuadernaciones produ-
cidas por máquina de encuadernar particular. La resistencia
puede ser medida registrando la fuerza requerida para
arrancar las páginas de la encuadernación. Si esta fuerza se
mide en libras, ¿cuántos libros deberán ser probados para
calcular la fuerza promedio requerida para romper la encua-
dernación dentro de 0.1 lb con 95% de confianza? Suponga
que se sabe que es de 0.8.
56. Es bien sabido que la exposición a la fibra de asbesto es un
riesgo para la salud. El artículo “The Acute Effects of Chry-
sotile Asbestos Exposure on Lung Function” (Environ. Re-
search, 1978: 360-372) reporta resultados sobre un estudio
basado en una muestra de trabajadores de la construcción
que habían estado expuestos a asbesto durante un periodo
prolongado. Entre los datos dados en el artículo se encon-
traron los siguientes valores (ordenados) de elasticidad pul-
monar (cm3
/cm H2O) por cada uno de los 16 sujetos 8
meses después del periodo de exposición (la elasticidad
pulmonar mide la elasticidad de los pulmones o cuán efec-
tivamente los pulmones son capaces de inhalar y exhalar):
167.9 180.8 184.8 189.8 194.8 200.2
201.9 206.9 207.2 208.4 226.3 227.7
228.5 232.4 239.8 258.6
a. ¿Es factible que la distribución de la población sea normal?
b. Calcule un intervalo de confianza de 95% para la elasticidad
pulmonar promedio verdadera después de la exposición.
c. Calcule un intervalo que, con un nivel de confianza de
95%, incluya por lo menos 95% de los valores de elasti-
cidad pulmonar en la distribución de la población.
57. En el ejemplo 6.8, se introdujo el concepto de experimento
censurado en el cual n componentes se prueban y el experi-
mento termina en cuanto r de los componentes fallan. Su-
ponga que las vidas útiles de los componentes son
independientes, cada uno con distribución exponencial y
parámetro . Sea Y1 el tiempo en el cual ocurre la primera
falla, Y2 el tiempo en el cual ocurre la segunda falla, y así
sucesivamente, de modo que Tr Y1 Yr (n r)
Yr, es la vida útil total acumulada. En ese caso se puede de-
mostrar que 2Tr, tiene una distribución ji cuadrada con 2r
grados de libertad. Use esto para desarrollar una fórmula
para un intervalo de confianza de 100(1 )% para una vi-
da útil promedio verdadera 1/. Calcule un intervalo de
confianza de 95% con los datos del ejemplo 6.8.
58. Sean X1, X2, . . . , Xn una muestra aleatoria de una distribu-
ción de probabilidad continua con mediana ~
(de modo que
P(Xi ~
) P(Xi
~
) 0.5).
a. Demuestre que
P(mín(Xi) ~
máx(Xi)) 1 1
2
n1
de modo que (mín(xi), máx(xi)) es un intervalo de confian-
za de 100(1 )% para ~
con 1
2n1
. [Sugerencia:
El complemento del evento {mín(Xi) ~
máx(Xi)} es
{máx(Xi) ~
} {mín(Xi) ~
}. Pero máx(Xi) ~
si y
sólo si Xi ~
con todas las i.]
b. Para cada uno de seis infantes normales varones, se de-
terminó la cantidad de alanina aminoácida (mg/100 ml)
mientras que los infantes llevaban un dieta libre de iso-
leucina y se obtuvieron los siguientes resultados
2.84 3.54 2.80 1.44 2.94 2.70
Calcule un intervalo de confianza de 97% para cantidad
mediana verdadera de alanina para infantes que llevaban
esa dieta (“The Essential Amino-Acid Requirements of
Infants”, Amer. J. Nutrition, 1964: 322-330).
c. Sean x(2) la segunda más pequeña de las xi y x(n1) la se-
gunda más grande de las xi. ¿Cuál es el coeficiente de
confianza del intervalo (x(2), x(n1)) para ~
?
59. Sean X1, X2, . . . , Xn una muestra aleatoria de una distribu-
ción uniforme en el intervalo [0, ], de modo que
f(x)
{1
0 x
0 de lo contrario
Entonces si Y máx(Xi), se puede demostrar que la varia-
ble aleatoria U Y/ tiene una función de densidad
fU(u) {nun1
0 u 1
0 de lo contrario
a. Use fU(u) para verificar que
P(/2)1/n
Y
(1 /2)1/n
1
y use ésta para derivar un intervalo de confianza de
100(1 )% para .
b. Verifique que P(1/n
Y/ 1) 1 y obtenga un
intervalo de confianza de 100(1 )% para basado en
esta proposición de probabilidad.
c. ¿Cuál de los dos intervalos derivados previamente es más
corto? Si mi tiempo de espera en la mañana de un camión
está uniformemente distribuido y los tiempos de espera
observados son x1 4.2, x2 3.5, x3 1.7, x4 1.2 y
x5 2.4 derive un intervalo de confianza de 95% para
utilizando el más corto de los dos intervalos.
60. Sea 0 . Entonces un intervalo de confianza de
100(1 )% para cuando n es grande es
x
z
s
n
, x
z
s
n
La opción de /2 da el intervalo usual derivado en la
sección 7.2; si /2, este intervalo no es simétrico con
respecto a x
. El ancho de este intervalo es w s(z
z )/n
. Demuestre que w se reduce al mínimo con la op-
c7_p225-283.qxd 3/12/08 4:15 AM Page 282](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-300-320.jpg)
![Bibliografía 283
ción /2, de modo que el intervalo simétrico sea el más
corto. [Sugerencia: a) Por definición de z, (z) 1 ,
de modo que z 1
(1 ); b) la relación entre la deri-
vada de una función y f(x) y la función inversa x f 1
(y)
es (d/dy) f 1
(y) 1/f (x).]
61. Suponga que x1, x2, . . . , xn son valores observados resultan-
tes de una muestra aleatoria tomada de una distribución si-
métrica pero posiblemente de cola gruesa. Sean x
~ y fs
la mediana muestral y la dispersión de los cuartos, respec-
tivamente. El capítulo 11 de Understanding Robust and
Exploratory Data Analysis (véase la bibliografía del capítu-
lo 6) sugiere el siguiente intervalo de confianza de 95%
robusto para la media de la población (punto de simetría):
x
~ !
fs
n
El valor de la cantidad entre paréntesis es 2.10 con n 10,
1.94 con n 20 y 1.91 con n 30. Calcule este intervalo
de confianza con los datos del ejercicio 45 y compare con
el intervalo de confianza t apropiado para distribución de
población normal.
62. a. Use los resultados del ejemplo 7.5 para obtener un lími-
te de confianza inferior de 95% para el parámetro de
una distribución exponencial y calcule el límite basado
en los datos dados en el ejemplo.
b. Si la vida útil tiene una distribución exponencial, la pro-
babilidad de que la vida útil exceda de t es P(X t)
e t
. Use el resultado del inciso a) para obtener un lími-
te de confianza inferior de 95% para la probabilidad de
que el tiempo de ruptura exceda de 100 min.
valor crítico t conservador
1.075
DeGroot, Morris y Mark Schervish, Probability and Statistics
(3a. ed.), Addison-Wesley, Reading MA, 2002. Una muy bue-
na exposición de los principios generales de inferencia esta-
dística.
Hahn, Gerald y William Meeker, Statistical Intervals, Wiley,
Nueva York, 1991. Todo lo que alguna vez quiso saber sobre
intervalos estadísticos (de confianza, predicción, tolerancia
y otros).
Larsen, Richard y Morris Marx, Introduction to Mathematical
Statistics: (2a. ed.), Prentice Hall, Englewood, Cliffs, NJ.,
1986. Similar a la presentación de DeGroot, pero un poco me-
nos matemática.
Bibliografía
c7_p225-283.qxd 3/12/08 4:15 AM Page 283](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-301-320.jpg)
![8.1 Hipótesis y procedimientos de prueba 293
EJERCICIOS Sección 8.1 (1-14)
1. Por cada una de las siguientes aseveraciones, exprese si es
una hipótesis estadística legítima y por qué:
a. H: 100 b. H: x
~ 45
c. H: s 0.20 d. H: 1/2 1
e. H: X
Y
5
f. H: 0.01 donde es el parámetro de una distribución
exponencial utilizada para modelar la vida útil de un
componente.
2. Para los siguientes pares de aseveraciones, indique cuáles
no satisfacen las reglas de establecer hipótesis y por qué
(los subíndices 1 y 2 diferencian las cantidades de dos po-
blaciones o muestras diferentes).
a. H0: 100, Ha: 100
b. H0: 20, Ha: 20
c. H0: p 0.25, Ha: p 0.25
d. H0: 1 2 25, Ha: 1 2 100
e. H0: S2
1 S2
2, Ha: S2
1 S2
2
f. H0: 120, Ha: 150
g. H0: 1/2 1, Ha: 1/2 1
h. H0: p1 p2 0.1, Ha: p1 p2 0.1
3. Para determinar si las soldaduras de las tuberías en una
planta de energía nuclear satisfacen las especificaciones, se
selecciona una muestra aleatoria de soldaduras y se realizan
pruebas en cada una de las soldaduras. La resistencia de la
soldadura se mide como la fuerza requerida para romperla.
Suponga que las especificaciones indican que la resistencia
media de las soldaduras deberá exceder de 100 lb/pulg2
; el
equipo de inspección decide probar H0: 100 contra Ha:
100. Explique por qué podría ser preferible utilizar
esta Ha en lugar de 100.
4. Sea el nivel de radioactividad promedio verdadero (pico-
curies por litro). Se considera que el valor 5 pCi/L es la lí-
nea divisoria entre agua segura e insegura. ¿Recomendaría
probar H0: 5 contra Ha: 5 o H0: 5 contra Ha:
5? Explique su razonamiento. [Sugerencia: Piense en
las consecuencias de un error de tipo I o de un error de tipo
II con cada posibilidad.]
5. Antes de aprobar un gran pedido de fundas de polietileno
para un tipo particular de cable de energía submarino relle-
no de aceite a alta presión, una compañía desea contar con
evidencia conclusiva de la desviación estándar verdadera
del espesor de la funda es de menos de 0.05 mm. ¿Qué hi-
pótesis deberán ser probadas y por qué? En este contexto,
¿Cuáles son los errores de tipo I y II?
6. Muchas casas viejas cuentan con sistemas eléctricos que uti-
lizan fusibles en lugar de cortacircuitos. Un fabricante de fu-
sibles de 40 amp desea asegurarse de que el amperaje medio
al cual se queman sus fusibles es en realidad de 40. Si el am-
peraje medio es menor que 40, los clientes se quejarán porque
los fusibles tienen que ser reemplazados con demasiada fre-
cuencia. Si el amperaje medio es de más de 40, el fabricante
podría ser responsable de los daños que sufra un sistema eléc-
trico a causa del funcionamiento defectuoso de los fusibles.
Para verificar el amperaje de los fusibles, se selecciona e ins-
pecciona una muestra de fusibles. Si tuviera que realizarse
una prueba de hipótesis con los datos resultantes, ¿Qué hipó-
tesis nula y alternativa sería de interés para el fabricante? Des-
criba los errores de tipo I y II en el contexto de este problema.
7. Se toman muestras de agua utilizada para enfriamiento al mo-
mento de ser descargada por una planta de energía en un río.
Se ha determinado que en tanto la temperatura media del agua
descargada sea cuando mucho de 150°F, no habrá efectos ne-
gativos en el ecosistema del río. Para investigar si la planta
cumple con los reglamentos que prohíben una temperatura
media por encima de 150° del agua de descarga, se tomarán al
azar 50 muestras de agua y se registrará la temperatura de ca-
da muestra. Los datos resultantes se utilizarán para probar la
hipótesis H0: 150° contra Ha: 150°. En el contexto
de esta situación, describa los errores de tipo I y tipo II. ¿Qué
tipo de error consideraría más serio? Explique.
8. Un tipo regular de laminado está siendo utilizado por un fa-
bricante de tarjetas de circuito. Un laminado especial ha si-
do desarrollado para reducir el alabeo. El laminado regular
será utilizado en una muestra de especímenes y el laminado
especial en otra muestra y se determinará entonces la canti-
dad de alabeo en cada espécimen. El fabricante cambiará
entonces al laminado especial sólo si puede demostrar que
la cantidad de alabeo promedio verdadera de dicho lamina-
do es menor que la del laminado regular. Formule las hipó-
tesis pertinentes y describa los errores de tipo I y de tipo II
en el contexto de esta situación.
9. Dos compañías diferentes han solicitado proporcionar el
servicio de televisión por cable en una cierta región. Sea p
la proporción de todos los suscriptores potenciales que
favorecen a la primera compañía sobre la segunda. Consi-
dere probar H0: p 0.5 contra Ha: p 0.5 basado en una
muestra aleatoria de 25 individuos. Sea X el número en
la muestra que favorece a la primera compañía y x el valor
observado de X.
a. ¿Cuál de las siguientes regiones de rechazo es más apro-
piada y por qué?
R1 {x: x 7 o x 18}, R2 {x: x 8},
R3 {x: x 17}
b. En el contexto de este problema, describa cuáles son los
errores de tipo I y de tipo II.
c. ¿Cuál es la distribución de probabilidad del estadístico
de prueba X cuando H0 es verdadera? Úsela para calcu-
lar la probabilidad de un error de tipo I.
d. Calcule la probabilidad de un error de tipo II en la región
seleccionada cuando p 0.3, otra vez cuando p 0.4 y
también con p 0.6 y p 0.7.
e. Utilizando la región seleccionada, ¿qué concluiría si 6 de
los 25 individuos encuestados favorecen a la compañía 1?
10. Una mezcla de cenizas combustibles pulverizadas y cemento
Portland utilizada para rellenar con lechada deberá tener
una resistencia a la compresión de más de 1300 KN/m2
.
La mezcla no será utilizada a menos que la evidencia expe-
rimental indique concluyentemente que la especificación de
resistencia ha sido satisfecha. Suponga que la resistencia a
la compresión de especímenes de esta muestra está normal-
mente distribuida con 60. Sea la resistencia a la com-
presión promedio verdadera.
c8_p284-324.qxd 3/12/08 4:17 AM Page 293](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-311-320.jpg)
![procedimientos generales y sus propiedades pueden ser desarrollados. La hipótesis nula en
los tres casos propondrá que tiene un valor numérico particular, el valor nulo, el cual se-
rá denotado por 0. Sean X1, . . . , Xn una muestra aleatoria de tamaño n de la población
normal. Entonces la media muestral X
tiene una distribución normal con valor esperado
X
y desviación estándar X
/n
. Cuando H0 es verdadera X
0. Considére-
se ahora el estadístico Z obtenido estandarizando X
de conformidad con la suposición de
que H0 es verdadera:
Z
Al sustituir la media muestral calculada x
se obtiene z, la distancia entre x
y 0 expresada
en “unidades de desviación estándar”. Por ejemplo, si la hipótesis nula es H0: 100,
X
/n
10/2
5
2.0 y x
103, entonces el valor estadístico de prueba es z
(103 – 100)/2.0 1.5. Es decir, el valor observado de x
es 1.5 desviaciones estándar (de X
)
más grande de lo que se espera sea cuando H0 es verdadera. El estadístico Z es una medida
natural de la distancia X
, el estimador de y su valor esperado cuando H0 es verdadera. Si
esta distancia es demasiado grande en una dirección consistente con Ha, la hipótesis nula de-
berá ser rechazada.
Supóngase primero que la hipótesis alternativa tiene la forma Ha: 0. Entonces
un valor de x
menor que 0 indudablemente no apoya a Ha. Tal x
corresponde a un valor ne-
gativo de z (puesto que x
0 es negativa y el divisor de /n
es positivo). Del mismo
modo, un valor de x
que exceda de 0 por sólo una pequeña cantidad (correspondiente a z
la cual es positiva aunque pequeña) no sugiere que H0 deberá ser rechazada a favor de Ha.
El rechazo de H0 es apropiado sólo cuando x
excede considerablemente de 0, es decir,
cuando el valor de z es positivo y grande. En suma, la región de rechazo apropiada basada
en el estadístico de prueba Z en lugar de X
tiene la forma z c.
Como se discutió en la sección 8.1, el valor de corte c deberá ser elegido para contro-
lar la probabilidad de un error de tipo I al nivel deseado. Esto es fácil de lograr porque la
distribución del estadístico de prueba Z cuando H0 es verdadera es la distribución normal es-
tándar (es por eso que 0 se restó al estandarizar). El valor c de corte requerido es el valor
crítico z que captura el área de la cola superior bajo la curva z. Como ejemplo, sea c
1.645, el valor que captura el área de cola 0.05 (z0.05 1.645). Entonces,
P(error de tipo I) P(H0 es rechazada cuando H0 es verdadera)
P(Z 1.645 cuando Z N(0, 1)) 1 (1.645) 0.05
Más generalmente, la región de rechazo z z tiene un probabilidad de error de tipo I . El
procedimiento de prueba es de cola superior porque la región de rechazo se compone de só-
lo valores grandes del estadístico de prueba.
Un razonamiento análogo para la hipótesis alternativa Ha: 0 sugiere una región
de rechazo de la forma z c, donde c es un número negativo adecuadamente seleccionado
(x
aparece muy debajo de 0 si y sólo si z es bastante negativo). Como Z tiene una distribu-
ción normal estándar cuando H0 es verdadera, con c z da P(error de tipo I) . Esta
es una prueba de cola inferior. Por ejemplo, z0.10 1.28 implica que la región de rechazo
z 1.28 especifica una prueba con nivel de significación de 0.10.
Por último, cuando la hipótesis alternativa es Ha: 0, H0 deberá ser rechazada si
x
está muy lejos a ambos lados de 0. Esto equivale a rechazar H0 si z c o si z c. Su-
póngase que se desea 0.05. Entonces,
0.05 P(Z c o Z c cuando Z tiene una distribución normal estándar)
(c) 1 (c) 2[1 (c)]
Por consiguiente c es tal que 1 (c), el área bajo la curva z a la derecha de c, es 0.025 (¡y
no 0.05!). De acuerdo con la sección 4.3 o la tabla A.3, c 1.96 y la región de rechazo
X
0
/n
8.2 Pruebas sobre una media de población 295
c8_p284-324.qxd 3/12/08 4:17 AM Page 295](https://image.slidesharecdn.com/probabilidadyestadisticaparaingenieriayciencias-jaydevore-septimaedicion-221220025744-1738d482/85/Probabilidad-y-Estadistica-para-Ingenieria-y-Ciencias-Jay-Devore-Septima-Edicion-pdf-313-320.jpg)
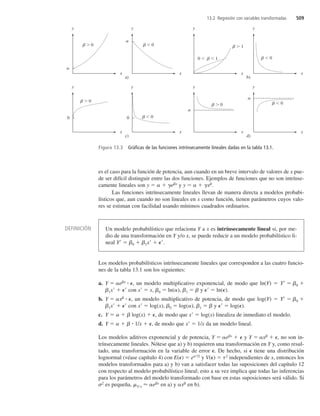
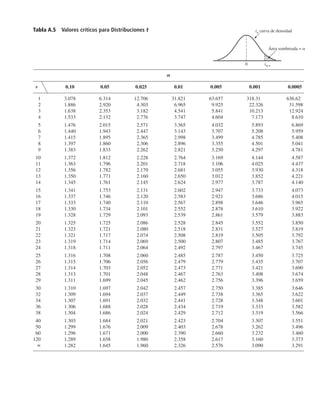
Probabilidad y Estadistica para Ingenieria y Ciencias - Jay Devore - Septima Edicion.pdf
- 2. 00Ander(i-xxviii).qxd 2/29/08 10:41 AM Page iv
- 3. SÉPTIMA EDICIÓN Probabilidad y Estadística para Ingeniería y Ciencias Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page i
- 4. Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page ii
- 5. Probabilidad y Estadística para Ingeniería y Ciencias JAY L. DEVORE California Polytechnic State University, San Luis Obispo Traducción Jorge Humberto Romo Traductor profesional Revisión Técnica A. Leonardo Bañuelos Saucedo Profesor de carrera titular Facultad de Ingeniería Universidad Nacional Autónoma de México Australia • Brasil • Corea • España • Estados Unidos • Japón • México • Singapur • Reino Unido SÉPTIMA EDICIÓN Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page iii
- 6. Probabilidad y Estadística para Ingeniería y Ciencias Séptima edición Jay L. Devore Presidente de Cengage Learning Latinoamérica: Javier Arellano Gutiérrez Director general México y Centroamérica: Héctor Enrique Galindo Iturribarría Director editorial Latinoamérica: José Tomás Pérez Bonilla Director de producción: Raúl D. Zendejas Espejel Editor: Sergio R. Cervantes González Editora de producción: Abril Vega Orozco Ilustrador: Lori Heckelman / Graphic World, International Typesetting and Composition Diseño de portada: Grupo Insigne OTA S. A. de C. V. Composición tipográfica: EDITEC, S.A. de C.V © D.R. 2008 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Corporativo Santa Fe Av. Santa Fe núm. 505, piso 12 Col. Cruz Manca, Santa Fe C.P. 05349, México, D.F. Cengage Learning™ es una marca registrada usada bajo permiso. DERECHOS RESERVADOS. Ninguna parte de este trabajo amparado por la Ley Federal del Derecho de Autor, podrá ser reproducida, transmitida, almacenada o utilizada en cualquier forma o por cualquier medio, ya sea gráfico, electrónico o mecánico, incluyendo, pero sin limitarse a lo siguiente: fotocopiado, reproducción, escaneo, digitalización, grabación en audio, distribución en Internet, distribución en redes de información o almacenamiento y recopilación en sistemas de información a excepción de lo permitido en el Capítulo III, Artículo 27 de la Ley Federal del Derecho de Autor, sin el consentimiento por escrito de la Editorial. Traducido del libro Probability and Statistics for Engineering and the Sciences. Seventh Edition. Publicado en inglés por Brooks/Cole © 2008 ISBN: 0-495-38217-5 Datos para catalogación bibliográfica: Devore, Jay L. Probabilidad y Estadística para Ingeniería y Ciencias. Séptima edición. ISBN-13: 978-607-481-338-8 ISBN-10: 607-481-338-8 Visite nuestro sitio en: http://latinoamerica.cengage.com Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page iv
- 7. v A mi esposa Carol: Su esmero en la enseñanza es una continua inspiración para mí. A mis hijas, Allison y Teresa: Con gran orgullo admito sus logros que no conocen ningún límite. Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page v
- 8. Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page vi
- 9. vii Contenido Introducción 1 1.1 Poblaciones, muestras y procesos 2 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 10 1.3 Medidas de localización 24 1.4 Medidas de variabilidad 31 Ejercicios suplementarios 42 Bibliografía 45 1 Generalidades y estadística descriptiva 2 Probabilidad Introducción 46 2.1 Espacios muestrales y eventos 47 2.2 Axiomas, interpretaciones y propiedades de probabilidad 51 2.3 Técnicas de conteo 59 2.4 Probabilidad condicional 67 2.5 Independencia 76 Ejercicios suplementarios 82 Bibliografía 85 Introducción 86 3.1 Variables aleatorias 87 3.2 Distribuciones de probabilidad para variables aleatorias discretas 90 3.3 Valores esperados 100 3.4 Distribución de probabilidad binomial 108 3.5 Distribuciones hipergeométricas y binomiales negativas 116 3.6 Distribución de probabilidad de Poisson 121 Ejercicios suplementarios 126 Bibliografía 129 3 Variables aleatorias discretas y distribuciones de probabilidad Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page vii
- 10. viii Contenido Introducción 130 4.1 Funciones de densidad de probabilidad 131 4.2 Funciones de distribución acumulativa y valores esperados 136 4.3 Distribución normal 144 4.4 Distribuciones exponencial y gama 157 4.5 Otras distribuciones continuas 163 4.6 Gráficas de probabilidad 170 Ejercicios suplementarios 179 Bibliografía 183 4 Variables aleatorias continuas y distribuciones de probabilidad Introducción 184 5.1 Variables aleatorias conjuntamente distribuidas 185 5.2 Valores esperados, covarianza y correlación 196 5.3 Estadísticos y sus distribuciones 202 5.4 Distribución de la media muestral 213 5.5 Distribución de una combinación lineal 219 Ejercicios suplementarios 224 Bibliografía 226 Introducción 254 7.1 Propiedades básicas de los intervalos de confianza 255 7.2 Intervalos de confianza de muestra grande para una media y proporción de población 263 Introducción 227 6.1 Algunos conceptos generales de estimación puntual 228 6.2 Métodos de estimación puntual 243 Ejercicios suplementarios 252 Bibliografía 253 5 Distribuciones de probabilidad conjunta y muestras aleatorias 6 Estimación puntual 7 Intervalos estadísticos basados en una sola muestra Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page viii
- 11. 7.3 Intervalos basados en una distribución de población normal 270 7.4 Intervalos de confianza para la varianza y desviación estándar de una población normal 278 Ejercicios suplementarios 281 Bibliografía 283 Contenido ix Introducción 284 8.1 Hipótesis y procedimientos de prueba 285 8.2 Pruebas sobre una media de población 294 8.3 Pruebas relacionadas con una proporción de población 306 8.4 Valores P 311 8.5 Algunos comentarios sobre la selección de una prueba 318 Ejercicios suplementarios 321 Bibliografía 324 Introducción 369 10.1 ANOVA unifactorial 370 10.2 Comparaciones múltiples en ANOVA 379 10.3 Más sobre ANOVA unifactorial 385 Ejercicios suplementarios 395 Bibliografía 396 Introducción 325 9.1 Pruebas z e intervalos de confianza para una diferencia entre dos medias de población 326 9.2 Prueba t con dos muestras e intervalo de confianza 336 9.4 Inferencias sobre una diferencia entre proporciones de población 353 9.5 Inferencias sobre dos varianzas de población 360 Ejercicios suplementarios 364 Bibliografía 368 8 Pruebas de hipótesis basadas en una sola muestra 9 Inferencias basadas en dos muestras 10 Análisis de la varianza Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page ix
- 12. Introducción 397 11.1 ANOVA bifactorial con Kij 1 398 11.2 ANOVA bifactorial con Kij 1 410 11.3 ANOVA con tres factores 419 11.4 Experimentos 2p factoriales 429 Ejercicios suplementarios 442 Bibliografía 445 x Contenido 12 Regresión lineal simple y correlación 13 Regresión múltiple y no lineal 11 Análisis de varianza con varios factores Introducción 446 12.1 Modelo de regresión lineal simple 447 12.2 Estimación de parámetros de modelo 454 12.3 Inferencias sobre el parámetro de pendiente 1 468 12.4 Inferencias sobre Yx* y predicción de valores Y futuros 477 12.5 Correlación 485 Ejercicios suplementarios 494 Bibliografía 499 Introducción 500 13.1 Aptitud y verificación del modelo 501 13.2 Regresión con variables transformadas 508 13.3 Regresión con polinomios 519 13.4 Análisis de regresión múltiple 528 13.5 Otros problemas en regresión múltiple 550 Ejercicios suplementarios 562 Bibliografía 567 Introducción 568 14.1 Pruebas de bondad de ajuste cuando las probabilidades categóricas se satisfacen por completo 569 14.2 Pruebas de bondad de ajuste para hipótesis compuestas 576 14 Pruebas de bondad de ajuste y análisis de datos categóricos Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page x
- 13. 14.3 Tablas de contingencia mutuas (o bidireccionales) 587 Ejercicios suplementarios 595 Bibliografía 598 Contenido xi 15 Procedimientos sin distribución 16 Métodos de control de calidad Apéndice/Tablas Introducción 599 15.1 La prueba Wilcoxon de rango con signo 600 15.2 Prueba Wilcoxon de suma de rangos 608 15.3 Intervalos de confianza sin distribución 614 15.4 ANOVA sin distribución 618 Ejercicios suplementarios 622 Bibliografía 624 Introducción 625 16.1 Comentarios generales sobre gráficas de control 626 16.2 Gráficas de control para ubicación de proceso 627 16.3 Gráficas de control para variación de proceso 637 16.4 Gráficas de control para atributos 641 16.5 Procedimientos CUSUM 646 16.6 Muestreo de aceptación 654 Ejercicios suplementarios 660 Bibliografía 661 A.1 Distribuciones binomiales acumulativas 664 A.2 Distribuciones acumulativas de Poisson 666 A.3 Áreas de la Curva normal estándar 668 A.4 La Función Gamma incompleta 670 A.5 Valores críticos para Distribuciones t 671 A.6 Valores críticos de tolerancia para distribuciones normales de población 672 A.7 Valores críticos para distribuciones chi-cuadrada 673 A.8 Curva t para áreas de cola 674 A.9 Valores críticos para distribuciones F 676 A.10 Valores críticos para distribuciones de rango estudentizado 682 Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page xi
- 14. A.11 Curvas chi-cuadrada para áreas de cola 683 A.12 Valores críticos para la prueba de normalidad Ryan-Joiner 685 A.13 Valores críticos para la prueba Wilcoxon de rangos con signo 686 A.14 Valores críticos para la prueba Wilcoxon de suma de rangos 687 A.15 Valores críticos para el intervalo Wilcoxon de rangos con signo 688 A.16 Valores críticos para el intervalo Wilcoxon de suma de rangos 689 A.17 Curvas para pruebas t 690 Respuestas a ejercicios seleccionados de número impar 691 Índice 710 xii Contenido Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page xii
- 15. xiii Propósito El uso de modelos de probabilidad y métodos estadísticos para analizar datos se ha conver- tido en una práctica común en virtualmente todas las disciplinas científicas. Este libro pre- tende introducir con amplitud aquellos modelos y métodos que con mayor probabilidad se encuentran y utilizan los estudiantes en sus carreras de ingeniería y las ciencias naturales. Aun cuando los ejemplos y ejercicios se diseñaron pensando en los científicos e ingenieros, la mayoría de los métodos tratados son básicos en los análisis estadísticos en muchas otras disciplinas, por lo que los estudiantes de las ciencias administrativas y sociales también se beneficiarán con la lectura del libro. Enfoque Los estudiantes de un curso de estadística diseñado para servir a otras especialidades de es- tudio al principio es posible que duden del valor pertinencia de la materia, pero mi experien- cia es que los estudiantes pueden ser conectados a la estadística con el uso de buenos ejemplos y ejercicios que combinen sus experiencias diarias con sus intereses científicos. Así pues, he trabajado duro para encontrar ejemplos reales y no artificiales, que alguien pen- só que valía la pena recopilar y analizar. Muchos de los métodos presentados, sobre todo en los últimos capítulos sobre inferencia estadística, se ilustran analizando datos tomados de una fuente publicada y muchos de los ejercicios también implican trabajar con dichos da- tos. En ocasiones es posible que el lector no esté familiarizado con el contexto de un pro- blema particular (como muchas veces yo lo estuve), pero me di cuenta que los problemas reales atraen más a los estudiantes con un contexto un tanto extraño que por problemas de- finitivamente artificiales en un entorno conocido. Nivel matemático La exposición es relativamente modesta en función de desarrollo matemático. El uso sus- tancial del cálculo se hace sólo en el capítulo 4 y en partes de los capítulos 5 y 6. En par- ticular, con excepción de una observación o nota ocasional, el cálculo aparece en la parte de inferencia del libro sólo en la segunda sección del capítulo 6. No se utiliza álgebra matricial en absoluto. Por lo tanto, casi toda la exposición deberá ser accesible para aquellos cuyo co- nocimiento matemático incluye un semestre o dos trimestres de cálculo diferencial e in- tegral. Contenido El capítulo 1 se inicia con algunos conceptos y terminología básicos (población, muestra, estadística descriptiva e inferencial, estudios enumerativos contra analíticos, y así sucesiva- mente) y continúa con el estudio de métodos descriptivos gráficos y numéricos importantes. En el capítulo 2 se ofrece el desarrollo un tanto tradicional de la probabilidad, seguido por distribuciones de probabilidad de variables aleatorias continuas y discretas en los capítulos 3 y 4, respectivamente. Las distribuciones conjuntas y sus propiedades se analizan en la pri- mera parte del capítulo 5. La última parte de este capítulo introduce la estadística y sus dis- tribuciones muestrales, las cuales constituyen el puente entre probabilidad e inferencia. Los siguientes tres capítulos se ocupan de la estimación puntual, los intervalos estadísticos y la comprobación de hipótesis basados en una muestra única. Los métodos de inferencia que implican dos muestras independientes y datos apareados se presentan en el capítulo 9. El análisis de la varianza es el tema de los capítulos 10 y 11 (unifactorial y multifactorial, Prefacio Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page xiii
- 16. xiv Prefacio respectivamente). La regresión aparece por primera vez en el capítulo 12 (el modelo de re- gresión lineal simple y correlación) y regresa para una amplia repetición en el capítulo 13. Los últimos tres capítulos analizan métodos de ji cuadrada, procedimientos sin distribución (no paramétricos) y técnicas de control de calidad estadístico. Ayuda para el aprendizaje de los estudiantes Aunque el nivel matemático del libro representará poca dificultad para la mayoría de los es- tudiantes de ciencia e ingeniería, es posible que el trabajo dirigido hacia la comprensión de los conceptos y apreciación del desarrollo lógico de la metodología en ocasiones requiera un esfuerzo sustancial. Para ayudar a que los estudiantes ganen en comprensión y aprecia- ción he proporcionado numerosos ejercicios de dificultad variable desde muchos que impli- can la aplicación rutinaria del material incluido en el texto hasta algunos que piden al lector que extienda los conceptos analizados en el texto a situaciones un tanto nuevas. Existen mu- chos ejercicios que la mayoría de los profesores desearía asignar durante cualquier curso particular, pero recomiendo que se les pida a los estudiantes que resuelvan un número sus- tancial de ellos; en una disciplina de solución de problemas, el compromiso activo de esta clase es la forma más segura de identificar y cerrar las brechas en el entendimiento que ine- vitablemente surgen. Las respuestas a la mayoría de los ejercicios impares aparecen en la sección de respuestas al final del texto. Además, está disponible un Manual de Soluciones para el Estudiante, que incluye soluciones resueltas de casi todos los ejercicios de número impar. Nuevo en esta edición • Ejercicios y ejemplos nuevos, muchos basados en fuentes publicadas que incluyen datos reales. Algunos de los ejercicios permiten una interpretación más amplia de los ejerci- cios tradicionales que incluyen cuestiones muy específicas y algunos de éstos implican material de las primeras secciones y capítulos. • El material de los capítulos 2 y 3 sobre propiedades de probabilidad, conteo y tipos de va- riables aleatorias se reescribió para alcanzar una mayor claridad. • La sección 3.6 sobre la distribución de Poisson ha sido revisada, incluido el material nue- vo sobre la aproximación de Poisson a la distribución binomial y la reorganización de la subsección sobre procesos de Poisson. • El material de la sección 4.4 sobre distribuciones gama y exponencial ha sido reordenado de tal suerte que las segundas aparecen antes que las primeras. Esto es muy conveniente para aquellos que desean abordar la distribución exponencial y evitar la distribución gama. • Una breve introducción al error en la media de los cuadrados en la sección 6.1 ahora apa- rece como ayuda para motivar la propiedad de insesgabilidad y se da un ejemplo nuevo que ilustra la posibilidad de tener más de un solo estimador insesgado razonable. • Existe un énfasis disminuido en los cálculos manuales en el ANOVA multifactorial para reflejar el hecho de que ahora hay software apropiado ampliamente disponible y ahora se incluyen gráficas residuales para verificar suposiciones de modelo. • Se han realizado miles de pequeños cambios en la redacción a lo largo del libro para me- jorar las explicaciones y pulir la exposición. • El sitio web incluye applets Java™ creados por Gary McClelland, específicamente para este texto basado en el cálculo, así como también conjuntos de datos tomados del texto principal. • WebAssign, el sistema de asignación de tareas más ampliamente utilizado en la educación superior, permite asignar, reunir, calificar y registrar tareas vía la web. Este comprobado sistema de asignación de tareas ha sido mejorado para incluir vínculos al contenido espe- cífico del texto, ejemplos de video y tutoriales propios del problema. Disponible para es- te libro, Enhanced WebAssign es más que un sistema de asignación de tareas; es un completo sistema de aprendizaje para los estudiantes. Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page xiv
- 17. Material de apoyo para el profesor Este libro cuenta con una serie de recursos para el profesor, los cuales están disponibles en el inglés y sólo se proporcionan a los docentes que lo adopten como texto en sus cursos. Para mayor información, póngase en contacto con el área de servicio a clientes en las siguientes direcciones de correo electrónico: Cengage Learning México y Centroamérica [email protected] Cengage Learning Caribe [email protected] Cengage Learning Cono Sur [email protected] Cengage Learning Paraninfo [email protected] Cengage Learning Pacto Andino [email protected] Los recursos disponibles se encuentran en el sitio web del libro: http: //latinoamerica.cengage.com/devore Las direcciones de los sitios web referidas en el texto no son administradas por Cengage Learning Latinoamérica, por lo que ésta no es responsable de los cambios o actualizaciones de las mismas. Prefacio xv Reconocimentos Mis colegas en Cal Poly me proporcionaron apoyo y retroalimentación invaluables durante el curso de los años. También agradezco a los muchos usuarios de ediciones previas que me sugirieron mejoras (y en ocasiones errores identificados). Una nota especial de agradecimien- to va para Matt Carlton por su trabajo en los dos manuales de soluciones, uno para profeso- res y el otro para estudiantes. Y me he beneficiado mucho de un diálogo que tuve con Doug Bates sobre el contenido, aun cuando no siempre he estado de acuerdo con sus muy preca- vidas sugerencias. La generosa retroalimentación provista por los siguientes revisores de ésta y previas ediciones, ha sido de mucha ayuda para mejorar el libro: Robert L. Armacost, University of Central Florida; Bill Bade, Lincoln Land Community College; Douglas M. Bates, Univer- sity of Wisconsin-Madison; Michael Berry, West Virginia Wesleyan College; Brian Bow- man, Auburn University; Linda Boyle, University of lowa; Ralph Bravaco, Stonehill College; Linfield C. Brown, Tufts University; Karen M. Bursic, University of Pittsburgh; Lynne Butler, Haverford College; Raj S. Chhikara, University of Houston-Clear Lake; Ed- win Chong, Colorado State University; David Clark, California State Polytechnic Univer- sity en Pomona; Ken Constantine, Taylor University; David M. Cresap, University of Portland; Savas Dayanik, Princeton University; Don E. Deal, University of Houston; Ann- janette M. Dodd, Humboldt State University; Jimmy Doi, California Polytechnic State Uni- versity-San Luis Obispo; Charles E. Donaghey, University of Houston; Patrick J. Driscoll, U.S. Military Academy; Mark Duva, University of Virginia; Nassir Eltinay, Lincoln Land Community College; Thomas English, College of the Mainland; Nasser S. Fard, Northeas- tern University; Ronald Fricker, Naval Postgraduate School; Steven T. Garren, James Madi- son University; Harland Glaz, University of Maryland; Ken Grace, Anoka-Ramsey Community College; Celso Grebogi, University of Maryland; Veronica Webster Griffis, Mi- chigan Technological University; Jose Guardiola, Texas AM University-Corpus Christi; K.L.D. Gunawardena, University of Wisconsin-Oshkosh; James J. Halavin, Rochester Institute of Technology; James Hartman, Marymount University; Tyler Haynes, Saginaw Valley State University; Jennifer Hoeting, Colorado State University; Wei-Min Huang, Lehigh University; Roger W. Johnson, South Dakota School of Mines Technology; Chih- wa Kao, Syracuse University; Saleem A. Kassam, University of Pennsylvania; Mohammad T. Khasawneh, State University of NewYork-Binghamton; Stephen Kokoska, Colgate Uni- versity; Sarah Lam, Binghamton University; M. Louise Lawson, Kennesaw State Univer- sity; Jialiang Li, University of Wisconsin-Madison; Wooi K. Lim, William Paterson Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page xv
- 18. xvi Prefacio University; Aquila Lipscomb, The Citadel; Manuel Lladser, University of Colorado en Boulder; Graham Lord, University of Califomia-Los Angeles; Joseph L. Macaluso, DeSales University; Ranjan Maitra, Iowa State University; David Mathiason, Rochester Institute of Technology; Arnold R. Miller, University of Denver; John J. Millson, University of Mary- land; Pamela Kay Miltenberger, West Virginia Wesleyan College; Monica Molsee, Portland State University; Thomas Moore, Naval Postgraduate School; Robert M. Norton, College of Charleston; Steven Pilnick, Naval Postgraduate School; Robi Polikar, Rowan University; Ernest Pyle, Houston Baptist University; Steve Rein, California Polytechnic State Uni- versity-San Luis Obispo; Tony Richardson, University of Evansville; Don Ridgeway, North Carolina State University; Larry J. Ringer, TexasAM University; Robert M. Schumacher, Ce- darville University; Ron Schwartz, Florida Atlantic University; Kevan Shafizadeh, California State University-Sacramento; Robert K. Smidt, California Polytechnic State University-San Luis Obispo; Alice E. Smith, Auburn University; James MacGregor Smith, University of Massachusetts; Paul J. Smith, University of Maryland; Richard M. Soland, The George Washington University; Clifford Spiegelman, Texas AM University; Jery Stedinger, Cor- nell University; David Steinberg, Tel Aviv University; William Thistleton, State University of New York Institute of Technology; G. Geoffrey Vining, University of Florida; Bhutan Wadhwa, Cleveland State University; Elaine Wenderholm, State University of New York- Oswego; Samuel P. Wilcock, Messiah College; Michael G. Zabetakis, University of Pitts- burgh y Maria Zack, Point Loma Nazarene University. Gracias a Merrill Peterson y sus colegas en Matrix Productions por hacer el proce- so de producción lo menos embarazoso posible. Una vez más me siento obligado a expresar mi gratitud a todas las personas que han hecho importantes contribuciones a lo largo de sie- te ediciones del libro. En particular, Carolyn Crockett ha sido tanto una editora de primera clase como una buena amiga. Jennifer Risden, Joseph Rogove, Ann Day, Elizabeth Gersh- man y Ashley Summers merecen una mención especial por sus recientes esfuerzos. También deseo extender mi aprecio a los cientos de representantes de ventas quienes durante los úl- timos 20 años han predicado hábilmente el evangelio sobre este libro y otros que he escri- to. Por último pero no menos importante, un sincero agradecimiento a mi esposa Carol por tolerar mi programa de trabajo y mis frecuentes y demasiadas quejas a lo largo de mi carre- ra de escritor. Jay Devore Prels_p00i-xvi.qxd 3/12/08 10:17 AM Page xvi
- 19. 1 1 Generalidades y estadística descriptiva INTRODUCCIÓN Los conceptos y métodos estadísticos no son sólo útiles sino que con frecuencia son in- dispensables para entender el mundo que nos rodea. Proporcionan formas de obtener ideas nuevas del comportamiento de muchos fenómenos que se presentarán en su campo de especialización escogido en ingeniería o ciencia. La disciplina de estadística nos enseña cómo realizar juicios inteligentes y tomar decisiones informadas entre la presencia de incertidumbre y variación. Sin incerti- dumbre y variación, habría poca necesidad de métodos estadísticos o de profesionales en estadística. Si cada componente de un tipo particular tuviera exactamente la mis- ma duración, si todos los resistores producidos por un fabricante tuvieran el mismo valor de resistencia, si las determinaciones del pH en muestras de suelo de un lugar particular dieran resultados idénticos, y así sucesivamente, entonces una sola obser- vación revelaría toda la información deseada. Una importante manifestación de variación surge en el curso de la medición de emisiones en vehículos automotores. Los requerimientos de costo y tiempo del Fede- ral Test Procedure (FTP, por sus siglas en inglés) impiden su uso generalizado en pro- gramas de inspección de vehículos. En consecuencia, muchas agencias han creado pruebas menos costosas y más rápidas, las que se espera reproduzcan los resultados obtenidos con el FTP. De acuerdo con el artículo “Motor Vehicle Emissions Variabi- lity” (J. of the Air and Waste Mgmt. Assoc., 1996: 667-675), la aceptación del FTP como patrón de oro ha llevado a la creencia ampliamente difundida de que las me- diciones repetidas en el mismo vehículo conducirían a resultados idénticos (o casi idénticos). Los autores del artículo aplicaron el FTP a siete vehículos caracterizados como “altos emisores”. He aquí los resultados de uno de los vehículos. HC (g/milla) 13.8 18.3 32.2 32.5 CO (g/milla) 118 149 232 236 c1_p001-045.qxd 3/12/08 2:31 AM Page 1
- 20. La variación sustancial en las mediciones tanto de HC como de CO proyecta una du- da considerable sobre la sabiduría convencional y hace mucho más difícil realizar eva- luaciones precisas sobre niveles de emisiones. ¿Cómo se pueden utilizar técnicas estadísticas para reunir información y sacar conclusiones? Supóngase, por ejemplo, que un ingeniero de materiales inventó un re- cubrimiento para retardar la corrosión en tuberías de metal en circunstancias específi- cas. Si este recubrimiento se aplica a diferentes segmentos de la tubería, la variación de las condiciones ambientales y de los segmentos mismos producirá más corrosión sus- tancial en algunos segmentos que en otros. Se podría utilizar un análisis estadístico en datos de dicho experimento para decidir si la cantidad promedio de corrosión excede un límite superior especificado de alguna clase o para predecir cuánta corrosión ocu- rrirá en una sola pieza de tubería. Por otra parte, supóngase que el ingeniero inventó el recubrimiento con la creen- cia de que será superior al recubrimiento actualmente utilizado. Se podría realizar un experimento comparativo para investigar esta cuestión aplicando el recubrimiento ac- tual a algunos segmentos de la tubería y el nuevo a otros segmentos. Esto debe reali- zarse con cuidado o se obtendrá una conclusión errónea. Por ejemplo, tal vez la cantidad promedio de corrosión sea idéntica con los dos recubrimientos. Sin embargo, el recubrimiento nuevo puede ser aplicado a segmentos que tengan una resistencia su- perior a la corrosión y en condiciones ambientales severas en comparación con los seg- mentos y condiciones del recubrimiento actual. El investigador probablemente observaría entonces una diferencia entre los dos recubrimientos atribuibles no a los recubrimien- tos mismos, sino sólo a variaciones extrañas. La estadística ofrece no sólo métodos para analizar resultados de experimentos una vez que se han realizado sino también suge- rencias sobre cómo pueden realizarse los experimentos de una manera eficiente para mitigar los efectos de variación y tener una mejor oportunidad de llegar a conclusiones correctas. 2 CAPÍTULO 1 Generalidades y estadística descriptiva 1.1 Poblaciones, muestras y procesos Los ingenieros y científicos constantemente están expuestos a la recolección de hechos o datos, tanto en sus actividades profesionales como en sus actividades diarias. La disciplina de estadística proporciona métodos de organizar y resumir datos y de sacar conclusiones ba- sadas en la información contenida en los datos. Una investigación típicamente se enfocará en una colección bien definida de objetos que constituyen una población de interés. En un estudio, la población podría consistir de todas las cápsulas de gelatina de un tipo particular producidas durante un periodo específi- co. Otra investigación podría implicar la población compuesta de todos los individuos que recibieron una licenciatura de ingeniería durante el año académico más reciente. Cuando la información deseada está disponible para todos los objetos de la población, se tiene lo que se llama un censo. Las restricciones de tiempo, dinero y otros recursos escasos casi siem- pre hacen que un censo sea impráctico o infactible. En su lugar, se selecciona un subcon- junto de la población, una muestra, de manera prescrita. Así pues, se podría obtener una c1_p001-045.qxd 3/12/08 2:31 AM Page 2
- 21. muestra de cojinetes de una corrida de producción particular como base para investigar si los cojinetes se ajustan a las especificaciones de fabricación, o se podría seleccionar una muestra de los graduados de ingeniería del último año para obtener retroalimentación sobre la calidad de los programas de estudio de ingeniería. Por lo general, existe interés sólo en ciertas características de los objetos en una po- blación: el número de grietas en la superficie de cada recubrimiento, el espesor de cada pa- red de cápsula, el género de un graduado de ingeniería, la edad a la cual el individuo se graduó, y así sucesivamente. Una característica puede ser categórica, tal como el género o tipo de funcionamiento defectuoso o puede ser de naturaleza numérica. En el primer caso, el valor de la característica es una categoría (p. ej., femenino o soldadura insuficiente), mientras que en el segundo caso, el valor es un número (p. ej., edad 23 años o diámetro 0.502 cm). Una variable es cualquier característica cuyo valor puede cambiar de un ob- jeto a otro en la población. Inicialmente las letras minúsculas del alfabeto denotarán las va- riables. Algunos ejemplos incluyen: x marca de la calculadora de un estudiante y número de visitas a un sitio web particular durante un periodo específico z distancia de frenado de un automóvil en condiciones específicas Se obtienen datos al observar o una sola variable o en forma simultánea dos o más varia- bles. Un conjunto de datos univariantes se compone de observaciones realizadas en una so- la variable. Por ejemplo, se podría determinar el tipo de transmisión automática (A) o manual (M) en cada uno de diez automóviles recientemente adquiridos en cierto concesio- nario y el resultado sería el siguiente conjunto de datos categóricos M A A A M A A M A A La siguiente muestra de duraciones (horas) de baterías D puestas en cierto uso es un con- junto de datos numéricos univariantes: 5.6 5.1 6.2 6.0 5.8 6.5 5.8 5.5 Se tienen datos bivariantes cuando se realizan observaciones en cada una de dos variables. El conjunto de datos podría consistir en un par (altura, peso) por cada jugador integrante del equipo de básquetbol, con la primera observación como (72, 168), la segunda como (75, 212), y así sucesivamente. Si un ingeniero determina el valor tanto de x componente de duración y y razón de la falla del componente, el conjunto de datos resultante es bivarian- te con una variable numérica y la otra categórica. Los datos multivariantes surgen cuando se realizan observaciones en más de una variable (por lo que bivariante es un caso especial de multivariante). Por ejemplo, un médico investigador podría determinar la presión sanguí- nea sistólica, la presión sanguínea diastólica y nivel de colesterol en suero de cada pacien- te participante en un estudio. Cada observación sería un triple de números, tal como (120, 80, 146). En muchos conjuntos de datos multivariantes, algunas variables son numéricas y otras son categóricas. Por lo tanto, el número anual dedicado al automóvil de Consumer Reports da valores de tales variables como tipo de vehículo (pequeño, deportivo, compacto, tamaño mediano, grande), eficiencia de consumo de combustible en la ciudad (mpg), efi- ciencia de consumo de combustible en carretera (mpg), tipo de tren motriz (ruedas traseras, ruedas delanteras, cuatro ruedas), etcétera. Ramas de la estadística Es posible que un investigador que ha recopilado datos desee resumir y describir caracterís- ticas importantes de los mismos. Esto implica utilizar métodos de estadística descriptiva. Algunos de ellos son de naturaleza gráfica; la construcción de histogramas, diagramas de caja y gráficas de puntos son ejemplos primordiales. Otros métodos descriptivos implican 1.1 Poblaciones, muestras y procesos 3 c1_p001-045.qxd 3/12/08 2:31 AM Page 3
- 22. el cálculo de medidas numéricas, tales como medias, desviaciones estándar y coeficientes de correlación. La amplia disponibilidad de programas de computadora estadísticos han he- cho que estas tareas sean más fáciles de realizar de lo que antes eran. Las computadoras son mucho más eficientes que los seres humanos para calcular y crear imágenes (¡una vez que han recibido las instrucciones apropiadas del usuario!). Esto significa que el investigador no tiene que esforzarse mucho en el “trabajo tedioso” y tendrá más tiempo para estudiar los da- tos y extraer mensajes importantes. A lo largo de este libro, se presentarán los datos de sa- lida de varios paquetes tales como MINITAB, SAS, S-Plus y R. El programa R puede ser descargado sin cargo del sitio http://www.r-project.org. La tragedia que sufrió el transbordador espacial Challenger y sus astronautas en 1986 con- dujo a varios estudios para investigar las razones de la falla de la misión. La atención se en- focó de inmediato en el comportamiento de los sellos anulares del motor del cohete. He aquí datos derivados de observaciones en x temperatura del sello anular (°F) en cada encendi- do de prueba o lanzamiento del motor del cohete del transbordador (Presidential Commis- sion on the Space Shuttle Challenger Accident, Vol. 1, 1986: 129-131). 84 49 61 40 83 67 45 66 70 69 80 58 68 60 67 72 73 70 57 63 70 78 52 67 53 67 75 61 70 81 76 79 75 76 58 31 Sin organización, es difícil tener una idea de cuál podría ser una temperatura típica o repre- sentativa, ya sea que los valores estén muy concentrados en torno a un valor típico o bastan- te esparcidos, ya sea que existan brechas en los datos, qué porcentaje de los valores están en los 60, y así sucesivamente. La figura 1.1 muestra lo que se conoce como gráfica de tallo y hojas de los datos, así como también un histograma. En breve, se discutirá la construcción e interpretación de estos resúmenes gráficos; por el momento se espera que se vea cómo es- tán distribuidos los valores de temperatura a lo largo de la escala de medición. Algunos de estos lanzamientos/encendidos fueron exitosos y otros fallaron. 4 CAPÍTULO 1 Generalidades y estadística descriptiva Ejemplo 1.1 Figura 1.1 Una gráfica de tallo y hojas e histograma generados con MINITAB de los datos de temperatura de los sellos anulares. Porcentaje Temperatura Tallo y hojas de temperatura N 36 Unidad de hojas 1.0 1 3 1 1 3 2 4 0 4 4 59 6 5 23 9 5 788 13 6 0113 (7) 6 6777789 16 7 000023 10 7 556689 4 8 0134 25 35 45 55 65 75 85 40 30 20 10 0 c1_p001-045.qxd 3/12/08 2:31 AM Page 4
- 23. La temperatura más baja es de 31 grados, mucho más baja que la siguiente temperatura más baja y ésta es la observación en relación con el desastre del Challenger. La investigación presidencial descubrió que se requerían temperaturas calientes para la operación exitosa de los sellos anulares y que 31 grados eran demasiado frío. En el capítulo 13 se presentará una relación entre temperatura y la probabilidad de un lanzamiento exitoso. ■ Después de haber obtenido una muestra de una población, un investigador con fre- cuencia desearía utilizar la información muestral para sacar algún tipo de conclusión (hacer una inferencia de alguna clase) con respecto a la población. Es decir, la muestra es un me- dio para llegar a un fin en lugar de un fin por sí misma. Las técnicas para generalizar desde una muestra hasta una población se congregan dentro de la rama de la disciplina llamada es- tadística inferencial. Las investigaciones de resistencia de materiales constituyen una rica área de aplicación de métodos estadísticos. El artículo “Effects of Aggregates and Microfillers on the Flexural Properties of Concrete” (Magazine of Concrete Research, 1997: 81-98) reportó sobre un es- tudio de propiedades de resistencia de concreto de alto desempeño obtenido con el uso de superplastificantes y ciertos aglomerantes. La resistencia a la compresión de dicho concre- to previamente había sido investigada, pero no se sabía mucho sobre la resistencia a la fle- xión (una medida de la capacidad de resistir fallas a flexión). Los datos anexos sobre resistencia a la flexión (en megapascales, MPa, donde 1 Pa (pascal) 1.45 104 lb/pulg2 ) aparecieron en el artículo citado: 5.9 7.2 7.3 6.3 8.1 6.8 7.0 7.6 6.8 6.5 7.0 6.3 7.9 9.0 8.2 8.7 7.8 9.7 7.4 7.7 9.7 7.8 7.7 11.6 11.3 11.8 10.7 Supóngase que se desea estimar el valor promedio de resistencia a la flexión de todas las vi- gas que pudieran ser fabricadas de esta manera (si se conceptualiza una población de todas esas vigas, se trata de estimar la media poblacional). Se puede demostrar que, con un alto gra- do de confianza, la resistencia media de la población se encuentra entre 7.48 MPa y 8.80 MPa; esto se llama intervalo de confianza o estimación de intervalo. Alternativamente, se podrían utilizar estos datos para predecir la resistencia a la flexión de una sola viga de este tipo. Con un alto grado de confianza, la resistencia de una sola viga excederá de 7.35 MPa; el núme- ro 7.35 se conoce como límite de predicción inferior. ■ El objetivo principal de este libro es presentar e ilustrar métodos de estadística infe- rencial que son útiles en el trabajo científico. Los tipos más importantes de procedimientos inferenciales, estimación puntual, comprobación de hipótesis y estimación por medio de in- tervalos de frecuencia, se introducen en los capítulos 6 a 8 y luego se utilizan escenarios más complicados en los capítulos 9 a 16. El resto de este capítulo presenta métodos de estadís- tica descriptiva que se utilizan mucho en el desarrollo de inferencia. Los capítulos 2 a 5 presentan material de la disciplina de probabilidad. Este material finalmente tiende un puente entre las técnicas descriptivas e inferenciales. El dominio de la pro- babilidad permite entender mejor cómo se desarrollan y utilizan los procedimientos inferencia- les, cómo las conclusiones estadísticas pueden ser traducidas al lenguaje diario e interpretadas y cuándo y dónde pueden ocurrir errores al aplicar los métodos. La probabilidad y estadística se ocupan de cuestiones que implican poblaciones y muestras, pero lo hacen de una “manera in- versa” una con respecto a la otra. En un problema de probabilidad, se supone que las propiedades de la población estu- diada son conocidas (p. ej., en una población numérica, se puede suponer una cierta distri- bución específica de valores de la población) y se pueden plantear y responder preguntas con respecto a una muestra tomada de una población. En un problema de estadística, el ex- perimentador dispone de las características de una muestra y esta información le permite sa- car conclusiones con respecto a la población. La relación entre las dos disciplinas se resume diciendo que la probabilidad discurre de la población a la muestra (razonamiento deductivo), 1.1 Poblaciones, muestras y procesos 5 Ejemplo 1.2 c1_p001-045.qxd 3/12/08 2:31 AM Page 5
- 24. mientras que la estadística inferencial discurre de la muestra a la población (razonamiento inductivo). Esto se ilustra en la figura 1.2. Antes de que se pueda entender lo que una muestra particular pueda decir sobre la po- blación, primero se deberá entender la incertidumbre asociada con la toma de una muestra de una población dada. Por eso se estudia la probabilidad antes que la estadística. Como un ejemplo del enfoque contrastante de la probabilidad y la estadística inferen- cial, el uso que los conductores hacen de los cinturones de seguridad manuales de regazo en carros equipados con sistemas de cinturones de hombro automáticos. (El artículo “Auto- mobile Seat Belts: Usage Patterns in Automatic Belt Systems”, Human Factors, 1998: 126-135, resume datos de uso.) Se podría suponer que probablemente 50% de todos los con- ductores de carros equipados de esta forma en cierta área metropolitana utilizan de manera regular su cinturón de regazo (una suposición sobre la población), así que se podría pregun- tar, “¿qué tan probable es que una muestra de 100 conductores incluirá por lo menos 70 que regularmente utilicen su cinturón de regazo?” o “¿cuántos de los conductores en una mues- tra de tamaño 100 se puede esperar que utilicen con regularidad su cinturón de regazo?” Por otra parte, en estadística inferencial se dispone de información sobre la muestra; por ejem- plo, una muestra de 100 conductores de tales vehículos reveló que 65 utilizan con regulari- dad su cinturón de regazo. Se podría entonces preguntar: “¿proporciona esto evidencia sustancial para concluir que más de 50% de todos los conductores en esta área utilizan con regularidad su cinturón de regazo?” En el último escenario, se intenta utilizar la informa- ción relativa a la muestra para responder una pregunta acerca de la estructura de toda la po- blación de la cual se seleccionó la muestra. En el ejemplo del cinturón de regazo, la población está bien definida y concreta: todos los conductores de carros equipados de una cierta manera en un área metropolitana particu- lar. En el ejemplo 1.1, sin embargo, una muestra de temperaturas de sello anular está dispo- nible, pero proviene de una población que en realidad no existe. En su lugar, conviene pensar en la población como compuesta de todas las posibles mediciones de temperatura que se po- drían hacer en condiciones experimentales similares. Tal población se conoce como pobla- ción conceptual o hipotética. Existen varias situaciones en las cuales las preguntas encajan en el marco de referencia de la estadística inferencial al conceptualizar una población. Estudios enumerativos contra analíticos W. E. Deming, estadístico estadounidense muy influyente quien fue una fuerza propulsora en la revolución de calidad de Japón durante las décadas de 1950 y 1960, introdujo la dis- tinción entre estudios enumerativos y estudios analíticos. En los primeros, el interés se en- foca en un conjunto de individuos u objetos finito, identificable y no cambiante que conforman una población. Un marco de muestreo, es decir, una lista de los individuos u ob- jetos que tienen que ser muestreados, está disponible para un investigador o puede ser cons- truida. Por ejemplo, el marco se podría componer de todas las firmas incluidas en una petición para calificar una cierta iniciativa para las boletas de votación en una elección próxi- ma; por lo general se elige una muestra para indagar si el número de firmas válidas sobre- pasa un valor especificado. Como otro ejemplo, el marco puede contener números de serie de todos los hornos fabricados por una compañía particular durante cierto periodo; se puede seleccionar una muestra para inferir algo sobre la duración promedio de estas unidades. El uso de métodos inferenciales presentados en este libro es razonablemente no controversial en tales escenarios (aun cuando los estadísticos continúan argumentando sobre qué métodos particulares deben ser utilizados). 6 CAPÍTULO 1 Generalidades y estadística descriptiva Población Probabilidad Estadística inferencial Muestra Figura 1.2 Relación entre probabilidad y estadística inferencial. c1_p001-045.qxd 3/12/08 2:31 AM Page 6
- 25. Un estudio analítico se define ampliamente como uno que no es de naturaleza enume- rativa. Tales estudios a menudo se realizan con el objetivo de mejorar un producto futuro al actuar sobre un proceso de una cierta clase (p. ej., recalibrar equipo o ajustar el nivel de al- guna sustancia tal como la cantidad de un catalizador). A menudo se obtienen datos sólo sobre un proceso existente, uno que puede diferir en aspectos importantes del proceso futu- ro. No existe por lo tanto un marco de muestreo que enliste los individuos u objetos de in- terés. Por ejemplo, una muestra de cinco turbinas con un nuevo diseño puede ser fabricada y probada para investigar su eficiencia. Estas cinco podrían ser consideradas como una muestra de la población conceptual de todos los prototipos que podrían ser fabricados en condiciones similares, pero no necesariamente representativas de la población de las unida- des fabricadas una vez que la producción futura esté en proceso. Los métodos para utilizar la información sobre muestras para sacar conclusiones sobre unidades de producción futu- ras pueden ser problemáticos. Se deberá llamar a alguien con los conocimientos necesarios en el área del diseño e ingeniería de turbinas (o de cualquier otra área pertinente) para que juzgue si tal extrapolación es sensible. Una buena exposición de estos temas se encuentra en el artículo “Assumptions for Statistical Inference”, de Gerald Hahn y William Meeker (The American Statistician, 1993: 1-11). Recopilación de datos La estadística se ocupa no sólo de la organización y análisis de datos una vez que han sido recopilados sino también con el desarrollo de técnicas de recopilación de datos. Si éstos no son apropiadamente recopilados, un investigador no puede ser capaz de responder las pre- guntas consideradas con un razonable grado de confianza. Un problema común es que la po- blación objetivo, aquella sobre la cual se van a sacar conclusiones, puede ser diferente de la población realmente muestreada. Por ejemplo, a los publicistas les gustaría contar con va- rias clases de información sobre los hábitos de ver televisión de sus clientes potenciales. La información más sistemática de esta clase proviene de colocar dispositivos de monitoreo en un pequeño número de casas a través de Estados Unidos. Se ha conjeturado que la coloca- ción de semejantes dispositivos por sí misma modifica el comportamiento del televidente, de modo que las características de la muestra pueden ser diferentes de aquellas de la pobla- ción objetivo. Cuando la recopilación de datos implica seleccionar individuos u objetos de un mar- co, el método más simple para garantizar una selección representativa es tomar una mues- tra aleatoria simple. Ésta es una para la cual cualquier subconjunto particular del tamaño especificado (p. ej., una muestra de tamaño 100) tiene la misma oportunidad de ser selec- cionada. Por ejemplo, si el marco se compone de 1000000 de números de serie, los núme- ros 1, 2, . . . , hasta 1000000 podrían ser anotados en trozos idénticos de papel. Después de colocarlos en una caja y mezclarlos perfectamente, se sacan uno por uno hasta que se ob- tenga el tamaño de muestra requisito. De manera alternativa (y mucho más preferible), se podría utilizar una tabla de números aleatorios o un generador de números aleatorios de computadora. En ocasiones se pueden utilizar métodos de muestreo alternativos para facilitar el pro- ceso de selección, a fin de obtener información extra o para incrementar el grado de con- fianza en conclusiones. Un método como ése, el muestreo estratificado, implica separar las unidades de la población en grupos no traslapantes y tomar una muestra de cada uno. Por ejemplo, un fabricante de reproductores de DVD podría desear información sobre la satis- facción del cliente para unidades producidas durante el año previo. Si tres modelos diferen- tes fueran fabricados y vendidos, se podría seleccionar una muestra distinta de cada uno de los estratos correspondientes. Esto daría información sobre los tres modelos y garantizaría que ningún modelo estuviera sobre o subrepresentado en toda la muestra. Con frecuencia, se obtiene una muestra de “conveniencia” seleccionando individuos u objetos sin aleatorización sistemática. Por ejemplo, un conjunto de ladrillos puede ser apilado 1.1 Poblaciones, muestras y procesos 7 c1_p001-045.qxd 3/12/08 2:31 AM Page 7
- 26. de tal modo que sea extremadamente difícil seleccionar a los que se encuentran en el cen- tro. Si los ladrillos localizados en la parte superior y a los lados de la pila fueran de algún modo diferentes a los demás, los datos muestrales resultantes no representarían la pobla- ción. A menudo un investigador supondrá que tal muestra de conveniencia representa en for- ma aproximada una muestra aleatoria, en cuyo caso el repertorio de métodos inferenciales de un estadístico puede ser utilizado; sin embargo, ésta es una cuestión de criterio. La ma- yoría de los métodos aquí analizados se basan en una variación del muestreo aleatorio sim- ple descrito en el capítulo 5. Los ingenieros y científicos a menudo reúnen datos realizando alguna clase de expe- rimento. Esto puede implicar cómo asignar varios tratamientos diferentes (tales como ferti- lizantes o recubrimientos anticorrosivos) a las varias unidades experimentales (parcelas o tramos de tubería). Por otra parte, un investigador puede variar sistemáticamente los niveles o categorías de ciertos factores (p. ej., presión o tipo de material aislante) y observar el efec- to en alguna variable de respuesta (tal como rendimiento de un proceso de producción). Un artículo en el New York Times (27 de enero de 1987) reportó que el riesgo de sufrir un ataque cardiaco podría ser reducido tomando aspirina. Esta conclusión se basó en un ex- perimento diseñado que incluía tanto un grupo de control de individuos que tomaron un placebo que tenía la apariencia de aspirina pero que se sabía era inerte y un grupo de tra- tamiento que tomó aspirina de acuerdo con un régimen específico. Los sujetos fueron asignados al azar a los grupos para protegerlos contra cualquier prejuicio de modo que se pudieran utilizar métodos basados en la probabilidad para analizar los datos. De los 11 034 individuos en el grupo de control, 189 subsecuentemente experimentaron ataques cardiacos, mientras que sólo 104 de los 11 037 en el grupo de aspirina sufrieron un ata- que cardiaco. La tasa de incidencia de ataques cardiacos en el grupo de tratamiento fue de sólo aproximadamente la mitad de aquella en el grupo de control. Una posible explica- ción de este resultado es la variación de la probabilidad, que la aspirina en realidad no tie- ne el efecto deseado y la diferencia observada es sólo una variación típica del mismo modo que el lanzamiento al aire de dos monedas idénticas por lo general produciría dife- rente cantidad de águilas. No obstante, en este caso, los métodos inferenciales sugieren que la variación de la probabilidad por sí misma no puede explicar en forma adecuada la magnitud de la diferencia observada. ■ Un ingeniero desea investigar los efectos tanto del tipo de adhesivo como del material con- ductor en la fuerza adhesiva cuando se monta un circuito integrado (CI) sobre cierto sustra- to. Se consideraron dos tipos de adhesivos y dos materiales conductores. Se realizaron dos observaciones por cada combinación de tipo de adhesivo/material conductor y se obtuvie- ron los datos anexos. Las fuerzas adhesivas promedio resultantes se ilustran en la figura 1.3. Parece que el adhe- sivo tipo 2 mejora la fuerza adhesiva en comparación con el tipo 1 en aproximadamente la misma cantidad siempre que se utiliza uno de los materiales conductores, con la combina- ción 2, 2 como la mejor. De nuevo se pueden utilizar métodos inferenciales para juzgar si estos efectos son reales o simplemente se deben a la variación de la probabilidad. Supóngase además que se consideran dos tiempos de curado y también dos tipos de posrecubrimientos de los circuitos integrados. Existen entonces 2 2 2 2 16 combi- naciones de estos cuatro factores y es posible que el ingeniero no disponga de suficientes ? ? ? 8 CAPÍTULO 1 Generalidades y estadística descriptiva Ejemplo 1.3 Ejemplo 1.4 Tipo de adhesivo Material conductor Fuerza de adhesión observada Promedio 1 1 82, 77 79.5 1 2 75, 87 81.0 2 1 84, 80 82.0 2 2 78, 90 84.0 c1_p001-045.qxd 3/12/08 2:31 AM Page 8
- 27. recursos para hacer incluso una observación sencilla para cada una de estas combinaciones. En el capítulo 11 se verá cómo la selección cuidadosa de una fracción de estas posibilida- des usualmente dará la información deseada. ■ 1.1 Poblaciones, muestras y procesos 9 Material conductor Fuerza promedio 1 2 80 85 Adhesivo tipo 2 Adhesivo tipo 1 Figura 1.3 Fuerzas de adhesión promedio en el ejemplo 1.4. EJERCICIOS Sección 1.1 (1-9) 1. Dé una posible muestra de tamaño 4 de cada una de las si- guientes poblaciones. a. Todos los periódicos publicados en Estados Unidos. b. Todas las compañías listadas en la Bolsa de Valores de Nueva York. c. Todos los estudiantes en su colegio o universidad. d. Todas las calificaciones promedio de los estudiantes en su colegio o universidad. 2. Para cada una de las siguientes poblaciones hipotéticas, dé una muestra posible de tamaño 4. a. Todas las distancias que podrían resultar cuando usted lan- za un balón de fútbol americano. b. Las longitudes de las páginas de libros publicados de aquí a 5 años. c. Todas las mediciones de intensidades posibles de terremo- tos (escala de Richter) que pudieran registrarse en Califor- nia durante el siguiente año. d. Todos los posibles rendimientos (en gramos) de una cierta reacción química realizada en un laboratorio. 3. Considere la población compuesta de todas las computadoras de una cierta marca y modelo y enfóquese en si una computadora necesita servicio mientras se encuentra dentro de la garantía. a. Plantee varias preguntas de probabilidad con base en la se- lección de 100 de esas computadoras. b. ¿Qué pregunta de estadística inferencial podría ser respondi- da determinando el número de dichas computadoras en una muestra de tamaño 100 que requieren servicio de garantía? 4. a. Dé tres ejemplos diferentes de poblaciones concretas y tres ejemplos distintos de poblaciones hipotéticas. b. Por cada una de sus poblaciones concretas e hipotéticas, dé un ejemplo de una pregunta de probabilidad y un ejemplo de pregunta de estadística inferencial. 5. Muchas universidades y colegios han instituido programas de instrucción suplementaria (IS), en los cuales un facilitador re- gularmente se reúne con un pequeño grupo de estudiantes inscritos en el curso para promover discusiones sobre el ma- terial incluido en el curso y mejorar el dominio de la materia. Suponga que los estudiantes inscritos en un largo curso de es- tadística (¿de qué más?) se dividen al azar en un grupo de control que no participará en la instrucción suplementaria y en un grupo de tratamiento que sí participará. Al final del cur- so, se determina la calificación total de cada estudiante en el curso. a. ¿Son las calificaciones del grupo IS una muestra de una población existente? De ser así, ¿cuál es? De no ser así, ¿cuál es la población conceptual pertinente? b. ¿Cuál piensa que es la ventaja de dividir al azar a los es- tudiantes en los dos grupos en lugar de permitir que cada estudiante elija el grupo al que desea unirse? c. ¿Por qué los investigadores no pusieron a todos los estu- diantes en el grupo de tratamiento? Nota: El artículo (“Supplemental Instruction: An Effective Component of Student Affairs Programming”, J. of College Student De- vel., 1997:577-586) discute el análisis de datos de varios programas de instrucción suplementaria. 6. El sistema de la Universidad Estatal de California (CSU, por sus siglas en inglés) consta de 23 terrenos universitarios, des- de la Estatal de San Diego en el sur hasta la Estatal Humboldt cerca de la frontera con Oregon. Un administrador de CSU desea hacer una inferencia sobre la distancia promedio entre la ciudad natal y sus terrenos universitarios. Describa y discuta diferentes métodos de muestreo, que pudieran ser empleados. ¿Éste sería un estudio enumerativo o un estudio analítico? Explique su razonamiento. 7. Cierta ciudad se divide naturalmente en diez distritos. ¿Cómo podría seleccionar un valuador de bienes raíces una muestra de casas unifamiliares que pudiera ser utilizada como base para desarrollar una ecuación para predecir el valor estimado a partir de características tales como antigüedad, tamaño, nú- mero de baños, distancia a la escuela más cercana y así suce- sivamente? ¿El estudio es enumerativo o analítico? c1_p001-045.qxd 3/12/08 2:31 AM Page 9
- 28. La estadística descriptiva se divide en dos temas generales. En esta sección, se considera la representación de un conjunto de datos por medio de técnicas visuales. En las secciones 1.3 y 1.4, se desarrollarán algunas medidas numéricas para conjuntos de datos. Es posible que usted ya conozca muchas técnicas visuales; tablas de frecuencia, hojas de contabilidad, his- togramas, gráficas de pastel, gráficas de barras, diagramas de puntos y similares. Aquí se se- leccionan algunas de estas técnicas que son más útiles y pertinentes a la estadística de probabilidad e inferencial. Notación Alguna notación general facilitará la aplicación de métodos y fórmulas a una amplia varie- dad de problemas prácticos. El número de observaciones en una muestra única, es decir, el tamaño de muestra, a menudo será denotado por n, de modo que n 4 para la muestra de universidades {Stanford, Iowa State, Wyoming, Rochester} y también para la muestra de lecturas de pH {6.3, 6.2, 5.9, 6.5}. Si se consideran dos muestras al mismo tiempo, m y n o n1 y n2 se pueden utilizar para denotar los números de observaciones. Por lo tanto, si {29.7, 31.6, 30.9} y {28.7, 29.5, 29.4, 30.3} son lecturas de eficiencia térmica de dos tipos diferentes de motores diesel, entonces m 3 y n 4. Dado un conjunto de datos compuesto de n observaciones de alguna variable x, enton- ces x1, x2, x3, . . . , xn denotarán las observaciones individuales. El subíndice no guarda nin- guna relación con la magnitud de una observación particular. Por lo tanto, x1 en general no será la observación más pequeña del conjunto, ni xn será la más grande. En muchas aplica- ciones, x1 será la primera observación realizada por el experimentador, x2 la segunda, y así sucesivamente. La observación i-ésima del conjunto de datos será denotada por xi. Gráficas de tallos y hojas Considérese un conjunto de datos numéricos x1, x2, . . . , xn para el cual xi se compone de por lo menos dos dígitos. Una forma rápida de obtener la representación visual informativa del conjunto de datos es construir una gráfica de tallos y hojas. 10 CAPÍTULO 1 Generalidades y estadística descriptiva 8. La cantidad de flujo a través de una válvula solenoide en el sistema de control de emisiones de un automóvil es una ca- racterística importante. Se realizó un experimento para estu- diar cómo la velocidad de flujo dependía de tres factores: la longitud de la armadura, la fuerza del resorte y la profundidad de la bobina. Se eligieron dos niveles diferentes (alto y bajo) de cada factor y se realizó una sola observación del flujo por ca- da combinación de niveles. a. ¿De cuántas observaciones consistió el conjunto de datos resultante? b. ¿Este estudio es enumerativo o analítico? Explique su ra- zonamiento. 9. En un famoso experimento realizado en 1882, Michelson y Newcomb obtuvieron 66 observaciones del tiempo que re- quería la luz para viajar entre dos lugares en Washington, D.C. Algunas de las mediciones (codificadas en cierta mane- ra) fueron, 31, 23, 32, 36, 2, 26, 27 y 31. a. ¿Por qué no son idénticas estas mediciones? b. ¿Es éste un estudio enumerativo? ¿Por qué sí o por qué no? 1.2 Métodos pictóricos y tabulares en la estadística descriptiva Pasos para construir una gráfica de tallos y hojas 1. Seleccione uno o más de los primeros dígitos para los valores de tallo. Los segun- dos dígitos se convierten en hojas. 2. Enumere los posibles valores de tallos en una columna vertical. 3. Anote la hoja para cada observación junto al valor de tallo. 4. Indique las unidades para tallos y hojas en algún lugar de la gráfica. c1_p001-045.qxd 3/12/08 2:31 AM Page 10
- 29. Si el conjunto de datos se compone de calificaciones de exámenes, cada uno entre 0 y 100, la calificación de 83 tendría un tallo de 8 y una hoja de 3. Para un conjunto de datos de efi- ciencias de consumo de combustible de automóviles (mpg), todas entre 8.1 y 47.8, se po- drían utilizar como el tallo, así que 32.6 tendría entonces una hoja de 2.6. En general, se recomienda una gráfica basada en tallos entre 5 y 20. El consumo de alcohol por parte de estudiantes universitarios preocupa no sólo a la comu- nidad académica sino también, a causa de consecuencias potenciales de salud y seguridad, a la sociedad en su conjunto. El artículo (“Health and Behavioral Consequences of Binge Drinking in College”, J. of the Amer. Med. Assoc., 1994: 1672-1677) presentó un amplio es- tudio sobre el consumo excesivo de alcohol en universidades a través de Estados Unidos. Un episodio de parranda se definió como cinco o más tragos en fila para varones y cuatro o más para mujeres. La figura 1.4 muestra una gráfica de tallo y hojas de 140 valores de x porcentaje de edades de los estudiantes de licenciatura bebedores. (Estos valores no apare- cieron en el artículo citado, pero la gráfica concuerda con una gráfica de los datos que sí lo hicieron.) La primera hoja de la fila 2 del tallo es 1, la cual dice que 21% de los estudiantes de una de las universidades de la muestra eran bebedores. Sin la identificación de los dígitos en los tallos y los dígitos en las hojas, no se sabría si la observación correspondiente al ta- llo 2, hoja 1 debería leerse como 21%, 2.1% o 0.21 por ciento. Cuando se crea una imagen a mano, la ordenación de las hojas de la más pequeña a la más grande en cada línea puede ser tediosa. Esta ordenación contribuye poco si no se dis- pone de información adicional. Supóngase que las observaciones hubieran sido puestas en lista en orden alfabético por nombre de la escuela, como 16% 33% 64% 37% 31% . . . Entonces la colocación de estos valores en la gráfica en este orden haría que la fila 1 del ta- llo tuviera 6 como su primera hoja y el principio de la fila 3 del tallo sería 3 ° 371 . . . La gráfica sugiere que un valor típico o representativo se encuentra en la fila 4 del ta- llo, tal vez en el rango medio de 40%. Las observaciones no aparecen muy concentradas en torno a este valor típico, como sería el caso si todos los valores estuvieran entre 20 y 49%. Esta gráfica se eleva a una sola cresta a medida que desciende, y luego declina; no hay bre- chas en la gráfica. La forma de la gráfica no es perfectamente simétrica, pero en su lugar pa- rece alargarse un poco más en la dirección de las hojas bajas que en la dirección de las hojas altas. Por último, no existen observaciones que se alejen inusualmente del grueso de los da- tos (ningunos valores apartados), como sería el caso si uno de los valores de 26% hubiera sido de 86%. La característica más sobresaliente de estos datos es que, en la mayoría de las universidades de la muestra, por lo menos una cuarta parte de los estudiantes son bebedo- res. El problema de beber en exceso en las universidades es mucho más extenso de lo que muchos hubieran sospechado. ■ 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 11 Ejemplo 1.5 0 4 1 1345678889 2 1223456666777889999 Tallo: dígitos de diez cifras 3 0112233344555666677777888899999 Hojas: dígitos de una cifra 4 111222223344445566666677788888999 5 00111222233455666667777888899 6 01111244455666778 Figura 1.4 Gráfica de tallo y hojas de porcentajes de bebedores en cada una de 140 universidades. c1_p001-045.qxd 3/12/08 2:31 AM Page 11
- 30. Una gráfica de tallos y hojas da información sobre los siguientes aspectos de los datos: • Identificación de un valor típico o representativo. • Grado de dispersión en torno al valor típico. • Presencia de brechas en los datos. • Grado de simetría en la distribución de los valores. • Número y localización de crestas. • Presencia de valores afuera de la gráfica. La figura 1.5 presenta gráficas de tallos y hojas de una muestra aleatoria de longitudes de campos de golf (yardas) designados por Golf Magazine como los más desafiantes en Esta- dos Unidos. Entre la muestra de 40 campos, el más corto es de 6 433 yardas de largo y el más largo es de 7280 yardas. Las longitudes parecen estar distribuidas de una manera aproximadamente uniforme dentro del rango de valores presentes en la muestra. Obsérvese que la selección de tallo en este caso de un solo dígito (6 ó 7) o de tres (643, . . . , 728) pro- duciría una gráfica no informativa, primero a causa de pocos tallos y segundo a causa de de- masiados. Los programas de computadora de estadística en general no producen gráficas con ta- llos de dígitos múltiples. La gráfica MINITAB que aparece en la figura 1.5(b) resulta de truncar cada observación al borrar los dígitos uno. Gráficas de puntos Una gráfica de puntos es un resumen atractivo de datos numéricos cuando el conjunto de datos es razonablemente pequeño o existen pocos valores de datos distintos. Cada observa- ción está representada por un punto sobre la ubicación correspondiente en una escala de me- dición horizontal. Cuando un valor ocurre más de una vez, existe un punto por cada ocurrencia y estos puntos se apilan verticalmente. Como con la gráfica de tallos y hojas, una gráfica de puntos da información sobre la localización, dispersión, extremos y brechas. La figura 1.6 muestra una gráfica de puntos para los datos de temperatura de los sellos anu- lares introducidos en el ejemplo 1.1 en la sección previa. Un valor de temperatura represen- tativo es uno que se encuentra entre la mitad de los 60 (°F) y existe poca dispersión en torno al centro. Los datos se alargan más en el extremo inferior que en el superior y la observa- ción más pequeña, 31, apenas puede ser descrita como valor extremo. 12 CAPÍTULO 1 Generalidades y estadística descriptiva Figura 1.5 Gráficas de tallo y hojas de yardajes de campos de golf: a) hojas de dos dígitos; b) gráfica generada por MINITAB con las hojas de un dígito truncadas. ■ 64 35 64 33 70 Tallo: dígitos de miles y cientos de cifras 65 26 27 06 83 Hojas: dígitos de decenas de cifras y una cifra 66 05 94 14 67 90 70 00 98 70 45 13 68 90 70 73 50 69 00 27 36 04 70 51 05 11 40 50 22 71 31 69 68 05 13 65 72 80 09 Tallo y hojas de yardaje N 40 Unidad de hojas 10 4 64 3367 8 65 0228 11 66 019 18 67 0147799 (4) 68 5779 18 69 0023 14 70 012455 8 71 013666 2 72 08 a) b) Ejemplo 1.6 Ejemplo 1.7 c1_p001-045.qxd 3/12/08 2:31 AM Page 12
- 31. Si el conjunto de datos del ejemplo 1.7 hubieran consistido en 50 o 100 observacio- nes de temperatura, cada una registrada a un décimo de grado, habría sido muy tedioso cons- truir una gráfica de puntos. La técnica siguiente es muy adecuada a situaciones como esas. Histogramas Algunos datos numéricos se obtienen contando para determinar el valor de una variable (el número de citatorios de tráfico que una persona recibió durante el año pasado, el número de personas que solicitan empleo durante un periodo particular), mientras que otros datos se obtienen tomando mediciones (peso de un individuo, tiempo de reacción a un estímulo par- ticular). La prescripción para trazar un histograma es en general diferente en estos dos casos. Una variable discreta x casi siempre resulta de contar, en cuyo caso posibles valores son 0, 1, 2, 3, . . . o algún subconjunto de estos enteros. De la toma de mediciones surgen variables continuas. Por ejemplo, si x es el pH de una sustancia química, entonces en teoría x podría ser cualquier número entre 0 y 14: 7.0, 7.03, 7.032 y así sucesivamente. Desde lue- go, en la práctica existen limitaciones en el grado de precisión de cualquier instrumento de medición, por lo que es posible que no se pueda determinar el pH, el tiempo de reacción, la altura y la concentración con un número arbitrariamente grande de decimales. Sin embargo, desde el punto de vista de crear modelos matemáticos de distribuciones de datos, conviene imaginar un conjunto completo continuo de valores posibles. Considérense datos compuestos de observaciones de una variable discreta x. La fre- cuencia de cualquier valor x particular es el número de veces que ocurre un valor en el con- junto de datos. La frecuencia relativa de un valor es la fracción o proporción de veces que ocurre el valor: Supóngase, por ejemplo, que el conjunto de datos se compone de 200 observaciones de x el número de cursos que un estudiante está tomando en este semestre. Si 70 de estos valo- res x es 3, entonces frecuencia del valor 3 de x: 70 frecuencia relativa del valor 3 de x: Si se multiplica una frecuencia relativa por 100 se obtiene un porcentaje en el ejemplo de cursos universitarios, 35% de los estudiantes de la muestra están tomando tres cursos. Las 70 200 5 0.35 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 13 Figura 1.6 Gráfica de puntos de los datos de temperatura de los sellos anulares (°F). ■ Temperatura 30 40 50 60 70 80 DEFINICIÓN Una variable numérica es discreta si su conjunto de valores posibles es finito o se puede enumerar en una sucesión infinita (una en la cual existe un primer número, un segundo número, y así sucesivamente). Una variable numérica es continua si sus va- lores posibles abarcan un intervalo completo sobre la línea de números. frecuencia relativa de un valor número de veces que ocurre el valor número de observaciones en el conjunto de datos c1_p001-045.qxd 3/12/08 2:31 AM Page 13
- 32. frecuencias relativas, o porcentajes, por lo general interesan más que las frecuencias mis- mas. En teoría, las frecuencias relativas deberán sumar 1, pero en la práctica la suma puede diferir un poco de 1 por el redondeo. Una distribución de frecuencia es una tabla de las frecuencias o de las frecuencias relativas, o de ambas. Esta construcción garantiza que el área de cada rectángulo es proporcional a la frecuencia relativa del valor. Por lo tanto, si las frecuencias relativas de x 1 y x 5 son 0.35 y 0.07, respectivamente, entonces el área del rectángulo sobre 1 es cinco veces el área del rectán- gulo sobre 5. ¿Qué tan inusual es un juego de béisbol sin hit o de un hit en las ligas mayores y cuán fre- cuentemente un equipo pega más de 10, 15 o incluso 20 hits? La tabla 1.1 es una distribu- ción de frecuencia del número de hits por equipo por juego de todos los juegos de nueve episodios que se jugaron entre 1989 y 1993. El histograma correspondiente en la figura 1.7 se eleva suavemente hasta una sola cresta y luego declina. El histograma se extiende un poco más hacia la derecha (hacia valo- res grandes) que hacia la izquierda, un poco “asimétrico positivo”. O con la información tabulada o con el histograma mismo, se puede determinar lo si- guiente: frecuencia frecuencia frecuencia relativa relativa relativa de x 0 de x 1 de x 2 0.0010 0.0037 0.0108 0.0155 14 CAPÍTULO 1 Generalidades y estadística descriptiva Construcción de un histograma para datos discretos En primer lugar, se determina la frecuencia y la frecuencia relativa de cada valor x. Luego se marcan los valores x posibles en una escala horizontal. Sobre cada valor, se traza un rectángulo cuya altura es la frecuencia relativa (o alternativamente, la fre- cuencia) de dicho valor. Ejemplo 1.8 Tabla 1.1 Distribución de frecuencia de hits en juegos de nueve episodios Número de Frecuencia Número de Frecuencia Hits/juego juegos relativa Hits/juego juegos relativa 0 20 0.0010 14 569 0.0294 1 72 0.0037 15 393 0.0203 2 209 0.0108 16 253 0.0131 3 527 0.0272 17 171 0.0088 4 1048 0.0541 18 97 0.0050 5 1457 0.0752 19 53 0.0027 6 1988 0.1026 20 31 0.0016 7 2256 0.1164 21 19 0.0010 8 2403 0.1240 22 13 0.0007 9 2256 0.1164 23 5 0.0003 10 1967 0.1015 24 1 0.0001 11 1509 0.0779 25 0 0.0000 12 1230 0.0635 26 1 0.0001 13 834 0.0430 27 1 0.0001 19383 1.0005 proporción de juegos a lo sumo de dos hits c1_p001-045.qxd 3/12/08 2:31 AM Page 14
- 33. Asimismo, proporción de juegos con 0.0752 0.1026 . . . 0.1015 0.6361 entre 5 y 10 hits (inclusive) Esto es, aproximadamente 64% de todos estos juegos fueron de entre 5 y 10 hits (inclu- sive). ■ La construcción de un histograma para datos continuos (mediciones) implica subdivi- dir el eje de medición en un número adecuado de intervalos de clase o clases, de tal suer- te que cada observación quede contenida en exactamente una clase. Supóngase, por ejemplo, que se hacen 50 observaciones de x eficiencia de consumo de combustible de un automóvil (mpg), la más pequeña de las cuales es 27.8 y la más grande 31.4. Entonces se podrían utilizar los límites de clase 27.5, 28.0, 28.5, . . . , y 31.5 como se muestra a con- tinuación: Una dificultad potencial es que de vez en cuando una observación está en un límite de cla- se así que por consiguiente no cae en exactamente un intervalo, por ejemplo, 29.0. Una for- ma de habérselas con este problema es utilizar límites como 27.55, 28.05, . . . , 31.55. La adición de centésimas a los límites de clase evita que las observaciones queden en los lí- mites resultantes. Otro método es utilizar las clases 27.5–28.0, 28.0–28.5, . . . , 31.0–31.5. En ese caso 29.0 queda en la clase 29.0–29.5 y no en la clase 28.5–29.0. En otras palabras, con esta convención, una observación que queda en el límite se coloca en el intervalo a la derecha del mismo. Así es como MINITAB construye un histograma. 27.5 28.0 28.5 29.0 29.5 30.0 30.5 31.0 31.5 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 15 Figura 1.7 Histograma de número de hits por juego de nueve episodios. 10 0.05 0 0.10 0 Hits/juego 20 Frecuencia relativa Construcción de un histograma para datos continuos: anchos de clase iguales Se determina la frecuencia y la frecuencia relativa de cada clase. Se marcan los límites de clase sobre un eje de medición horizontal. Sobre cada intervalo de cla- se, se traza un rectángulo cuya altura es la frecuencia relativa correspondiente (o frecuencia). c1_p001-045.qxd 3/12/08 2:31 AM Page 15
- 34. Las compañías eléctricas requieren información sobre el consumo de los clientes para obte- ner pronósticos precisos de demandas. Investigadores de Wisconsin Power and Light deter- minaron el consumo de energía (BTU) durante un periodo particular con una muestra de 90 hogares calentados con gas. Se calculó un valor de consumo promedio como sigue: consumo ajustado Esto dio por resultado los datos anexos (una parte del conjunto de datos guardados FUR- NACE.MTW disponible en MINITAB, el cual se ordenó desde el valor más pequeño al más grande). 2.97 4.00 5.20 5.56 5.94 5.98 6.35 6.62 6.72 6.78 6.80 6.85 6.94 7.15 7.16 7.23 7.29 7.62 7.62 7.69 7.73 7.87 7.93 8.00 8.26 8.29 8.37 8.47 8.54 8.58 8.61 8.67 8.69 8.81 9.07 9.27 9.37 9.43 9.52 9.58 9.60 9.76 9.82 9.83 9.83 9.84 9.96 10.04 10.21 10.28 10.28 10.30 10.35 10.36 10.40 10.49 10.50 10.64 10.95 11.09 11.12 11.21 11.29 11.43 11.62 11.70 11.70 12.16 12.19 12.28 12.31 12.62 12.69 12.71 12.91 12.92 13.11 13.38 13.42 13.43 13.47 13.60 13.96 14.24 14.35 15.12 15.24 16.06 16.90 18.26 Se permite que MINITAB seleccione los intervalos de clase. La característica del histogra- ma en la figura 1.8 que más llama la atención es su parecido a una curva en forma de cam- pana (y por consiguiente simétrico), con el punto de simetría aproximadamente en 10. Frecuencia 1–3 3–5 5–7 7–9 9–11 11–13 13–15 15–17 17–19 de clase 1 1 11 21 25 17 9 4 1 Frecuencia 0.011 0.011 0.122 0.233 0.278 0.189 0.100 0.044 0.011 relativa consumo (clima, en grados días)(área de casa) De acuerdo con el histograma, proporción de observaciones 0.01 0.01 0.12 0.23 0.37 (valor exacto menor que 9 34 90 5 0.378d 16 CAPÍTULO 1 Generalidades y estadística descriptiva Ejemplo 1.9 Figura 1.8 Histograma de los datos de consumo de energía del ejemplo 1.9. Porcentaje BTU 1 3 5 7 9 11 13 15 17 19 30 20 10 0 c1_p001-045.qxd 3/12/08 2:31 AM Page 16
- 35. La frecuencia relativa para la clase 9-11 es aproximadamente 0.27, así que se estima que en forma aproximada la mitad de ésta, o 0.135, queda entre 9 y 10. Por lo tanto proporción de observaciones 0.37 + 0.135 0.505 (poco más de 50%) menores que 10 El valor exacto de esta proporción es 47/90 0.522 ■ No existen reglas inviolables en cuanto al número de clases o la selección de las mis- mas. Entre 5 y 20 serán satisfactorias para la mayoría de los conjuntos de datos. En gene- ral, mientras más grande es el número de observaciones en un conjunto de datos, más clases deberán ser utilizadas. Una razonable regla empírica es número de clases n ú m e r o d e o b s e r v a c i o n e s Es posible que las clases de ancho-igual no sean una opción sensible si un conjunto de datos “se alarga” hacia un lado o el otro. La figura 1.9 muestra una curva de puntos de dicho conjunto de datos. Con un pequeño número de clases de ancho-igual casi todas las ob- servaciones quedan en exactamente una o dos de las clases. Si se utiliza un gran número de clases de ancho-igual las frecuencias de muchas clases será cero. Una buena opción es uti- lizar algunos intervalos más anchos cerca de las observaciones extremas y más angostos en la región de alta concentración. La corrosión del acero de refuerzo es un problema serio en estructuras de concreto localiza- das en ambientes afectados por condiciones climáticas severas. Por esa razón, los investiga- dores han estado estudiando el uso de barras de refuerzo hechas de un material compuesto. Se realizó un estudio para desarrollar indicaciones para adherir barras de refuerzo reforzadas con fibra de vidrio a concreto (“Design Recommendations for Bond of GFRP Rebars to Con- crete”, J. of Structural Engr., 1996: 247-254). Considérense las siguientes 48 observaciones de fuerza adhesiva medida: 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 17 a) b) c) Construcción de un histograma para datos continuos: anchos de clase desiguales Después de determinar las frecuencias y las frecuencias relativas, se calcula la altura de cada rectángulo con la fórmula altura del rectángulo Las alturas del rectángulo resultante en general se conocen como densidades y la es- cala vertical es la escala de densidades. Esta prescripción también funcionará cuan- do los anchos de clase son iguales. frecuencia relativa de la clase ancho de clase Figura 1.9 Selección de intervalos de clase para un conjunto “alargado” de puntos: a) interva- los angostos de ancho igual; b) intervalos amplios de ancho igual; c) intervalos de anchos dife- rentes. Ejemplo 1.10 c1_p001-045.qxd 3/12/08 2:31 AM Page 17
- 36. 11.5 12.1 9.9 9.3 7.8 6.2 6.6 7.0 13.4 17.1 9.3 5.6 5.7 5.4 5.2 5.1 4.9 10.7 15.2 8.5 4.2 4.0 3.9 3.8 3.6 3.4 20.6 25.5 13.8 12.6 13.1 8.9 8.2 10.7 14.2 7.6 5.2 5.5 5.1 5.0 5.2 4.8 4.1 3.8 3.7 3.6 3.6 3.6 Frecuencia 2–4 4–6 6–8 8–12 12–20 20–30 de clase 9 15 5 9 8 2 Frecuencia relativa 0.1875 0.3125 0.1042 0.1875 0.1667 0.0417 Densidad 0.094 0.156 0.052 0.047 0.021 0.004 El histograma resultante aparece en la figura 1.10. La cola derecha o superior se alarga mu- cho más que la izquierda o inferior, un sustancial alejamiento de la simetría. Cuando los anchos de clase son desiguales, si no se utiliza una escala de densidad se obtendrá una gráfica con áreas distorsionadas. Con anchos de clase iguales, el divisor es el mismo en cada cálculo de densidad y la aritmética adicional simplemente implica reescalar el eje vertical (es decir, el histograma que utiliza frecuencia relativa y el que utiliza densi- dad tendrán exactamente la misma apariencia). Un histograma de densidad tiene una pro- piedad interesante. Si se multiplican ambos miembros de la fórmula para densidad por el ancho de clase se obtiene frecuencia relativa (ancho de clase)(densidad) (ancho del rectángulo)(altura del rectángulo) área del rectángulo Es decir, el área de cada rectángulo es la frecuencia relativa de la clase correspondiente. Además, como la suma de frecuencias relativas debe ser 1, el área total de todos los rectán- gulos en un histograma de densidad es 1. Siempre es posible trazar un histograma de modo que el área sea igual a la frecuencia relativa (esto es cierto también para un histograma de datos discretos), simplemente se utiliza la escala de densidad. Esta propiedad desempeñará un importante papel al crear modelos de distribución en el capítulo 4. Formas de histograma Los histogramas se presentan en varias formas. Un histograma unimodal es el que se eleva a una sola cresta y luego declina. Uno bimodal tiene dos crestas diferentes. Puede ocurrir bimo- dalidad cuando el conjunto de datos se compone de observaciones de dos clases bastante dife- rentes de individuos u objetos. Por ejemplo, considérese un gran conjunto de datos compuesto de tiempos de manejo de automóviles que viajan entre San Luis Obispo, California 18 CAPÍTULO 1 Generalidades y estadística descriptiva Figura 1.10 Un histograma de densidad generado por MINITAB de los datos de fuerza adhesi- va del ejemplo 1.10. ■ Densidad Fuerza adhesiva 2 4 6 8 12 20 30 0.15 0.10 0.05 0.00 c1_p001-045.qxd 3/12/08 2:31 AM Page 18
- 37. y Monterey, California (sin contar el tiempo utilizado para ver puntos de interés, comer, etc.). Este histograma mostraría dos crestas, una para los carros que toman la ruta interior (aproximadamente 2.5 horas) y otra para los carros que viajan a lo largo de la costa (3.5-4 horas). Sin embargo, la bimodalidad no se presenta automáticamente en dichas situaciones. Sólo si los dos histogramas distintos están “muy alejados” en forma relativa con respecto a sus esparcimientos la bimodalidad ocurrirá en el histograma de datos combinados. Por consi- guiente un conjunto de datos grande compuesto de estaturas de estudiantes universitarios no producirá un histograma bimodal porque la altura típica de hombres de aproximadamente 69 pulgadas no está demasiado por encima de la altura típica de mujeres de aproximada- mente 64-65 pulgadas. Se dice que un histograma con más de dos crestas es multimodal. Por supuesto, el número de crestas dependerá de la selección de intervalos de clase, en par- ticular, con un pequeño número de observaciones. Mientras más grande es el número de clases, es más probable que se manifieste bimodalidad o multimodalidad. Un histograma es simétrico si la mitad izquierda es una imagen de espejo de la mi- tad derecha. Un histograma bimodal es positivamente asimétrico si la cola derecha o superior se alarga en comparación con la cola izquierda o inferior y negativamente asimé- trico si el alargamiento es hacia la izquierda. La figura 1.11 muestra histogramas “alisados” obtenidos superponiendo una curva alisada sobre los rectángulos, que ilustran varias posi- bilidades. Datos cualitativos Tanto una distribución de frecuencia y un histograma pueden ser construidos cuando el conjun- to de datos es de naturaleza cualitativa (categórico). En algunos casos, habrá un ordenamiento natural de las clases, por ejemplo, estudiantes de primer año, segundo, tercero, cuarto y gra- duados, mientras que en otros casos el orden será arbitrario, por ejemplo, católico, judío, pro- testante, etc. Con esos datos categóricos, los intervalos sobre los que se construyen rectángulos deberán ser de igual ancho. El Public Policy Institute of California realizó una encuesta telefónica de 2501 residentes adul- tos en California durante abril de 2006 para indagar qué pensaban sobre varios aspectos de la educación pública K-12. Una pregunta fue “En general, ¿cómo calificaría la calidad de las es- cuelas públicas de su vecindario hoy en día? La tabla 1.2 muestra las frecuencias y las frecuen- cias relativas y la figura 1.12 muestra el histograma correspondiente (gráfica de barras). 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 19 Figura 1.11 Histogramas alisados: a) unimodal simétrico; b) bimodal; c) positivamente asimé- trico y d) negativamente asimétrico. a) d) b) c) Ejemplo 1.11 Tabla 1.2 Distribución de frecuencia de calificaciones escolares Calificación Frecuencia Frecuencia relativa A 478 0.191 B 893 0.357 C 680 0.272 D 178 0.071 F 100 0.040 Desconocida 172 0.069 2501 1.000 c1_p001-045.qxd 3/12/08 2:31 AM Page 19
- 38. Más de la mitad de los encuestados otorgaron una calificación A o B y sólo un poco más de 10% otorgó una calificación D o F. Los porcentajes de padres de niños que asisten a escuelas públicas fueron un poco más favorables para las escuelas: 24, 40, 24, 6, 4 y 2 por ciento. ■ Datos multivariantes Los datos multivariantes en general son más difíciles de describir en forma visual. Varios métodos para hacerlo aparecen más adelante en el libro, notablemente en gráficas de pun- tos de datos numéricos bivariantes. 20 CAPÍTULO 1 Generalidades y estadística descriptiva Figura 1.12 Histograma de calificaciones de las escuelas obtenido con MINITAB. Frecuencia relativa Calificación 0.4 0.3 0.2 0.1 0.0 A B C D F Desconocida Gráfica de frecuencia relativa vs calificación EJERCICIOS Sección 1.2 (10-32) 10. Considere los datos de resistencia de las vigas del ejemplo 1.2. a. Construya una gráfica de tallos y hojas de los datos. ¿Cuál parece ser el valor de resistencia representativo? ¿Parecen estar las observaciones altamente concentradas en torno al valor representativo o algo dispersas? b. ¿Parece ser la gráfica razonablemente simétrica en torno a un valor representativo o describiría su forma de otra manera? c. ¿Parece haber algunos valores de resistencia extremos? d. ¿Qué proporción de las observaciones de resistencia en esta muestra exceden de 10 MPa? 11. Cada calificación en el siguiente lote de calificaciones de exámenes se encuentra en los 60, 70, 80 o 90. Una gráfica de tallos y hojas con sólo los cuatro tallos 6, 7, 8 y 9 no des- cribiría detalladamente la distribución de calificaciones. En tales situaciones, es deseable utilizar tallos repetidos. En es- te caso se repetiría el tallo 6 dos veces, utilizando 6L para las calificaciones en los 60 bajos (hojas 0, 1, 2, 3 y 4) y 6H para las calificaciones en los 60 altos (hojas 5, 6, 7, 8 y 9). Asimismo, los demás tallos pueden ser repetidos dos veces para obtener una gráfica de ocho filas. Construya la gráfi- ca para las calificaciones dadas. ¿Qué característica de los datos es resaltada por esta gráfica? 74 89 80 93 64 67 72 70 66 85 89 81 81 71 74 82 85 63 72 81 81 95 84 81 80 70 69 66 60 83 85 98 84 68 90 82 69 72 87 88 12. Los valores de densidad relativa anexos de varios tipos de madera utilizados en la construcción aparecieron en el artícu- lo (“Bolted Connection Design Values Based on European Yield Model”, J. of Structural Engr., 1993: 2169-2186): 0.31 0.35 0.36 0.36 0.37 0.38 0.40 0.40 0.40 0.41 0.41 0.42 0.42 0.42 0.42 0.42 0.43 0.44 0.45 0.46 0.46 0.47 0.48 0.48 0.48 0.51 0.54 0.54 0.55 0.58 0.62 0.66 0.66 0.67 0.68 0.75 Construya una gráfica de tallos y hojas con tallos repetidos (véase el ejercicio previo) y comente sobre cualquier carac- terística interesante de la gráfica. 13. Las propiedades mecánicas permisibles para el diseño es- tructural de vehículos aeroespaciales metálicos requieren un método aprobado para analizar estadísticamente datos de prueba empíricos. El artículo (“Establishing Mechanical Pro- perty Allowables for Metals”, J. of Testing and Evaluation, 1998: 293-299) utilizó los datos anexos sobre resistencia a la tensión última (lb/pulg2 ) como base para abordar las dificul- tades que se presentan en el desarrollo de dicho método. 122.2 124.2 124.3 125.6 126.3 126.5 126.5 127.2 127.3 127.5 127.9 128.6 128.8 129.0 129.2 129.4 129.6 130.2 130.4 130.8 131.3 131.4 131.4 131.5 131.6 131.6 131.8 131.8 132.3 132.4 132.4 132.5 132.5 132.5 132.5 132.6 132.7 132.9 133.0 133.1 133.1 133.1 133.1 133.2 133.2 133.2 133.3 133.3 133.5 133.5 133.5 133.8 133.9 134.0 134.0 134.0 134.0 134.1 134.2 134.3 134.4 134.4 134.6 c1_p001-045.qxd 3/12/08 2:31 AM Page 20
- 39. 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 21 134.7 134.7 134.7 134.8 134.8 134.8 134.9 134.9 135.2 135.2 135.2 135.3 135.3 135.4 135.5 135.5 135.6 135.6 135.7 135.8 135.8 135.8 135.8 135.8 135.9 135.9 135.9 135.9 136.0 136.0 136.1 136.2 136.2 136.3 136.4 136.4 136.6 136.8 136.9 136.9 137.0 137.1 137.2 137.6 137.6 137.8 137.8 137.8 137.9 137.9 138.2 138.2 138.3 138.3 138.4 138.4 138.4 138.5 138.5 138.6 138.7 138.7 139.0 139.1 139.5 139.6 139.8 139.8 140.0 140.0 140.7 140.7 140.9 140.9 141.2 141.4 141.5 141.6 142.9 143.4 143.5 143.6 143.8 143.8 143.9 144.1 144.5 144.5 147.7 147.7 a. Construya una gráfica de tallos y hojas de los datos eli- minando (truncando) los dígitos de décimos y luego re- pitiendo cada valor de tallo cinco veces (una vez para las hojas 1 y 2, una segunda vez para las hojas 3 y 4, etc.). ¿Por qué es relativamente fácil identificar un valor de re- sistencia representativo? b. Construya un histograma utilizando clases de ancho igual con la primera clase que tiene un límite inferior de 122 y un límite superior de 124. Enseguida comente so- bre cualquier característica interesante del histograma. 14. El conjunto de datos adjunto se compone de observaciones del flujo de una regadera (l/min) para una muestra de n 129 casas en Perth, Australia (“An Application of Bayes Methodology to the Analysis of Diary Records in a Water Use Study”, J. Amer. Stat. Assoc., 1987: 705-711): 4.6 12.3 7.1 7.0 4.0 9.2 6.7 6.9 11.5 5.1 11.2 10.5 14.3 8.0 8.8 6.4 5.1 5.6 9.6 7.5 7.5 6.2 5.8 2.3 3.4 10.4 9.8 6.6 3.7 6.4 8.3 6.5 7.6 9.3 9.2 7.3 5.0 6.3 13.8 6.2 5.4 4.8 7.5 6.0 6.9 10.8 7.5 6.6 5.0 3.3 7.6 3.9 11.9 2.2 15.0 7.2 6.1 15.3 18.9 7.2 5.4 5.5 4.3 9.0 12.7 11.3 7.4 5.0 3.5 8.2 8.4 7.3 10.3 11.9 6.0 5.6 9.5 9.3 10.4 9.7 5.1 6.7 10.2 6.2 8.4 7.0 4.8 5.6 10.5 14.6 10.8 15.5 7.5 6.4 3.4 5.5 6.6 5.9 15.0 9.6 7.8 7.0 6.9 4.1 3.6 11.9 3.7 5.7 6.8 11.3 9.3 9.6 10.4 9.3 6.9 9.8 9.1 10.6 4.5 6.2 8.3 3.2 4.9 5.0 6.0 8.2 6.3 3.8 6.0 a. Construya una gráfica de tallos y hojas de los datos. b. ¿Cuál es una velocidad de flujo o gasto típico o repre- sentativo? c. ¿Parece estar la gráfica altamente concentrada o dis- persa? d. ¿Es la distribución de valores razonablemente simétrica? Si no, ¿cómo describiría el alejamiento de la simetría? e. ¿Describiría cualquier observación como alejada del resto de los datos (un valor extremo)? 15. Un artículo de Consumer Reports sobre crema de cacahua- te (septiembre de 1990) reportó las siguientes calificaciones para varias marcas: Creamy 56 44 62 36 39 53 50 65 45 40 56 68 41 30 40 50 56 30 22 Crunchy 62 53 75 42 47 40 34 62 52 50 34 42 36 75 80 47 56 62 Construya una gráfica de tallos y hojas comparativa y pon- ga una lista de tallos a la mitad de la página y luego coloque las hojas “creamy” a la derecha y las “crunchy” a la izquier- da. Describa las similitudes y diferencias de los dos tipos. 16. El artículo citado en el ejemplo 1.2 también dio las obser- vaciones de resistencia adjuntas para los cilindros: 6.1 5.8 7.8 7.1 7.2 9.2 6.6 8.3 7.0 8.3 7.8 8.1 7.4 8.5 8.9 9.8 9.7 14.1 12.6 11.2 a. Construya una gráfica de tallos y hojas comparativa (véa- se el ejercicio previo) de los datos de la viga y el cilindro y luego responda las preguntas en las partes b)-d) del ejercicio 10 para las observaciones de los cilindros. b. ¿En qué formas son similares los dos lados de la gráfi- ca? ¿Existen algunas diferencias obvias entre las obser- vaciones de la viga y las observaciones del cilindro? c. Construya una gráfica de puntos de los datos del cilindro. 17. Transductores de temperatura de cierto tipo se envían en lotes de 50. Se seleccionó una muestra de 60 lotes y se determinó el número de transductores en cada lote que no cumplen con las especificaciones de diseño y se obtuvieron los datos siguientes: 2 1 2 4 0 1 3 2 0 5 3 3 1 3 2 4 7 0 2 3 0 4 2 1 3 1 1 3 4 1 2 3 2 2 8 4 5 1 3 1 5 0 2 3 2 1 0 6 4 2 1 6 0 3 3 3 6 1 2 3 a. Determine las frecuencias y las frecuencias relativas de los valores observados de x número de transductores en un lote que no cumple con las especificaciones. b. ¿Qué proporción de lotes muestreados tienen a lo sumo cinco transductores que no cumplen con las especificacio- nes? ¿Qué proporción tiene menos de cinco? ¿Qué propor- ción tienen por lo menos cinco unidades que no cumplen con las especificaciones? c. Trace un histograma de los datos que utilizan la frecuencia relativa en la escala vertical y comente sus características. 18. En un estudio de productividad de autores (“Lotka’s Test”, Collection Mgmt., 1982: 111-118), se clasificó a un gran nú- mero de autores de artículos de acuerdo con el número de ar- tículos que publicaron durante cierto periodo. Los resultados se presentaron en la distribución de frecuencia adjunta: Número de artículos 1 2 3 4 5 6 7 8 Frecuencia 784 204 127 50 33 28 19 19 Número de artículos 9 10 11 12 13 14 15 16 17 Frecuencia 6 7 6 7 4 4 5 3 3 a. Construya un histograma correspondiente a esta distri- bución de frecuencia. ¿Cuál es la característica más in- teresante de la forma de la distribución? b. ¿Qué proporción de estos autores publicó por lo menos cinco artículos? ¿Por lo menos diez artículos? ¿Más de diez artículos? c. Suponga que los cinco 15, los tres 6 y los tres 17 se agruparon en una sola categoría mostrada como “ 15”. ¿Podría trazar un histograma? Explique. c1_p001-045.qxd 3/12/08 2:31 AM Page 21
- 40. 22 CAPÍTULO 1 Generalidades y estadística descriptiva d. Suponga que los valores 15, 16 y 17 se enlistan por se- parado y se combinan en la categoría 15-17 con frecuen- cia 11. ¿Sería capaz de trazar un histograma? Explique. 19. Se determinó el número de partículas contaminadas en una oblea de silicio antes de cierto proceso de enjuague por ca- da oblea en una muestra de tamaño 100 y se obtuvieron las siguientes frecuencias: Número de partículas 0 1 2 3 4 5 6 7 Frecuencia 1 2 3 12 11 15 18 10 Número de partículas 8 9 10 11 12 13 14 Frecuencia 12 4 5 3 1 2 1 a. ¿Qué proporción de las obleas muestreadas tuvieron por lo menos una partícula? ¿Por lo menos cinco partículas? b. ¿Qué proporción de las obleas muestreadas tuvieron en- tre cinco y diez partículas, inclusive? ¿Estrictamente entre cinco y diez partículas? c. Trace un histograma con la frecuencia relativa en el eje vertical. ¿Cómo describiría la forma del histograma? 20. El artículo (“Determination of Most Representative Subdi- vision”, J. of Energy Engr., 1993: 43-55) dio datos sobre varias características de subdivisiones que podrían ser utili- zados para decidir si se suministra energía eléctrica con lí- neas elevadas o líneas subterráneas. He aquí los valores de la variable x longitud total de calles dentro de una subdi- visión: 1280 5320 4390 2100 1240 3060 4770 1050 360 3330 3380 340 1000 960 1320 530 3350 540 3870 1250 2400 960 1120 2120 450 2250 2320 2400 3150 5700 5220 500 1850 2460 5850 2700 2730 1670 100 5770 3150 1890 510 240 396 1419 2109 a. Construya una gráfica de hojas y tallos con las milési- mas como el tallo y las centésimas como las hojas y co- mente sobre algunas características de la gráfica. b. Construya un histograma con los límites de clase, 0, 1000, 2000, 3000, 4000, 5000 y 6000. ¿Qué proporción de subdivisiones tienen una longitud total menor que 2000? ¿Entre 2000 y 4000? ¿Cómo describiría la forma del histograma? 21. El artículo citado en el ejercicio 20 también da los siguien- tes valores de las variables y número de calles cerradas y z número de intersecciones: y 1 0 1 0 0 2 0 1 1 1 2 1 0 0 1 1 0 1 1 z 1 8 6 1 1 5 3 0 0 4 4 0 0 1 2 1 4 0 4 y 1 1 0 0 0 1 1 2 0 1 2 2 1 1 0 2 1 1 0 z 0 3 0 1 1 0 1 3 2 4 6 6 0 1 1 8 3 3 5 y 1 5 0 3 0 1 1 0 0 z 0 5 2 3 1 0 0 0 3 a. Construya un histograma con los datos y. ¿Qué propor- ción de estas subdivisiones no tenía calles cerradas? ¿Por lo menos una calle cerrada? b. Construya un histograma con los datos z. ¿Qué propor- ción de estas subdivisiones tenía cuando mucho cinco intersecciones? ¿Menos de cinco intersecciones? 22. ¿Cómo varía la velocidad de un corredor en el recorrido del curso de un maratón (una distancia de 42.195 km)? Consi- dere determinar tanto el tiempo de recorrido de los prime- ros 5 km y el tiempo de recorrido entre los 35 y 40 km, y luego reste el primer tiempo del segundo. Un valor posi- tivo de esta diferencia corresponde a un corredor que co- rre más lento hacia el final de la carrera. El histograma adjunto está basado en tiempos de corredores que partici- paron en varios maratones japoneses (“Factors Affecting Runners’ Maratón Performance”, Chance, otoño de 1993: 24-30). 0 100 200 400 50 100 150 200 –100 Diferencia de tiempo 300 500 600 700 800 Frecuencia Histograma del ejercicio 22 c1_p001-045.qxd 3/12/08 2:31 AM Page 22
- 41. 1.2 Métodos pictóricos y tabulares en la estadística descriptiva 23 ¿Cuáles son algunas características interesantes de este histograma? ¿Cuál es un valor de diferencia típico? ¿Apro- ximadamente qué proporción de los competidores corren la última distancia más rápido que la primera? 23. En un estudio de ruptura de la urdimbre durante el tejido de telas (Technometrics, 1982: 63), se sometieron a prueba 100 muestras de hilo. Se determinó el número de ciclos de es- fuerzo hasta ruptura para cada muestra de hilo y se obtuvie- ron los datos siguientes: 86 146 251 653 98 249 400 292 131 169 175 176 76 264 15 364 195 262 88 264 157 220 42 321 180 198 38 20 61 121 282 224 149 180 325 250 196 90 229 166 38 337 65 151 341 40 40 135 597 246 211 180 93 315 353 571 124 279 81 186 497 182 423 185 229 400 338 290 398 71 246 185 188 568 55 55 61 244 20 284 393 396 203 829 239 236 286 194 277 143 198 264 105 203 124 137 135 350 193 188 a. Construya un histograma de frecuencia relativa basado en los intervalos de clase 0-100, 100-200, . . . y co- mente sobre las características del histograma. b. Construya un histograma basado en los siguientes inter- valos de clase: 0-50, 50-100, 100-150, 150-200, 200-300, 300-400, 400-500, 500-600 y 600-900. c. Si las especificaciones de tejido requieren una resistencia a la ruptura de por lo menos 100 ciclos, ¿qué proporción de los especímenes de hilos en esta muestra sería consi- derada satisfactoria? 24. El conjunto de datos adjuntos consiste en observaciones de resistencia al esfuerzo cortante (lb) de soldaduras de puntos ultrasónicas aplicadas en un cierto tipo de lámina alclad. Construya un histograma de frecuencia relativa basado en diez clases de ancho igual con límites 4000, 4200, . . . [El histograma concordará con el que aparece en (“Comparison of Properties of Joints Prepared by Ultrasonic Welding and Other Means”, J. of Aircraft, 1983: 552-556).] Comente so- bre sus características. 5434 4948 4521 4570 4990 5702 5241 5112 5015 4659 4806 4637 5670 4381 4820 5043 4886 4599 5288 5299 4848 5378 5260 5055 5828 5218 4859 4780 5027 5008 4609 4772 5133 5095 4618 4848 5089 5518 5333 5164 5342 5069 4755 4925 5001 4803 4951 5679 5256 5207 5621 4918 5138 4786 4500 5461 5049 4974 4592 4173 5296 4965 5170 4740 5173 4568 5653 5078 4900 4968 5248 5245 4723 5275 5419 5205 4452 5227 5555 5388 5498 4681 5076 4774 4931 4493 5309 5582 4308 4823 4417 5364 5640 5069 5188 5764 5273 5042 5189 4986 25. Una transformación de valores de datos por medio de alguna función matemática, tal como o 1/x a menudo produce un conjunto de números que tienen “mejores” propiedades estadísticas que los datos originales. En particular, puede ser posible encontrar una función para la cual el histograma de valores transformados es más simétrico (o, incluso mejor, más parecido a una curva en forma de campana) que los datos originales. Por ejemplo, el artículo (“Time Lapse Cinemato- graphicAnalysis of Beryllium-Lung Fibroblast Interactions”, Environ. Research, 1983: 34-43) reportó los resultados de ex- perimentos diseñados para estudiar el comportamiento de ciertas células individuales que habían estado expuestas a be- rilio. Una importante característica de dichas células indivi- duales es su tiempo de interdivisión (IDT, por sus siglas en inglés). Se determinaron tiempos de interdivisión de un gran número de células tanto en condiciones expuestas (tratamien- to) como no expuestas (control). Los autores del artículo uti- lizaron una transformación logarítmica, es decir, valor transformado log(valor original). Considere los siguientes tiempos de interdivisión representativos. IDT log10(IDT) IDT log10(IDT) IDT log10(IDT) 28.1 1.45 60.1 1.78 21.0 1.32 31.2 1.49 23.7 1.37 22.3 1.35 13.7 1.14 18.6 1.27 15.5 1.19 46.0 1.66 21.4 1.33 36.3 1.56 25.8 1.41 26.6 1.42 19.1 1.28 16.8 1.23 26.2 1.42 38.4 1.58 34.8 1.54 32.0 1.51 72.8 1.86 62.3 1.79 43.5 1.64 48.9 1.69 28.0 1.45 17.4 1.24 21.4 1.33 17.9 1.25 38.8 1.59 20.7 1.32 19.5 1.29 30.6 1.49 57.3 1.76 21.1 1.32 55.6 1.75 40.9 1.61 31.9 1.50 25.5 1.41 28.9 1.46 52.1 1.72 Use los intervalos de clase 10–20, 20–30, . . . para cons- truir un histograma de los datos originales. Use los intervalos 1.1–1.2, 1.2–1.3, . . . para hacer lo mismo con los datos transformados. ¿Cuál es el efecto de la transformación? 26. En la actualidad se está utilizando la difracción retrodisper- sada de electrones en el estudio de fenómenos de fractura. La siguiente información sobre ángulo de desorientación (grados) se extrajo del artículo (“Observations on the Face- ted Initiation Site in the Dwell-Fatigue Tested Ti-6242 Alloy: Crystallographic Orientation and Size Effects”, Me- tallurgical and Materials Trans., 2006: 1507-1518). Clase: 0–5 5–10 10–15 15–20 Frec. rel.: 0.177 0.166 0.175 0.136 Clase: 20–30 30–40 40–60 60–90 Frec. rel.: 0.194 0.078 0.044 0.030 a. ¿Es verdad que más de 50% de los ángulos muestreados son más pequeños que 15°, como se afirma en el artículo? b. ¿Qué proporción de los ángulos muestreados son por lo menos de 30°? c. ¿Aproximadamente qué proporción de los ángulos son de entre 10° y 25°? d. Construya un histograma y comente sobre cualquier ca- racterística interesante. 2x c1_p001-045.qxd 3/12/08 2:31 AM Page 23
- 42. Los resúmenes visuales de datos son herramientas excelentes para obtener impresiones y percepciones preliminares. Un análisis de datos más formal a menudo requiere el cálculo e interpretación de medidas resumidas numéricas. Es decir, de los datos se trata de extraer va- rios números resumidos, números que podrían servir para caracterizar el conjunto de datos 24 CAPÍTULO 1 Generalidades y estadística descriptiva 27. El artículo (“Study on the Life Distribution of Microdrills”, J. of Engr. Manufacture, 2002: 301-305) reportó las si- guientes observaciones, listadas en orden creciente sobre la duración de brocas (número de agujeros que una broca fre- sa antes de que se rompa) cuando se fresaron agujeros en una cierta aleación de latón. 11 14 20 23 31 36 39 44 47 50 59 61 65 67 68 71 74 76 78 79 81 84 85 89 91 93 96 99 101 104 105 105 112 118 123 136 139 141 148 158 161 168 184 206 248 263 289 322 388 513 a. ¿Por qué una distribución de frecuencia no puede estar basada en los intervalos de clase 0-50, 50-100, 100-150 y así sucesivamente? b. Construya una distribución de frecuencia e histograma de los datos con los límites de clase 0, 50, 100, . . . y lue- go comente sobre las características interesantes. c. Construya una distribución de frecuencia e histograma de los logaritmos naturales de las observaciones de du- ración y comente sobre características interesantes. d. ¿Qué proporción de las observaciones de duración en esta muestra son menores que 100? ¿Qué proporción de las observaciones son de por lo menos 200? 28. Las mediciones humanas constituyen una rica área de apli- cación de métodos estadísticos. El artículo (“A Longitudinal Study of the Development of Elementary School Children’s Private Speech”, Merrill-Palmer Q., 1990: 443-463) repor- tó sobre un estudio de niños que hablan solos (conversación a solas). Se pensaba que la conservación a solas tenía que ver con el IQ, porque se supone que éste mide la madurez mental y se sabía que la conservación a solas disminuye conforme los estudiantes avanzan a través de los años de la escuela primaria. El estudio incluyó 33 estudiantes cuyas calificaciones de IQ de primer año se dan a continuación: 82 96 99 102 103 103 106 107 108 108 108 108 109 110 110 111 113 113 113 113 115 115 118 118 119 121 122 122 127 132 136 140 146 Describa los datos y comente sobre cualquier característica importante. 29. Considere los siguientes datos sobre el tipo de problemas de salud (J hinchazón de las articulaciones, F fatiga, B dolor de espalda, M debilidad muscular, C tos, N nariz suelta/irritación, O otro) que aquejan a los planta- dores de árboles. Obtenga las frecuencias y las frecuencias relativas de las diversas categorías y trace un histograma. (Los datos son consistentes con los porcentajes dados en el artículo (“Physiological Effects of Work Stress and Pestici- de Exposure in Tree Planting de British Columbia Silvicul- ture Workers”, Ergonomics, 1993: 951-961.) O O N J C F B B F O J O O M O F F O O N O N J F J B O C J O J J F N O B M O J M O B O F J O O B N C O O O M B F J O F N 30. Un diagrama de Pareto es una variación de un histograma de datos categóricos producidos por un estudio de control de calidad. Cada categoría representa un tipo diferente de no conformidad del producto o problema de producción. Las ca- tegorías se ordenaron de modo que la categoría con la fre- cuencia más grande aparezca a la extrema izquierda, luego la categoría con la segunda frecuencia más grande, y así sucesi- vamente. Suponga que se obtiene la siguiente información sobre no conformidades en paquetes de circuito: componen- tes averiados, 126; componentes incorrectos, 210; soldadura insuficiente, 67; soldadura excesiva, 54; componente faltan- te, 131. Construya un diagrama de Pareto. 31. La frecuencia acumulativa y la frecuencia relativa acumula- tiva de un intervalo de clase particular son la suma de frecuen- cias y frecuencias relativas, respectivamente, del intervalo y todos los intervalos que quedan debajo de él. Si, por ejem- plo, existen cuatro intervalos con frecuencias 9, 16, 13 y 12, entonces las frecuencias acumulativas son 9, 25, 38 y 50 y las frecuencias relativas acumulativas son 0.18, 0.50, 0.76 y 1.00 Calcule las frecuencias acumulativas y las frecuen- cias relativas de los datos del ejercicio 24. 32. La carga de incendio (MJ/m2 ) es la energía calorífica que po- dría ser liberada por metro cuadrado de área de piso por la combustión del contenido y la estructura misma. El artículo (“Fire Loads in Office Buildings”, J. of Structural Engr., 1997: 365-368) dio los siguientes porcentajes acumulativos (tomados de una gráfica) de cargas de fuego en una muestra de 388 cuartos: Valor 0 150 300 450 600 % acumulativo 0 19.3 37.6 62.7 77.5 Valor 750 900 1050 1200 1350 % acumulativo 87.2 93.8 95.7 98.6 99.1 Valor 1500 1650 1800 1950 % acumulativo 99.5 99.6 99.8 100.0 a. Construya un histograma de frecuencia relativa y co- mente sobre características interesantes. b. ¿Qué proporción de cargas de fuego es menor que 600? ¿Por lo menos de 1200? c. ¿Qué proporción de las cargas está entre 600 y 1200? 1.3 Medidas de localización c1_p001-045.qxd 3/12/08 2:31 AM Page 24
- 43. y comunicar algunas de sus características prominentes. El interés principal se concentrará en los datos numéricos; al final de la sección aparecen algunos comentarios con respecto a datos categóricos. Supóngase, entonces, que el conjunto de datos es de la forma x1, x2, . . . , xn, donde ca- da xi es un número. ¿Qué características del conjunto de números son de mayor interés y merecen énfasis? Una importante característica de un conjunto de números es su localiza- ción y en particular su centro. Esta sección presenta métodos para describir la localización de un conjunto de datos; en la sección 1.4 se regresará a los métodos para medir la variabi- lidad en un conjunto de números. La media Para un conjunto dado de números x1, x2, . . . , xn, la medida más conocida y útil del centro es la media o promedio aritmético del conjunto. Como casi siempre se pensará que los nú- meros xi constituyen una muestra, a menudo se hará referencia al promedio aritmético co- mo la media muestral y se la denotará por . x Para reportar , se recomienda utilizar una precisión decimal de un dígito más que la preci- sión de los números xi. Por consiguiente las observaciones son distancias de detención con x1 125, x2 131 y así sucesivamente, se podría tener 127.3 pies. El agrietamiento de hierro y acero provocado por corrosión producida por esfuerzo cáusti- co ha sido estudiado debido a las fallas que se presentan alrededor de los remaches en cal- deras de acero y fallas de rotores de turbinas de vapor. Considérense las observaciones adjuntas de x longitud de agrietamiento (m) derivadas de pruebas de corrosión con es- fuerzo constante en probetas de barras pulidas sometidas a tensión durante un periodo fijo. (Los datos concuerdan con un histograma y cantidades resumidas tomadas del artículo “On the Role of Phosphorus in the Caustic Stress Corrosion Cracking of Low Alloy Steels”, Co- rrosion Science, 1989: 53-68.) x1 16.1 x2 9.6 x3 24.9 x4 20.4 x5 12.7 x6 21.2 x7 30.2 x8 25.8 x9 18.5 x10 10.3 x11 25.3 x12 14.0 x13 27.1 x14 45.0 x15 23.3 x16 24.2 x17 14.6 x18 8.9 x19 32.4 x20 11.8 x21 28.5 La figura 1.13 muestra una gráfica de tallo y hojas de los datos; una longitud de agrietamien- to en los 20 bajos parece ser “típica”. x x 1.3 Medidas de ubicación 25 Ejemplo 1.12 DEFINICIÓN La media muestral de las observaciones x1, x2, . . . , xn está dada por El numerador de se escribe más informalmente como xi , donde la suma incluye todas las observaciones muestrales. x x 5 x1 1 x2 1 c 1 xn n 5 g n i51 xi n x Figura 1.13 Gráfica de tallo y hojas de los datos de la longitud de agrietamiento. 0H 96 89 1L 27 03 40 46 18 1H 61 85 2L 49 04 12 33 42 Tallo: dígitos de decenas 2H 58 53 71 85 Hojas: dígitos de unidades y decenas 3L 02 24 3H 4L 4H 50 c1_p001-045.qxd 3/12/08 2:31 AM Page 25
- 44. 26 CAPÍTULO 1 Generalidades y estadística descriptiva Con xi 444.8, la media muestral es un valor consistente conforme a la información dada por la gráfica de tallo y hojas. ■ Una interpretación física de demuestra cómo mide la ubicación (centro) de una muestra. Se traza y gradúa un eje de medición horizontal y luego se representa cada obser- vación muestral por una pesa de 1 lb colocada en el punto correspondiente sobre el eje. El único punto en el cual se puede colocar un punto de apoyo para equilibrar el sistema de pe- sas es el punto correspondiente al valor de (véase la figura 1.14). x x x 5 444.8 21 5 21.18 Así como representa el valor promedio de las observaciones incluidas en una mues- tra, se puede calcular el promedio de todos los valores incluidos en la población. Este pro- medio se llama media de la población y está denotada por la letra griega . Cuando existen N valores en la población (una población finita), entonces (suma de los N valores de población)/N. En los capítulos 3 y 4, se dará una definición más general de que se aplica tanto a poblaciones finitas y (conceptualmente) infinitas. Así como es una medida intere- sante e importante de la ubicación de la muestra, es una interesante e importante caracte- rística (con frecuencia la más importante) de una población. En los capítulos de inferencia estadística, se presentarán métodos basados en la media muestral para sacar conclusiones con respecto a una media de población. Por ejemplo, se podría utilizar la media muestral 21.18 calculada en el ejemplo 1.12 como una estimación puntual (un solo número que es la “mejor” conjetura) de la longitud de agrietamiento promedio verdadera de todas las probetas tratadas como se describe. La media sufre de una deficiencia que la hace ser una medida inapropiada del centro en algunas circunstancias: su valor puede ser afectado en gran medida por la presencia de incluso un solo valor extremo (una observación inusualmente grande o pequeña). En el ejemplo 1.12, el valor x14 45.0 es obviamente un valor extremo. Sin esta observación, 399.8/20 19.99; el valor extremo incrementa la media en más de 1 m. Si la obser- vación de 45.0 m fuera reemplazada por el valor catastrófico de 295.0 m, un valor real- mente extremo, entonces 694.8/21 33.09, ¡el cual es más grande que todos excepto una de las observaciones! Una muestra de ingresos a menudo produce algunos valores apartados (unos cuantos afortunados que gana cantidades astronómicas) y el uso del ingreso promedio como medi- da de ubicación con frecuencia será engañoso. Tales ejemplos sugieren que se busca una medida que sea menos sensible a los valores apartados que y momentáneamente se pro- pondrá una. Sin embargo, aunque sí tiene este defecto potencial, sigue siendo la medida más ampliamente utilizada, en gran medida porque existen muchas poblaciones para las cuales un valor extremo en la muestra sería altamente improbable. Cuando se muestrea una población como esa (una población normal o en forma de campana es el ejemplo más im- portante), la media muestral tenderá a ser estable y bastante representativa de la muestra. La mediana La palabra mediana es sinónimo de “medio” y la mediana muestral es en realidad el valor medio una vez que se ordenan las observaciones de la más pequeña a la más grande. Cuando las observaciones están denotadas por x1, . . . , xn, se utilizará el símbolo para representar la mediana muestral. x | x x x x x x x Figura 1.14 La media como punto de equilibrio de un sistema de pesas. 10 20 30 40 x = 21.18 c1_p001-045.qxd 3/12/08 2:31 AM Page 26
- 45. El riesgo de desarrollar deficiencia de hierro es especialmente alto durante el embarazo. El problema con la detección de tal deficiencia es que algunos métodos para determinar el es- tado del hierro pueden ser afectados por el estado de gravidez mismo. Considérense las si- guientes observaciones ordenadas de concentración de receptores de transferrina de una muestra de mujeres con evidencia de laboratorio de anemia por deficiencia de hierro eviden- te (“Serum Transferrin Receptor for the Detection of Iron Deficiency in Pregnancy”, Amer. J. of Clinical Nutrition, 1991: 1077-1081): 7.6 8.3 9.3 9.4 9.4 9.7 10.4 11.5 11.9 15.2 16.2 20.4 Como n 12 es par, el n/2 los valores sexto y séptimo ordenados deben ser promedia- dos: Note que si la observación más grande, 20.4, no hubiera aparecido en la muestra, la media- na muestral resultante de las n 11 observaciones habría sido el valor medio 9.7 [el (n + 1)/2 sexto valor ordenado]. La media muestral es , la cual es un tanto más grande que la mediana debido a los valores apartados 15.2, 16.2 y 20.4. ■ Los datos del ejemplo 1.13 ilustran una importante propiedad de en contraste con . La mediana muestral es muy insensible a los valores apartados. Si, por ejemplo, las dos xi más grandes se incrementan desde 16.2 y 20.4 hasta 26.2 y 30.4, respectivamente, no se vería afectada. Por lo tanto, en el tratamiento de valores apartados, y no son extremos opuestos de un espectro. Debido a que los valores grandes presentes en la muestra del ejemplo 1.13 afectan a más que , con esos datos. Aunque tanto como ubican el centro de un con- junto de datos, en general no serán iguales porque se enfocan en aspectos diferentes de la muestra. Análogo a como valor medio de la muestra es un valor medio de la población, la mediana poblacional, denotada por . Como con y , se puede pensar en utilizar la me- diana muestral para hacer una inferencia sobre . En el ejemplo 1.13, se podría utilizar 10.05 como estimación de la concentración de la mediana en toda la población de la cual se tomó la muestra. A menudo se utiliza una mediana para describir ingresos o sala- rios (debido a que no es influida en gran medida por unos pocos salarios grandes). Si el sa- lario mediano de una muestra de ingenieros fuera 66 416 dólares se podría utilizar como base para concluir que el salario mediano de todos los ingenieros es de más de 60 000 dólares. x | x | m | x | x m | x | x | x x x | x | x x | x x | x x | xi/n 5 139.3/12 5 11.61 x 5 x | 5 9.7 1 10.4 2 5 10.05 1.3 Medidas de ubicación 27 Ejemplo 1.13 DEFINICIÓN La mediana muestral se obtiene ordenando primero las n observaciones de la más pequeña a la más grande (con cualesquiera valores repetidos incluidos de modo que cada observación muestral aparezca en la lista ordenada). Entonces, El valor medio único si n es impar El promedio de los dos valores promedio de n 2 n-ésimo y n 2 1 n-ésimo valores ordenados medios si n es par x | ¨ « « « « © « « « « ª n 2 1 n-ésimo valor ordenado c1_p001-045.qxd 3/12/08 2:31 AM Page 27
- 46. 28 CAPÍTULO 1 Generalidades y estadística descriptiva La media y la mediana poblacionales en general no serán idénticas. Si la distri- bución de la población es positiva o negativamente asimétrica, como se ilustra en la figura 1.15, entonces . Cuando éste es el caso, al hacer inferencias primero se debe decidir cuál de las dos características de la población es de mayor interés y luego proceder como corresponda. Otras medidas de localización: cuartiles, percentiles y medias recortadas La mediana (poblacional o muestral) divide el conjunto de datos en dos partes iguales. Pa- ra obtener medidas de ubicación más finas, se podrían dividir los datos en más de dos par- tes. Tentativamente, los cuartiles dividen el conjunto de datos en cuatro partes iguales y las observaciones arriba del tercer cuartil constituyen el cuarto superior del conjunto de datos, el segundo cuartil es idéntico a la mediana y el primer cuartil separa el cuarto inferior de los tres cuartos superiores. Asimismo, un conjunto de datos (muestra o población) puede ser in- cluso más finamente dividido por medio de percentiles, el 99o percentil separa el 1% más alto del 99% más bajo, y así sucesivamente. A menos que el número de observaciones sea un múltiplo de 100, se debe tener cuidado al obtener percentiles. En el capítulo 4 se utiliza- rán percentiles con conexión con ciertos modelos de poblaciones infinitas y por tanto su dis- cusión se pospone hasta ese punto. La media es bastante sensible a un solo valor extremo, mientras que la mediana es in- sensible a muchos valores apartados. Como el comportamiento extremo de uno u otro tipo podría ser indeseable, se consideran brevemente medidas alternativas que no son ni sensi- bles como ni tan insensibles como . Para motivar estas alternativas, obsérvese que y se encuentran en extremos opuestos de la misma “familia” de medidas. La media es el pro- medio de todos los datos, mientras que la mediana resulta de eliminar todos excepto uno o dos valores medios y luego promediar. Parafraseando, la media implica recortar 0% de cada extremo de la muestra, mientras que en el caso de la mediana se recorta la cantidad máxima posible de cada extremo. Una muestra recortada es un término medio entre y . Una me- dia 10% recortada, por ejemplo, se calcularía eliminando el 10% más pequeño y el 10% más grande de la muestra y luego promediando lo que queda. La producción de Bidri es una artesanía tradicional de India. Las artesanías Bidri (tazones, recipientes, etc.) se funden con una aleación que contiene principalmente zinc y algo de co- bre. Considere las siguientes observaciones sobre contenido de cobre (%) de una muestra de artefactos Bidri tomada del Museo Victoria y Albert en Londres (“Enigmas of Bidri”, Sur- face Engr., 2005: 333-339), enlistadas en orden creciente. 2.0 2.4 2.5 2.6 2.6 2.7 2.7 2.8 3.0 3.1 3.2 3.3 3.3 3.4 3.4 3.6 3.6 3.6 3.6 3.7 4.4 4.6 4.7 4.8 5.3 10.1 La figura 1.16 es una gráfica de puntos de los datos. Una característica prominente es el valor extremo único en el extremo superior; la distribución está más dispersa en la región de valores grandes que en el caso de valores pequeños. La media muestral y la mediana son 3.65 y 3.35, respectivamente. Se obtiene una media recortada ( r) con un porcentaje de recorte de 100(2/26) 7.7% al eliminar las dos observaciones más pequeñas y las dos más grandes; esto da x x | x x | x x | x m 2 m | m | Ejemplo 1.14 Figura 1.15 Tres formas diferentes de una distribución de población. ~ ~ ~ a) Asimétrico negativo b) Simétrico c) Asimétrico positivo c1_p001-045.qxd 3/12/08 2:31 AM Page 28
- 47. . El recorte en este caso elimina el valor extremo más grande y por tanto aproxi- ma la media recortada hacia la mediana. ■ Una media recortada con un porcentaje de recorte moderado, algo entre 5 y 25%, pro- ducirá una medida del centro que no es ni tan sensible a los valores apartados como la me- dia ni tan insensible como la mediana. Si el porcentaje de recorte deseado es 100% y n no es un entero, la media recortada debe ser calculada por interpolación. Por ejemplo, considé- rese 0.10 para un porcentaje de recorte de 10% y n 26 como en el ejemplo 1.14. En- tonces sería el promedio ponderado apropiado de la media 7.7% recortada calculada allí y la media 11.5% recortada que resulta de recortar tres observaciones de cada extremo. Datos categóricos y proporciones muestrales Cuando los datos son categóricos, una distribución de frecuencia o una distribución de fre- cuencia relativa proporciona un resumen tabular efectivo de los datos. Las cantidades resumi- das numéricas naturales en esta situación son las frecuencias individuales y las frecuencias relativas. Por ejemplo, si se realiza una encuesta de personas que poseen cámaras digitales para estudiar la preferencia de marcas y cada persona en la muestra identifica la marca de cámara que él o ella posee, con lo cual se podría contar el número que poseen Cannon, Sony, Kodak, y así sucesivamente. Considérese muestrear una población dividida en dos partes, una que consiste en sólo dos categorías (tal como votó o no votó en la última elección, si posee o no una cámara digital, etc.). Si x denota el número en la muestra que cae en la categoría 1, entonces el número en el categoría 2 es n x. La frecuencia relativa o propor- ción muestral en la categoría 1 es x/n y la proporción muestral en la categoría 2 es 1 x/n. Que 1 denote una respuesta que cae en la categoría 1 y que 0 denote una respuesta que cae en la categoría 2. Un tamaño de muestra de n 10 podría dar entonces las respuestas 1, 1, 0, 1, 1, 1, 0, 0, 1, 1. La media muestral de esta muestra numérica es (como el número de unos x 7) Más generalmente, enfóquese la atención en una categoría particular y codifíquense los resultados de modo que se anote un 1 para una observación comprendida en la catego- ría y un 0 para una observación no comprendida en la categoría. Entonces la proporción muestral de observaciones comprendida en la categoría es la media muestral de la secuen- cia de los 1 y los 0. Por consiguiente se puede utilizar una media muestral para resumir los resultados de una muestra categórica. Estos comentarios también se aplican a situaciones en las cuales las categorías se definen agrupando valores en una muestra o población numéri- ca (p. ej., podría existir interés en saber si las personas han tenido su automóvil actual du- rante por lo menos 5 años, en lugar de estudiar la duración exacta de la tenencia). Análogo a la proporción muestral x/n de personas u objetos que caen en una catego- ría particular, que p represente la proporción de aquellos presentes en toda la población que cae en la categoría. Como con x/n, p es una cantidad entre 0 y 1 y mientras que x/n es una característica de muestra, p es una característica de la población. La relación entre las x1 1 c1 xn n 5 1 1 1 1 0 1 c1 1 1 1 10 5 7 10 5 x n 5 proporción muestral xrs10d xrs7.7d 5 3.42 1.3 Medidas de ubicación 29 Figura 1.16 Gráfica de puntos de contenidos de cobre del ejemplo 1.14. x ~ x – xr(7.7) – 1 2 3 4 5 6 7 8 9 10 11 c1_p001-045.qxd 3/12/08 2:31 AM Page 29
- 48. 30 CAPÍTULO 1 Generalidades y estadística descriptiva dos es igual a la relación entre y y entre y m. En particular, subsecuentemente se utili- zará x/n para hacer inferencias sobre p. Si, por ejemplo, una muestra de 100 propietarios de automóviles reveló que 22 tenían su automóvil desde por lo menos 5 años atrás, en tal caso se podría utilizar 22/100 0.22 como estimación puntual de la proporción de todos los propie- tarios que tenían su automóvil desde por lo menos 5 años atrás. Se estudiarán las propiedades de x/n como una estimación de p para ver cómo se puede utilizar x/n para responder otras pre- guntas inferenciales. Con k categorías (k 2), se pueden utilizar las k proporciones muestra- les para responder preguntas sobre las proporciones de población p1, . . . , pk. x m | x | EJERCICIOS Sección 1.3 (33-43) 33. El artículo (“The Pedaling Technique of Elite Endurance Cyclists”, Inst. J. of Sport Biomechanics, 1991: 29-53) re- portó los datos adjuntos sobre potencia de una sola pierna sometida a una alta carga de trabajo. 244 191 160 187 180 176 174 205 211 183 211 180 194 200 a. Calcule e interprete la media y la mediana muestral. b. Suponga que la primera observación hubiera sido 204 en lugar de 244. ¿Cómo cambiarían la media y la mediana? c. Calcule una media recortada eliminando las observacio- nes muestrales más pequeñas y más grandes. ¿Cuál es el porcentaje de recorte correspondiente? d. El artículo también reportó valores de potencia de una sola pierna con carga de trabajo baja. La media muestral de n 13 observaciones fue x 119.8 (en realidad 119.7692) y la 14a.observación, algo así como un valor ex- tremo, fue 159. ¿Cuál es el valor de x de toda la muestra? 34. La exposición a productos microbianos, especialmente en- dotoxina, puede tener un impacto en la vulnerabilidad a enfermedades alérgicas. El artículo (“Dust Sampling Methods for Endotoxin-An Essential, But Underestimated Issue”, Indoor Air, 2006: 20-27) consideró temas asociados con la determinación de concentración de endotoxina. Los siguien- tes datos sobre concentración (EU/mg) en polvo asentado de una muestra de hogares urbanos y otra de casas campes- tres fueron amablemente suministrados por los autores del artículo citado. U: 6.0 5.0 11.0 33.0 4.0 5.0 80.0 18.0 35.0 17.0 23.0 C: 4.0 14.0 11.0 9.0 9.0 8.0 4.0 20.0 5.0 8.9 21.0 9.2 3.0 2.0 0.3 a. Determine la media muestral de cada muestra. ¿Cómo se comparan? b. Determine la mediana muestral de cada muestra. ¿Cómo se comparan? ¿Por qué es la mediana de la muestra ur- bana tan diferente de la media de dicha muestra? c. Calcule la media recortada de cada muestra eliminando la observación más pequeña y más grande. ¿Cuáles son los porcentajes de recorte correspondientes? ¿Cómo se comparan los valores de estas medias recortadas a las medias y medianas correspondientes? 35. La presión de inyección mínima (lb/pulg2 ) de especímenes moldeados por inyección de fécula de maíz se determinó con ocho especímenes diferentes (la presión más alta co- rresponde a una mayor dificultad de procesamiento) y se obtuvieron las siguientes observaciones (tomadas de “Ther- moplastic Starch Blends with Polyethylene-Co-Vinyl Alco- hol: Processability and Physical Properties”, Polymer Engr. and Science, 1994: 17-23): 15.0 13.0 18.0 14.5 12.0 11.0 8.9 8.0 a. Determine los valores de la media muestral, la mediana muestral y la media 12.5% recortada y compare estos valores. b. ¿En cuánto se podría incrementar la observación de la muestra más pequeña, actualmente 8.0, sin afectar el va- lor de la mediana muestral? c. Suponga que desea los valores de la media y la mediana muestrales cuando las observaciones están expresadas en kilogramos por pulgada cuadrada (kg/pulg2 ) en lugar de lb/pulg2 . ¿Es necesario volver a expresar cada observación en kg/pulg2 o se pueden utilizar los valores calculados en el inciso a) directamente? [Sugerencia: 1 kg 2.2 lb.] 36. Una muestra de 26 trabajadores de plataforma petrolera ma- rina tomaron parte en un ejercicio de escape y se obtuvieron los datos adjuntos de tiempo (s) para completar el escape (“Oxygen Consumption and Ventilation During Escape from an Offshore Platform”, Ergonomics, 1997: 281-292): 389 356 359 363 375 424 325 394 402 373 373 370 364 366 364 325 339 393 392 369 374 359 356 403 334 397 a. Construya una gráfica de tallo y hojas de los datos. ¿Có- mo sugiere la gráfica que la media y mediana muestra- les se comparen? b. Calcule los valores de la media y mediana muestrales [Sugerencia: xi 9638.] c. ¿En cuánto se podría incrementar el tiempo más largo, actualmente de 424, sin afectar el valor de la mediana muestral? ¿En cuánto se podría disminuir este valor sin afectar el valor de la mediana muestral? d. ¿Cuáles son los valores de x y cuando las observacio- nes se reexpresan en minutos? 37. El artículo (“Snow Cover and Temperature Relationships in North America and Eurasia”, J. Climate and Applied Me- teorology, 1983: 460-469) utilizó técnicas estadísticas para relacionar la cantidad de cobertura de nieve sobre cada x | c1_p001-045.qxd 3/12/08 2:31 AM Page 30
- 49. El reporte de una medida de centro da sólo información parcial sobre un conjunto o distri- bución de datos. Diferentes muestras o poblaciones pueden tener medidas idénticas de cen- tro y aún diferir entre sí en otras importantes maneras. La figura 1.17 muestra gráficas de puntos de tres muestras con las mismas media y mediana, aunque el grado de dispersión en 1.4 Medidas de variabilidad 31 continente para promediar la temperatura continental. Los datos allí presentados incluyeron las siguientes diez obser- vaciones de la cobertura de nieve en octubre en Eurasia du- rante los años 1970-1979 (en millones de km2 ): 6.5 12.0 14.9 10.0 10.7 7.9 21.9 12.5 14.5 9.2 ¿Qué reportaría como valor representativo, o típico de co- bertura de nieve en octubre durante este periodo y qué mo- tivaría su elección? 38. Los valores de presión sanguínea a menudo se reportan a los 5 mmHg más cercanos (100, 105, 110, etc.). Suponga que los valores de presión sanguínea reales de nueve indivi- duos seleccionados al azar son 118.6 127.4 138.4 130.0 113.7 122.0 108.3 131.5 133.2 a. ¿Cuál es la mediana de los valores de presión sanguínea reportados? b. Suponga que la presión sanguínea del segundo indivi- duo es 127.6 en lugar de 127.4 (un pequeño cambio en un solo valor). ¿Cómo afecta esto a la mediana de los va- lores reportados? ¿Qué dice esto sobre la sensibilidad de la mediana al redondeo o agrupamiento en los datos? 39. La propagación de grietas provocadas por fatiga en varias partes de un avión ha sido el tema de extensos estudios en años recientes. Los datos adjuntos se componen de vidas de propagación (horas de vuelo/104 ) para alcanzar un tamaño de agrietamiento dado en orificios para sujetadores utiliza- dos en aviones militares (“Statistical Crack Propagation in Fastener Holes ander Spectrum Loading”, J. Aircraft, 1983: 1028-1032): 0.736 0.863 0.865 0.913 0.915 0.937 0.983 1.007 1.011 1.064 1.109 1.132 1.140 1.153 1.253 1.394 a. Calcule y compare los valores de la media y mediana muestrales. b. ¿En cuánto se podría disminuir la observación muestral más grande sin afectar el valor de la mediana? 40. Calcule la mediana muestral, media 25% recortada, media 10% recortada y media muestral de los datos de duración dados en el ejercicio 27 y compare estas medidas. 41. Se eligió una muestra de n 10 automóviles y cada uno se sometió a una prueba de choque a 5 mph. Denotando un ca- rro sin daños visibles por S (por éxito) y un carro con daños por F, los resultados fueron los siguientes: S S F S S S F F S S a. ¿Cuál es el valor de la proporción muestral de éxitos x/n? b. Reemplace cada S con 1 y cada F con 0. Acto seguido calcule x de esta muestra numéricamente codificada. ¿Cómo se compara x con x/n? c. Suponga que se decide incluir 15 carros más en el expe- rimento. ¿Cuántos de éstos tendrían que ser S para dar x/n 0.80 para toda la muestra de 25 carros? 42. a. Si se agrega una constante c a cada xi en una muestra y se obtiene yi xi c, ¿cómo se relacionan la media y mediana muestrales de las yi con la media y mediana muestrales de las xi? Verifique sus conjeturas. b. Si cada xi se multiplica por una constante c y se obtiene yi cxi, responda la pregunta del inciso a). De nuevo, verifique sus conjeturas. 43. Un experimento para estudiar la duración (en horas) de un cierto tipo de componente implicaba poner diez componentes en operación y observarlos durante 100 ho- ras. Ocho de ellos fallaron durante dicho periodo y se re- gistraron las duraciones. Denote las duraciones de dos componentes que continuaron funcionando después de 100 horas por 100. Las observaciones muestrales re- sultantes fueron: 48 79 100 35 92 86 57 100 17 29 ¿Cuáles de las medidas del centro discutidas en esta sección pueden ser calculadas y cuáles son los valores de dichas medidas? [Nota: Se dice que los datos obtenidos con este experimento están “censurados a la derecha”.] 1.4 Medidas de variabilidad Figura 1.17 Muestras con medidas idénticas de centro pero diferentes cantidades de variabilidad. 30 40 * * * * * * * * * 50 60 70 1: 2: 3: c1_p001-045.qxd 3/12/08 2:31 AM Page 31
- 50. 32 CAPÍTULO 1 Generalidades y estadística descriptiva torno al centro es diferente para las tres muestras. La primera tiene la cantidad más grande de variabilidad, la tercera tiene la cantidad más pequeña y la segunda es intermedia con res- pecto a las otras dos. Medidas de variabilidad de datos muestrales La medida más simple de variabilidad en una muestra es el rango, el cual es la diferencia entre los valores muestrales más grande y más pequeño. El valor del rango de la muestra 1 en la figura 1.17 es mucho más grande que el de la muestra 3, lo que refleja más variabilidad en la primera muestra que en la tercera. Un defecto del rango, no obstante, es que depende de sólo las dos observaciones más extremas y hace caso omiso de las posiciones de los n – 2 valores restantes. Las muestras 1 y 2 en la figura 1.17 tienen rangos idénticos, aunque cuan- do se toman en cuenta las observaciones entre los dos extremos, existe mucho menos varia- bilidad o dispersión en la segunda muestra que en la primera. Las medidas principales de variabilidad implican las desviaciones de la media, x1 x , x2 x , . . . , xn x . Es decir, las desviaciones de la media se obtienen restando x de cada una de la n observaciones muestrales. Una desviación será positiva si la observación es más grande que la media (a la derecha de la media sobre el eje de medición) y negativa si la observación es más pequeña que la media. Si todas las desviaciones son pequeñas en magnitud, entonces todas las xi se aproximan a la media y hay poca variabilidad. Alternati- vamente, si algunas de las desviaciones son grandes en magnitud, entonces algunas xi que- dan lejos de x lo que sugiere una mayor cantidad de variabilidad. Una forma simple de combinar las desviaciones en una sola cantidad es promediarlas. Desafortunadamente, esto es una mala idea: suma de desviaciones n i1 (xi x ) 0 por lo que la desviación promedio siempre es cero. La verificación utiliza varias reglas es- tándar y el hecho de que x x x x nx : (xi x ) xi x xi nx xi n 1 n xi 0 ¿Cómo se puede evitar que las desviaciones negativas y positivas se neutralicen entre sí cuando se combinan? Una posibilidad es trabajar con los valores absolutos de las desviacio- nes y calcular la desviación absoluta promedio °xi x °/n. Como la operación de valores absolutos conduce a dificultades teóricas, considérense en cambio las desviaciones al cua- drado (x1 x )2 , (x2 x )2 , . . . , (xn x )2 . En vez de utilizar la desviación al cuadrado pro- medio (xi x )2 /n, por varias razones se divide la suma de desviaciones al cuadrado entre n 1 en lugar de entre n. Obsérvese que s2 y s son no negativas. La unidad de s es la misma que la de cada una de las xi. Si por ejemplo, las observaciones son eficiencias de combustible en millas por galón, en- tonces se podría tener s 2.0 mpg. Una interpretación preliminar de la desviación estándar DEFINICIÓN La varianza muestral, denotada por s2 está dada por s2 ( n xi 1 x )2 n S xx 1 La desviación estándar muestral, denotada por s, es la raíz cuadrada (positiva) de la varianza s s2 c1_p001-045.qxd 3/12/08 2:31 AM Page 32
- 51. 1.4 Medidas de variabilidad 33 muestral es que es el tamaño de una desviación típica o representativa de la media muestral dentro de la muestra dada. Por tanto si s 2.0 mpg, entonces algunas xi en la muestra se aproximan más que 2.0 a x , en tanto que otras están más alejadas; 2.0 es una desviación re- presentativa (o “estándar”) de la eficiencia de combustible media. Si s 3.0 de una segunda muestra de carros de otro tipo, una desviación típica en esta muestra es aproximadamente 1.5 veces la de la primera muestra, una indicación de más variabilidad en la segunda muestra. La resistencia es una característica importante de los materiales utilizados en casas prefabri- cadas. Cada uno de n 11 elementos de placa prefabricados se sometieron a prueba de es- fuerzo severo y se registró el ancho máximo (mm) de las grietas resultantes. Los datos proporcionados (tabla 1.3) aparecieron en el artículo (“Prefabricated Ferrocement Ribbed Elements for Low-Cost Housing”, J. Ferrocement, 1984: 347-364). Los efectos de redondeo hacen que la suma de las desviaciones no sea exactamente cero. El numerador de s2 es 11.9359, por consiguiente s2 11.9359/(11 1) 11.9359/10 1.19359 y s 1 .1 9 3 5 9 1.0925 mm. ■ Motivación para s2 Para explicar el porqué del divisor n 1 en s2 , obsérvese primero que en tanto que s2 mide la variabilidad muestral, existe una medida de variabilidad en la población llamada varianza poblacional. Se utilizará 2 (el cuadrado de la letra griega sigma minúscula) para denotar la varianza poblacional y para denotar la desviación estándar poblacional (la raíz cuadrada de 2 ). Cuando la población es finita y se compone de N valores, 2 N i1 (xi )2 /N la cual es el promedio de todas las desviaciones al cuadrado con respecto a la media poblacio- nal (para la población, el divisor es N y no N 1). En los capítulos 3 y 4 aparecen definiciones más generales de 2 . Así como x se utilizará para hacer inferencias sobre la media poblacional , se de- berá definir la variancia muestral de modo que pueda ser utilizada para hacer inferencias sobre 2 . Ahora obsérvese que 2 implica desviaciones cuadradas con respecto a la me- dia poblacional . Si en realidad se conociera el valor de , entonces se podría definir la Ejemplo 1.15 Tabla 1.3 Datos del ejemplo 1.15 xi xi x (xi x )2 0.684 0.9841 0.9685 2.540 0.8719 0.7602 0.924 0.7441 0.5537 3.130 1.4619 2.1372 1.038 0.6301 0.3970 0.598 1.0701 1.1451 0.483 1.1851 1.4045 3.520 1.8519 3.4295 1.285 0.3831 0.1468 2.650 0.9819 0.9641 1.497 0.1711 0.0293 xi 18.349 (xi x ) 0.0001 Sxx (xi x )2 11.9359 x 18.349/11 1.6681 c1_p001-045.qxd 3/12/08 2:31 AM Page 33
- 52. 34 CAPÍTULO 1 Generalidades y estadística descriptiva varianza muestral como la desviación al cuadrado promedio de las xi de la muestra con respecto a . Sin embargo, el valor de casi nunca es conocido, por lo que se debe uti- lizar el cuadrado de la suma de las desviaciones con respecto a x . Pero las xi tienden a acercarse más a su valor promedio que el promedio poblacional , así que para compen- sar esto se utiliza el divisor n – 1 en lugar de n. En otras palabras, si se utiliza un divisor n en la varianza muestral, entonces la cantidad resultante tendería a subestimar 2 (se pro- ducen valores demasiado pequeños en promedio), mientras que si se divide entre el divi- sor un poco más pequeño n – 1 se corrige esta subestimación. Se acostumbra referirse a s2 que está basada en n – 1 grados de libertad (gl o df, por sus siglas en inglés). Esta terminología se deriva del hecho de que aunque s2 está basada en las n cantidades x1 x , x2 x , . . . , xn x , éstas suman 0, por lo que al especificar los valores de cualquier n – 1 de las cantidades se determina el valor restante. Por ejemplo, si n 4 y x1 x 8, x2 x 6 y x4 x 4, entonces automáticamente x3 x 2, así que sólo tres de los cuatro valores de xi x son libremente determinados (3 gl). Una fórmula para calcular s2 Es mejor obtener s2 con software estadístico o bien utilizar una calculadora que permita in- gresar datos en la memoria y luego ver s2 con un solo golpe de tecla. Si su calculadora no tiene esta capacidad, existe una fórmula alternativa para Sxx que evita calcular las desviacio- nes. La fórmula implica sumar (xi )2 , sumar y luego elevar al cuadrado y xi 2 , elevar al cuadrado y sumar. Comprobación Como x xi/n, nx 2 (xi )2 /n. Entonces (xi x )2 (x2 i 2x xi x 2 ) x2 i 2x xi (x )2 x2 i 2x nx n(x )2 x2 i n(x )2 La cantidad de luz reflejada por las hojas ha sido utilizada para varios propósitos, incluidas la evaluación del color del césped, la estimación del estado del nitrógeno y la medición de la bio- masa. El artículo (“Leaf Reflectance-Nitrogen-Chlorophyll Relations in Buffel-Grass”, Pho- togrammetric Engr. and Remote Sensing, 1985: 463-466) dio las siguientes observaciones obtenidas por medio de espectrofotogrametría, de la reflexión de las hojas en condiciones ex- perimentales. Una alternativa para el numerador de s2 es Sxx (xi x )2 x2 i ( n xi )2 Ejemplo 1.16 Observación xi x2 i Observación xi x2 i 1 15.2 231.04 9 12.7 161.29 2 16.8 282.24 10 15.8 249.64 3 12.6 158.76 11 19.2 368.64 4 13.2 174.24 12 12.7 161.29 5 12.8 163.84 13 15.6 243.36 6 13.8 190.44 14 13.5 182.25 7 16.3 265.69 15 12.9 166.41 8 13.0 169.00 xi 216.1 x2 i 3168.13 c1_p001-045.qxd 3/12/08 2:31 AM Page 34
- 53. La fórmula de cálculo ahora da Sxx x2 i ( n xi )2 3168.13 (21 1 6 5 .1)2 3168.13 3113.28 54.85 con la cual s2 Sxx /(n 1) 54.85/14 3.92 y s 1.98. ■ Tanto la fórmula definitoria como la de cálculo para s2 pueden ser sensibles al redondeo, por lo que en los cálculos intermedios se deberá usar tanta precisión decimal como sea posible. Algunas otras propiedades de s2 pueden mejorar el entendimiento y facilitar el cálculo. En palabras, el resultado 1 dice que si se suma una constante c (o resta) de cada valor de dato, la varianza no cambia. Esto es intuitivo, puesto que la adición o sustracción de c cambia la localización del conjunto de datos pero deja las distancias iguales entre los valores de datos. De acuerdo con el resultado 2, la multiplicación de cada xi por c hace que s2 sea multiplicada por un factor de c2 . Estas propiedades pueden ser comprobadas al observar que en el resul- tado 1, y x c y que en el resultado 2, y cx . Gráficas de caja Las gráficas de tallo y hojas e histogramas transmiten impresiones un tanto generales sobre un conjunto de datos, mientras que un resumen único tal como la media o la desviación están- dar se enfoca en sólo un aspecto de los datos. En años recientes, se ha utilizado con éxito un resumen gráfico llamado gráfica de caja para describir varias de las características más pro- minentes de un conjunto de datos. Estas características incluyen 1) el centro, 2) la disper- sión, 3) el grado y naturaleza de cualquier alejamiento de la simetría y 4) la identificación de las observaciones “extremas o apartadas” inusualmente alejadas del cuerpo principal de los datos. Como incluso un solo valor extremo puede afectar drásticamente los valores de x y s, una gráfica de caja está basada en medidas “resistentes” a la presencia de unos cuantos valo- res apartados, la mediana y una medida de variabilidad llamada dispersión de los cuartos. En general, la dispersión de los cuartos no se ve afectada por las posiciones de las observa- ciones comprendidas en el 25% más pequeño o el 25% más grande de los datos. Por consi- guiente es resistente a valores apartados. La gráfica de caja más simple se basa en el siguiente resumen de cinco números: xi más pequeñas cuarto inferior mediana cuarto superior xi más grandes 1.4 Medidas de variabilidad 35 Sean x1, x2, . . . , xn una muestra y c cualquier constante no cero. 1. Si y1 x1 c, y2 x2 c, . . . , yn xn c, entonces s2 y s2 x, y 2. Si y1 cx1, . . . , yn cxn, entonces s2 y c2 s2 x, sy °c°sx, donde s2 x es la varianza muestral de las x y s2 y es la varianza muestral de las y. Se ordenan las observaciones de la más pequeña a la más grande y se separa la mitad más pequeña de la más grande; se incluye la mediana ~ x en ambas mitades si n es im- par. En tal caso el cuarto inferior es la mediana de la mitad más pequeña y el cuar- to superior es la mediana de la mitad más grande. Una medida de dispersión que es resistente a los valores apartados es la dispersión de los cuartos fs, dada por fs cuarto superior – cuarto inferior PROPOSICIÓN DEFINICIÓN c1_p001-045.qxd 3/12/08 2:31 AM Page 35
- 54. 36 CAPÍTULO 1 Generalidades y estadística descriptiva Primero, se traza una escala de medición horizontal. Luego se coloca un rectángulo sobre es- te eje; el lado izquierdo del rectángulo está en el cuarto inferior y el derecho en el cuarto su- perior (por lo que el ancho de la caja fs). Se coloca un segmento de línea vertical o algún otro símbolo dentro del rectángulo en la ubicación de la mediana; la posición del símbolo de mediana con respecto a los dos lados da información sobre asimetría en el 50% medio de los datos. Por último, se trazan “bigotes” hacia fuera de ambos extremos del rectángulo hacia las observaciones más pequeñas y más grandes. También se puede trazar una gráfica de caja con orientación vertical mediante modificaciones obvias en el proceso de construcción. Se utilizó ultrasonido para reunir los datos de corrosión adjuntos de la placa de piso de un tanque elevado utilizado para almacenar petróleo crudo (“Statistical Analysis of UT Corro- sion Data from Floor Plates of a Crude Oil Aboveground Storage Tank”, Materials Eval., 1994: 846-849); cada observación es la profundidad de picadura más grande en la placa, ex- presada en milésimas de pulgada. 40 52 55 60 70 75 85 85 90 90 92 94 94 95 98 100 115 125 125 El resumen de cinco números es como sigue: xi más pequeña 40 cuarto inferior 72.5 90 cuarto superior 96.5 xi más grande 125 La figura 1.18 muestra la gráfica de caja resultante. El lado derecho de la caja está mucho más cerca a la mediana que el izquierdo, lo que indica una asimetría sustancial en la mitad derecha de los datos. El ancho de la caja (fs) también es razonablemente grande con respec- to al rango de datos (distancia entre las puntas de los bigotes). x | La figura 1.19 muestra los resultados obtenidos con MINITAB en respuesta a la pe- tición de describir los datos de corrosión. La media recortada es el promedio de las 17 ob- servaciones que permanecen después de eliminar los valores más grandes y más pequeños (porcentaje de recorte 5%), Q1 y Q3 son los cuartiles inferior y superior; éstos son si- milares a los cuartos pero se calculan de una manera diferente; el error estándar promedio (SE Mean) es s/n ; esta será una importante cantidad en el trabajo subsiguiente con res- pecto a inferencias en torno a . Gráficas de caja que muestran valores apartados Una gráfica de caja puede ser embellecida para indicar explícitamente la presencia de valo- res apartados. Muchos procedimientos inferenciales se basan en la suposición de que la dis- tribución de la población es normal (un cierto tipo de curva en forma de campana). Incluso Ejemplo 1.17 ¨ « « « « « « « © « « « « « « « « ª ¨ « « « « « « « « « © « « « « « « « « ª Figura 1.18 Gráfica de caja de los datos de corrosión. Figura 1.19 Descripción de MINITAB de los datos de profundidad de picaduras. ■ 40 50 60 70 80 90 100 110 120 130 Profundidad Profundidad N Media Media Media recortada Desv. estándar Media SE variable 19 86.32 90.00 86.76 23.32 5.35 Profundidad Mínima Máxima Q1 Q3 variable 40.00 125.00 70.00 98.00 c1_p001-045.qxd 3/12/08 2:31 AM Page 36
- 55. un solo valor apartado extremo que aparezca en la muestra advierte al investigador que ta- les procedimientos pueden ser no confiables y la presencia de varios valores apartados trans- mite el mismo mensaje. Modifíquese ahora la construcción previa de una gráfica de caja trazando un bigote que sale de cada extremo de la caja hacia las observaciones más pequeñas y más grandes que no son valores apartados. Cada valor apartado moderado está representado por un círculo cerra- do y cada valor apartado extremo por uno abierto. Algunos programas de computadora es- tadísticos no distinguen entre valores apartados moderados y extremos. Los efectos de descargas parciales en la degradación de materiales para cavidades aislantes tienen implicaciones importantes en relación con las duraciones de componentes de alto vol- taje. Considérese la siguiente muestra de n 25 anchos de pulso de descargas lentas en una cavidad cilíndrica de polietileno. (Estos datos son consistentes con un histograma de 250 observaciones en el artículo “Assessment of Dielectric Degradation by Ultrawide-band PD Detection”, IEEE Trans. on Dielectrics and Elec. Insul., 1995: 744-760.) El autor del artícu- lo señala el impacto de una amplia variedad de herramientas estadísticas en la interpretación de datos de descarga. 5.3 8.2 13.8 74.1 85.3 88.0 90.2 91.5 92.4 92.9 93.6 94.3 94.8 94.9 95.5 95.8 95.9 96.6 96.7 98.1 99.0 101.4 103.7 106.0 113.5 Las cantidades pertinentes son x̃ 94.8 cuarto inferior 90.2 cuarto superior 96.7 fs 6.5 1.5fs 9.75 3fs 19.50 Por lo tanto, cualquier observación menor que 90.2 9.75 80.45 o mayor que 96.7 9.75 106.45 es un valor apartado. Hay un valor apartado en el extremo superior de la muestra y cuatro en el extremo inferior. Debido a que 90.2 19.5 70.7, las tres observa- ciones 5.3, 8.2 y 13.8 son valores apartados extremos; los otros dos son moderados. Los bi- gotes se extienden a 85.3 y 106.0, las observaciones más extremas que no son valores apartados. La gráfica de caja resultante aparece en la figura 1.20. Existe una gran cantidad de asimetría negativa en la mitad media de la muestra así como también en toda la muestra. Gráficas de caja comparativas Una gráfica de caja comparativa o lado a lado es una forma muy efectiva de revelar similitu- des y diferencias entre dos o más conjuntos de datos compuestos de observaciones de la mis- ma variable, observaciones de eficiencia de consumo de combustible de cuatro tipos distintos de automóviles, rendimientos de cosechas de tres variedades diferentes y así sucesivamente. 1.4 Medidas de variabilidad 37 Figura 1.20 Gráfica de caja de los datos de ancho de pulso que muestra valores apartados mo- derados y extremos. ■ 0 50 100 Ancho de pulso Ejemplo 1.18 DEFINICIÓN Cualquier observación a más de 1.5fs del cuarto más cercano es un valor apartado (o atípico). Un valor apartado es extremo si se encuentra a más de 3fs del cuarto más cercano y moderado de lo contrario. c1_p001-045.qxd 3/12/08 2:31 AM Page 37
- 56. 38 CAPÍTULO 1 Generalidades y estadística descriptiva En años recientes, algunas evidencias sugieren que las altas concentraciones de radón bajo techo pueden estar ligadas al desarrollo de cánceres en niños, pero muchos profesionales de la salud aún no están convencidos. Un artículo reciente (“Indoor Radon and Childhood Can- cer”, The Lancet, 1991: 1537-1538) presentó los datos adjuntos sobre concentración de ra- dón (Bq/m3 ) en dos muestras diferentes de casas. La primera consistió en casas en las cuales un niño diagnosticado con cáncer había estado residiendo. Las casas en la segunda muestra no incluían casos registrados de cáncer infantil. La figura 1.21 presenta una gráfica de tallo y hojas de los datos. El resumen de cantidades numéricas es el siguiente: Los valores tanto de la media como de la mediana sugieren que la muestra de cáncer se en- cuentra en el centro un poco a la derecha de la muestra sin cáncer sobre la escala de medi- ción. La media, sin embargo, exagera la magnitud de este desplazamiento, en gran medida debido a la observación 210 en la muestra con cáncer. Los valores de s sugieren más varia- bilidad en la muestra con cáncer que en la muestra sin cáncer, pero las dispersiones de los cuartos contradicen esta impresión. De nuevo, la observación 210, un valor apartado extre- mo, es el culpable. La figura 1.22 muestra una gráfica de caja comparativa generada por el Ejemplo 1.19 Figura 1.21 Gráfica de tallo y hojas del ejemplo 1.19. 1. Con cáncer 2. Sin cáncer 9683795 0 95768397678993 86071815066815233150 1 12271713114 12302731 2 99494191 8349 3 839 5 4 7 5 55 6 7 Tallo: dígitos de decenas HI: 210 8 5 Hojas: dígitos de unidades s fs Con cáncer 22.8 16.0 31.7 11.0 Sin cáncer 19.2 12.0 17.0 18.0 x | x Figura 1.22 Gráfica de caja de los datos del ejemplo 1.19, obtenida con S-Plus. 0 50 100 150 200 Concentración de radón Sin cáncer Con cáncer c1_p001-045.qxd 3/12/08 2:31 AM Page 38
- 57. programa de computadora S-Plus. La caja sin cáncer aparece alargada en comparación con la caja con cáncer (fs 18 vs. fs 11) y las posiciones de las líneas medianas en las dos ca- jas muestran más asimetría en la mitad media de la muestra sin cáncer que la muestra con cáncer. Los valores apartados están representados por segmentos de línea horizontales y no hay distinción entre los valores apartados moderados y extremos. ■ 1.4 Medidas de variabilidad 39 EJERCICIOS Sección 1.4 (44-61) 44. El artículo (“Oxygen Consumption During Fire Suppres- sion: Error of Heart Rate Estimation”, Ergonomics, 1991: 1469-1474) reportó los siguientes datos sobre consumo de oxígeno (ml/kg/min) para una muestra de diez bomberos que realizaron un simulacro de supresión de incendio. 29.5 49.3 30.6 28.2 28.0 26.3 33.9 29.4 23.5 31.6 Calcule lo siguiente: a. El rango muestral. b. La varianza muestral s2 a partir de la definición (es de- cir, calculando primero las desviaciones y luego eleván- dolas al cuadrado, etcétera). c. La desviación estándar muestral. d. s2 utilizando el método más corto. 45. Se determinó el valor del módulo deYoung (GPa) de placas fundidas compuestas de ciertos sustratos intermetálicos y se obtuvieron las siguientes observaciones muestrales (“Strength and Modulus of a Molybdenum-Coated Ti- 25A1-10Nb-3U-1Mo Intermetallic”, J. of Materials Engr. and Performance, 1997: 46-50): 116.4 115.9 114.6 115.2 115.8 a. Calcule x y las desviaciones de la media. b. Use las desviaciones calculadas en el inciso a) para obtener la varianza muestral y la desviación estándar muestral. c. Calcule s2 utilizando la fórmula para el numerador Sxx. d. Reste 100 de cada observación para obtener una mues- tra de valores transformados. Ahora calcule la varianza muestral de estos valores transformados y compárela con s2 de los datos originales. 46. Las observaciones adjuntas de viscosidad estabilizada (cP) realizadas en probetas de un cierto grado de asfalto con 18% de caucho agregado se tomaron del artículo (“Visco- sity Characteristics of Rubber-Modified Asphalts”, J. of Materials in Civil Engr. 1996: 153-156): 2781 2900 3013 2856 2888 a. ¿Cuáles son los valores de la media y mediana mues- trales? b. Calcule la varianza muestral por medio de la fórmula de cálculo. [Sugerencia: Primero reste un número conve- niente de cada observación.] 47. Calcule e interprete los valores de la mediana muestral, la media muestral y la desviación estándar muestral de las si- guientes observaciones de resistencia a la fractura (MPa, leídas en una gráfica que aparece en el artículo (“Heat-Re- sistant Active Brazing of Silicon Nitride: Mechanical Eva- luation of Braze Joints”, Welding J., agosto de 1997): 87 93 96 98 105 114 128 131 142 168 48. El ejercicio 34 presentó los siguientes datos sobre concentra- ción de endotoxina en polvo asentado, obtenidos con una muestra de casas urbanas y una muestra de casas campestres: U: 6.0 5.0 11.0 33.0 4.0 5.0 80.0 18.0 35.0 17.0 23.0 C: 4.0 14.0 11.0 9.0 9.0 8.0 4.0 20.0 5.0 8.9 21.0 9.2 3.0 2.0 0.3 a. Determine el valor de la desviación estándar muestral de cada muestra, interprete estos valores y luego contraste la variabilidad en las dos muestras. [Sugerencia: xi 237.0 para la muestra urbana y 128.4 para la muestra campestre y x2 i 10 079 para la muestra urbana y 1617.94 para la muestra campestre.] b. Calcule la dispersión de los cuartos de cada muestra y compare. ¿Transmiten el mismo mensaje las dispersio- nes de los cuartos sobre la variabilidad que las desvia- ciones estándar? Explique. c. Los autores del artículo citado también proporcionan concentraciones de endotoxina en el polvo presente en bolsas captadoras de polvo: U: 34.0 49.0 13.0 33.0 24.0 24.0 35.0 104.0 34.0 40.0 38.0 1.0 C: 2.0 64.0 6.0 17.0 35.0 11.0 17.0 13.0 5.0 27.0 23.0 28.0 10.0 13.0 0.2 Construya una gráfica de caja comparativa (como se hizo en el artículo citado) y compare y contraste las cuatro muestras. 49. Un estudio de la relación entre edad y varias funciones vi- suales (tales como agudeza y percepción de profundidad) reportó las siguientes observaciones de área de la lámina es- clerótica (mm2 ) de las cabezas del nervio óptico humano (“Morphometry of Nerve Fiber Bundle Pores in the Optic Nerve Head of the Human”, Experimental Eye Research, 1988: 559-568): 2.75 2.62 2.74 3.85 2.34 2.74 3.93 4.21 3.88 4.33 3.46 4.52 2.43 3.65 2.78 3.56 3.01 a. Calcule xi y x2 i . b. Use los valores calculados en el inciso a) para calcular la varianza muestral s2 y luego la desviación estándar mues- tral s. 50. En 1997, una mujer demandó a un fabricante de teclados de computadora y lo acusó de que sus repetitivas lesiones por esfuerzo eran provocadas por el teclado (Genessy . Digital c1_p001-045.qxd 3/12/08 2:31 AM Page 39
- 58. 40 CAPÍTULO 1 Generalidades y estadística descriptiva Equipment Corp.). El jurado adjudicó $3.5 millones por el dolor y sufrimiento pero la corte anuló dicha adjudicación por considerarla una compensación irrazonable. Al hacer es- ta determinación, la corte identificó un grupo “normativo” de 27 casos similares y especificó una adjudicación razonable como una dentro de dos desviaciones estándar de la media de las adjudicaciones en los 27 casos. Las 27 adjudicaciones fueron (en el rango de los $1000) 37, 60, 75, 115, 135, 140, 149, 150, 238, 290, 340, 410, 600, 750, 750, 750, 1050, 1100, 1139, 1150, 1200, 1200, 1250, 1576, 1700, 1825 y 2000 con las cuales xi 20179, x2 i 24657511. ¿Cuál es la can- tidad máxima posible que podría ser adjudicada conforme a la regla de dos desviaciones estándar? 51. El artículo (“A Thin-Film Oxygen Uptake Test for the Eva- luation of Automotive Crankcase Lubricants”, Lubric. Engr., 1984: 75-83) reportó los siguientes datos sobre tiempo de in- ducción de oxidación (min) de varios aceites comerciales: 87 103 130 160 180 195 132 145 211 105 145 153 152 138 87 99 93 119 129 a. Calcule la varianza muestral y la desviación estándar. b. Si las observaciones se volvieran a expresar en horas, ¿cuáles serían los valores resultantes de la varianza de la muestra y la desviación estándar muestral? Responda sin realizar en realidad la reexpresión. 52. Las primeras cuatro desviaciones de la media en una mues- tra de n 5 tiempos de reacción fueron 0.3, 0.9, 1.0 y 1.3. ¿Cuál es la quinta desviación de la media? Dé una muestra para la cual estas son las cinco desviaciones de la media. 53. Reconsidere los datos sobre el área de lámina esclerótica dados en el ejercicio 49. a. Determine los cuartos inferior y superior. b. Calcule el valor de la dispersión de los cuartos. c. Si los dos valores muestrales más grandes, 4.33 y 4.52 hubieran sido 5.33 y 5.52, ¿cómo afectaría esto a fs? Ex- plique. d. ¿En cuánto se podría incrementar la observación 2.34 sin afectar a fs? Explique. e. Si la 18a. observación, x18 4.60, se suma a la muestra, ¿cuál es fs? 54. Considere las siguientes observaciones sobre resistencia al es- fuerzo cortante (MPa) de una junta unida de una manera par- ticular (tomadas de una gráfica que aparece en el artículo (“Diffusion of Silicon Nitride to Austenitic Stainless Steel without Interlayers”, Metallurgical Trans., 1993: 1835-1843). 22.2 40.4 16.4 73.7 36.6 109.9 30.0 4.4 33.1 66.7 81.5 a. ¿Cuáles son los valores de los cuartos y cuál es el valor de fs? b. Construya una gráfica de caja basada en el resumen de cinco números y comente sobre sus características. c. ¿Qué tan grande o pequeña tiene que ser una observa- ción para calificar como valor apartado? ¿Como valor apartado extremo? d. ¿En cuánto podría disminuir la observación más grande sin afectar fs? 55. He aquí una gráfica de tallo y hojas de los datos de tiempo de escape introducidos en el ejercicio 36 de este capítulo. 32 55 33 49 34 35 6699 36 34469 37 03345 38 9 39 2347 40 23 41 42 4 a. Determine el valor de la dispersión de los cuartos. b. ¿Hay algunos valores apartados en la muestra? ¿Algu- nos valores apartados extremos? c. Construya una gráfica de caja y comente sobre sus ca- racterísticas. d. ¿En cuánto se podría disminuir la observación más gran- de, actualmente de 424, sin afectar el valor de la disper- sión de los cuartos? 56. Se determinó la cantidad de contaminación por aluminio (ppm) en plástico de cierto tipo con una muestra de 26 probe- tas de plástico y se obtuvieron los siguientes datos (“The Log- normal Distribution for Modeling Quality Data when the Mean Is Near Zero”, J. of Quality Technology, 1990: 105-110): 30 30 60 63 70 79 87 90 101 102 115 118 119 119 120 125 140 145 172 182 183 191 222 244 291 511 Construya una gráfica de caja que muestre valores aparta- dos y comente sobre sus características. 57. Se seleccionó una muestra de 20 botellas de vidrio de un ti- po particular y se determinó la resistencia a la presión inter- na de cada botella. Considere la siguiente información parcial sobre la muestra: mediana 202.2 cuarto inferior 196.0 cuarto superior 216.8 Las tres observaciones más pequeñas 125.8 188.1 193.7 Las tres observaciones más grandes 221.3 230.5 250.2 a. ¿Hay valores apartados en la muestra? ¿Algunos valores apartados extremos? b. Construya una gráfica de caja que muestre valores apar- tados y comente sobre cualesquiera características inte- resantes. 58. Una compañía utiliza dos máquinas diferentes para fabricar piezas de cierto tipo. Durante un solo turno, se obtuvo una muestra de n 20 piezas producidas por cada máquina y se determinó el valor de una dimensión crítica particular de cada pieza. La gráfica de caja comparativa que aparece en la parte superior de la página 41 se construyó con los datos resultantes. Compare y contraste las dos muestras. 59. Se determinó la concentración de cocaína (mg/l) tanto con una muestra de individuos que murieron de delirio excitado (DE) inducido por el consumo de cocaína y con una mues- tra de aquellos que murieron de una sobredosis de cocaína sin delirio excitado; el tiempo de sobrevivencia de las personas c1_p001-045.qxd 3/12/08 2:31 AM Page 40
- 59. 1.4 Medidas de variabilidad 41 en ambos grupos fue a lo sumo de 6 horas. Los datos adjun- tos se tomaron de una gráfica de caja comparativa incluida en el artículo (“Fatal Excited Delirium Following Cocaine Use”, J. of Forensic Sciences, 1997: 25-31). Con DE 0 0 0 0 0.1 0.1 0.1 0.1 0.2 0.2 0.3 0.3 0.3 0.4 0.5 0.7 0.8 1.0 1.5 2.7 2.8 3.5 4.0 8.9 9.2 11.7 21.0 Sin DE 0 0 0 0 0 0.1 0.1 0.1 0.1 0.2 0.2 0.2 0.3 0.3 0.3 0.4 0.5 0.5 0.6 0.8 0.9 1.0 1.2 1.4 1.5 1.7 2.0 3.2 3.5 4.1 4.3 4.8 5.0 5.6 5.9 6.0 6.4 7.9 8.3 8.7 9.1 9.6 9.9 11.0 11.5 12.2 12.7 14.0 16.6 17.8 a. Determine las medianas, cuartos y dispersiones de los cuartos de las dos muestras, b. ¿Existen algunos valores apartados en una u otra mues- tra? ¿Algunos valores apartados extremos? c. Construya una gráfica de caja comparativa y utilícela como base para comparar y contrastar las muestras con DE y sin DE. 60. Se obtuvieron observaciones de resistencia al estallamiento (lb/pulg2 ) tanto con soldaduras de cierre de toberas de prueba como con soldaduras para toberas de envases de producción (“Proper Procedures Are the Key to Welding Radioactive Waste Cannisters”, Welding J., agosto de 1997: 61-67). Prueba 7200 6100 7300 7300 8000 7400 7300 7300 8000 6700 8300 Envase 5250 5625 5900 5900 5700 6050 5800 6000 5875 6100 5850 6600 Construya una gráfica de caja comparativa y comente sobre las características interesantes (el artículo citado no incluía tal gráfica, pero los autores comentaron que habían visto uno.) 61. La gráfica de caja comparativa adjunta de coeficientes de vapor de gasolina de vehículos en Detroit apareció en el ar- tículo (“Receptor Modeling Approach to VOC Emission In- ventory Validation”, J. of Envir. Engr., 1995: 483-490). Discuta las características interesantes. 85 1 2 95 105 115 Dimensión Máquina 6 a.m. 8a.m. 12 mediodía 2 p.m. 10 p.m. 10 0 20 30 40 50 60 70 Tiempo Coeficiente de vapor de gasolina Gráfica de caja comparativa del ejercicio 61 Gráfica de caja comparativa del ejercicio 58 c1_p001-045.qxd 3/12/08 2:31 AM Page 41
- 60. 42 CAPÍTULO 1 Generalidades y estadística descriptiva 62. Considere la siguiente información sobre resistencia a la tensión final (lb/pulg) de una muestra de n 4 probetas de alambre de cobre al zirconio duro (de “Characterization Methods for Fine Copper Wire”, Wire J. Intl., agosto de 1997: 74-80): 76 831 s 180, xi más pequeña 76 683, xi más grande 77 048. Determine los valores de las dos observaciones muestrales in- termedias (¡pero no lo haga mediante conjeturas sucesivas!) 63. La cantidad de radiación recibida en un invernadero desem- peña un importante papel al determinar el coeficiente de fo- tosíntesis. Las observaciones adjuntas sobre radiación solar incidente se leyeron en una gráfica que aparece en el artícu- lo (“Radiation Components over Bare Planted Soils in a Greenhouse”, Solar Energy, 1990: 1011-1016). 6.3 6.4 7.7 8.4 8.5 8.8 8.9 9.0 9.1 10.0 10.1 10.2 10.6 10.6 10.7 10.7 10.8 10.9 11.1 11.2 11.2 11.4 11.9 11.9 12.2 13.1 Use algunos de los métodos estudiados en este capítulo pa- ra describir y resumir estos datos. 64. Los siguientes datos sobre emisiones de HC y CO de un ve- hículo particular se dieron en la introducción del capítulo. HC (g/milla) 13.8 18.3 32.2 32.5 CO (g/milla) 118 149 232 236 a. Calcule las desviaciones estándar muestrales de las ob- servaciones de HC y CO. ¿Parece justificarse la creencia difundida? b. El coeficiente de variación muestral s/ x (o 100 s/ x ) eva- lúa el grado de variabilidad con respecto a la media. Los valores de este coeficiente para varios conjuntos de da- tos diferentes pueden ser comparados para determinar cuáles conjuntos de datos exhiben más o menos varia- ción. Realice la comparación con los datos dados. 65. La distribución de frecuencia adjunta de observaciones de resistencia a la fractura (MPa) de barras de cerámicas coci- das en un horno particular apareció en el artículo (“Evalua- ting Tunnel Kiln Performance”, Amer. Ceramic Soc. Bull., agosto de 1997: 59-63). Frecuencia 81–83 83–85 85–87 87–89 89–91 de clase 6 7 17 30 43 Frecuencia 91–93 93–95 95–97 97–99 de clase 28 22 13 3 a. Construya un histograma basado en frecuencias relati- vas y comente sobre cualesquiera características intere- santes. b. ¿Qué proporción de las observaciones de resistencia son por lo menos de 85? ¿Menores que 95? c. Aproximadamente, ¿qué proporción de las observacio- nes son menores que 90? 66. Una deficiencia de indicios de selenio en la dieta puede im- pactar negativamente el crecimiento, la inmunidad, la función muscular y neuromuscular y la fertilidad. La introducción de suplementos de selenio en vacas lecheras se justifica cuan- do las pasturas contienen niveles bajos de selenio. Los au- tores del artículo (“Effects of Short-Term Supplementation with Selenised Yeast on Milk Production and Composition of Lactating Cows”, Australian J. of Dairy Tech., 2004: 199-203) suministraron los siguientes datos sobre la con- centración de selenio en la leche (mg/l) obtenidos con una muestra de vacas a las que se les administró un suplemento de selenio y una muestra de control de vacas a las que no se les administró suplemento, tanto inicialmente como des- pués de un periodo de 9 días. a. ¿Parecen ser similares las concentraciones iniciales de Se en las muestras de suplemento y en las de control? Use varias técnicas de este capítulo para resumir los da- tos y responder la pregunta planteada. b. De nuevo use métodos de este capítulo para resumir los datos y luego describa cómo los valores de concentra- ción de Se finales en el grupo de tratamiento difieren de aquellos en el grupo de control. 67. Estenosis aórtica se refiere al estrechamiento de la válvula aór- tica en el corazón. El artículo (“Correlation Analysis of Steno- tic Aortic Valve Flow Patterns Using Phase Constrast MRI”, Annals of Biomed. Engr., 2005: 878-887) dio los siguientes datos sobre el diámetro de la raíz aórtica (cm) y el género de una muestra de pacientes con varios grados de estenosis aórtica: H: 3.7 3.4 3.7 4.0 3.9 3.8 3.4 3.6 3.1 4.0 3.4 3.8 3.5 M: 3.8 2.6 3.2 3.0 4.3 3.5 3.1 3.1 3.2 3.0 a. Compare y contraste los diámetros observados en los dos géneros. b. Calcule una media 10% recortada de cada una de las dos muestras y compare las demás medidas centrales (de la muestra de hombre, se debe utilizar el método de in- terpolación mencionado en la sección 1.3). x EJERCICIOS SUPLEMENTARIOS (62-83) Cont. Se Cont. Obs. Se inicial inicial final final 1 11.4 9.1 138.3 9.3 2 9.6 8.7 104.0 8.8 3 10.1 9.7 96.4 8.8 4 8.5 10.8 89.0 10.1 5 10.3 10.9 88.0 9.6 6 10.6 10.6 103.8 8.6 7 11.8 10.1 147.3 10.4 8 9.8 12.3 97.1 12.4 9 10.9 8.8 172.6 9.3 10 10.3 10.4 146.3 9.5 11 10.2 10.9 99.0 8.4 12 11.4 10.4 122.3 8.7 13 9.2 11.6 103.0 12.5 14 10.6 10.9 117.8 9.1 15 10.8 121.5 16 8.2 93.0 c1_p001-045.qxd 3/12/08 2:31 AM Page 42
- 61. Ejercicios suplementarios 43 68. a. ¿Con qué valor de c es mínima la cantidad (xi c)2 ? [Sugerencia: Tome la derivada con respecto a c, iguale a 0 y resuelva.] b. Utilizando el resultado del inciso a), ¿cuál de las dos cantidades (xi x )2 y (xi )2 será más pequeña que la otra (suponiendo que x )? 69. a. Sean a y b constantes y sea yi axi b con i 1, 2, . . . , n. ¿Cuáles son las relaciones entre x y y y entre y ? b. Una muestra de temperaturas para iniciar una cierta reacción química dio un promedio muestral (°C) de 87.3 y una desviación estándar muestral de 1.04. ¿Cuáles son el promedio muestral y la desviación estándar medidos en °F? [Sugerencia: F 9 5 C 32.] 70. El elevado consumo de energía durante el ejercicio continúa después de que termina la sesión de entrenamiento. Debido a que las calorías quemadas por ejercicio contribuyen a la pérdida de peso y tienen otras consecuencias, es importante entender el proceso. El artículo (“Effect of Weight Training Exercise and Treadmill Exercise on Post-Exercise Oxygen Consumption”, Medicine and Science in Sports and Exerci- se, 1998: 518-522) reportó los datos adjuntos tomados de un estudio en el cual se midió el consumo de oxígeno (litros) de forma continua durante 30 minutos de cada uno de 15 suje- tos tanto después de un entrenamiento con pesas como des- pués de una sesión de ejercicio en una caminadora. Sujeto 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Peso (x) 14.6 14.4 19.5 24.3 16.3 22.1 23.0 18.7 19.0 17.0 19.1 19.6 23.2 18.5 15.9 Caminadora (y) 11.3 5.3 9.1 15.2 10.1 19.6 20.8 10.3 10.3 2.6 16.6 22.4 23.6 12.6 4.4 a. Construya una gráfica de caja comparativa de las obser- vaciones del ejercicio con pesas y la caminadora y co- mente sobre lo que ve. b. Debido a que estos datos aparecen en pares (x, y), con mediciones de x y y de la misma variable en dos condi- ciones distintas, es natural enfocarse en las diferencias que existen en ellos: d1 x1 – y1, . . . , dn xn – yn. Construya una gráfica de caja de las diferencias mues- trales. ¿Qué sugiere la gráfica? 71. La siguiente es una descripción dada por MINITAB de los datos de resistencia dados en el ejercicio 13. Med. Desv. Media Resistencia N Media Mediana rec. est. SE variable 153 135.39 135.40 135.41 4.59 0.37 Resistencia Mínima Máxima Q1 Q3 variable 122.20 147.70 132.95 138.25 a. Comente sobre cualesquiera características interesantes (los cuartiles y los cuartos son virtualmente idénticos en este caso). b. Construya una gráfica de caja de los datos basada en los cuartiles y comente sobre lo que ve. 72. Los desórdenes y síntomas de ansiedad con frecuencia pue- den ser tratados exitosamente con benzodiazepina. Se sabe que los animales expuestos a estrés exhiben una disminu- ción de la ligadura de receptor de benzodiazepina en la cor- teza frontal. El artículo (“Decreased Benzodiazepine Receptor Binding in Prefrontal Cortex in Combat-Related Posttraumatic Stress Disorder”, Amer. J. of Psychiatry. 2000: 1120-1126) describió el primer estudio de ligadura de receptor de benzodiazepina en individuos que sufren de PTSD. Los datos anexos sobre una medición de ligadura a receptor (volumen de distribución ajustado) se leyeron en una gráfica que aparece en el artículo. PTSD: 10, 20, 25, 28, 31, 35, 37, 38, 38, 39, 39, 42, 46 Saludables: 23, 39, 40, 41, 43, 47, 51, 58, 63, 66, 67, 69, 72 Use varios métodos de este capítulo para describir y resu- mir los datos. 73. El artículo (“Can We Really Walk Straight?, Amer. J. of Physical Anthropology, 1992: 19-27) reportó sobre un ex- perimento en el cual a cada uno de 20 hombres saludables se les pidió que caminarán en línea recta como fuera posi- ble hacia un punto a 60 m de distancia a velocidad normal. Considérense las siguientes observaciones de cadencia (nú- mero de pasos por segundo): 0.95 0.85 0.92 .95 0.93 0.86 1.00 0.92 0.85 0.81 0.78 0.93 0.93 1.05 0.93 1.06 1.06 0.96 0.81 0.96 Use los métodos desarrollados en este capítulo para resumir los datos; incluya una interpretación o discusión en los ca- sos en que sea apropiado. [Nota: El autor del artículo utili- zó un análisis estadístico un tanto complejo para concluir que las personas no pueden caminar en línea recta y sugirió varias explicaciones para esto.] 74. La moda de un conjunto de datos numéricos es el valor que ocurre con más frecuencia en el conjunto. a. Determine la moda de los datos de cadencia dados en el ejercicio 73. b. Para una muestra categórica, ¿cómo definiría la catego- ría modal? 75. Se seleccionaron especímenes de tres tipos diferentes de ca- ble y se determinó el límite de fatiga (Mpa) de cada espéci- men y se obtuvieron los datos adjuntos. Tipo 1 350 350 350 358 370 370 370 371 371 372 372 384 391 391 392 Tipo 2 350 354 359 363 365 368 369 371 373 374 376 380 383 388 392 Tipo 3 350 361 362 364 364 365 366 371 377 377 377 379 380 380 392 a. Construya una gráfica de caja comparativa y comente sobre las similitudes y diferencias. b. Construya un diagrama de caja comparativo (una gráfi- ca de puntos de cada muestra con una escala común). Comente sobre las similitudes y diferencias. c. ¿Da la gráfica de caja comparativa del inciso a) una eva- luación informativa de similitudes y diferencias? Expli- que su razonamiento. sy 2 sx 2 c1_p001-045.qxd 3/12/08 2:31 AM Page 43
- 62. 44 CAPÍTULO 1 Generalidades y estadística descriptiva 76. Las tres medidas de centro introducidas en este capítulo son las media, la mediana y la media recortada. Dos medidas de centro adicionales que de vez en cuando se utilizan son el rango medio, el cual es el promedio de las observaciones más pequeñas y más grandes y el cuarto medio, el cual es el promedio de los dos cuartos. ¿Cuál de estas medidas de centro son resistentes a los efectos de los valores apartados y cuáles no? Explique su razonamiento. 77. Considere los siguientes datos sobre el tiempo de repara- ción activo (horas) de una muestra de n 46 receptores de comunicaciones aerotransportados: 0.2 0.3 0.5 0.5 0.5 0.6 0.6 0.7 0.7 0.7 0.8 0.8 0.8 1.0 1.0 1.0 1.0 1.1 1.3 1.5 1.5 1.5 1.5 2.0 2.0 2.2 2.5 2.7 3.0 3.0 3.3 3.3 4.0 4.0 4.5 4.7 5.0 5.4 5.4 7.0 7.5 8.8 9.0 10.3 22.0 24.5 Construya lo siguiente: a. Una gráfica de tallo y hojas en la cual los dos valores más grandes se muestran por separado en la fila HI. b. Un histograma basado en seis intervalos de clase con 0 como el límite inferior del primer intervalo y anchos de intervalo de 2, 2, 2, 4, 10 y 10, respectivamente. 78. Considere una muestra x1, x2, . . . , xn y suponga que los va- lores de , s2 y s han sido calculados. a. Sea yi xi con i 1, . . . , n. ¿Cómo se comparan los valores de s2 y s de las yi con los valores correspon- dientes de las xi? Explique. b. Sea zi (xi )/s con i 1, . . . , n. ¿Cuáles son los va- lores de la varianza muestral y la desviación estándar muestral de las zi? 79. Si y denotan la media y la varianza de la muestra x1, . . . , xn y si y denotan estas cantidades cuando se agrega una observación adicional xn1 a la muestra. a. Demuestre cómo se puede calcular con y . b. Demuestre que de modo que pueda ser calculada con xn1, , y . c. Suponga que una muestra de 15 torzales de hilo para te- las dio por resultado un alargamiento del hilo mediano muestral de 12.58 mm y una desviación estándar mues- tral de 0.512 mm. ¿Cuáles son los valores de la media muestral y la desviación estándar muestral de las 16 ob- servaciones de alargamiento? 80. Las distancias de recorrido de rutas de autobuses de cual- quier sistema de tránsito particular por lo general varían de una ruta a otra. El artículo (“Planning of City Bus Routes”, J. of the Institution of Engineers, 1995: 211-215) da la si- guiente información sobre las distancias (km) de un sistema particular. Distancia 6–8 8–10 10–12 12–14 14–16 Frecuencia 6 23 30 35 32 Distancia 16–18 18–20 20–22 22–24 24–26 Frecuencia 48 42 40 28 27 Distancia 26–28 28–30 30–35 35–40 40–45 Frecuencia 26 14 27 11 2 a. Trace un histograma correspondiente a estas frecuencias. b. ¿Qué proporción de estas distancias de ruta son menores que 20? ¿Qué proporción de estas rutas tienen distancias de recorrido de por lo menos 30? c. ¿Aproximadamente cuál es el valor de 90o percentil de la distribución de distancia de recorrido de las rutas? d. ¿Aproximadamente cuál es la distancia de recorrido de ruta mediana? 81. Un estudio realizado para investigar la distribución de tiem- po de frenado total (tiempo de reacción más tiempo de mo- vimiento de acelerador a freno, en ms) durante condiciones de manejo reales a 60 km/h da la siguiente información sobre la distribución de los tiempos (“A Field Study on Braking Response during Driving”, Ergonomics, 1995: 1903-1910): media 535 mediana 500 moda 500 Desv. estd. 96 mínima 220 máxima 925 5o percentil 400 10o percentil 430 90o percentil 640 95o percentil 720 ¿Qué puede concluir sobre la forma de un histograma de es- tos datos? Explique su razonamiento. 82. Los datos muestrales x1, x2, . . . , xn en ocasiones represen- tan una serie de tiempo, donde xt el valor observado de una variable de respuesta x en el tiempo t. A menudo la se- rie observada muestra una gran cantidad de variación alea- toria, lo que dificulta estudiar el comportamiento a largo plazo. En tales situaciones, es deseable producir una ver- sión alisada de la serie. Una técnica para hacerlo implica el alisamiento o atenuación exponencial. Se elige el valor de una constante de alisamiento (0 1). Luego con valor alisado o atenuado en el tiempo t se hace con t 2, 3, . . . , n, . a. Considere la siguiente serie de tiempo en la cual xt temperatura (°F) del efluente en una planta de tratamien- to de aguas negras en el día t: 47, 54, 53, 50, 46, 46, 47, 50, 51, 50, 46, 52, 50, 50. Trace cada xt contra t en un sistema de coordenadas de dos dimensiones (una gráfi- ca de tiempo-serie). ¿Parece haber algún patrón? b. Calcule las con 0.1. Repita con 0.5. ¿Qué valor de da una serie más atenuada? c. Sustituya en el miembro de la derecha de la expresión para , acto seguido sustituya en función de xt2, y , y así sucesivamente. ¿De cuántos de los valores x1, xt1, . . . , x1 depende ? ¿Qué le sucede al coeficiente de xtk conforme k se incrementa? d. Remítase al inciso c). Si t es grande, ¿qué tan sensible es a la inicialización ? Explique. [Nota: Una referencia pertinente es el artículo “Simple Sta- tistics for Interpreting Environmental Data”, Water Pollu- tion Control Fed. J., 1981: 167-175.] 83. Considere las observaciones numéricas x1, . . . , xn. Con fre- cuencia interesa saber si las xi están (por lo menos en forma aproximada) simétricamente distribuidas en torno al mismo valor. Si n es por lo menos grande de manera moderada, el grado de simetría puede ser valorado con una gráfica de ta- llo y hojas o un histograma. Sin embargo, si n no es muy grande, las gráficas mencionadas no son informativas en x1 5 x1 xt xt xt23 xt22 xt xt21 5 axt21 1 s1 2 adxt22 xt xt xt 5 axt 1 s1 2 adxt21 x1 5 x1 xt s2 n xn s2 n11 ns2 n11 5 sn 2 1ds2 n 1 n n 1 1 sxn11 2 xnd2 xn11 xn xn11 s2 n11 xn11 s2 n xn x x x c1_p001-045.qxd 3/12/08 2:31 AM Page 44
- 63. Bibliografía 45 particular. Considere la siguiente alternativa. Que y1 deno- te la xi más pequeña, y2 la segunda xi más pequeña y así sucesivamente. Luego coloque los siguientes pares como puntos en una sistema de coordenadas de dos dimensio- nes Existen n/2 puntos cuando n es par y (n – 1)/2 cuando n es impar. a. ¿Qué apariencia tiene esta gráfica cuando la simetría en los datos es perfecta? ¿Qué apariencia tiene cuando las observaciones se alargan más sobre la mediana que de- bajo de ella (una larga cola superior)? b. Los datos adjuntos sobre cantidad de lluvia (acres-pies) producida por 26 nubes bombardeadas se tomaron del ar- tículo (“A Bayesian Analysis of Multiplicative Treatment Effect in Weather Modification”, Technometrics, 1975: 161-166). Construya la gráfica y comente sobre el grado de simetría o la naturaleza del alejamiento de la misma. 4.1 7.7 17.5 31.4 32.7 40.6 92.4 115.3 118.3 119.0 129.6 198.6 200.7 242.5 255.0 274.7 274.7 302.8 334.1 430.0 489.1 703.4 978.0 1656.0 1697.8 2745.6 x | 2 y3d, c syn22 2 x |, syn21 2 x |, x | 2 y2d, syn 2 x |, x | 2 y1d, Bibliografía Chambers, John, William Cleveland, Beat Kleiner y Paul Tukey, Graphical Methods for Data Analysis, Brooks/Cole, Pacific Grove, CA, 1983. Una presentación altamente recomendada de varias metodologías gráficas y pictóricas en estadística. Cleveland, William, Visualizing Data, Hobart Press, Summit, NJ, 1993. Un entretenido recorrido de técnicas pictóricas. Devore, Jay y Roxy Peck, Statistics: The Exploration and Analy- sis of Data (5a. ed.), Thomson Brooks/Cole, Belmont, CA, 2005. Los primeros capítulos hacen un recuento no muy ma- temático de métodos para describir y resumir datos. Freedman, David, Robert Pisani y Roger Purves, Statistics (3a. ed.), Norton, Nueva York, 1998. Un excelente estudio no muy mate- mático de razonamiento y metodología estadísticos básicos. Hoaglin, David, Frederick Mosteller y John Tukey, Understan- ding Robust and Exploratory Data Analysis, Wiley, Nueva York, 1983. Discute el porqué y cómo deben ser utilizados los métodos exploratorios; es bueno por lo que se refiere a los de- talles de gráficas de tallo y hojas y gráficas de caja. Moore, David y William Notz, Statistics: Concepts and Contro- versies (6a. ed.), Freeman, San Francisco, 2006. Un libro de pasta blanda extremadamente fácil de leer y ameno que con- tiene una discusión intuitiva de problemas conectados con ex- perimentos de muestreo y diseñados. Peck, Roxy y colaboradores (eds.), Statistics: A Guide to the Unk- nown (4a. ed.), Thomson Brooks/Cole, Belmont, CA, 2006. Contiene muchos artículos no técnicos que describen varias aplicaciones de estadística. Verzani, John, Using R for Introductory Statistics, Chapman y Hall/CRC, Boca Ratón, FL, 2005. Una introducción muy agra- dable al paquete de “software” R. c1_p001-045.qxd 3/12/08 2:31 AM Page 45
- 64. Probabilidad 2 46 INTRODUCCIÓN El término probabilidad se refiere al estudio de azar y la incertidumbre en cualquier situación en la cual varios posibles sucesos pueden ocurrir; la disciplina de la proba- bilidad proporciona métodos de cuantificar las oportunidades y probabilidades aso- ciadas con varios sucesos. El lenguaje de probabilidad se utiliza constantemente de manera informal tanto en el contexto escrito como en el hablado. Algunos ejemplos incluyen enunciados tales como “es probable que el índice Dow-Jones se incremen- te al final del año”, “existen 50-50 probabilidades de que la persona con posesión de su cargo busque la reelección”, “probablemente se ofrecerá por lo menos una sección del curso el próximo año”, “las probabilidades favorecen la rápida solución de la huelga” y “se espera que se vendan por lo menos 20 000 boletos para el con- cierto”. En este capítulo, se introducen algunos conceptos de probabilidad, se indica cómo pueden ser interpretadas las probabilidades y se demuestra cómo pueden ser aplicadas las reglas de probabilidad para calcular las probabilidades de muchos eventos interesantes. La metodología de probabilidad permite entonces expresar en lengua- je preciso enunciados informales como los antes expresados. El estudio de la probabilidad como una rama de las matemáticas se remonta a más de 300 años, cuando nace en conexión con preguntas que implicaban juegos de azar. Muchos libros se han ocupado exclusivamente de la probabilidad, pero el ob- jetivo en este caso es cubrir sólo la parte de la materia que tiene más aplicación di- recta en problemas de inferencia estadística. c2_p046-085.qxd 3/12/08 3:58 AM Page 46
- 65. Un experimento es cualquier acción o proceso cuyo resultado está sujeto a la incertidum- bre. Aunque la palabra experimento en general sugiere una situación de prueba cuidadosa- mente controlada en un laboratorio, se le utiliza aquí en un sentido mucho más amplio. Por lo tanto, experimentos que pueden ser de interés incluyen lanzar al aire una moneda una vez o varias veces, seleccionar una carta o cartas de un mazo, pesar una hogaza de pan, el tiem- po de recorrido de la casa al trabajo en una mañana particular, obtener tipos de sangre de un grupo de individuos o medir las resistencias a la compresión de diferentes vigas de acero. El espacio muestral de un experimento El experimento más simple al que se aplica la probabilidad es uno con dos posibles resulta- dos. Tal experimento consiste en examinar un fusible para ver si está defectuoso. El espacio muestral de este experimento se abrevia como S {N, D}, donde N representa no defectuo- so, D representa defectuoso y las llaves se utilizan para encerrar los elementos de un con- junto. Otro experimento como ése implicaría lanzar al aire una tachuela y observar si cae punta arriba o punta abajo, con espacio muestral S {U, D} y otro más consistiría en ob- servar el sexo del siguiente niño nacido en el hospital, con S {H, M}. ■ Si se examinan tres fusibles en secuencia y se anota el resultado de cada examen, entonces un resultado del experimento es cualquier secuencia de letras N y D de longitud 3, por lo tanto S {NNN, NND, NDN, NDD, DNN, DND, DDN, DDD} Si se hubiera lanzado una tachuela tres veces, el espacio muestral se obtendría reemplazando N por U en la expresión S anterior y con un cambio de notación similar se obtendría el espacio muestral para el experimento en el cual se observan los sexos de tres niños recién nacidos. ■ Dos gasolinerías están localizadas en cierta intersección. Cada una dispone de 6 bombas de gasolina. Considérese el experimento en el cual se determina el número de bombas en uso a una hora particular del día en cada una de las gasolinerías. Un resultado experimental es- pecifica cuántas bombas están en uso en la primera gasolinería y cuántas están en uso en la segunda. Un posible resultado es (2, 2), otro es (4, 1) y otro más es (1, 4). Los 49 resulta- dos en S se muestran en la tabla adjunta. El espacio muestral del experimento en el cual un dado de 6 lados es lanzado dos veces se obtiene eliminando la fila 0 y la columna 0 de la ta- bla y se obtienen 36 resultados. Segunda gasolinería 0 1 2 3 4 5 6 0 (0, 0) (0, 1) (0, 2) (0, 3) (0, 4) (0, 5) (0, 6) 1 (1, 0) (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) Primera 2 (2, 0) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) gasolinería 3 (3, 0) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4, 0) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5, 0) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 0) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) ■ 2.1 Espacios muestrales y eventos 47 2.1 Espacios muestrales y eventos Ejemplo 2.1 Ejemplo 2.2 Ejemplo 2.3 DEFINICIÓN El espacio muestral de un experimento denotado por S, es el conjunto de todos los posibles resultados de dicho experimento. c2_p046-085.qxd 3/12/08 3:58 AM Page 47
- 66. Si el voltaje de una nueva batería tipo D para linterna queda fuera de ciertos límites, dicha batería se caracteriza como falla (F); si el voltaje de la batería se encuentra dentro de los lí- mites prescritos, se caracteriza como éxito (E). Supóngase un experimento que consiste en probar cada batería como sale de la línea de ensamble hasta que se observe primero un éxi- to. Aunque no es muy probable, un posible resultado de este experimento es que las prime- ras 10 (o 100 o 1000 o . . .) sean F y la siguiente sea un E. Es decir, para cualquier entero positivo n, es posible que se tenga que examinar n baterías antes de encontrar el primer E. El espacio muestral es S {E, FE, FFE, FFFE, . . .}, el cual contiene un número infinito de posibles resultados. La misma forma abreviada del espacio muestral es apropiada para un experimento en el cual, a partir de una hora especificada, se anota el sexo de cada infante recién nacido hasta que nazca un varón. ■ Eventos En el estudio de la probabilidad, interesan no sólo los resultados individuales de S sino tam- bién varias recopilaciones de resultados de S. Cuando se realiza un experimento, se dice que ocurre un evento particular A si el resultado experimental obtenido está contenido en A. En general, ocurrirá exactamente un evento sim- ple, pero muchos eventos compuestos ocurrirán al mismo tiempo. Considérese un experimento en el cual cada uno de tres vehículos que toman una salida de una autopista particular vira a la izquierda (L) o la derecha (R) al final de la rampa de sali- da. Los ocho posibles resultados que constituyen el espacio muestral son LLL, RLL, LRL, LLR, LRR, RLR, RRL y RRR. Así pues existen ocho eventos simples, entre los cuales están E1 {LLL} y E5 {LRR}. Algunos eventos compuestos incluyen A {RLL, LRL, LLR} el evento en que exactamente uno de los tres vehículos vire a la derecha. B {LLL, RLL, LRL, LLR} el evento en que cuando mucho uno de los vehículos vire a la derecha. C {LLL, RRR} el evento en que los tres vehículos viren en la misma dirección. Suponga que cuando se realiza el experimento, el resultado es LLL. Entonces ha ocurrido el evento simple E1 y por lo tanto también comprende los eventos B y C (pero no A). ■ Cuando se observa el número de bombas en uso en cada una de dos gasolinerías de 6 bombas, existen 49 posibles resultados, por lo que existen 49 eventos simples: E1 {(0, 0)}, E2 {(0, 1)}, . . . , E49 {(6, 6)}. Ejemplos de eventos compuestos son A {(0, 0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)} el evento en que el número de bombas en uso es el mismo en ambas gasolinerías. B {(0, 4), (1, 3) (2, 2), (3, 1), (4, 0)} el evento en que el número total de bombas en uso es cuatro. C {(0, 0), (0, 1), (1, 0), (1, 1)} el evento en que a lo sumo una bomba está en uso en cada gasolinería. ■ 48 CAPÍTULO 2 Probabilidad Ejemplo 2.4 Ejemplo 2.5 Ejemplo 2.6 (continuación del ejemplo 2.3) DEFINICIÓN Un evento es cualquier recopilación (subconjunto) de resultados contenidos en el es- pacio muestral S. Un evento es simple si consiste en exactamente un resultado y com- puesto si consiste en más de un resultado. c2_p046-085.qxd 3/12/08 3:58 AM Page 48
- 67. El espacio muestral del experimento del examen de las baterías contiene un número infini- to de resultados, por lo que existe un número infinito de eventos simples. Los eventos com- puestos incluyen A {E, FE, FFE} el evento en que cuando mucho se examinan tres baterías. E {FE, FFFE, FFFFFE,. . .} el evento en que se examina un número par de baterías. ■ Algunas relaciones de la teoría de conjuntos Un evento es simplemente un conjunto, así que las relaciones y resultados de la teoría ele- mental de conjuntos pueden ser utilizados para estudiar eventos. Se utilizarán las siguientes operaciones para crear eventos nuevos a partir de eventos dados. En el experimento en el cual se observa el número de bombas en uso en una sola gasoline- ría de seis bombas, sea A {0, 1, 2, 3, 4}, B {3, 4, 5, 6} y C {1, 3, 5}. Entonces A {5, 6}, A B {0, 1, 2, 3, 4, 5, 6} S, A C {0, 1, 2, 3, 4, 5}, A B {3, 4}, A C {1, 3}, (A C) {0, 2, 4, 5, 6} ■ En el experimento de la batería, defina A, B y C como A {E, FE, FFE}, B {E, FFE, FFFFE}, C {FE, FFFE, FFFFFE, . . .} Entonces A {FFFE, FFFFE, FFFFFE, . . .}, C {E, FFE, FFFFE, . . .} A B {E, FE, FFE, FFFFE}, A B {E, FFE} ■ En ocasiones A y B no tienen resultados en común, por lo que la intersección de A y B no contiene resultados. En una pequeña ciudad hay tres distribuidores de automóviles: un distribuidor GM que ven- de Chevrolets, Pontiacs y Buicks; un distribuidor Ford que vende Fords y Mercurys; y un distribuidor Chrysler que vende Plymouths y Chryslers. Si un experimento consiste en ob- servar la marca del siguiente carro vendido, entonces los eventos A {Chevrolet, Pontiac, Buick} y B {Ford, Mercury} son mutuamente excluyentes porque el siguiente carro ven- dido no puede ser tanto un producto GM como un producto Ford. ■ 2.1 Espacios muestrales y eventos 49 Ejemplo 2.7 (continuación del ejemplo 2.4) Ejemplo 2.8 (continuación del ejemplo 2.3) Ejemplo 2.9 (continuación del ejemplo 2.4) Ejemplo 2.10 DEFINICIÓN 1. El complemento de un evento A, denotado por A, es el conjunto de todos los re- sultados en S que no están contenidos en A. 2. La unión de dos eventos A y B, denotados por A B y leídos “A o B”, es el even- to que consiste en todos los resultados que están en A o en B o en ambos eventos (de tal suerte que la unión incluya resultados donde tanto A como B ocurren, así también resultados donde ocurre exactamente uno), es decir, todos los resultados en por lo menos uno de los eventos. 3. La intersección de dos eventos A y B, denotada por A B y leída “A y B”, es el evento que consiste en todos los resultados que están tanto en A como en B. DEFINICIÓN Que denote el evento nulo (el evento sin resultados). Cuando A B , se dice que A y B son eventos mutuamente excluyentes o disjuntos. c2_p046-085.qxd 3/12/08 3:58 AM Page 49
- 68. Las operaciones de unión e intersección pueden ser ampliadas a más de dos eventos. Para tres eventos cualesquiera A, B y C, el evento A B C es el conjunto de resultados contenidos en por lo menos uno de los tres eventos, mientras que A B C es el conjunto de resulta- dos contenidos en los tres eventos. Se dice que los eventos dados A1, A2, A3, . . . , son mutuamen- te excluyentes (disjuntos por pares) si ninguno de dos eventos tienen resultados en común. Con diagramas de Venn se obtiene una representación pictórica de eventos y manipula- ciones con eventos. Para construir un diagrama de Venn, se traza un rectángulo cuyo interior representará el espacio muestral S. En tal caso cualquier evento A se representa como el inte- rior de una curva cerrada (a menudo un círculo) contenido en S. La figura 2.1 muestra ejem- plos de diagramas de Venn. 50 CAPÍTULO 2 Probabilidad Figura 2.1 Diagramas de Venn. A B a) Diagrama de Venn de los eventos A y B A B e) Eventos mutuamente excluyentes A B c) La región sombreada es A B A d) La región sombreada es A' A B b) La región sombreada es A B 1. Cuatro universidades, 1, 2, 3 y 4, están participando en un torneo de básquetbol. En la primera ronda, 1 jugará con 2 y 3 jugará con 4. Acto seguido los ganadores jugarán por el campeonato y los dos perdedores también jugarán. Un po- sible resultado puede ser denotado por 1324 (1 derrota a 2 y 3 derrota a 4 en los juegos de la primera ronda y luego 1 derrota a 3 y 2 derrota a 4). a. Enumere todos los resultados en S. b. Que A denote el evento en que 1 gana el torneo. Enume- re los resultados en A. c. Que B denote el evento en que 2 gana el juego de cam- peonato. Enumere los resultados en B. d. ¿Cuáles son los resultados en A B y en A B? ¿Cuá- les son los resultados en A? 2. Suponga que un vehículo que toma una salida particular de una autopista puede virar a la derecha (R), virar a la izquier- da (L) o continuar de frente (S). Observe la dirección de cada uno de tres vehículos sucesivos. a. Elabore una lista de todos los resultados en el evento A en que los tres vehículos van en la misma dirección. b. Elabore una lista de todos los resultados en el evento B en que los tres vehículos toman direcciones diferentes. c. Elabore una lista de todos los resultados en el evento C en que exactamente dos de los tres vehículos dan vuelta a la derecha. d. Elabore una lista de todos los resultados en el evento D en que dos vehículos van en la misma dirección. e. Enumere los resultados en D, C D y C D. 3. Tres componentes están conectados para formar un sistema como se muestra en el diagrama adjunto. Como los compo- nentes del subsistema 2-3 están conectados en paralelo, di- cho subsistema funcionará si por lo menos uno de los dos componentes individuales funciona. Para que todo el siste- ma funcione, el componente 1 debe funcionar y por lo tan- to el subsistema 2-3 debe hacerlo. El experimento consiste en determinar la condición de cada componente [E (éxito) para un componente que funciona y F (falla) para un componente que no funciona]. a. ¿Qué resultados están contenidos en el evento A en que exactamente dos de los tres componentes funcionan? b. ¿Qué resultados están contenidos en el evento B en que por lo menos dos de los componentes funcionan? c. ¿Qué resultados están contenidos en el evento C en que el sistema funciona? d. Ponga en lista los resultados en C, A C, A C, B C y B C. 4. Cada muestra de cuatro hipotecas residenciales está clasi- ficada como tasa fija (F ) o tasa variable (V ). a. ¿Cuáles son los 16 resultados en S? b. ¿Qué resultados están en el evento en que exactamente tres de las hipotecas seleccionadas son de tasa fija? c. ¿Qué resultados están en el evento en que las cuatro hi- potecas son del mismo tipo? d. ¿Qué resultados están en el evento en que a lo sumo una de las cuatro es una hipoteca de tasa variable? e. ¿Cuál es la unión de eventos en los incisos c) y d) y cuál es la intersección de estos dos eventos? f. ¿Cuáles son la unión e intersección de los dos eventos en los incisos b) y c)? 5. Una familia compuesta de tres personas, A, B y C, pertene- ce a una clínica médica que siempre tiene disponible un doctor en cada una de las estaciones 1, 2 y 3. Durante cier- ta semana, cada miembro de la familia visita la clínica una vez y es asignado al azar a una estación. El experimento consiste en registrar la estación para cada miembro. Un EJERCICIOS Sección 2.1 (1-10) 2 1 3 c2_p046-085.qxd 3/12/08 3:58 AM Page 50
- 69. Dados un experimento y un espacio muestral S, el objetivo de la probabilidad es asignar a cada evento A un número P(A), llamado la probabilidad del evento A, el cual dará una me- dida precisa de la oportunidad de que A ocurra. Para garantizar que las asignaciones serán consistentes con las nociones intuitivas de la probabilidad, todas las asignaciones deberán sa- tisfacer los siguientes axiomas (propiedades básicas) de probabilidad. Se podría preguntar por qué el tercer axioma no contiene ninguna referencia a un con- junto finito de eventos mutuamente excluyentes. Es porque la propiedad correspondiente para un conjunto finito puede ser derivada de los tres axiomas. Se pretende que la lista de axio- mas sea tan corta como sea posible y que no contenga alguna propiedad que pueda ser de- rivada de los demás que aparecen en la lista. El axioma 1 refleja la noción intuitiva de que la 2.2 Axiomas, interpretaciones y propiedades de probabilidad 51 2.2 Axiomas, interpretaciones y propiedades de probabilidad resultado es (1, 2, 1) para A a la estación 1, B a la estación 2 y C a la estación 1. a. Elabore una lista de los 27 resultados en el espacio muestral. b. Elabore una lista de todos los resultados en el evento en que los tres miembros van a la misma estación. c. Elabore una lista de todos los resultados en que los tres miembros van a diferentes estaciones. d. Elabore una lista de los resultados en el evento en que ninguno va a la estación 2. 6. La biblioteca de una universidad dispone de cinco ejempla- res de un cierto texto en reserva. Dos ejemplares (1 y 2) son primeras impresiones y los otros tres (3, 4 y 5) son se- gundas impresiones. Un estudiante examina estos libros en orden aleatorio, y se detiene sólo cuando una segunda im- presión ha sido seleccionada. Un posible resultado es 5 y otro 213. a. Ponga en lista los resultados en S. b. Que A denote el evento en que exactamente un libro de- be ser examinado. ¿Qué resultados están en A? c. Sea B el evento en que el libro 5 es seleccionado. ¿Qué resultados están en B? d. Sea C el evento en que el libro 1 no es examinado. ¿Qué resultados están en C? 7. Un departamento académico acaba de votar secretamente para elegir un jefe de departamento. La urna contiene cua- tro boletas con votos para el candidato A y tres con votos para el candidato B. Suponga que estas boletas se sacan de la urna una por una. a. Ponga en lista todos los posibles resultados. b. Suponga que mantiene un conteo continuo de la boletas retiradas de la urna. ¿Para qué resultados A se mantiene adelante durante todo el conteo? 8. Una firma constructora de ingeniería en la actualidad está tra- bajando en plantas eléctricas en tres sitios diferentes. Que A denote el evento en que la planta localizada en el sitio i se com- pleta alrededor de la fecha contratada. Use las operaciones de unión, intersección y complemento para describir cada uno de los siguientes eventos en función de A1, A2 y A3, trace un diagrama y sombree la región que corresponde a cada uno. a. Por lo menos una planta se completa alrededor de la fe- cha contratada. b. Todas las plantas se completan alrededor de la fecha contratada. c. Sólo la planta localizada en el sitio 1 se completa alre- dedor de la fecha contratada. d. Exactamente una planta se completa alrededor de la fe- cha contratada. e. O la planta localizada en el sitio 1 o las otras dos plan- tas se completan alrededor de la fecha contratada. 9. Use diagramas de Venn para las dos siguientes relaciones para los eventos A y B (éstas se conocen como leyes De Morgan): a. (A B) A B b. (A B) A B 10. a. En el ejemplo 2.10, identifique tres eventos que son mu- tuamente excluyentes. b. Suponga que no hay ningún resultado común a los tres eventos A, B y C. ¿Son estos tres eventos necesariamen- te mutuamente excluyentes? Si su respuesta es sí, expli- que por qué; si su respuesta es no, dé un contraejemplo valiéndose del experimento del ejemplo 2.10. AXIOMA 1 AXIOMA 2 AXIOMA 3 Para cualquier evento A, P(A) 0. P(S ) 1. Si A1, A2, A3, . . . es un conjunto de eventos mutuamente excluyentes, entonces PsA1 ´ A2 ´ A3 ´ cd 5 g ` i51 PsAid c2_p046-085.qxd 3/12/08 3:58 AM Page 51
- 70. probabilidad de que ocurra A deberá ser no negativa. El espacio muestral es por definición el evento que debe ocurrir cuando se realiza el experimento (S contiene todos los posibles re- sultados), así se dice el axioma 2 que es la máxima probabilidad posible de 1 está asignada a S. El tercer axioma formaliza la idea que si se desea la probabilidad de que ocurra al me- nos uno de varios eventos, y no ocurran dos al mismo tiempo, entonces la probabilidad de que por lo menos uno ocurra es la suma de las probabilidades de los eventos individuales. Comprobación Primero considérese el conjunto infinito Como , los eventos en este conjunto son disjuntos y Ai . El tercer axioma da entonces Esto puede suceder sólo si P() 0. Ahora supóngase que A1, A2, . . . , Ak son eventos disjuntos y anéxense a éstos el con- junto finito De nuevo si se invoca el tercer axioma. como se deseaba. ■ Considere lanzar una tachuela al aire. Cuando se detiene en el suelo, o su punta estará ha- cia arriba (el resultado U) o hacia abajo (el resultado D). El espacio muestral de este even- to es por consiguiente S {U, D}. Los axiomas especifican P(S) 1, por lo que la asignación de probabilidad se completará determinando P(U) y P(D). Como U y D están desarticulados y su unión S, la siguiente proposición implica que 1 P(S ) P(U) P(D) Se desprende que P(D) 1 P(U). Una posible asignación de probabilidades es P(U) 0.5, P(D) 0.5, mientras que otra posible asignación es P(U ) 0.75, P(D) 0.25. De hecho, si p representa cualquier número fijo entre 0 y 1, P(U) p, P(D) 1 p es una asignación compatible con los axiomas. ■ Regresemos al experimento del ejemplo 2.4, en el cual se prueban las baterías que salen de la línea de ensamble una por una hasta que se encuentra una con el voltaje dentro de los límites prescritos. Los eventos simples son E1 {E}, E2 {FE}, E3 {FFE}, E4 {FFFE}, . . . . Suponga que la probabilidad de que cualquier batería resulte satisfactoria es de 0.99. Entonces se puede demostrar que P(E1) 0.99, P(E2) (0.01)(0.99), P(E3) (0.01)2 (0.99), . . . es una asignación de probabilidades a los eventos simples que satisface los axiomas. En particular, co- mo los Ei son disjuntos y S E1 E2 E3 . . . , debe ser el caso de que 1 P(S ) P(E1) P(E2) P(E3) . . . 0.99[1 0.01 (0.01)2 (0.01)3 . . .] Aquí se utilizó la fórmula para la suma de una serie geométrica: a 1 ar 1 ar2 1 ar3 1 c 5 a 1 2 r Pa ´ k i51 Aib 5 Pa ´ ` i51 Aib 5 g ` i51 PsAid 5 g k i51 PsAid Ak11 5 [, Ak12 5 [, Ak13 5 [, . . . . Ps[d 5 g Ps[d A1 5 [, A2 5 [, A3 5 [, . . . . 52 CAPÍTULO 2 Probabilidad PROPOSICIÓN P() 0 donde es el evento nulo (el evento que no contiene resultados en abso- luto). Esto a su vez implica que la propiedad contenida en el axioma 3 es válida para un conjunto finito de eventos. Ejemplo 2.11 Ejemplo 2.12 c2_p046-085.qxd 3/12/08 3:58 AM Page 52
- 71. Sin embargo, otra asignación de probabilidad legítima (de acuerdo con los axiomas) del mismo tipo “geométrico” se obtiene reemplazando 0.99 por cualquier otro número p en- tre 0 y 1 (y 0.01 por 1 p). ■ Interpretación de probabilidad Los ejemplos 2.11 y 2.12 muestran que los axiomas no determinan por completo una asig- nación de probabilidades a eventos. Los axiomas sirven sólo para excluir las asignaciones incompatibles con las nociones intuitivas de probabilidad. En el experimento de lanzar al ai- re tachuelas del ejemplo 2.11, se sugirieron dos asignaciones particulares. La asignación apro- piada o correcta depende de la naturaleza de la tachuela y también de la interpretación de probabilidad. La interpretación que más frecuentemente se utiliza y más fácil de entender está basada en la noción de frecuencias relativas. Considérese un experimento que pueda ser realizado repetidamente de una manera idéntica e independiente y sea A un evento que consiste en un conjunto fijo de resultados del experimento. Ejemplos simples de experimentos repetibles incluyen el lanzamiento al aire de tachuelas y dados previamente discutidos. Si el experimento se realiza n veces, en algunas de las réplicas el evento A ocurrirá (el resultado estará en el conjunto A) y en otros, A no ocurrirá. Que n(A) denote el número de réplicas en las cuales A sí ocurre. Entonces la relación n(A)/n se conoce como la frecuencia relativa de ocurrencia del evento A en la se- cuencia de n réplicas. La evidencia empírica basada en los resultados de muchas de estas secuencias de experimentos repetibles, indica que a medida que n se hace más grande, la frecuencia relativa n(A)/n se estabiliza, como se ilustra en la figura 2.2. Es decir, conforme n se hace arbitrariamente grande, la frecuencia relativa tiende a un valor límite al que se ha- ce referencia como frecuencia relativa límite del evento A. La interpretación objetiva de pro- babilidad identifica esta frecuencia relativa límite con P(A). Si se asignan probabilidades a eventos de acuerdo con sus frecuencias relativas límite, entonces se puede interpretar una aseveración tal como “la probabilidad de que una mone- da que cae con el águila hacia arriba cuando es lanzada al aire es 0.5” para dar a entender que en un gran número de los lanzamientos, aparecerá un águila en aproximadamente la mi- tad de los lanzamientos y un sol en la otra mitad. Se dice que esta interpretación de frecuencia relativa de probabilidad es objetiva por- que se apoya en una propiedad del experimento y no en cualquier individuo particular inte- resado en el experimento. Por ejemplo, dos observadores diferentes de una secuencia de lanzamiento de una moneda deberán utilizar la misma asignación de probabilidad puesto que los observadores no tienen nada que ver con la frecuencia relativa límite. En la práctica, la interpretación no es tan objetiva como pudiera parecer, puesto que la frecuencia relativa 2.2 Axiomas, interpretaciones y propiedades de probabilidad 53 Figura 2.2 Estabilización de la frecuencia relativa. n(A) Frecuencia n relativa 0 1 1 2 3 100 101 102 n x x x x x x x x x n Número de experimentos realizados c2_p046-085.qxd 3/12/08 3:58 AM Page 53
- 72. límite de un evento no será conocida. Por tanto, se tendrán que asignar probabilidades con ba- se en creencias sobre la frecuencia relativa límite de eventos en estudio. Afortunadamente, existen muchos experimentos para los cuales habrá consenso con respecto a asignaciones de probabilidad. Cuando se habla de una moneda imparcial, significa P(H) P(T) 0.5 y un dado imparcial es uno para el cual las frecuencias relativas límite de los seis resultados son 1/6, lo que sugiere las asignaciones de probabilidad P({1}) · · · P({6}) 1/6. Como la interpretación objetiva de probabilidad está basada en la noción de frecuen- cia límite, su aplicabilidad está restringida a situaciones experimentales repetibles. No obs- tante, el lenguaje de probabilidad a menudo se utiliza en conexión con situaciones que son inherentemente irrepetibles. Algunos ejemplos incluyen: “las probabilidades de un tratado de paz son buenas”; “es probable que el contrato le será otorgado a nuestra compañía”; y “como su mejor mariscal de campo está lesionado, espero que no anoten más de 10 puntos contra nosotros”. En tales situaciones se desearía, como antes, asignar probabilidades nu- méricas a varios resultados y eventos (p. ej., la probabilidad es 0.9 de que obtendremos el contrato). Por consiguiente se debe adoptar una interpretación alternativa de estas probabi- lidades. Como diferentes observadores pueden tener información y opiniones previas con respecto a tales situaciones experimentales, las asignaciones de probabilidad ahora pueden definir de un individuo a otro. Las interpretaciones en tales situaciones se conocen por lo tanto como subjetivas. El libro de Robert Winkler citado en las referencias del capítulo da un recuento muy fácil de leer de varias interpretaciones subjetivas. Más propiedades de probabilidad Comprobación En el axioma 3, sea k 2, A1 A y A2 A. Como por definición de A, A A S en tanto A y A sean eventos disjuntos, 1 P(S) P(A A) P(A) P(A). ■ Esta proposición es sorprendentemente útil porque se presentan muchas situaciones en las cuales P(A) es más fácil de obtener mediante métodos directos que P(A). Considere un sistema de cinco componentes idénticos conectados en serie, como se ilustra en la figura 2.3. Denote un componente que falla por F y uno que no lo hace por E (éxito). Sea A el evento en que el sistema falla. Para que ocurra A, por lo menos uno de los componentes individuales debe fallar. Los resultados en A incluyen EEFEE(1, 2, 4 y 5 funcionarán, pero 3 no). FFEEE, y así sucesivamente. Existen de hecho 31 resultados diferentes en A. Sin embargo, A, el evento en que el sistema funciona, consiste en el resultado único EEEEE. En la sección 2.5 se verá que si 90% de todos estos componentes no fallan y diferentes componentes lo hacen independientemente uno de otro, entonces P(A) P(EEEEE) 0.95 0.59. Así pues P(A) 1 0.59 0.41; por lo tanto, entre un gran número de sistemas como ése, aproximada- mente 41% fallarán. ■ En general, la proposición anterior es útil cuando el evento de interés puede ser expresado “por lo menos . . . ,” puesto que en ese caso puede ser más fácil trabajar con el 54 CAPÍTULO 2 Probabilidad PROPOSICIÓN Para cualquier evento A, P(A) + P(A) 1, a partir de la cual P(A) 1 – P(A). Ejemplo 2.13 Figura 2.3 Un sistema de cinco componentes conectados en serie. 1 2 3 4 5 c2_p046-085.qxd 3/12/08 3:58 AM Page 54
- 73. complemento “menos que . . .” (en algunos problemas es más fácil trabajar con “más que. . .” que con “cuando . . .”). Cuando se tenga dificultad al calcular P(A) directamente, habrá que pensar en determinar P(A). Esto se debe a que 1 P(A) P(A) P(A) puesto que P(A) 0. Cuando los eventos A y B son mutuamente excluyentes, P(A B) P(A) P(B). Para eventos que no son mutuamente excluyentes, la adición de P(A ) y P(B) da por resul- tado un “doble conteo” de los resultados en la intersección. El siguiente resultado muestra cómo corregir esto. Comprobación Obsérvese primero que A B puede ser descompuesto en dos eventos excluyentes, A y B A; la última es la parte B que queda afuera de A. Además, B por sí mismo es la unión de los dos eventos excluyentes A B y A B, por lo tanto P(B) P(A B) + P(A B). Por lo tanto P(A B) P(A) P(B A) P(A) [P(B) P(A B)] P(A) P(B) P(A B) En cierto suburbio residencial, 60% de las familias se suscriben al periódico en una ciudad cercana, 80% lo hacen al periódico local y 50% de todas las familias a ambos periódicos. Si se elige una familia al azar, ¿cuál es la probabilidad de que se suscriba a (1) por lo menos a uno de los dos periódicos y (2) exactamente a uno de los dos periódicos? Con A {se suscribe al periódico metropolitano} y B {se suscribe al periódico lo- cal}, la información dada implica que P(A) 0.6, P(B) 0.8 y P(A B) 0.5. La pro- posición precedente ahora lleva a P(se suscribe a por lo menos uno de los dos periódicos) P(A B) P(A) P(B) P(A B) 0.6 0.8 0.5 0.9 El evento en que una familia se suscribe a sólo el periódico local se escribe como A B [(no metropolitano) y local]. Ahora la figura 2.4 implica que 0.9 P(A B) P(A) P(A B) 0.6 P(A B) a partir de la cual P(A B) 0.3. Asimismo P(A B) P(A B) P(B) 0.1. Todo esto se ilustra en la figura 2.5, donde se ve que P(exactamente uno) P(A B) P(A B) 0.1 0.3 0.4 2.2 Axiomas, interpretaciones y propiedades de probabilidad 55 PROPOSICIÓN Para cualquier evento A, P(A) 1. PROPOSICIÓN Para dos eventos cualesquiera A y B. P(A B) P(A) P(B) P(A B) Ejemplo 2.14 Figura 2.4 Representación de A B como una unión de eventos excluyentes. ■ A B c2_p046-085.qxd 3/12/08 3:58 AM Page 55
- 74. La probabilidad de una unión de más de dos eventos se calcula en forma análoga. Esto se puede ver examinando un diagrama de Venn de A B C, el cual se muestra en la figura 2.6. Cuando P(A), P(B) y P(C) se agregan, ciertas intersecciones se cuentan dos veces, por lo que deben ser restadas, pero esto hace que P(A B C) se reste una vez en exceso. Determinación de probabilidades sistemáticamente Considérese un espacio muestral que es o finito o “contablemente infinito” (lo segundo sig- nifica que los resultados pueden ser puestos en lista en una secuencia infinita, por lo que existe un primer resultado, un segundo, un tercero, y así sucesivamente, por ejemplo, el es- cenario de prueba de baterías del ejemplo 2.4). Que E1, E2, E3, . . . denoten los eventos sim- ples correspondientes, cada uno compuesto de un solo resultado. Una estrategia sensible para el cálculo de probabilidad es determinar primero cada probabilidad de evento simple, con el requerimiento de que Entonces la probabilidad de cualquier evento compuesto A se calcula agregando los P(Ei) para todos los Ei que existen en A: Durante las horas no pico el tren que viaja entre los suburbios y la ciudad utiliza cinco carros. Suponga que existe el doble de probabilidades de que un usuario seleccione el carro interme- dio (#3) que cualquier carro adyacente (#2 o #4) y el doble de probabilidades de que seleccio- ne cualquier carro adyacente que cualquier carro extremo (#1 o #5). Sea pi P(carro i seleccionado) P(Ei). Entonces se tiene p3 2p2 2p4 y p2 2p1 2p5 p4. Esto da es decir, p1 p5 0.1, p2 p4 0.2, p3 0.4. La probabilidad de que uno de los tres ca- rros intermedios se seleccione (un evento compuesto) es entonces p2 + p3 + p4 0.8. ■ 1 5 gPsEid 5 p1 1 2p1 1 4p1 1 2p1 1 p1 5 10p1 PsAd 5 g todos los Ei en A PsEid PsEid 5 1. 56 CAPÍTULO 2 Probabilidad Figura 2.5 Probabilidades para el ejemplo 2.14. ■ 0.5 0.1 P(A' B) P(A B' ) 0.3 Figura 2.6 A B C. A B C Para tres eventos cualesquiera A, B y C, P(A B C) P(A) P(B) P(C) P(A B) P(A C) P(B C) P(A B C) Ejemplo 2.15 c2_p046-085.qxd 3/12/08 3:58 AM Page 56
- 75. Resultados igualmente probables En muchos experimentos compuestos de N resultados, es razonable asignar probabilidades iguales a los N eventos simples. Éstos incluyen ejemplos tan obvios como lanzar al aire una moneda o un dado imparciales una o dos veces (o cualquier número fijo de veces) o selec- cionar una o varias cartas de un mazo bien barajado de 52 cartas. Con p P(Ei) por cada i, 1 N i1 P(Ei) N i1 p p N por lo tanto p Es decir, si existen N resultados igualmente probables, la probabilidad de cada uno es 1/N. Ahora considérese un evento A, con N(A) como el número de resultados contenidos en A. Entonces P(A) Ei en A P(Ei) Ei en A Por lo tanto, cuando los resultados son igualmente probables, el cálculo de probabili- dades se reduce a contar: determinar tanto el número de resultados N(A) en A como el nú- mero de resultados N en S y formar su relación. Cuando dos dados se lanzan por separado, existen N 36 resultados (elimine la primera fila y la primera columna de la tabla del ejemplo 2.3). Si ambos dados son imparciales, los 36 resultados son igualmente probables, por lo tanto P(Ei) 3 1 6. Entonces el evento A {suma de dos números 7} consta de seis resultados (1, 6), (2, 5), (3, 4), (4, 3), (5, 2) y (6, 1), por lo tanto P(A) ■ 1 6 6 36 N(A) N N(A) N 1 N 1 N 2.2 Axiomas, interpretaciones y propiedades de probabilidad 57 Ejemplo 2.16 11. Una compañía de fondos de inversión mutua ofrece a sus clientes varios fondos diferentes: un fondo de mercado de dinero, tres fondos de bonos (a corto, intermedio y a largo plazos), dos fondos de acciones (de moderado y alto riesgo) y un fondo balanceado. Entre los clientes que poseen accio- nes en un solo fondo, los porcentajes de clientes en los di- ferentes fondos son como sigue: Mercado de dinero 20% Acciones de alto riesgo 18% Bonos a corto plazo 15% Acciones de riesgo Bonos a plazo moderado 25% intermedio 10% Balanceadas 7% Bonos a largo plazo 5% Se selecciona al azar un cliente que posee acciones en sólo un fondo. a. ¿Cuál es la probabilidad de que el individuo selecciona- do posea acciones en el fondo balanceado? b. ¿Cuál es la probabilidad de que el individuo posea ac- ciones en un fondo de bonos? c. ¿Cuál es la probabilidad de que el individuo selecciona- do no posea acciones en un fondo de acciones? 12. Considere seleccionar al azar un estudiante en cierta univer- sidad y que A denote el evento en que el individuo seleccio- nado tenga una tarjeta de crédito Visa y que B sea el evento análogo para la tarjeta MasterCard. Suponga que P(A) 0.5, P(B) 0.4 y P(A B) 0.25. a. Calcule la probabilidad de que el individuo seleccionado tenga por lo menos uno de los dos tipos de tarjetas (es de- cir, la probabilidad del evento A B). b. ¿Cuál es la probabilidad de que el individuo seleccionado no tenga ningún tipo de tarjeta? c. Describa, en función de A y B, el evento de que el estudian- te seleccionado tenga una tarjeta Visa pero no una Master- Card y luego calcule la probabilidad de este evento. 13. Una firma consultora de computación presentó propuestas en tres proyectos. Sea Ai {proyecto otorgado i}, con i 1, 2, 3 y suponga que P(A1) 0.22, P(A2) 0.25, P(A3) 0.28, P(A1 A2) 0.11, P(A1 A3) 0.05, P(A2 A3) 0.07, P(A1 A2 A3) 0.01. Exprese en palabras cada uno de los siguientes eventos y calcule la probabilidad de cada uno: a. A1 A2 b. A 1 A 2 [ Sugerencia: (A1 A2) A 1 A 2] c. A1 A2 A3 d. A 1 A 2 A 3 e. A 1 A 2 A3 f. (A 1 A 2) A3 14. Una compañía de electricidad ofrece una tarifa de consumo mínimo a cualquier usuario cuyo consumo de electricidad EJERCICIOS Sección 2.2 (11-28) c2_p046-085.qxd 3/12/08 3:58 AM Page 57
- 76. 58 CAPÍTULO 2 Probabilidad sea de menos de 240 kWh durante un mes particular. Si A denota el evento en que un usuario seleccionado al azar en una cierta comunidad no excede el consumo mínimo duran- te enero y B el evento análogo para el mes de julio (A y B se refieren al mismo usuario. Suponga P(A) 0.8, P(B) 0.7 y P(A B) 0.9. Calcule lo siguiente: a. P(A B). b. La probabilidad de que el consumo mínimo sea sobrepa- sado en exactamente uno de los dos meses. Describa es- te evento en función de A y B. 15. Considere el tipo de secadora de ropa (de gas o eléctrica) adquirida por cada uno de cinco clientes diferentes en cier- ta tienda. a. Si la probabilidad de que a lo sumo uno de éstos adquiera una secadora eléctrica es 0.428, ¿cuál es la probabilidad de que por lo menos dos adquieran una secadora eléctrica? b. Si P(los cinco compran una secadora de gas) 0.116 y P(los cinco compran una secadora eléctrica) 0.005, ¿cuál es la probabilidad de que por lo menos se adquie- ra una secadora de cada tipo? 16. A un individuo se le presentan tres vasos diferentes de refres- co de cola, designados C, D y P. Se le pide que pruebe los tres y que los ponga en lista en orden de preferencia. Suponga que se sirvió el mismo refresco de cola en los tres vasos. a. ¿Cuáles son los eventos simples en este evento de clasi- ficación y qué probabilidad le asignaría a cada uno? b. ¿Cuál es la probabilidad de que C obtenga el primer lugar? c. ¿Cuál es la probabilidad de que C obtenga el primer lu- gar y D el último? 17. Que A denote el evento en que la siguiente solicitud de ase- soría de un consultor de “software” estadístico tenga que ver con el paquete SPSS y que B denote el evento en que la siguiente solicitud de ayuda tiene que ver con SAS. Supon- ga que P(A ) 0.30 y P(B) 0.50. a. ¿Por qué no es el caso en que P(A) + P(B) 1? b. Calcule P(A). c. Calcule P(A B). d. Calcule P(A B). 18. Una caja contiene cuatro focos de 40 W, cinco de 60 W y seis de 75 W. Si los focos se eligen uno por uno en orden aleatorio, ¿cuál es la probabilidad de que por lo menos dos focos deban ser seleccionados para obtener uno de 75 W? 19. La inspección visual humana de uniones soldadas en un circuito impreso puede ser muy subjetiva. Una parte del problema se deriva de los numerosos tipos de defectos de soldadura (p. ej., almohadilla seca, visibilidad en escuadra, picaduras) e incluso el grado al cual una unión posee uno o más de estos defectos. Por consiguiente, incluso inspec- tores altamente entrenados pueden discrepar en cuanto a la disposición particular de una unión particular. En un lote de 10 000 uniones, el inspector A encontró 724 defectuo- sas, el inspector B, 751 y 1159 de las uniones fueron con- sideradas defectuosas por cuando menos uno de los inspectores. Suponga que se selecciona una de las 10 000 uniones al azar. a. ¿Cuál es la probabilidad de que la unión seleccionada no sea juzgada defectuosa por ninguno de los dos inspectores? b. ¿Cuál es la probabilidad de que la unión seleccionada sea juzgada defectuosa por el inspector B pero no por inspector A? 20. Cierta fábrica utiliza tres turnos diferentes. Durante el año pasado, ocurrieron 200 accidentes en la fábrica. Algunos de ellos pueden ser atribuidos por lo menos en parte a condi- ciones de trabajo inseguras. La tabla adjunta da el porcen- taje de accidentes que ocurren en cada tipo de categoría de accidente-turno. Condiciones No relacionados inseguras a condiciones Día 10% 35% Turno Tarde 8% 20% Noche 5% 22% Suponga que uno de los 200 reportes de accidente se selec- ciona al azar de un archivo de reportes y que el turno y el ti- po de accidente se determinan. a. ¿Cuáles son los eventos simples? b. ¿Cuál es la probabilidad de que el accidente selecciona- do se atribuya a condiciones inseguras? c. ¿Cuál es la probabilidad de que el accidente selecciona- do no ocurrió en el turno de día. 21. Una compañía de seguros ofrece cuatro diferentes niveles de deducible, ninguno, bajo, medio y alto, para sus tenedo- res de pólizas de propietario de casa y tres diferentes nive- les, bajo, medio y alto, para sus tenedores de pólizas de automóviles. La tabla adjunta da proporciones de las varias categorías de tenedores de pólizas que tienen ambos tipos de seguro. Por ejemplo, la proporción de individuos con de- ducible bajo de casa como deducible bajo de carro es 0.06 (6% de todos los individuos). Propietario de casa Auto N B M A B 0.04 0.06 0.05 0.03 M 0.07 0.10 0.20 0.10 A 0.02 0.03 0.15 0.15 Suponga que se elige al azar un individuo que posee ambos tipos de pólizas. a. ¿Cuál es la probabilidad de que el individuo tenga un de- ducible de auto medio y un deducible de casa alto? b. ¿Cuál es la probabilidad de que el individuo tenga un de- ducible de casa bajo y un deducible de auto bajo? c. ¿Cuál es la probabilidad de que el individuo se encuen- tre en la misma categoría de deducibles de casa y auto? d. Basado en su respuesta en el inciso c), ¿cuál es la proba- bilidad de que las dos categorías sean diferentes? e. ¿Cuál es la probabilidad de que el individuo tenga por lo menos un nivel deducible bajo? f. Utilizando la respuesta del inciso e). ¿cuál es la proba- bilidad de que ningún nivel deducible sea bajo? 22. La ruta utilizada por un automovilista para trasladarse a su trabajo contiene dos intersecciones con señales de tránsito. c2_p046-085.qxd 3/12/08 3:58 AM Page 58
- 77. Cuando los diversos resultados de un experimento son igualmente probables (la misma pro- babilidad es asignada a cada evento simple), la tarea de calcular probabilidades se reduce a contar. Sea N el número de resultados en un espacio muestral y N(A) el número de resulta- dos contenidos en un evento A. P(A) (2.1) N(A) N 2.3 Técnicas de conteo 59 La probabilidad de que tenga que detenerse en la primera señal es 0.4, el problema análogo para la segunda señal es 0.5 y la probabilidad de que tenga que detenerse en por lo menos una de las dos señales es 0.6. ¿Cuál es la probabili- dad de que tenga que detenerse a. En ambas señales? b. En la primera señal pero no en la segunda? c. En exactamente una señal? 23. Las computadoras de seis miembros del cuerpo de profeso- res en cierto departamento tienen que ser reemplazadas. Dos de ellos seleccionaron computadoras portátiles y los otros cuatro escogieron computadoras de escritorio. Su- ponga que sólo dos de las configuraciones pueden ser rea- lizadas en un día particular y las dos computadoras que van a ser configuradas se seleccionan al azar de entre las seis (lo que implica 15 resultados igualmente probables; si las computadoras se numeran 1, 2, . . . , 6 entonces un resultado se compone de las computadoras 1 y 2, otro de las compu- tadoras 1 y 3, y así sucesivamente). a. ¿Cuál es la probabilidad de que las dos configuraciones seleccionadas sean computadoras portátiles? b. ¿Cuál es la probabilidad de que ambas configuraciones se- leccionadas sean computadoras de escritorio? c. ¿Cuál es la probabilidad de que por lo menos una configu- ración seleccionada sea una computadora de escritorio? d. ¿Cuál es la probabilidad de que por lo menos una compu- tadora de cada tipo sea elegida para configurarla? 24. Demuestre que si un evento A está contenido en otro even- to B (es decir, A es un subconjunto de B), entonces P(A) P(B). [Sugerencia: Con los eventos A y B, A y B A son eventos excluyentes y B A (B A), como se ve en el diagrama de Venn.] Para los eventos A y B, ¿qué implica es- to sobre la relación entre P(A B), P(A) y P(A B)? 25. Las tres opciones principales en un tipo de carro nuevo son una transmisión automática (A), un quemacocos (B) y un estéreo con reproductor de discos compactos (C). Si 70% de todos los compradores solicitan A, 80% solicitan B, 75% so- licitan C, 85% solicitan A o B, 90% solicitan A o C, 95% solicitan B o C y 98% solicitan A o B o C, calcule las proba- bilidades de los siguientes eventos. [Sugerencia: “A o B” es el evento en que por lo menos una de las dos opciones es so- licitada; trate de trazar un diagrama de Venn y rotule todas las regiones.] a. El siguiente comprador solicitará por lo menos una de las tres opciones. b. El siguiente comprador no seleccionará ninguna de las tres opciones. c. El siguiente comprador solicitará sólo una transmisión automática y ninguna otra de las otras dos opciones. d. El siguiente comprador seleccionará exactamente una de estas tres opciones. 26. Un sistema puede experimentar tres tipos diferentes de defectos. Sea Ai (i 1, 2, 3) el evento en que el sistema tie- ne un defecto de tipo i. Suponga que P(A1) 0.12 P(A2) 0.07 P(A3) 0.05 P(A1 A2) 0.13 P(A1 A3) 0.14 P(A2 A3) 0.10 P(A1 A2 A3) 0.01 a. ¿Cuál es la probabilidad de que el sistema no tenga un defecto de tipo 1? b. ¿Cuál es la probabilidad de que el sistema tenga tanto defectos de tipo 1 como de tipo 2? c. ¿Cuál es la probabilidad de que el sistema tenga tanto defectos de tipo 1 como de tipo 2 pero no de tipo 3? d. ¿Cuál es la probabilidad de que el sistema tenga a lo su- mo dos de estos defectos? 27. Un departamento académico con cinco miembros del cuerpo de profesores, Anderson, Box, Cox, Cramer y Fisher, debe seleccionar dos de ellos para que participen en un comité de revisión de personal. Como el trabajo requerirá mucho tiem- po, ninguno está ansioso de participar, por lo que se decidió que el representante será elegido introduciendo cinco trozos de papel en una caja, revolviéndolos y seleccionando dos. a. ¿Cuál es la probabilidad de que tanto Anderson como Box serán seleccionados? [Sugerencia: Nombre los re- sultados igualmente probables.] b. ¿Cuál es la probabilidad de que por lo menos uno de los dos miembros cuyo nombre comienza con C sea selec- cionado? c. Si los cinco miembros del cuerpo de profesores han dado clase durante 3, 6, 7, 10 y 14 años, respectivamente, en la universidad, ¿cuál es la probabilidad de que los dos repre- sentantes seleccionados acumulen por lo menos 15 años de experiencia académica en la universidad? 28. En el ejercicio 5, suponga que cualquier individuo que en- tre a la clínica tiene las mismas probabilidades de ser asig- nado a cualquiera de las tres estaciones independientemente de adónde hayan sido asignados otros individuos. ¿Cuál es la probabilidad de que a. Los tres miembros de una familia sean asignados a la misma estación? b. A lo sumo dos miembros de la familia sean asignados a la misma estación? c. Cada miembro de la familia sea asignado a una estación diferente? 2.3 Técnicas de conteo c2_p046-085.qxd 3/12/08 3:58 AM Page 59
- 78. Si una lista de resultados es fácil de obtener y N es pequeño, entonces N y N(A) pueden ser determinadas sin utilizar ningún principio de conteo. Existen, sin embargo, muchos experimentos en los cuales el esfuerzo implicado al ela- borar la lista es prohibitivo porque N es bastante grande. Explotando algunas reglas de con- teo generales, es posible calcular probabilidades de la forma (2.1) sin una lista de resultados. Estas reglas también son útiles en muchos problemas que implican resultados que no son igualmente probables. Se utilizarán varias de las reglas desarrolladas aquí al estudiar distri- buciones de probabilidad en el siguiente capítulo. La regla de producto para pares ordenados La primera regla de conteo se aplica a cualquier situación en la cual un conjunto (evento) se compone de pares de objetos ordenados y se desea contar el número de pares. Por par orde- nado, se quiere decir que, si O1 y O2 son objetos, entonces el par (O1, O2) es diferente del par (O2, O1). Por ejemplo, si un individuo selecciona una línea aérea para un viaje de Los Ángeles a Chicago y (después de realizar transacciones de negocios en Chicago) un segun- do para continuar a Nueva York, una posibilidad es (American, United), otra es (United, American) y otra más es (United, United). El propietario de una casa que va a llevar a cabo una remodelación requiere los servicios tanto de un contratista de fontanería como de un contratista de electricidad. Si existen 12 contratistas de fontanería y 9 contratistas electricistas disponibles en el área, ¿de cuántas maneras pueden ser elegidos los contratistas? Sean P1, . . . , P12 los fontaneros y Q1, . . . , Q9 los electricistas, entonces se desea el número de pares de la forma (Pi, Qj). Con n1 12 y n2 9, la regla de producto da N (12)(9) 108 formas posibles de seleccionar los dos tipos de contratistas. ■ En el ejemplo 2.17, la selección del segundo elemento del par no dependió de qué pri- mer elemento ocurrió o fue elegido. En tanto exista el mismo número de opciones del se- gundo elemento por cada primer elemento, la regla de producto es válida incluso cuando el conjunto de posibles segundos elementos depende del primer elemento. Una familia se acaba de cambiar a una nueva ciudad y requiere los servicios tanto de un obs- tetra como de un pediatra. Existen dos clínicas médicas fácilmente accesibles y cada una tie- ne dos obstetras y tres pediatras. La familia obtendrá los máximos beneficios del seguro de salud si se une a la clínica y selecciona ambos doctores de la clínica. ¿De cuántas maneras se puede hacer esto? Denote los obstetras por O1, O2, O3 y O4 y los pediatras por P1, . . . , P6. Entonces se desea el número de pares (Oi,Pj) para los cuales Oi y Pj están asociados con la misma clínica. Como existen cuatro obstetras, n1 4, y por cada uno existen tres opcio- nes de pediatras, por lo tanto n2 3. Aplicando la regla de producto se obtienen N n1n2 12 posibles opciones. ■ En muchos problemas de conteo y probabilidad, se puede utilizar una configuración conoci- da como diagrama de árbol para representar pictóricamente todas las posibilidades. El dia- grama de árbol asociado con el ejemplo 2.18 aparece en la figura 2.7. Partiendo de un punto localizado en el lado izquierdo del diagrama, por cada posible primer elemento de un par emana un segmento de línea recta hacia la derecha. Cada una de estas líneas se conoce como 60 CAPÍTULO 2 Probabilidad PROPOSICIÓN Si el primer elemento u objeto de un par ordenado puede ser seleccionado de n1 ma- neras y por cada una de estas n1 maneras el segundo elemento del par puede ser se- leccionado de n2 maneras, entonces el número de pares es n1n2. Ejemplo 2.17 Ejemplo 2.18 c2_p046-085.qxd 3/12/08 3:58 AM Page 60
- 79. rama de primera generación. Ahora para cualquier rama de primera generación se constru- ye otro segmento de línea que emana de la punta de la rama por cada posible opción de un segundo elemento del par. Cada segmento de línea es una rama de segunda generación. Co- mo existen cuatro obstetras, existen cuatro ramas de primera generación y tres pediatras por cada obstetra se obtienen tres ramas de segunda generación que emanan de cada rama de primera generación. Generalizando, supóngase que existen n1 ramas de primera generación y por cada ra- ma de primera generación existen n2 ramas de segunda generación. El número total de ramas de segunda generación es entonces n1n2. Como el extremo de cada rama de segunda gene- ración corresponde a exactamente un posible par (la selección de un primer elemento y luego de un segundo nos sitúa en el extremo de exactamente una rama de segunda generación), existen n1n2 pares, lo que verifica la regla de producto. La construcción de un diagrama de árbol no depende de tener el mismo número de ra- mas de segunda generación que emanen de cada rama de primera generación. Si la segun- da clínica tenía cuatro pediatras, entonces habría sólo tres ramas que emanan de dos de las ramas de primera generación y cuatro que emanan de cada una de las otras dos ramas de pri- mera generación. Un diagrama de árbol puede ser utilizado por lo tanto para representar pic- tóricamente experimentos aparte de aquellos a los que se aplica la regla de producto. Una regla de producto más general Si se lanza al aire un dado de seis lados cinco veces en sucesión en lugar de sólo dos veces, entonces cada posible resultado es un conjunto ordenado de cinco números tal como (1, 3, 1, 2, 4) o (6, 5, 2, 2, 2). Un conjunto ordenado de k objetos recibirá el nombre de k-tupla (por tanto un par es un 2-tupla y un triple es un 3-tupla). Cada resultado del experimento del lanzamiento al aire de el dado es entonces un 5-tupla. 2.3 Técnicas de conteo 61 Regla de producto para k-tuplas Supóngase que un conjunto se compone de conjuntos ordenados de k elementos (k-tuplas) y que existen n1 posibles opciones para el primer elemento por cada opción del primer elemento, existen n2 posibles opciones del segundo elemento; . . . ; por cada posible opción de los primeros k 1 elementos, existen nk opciones del elemento k-ésimo. Existen entonces n1n2· · · · ·nk posibles k-tuplas. Figura 2.7 Diagrama de árbol para el ejemplo 2.18. O1 O2 O3 O4 P1 P2 P3 P1 P2 P3 P4 P5 P6 P4 P5 P6 c2_p046-085.qxd 3/12/08 3:59 AM Page 61
- 80. Esta regla más general también puede ser ilustrada por un diagrama de árbol; simple- mente se construye un diagrama más elaborado añadiendo una tercera generación de ramas que emanan de la punta de cada segunda generación, luego ramas de cuarta generación, y así sucesivamente, hasta que por último se agregan ramas de k-ésima generación. Suponga que el trabajo de remodelación de la casa implica adquirir primero varios utensi- lios de cocina. Se adquirirán en la misma tienda y hay cinco tiendas en el área. Con las tien- das denotadas por D1, . . . , D5, existen N n1n2n3 (5)(12)(9) 540 3 tuplas de la forma (Di, Pj, Qk), así que existen 540 formas de elegir primero una tienda, luego un contratista de fontanería y finalmente un contratista electricista. ■ Si cada clínica tiene dos especialistas en medicina interna y dos médicos generales, existen n1n2n3n4 (4)(3)(3)(2) 72 formas de seleccionar un doctor de cada tipo de tal suerte que todos los doctores practiquen en la misma clínica. ■ Permutaciones y combinaciones Considérese un grupo de n individuos u objetos distintos (“distintos” significa que existe al- guna característica que diferencia a cualquier individuo u objeto de cualquier otro). ¿Cuán- tas maneras existen de seleccionar un subconjunto de tamaño k del grupo? Por ejemplo, si un equipo de ligas menores tiene 15 jugadores registrados, ¿cuántas maneras existen de selec- cionar 9 jugadores para una alineación inicial? O si en su librero tiene 10 libros de misterio no leídos y desea seleccionar 3 para llevarlos consigo en unas vacaciones cortas, ¿cuántas ma- neras existen de hacerlo? Una respuesta a la pregunta general que se acaba de plantear requiere distinguir entre dos casos. En algunas situaciones, tal como el escenario del béisbol, el orden de la selección es importante. Por ejemplo, con Ángela como lanzador y Ben como receptor se obtiene una alineación diferente de aquella con Ángela como receptor y Ben como lanzador. A menudo, sin embargo, el orden no es importante y a nadie le interesa qué individuos u objetos sean seleccionados, como sería el caso en el escenario de selección de libros. El número de permutaciones se determina utilizando la primera regla de conteo para k-tuplas. Supóngase, por ejemplo, que un colegio de ingeniería tiene siete departamentos, denotados por a, b, c, d, e, f y g. Cada departamento tiene un representante en el consejo de estudiantes del colegio. De estos siete representantes, uno tiene que ser elegido como presiden- te, otro como vicepresidente y un tercero como secretario. ¿Cuántas maneras existen para se- leccionar los tres oficiales? Es decir, ¿cuántas permutaciones de tamaño 3 pueden ser formadas con los 7 representantes? Para responder esta pregunta, habrá que pensar en formar una tripleta (3-tupla) en la cual el primer elemento es el presidente, el segundo es el vicepresidente y el ter- cero es el secretario. Una tripleta es (a, g, b), otra es (b, g, a) y otra más es (d, f, b). Ahora bien el presidente puede ser seleccionado en cualesquiera de n1 7 formas. Por cada forma de se- leccionar el presidente, existen n2 6 formas de seleccionar el vicepresidente y por consiguien- te 7 6 42 (pares de presidente, vicepresidente). Por último, por cada forma de seleccionar un presidente y vicepresidente, existen n3 5 formas de seleccionar el secretario. Esto da P3,7 (7)(6)(5) 210 62 CAPÍTULO 2 Probabilidad Ejemplo 2.19 (continuación del ejemplo 2.17) Ejemplo 2.20 (continuación del ejemplo 2.18) DEFINICIÓN Un subconjunto ordenado se llama permutación. El número de permutaciones de ta- maño k que se puede formar con los n individuos u objetos en un grupo será denotado por Pk,n. Un subconjunto no ordenado se llama combinación. Una forma de denotar el número de combinaciones es Ck,n, pero en su lugar se utilizará una notación que es bas- tante común en libros de probabilidad: n k , que se lee “de n se eligen k”. B A c2_p046-085.qxd 3/12/08 3:59 AM Page 62
- 81. como el número de permutaciones de tamaño 3 que se pueden formar con 7 individuos dis- tintos. Una representación de diagrama de árbol mostraría tres generaciones de ramas. La expresión para P3,7 puede ser rescrita con la ayuda de notación factorial. Recuér- dese que 7! (se lee “factorial de 7”) es una notación compacta para el producto descenden- te de enteros (7)(6)(5)(4)(3)(2)(1). Más generalmente, para cualquier entero positivo m, m! m(m 1)(m 2)· · · · · (2)(1). Esto da 1! 1 y también se define 0! 1. Entonces Más generalmente . . . Multiplicando y dividiendo ésta por (n – k)! se obtiene una expresión compacta para el nú- mero de permutaciones. sn 2 sk 2 2ddsn 2 sk 2 1dd Pk,n 5 nsn 2 1dsn 2 2d P3,7 5 s7ds6ds5d 5 s7ds6ds5ds4!d s4!d 5 7! 4! Existen diez asistentes de profesor disponibles para calificar exámenes en un curso de cálculo en una gran universidad. El primer examen se compone de cuatro preguntas y el profesor desea seleccionar un asistente diferente para calificar cada pregunta (sólo un asis- tente por pregunta). ¿De cuántas maneras se pueden elegir los asistentes para calificar? En este caso n tamaño del grupo 10 y k tamaño del subconjunto 4. El número de per- mutaciones es Es decir, el profesor podría aplicar 5040 exámenes diferentes de cuatro preguntas sin utili- zar la misma asignación de calificadores a preguntas, ¡tiempo en el cual todos los asistentes seguramente habrán terminado sus programas de licenciatura! ■ Considérense ahora las combinaciones (es decir, subconjuntos ordenados). De nuevo habrá que remitirse al escenario de consejo estudiantil y supóngase que tres de los siete re- presentantes tienen que ser seleccionados para que asistan a una convención estatal. El or- den de selección no es importante; lo que importa es cuáles tres son seleccionados. Así que se busca (7 3), el número de combinaciones de 3 que se pueden formar con los 7 individuos. Considérese por un momento las combinaciones a, c, g. Estos tres individuos pueden ser or- denados en 3! 6 formas para producir el número de permutaciones: a,c,g a,g,c c,a,g c,g,a g,a,c g,c,a De manera similar, hay 3! 6 maneras para ordenar la combinación b, c, e para producir combinaciones y de hecho hay 3! modos para ordenar cualquier combinación particular de tamaño 3 para producir permutaciones. Esto implica la siguiente relación entre el número de combinaciones y el número de permutaciones. No sería difícil poner en lista las 35 combinaciones, pero no hay necesidad de hacerlo si só- lo interesa cuántas son. Obsérvese que el número 210 de permutaciones excede por mucho P3,7 5 s3!d ? Q 7 3 R 1 Q 7 3 R 5 P3,7 3! 5 7! s3!ds4!d 5 s7ds6ds5d s3ds2ds1d 5 35 P4,10 5 10! s10 2 4d! 5 10! 6! 5 10s9ds8ds7d 5 5040 2.3 Técnicas de conteo 63 Ejemplo 2.21 PROPOSICIÓN Pk,n 5 n! sn 2 kd! c2_p046-085.qxd 3/12/08 3:59 AM Page 63
- 82. el número de combinaciones; el segundo es más grande que el primero por un factor de 3! puesto que así es como cada combinación puede ser ordenada. Generalizando la línea de razonamiento anterior se obtiene una relación simple entre el número de permutaciones y el número de combinaciones que produce una expresión con- cisa para la última cantidad. Nótese que (n n) 1 y (n 0) 1 puesto que hay sólo una forma de seleccionar un conjunto de (todos) n elementos o de ningún elemento y (n 1) n puesto que existen n subconjun- tos de tamaño 1. Una mano de bridge se compone de 13 cartas seleccionadas de entre un mazo de 52 cartas sin importar el orden. Existen (5 1 2 3) 52!/13!39! manos de bridge diferentes, lo que asciende a aproximadamente 635 000 millones. Como existen 13 cartas de cada palo, el número de ma- nos compuestas por completo de tréboles y/o espadas (nada de cartas rojas) es (2 1 6 3) 26!/13!13! 10400600. Una de estas manos (2 1 6 3)se compone por completo de espadas y una se compone por completo de tréboles, por lo tanto existen [(2 1 6 3) 2] manos compuestas por completo de tréboles y espadas con ambos palos representados en la mano. Supóngase que una mano de bridge repartida de un mazo bien barajado (es decir, 13 cartas se seleccionan al azar de entre 52 posibilidades) y si A {la mano se compone por completo de espadas y tréboles con ambos palos re- presentados} B {la mano se compone de exactamente dos palos} Los N (5 1 2 3) posibles resultados son igualmente probables, por lo tanto P(A) 0.0000164 Como existen (4 2) 6 combinaciones compuestas de dos palos, de las cuales espadas y tré- boles es una de esas combinaciones, P(B) 0.0000983 Es decir, una mano compuesta por completo de cartas de exactamente dos de los cuatro pa- los ocurrirá aproximadamente una vez por cada 100 000 manos. Si juega bridge sólo una vez al mes, es probable que nunca le repartan semejante mano. ■ El almacén de una universidad recibió 25 impresoras, de las cuales 10 son impresoras láser y 15 son modelos de inyección de tinta. Si 6 de estas 25 se seleccionan al azar para que las revise un técnico particular, ¿cuál es la probabilidad de que exactamente 3 de las seleccio- nadas sean impresoras láser (de modo que las otras 3 sean de inyección de tinta)? Sea D3 {exactamente 3 de las 6 seleccionadas son impresoras de inyección de tin- ta}. Suponiendo que cualquier conjunto particular de 6 impresoras es tan probable de ser ele- gido como cualquier otro conjunto de 6, se tienen resultados igualmente probables, por lo tanto P(D3) N(D3)/N, donde N es el número de formas de elegir 6 impresoras de entre las 25 y N(D3) es el número de formas de elegir 3 impresoras láser y 3 de inyección de tinta. Por lo tanto N (2 6 5 ). Para obtener N(D3), primero se piensa en elegir 3 de las 15 impresoras de inyección de tinta y luego 3 de las impresoras láser. Existen (1 3 5 ) formas de elegir las 3 im- presoras de inyección de tinta y (1 3 0 ) formas de elegir las 3 impresoras láser; N(D3) es ahora 6 2 1 6 3 2 5 1 2 3 2 1 6 3 2 5 1 2 3 N(A) N 64 CAPÍTULO 2 Probabilidad PROPOSICIÓN n! k!(n k)! Pk,n k! n k Ejemplo 2.22 Ejemplo 2.23 c2_p046-085.qxd 3/12/08 3:59 AM Page 64
- 83. el producto de estos dos números (visualícese un diagrama de árbol, en realidad aquí se está utilizando el argumento de la regla de producto), por lo tanto P(D3) 0.3083 Sea D4 {exactamente 4 de las 6 impresoras seleccionadas son impresoras de inyección de tinta} y defínanse D5 y D6 del mismo modo. Entonces la probabilidad de seleccionar por lo menos 3 impresoras de inyección de tinta es P(D3 D4 D5 D6) P(D3) P(D4) P(D5) P(D6) 0.8530 ■ 1 6 5 1 0 0 2 6 5 1 5 5 1 1 0 2 6 5 1 4 5 1 2 0 2 6 5 1 3 5 1 3 0 2 6 5 3 1 !1 5 2 ! ! 3 1 ! 0 7 ! ! 6 2 !1 5 9 ! ! 1 3 5 1 3 0 2 6 5 N(D3) N 2.3 Técnicas de conteo 65 29. Con fecha de abril de 2006, aproximadamente 50 millones de nombres de dominio web.com fueron registrados (p. ej., yahoo.com). a. ¿Cuántos nombres de dominio compuestos de exacta- mente dos letras pueden ser formados? ¿Cuántos nom- bres de dominio de dos letras existen si como caracteres se permiten dígitos y números? [Nota: Una longitud de carácter de tres o más ahora es obligatoria.] b. ¿Cuántos nombres de dominio existen compuestos de tres letras en secuencia? ¿Cuántos de esta longitud exis- ten si se permiten letras o dígitos? [Nota: En la actuali- dad todos están utilizados.] c. Responda las preguntas hechas en b) para secuencias de cuatro caracteres. d. Con fecha de abril de 2006, 97 786 de las secuencias de cuatro caracteres utilizando letras o dígitos aún no ha- bían sido reclamadas. Si se elige un nombre de cuatro caracteres al azar, ¿cuál es la probabilidad de que ya ten- ga dueño? 30. Un amigo mío va a ofrecer una fiesta. Sus existencias actua- les de vino incluyen 8 botellas de zinfandel, 10 de merlot y 12 de cabernet (él sólo bebe vino tinto), todos de diferentes fábricas vinícolas. a. Si desea servir 3 botellas de zinfandel y el orden de servi- cio es importante, ¿cuántas formas existen de hacerlo? b. Si 6 botellas de vino tienen que ser seleccionadas al azar de las 30 para servirse, ¿cuántas formas existen de ha- cerlo? c. Si se seleccionan al azar 6 botellas, ¿cuántas formas existen de obtener dos botellas de cada variedad? d. Si se seleccionan 6 botellas al azar, ¿cuál es la probabili- dad de que el resultado sea dos botellas de cada variedad? e. Si se eligen 6 botellas al azar, ¿cuál es la probabilidad de que todas ellas sean de la misma variedad. 31. a. Beethoven escribió 9 sinfonías y Mozart 27 conciertos para piano. Si el locutor de una estación de radio de una universidad desea tocar primero una sinfonía de Beetho- ven y luego un concierto de Mozart, ¿de cuántas mane- ras puede hacerlo? b. El gerente de la estación decide que en cada noche sucesi- va (7 días a la semana), se tocará una sinfonía de Beetho- ven, seguida por un concierto para piano de Mozart, seguido por un cuarteto de cuerdas de Schubert (de los cuales existen 15). ¿Durante aproximadamente cuántos años se podría continuar con esta política antes de que exactamente el mismo programa se repitiera? 32. Una tienda de equipos de sonido está ofreciendo un precio especial en un juego completo de componentes (receptor, reproductor de discos compactos, altavoces, casetera). Al comprador se le ofrece una opción de fabricante por ca- da componente. Receptor: Kenwood, Onkyo, Pioneer, Sony, Sherwood Reproductor de discos compactos: Onkyo, Pioneer, Sony, Technics Altavoces: Boston, Infinity, Polk Casetera: Onkyo, Sony, Teac, Technics Un tablero de distribución en la tienda permite al cliente co- nectar cualquier selección de componentes (compuesta de uno de cada tipo). Use las reglas de producto para respon- der las siguientes preguntas. a. ¿De cuántas maneras puede ser seleccionado un compo- nente de cada tipo? b. ¿De cuántas maneras pueden ser seleccionados los com- ponentes si tanto el receptor como el reproductor de dis- cos compactos tienen que ser Sony? EJERCICIOS Sección 2.3 (29-44) c2_p046-085.qxd 3/12/08 3:59 AM Page 65
- 84. 66 CAPÍTULO 2 Probabilidad c. ¿De cuántas maneras pueden ser seleccionados los com- ponentes si ninguno tiene que ser Sony? d. ¿De cuántas maneras se puede hacer una selección si por lo menos se tiene que incluir un componente Sony? e. Si alguien mueve los interruptores en el tablero de distri- bución completamente al azar, ¿cuál es la probabilidad de que el sistema seleccionado contenga por lo menos un componente Sony? ¿Exactamente un componente Sony? 33. De nuevo considere el equipo de ligas menores que tiene 15 jugadores en su plantel. a. ¿Cuántas formas existen de seleccionar 9 jugadores pa- ra la alineación inicial? b. ¿Cuántas formas existen de seleccionar 9 jugadores para la alineación inicial y un orden al bat de los 9 inicialistas? c. Suponga que 5 de los 15 jugadores son zurdos. ¿Cuántas formas existen de seleccionar 3 jardineros zurdos y tener las otras 6 posiciones ocupadas por jugadores derechos? 34. Poco tiempo después de ser puestos en servicio, algunos au- tobuses fabricados por una cierta compañía presentaron grietas debajo del chasis principal. Suponga que una ciudad particular utiliza 25 de estos autobuses y que en 8 de ellos aparecieron grietas. a. ¿Cuántas maneras existen de seleccionar una muestra de 5 autobuses de entre los 25 para una inspección completa? b. ¿De cuántas maneras puede una muestra de 5 autobuses contener exactamente 4 con grietas visibles? c. Si se elige una muestra de 5 autobuses al azar, ¿cuál es la probabilidad de que exactamente 4 de los 5 tengan grietas visibles? d. Si los autobuses se seleccionan como en el inciso c), ¿cuál es la probabilidad de que por lo menos 4 de los seleccionados tengan grietas visibles? 35. Una empresa de producción emplea 20 trabajadores en el turno de día, 15 en el turno de tarde y 10 en el turno de me- dianoche. Un consultor de control de calidad va a seleccionar 6 de estos trabajadores para entrevistas a fondo. Suponga que la selección se hace de tal modo que cualquier grupo particular de 6 trabajadores tiene la misma oportunidad de ser seleccionado al igual que cualquier otro grupo (sacando 6 papelitos de entre 45 sin reemplazarlos). a. ¿Cuántas selecciones resultarán en que los 6 trabajado- res seleccionados provengan del turno de día? b. ¿Cuál es la probabilidad de que los 6 trabajadores selec- cionados sean del mismo turno? c. ¿Cuál es la probabilidad de que por lo menos dos turnos diferentes estarán representados entre los trabajadores seleccionados? d. ¿Cuál es la probabilidad de que por lo menos uno de los turnos no estará representado en la muestra de tra- bajadores? 36. Un departamento académico compuesto de cinco profeso- res limitó su opción para jefe de departamento a el candida- to A o el candidato B. Cada miembro votó entonces con un papelito por uno de los candidatos. Suponga que en realidad existen tres votos para A y dos para B. Si los papelitos se cuentan al azar, ¿cuál es la probabilidad de que A perma- nezca delante de B durante todo el conteo de votos (p. ej. ¿ocurre este evento si el orden seleccionado es AABAB pe- ro no si es ABBAA)? 37. Un experimentador está estudiando los efectos de la tempe- ratura, la presión y el tipo de catalizador en la producción de cierta reacción química. Tres diferentes temperaturas, cuatro presiones distintas y cinco catalizadores diferentes se están considerando. a. Si cualquier experimento particular implica utilizar una temperatura, una presión y un catalizador, ¿cuántos ex- perimentos son posibles? b. ¿Cuántos experimentos existen que impliquen el uso de la temperatura más baja y dos presiones bajas? c. Suponga que se tienen que realizar cinco experimentos diferentes el primer día de experimentación. Si los cin- co se eligen al azar de entre todas las posibilidades, de modo que cualquier grupo de cinco tenga la misma pro- babilidad de selección, ¿cuál es la probabilidad de que se utilice un catalizador diferente en cada experimento? 38. Una caja en un almacén contiene cuatro focos de 40 W, cin- co de 60 W y seis de 75 W. Suponga que se eligen al azar tres focos. a. ¿Cuál es la probabilidad de que exactamente dos de los focos seleccionados sean de 75 W? b. ¿Cuál es la probabilidad de que los tres focos seleccio- nados sean de los mismos watts? c. ¿Cuál es la probabilidad de que se seleccione un foco de cada tipo? d. Suponga ahora que los focos tienen que ser selecciona- dos uno por uno hasta encontrar uno de 75 W. ¿Cuál es la probabilidad de que sea necesario examinar por lo menos seis focos? 39. Quince teléfonos acaban de llegar a un centro de servicio autorizado. Cinco de éstos son celulares, cinco inalámbri- cos y los otros cincos alámbricos. Suponga que a estos com- ponentes se les asignan al azar los números 1, 2, . . . , 15 para establecer el orden en que serán reparados. a. ¿Cuál es la probabilidad de que los teléfonos inalámbri- cos estén entre los primeros diez que van a ser reparados? b. ¿Cuál es la probabilidad de que después de reparar diez de estos teléfonos, sólo dos de los tres tipos de teléfonos queden para ser reparados? c. ¿Cuál es la probabilidad que dos teléfonos de cada tipo estén entre los primeros seis reparados? 40. Tres moléculas de tipo A, tres de tipo B, tres de tipo C y tres de tipo D tienen que ser unidas para formar una cadena mo- lecular. Una cadena molecular como esa es ABCDABC- DABCD y otra es BCDDAAABDBCC. a. ¿Cuántas moléculas en cadena hay? [Sugerencia: si se pudieran distinguir entre sí las tres letras A, A1, A2, A3, y también las letras B, C y D, ¿cuántas moléculas del tipo habría? ¿Cómo se reduce este número cuando se elimi- nan de las letras A los subíndices? b. Suponga que se elige al azar una molécula del tipo des- crito. ¿Cuál es la probabilidad de que las tres molécu- las de cada tipo terminen una junto a la otra (como en BBBAAADDDCCC)? 41. Una profesora de matemáticas desea programar una cita con cada uno de sus ochos asistentes, cuatro hombres y cua- tro mujeres, para discutir su curso de cálculo. Suponga que todos los posibles ordena mientos de citas tienen la misma probabilidad de ser seleccionados. c2_p046-085.qxd 3/12/08 3:59 AM Page 66
- 85. Las probabilidades asignadas a varios eventos dependen de lo que se sabe sobre la situación experimental cuando se hace la asignación. Subsiguiente a la asignación inicial puede lle- gar a estar disponible información parcial pertinente al resultado del experimento. Tal infor- mación puede hacer que se revisen algunas de las asignaciones de probabilidad. Para un evento particular A, se ha utilizado P(A) para representar la probabilidad asignada a A; aho- ra se considera P(A) como la probabilidad original no condicional del evento A. En esta sección, se examina cómo afecta la información de que “un evento B ha ocu- rrido” a la probabilidad asignada a A. Por ejemplo, A podría referirse a un individuo que su- fre una enfermedad particular en la presencia de ciertos síntomas. Si se realiza un examen de sangre en el individuo y el resultado es negativo (B examen de sangre negativo), en- tonces la probabilidad de que tenga la enfermedad cambiará (deberá reducirse, pero no a ce- ro, puesto que los exámenes de sangre no son infalibles). Se utilizará la notación P(A | B) para representar la probabilidad condicional de A dado que el evento B haya ocurrido. B es el “evento condicionante”. Por ejemplo, considérese el evento A en que un estudiante seleccionado al azar en su universidad obtuvo todas las clases deseadas durante el ciclo de inscripciones del semestre anterior. Presumiblemente P(A) no es muy grande. Sin embargo, supóngase que el estudian- te seleccionado es un atleta con prioridad de inscripción especial (el evento B). Entonces P(A | B) deberá ser sustancialmente más grande que P(A), aunque quizá aún no cerca de 1. En una planta se ensamblan componentes complejos en dos líneas de ensamble diferentes, A y A. La línea A utiliza equipo más viejo que A, por lo que es un poco más lenta y me- nos confiable. Suponga que en un día dado la línea A ensambla 8 componentes, de los cua- les 2 han sido identificados como defectuosos (B) y 6 como no defectuosos (B), mientras que A ha producido 1 componente defectuoso y 9 no defectuosos. Esta información se re- sume en la tabla adjunta. Ajeno a esta información, el gerente de ventas selecciona al azar 1 de estos 18 componen- tes para una demostración. Antes de la demostración 2.4 Probabilidad condicional 67 a. ¿Cuál es la probabilidad de que por lo menos una mujer asistente quede entre los primeros tres con quien la pro- fesora se reúna? b. ¿Cuál es la probabilidad de que después de las primeras cinco citas se haya reunido con todas las asistentes mu- jeres? c. Suponga que la profesora tiene los mismos ocho asisten- tes el siguiente semestre y de nuevo programa citas sin importar el orden que hubo durante el primer semestre. ¿Cuál es la probabilidad de que los ordenamientos de las citas sean diferentes? 42. Tres parejas de casados compraron boletos para el teatro y están sentados en una fila compuesta de sólo seis asientos. Si ocupan sus asientos de un modo completamente al azar (orden aleatorio), ¿cuál es la probabilidad de que Jim y Paula (esposo y esposa) se sienten en los dos asientos extremos del lado izquierdo? ¿Cuál es la probabilidad de que Jim y Paula terminen sentándose uno junto al otro? ¿Cuál es la probabilidad de que por lo menos dos de las esposas termi- nen sentándose al lado de su esposo? 43. En un juego de póker de cinco cartas, una escalera se com- pone de cinco cartas con denominaciones adyacentes (p. ej. 9 de tréboles, 10 de corazones, joto de corazones, reina de espadas y rey de tréboles). Suponiendo que los ases pue- den estar arriba o abajo, si le reparten una mano de cinco cartas, ¿cuál es la probabilidad que será una escalera con un 10 como carta alta? ¿Cuál es la probabilidad de que sea una escalera del mismo palo? 44. Demuestre que (n k) (n n k). Dé una interpretación que im- plique subconjuntos. 2.4 Probabilidad condicional Condición B B A 2 6 Línea A 1 9 Ejemplo 2.24 c2_p046-085.qxd 3/12/08 3:59 AM Page 67
- 86. P(componente de la línea A seleccionado) P(A) 0.44 No obstante, si el componente seleccionado resulta defectuoso, entonces el evento B ha ocu- rrido, por lo que el componente debe haber sido 1 de los 3 de la columna B de la tabla. Co- mo estos 3 componentes son igualmente probables entre ellos mismos una vez que B ha ocurrido, P(A°B) 2 3 (2.2) ■ En la ecuación (2.2), la probabilidad condicional está expresada como una razón de probabilidades incondicionales. El numerador es la probabilidad de la intersección de los dos eventos, en tanto que el denominador es la probabilidad del evento condicionante B. Un diagrama de Venn ilustra esta relación (figura 2.8). P(A B) P(B) 1 2 8 1 3 8 8 18 N(A) N Dado que B ha ocurrido, el espacio muestral pertinente ya no es S pero consta de re- sultados en B; A ha ocurrido si y sólo si uno de los resultados en la intersección ocurrió, así que la probabilidad condicional de A dado B es proporcional a P(A B). Se utiliza la cons- tante de proporcionalidad 1/P(B) para garantizar que la probabilidad P(B | B) del nuevo es- pacio muestral B sea igual a 1. Definición de probabilidad condicional El ejemplo 2.24 demuestra que cuando los resultados son igualmente probables, el cálculo de probabilidades condicionales puede basarse en intuición. Cuando los experimentos son más complicados, la intuición puede fallar, así que se requiere una definición general de pro- babilidad condicional que dé respuestas intuitivas en problemas simples. El diagrama de Venn y la ecuación (2.2) sugieren cómo proceder. Supóngase que de todos los individuos que compran cierta cámara digital, 60% incluye una tarjeta de memoria opcional en su compra, 40% incluyen una batería extra y 30% inclu- yen tanto una tarjeta como una batería. Considere seleccionar al azar un comprador y sea A {tarjeta de memoria adquirida} y B {batería adquirida}. Entonces P(A) 0.60, P(B) 0.40 y P(ambas adquiridas) P(A B) 0.30. Dado que el individuo seleccionado adquirió una batería extra, la probabilidad de que una tarjeta opcional también sea adquirida es P(A°B) 0.75 0.30 0.40 P(A B) P(B) 68 CAPÍTULO 2 Probabilidad Figura 2.8 Motivación para la definición de probabilidad condicional. A B DEFINICIÓN Para dos eventos cualesquiera A y B con P(B) 0, la probabilidad condicional de A dado que B ha ocurrido está definida por P(A°B) (2.3) P(A B) P(B) Ejemplo 2.25 c2_p046-085.qxd 3/12/08 3:59 AM Page 68
- 87. Es decir, de todos los que adquieren una batería extra, 75% adquirieron una tarjeta de me- moria opcional. Asimismo, P(batería | tarjeta de memoria) P(B°A) 0.50 Obsérvese que P(A | B) P(A) y P(B | A) P(B). ■ El evento cuya probabilidad se desea podría ser una unión o intersección de otros eventos y lo mismo podría ser cierto del evento condicionante. Una revista de noticias publica tres columnas tituladas “Arte” (A), “Libros” (B) y “Cine” (C). Los hábitos de lectura de un lector seleccionado al azar con respecto a estas columnas son Lee con regularidad A B C A B A C B C A B C Probabilidad 0.14 0.23 0.37 0.08 0.09 0.13 0.05 La figura 2.9 ilustra las probabilidades pertinentes. 0.30 0.60 P(A B) P(A) Por lo tanto se tiene P(A°B) 0.348 P(A°B C) 0.255 P(A°lee por lo menos una) P(A°A B C) 0.286 y P(A B°C) 0.459 ■ Regla de multiplicación para P(A B) La definición de probabilidad condicional da el siguiente resultado, obtenido multiplicando ambos miembros de la ecuación (2.3) por P(B). 0.04 0.05 0.08 0.37 P((A B) C) P(C) 0.14 0.49 P(A) P(A B C) P(A (A B C)) P(A B C) 0.12 0.47 0.04 0.05 0.03 0.47 P(A (B C)) P(B C) 0.08 0.23 P(A B) P(B) 2.4 Probabilidad condicional 69 Figura 2.9 Diagrama de Venn para el ejemplo 2.26. 0.02 0.03 0.07 0.05 0.04 0.08 0.20 0.51 A B C La regla de multiplicación P(A B) P(A°B) P(B) Ejemplo 2.26 c2_p046-085.qxd 3/12/08 3:59 AM Page 69
- 88. Esta regla es importante porque a menudo se desea obtener P(A B), en tanto que P(B) y P(A | B) pueden ser especificadas a partir de la descripción del problema. La consi- deración de P(B | A) da P(A B) = P(B | A) P(A). Cuatro individuos han respondido a una solicitud de un banco de sangre para donaciones de sangre. Ninguno de ellos ha donado antes, por lo que sus tipos de sangre son desconocidos. Suponga que sólo se desea el tipo O y sólo uno de los cuatro tiene ese tipo. Si los dona- dores potenciales se seleccionan en orden aleatorio para determinar su tipo de sangre, ¿cuál es la probabilidad de que por los menos tres individuos tengan que ser examinados para de- terminar su tipo de sangre y obtener el tipo deseado? Haciendo la identificación B {primer tipo no O} y A {segundo tipo no O}, P(B) 3 4. Dado que el primer tipo no es O, dos de los tres individuos que quedan no son O, por lo tanto P(A°B) 2 3. La regla de multiplicación ahora da P(por lo menos tres individuos fueron examinados para determinar su tipo de sangre) P(A B) P(A°B) P(B) 0.5 ■ La regla de multiplicación es más útil cuando los experimentos se componen de va- rias etapas en sucesión. El evento condicionante B describe entonces el resultado de la pri- mera etapa y A el resultado de la segunda, de modo que P(A | B), condicionada en lo que ocurra primero, a menudo será conocida. La regla es fácil de ser ampliada a experimentos que implican más de dos etapas. Por ejemplo, P(A1 A2 A3) P(A3°A1 A2) P(A1 A2) P(A3°A1 A2) P(A2°A1) P(A1) (2.4) donde A1 ocurre primero, seguido por A2 y finalmente A3. Para el experimento de determinación de tipo de sangre del ejemplo 2.27, P(el tercer tipo es O) P(el tercero es | el primero no es el segundo no es) P(el segundo no es | el primero no es) P(el primero no es) 0.25 ■ Cuando el experimento de interés se compone de una secuencia de varias etapas, es conveniente representarlas con diagrama de árbol. Una vez que se tiene un diagrama de ár- bol apropiado, las probabilidades y las probabilidades condicionales pueden ser ingresadas en las diversas ramas; esto implicará el uso repetido de la regla de multiplicación. Una cadena de tiendas de video vende tres marcas diferentes de reproductores de DVD. De sus ventas de reproductores de DVD, 50% son de la marca 1 (la menos cara), 30% son de la marca 2 y 20% son de la marca 3. Cada fabricante ofrece 1 año de garantía en las partes y mano de obra. Se sabe que 25% de los reproductores de DVD de la marca 1 requieren tra- bajo de reparación dentro del periodo de garantía, mientras que los porcentajes correspon- dientes de las marcas 2 y 3 son 20% y 10%, respectivamente. 1. ¿Cuál es la probabilidad de que un comprador seleccionado al azar haya adquirido un repro- ductor de DVD marca 1 que necesitará reparación mientras se encuentra dentro de garantía? 2. ¿Cuál es la probabilidad de que un comprador seleccionado al azar haya comprado un re- productor de DVD que necesitará reparación mientras se encuentra dentro de garantía. 3. Si un cliente regresa a la tienda con un reproductor de DVD que necesita reparación den- tro de garantía, ¿cuál es la probabilidad de que sea un reproductor de DVD marca 1? ¿Un reproductor de DVD marca 2? ¿Un reproductor de DVD marca 3? 1 4 3 4 2 3 1 2 6 12 3 4 2 3 70 CAPÍTULO 2 Probabilidad Ejemplo 2.27 Ejemplo 2.28 Ejemplo 2.29 c2_p046-085.qxd 3/12/08 3:59 AM Page 70
- 89. La primera etapa del problema implica un cliente que selecciona una de las tres mar- cas de reproductor de DVD. Sea Ai {marca i adquirida}, con i 1, 2 y 3. Entonces P(A1 0.50, P(A2) 0.30 y P(A3) 0.20. Una vez que se selecciona una marca de reproductor de DVD, la segunda etapa implica observar si el reproductor de DVD seleccionado necesita reparación dentro de garantía. Con B {necesita reparación} y B {no necesita repara- ción}, la información dada implica que P(B | A1) 0.25, P(B | A2) 0.20 y P(B | A3) 0.10. El diagrama de árbol que representa esta situación experimental se muestra en la fi- gura 2.10. Las ramas iniciales corresponden a marcas diferentes de reproductores de DVD; hay dos ramas de segunda generación que emanan de la punta de cada rama inicial, una pa- ra “necesita reparación” y la otra para “no necesita reparación”. La probabilidad de que P(Ai) aparezca en la rama i-ésima inicial, en tanto que las probabilidades condicionales P(B | Ai) y P(B | Ai) aparecen en las ramas de segunda generación. A la derecha de cada ra- ma de segunda generación correspondiente a la ocurrencia de B, se muestra el producto de probabilidades en las ramas que conducen hacia fuera de dicho punto. Ésta es simplemente la regla de multiplicación en acción. La respuesta a la pregunta planteada en 1 es por lo tan- to P(A1 B) P(B°A1) P(A1) 0.125. La respuesta a la pregunta 2 es P(B) P[(marca 1 y reparación) o (marca 2 y reparación) o (marca 3 y reparación)] P(A1 B) P(A2 B) P(A3 B) 0.125 0.060 0.020 0.205 Finalmente, P(A1°B) 0.61 P(A2°B) 0.29 y P(A3°B) 1 P(A1°B) P(A2°B) 0.10 0.060 0.205 P(A2 B) P(B) 0.125 0.205 P(A1 B) P(B) 2.4 Probabilidad condicional 71 Figura 2.10 Diagrama de árbol para el ejemplo 2.29. Marca 2 M arca 1 M arca 3 P(A 3 ) 0.20 P(A1 ) 0.50 P(A2) 0.30 P(B A2) 0.20 Reparación P(B' A2) 0.80 Ninguna reparación P(B A3) 0.10 Reparación P(B' A3) 0.90 Ninguna reparación P(B' A1) 0.75 Ninguna reparación P(B A1) 0.25 Reparación P(B A3) P(A3) P(B A3) 0.020 P(B A2) P(A2) P(B A2) 0.060 P(B A1) P(A1) P(B A1) 0.125 P(B) 0.205 c2_p046-085.qxd 3/12/08 3:59 AM Page 71
- 90. La probabilidad previa o inicial de la marca 1 es 0.50. Una vez que se sabe que el repro- ductor de DVD seleccionado necesitaba reparación, la probabilidad posterior de la marca 1 se incrementa a 0.61. Esto se debe a que es más probable que los reproductores de DVD marca 1 necesiten reparación de garantía que las demás marcas. La probabilidad posterior de la marca 3 es P(A3 | B) 0.10, la cual es mucho menor que la probabilidad previa P(A3) 0.20. ■ Teorema de Bayes El cálculo de una probabilidad posterior P(Aj | B) a partir de probabilidades previas dadas P(Ai) y probabilidades condicionales P(B | Ai) ocupa una posición central en la probabilidad elemental. La regla general de dichos cálculos, los que en realidad son una aplicación sim- ple de la regla de multiplicación, se remonta al reverendo Thomas Bayes, quien vivió en el siglo XVIII. Para formularla primero se requiere otro resultado. Recuérdese que los eventos A1, . . . , Ak son mutuamente excluyentes si ninguno de los dos tiene resultados comunes. Los eventos son exhaustivos si un Ai debe ocurrir, de modo que A1 Ak S. Comprobación Como los eventos Ai son mutuamente excluyentes y exhaustivos, si B ocu- rre debe ser en forma conjunta con uno de los eventos Ai de manera exacta. Es decir, B (A1 B) . . . (Ak B), donde los eventos (Ai B) son mutuamente excluyentes. Esta “partición de B” se ilustra en la figura 2.11. Por lo tanto P(B) k i1 P(Ai B) k i1 P(B°Ai)P(Ai) como se deseaba. Un ejemplo del uso de la ecuación (2.5) apareció al responder la pregunta 2 del ejemplo 2.29, donde A1 {marca 1}, A2 {marca 2}, A3 {marca 3} y B {repa- ración}. 72 CAPÍTULO 2 Probabilidad Ley de probabilidad total Sean A1, . . . , Ak eventos mutuamente excluyentes y exhaustivos. Entonces para cual- quier otro evento B, P(B) P(B°A1)P(A1) . . . P(B°Ak)P(Ak) (2.5) k i1 P(B°Ai)P(Ai) Figura 2.11 División de B entre Ai’ mutuamente excluyentes y exhaustivas. ■ A1 A2 A3 B A4 c2_p046-085.qxd 3/12/08 3:59 AM Page 72
- 91. La transición de la segunda a la tercera expresión en (2.6) se apoya en el uso de la re- gla de multiplicación en el numerador y la ley de probabilidad total en el denominador. La proliferación de eventos y subíndices en (2.6) puede ser un poco intimidante para los recién llegados a la probabilidad. Mientras existan relativamente pocos eventos en la repartición, se puede utilizar un diagrama de árbol (como en el ejemplo 2.29) como base para calcular probabilidades posteriores sin jamás referirse de manera explícita al teorema de Bayes. Incidencia de una enfermedad rara. Sólo 1 de 1000 adultos padece una enfermedad rara pa- ra la cual se ha creado una prueba de diagnóstico. La prueba es tal que cuando un individuo que en realidad tiene la enfermedad, un resultado positivo se presentará en 99% de las ve- ces mientras que en individuos sin enfermedad el examen será positivo sólo en un 2% de las veces. Si se somete a prueba un individuo seleccionado al azar y el resultado es positivo, ¿cuál es la probabilidad de que el individuo tenga la enfermedad? Para utilizar el teorema de Bayes, sea A1 {el individuo tiene la enfermedad}, A2 {el individuo no tiene la enfermedad} y B {resultado de prueba positivo}. Entonces P(A1) 0.001, P(A2) 0.999, P(B | A1) 0.99 y P(B | A2) 0.02. El diagrama de árbol para este problema aparece en la figura 2.12. Junto a cada rama correspondiente a un resultado positivo de prueba, la regla de mul- tiplicación da las probabilidades anotadas. Por consiguiente, P(B) 0.00099 0.01998 0.02097, a partir de la cual se tiene P(A1°B) 0.047 Este resultado parece contraintuitivo; la prueba de diagnóstico parece tan precisa que es al- tamente probable que alguien con un resultado positivo de prueba tenga la enfermedad, mien- tras que la probabilidad condicional calculada es de sólo 0.047. Sin embargo, como la enfermedad es rara y la prueba es sólo moderadamente confiable, surgen más resultados 0.00099 0.02097 P(A1 B) P(B) 2.4 Probabilidad condicional 73 Teorema de Bayes Sean A1, A2, . . . , Ak un conjunto de eventos mutuamente excluyentes y exhaustivos con probabilidades previas P(Ai)(i 1, . . . , k). Entonces para cualquier otro evento B para el cual P(B) 0, la probabilidad posterior de Aj dado que B ha ocurrido es P(Aj°B) j 1, . . . , k (2.6) P(B°Aj)P(Aj) k i1 P(B°Ai) P(Ai) P(Aj B) P(B) Figura 2.12 Diagrama de árbol para el problema de la enfermedad rara. A2 no tiene la enfermedad A1 tiene la enfermedad 0.001 0.999 0.02 B Prueba 0.98 B' Prueba 0.01 B' Prueba 0.99 B Prueba P(A1 B) 0.00099 P(A2 B) 0.01998 Ejemplo 2.30 c2_p046-085.qxd 3/12/08 3:59 AM Page 73
- 92. positivos de prueba a causa de errores y no de individuos enfermos. La probabilidad de tener la enfermedad se ha incrementado por un factor de multiplicación de 47 (desde la probabili- dad previa de 0.001 hasta la probabilidad posterior de 0.047); pero para incrementar aún más la probabilidad posterior, se requiere una prueba de diagnóstico con tasas de error mucho más pequeñas. Si la enfermedad no fuera tan rara (p. ej., 25% de incidencia en la población), entonces las tasas de error de la prueba actual proporcionaría buenos diagnósticos. ■ 74 CAPÍTULO 2 Probabilidad 45. La población de un país particular se compone de tres gru- pos étnicos. Cada individuo pertenece a uno de los cuatro grupos sanguíneos principales. La tabla de probabilidad conjunta anexa da la proporción de individuos en las diver- sas combinaciones de grupo étnico-grupo sanguíneo. Suponga que se selecciona un individuo al azar de la pobla- ción y que los eventos se definen como A {tipo A seleccio- nado}, B {tipo B seleccionado} y C {grupo étnico 3 seleccionado}. a. Calcule P(A), P(C ) y P(A C). b. Calcule tanto P(A | C) y P(C | A) y explique en contex- to lo que cada una de estas probabilidades representa. c. Si el individuo seleccionado no tiene sangre de tipo B, ¿cuál es la probabilidad de que él o ella pertenezca al grupo étnico 1? 46. Suponga que un individuo es seleccionado al azar de la po- blación de todos los adultos varones que viven en Estados Unidos. Sea A el evento en que el individuo seleccionado tiene una estatura de más de 6 pies y sea B el evento en que el individuo seleccionado es un jugador profesional de básquetbol. ¿Cuál piensa que es más grande, P(A | B) o P(B | A)? ¿Por qué? 47. Regrese al escenario de la tarjeta de crédito del ejercicio 12 (sección 2.2), donde A {Visa}, B {MasterCard}, P(A) 0.5, P(B) 0.4 y P(A B) 0.25. Calcule e interprete ca- da una de las siguientes probabilidades (un diagrama de Venn podría ayudar). a. P(B°A) b. P(B°A) c. P(A°B) d. P(A°B) e. Dado que el individuo seleccionado tiene por lo menos una tarjeta, ¿cuál es la probabilidad de que él o ella ten- ga una tarjeta Visa? 48. Reconsidere la situación del sistema defectuoso descrito en el ejercicio 26 (sección 2.2). a. Dado que el sistema tiene un defecto de tipo 1, ¿cuál es la probabilidad de que tenga un defecto de tipo 2? b. Dado que el sistema tiene un defecto de tipo 1, ¿cuál es la probabilidad de que tenga los tres tipos de defectos? c. Dado que el sistema tiene por lo menos un tipo de defec- to, ¿cuál es la probabilidad de que tenga exactamente un tipo de defecto? d. Dado que el sistema tiene los primeros dos tipos de defectos, ¿cuál es la probabilidad de que no tenga el ter- cer tipo de defecto? 49. Si se seleccionan al azar dos focos de la caja descrita en el ejercicio 38 (sección 2.3) y por lo menos uno de ellos es de 75 W, ¿cuál es la probabilidad de que los dos sean de 75 W? Dado que por lo menos uno de los dos seleccionados no es de 75 W, ¿cuál es la probabilidad de que los dos focos se- leccionados sean de la misma clase? 50. Una tienda de departamentos vende camisas sport en tres tallas (chica, mediana y grande), tres diseños (a cuadros, es- tampadas y a rayas) y dos largos de manga (larga y corta). Las tablas adjuntas dan las proporciones de camisas vendi- das en las combinaciones de categoría. Manga corta Diseño Talla Cuadros Estampada Rayas CH 0.04 0.02 0.05 M 0.08 0.07 0.12 G 0.03 0.07 0.08 Manga larga Diseño Talla Cuadros Estampada Rayas CH 0.03 0.02 0.03 M 0.10 0.05 0.07 G 0.04 0.02 0.08 a. ¿Cuál es la probabilidad de que la siguiente camisa ven- dida sea una camisa mediana estampada de manga larga? b. ¿Cuál es la probabilidad de que la siguiente camisa ven- dida sea una camisa estampada mediana? c. ¿Cuál es la probabilidad de que la siguiente camisa ven- dida sea de manga corta? ¿De manga larga? d. ¿Cuál es la probabilidad de que la talla de la siguiente camisa vendida sea mediana? ¿Que la siguiente camisa vendida sea estampada? e. Dado que la camisa que se acaba de vender era de man- ga corta a cuadros, ¿cuál es la probabilidad de que fuera mediana? f. Dado que la camisa que se acaba de vender era mediana a cuadros, ¿cuál es la probabilidad de que fuera de man- ga corta? ¿De manga larga? EJERCICIOS Sección 2.4 (45-69) Grupo sanguíneo O A B AB 1 0.082 0.106 0.008 0.004 Grupo étnico 2 0.135 0.141 0.018 0.006 3 0.215 0.200 0.065 0.020 c2_p046-085.qxd 3/12/08 3:59 AM Page 74
- 93. 2.4 Probabilidad condicional 75 51. Una caja contiene seis pelotas rojas y cuatro verdes y una se- gunda caja contiene siete pelotas rojas y tres verdes. Se selec- ciona una pelota al azar de la primera caja y se le coloca en la segunda caja. Luego se selecciona al azar una pelota de la segunda caja y se le coloca en la primera caja. a. ¿Cuál es la probabilidad de que se seleccione una pelo- ta roja de la primera caja y de que se seleccione una pe- lota roja de la segunda caja? b. Al final del proceso de selección, ¿cuál es la probabilidad de que los números de pelotas rojas y verdes que hay en la primera caja sean idénticas a los números iniciales? 52. Un sistema se compone de bombas idénticas, #1 y #2. Si una falla, el sistema seguirá operando. Sin embargo, debido al esfuerzo adicional, ahora es más probable que la bom- ba restante falle de lo que era originalmente. Es decir, r P(#2 falla | #1 falla) P(#2 falla) q. Si por lo menos una bomba falla alrededor del final de su vida útil en 7% de todos los sistemas y ambas bombas fallan durante dicho pe- riodo en sólo 1%, ¿cuál es la probabilidad de que la bomba #1 falle durante su vida útil de diseño? 53. Un taller repara tanto componentes de audio como de vi- deo. Sea A el evento en que el siguiente componente traído a reparación es un componente de audio y sea B el evento en que el siguiente componente es un reproductor de discos compactos (así que el evento B está contenido en A). Su- ponga que P(A) 0.6 y P(B) 0.05. ¿Cuál es P(B | A)? 54. En el ejercicio 13, Ai {proyecto otorgado i}, con i 1, 2, 3. Use las probabilidades dadas allí para calcular las siguien- tes probabilidades y explique en palabras el significado de cada una. a. P(A2°A1) b. P(A2 A3°A1) c. P(A2 A3°A1) d. P(A1 A2 A3°A1 A2 A3). 55. Las garrapatas de venados pueden ser portadoras de la en- fermedad de Lyme o de la Erhlichiosis granulocítica huma- na (HGE, por sus siglas en inglés). Con base en un estudio reciente, suponga que 16% de todas las garrapatas en cierto lugar portan la enfermedad de Lyme, 10% portan HGE y 10% de las garrapatas que portan por lo menos una de estas enfermedades en realidad portan las dos. Si determina que una garrapata seleccionada al azar ha sido portadora de HGE, ¿cuál es la probabilidad de que la garrapata seleccio- nada también porte la enfermedad de Lyme? 56. Para los eventos A y B con P(B) 0, demuestre que P(A | B) P(A | B) 1. 57. Si P(B | A) P(B), demuestre que P(B|A) P(B). [Suge- rencia: Sume P(B | A) a ambos lados de la desigualdad da- da y luego utilice el resultado del ejercicio 56.] 58. Demuestre que para tres eventos cualesquiera A, B y C con P(C) 0, P(A B | C) P(A | C) P(B | C) – P(A B | C). 59. En una gasolinería, 40% de los clientes utilizan gasolina re- gular (A1), 35% usan gasolina plus (A2) y 25% utilizan pre- mium (A3). De los clientes que utilizan gasolina regular, sólo 30% llenan sus tanques (evento B). De los clientes que utili- zan plus, 60% llenan sus tanques, mientras que los que uti- lizan premium, 50% llenan sus tanques. a. ¿Cuál es la probabilidad de que el siguiente cliente pida gasolina plus y llene el tanque (A2 B)? b. ¿Cuál es la probabilidad de que el siguiente cliente lle- ne el tanque? c. Si el siguiente cliente llena el tanque, ¿cuál es la proba- bilidad que pida gasolina regular? ¿Plus? ¿Premium? 60. El 70% de las aeronaves ligeras que desaparecen en vuelo en cierto país son posteriormente localizadas. De las aero- naves que son localizadas, 60% cuentan con un localizador de emergencia, mientras que 90% de las aeronaves no locali- zadas no cuentan con dicho localizador. Suponga que una aeronave ligera ha desaparecido. a. Si tiene un localizador de emergencia, ¿cuál es la proba- bilidad de que no sea localizada? b. Si no tiene un localizador de emergencia, ¿cuál es la probabilidad de que sea localizada? 61. Componentes de cierto tipo son enviados a un distribuidor en lotes de diez. Suponga que 50% de dichos lotes no contie- nen componentes defectuosos, 30% contienen un componente defectuoso y 20% contienen dos componentes defectuosos. Se seleccionan al azar dos componentes de un lote y se prueban. ¿Cuáles son las probabilidades asociadas con 0, 1 y 2 componentes defectuosos que están en el lote en cada una de las siguientes condiciones? a. Ningún componente probado está defectuoso. b. Uno de los dos componentes probados está defectuoso. [Sugerencia: Trace un diagrama de árbol con tres ramas de primera generación correspondientes a los tres tipos diferentes de lotes.] 62. Una compañía que fabrica cámaras de video produce un mo- delo básico y un modelo de lujo. Durante el año pasado, 40% de las cámaras vendidas fueron del modelo básico. De aquellos que compraron el modelo básico, 30% adquirieron una garantía ampliada, en tanto que 50% de los que compra- ron el modelo de lujo también lo hicieron. Si sabe que un comprador seleccionado al azar tiene una garantía ampliada, ¿qué tan probable es que él o ella tengan un modelo básico? 63. Para los clientes que compran un refrigerador en una tienda de aparatos domésticos, sea A el evento en que el refrigera- dor fue fabricado en EU, B el evento en que el refrigerador contaba con una máquina de hacer hielos y C el evento en que el cliente adquirió una garantía ampliada. Las probabi- lidades pertinentes son P(A) 0.75 P(B°A) 0.9 P(B°A) 0.8 P(C°A B) 0.8 P(C°A B) 0.6 P(C°A B) 0.7 P(C°A B) 0.3 a. Construya un diagrama de árbol compuesto de ramas de primera, segunda y tercera generaciones y anote el even- to y la probabilidad apropiada junto a cada rama. b. Calcule P(A B C). c. Calcule P(B C). d. Calcule P(C). e. Calcule P(A | B C), la probabilidad de la compra de un refrigerador fabricado en EU dado que también se adquirie- ron una máquina de hacer hielos y una garantía ampliada. 64. En el ejemplo 2.30, suponga que la tasa de incidencia de la enfermedad es de 1 en 25 y no de 1 en 1000. ¿Cuál es en- tonces la probabilidad de un resultado de prueba positivo? Dado que el resultado de prueba es positivo, ¿cuál es la pro- babilidad de que el individuo tenga la enfermedad? Dado un resultado de prueba negativo, ¿cuál es la probabilidad de que el individuo no tenga la enfermedad? c2_p046-085.qxd 3/12/08 3:59 AM Page 75
- 94. La definición de probabilidad condicional permite revisar la probabilidad P(A) originalmente asignada a A cuando después se informa que otro evento B ha ocurrido; la nueva probabilidad de A es P(A | B). En los ejemplos, con frecuencia fue el caso de que P(A | B) difería de la pro- babilidad no condicional P(A), lo que indica que la información “B ha ocurrido” cambia la probabilidad de que ocurra A. A menudo la probabilidad de que ocurra o haya ocurrido A no se ve afectada por el conocimiento de que B ha ocurrido, así que P(A | B) P(A). Es entonces 76 CAPÍTULO 2 Probabilidad 2.5 Independencia 65. En una gran universidad, en la búsqueda que nunca termina de un libro de texto satisfactorio, el Departamento de Estadís- tica probó un texto diferente durante cada uno de los últimos tres trimestres. Durante el trimestre de otoño, 500 estudiantes utilizaron el texto del profesor Mean; durante el trimestre de invierno, 300 estudiantes usaron el texto del profesor Median y durante el trimestre de primavera, 200 estudiantes utiliza- ron el texto del profesor Mode. Una encuesta realizada al fi- nal de cada trimestre mostró que 200 estudiantes se sintieron satisfechos con el libro de Mean, 150 con el libro de Median y 160 con el libro de Mode. Si se selecciona al azar un estu- diante que cursó estadística durante uno de estos trimestres y admite haber estado satisfecho con el texto, ¿es probable que el estudiante haya utilizado el libro de Mean, Median o Mo- de? ¿Quién es el autor menos probable? [Sugerencia: Trace un diagrama de árbol o use el teorema de Bayes.] 66. Considere la siguiente información sobre vacacionistas (ba- sada en parte en una encuesta reciente de Travelocity): 40% revisan su correo electrónico de trabajo, 30% utilizan un te- léfono celular para permanecer en contacto con su trabajo, 25% trajeron una computadora portátil consigo, 23% revisan su correo electrónico de trabajo y utilizan un teléfono celular para permanecer en contacto y 51% ni revisan su correo elec- trónico de trabajo ni utilizan un teléfono celular para per- manecer en contacto ni trajeron consigo una computadora portátil. Además, 88 de cada 100 que traen una computado- ra portátil también revisan su correo electrónico de trabajo y 70 de cada 100 que utilizan un teléfono celular para perma- necer en contacto también traen una computadora portátil. a. ¿Cuál es la probabilidad de que un vacacionista selec- cionado al azar que revisa su correo electrónico de tra- bajo también utilice un teléfono celular para permanecer en contacto. b. ¿Cuál es la probabilidad de que alguien que trae una computadora portátil también utilice un teléfono celular para permanecer en contacto. c. Si el vacacionista seleccionado al azar revisó su correo electrónico de trabajo y trajo una computadora portátil, ¿cuál es la probabilidad de que él o ella utilice un telé- fono celular para permanecer en contacto? 67. Ha habido una gran controversia durante los últimos años con respecto a qué tipos de vigilancia son apropiados para impedir el terrorismo. Suponga que un sistema de vigilancia particular tiene 99% de probabilidades de identificar correc- tamente a un futuro terrorista y 99.9% de probabilidades de identificar correctamente a alguien que no es un futuro terro- rista. Si existen 1000 futuros terroristas en una población de 300 millones y se selecciona al azar uno de estos 300 millones, examinado por el sistema e identificado como futuro terro- rista, ¿cuál es la probabilidad de él o ella que sean futuros te- rroristas? ¿Le inquieta el valor de esta probabilidad sobre el uso del sistema de vigilancia? Explique. 68. Una amiga que vive en Los Ángeles hace viajes frecuentes de consultoría a Washington, D.C.; 50% del tiempo viaja en la línea aérea #1, 30% del tiempo en la aerolínea #2 y el 20% restante en la aerolínea #3. Los vuelos de la aerolínea #1 llegan demorados a D.C. 30% del tiempo y 10% del tiempo llegan demorados a L.A. Para la aerolínea #2, estos porcentajes son 25% y 20%, en tanto que para la aerolínea #3 los porcentajes son 40% y 25%. Si se sabe que en un via- je particular ella llegó demorada a exactamente uno de los destinos, ¿cuáles son las probabilidades posteriores de haber volado en las aerolíneas #1, #2 y #3? Suponga que la proba- bilidad de arribar con demora a L.A. no se ve afectada por lo que suceda en el vuelo a D.C. [Sugerencia: Desde la punta de cada rama de primera generación en un diagrama de árbol, trace tres ramas de segunda generación identificadas, respec- tivamente, como, 0 demorado, 1 demorado y 2 demorado.] 69. En el ejercicio 59, considere la siguiente información adi- cional sobre el uso de tarjetas de crédito: El 70% de todos los clientes que utilizan gasolina regular y que llenan el tanque usan una tarjeta de crédito. El 50% de todos los clientes que utilizan gasolina regular y que no llenan el tanque usan una tarjeta de crédito. El 60% de todos los clientes que llenan el tanque con gaso- lina plus usan una tarjeta de crédito. El 50% de todos los clientes que utilizan gasolina plus y que no llenan el tanque usan una tarjeta de crédito. El 50% de todos los clientes que utilizan gasolina premium y que llenan el tanque usan una tarjeta de crédito. El 40% de todos los clientes que utilizan gasolina premium y que no llenan el tanque usan una tarjeta de crédito. Calcule la probabilidad de cada uno de los siguientes even- tos para el siguiente cliente que llegue (un diagrama de ár- bol podría ayudar). a. {Plus, tanque lleno y tarjeta de crédito} b. {Premium, tanque no lleno y tarjeta de crédito} c. {Premium y tarjeta de crédito} d. {Tanque lleno y tarjeta de crédito} e. {Tarjeta de crédito} f. Si el siguiente cliente utiliza una tarjeta de crédito, ¿cuál es la probabilidad de que pida premium? c2_p046-085.qxd 3/12/08 3:59 AM Page 76
- 95. natural considerar a A y B como eventos independientes, es decir que la ocurrencia o no ocu- rrencia de un evento no afecta la probabilidad de que el otro ocurra. La definición de independencia podría parecer “no simétrica” porque no demanda también que P(B | A) P(B). Sin embargo, utilizando la definición de probabilidad condi- cional y la regla de multiplicación, P(B°A) (2.7) El lado derecho de la ecuación (2.7) es P(B) si y sólo si P(A | B) P(A) (independen- cia), así que la igualdad en la definición implica la otra igualdad (y viceversa). También es fácil demostrar que si A y B son independientes, entonces también lo son los pares de even- tos: (1) A y B, (2) A y B y (3) A y B. Considere una gasolinería con seis bombas numeradas 1, 2, . . . , 6 y sea Ei el evento simple en que un cliente seleccionado al azar utiliza la bomba i (i 1, . . . , 6). Suponga que P(E1) P(E6) 0.10, P(E2) P(E5) 0.15 y P(E3) P(E4) 0.25. Defina los eventos A, B, C como A {2, 4, 6}, B {1, 2, 3} y C {2, 3, 4, 5}. Luego se tiene P(A) 0.50, P(A | B) 0.30 y P(A | C) 0.50. Es decir, los eventos A y B son dependientes, en tanto que los eventos A y C son independientes. Intuitivamente, A y C son independientes porque la división de pro- babilidad relativa entre las bombas pares e impares es la misma entre las bombas 2, 3, 4, 5 como lo es entre todas las seis bombas. ■ Sean A y B dos eventos excluyentes cualesquiera con P(A) 0. Por ejemplo, para un auto- móvil seleccionado al azar, sea A {el carro es de cuatro cilindros} y B {el carro es de seis cilindros}. Como los eventos son mutuamente excluyentes, si B ocurre, entonces A quizá no puede haber ocurrido, así que P(A | B) 0 P(A). El mensaje aquí es que si dos eventos son mutuamente excluyentes, no pueden ser independientes. Cuando A y B son mutuamen- te excluyentes, la información de que A ocurrió dice algo sobre B (no puede haber ocurri- do), así que se impide la independencia. ■ Regla de multiplicación para P(A B) Con frecuencia la naturaleza de un experimento sugiere que dos eventos A y B deben su- ponerse independientes. Este es el caso, por ejemplo, si un fabricante recibe una tarjeta de circuito de cada uno de dos proveedores diferentes, cada tarjeta se somete a prueba al llegar y A {la primera está defectuosa} y B {la segunda está defectuosa}. Si P(A) 0.1, tam- bién deberá ser el caso de que P(A | B) 0.1; sabiendo que la condición de la segunda tar- jeta no informa sobre la condición de la primera. El siguiente resultado muestra cómo calcular P(A B) cuando los eventos son independientes. P(A°B)P(B) P(A) P(A B) P(A) 2.5 Independencia 77 DEFINICIÓN Los eventos A y B son independientes si P(A | B) P(A) y son dependientes de lo contrario. PROPOSICIÓN A y B son independientes si y sólo si P(A B) P(A) P(B) (2.8) Ejemplo 2.31 Ejemplo 2.32 c2_p046-085.qxd 3/12/08 3:59 AM Page 77
- 96. 78 CAPÍTULO 2 Probabilidad Parafraseando la proposición, A y B son independientes si y sólo si la probabilidad de que ambos ocurran (A B) es el producto de las dos probabilidades individuales. La veri- ficación es como sigue: P(A B) P(A°B) P(B) P(A) P(B) (2.9) donde la segunda igualdad en la ecuación (2.9) es válida si y sólo si A y B son independien- tes. Debido a la equivalencia de independencia con la ecuación (2.8), la segunda puede ser utilizada como definición de independencia. Se sabe que 30% de las lavadoras de cierta compañía requieren servicio mientras se encuen- tran dentro de garantía, en tanto que sólo 10% de sus secadoras necesitan dicho servicio. Si alguien adquiere tanto una lavadora como una secadora fabricadas por esta compañía, ¿cuál es la probabilidad de que ambas máquinas requieran servicio de garantía? Sea A el evento en que la lavadora necesita servicio mientras se encuentra dentro de garantía y defina B de forma análoga para la secadora. Entonces P(A) 0.30 y P(B) 0.10. Suponiendo que las dos máquinas funcionan independientemente una de otra, la probabili- dad deseada es P(A B) P(A) P(B) (0.30)(0.10) 0.03 ■ Es fácil demostrar que A y B son independientes si y sólo si A y B son independientes, A y B son independientes y A y B son independientes. Por lo tanto, en el ejemplo 2.33, la pro- babilidad de que ninguna máquina necesite servicio es P(A B) P(A) P(B) (0.70)(0.90) 0.63 Cada día, de lunes a viernes, un lote de componentes enviado por un primer proveedor arri- ba a una instalación de inspección. Dos días a la semana, también arriba un lote de un se- gundo proveedor. El 80% de todos los lotes del proveedor 1 son inspeccionados y 90% de los del proveedor 2 también lo son. ¿Cuál es la probabilidad de que, en un día seleccionado al azar, dos lotes sean inspeccionados? Esta pregunta se responderá suponiendo que en los días en que se inspeccionan dos lotes, si el primer lote pasa es independiente de si el segun- do también lo hace. La figura 2.13 muestra la información pertinente. P(dos pasan) P(dos recibidos ambos pasan) P(ambos pasan | dos recibidos) P(dos recibidos) [(0.8)(0.9)(0.4) 0.288 ■ Ejemplo 2.33 Ejemplo 2.34 Figura 2.13 Diagrama de árbol para el ejemplo 2.34. Lote de proveedor 2 Lote de proveedor 1 0.6 0.4 0.8 1o. pasa 0.2 1o. falla 0.2 Falla 0.8 Pasa 0.9 2o. pasa 0.1 2o. falla 0.9 2o. pasa 0.1 2o. falla 0.4 (0.8 0.9) c2_p046-085.qxd 3/12/08 3:59 AM Page 78
- 97. Independencia de más de dos eventos La noción de independencia de dos eventos puede ser ampliada a conjuntos de más de dos eventos. Aunque es posible ampliar la definición para dos eventos independientes trabajan- do en función de probabilidades condicionales y no condicionales, es más directo y menos tedioso seguir las líneas de la última proposición. Parafraseando la definición, los eventos son mutuamente independientes si la probabili- dad de la intersección de cualquier subconjunto de “n”-elementos, es igual al producto de las probabilidades individuales. Al utilizar la propiedad de multiplicación para más de dos eventos independientes, es legítimo reemplazar una o más de las Ai por su complemento (p. ej., si A1, A2 y A3 son eventos independientes, también lo son A1 , A2 y A3 ). Como fue el caso con dos even- tos, con frecuencia se especifica al principio de un problema la independencia de ciertos eventos. La probabilidad de una intersección puede entonces ser calculada vía multiplicación. El artículo “Reliability Evaluation of Solar Photovoltaic Arrays” (Solar Energy, 2002: 129–141) presenta varias configuraciones de redes fotovoltaicas solares compuestas de celdas solares de silicio cristalino. Considérese primero el sistema ilustrado en la figura 2.14(a). Existen dos subsistemas conectados en paralelo y cada uno contiene tres celdas. Para que el sistema funcione, por lo menos uno de los dos subsistemas en paralelo debe funcionar. Den- tro de cada subsistema, las tres celdas están conectadas en serie, así que un subsistema fun- cionará sólo si todas sus celdas funcionan. Considere un valor de duración particular t0 y suponga que desea determinar la probabilidad de que la duración del sistema exceda de t0. Sea Ai el evento en que la duración de la celda i excede de t0 (i 1, 2, . . . , 6). Se supone que las Ai son eventos independientes (ya sea que cualquier celda particular que dure más de t0 horas no tenga ningún efecto en sí o no cualquier otra celda lo hace) y que P(Ai) 0.9 por cada i puesto que las celdas son idénticas. Entonces P(la duración del sistema excede de t0) P[(A1 A2 A3) (A4 A5 A6)] P(A1 A2 A3) P(A4 A5 A6) P [(A1 A2 A3) (A4 A5 A6)] (0.9)(0.9)(0.9) (0.9)(0.9)(0.9) (0.9)(0.9)(0.9)(0.9)(0.9)(0.9) 0.927 Alternativamente, P(la duración del sistema excede de t0) 1 P(ambas duraciones del subsistema son t0) 1 [P(la duración del subsistema es t0)]2 1 [1 P(la duración del subsistema es t0)]2 1 [1 (0.9)3 ]2 0.927 2.5 Independencia 79 Ejemplo 2.35 Figura 2.14 Configuración del sistema para el ejemplo 2.35: (a) en serie-paralelo; (b) vinculado en cruz total. 1 2 3 4 5 6 1 2 3 4 5 6 (a) (b) DEFINICIÓN Los eventos A1, . . . , An son mutuamente independientes si por cada k (k 2, 3, . . . , n) y cada subconjunto de índices i1, i2, . . . , ik, P(Ai1 Ai2 . . . Aik ) P(Ai1 ) P(Ai2 ) . . . P(Aik ). c2_p046-085.qxd 3/12/08 3:59 AM Page 79
- 98. 80 CAPÍTULO 2 Probabilidad Considérese a continuación el sistema vinculado en cruz mostrado en la figura 2.14(b), ob- tenido a partir de la red conectada en serie-paralelo mediante la conexión de enlaces a tra- vés de cada columna de uniones. Ahora bien, el sistema falla en cuanto toda una columna falla y la duración del sistema excede de t0 sólo si la duración de cada columna lo hace. Pa- ra esta configuración, P(la duración del sistema es de por lo menos t0) [P(la duración de la columna excede de t0)]3 [1 P(duración de la columna t0)]3 [1 P(la duración de ambas celdas en una columna es t0)]3 [1 (1 0.9)2 ]3 0.970 ■ 70. Reconsidere el escenario de la tarjeta de crédito del ejercicio 47 (sección 2.4) y demuestre que A y B son dependientes uti- lizando primero la definición de independencia y luego ve- rificando que la propiedad de multiplicación no prevalece. 71. Una compañía de exploración petrolera en la actualidad tie- ne dos proyectos activos, uno enAsia y el otro en Europa. Sea A el evento en que el proyecto asiático tiene éxito y B el even- to en que el proyecto europeo tiene éxito. Suponga que A y B son eventos independientes con P(A) 0.4 y P(B) 0.7. a. Si el proyecto asiático no tiene éxito, ¿cuál es la proba- bilidad de que el europeo también fracase? Explique su razonamiento. b. ¿Cuál es la probabilidad de que por lo menos uno de los dos proyectos tenga éxito? c. Dado que por lo menos uno de los dos proyectos tiene éxito, ¿cuál es la probabilidad de que sólo el proyecto asiático tenga éxito? 72. En el ejercicio 13, ¿es cualquier Ai independiente de cual- quier otro Aj? Responda utilizando la propiedad de multipli- cación para eventos independientes. 73. Si A y B son eventos independientes, demuestre que A y B también son independientes. [Sugerencia: Primero establez- ca una relación entre P(A B), P(B) y P(A B).] 74. Suponga que las proporciones de fenotipos sanguíneos en una población son las siguientes: A B AB O 0.42 0.10 0.04 0.44 Suponiendo que los fenotipos de dos individuos selecciona- dos al azar son independientes uno de otro, ¿cuál es la pro- babilidad de que ambos fenotipos sean O? ¿Cuál es la probabilidad de que los fenotipos de dos individuos selec- cionados al azar coincidan? 75. Una de las suposiciones que sustentan la teoría de las gráfi- cas de control (véase el capítulo 16) es que los puntos dibu- jados consecutivamente son independientes entre sí. Cada punto puede señalar que un proceso de producción está fun- cionando correctamente o que existe algún funcionamiento defectuoso. Aun cuando un proceso esté funcionando de manera correcta, existe una pequeña probabilidad de que un punto particular señalará un problema con el proceso. Supon- ga que esta probabilidad es de 0.05. ¿Cuál es la probabilidad de que por lo menos uno de 10 puntos sucesivos indique un problema cuando de hecho el proceso está operando correc- tamente? Responda está pregunta para 25 puntos sucesivos. 76. La probabilidad de que un calificador se equivoque al mar- car cualquier pregunta particular de un examen de opciones múltiples es de 0.1. Si existen diez preguntas y éstas se mar- can en forma independiente, ¿cuál es la probabilidad de que no se cometan errores? ¿Que por lo menos se cometa un error? Si existen n preguntas y la probabilidad de un error de marcado es p en lugar de 0.1, dé expresiones para estas dos probabilidades. 77. La costura de un avión requiere 25 remaches. La costura tendrá que ser retrabajada si alguno de los remaches está defectuoso. Suponga que los remaches están defectuosos independientemente uno de otro, cada uno con la misma probabilidad. a. Si 20% de todas las costuras tienen que ser retrabajadas, ¿cuál es la probabilidad de que un remache esté defec- tuoso? b. ¿Qué tan pequeña deberá ser la probabilidad de un re- mache defectuoso para garantizar que sólo 10% de las costuras tienen que ser retrabajadas? 78. Una caldera tiene cinco válvulas de alivio idénticas. La pro- babilidad de que cualquier válvula particular se abra en un momento de demanda es de 0.95. Suponiendo que operan independientemente, calcule P(por lo menos una válvula se abre) y P(por lo menos una válvula no se abre). 79. Dos bombas conectadas en paralelo fallan independiente- mente una de otra en cualquier día dado. La probabilidad de que falle sólo la bomba más vieja es de 0.10 y la probabili- dad de que sólo la bomba más nueva falle es de 0.05. ¿Cuál es la probabilidad de que el sistema de bombeo falle en cualquier día dado (lo que sucede si ambas bombas fallan)? 80. Considere el sistema de componentes conectados como en la figura adjunta. Los componentes 1 y 2 están conectados en paralelo, de modo que el subsistema trabaja si y sólo si EJERCICIOS Sección 2.5 (70-89) c2_p046-085.qxd 3/12/08 3:59 AM Page 80
- 99. 2.5 Independencia 81 1 o 2 trabaja; como 3 y 4 están conectados en serie, qué sub- sistema trabaja si y sólo si 3 y 4 trabajan. Si los componen- tes funcionan independientemente uno de otro y P(el componente trabaja) 0.9, calcule P(el sistema trabaja). 81. Remítase otra vez al sistema en serie-paralelo introducido en el ejemplo 2.35 y suponga que existen sólo dos celdas en lugar de tres en cada subsistema en paralelo [en la figura 2.14(a), elimine las celdas 3 y 6 y renumere las celdas 4 y 5 como 3 y 4]. Utilizando P(Ai) 0.9, es fácil ver que la probabilidad de que la duración del sistema exceda de t0 es de 0.9639. ¿A qué valor tendría que cambiar 0.9 para incre- mentar la duración del sistema de 0.9639 a 0.99? [Sugeren- cia: Sea P(Ai) p, exprese la confiabilidad del sistema en función de p, luego haga x p2 .] 82. Considere lanzar en forma independiente dos dados impar- ciales, uno rojo y otro verde. Sea A el evento en que el da- do rojo muestra 3 puntos, B el evento en que el dado verde muestra 4 puntos y C el evento en que el número total de puntos que muestran los dos dados es 7. ¿Son estos eventos independientes por pares (es decir, ¿son A y B eventos inde- pendientes, son A y C independientes y son B y C indepen- dientes? ¿Son los tres eventos mutuamente independientes? 83. Los componentes enviados a un distribuidor son revisados en cuanto a defectos por dos inspectores diferentes (cada componente es revisado por ambos inspectores). El primero detecta 90% de todos los defectuosos que están presentes y el segundo hace lo mismo. Por lo menos un inspector no de- tecta un defecto en 20% de todos los componentes defectuo- sos. ¿Cuál es la probabilidad de que ocurra lo siguiente? a. ¿Un componente defectuoso será detectado sólo por el primer inspector? ¿Por exactamente uno de los dos ins- pectores? b. ¿Los tres componentes defectuosos en un lote no son detectados por ambos inspectores (suponiendo que las inspecciones de los diferentes componentes son inde- pendientes unas de otras)? 84. El 70% de todos los vehículos examinados en un centro de ve- rificación de emisiones pasan la inspección. Suponiendo que vehículos sucesivos pasan o fallan independientemente uno de otro, calcule las siguientes probabilidades: a. P(los tres vehículos siguientes inspeccionados pasan). b. P(por lo menos uno de los tres vehículos siguientes pasa). c. P(exactamente uno de los tres vehículos siguientes pasa). d. P(cuando mucho uno de los tres vehículos siguientes inspeccionados pasa). e. Dado que por lo menos uno de los tres vehículos si- guientes pasa la inspección, ¿cuál es la probabilidad de que los tres pasen (una probabilidad condicional)? 85. Un inspector de control de calidad verifica artículos recién producidos en busca de fallas. El inspector examina un artículo en busca de fallas en una serie de observaciones in- dependientes, cada una de duración fija. Dado que en reali- dad está presente una imperfección, sea p la probabilidad de que la imperfección sea detectada durante cualquier obser- vación (este modelo se discute en “Human Performance in Sampling Inspection”, Human Factors, 1979: 99–105). a. Suponiendo que un artículo tiene una imperfección, ¿cuál es la probabilidad de que sea detectada al final de la se- gunda observación (una vez que una imperfección ha si- do detectada, la secuencia de observaciones termina)? b. Dé una expresión para la probabilidad de que una imper- fección sea detectada al final de la n-ésima observación. c. Si cuando en tres observaciones no ha sido detectada una imperfección, el artículo es aprobado, ¿cuál es la probabi- lidad de que un artículo imperfecto pase la inspección? d. Suponga que 10% de todos los artículos contienen una imperfección [P(artículo seleccionado al azar muestra una imperfección) 0.1]. Con la suposición del inciso c), ¿cuál es la probabilidad de que un artículo seleccio- nado al azar pase la inspección (pasará automáticamen- te si no tiene imperfección, pero también podría pasar si tiene una imperfección)? e. Dado que un artículo ha pasado la inspección (sin imper- fecciones en tres observaciones), ¿cuál es la probabilidad de que sí tenga una imperfección? Calcule para p 0.5. 86. a. Una compañía maderera acaba de recibir un lote de 10 000 tablas de 2 4. Suponga que 20% de estas tablas (2 000) en realidad están demasiado tiernas o verdes para ser utilizadas en construcción de primera calidad. Se eli- gen dos tablas al azar, una después de la otra. Sea A {la primera tabla está verde} y B {la segunda tabla es- tá verde}. Calcule P(A), P(B) y P(A B) (un diagrama de árbol podría ayudar). ¿Son A y B independientes? b. Con A y B independientes y P(A) P(B) 0.2, ¿cuál es P(A B)? ¿Cuánta diferencia existe entre esta res- puesta y P(A B) en el inciso a)? Para propósitos de cálculo P(A B), ¿se puede suponer que A y B del in- ciso a) son independientes para obtener en esencia la probabilidad correcta? c. Suponga que un lote consta de 10 tablas, de las cuales dos están verdes. ¿Produce ahora la suposición de inde- pendencia aproximadamente la respuesta correcta para P(A B)? ¿Cuál es la diferencia crítica entre la situación en este caso y la del inciso a)? ¿Cuándo piensa que una suposición de independencia sería válida al obtener una respuesta aproximadamente correcta a P(A B)? 87. Remítase a las suposiciones manifestadas en el ejercicio 80 y responda la pregunta planteada allí para el sistema de la figura adjunta. ¿Cómo cambiaría la probabilidad si ésta fue- ra un subsistema conectado en paralelo al subsistema ilus- trado en la figura 2.14(a)? 88. El profesor Stan der Deviation puede tomar una de las rutas en el trayecto del trabajo a su casa. En la primera ruta, hay 2 1 5 3 6 7 4 2 1 3 4 c2_p046-085.qxd 3/12/08 3:59 AM Page 81
- 100. 82 CAPÍTULO 2 Probabilidad cuatro cruces de ferrocarril. La probabilidad de que sea de- tenido por un tren en cualquiera de los cruces es 0.1 y los trenes operan independientemente en los cuatro cruces. La otra ruta es más larga pero sólo hay dos cruces, indepen- dientes uno de otro, con la misma posibilidad de que sea de- tenido por un tren al igual que en la primera ruta. En un día particular, el profesor Deviation tiene una reunión progra- mada en casa durante cierto tiempo. Cualquiera ruta que to- me, calcula que llegará tarde si es detenido por los trenes en por lo menos la mitad de los cruces encontrados. a. ¿Cuál ruta deberá tomar para reducir al mínimo la pro- babilidad de llegar tarde a la reunión? b. Si lanza al aire una moneda imparcial para decidir que ru- ta tomar y llega tarde, ¿cuál es la probabilidad de que tomó la ruta de los cuatro cruces? 89. Suponga que se colocan etiquetas idénticas en las dos ore- jas de un zorro. El zorro es dejado en libertad durante un tiempo. Considere los dos eventos C1 {se pierde la eti- queta de la oreja izquierda} y C2 {se pierde la etiqueta de la oreja derecha}. Sea P(C1) P(C2) y suponga que C1 y C2 son eventos independientes. Derive una expresión (que implique ) para la probabilidad de que exactamente una etiqueta se pierda dado que cuando mucho una se pier- de (“Ear Tag Loss in Red Foxes”, J. Wildlife Mgmt., 1976: 164–167). [Sugerencia: Trace un diagrama de árbol en el cual las dos ramas iniciales se refieren a si la etiqueta de la oreja izquierda se pierde.] 90. Una pequeña compañía manufacturera iniciará un turno de no- che. Hay 20 mecánicos empleados por la compañía. a. Si una cuadrilla nocturna se compone de 3 mecánicos, ¿cuántas cuadrillas diferentes son posibles? b. Si los mecánicos están clasificados 1, 2, . . . , 20 en or- den de competencia, ¿cuántas de estas cuadrillas no in- cluirían al mejor mecánico? c. ¿Cuántas de las cuadrillas tendrían por lo menos 1 de los 10 mejores mecánicos? d. Si se selecciona al azar una de estas cuadrillas para que trabajen una noche particular, ¿cuál es la probabilidad de que el mejor mecánico no trabaje esa noche? 91. Una fábrica utiliza tres líneas de producción para fabricar latas de cierto tipo. La tabla adjunta da porcentajes de latas que no cumplen con las especificaciones, categorizadas por tipo de incumplimiento de las especificaciones, para cada una de las tres líneas durante un periodo particular. Línea 1 Línea 2 Línea 3 Manchas 15 12 20 Grietas 50 44 40 Problema con la argolla de apertura 21 28 24 Defecto superficial 10 8 15 Otros 4 8 2 Durante este periodo, la línea 1 produjo 500 latas fuera de especificación, la 2 produjo 400 latas como esas y la 3 fue responsable de 600 latas fuera de especificación. Suponga que se selecciona al azar una de estas 1500 latas. a. ¿Cuál es la probabilidad de que la lata la produjo la lí- nea 1? ¿Cuál es la probabilidad de que la razón del in- cumplimiento de la especificación es una grieta? b. Si la lata seleccionada provino de la línea 1, ¿cuál es la probabilidad de que tenía una mancha? c. Dado que la lata seleccionada mostró un defecto superfi- cial, ¿cuál es la probabilidad de que provino de la línea 1? 92. Un empleado de la oficina de inscripciones en una univer- sidad en este momento tiene diez formas en su escritorio en espera de ser procesadas. Seis de éstas son peticiones de ba- ja y las otras cuatro son solicitudes de sustitución de curso. a. Si selecciona al azar seis de estas formas para dárselas a un subordinado, ¿cuál es la probabilidad de que sólo uno de los dos tipos permanezca en su escritorio? b. Suponga que tiene tiempo para procesar sólo cuatro de estas formas antes de salir del trabajo. Si estas cuatro se seleccionan al azar una por una, ¿cuál es la probabilidad de que cada forma subsiguiente sea de un tipo diferente de su predecesora? 93. Un satélite está programado para ser lanzado desde Cabo Ca- ñaveral en Florida y otro lanzamiento está programado para la Base de la Fuerza Aérea Vandenberg en California. Sea A el evento en que el lanzamiento en Vandenberg se hace a la hora programada y B el evento en que el lanzamiento en Ca- bo Cañaveral se hace a la hora programada. Si A y B son eventos independientes con P(A) P(B) y P(A B) 0.626, P(A B) 0.144, determine los valores de P(A) y P(B). 94. Un transmisor envía un mensaje utilizando un código bina- rio, esto es, una secuencia de ceros y unos. Cada bit trans- mitido (0 o 1) debe pasar a través de tres relevadores para llegar al receptor. En cada relevador, la probabilidad es 0.20 de que el bit enviado será diferente del bit recibido (una in- versión). Suponga que los relevadores operan independien- temente uno de otro. Transmisor A Relevador 1 A Relevador 2 A Relevador 3 A Receptor a. Si el transmisor envía un 1, ¿cuál es la probabilidad de que los tres relevadores envíen un 1? b. Si el transmisor envía un 1, ¿cuál es la probabilidad de que el receptor reciba un 1? [Sugerencia: Los ocho re- sultados experimentales pueden ser mostrados en un diagrama de árbol con tres ramas de generación, una por cada relevador.] c. Suponga que 70% de todos los bits enviados por el transmisor son 1. Si el receptor recibe un 1, ¿cuál es la probabilidad de que un 1 fue enviado? 95. El individuo A tiene un círculo de cinco amigos cercanos (B, C, D, E y F). A escuchó cierto rumor originado fuera del círculo e invitó a sus cinco amigos a una fiesta para contar- les el rumor. Para empezar, A escoge a uno de los cinco al EJERCICIOS SUPLEMENTARIOS (90-114) c2_p046-085.qxd 3/12/08 3:59 AM Page 82
- 101. Ejercicios suplementarios 83 azar y se lo cuenta. Dicho individuo escoge entonces al azar a uno de los cuatro individuos restantes y repite el rumor. Después, de aquellos que ya oyeron el rumor uno se lo cuenta a otro nuevo individuo y así hasta que todos oyen el rumor. a. ¿Cuál es la probabilidad de que el rumor se repita en el orden B, C, D, E y F? b. ¿Cuál es la probabilidad de que F sea la tercera perso- na en la reunión a quien se cuenta el rumor? c. ¿Cuál es la probabilidad de que F sea la última persona en oír el rumor? 96. Remítase al ejercicio 95. Si en cada etapa la persona que actualmente “oyó” el rumor no sabe quién ya lo oyó y se- lecciona el siguiente receptor al azar de entre todos los cin- co probables individuos, ¿cuál es la probabilidad de que F aún no haya escuchado el rumor después de que el rumor haya sido contado diez veces en la reunión? 97. Un ingeniero químico está interesado en determinar si cierta impureza está presente en un producto. Un experimento tie- ne una probabilidad de 0.80 de detectarla si está presente. La probabilidad de no detectarla si está ausente es de 0.90. Las probabilidades previas de que la impureza esté presen- te o ausente son de 0.40 y 0.60, respectivamente. Tres expe- rimentos distintos producen sólo dos detecciones. ¿Cuál es la probabilidad posterior de que la impureza esté presente? 98. A cada concursante en un programa de preguntas se le pi- de que especifique una de seis posibles categorías de entre las cuales se le hará una pregunta. Suponga P(el concur- sante escoge la categoría i) 1 6 y concursantes sucesivos escogen sus categorías independientemente uno de otro. Si participan tres concursantes en cada programa y los tres en un programa particular seleccionan diferentes categorías, ¿cuál es la probabilidad de que exactamente uno seleccio- ne la categoría 1? 99. Los sujetadores roscados utilizados en la fabricación de aviones son levemente doblados para que queden bien apretados y no se aflojen durante vibraciones. Suponga que 95% de todos los sujetadores pasan una inspección ini- cial. De 5% que fallan, 20% están tan seriamente defectuo- sos que deben ser desechados. Los sujetadores restantes son enviados a una operación de redoblado, donde 40% no pueden ser recuperados y son desechados. El otro 60% de estos sujetadores son corregidos por el proceso de redobla- do y posteriormente pasan la inspección. a. ¿Cuál es la probabilidad de que un sujetador que acaba de llegar seleccionado al azar pase la inspección inicial- mente o después del redoblado? b. Dado que un sujetador pasó la inspección, ¿cuál es la probabilidad de que apruebe la inspección inicial y de que no necesite redoblado? 100. Un porcentaje de todos los individuos en una población son portadores de una enfermedad particular. Una prue- ba de diagnóstico para esta enfermedad tiene una tasa de detección de 90% para portadores y de 5% para no porta- dores. Suponga que la prueba se aplica independientemen- te a dos muestras de sangre diferentes del mismo individuo seleccionado al azar. a. ¿Cuál es la probabilidad de que ambas pruebas den el mismo resultado? b. Si ambas pruebas son positivas, ¿cuál es la probabilidad de que el individuo seleccionado sea un portador? 101. Un sistema consta de dos componentes. La probabilidad de que el segundo componente funcione de manera satisfacto- ria durante su duración de diseño es de 0.9, la probabilidad de que por lo menos uno de los dos componentes lo haga es de 0.96 y la probabilidad de que ambos componentes lo hagan es de 0.75. Dado que el primer componente funciona de manera satisfactoria durante toda su duración de diseño, ¿cuál es la probabilidad de que el segundo también lo haga? 102. Cierta compañía envía 40% de sus paquetes de correspon- dencia nocturna vía un servicio de correo Express E1. De estos paquetes, 2% llegan después del tiempo de entrega garantizado (sea L el evento “entrega demorada”). Si se selecciona al azar un registro de correspondencia nocturna del archivo de la compañía, ¿cuál es la probabilidad de que el paquete se fue vía E1 y llegó demorado? 103. Remítase al ejercicio 102. Suponga que 50% de los paque- tes nocturnos se envían vía servicio de correo Express E2 y el 10% restante se envía por E3. De los paquetes enviados vía E2, sólo 1% llegan demorados, en tanto que 5% de los paquetes manejados por E3 llegan demorados. a. ¿Cuál es la probabilidad de que un paquete selecciona- do al azar llegue demorado? b. Si un paquete seleccionado al azar llegó a tiempo, ¿cuál es la probabilidad de que no fue mandado vía E1? 104. Una compañía utiliza tres líneas de ensamble diferentes: A1, A2 y A3, para fabricar un componente particular. De los fa- bricados por la línea A1, 5% tienen que ser retrabajados para corregir un defecto, mientras que 8% de los componentes de A2 tienen que ser retrabajados y 10% de los componentes de A3 tienen que ser retrabajados. Suponga que 50% de to- dos los componentes los produce la línea A1, 30% la línea A2 y 20% la línea A3. Si un componente seleccionado al azar tiene que ser retrabajado, ¿cuál es la probabilidad de que provenga de la línea A1? ¿De la línea A2? ¿De la línea A3? 105. Desechando la posibilidad de cumplir años el 29 de febre- ro, suponga que es igualmente probable que un individuo seleccionado al azar haya nacido en cualquiera de los de- más 365 días. a. Si se seleccionan al azar diez personas, ¿cuál es la pro- babilidad que tendrán diferentes cumpleaños? ¿De que por lo menos dos tengan el mismo cumpleaños? b. Si k reemplaza a diez en el inciso a), ¿cuál es la k más pequeña para la cual existe por lo menos una probabili- dad de 50-50 de que dos o más personas tengan el mis- mo cumpleaños? c. Si seleccionan diez personas al azar, ¿cuál es la proba- bilidad de que por los menos dos tengan el mismo cum- pleaños o por lo menos dos tengan los mismos tres últimos dígitos de sus números del Seguro Social? [No- ta: El artículo “Methods for Studying Coincidences” (F. Mosteller y P. Diaconis, J. Amer. Stat. Assoc., 1989: 853–861) discute problemas de este tipo.] 106. Un método utilizado para distinguir entre rocas graníticas (G) y basálticas (B) es examinar una parte del espectro infra- rrojo de la energía solar reflejada por la superficie de la ro- ca. Sean R1, R2 y R3 intensidades espectrales medidas a tres c2_p046-085.qxd 3/12/08 3:59 AM Page 83
- 102. 84 CAPÍTULO 2 Probabilidad longitudes de onda diferentes, en general, para granito R1 R2 R3, en tanto que para basalto R3 R1 R2. Cuando se hacen mediciones a distancia (mediante un avión), varios or- denamientos de Ri pueden presentarse ya sea que la roca sea basalto o granito. Vuelos sobre regiones de composición co- nocida han arrojado la siguiente información: Granito Basalto R1 R2 R3 60% 10% R1 R3 R2 25% 20% R3 R1 R2 15% 70% Suponga que para una roca seleccionada al azar en cierta región P(granito) 0.25 y P(basalto) 0.75. a. Demuestre que P(granito | R1 R2 R3) P(basalto | R1 R2 R3). Si las mediciones dieron R1 R2 R3, ¿clasificaría la roca como granito o como basalto? b. Si las mediciones dieron R1 R3 R2, ¿cómo clasifi- caría la roca? Responda la misma pregunta para R3 R1 R2. c. Con las reglas de clasificación indicadas en los incisos a) y b) cuando se seleccione una roca de esta región, ¿cuál es la probabilidad de una clasificación errónea? [Sugerencia: G podría ser clasificada como B o B como G y P(B) y P(G) son conocidas.] d. Si P(granito p en lugar de 0.25, ¿existen valores de p (aparte de 1) para los cuales una roca siempre sería cla- sificada como granito? 107. A un sujeto se le permite una secuencia de vistazos para de- tectar un objetivo. Sea Gi {el objetivo es detectado en el vistazo i-ésimo}, con pi P(Gi). Suponga que los Gi son eventos independientes y escriba una expresión para la pro- babilidad de que el objetivo haya sido detectado al final del vistazo n-ésimo. [Nota: Este modelo se discute en “Predicting Aircraft Detectability”, Human Factors, 1979: 277–291.] 108. En un juego de béisbol de Ligas menores, el lanzador del equipo A lanza un “strike” 50% del tiempo y una bola 50% del tiempo; los lanzamientos sucesivos son independientes unos de otros y el lanzador nunca golpea a un bateador. Sa- biendo esto, el “mánager” del equipo B ha instruido al pri- mer bateador que no le batee a nada. Calcule la probabilidad de que: a. El bateador reciba base por bolas en el cuarto lanza- miento. b. El bateador reciba base por bolas en el sexto lanza- miento (por lo que dos de los primeros cinco deben ser “strikes”), por medio de un argumento de conteo o un diagrama de árbol. c. El bateador recibe base por bolas. d. El primer bateador en el orden al bat anota mientras no hay ningún “out” (suponiendo que cada bateador utili- za la estrategia de no batearle a nada). 109. Cuatro ingenieros, A, B, C y D han sido citados para entre- vistas de trabajo a las 10 A.M., el viernes 13 de enero, en Random Sampling, Inc. El gerente de personal ha progra- mado a los cuatro para las oficinas de entrevistas 1, 2, 3 y 4, respectivamente. Sin embargo, el secretario del gerente no está enterado de esto, por lo que los asigna a las oficinas de un modo completamente aleatorio (¡Qué más!) ¿Cuál es la probabilidad de que a. Los cuatro terminen en las oficinas correctas? b. Ninguno de los cuatro termine en la oficina correcta? 110. Una aerolínea particular opera vuelos a las 10 A.M., de Chicago a Nueva York, Atlanta y Los Ángeles. Sea A el evento en que el vuelo a Nueva York está lleno y defina los eventos B y C en forma análoga para los otros dos vuelos. Suponga que P(A) 0.6, P(B) 0.5, P(C) 0.4 y los tres eventos son independientes. ¿Cuál es la probabilidad de que a. Los tres vuelos estén llenos? Que por lo menos uno no esté lleno? b. Sólo el vuelo a Nueva York esté lleno? Que exactamen- te uno de los tres vuelos esté lleno? 111. Un gerente de personal va a entrevistar cuatro candidatos para un puesto. Éstos están clasificados como 1, 2, 3 y 4 en orden de preferencia y serán entrevistados en orden aleato- rio. Sin embargo, al final de cada entrevista, el gerente sa- brá sólo cómo se compara el candidato actual con los candidatos previamente entrevistados. Por ejemplo, el or- den de entrevista 3, 4, 1, 2 no genera información después de la primera entrevista, muestra que el segundo candidato es peor que el primero y que el tercero es mejor que los pri- meros dos. Sin embargo, el orden 3, 4, 2, 1 generaría la misma información después de cada una de las primeras tres entrevistas. El gerente desea contratar al mejor candi- dato pero debe tomar una decisión irrevocable de contratar- lo o no contratarlo después de cada entrevista. Considere la siguiente estrategia: Rechazar automáticamente a los pri- meros s candidatos y luego contratar al primer candidato subsiguiente que resulte mejor entre los que ya fueron en- trevistados (si tal candidato no aparece, el último entrevis- tado es el contratado). Por ejemplo, con s 2, el orden 3, 4, 1, 2 permitiría con- tratar al mejor, en tanto que el orden 3, 1, 2, 4 no. De los cua- tro posibles valores de s (0, 1, 2 y 3), ¿cuál incrementa al máximo a P(el mejor es contratado)? [Sugerencia: los 24 or- denamientos de entrevista igualmente probables: s 0 signi- fica que el primer candidato es automáticamente contratado.] 112. Considere cuatro eventos independientes A1, A2, A3 y A4 y sea pi P(Ai) con i 1, 2, 3, 4. Exprese la probabilidad de que por lo menos uno de estos eventos ocurra en fun- ción de las pi y haga lo mismo para la probabilidad de que por lo menos dos de los eventos ocurran. 113. Una caja contiene los siguientes cuatro papelitos y cada uno tiene exactamente las mismas dimensiones: (1) gana el premio 1; (2) gana el premio 2; (3) gana el premio 3; (4) ganan los premios 1, 2 y 3. Se selecciona un papelito al azar. Sea A1 {gana el premio 1}, A2 {gana el premio 2} y A3 {gana el premio 3}. Demuestre que A1 y A2 son independientes, que A1 y A3 son independientes y que A2 y A3 también son independientes (esta es una independencia por pares). Sin embargo, demuestre que P(A1 A2 A3) P(A1) P(A2) · P(A3), así que los tres eventos no son mu- tuamente independientes. 114. Demuestre que si A1, A2 y A3 son eventos independientes, entonces P(A1 | A2 A3) P(A1). c2_p046-085.qxd 3/12/08 3:59 AM Page 84
- 103. Blibliografía 85 Bibliografía Durrett, Richard, The Essentials of Probability, Duxbury Press, Belmont, CA, 1993. Una presentación concisa a un nivel un poco más alto que este texto. Mosteller, Frederick, Robert Rourke y George Thomas, Probabi- lity with Statistical Applications (2a. ed.), Addison-Wesley, Reading, MA, 1970. Una muy buena introducción a la proba- bilidad con muchos ejemplos entretenidos; especialmente buenos con respecto a reglas de conteo y su aplicación. Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models and Application (2a. ed.), Macmillan, Nueva York, 1994. Una amplia introducción a la probabilidad escrita a un nivel mate- mático un poco más alto que este texto pero que contiene mu- chos buenos ejemplos. Ross, Sheldon, A First Course in Probability (6a. ed.), Macmi- llan, Nueva York, 2002. Algo concisamente escrito y más ma- temáticamente complejo que este texto pero contiene una gran cantidad de ejemplos y ejercicios interesantes. Winkler, Robert, Introducction to Bayesian Inference and Deci- sion, Holt, Rinehart Winston, Nueva York, 1972. Una muy buena introducción a la probabilidad subjetiva. c2_p046-085.qxd 3/12/08 3:59 AM Page 85
- 104. Variables aleatorias discretas y distribuciones de probabilidad 3 86 INTRODUCCIÓN Ya sea que un experimento produzca resultados cualitativos o cuantitativos, los mé- todos de análisis estadístico requieren enfocarse en ciertos aspectos numéricos de los datos (como la proporción muestral x/n, la media x _ o la desviación estándar s). El concepto de variable aleatoria permite pasar de los resultados experimentales a la función numérica de los resultados. Existen dos tipos fundamentalmente diferentes de variables aleatorias: las variables aleatorias discretas y las variables aleatorias con- tinuas. En este capítulo, se examinan las propiedades básicas y se discuten los ejem- plos más importantes de variables discretas. El capítulo 4 se enfoca en las variables aleatorias continuas. c3_p086-129.qxd 3/12/08 4:01 AM Page 86
- 105. En cualquier experimento, existen numerosas características que pueden ser observadas o medidas, pero en la mayoría de los casos un experimentador se enfoca en algún aspecto es- pecífico o aspectos de una muestra. Por ejemplo, en un estudio de patrones de viaje entre los suburbios y la ciudad en un área metropolitana, a cada individuo en una muestra se le podría preguntar sobre la distancia que recorre para ir de su casa al trabajo y viceversa y el número de personas que lo hacen en el mismo vehículo, pero no sobre su coeficiente inte- lectual, ingreso, tamaño de su familia y otras características. Por otra parte, un investigador puede probar una muestra de componentes y anotar sólo el número de los que han fallado dentro de 1000 horas, en lugar de anotar los tiempos de falla individuales. En general, cada resultado de un experimento puede ser asociado con un número es- pecificando una regla de asociación (p. ej., el número entre la muestra de diez componentes que no duran 1000 horas o el peso total del equipaje en una muestra de 25 pasajeros de ae- rolínea). Semejante regla de asociación se llama variable aleatoria, variable porque dife- rentes valores numéricos son posibles y aleatoria porque el valor observado depende de cuál de los posibles resultados experimentales resulte (figura 3.1). 3.1 Variables aleatorias 87 3.1 Variables aleatorias Se acostumbra denotar las variables aleatorias con letras mayúsculas, tales como X y Y, que son las de cerca del final del alfabeto. En contraste al uso previo de una letra minúscu- la, tal como x, para denotar una variable, ahora se utilizarán letras mayúsculas para repre- sentar algún valor particular de la variable aleatoria correspondiente. La notación X(s) x significa que x es el valor asociado con el resultado s por la va X. Cuando un estudiante intenta entrar a un sistema de tiempo compartido de computadora, o todos los puertos están ocupados (F), en cuyo caso el estudiante no podrá tener acceso o hay por lo menos un puerto libre (S), en cuyo caso el estudiante sí podrá tener acceso al siste- ma. Con S {S, F}, la va X se define como X(S) 1 X(F) 0 La va X indica si (1) o no (2) el estudiante puede entrar al sistema. ■ La va X en el ejemplo 3.1 se especificó al poner en lista explícitamente cada elemen- to de S y el número asociado. Una lista como esa es tediosa si S contiene más de algunos cuantos resultados, pero con frecuencia puede ser evitada. Figura 3.1 Una variable aleatoria. 2 1 0 1 2 DEFINICIÓN Para un espacio muestral dado S de algún experimento, una variable aleatoria (va, o rv, por sus siglas en inglés) es cualquier regla que asocia un número con cada resul- tado en S. En lenguaje matemático, una variable aleatoria es una función cuyo domi- nio es el espacio muestral y cuyo rango es el conjunto de números reales. Ejemplo 3.1 c3_p086-129.qxd 3/12/08 4:01 AM Page 87
- 106. Considere el experimento en el cual un número telefónico en cierto código de área es elegi- do con un marcador de números aleatorio (tales dispositivos los utilizan en forma extensa organizaciones encuestadoras) y defina una va Y como Y {1 si el número seleccionado no aparece en el directorio 0 si el número seleccionado sí aparece en el directorio Por ejemplo, si 5282966 aparece en el directorio telefónico, entonces Y(5282966) 0 en tanto que Y(7727350) dice que el número 7727350 no aparece en el directorio telefóni- co. Una descripción en palabras de esta índole es más económica que una lista completa, por lo que se utilizará tal descripción siempre que sea posible. ■ En los ejemplos 3.1 y 3.2, los únicos valores posibles de la variable aleatoria fueron 0 y 1. Tal variable aleatoria se presenta con suficiente frecuencia como para darle un nom- bre especial, en honor del individuo que la estudió primero. 88 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.2 DEFINICIÓN Cualquier variable aleatoria cuyos únicos valores posibles son 0 y 1 se llama varia- ble aleatoria de Bernoulli. En ocasiones se deseará definir y estudiar varias variables diferentes del mismo espa- cio muestral. El ejemplo 2.3 describe un experimento en el cual se determinó el número de bombas en uso en cada una de dos gasolinerías. Defina las variables aleatorias X, Y y U como X el número total de bombas en uso en las dos gasolinerías. Y la diferencia entre el número de bombas en uso en la gasolinería 1 y el número en uso en la gasolinería 2. U el máximo de los números de bombas en uso en las dos gasolinerías. Si se realiza este experimento y s (2, 3) se obtiene entonces X((2, 3)) 2 3 5, por lo que se dice que el valor observado de X fue x 5. Asimismo, el valor observado de Y se- ría y 2 3 1 y el de U sería u máx(2, 3) 3. ■ Cada una de las variables aleatorias de los ejemplos 3.1–3.3 puede asumir sólo un nú- mero finito de posibles valores. Éste no tiene que ser el caso. En el ejemplo 2.4, se consideraron experimentos en los cuales se examinaron baterías has- ta que se obtuvo una buena (S). El espacio muestral fue S {S, FS, FFS, . . .}. Defina una variable aleatoria X como X el número de baterías examinadas antes que se termine el experimento. En ese caso X(S) 1, X(FS) 2, X(FFS) 3, . . . , X(FFFFFFS) 7, y así sucesivamen- te. Cualquier entero positivo es un valor positivo de X, así que el conjunto de valores posi- bles es infinito. ■ Suponga que del mismo modo aleatorio, se selecciona un lugar (latitud y longitud) en los Estados Unidos continentales. Defina una variable aleatoria Y como Y la altura sobre el nivel del mar en el lugar seleccionado. Por ejemplo, si el lugar seleccionado fuera (39° 50N, 98° 35O, entonces se podría tener Y((39° 50N, 98° 35O)) 1748.26 pies. El valor más grande posible de Y es 14 494 Ejemplo 3.3 Ejemplo 3.4 Ejemplo 3.5 c3_p086-129.qxd 3/12/08 4:01 AM Page 88
- 107. (Monte Whitney) y el valor más pequeño posible es 282 (Valle de la Muerte). El conjun- to de todos los valores posibles de Y es el conjunto de todos los números en el intervalo en- tre 282 y 14 494, es decir, {y: y es un número, 282 y 14 494} y existe un número infinito de números en este intervalo. ■ Dos tipos de variables aleatorias En la sección 1.2, se distinguió entre los datos que resultan de observaciones de una varia- ble de conteo y los datos obtenidos observando valores de una variable de medición. Una distinción un poco más formal caracteriza dos tipos diferentes de variables aleatorias. 3.1 Variables aleatorias 89 DEFINICIÓN Una variable aleatoria discreta es una variable aleatoria cuyos valores posibles o constituyen un conjunto finito o bien pueden ser puestos en lista en una secuencia in- finita en la cual existe un primer elemento, un segundo elemento, y así sucesivamen- te (“contablemente” infinita). Una variable aleatoria es continua si ambas de las siguientes condiciones aplican: 1. Su conjunto de valores posibles se compone de o todos los números que hay en un solo intervalo sobre la línea de numeración (posiblemente de extensión infinita, es decir, desde hasta ) o todos los números en una unión excluyente de dichos intervalos (p. ej., [0, 10] [20, 30]). 2. Ningún valor posible de la variable aleatoria tiene probabilidad positiva, esto es, P(X c) 0 con cualquier valor posible de c. Aunque cualquier intervalo sobre la línea de numeración contiene un número infinito de nú- meros, se puede demostrar que no existe ninguna forma de crear una lista infinita de todos estos valores, existen sólo demasiados de ellos. La segunda condición que describe una va- riable aleatoria continua es tal vez contraintuitiva, puesto que parecería que implica una pro- babilidad total de cero con todos los valores posibles. Pero en el capítulo 4 se verá que los intervalos de valores tienen probabilidad positiva; la probabilidad de un intervalo se reduci- rá a cero a medida que su ancho tienda a cero. Todas las variables aleatorias de los ejemplos 3.1-3.4 son discretas. Como otro ejemplo, su- ponga que se eligen al azar parejas de casados y que a cada persona se le hace una prueba de sangre hasta encontrar un esposo y esposa con el mismo factor Rh. Con X el núme- ro de pruebas de sangre que serán realizadas, los posibles valores de X son D {2, 4, 6, 8, . . .}. Como los posibles valores se dieron en secuencia, X es una variable aleatoria discreta. ■ Para estudiar las propiedades básicas de las variables aleatorias discretas, sólo se re- quieren las herramientas de matemáticas discretas: sumas y diferencias. El estudio de varia- bles continuas requiere las matemáticas continuas del cálculo: integrales y derivadas. Ejemplo 3.6 EJERCICIOS Sección 3.1 (1-10) 1. Una viga de concreto puede fallar o por esfuerzo cortante (S) o flexión (F). Suponga que se seleccionan al azar tres vigas que fallaron y que se determina el tipo de falla de cada una. Sea X el número de vigas entre las tres seleccionadas que fallaron por cortante. Ponga en lista cada resultado en el es- pacio muestral junto con el valor asociado de X. 2. Dé tres ejemplos de variables aleatorias de Bernoulli (apar- te de los que aparecen en el texto). 3. Con el experimento del ejemplo 3.3, defina dos variables aleatorias más y mencione los valores posibles de cada una. 4. Sea X el número de dígitos no cero en un código postal seleccionado al azar. ¿Cuáles son los posibles valores de X? Dé tres posibles resultados y sus valores X asociados. 5. Si el espacio muestral S es un conjunto infinito, ¿implica es- to necesariamente que cualquier variable aleatoria X definida c3_p086-129.qxd 3/12/08 4:01 AM Page 89
- 108. a partir de S tendrá un conjunto infinito de posibles valores? Si la respuesta es sí, diga por qué. Si es no, dé un ejemplo. 6. A partir de una hora fija, cada carro que entra a una intersec- ción es observado para ver si da vuelta a la izquierda (L), la derecha (R) o si sigue de frente (A). El experimento termina en cuanto se observa que un carro da vuelta a la izquierda. Sea X el número de carros observados. ¿Cuáles son los posibles valores de X? Dé cinco resultados y sus valores X asociados. 7. Para cada variable definida aquí, describa el conjunto de po- sibles valores de la variable y diga si la variable es discreta. a. X el número de huevos no quebrados en una caja de huevos estándar seleccionada al azar. b. Y el número de estudiantes en una lista de clase de un curso particular que no asisten el primer día de clases. c. U el número de veces que un novato tiene que hacerle “swing” a una pelota de golf antes de golpearla. d. X la longitud de una serpiente de cascabel selecciona- da en forma aleatoria. e. Z la cantidad de regalías devengada por la venta de la primera edición de 10 000 libros de texto. f. Y el pH de una muestra de suelo elegida al azar. g. X la tensión (lb/pulg2 ) a la cual una raqueta de tenis se- leccionada al azar fue encordada. h. X el número total de lanzamientos al aire de una mo- neda requerido para que tres individuos obtengan una coincidencia (HHH o TTT ). 8. Cada vez que un componente se somete a prueba, ésta es un éxito (E) o una falla (F). Suponga que el componente se prueba repetidamente hasta que ocurre un éxito en tres pruebas consecutivas. Sea Y el número de pruebas necesa- rio para lograrlo. Haga una lista de todos los resultados correspondientes a los primeros posibles valores más peque- ños de Y y diga qué valor de Y está asociado con cada uno. 9. Un individuo de nombre Claudius se encuentra en el punto 0 del diagrama adjunto. Con un dispositivo de aleatorización apropiado (tal como un dado tetraédrico, uno que tiene cuatro lados), Claudius pri- mero se mueve a uno de los cuatro lugares B1, B2, B3, B4. Una vez que está en uno de estos lugares, se utiliza otro dis- positivo de aleatorización para decidir si Claudius regresa a 0 o visita uno de los otros dos lugares adyacentes. Este proceso continúa entonces; después de cada movimiento, se determina otro movimiento a uno de los (nuevos) pun- tos adyacentes lanzando al aire un dado o moneda apro- piada. a. Sea X el número de movimientos que Claudius hace antes de regresar a 0. ¿Cuáles son los posibles valores de X? ¿Es X discreta o continua? b. Si también se permiten movimientos a lo largo de los tra- yectos diagonales que conectan 0 con A1, A2, A3 y A4, res- pectivamente, responda la pregunta del inciso a). 10. Se determinará el número de bombas en uso tanto en la ga- solinería de seis bombas como en la gasolinería de cuatro bombas. Dé los posibles valores de cada una de las siguien- tes variables aleatorias: a. T el número total de bombas en uso. b. X la diferencia entre el número en uso en las gasoline- rías 1 y 2. c. U el número máximo de bombas en uso en una u otra gasolinería. d. Z el número de gasolinerías que tienen exactamente dos bombas en uso. 90 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad B2 A3 A2 0 B1 A1 B4 A4 B3 Las probabilidades asignadas a varios resultados en S determinan a su vez las probabilidades asociadas con los valores de cualquier variable aleatoria X particular. La distribución de pro- babilidad de X dice cómo está distribuida (asignada) la probabilidad total de 1 entre los va- rios posibles valores de X. Supóngase, por ejemplo, que una empresa acaba de adquirir cuatro impresoras láser y sea X el número entre éstas que requieren servicio durante el periodo de garantía. Los posibles valores de X son entonces 0, 1, 2, 3 y 4. La distribución de probabili- dad dirá cómo está subdividida la probabilidad de 1 entre estos cinco posibles valores: cuán- ta probabilidad está asociada con el valor 0 de X, cuánta está adjudicada al valor 1 de X, y así sucesivamente. Se utilizará la siguiente notación para las probabilidades en la notación: p(0) la probabilidad del valor 0 de X P(X 0) p(1) la probabilidad del valor 1 de X P(X 1) y así sucesivamente. En general, p(x) denotará la probabilidad asignada al valor de x. 3.2 Distribuciones de probabilidad para variables aleatorias discretas c3_p086-129.qxd 3/12/08 4:01 AM Page 90
- 109. En palabras, para cada valor posible x de la variable aleatoria, la función masa de pro- babilidad especifica la probabilidad de observar dicho valor cuando se realiza el experimen- to. Se requieren las condiciones p(x) 0 y todas las x posibles p(x) 1 de cualquier función masa de probabilidad. La función masa de probabilidad de X en el ejemplo previo se dio simplemente en la descripción del problema. A continuación se consideran varios ejemplos en los cuales va- rias propiedades de probabilidad son explotadas para obtener la distribución deseada. Seis lotes de componentes están listos para ser enviados por un proveedor. El número de componentes defectuosos en cada lote es como sigue: Lote 1 2 3 4 5 6 Número de defectuosos 0 2 0 1 2 0 Uno de estos lotes tiene que ser seleccionado al azar para ser enviado a un cliente particu- lar. Sea X el número de defectuosos en el lote seleccionado. Los tres posibles valores de X Una cierta gasolinería tiene seis bombas. Sea X el número de bombas que están en servicio a una hora particular del día. Suponga que la distribución de probabilidad de X es como se da en la tabla siguiente; la primera fila de la tabla contiene los posibles valores de X y la se- gunda da la probabilidad de dicho valor. 3.2 Distribuciones de probabilidad para variables aleatorias discretas 91 Ejemplo 3.7 x 0 1 2 3 4 5 6 p(x) 0.05 0.10 0.15 0.25 0.20 0.15 0.10 Ahora se pueden usar propiedades de probabilidad elemental para calcular otras probabili- dades de interés. Por ejemplo, la probabilidad de que cuando mucho dos bombas estén en servicio es P(X 2) P(X 0 o 1 o 2) p(0) p(1) p(2) 0.05 0.10 0.15 0.30 Como el evento de que por lo menos 3 bombas estén en servicio es complementario a cuan- do mucho 2 bombas están en servicio. P(X 3) 1 P(X 2) 1 0.30 0.70 la que, desde luego, también se obtiene sumando las probabilidades de los valores 3, 4, 5 y 6. La probabilidad de que entre 2 y 5 bombas inclusive estén en servicio es P(2 X 5) P(X 2, 3, 4 o 5) 0.15 0.25 0.20 0.15 0.75 en tanto que la probabilidad de que el número de bombas en servicio esté estrictamente en- tre 2 y 5 es P(2 X 5) P(X 3 o 4) 0.25 0.20 0.45 ■ DEFINICIÓN La distribución de probabilidad o función masa de probabilidad (fmp) de una va- riable discreta se define para cada número x como p(x) P(X x) P(todas las s S: X(s) x). Ejemplo 3.8 c3_p086-129.qxd 3/12/08 4:01 AM Page 91
- 110. son 0, 1 y 2. De los seis eventos simples igualmente probables, tres dan por resultado X 0, uno X 1 y los otros dos X 2. Entonces p(0) P(X 0) P(el lote 1 o 3 o 6 es enviado) 3 6 0.5 p(1) P(X 1) P(el lote 4 es enviado) 1 6 0.167 p(2) P(X 2) P(el lote 2 o 5 es enviado) 2 6 0.333 Es decir, una probabilidad de 0.5 se asigna al valor 0 de X, una probabilidad de 0.167 se asigna al valor 1 de X y la probabilidad restante 0.333 se asocia con el valor 2 de X. Los va- lores de X junto con sus probabilidades especifican la función de masa de probabilidad. Si este experimento se repitiera una y otra vez, a la larga X 0 ocurriría la mitad del tiempo, X 1 un sexto del tiempo y X 2 un tercio del tiempo. ■ Considere si la siguiente persona que compre una computadora en una librería universitaria comprará un modelo portátil o uno de escritorio. Sea X {1 si el cliente compra una computadora portátil 0 si el cliente compra una computadora de escritorio Si 20% de todas las compras durante esa semana seleccionan una portátil, la función masa de probabilidad de X es p(0) P(X 0) P(el siguiente cliente compra un modelo de escritorio) 0.8 p(1) P(X 1) P(el siguiente cliente compra un modelo portátil) 0.2 p(x) P(X x) 0 con x 0 o 1 Una descripción equivalente es p(x) { 0.8 si x 0 0.2 si x 1 0 si x 0 o 1 La figura 3.2 es una ilustración de esta función masa de probabilidad, llamada gráfica li- neal. X es, desde luego, una variable aleatoria de Bernoulli y p(x) es una función masa de probabilidad de Bernoulli. 92 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.9 Ejemplo 3.10 1 1 x p(x) 0 Figura 3.2 Gráfica lineal de la función de masa de probabilidad en el ejemplo 3.9. ■ Considere un grupo de cinco donadores de sangre potenciales, a, b, c, d y e, de los cuales sólo a y b tienen sangre tipo O. Se determinará en orden aleatorio el tipo de sangre con cinco muestras, una de cada individuo hasta que se identifique un individuo O. Sea la c3_p086-129.qxd 3/12/08 4:01 AM Page 92
- 111. variable aleatoria Y el número de exámenes de sangre para identificar un individuo O. Entonces la función masa de probabilidad de Y es p(1) P(Y 1) P(a o b examinados primero) 0.4 p(2) P(Y 2) P(c, d o e primero y luego a o b) P(c, d o e primero) P(a o b a continuación°c, d o e primero) 0.3 p(3) P(Y 3) P(c, d o e primero y segundo y luego a o b) 0.2 p(4) P(Y 4) P(c, d y e primero) 0.1 p(y) 0 si y 1, 2, 3, 4 En forma tabular, la función de masa de probabilidad es 1 3 2 4 3 5 2 3 2 4 3 5 2 4 3 5 2 5 3.2 Distribuciones de probabilidad para variables aleatorias discretas 93 y 1 2 3 4 p(y) 0.4 0.3 0.2 0.1 donde cualquier valor de y que no aparece en la tabla recibe cero probabilidad. La figura 3.3 muestra una gráfica lineal de la función de masa de probabilidad. 0.5 p(y) 1 y 0 2 3 4 0 1 1 2 3 4 a) b) Figura 3.3 Gráfica lineal de la función de masa de probabilidad en el ejemplo 3.10. ■ Figura 3.4 Histogramas de probabilidad: a) ejemplo 3.9; b) ejemplo 3.10. Un modelo utilizado en física para un sistema de “masas puntuales” sugirió el nom- bre “función masa de probabilidad”. En este modelo, las masas están distribuidas en varios x lugares a lo largo de un eje unidimensional. La función masa de probabilidad describe có- mo está distribuida la masa de probabilidad total de 1 en varios puntos a lo largo del eje de posibles valores de la variable aleatoria (dónde y cuánta masa hay en cada x). Otra representación pictórica útil de una función de masa de probabilidad, llamada histograma de probabilidad, es similar a los histogramas discutidos en el capítulo 1. So- bre cada y con p(y) 0, se construye un rectángulo con su centro en y. La altura de cada rectángulo es proporcional a p(y) y la base es la misma para todos los rectángulos. Cuando los valores posibles están equidistantes, con frecuencia se selecciona la base como la dis- tancia entre valores y sucesivos (aunque podría ser más pequeña). La figura 3.4 muestra dos histogramas de probabilidad. c3_p086-129.qxd 3/12/08 4:01 AM Page 93
- 112. A menudo es útil pensar en una función masa de probabilidad como un modelo matemáti- co de una población discreta. Considere seleccionar al azar un estudiante de entre los 15 000 inscritos en el semestre ac- tual en la Universidad Mega. Sea X el número de cursos en los cuales el estudiante selec- cionado está inscrito y suponga que X tiene la siguiente función masa de probabilidad. 94 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.11 x 1 2 3 4 5 6 7 p(x) 0.01 0.03 0.13 0.25 0.39 0.17 0.02 Una forma de ver esta situación es pensar en la población como compuesta de 15 000 individuos, cada uno con su propio valor X; la proporción con cada valor de X está dada por p(x). Un punto de vista alternativo es olvidarse de los estudiantes y pensar en la población como compuesta de los valores X: Existen algunos 1 en la población, algunos 2, . . . y final- mente algunos 7. La población se compone entonces de los números, 1, 2, . . . , 7 (por lo tan- to es discreta) y p(x) da un modelo para la distribución de los valores de población. ■ Una vez que se tiene el modelo de la población, se utilizará para calcular valores de características de la población (p. ej., la media ) y para hacer inferencias sobre tales carac- terísticas. Parámetro de una distribución de probabilidad En el ejemplo 3.9, se tuvo p(0) 0.8 y p(1) 0.2 porque 20% de todos los compradores seleccionaron una computadora portátil. En otra librería, puede ser el caso que p(0) 0.9 y p(1) 0.1. Más generalmente, la función masa de probabilidad de cualquier variable alea- toria de Bernoulli puede ser expresada en la forma p(1) y p(0) 1 , donde 0 1. Como la función masa de probabilidad depende del valor particular de , con frecuencia se escribe p(x; ) en lugar de sólo p(x): p(x; ) { 1 si x 0 si x 1 (3.1) 0 de lo contrario Entonces cada opción de en la expresión (3.1) da una función de masa de probabilidad di- ferente. DEFINICIÓN Supóngase que p(x) depende de la cantidad que puede ser asignada a cualesquiera de varios valores posibles y cada valor determina una distribución de probabilidad dife- rente. Tal cantidad se llama parámetro de distribución. El conjunto de todas las dis- tribuciones de probabilidad con diferentes valores del parámetro se llama familia de distribuciones de probabilidad. La cantidad en la expresión (3.1) es un parámetro. Cada número diferente entre 0 y 1 determina un miembro diferente de una familia de distribuciones; dos de esos miem- bros son p(x; 0.6) { 0.4 si x 0 y p(x; 0.5) { 0.5 si x 0 0.6 si x 1 0.5 si x 1 0 de lo contrario 0 de lo contrario Toda distribución de probabilidad de una variable aleatoria de Bernoulli tiene la forma de la expresión (3.1), por lo tanto se llama familia de distribuciones de Bernoulli. c3_p086-129.qxd 3/12/08 4:01 AM Page 94
- 113. A partir de un tiempo fijo, se observa el sexo de cada niño recién nacido en un hospital has- ta que nace un varón (B). Sea p P(B) y suponga que los nacimientos sucesivos son inde- pendientes y defina la variable aleatoria X como X número de nacimientos observados. Entonces p(1) P(X 1) P(B) p p(2) P(X 2) P(GB) P(G) P(B) (1 p)p y p(3) P(X 3) P(GGB) P(G) P(G) P(B) (1 p)2 p Continuando de esta manera, emerge una fórmula general: p(x) {(1 p)x1 p x 1, 2, 3, . . . 0 de lo contrario (3.2) La cantidad p en la expresión (3.2) representa un número entre 0 y 1 y es un parámetro de la distribución de probabilidad. En el ejemplo de sexo, p 0.51 podría ser apropiada, pero si se estuviera buscando el primer niño con sangre Rh positivo, entonces se podría tener p 0.85. ■ Función de distribución acumulativa Para algún valor fijo x, a menudo se desea calcular la probabilidad de que el valor obser- vado de X será cuando mucho x. Por ejemplo, la función masa de probabilidad en el ejem- plo 3.8 fue ¨ 0.500 x 0 p(x) ©0.167 x 1 0.333 x 2 ª 0 de lo contrario La probabilidad de que X sea cuando mucho de 1 es entonces P(X 1) p(0) p(1) 0.500 0.167 0.667 En este ejemplo, X 1.5 si y sólo si X 1, por lo tanto P(X 1.5) P(X 1) 0.667 Asimismo, P(X 0) P(X 0) 0.5, P(X 0.75) 0.5 y de hecho con cualquier x que satisfaga 0 x 1, P(X x) 0.5. El valor X más grande posible es 2, por lo tanto P(X 2) 1, P(X 3.7) 1, P(X 20.5) 1 y así sucesivamente. Obsérvese que P(X 1) P(X 1) puesto que la segunda parte de la desigualdad incluye la probabilidad del valor 1 de X, en tanto que la primera no. Más generalmente, cuando X es discreta y x es un valor posible de la variable, P(X x) P(X x). 3.2 Distribuciones de probabilidad para variables aleatorias discretas 95 Ejemplo 3.12 DEFINICIÓN La función de distribución acumulativa (fda) F(x) de una variable aleatoria discre- ta X con función masa de probabilidad p(x) se define para cada número x como F(x) P(X x) y: yx p(y) (3.3) Para cualquier número x, F(x) es la probabilidad de que el valor observado de X será cuando mucho x. c3_p086-129.qxd 3/12/08 4:01 AM Page 95
- 114. La función masa de probabilidad de Y (el número de determinaciones de tipo de sangre) en el ejemplo 3.10 fue 96 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.13 y 1 2 3 4 p(y) 0.4 0.3 0.2 0.1 Primero se determina F(y) para cada uno de los valores posibles del conjunto (1, 2, 3, 4): F(1) P(Y 1) P(Y 1) p(1) 0.4 F(2) P(Y 2) P(Y 1 o 2) p(1) p(2) 0.7 F(3) P(Y 3) P(Y 1 o 2 o 3) p(1) p(2) p(3) 0.9 F(4) P(Y 4) P(Y 1 o 2 o 3 o 4) 1 Ahora con cualquier otro número y, F(y) será igual al valor de F con el valor más próximo posible de Y a la izquierda de y. Por ejemplo, F(2,7) P(Y 2.7) P(Y 2) 0.7 y F(3.999) F(3) 0.9. La función de distribución acumulativa es por lo tanto ¨ 0 si y 1 « 0.4 si 1 y 2 F(y) © 0.7 si 2 y 3 « 0.9 si 3 y 4 ª 1 si 4 y En la figura 3.5 se muestra una gráfica de F(y). Para una variable aleatoria discreta X, la gráfica de F(x) mostrará un salto con cada valor posible de X y será plana entre los valores posibles. Tal gráfica se conoce como fun- ción escalonada. En el ejemplo 3.12, cualquier entero fue un valor posible de X y la comprobación fue p(x) {(1 p)x1 p x 1, 2, 3, . . . 0 de lo contrario Con cualquier entero positivo x, F(x) yx p(y) x y1 (1 p)y1 p p x 1 y0 (1 p)y (3.4) Para evaluar esta suma, se utiliza el hecho de que la suma parcial de una serie geométrica es k y0 ay Utilizando esta ecuación (3.4), con a 1 p y k x 1, se obtiene F(x) p 1 (1 p)x un entero positivo x 1 (1 p)x 1 (1 p) 1 ak1 1 a 1 y F(y) 2 3 4 1 Figura 3.5 Gráfica de la función de distribución acumulativa del ejemplo 3.13. ■ Ejemplo 3.14 c3_p086-129.qxd 3/12/08 4:01 AM Page 96
- 115. Como F es una constante entre enteros positivos F(x) { 0 x 1 1 (1 p)[x] x 1 (3.5) donde [x] es el entero más grande x (p. ej., [2.7] 2). Así pues, si p 0.51 como el ejem- plo de los nacimientos, entonces la probabilidad de tener que examinar cuando mucho cinco nacimientos para ver el primer niño es F(5) 1 (0.49)5 1 0.0282 0.9718, mien- tras que F(10) 1.0000. Esta función de distribución acumulativa se ilustra en la figura 3.6. 3.2 Distribuciones de probabilidad para variables aleatorias discretas 97 En los ejemplos presentados hasta ahora, la función de distribución acumulativa se de- rivó de la función masa de probabilidad. Este proceso puede ser invertido para obtener la función masa de probabilidad de la función de distribución acumulativa siempre que ésta esté disponible. Por ejemplo, considérese otra vez la variable aleatoria del ejemplo 3.7 (el número de bombas en servicio en una gasolinería); los valores posibles de X son 0, 1, . . . , 6. Entonces p(3) P(X 3) [p(0) p(1) p(2) p(3)] [p(0) p(1) p(2)] P(X 3) P(X 2) F(3) F(2) Más generalmente, la probabilidad de que X quede dentro de un intervalo especificado es fácil de obtener a partir de la función de distribución acumulativa. Por ejemplo, P(2 X 4) p(2) p(3) p(4) [p(0) . . . p(4)] [p(0) p(1)] P(X 4) P(X 1) F(4) F(1) Obsérvese que P(2 X 4) F(4) F(2). Esto es porque el valor 2 de X está incluido en 2 X 4, así que no se desea restar su probabilidad. Sin embargo, P(2 X 4) F(4) F(2) porque X 2 no está incluido en el intervalo 2 X 4. x F(x) 1 0 1 2 3 4 5 50 51 Figura 3.6 Gráfica de F(x) del ejemplo 3.14. ■ PROPOSICIÓN Para dos números cualesquiera a y b con a b. P(a X b) F(b) F(a ) donde “a” representa el valor posible de X más grande que es estrictamente menor que a. En particular, si los únicos valores posibles son enteros y si a y b son enteros, entonces P(a X b) P(X a o a 1 o . . . o b) F(b) F(a 1) Con a b se obtiene P(X a) F(a) F(a 1) en este caso. c3_p086-129.qxd 3/12/08 4:01 AM Page 97
- 116. La razón para restar F(a) en lugar de F(a) es que se desea incluir P(X a); F(b) F(a) da P(a X b). Esta proposición se utilizará extensamente cuando se calcu- len las probabilidades binomial y de Poisson en las secciones 3.4 y 3.6. Sea X el número de días de ausencia por enfermedad tomados por un empleado seleccio- nado al azar de una gran compañía durante un año particular. Si el número máximo de días de ausencia por enfermedad permisibles al año es de 14, los valores posibles de X son 0, 1, . . . , 14. Con F(0) 0.58, F(1) 0.72, F(2) 0.76, F(3) 0.81, F(4) 0.88 y F(5) 0.94, P(2 X 5) P(X 2, 3, 4 o 5) F(5) F(1) 0.22 y P(X 3) F(3) F(2) 0.05 ■ 98 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.15 EJERCICIOS Sección 3.2 (11-28) 11. En un taller de servicio automotriz especializado en afinacio- nes se sabe que 45% de todas las afinaciones se realizan en automóviles de cuatro cilindros, 40% en automóviles de seis cilindros y 15% en automóviles de ocho cilindros. Sea X el número de cilindros en el siguiente carro que va a ser afinado. a. ¿Cuál es la función masa de probabilidad de X? b. Trace tanto una gráfica lineal como un histograma de probabilidad de la función masa de probabilidad del inciso a). c. ¿Cuál es la probabilidad de que el siguiente carro afinado sea de por lo menos seis cilindros? ¿Más de seis cilin- dros? 12. Las líneas aéreas en ocasiones venden boletos de más. Su- ponga que para un avión de 50 asientos, 55 pasajeros tienen boletos. Defina la variable aleatoria Y como el número de pasajeros con boletos que en realidad aparecen para el vue- lo. La función masa de probabilidad de Y aparece en la tabla adjunta. a. ¿Cuál es la probabilidad de que el vuelo acomodará a to- dos los pasajeros con boleto que aparecieron? b. ¿Cuál es la probabilidad de que no todos los pasajeros con boleto que aparecieron puedan ser acomodados? c. Si usted es la primera persona en la lista de espera (lo que significa que será el primero en abordar el avión si hay boletos disponibles después de que todos los pasajeros con boleto hayan sido acomodados), ¿cuál es la probabi- lidad de que podrá tomar el vuelo? ¿Cuál es esta proba- bilidad si usted es la tercera persona en la lista de espera? 13. Una empresa de ventas en línea dispone de seis líneas telefó- nicas. Sea X el número de líneas en uso en un tiempo espe- cificado. Suponga que la función masa de probabilidad de X es la que se da en la tabla adjunta. Calcule la probabilidad de cada uno de los siguientes eventos. a. {cuando mucho tres líneas están en uso} b. {menos de tres líneas están en uso} c. {por lo menos tres líneas están en uso} d. {entre dos y cinco líneas, inclusive, están en uso} e. {entre dos y cuatro líneas, inclusive, no están en uso f. {por lo menos cuatro líneas no están en uso} 14. El departamento de planeación de un condado requiere que un contratista presente uno, dos, tres, cuatro o cinco formas (según la naturaleza del proyecto) para solicitar un permiso de construcción. Sea Y número de formas requeridas del siguiente solicitante. Se sabe que la probabilidad de que se requieran y formas es proporcional a y, es decir, p(y) ky con y 1, . . . , 5. a. ¿Cuál es el valor de k? [Sugerencia: 5 y1 p(y) 1.] b. ¿Cuál es la probabilidad de que cuando mucho se requie- ran tres formas? c. ¿Cuál es la probabilidad de que se requieran entre dos y cuatro formas (inclusive)? d. ¿Podría ser p(y) y2 /50 con y 1, . . . , 5 la función masa de probabilidad de Y? 15. Muchos fabricantes cuentan con programas de control de ca- lidad que incluyen la inspección de los materiales recibidos en busca de defectos. Suponga que un fabricante de compu- tadoras recibe tarjetas madre en lotes de cinco. Se seleccio- nan dos tarjetas de cada lote para inspeccionarlas. Se pueden representar los posibles resultados del proceso de selección por pares. Por ejemplo, el par (1, 2) representa la selec- ción de las tarjetas 1 y 2 para inspección. a. Mencione los diez posibles resultados diferentes. b. Suponga que las tarjetas 1 y 2 son las únicas tarjetas de- fectuosas en un lote de cinco. Dos tarjetas tienen que ser seleccionadas al azar. Defina X como el número de tarje- tas defectuosas observadas entre las inspeccionadas. En- cuentre la distribución de probabilidad de X. c. Sea F(x) la función de distribución acumulativa de X. Pri- mero determine F(0) P(X 0), F(1) y F(2); luego ob- tenga F(x) para todas las demás x. 16. Algunas partes de California son particularmente propensas a los temblores. Suponga que en un área metropolitana, 30% de todos los propietarios de casa están asegurados contra da- ños provocados por terremotos. Se seleccionan al azar cuatro y 45 46 47 48 49 50 51 52 53 54 55 p(y) 0.05 0.10 0.12 0.14 0.25 0.17 0.06 0.05 0.03 0.02 0.01 x 0 1 2 3 4 5 6 p(x) 0.10 0.15 0.20 0.25 0.20 0.06 0.04 c3_p086-129.qxd 3/12/08 4:01 AM Page 98
- 117. propietarios de casa, sea X el número entre los cuatro que es- tán asegurados contra terremotos. a. Encuentre la distribución de probabilidad de X [Sugeren- cia: Sea S un propietario de casa asegurado y F uno no asegurado. Entonces un posible resultado es SFSS, con probabilidad (0.3)(0.7)(0.3)(0.3) y el valor 3 de X asocia- do. Existen otros 15 resultados.] b. Trace el histograma de probabilidad correspondiente. c. ¿Cuál es el valor más probable de X? d. ¿Cuál es la probabilidad de que por lo menos dos de los cuatro seleccionados estén asegurados contra terremotos? 17. El voltaje de una batería nueva puede ser aceptable (A) o inaceptable (U). Una linterna requiere dos baterías, así que las baterías serán independientemente seleccionadas y pro- badas hasta encontrar dos aceptables. Suponga que 90% de todas las baterías tienen voltajes aceptables. Sea Y el núme- ro de baterías que deben ser probadas. a. ¿Cuál es p(2), es decir P(Y 2)? b. ¿Cuál es p(3)? [Sugerencia: Existen dos resultados dife- rentes que producen Y 3.] c. Para tener Y 5, ¿qué debe ser cierto de la quinta bate- ría seleccionada? Mencione los cuatro resultados con los cuales Y 5 y luego determine p(5). d. Use el patrón de sus respuestas en los incisos a)–c) para obtener una fórmula general para p(y). 18. Dos dados de seis caras son lanzados al aire en forma inde- pendiente. Sea M el máximo de los dos lanzamientos (por lo tanto M(1, 5) 5, M(3, 3) 3, etcétera). a. ¿Cuál es la función masa de probabilidad de M? [Suge- rencia: Primero determine p(1), luego p(2), y así sucesi- vamente.] b. Determine la función de distribución acumulativa de M y dibújela. 19. Una biblioteca se suscribe a dos revistas de noticias semana- les, cada una de las cuales se supone que llega en el correo de los miércoles. En realidad, cada una puede llegar el miér- coles, jueves, viernes o sábado. Suponga que las dos llegan independientemente una de otra y para cada una P(mié) 0.3, P(jue) 0.4, P(vie) 0.2 y P(sáb) 0.1. Sea Y el número de días después del miércoles que pasan para que am- bas revistas lleguen (por lo tanto los posibles valores de Y son 0, 1, 2 o 3). Calcule la función masa de probabilidad de Y [Sugerencia: Hay 16 posibles resultados: Y(M, M) 0, Y(V, J) 2, y así sucesivamente.] 20. Tres parejas y dos individuos solteros han sido invitados a un seminario de inversión y han aceptado asistir. Suponga que la probabilidad de que cualquier pareja o individuo particular llegue tarde es de 0.4 (una pareja viajará en el mismo ve- hículo, así que ambos llegarán a tiempo o bien ambos llega- rán tarde). Suponga que diferentes parejas e individuos llegan puntuales o tarde independientemente unos de otros. Sea X el número de personas que llegan tarde al seminario. a. Determine la función masa de probabilidad de X. [Suge- rencia: Designe las tres parejas #1, #2 y #3 y los dos in- dividuos #4 y #5.] b. Obtenga la función de distribución acumulativa de X y úsela para calcular P(2 X 6). 21. Suponga que lee los números de este año del NewYork Times y que anota cada número que aparece en un artículo de noticias: el ingreso de un oficial ejecutivo en jefe, el número de cajas de vino producidas por una compañía vinícola, la contribución ca- ritativa total de un político durante el año fiscal previo, la edad de una celebridad y así sucesivamente. Ahora enfóquese en el primer dígito de cada número, el cual podría ser 1, 2, . . . , 8 o 9. Su primer pensamiento podría ser que el primer dígito X de un número seleccionado al azar sería igualmente probable que fuera una de las nueve posibilidades (una distribución uniforme discreta). Sin embargo, mucha evidencia empírica así como también algunos argumentos teóricos, sugieren una dis- tribución de probabilidad alternativa llamada ley de Benford: p(x) P(el primer dígito es x) log10 (1 1/x) x 1, 2, . . . , 9 a. Calcule las probabilidades individuales y compare con la distribución uniforme discreta correspondiente. b. Obtenga la función de distribución acumulativa de X. c. Utilizando la función de distribución acumulativa, ¿cuál es la probabilidad de que el primer dígito sea cuando mu- cho 3? ¿Por lo menos 5? [Nota: La ley de Benford es la base de algunos procedimien- tos de auditoría utilizados para detectar fraudes en reportes fi- nancieros, por ejemplo, por el Servicio de Ingresos Internos.] 22. Remítase al ejercicio 13 y calcule y trace la gráfica de la fun- ción de distribución acumulativa F(x). Luego utilícela para calcular las probabilidades de los eventos dados en los inci- sos a)–d) de dicho problema. 23. Una organización de protección al consumidor que habitual- mente evalúa automóviles nuevos reporta el número de defectos importantes encontrados en cada carro examinado. Sea X el número de defectos importantes en un carro selec- cionado al azar de cierto tipo. La función de distribución acumulativa de X es la siguiente: ¨ 0 x 0 «0.06 0 x 1 «0.19 1 x 2 F(x) ©0.39 2 x 3 « 0.67 3 x 4 «0.92 4 x 5 «0.97 5 x 6 ª 1 6 x Calcule las siguientes probabilidades directamente con la función de probabilidad acumulativa: a. p(2), es decir, P(X 2) b. P(X 3) c. P(2 X 5) d. P(2 X 5) 24. Una compañía de seguros ofrece a sus asegurados varias opcio- nes diferentes de pago de primas. Para un asegurado seleccio- nado al azar, sea X el número de meses entre pagos sucesivos. La función de distribución acumulativa es la siguiente: ¨ 0 x 1 «0.30 1 x 3 F(x) © 0.40 3 x 4 0.45 4 x 6 «0.60 6 x 12 ª 1 12 x 3.2 Distribuciones de probabilidad para variables aleatorias discretas 99 c3_p086-129.qxd 3/12/08 4:01 AM Page 99
- 118. a. ¿Cuál es la función de masa de probabilidad de X? b. Con sólo la función de distribución acumulativa, calcule P(3 X 6) y P(4 X). 25. En el ejemplo 3.12, sea Y el número de niñas nacidas antes de que termine el experimento. Con p P(B) y 1 – p P(G), ¿cuál es la función masa de probabilidad de Y? [Sugerencia: Primero ponga en lista los posibles valores de Y, inicie con el más pequeño y continúe hasta que encuentre una fórmu- la general.] 26. Alvie Singer vive en 0 en el diagrama adjunto y sus cuatro amigos viven en A, B, C y D. Un día Alvie decide visitarlos, así que lanza al aire una moneda imparcial dos veces para decidir a cuál de los cuatro visitar. Una vez que está en la casa de uno de sus amigos, o regresará a su casa o bien pro- seguirá a una de las dos casas adyacentes (tales como 0, A o C, cuando está en B) con cada una de las tres posibilidades cuya probabilidad es 1 3. De este modo, Alvie continúa visi- tando a sus amigos hasta que regresa a casa. a. Sea X el número de veces que Alvie visita a un amigo. Obtenga la función masa de probabilidad de X. b. Sea Y el número de segmentos de línea recta que Alvie recorre (incluidos los que conducen a o que parten de 0). ¿Cuál es la función masa de probabilidad de Y? c. Suponga que sus amigas viven en A y C y sus amigos en B y D. Si Z el número de visitas a amigas, ¿cuál es la función masa de probabilidad de Z? 27. Después de que todos los estudiantes salieron del salón de clases, un profesor de estadística nota que cuatro ejemplares del texto se quedaron debajo de los escritorios. Al principio de la siguiente clase, el profesor distribuye los cuatro libros al azar a cada uno de los cuatro estudiantes (1, 2, 3 y 4) que dicen haber dejado los libros. Un posible resultado es que 1 reciba el libro de 2, que 2 reciba el libro de 4 y que 3 reciba su propio libro y que 4 reciba el libro de 1. Este resultado puede ser abreviado como (2, 4, 3, 1). a. Mencione los otros 23 posibles resultados. b. Si X es el número de estudiantes que reciben su propio li- bro, determine la función masa de probabilidad de X. 28. Demuestre que la función de distribución acumulativa de F(x) es una función no decreciente; es decir, x1 x2 im- plica que F(x1) F(x2). ¿En qué condición será F(x1) F(x2)? 100 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad B C A D 0 Considérese una universidad que tiene 15 000 estudiantes y sea X el número de cursos en los cuales está inscrito un estudiante seleccionado al azar. La función de masa de probabi- lidad de X se determina como sigue. Como p(1) 0.01, se sabe que (0.01) (15000) 150 de los estudiantes están inscritos en un curso y asimismo con los demás valores de x. (3.6) El número promedio de cursos por estudiante o el valor promedio de X en la población se obtiene al calcular el número total de cursos tomados por todos los estudiantes y al dividir entre el número total de estudiantes. Como cada uno de los 150 estudiantes está tomando un curso, estos 150 contribuyen con 150 cursos al total. Asimismo, 450 estudiantes contribuyen con 2(450) cursos, y así sucesivamente. El valor promedio de la población de X es entonces 4.57 (3.7) Como 150/15 000 0.01 p(1), 450/15000 0.03 p(2), y así sucesivamente, una ex- presión alterna para (3.7) es 1 p(1) 2 p(2) . . . 7 p(7) (3.8) La expresión (3.8) muestra que para calcular el valor promedio de la población de X, sólo se necesitan los valores posibles de X junto con las probabilidades (proporciones). En particular, el tamaño de la población no viene al caso en tanto la función masa de probabi- lidad esté dada por (3.6). El valor promedio o medio de X es entonces el promedio ponde- rado de los posibles valores 1, . . . , 7, donde las ponderaciones son las probabilidades de esos valores. 1(150) 2(450) 3(1950) . . . 7(300) 15000 3.3 Valores esperados x 1 2 3 4 5 6 7 p(x) 0.01 0.03 0.13 0.25 0.39 0.17 0.02 Número de inscrito 150 450 1950 3750 5850 2550 300 c3_p086-129.qxd 3/12/08 4:01 AM Page 100
- 119. Valor esperado de X 3.3 Valores esperados 101 DEFINICIÓN Sea X una variable aleatoria discreta con un conjunto de valores posibles D y una fun- ción masa de probabilidad p(x). El valor esperado o valor medio de X, denotado por E(X) o X, es E(X) X xD x p(x) Cuando está claro a que X se refiere el valor esperado, a menudo se utiliza en lugar de X. Para la función masa de probabilidad en (3.6), 1 p(1) 2 p(2) . . . 7 p(7) (1)(0.01) 2(0.03) . . . (7)(0.02) 0.01 0.06 0.39 1.00 1.95 1.02 0.14 4.57 Si se piensa en la población como compuesta de los valores 1, 2, . . . , 7, de X, entonces 4.57 es la media de la población. En lo que sigue, a menudo se hará referencia a como la media de la población en lugar de la media de X en la población. ■ En el ejemplo 3.16, el valor esperado fue 4.57, el cual no es un valor posible de X. La palabra esperado deberá interpretarse con precaución porque no se esperaría ver un va- lor de X de 4.57 cuando se selecciona un solo estudiante. Exactamente después de nacer, cada niño recién nacido es evaluado en una escala llamada escala de Apgar. Las evaluaciones posibles son 0, 1, . . . , 10, con la evaluación del niño de- terminada por color, tono muscular, esfuerzo para respirar, ritmo cardiaco e irritabilidad re- fleja (la mejor evaluación posible es 10). Sea X la evaluación Apgar de un niño seleccionado al azar nacido en cierto hospital durante el siguiente año y supóngase que la función masa de probabilidad de X es x 0 1 2 3 4 5 6 7 8 9 10 p(x) 0.002 0.001 0.002 0.005 0.02 0.04 0.18 0.37 0.25 0.12 0.01 Entonces el valor medio de X es E(X) 0(0.002) 1(0.001) 2(0.002) . . . 8(0.25) 9(0.12) 10(0.01) 7.15 De nuevo, no es un valor posible de la variable X. Además, como la variable se refiere a un niño futuro, no existe ninguna población existente concreta a la cual se podría referir . En cambio, la función masa de probabilidad se considera como un modelo de una población compuesta de los valores 0, 1, 2, . . . , 10. El valor medio de esta población conceptual es entonces 7.15. ■ Sea X 1 si un componente seleccionado al azar necesita servicio de garantía y 0 si no. Entonces X es una variable aleatoria de Bernoulli con función masa de probabilidad ¨ 1 p x 0 p(x) © p x 1 ª 0 x 0, 1 Ejemplo 3.16 Ejemplo 3.17 Ejemplo 3.18 c3_p086-129.qxd 3/12/08 4:01 AM Page 101
- 120. a partir de la cual E(X) 0 p(0) 1 p(1) 0(1 p) 1(p) p. Es decir, el valor es- perado de X es exactamente la probabilidad de que X tome el valor 1. Si se conceptualiza una población compuesta de ceros en la proporción de 1 p y unos en la proporción de p, entonces el promedio de la proporción es p. ■ La forma general de función de masa de probabilidad de X número de niños nacidos has- ta e incluido el primer varón es p(x) {p(1 p)x1 x 1, 2, 3, . . . 0 de lo contrario De acuerdo con la definición, E(X) D x p(x) x1 xp(1 p)x1 p x1 (1 p)x (3.9) Si se intercambia el orden de tomar la derivada y la suma, ésta es la de una serie geométri- ca. Una vez que se calcula la suma, se toma la derivada y el resultado final es E(X) 1/p. Si p se aproxima a 1, se espera ver que nazca un varón muy pronto, mientras que si p se aproxima a 0, se esperan muchos nacimientos antes del primer varón. Con p 0.5, E(X) 2. ■ Existe otra interpretación frecuentemente utilizada de . Considérese la función ma- sa de probabilidad p(x) {(0.5) (0.5)x1 si x 1, 2, 3, . . . 0 de lo contrario Esta es la función masa de probabilidad de X el número de lanzamientos al aire de una moneda imparcial necesarios para obtener la primera H (cara) (un caso especial del ejem- plo 3.19). Supóngase que se observa un valor x de esta función masa de probabilidad (lan- zar al aire una moneda hasta que aparezca una H (cara), luego se observa de modo independiente otro valor (sígase lanzando al aire la moneda), luego otro y así sucesivamen- te. Si después de observar un número muy grande de valores x se promedian, el promedio muestral resultante se aproximará a 2. Es decir, puede ser interpretado como el valor promedio observado a largo plazo de X cuando el experimento se realiza de manera repetida. X es el número de entrevistas que un estudiante sostiene antes de conseguir un trabajo y tie- ne la función masa de probabilidad p(x) {k/x2 x 1, 2, 3, . . . 0 de lo contrario donde k se elige de modo que x1 (k/x2 ) 1. (En un curso de matemáticas de series infi- nitas, se demostró que x1 (1/x2 ) , lo cual implica que tal k existe, pero su valor exac- to no interesa.) El valor esperado de X es E(X) x1 x k x1 (3.10) La suma del lado derecho de la ecuación (3.10) es la famosa serie armónica de mate- máticas y se puede demostrar que tiende a . E(X) no es finita en este caso porque p(x) no disminuye suficientemente rápido a medida que x se incrementa; los estadísticos dicen que la distribución de probabilidad de X tiene “una cola gruesa”. Si se selecciona una secuencia de valores X utilizando esta distribución, el promedio muestral no se establecerá en un nú- mero finito sino que tenderá a crecer sin límite. Los estadísticos utilizan la frase “colas gruesas” en conexión con cualquier distribu- ción con una gran cantidad de probabilidad alejada de (así que las colas gruesas no re- quieren ). Tales colas gruesas hacen difícil hacer inferencias sobre . ■ 1 x k x2 d dp 102 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.19 Ejemplo 3.20 c3_p086-129.qxd 3/12/08 4:01 AM Page 102
- 121. Valor esperado de una función A menudo interesará el valor esperado de alguna función h(X) en lugar de X propiamente dicha. Suponga que una librería adquiere diez ejemplares de un libro a $6.00 cada uno para ven- derlos a $12.00 en el entendimiento de que al final de un periodo de 3 meses cualquier ejemplar no vendido puede ser compensado por $2.00. Si X el número de ejemplares ven- didos, entonces el ingreso neto h(X) 12X 2(10 X) 60 10X 40. ■ El siguiente ejemplo sugiere una forma fácil de calcular el valor esperado de h(X). Sea X el número de cilindros del motor del siguiente carro que va a ser afinado en cierto taller. El costo de una afinación está relacionado con X mediante h(X) 20 3X 0.5X2 . Como X es una variable aleatoria, también lo es h(X); denote esta última variable aleatoria por Y. Las funciones de masa de probabilidad de X y Y son las siguientes: 3.3 Valores esperados 103 Ejemplo 3.21 Ejemplo 3.22 x 4 6 8 y 40 56 76 p(x) 0.5 0.3 0.2 p(y) 0.5 0.3 0.2 Con D* denotando posibles valores de Y, E(Y) E[h(X)] D* y p(y) (3.11) (40)(0.5) (56)(0.3) (76)(0.2) h(4) (0.5) h(6) (0.3) h(8) (0.2) D h(x) p(x) De acuerdo con la ecuación (3.11), no fue necesario determinar la función masa de proba- bilidad de Y para obtener E(Y); en su lugar, el valor esperado deseado es un promedio pon- derado de los posibles valores de h(x) (y no de x). ■ Esto es, E[h(X)] se calcula del mismo modo que E(X), excepto que h(x) sustituye a x. Una tienda de computadoras adquirió tres computadoras de un tipo a $500 cada una. Las venderá a $1000 cada una. El fabricante se comprometió a readquirir cualquier computado- ra que no se haya vendido después de un periodo especificado a $200 cada una. Sea X el nú- mero de computadoras vendidas y suponga que p(0) 0.1, p(1) 0.2, p(2) 0.3 y p(3) 0.4. Con h(X) denotando la utilidad asociada con la venta de X unidades, la informa- ción dada implica que h(X) ingreso costo 1000X 200(3 X) 1500 800X 900. La utilidad esperada es entonces E[h(X)] h(0) p(0) h(1) p(1) h(2) p(2) h(3) p(3) ( 900)(0.1) ( 100)(0.2) (700)(0.3) (1500)(0.4) $700 ■ PROPOSICIÓN Si la variable aleatoria X tiene un conjunto de posibles valores D y una función masa de probabilidad p(x), entonces el valor esperado de cualquier función h(X), de- notada por E[h(X)] o h(X), se calcula con E[h(X)] D h(x) p(x) Ejemplo 3.23 c3_p086-129.qxd 3/12/08 4:01 AM Page 103
- 122. Reglas de valor esperado La función de interés h(X) con bastante frecuencia es una función lineal aX b. En este caso, E[h(X)] es fácil de calcular a partir de E(X). 104 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad PROPOSICIÓN E(aX b) a E(X) b (O, con notación alternativa, aX b X b.) Parafraseando, el valor esperado de una función lineal es igual a la función lineal eva- luada con el valor esperado E(X). Como h(X) en el ejemplo 3.23 es lineal y E(X) 2, E[h(X)] 800(2) 900 $700, como antes. Comprobación E(aX b) D (ax b) p(x) a D x p(x) b D p(x) aE(X) b ■ Dos casos especiales de proposición producen dos reglas importantes de valor espe- rado. 1. Con cualquier constante a, E(aX) a E(X) (considérese b 0). (3.12) 2. Con cualquier constante b, E(X b) E(X) b (considérese a 1). La multiplicación de X por una constante cambia la unidad de medición (de dólares a centavos, donde a 100, pulgadas a centímetros, donde a 2.54, etc.). La regla 1 dice que el valor esperado en las nuevas unidades es igual al valor esperado en las viejas unidades multiplicado por el factor de conversión a. Asimismo, si se agrega una constante b a cada valor posible de X, entonces el valor esperado se desplazará en esa misma cantidad cons- tante. Varianza de X El valor esperado de X describe dónde está centrada la distribución de probabilidad. Utili- zando la analogía física de colocar una masa puntual p(x) en el valor x sobre un eje unidi- mensional, si el eje estuviera entonces soportado por un fulcro colocado en , el eje no tendería a ladearse. Esto se ilustra para dos distribuciones diferentes en la figura 3.7. p(x) 0.5 1 2 3 (a ) 5 p(x) 0.5 1 2 3 5 6 7 8 (b ) Figura 3.7 Dos distribuciones de probabilidad diferentes con 4. Aunque ambas distribuciones ilustradas en la figura 3.7 tienen el mismo centro , la distribución de la figura 3.7(b) tiene una mayor dispersión o variabilidad que la de la figu- ra 3.7(a). Se utilizará la varianza de X para evaluar la cantidad de variabilidad en (la distri- bución de) X, del mismo modo que se utilizó s2 en el capítulo 1 para medir la variabilidad en una muestra. c3_p086-129.qxd 3/12/08 4:01 AM Page 104
- 123. La cantidad h(X) (X – )2 es la desviación al cuadrado de X con respecto a su me- dia y 2 es la desviación al cuadrado esperada, es decir, el promedio ponderado de desvia- ciones al cuadrado, donde las ponderaciones son probabilidades de la distribución. Si la mayor parte de la distribución de probabilidad está cerca de , entonces 2 será relativamen- te pequeña. Sin embargo, existen valores x alejados de que tienen una gran p(x), en ese caso 2 será bastante grande. Si X es el número de cilindros del siguiente carro que va a ser afinado en un taller de servi- cio, con la función masa de probabilidad dada en el ejemplo 3.22 [p(4) 0.5, p(6) 0.3, p(8) 0.2, a partir de la cual 5.4], entonces V(X) 2 8 x4 (x 5.4)2 p(x) (4 5.4)2 (0.5) (6 5.4)2 (0.3) (8 5.4)2 (0.2) 2.44 La desviación estándar de X es 2 .4 4 1.562. ■ Cuando la función masa de probabilidad p(x) especifica un modelo matemático para la distribución de los valores de la población, tanto 2 como miden la dispersión de los valores en la población; 2 es la varianza de la población y es su desviación estándar. Fórmula abreviada para 2 El número de operaciones aritméticas necesarias para calcular 2 pueden reducirse si se uti- liza una fórmula de cálculo alternativa. 3.3 Valores esperados 105 DEFINICIÓN Sea p(x) la función masa de probabilidad de X y su valor esperado. En ese caso la varianza de X, denotada por V(X) o 2 X o simplemente 2 , es V(X) D (x )2 p(x) E[(X )2 ] La desviación estándar (DE) de X es X 2 X PROPOSICIÓN V(X) 2 D x2 p(x) 2 E(X2 ) [E(X)]2 Al utilizar esta fórmula, E(X2 ) se calcula primero sin ninguna sustracción; acto seguido E(X) se calcula, se eleva al cuadrado y se resta (una vez) de E(X2 ). La función masa de probabilidad del número de cilindros X del siguiente carro que va a ser afinado en un taller se dio en el ejemplo 3.24 como p(4) 0.5, p(6) 0.3 y p(8) 0.2, a partir de las cuales 5.4 y E(X2 ) (42 )(0.5) (62 )(0.3) (82 )(0.2) 31.6 Por lo tanto 2 31.6 (5.4)2 2.44 en el ejemplo 3.24. ■ Ejemplo 3.24 Ejemplo 3.25 c3_p086-129.qxd 3/12/08 4:01 AM Page 105
- 124. Comprobación de la fórmula abreviada Expándase (x )2 en la definición de 2 para obtener x2 2x 2 y luego lleve a cada uno de los tres términos: 2 D x2 p(x) 2 D x p(x) 2 D p(x) E(X2 ) 2 2 E(X2 ) 2 ■ Reglas de varianza La varianza de h(X) es el valor esperado de la diferencia al cuadrado entre h(X) y su valor esperado: V[h(X)] 2 h (X) D {h(x) E[h(X)]}2 p(x) (3.13) Cuando h(X) aX b, una función lineal h(x) E[h(X)] ax b (a b) a(x ) Sustituyendo esto en la ecuación (3.13) se obtiene una relación simple entre V[h(X)] y V(X): 106 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad El valor absoluto es necesario porque a podría ser negativa, no obstante una desviación es- tándar no puede serlo. Casi siempre la multiplicación por a corresponde a un cambio de la unidad de medición (p. ej., kg a lb o dólares a euros). De acuerdo con la primera relación en (3.14), la desviación estándar en la nueva unidad es la desviación estándar original mul- tiplicada por el factor de conversión. La segunda relación dice que la adición o sustracción de una constante no impacta la variabilidad; simplemente desplaza la distribución a la dere- cha o izquierda. En el problema de ventas de computadoras del ejemplo 3.23, E(X) 2 y E(X2 ) (0)2 (0.1) (1)2 (0.2) (2)2 (0.3) (3)2 (0.4) 5 así que V(X) 5 (2)2 1. La función de utilidad h(X) 800X 900 tiene entonces la varianza (800)2 · V(X) (640 000)(1) 640 000 y la desviación estándar 800. ■ 29. La función masa de probabilidad de X el número de de- fectos importantes en un aparato eléctrico de un tipo selec- cionado al azar es Calcule lo siguiente: a. E(X). b. V(X) directamente a partir de la definición. c. La desviación estándar de X. d. V(X) por medio de la fórmula abreviada. 30. Se selecciona al azar un individuo que tiene asegurado su au- tomóvil con una compañía. Sea Y el número de infracciones de tránsito por las que el individuo fue citado durante los úl- timos 3 años. La función masa de probabilidad de Y es PROPOSICIÓN En particular, (3.14) saX 5 |a| ? sX, sX1b 5 sX VsaX 1 bd 5 s2 aX1b 5 a2 ? s2 X and saX1b 5 |a| ? sx Ejemplo 3.26 EJERCICIOS Sección 3.3 (29-45) x 0 1 2 3 4 p(x) 0.08 0.15 0.45 0.27 0.05 y 0 1 2 3 p(y) 0.60 0.25 0.10 0.05 c3_p086-129.qxd 3/12/08 4:01 AM Page 106
- 125. a. Calcule E(Y). b. Suponga que un individuo con Y infracciones incurre en un recargo de $100Y2 . Calcule la cantidad esperada del recargo. 31. Remítase al ejercicio 12 y calcule V(Y) y Y. Determine en- tonces la probabilidad de que Y esté dentro de una desvia- ción estándar de 1 de su valor medio. 32. Un distribuidor de enseres para el hogar vende tres mode- los de congeladores verticales de 13.5, 15.9 y 19.1 pies cú- bicos de espacio de almacenamiento, respectivamente. Sea X la cantidad de espacio de almacenamiento adquirido por el siguiente cliente que compre un congelador. Suponga que X tiene la función masa de probabilidad a. Calcule E(X), E(X2 ) y V(X). b. Si el precio de un congelador de X pies cúbicos de capa- cidad es 25X 8.5, ¿cuál es el precio esperado pagado por el siguiente cliente que compre un congelador? c. ¿Cuál es la varianza del precio 25X 8.5 pagado por el siguiente cliente? d. Suponga que aunque la capacidad nominal de un conge- lador X, la real es h(X) X 0.01X2 . ¿Cuál es la capa- cidad real esperada del congelador adquirido por el siguiente cliente? 33. Sea X una variable aleatoria de Bernoulli con función masa de probabilidad como en el ejemplo 3.18. a. Calcule E(X2 ). b. Demuestre que V(X) p(1 p). c. Calcule E(X79 ). 34. Suponga que el número de plantas de un tipo particular en- contradas en una región particular (llamada cuadrante por ecologistas) en cierta área geográfica es una variable aleato- ria X con función masa de probabilidad p(x) {c/x3 x 1, 2, 3, . . . 0 de lo contrario ¿Es E(X) finita? Justifique su respuesta (ésta es otra distribu- ción que los estadísticos llamarían de cola gruesa). 35. Un pequeño mercado ordena ejemplares de cierta revista para su exhibidor de revistas cada semana. Sea X deman- da de la revista, con función masa de probabilidad Suponga que el propietario de la tienda paga $1.00 por cada ejemplar de la revista y el precio para los consumidores es de $2.00. Si las revistas que se quedan al final de la semana no tienen valor de recuperación, ¿es mejor ordenar tres o cuatro ejemplares de la revista? [Sugerencia: Tanto para tres o cuatro ejemplares ordenados, exprese un ingreso neto como una función de la demanda X y luego calcule el ingre- so esperado.] 36. Sea X el daño incurrido (en dólares) en un tipo de accidente durante un año dado. Valores posibles de X son 0, 1000, 5000 y 10000 dólares con probabilidades de 0.8, 0.1, 0.08, y 0.02, respectivamente. Una compañía particular ofrece una póliza con deducible de $500. Si la compañía desea que su utilidad esperada sea de $100, ¿qué cantidad de prima debe- rá cobrar? 37. Los n candidatos para un trabajo fueron clasificados como 1, 2, 3, . . . , n. Sea X el rango de un candidato seleccio- nado al azar, de modo que X tenga la función masa de pro- babilidad p(x) {1/n x 1, 2, 3, . . . , n 0 de lo contrario (ésta se llama distribución uniforme discreta). Calcule E(X) y V(X) por medio de la fórmula abreviada. [Sugerencia: La suma de los primeros n enteros positivos es n(n 1)/2, mientras que la suma de sus cuadrados es n(n 1)(2n 1) /6.] 38. Sea X el resultado cuando un dado imparcial es lanzado una vez. Si antes de lanzar el dado le ofrecen o (1/3.5) dóla- res o h(X) 1/X dólares, ¿aceptaría la suma garantizada o jugaría? [Nota: Generalmente no es cierto que 1(E/X) E(1/X).] 39. Una compañía de productos químicos en la actualidad tiene en existencia 100 lb de un producto químico, el cual se ven- de a sus clientes en lotes de 5 lb. Sea X el número de lo- tes solicitados por un cliente seleccionado al azar y suponga que X tiene la función masa de probabilidad Calcule E(X) y V(X). Calcule enseguida el número esperado de libras que quedan una vez que se envía el pedido del si- guiente cliente y la varianza del número de libras sobrantes. [Sugerencia: El número de libras que quedan es una función lineal de X.] 40. a. Trace una gráfica lineal de la función masa de probabi- lidad de X en el ejercicio 35. Enseguida determine la función masa de probabilidad de X y trace su gráfica li- neal. Con base en estas dos figuras, ¿qué se puede decir sobre V(X) y V(X)? b. Use la proposición que implica V(aX b) para estable- cer una relación general entre V(X) y V(X). 41. Use la definición en la expresión (3.13) para comprobar que V(aX b) a2 2 X. [Sugerencia: Con h(X) aX b, E[h(X)] a b, donde E(X).] 42. Suponga E(X) 5 y E[X(X 1)] 27.5. ¿Cuál es a. E(X2 )? [Sugerencia: E[X(X 1)] E(X2 X] E(X2 ) E(X)]? b. V(X)? c. La relación general entre las cantidades E(X), E[X(X) 1)] y V(X)? 43. Escriba una regla general para E(X c), donde c es una constante. ¿Qué sucede cuando hace c , el valor espera- do de X? 44. Un resultado llamado desigualdad de Chebyshev establece que para cualquier distribución de probabilidad de una 3.3 Valores esperados 107 x 13.5 15.9 19.1 p(x) 0.2 0.5 0.3 x 1 2 3 4 5 6 p(x) 1 1 5 1 2 5 1 3 5 1 4 5 1 3 5 1 2 5 x 1 2 3 4 p(x) 0.2 0.4 0.3 0.1 c3_p086-129.qxd 3/12/08 4:01 AM Page 107
- 126. variable aleatoria X y cualquier número k que por lo menos sea 1, P(°X ° k) 1/k2 . En palabras, la posibilidad de que el valor de X quede por lo menos a k desviaciones es- tándar de su media es cuando mucho 1/k2 . a. ¿Cuál es el valor del límite superior con k 2?, ¿k 3?, ¿k 4?, ¿k 5?, ¿k 10? b. Calcule y para la distribución del ejercicio 13. Eva- lúe enseguida P(|X | * k) con los valores de k dados en el inciso a). ¿Qué sugiere esto sobre el límite superior con respecto a la probabilidad correspondiente? c. Que X tenga los valores posibles 1, 0 y 1, con las proba- bilidades 1 1 8, 8 9 y 1 1 8, respectivamente. ¿Cuál es P(°X ° 3) y cómo se compara con el límite correspondiente? d. Dé una distribución con la cual P(°X ° 5) 0.04. 45. Si a X b, demuestre que a E(X) b. 108 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Existen muchos experimentos que se ajustan exacta o aproximadamente a la siguiente lista de requerimientos: 1. El experimento consta de una secuencia de n experimentos más pequeños llamados en- sayos, donde n se fija antes del experimento. 2. Cada ensayo puede dar por resultado uno de los mismos dos resultados posibles (ensa- yos dicotómicos), los cuales se denotan como éxito (E) y falla (F). 3. Los ensayos son independientes, de modo que el resultado en cualquier ensayo particu- lar no influye en el resultado de cualquier otro ensayo. 4. La probabilidad de éxito es constante de un ensayo a otro; esta probabilidad se denota por p. 3.4 Distribución de probabilidad binomial La misma moneda se lanza al aire sucesiva e independientemente n veces. De manera arbi- traria se utiliza E para denotar el resultado H (caras) y F para denotar el resultado T (cru- ces). Entonces este experimento satisface las condiciones 1–4. El lanzamiento al aire de una tachuela n veces, con E punta hacia arriba y F punta hacia abajo), también da por resultado un experimento binomial. ■ Muchos experimentos implican una secuencia de ensayos independientes para los cuales existen más de dos resultados posibles en cualquier ensayo. Entonces, un experimen- to binomial puede crearse dividiendo los posibles resultados en dos grupos. El color de las semillas de chícharo lo determina un solo lugar geométrico genético. Si los dos alelos en este lugar geométrico son AA o Aa (el genotipo), entonces el chícharo será amarillo (el fenotipo) y si el alelo es aa, el chícharo será verde. Suponga que aparean 20 se- millas Aa y se cruzan las dos semillas en cada uno de los diez pares para obtener diez nue- vos genotipos. Designe a cada nuevo genotipo como éxito (E) si es aa y falla (F ) si es lo contrario. Entonces con esta identificación de S y F, el experimento es binomial con n 10 y p P (genotipo aa). Si es igualmente probable que cada miembro del par contribuya con a o A, entonces p P(a) P(a) (1 2)(1 2) 1 4. ■ Suponga que una ciudad tiene 50 restaurantes autorizados, de los cuales 15 han cometido en la actualidad una seria violación del código sanitario y los otros 35 no han cometido viola- ciones serias. Hay cinco inspectores, cada uno de los cuales inspeccionará un restaurante durante la semana entrante. El nombre de cada restaurante se anota en un pedacito de papel diferente y a continuación se mezclan perfectamente, cada inspector a su vez saca uno de DEFINICIÓN Un experimento para el que se satisfacen las condiciones 1–4 se llama experimento binomial. Ejemplo 3.27 Ejemplo 3.28 Ejemplo 3.29 c3_p086-129.qxd 3/12/08 4:01 AM Page 108
- 127. los papelitos sin reemplazarlos. Anótese el ensayo i-ésimo como éxito si el restaurante i-ési- mo seleccionado (i 1, . . . , 5) no ha cometido violaciones serias. Entonces ■ P(E en el primer ensayo) 0.70 y P(E en el segundo ensayo) P(EE) P(FE) P(segundo E°primer E) P(primer E) P(segundo E°primer F) P(primer F) 0.70 Asimismo, se puede demostrar que P(E en el ensayo i-ésimo) 0.70 con i 3, 4, 5. Sin embargo, P(E en el quinto ensayo°EEEE) 0.67 puesto que P(E en el quinto ensayo°FFFF) 0.76 El experimento no es binomial porque los ensayos no son independientes. En general, si se muestrea sin reemplazo, el experimento no producirá ensayos independientes. Si cada papelito hubiera sido reemplazado después de ser sacado, entonces los ensayos habrían sido independientes, pero esto podría haber dado por resultado que el mismo restaurante fuera inspeccionado por más de un inspector. ■ Un estado tiene 500000 conductores con licencia, de los cuales 400 000 están asegurados. Se selecciona una muestra de 10 conductores sin reemplazo. El ensayo i-ésimo se denota S si el conductor i-ésimo seleccionado está asegurado. Aunque está situación parecería idén- tica a la del ejemplo 3.29, la diferencia importante es que el tamaño de la población mues- treada es muy grande con respecto al tamaño de la muestra. En este caso P(E en 2°E en 1) 0.80000 y P(E en 10°E en los primeros 9) 0.799996 0.80000 Estos cálculos sugieren que aunque los ensayos no son exactamente independientes, las pro- babilidades condicionales difieren tan poco una de otra que en la práctica los ensayos se consideran independientes con la constante P(E) 0.8. Por lo tanto, para una muy buena aproximación, el experimento es binomial con n 10 y p 0.8. ■ Se utilizará la siguiente regla empírica para decidir si un experimento “sin reempla- zo” puede ser tratado como experimento binomial. 399 991 499 991 399 999 499 999 35 46 31 46 35 50 15 49 34 49 35 50 15 50 35 49 35 50 34 49 35 50 3.4 Distribución de probabilidad binomial 109 Ejemplo 3.30 Por “analizado” se quiere decir que las probabilidades basadas en suposiciones de experi- mento binomial se aproximarán bastante a las probabilidades reales “sin reemplazo”, las REGLA Considérese muestreo sin reemplazo de una población dicotómica de tamaño N. Si el tamaño de la muestra (número de ensayos) n es cuando mucho 5% del tamaño de la población, el experimento puede ser analizado como si fuera exactamente un experi- mento binomial. c3_p086-129.qxd 3/12/08 4:01 AM Page 109
- 128. que generalmente son más difíciles de calcular. En el ejemplo 3.29, n/N 5/50 0.1 0.05, de modo que el experimento binomial no es una buena aproximación, pero en el ejemplo 3.30, n/N 10/500 000 0.05. Variable aleatoria binomial y distribución En la mayoría de los experimentos binomiales, lo que interesa es el número total de los éxi- tos (E), en lugar del conocimiento de qué ensayos dieron los éxitos. 110 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Supóngase, por ejemplo, que n 3. Entonces existen ocho posibles resultados para el ex- perimento: EEE EEF EFE EFF FEE FEF FFE FFF Por la definición de X, X(EEF) 2, X(EFF) 1 y así sucesivamente. Valores posibles de X en un experimento de n ensayos son x 0, 1, 2, . . . , n. A menudo se escribirá X Bin(n, p) para indicar que X es una variable aleatoria binomial basada en n ensayos con probabilidad de éxito p. Considérese primero el caso n 4 para el cual cada resultado, su probabilidad y valor x correspondiente se dan en la tabla 3.1. Por ejemplo, P(EEFE) P(E) P(E) P(F) P(E) (ensayos independientes) p p (1 p) p (constante P(E)) p3 (1 p) DEFINICIÓN La variable aleatoria binomial X asociada con un experimento binomial que consis- te en n ensayos se define como X el número de los E entre los n ensayos NOTACIÓN Como la función masa de probabilidad de una variable aleatoria binomial X depen- de de los dos parámetros n y p, la función masa de probabilidad se denota por b(x; n, p). Tabla 3.1 Resultados y probabilidades de un experimento binomial con cuatro ensayos Resultado x Probabilidad Resultado x Probabilidad EEEE 4 p4 FEEE 3 p3 (1 p) EEEF 3 p3 (1 p) FEEF 2 p2 (1 p)2 EEFE 3 p3 (1 p) FEFE 2 p2 (1 p)2 EEFF 2 p2 (1 p)2 FEFF 1 p(1 p)3 EFEE 3 p3 (1 p) FFEE 2 p2 (1 p)2 EFEF 2 p2 (1 p)2 FFEF 1 p(1 p)3 EFFE 2 p2 (1 p)2 FFFE 1 p(1 p)3 EFFF 1 p(1 p)3 FFFF 0 (1 p)4 En este caso especial, se desea b(x; 4, p) con x 0, 1, 2, 3 y 4. Para b(3; 4, p), iden- tifíquese cuál de los 16 resultados dan un valor x de 3 y sume las probabilidades asociadas con cada resultado. b(3; 4, p) P(FEEE) P(EFEE) P(EEFE) P(EEEF) 4p3 (1 p) c3_p086-129.qxd 3/12/08 4:01 AM Page 110
- 129. Existen cuatro resultados con x 3 y la probabilidad de cada uno es p3 (1 p) (el orden de los E y las F no es importante, sino sólo el número de los E), por lo tanto b(3; 4, p) {número de resultados } {probabilidad de cualquier resultado } con X 3 con X 3 Asimismo, b(2; 4, p) 6p2 (1 p)2 , la cual también es el producto del número de resulta- dos con X 2 y la probabilidad de cualquier resultado como ese. En general, b(x; n, p) {número de secuencias de longitud n } {probabilidad de cualquier } compuestas de los éxitos de x secuencia como esa Como el orden de los E y las F no es importante, el segundo factor en la ecuación previa es px (1 p)nx (p. ej., los primeros x ensayos producen E y los últimos n x producen F. El primer factor es el número de formas de escoger x de los n ensayos para que sean los E, es decir, el número de combinaciones de tamaño x que pueden ser construidas con n objetos distintos (ensayos en este caso). 3.4 Distribución de probabilidad binomial 111 TEOREMA b(x; n, p) { px (1 p)nx x 0, 1, 2, . . . n 0 de lo contrario n x A cada uno de seis bebedores de refrescos de cola seleccionados al azar se le sirve un vaso de refresco de cola A y uno de refresco de cola B. Los vasos son idénticos en apariencia ex- cepto por un código que viene en el fondo para identificar el refresco de cola. Suponga que en realidad no existe una tendencia entre los bebedores de refresco de cola de preferir un re- fresco de cola al otro. Entonces p P(un individuo seleccionado prefiere A) 0.5, así que con X el número entre los seis que prefieren A, X Bin(6, 0.5). Por lo tanto P(X 3) b(3; 6, 0.5) (0.5)3 (0.5)3 20(0.5)6 0.313 La probabilidad de que por lo menos tres prefieran A es P(3 X) 6 x3 b(x; 6, 0.5) 6 x3 (0.5)x (0.5)6x 0.656 y la probabilidad de que cuando mucho uno prefiera A es P(X 1) 1 x0 b(x; 6, 0.5) 0.109 ■ Utilización de tablas binomiales* Incluso con un valor relativamente pequeño de n, el cálculo de probabilidades binomiales es tedioso. La tabla A.1 del apéndice tabula la función de distribución acumulativa F(x) P(X x) con n 5, 10, 15, 20, 25 en combinación con valores seleccionados de p. Varias otras probabilidades pueden entonces ser calculadas por medio de la proposición sobre funciones de distribución acumulativas de la sección 3.2. Una anotación de 0 en la tabla significa úni- camente que la probabilidad es 0 a tres dígitos significativos puesto que todos los valores ingresados en la tabla en realidad son positivos. 6 x 6 3 Ejemplo 3.31 * Los paquetes de programas estadísticos tales como MINITAB y R proporcionan la función masa de probabili- dad o la función de distribución acumulativa en forma casi instantánea al solicitarla para cualquier valor de p y n hasta 2 millones. También existe un comando en R para calcular la probabilidad de que X quede en el mismo intervalo. c3_p086-129.qxd 3/12/08 4:01 AM Page 111
- 130. Suponga que 20% de todos los ejemplares de un libro de texto particular no pasan una prue- ba de resistencia de encuadernación. Sea X el número entre 15 ejemplares seleccionados al azar que no pasan la prueba. Entonces X tiene una distribución binomial con n 15 y p 0.2. 1. La probabilidad de que cuando mucho 8 no pasen la prueba es P(X 8) 8 y0 b(y; 15, 0.2) B(8; 15, 0.2) la cual es el ingreso en la fila x 8 y la columna p 0.2 de la tabla binomial n 15. Según la tabla A.1 del apéndice, la probabilidad es B(8; 15, 0.2) 0.999. 2. La probabilidad de que exactamente 8 fallen es P(X 8) P(X 8) P(X 7) B(8; 15, 0.2) B(7; 15, 0.2) la cual es la diferencia entre dos ingresos consecutivos en la columna p 0.2. El resul- tado es 0.999 0.996 0.003. 3. La probabilidad de que por lo menos 8 fallen es P(X 8) 1 P(X 7) 1 B(7; 15, 0.2) 1 ingreso en x 7 fila de columna p 0.2 1 0.996 0.004 4. Finalmente, la probabilidad de que entre 4 y 7, inclusive, fallen es P(4 X 7) P(X 4, 5, 6 o 7) P(X 7) P(X 3) B(7; 15, 0.2) B(3; 15, 0.2) 0.996 0.648 0.348 Obsérvese que esta última probabilidad es la diferencia entre los ingresos en las filas x 7 y x 3, no en las filas x 7 y x 4. ■ Un fabricante de aparatos electrónicos afirma que cuando mucho 10% de sus unidades de suministro de potencia necesitan servicio durante el periodo de garantía. Para investigar esta afirmación, técnicos en un laboratorio de prueba adquieren 20 unidades y someten a cada una a una prueba acelerada para simular el uso durante el periodo de garantía. Sea p la probabilidad de que una unidad de suministro de potencia necesite reparación durante el periodo (proporción de unidades que requieren reparación). Los técnicos de laboratorio deben decidir si los datos obtenidos con el experimento respaldan la afirmación de que p 0.10. Sea X el número entre las 20 muestreadas que necesitan reparación, así que X Bin(20, p). Con- sidere la regla de decisión Rechazar la afirmación de que p 0.10 a favor de la conclusión de que p 0.10 si x 5 (donde x es el valor observado de X) y considere posible la afirmación si x 4. La probabilidad de que la afirmación sea rechazada cuando p 0.10 (una conclusión inco- rrecta) es P(X 5 cuando p 0.10) 1 B(4; 20, 0.1) 1 0.957 0.043 112 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad NOTACIÓN Para X Bin(n, p), la función de distribución acumulativa será denotada por P(X x) B(x; n, p) x y0 b(y; n, p) x 0, 1, . . . , n Ejemplo 3.32 Ejemplo 3.33 c3_p086-129.qxd 3/12/08 4:01 AM Page 112
- 131. La probabilidad de que la afirmación no sea rechazada cuando p 0.20 (un tipo diferente de conclusión incorrecta) es P(X 4 cuando p 0.2) B(4; 20, 0.2) 0.630 La primera probabilidad es algo pequeña, pero la segunda es intolerablemente grande. Cuando p 0.20, significa que el fabricante subestimó de manera excesiva el porcenta- je de unidades que necesitan servicio y si se utiliza la regla de decisión establecida, ¡el 63% de las muestras dan como resultado que la afirmación del fabricamte se considere plausible! Se podría pensar que la probabilidad de este segundo tipo de conclusión errónea po- dría hacerse más pequeña cambiando el valor de corte de 5 en la regla de decisión por algún otro. Sin embargo, aunque el reemplazo de 5 por un número más pequeño daría una proba- bilidad más pequeña que 0.630, la otra probabilidad se incrementaría entonces. La única forma de hacer ambas “probabilidades de error” pequeñas es basar la regla de decisión en un experimento que implique muchas más unidades. ■ La media y varianza de X Con n 1, la distribución binomial llega a ser la distribución de Bernoulli. De acuerdo con el ejemplo 3.18, el valor medio de una variable de Bernoulli es p, así que el número esperado de los S en cualquier ensayo único es p. Como un experimento binomial se com- pone de n ensayos, la intuición sugiere que para X Bin(n, p), E(X) np, el producto del número de ensayos y la probabilidad de éxito en un solo ensayo. La expresión para V(X) no es tan intuitiva. 3.4 Distribución de probabilidad binomial 113 Por tanto, para calcular la media y varianza de una variable aleatoria binomial no se requie- re evaluar las sumas. La comprobación del resultado para E(X) se ilustra en el ejercicio 64. Si 75% de todas las compras en una tienda se hacen con tarjeta de crédito y X es el número entre diez compras seleccionadas al azar realizadas con tarjeta de crédito, entonces X Bin(10, 0.75). Por lo tanto, E(X) np (10)(0.75) 7.5, V(X) npq 10(0.75)(0.25) 1.875 y 1. 87 5 . Otra vez, aun cuando X puede tomar sólo valores enteros, E(X) no tiene que ser un entero. Si se realiza un gran número de experimentos binomiales independientes, cada uno con n 10 ensayos y p 0.75, entonces el número promedio de los E por expe- rimento se acercará a 7.5. ■ PROPOSICIÓN Si X Bin(n, p), entonces E(X) np, V(X) np(1 p) npq y X n p q (don- de q 1 p). Ejemplo 3.34 EJERCICIOS Sección 3.4 (46-67) 46. Calcule las siguientes probabilidades binomiales directamen- te con la fórmula para b(x; n, p): a. b(3; 8, 0.35) b. b(5; 8, 0.6) c. P(3 X 5) cuando n 7 y p 0.6 d. P(1 X) cuando n 9 y p 0.1 47. Use la tabla A.1 del apéndice para obtener las siguientes probabilidades: a. B(4; 15, 0.3) b. b(4; 15, 0.3) c. b(6; 15, 0.7) d. P(2 X 4) cuando X Bin(15, 0.3) e. P(2 X) cuando X Bin(15, 0.3) f. P(X 1) cuando X Bin(15, 0.7) g. P(2 X 6) cuando X Bin(15, 0.3) 48. Cuando se utilizan tarjetas de circuito en la fabricación de reproductores de discos compactos se prueban; el porcenta- je de defectuosas es de 5%. Sea X el número de tarjetas defectuosas en una muestra aleatoria de tamaño n 25, así que X Bin(25, 0.05). c3_p086-129.qxd 3/12/08 4:01 AM Page 113
- 132. a. Determine P(X 2). b. Determine P(X 5). c. Determine P(1 X 4). d. ¿Cuál es la probabilidad que ninguna de estas 25 tarjetas esté defectuosa? e. Calcule el valor esperado y la desviación estándar X. 49. Una compañía que produce cristales finos sabe por expe- riencia que 10% de sus copas de mesa tienen imperfecciones cosméticas y deben ser clasificadas como “de segunda”. a. Entre seis copas seleccionadas al azar, ¿qué tan probable es que sólo una sea de segunda? b. Entre seis copas seleccionadas al azar, ¿qué tan probable es que por lo menos dos sean de segunda? c. Si las copas se examinan una por una, ¿cuál es la proba- bilidad de cuando mucho cinco deban ser seleccionadas para encontrar cuatro que no sean de segunda? 50. Se utiliza un número telefónico particular para recibir tanto lla- madas de voz como faxes. Suponga que 25% de las llamadas entrantes son faxes y considere una muestra de 25 llamadas en- trantes. ¿Cuál es la probabilidad de que a. Cuando mucho 6 de las llamadas sean un fax? b. Exactamente 6 de las llamadas sean un fax? c. Por lo menos 6 de las llamadas sean un fax? d. Más de 6 de las llamadas sean un fax? 51. Remítase al ejercicio previo. a. ¿Cuál es el número esperado de llamadas entre las 25 que impliquen un fax? b. ¿Cuál es la desviación estándar del número entre las 25 llamadas que implican un fax? c. ¿Cuál es la probabilidad de que el número de llamadas entre las 25 que implican una transmisión de fax so- brepase el número esperado por más de 2 desviaciones estándar? 52. Suponga que 30% de todos los estudiantes que tienen que comprar un texto para un curso particular desean un ejem- plar nuevo (¡los exitosos!), mientras que el otro 70% desea comprar un ejemplar usado. Considere seleccionar 25 com- pradores al azar. a. ¿Cuáles son el valor medio y la desviación estándar del número que desea un ejemplar nuevo del libro? b. ¿Cuál es la probabilidad de que el número que desea ejemplares nuevos esté a más de dos desviaciones están- dar del valor medio? c. La librería tiene 15 ejemplares nuevos y 15 usados en exis- tencia. Si 25 personas llegan una por una a comprar el tex- to, ¿cuál es la probabilidad de las 25 que obtengan el tipo de libro que desean de las existencias actuales? [Sugeren- cia: Sea X el número que desea un ejemplar nuevo. ¿Con qué valores de X obtendrán las 15 lo que desean?] d. Suponga que los ejemplares nuevos cuestan $100 y los usados $70. Suponga que la librería en la actualidad tie- ne 50 ejemplares nuevos y 50 usados. ¿Cuál es el valor esperado del ingreso total por la venta de los siguientes 25 ejemplares comprados? Asegúrese de indicar qué re- gla de valor esperado está utilizando. [Sugerencia: Sea h(X) el ingreso cuando X de los 25 compradores de- sean ejemplares nuevos. Exprese esto como una función lineal.] 53. El ejercicio 30 (sección 3.3) dio la función masa de proba- bilidad de Y, el número de citaciones de tránsito de un indi- viduo seleccionado al azar asegurado por una compañía particular. ¿Cuál es la probabilidad de que entre 15 indivi- duos seleccionados al azar a. por lo menos 10 no tengan citaciones? b. menos de la mitad tengan por lo menos una citación? c. el número que tengan por lo menos una citación esté en- tre 5 y 10, inclusive?* 54. Un tipo particular de raqueta de tenis viene en tamaño me- diano y en tamaño extragrande. El 60% de todos los clientes en una tienda desean la versión extragrande. a. Entre diez clientes seleccionados al azar que desean este tipo de raqueta, ¿cuál es la probabilidad de que por lo menos seis deseen la versión extragrande? b. Entre diez clientes seleccionados al azar, ¿cuál es la proba- bilidad de que el número que desea la versión extragrande esté dentro de una desviación estándar del valor medio? c. La tienda dispone actualmente de siete raquetas de cada versión. ¿Cuál es la probabilidad de que los siguientes diez clientes que desean esta raqueta puedan obtener la versión que desean de las existencias actuales? 55. El 20% de todos los teléfonos de cierto tipo son llevados a servicio mientras se encuentran dentro de la garantía. De és- tos, 60% puede ser reparado, mientras el 40% restante debe ser reemplazado con unidades nuevas. Si una compañía ad- quiere diez de estos teléfonos, ¿cuál es la probabilidad de que exactamente dos sean reemplazados bajo garantía? 56. La Junta de Educación reporta que 2% de los dos millones de estudiantes de preparatoria que toman el SAT cada año reciben un trato especial a causa de discapacidades documen- tadas (Los Angeles Times, 16 de julio de 2002). Considere una muestra aleatoria de 25 estudiantes que recientemente presentaron el examen. a. ¿Cuál es la probabilidad de que exactamente 1 reciba un trato especial? b. ¿Cuál es la posibilidad de que por lo menos 1 reciba un trato especial? c. ¿Cuál es la probabilidad de que por lo menos 2 reciban un trato especial? d. ¿Cuál es la probabilidad de que el número entre los 25 que recibieron un trato especial esté dentro de 2 desvia- ciones estándar del número que esperaría reciba un trato especial? e. Suponga que a un estudiante que no recibe un trato espe- cial se le permiten 3 horas para el examen, mientras que a un estudiante que recibió un trato especial se le permi- ten 4.5 horas. ¿Qué tiempo promedio piensa que le sería permitido a los 25 estudiantes seleccionados? 57. Suponga que 90% de todas las baterías de cierto proveedor tienen voltajes aceptables. Un tipo de linterna requiere que las dos baterías sean tipo D y la linterna funcionará sólo si sus dos baterías tienen voltajes aceptables. Entre diez lin- ternas seleccionadas al azar, ¿cuál es la probabilidad de que por lo menos nueve funcionarán? ¿Qué suposiciones hizo para responder la pregunta planteada? 114 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad * “Entre a y b, inclusive” equivale a (a X b). c3_p086-129.qxd 3/12/08 4:01 AM Page 114
- 133. 58. Un distribuidor recibe un lote muy grande de componentes. El lote sólo puede ser caracterizado como aceptable si la proporción de componentes defectuosos es cuando mucho de 10. El distribuidor decide seleccionar 10 componentes al azar y aceptar el lote sólo si el número de componentes de- fectuosos presentes en la muestra es cuando mucho de 2. a. ¿Cuál es la probabilidad de que el lote será aceptado cuando la proporción real de componentes defectuosos es de 0.01?, 0.05? 0.10? 0.20? 0.25? b. Sea p la proporción real de componentes defectuosos presentes en el lote. Una gráfica de P(se acepta el lote) en función de p y con p sobre el eje horizontal y P(se acep- ta el lote) sobre el eje vertical, se llama curva caracterís- tica de operación del plan de muestreo de aceptación. Use los resultados del inciso a) para trazar esta curva con 0 p 1. c. Repita los incisos a) y b) con “1” reemplazando a “2” en el plan de muestreo de aceptación. d. Repita los incisos a) y b) con “15” reemplazando a “10” en el plan de muestreo de aceptación. e. ¿Cuál de estos planes de muestreo, el del inciso a), c) o d) parece más satisfactorio y por qué? 59. Un reglamento que requiere que se instale un detector de humo en todas las casas previamente construidas ha estado en vigor en una ciudad particular durante 1 año. Al departa- mento de bomberos le preocupa que muchas casas perma- nezcan sin detectores. Sea p la proporción verdadera de las casas que tienen detectores y suponga que se inspeccio- na una muestra aleatoria de 25 casas. Si ésta indica marca- damente que menos de 80% de todas las casas tienen un detector, el departamento de bomberos lanzará una campaña para la puesta en ejecución de un programa de inspección obligatorio. Debido a lo caro del programa, el departamento prefiere no requerir tales inspecciones a menos que una evi- dencia muestral indique que se requieren. Sea X el número de casas con detectores entre las 25 muestreadas. Considere rechazar el requerimiento de que p 0.8 si x 15. a. ¿Cuál es la probabilidad de que el requerimiento sea re- chazado cuando el valor real de p es 0.8? b. ¿Cuál es la probabilidad de no rechazar el requerimiento cuando p 0.7? ¿Cuándo p 0.6? c. ¿Cómo cambian las “probabilidades de error” de los inci- sos a) y b) si el valor 15 en la regla de decisión es reem- plazado por 14? 60. Un puente de cuota cobra $1.00 por cada automóvil de uso particular y $2.50 por cualquier otro vehículo. Suponga que durante el día 60% son vehículos de uso particular. Si 25 vehículos cruzan el puente durante un periodo determinado del día, ¿cuál es la expectativa de ingresos resultantes en el día? [Sugerencia: Exprese X número de automóviles de uso particular; cuando el ingreso por concepto de cuota h(X) es una función lineal de X]. 61. Un estudiante que está tratando de escribir un ensayo para un curso tiene la opción de dos temas, A y B. Si selecciona el tema A, el estudiante pedirá dos libros mediante préstamo interbiblioteca, mientras que si selecciona el tema B, el es- tudiante pedirá cuatro libros. El estudiante cree que un buen ensayo necesita recibir y utilizar por lo menos la mitad de los libros pedidos para uno u otro tema seleccionado. Si la probabilidad de que un libro pedido mediante préstamo inter- biblioteca llegue a tiempo es de 0.9 y los libros llegan inde- pendientemente uno de otro, ¿qué tema deberá seleccionar el estudiante para incrementar al máximo la probabilidad de es- cribir un buen ensayo? ¿Qué pasa si la probabilidad de que lle- guen los libros es de sólo 0.5 en lugar de 0.9? 62. a. Con n fijo, ¿hay valores de p(0 p 1) para los cuales V(X) 0? Explique por qué esto es así. b. ¿Con qué valor de p se incrementa al máximo V(X)? [Su- gerencia: Trace la gráfica de V(X) en función de p o bien tome una derivada.] 63. a. Demuestre que b(x; n, 1 p) b(n x; n, p). b. Demuestre que B(x; n, 1 p) 1 B(n x 1; n, p). [Sugerencia: Cuando mucho x éxitos (S) equivalen a por lo menos (n x) fracasos (F).] c. ¿Qué implican los incisos a) y b) sobre la necesidad de incluir valores de p más grandes que 0.5 en la tabla A.1 del apéndice? 64. Demuestre que E(X) np cuando X es una variable aleatoria binomial [Sugerencia: Primero exprese E(X) como una suma con límite inferior x 1. Luego saque a np como factor, sea y x 1 de modo que la suma sea de y 0 a y n 1 y demuestre que la suma es igual a 1.] 65. Los clientes en una gasolinería pagan con tarjeta de crédi- to (A), tarjeta de débito (B) o efectivo (C). Suponga qué clientes sucesivos toman decisiones independientes con P(A) 0.5, P(B) 0.2 y P(C) 0.3. a. Entre los siguientes 100 clientes, ¿cuáles son la media y varianza del número que paga con tarjeta de débito? Ex- plique su razonamiento. b. Conteste el inciso a) para el número entre 100 que no pa- gan con efectivo. 66. Una limusina de aeropuerto puede transportar hasta cuatro pasajeros en cualquier viaje. La compañía aceptará un máxi- mo de seis reservaciones para un viaje y un pasajero debe te- ner una reservación. Según registros previos, 20% de los que reservan no se presentan para el viaje. Responda las siguien- tes preguntas, suponiendo independencia en los casos en que sea apropiado. a. Si se hacen seis reservaciones, ¿cuál es la probabilidad de que por lo menos un individuo con reservación no pueda ser acomodado en el viaje? b. Si se hacen seis reservaciones, ¿cuál es el número espe- rado de lugares disponibles cuando la limusina parte? c. Suponga que la distribución de probabilidad del número de reservaciones hechas se da en la tabla adjunta. Sea X el número de pasajeros en un viaje seleccionado al azar. Obtenga la función masa de probabilidad de X. 67. Remítase a la desigualdad de Chebyshev dada en el ejercicio 44. Calcule P(°X ° k) con k 2 y k 3 cuando X Bin (20, 0.5) y compare con el límite superior corres- pondiente. Repita para X Bin(20, 0.75). 3.4 Distribución de probabilidad binomial 115 Número de reservaciones 3 4 5 6 Probabilidad 0.1 0.2 0.3 0.4 c3_p086-129.qxd 3/12/08 4:01 AM Page 115
- 134. Las distribuciones hipergeométricas y binomiales negativas están relacionadas con la distri- bución binomial. En tanto que la distribución binomial es el modelo de probabilidad apro- ximada de muestreo sin reemplazo de una población dicotómica finita (E–F), la distribución hipergeométrica es el modelo de probabilidad exacta del número de éxitos (E) en la mues- tra. La variable aleatoria binomial X es el número de éxitos cuando el número n de ensayos es fijo, mientras que la distribución binomial surge de fijar el número de éxitos deseados y de permitir que el número de ensayos sea aleatorio. Distribución hipergeométrica Las suposiciones que conducen a la distribución hipergeométrica son las siguientes: 1. La población o conjunto que se va a muestrear se compone de N individuos, objetos o elementos (una población finita). 2. Cada individuo puede ser caracterizado como éxito (E) o falla (F) y hay M éxitos en la población. 3. Se selecciona una muestra de n individuos sin reemplazo de tal modo que cada subcon- junto de tamaño n es igualmente probable de ser seleccionado. La variable aleatoria de interés es X el número de éxitos en la muestra. La distribución de probabilidad de X depende de los parámetros n, M y N, así que se desea obtener P(X x) h(x; n, M, N). Durante un periodo particular una oficina de tecnología de la información de una universi- dad recibió 20 solicitudes de servicio de problemas con impresoras, de las cuales 8 eran im- presoras láser y 12 eran modelos de inyección de tinta. Se tiene que seleccionar una muestra de 5 de estas solicitudes de servicio completamente al azar, de modo que cualquier subcon- junto de tamaño 5 tenga la misma probabilidad de ser seleccionado como cualquier otro subconjunto (piense en escribir los números 1, 2, . . . , 20 en 20 papelitos idénticos, mez- clarlos y seleccionar 5 de ellos). ¿Cuál es entonces la probabilidad de que exactamente x(x 0, 1, 2, 3, 4 o 5) de las solicitudes de servicio fueran para impresoras de inyección de tinta? En este caso, el tamaño de la población es N 20, el tamaño de la muestra es n 5 y el número de éxitos (inyección de tinta E) y las fallas (F) en la población son M 12 y N M 8, respectivamente. Considérese el valor x 2. Como todos los resultados (ca- da uno consta de 5 solicitudes particulares) son igualmente probables. P(X 2) h(2; 5, 12, 20) El número de posibles resultados en el experimento es el número de formas de seleccionar 5 de los 20 objetos sin importar el orden, es decir, (2 5 0 ). Para contar el número de resultados con X 2, obsérvese que existen (1 2 2 ) formas de seleccionar 2 de la solicitudes para impresoras de inyección de tinta, y por cada forma existen (8 3) formas de seleccionar las 3 solicitudes pa- ra impresoras láser a fin de completar la muestra. La regla de producto del capítulo 2 da en- tonces (1 2 2 )(8 3) como el número de resultados con X 2, por lo tanto h(2; 5, 12, 20) 0.238 ■ 77 323 1 2 2 8 3 2 5 0 número de resultados con X 2 número de posibles resultados 116 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad 3.5 Distribuciones hipergeométricas y binomiales negativas Ejemplo 3.35 c3_p086-129.qxd 3/12/08 4:01 AM Page 116
- 135. En general, si el tamaño de la muestra n es más pequeño que el número de éxitos en la población (M), entonces el valor de X más grande posible es n. Sin embargo, si M n (p. ej., un tamaño de muestra de 25 y sólo hay 15 éxitos en la población), entonces X puede ser cuando mucho M. Asimismo, siempre que el número de fallas en la población (N M) so- brepase el tamaño de la muestra, el valor más pequeño de X es 0 (puesto que todos los in- dividuos muestreados podrían entonces ser fallas). Sin embargo, si N M n, el valor más pequeño posible de X es n (N M). Por lo tanto, los posibles valores de X satisfacen la restricción máx(0, n (N M)) x mín(n, M). Un argumento paralelo al del ejemplo previo da la función masa de probabilidad de X. 3.5 Distribuciones hipergeométricas y binomiales negativas 117 PROPOSICIÓN Si X es el número de éxitos (E) en una muestra completamente aleatoria de tamaño n extraída de la población compuesta de M éxitos y (N M) fallas, entonces la distri- bución de probabilidad de X llamada distribución hipergeométrica, es P(X x) h(x; n, M, N) (3.15) con x un entero que satisface máx(0, n N M) x mín(n, M). M x N n M x N n Ejemplo 3.36 En el ejemplo 3.35, n 5, M 12 y N 20, por lo tanto h(x; 5, 12, 20) con x 0, 1, 2, 3, 4, 5 se obtiene sustituyendo estos números en la ecuación (3.15). Se capturaron, etiquetaron y liberaron cinco individuos de una población de animales que se piensa están al borde de la extinción en una región para que se mezclen con la población. Después de haber tenido la oportunidad de mezclarse, se selecciona una muestra aleatoria de 10 de estos animales. Sea X el número de animales etiquetados en la segunda mues- tra. Si en realidad hay 25 animales de este tipo en la región, ¿cuál es la probabilidad de que a) X 2? b) ¿X 2? Los valores de los parámetros son n 10, M 5 (cinco animales etiquetados en la población) y N 25, por lo tanto h(x; 10, 5, 25) x 0, 1, 2, 3, 4, 5 Para el inciso a) P(X 2) h(2; 10, 5, 25) 0.385 Para el inciso b) P(X 2) P(X 0, 1 o 2) 2 x0 h(x; 10, 5, 25) 0.057 0.257 0.385 0.699 ■ Están disponibles tablas amplias de la distribución hipergeométrica, pero como la dis- tribución tiene tres parámetros, estas tablas requieren mucho más espacio que las tablas 5 2 2 8 0 2 1 5 0 5 x10 2 0 x 2 1 5 0 c3_p086-129.qxd 3/12/08 4:01 AM Page 117
- 136. para la distribución binomial. MINITAB y otros paquetes de software de estadística gene- ran con facilidad las probabilidades hipergeométricas. Como en el caso binomial, existen expresiones simples para E(X) y V(X) para varia- bles aleatorias hipergeométricas. 118 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad La razón M/N es la proporción de éxitos en la población. Si se reemplaza M/N por p en E(X) y V(X), se obtiene E(X) np V(X) np(1 p) (3.16) La expresión (3.16) muestra que las medias de las variables aleatorias binomiales e hiper- geométricas son iguales, en tanto que las varianzas de las dos variables aleatorias difieren por el factor (N n)/(N 1), a menudo llamado factor de corrección por población finita. Este factor es menor que 1, así que la variable hipergeométrica tiene una varianza más pe- queña que la variable aleatoria binomial. El factor de corrección puede escribirse como (1 n/N)(1 1/N), el cual es aproximadamente 1 cuando n es pequeño con respecto a N. En el ejemplo de etiquetación de animales, n 10, M 5 y N 25, por lo tanto p 2 5 5 0.2 y E(X) 10(0.2) 2 V(X) (10)(0.2)(0.8) (0.625)(1.6) 1 Si el muestreo se realizó con reemplazo, V(X) 1.6. Suponga que en realidad no se conoce el tamaño de la población N, así que se obser- va el valor x y se desea estimar N. Es razonable igualar la proporción muestral observada de éxitos, x/n, y la proporción de la población, M/N da la estimación N̂ Si M 100, n 40 y x 16, entonces N̂ 250. ■ La regla general empírica dada en la sección 3.4 plantea que si el muestreo se realizó sin reemplazo pero n/N era cuando mucho de 0.05, entonces la distribución binomial podría ser utilizada para calcular probabilidades aproximadas que implican el número de éxitos en la muestra. Un enunciado más preciso es el siguiente. Permita que el tamaño de la pobla- ción N y el número de M éxitos presentes en la población, se hagan más grandes a medida que la razón M/N tiende a p. Entonces h(x; n, M, N) tiende a b(x; n, p); así que con n/N pe- queña, las dos son aproximadamente iguales siempre que p no esté muy cerca de 0 o 1. Este es el razonamiento de la regla empírica. Distribución binomial negativa La variable aleatoria y la distribución binomial negativa se basan en un experimento que sa- tisface las siguientes condiciones: M n x 15 24 N n N 1 PROPOSICIÓN La media y la varianza de la variable aleatoria hipergeométrica X cuya función masa de probabilidad es h(x; n, M, N) son E(X) n V(X) n 1 M N M N N n N 1 M N Ejemplo 3.37 (continuación del ejemplo 3.36) c3_p086-129.qxd 3/12/08 4:01 AM Page 118
- 137. 1. El experimento consiste en una secuencia de ensayos independientes. 2. Cada ensayo puede dar por resultado un éxito (E) o una falla (F). 3. La probabilidad de éxito es constante de un ensayo a otro, por lo tanto P(E en el ensayo i) p con i 1, 2, 3. . . . 4. El experimento continúa (se realizan ensayos) hasta que un total de r éxitos hayan sido observados, donde r es un entero positivo especificado. La variable aleatoria de interés es X el número de fallas que preceden al r-ésimo éxito; X se llama variable aleatoria binomial negativa porque, en contraste con la variable aleato- ria binomial, el número de éxitos es fijo y el número de ensayos es aleatorio. Posibles valores de X son 0, 1, 2, . . . . Sea nb(x; r, p) la función masa de probabilidad de X. El evento {X x} equivale a {r 1 éxitos en los primeros (x r 1) ensayos y un éxito (E) en el ensayo (x r) perceptil} (p. ej., si r 5 y x 10, entonces debe haber cua- tro éxitos en los primeros 14 ensayos y en el ensayo 15 debe ser un éxito). Como los ensa- yos son independientes, nb(x; r, p) P(X x) P(r 1 éxitos en los primeros x r 1 ensayos) P(E) (3.17) La primera probabilidad en el miembro de más a la derecha de la expresión (3.17) es la pro- babilidad binomial pr1 (1 p)x donde P(E) p x r 1 r 1 3.5 Distribuciones hipergeométricas y binomiales negativas 119 Un pediatra desea reclutar cinco parejas, cada una de las cuales espera a su primer hijo, para participar en un nuevo régimen de alumbramiento natural. Sea p P(una pareja selec- cionada al azar está de acuerdo en participar). Si p 0.2, ¿cuál es la probabilidad de que 15 parejas tengan que ser entrevistadas antes de encontrar cinco que estén de acuerdo en parti- cipar? Es decir, E {está de acuerdo en participar}, ¿cuál es la probabilidad de que ocurran 10 fallas antes del quinto éxito? Sustituyendo r 5, p 0.2 y x 10 en nb(x; r, p) da nb(10; 5, 0.2) (0.2)5 (0.8)10 0.034 La probabilidad de que cuando mucho se observen 10 fallas (cuando mucho con 15 parejas entrevistadas) es P(X 10) 10 x0 nb(x; 5, 0.2) (0.2)5 10 x0 (0.8)x 0.164 ■ En algunas fuentes, la variable aleatoria binomial negativa se considera como el nú- mero de ensayos X r en lugar del número de fallas. En el caso especial r 1, la función masa de probabilidad es nb(x; 1, p) (1 p)x p x 0, 1, 2, . . . (3.18) En el ejemplo 3.12, la función masa de probabilidad se derivó para el número de ensayos necesarios para obtener el primer éxito (E ) y allí la función masa de probabilidad es simi- lar a la expresión (3.18). En la literatura se hace referencia tanto a X número de fallas (F) como a Y número de ensayos ( 1 X) como variables aleatorias geométricas y la función masa de probabilidad en la expresión (3.18) se llama distribución geométrica. x 4 4 14 4 PROPOSICIÓN La función masa de probabilidad de la variable aleatoria binomial negativa X con los parámetros r número de éxitos (E) y p P(E) es nb(x; r, p) pr (1 p)x x 0, 1, 2, . . . x r 1 r 1 Ejemplo 3.38 c3_p086-129.qxd 3/12/08 4:01 AM Page 119
- 138. En el ejemplo 3.19, se demostró que el número esperado de ensayos hasta que apare- ce el primer éxito es 1/p, así que el número esperado de fallas hasta que aparece el primer éxito es (1/p) 1 (1 p)/p. Intuitivamente, se esperaría ver r (1 p)/p fallas antes del r-ésimo éxito y éste en realidad es E(X). También existe una fórmula simple para V(X). 120 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Por último, al expandir el coeficiente binomial en frente de pr (1 p)x y haciendo alguna re- ducción o cancelación, se ve que nb(x; r, p) está bien definido incluso cuando r no es un en- tero. Se ha encontrado la distribución binomial negativa generalizada para ajustar muy bien los datos observados en una amplia variedad de aplicaciones. PROPOSICIÓN Si X es una variable aleatoria binomial negativa con función masa de probabilidad nb(x; r, p), entonces E(X) V(X) r(1 p) p2 r(1 p) p 68. Un tipo de cámara digital viene en una versión de 3 megapi- xeles o una versión de 4 megapixeles. Una tienda de cáma- ras recibió un envío de 15 de estas cámaras, de las cuales 6 tienen una resolución de 3 megapixeles. Suponga que se seleccionan al azar 5 de estas cámaras para guardarlas detrás del mostrador; las otras 10 se colocan en una bodega. Sea X el número de cámaras de 3 megapixeles entre las 5 se- leccionadas para guardarlas detrás del mostrador. a. ¿Qué distribución tiene X (nombre y valores de todos los parámetros)? b. Calcule P(X 2), P(X 2) y P(X 2). c. Calcule el valor medio y la desviación estándar de X. 69. Cada uno de 12 refrigeradores de un tipo ha sido regresado a un distribuidor debido a un ruido agudo audible producido por oscilación cuando el refrigerador está funcionando. Su- ponga que 7 de estos refrigeradores tienen un compresor de- fectuoso y que los otros 5 tienen problemas menos serios. Si los refrigeradores se examinan en orden aleatorio, sea X el número entre los primeros 6 examinados que tienen un com- presor defectuoso. Calcule lo siguiente: a. P(X 5) b. P(X 4) c. La probabilidad de que X exceda su valor medio por más de una desviación estándar. d. Considere un gran envío de 400 refrigeradores, 40 de los cuales tienen compresores defectuosos. Si X es el núme- ro entre 15 refrigeradores seleccionados al azar que tie- nen compresores defectuosos, describa una forma menos tediosa de calcular (por lo menos de forma aproximada) P(X 5) que utilizar la función masa de probabilidad hi- pergeométrica. 70. Un instructor que impartió dos secciones de estadística de ingeniería el semestre pasado, la primera con 20 estudiantes y la segunda con 30, decidió asignar un proyecto semestral. Una vez que todos los proyectos le fueron entregados, el ins- tructor los ordenó al azar antes de calificarlos. Considere los primeros 15 proyectos calificados. a. ¿Cuál es la probabilidad de que exactamente 10 de estos sean de la segunda sección? b. ¿Cuál es la probabilidad de que por lo menos 10 de estos sean de la segunda sección? c. ¿Cuál es la probabilidad de que por lo menos 10 de estos sean de la misma sección? d. ¿Cuáles son el valor medio y la desviación estándar del número entre estos 15 que son de la segunda sección? e. ¿Cuáles son el valor medio y la desviación estándar del número de proyectos que no están entre estos primeros 15 que son de la segunda sección? 71. Un geólogo recolectó 10 especímenes de roca basáltica y 10 especímenes de granito. Él le pide a su ayudante de labora- torio que seleccione al azar 15 de los especímenes para ana- lizarlos. a. ¿Cuál es la función masa de probabilidad del número de especímenes de granito seleccionados para su aná- lisis? b. ¿Cuál es la probabilidad de que todos los especímenes de uno de los dos tipos de roca sean seleccionados para su análisis? c. ¿Cuál es la probabilidad de que el número de especíme- nes de granito seleccionados para analizarlos esté dentro de una desviación estándar de su valor medio? 72. Un director de personal que va a entrevistar a 11 ingenieros para cuatro vacantes de trabajo ha programado seis entrevis- tas para el primer día y cinco para el segundo. Suponga que los candidatos son entrevistados en orden aleatorio. a. ¿Cuál es la probabilidad que x de los cuatro mejores can- didatos sean entrevistados el primer día? b. ¿Cuántos de los mejores cuatro candidatos se espera que puedan ser entrevistados el primer día? 73. Veinte parejas de individuos que participan en un torneo de bridge han sido sembrados del 1, . . . , 20. En esta primera parte del torneo, los 20 son divididos al azar en 10 parejas este-oeste y 10 parejas norte-sur. EJERCICIOS Sección 3.5 (68-78) c3_p086-129.qxd 3/12/08 4:01 AM Page 120
- 139. a. ¿Cuál es la probabilidad de que x de las 10 mejores pare- jas terminen jugando este-oeste? b. ¿Cuál es la probabilidad de que las cinco mejores parejas terminen jugando en la misma dirección? c. Si existen 2n parejas, ¿cuál es la función masa de proba- bilidad de X el número entre las mejores n parejas que terminan jugando este-oeste? ¿Cuáles son E(X) y V(X)? 74. Una alerta contra el esmog de segunda etapa ha sido emiti- da en una área del condado de Los Ángeles en la cual hay 50 firmas industriales. Un inspector visitará 10 firmas seleccio- nadas al azar para ver si no han violado los reglamentos. a. Si 15 de las firmas sí están violando por lo menos un re- glamento, ¿cuál es la función masa de probabilidad del número de firmas visitadas por el inspector que violan por lo menos un reglamento? b. Si existen 500 firmas en el área, 150 de las cuales violan algún reglamento, represente de forma aproximada la función masa de probabilidad del inciso a) con una fun- ción masa de probabilidad más simple. c. Con X el número entre las 10 visitadas que violan al- gún reglamento, calcule E(X) y V(X) ambas para la fun- ción masa de probabilidad exacta y función masa de probabilidad aproximada del inciso b). 75. Suponga que p P(nacimiento de un varón) 0.5. Una pa- reja desea tener exactamente dos niñas en su familia. Ten- drán hijos hasta que esta condición se satisfaga. a. ¿Cuál es la probabilidad de que la familia tenga x varones? b. ¿Cuál es la probabilidad de que la familia tenga cuatro hijos? c. ¿Cuál es la probabilidad de que la familia tenga cuando mucho cuatro hijos? d. ¿Cuántos varones cree que tenga esta familia? ¿Cuántos hijos esperaría que tenga esta familia? 76. Una familia decide tener hijos hasta que tengan tres del mismo sexo. Suponiendo P(B) P(G) 0.5, ¿cuál es la función ma- sa de probabilidad de X el número de hijos en la familia? 77. Tres hermanos y sus esposas deciden tener hijos hasta que cada familia tenga dos niñas. ¿Cuál es la función masa de probabilidad de X el número total de varones procreados por los hermanos? ¿Cuál es E(X) y cómo se compara con el número esperado de varones procreados por cada hermano? 78. El individuo A tiene un dado rojo y el B uno verde (ambos imparciales). Si cada uno los lanza hasta que obtiene cinco “dobles” (11, . . . , 66), ¿cuál es la función masa de pro- babilidad de X el número total de veces que un dado es lanzado? ¿Cuáles son E(X) y V(X)? 3.6 Distribución de probabilidad de Poisson 121 Las distribuciones binomiales, hipergeométricas y binomiales negativas se derivaron par- tiendo de un experimento compuesto de ensayos o sorteos y aplicando las leyes de probabi- lidad a varios resultados del experimento. No existe un experimento simple en el cual esté basada la distribución de Poisson, aun cuando en breve se describirá cómo puede ser obte- nida mediante ciertas operaciones restrictivas. 3.6 Distribución de probabilidad de Poisson DEFINICIÓN Se dice que una variable aleatoria X tiene una distribución de Poisson con paráme- tro ( 0) si la función masa de probabilidad de X es p(x; ) x 0, 1, 2, . . . e x x! El valor de es con frecuencia un valor por unidad de tiempo o por unidad de área. La letra e en p(x; ) representa la base del sistema de logaritmos naturales; su valor numé- rico es aproximadamente 2.71828. Como debe ser positiva, p(x; ) 0 con todos los va- lores posibles x. El hecho de que x0 p(x; ) 1 es una consecuencia de la expansión de la serie infinita de Maclaurin de e , la cual aparece en la mayoría de los textos de cálculo: e 1 . . . x0 (3.19) Si los dos términos extremos de la expresión (3.19) se multiplican por e y luego e se coloca adentro de la suma, el resultado es 1 x0 e lo que demuestra que p(x; ) satisface la segunda condición necesaria para especificar una función masa de probabilidad. x x! x x! 3 3! 2 2! c3_p086-129.qxd 3/12/08 4:01 AM Page 121
- 140. Sea X el número de criaturas de un tipo particular capturadas en una trampa durante un periodo determinado. Suponga que X tiene una distribución de Poisson con 4.5, así que en promedio las trampas contendrán 4.5 criaturas [El artículo “Dispersal Dynamics of the Bivalve Gemma Gemma in a Patchy Environment (Ecological Monographs, 1995: 1–20) su- giere este modelo: el molusco bivalvo Gemma gemma es una pequeña almeja.] La probabi- lidad de que una trampa contenga exactamente cinco criaturas es P(X 5) 0.1708 La probabilidad de que una trampa contenga cuando mucho cinco criaturas es P(X 5) 5 x0 e 4.5 1 4.5 . . . 0.7029 ■ La distribución de Poisson como límite La siguiente proposición proporciona el razonamiento para utilizar la distribución de Pois- son en muchas situaciones. (4.5)5 5! (4.5)2 2! e 4.5 (4.5)x x! e 4.5 (4.5)5 5! 122 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad Ejemplo 3.39 De acuerdo con esta proposición, en cualquier experimento binomial en el cual n es grande y p es pequeña, b(x; n, p) p(x; ), donde np. Como regla empírica, esta apro- ximación puede ser aplicada con seguridad si n 50 y np 5. Si un editor de libros no técnicos hace todo lo posible porque sus libros estén libres de erro- res tipográficos, de modo que la probabilidad de que cualquier página dada contenga por lo menos uno de esos errores es de 0.005 y los errores son independientes de una página a otra, ¿cuál es la probabilidad de que una de sus novelas de 400 páginas contenga exactamente una página con errores? ¿Cuándo mucho tres páginas con errores? Con S denotando una página que contiene por lo menos un error y F una página libre de errores, el número X de páginas que contienen por lo menos un error es una variable alea- toria binomial con n 400 y p 0.005, así que np 2. Se desea P(X 1) b(1; 400, 0.005) p(1; 2) 0.270671 El valor binomial es b(1; 400, 0.005) 0.270669, así que la aproximación es muy buena. Asimismo P(X 3) 3 x0 p(x, 2) 3 x0 e 2 0.135335 0.270671 0.270671 0.180447 0.8571 y éste de nuevo se aproxima bastante al valor binomial P(X 3) 0.8576. ■ La tabla 3.2 muestra la distribución de Poisson con 3 junto con las tres distribu- ciones binomiales con np 3 y la figura 3.8 (generada por S-Plus) ilustra una gráfica de la distribución de Poisson junto con las dos primeras distribuciones binomiales. La aproxima- ción es de uso limitado con n 30, pero desde luego la precisión es mejor con n 100 y mucho mejor con n 300. 2x x! e 2 (2)1 1! PROPOSICIÓN Suponga que en la función masa de probabilidad binomial b(x; n, p), si n A y p A 0 de tal modo que np tienda a un valor 0. Entonces b(x; n, p) A p(x; ). Ejemplo 3.40 c3_p086-129.qxd 3/12/08 4:01 AM Page 122
- 141. La tabla A.2 del apéndice muestra la función de distribución acumulativa F(x; ) para 0.1, 0.2, . . . , 1, 2, . . . , 10, 15 y 20. Por ejemplo, si 2 entonces P(X 3) F(3; 2) 0.857 como en el ejemplo 3.40, en tanto que P(X 3) F(3; 2) F(2; 2) 0.180. Alternativamente, muchos paquetes de computadora estadísticos generarán p(x; ) y F(x; ) al solicitarlo. Media y varianza de X Como b(x; n, p) A p(x; ) a medida que n A , p A 0, np A , la media y varianza de una variable binomial deberán aproximarse a las de una variable de Poisson. Estos límites son np A y np(1 p) A . 3.6 Distribución de probabilidad de Poisson 123 Tabla 3.2 Comparación de la distribución de Poisson con tres distribuciones binomiales x n 30, p 0.1 n 100, p 0.03 n 300, p 0.01 Poisson, 3 0 0.042391 0.047553 0.049041 0.049787 1 0.141304 0.147070 0.148609 0.149361 2 0.227656 0.225153 0.224414 0.224042 3 0.236088 0.227474 0.225170 0.224042 4 0.177066 0.170606 0.168877 0.168031 5 0.102305 0.101308 0.100985 0.100819 6 0.047363 0.049610 0.050153 0.050409 7 0.018043 0.020604 0.021277 0.021604 8 0.005764 0.007408 0.007871 0.008102 9 0.001565 0.002342 0.002580 0.002701 10 0.000365 0.000659 0.000758 0.000810 0 2 4 6 8 10 x 0.25 0.20 0.15 0.10 0.05 0 o x o x o x o x o x o x o x o x o x o x o x Bin, n30 (o); Bin, n100 (x); Poisson ( ) p(x) Figura 3.8 Comparación de una distribución de Poisson con dos distribuciones binomiales. PROPOSICIÓN Si X tiene una distribución de Poisson con parámetro , entonces E(X) V(X) . Estos resultados también pueden ser derivados directamente de la definición de media y va- rianza. Tanto el número esperado de criaturas atrapadas como la varianza de éste son iguales a 4.5, y X 4 .5 2.12. ■ Ejemplo 3.41 (continuación del ejemplo 3.39) c3_p086-129.qxd 3/12/08 4:01 AM Page 123
- 142. Proceso de Poisson Una aplicación muy importante de la distribución de Poisson surge en conexión con la ocu- rrencia de eventos de algún tipo en el transcurso del tiempo. Eventos de interés podrían ser visitas a un sitio web particular, pulsos de alguna clase registrados por un contador, mensa- jes de correo electrónico enviados a una dirección particular, accidentes en una instalación industrial o lluvias de rayos cósmicos observados por astrónomos en un observatorio par- ticular. Se hace la siguiente suposición sobre la forma en que los eventos de interés ocurren: 1. Existe un parámetro 0 de tal modo que durante cualquier intervalo de tiempo corto t, la probabilidad de que ocurra exactamente un evento es t o(t).* 2. La probabilidad de que ocurra más de un evento durante t es o(t) [la que junto con la suposición 1, implica que la probabilidad de cero eventos durante t es 1 t o(t)]. 3. El número de eventos ocurridos durante este intervalo de tiempo t es independiente del número ocurrido antes de este intervalo de tiempo. Informalmente, la suposición 1 dice que durante un corto intervalo de tiempo, la probabili- dad de que ocurra un solo evento es aproximadamente proporcional a la duración del inter- valo de tiempo, donde es la constante de proporcionalidad. Ahora sea Pk(t) la probabilidad de que k eventos serán observados durante cualquier intervalo de tiempo particular de dura- ción t. 124 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad PROPOSICIÓN Pk(t) et (t)k /k!, de modo que el número de eventos durante un intervalo de tiempo de duración t es una variable de Poisson con parámetro t. El número es- perado de eventos durante cualquier intervalo de tiempo es entonces t, así que el nú- mero esperado durante un intervalo de tiempo unitario es . La ocurrencia de eventos en el transcurso del tiempo como se describió se llama proceso de Poisson; el parámetro especifica el ritmo del proceso. Suponga que llegan pulsos a un contador a un ritmo promedio de seis por minuto, así que 6. Para determinar la probabilidad de que en un intervalo de 0.5 min se reciba por lo menos un pulso, obsérvese que el número de pulsos en ese intervalo tiene una distribución de Poisson con parámetro t 6(0.5) 3 (se utiliza 0.5 min porque está expresada co- mo ritmo por minuto). Entonces con X el número de pulsos recibidos en el intervalo de 30 segundos, P(1 X) 1 P(X 0) 1 0.950 ■ En lugar de observar eventos en el transcurso del tiempo, considere observar eventos de algún tipo que ocurren en una región de dos o tres dimensiones. Por ejemplo, se podría seleccionar un mapa de una región R de un bosque, ir a dicha región y contar el número de árboles. Cada árbol representaría un evento que ocurre en un punto particular del espacio. Conforme a suposiciones similares a 1–3, se puede demostrar que el número de eventos que ocurren en una región R tiene una distribución de Poisson con parámetro a(R), donde a(R) es el área de R. La cantidad es el número esperado de eventos por unidad de área o volumen. e 3 (3)0 0! Ejemplo 3.42 * Una cantidad es o(t) (léase “o minúscula de delta t”) si, a medida que t tiende a cero, también lo hace o(t)/t. Es decir, o(t) es incluso más insignificante (tiende a 0 más rápido) que t mismo. La cantidad (t)2 tiene esta pro- piedad, pero sen(t) no. c3_p086-129.qxd 3/12/08 4:01 AM Page 124
- 143. 79. Sea X el número de imperfecciones superficiales de una cal- dera seleccionada al azar de un tipo que tiene una distribu- ción de Poisson con parámetro 5. Use la tabla A.2 del apéndice para calcular las siguientes probabilidades: a. P(X 8) b. P(X 8) c. P(9 X) d. P(5 X 8) e. P(5 X 8) 80. Suponga que el número X de tornados observados en una re- gión particular durante un año tiene una distribución de Poisson con 8. a. Calcule P(X 5). b. Calcule P(6 X 9). c. Calcule P(10 X). d. ¿Cuál es la probabilidad de que el número observado de tornados sobrepase el número esperado por más de una desviación estándar? 81. Suponga que el número de conductores que viajan entre un origen y destino particulares durante un periodo designado tiene una distribución de Poisson con parámetro 20 (su- gerido en el artículo “Dynamic Ride Sharing: Theory and Practice”, J. of Transp. Engr., 1997: 308–312). ¿Cuál es la probabilidad de que el número de conductores a. sea cuando mucho de 10? b. sea de más de 20? c. sea de entre 10 y 20, inclusive? ¿Sea estrictamente de en- tre 10 y 20? d. esté dentro de dos desviaciones estándar del valor medio? 82. Considere escribir en un disco de computadora y luego enviar- lo a través de un certificador que cuenta el número de pulsos faltantes. Suponga que este número X tiene una distribución de Poisson con parámetro 0.2. (Sugerido en “Average Sample Number for Semi-Curtailed Sampling Using the Pois- son Distribution”, J. Quality Technology, 1983: 126–129.) a. ¿Cuál es la probabilidad de que un disco tenga exacta- mente un pulso faltante? b. ¿Cuál es la probabilidad de que un disco tenga por lo me- nos dos pulsos faltantes? c. Si seleccionan dos discos independientemente, ¿cuál es la probabilidad de que ninguno contenga un pulso faltante? 83. Un artículo en Los Ángeles Times (3 de diciembre de 1993) reporta que una de cada 200 personas portan el gen defec- tuoso que provoca cáncer de colon hereditario. En una muestra de 1000 individuos, ¿cuál es la distribución aproxi- mada del número que porta este gen? Use esta distribución para calcular la probabilidad aproximada de que a. Entre 5 y 8 (inclusive) porten el gen. b. Por lo menos 8 porten el gen. 84. Suponga que sólo 0.10% de todas las computadoras de cier- to tipo experimentan fallas del CPU durante el periodo de garantía. Considere una muestra de 10 000 computadoras. a. ¿Cuáles son el valor esperado y la desviación estándar del número de computadoras en la muestra que tienen el defecto? b. ¿Cuál es la probabilidad (aproximada) de que más de 10 computadoras muestreadas tengan el defecto? c. ¿Cuál es la probabilidad (aproximada) de que ninguna computadora muestreada tenga el defecto? 85. Suponga que una pequeña aeronave aterriza en un aeropuer- to de acuerdo con un proceso de Poisson con razón 8 por hora de modo que el número de aterrizajes durante un periodo de t horas es una variable aleatoria de Poisson con parámetro 8t. a. ¿Cuál es la probabilidad de que exactamente seis aerona- ves pequeñas aterricen durante un intervalo de una hora? ¿Por lo menos seis? ¿Por lo menos 10? b. ¿Cuáles son el valor esperado y la desviación estándar del número de aeronaves pequeñas que aterrizan durante un lapso de 90 min? c. ¿Cuál es la probabilidad de que por lo menos 20 aerona- ves pequeñas aterricen durante un lapso de 2 1 2-horas? ¿De qué cuando mucho aterricen 10 durante este periodo? 86. El número de personas que llegan para tratamiento a una sala de urgencias puede ser modelado mediante un proceso de Poisson con parámetro de razón de cinco por hora. a. ¿Cuál es la probabilidad de que ocurran exactamente cuatro arribos durante una hora particular? b. ¿Cuál es la probabilidad de que por lo menos cuatro per- sonas arriben durante una hora particular? c. ¿Cuántas personas espera que arriben durante un periodo de 45 min? 87. El número de solicitudes de ayuda recibidas por un servicio de grúas es un proceso de Poisson con razón 4 por hora. a. Calcule la probabilidad de que exactamente diez solicitu- des sean recibidas durante un periodo particular de 2 horas. b. Si los operadores del servicio de grúas hacen una pausa de 30 min para el almuerzo, ¿cuál es la probabilidad de que no dejen de atender llamadas de ayuda? c. ¿Cuántas llamadas esperaría durante esta pausa? 88. Al someter a prueba tarjetas de circuito, la probabilidad de que cualquier diodo particular falle es de 0.01. Suponga que una tarjeta de circuito contiene 200 diodos. a. ¿Cuántos diodos esperaría que fallen y cuál es la desvia- ción estándar del número que se espera fallen? b. ¿Cuál es la probabilidad (aproximada) de que por lo menos cuatro diodos fallen en una tarjeta seleccionada al azar? c. Si se envían cinco tarjetas a un cliente particular, ¿qué tan probable es que por lo menos cuatro de ellas funcionen apropiadamente? (Una tarjeta funciona apropiadamente sólo si todos sus diodos funcionan.) 89. El artículo “Reliability-Based Service-Life Assessment of Aging Concrete Structures”. (J. Structural Engr., 1993: 1600–1621) sugiere que un proceso de Poisson puede ser utilizado para representar la ocurrencia de cargas estructura- les en el transcurso del tiempo. Suponga que el tiempo medio entre ocurrencias de cargas es de 0.5 al año. a. ¿Cuántas cargas se espera que ocurran durante un perio- do de 2 años? b. ¿Cuál es la probabilidad de que ocurran más de cinco cargas durante un periodo de 2 años? c. ¿Qué tan largo debe ser un periodo de modo que la pro- babilidad de que no ocurran cargas durante dicho periodo sea cuando mucho de 0.1? 3.6 Distribución de probabilidad de Poisson 125 EJERCICIOS Sección 3.6 (79-93) c3_p086-129.qxd 3/12/08 4:01 AM Page 125
- 144. 94. Considere un mazo compuesto de siete cartas, marcadas 1, 2, . . . , 7. Se seleccionan al azar tres de estas cartas. Defina una variable aleatoria W como W la suma de los números resultantes y calcule la función masa de probabilidad de W. Calcule entonces y 2 . [Sugerencia: Considere los resul- tados sin orden, de modo que (1, 3, 7) y (3, 1, 7) no son re- sultados diferentes. Entonces existen 35 resultados y pueden ser puestos en lista. (Este tipo de variable aleatoria en reali- dad se presenta en conexión con una prueba de hipótesis lla- mada prueba de suma de filas de Wilcoxon, en la cual hay una muestra x y una muestra y y W es la suma de las filas de x en la muestra combinada.)] 95. Después de barajar un mazo de 52 cartas, un tallador repar- te 5. Sea X el número de palos representados en la mano de 5 cartas. a. Demuestre que la función masa de probabilidad de X es [Sugerencia: p(1) 4P(todas son espadas), p(2) 6P(sólo espadas y corazones con por lo menos una de cada palo) y p(4) 4P(2 espadas una de cada otro palo).] b. Calcule , 2 y . 96. La variable aleatoria binomial negativa X se definió como el nú- mero de fallas (F) que preceden al r-ésimo éxito (S). Sea Y el número de ensayos necesarios para obtener el r-ésimo éxito (S). Del mismo modo en que fue derivada la función masa de probabilidad, derive la función masa de probabilidad de Y. 97. De todos los clientes que adquieren abrepuertas de cochera automáticas, 75% adquieren el modelo de transmisión por cadena. Sea X el número entre los siguientes 15 compra- dores que seleccionan el modelo de transmisión por cadena. a. ¿Cuál es la función masa de probabilidad de X? b. Calcule P(X 10). c. Calcule P(6 X 10). d. Calcule y 2 . e. Si la tienda actualmente tiene en existencia 10 modelos de transmisión por cadena y 8 modelos de transmisión por flecha, ¿cuál es la probabilidad de que las solicitudes de estos 15 clientes puedan ser satisfechas con las exis- tencias actuales? 98. Un amigo recientemente planeó un viaje de campamento. Tenía dos linternas, una que requería una sola batería de 6 V y otra que utilizaba dos baterías de tamaño D. Antes había empacado dos baterías de 6 V y cuatro tamaño D en su “camper”. Suponga que la probabilidad de que cualquier ba- tería particular funcione es p y que las baterías funcionan o fallan independientemente una de otra. Nuestro amigo desea llevar sólo una linterna. ¿Con qué valores de p deberá llevar la linterna de 6 V? 99. Un sistema k de n es uno que funcionará si y sólo si por lo menos k de los n componentes individuales en el sistema funcionan. Si los componentes individuales funcionan inde- pendientemente uno de otro, cada uno con probabilidad de 0.9, ¿cuál es la probabilidad de que un sistema 3 de 5 fun- cione? 90. Si X tiene una distribución de Poisson con parámetro . De- muestre que E(X) derivada directamente de la defini- ción de valor esperado. [Sugerencia: El primer término en la suma es igual a 0 y luego x puede ser eliminada. Ahora sa- que como factor a y demuestre que la suma es uno.] 91. Suponga que hay árboles distribuidos en un bosque de acuerdo con un proceso de Poisson bidimensional con pará- metro , el número esperado de árboles por acre es de 80. a. ¿Cuál es la probabilidad de que en un terreno de un cuar- to de acre, haya cuando mucho 16 árboles? b. Si el bosque abarca 85 000 acres, ¿cuál es el número es- perado de árboles en el bosque? c. Suponga que selecciona un punto en el bosque y constru- ye un círculo de 0.1 milla de radio. Sea X el número de árboles dentro de esa región circular. ¿Cuál es la función masa de probabilidad de X? [Sugerencia: 1 milla cuadra- da 640 acres.] 92. A una estación de inspección de equipo vehicular llegan au- tomóviles de acuerdo con un proceso de Poisson con razón 10 por hora. Suponga que un vehículo que llega con probabilidad de 0.5 no tendrá violaciones de equipo. a. ¿Cuál es la probabilidad de que exactamente diez lleguen durante la hora y que los diez no tengan violaciones? b. Con cualquier y 10 fija, ¿cuál es la probabilidad de que y automóviles lleguen durante la hora, diez de los cuales no tengan violaciones? c. ¿Cuál es la probabilidad de que lleguen diez carros “sin violaciones” durante la siguiente hora? [Sugerencia: Sume la probabilidades en el inciso b) desde y 10 hasta .] 93. a. En un proceso de Poisson, ¿qué tiene que suceder tanto en el intervalo de tiempo (0, t) como en el intervalo (t, t t) de modo que no ocurran eventos en todo el intervalo (0, t t)? Use esto y las suposiciones 1–3 para escribir una relación entre P0(t t) y P0(t). b. Use el resultado del inciso a) para escribir una expresión para la diferencia P0(t t) P0(t). Divida entonces en- tre t y permita que t A 0 para obtener una ecuación que implique (d/dt)P0(t), la derivada de P0(t) con respec- to a t. c. Verifique que P0(t) et satisface la ecuación del in- ciso b). d. Se puede demostrar de manera similar a los incisos a) y b) que Pk(t)s debe satisfacer el sistema de ecuaciones di- ferenciales Pk(t) Pk1(t) Pk(t) k 1, 2, 3, . . . Verifique que Pk(t) e t (t)k /k! satisface el sistema. (En realidad esta es la única solución.) d dt 126 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad EJERCICIOS SUPLEMENTARIOS (94-122) x 1 2 3 4 p(x) 0.002 0.146 0.588 0.264 c3_p086-129.qxd 3/12/08 4:01 AM Page 126
- 145. 100. Un fabricante de baterías para linternas desea controlar la calidad de sus productos rechazando cualquier lote en el que la proporción de baterías que tienen un voltaje inacep- table parezca ser demasiado alto. Con esta finalidad, de cada lote de 10 000 baterías, se seleccionaron y probarán 25. Si por lo menos 5 de estas generan un voltaje inacepta- ble, todo el lote será rechazado. ¿Cuál es la probabilidad de que un lote será rechazado si a. 5% de las baterías en el lote tienen voltajes inaceptables? b. 10% de las baterías en el lote tienen voltajes inacepta- bles? c. 20% de las baterías en el lote tienen voltajes inacepta- bles? d. ¿Qué les sucedería a las probabilidades en los incisos a)–c) si el número de rechazo crítico se incrementara de 5 a 6? 101. De las personas que pasan a través de un detector de meta- les en un aeropuerto, el 0.5% lo activan; sea X el núme- ro entre un grupo de 500 seleccionado al azar que activan el detector. a. ¿Cuál es la función masa de probabilidad (aproximada) de X? b. Calcule P(X 5). c. Calcule P(5 X). 102. Una firma consultora educativa está tratando de decidir si los estudiantes de preparatoria que nunca antes han utiliza- do una calculadora de mano pueden resolver cierto tipo de problema más fácilmente con una calculadora que utiliza lógica polaca inversa o una que no utiliza esta lógica. Se selecciona una muestra de 25 estudiantes y se les permite practicar con ambas calculadoras. Luego a cada estudiante se le pide que resuelva un problema con la calculadora po- laca inversa y un problema similar con la otra. Sea p P(S), donde S indica que un estudiante resolvió el proble- ma más rápido con la lógica polaca inversa que sin ella y sea X número de éxitos. a. Si p 0.5, ¿cuál es P(7 X 18)? b. Si p 0.8, ¿cuál es P(7 X 18)? c. Si la pretensión de que p 0.5 tiene que ser rechazada cuando X 7 o X 18, ¿cuál es la probabilidad de re- chazar la pretensión cuando en realidad es correcta? d. Si la decisión de rechazar la pretensión p 0.5 se hace como en el inciso c), ¿cuál es la probabilidad de que la pretensión no sea rechazada cuando p 0.6? ¿Cuándo p 0.8? e. ¿Qué regla de decisión escogería para rechazar la pre- tensión de que p 0.5 si desea que la probabilidad en el inciso c) sea cuando mucho de 0.01? 103. Considere una enfermedad cuya presencia puede ser iden- tificada por medio de un análisis de sangre. Sea p la proba- bilidad de que un individuo seleccionado al azar tenga la enfermedad. Suponga se seleccionan independientemente n individuos para analizarlos. Una forma de proceder es analizar cada una de las n muestras de sangre. Un proce- dimiento potencialmente más económico, de análisis en grupo se introdujo durante la Segunda Guerra Mundial pa- ra identificar hombres sifilíticos entre los reclutas. En pri- mer lugar, se toma una parte de cada muestra de sangre, se combinan estos especímenes y se realiza un solo análisis. Si ninguno tiene la enfermedad, el resultado será negativo y sólo se requiere un análisis. Si por lo menos un individuo está enfermo, el análisis de la muestra combinada dará un resultado positivo, en cuyo caso se realizan los análisis de los n individuos. Si p 0.1 y n 3, ¿cuál es el número es- perado de análisis si se utiliza este procedimiento? ¿Cuál es el número esperado cuando n 5? [El artículo “Ran- dom Multiple-Access Communication and Group Testing” (IEEE Trans. on Commun., 1984: 769–774) aplicó estas ideas a un sistema de comunicación en el cual la dicotomía fue usuario ocioso/activo en lugar de enfermo/no enfermo.] 104. Sea p1 la probabilidad de que cualquier símbolo de código particular sea erróneamente transmitido a través de un sistema de comunicación. Suponga que en diferentes sím- bolos, ocurren errores de manera independiente uno de otro. Suponga también que con probabilidad p2 un símbo- lo erróneo es corregido al ser recibido. Sea X el número de símbolos correctos en un bloque de mensaje compuesto de n símbolos (una vez que el proceso de corrección ha ter- minado). ¿Cuál es la distribución de probabilidad de X? 105. El comprador de una unidad generadora de potencia requie- re de arranques consecutivos exitosos antes de aceptar la uni- dad. Suponga que los resultados de arranques individuales son independientes entre sí. Sea p la probabilidad de que cualquier arranque particular sea exitoso. La variable aleato- ria de interés es X el número de arranques que deben ha- cerse antes de la aceptación. Dé la función masa de probabilidad de X en el caso c 2. Si p 0.9, ¿cuál es P(X 8)? [Sugerencia: Con x 5, exprese p(x) “recursivamen- te” en términos de la función masa de probabilidad evalua- da con los valores más pequeños x 3, x 4, . . . , 2.] (Este problema fue sugerido del artículo “Evaluation of a Start-Up Demonstration Test”, J. Quality Technology, 1983: 103–106.) 106. Una aerolínea ha desarrollado un plan para un club de via- jeros ejecutivos sobre la premisa de que 10% de sus clien- tes actuales calificarían para membresía. a. Suponiendo la validez de esta premisa, entre 25 clientes actuales seleccionados al azar, ¿cuál es la probabilidad de que entre 2 y 6 (inclusive) califiquen para membresía? b. De nuevo suponiendo la validez de la premisa, ¿cuál es el número esperado de clientes que califican y la desvia- ción estándar del número que califica en una muestra aleatoria de 100 clientes actuales? c. Sea X el número en una muestra al azar de 25 clientes actuales que califican para membresía. Considere recha- zar la premisa de la compañía a favor de la pretensión de que p 0.10 si x 7. ¿Cuál es la probabilidad de que la premisa de la compañía sea rechazada cuando en realidad es válida? d. Remítase a la regla de decisión introducida en el inciso c). ¿Cuál es la probabilidad de que la premisa de la compañía no sea rechazada aun cuando p 0.20 (es de- cir, 20% califican)? 107. 40% de las semillas de mazorcas de maíz (maíz moderno) portan sólo una espiga y el 60% restante portan dos espigas. Una semilla con una espiga producirá una mazorca con es- pigas únicas 29% del tiempo, en tanto que una semilla con dos espigas producirán una mazorca con espigas únicas 26% del tiempo. Considere seleccionar al azar diez semillas. Ejercicios suplementarios 127 c3_p086-129.qxd 3/12/08 4:01 AM Page 127
- 146. a. ¿Cuál es la probabilidad de que exactamente cinco de es- tas semillas porten una sola espiga y de que produzcan una mazorca con una sola espiga? b. ¿Cuál es la probabilidad de que exactamente cinco de estas mazorcas producidas por estas semillas tengan es- pigas únicas? ¿Cuál es la probabilidad de que cuando mucho cinco mazorcas tengan espigas únicas? 108. Un juicio terminó con el jurado en desacuerdo porque ocho de sus miembros estuvieron a favor de un veredicto de cul- pabilidad y los otros cuatro estuvieron a favor de la abso- lución. Si los jurados salen de la sala en orden aleatorio y cada uno de los primeros cuatro que salen de la sala es aco- sado por un reportero para entrevistarlo, ¿cuál es la función masa de probabilidad de X el número de jurados a favor de la absolución entre los entrevistados? ¿Cuántos de los que están a favor de la absolución espera que sean entrevis- tados? 109. Un servicio de reservaciones emplea cinco operadores de información que reciben solicitudes de información inde- pendientemente uno de otro, cada uno de acuerdo con un proceso de Poisson con razón 2 por minuto. a. ¿Cuál es la probabilidad de que durante un periodo de un min dado, el primer operador no reciba solicitudes? b. ¿Cuál es la probabilidad de que durante un periodo de un min dado, exactamente cuatro de los cinco operado- res no reciban solicitudes? c. Escriba una expresión para la probabilidad de que du- rante un periodo de un min dado, todos los operadores reciban exactamente el mismo número de solicitudes. 110. En un gran campo se distribuyen al azar las langostas de acuerdo con una distribución de Poisson con parámetro 2 por yarda cuadrada. ¿Qué tan grande deberá ser el radio R de una región de muestreo circular para que la pro- babilidad de hallar por lo menos una en la región sea igual a 0.99? 111. Un puesto de periódicos ha pedido cinco ejemplares de cierto número de una revista de fotografía. Sea X el nú- mero de individuos que vienen a comprar esta revista. Si X tiene una distribución de Poisson con parámetro 4, ¿cuál es el número esperado de ejemplares que serán ven- didos? 112. Los individuos A y B comienzan a jugar una secuencia de partidas de ajedrez. Sea S {A gana un juego} y suponga que los resultados de juegos sucesivos son independientes con P(S) p y P(F) 1 p (nunca empatan). Jugarán hasta que uno de ellos gane diez juegos. Sea X el núme- ro de partidas jugadas (con posibles valores 10, 11, . . . , 19). a. Con x 10, 11, . . . , 19, obtenga una expresión para p(x) P(X x). b. Si un empate es posible, con p P(S), q P(F), 1 p q P(empate), ¿cuáles son los posibles valores de X? ¿Cuál es P(20 X)? [Sugerencia: P(20 X) 1 P(X 20).] 113. Un análisis para detectar la presencia de una enfermedad tiene una probabilidad de 0.20 de dar un resultado falso po- sitivo (lo que indica que un individuo tiene la enfermedad cuando éste no es el caso) y una probabilidad de 0.10 de dar un resultado falso negativo. Suponga que diez individuos son analizados, cinco de los cuales tienen la enfermedad y cinco de los cuales no. Sea X el número de lecturas posi- tivas que resultan. a. ¿Tiene X una distribución binomial? Explique su razo- namiento. b. ¿Cuál es la probabilidad de que exactamente tres de diez resultados sean positivos? 114. La función masa de probabilidad binomial negativa gene- ralizada está dada por nb(x; r, p) k(r, x) pr (1 p)x x 0, 1, 2, . . . Sea X el número de plantas de cierta especie encontrada en una región particular y tenga esta distribución con p 0.3 y r 2.5. ¿Cuál es P(X 4)? ¿Cuál es la probabilidad de que por lo menos se encuentre una planta? 115. Defina una función p(x; , ) mediante p(x; , ) { e e x 0, 1, 2, . . . 0 de lo contrario a. Demuestre que p(x; , ) satisface las dos condiciones necesarias para especificar una función masa de proba- bilidad. [Nota: Si una firma emplea dos mecanógrafos, uno de los cuales comete errores tipográficos a razón de por página y el otro a razón de por página y cada uno ellos realiza la mitad del trabajo de mecanografía de la firma, entonces p(x; , ) es la función masa de probabilidad de X el número de errores en una pági- na escogida al azar.] b. Si el primer mecanógrafo (razón ) teclea 60% de todas las páginas, ¿cuál es la función masa de probabilidad de X del inciso a)? c. ¿Cuál es E(X) para p(x; , ) dada por la expresión mos- trada? d. ¿Cuál es 2 para p(x; , ) dada por esta expresión? 116. La moda de una variable aleatoria discreta X con función masa de probabilidad p(x) es ese valor x* con el cual p(x) alcanza su valor más grande (el valor x más probable). a. Sea X Bin(n, p). Considerando la razón b(x 1; n, p)/b(x; n, p), demuestre que b(x; n, p) se incrementa con x en tanto x np (1 p). Concluya que el modo x* es el entero que satisface (n 1)p 1 x* (n 1)p. b. Demuestre que si X tiene una distribución de Poisson con parámetro , la moda es el entero más grande me- nor que . Si es un entero, demuestre que tanto 1 como son modas. 117. Un disco duro de computadora tiene diez pistas concéntri- cas, numeradas 1, 2, . . . , 10 desde la más externa hasta la más interna y un solo brazo de acceso. Sea pi la proba- bilidad de que cualquier solicitud particular de datos hará que el brazo se vaya a la pista i (i 1, . . . , 10. Supon- ga que las pistas accesadas en búsquedas sucesivas son in- dependientes. Sea X el número de pistas sobre las cuales pasa el brazo de acceso durante dos solicitudes sucesivas (excluida la pista que el brazo acaba de dejar, así que los x x! 1 2 x x! 1 2 128 CAPÍTULO 3 Variables aleatorias discretas y distribuciones de probabilidad c3_p086-129.qxd 3/12/08 4:01 AM Page 128
- 147. valores posibles son x 0, 1, . . . , 9). Calcule la función masa de probabilidad de X [Sugerencia: P(el brazo está ahora sobre la pista i y X j) P(X j°el brazo está ahora sobre i) pi. Una vez que se escribe la probabilidad condicional en función de p1, . . . , p10, me- diante la ley de la probabilidad total, se obtiene la probabi- lidad deseada sumando a lo largo de i.] 118. Si X es una variable aleatoria hipergeométrica demuestre directamente con la definición que E(X) nM/N (conside- re sólo el caso n M). [Sugerencia: Saque como factor a nM/N de la suma para E(X) y demuestre que los términos adentro de la suma son de la forma h(y; n 1, M 1, N 1) donde y x 1.] 119. Use el hecho de que todos x (x )2 p(x) x:°x° k (x )2 p(x) para comprobar la desigualdad de Chebyshev dada en el ejercicio 44. 120. El proceso de Poisson simple de la sección 3.6 está carac- terizado por una razón constante a la cual los eventos ocu- rren por unidad de tiempo. Una generalización de esto es suponer que la probabilidad de que ocurra exactamente un evento en el intervalo [t, t t] es (t) t o(t). Se puede demostrar entonces que el número de eventos que ocurren durante un intervalo [t1, t2] tiene una distribución de Poisson con parámetro t2 t1 (t) dt La ocurrencia de eventos en el transcurso del tiempo en esta situación se llama proceso de Poisson no homogéneo. El artículo “Inference Based on Retrospective Ascertain- ment”, J. Amer. Stat. Assoc., 1989: 360–372, considera la función de intensidad (t) eabt en su forma apropiada para eventos que implican la trans- misión VIH (el virus del SIDA) vía transfusiones sanguí- neas. Suponga que a 2 y b 0.6 (cercanos a los valores sugeridos en el artículo), con el tiempo en años. a. ¿Cuál es el número esperado de eventos en el intervalo [0, 4?]? ¿En [2, 6]? b. ¿Cuál es la probabilidad de que cuando mucho ocurran 15 eventos en el intervalo [0, 0.9907]? 121. Considere un conjunto de A1, . . . , Ak de eventos mutua- mente excluyentes y exhaustivos y una variable aleatoria X cuya distribución depende de cuál de los eventos Ai ocurra (p. ej., un viajero abonado podría seleccionar una de tres rutas posibles de su casa al trabajo, con X como el tiempo de recorrido). Sea E(X°Ai) el valor esperado de X dado que el evento Ai ocurre. Entonces se puede demostrar que E(X) E (X°Ai) P(Ai) el promedio ponderado de las “expec- tativas condicionales” individuales donde las ponderacio- nes son las probabilidades de la división de eventos. a. La duración esperada de una llamada de voz a un núme- ro telefónico particular es de 3 minutos, mientras que la duración esperada de una llamada de datos a ese mismo número es de 1 minuto. Si 75% de las llamadas son de voz, ¿cuál es la duración esperada de la siguiente lla- mada? b. Una pastelería vende tres diferentes tipos de galletas con briznas de chocolate. El número de briznas de cho- colate en un tipo de galleta tiene una distribución de Poisson con parámetro i i 1 (i 1, 2, 3). Si 20% de todos los clientes que compran una galleta con briz- nas de chocolate selecciona el primer tipo, 50% elige el segundo tipo y el 30% restante opta por el tercer tipo, ¿cuál es el número esperado de briznas en una galleta comprada por el siguiente cliente? 122. Considere una fuente de comunicaciones que transmite pa- quetes que contienen lenguaje digitalizado. Después de cada transmisión, el receptor envía un mensaje que indica si la transmisión fue exitosa o no. Si una transmisión no es exitosa, el paquete es reenviado. Suponga que el paquete de voz puede ser transmitido un máximo de 10 veces. Supo- niendo que los resultados de transmisiones sucesivas son independientes una de otra y que la probabilidad de que cualquier transmisión particular sea exitosa es p, determine la función masa de probabilidad de la variable aleatoria X el número de veces que un paquete es transmitido. Luego obtenga una expresión para el número de veces es- perado que un paquete es transmitido. ? Ejercicios suplementarios 129 Bibliografía Johnson, Norman, Samuel Kotz y Adrienne Kemp. Discrete Uni- variate Distributions. Wiley, Nueva York, 1972. Una enciclo- pedia de información sobre distribuciones discretas. Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models and Applications (2a. ed.), Macmillan, Nueva York, 1994. Contiene una discusión a fondo tanto de las propiedades gene- rales de distribuciones discretas y continuas como los resulta- dos para distribuciones específicas. Ross, Sheldon, Introduction to Probability Models (7a. ed.), Aca- demic Press, Nueva York, 2003. Una fuente de material sobre el proceso de Poisson y generalizaciones y una amena intro- ducción a otros temas de probabilidad aplicada. c3_p086-129.qxd 3/12/08 4:01 AM Page 129
- 148. Variables aleatorias continuas y distribuciones de probabilidad 4 130 INTRODUCCIÓN El capítulo 3 se concentró en el desarrollo de distribuciones de probabilidad de varia- bles aleatorias discretas. En este capítulo se estudia el segundo tipo general de variable aleatoria que se presenta en muchos problemas aplicados. Las secciones 4.1 y 4.2 presentan las definiciones y propiedades básicas de las variables aleatorias continuas y sus distribuciones de probabilidad. En la sección 4.3, se estudia en detalle la varia- ble aleatoria normal y su distribución, sin duda la más importante y útil en la proba- bilidad y estadística. Las secciones 4.4 y 4.5 se ocupan de otras distribuciones continuas utilizadas con frecuencia en trabajo aplicado. En la sección 4.6, se introdu- ce un método de evaluar si un dato muestral es compatible con una distribución es- pecificada. c4_p130-183.qxd 3/12/08 4:04 AM Page 130
- 149. Una variable aleatoria (va) discreta es una cuyos valores posibles o constituyen un conjun- to finito o bien pueden ser puestos en lista en una secuencia infinita (una lista en la cual exis- te un primer elemento, un segundo elemento, etc.). Una variable aleatoria cuyo conjunto de valores posibles es un intervalo completo de números no es discreta. Recuérdese de acuerdo con el capítulo 3 que una variable aleatoria X es continua si 1) sus valores posibles comprenden un solo intervalo sobre la línea de numeración (para al- guna A B, cualquier número x entre A y B es un valor posible) o una unión de intervalos disjuntos y 2) P(X c) 0 para cualquier número c que sea un valor posible de X. En el estudio de la ecología de un lago, se mide la profundidad en lugares seleccionados, entonces X la profundidad en ese lugar es una variable aleatoria continua. En este caso A es la profundidad mínima en la región muestreada y B es la profundidad máxima. ■ Si se selecciona al azar un compuesto químico y se determina su pH X, entonces X es una variable aleatoria continua porque cualquier valor pH entre 0 y 14 es posible. Si se conoce más sobre el compuesto seleccionado para su análisis, entonces el conjunto de posibles va- lores podría ser un subintervalo de [0, 14], tal como 5.5 x 6.5 pero X seguiría siendo continua. ■ Sea X la cantidad de tiempo que un cliente seleccionado al azar pasa esperando que le cor- ten el pelo antes de que comience su corte de pelo. El primer pensamiento podría ser que X es una variable aleatoria continua, puesto que se requiere medirla para determinar su valor. Sin embargo, existen clientes suficientemente afortunados que no tienen que esperar antes de sentarse en el sillón del peluquero. Así que el caso debe ser P(X 0) 0. Condicional en cuanto a los sillones vacíos, aun cuando, el tiempo de espera será continuo puesto que X podría asumir entonces cualquier valor entre un tiempo mínimo posible A y un tiempo má- ximo posible B. Esta variable aleatoria no es ni puramente discreta ni puramente continua sino que es una mezcla de los dos tipos. ■ Se podría argumentar que aunque en principio las variables tales como altura, peso y temperatura son continuas, en la práctica las limitaciones de los instrumentos de medición nos restringen a un mundo discreto (aunque en ocasiones muy finamente subdividido). Sin embargo, los modelos continuos a menudo representan muy bien de forma aproximada si- tuaciones del mundo real y con frecuencia es más fácil trabajar con matemáticas continuas (el cálculo) que con matemáticas de variables discretas y distribuciones. Distribuciones de probabilidad de variables continuas Supóngase que la variable X de interés es la profundidad de un lago en un punto sobre la su- perficie seleccionado al azar. Sea M la profundidad máxima (en metros), así que cual- quier número en el intervalo [0, M] es un valor posible de X. Si se “discretiza” X midiendo la profundidad al metro más cercano, entonces los valores posibles son enteros no negativos menores que o iguales a M. La distribución discreta resultante de profundidad se ilustra con un histograma de probabilidad. Si se traza el histograma de modo que el área del rectángu- lo sobre cualquier entero posible k sea la proporción del lago cuya profundidad es (al me- tro más cercano) k, entonces el área total de todos los rectángulos es 1. En la figura 4.1a) aparece un posible histograma. Si se mide la profundidad con mucho más precisión y se utiliza el mismo eje de me- dición de la figura 4.1a), cada rectángulo en el histograma de probabilidad resultante es mu- cho más angosto, aun cuando el área total de todos los rectángulos sigue siendo 1. En la 4.1 Funciones de densidad de probabilidad 131 4.1 Funciones de densidad de probabilidad Ejemplo 4.1 Ejemplo 4.2 Ejemplo 4.3 c4_p130-183.qxd 3/12/08 4:04 AM Page 131
- 150. figura 4.1b) se ilustra un posible histograma; tiene una apariencia mucho más regular que el histograma de la figura 4.1a). Si se continúa de esta manera midiendo la profundidad más y más finamente, la secuencia resultante de histogramas se aproxima a una curva más regular, tal como la ilustrada en la figura 4.1c). Como en cada histograma el área total de todos los rectángulos es igual a 1, el área total bajo la curva regular también es 1. La probabilidad de que la profundidad en un punto seleccionado al azar se encuentre entre a y b es simplemen- te el área bajo la curva regular entre a y b. Es de manera exacta una curva regular del tipo ilustrado en la figura 4.1c) la que especifica un distribución de probabilidad continua. Para que f(x) sea una función de densidad de probabilidad legítima, debe satisfacer las dos siguientes condiciones: 1. f(x) 0 con todas las x 2. f(x) dx área bajo la curva f(x) 1 La dirección de una imperfección con respecto a una línea de referencia sobre un objeto circu- lar tal como un neumático, un rotor de freno o un volante está, en general, sujeta a incertidum- bre. Considérese la línea de referencia que conecta el vástago de la válvula de un neumático con su punto central y sea X el ángulo medido en el sentido de las manecillas del reloj con respecto a la ubicación de una imperfección. Una posible función de densidad de probabilidad de X es f(x) 3 1 60 0 x 360 0 de lo contrario 132 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad DEFINICIÓN Sea X una variable aleatoria continua. Entonces, una distribución de probabilidad o función de densidad de probabilidad (fdp) de X es una función f(x) tal que para dos números cualesquiera a y b con a b, P(a X b) b a f(x) dx Es decir, la probabilidad de que X asuma un valor en el intervalo [a, b] es el área so- bre este intervalo y bajo la gráfica de la función de densidad, como se ilustra en la fi- gura 4.2. La gráfica de f(x) a menudo se conoce como curva de densidad. Figura 4.1 a) Histograma de probabilidad de profundidad medida al metro más cercano; b) histograma de probabilidad de profundidad medida al centímetro más cercano; c) un límite de una secuencia de histo- gramas discretos. a) b) c) 0 M 0 M 0 M Figura 4.2 P(a X b) el área debajo de la curva de densidad entre a y b. a b x Ejemplo 4.4 Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 132
- 151. La función de densidad de probabilidad aparece dibujada en la figura 4.3. Claramente f(x) 0. El área bajo la curva de densidad es simplemente el área de un rectángulo (altura) (base) (3 1 60)(360) 1. La probabilidad de que el ángulo esté entre 90° y 180° es P(90 X 180) 180 90 dx ° x180 x90 0.25 La probabilidad de que el ángulo de ocurrencia esté dentro de 90° de la línea de referencia es P(0 X 90) P(270 X 360) 0.25 0.25 0.50 1 4 x 360 1 360 Como siempre que 0 a b 360 en el ejemplo 4.4, P(a X b) depende sólo del an- cho b a del intervalo, se dice que X tiene una distribución uniforme. La gráfica de cualquier función de densidad de probabilidad uniforme es como la de la fi- gura 4.3 excepto que el intervalo de densidad positiva es [A, B] en lugar de [0, 360]. En el caso discreto, una función masa de probabilidad indica cómo estan distribuidas pequeñas “manchas” de masa de probabilidad de varias magnitudes a lo largo del eje de medición. En el caso continuo, la densidad de probabilidad está “dispersa” en forma conti- nua a lo largo del intervalo de posibles valores. Cuando la densidad está dispersa uniforme- mente a lo largo del intervalo, se obtiene una función de densidad de probabilidad uniforme como en la figura 4.3. Cuando X es una variable aleatoria discreta, a cada valor posible se le asigna una pro- babilidad positiva. Esto no es cierto en el caso de una variable aleatoria continua (es decir, se satisface la segunda condición de la definición) porque el área bajo una curva de densi- dad situada sobre cualquier valor único es cero: c c c e c e El hecho de que P(X c) 0 cuando X es continua tiene una importante consecuen- cia práctica: La probabilidad de que X quede en algún intervalo entre a y b no depende de si el límite inferior a o el límite superior b está incluido en el cálculo de probabilidad P(a X b) P(a X b) P(a X b) P(a X b) (4.1) fsxddx 5 0 fsxddx 5 lim eS0 PsX 5 cd 5 4.1 Funciones de densidad de probabilidad 133 DEFINICIÓN Se dice que una variable aleatoria continua X tiene una distribución uniforme en el intervalo [A, B] si la función de densidad de probabilidad de X es f(x; A, B) B 1 A A x B 0 de lo contrario Figura 4.3 Función de densidad de probabilidad del ejemplo 4.4. ■ Área sombreada P(90 X 180) x 1 360 f(x) 0 360 x f(x) 360 270 180 90 Ï Ì Ó ´ c4_p130-183.qxd 3/12/08 4:04 AM Page 133
- 152. Si X es discreta y tanto a como b son valores posibles (p. ej., X es binomial con n 20 y a 5, b 10), entonces cuatro de estas probabilidades son diferentes. La condición de probabilidad cero tiene un análogo físico. Considérese una barra circular sólida con área de sección transversal 1 pulg2 . Coloque la barra a lo largo de un eje de medición y supóngase que la densidad de la barra en cualquier punto x está dada por el valor f(x) de una función de densidad. Entonces si la barra se rebana en los puntos a y b y este segmento se retira, la cantidad de masa eliminada es b a f(x) dx; si la barra se rebana exactamente en el punto c, no se elimina masa. Se asigna masa a segmentos de intervalo de la barra pero no a puntos individuales. “Intervalo de tiempo” en el flujo de tránsito es el tiempo transcurrido entre el tiempo en que un carro termina de pasar por un punto fijo y el instante en que el siguiente carro comienza a pasar por ese punto. Sea X el intervalo de tiempo de dos carros consecutivos seleccio- nados al azar en una autopista durante un periodo de tráfico intenso. La siguiente función de densidad de probabilidad de X es en esencia el sugerido en “The Statistical Properties of Freeway Traffic” (Transp. Res. vol. 11: 221-228): f(x) 0.15e 0.15(x0.5) x 0.5 0 de lo contrario La gráfica de f(x) se da en la figura 4.4; no hay ninguna densidad asociada con inter- valos de tiempo de menos de 0.5 y la densidad del intervalo decrece con rapidez (exponen- cial) a medida que x se incrementa a partir de 0.5. Claramente, f(x) 0; para demostrar que f(x) dx 1, se utiliza el resultado obtenido con cálculo integral a e kx dx (1/k)e k a . Entonces f(x) dx 0.5 0.15e 0.15(x0.5) dx 0.15e0.075 0.5 e 0.15x dx 0.15e0.075 0.1 1 5 e (0.15)(0.5) 1 La probabilidad de que el intervalo de tiempo sea cuando mucho de 5 segundos es P(X 5) 5 f(x) dx 5 0.5 0.15e 0.15(x0.5) dx 0.15e0.075 5 0.5 e 0.15x dx 0.15e0.075 0.1 1 5 e 0.15x ° x5 x0.5 e0.075 ( e 0.75 e 0.075 ) 1.078( 0.472 0.928) 0.491 P(menos de 5 seg) P(X 5) ■ A diferencia las distribuciones discretas tales como la binomial, la hipergeométrica y la binomial negativa, la distribución de cualquier variable aleatoria continua dada en gene- ral no puede ser derivada mediante simples argumentos probabilísticos. En cambio, se debe hacer una selección juiciosa de la función de densidad de probabilidad basada en conoci- mientos previos y en los datos disponibles. Afortunadamente, existen algunas familias ge- nerales de funciones de densidad de probabilidad que se ajustan bien a una amplia variedad de situaciones experimentales; varias de éstas se discuten más adelante en el capítulo. 134 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad Ejemplo 4.5 Ï Ì Ó Figura 4.4 Curva de densidad del intervalo de tiempo entre vehículos en el ejemplo 4.5. 0 0.15 2 0.5 4 6 8 10 x f(x) P(X 5) c4_p130-183.qxd 3/12/08 4:04 AM Page 134
- 153. Exactamente como en el caso discreto, a menudo es útil pensar en la población de interés como compuesta de valores X en lugar de individuos u objetos. La función de densidad de pro- babilidad es entonces un modelo de la distribución de valores en esta población numérica y con base en este modelo se pueden calcular varias características de la población (tal como la media). 4.1 Funciones de densidad de probabilidad 135 EJERCICIOS Sección 4.1 (1-10) 1. Sea X la cantidad de tiempo durante la cual un libro puesto en reserva durante dos horas en la biblioteca de una univer- sidad es solicitado en préstamo por un estudiante seleccio- nado y suponga que X tiene la función de densidad f(x) 0.5x 0 x 2 0 de lo contrario Calcule las siguientes probabilidades: a. P(X 1) b. P(0.5 X 1.5) c. P(1.5 X) 2. Suponga que la temperatura de reacción X (en °C) en cier- to proceso químico tiene una distribución uniforme con A 5 y B 5. a. Calcule P(X 0). b. Calcule P( 2.5 X 2.5). c. Calcule P( 2 X 3). d. Para que k satisfaga 5 k k 4 5, calcule P(k X k 4). 3. El error implicado al hacer una medición es una variable aleatoria continua X con función de densidad de probabilidad f(x) 0.09375(4 x2 ) 2 x 2 0 de lo contrario a. Bosqueje la gráfica de f(x). b. Calcule P(X 0). c. Calcule P( 1 X 1). d. Calcule P(X 0.5 o X 0.5). 4. Sea X el esfuerzo vibratorio (lb/pulg2 ) en el aspa de una tur- bina de viento a una velocidad del viento particular en un túnel aerodinámico. El artículo “Blade Fatigue Life Assess- ment with Application to VAWTS” (J. Solar Energy Engr. 1982: 107-111) propone la distribución Rayleigh, con fun- ción de densidad de probabilidad f(x; ) x 2 e x 2 /(2 2 ) x 0 0 de lo contrario como modelo de la distribución X. a. Verifique que f(x; ) es una función de densidad de pro- babilidad legítima. b. Suponga que 100 (un valor sugerido por una gráfica en el artículo). ¿Cuál es la probabilidad de que X es cuan- do mucho de 200? ¿Menos de 200? ¿Por lo menos de 200? c. ¿Cuál es la probabilidad de que X esté entre 100 y 200 (de nuevo con 100)? d. Dé una expresión para P(X x). 5. Un profesor universitario nunca termina su disertación an- tes del final de la hora y siempre termina dentro de 2 minu- tos después de la hora. Sea X el tiempo que transcurre entre el final de la hora y el final de la disertación y supon- ga que la función de densidad de probabilidad de X es f(x) kx2 0 x 2 0 de lo contrario a. Determine el valor de k y trace la curva de densidad co- rrespondiente. [Sugerencia: El área total bajo la gráfica de f(x) es 1.] b. ¿Cuál es la probabilidad de que la disertación termine dentro de un minuto del final de la hora? c. ¿Cuál es la probabilidad de que la disertación continúe después de la hora durante entre 60 y 90 segundos. d. ¿Cuál es la probabilidad de que la disertación continúe durante por lo menos 90 segundos después del final de la hora? 6. El peso de lectura real de una pastilla de estéreo ajustado a 3 gramos en un tocadiscos particular puede ser considerado como una variable aleatoria continua X con función de den- sidad de probabilidad f(x) k[1 (x 3)2 ] 2 x 4 0 de lo contrario a. Trace la gráfica de f(x). b. Determine el valor de k. c. ¿Cuál es la probabilidad de que el peso real de lectura sea mayor que el peso prescrito? d. ¿Cuál es la probabilidad de que el peso real de lectura esté dentro de 0.25 gramos del peso prescrito? e. ¿Cuál es la probabilidad de que el peso real difiera del peso prescrito por más de 0.5 gramos? 7. Se cree que el tiempo X (min) para que un ayudante de la- boratorio prepare el equipo para cierto experimento tiene una distribución uniforme con A 25 y B 35. a. Determine la función de densidad de probabilidad de X y trace la curva de densidad de correspondiente. b. ¿Cuál es la probabilidad de que el tiempo de preparación exceda de 33 min? c. ¿Cuál es la probabilidad de que el tiempo de preparación esté dentro de dos min del tiempo medio? [Sugerencia: Identifique en la gráfica de f(x).] d. Con cualquier a de modo que 25 a a 2 35, ¿cuál es la probabilidad de que el tiempo de preparación esté entre a y a 2 min? 8. Para ir al trabajo, primero tengo que tomar un camión cerca de mi casa y luego tomar un segundo camión. Si el tiempo de espera (en minutos) en cada parada tiene una distribución uniforme con A 0 y B 5, entonces se puede demostrar que el tiempo de espera total Y tiene la función de densidad de probabilidad Ï Ì Ó Ï Ì Ó Ï Ì Ó Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 135
- 154. Varios de los más importantes conceptos introducidos en el estudio de distribuciones discre- tas también desempeñan un importante papel en las distribuciones continuas. Definiciones análogas a las del capítulo 3 implican reemplazar la suma por integración. Función de distribución acumulativa La función de distribución acumulativa F(x) de una variable aleatoria discreta X da, con cualquier número especificado x, la probabilidad P(X x). Se obtiene sumando la función masa de pro- babilidad p(y) a lo largo de todos los valores posibles y que satisfacen y x. La función de dis- tribución acumulativa de una variable aleatoria continua da las mismas probabilidades P(X x) y se obtiene integrando la función de densidad de probabilidad f(y) entre los límites y x. 136 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad 2 1 5 y 0 y 5 f(y) 2 5 2 1 5 y 5 y 10 0 y 0 o y 10 a. Trace la gráfica de la función de densidad de probabili- dad de Y. b. Verifique que f(y) dy 1. c. ¿Cuál es la probabilidad de que el tiempo de espera to- tal sea cuando mucho de tres minutos? d. ¿Cuál es la probabilidad de que el tiempo de espera total sea cuando mucho de ocho minutos? e. ¿Cuál es la probabilidad de que el tiempo de espera to- tal esté entre tres y ocho minutos? f. ¿Cuál es la probabilidad de que el tiempo de espera to- tal sea de menos de 2 minutos o de más de 6 minutos? 9. Considere de nuevo la función de densidad de probabilidad de X intervalo de tiempo dado en el ejemplo 4.5. ¿Cuál es la probabilidad de que el intervalo de tiempo sea a. Cuando mucho de seis segundos? b. De más de seis segundos? ¿Por lo menos de seis segundos? c. De entre cinco y seis segundos? 10. Una familia de funciones de densidad de probabilidad que ha sido utilizada para aproximar la distribución del ingreso, el tamaño de la población de una ciudad y el tamaño de fir- mas es la familia Pareto. La familia tiene dos parámetros, k y , ambos 0 y la función de densidad de probabilidad es f(x; k, ) k x k1 k x 0 x a. Trace la gráfica de f(x; k, ). b. Verifique que el área total bajo la gráfica es igual a 1. c. Si la variable aleatoria X tiene una función de densidad de probabilidad f(x; k, ), con cualquier b , obtenga una expresión para P(X b). d. Con a b, obtenga una expresión para la probabi- lidad P(a X b). Ï Ì Ó Ï Ì Ó 4.2 Funciones de distribución acumulativa y valores esperados Figura 4.5 Una función de densidad de probabilidad y función de distribución acumulativa asociada. f(x) F(x) F(8) x x F(8) 5 8 10 5 8 10 0.5 1 DEFINICIÓN La función de distribución acumulativa F(x) de una variable aleatoria continua X se define para todo número x como F(x) P(X x) x f(y) dy Con cada x, F(x) es el área bajo la curva de densidad a la izquierda de x. Esto se ilustra en la figura 4.5, donde F(x) se incrementa con regularidad a medida que x se incrementa. c4_p130-183.qxd 3/12/08 4:04 AM Page 136
- 155. Sea X el espesor de una cierta lámina de metal con distribución uniforme en [A, B]. La fun- ción de densidad se muestra en la figura 4.6. Con x A, F(x) 0, como no hay área bajo la gráfica de la función de densidad a la izquierda de la x. Con x B, F(x) 1, puesto que toda el área está acumulada a la izquierda de la x. Finalmente con A x B, F(x) x f(y) dy x A B 1 A dy B 1 A y ° ° ° yx yA B x A A La función de distribución acumulativa completa es 0 x A F(x) B x A A A x B 1 x B La gráfica de esta función de distribución acumulativa aparece en la figura 4.7. Utilización de F(x) para calcular probabilidades La importancia de la función de distribución acumulativa en este caso, lo mismo que para va- riables aleatorias discretas, es que las probabilidades de varios intervalos pueden ser calculadas con una fórmula o una tabla de F(x). 4.2 Funciones de distribución acumulativa y valores esperados 137 PROPOSICIÓN Sea X una variable aleatoria continua con función de densidad de probabilidad f(x) y función de distribución acumulativa F(x). Entonces con cualquier número a, P(X a) 1 F(a) y para dos números cualesquiera a y b con a b. P(a X b) F(b) F(a) Ejemplo 4.6 Figura 4.6 Función de densidad de probabilidad de una distribución uniforme. f(x) 1 BA A B 1 BA A B x x Área sombreada F(x) Figura 4.7 Función de distribución acumulativa de una distribución uniforme. ■ F(x) A B x 1 Ï ÌÓ c4_p130-183.qxd 3/12/08 4:04 AM Page 137
- 156. 138 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad La figura 4.8 ilustra la segunda parte de esta proposición; la probabilidad deseada es el área sombreada bajo la curva de densidad entre a y b y es igual a la diferencia entre las dos áreas sombreadas acumulativas. Esto es diferente de lo que es apropiado para una variable aleatoria discreta de valor entero (p. ej., binomial o Poisson): P(a X b) F(b) F(a 1) cuando a y b son enteros. Suponga que la función de densidad de probabilidad de la magnitud X de una carga dinámi- ca sobre un puente (en newtons) está dada por f(x) 1 8 3 8 x 0 x 2 0 de lo contrario Para cualquier número x entre 0 y 2, F(x) x f(y) dy x 0 1 8 3 8 y dy 8 x 1 3 6 x2 Por lo tanto 0 x 0 F(x) 8 x 1 3 6 x2 0 x 2 1 2 x Las gráficas de f(x) y F(x) se muestran en la figura 4.9. La probabilidad de que la carga esté entre 1 y 1.5 es P(1 X 1.5) F(1.5) F(1) 1 8 (1.5) 1 3 6 (1.5)2 1 8 (1) 1 3 6 (1)2 1 6 9 4 0.297 La probabilidad de que la carga sea de más de uno es P(X 1) 1 P(X 1) 1 F(1) 1 1 8 (1) 1 3 6 (1)2 1 1 1 6 0.688 Figura 4.8 Cálculo de P(a X b) a partir de probabilidades acumulativas. a b f(x) b a Figura 4.9 Función de densidad de probabilidad y función de distribución acumulativa del ejemplo 4.7. ■ 1 8 7 8 0 2 f(x) 2 F(x) 1 x x Ejemplo 4.7 Ï Ì Ó Ï ÌÓ c4_p130-183.qxd 3/12/08 4:04 AM Page 138
- 157. Una vez que se obtiene la función de distribución acumulativa, cualquier probabilidad que implique X es fácil de calcular sin cualquier integración adicional. Obtención de f(x) a partir de F(x) Para X discreta, la función masa de probabilidad se obtiene a partir de la función de distri- bución acumulativa considerando la diferencia entre dos valores F(x). El análogo continuo de una diferencia es una derivada. El siguiente resultado es una consecuencia del teorema fundamental del cálculo. Cuando X tiene una distribución uniforme, F(x) es derivable excepto con x A y x B, don- de la gráfica de F(x) tiene esquinas afiladas. Como F(x) 0 con x A y F(x) 1 con x B. F(x) 0 f(x) con dicha x. Con A x B, F(x) d d x B x A A B 1 A f(x) ■ Percentiles de una distribución continua Cuando se dice que la calificación de un individuo en una prueba fue el 85o percentil de la población, significa que 85% de todas las calificaciones de la población estuvieron por de- bajo de dicha calificación y que 15% estuvo arriba. Asimismo, el 40o percentil es la califi- cación que sobrepasa 40% de todas las calificaciones y que es superada por 60% de todas las calificaciones. De acuerdo con la expresión (4.2), (p) es ese valor sobre el eje de medición de tal suerte que el 100p% del área bajo la gráfica de f(x) queda a la izquierda de (p) y 100(1 p)% que- da a la derecha. Por lo tanto, (0.75), el 75o percentil, es tal que el área bajo la gráfica de f(x) a la izquierda de (0.75) es 0.75. La figura 4.10 ilustra la definición. 4.2 Funciones de distribución acumulativa y valores esperados 139 Figura 4.10 El (100p)o percentil de una distribución continua. Área sombreada p (p) f(x) F(x) p F( (p)) x x 1 (p) PROPOSICIÓN Si X es una variable aleatoria continua con función de densidad de probabilidad f(x) y función de distribución acumulativa F(x), entonces con cada x hace posible que la derivada F(x) exista, F(x) f(x). DEFINICIÓN Sea p un número entere 0 y 1. El (100p)o percentil de la distribución de una variable aleatoria continua X, denotada por (p), se define como p F( (p)) (p) f(y) dy (4.2) Ejemplo 4.8 (continuación del ejemplo 4.6) c4_p130-183.qxd 3/12/08 4:04 AM Page 139
- 158. 140 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad La distribución de la cantidad de grava (en toneladas) vendida por una compañía de mate- riales para la construcción particular en una semana dada es una variable aleatoria continua X con función de densidad de probabilidad f(x) 3 2 (1 x2 ) 0 x 1 0 de lo contrario La función de distribución acumulativa de las ventas para cualquier x entre 0 y 1 es F(x) x 0 3 2 (1 y2 ) dy 3 2 y y 3 3 ° ° ° yx y0 3 2 x x 3 3 Las gráficas tanto de f(x) como de F(x) aparecen en la figura 4.11. El (100p)o percentil de esta distribución satisface la ecuación p F( (p)) 3 2 (p) ( ( 3 p))3 es decir, ( (p))3 3 (p) 2p 0 Para el 50o percentil, p 0.5 y la ecuación que se tiene que resolver es 3 3 1 0; la solución es (0.5) 0.347. Si la distribución no cambia de una semana a otra, en- tonces a la larga 50% de todas las semanas se realizarán ventas de menos de 0.347 ton y 50% de más de 0.347 ton. Una distribución continua cuya función de densidad de probabilidad es simétrica, lo cual significa que la gráfica a la izquierda de un punto en particular es una imagen a espejo de la gráfica a la derecha de dicho punto, tiene una mediana ˜ igual al punto de simetría, puesto que la mitad del área bajo la curva queda a uno u otro lado de este punto. La figura 4.12 da varios ejemplos. A menudo se supone que el error en la medición de una cantidad física tie- ne una distribución simétrica. Ejemplo 4.9 Ï Ì Ó Figura 4.11 Función de densidad de probabilidad y función de distribución acumulativa del ejemplo 4.9.■ 1.5 0 1 x f(x) 1 0 1 x F(x) 0.5 0.347 Figura 4.12 Medianas y distribuciones simétricas. f(x) x x x f(x) f(x) A B ˜ ˜ ˜ DEFINICIÓN La mediana de una distribución continua, denotada por ˜ , es el 50o percentil, así que ˜ satisface 0.5 F( ˜ ). Es decir, la mitad del área bajo la curva de densidad se en- cuentra a la izquierda de ˜ y la mitad a la derecha de ˜ . c4_p130-183.qxd 3/12/08 4:04 AM Page 140
- 159. Valores esperados Para una variable aleatoria discreta X, E(X) se obtuvo sumando x p(x) a lo largo de posibles valores de X. Aquí se reemplaza la suma con la integración y la función masa de probabilidad por la función de densidad de probabilidad para obtener un promedio ponderado continuo. La función de densidad de probabilidad de las ventas semanales de grava X fue f(x) 3 2 (1 x2 ) 0 x 1 0 de lo contrario por lo tanto E(X) x f(x) dx 1 0 x 3 2 (1 x2 ) dx 3 2 1 0 (x x3 ) dx 3 2 x 2 2 x 4 4 ° ° ° x1 x0 3 8 ■ Cuando la función de densidad de probabilidad f(x) especifica un modelo para la dis- tribución de valores en una población numérica, entonces es la media de la población, la cual es la medida más frecuentemente utilizada de la ubicación o centro de la población. Con frecuencia se desea calcular el valor esperado de alguna función h(X) de la varia- ble aleatoria X. Si se piensa en h(X) como una nueva variable aleatoria Y, se utilizan técni- cas de estadística matemática para derivar la función de densidad de probabilidad de Y y E(Y) se calcula a partir de la definición. Afortunadamente, como en el caso discreto, existe una forma más fácil de calcular E[h(X)]. Dos especies compiten en una región por el control de una cantidad limitada de un cierto re- curso. Sea X la proporción del recurso controlado por la especie 1 y suponga que la fun- ción de densidad de probabilidad de X es f(x) 1 0 x 1 0 de lo contrario la cual es una distribución uniforme en [0, 1]. (En su libro Ecological Diversity, E. C. Pielou llama a esto el modelo del “palo roto” para la asignación de recursos, puesto que es análogo 4.2 Funciones de distribución acumulativa y valores esperados 141 Ejemplo 4.11 DEFINICIÓN El valor esperado o valor medio de una variable aleatoria continua X con función de densidad de probabilidad f(x) es X E(X) x f(x) dx PROPOSICIÓN Si X es una variable aleatoria continua con función de densidad de probabilidad f(x) y h(X) es cualquier función de X, entonces E[h(X)] h(X) h(x) f(x) dx Ejemplo 4.10 (continuación del ejemplo 4.9) Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 141
- 160. 142 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad a la ruptura de un palo en un lugar seleccionado al azar.) Entonces la especie que controla la mayor parte de este recurso controla la cantidad h(X) máx(X, 1 X) 1 X si 0 X 1 2 X si 1 2 X 1 La cantidad esperada controlada por la especie que controla la mayor parte es entonces E[h(X)] máx(x, 1 x) f(x) dx 1 0 máx(x, 1 x) 1 dx 1/2 0 (1 x) 1 dx 1 1/2 x 1 dx 3 4 ■ Para h(X) una función lineal, E[h(X)] E(aX b) aE(X) b. En el caso discreto, la varianza de X se definió como la desviación al cuadrado esperada con respecto a y se calculó por medio de suma. En este caso de nuevo la integración reempla- za a la suma. La varianza y la desviación estándar dan medidas cuantitativas de cuánta dispersión hay en la distribución o población de valores x. La forma más fácil de calcular 2 es utilizar una fórmula abreviada. Para X ventas semanales de grava, se calcula E(X) 3 8. Como E(X2 ) x2 f(x) dx 1 0 x2 3 2 (1 x2 ) dx 1 0 3 2 (x2 x4 ) dx 1 5 V(X) 1 5 3 8 2 3 1 2 9 0 0.059 y X 0.244 ■ Cuando h(X) aX b, el valor esperado y la varianza de h(X) satisfacen las mismas pro- piedades que en el caso discreto: E[h(X)] a b y V[h(X)] a2 2 . Ï Ì Ó DEFINICIÓN La varianza de una variable aleatoria continua X con función de densidad de proba- bilidad f(x) y valor medio es 2 X V(X) (x )2 f(x) dx E[(X )2 ] La desviación estándar (DE) de X es X V (X ) . PROPOSICIÓN V(X) E(X2 ) [E(X)]2 EJERCICIOS Sección 4.2 (11-27) 11. La función de distribución acumulativa del tiempo de prés- tamo X como se describe en el ejercicio 1 es x 0 F(x) x 4 2 0 x 2 1 2 x Use ésta para calcular lo siguiente: a. P(X 1) b. P(0.5 X 1) c. P(X 0.5) d. El tiempo de préstamo medio ˜ [resolver 0.5 F( ˜ )] e. F(x) para obtener la función de densidad f(x) Ï ÌÓ Ejemplo 4.12 (continuación del ejemplo 4.10) c4_p130-183.qxd 3/12/08 4:04 AM Page 142
- 161. 4.2 Funciones de distribución acumulativa y valores esperados 143 f. E(X) g. V(X) y X h. Si al prestatario se le cobra una cantidad h(X) X2 cuan- do el tiempo de préstamo es X, calcule el cobro esperado E[h(X)]. 12. La función de distribución acumulativa de X ( error de medición) del ejercicio 3 es 0 x 2 F(x) 1 2 3 3 2 4x x 3 3 2 x 2 1 2 x a. Calcule P(X 0). b. Calcule P(1 X 1). c. Calcule P(0.5 X). d. Verifique que f(x) está dada en el ejercicio 3 obteniendo F’(x). e. Verifique que ˜ 0. 13. El ejemplo 4.5 introdujo el concepto de intervalo de tiempo en el flujo de tránsito y propuso una distribución particular para X el intervalo de tiempo entre dos carros consecuti- vos seleccionados al azar (s). Suponga que en un entorno de tránsito diferente, la distribución del intervalo de tiempo tiene la forma f(x) k x4 x 1 0 x 1 a. Determine el valor de k con el cual f(x) es una función de densidad de probabilidad legítima. b. Obtenga la función de distribución acumulativa. c. Use la función de distribución acumulativa de (b) para determinar la probabilidad de que el intervalo de tiempo exceda de 2 segundos y también la probabilidad de que el intervalo esté entre 2 y 3 segundos. d. Obtenga un valor medio del intervalo de tiempo y su desviación estándar. e. ¿Cuál es la probabilidad de que el intervalo de tiempo quede dentro de una desviación estándar del valor medio? 14. El artículo “Modeling Sediment and Water Column Interac- tions for Hidrophobic Pollutants” (Water Research, 1984: 1169-1174) sugiere la distribución uniforme en el intervalo 7.5, 20) como modelo de profundidad (cm) de la capa de bioturbación en sedimento en una región. a. ¿Cuáles son la media y la varianza de la profundidad? b. ¿Cuál es la función de distribución acumulativa de la profundidad? c. ¿Cuál es la probabilidad de que la profundidad observa- da sea cuando mucho de 10? ¿Entre 10 y 15? d. ¿Cuál es la probabilidad de que la profundidad observa- da esté dentro de una desviación estándar del valor me- dio? ¿Dentro de dos desviaciones estándar? 15. Sea X la cantidad de espacio ocupado por un artículo colo- cado en un contenedor de un pie3 . La función de densidad de probabilidad de X es f(x) 90x8 (1 x) 0 x 1 0 de lo contrario a. Dibuje la función de densidad de probabilidad. Luego obtenga la función de distribución acumulativa de X y dibújela. b. ¿Cuál es P(X 0.5) [es decir, F(0.5)]? c. Con la función de distribución acumulativa de (a), ¿cuál es P(0.25 X 0.5)? ¿Cuál es P(0.25 X 0.5)? d. ¿Cuál es el 75o percentil de la distribución? e. Calcule E(X) y X. f. ¿Cuál es la probabilidad de que X esté a más de una des- viación estándar de su valor medio? 16. Responda los incisos a)-f) del ejercicio 15 con X tiempo de disertación después de la hora dado en el ejercicio 5. 17. Si la distribución de X en el intervalo [A, B] es uniforme. a. Obtenga una expresión para el (100p)o percentil. b. Calcule E(X), V(X) y X. c. Con n, un entero positivo, calcule E(Xn ). 18. Sea X el voltaje a la salida de un micrófono y suponga que X tiene una distribución uniforme en el intervalo de 1 a 1. El voltaje es procesado por un “limitador duro” con valores de corte de 0.5 y 0.5, de modo que la salida del limitador es una variable aleatoria Y relacionada con X por Y X si |X| 0.5, Y 0.5 si X 5 y Y 0.5 si X 0.5. a. ¿Cuál es P(Y 0.5)? b. Obtenga la función de distribución acumulativa de Y y dibújela. 19. Sea X una variable aleatoria continua con función de distri- bución acumulativa 0 x 0 F(x) 4 x 1 ln 4 x 0 x 4 1 x 4 [Este tipo de función de distribución acumulativa es sugeri- do en el artículo “Variabilitiy in Measured Bedload-Trans- port Rates” (Water Resources Bull., 1985: 39-48) como modelo de cierta variable hidrológica.] Determinar: a. P(X 1) b. P(1 X 3) c. La función de densidad de probabilidad de X 20. Considere la función de densidad de probabilidad del tiem- po de espera total Y de dos camiones 2 1 5 y 0 y 5 f(y) 2 5 2 1 5 y 5 y 10 0 de lo contrario introducida en el ejercicio 8. a. Calcule y trace la función de distribución acumulativa de Y. [Sugerencia: Considere por separado 0 y 5 y 5 y 10 al calcular F(y). Una gráfica de la función de densidad de probabilidad debe ser útil.] b. Obtenga una expresión para el (100p)o percentil. [Sugeren- cia: Considere por separado 0 p 0.5 y 0.5 p 1.] c. Calcule E(Y) y V(Y). ¿Cómo se comparan estos valores con el tiempo de espera probable y la varianza de un solo camión cuando el tiempo está uniformemente dis- tribuido en [0, 5]? 21. Un ecólogo desea marcar una región de muestreo circular de 10 m de radio. Sin embargo, el radio de la región resul- tante en realidad es una variable aleatoria R con función de densidad de probabilidad Ï ÌÓ Ï Ì Ó Ï Ì Ó Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 143
- 162. 144 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad La distribución normal es la más importante en toda la probabilidad y estadística. Muchas po- blaciones numéricas tienen distribuciones que pueden ser representadas muy fielmente por una curva normal apropiada. Los ejemplos incluyen estaturas, pesos y otras características fí- sicas (el famoso artículo Biométrica 1903 “On the Laws of Inheritance in Man” discutió mu- chos ejemplos de esta clase), errores de medición en experimentos científicos, mediciones antropométricas en fósiles, tiempos de reacción en experimentos psicológicos, mediciones de inteligencia y aptitud, calificaciones en varios exámenes y numerosas medidas e indicadores económicos. Incluso cuando la distribución subyacente es discreta, la curva normal a menu- do da una excelente aproximación. Además, aun cuando las variables individuales no estén ¿Cuál es el área esperada de la región circular resultante? 22. La demanda semanal de gas propano (en miles de galones) de una instalación particular es una variable aleatoria X con función de densidad de probabilidad f(x) 21 x 1 2 1 x 2 0 de lo contrario a. Calcule la función de distribución acumulativa de X. b. Obtenga una expresión para el (100p)o percentil. ¿Cuál es el valor de ˜ ? c. Calcule E(X) y V(X). d. Si 1500 galones están en existencia al principio de la se- mana y no se espera ningún nuevo suministro durante la semana, ¿cuántos de los 1500 galones se espera que queden al final de la semana? [Sugerencia: Sea h(x) cantidad que queda cuando la demanda es x.] 23. Si la temperatura a la cual cierto compuesto se funde es una variable aleatoria con valor medio de 120°C y desviación es- tándar de 2°C, ¿cuáles son la temperatura media y la desvia- ción estándar medidas en °F? [Sugerencia: °F 1.8°C 32.] 24. La función de densidad de probabilidad de Pareto de X es f(x; k, ) k x k1 k x 0 x introducida en el ejercicio 10. a. Si k 1, calcule E(X). b. ¿Qué se puede decir sobre E(X) si k 1? c. Si k 2, demuestre que V(X) k 2 (k 1)2 (k 2)1 . d. Si k 2, ¿qué se puede decir sobre V(X)? e. ¿Qué condiciones en cuanto a k son necesarias para ga- rantizar que E(Xn ) es finito? 25. Sea X la temperatura en °C a la cual ocurre una reacción quí- mica y sea Y la temperatura en °F (así que Y 1.8X 32). a. Si la mediana de la distribución X es ˜ , demuestre que 1.8 ˜ 32 es la mediana de la distribución Y. b. ¿Cómo está relacionado el 90o percentil de la distribu- ción Y con el 90o de la distribución X? Verifique su con- jetura. c. Más generalmente, si Y aX b, ¿cómo está relacio- nado cualquier percentil de la distribución Y con el per- centil correspondiente de la distribución X? 26. Sea X los gastos médicos totales (en miles de dólares) in- curridos por un individuo particular durante un año dado. Aunque X es una variable aleatoria discreta, suponga que su distribución es bastante bien aproximada por una distri- bución continua con función de densidad de probabilidad f(x) k(1 x/2.5)7 con x 0. a. ¿Cuál es el valor de k? b. Dibuje la función de densidad de probabilidad de X. c. ¿Cuáles son el valor esperado y la desviación estándar de los gastos médicos totales? d. Un individuo está cubierto por un plan de aseguramiento que le impone una provisión deducible de $500 (así que los primeros $500 de gastos son pagados por el individuo). Luego el plan pagará 80% de cualquier gasto adicional que exceda de $500 y el pago máximo por parte del individuo (incluida la cantidad deducible) es de $2500. Sea Y la can- tidad de gastos médicos de este individuo pagados por la compañía de seguros. ¿Cuál es el valor esperado de Y? [Sugerencia: Primero indague qué valor de X correspon- de al gasto máximo que sale del bolsillo de $2500. Lue- go escriba una expresión para Y como una función de X (la cual implique varios precios diferentes) y calcule el valor esperado de la función.] 27. Cuando se lanza un dardo a un blanco circular, considere la ubicación del punto de aterrizaje respecto al centro. Sea X el ángulo en grados medido con respecto a la horizontal y suponga que X está uniformemente distribuida en [0, 360]. Defina Y como la variable transformada Y h(X) (2/360)X , por lo tanto, Y es el ángulo medido en ra- dianes y Y está entre y . Obtenga E(Y) y y obteniendo primero E(X) y X y luego utilizando el hecho de que h(X) es una función lineal de X. f(r) 3 4 [1 (10 r)2 ] 9 r 11 0 de lo contrario Ï Ì Ó Ï Ì Ó Ï Ì Ó 4.3 Distribución normal c4_p130-183.qxd 3/12/08 4:04 AM Page 144
- 163. normalmente distribuidas, las sumas y promedios de las variables en condiciones adecuadas tendrán de manera aproximada una distribución normal; este es el contenido del Teorema del Límite Central discutido en el siguiente capítulo. De nuevo e denota la base del sistema de logaritmos naturales y es aproximadamente igual a 2.71828 y representa la conocida constante matemática con un valor aproximado de 3.14159. El enunciado de que X está normalmente distribuida con los parámetros y 2 a menudo se abrevia como X N(, 2 ). Claramente f(x; , ) 0 aunque se tiene que utilizar un argumento de cálculo un tanto complicado para verificar que f(x; , ) dx 1. Se puede demostrar que E(X) y V(X) 2 , de modo que los parámetros son la media y la desviación estándar de X. La fi- gura 4.13 representa gráficas de f(x; , ) de varios pares diferentes (, ). Cada curva de densidad es simétrica con respecto a y acampanada, de modo que el centro de la campa- na (punto de simetría) es tanto la media de la distribución como la mediana. El valor de es la distancia desde hasta los puntos de inflexión de la curva (los puntos donde la curva cambia de virar hacia abajo a virar hacia arriba). Los grandes valores de producen gráfi- cas que están bastante extendidas en torno a , en tanto que los valores pequeños de dan gráficas con una alta cresta sobre y la mayor parte del área bajo de la gráfica bastante cer- ca de . Así pues, una grande implica que se puede observar muy bien un valor de X ale- jado de , en tanto que dicho valor es bastante improbable cuando es pequeña. Distribución normal estándar Para calcular P(a X b) cuando X es una variable aleatoria normal con parámetros y , se debe determinar b a e (x) 2 /(2 2 ) dx (4.4) Ninguna de las técnicas estándar de integración puede ser utilizada para evaluar la expre- sión (4.4). En cambio, con 0 y 1, se calculó la expresión (4.4) por medio de téc- nicas numéricas y se tabuló para ciertos valores de a y b. Esta tabla también puede ser utilizada para calcular probabilidades con cualesquiera otros valores de y considerados. 1 22p s 4.3 Distribución normal 145 DEFINICIÓN Se dice que una variable aleatoria continua X tiene una distribución normal con pa- rámetros y (o y 2 ), donde y o, si la función de densidad de probabilidad de X es f(x; , ) e (x) 2 /(2 2 ) x (4.3) 1 22p s Figura 4.13 Curvas de densidad normal. ⎧ ⎨ ⎩ c4_p130-183.qxd 3/12/08 4:04 AM Page 145
- 164. 146 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad La distribución normal estándar no sirve con frecuencia como modelo de una pobla- ción que surge naturalmente. En cambio, es una distribución de referencia de la que se puede obtener información sobre otra distribución normal. La tabla A.3 del apéndice, da (z) P(Z z), el área bajo la curva de densidad normal estándar a la izquierda de z con z 3.49, 3.48, . . . , 3.48, 3.49. La figura 4.14 ilustra el tipo de área acumulativa (pro- babilidad) tabulada en la tabla A.3. Con esta tabla, varias probabilidades que implican Z pueden ser calculadas. Determínense las siguientes probabilidades normales estándar: (a) P(Z 1.25), (b) P(Z 1.25), (c) P(Z 1.25) y (d) P(0.38 Z 1.25). a. P(Z 1.25) (1.25), una probabilidad tabulada en la tabla A.3 del apéndice en la in- tersección de la fila 1.2 y la columna 0.05. El número allí es 0.8944, así que P(Z 1.25) 0.8944. La figura 4.15(a) ilustra esta probabilidad. b. P(Z 1.25) 1 P(Z 1.25) 1 (1.25), el área bajo la curva z a la derecha de 1.25 (un área de cola superior). En ese caso (1.25) 0.8944 implica que P(Z 1.25) 0.1056. Como Z es una variable aleatoria continua, P(Z 1.25) 0.1056. Véase la figura 4.15(b). c. P(Z 1.25) (1.25), un área de cola inferior. Directamente de la tabla A.3 del apéndice (1.25) 0.1056. Por simetría de la curva z, ésta es la misma respuesta del inciso b). DEFINICIÓN La distribución normal con valores de parámetro 0 y 1 se llama distribu- ción normal estándar. Una variable aleatoria que tiene una distribución normal es- tándar se llama variable aleatoria normal estándar y se denotará por Z. La función de densidad de probabilidad de Z es f(z; 0, 1) 1 2 e z 2 /2 z La gráfica de f(z; 0, 1) se llama curva normal estándar (o z). La función de distribu- ción acumulativa de Z es P(Z z) z f(y; 0, 1) dy, la cual será denotada por (z). Figura 4.14 Áreas acumulativas normales estándar tabuladas en la tabla A.3 del apéndice. 0 z Área sombreada (z) Curva normal estándar (z) Figura 4.15 Áreas (probabilidades) de curvas normales del ejemplo 4.13. Área sombreada (1.25) curva z 0 a) 1.25 curva z 0 b) 1.25 Ejemplo 4.13 c4_p130-183.qxd 3/12/08 4:04 AM Page 146
- 165. d. P(0.38 Z 1.25) es el área bajo la curva normal estándar sobre el intervalo cuyo punto extremo izquierdo es 0.38 y cuyo punto extremo derecho es 1.25. Según la sec- ción 4.2, si X es una variable aleatoria continua con función de distribución acumulativa F(x), entonces P(a X b) F(b) F(a). Por lo tanto, P(0.38 Z 1.25) (1.25) (0.38) 0.8944 0.3520 0.5424. (Véase la figura 4.16.) Percentiles de la distribución normal estándar Con cualquier p entre 0 y 1, se puede utilizar la tabla A.3 del apéndice para obtener el (100p)o percentil de la distribución normal estándar. El 99o percentil de la distribución normal estándar es el valor sobre el eje horizontal tal que el área bajo la curva z a la izquierda de dicho valor es 0.9900. La tabla A.3 del apéndice da con z fija el área bajo la curva normal estándar a la izquierda de z, mientras que aquí se tiene el área y se desea el valor de z. Este es problema “inverso” a P(Z z) ? así que la tabla se utiliza a la inversa: Encuentre en la mitad de la tabla 0.9900; la fila y la columna en la que se encuentra identificado el 99o percentil z. En este caso 0.9901 queda en la intersección de la fila 2.3 y la columna 0.03, así que el 99o percentil es (aproximadamente) z 2.33. (Véase la figura 4.17). Por simetría, el primer percentil está tan debajo de 0 como el 99o está sobre 0, así que es igual a 2.33 (1% queda debajo del primero y también sobre el 99o ). (Véase la figura 4.18.) 4.3 Distribución normal 147 Figura 4.16 P(0.38 Z 1.25) como la diferencia entre dos áreas acumulativas. ■ 0 0.38 1.25 0 1.25 0 0.38 curva z Figura 4.17 Localización del 99o percentil. Área sombreada 0.9900 curva z 99o percentil 0 Figura 4.18 Relación entre el 1er y 99o percentiles. ■ Área sombreada 0.01 curva z 2.33 99o percentil 2.33 1er percentil 0 Ejemplo 4.14 c4_p130-183.qxd 3/12/08 4:04 AM Page 147
- 166. 148 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad En general, la fila y la columna de la tabla A.3 del apéndice, donde el ingreso p está localizado identifican el (100p)o percentil (p. ej., el 67o percentil se obtiene localizando 0.6700 en el cuerpo de la tabla, la cual da z 0.44). Si p no aparece, a menudo se utiliza el número más cercano a él, aunque la interpolación lineal da una respuesta más precisa. Por ejemplo, para encontrar el 95o percentil, se busca 0.9500 adentro de la tabla. Aunque 0.9500 no aparece, tanto 0.9495 como 0.9505 sí, correspondientes a z 1.64 y 1.65, respectiva- mente. Como 0.9500 está a la mitad entre las dos probabilidades que sí aparecen, se utiliza- rá 1.645 como el 95o percentil y 1.645 como el 5o percentil. Notación z En inferencia estadística, se necesitan valores sobre el eje horizontal z que capturen ciertas áreas de cola pequeña bajo la curva normal estándar. Por ejemplo, z0.10 captura el área de cola superior 0.10 y z0.01 captura el área de cola superior 0.01. Como del área bajo la curva z queda a la derecha de z, 1 del área queda a su izquierda. Por lo tanto, z es el 100(1 )o percentil de la distribución normal estándar. Por simetría el área bajo la curva normal estándar a la izquierda de z también es . Los valores z en general se conocen como valores críticos z. La tabla 4.1 incluye los percenti- les z y los valores z más útiles. Tabla 4.1 Percentiles normales estándar y valores críticos Percentil 90 95 97.5 99 99.5 99.9 99.95 (área de cola) 0.1 0.05 0.025 0.01 0.005 0.001 0.0005 z 100(1 )o 1.28 1.645 1.96 2.33 2.58 3.08 3.27 percentil z0.05 es el 100(1 0.05)o 95o percentil de la distribución normal estándar, por lo tanto z0.05 1.645. El área bajo la curva normal estándar a la izquierda de z0.05 también es 0.05. (Véase la figura 4.20.) Notación z denotará el valor sobre el eje z para el cual del área bajo la curva z queda a la de- recha de z. (Véase la figura 4.19.) Ejemplo 4.15 Figura 4.19 Notación z ilustrada. Área sombreada P(Z z) curva z z 0 c4_p130-183.qxd 3/12/08 4:04 AM Page 148
- 167. Distribuciones normales no estándar Cuando X N(, 2 ), las probabilidades que implican X se calculan “estandarizando”. La variable estandarizada es (X ) . Al restar la media cambia de a cero y luego al dividir entre cambian las escalas de la variable de modo que la desviación estándar es uno en lugar de . La idea clave de la proposición es que estandarizando cualquier probabilidad que implique X puede ser expresada como una probabilidad que implica una variable aleatoria normal es- tándar Z, de modo que se pueda utilizar la tabla A.3 del apéndice. Esto se ilustra en la figu- ra 4.21. La proposición se comprueba escribiendo la función de distribución acumulativa de Z (X )/ como P(Z z) P(X z ) z f(x; , ) dx Utilizando un resultado del cálculo, esta integral puede ser derivada con respecto a z para que dé la función de densidad de probabilidad deseada f(z; 0, 1). 4.3 Distribución normal 149 Figura 4.20 Determinación de z0.05. ■ Área sombreada 0.05 Área sombreada 0.05 curva z z0.05 95o percentil 1.645 1.645 z0.05 0 Figura 4.21 Igualdad de áreas de curvas normales estándar y no estándar. x 0 N( , 2) N(0, 1) (x )/ PROPOSICIÓN Si X tiene una distribución normal con media y desviación estándar , entonces Z X tiene una distribución normal estándar. Por lo tanto, P(a X b) P a Z b b a P(X a) a P(X b) 1 b c4_p130-183.qxd 3/12/08 4:04 AM Page 149
- 168. 150 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad El tiempo que requiere un conductor para reaccionar a las luces de freno de un vehículo que está desacelerando es crítico para evitar colisiones por alcance. El artículo “Fast-Rise Bra- ke Lamp as a Collision-Prevention Device” (Ergonomics, 1993: 391-395), sugiere que el tiempo de reacción de respuesta en tráfico a una señal de freno de luces de freno estándar puede ser modelado con una distribución normal que tiene un valor medio de 1.25 s y des- viación estándar de 0.46 s. ¿Cuál es la probabilidad de que el tiempo de reacción esté entre 1.00 s y 1.75 s? Si X denota el tiempo de reacción, entonces estandarizando se obtiene 1.00 X 1.75 si y sólo si 1.00 4 . 6 1.25 X .4 1 6 .25 1.75 . 46 1.25 Por lo tanto P(1.00 X 1.75) P 1.00 . 46 1.25 Z 1.75 . 46 1.25 P( 0.54 Z 1.09) (1.09) ( 0.54) 0.8621 0.2946 0.5675 Esto se ilustra en la figura 4.22. Asimismo, si se ven los 2 s como un tiempo de reacción crí- ticamente largo, la probabilidad de que el tiempo de reacción real exceda este valor es P(X 2) P Z 2 .4 1 6 .25 P(Z 1.63) 1 (1.63) 0.0516 ■ Estandarizar no lleva nada más que a calcular una distancia al valor medio y luego reexpre- sarla como algún número de desviaciones estándar. Por lo tanto, si 100 y 15, en- tonces x 130 corresponde a z (130 100)/15 30/15 2.00. Es decir, 130 está a 2 desviaciones estándar sobre (a la derecha de) el valor medio. Asimismo, estandarizando 85 se obtiene (85 100)/15 1.00, por lo tanto, 85 está a una desviación estándar por de- bajo de la media. La tabla z se aplica a cualquier distribución normal siempre que se pien- se en función del número de desviaciones estándar de alejamiento del valor medio. Se sabe que el voltaje de ruptura de un diodo seleccionado al azar de un tipo particular está normalmente distribuido. ¿Cuál es la probabilidad de que el voltaje de ruptura de un diodo esté dentro de una desviación estándar de su valor medio? Esta pregunta puede ser respondi- Ejemplo 4.16 Ejemplo 4.17 Figura 4.22 Curvas normales del ejemplo 4.16. 1.25 1.75 1.00 0 1.09 0.54 normal 1.25, 0.46 P(1.00 X 1.75) curva z 0.46 0.46 0.46 0.46 0.46 0.46 c4_p130-183.qxd 3/12/08 4:04 AM Page 150
- 169. da sin conocer o , en tanto se sepa que la distribución es normal; la respuesta es la mis- ma para cualquier distribución normal: P(X está dentro de 1 desviación estándar de su media) P( X ) P Z P(1.00 Z 1.00) (1.00) (1.00) 0.6826 La probabilidad de que X esté dentro de dos desviaciones estándar es P( 2.00 Z 2.00) 0.9544 y dentro de tres desviaciones estándar es P( 3.00 Z 3.00) 0.9974. ■ Los resultados del ejemplo 4.17 a menudo se reportan en forma de porcentaje y se les conoce como regla empírica (porque la evidencia empírica ha demostrado que los histogra- mas de datos reales con frecuencia pueden ser aproximados por curvas normales). 4.3 Distribución normal 151 Si la distribución de la población de una variable es (aproximadamente) normal, entonces 1. Aproximadamente 68% de los valores están dentro de 1 DE de la media. 2. Aproximadamente 95% de los valores están dentro de 2 DE de la media. 3. Aproximadamente 99.7% de los valores están dentro de 3 DE de la media. En realidad es inusual observar un valor de una población normal que esté mucho más le- jos de 2 desviaciones estándar de . Estos resultados serán importantes en el desarrollo de procedimientos de prueba de hipótesis en capítulos posteriores. Percentiles de una distribución normal arbitraria El (100p)o percentil de una distribución normal con media y desviación estándar es fá- cil de relacionar con el (100p)o percentil de la distribución normal estándar. Otra forma de decir es que si z es el percentil deseado de la distribución normal estándar, entonces el percentil deseado de la distribución (, ) normal está a z desviaciones están- dar de . La cantidad de agua destilada despachada por una cierta máquina está normalmente distri- buida con valor medio de 64 oz y desviación estándar de 0.78 oz. ¿Qué tamaño de contene- dor c asegurará que ocurra rebosamiento sólo 0.5% del tiempo? Si X denota la cantidad despachada, la condición deseada es que P(X c) 0.005, o, en forma equivalente, que P(X c) 0.995. Por lo tanto, c es el 99.5o percentil de la distribución normal con 64 y 0.78. El 99.5o percentil de la distribución normal estándar es de 2.58, por lo tanto, c (0.995) 64 (2.58)(0.78) 64 2.0 66 oz Esto se ilustra en la figura 4.23. PROPOSICIÓN (100p)o percentil de normal estándar (100p)o percentil de (m, s) normal Ejemplo 4.18 c4_p130-183.qxd 3/12/08 4:04 AM Page 151
- 170. 152 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad Distribución normal y poblaciones discretas La distribución normal a menudo se utiliza como una aproximación a la distribución de va- lores en una población discreta. En semejantes situaciones, se debe tener un cuidado espe- cial para asegurarse de que las probabilidades se calculen con precisión. Se sabe que el coeficiente intelectual en una población particular (medido con una prueba estándar) está más o menos normalmente distribuido con 100 y 15. ¿Cuál es la probabilidad de que un individuo seleccionado al azar tenga un CI de por lo menos 125? Con X el CI de una persona seleccionada al azar, se desea P(X 125). La tentación en este caso es estandarizar X 125 como en ejemplos previos. Sin embargo, la distribución de la población de coeficientes intelectuales en realidad es discreta, puesto que los coefi- cientes intelectuales son valores enteros. Así que la curva normal es una aproximación a un histograma de probabilidad discreto como se ilustra en la figura 4.24. Los rectángulos del histograma están centrados en enteros, por lo que los coeficien- tes intelectuales de por lo menos 125 corresponden a rectángulos que comienzan en 124.5, la zona sombreada en la figura 4.24. Por lo tanto, en realidad se desea el área bajo la curva aproximadamente normal a la derecha de 124.5. Si se estandariza este valor se obtiene P(Z 1.63) 0.0516, en tanto que si se estandariza 125 se obtiene P(Z 1.67 0.0475. La diferencia no es grande, pero la respuesta 0.0516 es más precisa. Asimismo, P(X 125) se- ría aproximada por el área entre 124.5 y 125.5, puesto que el área bajo la curva normal so- bre el valor único de 125 es cero. La corrección en cuanto a discrecionalidad de la distribución subyacente en el ejem- plo 4.19 a menudo se llama corrección por continuidad. Es útil en la siguiente aplicación de la distribución normal al cálculo de probabilidades binomiales. Aproximación de la distribución binomial Recuérdese que el valor medio y la desviación estándar de una variable aleatoria binomial X son X np y X n p q , respectivamente. La figura 4.25 muestra una histograma de probabilidad binomial de la distribución binomial con n 20, p 0.6 con el cual 20(0.6) 12 y 2 0 (0 . 6 )( 0 .4 ) 2.19. Sobre el histograma de probabilidad se super- puso una curva normal con esas y . Aunque el histograma de probabilidad es un poco Área sombreada 0.995 c 99.5o percentil 66.0 6 4 Figura 4.23 Distribución de la cantidad despachada en el ejemplo 4.18. ■ Ejemplo 4.19 125 Figura 4.24 Aproximación normal a una distribución discreta. ■ c4_p130-183.qxd 3/12/08 4:04 AM Page 152
- 171. asimétrico (debido a que p 0.5), la curva normal da una muy buena aproximación, sobre todo en la parte media de la figura. El área de cualquier rectángulo (probabilidad de cual- quier valor X particular), excepto la de los localizados en las colas extremas, puede ser aproximada con precisión mediante el área de la curva normal correspondiente. Por ejem- plo, P(X 10) B(10; 20, 0.6) B(9; 20, 0.6) 0.117, mientras que el área bajo la curva normal entre 9.5 y 10.5 es P(1.14 Z 0.68) 0.1212. En términos generales, en tanto que el histograma de probabilidad binomial no sea de- masiado asimétrico, las probabilidades binomiales pueden ser aproximadas muy bien por áreas de curva normal. Se acostumbra entonces decir que X tiene aproximadamente una dis- tribución normal. 4.3 Distribución normal 153 Una comprobación directa de este resultado es bastante difícil. En el siguiente capítulo se ve- rá que es una consecuencia de un resultado más general llamado Teorema del Límite Central. Con toda honestidad, esta aproximación no es tan importante en el cálculo de probabilidad como una vez lo fue. Esto se debe a que los programas de computadora ahora son capaces de calcular probabilidades binomiales con exactitud con valores bastante grandes de n. Suponga que 25% de los conductores con licencia de manejo en un estado particular no están asegurados. Sea X el número de conductores no asegurados en una muestra aleato- ria de tamaño 50 (algo perversamente, un éxito es un conductor no asegurado), de modo que PROPOSICIÓN Sea X una variable aleatoria normal basada en n ensayos con probabilidad de éxito p. Luego si el histograma de probabilidad binomial no es demasiado asimétrico, X tiene aproximadamente una distribución normal con np y n p q . En particular, con x un valor posible de X, P(X x) B(x; n, p) x 0.5 n p q np En la práctica, la aproximación es adecuada siempre que tanto np 10 como nq 10, puesto que en ese caso existe bastante simetría en la distribución binomial subya- cente. área bajo la curva normal a la izquierda de x 0.5 Ejemplo 4.20 0 2 4 6 8 10 12 14 16 18 20 Curva normal, 12, 2.19 0.20 0.15 0.10 0.05 μ σ Figura 4.25 Histograma de probabilidad binomial para n 20, p 0.6 con curva de aproximación normal sobrepuesta. c4_p130-183.qxd 3/12/08 4:04 AM Page 153
- 172. 154 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad p 0.25. Entonces 12.5 y 3.06. Como np 50(0.25) 12.5 10 y nq 37.5 10, la aproximación puede ser aplicada con seguridad: P(X 10) B(10; 50, 0.25) 10 3 0.5 .0 6 12.5 ( 0.65) 0.2578 Asimismo, la probabilidad de que entre 5 y 15 (inclusive) de los conductores seleccionados no estén asegurados es P(5 X 15) B(15; 50, 0.25) B(4; 50, 0.25) 15.5 3 .06 12.5 4.5 3 .06 12.5 0.8320 Las probabilidades exactas son 0.2622 y 0.8348, respectivamente, así que las aproximacio- nes son bastante buenas. En el último cálculo, la probabilidad P(5 X 15) está siendo aproximada por el área bajo la curva normal entre 4.5 y 15.5, se utiliza la corrección de con- tinuidad tanto para el límite superior como para el inferior. ■ Cuando el objetivo de la investigación es hacer una inferencia sobre una proporción de población p, el interés se enfocará en la proporción muestral de X/n éxitos y no en X. Como esta proporción es exactamente X multiplicada por la constante 1/n, también tendrá apro- ximadamente una distribución normal (con media p y desviación estándar p q /n ), siempre que tanto np 10 como nq 10. Esta aproximación normal es la base de varios procedimientos inferenciales que se discutirán en capítulos posteriores. 28. Sea Z una variable aleatoria normal estándar y calcule las siguientes probabilidades, trace las figuras siempre que sea apropiado. a. P(0 Z 2.17) b. P(0 Z 1) c. P( 2.50 Z 0) d. P( 2.50 Z 2.50) e. P(Z 1.37) f. P( 1.75 Z) g. P( 1.50 Z 2.00) h. P(1.37 Z 2.50) i. P(1.50 Z) j. P(°Z° 2.50) 29. En cada caso, determine el valor de la constante c que hace que el enunciado de probabilidad sea correcto. a. (c) 0.9838 b. P(0 Z c) 0.291 c. P(c Z) 0.121 d. P( c Z c) 0.668 e. P(c °Z°) 0.016 30. Encuentre los siguientes percentiles de la distribución normal estándar. Interpole en los casos en que sea apro- piado. a. 91o b. 9o c. 75o d. 25o e. 6o 31. Determine z para lo siguiente: a. 0.0055 b. 0.09 c. 0.663 32. Si X es una variable aleatoria normal con media 80 y des- viación estándar 10, calcule las siguientes probabilidades mediante estandarización: a. P(X 100) b. P(X 80) c. P(65 X 100) d. P(70 X) e. P(85 X 95) f. P(°X 80° 10) 33. Suponga que la fuerza que actúa en una columna que ayu- da a soportar un edificio está normalmente distribuida con media de 15.0 kips y desviación estándar de 1.25 kips. ¿Cuál es la probabilidad de que la fuerza a. sea de más de 18 kips? b. esté entre 10 y 12 kips? c. Difiera de 15.0 kips en cuando mucho 1.5 desviaciones estándar? 34. El artículo “Reliability of Domestic-Waste Biofilm Reactors” (J. of Envir. Engr., 1995: 785-790) sugiere que la concentra- ción de sustrato (mg/cm3 ) del afluente que llega a un reactor está normalmente distribuida con 0.30 y 0.06. a. ¿Cuál es la probabilidad de que la concentración exceda de 0.25? b. ¿Cuál es la probabilidad de que la concentración sea cuando mucho de 0.10? c. ¿Cómo caracterizaría el 5% más grande de todos los va- lores de concentración? EJERCICIOS Sección 4.3 (28-58) c4_p130-183.qxd 3/12/08 4:04 AM Page 154
- 173. 4.3 Distribución normal 155 35. Suponga que el diámetro a la altura del pecho (pulg) de ár- boles de un tipo está normalmente distribuido con 8.8 y 2.8 como se sugiere en el artículo “Simulating a Har- vester-Forwarder Softwood Thinning” (Forest Products J. mayo de 1997; 36-41). a. ¿Cuál es la probabilidad de que el diámetro de un árbol seleccionado al azar sea por lo menos de 10 pulg? ¿Mayor de 10 pulg? b. ¿Cuál es la probabilidad de que el diámetro de un árbol seleccionado al azar sea de más de 20 pulg? c. ¿Cuál es la probabilidad de que el diámetro de un árbol seleccionado al azar esté entre 5 y 10 pulg? d. ¿Qué valor c es tal que el intervalo (8.8 c, 8.8 c) in- cluya 98% de todos los valores de diámetro? e. Si se seleccionan cuatro árboles al azar, ¿cuál es la pro- babilidad de que por lo menos uno tenga un diámetro de más de 10 pulg? 36. La deriva de las atomizaciones de pesticidas es una preocu- pación constante de los fumigadores y productores agrícolas. La relación inversa entre el tamaño de gota y el potencial de deriva es bien conocida. El artículo “Effects of 2,4-D Formu- lation and Quinclorac on Spray Droplet Size and Deposition” (Weed Technology, 2005: 1030-1036) investigó los efectos de formulaciones de herbicidas en atomizaciones. Una figura en el artículo sugirió que la distribución normal con media de 1050 m y desviación estándar de 150 m fue un modelo ra- zonable de tamaño de gotas de agua (el “tratamiento de con- trol”) pulverizada a través de una boquilla de 760 ml/min. a. ¿Cuál es la probabilidad de que el tamaño de una sola go- ta sea de menos de 1500 m? ¿Por lo menos de 1000 m? b. ¿Cuál es la probabilidad de que el tamaño de una sola gota esté entre 1000 y 1500 m? c. ¿Cómo caracterizaría el 2% más pequeño de todas las gotas? d. Si se miden los tamaños de cinco gotas independiente- mente seleccionadas, ¿cuál es la probabilidad de que por lo menos una exceda de 1500 m? 37. Suponga que la concentración de cloruro en sangre (mmol/L) tiene una distribución normal con media de 104 y desvia- ción estándar de 5 (información en el artículo “Matemathi- cal Model of Chloride Concentration in Human Blood”, J. of Med. Engr. and Tech., 2006; 25-30, incluida una gráfica de probabilidad normal como se describe en la sección 4.6, apoyando esta suposición). a. ¿Cuál es la probabilidad de que la concentración de clo- ruro sea igual a 105? ¿Sea menor que 105? ¿Sea cuando mucho de 105? b. ¿Cuál es la probabilidad de que la concentración de clo- ruro difiera de la media por más de una desviación están- dar? ¿Depende esta probabilidad de los valores de y ? c. ¿Cómo caracterizaría el 0.1% más extremo de los valores de concentración de cloruro? 38. Hay dos máquinas disponibles para cortar corchos para usarse en botellas de vino. La primera produce corchos con diáme- tros que están normalmente distribuidos con media de 3 cm y desviación estándar de 0.1 cm. La segunda máquina produce corchos con diámetros que tienen una distribución normal con media de 3.04 cm y desviación estándar de 0.02 cm. Los cor- chos aceptables tienen diámetros entre 2.9 y 3.1 cm. ¿Cuál máquina es más probable que produzca un corcho aceptable? 39. a. Si una distribución normal tiene 30 y 5, ¿cuál es el 91o percentil de la distribución? b. ¿Cuál es el 6o percentil de la distribución? c. El ancho de una línea grabada en un “chip” de circuito in- tegrado normalmente está distribuida con media de 3.000 m y desviación estándar de 0.140. ¿Qué valor de ancho separa 10% de las líneas más anchas del 90% restante? 40. El artículo “Monte Carlo Simulation-Tool for Better Un- derstanding of LRFD” (J. Structural Engr., 1993: 1586- 1599) sugiere que la resistencia a ceder (lb/pulg2 ) de un acero grado A36 está normalmente distribuida con 43 y 4.5. a. ¿Cuál es la probabilidad de que la resistencia a ceder sea cuando mucho de 40? ¿De más de 60? b. ¿Qué valor de resistencia a ceder separa al 75% más re- sistente del resto? 41. El dispositivo de apertura automática de un paracaídas de carga militar se diseñó para que abriera el paracaídas a 200 m sobre el suelo. Suponga que la altitud de abertura en realidad tiene una distribución normal con valor medio de 200 m y desviación estándar de 30 m. La carga útil se dañará si el paracaídas se abre a menos de 100 m. ¿Cuál es la probabi- lidad de que se dañe la carga útil de cuando menos uno de cinco paracaídas lanzados en forma independiente? 42. La lectura de temperatura tomada con un termopar colocado en un medio a temperatura constante normalmente está dis- tribuida con media , la temperatura real del medio y la des- viación estándar . ¿Qué valor tendría para asegurarse de que el 95% de todas las lecturas están dentro de 0.1º de ? 43. Se sabe que la distribución de resistencia de resistores de un tipo es normal y la resistencia del 10% de ellos es mayor de 10.256 ohms y la del 5% es de una resistencia menor de 9.671 ohms. ¿Cuáles son el valor medio y la desviación estándar de la distribución de resistencia? 44. Si la longitud roscada de un perno está normalmente distri- buida, ¿cuál es la probabilidad de que la longitud roscada de un perno seleccionado al azar esté a. dentro de 1.5 desviaciones estándar de su valor medio? b. a más de 2.5 desviaciones estándar de su valor medio? c. entre una y dos desviaciones estándar de su valor medio? 45. Una máquina que produce cojinetes de bolas inicialmente se ajustó de modo que el diámetro promedio verdadero de los cojinetes que produce sea de 0.500 pulg. Un cojinete es aceptable si su diámetro está dentro de 0.004 pulg de su va- lor objetivo. Suponga, sin embargo, que el ajuste cambia du- rante el curso de la producción, de modo que los cojinetes tengan diámetros normalmente distribuidos con valor medio de 0.499 pulg y desviación estándar de 0.002 pulg. ¿Qué porcentaje de los cojinetes producidos no será aceptable? 46. La dureza Rockwell de un metal se determina hincando una punta endurecida en la superficie del metal y luego midien- do la profundidad de penetración de la punta. Suponga que la dureza Rockwell de una aleación particular está normal- mente distribuida con media de 70 y desviación estándar de 3. (La dureza Rockwell se mide en una escala continua.) c4_p130-183.qxd 3/12/08 4:04 AM Page 155
- 174. 156 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad a. Una probeta es aceptable sólo si su dureza oscila entre 67 y 75, ¿cuál es la probabilidad de que una probeta se- leccionada al azar tenga una dureza aceptable? b. Si el rango de dureza aceptable es (70 c, 70 c), ¿con qué valor de c tendría 95% de todas las probetas una du- reza aceptable? c. Si el rango de dureza aceptable es como el del inciso a) y la dureza de cada una de diez probetas seleccionadas al azar se determina de forma independiente, ¿cuál es el valor esperado de probetas aceptables entre las diez? d. ¿Cuál es la probabilidad de que cuando mucho ocho de diez probetas independientemente seleccionadas tengan una dureza de menos de 73.84? [Sugerencia: Y el nú- mero de entre las diez probetas con dureza de menos de 73.84 es una variable binomial; ¿cuál es p?] 47. La distribución de peso de paquetes enviados de cierta ma- nera es normal con valor medio de 12 lb y desviación están- dar de 3.5 lb. El servicio de paquetería desea establecer un valor de peso c más allá del cual habrá un cargo extra. ¿Qué valor de c es tal que 99% de todos los paquetes estén por lo menos 1 lb por debajo del peso de cargo extra? 48. Suponga que la tabla A.3 del apéndice contiene (z) sólo para z 0. Explique cómo aún así podría calcular a. P( 1.72 Z 0.55) b. P( 1.72 Z 0.55) ¿Es necesario tabular (z) para z negativo? ¿Qué propiedad de la curva normal estándar justifica su respuesta? 49. Considere los bebés nacidos en el rango “normal” de 37-43 semanas de gestación. Datos extensos sustentan la suposi- ción de que el peso de nacimiento de estos bebés nacidos en Estados Unidos está normalmente distribuido con media de 3432 g y desviación estándar de 482 g. [El artículo “Are Ba- bies Normal?” (The American Statistician (1999): 298-302) analizó datos de un año particular; con una selección sensi- ble de intervalos de clase, un histograma no parecía del todo normal pero después de una investigación se determinó que esto se debía a que en algunos hospitales medían el peso en gramos, en otros lo medían a la onza más cercana y luego lo convertían en gramos. Una selección modificada de interva- los de clase que permitía esto produjo un histograma que era descrito muy bien por una distribución normal.] a. ¿Cuál es la probabilidad de que el peso de nacimiento de un bebé seleccionado al azar de este tipo exceda de 4000 gramos? ¿Esté entre 3000 y 4000 gramos? b. ¿Cuál es la probabilidad de que el peso de nacimiento de un bebé seleccionado al azar de este tipo sea de menos de 2000 gramos o de más de 5000 gramos? c. ¿Cuál es la probabilidad de que el peso de nacimiento de un bebé seleccionado al azar de este tipo exceda de 7 libras? d. ¿Cómo caracterizaría el 0.1% más extremo de todos los pesos de nacimiento? e. Si X es una variable aleatoria con una distribución nor- mal y a es una constante numérica (a 0), entonces Y aX también tiene una distribución normal. Use esto para determinar la distribución de pesos de nacimiento expresados en libras (forma, media y desviación están- dar) y luego calcule otra vez la probabilidad del inciso c) ¿Cómo se compara ésta con su respuesta previa? 50. En respuesta a preocupaciones sobre el contenido nutricional de las comidas rápidas. McDonald’s ha anunciado que utili- zará un nuevo aceite de cocinar para sus papas a la francesa que reducirá sustancialmente los niveles de ácidos grasos e incrementará la cantidad de grasa poliinsaturada más benéfi- ca. La compañía afirma que 97 de 100 personas no son capa- ces de detectar una diferencia de sabor entre los nuevos y los viejos aceites. Suponiendo que esta cifra es correcta (como proporción de largo plazo) ¿cuál es la probabilidad aproxi- mada de que en una muestra aleatoria de 1000 individuos que han comprado papas a la francesa en McDonald’s: a. ¿Por lo menos 40 puedan notar la diferencia de sabor en- tre los dos aceites? b. Cuando mucho 5% pueda notar la diferencia de sabor entre los dos aceites? 51. La desigualdad de Chebyshev (véase el ejercicio 44 del capítulo 3), es válida para distribuciones continuas y dis- cretas. Estipula que para cualquier número k que satisfaga k 1, P(°X ° k) 1/k2 (véase el ejercicio 44 en el capítulo 3 para una interpretación). Obtenga esta proba- bilidad en el caso de una distribución normal con k 1, 2, 3 y compare con el límite superior. 52. Sea X el número de defectos en un carrete de cinta magné- tica de 100 m (una variable de valor entero). Suponga que X tiene aproximadamente una distribución normal con 25 y 5. Use la corrección por continuidad para calcu- lar la probabilidad de que el número de defectos sea: a. Entre 20 y 30, inclusive. b. Cuando mucho 30. Menos de 30. 53. Si X tiene una distribución binomial con parámetros n 25 y p, calcule cada una de las siguientes probabilidades mediante la aproximación normal (con la corrección por continuidad) en los casos p 0.5, 0.6, y 0.8 y compare con las probabili- dades exactas calculadas con la tabla A.1 del apéndice. a. P(15 X 20) b. P(X 15) c. P(20 X) 54. Suponga que 10% de todas las flechas de acero producidas por medio de un proceso no cumplen con las especificacio- nes pero pueden ser retrabajadas (en lugar de ser desecha- das). Considere una muestra aleatoria de 200 flechas y sea X el número entre éstas que no cumplen con las especifica- ciones y pueden ser retrabajadas. ¿Cuál es la probabilidad aproximada de que X sea a. Cuando mucho 30? b. Menos que 30? c. Entre 15 y 25 (inclusive)? 55. Suponga que sólo 75% de todos los conductores en un esta- do usan con regularidad el cinturón de seguridad. Se selec- ciona una muestra aleatoria de 500 conductores. ¿Cuál es la probabilidad de que a. Entre 360 y 400 (inclusive) de los conductores en la muestra usen con regularidad el cinturón de seguridad? b. Menos de 400 de aquellos en la muestra usen con regu- laridad el cinturón de seguridad? c4_p130-183.qxd 3/12/08 4:04 AM Page 156
- 175. 56. Demuestre que la relación entre un percentil normal gene- ral y el percentil z correspondiente es como se estipuló en esta sección. 57. a. Demuestre que si X tiene una distribución normal con parámetros y , entonces Y aX b (una función li- neal de X) también tiene una distribución normal. ¿Cuá- les son los parámetros de la distribución de Y [es decir, E(Y) y V(Y)]? [Sugerencia: Escriba la función de distri- bución acumulativa de Y, P(Y y), como una integral que implique la función de densidad de probabilidad de X y luego derive con respecto a y para obtener la función de densidad de probabilidad de Y.] b. Si cuando se mide en °C, la temperatura está normal- mente distribuida con media de 115 y desviación están- dar de dos, ¿qué se puede decir sobre la distribución de temperatura medida en °F? 58. No existe una fórmula exacta para función de distribución acumulativa normal estándar (z), aunque se han publicado varias aproximaciones en artículos. La siguiente se tomó de “Approximations for Hand Calculators Using Small Integer Coefficients” (Mathematics of Computation, 1977: 214- 222). Con 0 z 5.5, P(Z z) 1 (z) 0.5 exp El error relativo de esta aproximación es de menos de 0.042%. Úsela para calcular aproximaciones a las siguientes probabi- lidades y compare siempre que sea posible con las probabili- dades obtenidas con la tabla A.3 del apéndice. a. P(Z 1) b. P(Z 3) c. P( 4 Z 4) d. P(Z 5) (83z 351)z 562 703/z 165 4.4 Distribuciones exponencial y gama 157 La curva de densidad correspondiente a cualquier distribución normal tiene forma de campa- na y por consiguiente es simétrica. Existen muchas situaciones prácticas en las cuales la va- riable de interés para un investigador podría tener una distribución asimétrica. Una familia de distribuciones que tiene esta propiedad es la familia gama. Primero se considera un caso es- pecial, la distribución exponencial y luego se le generaliza más adelante en esta sección. Distribución exponencial La familia de distribuciones exponenciales proporciona modelos de probabilidad que son muy utilizados en disciplinas de ingeniería y ciencias. 4.4 Distribuciones exponencial y gama Algunas fuentes escriben la función de densidad de probabilidad exponencial en la forma (1/b)ex/b , de modo que 1/. El valor esperado de una variable aleatoria exponencial- mente distribuida X es E(X) 0 x ex dx Para obtener este valor esperado se requiere integrar por partes. La varianza de X se calcula utilizando el hecho de que V(X) E(X2 ) [E(X)]2 . La determinación de E(X2 ) requiere inte- grar por partes dos veces en sucesión. Los resultados de estas integraciones son los siguientes: Tanto la media como la desviación estándar de la distribución exponencial son iguales a 1/. En la figura 4.26 aparecen algunas gráficas de varias funciones de densidad de probabilidad exponenciales. m 5 1 l s2 5 1 l2 DEFINICIÓN Se dice que X tiene una distribución exponencial con parámetro ( 0) si la fun- ción de densidad de probabilidad de X es f(x; ) elx x 0 0 de lo contrario (4.5) Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 157
- 176. 158 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad 0.5 1 2 x 2 0.5 1 f(x; ) Figura 4.26 Curvas de densidad exponencial. La función de densidad de probabilidad exponencial es fácil de integrar para obtener la fun- ción de densidad acumulativa. Suponga que el tiempo de respuesta X en una terminal de computadora en línea (el tiempo transcurrido entre el final de la consulta de un usuario y el inicio de la respuesta del siste- ma a dicha consulta) tiene una distribución exponencial con tiempo de respuesta esperado de 5 s. Entonces E(X) 1/ 5, por lo tanto 0.2. La probabilidad de que el tiempo de respuesta sea cuando mucho de 10 s es P(X 10) F(10; 0.2) 1 e(0.2)(10) 1 e2 1 0.135 0.865 La probabilidad de que el tiempo de respuesta sea de entre 5 y 10 s es P(5 X 10) F(10; 0.2) F(5; 0.2) (1 e2 ) (1 e1 ) 0.233 ■ La distribución exponencial se utiliza con frecuencia como modelo de la distribución de tiempos entre la ocurrencia de eventos sucesivos, tales como clientes que llegan a una instalación de servicio o llamadas que entran a un conmutador. La razón de esto es que la distribución exponencial está estrechamente relacionada con el proceso de Poisson discuti- do en el capítulo 3. Aunque una comprobación completa queda fuera del alcance de este libro, el resultado es fácil de verificar para el tiempo X1 hasta que ocurre el primer evento: P(X1 t) 1 P(X1 t) 1 P[ningún evento en (0, t)] 1 et 0 ! (t)0 1 et la cual es exactamente la función de distribución acumulativa de la distribución exponencial. Ï Ì Ó Ejemplo 4.21 PROPOSICIÓN Suponga que el número de eventos que ocurren en cualquier intervalo de tiempo de duración t tiene una distribución de Poisson con parámetro t (donde , la razón del proceso de eventos, es el número esperado de eventos que ocurren en una unidad de tiempo) y que los números de ocurrencias en intervalos no traslapantes son indepen- dientes uno de otro. Entonces la distribución del tiempo transcurrido entre la ocu- rrencia de dos eventos sucesivos es exponencial con parámetro . F(x; ) 0 x 0 1 ex x 0 c4_p130-183.qxd 3/12/08 4:04 AM Page 158
- 177. Suponga que se reciben llamadas durante las 24 horas en una “línea de emergencia para pre- vención del suicidio” de acuerdo con un proceso de Poisson a razón 0.5 llamadas por día. Entonces el número de días X entre llamadas sucesivas tiene una distribución exponen- cial con valor de parámetro 0.5, así que la probabilidad de que transcurran más de dos días entre llamadas es P(X 2) 1 P(X 2) 1 F(2; 0.5) e(0.5)(2) 0.368 El tiempo esperado entre llamadas sucesivas es 1/0.5 2 días. ■ Otra aplicación importante de la distribución exponencial es modelar la distribución de la duración de un componente. Una razón parcial de la popularidad de tales aplicaciones es la propiedad de “ falta de memoria o amnesia” de la distribución exponencial. Supon- ga que la duración de un componente está exponencialmente distribuida con parámetro . Después de poner el componente en servicio, se deja que pase un periodo de t0 horas y lue- go se ve si el componente sigue trabajando; ¿cuál es ahora la probabilidad de que dure por lo menos t horas más? En símbolos, se desea P(X t t0°X t0). Por la definición de pro- babilidad condicional, P(X t t0°X t0) Pero el evento X t0 en el numerador es redundante, puesto que ambos eventos pueden ocu- rrir si y sólo si X t t0. Por consiguiente, P(X t t0°X t0) P( P X (X t t0) t0) et Esta probabilidad condicional es idéntica a la probabilidad original P(X t) de que el com- ponente dure t horas. Por lo tanto, la distribución de duración adicional es exactamente la misma que la distribución original de duración, así que en cada punto en el tiempo el com- ponente no muestra ningún efecto de desgaste. En otras palabras, la distribución de la dura- ción restante es independiente de la antigüedad actual. Aunque la propiedad de amnesia se justifica por lo menos en forma aproximada en muchos problemas aplicados, en otras situaciones los componentes se deterioran con el tiempo o de vez en cuando mejoran con él (por lo menos hasta cierto punto). Las distribu- ciones gama, Weibull y lognormales proporcionan modelos de duración más generales (las últimas dos se discuten en la siguiente sección). La función gama Para definir la familia de distribuciones gama, primero se tiene que introducir una función que desempeña un importante papel en muchas ramas de las matemáticas. 1 F(t t0; ) 1 F(t0; ) P[(X t t0) (X t0)] P(X t0) 4.4 Distribuciones exponencial y gama 159 Ejemplo 4.22 Las propiedades más importantes de la función gama son las siguientes: 1. Con cualquier 1, () ( 1) ( 1) [vía integración por partes]. 2. Con cualquier entero positivo, n, (n) (n 1)! 3. 1 2 . DEFINICIÓN Con 0, la función gama () se define como () 0 x1 ex dx (4.6) c4_p130-183.qxd 3/12/08 4:04 AM Page 159
- 178. 160 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad De acuerdo con la expresión (4.6), si f(x; ) x ( 1 e ) x x 0 0 de lo contrario (4.7) entonces f (x; ) 0 y 0 f(x; ) dx ()/() 1, así que f(x; ) satisface las dos pro- piedades básicas de una función de densidad de probabilidad. La distribución gama La distribución exponencial se deriva de considerar 1 y 1/. La figura 4.27(a) ilustra las gráficas de la función de densidad de probabilidad gama f(x; , ) (4.8) para varios pares (, ), en tanto que la figura 4.27(b) presenta gráficas de la función de densidad de probabilidad gama estándar. Para la función de densidad de pro- babilidad estándar cuando 1, f(x; ) es estrictamente decreciente a medida que x se in- crementa desde 0; cuando 1, f(x; ) se eleva desde 0 en x 0 hasta un máximo y luego decrece. El parámetro en (4.8) se llama parámetro de escala porque los valores diferen- tes de uno alargan o comprimen la función de densidad de probabilidad en la dirección x. La media y la varianza de una variable aleatoria X que tiene la distribución gama f(x; , ) son E(X) V(X) 2 2 Cuando X es una variable aleatoria gama estándar, la función de distribución acumu- lativa de X, F(x; ) x 0 y ( 1 e ) y dy x 0 (4.9) DEFINICIÓN Se dice que una variable aleatoria continua X tiene una distribución gama si la fun- ción de densidad de probabilidad de X es f(x; , ) 1 () x1 e x/ x 0 (4.8) 0 de lo contrario donde los parámetros y satisfacen 0, 0. La distribución gama están- dar tiene 1, así que (4.7) da la función de densidad de probabilidad de una va- riable aleatoria gama estándar. 7 6 5 4 3 2 1 0 0.5 1.0 2, 1 3 1, 1 2, 2 2, 1 (a ) x f(x; , ) 5 4 3 2 1 0 0.5 1.0 1 0.6 2 5 (b ) x f(x; ) Figura 4.27 (a) Curvas de densidad gama; (b) Curvas de densidad gama estándar. Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 160
- 179. se llama función gama incompleta [en ocasiones la función gama incompleta se refiere a la expresión (4.9) sin el denominador () en el integrando]. Existen tablas extensas de F(x; ) disponibles; en la tabla A.4 del apéndice se presenta una pequeña tabulación para 1, 2, . . . , 10 y x 1, 2, . . . , 15. Suponga que el tiempo de reacción X de un individuo seleccionado al azar a un estímulo tie- ne una distribución gama estándar con 2. Como P(a X b) F(b) F(a) cuando X es continua, P(3 X 5) F(5; 2) F(3; 2) 0.960 0.801 0.159 La probabilidad de que el tiempo de reacción sea de más de 4 s es P(X 4) 1 P(X 4) 1 F(4; 2) 1 0.908 0.092 ■ La función gama incompleta también se utiliza para calcular probabilidades que im- plican distribuciones gama no estándar. Estas probabilidades también se obtienen casi ins- tantáneamente con varios paquetes de software. Suponga que el tiempo de sobrevivencia de un ratón macho seleccionado al azar expuesto a 240 rads de radiación gama tiene una distribución gama con 8 y 15. (Datos en Sur- vival Distributions: Reliability Applications in the Biomedical Services, de A. J. Gross y V. Clark, sugiere 8.5 y 13.3.) El tiempo de sobrevivencia esperado es E(X) (8)(15) 120 semanas, en tanto que V(X) (8)(15)2 1800 y X 1 8 0 0 42.43 semanas. La probabilidad de que un ratón sobreviva entre 60 y 120 semanas es P(60 X 120) P(X 120) P(X 60) F(120/15; 8) F(60/15; 8) F(8; 8) F(4; 8) 0.547 0.051 0.496 La probabilidad de que un ratón sobreviva por lo menos 30 semanas es P(X 30) 1 P(X 30) 1 P(X 30) 1 F(30/15; 8) 0.999 ■ Distribución ji cuadrada La distribución ji cuadrada es importante porque es la base de varios procedimientos de in- ferencia estadística. El papel central desempeñado por la distribución ji cuadrada en infe- rencia se deriva de su relación con distribuciones normales (véase el ejercicio 71). Se discutirá esta distribución con más detalle en capítulos posteriores. 4.4 Distribuciones exponencial y gama 161 Ejemplo 4.23 Ejemplo 4.24 PROPOSICIÓN Si X tiene una distribución gama con parámetros y entonces con cualquier x 0, la función de distribución acumulativa de X es P(X x) F(x; , ) F x ; donde F(; ) es la función gama incompleta. c4_p130-183.qxd 3/12/08 4:04 AM Page 161
- 180. 162 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad DEFINICIÓN Sea un entero positivo. Se dice entonces que una variable aleatoria X tiene una dis- tribución ji cuadrada con parámetro si la función de densidad de probabilidad de X es la densidad gama con /2 y 2. La función de densidad de probabilidad de una variable aleatoria ji cuadrada es por lo tanto f(x; ) 2 /2 1 ( /2) x( /2)1 ex/2 x 0 (4.10) 0 x 0 El parámetro se llama número de grados de libertad (gl) de X. A menudo se uti- liza el símbolo 2 en lugar de “ji cuadrada”. EJERCICIOS Sección 4.4 (59-71) 59. Sea X el tiempo entre dos llegadas sucesivas a la ventanilla de autopago de un banco local. Si X tiene una distribución ex- ponencial con 1 (la cual es idéntica a una distribución gama estándar con 1), calcule lo siguiente: a. El tiempo esperado entre dos llegadas sucesivas. b. La desviación estándar del tiempo entre dos llegadas su- cesivas. c. P(X 4) d. P(2 X 5) 60. Sea X la distancia (m) que un animal recorre desde el sitio de su nacimiento hasta el primer territorio vacante que encuen- tra. Suponga que ratas canguro con etiqueta en la cola, X tie- ne una distribución exponencial con parámetro 0.01386 (como lo sugiere el artículo “Competition and Dispersal from Multiple Nests”, Ecology, 1997: 873-883). a. ¿Cuál es la probabilidad de que la distancia sea cuando mucho de 100 m? ¿Cuándo mucho de 200? ¿Entre 100 y 200 m? b. ¿Cuál es la probabilidad de que la distancia exceda la distancia media por más de dos desviaciones estándar? c. ¿Cuál es el valor de la distancia mediana? 61. La amplia experiencia con ventiladores de un tipo utiliza- dos en motores diesel ha sugerido que la distribución ex- ponencial proporciona un buen modelo del tiempo hasta la falla. Suponga que el tiempo medio hasta la falla es de 25 000 horas. ¿Cuál es la probabilidad de que a. Un ventilador seleccionado al azar dure por lo menos 20 000 horas? ¿Cuándo mucho 30 000 horas? ¿Entre 20 000 y 30 000 horas? b. ¿Exceda la duración de un ventilador el valor medio por más de dos desviaciones estándar? ¿Más de tres desvia- ciones estándar? 62. El artículo “Microwave Observations of Daily Antarctic Sea- Ice Edge Expansion and Contribution Rates” (IEEE Geosci. and Remote Sensing Letters, 2006: 54-58) establece que “la distribución del avance/retroceso diarios del hielo marino con respecto a cada sensor es similar y es aproximadamente una exponencial doble”. La distribución exponencial doble pro- puesta tiene una función de densidad f(x) 0.5e|x| para x . La desviación estándar se da como 40.9 km. a. ¿Cuál es el valor del parámetro ? b. ¿Cuál es la probabilidad de que la extensión del cambio del hielo marino esté dentro de una desviación estándar del valor medio? 63. Un consumidor está tratando de decidir entre dos planes de llamadas de larga distancia. El primero aplica una sola tari- fa de 10¢ por minuto, en tanto que el segundo cobra una ta- rifa de 99¢ por llamadas hasta de 20 minutos y luego 10¢ por cada minuto adicional que exceda de 20 (suponga que las llamadas que duran un número no entero de minutos son cobradas proporcionalmente a un cargo por minuto entero). Suponga que la distribución de duración de llamadas del consumidor es exponencial con parámetro . a. Explique intuitivamente cómo la selección del plan de llama- das deberá depender de cuál sea la duración de las llamadas. b. ¿Cuál plan es mejor si la duración esperada de las llama- das es de 10 minutos? ¿Y de 15 minutos? [Sugerencia: Sea h1(x) el costo del primer plan cuando la duración de las llamadas es de x minutos y sea h2(x) la función de costo del segundo plan. Dé expresiones para estas dos funciones de costo y luego determine el costo esperado de cada plan.] 64. Evalúe lo siguiente: a. (6) b. (5/2) c. F(4; 5) (la función gama incompleta) d. F(5; 4) e. F(0; 4) 65. Si X tiene una distribución gama estándar con 7 evalúe lo siguiente: a. P(X 5) b. P(X 5) c. P(X 8) d. P(3 X 8) e. P(3 X 8) f. P(X 4 o X 6) 66. Suponga que el tiempo empleado por un estudiante seleccio- nado al azar que utiliza una terminal conectada a un sistema de computadoras de tiempo compartido tiene una distribu- ción gama con media de 20 min y varianza de 80 min2 . a. ¿Cuáles son los valores de y ? b. ¿Cuál es la probabilidad de que un estudiante utilice la terminal durante cuando mucho 24 min? c. ¿Cuál es la probabilidad de que un estudiante utilice la terminal durante entre 20 y 40 min? Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 162
- 181. Las familias de distribuciones normal, gama (incluida la exponencial) y uniforme propor- cionan una amplia variedad de modelos de probabilidad de variables continuas, pero exis- ten muchas situaciones prácticas en las cuales ningún miembro de estas familias se adapta bien a un conjunto de datos observados. Los estadísticos y otros investigadores han desarro- llado otras familias de distribuciones que a menudo son apropiadas en la práctica. Distribución Weibull El físico sueco Waloddi Weibull introdujo la familia de distribuciones Weibull en 1939; su artículo de 1951 “A Statistical Distribution Function of Wide Applicability” (J. Applied Me- chanics, vol. 18: 293-297) discute varias aplicaciones. 4.5 Otras distribuciones continuas 163 67. Suponga que cuando un transistor de cierto tipo se somete a una prueba de duración acelerada, la duración X (en sema- nas) tiene una distribución gama acelerada con media de 24 semanas y desviación estándar de 12 semanas. a. ¿Cuál es la probabilidad de que un transistor dure entre 12 y 24 semanas? b. ¿Cuál es la probabilidad de que un transistor dure cuan- do mucho 24 semanas? ¿Es la mediana de la distribu- ción de duración menor que 24? ¿Por qué si o por qué no? c. ¿Cuál es el 99o percentil de la distribución de duración? d. Suponga que la prueba termina en realidad después de t semanas. ¿Qué valor de t es tal que sólo el 0.5% de todos los transistores continuarán funcionando al término de la prueba? 68. El caso especial de la distribución gama en la cual es un entero positivo n se llama distribución Erlang. Si se reem- plaza por 1/ en la expresión (4.8), la función de densi- dad de probabilidad Erlang es f(x; , n) ( ( n x )n 1 1 e ) ! x x 0 0 x 0 Se puede demostrar que si los tiempos entre eventos sucesi- vos son independientes, cada uno con distribución exponen- cial con parámetro , entonces el tiempo total que transcurre antes de que ocurran los siguientes n eventos tiene una fun- ción de densidad de probabilidad f(x; , n). a. ¿Cuál es el valor esperado de X? Si el tiempo (en minu- tos) entre llegadas de clientes sucesivos está exponen- cialmente distribuido con 0.5, ¿cuánto tiempo se puede esperar que transcurra antes de que llegue el déci- mo cliente? b. Si el tiempo entre llegadas de clientes está exponencial- mente distribuido con 0.5, ¿cuál es la probabilidad de que el décimo cliente (después del que acaba de lle- gar) llegue dentro de los siguientes 30 min? c. El evento {X t} ocurre si y sólo si ocurren n eventos en el siguiente t. Use el hecho de que el número de even- tos que ocurren en un intervalo de duración t tiene una distribución de Poisson con parámetro t para escribir una expresión (que implique probabilidades de Poisson) para la función de distribución acumulativa de Erlang F(t; , n) P(X t). 69. Un sistema consta de cinco componentes idénticos conecta- dos en serie como se muestra: En cuanto un componente falla, todo el sistema lo hace. Su- ponga que cada componente tiene una duración que está ex- ponencialmente distribuida con 0.01 y que los componentes fallan de manera independiente uno de otro. Defina los eventos Ai {el componente i-ésimo dura por lo menos t horas}, i 1, . . . , 5, de modo que los Ai son even- tos independientes. Sea X el tiempo al cual el sistema fa- lla, es decir, la duración más corta (mínima) entre los cinco componentes. a. ¿A qué evento equivale el evento {X t} que implique A1, . . . , A5? b. Utilizando la independencia de los eventos Ai, calcule P(X t). Luego obtenga F(t) P(X t) y la función de densidad de probabilidad de X. ¿Qué tipo de distribu- ción tiene X? c. Suponga que existen n componentes y cada uno tiene una duración exponencial con parámetro . ¿Qué tipo de distribución tiene X? 70. Si X tiene una distribución exponencial con parámetro , derive una expresión general para el (100p)o percentil de la distribución. Luego especifique cómo obtener la mediana. 71. a. ¿A qué evento equivale el evento {X2 y} que implique a X misma? b. Si X tiene una distribución normal estándar, use el inciso a) para escribir la integral que es igual a P(X2 y). Lue- go derive con respecto a y para obtener la función de den- sidad de probabilidad de X2 [el cuadrado de una variable N(0, 1)]. Por último, demuestre que X2 tiene una distribución ji cuadrada con 1 grados de libertad [véase (4.10)]. [Sugerencia: Use la siguiente identidad.] d d y b(y) a(y) f(x) dx f[b(y)] b(y) f[a(y)] a(y) 1 2 3 4 5 Ï Ì Ó Ï Ì Ó Ï Ì Ó 4.5 Otras distribuciones continuas c4_p130-183.qxd 3/12/08 4:04 AM Page 163
- 182. 164 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad En algunas situaciones, existen justificaciones teóricas para la pertinencia de la distri- bución Weibull, pero en muchas aplicaciones f(x; , ) simplemente proporciona una con- cordancia con los datos observados con valores particulares de y . Cuando 1, la función de densidad de probabilidad se reduce a la distribución exponencial (con 1/), de modo que la distribución exponencial es un caso especial tanto de la distribución gama como de la distribución Weibull. No obstante, existen distribuciones gama que no son Wei- bull y viceversa, por lo que una familia no es un subconjunto de la otra. Tanto como pueden ser variadas para obtener diferentes formas distribucionales, como se ilustra en la fi- gura 4.28. es un parámetro de escala, así que diferentes valores alargan o comprimen la gráfica en la dirección x. Si se integra para obtener E(X) y E(X2 ) se tiene 1 1 2 2 1 2 1 1 2 El cálculo de y 2 requiere por lo tanto el uso de la función gama. La integración x 0 f(y; , ) dy es fácil de realizar para obtener la función de distribu- ción acumulativa de X. En años recientes la distribución Weibull ha sido utilizada para modelar emisiones de va- rios contaminantes de motores. Sea X la cantidad de emisiones de NOx (g/gal) de un mo- tor de cuatro tiempos de un tipo seleccionado al azar y suponga que X tiene una distribución Weibull con 2 y 10 (sugeridos por la información que aparece en el artículo “Quantification of Variability and Uncertainty in Lawn and Garden Equipment NOx and Total Hydrocarbon Emission Factors”, J. of the Air and Waste Management As- soc., 2002: 435-448). La curva de densidad correspondiente se ve exactamente como la de la figura 4.28 con 2, 1 excepto que ahora los valores 50 y 100 reemplazan a 5 y 10 en el eje horizontal (debido a que es un “parámetro de escala”). Entonces P(X 10) F(10; 2, 10) 1 e(10/10) 2 1 e1 0.632 Asimismo, P(X 25) 0.998, así que la distribución está concentrada casi por completo en valores entre 0 y 25. El valor c, el cual separa 5% de todos los motores que emiten las más grandes cantidades de NOx del 95% restante, satisface 0.95 1 e(c/10) 2 Aislando el término exponencial en un lado, tomando logaritmos y resolviendo la ecuación resultante se obtiene c 17.3 como el 95o percentil de la distribución de emisiones. ■ DEFINICIÓN Se dice que una variable aleatoria X tiene una distribución Weibull con parámetros y ( 0, 0) si la función de densidad de probabilidad de X es f(x; , ) x1 e(x /) x 0 (4.11) 0 x 0 La función de distribución acumulativa de una variable aleatoria de Weibull con pa- rámetros y es 0 x 0 F(x; , ) 1 e(x/) x 0 (4.12) Ejemplo 4.25 Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 164
- 183. En situaciones prácticas, un modelo de Weibull puede ser razonable excepto que el valor de X más pequeño posible puede ser algún valor que no se supone sea cero (esto también se aplicaría a un modelo gama). La cantidad puede entonces ser considerada co- mo un tercer parámetro de la distribución, lo cual es lo que Weibull hizo en su trabajo ori- ginal. Con, por ejemplo, 3, todas las curvas que aparecen en la figura 4.28 se desplazarían 3 unidades a la derecha. Esto equivale a decir que X tiene la función de densidad de probabilidad (4.11) de modo que la función de distribución acumulativa de X se obtiene reemplazando x en (4.12) por x . Sea X la pérdida de peso por corrosión de una pequeña placa de aleación de magnesio cuadrada sumergida durante 7 días en una solución inhibida acuosa al 20% de MgBr2. Su- ponga que la pérdida de peso mínima posible es 3 y que el exceso X 3 sobre esta mínima tiene una distribución Weibull con 2 y 4. (Este ejemplo se consideró en “Practical Applications of the Weibull Distribution”, Industrial Quality Control, agosto de 1964: 71-78; los valores de y se consideraron como 1.8 y 3.67, respectivamente, aun cuando en el artículo se utilizó una selección de parámetros un poco diferente.) La función de distribución acumulativa de X es entonces 0 x 3 F(x; , , ) F(x; 2, 4, 3) 1 e[(x3)/4] 2 x 3 4.5 Otras distribuciones continuas 165 Ejemplo 4.26 0.5 1 0 5 10 f(x) 2 0 4 6 8 0.5 0 1.0 1.5 2.0 2.5 f(x) x x a = 2, b = 1 a = 2, b = 0.5 a = 1, b = 1 (exponencial) a = 10, b = 2 a = 10, b = 1 a = 10, b = 0.5 Figura 4.28 Curvas de densidad Weibull. Ï Ì Ó c4_p130-183.qxd 3/12/08 4:04 AM Page 165
- 184. 166 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad Por consiguiente, P(X 3.5) 1 F(3.5; 2, 4, 3) e0.0156 0.985 y P(7 X 9) 1 e2.25 (1 e1 ) 0.895 0.632 0.263 ■ Distribución lognormal Hay que tener cuidado aquí; los parámetros y no son la media y la desviación estándar de X sino de ln(X). Se puede demostrar que la media y varianza de X son E(X) e 2 /2 V(X) e2 2 (e 2 1) En el capítulo 5, se presenta una justificación teórica para esta distribución en cone- xión con el Teorema del Límite Central, pero como con cualesquiera otras distribuciones, se puede utilizar la lognormal como modelo incluso en la ausencia de semejante justificación. La figura 4.29 ilustra gráficas de la función de densidad de probabilidad lognormal; aunque una curva normal es simétrica, una curva lognormal tiene una asimetría positiva. Como el ln(X) tiene una distribución normal, la función de distribución acumulativa de X puede ser expresada en términos de la función de distribución acumulativa (z) de una variable aleatoria normal estándar Z. DEFINICIÓN Se dice que una variable aleatoria no negativa X tiene una distribución lognormal si la variable aleatoria Y ln(X) tiene una distribución normal. La función de densidad de probabilidad resultante de una variable aleatoria lognormal cuando el ln(X) está normalmente distribuido con parámetros y es f(x; , ) 2 1 x e[ln(x)] 2 /(2 2 ) x 0 0 x 0 F(x; , ) P(X x) P[ln(X) ln(x)] PZ ln(x) ln(x) , x 0 (4.13) Ï ÌÓ 0.05 0 0.10 0.15 0.20 0.25 0 5 10 15 20 25 f(x) x m = 1, s = 1 m = 3, s = 1 m = 3, s = √3 Figura 4.29 Curvas de densidad lognormal. c4_p130-183.qxd 3/12/08 4:04 AM Page 166
- 185. La distribución lognormal se utiliza con frecuencia como modelo de varias propiedades de materiales. El artículo “Reliability of Wood Joist Floor Systems with Creep” (J. of Structu- ral Engr., 1995: 946-954) sugiere que la distribución lognormal con 0.375 y 0.25 es un modelo factible de X el módulo de elasticidad (MDE, en 106 lb/pulg2 ) de sistemas de piso de viguetas de madera de pino grado #2. La media y varianza del módulo de elasti- cidad son E(X) e0.375 (0.25) 2 /2 e0.40625 1.50 V(X) e0.8125 (e0.0625 1) 0.1453 La probabilidad de que el módulo de elasticidad esté entre uno y dos es P(1 X 2) P(ln(1) ln(X) ln(2)) P(0 ln(X) 0.693) P Z (1.27) ( 1.50) 0.8312 ¿Qué valor de c es tal que sólo el 1% de todos los sistemas tienen un módulo de elasticidad que excede c? Se desea el valor de c con el cual 0.99 P(X c) P Z con la cual (ln(c) 0.375)/0.25 2.33 y c 2.605. Por lo tanto, 2.605 es el 99o percentil de la distribución del módulo de elasticidad. ■ Distribución beta Todas las familias de distribuciones continuas estudiadas hasta ahora, excepto la distribu- ción uniforme, tienen densidad positiva a lo largo de un intervalo infinito (aunque por lo ge- neral la función de densidad se reduce con rapidez a cero más allá de unas cuantas desviaciones estándar de la media). La distribución beta proporciona densidad positiva sólo para X en un intervalo de longitud finita. In(c) 0.375 0.25 0.693 0.375 0.25 0 0.375 0.25 La figura 4.30 ilustra varias funciones de densidad de probabilidad beta estándar. Las gráfi- cas de la función de densidad de probabilidad son similares, excepto que están desplazadas y luego alargadas o comprimidas para ajustarse al intervalo [A, B]. A menos que y sean enteros, la integración de la función de densidad de probabilidad para calcular probabilida- des es difícil. Se deberá utilizar una tabla de la función beta incompleta o un programa de computadora apropiado. La media y varianza de X son A (B A) 2 (B A)2 ( )2 ( 1) 4.5 Otras distribuciones continuas 167 DEFINICIÓN Se dice que una variable aleatoria X tiene una distribución beta con parámetros , (ambos positivos), A y B si la función de densidad de probabilidad de X es f(x; , , A, B) B 1 A ( ( ) ( ) ) B x A A 1 B B A x 1 A x B 0 de lo contrario El caso A 0, B 1 da la distribución beta estándar. Ejemplo 4.27 Ï ÌÓ c4_p130-183.qxd 3/12/08 4:04 AM Page 167
- 186. 168 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad Los gerentes de proyectos a menudo utilizan un método llamado PERT (técnica de revisión y evaluación de programas) para coordinar las diversas actividades que conforman un gran proyecto. (Una aplicación exitosa ocurrió en la construcción de la nave espacial Apolo.) Una suposición estándar en el análisis PERT es que el tiempo necesario para completar cualquier actividad particular una vez que se ha iniciado tiene una distribución beta con A el tiem- po optimista (si todo sale bien) y B tiempo pesimista (si todo sale mal). Suponga que al construir una casa unifamiliar, el tiempo X (en días) necesario para echar los cimientos tie- ne una distribución beta con A 2, B 5, 2 y 3. Entonces, /( ) 0.4, así que E(X) 2 (3)(0.4) 3.2. Con estos valores de y , la función de densidad de pro- babilidad de X es una función polinomial simple. La probabilidad de que se requieran a lo sumo tres días para echar los cimientos es P(X 3) 3 2 1 3 1 4 !2 ! ! x 3 2 5 3 x 2 dx 2 4 7 3 2 (x 2)(5 x)2 dx 2 4 7 1 4 1 1 2 1 7 0.407 ■ La distribución beta estándar se utiliza comúnmente para modelar la variación en la proporción o porcentaje de una cantidad que ocurre en diferentes muestras, tal como la pro- porción de un día de 24 horas que un individuo está despierto o la proporción de un cierto elemento químico en un compuesto. 0.2 0.4 0.6 0.8 1 1 2 3 4 5 0 0.5 2 0.5 5 2 x f(x; , ) Figura 4.30 Curvas de densidad beta estándar. Ejemplo 4.28 EJERCICIOS Sección 4.5 (72-86) 72. La duración X (en cientos de horas) de un tipo de tubo de vacío tiene una distribución de Weibull con parámetros 2 y 3. Calcule lo siguiente: a. E(X) y V(X) b. P(X 6) c. P(1.5 X 6) (Esta distribución de Weibull se sugiere como modelo de tiempo de servicio en “On the Assessment of Equipment Reliability: Trading Data Collection Costs for Precision”, J. Engr. Manuf., 1991: 105-109.) 73. Los autores del artículo “A Probabilistic Insulation Life Mo- del for Combined Thermal-Electrical Stresses” (IEEE Trans. on Elect. Insulation, 1985: 519-522) expresa que “la distri- bución de Weibull se utiliza mucho en problemas estadísti- cos relacionados con el envejecimiento de materiales sólidos aislantes sometidos a envejecimiento y esfuerzo”. Proponen el uso de la distribución como modelo del tiempo (en ho- ras) hasta la falla de especímenes aislantes sólidos someti- dos a voltaje de CA. Los valores de los parámetros dependen del voltaje y temperatura, suponga 2.5 y 200 (va- lores sugeridos por datos que aparecen en el artículo). c4_p130-183.qxd 3/12/08 4:04 AM Page 168
- 187. 4.5 Otras distribuciones continuas 169 a. ¿Cuál es la probabilidad de que la duración de un espé- cimen sea cuando mucho de 250? ¿De menos de 250? ¿De más de 300? b. ¿Cuál es la probabilidad de que la duración de un espé- cimen esté entre 100 y 250? c. ¿Qué valor es tal que exactamente 50% de todos los es- pecímenes tengan duraciones que sobrepasen ese valor? 74. Sea X el tiempo (en 101 semanas) desde el envío de un producto defectuoso hasta que el cliente lo devuelve. Supon- ga que el tiempo de devolución mínimo es 3.5 y que el excedente X 3.5 sobre el mínimo tiene una distribución de Weibull con parámetros 2 y 1.5 (véase el artículo Industrial Quality Control, citado en el ejemplo 4.26). a. ¿Cuál es la función de distribución acumulativa de X? b. ¿Cuáles son el tiempo de devolución esperado y la va- rianza del tiempo de devolución? [Sugerencia: Primero obtenga E(X 3.5) y V(X 3.5).] c. Calcule P(X 5). d. Calcule P(5 X 8). 75. Si X tiene una distribución de Weibull con la función de den- sidad de probabilidad de la expresión (4.11), verifique que (1 1/). [Sugerencia: En la integral para E(X) cambie la variable y (x/) , de modo que x y1/ .] 76. a. En el ejercicio 72, ¿cuál es la duración mediana de los tubos? [Sugerencia: Use la expresión (4.12).] b. En el ejercicio 74, ¿cuál es el tiempo de devolución mediano? c. Si X tiene una distribución de Weibull con la función de distribución acumulativa de la expresión (4.12), obtenga una expresión general para el percentil (100p)o de la dis- tribución. d. En el ejercicio 74, la compañía desea negarse a aceptar devoluciones después de t semanas. ¿Para qué valor de t sólo el 10% de todas las devoluciones serán rechazadas? 77. Los autores del artículo del cual se extrajeron los datos en el ejercicio 1.27 sugirieron que un modelo de probabilidad razonable de la duración de las brocas era una distribución lognormal con 4.5 y 0.8. a. ¿Cuáles son el valor medio y la desviación estándar de la duración? b. ¿Cuál es la probabilidad de que la duración sea cuando mucho de 100? c. ¿Cuál es la probabilidad de que la duración sea por lo menos de 200? ¿De más de 200? 78. El artículo “On Assessing the Accuracy of Offshore Wind Turbine Reliability-Based Design Loads from the Environ- mental Contour Method” (Intl. J. of Offshore and Polar Engr., 2005: 132-140) propone la distribución de Weibull con 1.817 y 0.863 como modelo de una altura (m) de olas significativa durante una hora en un sitio. a. ¿Cuál es la probabilidad de que la altura de las olas sea cuando mucho de 0.5 m? b. ¿Cuál es la probabilidad de que la altura de las olas ex- ceda su valor medio por más de una desviación estándar? c. ¿Cuál es la mediana de la distribución de la altura de las olas? d. Para 0 p 1, dé una expresión general para el percen- til (100p)o de la distribución de altura de olas. 79. Sea X la potencia mediana por hora (en decibeles) de se- ñales de radio transmitidas entre dos ciudades. Los autores del artículo “Families of Distributions for Hourly Median Power and Instantaneous Power of Received Radio Sig- nals” (J. Research National Bureau of Standards, vol. 67D, 1963: 753-762) argumentan que la distribución lognormal proporciona un modelo de probabilidad razonable para X. Si los valores de parámetros son 3.5 y 1.2, calcu- le lo siguiente: a. El valor medio y la desviación estándar de la potencia recibida. b. La probabilidad de que la potencia recibida esté entre 50 y 250 dB. c. La probabilidad de que X sea menor que su valor medio. ¿Por qué esta probabilidad no es de 0.5? 80. a. Use la ecuación (4.13) para escribir una fórmula para la mediana ~ de la distribución lognormal. ¿Cuál es la me- diana de la distribución de potencia del ejercicio 79? b. Recordando que z es la notación para el percentil 100(1 ) de la distribución normal estándar, escriba una expresión para el percentil 100(1 ) de la distri- bución lognormal. En el ejercicio 79, ¿qué valor exce- derá la potencia recibida sólo 5% del tiempo? 81. Una justificación teórica basada en el mecanismo de falla de cierto material sustenta la suposición de que la resisten- cia dúctil X de un material tiene una distribución lognormal. Suponga que los parámetros son 5 y 0.1. a. Calcule E(X) y V(X). b. Calcule P(X 125). c. Calcule P(110 X 125). d. ¿Cuál es el valor de la resistencia dúctil mediana? e. Si diez muestras diferentes de un acero de aleación de es- te tipo se sometieran a una prueba de resistencia, ¿cuántas esperaría que tengan una resistencia de por lo menos 125? f. Si 5% de los valores de resistencia más pequeños fueran inaceptables, ¿cuál sería la resistencia mínima aceptable? 82. El artículo “The Statistics of Phytotoxic Air Pollutants” (J. Royal Stat. Soc., 1989:183-198) sugiere la distribución lognormal como modelo de la concentración de SO2 sobre un cierto bosque. Suponga que los valores de parámetro son 1.9 y 0.9. a. ¿Cuáles son el valor medio y la desviación estándar de la concentración? b. ¿Cuál es la probabilidad de que la concentración sea cuando mucho de 10? ¿De entre 5 y 10? 83. ¿Qué condición en relación con y es necesaria para que la función de densidad de probabilidad beta estándar sea si- métrica? 84. Suponga que la proporción X de área en un cuadrado selec- cionado al azar que está cubierto por cierta planta tiene una distribución beta estándar con 5 y 2. a. Calcule E(X) y V(X). b. Calcule P(X 0.2). c. Calcule P(0.2 X 0.4). d. ¿Cuál es la proporción esperada de la región de mues- treo no cubierta por la planta? 85. Si X tiene una densidad beta estándar con parámetros y . a. Verifique la fórmula para E(X) dada en la sección. b. Calcule E[(1 X)m ]. Si X representa la proporción de una sustancia compuesta de un ingrediente particular, ¿cuál es la proporción esperada que no se compone de ese ingrediente? c4_p130-183.qxd 3/12/08 4:04 AM Page 169
- 188. 170 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad Un investigador a menudo ha obtenido una muestra numérica x1, x2, . . . , xn y desea saber si es factible que provenga de una distribución de población de un tipo particular (p. ej., de una distribución normal). Entre otras cosas, muchos procedimientos formales de inferen- cia estadística están basados en la suposición de que la distribución de población es de un tipo específico. El uso de un procedimiento como esos es inapropiado si la distribución de pro- babilidad subyacente existente difiere en gran medida del tipo supuesto. Además, el enten- dimiento de la distribución subyacente en ocasiones puede dar una idea de los mecanismos físicos implicados en la generación de los datos. Una forma efectiva de verificar una suposi- ción distribucional es construir una gráfica de probabilidad. La esencia de una gráfica como ésa es que si la distribución en la cual está basada es correcta, los puntos en la gráfica queda- rán casi en una línea recta. Si la distribución real es bastante diferente de la utilizada para cons- truir la curva, los puntos deberán apartarse sustancialmente de un patrón lineal. Percentiles muestrales Los detalles implicados al construir gráficas de probabilidad difieren un poco de una fuen- te a otra. La base de la construcción es una comparación entre percentiles de los datos mues- trales y los percentiles correspondientes de la distribución considerada. Recuérdese que el percentil (100p)o de una distribución continua con función de distribución acumulativa F() es el número (p) que satisface F( (p)) p. Es decir, (p) es el número sobre la escala de medición de modo que el área bajo la curva de densidad a la izquierda de (p) es p. Por lo tanto el percentil 50o (0.5) satisface F( (0.5)) 0.5 y el percentil 90o satisface F( (0.9)) 0.9. Considere como ejemplo la distribución normal estándar, para la cual la función de distribución acumulativa es (). En la tabla A.3 del apéndice, el 20o percentil se halla lo- calizando la fila y columna en la cual aparece 0.2000 (o un número tan cerca de él como es posible) en el interior de la tabla. Como 0.2005 aparece en la intersección de la fila 0.8 y la columna 0.04, el 20o percentil es aproximadamente 0.84. Asimismo el 25o percentil de la distribución normal estándar es (utilizando interpolación lineal) aproximadamente 0.675. En general, los percentiles muestrales se definen del mismo modo que se definen los percentiles de una distribución de población. El 50o percentil muestral deberá separarse del 50% más pequeño de la muestra del 50% más grande, el 90o percentil deberá ser tal que el 90% de la muestra quede debajo de ese valor y el 10% quede sobre ese valor, y así de ma- nera sucesiva. Desafortunadamente, se presentan problemas cuando en realidad se trata de calcular los percentiles muestrales de una muestra particular de n observaciones. Si, por ejemplo, n 10, se puede separar 20% de estos valores o 30% de los datos, pero no hay ningún valor que separe con exactitud 23% de estas diez observaciones. Para ir más allá, se requiere una definición operacional de percentiles muestrales (este es un lugar donde dife- rentes personas hacen cosas un poco diferentes). Recuérdese que cuando n es impar, la me- diana muestral o el 50o percentil muestral es el valor medio en la lista ordenada, por ejemplo, el sexto valor más grande cuando n 11. Esto equivale a considerar la observa- ción media como la mitad en la mitad inferior de los datos y la mitad en la mitad superior. Asimismo, supóngase que n 10. Entonces, si a este tercer valor más pequeño se le da el nombre de 25o percentil, ese valor se está considerando como la mitad en el grupo inferior (compuesto de las dos observaciones más pequeñas) y la mitad en el grupo superior (las siete 86. Se aplica esfuerzo a un barra de acero de 20 pulg sujeta por cada extremo en una posición fija. Sea Y la distancia del extremo izquierdo al punto donde se rompe la barra. Su- ponga que Y/20 tiene una distribución beta estándar con E(Y) 10 y V(Y) 10 7 0 . a. ¿Cuáles son los parámetros de la distribución beta están- dar de interés? b. Calcule P(8 Y 12). c. Calcule la probabilidad de que la barra se rompa a más de 2 pulg de donde esperaba que se rompiera. 4.6 Gráficas de probabilidad c4_p130-183.qxd 3/12/08 4:05 AM Page 170
- 189. observaciones más grandes). Esto conduce a la siguiente definición general de percentiles muestrales. Una vez que se han calculado los valores porcentuales 100(i 0.5)/n(i 1, 2, . . . , n), se pueden obtener los percentiles muestrales correspondientes a porcentajes intermedios mediante interpolación lineal. Por ejemplo, si n 10, los porcentajes correspondientes a las observaciones muestrales ordenadas son 100(1 0.5)/10 5%, 100(2 0.5)/10 15%, 25%, . . . , y 100(10 0.5)/10 95%. El 10o percentil está entonces a la mitad entre el 5o percentil (observación muestral más pequeña) y el 15o (segunda observación más pe- queña). Para los propósitos, en este caso, tal interpolación no es necesaria porque una grá- fica de probabilidad se basa sólo en los porcentajes 100(i 0.5)/n correspondientes a las n observaciones muestrales. Gráfica de probabilidad Supóngase ahora que para los porcentajes 100(i 0.5)/n(i 1, . . . , n) se determinan los percentiles de una distribución de población especificada cuya factibilidad está siendo in- vestigada. Si la muestra en realidad se seleccionó de la distribución especificada, los per- centiles muestrales (observaciones muestrales ordenadas) deberán estar razonablemente próximos a los percentiles de distribución de población correspondientes. Es decir, con i 1, 2, . . . , n deberá haber una razonable concordancia entre la i-ésima observación muestral más pequeña y el [100(i 0.5)/n]o percentil de la distribución especificada. Considérense los (percentil poblacional, percentil muestral) pares, es decir, los pares , con i 1, . . . , n. Cada uno de esos pares se dibuja como un punto en un sistema de coor- denadas bidimensional. Si los percentiles muestrales se acercan a los percentiles de distri- bución de población correspondientes, el primer número en cada par será aproximadamente igual al segundo número. Los puntos dibujados se quedarán entonces cerca de una línea a 45°. Desviaciones sustanciales de los puntos dibujados con respecto a una línea a 45° hacen dudar de la suposición de que la distribución considerada es la correcta. Un experimentador conoce el valor de cierta constante física. El experimentador realiza n 10 mediciones independientes de este valor por medio de un dispositivo de medición particu- lar y anota los errores de medición resultantes (error valor observado valor verdade- ro). Estas observaciones aparecen en la tabla adjunta. Porcentaje 5 15 25 35 45 Percentil z 1.645 1.037 0.675 0.385 0.126 Observación muestral 1.91 1.25 0.75 0.53 0.20 Porcentaje 55 65 75 85 95 Percentil z 0.126 0.385 0.675 1.037 1.645 Observación muestral 0.35 0.72 0.87 1.40 1.56 i-ésima observación muestral más pequeña [100(i 0.5)/n]o percentil de la distribución 4.6 Gráficas de probabilidad 171 DEFINICIÓN Se ordenan las n observaciones muestrales de la más pequeña a la más grande. Enton- ces la observación i-ésima más pequeña en la lista se considera que es el [100(i 0.5)/n]o percentil muestral. Ejemplo 4.29 c4_p130-183.qxd 3/12/08 4:05 AM Page 171
- 190. 172 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad ¿Es factible que el error de medición de una variable aleatoria tenga una distribución nor- mal estándar? Los percentiles (z) normales estándares requeridos también se muestran en la tabla. Por lo tanto, los puntos en la gráfica de probabilidad son (1.645, 1.91), (1.037, 1.25), . . . , y (1.645, 1.56). La figura 4.31 muestra la gráfica resultante. Aunque los puntos se desvían un poco de la línea a 45°, la impresión predominante es que la línea se adapta a los puntos muy bien. La gráfica sugiere que la distribución normal estándar es un modelo de probabilidad razonable de error de medición. La figura 4.32 muestra una gráfica de pares (percentil z¸ observación) de una segunda muestra de diez observaciones. La línea a 45° da una buena adaptación a la parte media de la muestra pero no a los extremos. La gráfica tiene apariencia S bien definida. Las dos ob- servaciones muestrales más pequeñas son considerablemente más grandes que los percenti- les z correspondientes Valor observado Percentil z Línea a 45˚ 1.6 1.2 0.8 1.6 1.2 0.8 0.4 0.4 0.8 1.2 1.6 0.4 0.4 0.8 1.2 1.6 1.8 Figura 4.31 Gráficas de pares (percentil z, valor observado) con los datos del ejemplo 4.29: primera muestra. Valor observado Percentil z Línea a 45˚ 1.2 0.8 1.6 1.2 0.8 0.4 0.4 0.8 1.2 1. 6 0.4 0.4 0.8 1.2 Curva en forma de S Figura 4.32 Gráficas de pares (percentil z, valor observado) con los datos del ejemplo 4.29: segunda muestra. c4_p130-183.qxd 3/12/08 4:05 AM Page 172
- 191. (los puntos a la extrema izquierda de la gráfica están bien por arriba de la línea a 45°). Asimis- mo, las dos observaciones muestrales más grandes son mucho más pequeñas que los percen- tiles z asociados. Esta gráfica indica que la distribución normal estándar no sería una opción factible del modelo de probabilidad que dio lugar a estos errores de medición observados. ■ A un investigador en general no le interesa saber con exactitud si una distribución de probabilidad especificada, tal como la distribución normal estándar (normal con 0 y 1) o la distribución exponencial con 0.1, es un modelo factible de la distribución de población de la cual se seleccionó la muestra. En cambio, la cuestión es si algún miembro de una familia de distribuciones de probabilidad especifica un modelo factible, la familia de distribuciones normales, la familia de distribuciones exponenciales, la familia de distribu- ciones Weibull, y así sucesivamente. Los valores de los parámetros de una distribución casi nunca se especifican al principio. Si la familia de distribuciones Weibull se considera como modelo de datos de duración, ¿existen algunos valores de los parámetros y con los cuales la distribución de Weibull correspondiente se adapta bien a los datos? Afortunadamente, casi siempre es el caso de que sólo una gráfica de probabilidad bastará para evaluar la factibilidad de una familia completa. Si la gráfica se desvía sustancialmente de una línea recta, ningún miembro de la familia es factible. Cuando la gráfica es bastante recta, se requiere más tra- bajo para estimar valores de los parámetros que generen la distribución más razonable del tipo especificado. Habrá que enfocarse en una gráfica para verificar la normalidad. Tal gráfica es útil en trabajo aplicado porque muchos procedimientos estadísticos formales dan inferencias pre- cisas sólo cuando la distribución de población es por lo menos aproximadamente normal. Estos procedimientos en general no deben ser utilizados si la gráfica de probabilidad nor- mal muestra un alejamiento muy pronunciado de la linealidad. La clave para construir una gráfica de probabilidad normal que comprenda varios elementos es la relación entre los per- centiles (z) normales estándares y aquellos de cualquier otra distribución normal: ( percentil z correspondiente) Considérese primero el caso, 0. Si cada observación es exactamente igual al percentil normal correspondiente con algún valor de , los pares ( [percentil z], observación) que- dan sobre una línea a 45°, cuya pendientes es 1. Esto implica que los pares (percentil z, ob- servación) quedan sobre una línea que pasa por (0, 0) (es decir, una con intercepción y en 0) pero con pendiente en lugar de 1. El efecto del valor no cero de es simplemente cambiar la intercepción y de 0 a . percentil de una distribución normal (, ) La muestra adjunta compuesta de n 20 observaciones de voltaje de ruptura dieléctrica de un pedazo de resina epóxica apareció en el artículo “Maximum Likelihood Estimation in the 3-Parameter Weibull Distribution” (IEEE Trans. on Dielectrics and Elec. Insul., 4.6 Gráficas de probabilidad 173 Una gráfica de los n pares ([100(i 0.5)/n]o percentil z, observación i-ésima más pequeña) en un sistema de coordenadas bidimensional se llama gráfica de probabilidad nor- mal. Si las observaciones muestrales se extraen en realidad de una distribución normal con valor medio y desviación estándar , los puntos deberán quedar cerca de una línea recta con pendiente e intercepción en . Así pues, una gráfica en la cual los puntos quedan cerca de alguna línea recta sugiere que la suposición de una distribución de población normal es factible. Ejemplo 4.30 c4_p130-183.qxd 3/12/08 4:05 AM Page 173
- 192. 174 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad 1996: 43-55). Los valores de (i 0.5)/n para los cuales se requieren los percentiles z son (1 0.5)/20 0.025, (2 0.5)/20 0.075, . . . , y 0.975. Observación 24.46 25.61 26.25 26.42 26.66 27.15 27.31 27.54 27.74 27.94 Percentil z 1.96 1.44 1.15 0.93 0.76 0.60 0.45 0.32 0.19 0.06 Observación 27.98 28.04 28.28 28.49 28.50 28.87 29.11 29.13 29.50 30.88 Percentil z 0.06 0.19 0.32 0.45 0.60 0.76 0.93 1.15 1.44 1.96 La figura 4.33 muestra la gráfica de probabilidad normal resultante. La configuración en la gráfica es bastante recta, lo que indica que es factible que la distribución de la población de voltaje de ruptura dieléctrica es normal. Existe una versión alternativa de una curva de probabilidad normal en la cual el eje de los percentiles z es reemplazado por un eje de probabilidad no lineal. La graduación a escala de este eje se construye de modo que los puntos graficados de nuevo queden cerca de una lí- nea cuando la distribución muestreada es normal. La figura 4.34 muestra una gráfica como esa generada por MINITAB con los datos de voltaje de ruptura del ejemplo 4.30. –2 –1 25 24 0 1 2 26 27 28 29 30 31 Percentil z Voltaje Figura 4.33 Gráfica de probabilidad normal de la muestra de voltaje de ruptura dieléctrica. ■ 0.999 0.99 0.95 0.80 0.50 0.20 0.05 0.01 0.001 Probabilidad 24.2 25.2 26.2 27.2 28.2 29.2 30.2 31.2 Voltaje Figura 4.34 Gráfica de probabilidad normal de los datos de voltaje de ruptura generada por MINITAB. c4_p130-183.qxd 3/12/08 4:05 AM Page 174
- 193. Una distribución de población no normal a menudo puede ser colocada en una de las siguientes tres categorías: 1. Es simétrica y tiene “colas más livianas” que una distribución normal; es decir la curva de densidad declina con más rapidez en la cola de lo que lo hace una curva normal. 2. Es simétrica y con colas pesadas en comparación con una distribución normal. 3. Es asimétrica. Una distribución uniforme es de cola liviana, puesto que su función de densidad se reduce a cero afuera de un intervalo finito. La función de densidad f(x) 1/[(1 x2 )] en x es de cola pesada, puesto que 1/(1 x2 ) declina mucho menos rápidamente que ex2/2 . Las dis- tribuciones lognormal y Weibull se encuentran entre aquellas que son asimétricas. Cuando los puntos en una gráfica de probabilidad normal no se adhieren a una línea recta, la confi- guración con frecuencia sugerirá que la distribución de la población se encuentra en una ca- tegoría particular de estas tres categorías. Cuando la distribución de la cual se selecciona la muestra es de cola liviana, las ob- servaciones más grandes y más pequeñas en general no son tan extremas como podría espe- rarse de una muestra aleatoria normal. Visualícese una línea recta trazada a través de la parte media de la gráfica; los puntos a la extrema derecha tienden a estar debajo de la línea (va- lor observado el percentil z) en tanto que los puntos a la extrema izquierda de la gráfica tienden a quedar sobre la línea recta (valor observado percentil z). El resultado es una configuración en forma de S del tipo ilustrado en la figura 4.32. Una muestra tomada de una distribución de cola pesada también tiende a producir una gráfica en forma de S. Sin embargo, en contraste con el caso de cola liviana, el extremo iz- quierdo de la gráfica se curva hacia abajo (observado percentil z), como se muestra en la figura 4.35a). Si la distribución subyacente es positivamente asimétrica (una cola izquierda corta y una cola derecha larga), las observaciones muestrales más pequeñas serán más gran- des que las esperadas con una muestra normal y también lo serán las observaciones más grandes. En este caso, los puntos en ambos extremos de la gráfica quedarán sobre una línea recta que pasa por la parte media, que produce una configuración curvada, como se ilustra en la figura 4.35b). Una muestra tomada de una distribución lognormal casi siempre produ- cirá la configuración mencionada. Una gráfica de (percentil z, ln(x)) pares deberán parecer- se entonces a una línea recta. 4.6 Gráficas de probabilidad 175 Observación Percentil z a) Observación Percentil z b) Figura 4.35 Gráficas de probabilidad que sugieren una distribución no normal: a) una gráfica compatible con una distribución de cola pesada; b) una gráfica compatible con una distribución positivamente asimétrica. c4_p130-183.qxd 3/12/08 4:05 AM Page 175
- 194. Aun cuando la distribución de la población sea normal, los percentiles muestrales no coincidirán exactamente con los teóricos debido a la variabilidad del muestreo. ¿Qué tanto pueden desviarse los puntos de la gráfica de probabilidad de un patrón de línea recta antes de que la suposición de normalidad ya no sea factible? Esta no es una pregunta fácil de res- ponder. En general, es más probable que una pequeña muestra de una distribución normal produzca una gráfica con un patrón no lineal que una grande. El libro Fitting Equations to Data (véase la bibliografía del capítulo 13) presenta los resultados de un estudio de simulación en el cual se seleccionaron numerosas muestras de diferentes tamaños de distribuciones nor- males. Los autores concluyeron que en general varía mucho la apariencia de la gráfica de probabilidad con tamaños de muestra de menos de 30 y sólo con tamaños de muestra mu- cho más grandes en general predomina el patrón lineal. Cuando una gráfica está basada en un pequeño tamaño de muestra, sólo un alejamiento muy sustancial de la linealidad se de- berá considerar como evidencia concluyente de no normalidad. Un comentario similar se aplica a gráficas de probabilidad para comprobar la factibilidad de otros tipos de distribu- ciones. Más allá de la normalidad Considérese una familia de distribuciones de probabilidad que implica dos parámetros 1 y 2 y sea F(x; 1, 2) la función de distribución acumulativa correspondiente. La familia de dis- tribuciones normales es una de esas familias, con 1 , 2 y F(x; , ) [(x )/]. Otro ejemplo es la familia Weibull, con 1 , 2 y F(x; , ) 1 e(x/) Otra familia más de este tipo es la familia gama, para la cual la función de distribución acumulativa es una integral que implica la función gama incompleta que no puede ser ex- presada en cualquier forma más simple. Se dice que los parámetros 1 y 2 son parámetros de ubicación y escala, respecti- vamente, si F(x; 1, 2) es una función de (x 1)/ 2. Los parámetros y de la familia normal son los parámetros de ubicación y escala, respectivamente. Al cambiar la curva de densidad acampanada se desplaza a la derecha o izquierda y al cambiar se alarga o com- prime la escala de medición (la escala sobre el eje horizontal cuando se dibuja la función de densidad). La función de distribución acumulativa da otro ejemplo F(x; 1, 2) 1 ee(x 1 )/ 2 x Se dice que una variable aleatoria con esta función de distribución acumulativa tiene una distribución de valor extremo. Se utiliza en aplicaciones que implican la duración de un componente y la resistencia de un material. Aunque la forma de la función de distribución acumulativa de valor extremo a prime- ra vista pudiera sugerir que 1 es el punto de simetría de la función de densidad y por ende la media y la mediana, éste no es el caso. En cambio, P(X 1) F( 1; 1, 2) 1 e1 0.632, y la función de densidad f(x; 1, 2) F(x; 1, 2) es negativamente asimétrica (una larga cola inferior). Asimismo, el parámetro de escala 2 no es la desviación estándar ( 1 0.5772 2 y 1.283 2). Sin embargo, al cambiar el valor de 1 cambia la ubicación de la curva de densidad, mientras que al cambiar 2 cambia la escala del eje de medición. El parámetro de la distribución de Weibull es un parámetro de escala, pero no es un parámetro de ubicación. El parámetro en general se conoce como parámetro de forma. Un comentario similar es pertinente para los parámetros y de la distribución gama. En la forma usual, la función de densidad de cualquier miembro de o la distribución gama o Wei- bull es positiva con x 0 y cero de lo contrario. Un parámetro de ubicación puede ser in- troducido como tercer parámetro (se hizo esto para la distribución de Weibull) para desplazar la función de densidad de modo que sea positiva si x y cero de lo contrario. 176 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad c4_p130-183.qxd 3/12/08 4:05 AM Page 176
- 195. Cuando la familia considerada tiene sólo parámetros de ubicación y escala, el tema de si cualquier miembro de la familia es una distribución de población factible puede ser abor- dado vía una gráfica de probabilidad única de fácil construcción. Primero se obtienen los percentiles de la distribución estándar, una con 1 0 y 2 1, con los porcentajes 100 (i 0.5)/n (i 1, . . . , n). Los n pares (percentil estandarizado, observación) dan los puntos en la gráfica. Esto es exactamente lo que se hizo para obtener una gráfica de proba- bilidad normal ómnibus. Un tanto sorprendentemente, esta metodología puede ser aplicada para dar una gráfica de probabilidad Weibull ómnibus. El resultado clave es que X tiene una distribución de Weibull con parámetro de forma y parámetro de escala , entonces la va- riable transformada ln(X) tiene una distribución de valor extremo con parámetro de ubica- ción 1 ln() y parámetro de escala 1/. Así pues una gráfica de los pares (percentil estandarizado de valor extremo, ln(x)) que muestre un fuerte patrón lineal apoya la selec- ción de la distribución de Weibull como modelo de una población. Las observaciones adjuntas son de la duración (en horas) del aislamiento de aparatos eléc- tricos cuando la aceleración del esfuerzo térmico y eléctrico se mantuvo fijo a valores par- ticulares (“On the Estimation of Life of Power Apparatus Insulation Under Combined Electrical and Thermal Stress”, IEEE Trans. on Electrical Insulation, 1985: 70-78). Una gráfica de probabilidad de Weibull necesita calcular primero los percentiles 5o , 15o , . . . , y 95o de la distribución de valor extremo estándar. El (100p)o percentil (p) satisface p F( (p)) 1 ee (p) de donde (p) ln[ln(1 p)]. Percentil 2.97 1.82 1.25 0.84 0.51 x 282 501 741 851 1072 ln(x) 5.64 6.22 6.61 6.75 6.98 Percentil 0.23 0.05 0.33 0.64 1.10 x 1122 1202 1585 1905 2138 ln(x) 7.02 7.09 7.37 7.55 7.67 Los pares (2.97, 5.64), (1.82, 6.22), . . . , (1.10, 7.67) se dibujan como puntos en la fi- gura 4.36. La forma recta de la gráfica hacia la derecha argumenta firmemente a favor del uso de la distribución de Weibull como modelo de duración de aislamiento, una conclusión también alcanzada por el autor del citado artículo. 4.6 Gráficas de probabilidad 177 Ejemplo 4.31 3 5 8 7 6 2 1 0 1 ln(x) Percentil Figura 4.36 Gráfica de probabilidad Weibull de los datos de duración del aislamiento. ■ c4_p130-183.qxd 3/12/08 4:05 AM Page 177
- 196. 178 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad La distribución gama es un ejemplo de una familia que implica un parámetro de for- ma para el cual no hay ninguna transformación h(·) de tal suerte que h(X) tenga una distri- bución que dependa sólo de los parámetros de ubicación y escala. Para construir una gráfica de probabilidad primero se tiene que estimar el parámetro de forma de los datos muestrales (algunos métodos para realizar lo anterior se describen en el capítulo 6). En ocasiones un investigador desea saber si la variable transformada X tiene una distribución normal con al- gún valor de (por convención, 0 es idéntica a la transformación, en cuyo caso X tie- ne una distribución lognormal). El libro Graphical Methods for Data Analysis, citado en la bibliografía del capítulo 1, discute este tipo de problema así como también otros refinamien- tos de construcción de gráficas de probabilidad. Afortunadamente, la amplia disponibilidad de varias gráficas de probabilidad junto con paquetes de software estadísticos significa que el usuario con frecuencia puede evitar los detalles técnicos. EJERCICIOS Sección 4.6 (87-97) 87. La gráfica de probabilidad normal adjunta se construyó con una muestra de 30 lecturas de tensión de pantallas de malla localizadas detrás de la superficie de tubos de visualización de video utilizadas en monitores de computadora. ¿Parece factible que la distribución de tensión sea normal? 88. Considere las siguientes diez observaciones de duración de cojinetes (en horas): 152.7 172.0 172.5 173.3 193.0 204.7 216.5 234.9 262.6 422.6 Construya una gráfica de probabilidad normal y comente sobre la factibilidad de la distribución normal como mode- lo de la duración de cojinetes (datos de “Modified Moment Estimation for the Three-Parameter Lognormal Distribu- tion”, J. Quality Technology, 1985: 92-99). 89. Construya una gráfica de probabilidad normal con la siguien- te muestra de observaciones de espesor de recubrimiento de pintura de baja viscosidad (“Achieving a Target Value for a Manufacturing Process: A Case Study”, J. of Quality Tech- nology, 1992: 22-26). ¿Se sentiría cómodo estimando el es- pesor medio de la población con un método que supuso una distribución de población normal? 0.83 0.88 0.88 1.04 1.09 1.12 1.29 1.31 1.48 1.49 1.59 1.62 1.65 1.71 1.76 1.83 90. El artículo “A Probabilistic Model of Fracture in Concrete and Size Effects on Fracture Toughness” (Magazine of Con- crete Res., 1996: 311-320) da argumentos de por qué la dis- tribución de tenacidad a la fractura en especímenes de concreto deben tener una distribución de Weibull y presen- tar varios histogramas de datos a los que adaptan bien cur- vas de Weibull superpuestas. Considere la siguiente muestra de tamaño n 18 observaciones de tenacidad de concreto de alta resistencia (compatible con uno de los histogramas); también se dan los valores de pi (i 0.5)/18. Observación 0.47 0.58 0.65 0.69 0.72 0.74 pi 0.0278 0.0833 0.1389 0.1944 0.2500 0.3056 Observación 0.77 0.79 0.80 0.81 0.82 0.84 pi 0.3611 0.4167 0.4722 0.5278 0.5833 0.6389 Observación 0.86 0.89 0.91 0.95 1.01 1.04 pi 0.6944 0.7500 0.8056 0.8611 0.9167 0.9722 Construya una gráfica de probabilidad Weibull y comente acerca de ella. 91. Construya una gráfica de probabilidad normal con los datos de propagación de grietas por fatiga dados en el ejercicio 39 (capítulo 1). ¿Parece factible que la duración de la propaga- ción tenga una distribución normal? Explique. 92. El artículo “The Load-Life Relationship for M50 Bea- rings with Silicon Nitride Ceramic Balls” (Lubrication Engr., 1984: 153-159) reporta los datos adjuntos de dura- ción de cojinetes (millones de revs.) probados con una carga de 6.45 kN. 47.1 68.1 68.1 90.8 103.6 106.0 115.0 126.0 146.6 229.0 240.0 240.0 278.0 278.0 289.0 289.0 367.0 385.9 392.0 505.0 a. Construya una gráfica de probabilidad normal. ¿Es fac- tible la normalidad? b. Construya una gráfica de probabilidad de Weibull. ¿Es factible la familia de distribución Weibull? –2 –1 200 0 1 2 250 300 350 Percentil z Tensión c4_p130-183.qxd 3/12/08 4:05 AM Page 178
- 197. Ejercicios suplementarios 179 EJERCICIOS SUPLEMENTARIOS (98-128) 98. Sea X el tiempo que una cabeza de lectura/escritura re- quiere para localizar un registro deseado en un dispositivo de memoria de disco de computadora una vez que la cabe- za se ha colocado sobre la pista correcta. Si los discos giran una vez cada 25 milisegundos, una suposición razonable es que X está uniformemente distribuida en el intervalo [0, 25]. a. Calcule P(10 X 20). b. Calcule P(X 10). c. Obtenga la función de distribución acumulativa F(X). d. Calcule E(X) y X. 99. Una barra de 12 pulg que está sujeta por ambos extremos se somete a una cantidad creciente de esfuerzo hasta que se rompe. Sea Y la distancia del extremo izquierdo al punto donde ocurre la ruptura. Suponga que Y tiene la fun- ción de densidad de probabilidad f(y) 2 1 4y1 1 y 2 0 y 12 0 de lo contrario Calcule lo siguiente: a. La función de densidad de probabilidad de Y y dibújela. b. P(Y 4), P(Y 6) y P(4 Y 6) c. E(Y), E(Y2 ) y V(Y). d. La probabilidad de que el punto de ruptura ocurra a más de 2 pulg del punto de ruptura esperado. e. La longitud esperada del segmento más corto cuando ocurre la ruptura. 100. Sea X el tiempo hasta la falla (en años) de cierto compo- nente hidráulico. Suponga que la función de densidad de probabilidad de X es f(x) 32/(x 4)3 con x 0. a. Verifique que f(x) es una función de densidad de proba- bilidad legítima. b. Determine la función de distribución acumulativa. c. Use el resultado del inciso b) para calcular la probabi- lidad de que el tiempo hasta la falla esté entre dos y cin- co años. d. ¿Cuál el tiempo esperado hasta la falla? e. Si el componente tiene un valor de recuperación igual a 100/(4 x) cuando su tiempo para la falla es x, ¿cuál es el valor de recuperación esperado? 101. El tiempo X para la terminación de cierta tarea tiene una función de distribución acumulativa F(x) dada por 0 x 0 x 3 3 0 x 1 1 1 2 7 3 x 7 4 3 4 x 1 x 7 3 1 x 7 3 a. Obtenga la función de densidad de probabilidad f(x) y trace su gráfica. b. Calcule P(0.5 X 2). c. Calcule E(X). 93. Construya una gráfica de probabilidad que le permita evaluar la factibilidad de la distribución lognormal como modelo de los datos de cantidad de lluvia del ejercicio 83 (capítulo 1). 94. Las observaciones adjuntas son valores de precipitación du- rante marzo a lo largo de un periodo de 30 años en Minnea- polis-St. Paul. a. Construya e interprete una gráfica de probabilidad nor- mal con este conjunto de datos. b. Calcule la raíz cuadrada de cada valor y luego constru- ya una gráfica de probabilidad normal basada en estos datos transformados. ¿Parece factible que la raíz cuadra- da de la precipitación esté normalmente distribuida? c. Repita el inciso b) después de transformar por medio de raíces cúbicas. 95. Use un paquete de software estadístico para construir una grá- fica de probabilidad normal de los datos de resistencia última a la tensión dados en el ejercicio 13 del capítulo 1 y comente. 96. Sean y1, y2, . . . , yn, las observaciones muestrales ordenadas (con y1 como la más pequeña y yn como la más grande). Una verificación sugerida de normalidad es dibujar los pares (1 ((i 0.5)/n), yi). Suponga que se cree que las observa- ciones provienen de una distribución con media 0 y sean w1, . . . , wn los valores absolutos ordenados de las xi. Una gráfica medio normal es una gráfica de probabilidad de las wi. Más específicamente, como P(°Z° w) P(w w) 2(w) 1, una gráfica medio normal es una grá- fica de los pares (1 {[(i 0.5)/n 1]/2}, wi) La virtud de esta gráfica es que los valores apartados pequeños o grandes en la muestra original ahora aparecerán sólo en el extremo superior de la gráfica y no en ambos extremos. Construya una gráfica medio normal con la siguiente muestra de errores de medición y comente: 3.78, 1.27, 1.44, 0.39, 12.38, 43.40, 1.15, 3.96, 2.34, 30.84. 97. Las siguientes observaciones de tiempo de falla (miles de horas) se obtuvieron con una prueba de duración acelerada de 16 chips de circuitos integrados de un tipo: Use los percentiles correspondientes de la distribución exponencial con 1 para construir una gráfica de pro- babilidad. Luego explique por qué la gráfica valora la facti- bilidad de la muestra habiendo sido generada con cualquier distribución exponencial. 0.77 1.20 3.00 1.62 2.81 2.48 1.74 0.47 3.09 1.31 1.87 0.96 0.81 1.43 1.51 0.32 1.18 1.89 1.20 3.37 2.10 0.59 1.35 0.90 1.95 2.20 0.52 0.81 4.75 2.05 82.8 11.6 359.5 502.5 307.8 179.7 242.0 26.5 244.8 304.3 379.1 212.6 229.9 558.9 366.7 204.6 Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:05 AM Page 179
- 198. 180 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad 102. Se sabe que el voltaje de ruptura de un diodo seleccionado al azar de cierto tipo está normalmente distribuido con va- lor medio de 40 V y desviación estándar de 1.5 V. a. ¿Cuál es la probabilidad de que el voltaje de un solo diodo esté entre 39 y 42? b. ¿Qué valor es tal que sólo 15% de todos los diodos ten- gan voltajes que excedan ese valor? c. Si se seleccionan cuatro diodos independientemente, ¿cuál es la probabilidad de que por lo menos uno tenga un voltaje de más de 42? 103. El artículo “Computer Assisted Net Weight Control” (Qua- lity Progress, 1983: 22-25) sugiere una distribución normal con media de 137.2 oz y desviación estándar de 1.6 oz del contenido de frascos de cierto tipo. El contenido declarado fue de 135 oz. a. ¿Cuál es la probabilidad de que un solo frasco conten- ga más que el contenido declarado? b. Entre diez frascos seleccionados al azar, ¿cuál es la pro- babilidad de que por lo menos ocho contengan más del contenido declarado? c. Suponiendo que la media permanece en 137.2, ¿a qué valor se tendría que cambiar la desviación estándar de modo que 95% de todos los frascos contengan más que el contenido declarado? 104. Cuando tarjetas de circuito utilizadas en la fabricación de reproductores de discos compactos se someten a prueba, el porcentaje de tarjetas defectuosas es de 5%. Suponga que se recibió un lote de 250 tarjetas y que la condición de cualquier tarjeta particular es independiente de las demás. a. ¿Cuál es la probabilidad aproximada de que por lo menos 10% de las tarjetas en el lote sean defectuosas? b. ¿Cuál es la probabilidad aproximada de que haya exac- tamente 10 defectuosas en el lote? 105. El artículo “Characterization of Room Temperature Dam- ping in Aluminum-Indium Alloys” (Metallurgical Trans. 1993: 1611-1619) sugiere que el tamaño de grano de ma- triz A1 (m) de una aleación compuesta de 2% de indio podría ser modelado con una distribución normal con valor medio de 96 y desviación estándar de 14. a. ¿Cuál es la probabilidad de que el tamaño de grano ex- ceda de 100? b. ¿Cuál es la probabilidad de que el tamaño de grano esté entre 50 y 80? c. ¿Qué intervalo (a, b) incluye 90% central de todos los tamaños de grano (de modo que 5% esté por debajo de a y 5% por encima de b)? 106. El tiempo de reacción (en segundos) a un estímulo es una variable aleatoria continua con función de densidad de pro- babilidad f(x) 3 2 x 1 2 1 x 3 0 de lo contrario a. Obtenga la función de distribución acumulativa. b. ¿Cuál es la probabilidad de que el tiempo de reacción sea cuando mucho de 2.5 s? ¿De entre 1.5 y 2.5 s? c. Calcule el tiempo de reacción esperado. d. Calcule la desviación estándar del tiempo de reacción. e. Si un individuo requiere más de 1.5 s para reaccionar a una luz que se enciende y permanece encendida hasta que transcurre un segundo más o hasta que la persona reaccio- na (lo que suceda primero). Determine la cantidad de tiempo esperado de que la luz permanezca encendida. [Sugerencia: Sea h(X) el tiempo que la luz está encen- dida como una función del tiempo de reacción X.] 107. Sea X la temperatura a la cual ocurre una reacción química. Suponga que X tiene una función de densidad de probabilidad f(x) 1 9 (4 x2 ) 1 x 2 0 de lo contrario a. Trace la gráfica de f(x). b. Determine la función de distribución acumulativa y dibújela. c. ¿Es cero la temperatura mediana a la cual ocurre la reacción? Si no, ¿es la temperatura mediana menor o mayor que cero? d. Suponga que esta reacción es independientemente reali- zada una vez en cada uno de diez laboratorios diferentes y que la función de densidad de probabilidad del tiempo de reacción en cada laboratorio es como se da. Sea Y el número entre los diez laboratorios en los cuales la temperatura excede de uno. ¿Qué clase de distribución tiene Y? (Dé el nombre y valores de los parámetros.) 108. El artículo “Determination of the MTF of Positive Photore- sists Using the Monte Carlo Method” (Photographic Sci. and Engr., 1983: 254-260) propone la distribución exponen- cial con parámetro 0.93 como modelo de la distribución de una longitud de trayectoria libre de fotones (m) en cier- tas circunstancias. Suponga que éste es el modelo correcto. a. ¿Cuál es la longitud de trayectoria esperada y cuál es su desviación estándar? b. ¿Cuál es la probabilidad de que la longitud de trayecto- ria exceda de 3.0? ¿Cuál es la probabilidad de que la longitud de trayectoria esté entre 1.0 y 3.0? c. ¿Qué valor es excedido por sólo 10% de todas las lon- gitudes de trayectoria? 109. El artículo “The Prediction of Corrosion by Statistical Analysis of Corrosion Profiles” (Corrosion Science, 1985: 305-315) sugiere la siguiente función de distribución acumu- lativa de la profundidad X de la picadura más profunda en un experimento que implica la exposición de acero al man- ganeso de carbono a agua de mar acidificada. F(x; , ) ee(x)/ x Los autores proponen los valores 150 y 90. Su- ponga que éste es el modelo correcto. a. ¿Cuál es la probabilidad de que la profundidad de la pi- cadura más profunda sea cuando mucho de 150? ¿Cuándo mucho 300? ¿De entre 150 y 300? b. ¿Por debajo de qué valor será observada la profundidad de la picadura máxima en 90% de todos los experimentos? c. ¿Cuál es la función de densidad de X? d. Se puede demostrar que la función de densidad es unimo- dal (una sola cresta). ¿Por encima de qué valor sobre el eje de medición ocurre esta cresta? (Este valor es el modo.) e. Se puede demostrar que E(X) 0.5772 . ¿Cuál es la media de los valores dados de y y cómo se Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:05 AM Page 180
- 199. Ejercicios suplementarios 181 compara con la mediana y el modo? Trace la gráfica de la función de densidad. [Nota: Ésta se conoce como distribución de valor extremo más grande.] 110. Un componente tiene una duración X exponencialmente distribuida con parámetro . a. Si el costo de operación por unidad de tiempo es c, ¿cuál es el costo esperado de operación de este compo- nente durante el tiempo que dura? b. En lugar de un coeficiente de costos constante como en el inciso a), suponga que el coeficiente de costos es c(1 0.5eax ) con a 0, de modo que el costo por uni- dad de tiempo es menor que c cuando el componente es nuevo y se vuelve más caro a medida que el componen- te envejece. Ahora calcule el costo de operación espe- rado durante la duración del componente. 111. La moda de una distribución continua es el valor x* que in- crementa al máximo f(x). a. ¿Cuál es la moda de una distribución normal con pará- metros y ? b. ¿Tiene una sola moda la distribución uniforme con pa- rámetros A y B? ¿Por qué sí o por qué no? c. ¿Cuál es la moda de una distribución exponencial con parámetro ? (Trace una gráfica.) d. Si X tiene una distribución gama con parámetros y y 1, halle la moda [Sugerencia: ln[f(x)] se incremen- tará al máximo si y sólo si f(x) es, y puede ser más sim- ple considerar la derivada de ln[f(x)]. e. ¿Cuál es la moda de una distribución ji cuadrada con grados de libertad? 112. El artículo “Error Distribution in Navigation” (J. Institute of Navigation, 1971: 429-442) sugiere que una distribución exponencial reproduce con más o menos precisión a una distribución de frecuencia de errores positivos (magnitudes de errores). Sea X el error de posición lateral (millas náu- ticas), el cual puede ser positivo o negativo. Suponga que la función de densidad de probabilidad de X es f(x) (0.1)e .2°x° x a. Trace una gráfica de f(x) y compruebe que f(x) es una función de densidad de probabilidad legítima (demues- tre que se integra a 1). b. Obtenga la función de distribución acumulativa de X y trácela. c. Calcule P(X 0), P(X 2), P( 1 X 2), y la pro- babilidad de cometer un error de más de dos millas. 113. En algunos sistemas, un cliente es asignado a una o dos pres- tadoras de servicios. Si el tiempo para que el cliente sea aten- dido por la prestadora de servicios i tiene una distribución exponencial con parámetro i (i 1, 2) y p es la proporción de todos los clientes atendidos por la prestadora de servicios 1, entonces la función de densidad de probabilidad de X el tiempo para ser atendido de un cliente seleccionado al azar es f(x; 1, 2, p) p1e1 x (1 p)2e2 x x 0 0 de lo contrario Ésta a menudo se llama distribución hiperexponencial o ex- ponencial combinada. Esta distribución también se propone como modelo de la cantidad de lluvia en “Modeling Mon- soon Affected Rainfall of Pakistan by Point Processes” (J. Water Resources Planning and Mgmnt., 1992: 671-688). a. Verifique que f(x; 1, 2, p) es una función de densidad de probabilidad. b. ¿Cuál es la función de distribución acumulativa F(x; 1, 2, p)? c. Si f(x; 1, 2, p) es la función de densidad de probabili- dad de X, ¿cuál es E(X)? d. Utilizando el hecho de que E(X2 ) 2/2 cuando X tiene una distribución exponencial con parámetro , calcule E(X2 ) cuando X tiene la función de densidad de proba- bilidad f(x; 1, 2, p). Luego calcule V(X). e. El coeficiente de variación de una variable aleatoria (o dis- tribución) es CV /. ¿Cuál es CV para una variable aleatoria exponencial? ¿Qué puede decir sobre el valor de CV cuando X tiene una distribución hiperexponencial? f. ¿Cuál es el CV de una distribución Erlang con paráme- tros y n como se definen en el ejercicio 68? [Nota: En trabajo aplicado, el CV muestral se utiliza para decidir cuál de las tres distribuciones podría ser apropiada.] 114. Suponga que en un estado particular se permite que las per- sonas físicas que presentan su declaración de impuestos de- tallen sus deducciones sólo si el total de las deducciones detalladas es por lo menos de $5000. Sea X (en miles de dó- lares) el total de deducciones detalladas en un formulario seleccionado al azar. Suponga que X tiene la función de densidad de probabilidad f(x; ) k/x x 5 0 de lo contrario a. Encuentre el valor de k. ¿Qué restricción en es necesaria? b. ¿Cuál es la función de distribución acumulativa de X? c. ¿Cuál es la deducción total esperada en un formulario seleccionado al azar? ¿Qué restricción en es necesa- ria para que E(X) sea finita? d. Demuestre que ln(X/5) tiene una distribución exponen- cial con parámetro 1. 115. Sea Ii la corriente de entrada a un transistor e I0 la corrien- te de salida. En ese caso la ganancia de corriente es pro- porcional a ln(I0/Ii). Suponga que la constante de proporcionalidad es 1 (lo que conduce a seleccionar una unidad de medición particular), así que la ganancia de co- rriente X ln(I0/Ii). Suponga que X está normalmente distribuida con 1 y 0.05. a. ¿Qué tipo de distribución tiene la razón I0/Ii? b. ¿Cuál es la probabilidad de que la corriente de salida sea más de dos veces la corriente de entrada? c. ¿Cuáles son el valor esperado y la varianza de la razón de corriente de salida a corriente de entrada? 116. El artículo “Response of SiCf/Si3N4 Composites Under Static and Cyclic Loading-An Experimental and Statistical Analysis” (J. of Engr. Materials and Technology, 1997: 186-193) sugiere que la resistencia a la tensión (MPa) de compuestos en condiciones especificadas puede ser mode- lada por una distribución de Weibull con 9 y 180. a. Trace una gráfica de la función de densidad. b. ¿Cuál es la probabilidad de que la resistencia de un es- pécimen seleccionado al azar exceda de 175? ¿Sea de entre 150 y 175? c. Si se seleccionan al azar dos especímenes y sus resistencias son independientes entre sí, ¿cuál es la probabilidad de que por lo menos uno tenga una resistencia entre 150 y 175? Ï Ì Ó Ï Ì Ó c4_p130-183.qxd 3/12/08 4:05 AM Page 181
- 200. 182 CAPÍTULO 4 Variables aleatorias continuas y distribuciones de probabilidad d. ¿Qué valor de resistencia separa al 10% de todos los es- pecímenes más débiles del 90% restante? 117. Si Z tiene una distribución normal estándar, defina una nueva variable aleatoria Y como Y Z . Demuestre que Y tiene una distribución normal con parámetros y . [Sugerencia: Y y si y sólo si Z ? Use ésta para definir la función de distribución acumulativa de Y y luego derí- vela con respecto a y.] 118. a. Suponga que la duración X de un componente, medida en horas, tiene una distribución gama con parámetros y . Sea Y la duración medida en minutos. Deduzca la función de densidad de probabilidad de Y. [Sugerencia: Y y si y sólo si X y/60. Use esto para obtener la fun- ción de distribución acumulativa de Y y luego derívela pa- ra obtener la función de densidad de probabilidad.] b. Si X tiene una distribución gama con parámetros y , ¿cuál es la distribución de probabilidad de Y cX? 119. En los ejercicios 111 y 112, así como también en muchas otras situaciones, se tiene la función de densidad de proba- bilidad f(x) de X y se desea conocer la función de densidad de probabilidad de Y h(X). Suponga que h() es una fun- ción invertible, de modo que y h(x) se resuelve para x a fin de obtener x k(y). Entonces se puede demostrar que la función de densidad de probabilidad de Y es g(y) f [k(y)] °k(y)° a. Si X tiene una distribución uniforme con A 0 y B 1, derive la función de densidad de probabilidad de Y ln(X). b. Resuelva el ejercicio 117, utilizando este resultado. c. Resuelva el ejercicio 118(b), utilizando este resultado. 120. Basado en los datos del experimento de lanzamiento de dar- do, el artículo “Shooting Darts” (Chance, verano de 1997: 16-19) propuso que los errores horizontales y verticales al apuntar a un blanco deben ser independientes unos de otros, cada uno con una distribución normal con media 0 y varianza 2 . Se puede demostrar entonces que la distancia V del blanco al punto de aterrizaje es f(v) ev2/22 v 0 a. ¿De qué familia introducida en este capítulo es esta función de densidad de probabilidad? b. Si 20 mm (cerca del valor sugerido por el artículo), ¿Cuál es la probabilidad de que un dardo aterrice dentro de 25 mm (aproximadamente una pulg) del blanco? 121. El artículo “Three Sisters Give Birth on the Same Day” (Chance, primavera de 2001, 23-25) utilizó el hecho de que tres hermanas de Utah dieron a luz el 11 de marzo de 1998 como base para plantear algunas preguntas interesantes con respecto a coincidencias de fechas de nacimiento. a. No haciendo caso del año bisiesto y suponiendo que los otros 365 días son igualmente probables, ¿cuál es la probabilidad de que tres nacimientos seleccionados al azar ocurran el 11 de marzo? Asegúrese de indicar qué, si las hay, suposiciones adicionales está haciendo. b. Con las suposiciones utilizadas en el inciso a), ¿cuál es la probabilidad de que tres nacimientos seleccionados al azar ocurran el mismo día? c. El autor sugirió, basado en datos extensos, que el tiempo de gestación (tiempo entre la concepción y el nacimiento) podía ser modelado como si tuviera una distribución normal con valor medio de 280 días y desviación están- dar de 19.88 días. Las fechas esperadas para las tres her- manas de Utah fueron el 15 de marzo, el 1 de abril y el 4 de abril, respectivamente. Suponiendo que las tres fe- chas esperadas están en la media de la distribución, ¿cuál es la probabilidad de que los nacimientos ocurrie- ran el 11 de marzo? [Sugerencia: La desviación de la fe- cha de nacimiento con respecto a la fecha esperada está normalmente distribuida con media 0.] d. Explique cómo utilizaría la información del inciso c) para calcular la probabilidad de una fecha de nacimien- to común. 122. Sea X la duración de un componente, con f(x) y F(x) la fun- ción de densidad de probabilidad y la función de distribución acumulativa de X. La probabilidad de que el componente fa- lle en el intervalo (x, x x) es aproximadamente f(x) x. La probabilidad condicional de que falle en (x, x x) dado que ha durado por lo menos x es f(x) x/[1 F(x)]. Divi- diendo ésta entre x se produce la función de coeficiente de falla: r(x) 1 f(x F ) (x) Una función de coeficiente de falla creciente indica que la probabilidad de que los componentes viejos se desgasten es cada vez más grande, mientras que un coeficiente de falla decreciente evidencia una confiabilidad cada vez más grande con la edad. En la práctica, a menudo se supone una falla “en forma de tina de baño”. a. Si X está exponencialmente distribuida, ¿cuál es r(x)? b. Si X tiene una distribución de Weibull con parámetros y , ¿cuál es r(x)? ¿Con qué valores de parámetros se incrementará r(x)? ¿Con qué valores de parámetro de- crecerá r(x) con x? c. Como r(x)(d/dx)ln[1F(x)], ln[1F(x)] r(x) dx. Suponga r(x) 1 x 0 x 0 de lo contrario de modo que si un componente dura horas, durará por siempre (si bien parece irrazonable, este modelo puede ser utilizado para estudiar el “desgaste inicial”). ¿Cuá- les son la función de distribución acumulativa y la fun- ción de densidad de probabilidad de X? 123. Sea que U tenga una distribución uniforme en el intervalo [0, 1]. Entonces los valores observados que tienen esta dis- tribución se obtienen con un generador de números aleato- rios de computadora. Sea X (1/)ln(1 U). a. Demuestre que X tiene una distribución exponencial con parámetro . [Sugerencia: La función de distribu- ción acumulativa de X es F(x) P(X x); X x equi- vale a U ?] b. ¿Cómo utilizaría el inciso a) y un generador de números aleatorios para obtener valores observados derivados de una distribución exponencial con parámetro 10? 124. Considere una variable aleatoria con media y desviación estándar y sea g(X) una función especificada de X. La aproximación de la serie de Taylor de primer grado a g(X) en la cercanía de es g(X) g() g() (X ) v 2 Ï Ì Ó c4_p130-183.qxd 3/12/08 4:05 AM Page 182
- 201. Bibliografía 183 El miembro del lado derecho de esta ecuación es una función lineal de X. Si la distribución de X está concentrada en un in- tervalo a lo largo del cual g() es aproximadamente lineal [p. ej., x es aproximadamente lineal en (1, 2)], entonces la ecuación produce aproximaciones a E(g(X)) y V(g(X)). a. Dé expresiones para estas aproximaciones. [Sugeren- cia: Use reglas de valor esperado y varianza de una fun- ción lineal aX b.] b. Si el voltaje a través de un medio se mantiene fijo pero la corriente I es aleatoria, entonces la resistencia también será una variable aleatoria relacionada con I por R v/I. Si I 20 y I 0.5, calcule aproxima- ciones a R y R. 125. Una función g(x) es convexa si la cuerda que conecta dos puntos cualesquiera de su gráfica quedan sobre ésta. Cuan- do g(x) es derivable, una condición equivalente es que pa- ra cada x, la línea tangente en x queda por completo sobre o debajo de la gráfica. (Véanse las figuras a continuación.) ¿Cómo se compara g() g(E(X)) con E(g(X))? [Sugeren- cia: La ecuación de la línea tangente en x es y g() g() (x ). Use la condición de convexidad, sustituya x por X y considere los valores esperados. Nota: A menos que g(x) sea lineal, la desigualdad resultante (por lo general llamada desigualdad de Jensen) es estricta ( en lugar de ); es válida tanto con variables aleatorias conti- nuas como discretas.] 126. Si X tiene una distribución de Weibull con parámetros 2 y , demuestre que Y 2X2 /2 tiene una distribución ji cuadrada con 2. [Sugerencia: La función de distribución acumulativa de Y es P(Y y); exprese esta probabilidad en la forma P(X g(y)), use el hecho de que X tiene una fun- ción de distribución acumulativa de la forma de la expresión (4.12) y derive con respecto a y para obtener la función de densidad de probabilidad de Y.] 127. El registro crediticio de un individuo es un número calcu- lado basado en el historial crediticio de dicho individuo el cual ayuda a un prestamista a determinar cuánto se le pue- de prestar o qué límite de crédito debe ser establecido para una tarjeta de crédito. Un artículo en los Los Angeles Times presentó datos que sugerían que una distribución beta con parámetros A 150 y B 850, 8, 2 pro- porcionaría una aproximación razonable a la distribución de registros de crédito estadounidenses [Nota: Los regis- tros de crédito son valores enteros]. a. Sea X un registro estadounidense de crédito selecciona- do al azar. ¿Cuáles son el valor medio y la desviación estándar de esta variable aleatoria? ¿Cuál es la probabi- lidad de que X esté dentro de una desviación estándar de su valor medio? b. ¿Cuál es la probabilidad aproximada de que un registro seleccionado al azar excederá de 750 (lo que los presta- mistas consideran un muy buen registro)? 128. Sea V el volumen de lluvia y W el volumen de escurrimien- to (ambos en mm). De acuerdo con el artículo “Runoff Quality Analysis of Urban Catchments with Analytical Probability Models” (J. of Water Resource Planning and Management, 2006: 4-14), el volumen de escurrimiento será 0 si V d y será k(V d) si V vd. Aquí d es el volumen de almacenamiento en una depresión (una cons- tante) y k (también una constante) es el coeficiente de es- currimiento. El artículo citado propone una distribución exponencial con parámetro para V. a. Obtenga una expresión para la función de distribución acumulativa de W. [Nota: W no es ni puramente conti- nua ni puramente discreta; en cambio tiene una distri- bución “combinada” con un componente discreto en 0 y es continua con valores w 0.] b. ¿Cuál es la función de densidad de probabilidad de W con w 0? Úsela para obtener una expresión para el valor esperado de volumen de escurrimiento. Línea tangente x Bibliografía Bury, Kart, Statistical Distributions in Engineering, Cambridge Univ. Press, Cambridge, Inglaterra, 1999. Un estudio informa- tivo y fácil de leer de distribuciones y sus propiedades. Johnson, Norman, Samuel Kotz y N. Balakrishnan Continuous Univariate Distributions, vols. 1-2, Wiley, Nueva York, 1994. Estos dos volúmenes presentan un estudio exhaustivo de va- rias distribuciones continuas. Nelson, Wayne, Applied Life Data Analysis, Wiley, Nueva York, 1982. Presenta amplia discusión de distribuciones y métodos que se utilizan en el análisis de datos de vida útil. Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models and Applications (2a. ed.), Macmillan, NuevaYork, 1994. Una buena cobertura de las propiedades generales y distribuciones específicas. c4_p130-183.qxd 3/12/08 4:05 AM Page 183
- 202. Distribuciones de probabilidad conjunta y muestras aleatorias 5 184 INTRODUCCIÓN En los capítulos 3 y 4 se estudiaron modelos de probabilidad para una sola variable aleatoria. Muchos problemas de probabilidad y estadística implican diversas varia- bles aleatorias al mismo tiempo. En este capítulo, primero se discuten modelos de probabilidad del comportamiento conjunto (es decir, simultáneo) de diversas varia- bles aleatorias, con énfasis especial en el caso en el cual las variables son independien- tes una de otra. Enseguida se estudian los valores esperados de funciones de diversas variables aleatorias, incluidas la covarianza y la correlación como medidas del grado de asociación entre dos variables. Las últimas tres secciones del capítulo consideran funciones de n variables alea- torias X1, X2, . . . , Xn, con un enfoque especial en su promedio (X1 · · · Xn)/n. A cualquier función de esta clase, que por sí misma es una variable aleatoria, se le lla- ma estadística. Se utilizan métodos de probabilidad para obtener información sobre la distribución de un estadístico. El resultado principal de este tipo es el Teorema del Límite Central (TLC), la base de muchos procedimientos inferenciales que implican tamaños de muestra grandes c5_p184-226.qxd 3/12/08 4:07 AM Page 184
- 203. Existen muchas situaciones experimentales en las cuales más de una variable aleatoria será de interés para un investigador. Primero se consideran las distribuciones de probabilidad conjunta para dos variables aleatorias discretas, enseguida para dos variables continuas y por último para más de dos variables. Dos variables aleatorias discretas La función masa de probabilidad (fmp) de una sola variable aleatoria discreta X especifica cuánta masa de probabilidad está colocada en cada valor posible de X. La función masa de probabilidad conjunta de dos variables aleatorias discretas X y Y describe cuánta masa de pro- babilidad se coloca en cada par posible de valores (x, y). Una gran agencia de seguros presta servicios a numerosos clientes que han adquirido tanto una póliza de propietario de casa como una póliza de automóvil en la agencia. Por cada tipo de póliza, se debe especificar una cantidad deducible. Para una póliza de automóvil, las opciones son $100 y $250, mientras que para la póliza de propietario de casa, las opciones son 0, $100 y $200. Suponga que se selecciona al azar un individuo con ambos tipos de póli- za de los archivos de la agencia. Sea X la cantidad deducible sobre la póliza de auto y Y la cantidad deducible sobre la póliza de propietario de casa. Los posibles pares (X, Y) son entonces (100, 0), (100, 100), (100, 200), (250, 0), (250, 100) y (250, 200); la función masa de probabilidad conjunta especifica la probabilidad asociada con cada uno de estos pares, con cualquier otro par tiene probabilidad cero. Suponga que la tabla de probabilidad con- junta siguiente da la función masa de probabilidad conjunta: y p(x, y) | 0 100 200 x 100 | 0.20 0.10 0.20 250 | 0.05 0.15 0.30 Entonces p(100, 100) P(X 100 y Y 100) P($100 deducible sobre ambas pólizas) 0.10. La probabilidad P(Y 100) se calcula sumando las probabilidades de todos los pares (x, y) para los cuales y 100: P(Y 100) p(100, 100) p(250, 100) p(100, 200) p(250, 200) 0.75 ■ 5.1 Variables aleatorias conjuntamente distribuidas 185 5.1 Variables aleatorias conjuntamente distribuidas Ejemplo 5.1 DEFINICIÓN Sean X y Y dos variables aleatorias discretas definidas en el espacio muestral S de un experimento. La función masa de probabilidad conjunta p(x, y) se define para cada par de números (x, y) como p(x, y) P(X x y Y y) Debe cumplirse que p(x, y) 0 y x y p(x, y) 1. Ahora sea A cualquier conjunto compuesto de pares de valores (x, y) (p. ej., A {(x, y): x y 5} o {(x, y): máx(x, y) 3}). Entonces la probabilidad P[(X, Y) A] se obtiene sumando la función masa de probabilidad conjunta incluidos todos los pares en A: P[(X, Y) A] (x, y) A p(x, y) c5_p184-226.qxd 3/12/08 4:07 AM Page 185
- 204. La función masa de probabilidad de una de las variables sola se obtiene sumando p(x, y) con los valores de la otra variable. El resultado se llama función masa de probabilidad marginal cuando los valores p(x, y) aparecen en una tabla rectangular, las sumas son totales marginales (filas o columnas). Así pues para obtener la función masa de probabilidad marginal de X evaluada en, por ejem- plo, x 100, las probabilidades p(100, y) se suman con todos los valores posibles de y. Si se hace esto por cada valor posible de X se obtiene la función masa de probabilidad marginal de X sola (sin referencia a Y). Con las funciones masa de probabilidad marginal, se pueden calcular las probabilidades de eventos que implican sólo X o sólo Y. Los valores posibles de X son x 100 y x 250, por lo que si se calculan los totales en las filas de la tabla de probabilidad conjunta se obtiene pX(100) p(100, 0) p(100, 100) p(100, 200) 0.50 y pX(250) p(250, 0) p(250, 100) p(250, 200) 0.50 La función masa de probabilidad marginal de X es entonces pX(x) {0.5 x 100, 250 0 de lo contrario Asimismo, la función masa de probabilidad marginal de Y se obtiene con los totales de las columnas como ¨0.25 y 0, 100 pY(y) ©0.50 y 200 ª0 de lo contrario Por lo tanto, P(Y 100) pY(100) pY(200) 0.75 como antes. ■ Dos variables aleatorias continuas La probabilidad de que el valor observado de una variable aleatoria continua X esté en un conjunto unidimensional A (tal como un intervalo) se obtiene integrando la función de den- sidad de probabilidad f(x) a lo largo del conjunto A. Asimismo, la probabilidad de que el par (X, Y) de variables aleatorias continuas quede en un conjunto A en dos dimensiones (tal como un rectángulo) se obtiene integrando una función llamada función de densidad conjunta. 186 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias DEFINICIÓN Las funciones masa de probabilidad marginal de X y de Y, denotadas por pX(x) y pY(y), respectivamente, están dadas por pX(x) y p(x, y) pY(y) x p(x, y) DEFINICIÓN Sean X y Y variables aleatorias continuas. Una función de densidad de probabili- dad conjunta f(x, y) de estas dos variables es una función que satisface f(x, y) 0 y f(x, y) dx dy 1. Entonces para cualquier conjunto A en dos dimensiones P[(X, Y) A] A f(x, y) dx dy En particular, si A es el rectángulo {(x, y): a x b, c y d}, entonces P[(X, Y) A] P(a X b, c Y d) b a d c f(x, y) dy dx Ejemplo 5.2 (continuación del ejemplo 5.1) c5_p184-226.qxd 3/12/08 4:07 AM Page 186
- 205. Se puede considerar que f(x, y) especifica una superficie situada a una altura f(x, y) sobre el punto (x, y) en un sistema de coordenadas tridimensional. Entonces P[(X, Y) A] es el volumen debajo de esta superficie y sobre la región A, similar al área bajo una curva en el caso unidimensional. Esto se ilustra en la figura 5.1. Un banco dispone tanto de una ventanilla para automovilistas como de una ventanilla nor- mal. En un día seleccionado al azar, sea X la proporción de tiempo que la ventanilla para automovilistas está en uso (por lo menos un cliente está siendo atendido o está esperan- do ser atendido) y Y la proporción del tiempo que la ventanilla normal está en uso. Entonces el conjunto de valores posibles de (X, Y) es el rectángulo D {(x, y): 0 x 1, 0 y 1}. Suponga que la función de densidad de probabilidad conjunta de (X, Y ) está dada por f(x, y) { (x y2 ) 0 x 1, 0 y 1 0 de lo contrario Para verificar que ésta es una función de densidad de probabilidad legítima, obsérvese que f(x, y) 0 y f(x, y) dx dy 1 0 1 0 6 5 (x y2 ) dx dy 1 0 1 0 6 5 x dx dy 1 0 1 0 6 5 y2 dx dy 1 0 6 5 x dx 1 0 6 5 y2 dy 1 6 0 1 6 5 1 La probabilidad de que ninguna ventanilla esté ocupada más de un cuarto del tiempo es P0 X 1 4 , 0 Y 1 4 1/4 0 1/4 0 6 5 (x y2 ) dx dy 6 5 1/4 0 1/4 0 x dx dy 6 5 1/4 0 1/4 0 y2 dx dy 2 6 0 x 2 2 ° x1/4 x0 2 6 0 y 3 3 ° y1/4 y0 6 7 40 .0109 ■ Como con las funciones masa de probabilidad conjunta, con la función de densidad de probabilidad conjunta de X y Y, se puede calcular cada una de las dos funciones de densi- dad marginal. 6 5 5.1 Variables aleatorias conjuntamente distribuidas 187 Figura 5.1 P(X, Y) A volumen bajo la superficie de densidad sobre A. f(x, y) y x A Rectángulo sombreado Superficie f(x, y) Ejemplo 5.3 c5_p184-226.qxd 3/12/08 4:07 AM Page 187
- 206. La función de densidad de probabilidad marginal de X, la cual da la distribución de proba- bilidad del tiempo que permanece ocupada la ventanilla para automovilistas sin referencia a la ventanilla normal, es fX(x) f(x, y) dy 1 0 6 5 (x y2 ) dy 6 5 x 2 5 con 0 x 1 y 0 de lo contrario. La función de densidad de probabilidad marginal de Y es fY(y) {6 5 y2 3 5 0 y 1 0 de lo contrario Entonces P 1 4 Y 3 4 3/4 1/4 fY (y) dy 3 8 7 0 0.4625 ■ En el ejemplo 5.3, la región de densidad conjunta positiva fue un rectángulo, el cual facilitó el cálculo de las funciones de densidad de probabilidad marginal. Considere ahora un ejemplo en el cual la región de densidad positiva es más complicada. Una compañía de nueces comercializa latas de nueces combinadas de lujo que contienen almendras, nueces de acajú y cacahuates. Suponga que el peso neto de cada lata es exacta- mente de 1 lb, pero la contribución al peso de cada tipo de nuez es aleatoria. Como los tres pesos suman 1, un modelo de probabilidad conjunta de dos cualquiera da toda la informa- ción necesaria sobre el peso del tercer tipo. Sea X el peso de las almendras en una lata seleccionada y Y el peso de las nueces de acajú. Entonces la región de densidad positiva es D {(x, y): 0 x 1, 0 y 1, x y 1}, región sombreada ilustrada en la figura 5.2. Ahora sea la función de densidad de probabilidad conjunta de (X, Y) f(x, y) {24xy 0 x 1, 0 y 1, x y 1 0 de lo contrario 188 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Ejemplo 5.4 (continuación del ejemplo 5.3) DEFINICIÓN Las funciones de densidad de probabilidad marginal de X y Y, denotadas por fX(x) y fY(y), respectivamente, están dadas por fX(x) f(x, y) dy con x fY (y) f(x, y) dx con y Ejemplo 5.5 Figura 5.2 Región de densidad positiva para el ejemplo 5.5. x (0, 1) x (x, 1 x) (1, 0) y c5_p184-226.qxd 3/12/08 4:07 AM Page 188
- 207. Con cualquier x fija, f (x, y) se incrementa con y; con y fija, f (x, y) se incrementa con x. Esto es apropiado porque las palabras de lujo implican que la mayor parte de la lata deberá estar compuesta de almendras y nueces de acajú en lugar de cacahuates, así que la función de densidad deberá ser grande cerca del límite superior y pequeña cerca del origen. La super- ficie determinada por f(x, y) se inclina hacia arriba desde cero a medida que (x, y) se alejan de uno u otro eje. Claramente, f(x, y) 0. Para verificar la segunda condición sobre una función de den- sidad de probabilidad conjunta, recuérdese que una integral doble se calcula como una inte- gral iterada manteniendo una variable fija (tal como x en la figura 5.2), integrando con los valores de la otra variable localizados a lo largo de la línea recta que pasa a través de la variable fija y finalmente integrando todos los valores posibles de la variable fija. Así pues f(x, y) dy dx D f(x, y) dy dx 1 0 1x 0 24xy dy dx 1 0 24x y 2 2 ° y1x y0 dx 1 0 12x(1 x)2 dx 1 Para calcular la probabilidad de que los dos tipos de nueces conformen cuando mucho 50% de la lata, Sea A {(x, y): 0 x 1, 0 y 1, y x y 0.5}, como se muestra en la figura 5.3. Entonces P((X, Y) A) A f(x, y) dx dy 0.5 0 0.5x 0 24xy dy dx 0.0625 La función de densidad de probabilidad marginal de las almendras se obtiene manteniendo X fija en x e integrando la función de densidad de probabilidad conjunta f(x, y) a lo largo de la línea vertical que pasa por x: fX(x) f(x, y) dy { 1x 0 24xy dy 12x(1 x)2 0 x 1 0 de lo contrario Por simetría de f(x, y) y la región D, la función de densidad de probabilidad marginal de Y se obtiene reemplazando x y X en fX(x) por y y Y, respectivamente. ■ Variables aleatorias independientes En muchas situaciones, la información sobre el valor observado de una de las dos variables X y Y da información sobre el valor de la otra variable. En el ejemplo 5.1, la probabilidad marginal de X con x 250 fue de 0.5, como lo fue la probabilidad de que X 100. Sin embargo, si se sabe que el individuo seleccionado tuvo Y 0, entonces X 100 es cuatro veces más probable que X 250. Por lo tanto, existe dependencia entre las dos variables. 5.1 Variables aleatorias conjuntamente distribuidas 189 Figura 5.3 Calcule de P[(X, Y) A] para el ejemplo 5.5. x 1 1 x y 0 . 5 x y 1 A Región sombreada y 0.5 x c5_p184-226.qxd 3/12/08 4:07 AM Page 189
- 208. En el capítulo 2, se señaló que una forma de definir la independencia de dos eventos es vía la condición de que P(A B) P(A) P(B). A continuación se da una definición análoga de la independencia de dos variables aleatorias. La definición dice que dos variables son independientes si su función masa de probabili- dad conjunta o función de densidad de probabilidad conjunta es el producto de las dos funciones masa de probabilidad marginal o de las funciones de densidad de probabilidad marginal. En la situación de la agencia de seguros de los ejemplos 5.1 y 5.2, p(100, 100) 0.10 (0.5)(0.25) pX(100) pY(100) de modo que X y Y no son independientes. La independencia de X y Y requiere que toda entrada en la tabla de probabilidad conjunta sea el producto de las probabilidades margina- les que aparecen en la filas y columnas correspondientes. ■ Como f(x, y) tiene la forma de un producto, X y Y parecerían ser independientes. Sin embar- go, aunque fX(3 4) fY(3 4) 1 9 6, f( 3 4, 3 4) 0 1 9 6 1 9 6, de modo que las variables no son en rea- lidad independientes. Para que sean independientes f (x, y) debe tener la forma g(x) h(y) y la región de densidad positiva debe ser un rectángulo con sus lados paralelos a los ejes de coordenadas. ■ La independencia de dos variables aleatorias es más útil cuando la descripción del expe- rimento en estudio sugiere que X y Y no tienen ningún efecto entre ellas. Entonces, una vez que las funciones masa de probabilidad y de densidad de probabilidad marginales han sido especificadas, la función masa de probabilidad conjunta o la función de densidad de probabi- lidad conjunta es simplemente el producto de dos funciones marginales. Se desprende que P(a X b, c Y d) P(a X b) P(c Y d) Suponga que las duraciones de dos componentes son independientes entre sí y que la distri- bución exponencial de la primera duración es X1 con parámetro 1, mientras que la distribu- ción exponencial de la segunda es X2 con parámetro 2. Entonces la función de densidad de probabilidad conjunta es f(x1, x2) fX1 (x1) fX2 (x2) 1e1x1 2e2x2 12e1x12x2 x1 0, x2 0 0 de lo contrario Sean 1 1/1000 y 2 1/1200, de modo que las duraciones esperadas son 1000 y 1200 horas, respectivamente. La probabilidad de que ambas duraciones sean de por lo menos 1500 horas es P(1500 X1, 1500 X2) P(1500 X1) P(1500 X2) e1(1500) e2(1500) (0.2231)(0.2865) 0.0639 ■ 190 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias DEFINICIÓN Se dice que dos variables aleatorias X y Y son independientes si por cada par de valo- res x y y, p(x, y) pX(x) pY(y) cuando X y Y son discretas o (5.1) f(x, y) fX(x) fY(y) cuando X y Y son continuas Si (5.1) no se satisface con todos los pares (x, y), entonces se dice que X y Y son dependientes. Ejemplo 5.6 Ejemplo 5.8 Ejemplo 5.7 (continuación del ejemplo 5.5) c5_p184-226.qxd 3/12/08 4:07 AM Page 190
- 209. Más de dos variables aleatorias Para modelar el comportamiento conjunto de más de dos variables aleatorias, se amplía el concepto de una distribución conjunta de dos variables. En un experimento binomial, cada ensayo podría dar por resultado uno de sólo dos posibles resultados. Considérese ahora un experimento compuesto de n ensayos indepen- dientes e idénticos, en los que cada ensayo puede dar uno cualquiera de r posibles resulta- dos. Sea p1 P(resultado i en cualquier ensayo particular) y defínanse las variables aleatorias como Xi el número de ensayos que dan el resultado i(i 1, . . . , r). Tal expe- rimento se llama experimento multinomial y la función masa de probabilidad conjunta de X1, . . . , Xr se llama distribución multinomial. Utilizando un argumento de conteo análo- go al utilizado al derivar la distribución binomial, la función masa de probabilidad conjun- ta de X1, . . . , Xr, se puede demostrar que es p(x1, . . . , xr) { p1 x1 . . . pxr r xi 0, 1, 2, . . . , con x1 . . . xr n 0 de lo contrario El caso r 2 da la distribución binomial, con X1 número de éxitos y X2 n X1 número de fallas. Si se determina el alelo de cada una de diez secciones de un chícharo obtenidas indepen- dientemente y p1 P(AA), p2 P(Aa), p3 P(aa), X1 número de AA, X2 número de Aa y X3 número de aa, entonces la función masa de probabilidad multinomial para estas Xi es p(x1, x2, x3) px1 1 px2 2 px3 3 xi 0, 1, . . . y x1 x2 x3 10 con p1 p3 0.25, p2 0.5. P(X1 2, X2 5, X3 3) p(2, 5, 3) (0.25)2 (0.5)5 (0.25)3 0.0769 ■ Cuando se utiliza cierto método para recolectar un volumen fijo de muestras de roca en una región, existen cuatro tipos de roca. Sean X1, X2 y X3 la proporción por volumen de los tipos de roca 1, 2 y 3 en una muestra aleatoriamente seleccionada (la proporción del tipo de roca 4 es 1 X1 X2 X3, de modo que una variable X4 sería redundante). Si la función de densidad de probabilidad conjunta de X1, X2, X3 es f(x1, x2, x3) kx1x2(1 x3) 0 x1 1, 0 x2 1, 0 x3 1, x1 x2 x3 1 0 de lo contrario 10! 2! 5! 3! 10! (x1!)(x2!)(x3!) n! (x1!)(x2!) . . . (xr!) 5.1 Variables aleatorias conjuntamente distribuidas 191 DEFINICIÓN Si X1, X2, . . . , Xn son variables aleatorias discretas, la función masa de probabilidad conjunta de las variables es la función p(x1, x2, . . . , xn) P(X1 x1, X2 x2, . . . , Xn xn) Si las variables son continuas, la función de densidad de probabilidad conjunta de X1, . . . , Xn es la función f(x1, x2, . . . , xn) de modo que para n intervalos cualesquiera [a1, b1], . . . , [an, bn], P(a1 X1 b1, . . . , an Xn bn) b1 a1 . . . bn an f(x1, . . . , xn) dxn . . . dx1 Ejemplo 5.9 Ejemplo 5.10 c5_p184-226.qxd 3/12/08 4:07 AM Page 191
- 210. entonces k se determina como sigue 1 f(x1, x2, x3) dx3 dx2 dx1 1 0 1x1 0 1x1x2 0 kx1x2(1 x3) dx3 dx2 dx1 El valor de la integral iterada es k/144, por lo tanto k 144. La probabilidad de que las rocas de los tipos 1 y 2 integren más de 50% de la muestra es P(X1 X2 0.5) f(x1, x2, x3) dx3 dx2 dx1 0xi1 para i1, 2, 3 {x1x2x31, x1x20.5} 0.5 0 0.5x1 0 1x1x2 0 144x1x2(1 x3) dx3 dx2 dx1 0.6066 ■ La noción de independencia de más de dos variables aleatorias es similar a la noción de independencia de más de dos eventos. Así pues si las variables son independientes con n 4, entonces la función masa de proba- bilidad conjunta o función de densidad de probabilidad conjunta de dos variables cuales- quiera es el producto de las dos marginales y asimismo para tres variables cualesquiera y las cuatro variables juntas. Aún más importante, una vez que se dice que n variables son independientes, entonces la función masa de probabilidad conjunta o función de densidad de probabilidad conjunta es el producto de las n marginales. Si X1, . . . , Xn representan las duraciones de n componentes y éstos operan de manera inde- pendiente uno de otro y cada duración está exponencialmente distribuida con parámetro , entonces f(x1, x2, . . . , xn) (ex1 ) (ex2 ) . . . (exn ) n exi x1 0, x2 0, . . . , xn 0 0 de lo contrario Si estos n componentes constituyen un sistema que fallará en cuanto un solo componente lo haga, entonces la probabilidad de que el sistema dure más allá del tiempo t es P(X1 t, . . . , Xn t) ' t . . . ' t f(x1, . . . , xn) dx1 . . . dxn ' t ex1 dx1. . . ' t exn dxn (et )n ent Por consiguiente, P(duración del sistema t) 1 ent con t 0 192 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias DEFINICIÓN Se dice que las variables aleatorias X1, X2, . . . , Xn son independientes si para cada subconjunto Xi1 , Xi2 , . . . , Xik de las variables (cada par, cada tripleta, y así sucesiva- mente), la función masa de probabilidad conjunta o función de densidad de probabi- lidad conjunta del subconjunto es igual al producto de funciones masa de probabilidad o funciones de densidad de probabilidad marginales. Ejemplo 5.11 c5_p184-226.qxd 3/12/08 4:07 AM Page 192
- 211. lo que demuestra que la distribución de la duración del sistema es exponencial con paráme- tro n; el valor esperado de la duración del sistema es 1/n. ■ En muchas situaciones exponenciales que se considerarán en este libro, la indepen- dencia es una suposición razonable, de modo que la especificación de la distribución con- junta se reduce a decidir sobre distribuciones marginales apropiadas. Distribuciones condicionales Suponga X el número de defectos mayores en un automóvil nuevo seleccionado al azar y Y el número de defectos menores en el mismo auto. Si se sabe que el carro seleccionado tiene un defecto mayor, ¿cuál es ahora la probabilidad de que el carro tenga cuando mucho tres defectos menores?, es decir, ¿cuál es P(Y 3 | X 1)? Asimismo, si X y Y denotan las duraciones de los neumáticos delantero y trasero de una motocicleta y sucede que X 10 000 millas, ¿cuál es ahora la probabilidad de que Y sea cuando mucho de 15 000 millas y cuál es la duración esperada del neumático trasero “condicionada en” este valor de X? Preguntas de esta clase pueden ser respondidas estudiando distribuciones de probabilidad condicional. Obsérvese que la definición de fY | X(y | x) es igual a la de P(B | A), la probabilidad condi- cional de que B ocurra, dado que A ha ocurrido. Una vez que la función de densidad de pro- babilidad o la función masa de probabilidad ha sido determinada, preguntas del tipo planteado al principio de esta subsección pueden ser respondidas integrando o sumando a lo largo de un conjunto apropiado de valores Y. Reconsidere la situación del ejemplo 5.3 y 5.4 que implica X la proporción del tiempo que la ventanilla para automovilista de un banco está ocupada y Y la proporción análoga de ven- tanilla normal. La función de densidad de probabilidad condicional de Y dado que X 0.8 es fY°X(y°0.8) 1 1 . . 2 2 ( ( 0 0 . . 8 8 ) y 0 2 . ) 4 3 1 4 (24 30y2 ) 0 y 1 La probabilidad de que la ventanilla normal esté ocupada cuando mucho la mitad del tiem- po dado que X 0.8 es entonces P(Y 0.5°X 0.8) 0.5 fY°X(y°0.8) dy 0.5 0 3 1 4 (24 30y2 ) dy 0.390 Utilizando la función de densidad de probabilidad marginal de Y se obtiene P(Y 0.5) 0.350. Además E(Y) 0.6, mientras que la proporción esperada del tiempo que la ventani- lla normal está ocupada dado que X 0.8 (una expectativa condicional) es E(Y°X 0.8) y fY°X(y°0.8) dy 3 1 4 1 0 y(24 30y2 ) dy 0.574 ■ f(0.8, y) fX (0.8) 5.1 Variables aleatorias conjuntamente distribuidas 193 DEFINICIÓN Sean X y Y dos variables aleatorias continuas con función de densidad de probabili- dad conjunta f (x, y) y función de densidad de probabilidad marginal X fX(x). Entonces para cualquier valor x de X con el cual fX(x) 0, la función de densidad de proba- bilidad condicional de Y dado que X x es fY°X (y°x) f f ( X x ( , x y ) ) y Si X y Y son discretas, si en esta definición se reemplazan las funciones de densidad de probabilidad por funciones masa de probabilidad en esta definición da la función masa de probabilidad condicional de Y cuando X x. Ejemplo 5.12 c5_p184-226.qxd 3/12/08 4:07 AM Page 193
- 212. 194 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias EJERCICIOS Sección 5.1 (1-21) 1. Una gasolinería cuenta tanto con islas de autoservicio como de servicio completo. En cada isla, hay una sola bomba de gaso- lina sin plomo regular con dos mangueras. Sea X el número de mangueras utilizadas en la isla de autoservicio y en un tiempo particular y sea Y el número de mangueras en uso en la isla de servicio completo en ese tiempo. La función masa de probabi- lidad conjunta de X y Y aparece en la tabla adjunta. p(x, y) | 0 2 0 | 0.10 0.04 0.02 x 1 | 0.08 0.20 0.06 2 | 0.06 0.14 0.30 a. ¿Cuál es P(X 1 y Y 1)? b. Calcule P(X 1 y Y 1). c. Describa el evento (X 0 y Y 0) y calcule su proba- bilidad. d. Calcule la función masa de probabilidad marginal de X y Y. Utilizando pX(x), ¿cuál es P(X 1)? e. ¿Son X y Y variables aleatorias independientes? Explique. 2. Cuando un automóvil es detenido por una patrulla de segu- ridad, cada uno de los neumáticos es revisado en cuanto a desgaste y cada uno de los faros es revisado para ver si está apropiadamente alineado. Sean X el número de faros que necesitan ajuste y Y el número de neumáticos defectuosos. a. Si X y Y son independientes con pX(0) 0.5, pX(1) 0.3, pX(2) 0.2 y pY(0) 0.6, pY(1) 0.1, pY(2) pY(3) 0.05, pY(4) 0.2, muestre la función masa de probabi- lidad conjunta de (X, Y) en una tabla de probabilidad conjunta. b. Calcule P(X 1 y Y 1) con la tabla de probabilidad conjunta y verifique que es igual al producto P(X 1) P(Y 1). c. ¿Cuál es P(X Y 0) (la probabilidad de ninguna vio- lación)? d. Calcule P(X Y 1). 3. Un supermercado cuenta tanto con una caja rápida como con una superrápida. Sea X1 el número de clientes formados en la caja rápida a una hora particular del día y sea X2 el número de clientes formados en la caja superrápida a la misma hora. Suponga que la función masa de probabilidad de X1 y X2 es la que aparece en la tabla adjunta. x2 | 0 1 2 3 0 | 0.08 0.07 0.04 0.00 1 | 0.06 0.15 0.05 0.04 x1 2 | 0.05 0.04 0.10 0.06 3 | 0.00 0.03 0.04 0.07 4 | 0.00 0.01 0.05 0.06 a. ¿Cuál es P(X1 1, X2 1), es decir, la probabilidad de que haya exactamente un cliente en cada caja? b. ¿Cuál es P(X1 X2), es decir, la probabilidad de que los números de clientes en las dos cajas sean idénticos? c. Sea A el evento en que hay por lo menos dos clientes más en una caja que en la otra. Exprese A en función de X1 y X2 y calcule la probabilidad de este evento. d. ¿Cuál es la probabilidad de que el número total de clien- tes en las dos líneas sea exactamente cuatro? ¿Por lo menos cuatro? 4. Regrese a la situación descrita en el ejercicio 3. a. Determine la función masa de probabilidad marginal de X1 y enseguida calcule el número esperado de clientes formados en la caja rápida. b. Determine la función masa de probabilidad marginal de X2. c. Por inspección de las probabilidades P(X1 4), P(X2 0) y P(X1 4, X2 0), ¿son X1 y X2 variables aleatorias independientes? Explique. 5. El número de clientes que esperan en el servicio de envoltu- ra de regalos en una tienda de departamentos es una variable aleatoria X con valores posibles 0, 1, 2, 3, 4 y probabilidades correspondientes 0.1, 0.2, 0.3, 0.25, 0.15. Un cliente selec- cionado al azar tendrá 1, 2 ó 3 paquetes para envoltura con probabilidades de 0.6, 0.3 y 0.1, respectivamente. Sea Y el número total de paquetes que van a ser envueltos para los clientes que esperan formados en la fila (suponga que el número de paquetes entregado por un cliente es indepen- diente del número entregado por cualquier otro cliente). a. Determine P(X 3, Y 3), es decir, p(3, 3). b. Determine p(4, 11) 6. Sea X el número de cámaras digitales Canon vendidas durante una semana particular por una tienda. La función masa de probabilidad de X es x | 0 1 2 3 4 pX(x) | 0.1 0.2 0.3 0.25 0.15 El 60% de todos los clientes que compran estas cámaras también compran una garantía extendida. Sea Y el número de compradores durante esta semana que compran una garantía extendida. a. ¿Cuál es P(X 4, Y 2)? [Sugerencia: Esta probabili- dad es igual a P(Y 2|X 4) P(X 4); ahora piense en las cuatro compras como cuatro ensayos de un expe- rimento binomial, con el éxito en un ensayo correspon- diente a comprar una garantía extendida.] b. Calcule P(X Y). c. Determine la función masa de probabilidad conjunta de X y Y y luego la función masa de probabilidad marginal de Y. 7. La distribución de probabilidad conjunta del número X de carros y el número Y de autobuses por ciclo de señal en un carril de vuelta a la izquierda propuesto se muestra en la tabla de probabilidad conjunta anexa. p(x, y) | 0 2 0 | 0.025 0.015 0.010 1 | 0.050 0.030 0.020 2 | 0.125 0.075 0.050 x 3 | 0.150 0.090 0.060 4 | 0.100 0.060 0.040 5 | 0.050 0.030 0.020 y 1 y 1 c5_p184-226.qxd 3/12/08 4:07 AM Page 194
- 213. 5.1 Variables aleatorias conjuntamente distribuidas 195 a. ¿Cuál es la probabilidad de que haya exactamente un carro y exactamente un autobús durante un ciclo? b. ¿Cuál es la probabilidad de que haya cuando mucho un carro y cuando mucho un autobús durante un ciclo? c. ¿Cuál es la probabilidad de que haya exactamente un carro durante un ciclo? ¿Exactamente un autobús? d. Suponga que el carril de vuelta a la izquierda tiene una capacidad de cinco carros y un autobús que equivale a tres carros. ¿Cuál es la probabilidad de un exceso de vehículos durante un ciclo? e. ¿Son X y Y variables aleatorias independientes? Explique. 8. Un almacén cuenta con 30 componentes de un tipo, de los cua- les 8 fueron surtidos por el proveedor 1, 10 por el proveedor 2 y 12 por el proveedor 3. Seis de éstos tienen que ser seleccio- nados al azar para un ensamble particular. Sea X el número de componentes del proveedor 1 seleccionados, Y el núme- ro de componentes del proveedor 2 seleccionados y que p(x, y) denote la función masa de probabilidad conjunta de X y Y. a. ¿Cuál es p(3, 2)? [Sugerencia: La probabilidad de que cada muestra de tamaño 6 sea seleccionada es igual. Por consiguiente, p(3, 2) (número de resultados con X 3 y Y 2)/(el número total de resultados). Ahora use la regla de producto de conteo para obtener el numerador y denominador.] b. Utilizando la lógica del inciso a), obtenga p(x, y). (Esto puede ser considerado como un muestreo con distribu- ción hipergeométrica multivariante sin reemplazo de una población finita compuesta de más de dos categorías.) 9. Se supone que cada neumático delantero de un tipo particu- lar de vehículo está inflado a una presión de 26 lb/pulg2 . Suponga que la presión de aire real en cada neumático es una variable aleatoria: X para el neumático derecho y Y para el izquierdo con función de densidad de probabilidad conjunta f(x, y) {K(x2 y2 ) 20 x 30, 20 y 30 0 de lo contrario a. ¿Cuál es el valor de K? b. ¿Cuál es la probabilidad de que ambos neumáticos estén inflados a menos presión? c. ¿Cuál es la probabilidad de que la diferencia en la pre- sión del aire entre los dos neumáticos sea de cuando mucho 2 lb/pulg2 ? d. Determine la distribución (marginal) de la presión del aire en el neumático derecho. e. ¿Son X y Y variables aleatorias independientes? 10. Annie y Alvie acordaron encontrarse entre las 5:00 P.M. y las 6:00 P.M. para cenar en un restaurante local de comida salu- dable. Sea X la hora de llegada de Annie y Y la hora de llegada de Alvie. Suponga que X y Y son independientes con cada una distribuida uniformemente en el intervalo [5, 6]. a. ¿Cuál es la función de densidad de probabilidad conjun- ta de X y Y? b. ¿Cuál es la probabilidad de que ambos lleguen entre las 5:15 y las 5:45? c. Si el primero en llegar espera sólo 10 min antes de irse a comer a otra parte, ¿cuál es la probabilidad de que cenen en el restaurante de comida saludable? [Sugerencia: El evento de interés es A {(x, y):°x y° 1 6}.] 11. Dos profesores acaban de entregar los exámenes finales para su copia. Sea X el número de errores tipográficos en el examen del primer profesor y Y el número de tales errores en el segundo examen. Suponga que X tiene una distribución de Poisson con parámetro , que Y tiene una distribución de Poisson con parámetro y que X y Y son independientes. a. ¿Cuál es la función masa de probabilidad conjunta de X y Y? b. ¿Cuál es la probabilidad de que se cometa cuando mucho un error en ambos exámenes combinados? c. Obtenga una expresión general para la probabilidad de que el número total de errores en los dos exámenes sea m (don- de m es un entero no negativo). [Sugerencia: A {(x, y): x y m} {(m, 0), (m 1, 1), . . . , (1, m 1), (0, m)}. Ahora sume la función masa de probabilidad con- junta a lo largo de (x, y) A y use el teorema binomial, el cual dice que m k0 ak bmk (a b)m con cualquier a, b.] 12. Dos componentes de una minicomputadora tienen la siguiente función de densidad de probabilidad conjunta de sus vidas útiles X y Y: f(x, y) {xex(1y) x 0 y y 0 0 de lo contrario a. ¿Cuál es la probabilidad de que la vida útil X del primer componente exceda de 3? b. ¿Cuáles son las funciones de densidad de probabilidad marginal de X y Y? ¿Son las dos vidas útiles indepen- dientes? Explique. c. ¿Cuál es la probabilidad de que la vida útil de por lo menos un componente exceda de 3? 13. Tiene dos focos para una lámpara particular. Sea X la vida útil del primer foco y Y la vida útil del segundo (ambas en miles de horas). Suponga que X y Y son inde- pendientes y que cada una tiene una distribución exponen- cial con parámetro 1. a. ¿Cuál es la función de densidad de probabilidad conjun- ta de X y Y? b. ¿Cuál es la probabilidad de que cada foco dure cuando mucho 1000 horas (es decir, X 1 y Y 1)? c. ¿Cuál es la probabilidad de que la vida útil total de los dos focos sea cuando mucho de 2? [Sugerencia: Trace una figura de la región A {(x, y): x 0, y 0, x y 2} antes de integrar.] d. ¿Cuál es la probabilidad de que la vida útil total esté entre 1 y 2? 14. Suponga que tiene diez focos y que la vida útil de cada uno es independiente de la de los demás y que la distribución de cada vida útil es exponencial con parámetro . a. ¿Cuál es la probabilidad de que los diez focos fallen antes del tiempo t? b. ¿Cuál es la probabilidad de que exactamente k de los diez focos fallen antes del tiempo t? c. Suponga que nueve de los focos tienen vidas útiles exponencialmente distribuidas con parámetro y que el foco restante tiene una vida útil que está exponencial- mente distribuida con parámetro (fue hecho por otro fabricante). ¿Cuál es la probabilidad de que exactamen- te cinco de los diez focos fallen antes del tiempo t? m k c5_p184-226.qxd 3/12/08 4:07 AM Page 195
- 214. Previamente se vio que cualquier función h(X) de una sola variable aleatoria X es por sí misma una variable aleatoria. Sin embargo, para calcular E[h(X)], no fue necesario obtener la distribución de probabilidad de h(X); en cambio, E[h(X)] se calculó como un promedio ponderado de valores de h(x), donde la función de ponderación fue la función masa de pro- babilidad p(x) o la función de densidad de probabilidad f(x) de X. Se obtiene un resultado similar para una función h(X, Y) de dos variables aleatorias conjuntamente distribuidas. 196 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias 15. Considere un sistema compuesto de tres componentes como se ilustra. El sistema continuará funcionando en tanto el pri- mer componente funcione y o el componente 2 o el compo- nente 3 funcione. Sean X1, X2 y X3 las vidas útiles de los componentes 1, 2 y 3, respectivamente. Suponga que las Xi son independientes una de otra y que cada Xi tiene una dis- tribución exponencial con parámetro . a. Sea Y la vida útil del sistema. Obtenga la función de dis- tribución acumulativa de Y y derívela para obtener la función de densidad de probabilidad. [Sugerencia: F(y) P(Y y); exprese el evento {Y y} en función de uniones y/o intersecciones de los tres eventos {X1 y}, {X2 y} y {X3 y}.] b. Calcule la vida útil esperada del sistema. 16. a. Con f(x1, x2, x3) del ejemplo 5.10, calcule la función de densidad marginal conjunta de X1 y X3 (integrando para x2). b. ¿Cuál es la probabilidad de que las rocas de tipos 1 y 3 constituyan cuando mucho 50% de la muestra? [Suge- rencia: Use el resultado del inciso a).] c. Calcule la función de densidad de probabilidad marginal de X1 [Sugerencia: Use el resultado del inciso a).] 17. Un ecólogo desea seleccionar un punto adentro de una región de muestreo circular de acuerdo con una distribución unifor- me (en la práctica esto podría hacerse seleccionando primero una dirección y luego una distancia a partir del centro en esa dirección). Sea X la coordenada x del punto seleccionado y Y la coordenada y del punto seleccionado. Si el círculo tiene su centro en (0, 0) y su radio es R, entonces la función de densidad de probabilidad conjunta de X y Y es f(x, y) { 1 R2 x2 y2 R2 0 de lo contrario a. ¿Cuál es la probabilidad de que el punto seleccionado quede dentro de R/2 del centro de la región circular? [Sugerencia: Trace una figura de la región de densidad positiva D. Como f(x, y) es constante en D, el cálculo de probabilidad se reduce al cálculo de un área.] b. ¿Cuál es la probabilidad de que tanto X como Y difieran de 0 por cuando mucho R/2? c. Responda el inciso b) con R/2 reemplazando a R/2. d. ¿Cuál es la función de densidad de probabilidad margi- nal de X? ¿De Y? ¿Son X y Y independientes? 18. Remítase al ejercicio 1 y responda las siguientes preguntas: a. Dado que X 1, determine la función masa de probabi- lidad condicional de Y, es decir, pY°X (0°1), pY°X (1°1) y pY°X (2°1). b. Dado que dos mangueras están en uso en la isla de auto- servicio, ¿cuál es la función masa de probabilidad con- dicional del número de mangueras en uso en la isla de servicio completo? c. Use el resultado del inciso b) para calcular la probabili- dad condicional P(Y 1|X 2). d. Dado que dos mangueras están en uso en la isla de servicio completo, ¿Cuál es la función masa de probabi- lidad condicional del número en uso en la isla de auto- servicio? 19. La función de densidad de probabilidad conjunta de las pre- siones de los neumáticos delanteros derecho e izquierdo se da en el ejercicio 9. a. Determine la función de densidad de probabilidad con- dicional de Y dado que X x y la función de densidad de probabilidad condicional de X dado que Y y. b. Si la presión del neumático derecho es de 22 lb/pulg2 , ¿cuál es la probabilidad de que la presión del neumático izquierdo sea de por lo menos 25 lb/pulg2 ? Compare con P(Y 25). c. Si la presión del neumático derecho es de 22 lb/pulg2 , ¿cuál es la presión esperada en el neumático izquierdo y cuál es la desviación estándar de la presión en este neu- mático? 20. Sean X1, X2, X3, X4, X5 y X6 los números de lunetas MM azules, cafés, verdes, naranjas, rojas y amarillas, respectiva- mente, en una muestra de tamaño n. Entonces estas Xi tie- nen una distribución multinomial. De acuerdo con el sitio web de MM, las proporciones de colores son p1 0.24, p2 0.13, p3 0.16, p4 0.20, p5 0.13 y p6 0.14. a. Si n 12, ¿cuál es la probabilidad de que haya exacta- mente dos lunetas MM de cada color? b. Con n 20, ¿cuál es la probabilidad de que haya cuan- do mucho cinco lunetas naranjas? [Sugerencia: Consi- dere la luneta naranja como un éxito y cualquier otro color como falla.] c. En una muestra de 20 lunetas MM, ¿cuál es la proba- bilidad de que el número de lunetas azules, verdes o naranjas sea por lo menos 10? 21. Sean X1, X2 y X3 las vidas útiles de los componentes 1, 2 y 3 en un sistema de tres componentes. a. ¿Cómo definiría la función de densidad de probabilidad condicional de X3 dado que X1 x1 y X2 x2? b. ¿Cómo definiría la función de densidad de probabilidad conjunta condicional de X2 y X3 dado que X1 x1? 1 3 2 5.2 Valores esperados, covarianza y correlación c5_p184-226.qxd 3/12/08 4:07 AM Page 196
- 215. 5.2 Valores esperados, covarianza y correlación 197 Cinco amigos compraron boletos para un concierto. Si los boletos son para asientos 1-5 en una fila particular y los boletos se distribuyen al azar entre los cinco, ¿cuál es el número esperado de asientos que separen a cualquiera dos de los cinco? Sean X y Y los números de asiento del primer y segundo individuos, respectivamente. Los pares posibles (X, Y) son (1, 2), (1, 3), . . . , (5, 4) y la función masa de probabilidad conjunta de (X, Y) es p(x, y) {2 1 0 x 1, . . . , 5; y 1, . . . , 5; x y 0 de lo contrario El número de asientos que separan a los dos individuos es h(X, Y) |X Y| 1. La tabla adjunta da h(x, y) para cada par posible (x, y). h(x, y) | 1 2 4 5 1 | — 0 1 2 3 2 | 0 — 0 1 2 y 3 | 1 0 — 0 1 4 | 2 1 0 — 0 5 | 3 2 1 0 — Por lo tanto E[h(X, Y)] (x, y) h(x, y) p(x, y) 5 x1 5 y1 (°x y° 1) 1 ■ x y En el ejemplo 5.5, la función de densidad de probabilidad conjunta de la cantidad X de almendras y la cantidad de nueces de acajú en una lata de una lb de nueces fue f(x, y) {24xy 0 x 1, 0 y 1, x y 1 0 de lo contrario Si una lb de almendras le cuesta a la compañía $1.00, una lb de nuez de acajú le cuesta $1.50 y una lb de cacahuates le cuesta $0.50, entonces el costo total del contenido de una lata es h(X, Y) (1)X (1.5)Y (0.5)(1 X Y) 0.5 0.5X Y (puesto que 1 X Y del peso se compone de cacahuates). El costo esperado total es E[h(X, Y)] h(x, y) f(x, y) dx dy 1 0 1x 0 (0.5 0.5x y) 24xy dy dx $1.10 ■ El método de calcular el valor esperado de una función h(X1, . . . , Xn) de n variables aleatorias es similar al de dos variables aleatorias. Si las Xi son discretas, E[h(X1, . . . , Xn)] es una suma de n dimensiones; si las Xi son continuas, es una integral de n dimensiones. 1 20 x 3 PROPOSICIÓN Sean X y Y variables aleatorias conjuntamente distribuidas con función masa de pro- babilidad p(x, y) o función de densidad de probabilidad f (x, y) ya sea que las varia- bles sean discretas o continuas. Entonces el valor esperado de una función h(X, Y) denotada por E[h(X, Y)] o h(X, Y) está dada por E[h(X, Y)] x y h(x, y) p(x, y) Si X y Y son discretas {' ' ' ' h(x, y) f(x, y) dx dy Si X y Y son continuas Ejemplo 5.13 Ejemplo 5.14 c5_p184-226.qxd 3/12/08 4:07 AM Page 197
- 216. 198 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Covarianza Cuando dos variables aleatorias X y Y no son independientes, con frecuencia es de interés valorar qué tan fuerte están relacionadas una con otra. Es decir, como X X y Y Y son las desviaciones de las dos variables con respecto a sus valores medios, la covarianza es el producto esperado de las desviaciones. Obsérvese que Cov(X, X) E[(X X)2 ] V(X). La exposición razonada para la definición es como sigue. Suponga que X y Y tienen una fuerte relación positiva entre ellas, lo que significa que los valores grandes de X tienden a ocurrir con valores grandes de Y y los valores pequeños de X con los valores pequeños de Y. Entonces la mayor parte de la masa o densidad de probabilidad estará asociada con (x X) y (y Y) o ambos positivos (tanto X como Y sobre sus respectivas medias) o ambos negativos, así que el producto (x X)(y Y) tenderá a ser positivo. Por tanto con una fuerte relación positiva, Cov(X, Y) deberá ser bastante positiva. Con una fuerte relación negativa los signos de (x X) y (y Y) tenderán a ser opuestos, lo que da un producto nega- tivo. Por tanto con una fuerte relación negativa, Cov(X, Y) deberá ser bastante negativa. Si X y Y no están fuertemente relacionadas, los productos positivo y negativo tenderán a eli- minarse entre sí, lo que da una covarianza de cerca de 0. La figura 5.4 ilustra las diferentes posibilidades. La covarianza depende tanto del conjunto de pares posibles como de las pro- babilidades. En la figura 5.4, las probabilidades podrían ser cambiadas sin que se altere el conjunto de pares posibles y esto podría cambiar drásticamente el valor de Cov(X, Y). Las funciones masa de probabilidad conjunta y marginal de X cantidad deducible sobre una póliza de automóvil y Y cantidad deducible sobre póliza de propietario de casa en el ejemplo 5.1 fueron p(x, y) | 0 200 x | 100 250 y | 0 100 200 x 100 | 0.20 0.10 0.20 pX(x) | 0.5 0.5 pY(y) | 0.25 0.25 0.5 250 | 0.05 0.15 0.30 y 100 DEFINICIÓN La covarianza entre dos variables aleatorias X y Y es Cov(X, Y) E[(X X)(Y Y)] x y (x X)(y Y)p(x, y) X, Y discretas { (x X)(y Y)f(x, y) dx dy X, Y continuas Ejemplo 5.15 Figura 5.4 p(x, y) 1/10 de cada uno de los diez pares correspondientes a los puntos indicados; a) cova- rianza positiva; b) covarianza negativa; c) covarianza cerca de cero. X c) X b) Y Y y Y X a) x y x y x c5_p184-226.qxd 3/12/08 4:07 AM Page 198
- 217. de la cual X xpX(x) 175 y Y 125. Por consiguiente, Cov(X, Y) (x, y) (x 175)(y 125)p(x, y) (100 175)(0 125)(0.20) . . . (250 175)(200 125)(0.30) 1875 ■ La siguiente fórmula abreviada para Cov(X, Y) simplifica los cálculos. De acuerdo con esta fórmula, no se requieren sustracciones intermedias; sólo al final de cálculo X Y se resta de E(XY). La comprobación implica expandir (X X)(Y Y) y luego considerar el valor esperado de cada término por separado. Las funciones de densidad de probabilidad conjunta y marginal de X cantidad de almen- dras y Y cantidad de nueces de acajú fueron f(x, y) {24xy 0 x 1, 0 y 1, x y 1 0 de lo contrario fX(x) {12x(1 x)2 0 x 1 0 de lo contrario con fY(y) obtenida reemplazando x por y en fX(x). Es fácil verificar que X Y 2 5, y E(XY) xy f(x, y) dx dy 1 0 1x 0 xy 24xy dy dx 8 1 0 x2 (1 x)3 dx 1 2 5 Por lo tanto, Cov(X, Y) 1 2 5 (2 5)(2 5) 1 2 5 2 4 5 7 2 5. Una covarianza negativa se consi- dera razonable en este caso porque más almendras contenidas en la lata implican menos nueces de acajú. ■ Pudiera parecer que la relación en el ejemplo de los seguros es bastante fuerte puesto que Cov(X, Y) 1875, mientras que Cov(X, Y) 7 2 5 en el ejemplo de las nueces parece- ría implicar una relación bastante débil. Desafortunadamente, la covarianza tiene un serio defecto que hace imposible interpretar un valor calculado. En el ejemplo de los seguros, suponga que la cantidad deducible se expresó en centavos en lugar de dólares. Entonces 100X reemplazaría a X, 100Y reemplazaría a Y y la covarianza resultante sería Cov(100X, 100Y) (100)(100)Cov(X, Y) 18 750 000. Si, por otra parte, la cantidad deducible se hubiera expresado en cientos de dólares, la covarianza calculada habría sido (0.01)(0.01)(1875) 0.1875. El defecto de la covarianza es que su valor calculado depen- de críticamente de las unidades de medición. De manera ideal, la selección de las unida- des no debe tener efecto en la medida de la fuerza de la relación. Esto se logra graduando a escala la covarianza. 5.2 Valores esperados, covarianza y correlación 199 PROPOSICIÓN Cov(X, Y) E(XY) X Y Ejemplo 5.16 (continuación del ejemplo 5.5) c5_p184-226.qxd 3/12/08 4:07 AM Page 199
- 218. 200 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Correlación Es fácil verificar que en el escenario de los seguros del ejemplo 5.15, E(X2 ) 36250, 2 X 36250 (175)2 5625, X 75, E(Y2 ) 22500, 2 Y 6875, y Y 82.92. Esto da 0.301 ■ La siguiente proposición muestra que remedia el defecto de Cov(X, Y) y también sugiere cómo reconocer la existencia de una fuerte relación (lineal). 1875 (75)(82.92) La proposición 1 dice precisamente que el coeficiente de correlación no se ve afectado por un cambio lineal en las unidades de medición (si, por ejemplo, X temperatura en °C, entonces 9X/5 32 temperatura en °F). De acuerdo con la proposición 2, la relación positiva más fuerte posible es puesta en evidencia por 1, en tanto que la relación nega- tiva más fuerte posible corresponde a 1. La comprobación de la primera proposición se ilustra en el ejercicio 35, y la de la segunda aparece en el ejercicio suplementario 87 al final del capítulo. Para propósitos descriptivos, la relación se describirá como fuerte si || 0.8, moderada si 0.5 || 0.8 y débil si || 0.5. Si se considera que p(x, y) o f(x, y) prescribe un modelo matemático de cómo las dos variables numéricas X y Y están distribuidas en alguna población (estatura y peso, califica- ción SAT verbal y calificación SAT cuantitativa, etc.), entonces es una característica o parámetro de población que mide cuán fuertemente X y Y están relacionadas en la pobla- ción. En el capítulo 12, se considerará tomar una muestra de pares (x1, y1), . . . , (xn, yn) de la población. El coeficiente de correlación muestral r se definirá y utilizará entonces para hacer inferencias con respecto a . El coeficiente de correlación no es en realidad una medida completamente general de la fuerza de una relación. Esta proposición dice que mide el grado de asociación lineal entre X y Y y sólo cuando las dos variables están perfectamente relacionadas de una manera lineal será tan positivo o negativo como pueda ser. Un menor que 1 en valor absoluto indica sólo que la relación no es completamente lineal, sino que aún puede haber una fuerte relación no lineal. Además, DEFINICIÓN El coeficiente de correlación de X y Y, denotado por Corr(X, Y), X,Y o simplemente , está definido por X,Y C ov X ( X , Y Y) Ejemplo 5.17 PROPOSICIÓN 1. Si a y c son ambas positivas o ambas negativas, Corr(aX b, cY d) Corr(X, Y) 2. Para dos variables aleatorias cualesquiera X y Y, 1 Corr(X, Y) 1. PROPOSICIÓN 1. Si X y Y son independientes, entonces 0, pero 0 no implica independencia. 2. 1 o 1 si y sólo si Y aX b con algunos números a y b con a 0. c5_p184-226.qxd 3/12/08 4:07 AM Page 200
- 219. 0 no implica que X y Y son independientes, sino sólo que existe una ausencia comple- ta de relación lineal. Cuando 0, se dice que X y Y no están correlacionadas. Dos varia- bles podrían estar no correlacionadas y no obstante ser altamente dependientes porque existe una fuerte relación no lineal, así que se debe tener cuidado de no concluir demasiado del hecho de que 0. Sean X y Y variables aleatorias discretas con función masa de probabilidad conjunta p(x, y) {1 4 (x, y) ( 4, 1), (4, 1), (2, 2), ( 2, 2) 0 de lo contrario Los puntos que reciben masa de probabilidad positiva están identificados en el sistema de coordenadas (x, y) en la figura 5.5. Es evidente por la figura que el valor de X está com- pletamente determinado por el valor de Y y viceversa, de modo que las dos variables son completamente dependientes. Sin embargo, por simetría X Y 0 y E(XY) ( 4) 1 4 ( 4) 1 4 (4) 1 4 (4) 1 4 0, por tanto Cov(X, Y) E(XY) X Y 0 y por consiguiente X,Y 0. ¡Aunque hay una dependencia perfecta, también hay una ausencia completa de cualquier relación lineal! Un valor de próximo a 1 no necesariamente implica que el incremento del valor de X hace que se incremente Y. Implica sólo que los valores grandes de X están asociados con valores grandes de Y. Por ejemplo, en la población de niños, el tamaño del vocabulario y el número de caries están bastante correlacionados positivamente, pero con certeza no es cier- to que las caries hagan que crezca el vocabulario. En cambio, los valores de estas dos varia- bles tienden a incrementarse conforme el valor de la edad, una tercera variable, se incrementa. Para niños de una edad fija, quizá existe una muy baja correlación entre el número de caries y el tamaño del vocabulario. En suma, asociación (una alta correlación) no es lo mismo que causa. 5.2 Valores esperados, covarianza y correlación 201 Ejemplo 5.18 Figura 5.5 Población de pares del ejemplo 5.18. ■ 2 1 1 2 1 2 3 4 1 2 3 4 EJERCICIOS Sección 5.2 (22-36) 22. Un instructor aplicó un corto examen compuesto de dos par- tes. Para un estudiante seleccionado al azar, sea X el núme- ro de puntos obtenidos en la primera parte y Y el número de puntos obtenidos en la segunda parte. Suponga que la fun- ción masa de probabilidad conjunta de X y Y se da en la tabla adjunta. y p(x, y) | 0 5 10 15 0 | 0.02 0.06 0.02 0.10 x 5 | 0.04 0.15 0.20 0.10 10 | 0.01 0.15 0.14 0.01 a. Si la calificación anotada en la libreta de calificaciones es el número total de puntos obtenidos en las dos partes, ¿cuál es la calificación anotada esperada E(X Y)? b. Si se anota la máxima de las dos calificaciones, ¿cuál es la calificación anotada esperada? 23. La diferencia entre el número de clientes formados en la caja rápida y el número formado en la caja superrápida del ejercicio 3 es X1 X2. Calcule la diferencia esperada. 24. Seis individuos, incluidos A y B, se sientan alrededor de una tabla circular de una forma completamente al azar. Suponga que los asientos están numerados 1, . . . , 6. Sea X el c5_p184-226.qxd 3/12/08 4:08 AM Page 201
- 220. 202 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias En el capítulo 1, x1, x2, . . . , xn denotaron las observaciones en una sola muestra. Considérese seleccionar dos muestras diferentes de tamaño n de la misma distribución de población. Las xi en la segunda muestra virtualmente siempre diferirán por lo menos un poco de aquellas en la primera muestra. Por ejemplo, una primera muestra de n 3 carros de un tipo particular podría producir eficiencias de combustible x1 30.7, x2 29.4, x3 31.1, mientras que una segunda muestra puede dar x1 28.8, x2 30.0 y x3 31.1. Antes de obtener datos, existe incertidumbre sobre el valor de cada xi. Debido a esta incertidumbre, antes de que los datos estén disponibles, cada observación se considera como una variable aleatoria y la muestra se denota por X1, X2, . . . , Xn (letras mayúsculas para variables aleatorias). Esta variación en los valores observados implica a su vez que el valor de cualquier función de las observaciones muestrales, tal como la media muestral, la desviación estándar muestral o la dispersión de los cuartos muestrales, también varía de una muestra a otra. Es decir, antes de obtener x1, . . . , xn, existe incertidumbre en cuanto al valor de x , el valor de s, y así sucesivamente. Suponga que la resistencia del material de un especimen seleccionado al azar de un tipo particular tiene una distribución Weibull con valores de parámetro 2 (forma) y 5 número de asiento de A y Y el número de asiento de B. Si A envía un mensaje escrito alrededor de la mesa a B en la dirección en la cual están más cerca, ¿cuántos individuos (incluidos A y B) esperarían manipular el mensaje? 25. Un topógrafo desea delimitar una región cuadrada con L de lado. Sin embargo, debido a un error de medición, delimita en cambio un rectángulo en el cual los lados norte-sur son de longitud X y los lados este-oeste son de longitud Y. Suponga que X y Y son independientes y que cada uno está uniformemente distribuido en el intervalo [L A, L A] (donde 0 A L). ¿Cuál es el área esperada del rectángu- lo resultante? 26. Considere un pequeño transbordador que puede transportar carros y autobuses. La cuota para carros es de $3 y para autobuses es de $10. Sean X y Y el número de carros y auto- buses, respectivamente, transportados en un solo viaje. Suponga que la distribución conjunta de X y Y aparece en la tabla del ejercicio 7. Calcule el ingreso esperado en un solo viaje. 27. Annie y Alvie quedaron de encontrarse para desayunar entre el mediodía (0:00 M.) y 1:00 P.M. Denote la hora de llegada de Annie por X, y la de Alvie por Y y suponga que X y Y son independientes con funciones de densidad de pro- babilidad fX(x) {3x2 0 x 1 0 de lo contrario fY(y) {2y 0 y 1 0 de lo contrario ¿Cuál es la cantidad esperada de tiempo que el que llega primero debe esperar a la otra persona? [Sugerencia: h(X, Y) |X Y|.] 28. Demuestre que si X y Y son variables aleatorias indepen- dientes, entonces E(XY) E(X) E(Y). Luego aplique esto en el ejercicio 25. [Sugerencia: Considere el caso continuo con f(x, y) fX(x) fY(y).] 29. Calcule el coeficiente de correlación , de X y Y del ejem- plo 5.16 (ya se calculó la covarianza). 30. a. Calcule la covarianza de X y Y en el ejercicio 22. b. Calcule para X y Y en el mismo ejercicio. 31. a. Calcule la covarianza entre X y Y en el ejercicio 9. b. Calcule el coeficiente de correlación para X y Y. 32. Reconsidere las vidas útiles de los componentes de mini- computadoras X y Y como se describe en el ejercicio 12. Determine E(XY). ¿Qué se puede decir sobre Cov(X, Y) y ? 33. Use el resultado del ejercicio 28 para demostrar que cuan- do X y Y son independientes Cov(X, Y) Corr(X, Y) 0. 34. a. Recordando la definición de 2 para una sola variable aleatoria X, escriba una fórmula que sería apropiada para calcular la varianza de una función h(X, Y) de dos varia- bles aleatorias. [Sugerencia: Recuerde que la varianza es simplemente un valor especial esperado.] b. Use esta fórmula para calcular la varianza de la califica- ción anotada h(X, Y) [ máx(X, Y)] en el inciso b) del ejercicio 22. 35. a. Use las reglas de valor esperado para demostrar que Cov(aX b, cY d) ac Cov(X, Y). b. Use el inciso a) junto con las reglas de varianza y desvia- ción estándar para demostrar que Corr(aX b, cY d) Corr(X, Y) cuando a y c tienen el mismo signo. c. ¿Qué sucede si a y c tienen signos opuestos? 36. Demuestre que si Y aX b (a 0), entonces Corr(X, Y) 1 o 1. ¿En que condiciones será 1? Ejemplo 5.19 5.3 Estadísticos y sus distribuciones c5_p184-226.qxd 3/12/08 4:08 AM Page 202
- 221. (escala). La curva de densidad correspondiente se muestra en la figura 5.6. Fórmulas de la sección 4.5 dan E(X) 4.4311 ~ 4.1628 2 V(X) 5.365 2.316 La media excede a la mediana debido a la asimetría positiva de la distribución. Se utilizó MINITAB para generar seis muestras diferentes, cada una con n 10, de esta distribución (resistencias de material de seis diferentes grupos de diez especímenes cada uno). Los resultados aparecen en la tabla 5.1, seguidos por los valores de la media, la mediana y la desviación estándar de cada muestra. Obsérvese en primer lugar que las diez observaciones en cualquier muestra particular son diferentes de aquellas en cualquier otra muestra. En segundo lugar, los seis valores de la media son diferentes entre sí, como lo son los seis valores de la mediana y los seis valores de la desviación estándar. Lo mismo es cierto para las medias 10% recortadas, la dispersiones de los cuartos de las muestras, y así sucesivamente. 5.3 Estadísticos y sus distribuciones 203 Figura 5.6 Curva de densidad Weibull del ejemplo 5.19. 0 5 10 0 15 0.05 0.10 0.15 x f(x) Tabla 5.1 Muestras de la distribución Weibull del ejemplo 5.19 Muestra 1 2 3 4 5 6 1 6.1171 5.07611 3.46710 1.55601 3.12372 8.93795 2 4.1600 6.79279 2.71938 4.56941 6.09685 3.92487 3 3.1950 4.43259 5.88129 4.79870 3.41181 8.76202 4 0.6694 8.55752 5.14915 2.49759 1.65409 7.05569 5 1.8552 6.82487 4.99635 2.33267 2.29512 2.30932 6 5.2316 7.39958 5.86887 4.01295 2.12583 5.94195 7 2.7609 2.14755 6.05918 9.08845 3.20938 6.74166 8 10.2185 8.50628 1.80119 3.25728 3.23209 1.75468 9 5.2438 5.49510 4.21994 3.70132 6.84426 4.91827 10 4.5590 4.04525 2.12934 5.50134 4.20694 7.26081 4.401 5.928 4.229 4.132 3.620 5.761 x̃ 4.360 6.144 4.608 3.857 3.221 6.342 s 2.642 2.062 1.611 2.124 1.678 2.496 x c5_p184-226.qxd 3/12/08 4:08 AM Page 203
- 222. 204 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Además, el valor de la media de cualquier muestra puede ser considerada como esti- mación puntual (“puntual” porque es un solo número, correspondiente a un solo punto sobre la línea de numeración) de la media de la población , cuyo valor se sabe que es 4.4311. Ninguna de las estimaciones de estas seis muestras es idéntica a la que se está estimando. Las estimaciones de la segunda y sexta muestras son demasiado grandes, en tanto que la quinta da una subestimación sustancial. Asimismo, la desviación estándar muestral da una estimación puntual de la desviación estándar de la población. Las seis estimaciones resul- tantes están equivocadas por lo menos en una pequeña cantidad. En resumen, los valores de cada una de las observaciones muestrales varían de una muestra a otra, así que en general el valor de cualquier cantidad calculado a partir de los datos de la muestra, y el valor de una característica muestral utilizado como estimación de la característica poblacional correspondiente, prácticamente nunca coincidirá con lo que está siendo estimado. ■ Por lo tanto la media muestral, considerada como estadístico (antes de seleccionar una muestra o realizar un experimento), está denotada por X ; el valor calculado de este estadís- tico es x . Del mismo modo, S representa la desviación estándar muestral considerada como estadístico y su valor calculado es s. Si se seleccionan muestras de dos tipos diferentes de ladrillos y las resistencias a la compresión individuales se denotan por X1, . . . , Xm y Y1, . . . , Yn, respectivamente, entonces el estadístico X Y , la diferencia entre las dos resis- tencias muestrales medias a la compresión, a menudo es de gran interés. Cualquier estadístico, por el hecho de ser una variable aleatoria, tiene una distribución de probabilidad. En particular, la media muestral X tiene una distribución de probabilidad. Supóngase, por ejemplo, que n 2 componentes se seleccionan al azar y que el número de descomposturas mientras se encuentran dentro de garantía se determina para cada uno. Los valores posibles del número medio muestral de descomposturas X son 0 (si X1 X2 0), 0.5 (si o X1 0 y X2 1 o X1 1 y X2 0), 1, 1.5, . . . La distribución de probabilidad de X especifica P(X 0), P(X 0.5), y así sucesivamente, a partir de las cuales otras probabi- lidades tales como P(1 X 3) y P(X 2.5) pueden ser calculadas. Asimismo, si para una muestra de tamaño n 2, los únicos valores posibles de la varianza muestral son 0, 12.5 y 50 (el cual es el caso si X1 y X2 pueden tomar sólo los valores 40, 45 o 50), entonces la dis- tribución de probabilidad de S2 da P(S2 0), P(S2 12.5) y P(S2 50). La distribución de probabilidad de un estadístico en ocasiones se conoce como distribución de muestreo para enfatizar que describe cómo varía el valor del estadístico a través de todas las muestras que pudieran ser seleccionadas. Muestras aleatorias La distribución de probabilidad de cualquier estadístico particular depende no sólo de la dis- tribución de la población (normal, uniforme, etc.) y el tamaño de muestra n sino también del método de muestreo. Considérese seleccionar una muestra de tamaño n 2 de una pobla- ción compuesta de sólo los tres valores 1, 5 y 10 y supóngase que el estadístico de interés es la varianza muestral. Si el muestreo se realiza “con reemplazo”, entonces S2 0 resulta- rá si X1 X2. Sin embargo, S2 no puede ser igual a 0 si el muestreo se realiza “sin reem- plazo”. Por tanto P(S2 0) 0 con un método de muestreo, y esta probabilidad es positiva DEFINICIÓN Un estadístico es cualquier cantidad cuyo valor puede ser calculado a partir de datos muestrales. Antes de obtener los datos, existe incertidumbre sobre qué valor de cual- quier estadístico particular resultará. Por consiguiente, un estadístico es una variable aleatoria y será denotada por una letra mayúscula; se utiliza una letra minúscula para representar el valor calculado u observado del estadístico. c5_p184-226.qxd 3/12/08 4:08 AM Page 204
- 223. con el otro método. La siguiente definición describe un método de muestreo encontrado a menudo (por lo menos aproximadamente) en la práctica. Las condiciones 1 y 2 pueden ser parafraseadas diciendo que las Xi son independientes e idénticamente distribuidas (iid). Si el muestreo se realiza con reemplazo o de una población infinita (conceptual), las condiciones 1 y 2 se satisfacen con exactitud. Estas condiciones serán aproximadamente satisfechas si el muestreo se realiza sin reemplazo, aunque el tama- ño de la muestra sea mucho más pequeño que el tamaño de la población N. En la práctica, si n/N 0.05 (cuando mucho 5% de la población se muestrea), se puede proceder como si las Xi formarán una muestra aleatoria. La virtud de este método de muestreo es que la dis- tribución de probabilidad de cualquier estadístico es más fácil de obtener que con cualquier otro método de muestreo. Existen dos métodos generales de obtener información sobre una distribución de muestreo estadístico. Uno implica cálculos basados en reglas de probabilidad y el otro implica realizar un experimento de simulación. Derivación de una distribución de muestreo Se pueden utilizar reglas de probabilidad para obtener la distribución de un estadístico siem- pre que sea una función “bastante simple” de las Xi y o existen relativamente pocos valores X diferentes en la población o bien la distribución de la población tiene una forma “accesi- ble”. Los dos ejemplos siguientes ilustran tales situaciones. Un gran centro de servicio automotriz cobra $40, $45 y $50 por la afinación de carros de cuatro, seis y ocho cilindros, respectivamente. Si 20% de sus afinaciones se realizan en carros de cuatro cilindros, 30% en carros de seis cilindros y 50% en carros de ocho cilin- dros, entonces la distribución de probabilidad de los ingresos por una afinación selecciona- da al azar está dada por x | 40 45 50 p(x) | 0.2 0.3 0.5 con 46.5, 2 15.25 (5.2) Suponga que en un día particular sólo se realizan dos trabajos de servicio que implican afi- naciones. Sea X1 el ingreso por la primera afinación y X2 el ingreso por la segunda. Suponga que X1 y X2 son independientes, cada una con la distribución de probabilidad mos- trada en (5.2) [de modo que X1 y X2 constituyen una muestra aleatoria de la distribución (5.2)]. La tabla 5.2 pone en lista pares posibles (x1, x2), la probabilidad de cada uno [calcu- lado por medio de (5.2) y la suposición de independencia] y los valores x y s2 resultantes. Ahora para obtener la distribución de probabilidad de X , el ingreso promedio muestral por afinación, se debe considerar cada valor posible de x y calcular su probabilidad. Por ejem- plo, x 45 ocurre tres veces en la tabla con probabilidades 0.10, 0.09 y 0.10, por lo tanto pX (45) P(X 45) 0.10 0.09 0.10 0.29 Asimismo pS2(50) P(S2 50) P(X1 40, X2 50 o X1 50, X2 40) 0.10 0.10 0.20 5.3 Estadísticos y sus distribuciones 205 DEFINICIÓN Se dice que las variables aleatorias X1, X2, . . . , Xn forman una muestra aleatoria sim- ple de tamaño n si 1. Las Xi son variables aleatorias independientes. 2. Cada Xi tiene la misma distribución de probabilidad. Ejemplo 5.20 c5_p184-226.qxd 3/12/08 4:08 AM Page 205
- 224. 206 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Las distribuciones de muestreo completas de X y S2 aparecen en (5.3) y (5.4). x | 40 42.5 45 47.5 50 pX (x ) | 0.04 0.12 0.29 0.30 0.25 (5.3) s2 | 0 12.5 50 pS2(s2 ) | 0.38 0.42 0.20 (5.4) La figura 5.7 ilustra un histograma de probabilidad tanto de la distribución original (5.2) como la distribución X (5.3). La figura sugiere primero que la media (valor esperado) de la distribución X es igual a la media 46.5 de la distribución original, puesto que ambos histo- gramas parecen estar centrados en el mismo lugar. De acuerdo con (5.3), X E(X ) x pX (x ) (40)(0.04) . . . (50)(0.25) 46.5 En segundo lugar, parece que la distribución X tiene una dispersión más pequeña (variabili- dad) que la distribución original, puesto que la masa de probabilidad se movió hacia la media. De nuevo de acuerdo con (5.3), 2 X V(X ) x 2 pX (x ) 2 X (40)2 (0.04) . . . (50)2 (0.25) (46.5)2 7.625 La varianza de X es precisamente la mitad de la varianza original (porque n 2). El valor medio de S2 es S2 E(S2 ) s2 pS2(s2 ) (0)(0.38) (12.5)(0.42) (50)(0.20) 15.25 2 2 2 15.25 2 Tabla 5.2 Resultados, probabilidades y valores de x y s2 en el ejemplo 5.20 x1 x2 p(x1, x2) x s2 40 40 0.04 40 0 40 45 0.06 42.5 12.5 40 50 0.10 45 50 45 40 0.06 42.5 12.5 45 45 0.09 45 0 45 50 0.15 47.5 12.5 50 40 0.10 45 50 50 45 0.15 47.5 12.5 50 50 0.25 50 0 Figura 5.7 Histogramas de probabilidad de la distribución subyacente y distribución X en el ejemplo 5.20. 0.3 0.2 0.5 0.04 0.12 0.29 0.30 0.25 45 40 50 40 42.5 45 47.5 50 c5_p184-226.qxd 3/12/08 4:08 AM Page 206
- 225. Es decir, la distribución de muestreo X tiene su centro en la media de la población y la distribución de muestreo S2 está centrada en la varianza de la población 2 . Si se hubieran realizado cuatro afinaciones en el día de interés, el ingreso promedio muestral X estaría basado en una muestra aleatoria de cuatro Xi, cada una con la distribución (5.2). Con más cálculos se obtiene la función masa de probabilidad de X con n 4 como x | 40 41.25 42.5 43.75 45 46.25 47.5 48.75 50 pX (x ) | 0.0016 0.0096 0.0376 0.0936 0.1761 0.2340 0.2350 0.1500 0.0625 De acuerdo con esta, X 46.50 y 2 X 3.8125 2 /4. La figura 5.8 es un histogra- ma de probabilidad de esta función masa de probabilidad. El ejemplo 5.20 sugiere que el cálculo de pX (x ) y pS 2(s2 ) puede ser tedioso. Si la distri- bución original (5.2) hubiera permitido más de tres valores posibles, 40, 45 y 50, entonces incluso con n 2 los cálculos hubieran sido más complicados. El ejemplo también sugiere, sin embargo, que existen algunas relaciones generales entre E(X ), V(X ), E(S2 ), y la media y la varianza 2 de la distribución original. Éstas se formulan en la siguiente sección. Ahora considérese un ejemplo en el cual la muestra aleatoria se extrae de una distribución continua. Tiempo de servicio para un tipo de transacción bancaria es una variable aleatoria con dis- tribución exponencial y parámetro . Suponga que X1 y X2 son tiempos de servicio para dos clientes diferentes, supuestos independientes entre sí. Considere el tiempo de servicio total To X1 X2 para los dos clientes, también un estadístico. La función de distribución acumu- lativa de To con t 0, FT0 (t) P(X1 X2 t) f(x1, x2) dx1 dx2 {(x1, x2):x1x2t} t 0 tx1 0 ex1 ex2 dx2 dx1 t 0 [ex1 et ] dx1 1 et tet La región de integración se ilustra en la figura 5.9. 5.3 Estadísticos y sus distribuciones 207 Figura 5.8 Histograma de probabilidad de X basado en el n 4 en el ejemplo 5.20. ■ 40 42.5 45 47.5 50 Figura 5.9 Región de integración para obtener la función de distribución acumulativa de To en el ejemplo 5.21. x1 x2 x1 x1 x2 t (x1, t x1) Ejemplo 5.21 c5_p184-226.qxd 3/12/08 4:08 AM Page 207
- 226. 208 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias La función de densidad de probabilidad de To se obtiene derivando FTo (t): fT0 (t) {2 tet t 0 0 t 0 (5.5) Esta es una función de densidad de probabilidad gama ( 2 y 1/). La función de densidad de probabilidad de X To/2 se obtiene a partir de la relación {X x } si y sólo si {To 2x } como fX (x ) {42 x e 2x x 0 0 x 0 (5.6) La media y la varianza de la distribución exponencial subyacente son 1/ y 2 1/2 . Con las expresiones (5.5) y (5.6) se puede verificar que E(X ) 1/, V(X ) 1/(22 ), E(To) 2/, y V(To) 2/2 . Estos resultados sugieren de nuevo algunas relaciones generales entre medias y varianzas de X , To y la distribución subyacente. ■ Experimentos de simulación El segundo método de obtener información sobre distribución de muestreo estadístico es realizar un experimento de simulación. Este método casi siempre se utiliza cuando la obtención vía reglas de probabilidad es demasiado difícil o complicada de realizar. Tal experimento vir- tualmente siempre se realiza con la ayuda de una computadora. Las siguientes características de un experimento deben ser especificadas: 1. El estadístico de interés (X , S, una media recortada particular, etcétera). 2. La distribución de la población (normal con 100 y 15, uniforme con límite inferior A 5 y superior B 10, etcétera). 3. El tamaño de muestra n(p. ej., n 10 o n 50). 4. El número de réplicas k (p. ej., k 500). Luego se utiliza una computadora para obtener k diferentes muestras aleatorias, cada una de tamaño n, de la distribución de población designada. Para cada una de las muestras, calcu- le el valor del estadístico y construya un histograma de los k valores calculados. Este histo- grama da la distribución de muestreo aproximada del estadístico. Mientras más grande es el valor de k, mejor tenderá a ser la aproximación (la distribución de muestreo real emerge a medida que k A ). En la práctica k 500 o 1000 casi siempre es suficiente si el estadís- tico es “bastante simple”. La distribución de la población del primer estudio de simulación es normal con 8.25 y 0.75, como se ilustra en la figura 5.10. [El artículo “Platelet Size in Myocardial Infarction” (British Med. J., 1983: 449-451) sugiere esta distribución de volumen de pla- quetas en individuos sin historial clínico de problemas de corazón serios.] Ejemplo 5.22 Figura 5.10 Distribución normal, con 8.25 y 0.75. 6.00 6.75 7.50 9.00 9.75 10.50 8.25 ¨ © ª 0.75 c5_p184-226.qxd 3/12/08 4:08 AM Page 208
- 227. En realidad se realizaron cuatro experimentos diferentes, con 500 réplicas por cada uno. En el primero, se generaron 500 muestras de n 5 observaciones cada una con MINITAB y los tamaños de las otras tres muestras fueron n 10, n 20 y n 30, respectivamente. La media muestral se calculó para cada muestra y los histogramas resultantes de valores x apa- recen en la figura 5.11. Lo primero que se nota en relación con los histogramas es su forma. En cuanto a una razonable aproximación, cada uno de los cuatro se ve como una curva normal. El parecido sería aún más impactante si cada histograma se hubiera basado en más de 500 x valores. En segundo lugar, cada histograma está centrado aproximadamente en 8.25, la media de la población muestreada. Si los histogramas se hubieran basado en un secuencia interminable de valores x , sus centros habrían sido exactamente la media de la población, 8.25. 5.3 Estadísticos y sus distribuciones 209 Figura 5.11 Histogramas muestrales de x basados en 500 muestras, cada uno compuesto de n observa- ciones: a) n 5; b) n 10; c) n 20; d) n 30. 7.35 7.65 7.95 8.25 8.55 8.85 9.15 7.50 7.80 8.10 8.40 8.70 9.00 9.30 0.05 0.10 0.15 0.20 0.25 Frecuencia relativa x 7.65 7.95 8.25 8.55 8.85 7.50 7.80 8.10 8.40 8.70 0.05 0.10 0.15 0.20 0.25 x 0.05 0.10 0.15 0.20 0.25 Frecuencia relativa Frecuencia relativa Frecuencia relativa x 7.80 8.10 8.40 8.70 7.95 8.25 8.55 0.05 0.10 0.15 0.20 0.25 x 7.80 8.10 8.40 8.70 7.95 8.25 8.55 a) b) c) d) c5_p184-226.qxd 3/12/08 4:08 AM Page 209
- 228. 210 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias El aspecto final del histograma es su dispersión uno con respecto al otro. Mientras más pequeño es el valor de n, más grande es la extensión hacia la cual la distribución se esparce con respecto al valor medio. Por eso los histogramas con n 20 y n 30 están basados en intervalos de clase más angostos que aquellos de los dos tamaños de muestra más pequeños. Con los tamaños de muestra más grandes, la mayoría de los valores x están bastante cerca de 8.25. Este es el efecto de promediar. Cuando n es pequeño, un valor x inusual puede dar por resultado un valor x alejado del centro. Con un tamaño de muestra grande, cualesquiera valores x inusuales, cuando se promedian con los demás valores muestrales, seguirá tendiendo a producir un valor x próximo a . Si se combinan estas ideas se obtiene un resultado muy apegado a su intuición: X basado en n grande tiende a acercarse más a que X basado en n pequeño. ■ Considere un experimento de simulación en el cual la distribución de la población es bastan- te asimétrica. La figura 5.12 muestra la curva de densidad de las vidas útiles de un tipo de control electrónico [ésta es en realidad una distribución lognormal con E(ln(X)) 3 y V(ln(X)) 0.16]. De nueva cuenta el estadístico de interés es la media muestral X . El experi- mento utilizó 500 réplicas y consideró los mismos cuatro tamaños de muestra que en el ejem- plo 5.22. Los histogramas resultantes junto con una curva de probabilidad normal generada por MINITAB con los 500 x valores basados en n 30 se muestran en la figura 5.13. A diferencia del caso normal, estos histogramas difieren en cuanto a forma. En particular, se vuelven progresivamente menos asimétricos a medida que el tamaño de muestra n se incrementa. El promedio de los 500 x valores con los cuatro tamaños de muestra diferentes se aproximan bastante al valor medio de la distribución de la población. Si cada histograma se hubiera basado en una secuencia interminable de valores x en lugar de sólo 500, los cuatro habrían tenido su centro en exactamente 21.7584. Por tanto los valores diferentes de n cam- bian la forma mas no el centro de la distribución de muestreo de X . La comparación de los cuatro histogramas en la figura 5.13 también muestra que conforme n se incrementa, la dis- persión de los histogramas decrece. El incremento de n produce un mayor grado de con- centración en torno al valor medio de la población y hace que el histograma se vea más como una curva normal. El histograma de la figura 5.13d) y la curva de probabilidad nor- mal en la figura 5.13e) proporcionan una evidencia convincente de que un tamaño de mues- tra de n 30 es suficiente para superar la asimetría de la distribución de la población y para producir una distribución de muestreo X aproximadamente normal. Ejemplo 5.23 Figura 5.12 Curva de densidad del experimento de simulación del ejemplo 5.23 [E(X) 21.7584, V(X) 82.1449]. 0 25 50 75 0.01 0.02 0.03 0.04 0.05 x f(x) c5_p184-226.qxd 3/12/08 4:08 AM Page 210
- 229. 5.3 Estadísticos y sus distribuciones 211 Figura 5.13 Resultados del experimento de simulación del ejemplo 5.23: a) histograma de x con n 5; b) histograma de x con n 10; c) histograma de x con n 20; d) histograma de x con n 30; e) curva de probabilidad normal con n 30 (generados por MINITAB). ■ 0.05 0.10 0 10 20 a) b) 30 40 n = 5 n = 10 n = 20 n = 30 0.05 0.10 0 10 20 30 40 x x 0.1 0.2 0 15 20 c) 25 Densidad x 0.1 0.2 0 15 20 d) 25 Densidad x Media 30 e) Prueba W de normalidad R: 0.9975 Valor P (aprox.): 0.1000 Promedio: 21.7891 Desv. Est. = 1.57396 N: 500 0.999 0.99 0.95 0.80 0.50 0.20 0.05 0.01 0.001 Probabilidad 18 19 20 21 22 23 24 25 26 27 c5_p184-226.qxd 3/12/08 4:08 AM Page 211
- 230. 212 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias EJERCICIOS Sección 5.3 (37-45) 37. Una marca particular de jabón para lavadora de platos se vende en tres tamaños: 25 oz, 40 oz y 65 oz. El 20% de to- dos los compradores seleccionan la caja de 25 oz, 50% se- leccionan una caja de 40 oz y el 30% restante seleccionan la caja de 65 oz. Sean X1 y X2 los tamaños de paquete selec- cionados por dos compradores independientemente seleccio- nados. a. Determine la distribución de muestreo de X , calcule E(X ), y compare con . b. Determine la distribución de muestreo de la varianza muestral S2 , calcule E(S2 ) y compare con 2 . 38. Hay dos semáforos en mi camino al trabajo. Sea X1 el número de semáforos en los cuales me tengo que detener y suponga que la distribución X1 es como sigue: x1 | 0 1 2 1.1, 2 0.49 p(x1) | 0.2 0.5 0.3 Sea X2 el número de semáforos en los cuales me tengo que detener camino a casa; X2 es independiente de X1. Suponga que X2 tiene la misma distribución que X1, de modo que X1, X2 es una muestra aleatoria de tamaño n 2. a. Sea To X1 X2, y determine la distribución de proba- bilidad de To. b. Calcule To . ¿Cómo se relaciona con , la media de la población? c. Calcule 2 To . ¿Cómo se relaciona con 2 , la varianza de la población? 39. Se sabe que 80% de todos los discos de almacenamiento extraíbles funcionan satisfactoriamente durante el periodo de garantía (son “éxitos”). Suponga que se seleccionan al azar n 10 unidades de disco. Sea X el número de éxi- tos en la muestra. El estadístico X/n es la proporción de la muestra (fracción) de éxitos. Obtenga la distribución mues- tral de este estadístico. [Sugerencia: Un posible valor de X/n es 0.3, correspondiente a X 3. ¿Cuál es la probabilidad de este valor (qué clase de variable aleatoria es X)?] 40. Una caja contiene diez sobres sellados numerados 1, . . . , 10. Los primeros cinco no contienen dinero, cada uno de los siguientes tres contiene $5 y hay un billete de $10 en cada uno de los últimos dos. Se selecciona un tamaño de mues- tra de 3 con reemplazo (así que se tiene una muestra alea- toria) y se obtiene la cantidad más grande en cualquiera de los sobres seleccionados. Si X1, X2 y X3 denotan las canti- dades en los sobres seleccionados, el estadístico de interés es M el máximo de X1, X2 y X3. a. Obtenga la distribución de probabilidad de este estadís- tico. b. Describa cómo realizaría un experimento de simulación para comparar las distribuciones de M con varios tama- ños de muestra. ¿Cómo piensa que cambiaría la distri- bución a medida que n se incrementa? 41. Sea X el número de paquetes enviados por un cliente selec- cionado al azar vía una compañía de paquetería y mensaje- ría. Suponga que la distribución de X es como sigue: x | 1 2 3 4 p(x) | 0.4 0.3 0.2 0.1 a. Considere una muestra aleatoria de tamaño n 2 (dos clientes) y sea X el número medio muestral de paquetes enviados. Obtenga la distribución de probabilidad de X . b. Remítase al inciso a) y calcule P(X 2.5). c. De nuevo considere una muestra aleatoria de tamaño n 2, pero ahora enfóquese en el estadístico R el ran- go muestral (diferencia entre los valores más grande y más pequeño en la muestra). Obtenga la distribución de R. [Sugerencia: Calcule el valor de R por cada resultado y use las probabilidades del inciso a).] d. Si se selecciona una muestra aleatoria de tamaño n 4, ¿Cuál es P(X 1.5)? [Sugerencia: No tiene que dar todos los resultados posibles, sólo aquellos para los cua- les x 1.5.] 42. Una compañía mantiene tres oficinas en una región, cada una manejada por dos empleados. Información concernien- te a salarios anuales (miles de dólares) es la siguiente: Oficina 1 1 2 2 3 3 Empleado 1 2 3 4 5 6 Salario 29.7 33.6 30.2 33.6 25.8 29.7 a. Suponga que dos de estos empleados se seleccionan al azar de entre los seis (sin reemplazo). Determine la dis- tribución del salario medio muestral X . b. Suponga que se selecciona al azar una de las tres ofici- nas. Sean X1 y X2 los salarios de los dos empleados. Determine la distribución muestral de X . c. ¿Cómo se compara E(X ) de los incisos a) y b) con el salario medio de la población ? 43. Suponga que la cantidad de líquido despachado por una máquina está uniformemente distribuida con límite inferior A 8 oz y límite superior B 10 oz. Describa cómo rea- lizaría experimentos de simulación para comparar la distri- bución de la (muestra) dispersión de los cuartos con tamaños de muestra n 5, 10, 20 y 30. 44. Realice un experimento con un programa de computadora estadístico u otro programa para estudiar la distribución muestral de X cuando la distribución de la población es Weibull con 2 y 5, como en el ejemplo 5.19. Considere los cuatro tamaños de muestra n 5, 10, 20 y 30 y en cada caso utilice 500 réplicas. ¿Con cuál de estos tamaños de muestra la distribución muestral X parece ser aproximadamente normal? 45. Realice un experimento de simulación con un programa de computadora estadístico u otro programa para estudiar la distribución muestral de X cuando la distribución de la población es lognormal con E(ln(X)) 3 y V(ln(X)) 1. Considere los cuatro tamaños de muestra n 10, 20, 30 y 50 y en cada caso utilice 500 réplicas. ¿Con cuál de estos tamaños de muestra la distribución muestral X parece ser aproximadamente normal? c5_p184-226.qxd 3/12/08 4:08 AM Page 212
- 231. La importancia de la medía muestral X proviene de su uso al sacar conclusiones sobre la media de la población . Algunos de los procedimientos inferenciales más frecuentemen- te utilizados están basados en propiedades de la distribución muestral de X . Un examen previo de estas propiedades apareció en los cálculos y experimentos de simulación de la sección previa, donde se observaron las relaciones entre E(X ) y y también entre V(X ), 2 y n. Comprobaciones de estos resultados se difieren a la siguiente sección. De acuerdo con el resultado 1, la distribución (es decir, probabilidad) muestral de X está centrada precisamente en la media de la población de la cual se seleccionó la muestra. El resultado 2 muestra que la distribución X se concentra más en torno a a medida que se incrementa el tamaño de la muestra n. En un marcado contraste, la distribución de To se dispersa más a medida que n se incrementa. Al promediar la probabilidad se mueve hacia la parte media, en tanto que al tota- lizar la probabilidad se dispersa sobre un rango más y más amplio de valores. En una prueba de fatiga por tensión con un espécimen de titanio, el número esperado de ciclos hasta la primera emisión acústica (utilizada para indicar la iniciación del agrieta- miento) es 28 000 y la desviación estándar del número de ciclos es 5000. Sean X1, X2, . . . , X25 una muestra aleatoria de tamaño 25, donde cada Xi es el número de ciclos en un espécimen diferente seleccionado al azar. Entonces el valor esperado del número de ciclos medio muestral hasta la primera emisión es E(X ) 28000, y el número total esperado de ciclos para los 25 especímenes es E(To) n 25(28000) 700000. La des- viación estándar de X y To son X /n 1000 To n 2 5 (5000) 25 000 Si el tamaño de muestra se incrementa a n 100, E(X ) no cambió, pero 500, la mitad de su valor previo (el tamaño de muestra debe ser cuadruplicado al dividir a la mitad la des- viación estándar de X ). ■ El caso de una distribución de población normal El experimento de simulación del ejemplo 5.22 indicó que cuando la distribución de la población es normal, cada histograma de valores x se representa muy bien con una curva normal. 5000 2 5 5.4 Distribución de la media muestral 213 5.4 Distribución de la media muestral PROPOSICIÓN Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución con valor medio y desviación estándar . Entonces 1. E(X ) X 2. V(X ) 2 X 2 /n y X /n Además, con To X1 . . . Xn (el total de la muestra), E(To) n, V(To) n2 y To n . Ejemplo 5.24 c5_p184-226.qxd 3/12/08 4:08 AM Page 213
- 232. 214 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Se sabe todo lo que se tiene que saber sobre las distribuciones X y To cuando la distribu- ción de la población es normal. En particular, las probabilidades de modo que P(a X b) y P(c To d) se obtienen simplemente estandarizando. La figura 5.14 ilustra la pro- posición. El tiempo que requiere una rata de cierta subespecie seleccionada al azar para encontrar su camino a través de un laberinto es una variable aleatoria normalmente distribuida con 1.5 min y 0.35 min. Suponga que se seleccionan cinco ratas. Sean X1, . . . , X5 sus tiem- pos en el laberinto. Suponiendo que las Xi son una muestra aleatoria de esta distribución nor- mal, ¿cuál es la probabilidad de que el tiempo total To X1 · · · X5 de las cinco sea de entre 6 y 8 min? De acuerdo con la proposición, To tiene una distribución normal con To n 5(1.5) 7.5 y varianza 2 To n2 5(0.1225) 0.6125, por tanto To 0.783. Para estandarizar To, reste To y divida entre To : P(6 To 8) P Z P( 1.92 Z 0.64) (0.64) ( 1.92) 0.7115 La determinación de la probabilidad de que el tiempo promedio muestral X (una variable normalmente distribuida) sea cuando mucho de 2.0 min requiere X 1.5 y X /n 0.35/5 0.1565. Entonces P(X 2.0) P Z P(Z 3.19) (3.19) 0.9993 ■ 2.0 1.5 0.1565 8 7.5 0.783 6 7.5 0.783 PROPOSICIÓN Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución normal con media y desviación estándar . Entonces con cualquier n, X está normalmente distribuida (con media y desviación estándar /n ), al igual que To (con media n y desvia- ción estándar n ).* Ejemplo 5.25 Figura 5.14 Distribución de la población normal y distribuciones muestrales X . Distribución X cuando n 10 Distribución X cuando n 4 Distribución de población * Una comprobación del resultado para To cuando n 2 es posible si se utiliza el método del ejemplo 5.21, pero los detalles son complicados. El resultado general casi siempre se comprueba por medio de una herramienta teó- rica llamada función generadora de momentos. Se puede consultar una de las referencias del capítulo para más información. c5_p184-226.qxd 3/12/08 4:08 AM Page 214
- 233. Teorema del límite central Cuando las Xi están normalmente distribuidas, también lo está X con cada tamaño de mues- tra n. El experimento de simulación del ejemplo 5.23, sugiere que incluso cuando la distri- bución de la población es altamente no normal, el cálculo de promedios produce una distribución más acampanada que la que está siendo muestreada. Una conjetura razonable es que si n es grande, una curva normal apropiada representará de forma más o menos apro- ximada la distribución real de X . La proposición formal de este resultado es el teorema de probabilidad más importante. La figura 5.15 ilustra el teorema del límite central. De acuerdo con el TLC, cuando n es grande y se desea calcular una probabilidad tal como P(a X b), lo único que se requiere es “pretender” que X es normal, estandarizarla y utilizar la tabla normal. La respuesta resul- tante será aproximadamente correcta. Se podría obtener la respuesta correcta determinando primero la distribución de X así que el TLC proporciona un a tajo verdaderamente impre- sionante. La comprobación del teorema implica muchas matemáticas avanzadas. La cantidad de una impureza particular en un lote de cierto producto químico es una varia- ble aleatoria con valor medio de 4.0 g y desviación estándar de 1.5 g. Si se preparan 50 lotes en forma independiente, ¿cuál es la probabilidad (aproximada) de que la cantidad prome- dio muestral de la impureza X sea de 3.5 a 3.8 g? De acuerdo con la regla empírica que se formulará en breve, n 50 es suficientemente grande como para que el TLC sea aplicable. En ese caso X tiene aproximadamente una distribución normal con valor medio X 4.0 y X 1.5/5 0 0.2121, por lo tanto P(3.5 X 3.8) P Z ( 0.94) ( 2.36) 0.1645 ■ Una organización de protección al consumidor reporta cotidianamente el número de defectos mayores de cada automóvil nuevo que prueba. Suponga que el número de tales defectos en cierto modelo es una variable aleatoria con valor medio de 3.2 y desviación estándar de 2.4. 3.8 4.0 0.2121 3.5 4.0 0.2121 5.4 Distribución de la media muestral 215 Ejemplo 5.26 Ejemplo 5.27 Figura 5.15 Teorema del límite central ilustrado. Distribución X pequeño a moderado n Distribución de población Distribución X con n grande (aproximadamente normal) TEOREMA Teorema del límite central (TLC) Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución con media y varian- za 2 . Entonces si n es suficientemente grande, X tiene aproximadamente una distri- bución normal con X y 2 X 2 /n, y To también tiene aproximadamente una distribución normal con To n, 2 To n2 . Mientras más grande es el valor de n, mejor es la aproximación. Distribución de población Distribución Distribución c5_p184-226.qxd 3/12/08 4:08 AM Page 215
- 234. 216 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Entre 100 carros seleccionados al azar de este modelo, ¿qué tan probable es que el número promedio muestral de defectos mayores exceda de 4? Sea Xi el número de defectos mayo- res del i-ésimo carro en la muestra aleatoria. Obsérvese que Xi es una variable aleatoria dis- creta, pero el TLC es aplicable si la variable de interés es discreta o continua. Además, aunque el hecho de que la desviación estándar de esta variable no negativa es bastante grande con respecto al valor medio sugiere que su distribución es positivamente asimétrica, el gran tamaño de muestra implica que X sí tiene aproximadamente una distribución normal. Con X 3.2 y X 0.24, P(X 4) P Z 1 (3.33) 0.0004 ■ El TLC da una idea de por qué muchas variables aleatorias tienen distribuciones de probabilidad que son aproximadamente normales. Por ejemplo, el error de medición en un experimento científico puede ser considerado como la suma de varias perturbaciones y erro- res subyacentes de pequeña magnitud. Aunque la utilidad del TLC para inferencia pronto será evidente, el contenido intuitivo del resultado presenta muchas dificultades para los estudiantes novicios. De nuevo regresan- do a la figura 5.7, el histograma de probabilidad a la izquierda ilustra la distribución que se está muestreando. Es discreta y bastante asimétrica de modo que no se vea en absoluto como una distribución normal. La distribución de X con n 2 comienza a exhibir algo de simetría y ésta incluso es más pronunciada con n 4 en la figura 5.8. La figura 5.16 contiene la dis- tribución de probabilidad X con n 8, así como también un histograma de probabilidad de esta distribución. Con X 46.5 y X /n 3.905/8 1.38, si se ajusta una cur- va normal con esta media y desviación estándar al histograma de X , el área de los rectángulos en el histograma de probabilidad son razonablemente bien aproximadas por las áreas de curva normal, por lo menos en la parte central de la distribución. La figura de To es similar excepto que la escala horizontal está mucho más dispersa, con To dentro de 320 (x 40) a 400 (x 50). x | 40 40.625 41.25 41.875 42.5 43.125 p(x ) | 0.0000 0.0000 0.0003 0.0012 0.0038 0.0112 x | 43.75 44.375 45 45.625 46.25 46.875 p(x ) | 0.0274 0.0556 0.0954 0.1378 0.1704 0.1746 x | 47.5 48.125 48.75 49.375 50 p(x ) | 0.1474 0.0998 0.0519 0.0188 0.0039 4 3.2 0.24 Figura 5.16 a) Distribución de probabilidad de X con n 8; b) histograma de probabilidad y aproxi- mación normal a la distribución de X cuando la distribución original es como en el ejemplo 5.20. 0.175 0.15 0.125 0.10 0.075 0.05 0.025 42.5 45 47.5 50 40 a) b) c5_p184-226.qxd 3/12/08 4:08 AM Page 216
- 235. Una dificultad práctica al aplicar el teorema del límite central es saber cuándo n es suficientemente grande. El problema es que la precisión de la aproximación con una n particular depende de la forma de la distribución subyacente original que está siendo muestreada. Si la distribución subyacente tiende a una curva de densidad normal, entonces la aproximación será buena incluso con n pequeña, mientras que si está lejos de ser normal, entonces se requerirá una n grande. Existen distribuciones de población para las cuales una n de 40 o 50 no son suficientes, pero tales distribuciones rara vez se encuentran en la práctica. Por otra parte, la regla empírica a menudo es conservadora; para muchas distribuciones de población, una n mucho menor que 30 serían suficientes. Por ejemplo, en el caso de una distribución de población uniforme, el teorema del límite central da una buena aproximación con n 12. Otras aplicaciones del teorema del límite central El teorema del límite central puede ser utilizado para justificar la aproximación normal a la distribución binomial discutida en el capítulo 4. Recuérdese que una variable binomial X es el número de éxitos en una experiencia binomial compuesta de n ensayos independien- tes con éxitos/fallas y p P(S) para cualquier ensayo particular. Defínanse nuevas varia- bles aleatorias X1, X2, . . . , Xn como Xi {1 Si el i-ésimo ensayo produce un éxito (i 1, . . . , n) 0 Si el i-ésimo ensayo produce una falla Como los ensayos son independientes y P(S) es constante de un ensayo a otro, las Xi son idénticas (una muestra aleatoria de una distribución de Bernoulli). El teorema del límite cen- tral implica entonces que si n es suficientemente grande, tanto la suma como el promedio de las Xi tienen distribuciones normales de manera aproximada. Cuando se suman las Xi, se agrega un 1 por cada S (éxito) que ocurra y un 0 por cada F (falla), por tanto X1 · · · Xn X. La media muestral de las Xi es X/n, la proporción muestral de éxitos. Es decir, tanto X como X/n son aproximadamente normales cuando n es grande. El tamaño de muestra nece- sario para esta aproximación depende del valor de p: Cuando p se acerca a 0.5, la distribu- ción de cada Xi es razonablemente simétrica (véase la figura 5.17), mientras que la distribución es bastante asimétrica cuando p se acerca a 0 o 1. Utilizando la aproximación sólo si tanto np 10 como a n(1 p) 10 garantiza que n es suficientemente grande para superar cualquier asimetría en la distribución de Bernoulli subyacente. Recuérdese por la sección 4.5 que X tiene una distribución lognormal si ln(X) tiene una distribución normal. 5.4 Distribución de la media muestral 217 Figura 5.17 Dos distribuciones de Bernoulli: a) p 5 4 (razonablemente simétrica); b) p 5 1 (muy asimétrica). 0 1 a) 0 1 b) Regla empírica Si n 30, se puede utiliza el teorema del límite central. PROPOSICIÓN Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución para la cual sólo valo- res positivos son posibles [P(Xi 0) 1]. Entonces si n es suficientemente grande, el producto Y X1X2 · · · · · Xn tiene aproximadamente una distribución lognormal. c5_p184-226.qxd 3/12/08 4:08 AM Page 217
- 236. 218 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Para verificar esto, obsérvese que ln(Y) ln(X1) ln(X2) . . . ln(Xn) Como ln(Y) es una suma de variables aleatorias independientes y distribuidas de manera idéntica [las ln(Xi)], es aproximadamente normal cuando n es grande, así que Y tiene apro- ximadamente una distribución lognormal. Como ejemplo de la aplicabilidad de este resul- tado, Bury (Statistical Models in Applied Science, Wiley, p. 590) argumenta que el proceso de daños en el flujo plástico y en la propagación de grietas es un proceso multiplicativo, de modo que las variables tales como porcentaje de alargamiento y resistencia a la ruptura tie- nen aproximadamente distribuciones lognormales. EJERCICIOS Sección 5.4 (46-57) 46. El diámetro interno de un anillo de pistón seleccionado al azar es una variable aleatoria con valor medio de 12 cm y desviación estándar de 0.04 cm. a. Si X es el diámetro medio en una muestra aleatoria de n 16 anillos, ¿dónde está centrada la distribución muestral de X y cuál es la desviación estándar de la distribución X ? b. Responda las preguntas planteadas en el inciso a) con un tamaño de muestra de n 64 anillos. c. ¿Con cuál de las dos muestras aleatorias, la del inciso a) o la del inciso b), es más probable que X esté dentro de 0.01 cm de 12 cm? Explique su razonamiento. 47. Remítase al ejercicio 46. Suponga que el diámetro de la dis- tribución es normal. a. Calcule P(11.99 X 12.01) cuando n 16. b. ¿Qué tan probable es que el diámetro medio muestral exceda de 12.01 cuando n 25? 48. Sean X1, X2, . . . , X100 los pesos netos reales de 100 sacos de 50 lb de fertilizante seleccionados al azar. a. Si el peso esperado de cada saco es de 50 lb y la varian- za es uno, calcule P(49.9 X 50.1) (aproximada- mente) por medio del teorema del límite central. b. Si el peso esperado es de 49.8 lb en lugar de 50 lb de modo que en promedio los sacos están menos llenos, calcule P(49.9 X 50.1). 49. Hay 40 estudiantes en una clase de estadística elemental. Basado en años de experiencia, el instructor sabe que el tiempo requerido para calificar un primer examen seleccio- nado al azar es una variable aleatoria con un valor esperado de seis min y una desviación estándar de seis min. a. Si los tiempos de calificación son independientes y el instructor comienza a calificar a las 6:50 p.m. y califica en forma continua, ¿cuál es la probabilidad (aproxima- da) de que termine de calificar antes de que se inicie el programa de noticias de las 11:00 p.m.? b. Si el reporte de deportes se inicia a la 11:10, ¿cuál es la probabilidad de que se pierda una parte del reporte si se espera hasta que termine de calificar antes de prender la TV? 50. La resistencia a la ruptura de un remache tiene un valor medio de 10 000 lb/pulg2 y una desviación estándar de 500 lb/pulg2 . a. ¿Cuál es la probabilidad de que la resistencia a la ruptu- ra media de una muestra aleatoria de 40 remaches sea de entre 9900 y 10 200? b. Si el tamaño de muestra hubiera sido de 15 y no de 40, ¿se podría calcular la probabilidad solicitada en el inci- so a) con la información dada? 51. El tiempo requerido por un solicitante seleccionado al azar de una hipoteca para llenar un formulario tiene una distri- bución normal con valor medio de 10 min y desviación estándar de dos min. Si cinco individuos llenan un formula- rio en un día y seis en otro, ¿cuál es la probabilidad de que la cantidad promedio muestral de tiempo requerido cada día sea cuando mucho de 11 min? 52. La vida útil de un tipo de batería está normalmente distribuida con valor medio de 10 horas y desviación estándar de una hora. Hay cuatro baterías en un paquete. ¿Qué valor de vida útil es tal que la vida útil total de todas las baterías contenidas en un paquete exceda de ese valor en sólo 5% de todos los paquetes? 53. Se sabe que la dureza Rockwell de “pernos” de un tipo tie- ne un valor medio de 50 y una desviación estándar de 1.2. a. Si la distribución es normal, ¿cuál es la probabilidad de que la dureza media de una muestra aleatoria de 9 per- nos sea por lo menos de 51? b. ¿Cuál es la probabilidad (aproximada) de que la dureza media de una muestra aleatoria de 40 pernos sea por lo menos de 51? 54. Suponga que la densidad de un sedimento (g/cm) de un espécimen seleccionado al azar de cierta región está nor- malmente distribuida con media de 2.65 y desviación están- dar de 0.85 (sugerida en “Modeling Sediment and Water Column Interactions for Hydrophobic Pollutants”, Water Research, 1984: 1169-1174). a. Si se selecciona una muestra aleatoria de 25 especíme- nes, ¿cuál es la probabilidad de que la densidad del sedi- mento promedio muestral sea cuando mucho de 3.00? ¿De entre 2.65 y 3.00? b. ¿Qué tan grande debe ser un tamaño de muestra para garantizar que la primera probabilidad en el inciso a) sea por lo menos de 0.99? 55. El número de infracciones de estacionamiento aplicadas en una ciudad en cualquier día de la semana dado tiene una distribución de Poisson con parámetro 50. ¿Cuál es la probabilidad aproximada de que a. entre 35 y 70 infracciones sean aplicadas en un día par- ticular? [Sugerencia: Cuando es grande, una variable aleatoria de Poisson tiene aproximadamente una distri- bución normal.] c5_p184-226.qxd 3/12/08 4:08 AM Page 218
- 237. La media muestral X y el total muestral To son casos especiales de un tipo de variable alea- toria que surgen con frecuencia en aplicaciones estadísticas. Con a1 a2 . . . an 1 se obtiene Y X1 . . . Xn To, y a1 a2 . . . an 1 n da Y 1 n X1 . . . 1 nXn 1 n(X1 . . . Xn) 1 nTo X . Obsérvese que no se requiere que las Xi sean independientes o que estén idénticamente distribuidas. Todas las Xi podrían tener distribuciones diferentes y por consiguiente valores y varianzas medias diferentes. Primero se considera el valor y la varianza esperados de una combinación lineal. 5.5 Distribución de una combinación lineal 219 b. el número total de infracciones aplicadas durante una semana de 5 días sea de entre 225 y 275? 56. Un canal de comunicación binaria transmite una secuencia de “bits” (ceros y unos). Suponga que por cualquier bit par- ticular transmitido, existe una probabilidad de 0.1 de que ocurra un error en la transmisión (un 0 se convierte en 1 o un 1 se convierte en 0). Suponga que los errores en los bits ocurren independientemente uno de otro. a. Considere transmitir 1000 bits. ¿Cuál es la probabilidad aproximada de que cuando mucho ocurran 125 errores de transmisión? b. Suponga que el mismo mensaje de 1000 bits es enviado en dos momentos diferentes independientemente uno de otro? ¿Cuál es la probabilidad aproximada de que el número de errores en la primera transmisión sea dentro de 50 del número en la segunda? 57. Suponga que la distribución del tiempo X (en horas) utili- zado por estudiantes en cierta universidad en un proyecto particular es gama con parámetros 50 y 2. Como es grande, se puede demostrar que X tiene aproximada- mente una distribución normal. Use este hecho para calcu- lar la probabilidad de que un estudiante seleccionado al azar utilice cuando mucho 125 horas en el proyecto. 5.5 Distribución de una combinación lineal PROPOSICIÓN Si X1, X2, . . . , Xn tienen valores medios 1, . . . , n, respectivamente y varianzas 2 1, . . . , 2 n, respectivamente. 1. Si las Xi son independientes o no. E(a1X1 a2X2 . . . anXn) a1E(X1) a2E(X2) . . . anE(Xn) a11 . . . ann (5.8) 2. Si X1, . . . , Xn son independientes, V(a1X1 a2X2 . . . anXn) a2 1V(X1) a2 2V(X2) . . . a2 nV(Xn) a2 12 1 . . . a2 n2 n (5.9) y a1X1. . .anXn a2 12 1 . . . a2 n 2 n (5.10) 3. Con cualquiera X1, . . . , Xn, V(a1X1 . . . anXn) n i1 n j1 aiaj COV(Xi, Xj) (5.11) DEFINICIÓN Dado un conjunto de n variables aleatorias X1, . . . , Xn y n constantes numéricas a1,..., an, la variable aleatoria Y a1X1 . . . anXn n i1 aiXi (5.7) se llama combinación lineal de las Xi. c5_p184-226.qxd 3/12/08 4:08 AM Page 219
- 238. 220 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias Las comprobaciones se dan al final de la sección. Un parafraseo de (5.8) es que el valor espe- rado de una combinación lineal es la misma combinación lineal de los valores esperados, por ejemplo, E(2X1 5X2) 21 52. El resultado (5.9) en la proposición 2 es un caso especial de (5.11) en la proposición 3; cuando las Xi son independientes, Cov(Xi, Xj) 0 con i j e igual a V(Xi) con i j (esta simplificación en realidad ocurre cuando las Xi no están correla- cionadas, una condición más débil que la de independencia). Especializando al caso de una muestra aleatoria (Xi idénticamente distribuidas) con ai 1/n con cada i da E(X ) y V(X ) 2 /n, como se discutió en la sección 5.4. Un comentario similar se aplica a las reglas para To. Una gasolinería vende tres grados de gasolina; regular, extra y súper. Éstas se venden a $21.20, $21.35 y $21.50 por galón, respectivamente. Sean X1, X2 y X3 las cantidades (galo- nes) de estas gasolinas compradas en un día particular. Suponga que las Xi son indepen- dientes con 1 1000, 2 500, 3 300, 1 100, 2 80, y 3 50. El ingreso por las ventas es Y 21.2X1 21.35X2 21.5X3 y E(Y) 21.21 21.352 21.53 $4125 V(Y) (21.2)2 2 1 (21.35)2 2 2 (21.5)2 2 3 104 025 Y 10402 5 $322.53 ■ Diferencia entre dos variables aleatorias Un caso especial importante de una combinación lineal se presenta con n 2, a1 1 y a2 1: Y a1X1 a2X2 X1 X2 Entonces se tiene el siguiente corolario de la proposición. El valor esperado de una diferencia es la diferencia de los dos valores esperados, pero la varianza de una diferencia entre dos variables independientes es la suma, no la diferencia, de las dos varianzas. Existe tanta variabilidad en X1 X2 como en X1 X2 [escribiendo X1 X2 X1 (1)X2, (1)X2 tiene la misma cantidad de variabilidad que X2]. Una compañía automotriz equipa un modelo particular con un motor de seis cilindros o un motor de cuatro cilindros. Sean X1 y X2 eficiencias de combustible de carros de seis y cua- tro cilindros seleccionados en forma independiente al azar, respectivamente. Con 1 22, 2 26, 1 1.2 y 2 1.5, E(X1 X2) 1 2 22 26 4 V(X1 X2) 2 1 2 2 (1.2)2 (1.5)2 3.69 X1X2 3 .6 9 1.92 Si se cambia la notación de modo que X1 se refiera al carro de cuatro cilindros, entonces E(X1 X2) 4, pero la varianza de la diferencia sigue siendo de 3.69. ■ El caso de variables aleatorias normales Cuando las Xi forman una muestra aleatoria de una distribución normal, X y To están normal- mente distribuidas. He aquí un resultado más general con respecto a combinaciones lineales. Ejemplo 5.28 Ejemplo 5.29 COROLARIO E(X1 X2) E(X1) E(X2) y, si X1 y X2 son independientes, V(X1 X2) V(X1) V(X2). c5_p184-226.qxd 3/12/08 4:08 AM Page 220
- 239. El ingreso total por la venta de los tres grados de gasolina en un día particular fue Y 21.2X1 21.35X2 21.5X3, y se calculó Y 4125 y (suponiendo independencia) Y 322.53. Si las Xi están normalmente distribuidas, la probabilidad de que el ingreso sea de más de 4500 es P(Y 4500) P Z P(Z 1.16) 1 (1.16) 0.1230 ■ El teorema del límite central también puede ser generalizado para aplicarlo a ciertas combina- ciones lineales. En general, si n es grande y no es probable que algún término individual con- tribuya demasiado al valor total, entonces Y tiene aproximadamente una distribución normal. Comprobaciones en el caso n 2 En cuanto al resultado por lo concerniente a los valores esperados, suponga que X1 y X2 son continuas con función de densidad de probabilidad conjunta f(x1, x2). Entonces E(a1X1 a2X2) (a1x1 a2x2)f(x1, x2) dx1 dx2 a1 x1 f(x1, x2) dx2 dx1 a2 x2 f(x1, x2) dx1 dx2 a1 x1 fX1 (x1) dx1 a2 x2 fX2 (x2) dx2 a1E(X1) a2E(X2) La suma reemplaza a la integración en el caso discreto. El argumento en cuanto a la varian- za resultante no requiere especificar si la variable es discreta o continua. Recordando que V(Y) E[(Y Y)2 ], V(a1X1 a2X2) E{[a1X1 a2X2 (a11 a22)]2 } E{a2 1(X1 1)2 a2 2(X2 2)2 2a1a2(X1 1)(X2 2)} La expresión adentro de las llaves es una combinación lineal de las variables Y1 (X1 1)2 , Y2 (X2 2)2 y Y3 (X1 1)(X2 2), así que si se acarrea la operación E a través de los tres términos se obtiene a2 1V(X1) a2 2V(X2) 2a1a2 Cov(X1, X2) como se requiere. ■ 4500 4125 322.53 5.5 Distribución de una combinación lineal 221 PROPOSICIÓN Si X1, X2, . . . , Xn son variables aleatorias independientes normalmente distribuidas (con quizá diferentes medias y/o varianzas), entonces cualquier combinación lineal de las Xi también tiene una distribución normal. En particular, la diferencia X1 X2 entre dos variables independientes normalmente distribuidas también está distribuida en forma normal. Ejemplo 5.30 (continuación del ejemplo 5.28) EJERCICIOS Sección 5.5 (58-74) 58. Una compañía naviera maneja contenedores en tres dife- rentes tamaños: (1) 27 pies3 (3 3 3), (2) 125 pies3 y (3) 512 pies3 . Sea Xi (i 1, 2, 3) el número de contenedores de tipo i embarcados durante una semana dada. Con i E(Xi) y 2 i V(Xi), suponga que los valores medios y las desvia- ciones estándar son como sigue: 1 200 2 250 3 100 1 10 2 12 3 8 c5_p184-226.qxd 3/12/08 4:08 AM Page 221
- 240. 222 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias a. Suponiendo que X1, X2, X3 son independientes, calcule el valor esperado y la varianza del volumen total embarca- do [Sugerencia: Volumen 27X1 125X2 512X3.] b. ¿Serían sus cálculos necesariamente correctos si las Xi no fueran independientes? Explique. 59. Si X1, X2 y X3 representan los tiempos necesarios para rea- lizar tres tareas de reparación sucesivas en cierto taller de servicio. Suponga que son variables aleatorias normales independientes con valores esperados 1, 2 y 3 y varian- zas 2 1, 2 2 y 2 3, respectivamente. a. Si 2 3 60 y 2 1 2 2 2 3 15, calcule P(X1 X2 X3 200). ¿Cuál es P(150 X1 X2 X3 200)? b. Con las i y i dadas en el inciso a), calcule P(55 X ) y P(58 X 62). c. Con las i y i dadas en el inciso a), calcule P(10 X1 0.5X2 0.5X3 5). d. Si 1 40, 2 50, 3 60, 2 1 10, 2 2 12, y 2 3 14, calcule P(X1 X2 X3 160) y P(X1 X2 2 X3). 60. Cinco automóviles del mismo tipo tienen que realizar un viaje de 300 millas. Los primeros dos utilizarán una marca económica de gasolina y los otros tres una marca de renom- bre. Sean X1, X2, X3, X4 y X5 las eficiencias de combustible observadas (mpg) de los cinco carros. Suponga que estas variables son independientes y normalmente distribuidas con 1 2 20, 3 4 5 21 y 2 4 con la mar- ca económica y 3.5 con la marca de renombre. Defina una variable aleatoria Y como Y de modo que Y mide la diferencia de eficiencia entre la gasolina económica y la de renombre. Calcule P(0 Y) y P(1 Y 1). [Sugerencia: Y a1X1 . . . a5X5, con a1 2 1 , . . . , a5 1 3.] 61. El ejercicio 26 introdujo variables aleatorias X y Y, el núme- ro de carros y autobuses, respectivamente, transportados por un transbordador en un solo viaje. La función masa de probabilidad conjunta de X y Y se da en la tabla del ejerci- cio 7. Es fácil verificar que X y Y son independientes. a. Calcule el valor esperado, la varianza y la desviación estándar del número total de vehículos en un solo viaje. b. Si a cada carro se le cobran $3 y a cada autobús $10, calcule el valor esperado, la varianza y la desviación estándar del ingreso resultante de un solo viaje. 62. Un fabricante de un cierto componente requiere tres opera- ciones de maquinado diferentes. El tiempo de maquinado de cada operación tiene una distribución normal y los tres tiem- pos son independientes entre sí. Los valores medios son 15, 30 y 20 min, respectivamente y las desviaciones estándar son 1, 2 y 1.5 min respectivamente. ¿Cuál es la probabilidad de que se requiera cuando mucho una hora de tiempo de maquinado para producir un componente seleccionado al azar? 63. Remítase al ejercicio 3. a. Calcule la covarianza entre X1 el número de clientes en la caja rápida y X2 el número de clientes en la caja súperrápida. b. Calcule V(X1 X2). ¿Cómo se compara con V(X1) V(X2)? 64. Suponga que el tiempo de espera para un autobús en la maña- na está uniformemente distribuido en [0, 8], mientras que el tiempo de espera en la noche está uniformemente distribuido en [0, 10] independiente del tiempo de espera en la mañana. a. Si toma el autobús en la mañana y en la noche durante una semana, ¿cuál es su tiempo de espera total espera- do? [Sugerencia: Defina las variables aleatorias X1, . . . , X10 y use una regla de valor esperado.] b. ¿Cuál es la varianza de su tiempo de espera total? c. ¿Cuáles son el valor esperado y la varianza de la dife- rencia entre los tiempos de espera en la mañana y en la noche en un día dado? d. ¿Cuáles son el valor esperado y la varianza de la diferencia entre el tiempo de espera total en la mañana y el tiempo de espera total en la noche durante una semana particular? 65. Suponga que cuando el pH de cierto compuesto químico es 5.00, el pH medido por un estudiante de química de primer año seleccionado al azar es una variable aleatoria con media de 5.00 y desviación estándar de 0.2. Un gran lote del com- puesto se subdivide y a cada estudiante se le da una mues- tra en un laboratorio matutino y a cada estudiante en un laboratorio vespertino. Sea X el pH promedio determina- do por los estudiantes matutinos y Y el pH promedio determinado por los estudiantes vespertinos. a. Si el pH es una variable normal y hay 25 estudiantes en cada laboratorio, calcule P(0.1 X Y 0.1). [Sugerencia: X Y es una combinación lineal de varia- bles normales, así que está normalmente distribuida. Calcule X Y y X Y .] b. Si hay 36 estudiantes en cada laboratorio, pero las deter- minaciones del pH no se suponen normales, calcule (aproximadamente) P(0.1 X Y 0.1). 66. Si se aplican dos cargas a una viga en voladizo como se muestra en la figura adjunta, el momento de flexión en 0 debido a las cargas es a1X1 a2X2. a. Suponga que X1 y X2 son variables independientes con medias de 2 y 4 klb, respectivamente y desviación estándar de 0.5 y 1.0 klb, respectivamente. Si a1 5 pies y a2 10 pies, ¿cuál es el momento de flexión esperado y cuál es la desviación estándar del momento de flexión? b. Si X1 y X2 están normalmente distribuidas, ¿cuál es la probabilidad de que el momento de flexión sea de más de 75 klb-pie? c. Suponga que las posiciones de las dos cargas son varia- bles aleatorias. Denotándolas por A1 y A2, suponga que estas variables tienen medias de 5 y 10 pies, respectiva- mente, que cada una tiene una desviación estándar de 0.5 y que todas las Ai y Xi son independientes entre sí. ¿Cuál es el momento esperado ahora? d. En la situación del inciso c), ¿cuál es la varianza del momento de flexión? X1 X2 a1 a2 0 X3 X4 X5 3 X1 X2 2 c5_p184-226.qxd 3/12/08 4:08 AM Page 222
- 241. 5.5 Distribución de una combinación lineal 223 e. Si la situación es como se describe en el inciso a) excep- to que Corr(X1, X2) 0.5 (de modo que las dos cargas no sean independientes), ¿cuál es la varianza del mo- mento de flexión? 67. Un tramo de tubería de PVC tiene que ser insertado en otro tramo. La longitud del primer tramo está normalmente dis- tribuido con valor medio de 20 pulg y desviación estándar de 0.5 pulg. El segundo tramo es una variable aleatoria nor- mal con media y desviación estándar de 15 pulg y 0.4 pulg, respectivamente. La cantidad de traslape está normalmente distribuido con valor medio de una pulg y desviación están- dar de 0.1 pulg. Suponiendo que los tramos y cantidad de traslape son independientes entre sí, ¿cuál es la probabili- dad de que la longitud total después de la inserción esté entre 34.5 pulg y 35 pulg? 68. Dos aviones vuelan en la misma dirección en dos corredo- res adyacentes. En el instante t 0, el primer avión está a 10 km adelante del segundo. Suponga que la velocidad del primero (km/h) está normalmente distribuida con media de 520 y desviación estándar de 10 y que la velocidad del segundo también está normalmente distribuida con media y desviación estándar de 500 y 10, respectivamente. a. ¿Cuál es la probabilidad de que después de 2 horas de vuelo, el segundo avión no haya alcanzado al primer avión? b. Determine la probabilidad de que los aviones estén separados cuando mucho 10 km después de 2 horas. 69. Tres carreteras diferentes entroncan en una autopista particu- lar. Suponga que durante un tiempo fijo, el número de carros que llegan por cada carretera a la autopista es una variable aleatoria, con valor esperado y desviación estándar como se dan en la tabla | Carretera 1 Carretera 2 Carretera 3 Valor esperado | 800 1000 600 Desviación estándar | 16 25 18 a. ¿Cuál es el número de carros total esperado que entran a la autopista en este punto durante el periodo? [Sugerencia: Sea Xi el número de la carretera i.] b. ¿Cuál es la varianza del número total de carros que entran? ¿Ha hecho suposiciones sobre la relación entre los números de carros en las diferentes carreteras? c. Con Xi denotando el número de carros que entran de la carretera i durante el periodo, suponga que Cov(X1, X2) 80, Cov(X1, X3) 90 y Cov(X2, X3) 100 (de modo que las tres corrientes de tráfico no son indepen- dientes). Calcule el número total esperado de los carros que entran y la desviación estándar del total. 70. Considere una muestra aleatoria de tamaño n tomada de una distribución continua con mediana 0 de modo que la proba- bilidad de cualquier observación sea positiva de 0.5. Ha- ciendo caso omiso de los signos de las observaciones, clasifíquelas desde la más pequeña a la más grande en valor absoluto y sea W la suma de las filas de las observacio- nes con signos positivos. Por ejemplo, si las observaciones son 0.3, 0.7, 2.1 y 2.5, entonces las filas de obser- vaciones positivas son 2 y 3, de modo que W 5. En el capítulo 15, W se llamará estadístico de filas con signo de Wilcoxon. W puede representarse como sigue: W 1 Y1 2 Y2 3 Y3 . . . n Yn n i1 i Yi donde las Yi son variables aleatorias independientes de Bernoulli, cada una con p 0.5(Yi 1 corresponde a la observación con fila i positiva). a. Determine E(Yi) y luego E(W) utilizando la ecuación para W. [Sugerencia: Los primeros n enteros positivos suman n(n 1)/2.] b. Determine V(Yi) y luego V(W). [Sugerencia: La suma de los cuadrados de los primeros n enteros positivos puede expresarse como n(n 1)(2n 1)/6.] 71. En el ejercicio 66, el peso de viga contribuye al momento de flexión. Suponga que la viga es de espesor y densidad uniformes, de modo que la carga resultante esté uniforme- mente distribuida en la viga. Si el peso de ésta es aleatorio, la carga resultante a consecuencia del peso también es alea- toria; denote esta carga por W(klb-pies). a. Si la viga es de 12 pies de largo, W tiene una media de 1.5 y una desviación estándar de 0.25 y las cargas fijas son como se describen en el inciso a) del ejercicio 66, ¿cuáles son el valor esperado y la varianza del momen- to de flexión? [Sugerencia: Si la carga originada por la viga fuera w klb-pies, la contribución al momento de fle- xión sería w 12 0 x dx.] b. Si las tres variables (X1, X2 y W) están normalmente dis- tribuidas, ¿cuál es la probabilidad de que el momento de flexión será cuando mucho de 200 klb-pies? 72. Tengo tres encargos que atender en el edificio de administra- ción. Sea Xi el tiempo que requiere el i-ésimo encargo (i 1, 2, 3) y sea X4 el tiempo total en minutos que me pa- so caminando hasta y desde el edificio y entre cada encargo. Suponga que las Xi son independientes y normalmente distri- buidas con las siguientes medias y desviaciones estándar 1 15, 1 4, 2 5, 2 1, 3 8, 3 2, 4 12, 4 3. Pienso salir de mi oficina precisamente a las 10:00 a.m. y deseo pegar una nota en la puerta que diga “Regreso al- rededor de las t a.m.”. ¿Qué hora debo escribir si deseo que la probabilidad de mi llegada después de t sea de 0.01? 73. Suponga que la resistencia a la tensión de acero tipo A es de 105 klb2 y que la desviación estándar de la resistencia a la tensión es de 8 klb2 . Para acero tipo B, suponga que la resistencia a la tensión esperada y la desviación estándar de la resistencia a la tensión son de 100 klb2 y 6 klb2 , respec- tivamente. Sea X la resistencia a la tensión promedio de una muestra aleatoria de 40 especímenes tipo A y sea Y la resistencia a la tensión promedio de una muestra aleato- ria de 35 especímenes tipo B. a. ¿Cuál es la distribución aproximada de X ? ¿De Y ? b. ¿Cuál es la distribución aproximada de X Y ? Justifi- que su respuesta. c. Calcule (aproximadamente) P(1 X Y 1). d. Calcule P(X Y 10). Si en realidad observó X Y 10, dudaría que 1 2 5? c5_p184-226.qxd 3/12/08 4:08 AM Page 223
- 242. 224 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias 74. En un área de suelo arenoso se plantaron 50 árboles pequeños de un cierto tipo y otros 50 se plantaron en un área de suelo arcilloso. Sea X el número de árboles plantados en suelo arenoso que sobreviven un año y Y el número de árboles plantados en suelo arcilloso que sobre- viven un año. Si la probabilidad de que un árbol plantado en suelo arenoso sobreviva un año es de 0.7 y la probabili- dad de sobrevivencia de un año en suelo arcilloso es de 0.6, calcule una aproximación a P(5 X Y 5) (no se moleste con la corrección de continuidad). 75. Un restaurante sirve tres comidas que cuestan $12, $15 y $20. Para una pareja seleccionada al azar que está comien- do en este restaurante, sea X el costo de la comida del hombre y Y el costo de la comida de la mujer. La función masa de probabilidad conjunta de X y Y se da en la siguien- te tabla: y p(x, y) | 12 15 20 12 | 0.05 0.05 0.10 x 15 | 0.05 0.10 0.35 20 | 0 0.20 0.10 a. Calcule las funciones masa de probabilidad marginal de X y Y. b. ¿Cuál es la probabilidad de que las comidas del hombre y la mujer cuesten cuando mucho $15 cada una? c. ¿Son X y Y independientes? Justifique su respuesta. d. ¿Cuál es el costo total esperado de la comida de las dos personas? e. Suponga que cuando una pareja abre las galletas de la fortuna al final de la comida, encuentran el mensaje “Recibirá como reembolso la diferencia entre el costo de la comida más cara y la menos cara que eligió”. ¿Cuánto espera reembolsar el restaurante? 76. En una estimación de costos, el costo total de un proyecto es la suma de los costos de las tareas componentes. Cada uno de estos costos es una variable aleatoria con distribución de probabilidad. Se acostumbra obtener información sobre la distribución de costos total sumando las características de las distribuciones de costo de componente individuales; esto se conoce como procedimiento de “despliegue”. Por ejemplo, E(X1 . . . Xn) E(X1) . . . E(Xn), así que el procedimiento de despliegue es válido para costo medio. Suponga que hay dos tareas componentes y que X1 y X2 son variables aleatorias independientes normalmente distribui- das. ¿Es válido el procedimiento de despliegue para el 75º percentil? Es decir, ¿Es el 75º percentil de la distribución de X1 X2 el mismo que la suma de los 75º percentiles de las dos distribuciones individuales? Si no, ¿cuál es la relación entre el percentil de la suma y la suma de los percentiles? ¿Con qué percentiles es válido el procedimiento de desplie- gue en este caso? 77. Una tienda de comida saludable vende dos marcas diferen- tes de un tipo de grano. Sea X la cantidad (lb) de la mar- ca A disponible y Y la cantidad de la marca B, disponible. Suponga que la función de densidad de probabilidad con- junta de X y Y es f(x, y) {kxy x 0, y 0, 20 x y 30 0 de lo contrario a. Trace la región de densidad positiva y determine el valor de k. b. ¿Son X y Y independientes? Responda obteniendo pri- mero la función de densidad de probabilidad marginal de cada variable. c. Calcule P(X Y 25). d. ¿Cuál es la cantidad total esperada de este grano dis- ponible? e. Calcule Cov(X, Y) y Corr(X, Y). f. ¿Cuál es la varianza de la cantidad total de grano disponible? 78. Sean X1, X2, . . . , Xn variables aleatorias que denotan n pos- turas independientes para un artículo que está a la venta. Suponga que cada Xi está uniformemente distribuida en el intervalo [100, 200]. Si el vendedor se lo vende al postor más alto, ¿cuánto puede esperar ganar en la venta? [Sugerencia: Sea Y máx(X1, X2, . . . , Xn). Primero halle FY(y) observan- do que Y y si y sólo si cada Xi es y. Luego obtenga la función de densidad de probabilidad y E(Y).] 79. Suponga que para un individuo, la ingesta de calorías en el desayuno es una variable aleatoria con valor esperado de 500 y desviación estándar de 50, la ingesta de calorías en el almuerzo es aleatoria con valor esperado de 900 y desvia- ción estándar de 100 y la ingesta de calorías en la comida es una variable aleatoria con valor esperado de 2000 y des- viación estándar de 180. Suponiendo que las ingestas en las diferentes comidas son independientes entre sí, ¿cuál es la probabilidad de que la ingesta de calorías promedio por día durante el siguiente año (365 días) sea cuando mucho de 3500? [Sugerencia: Sean Xi, Yi y Zi las tres ingestas de calo- rías en el día i. Entonces la ingesta total es (Xi Yi Zi).] 80. El peso medio del equipaje documentado por un pasajero de clase turista seleccionado al azar que vuela entre dos ciuda- des en cierta aerolínea es de 40 lb y la desviación estándar es de 10 lb. La media y la desviación estándar de un pasa- jero de clase de negocios son 30 lb y 6 lb, respectivamente. a. Si hay 12 pasajeros de clase de negocios y 50 de clase turista en un vuelo particular, ¿cuáles son el valor espe- rado y la desviación estándar del peso total del equipaje? b. Si los pesos individuales de los equipajes son variables aleatorias independientes normalmente distribuidas, ¿cuál es la probabilidad de que el peso total del equipa- je sea cuando mucho de 2500 lb? 81. Se ha visto que si E(X1) E(X2) . . . E(Xn) , entonces E(X1 . . . Xn) n. En algunas aplicacio- nes, el número de Xi considerado no es un número fijo n sino una variable aleatoria N. Por ejemplo, sea N el número de componentes que son traídos a un taller de repa- ración en un día particular y sea Xi el tiempo de reparación EJERCICIOS SUPLEMENTARIOS (75-95) c5_p184-226.qxd 3/12/08 4:08 AM Page 224
- 243. Ejercicios suplementarios 225 del i-ésimo componente, entonces el tiempo de reparación total es X1 X2 . . . XN, la suma de un número aleato- rio de variables aleatorias. Cuando N es independiente de las Xi se puede demostrar que E(X1 . . . XN) E(N) a. Si el número de componentes traídos en un día particu- lar es 10 y el tiempo de reparación esperado de un com- ponente seleccionado al azar es de 40 min, ¿cuál es el tiempo de reparación total de componentes entregados en cualquier día particular? b. Suponga que componentes de un tipo llegan para ser repa- rados de acuerdo en un proceso de Poisson a razón de cin- co por hora. El número esperado de defectos por componente es de 3.5. ¿Cuál es el valor esperado del número total de defectos en componentes traídos a repara- ción durante un periodo de cuatro horas? Asegúrese de indicar cómo su respuesta se deriva del resultado general que se acaba de dar. 82. Suponga que la proporción de votantes rurales en un estado que favorecen a un candidato particular es de 0.45 y que la proporción de votantes suburbanos y urbanos que favorecen al candidato es de 0.60. Si se obtiene una muestra de 200 votantes rurales y 300 votantes suburbanos y urbanos, ¿cuál es la probabilidad aproximada de que por lo menos 250 de estos votantes favorezcan a este candidato? 83. Sea el pH verdadero de un compuesto químico. Se reali- zará una secuencia de n determinaciones de pH muestrales independientes. Suponga que cada pH muestra es una varia- ble aleatoria con valor esperado y desviación estándar de 0.1. ¿Cuántas determinaciones se requieren si se desea que la probabilidad de que el promedio muestral esté dentro de 0.02 de pH verdadero sea por lo menos de 0.95? ¿Qué teorema justifica su cálculo de probabilidad? 84. Si la cantidad de refresco que consumo en cualquier día dado es independiente del consumo en cualquier otro día y está normalmente distribuido con 13 oz y 2 y en este momento tengo dos paquetes de seis botellas de 16 oz, ¿cuál es la probabilidad de que todavía tenga algo de refresco al cabo de 2 semanas (14 días)? 85. Remítase al ejercicio 58 y suponga que las Xi son indepen- dientes entre sí y que cada una tiene una distribución nor- mal. ¿Cuál es la probabilidad de que el volumen total embarcado sea cuando mucho de 100 000 pies3 ? 86. Un estudiante tiene una clase que se supone termina a las 9:00 a.m. y otra que se supone comienza a las 9:10 a.m. Su- ponga que el tiempo real de terminación de la clase de las 9:00 a.m. es una variable aleatoria normalmente distribuida X1 con media de 9:02 y desviación estándar de 1.5 min y que la hora de inicio de la siguiente clase también es una varia- ble aleatoria normalmente distribuida X2 con media de 9:10 y desviación estándar de un min. Suponga que el tiempo ne- cesario para ir de un salón de clases al otro es una variable aleatoria normalmente distribuida X3 con media de seis min y desviación estándar de un min. ¿Cuál es la proba- bilidad de que el estudiante llegue a la segunda clase antes de que comience? (Suponga independencia de X1, X2 y X3, la cual es razonable si el estudiante no presta atención a la hora de terminación de la primera clase.) 87. a. Use la fórmula general de la varianza de una combinación lineal para escribir una expresión para V(aX Y). Luego si a Y/X, y demuestre que 1. [Sugerencia: La varianza siempre es 0 y Cov(X, Y) X Y .] b. Considerando que V(aX Y), concluya que 1. c. Use el hecho de que V(W) 0 sólo si W es una cons- tante para demostrar que 1 sólo si Y aX b. 88. Suponga que una calificación oral X y una calificación cuantitativa Y de un individuo seleccionado al azar en un examen de aptitud aplicado a nivel nacionalmente tienen una función de densidad de probabilidad conjunta f(x, y) { 2 5 (2x 3y) 0 x 1, 0 y 1 0 de lo contrario Se le pide que haga una predicción t de la calificación total X Y del individuo. El error de predicción es la media del error al cuadrado E[(X Y t)2 ]. ¿Qué valor de t reduce al mínimo el error de predicción? 89. a. Que Xi tenga una distribución ji cuadrada con parámetro 1 (véase la sección 4.4) y que X2 sea independiente de X1 y que tenga una distribución ji cuadrada con paráme- tro 2. Use la técnica del ejemplo 5.21 para demostrar que X1 X2 tiene una distribución ji cuadrada con pará- metro 1 2. b. En el ejercicio 71 del capítulo 4, se le pidió que demos- trara que si Z es una variable normal estándar, entonces Z2 tiene una distribución ji cuadrada con 1. Sean Z1, Z2, . . . , Zn n variables aleatorias normales estándar. ¿Cuál es la distribución de Z2 1 . . . Z2 n? Justifique su respuesta. c. Sean X1, . . . , Xn una muestra aleatoria de una distribu- ción normal con media y varianza 2 . ¿Cuál es la dis- tribución de la suma Y n i1 [(Xi )/]2 ? Justifique su respuesta. 90. a. Demuestre que Cov(X, Y Z) Cov(X, Y) Cov(X, Z). b. Sean X1 y X2 calificaciones cuantitativas y orales en un examen de aptitud y sean Y1 y Y2 calificaciones corres- pondientes en otro examen. Si Cov(X1, Y1) 5, Cov(X1, Y2) 1, Cov(X2, Y1) 2 y Cov(X2, Y2) 8, ¿cuál es la covarianza entre las dos calificaciones totales X1 X2 y Y1 Y2? 91. Se selecciona al azar y se pesa dos veces un espécimen de roca de un área particular. Sea W el peso real y X1 y X2 los dos pesos medidos. Entonces X1 W E1 y X2 W E2, donde E1 y E2 son los dos errores de medición. Suponga que los Ei son independientes entre sí y de W y que V(E1) V(E2) 2 E. a. Exprese , el coeficiente de correlación entre los dos pesos medidos X1 y X2 en función de 2 W, la varianza del peso real y 2 x , la varianza del peso medido. b. Calcule cuando W 1 kg y E 0.01 kg. 92. Sea A el porcentaje de un constituyente en un espécimen de roca seleccionado al azar y sea B el porcentaje de un segundo constituyente en ese mismo espécimen. Suponga que D y E son errores de medición al determinar los valores de A y B de modo que los valores medidos sea X A D y Y B E, respectivamente. Suponga que los errores de medición son independientes entre sí y de los valores reales. c5_p184-226.qxd 3/12/08 4:08 AM Page 225
- 244. 226 CAPÍTULO 5 Distribuciones de probabilidad conjunta y muestras aleatorias a. Demuestre que Corr(X, Y) Corr(A, B) C o rr (X 1, X 2) C o rr (Y 1, Y 2) donde X1 y X2 son mediciones replicadas del valor de A y Y1 y Y2 se definen análogamente con respecto a B. ¿Qué efecto tiene la presencia del error de medición en la correlación? b. ¿Cuál es valor máximo de Corr(X, Y) cuando Corr(X1, X2) 0.8100 y Corr(Y1, Y2) 0.9025? ¿Es esto per- turbador? 93. Sean X1, . . . , Xn variables aleatorias independientes con valores medios 1, . . . , n y varianzas 2 1, . . . , 2 n. Considere una función h(x1, . . . , xn) y úsela para definir una nueva variable aleatoria Y h(X1, . . . , Xn). En condiciones un tanto generales en cuanto a la función h, si las i son pequeñas con respecto a las i correspondientes se puede demostrar que E(Y) h(1, . . . , n) y V(Y) 2 2 1 . . . 2 2 n donde cada derivada parcial se evalúa en (x1, . . . , xn) (1, . . . , n). Suponga tres resistores con resistencias X1, X2, X3 conectadas en paralelo a través de una batería con voltaje X4. Luego, según la ley de Ohm, la corriente es Y X4 X 1 1 X 1 2 X 1 3 Sea 1 10 ohms, 1 1.0 ohms, 2 15 ohms, 2 1.0 ohms, 3 20 ohms, 3 1.5 ohms, 4 120 V, 4 4.0 V. Calcule el valor esperado aproximado y la desviación están- dar de la corriente (sugerido por “Random Samplings”, CHEMTECH, 1984: 696-697). 94. Una aproximación más precisa a E[h(X1, . . . , Xn)] en el ejercicio 93 es h(1, . . . , n) 1 2 2 1 . . . 1 2 2 n Calcule esto con Y h(X1, X2, X3, X4) dada en el ejercicio 93 y compárela con el primer término h(1, . . . , n). 95. Sean X y Y variables aleatorias normales estándar indepen- dientes y defina una nueva variable aleatoria como U 0.6X 0.8Y. a. Determine Corr(X, U). b. ¿Cómo modificaría U para obtener Corr(X, U) con un valor especificado de ? ,2 h ,x2 n ,2 h ,x2 1 ,h ,xn ,h ,x1 Bibliografía Devore, Jay y Kenneth Berk, Modern Mathematical Statistics with Applications, Thomson-Brooks/Cole, Belmont, CA, 2007. Una exposición un poco más complicada de temas de probabilidad que en el presente libro. Olkin, Ingram, Cyrus Derman y Leon Gleser, Probability Models and Applications (2a. ed.). Macmillan, Nueva York, 1994. Contiene una cuidadosa y amplia exposición de distribuciones conjuntas, reglas de probabilidad y teoremas de límites. c5_p184-226.qxd 3/12/08 4:08 AM Page 226
- 245. 6 227 Estimación puntual INTRODUCCIÓN Dado un parámetro de interés, tal como la media o la proporción p de una pobla- ción, el objetivo de la estimación puntual es utilizar una muestra para calcular un número que representa en cierto sentido una buena suposición del valor verdadero del parámetro. El número resultante se llama estimación puntual. En la sección 6.1, se presentan algunos conceptos generales de estimación puntual. En la sección 6.2, se describen e ilustran dos métodos importantes de obtener estimaciones puntuales: el método de momentos y el método de máxima probabilidad. c6_p227-253.qxd 3/12/08 4:12 AM Page 227
- 246. 228 CAPÍTULO 6 Estimación puntual 6.1 Algunos conceptos generales de estimación puntual El objetivo de la inferencia estadística casi siempre es sacar algún tipo de conclusión sobre uno o más parámetros (características de la población). Para hacer eso un investigador tie- ne que obtener datos muestrales de cada una de las poblaciones estudiadas. Las conclusio- nes pueden entonces basarse en los valores calculados de varias cantidades muestrales. Por ejemplo, sea (un parámetro) la resistencia a la ruptura promedio verdadera de conexiones alámbricas utilizadas en la unión de obleas semiconductoras. Se podría tomar una muestra aleatoria de n 10 conexiones y determinar la resistencia a la ruptura de cada una y se ten- drían las resistencias observadas x1, x2, . . . , x10. La resistencia a la ruptura media muestral x se utilizaría entonces para sacar una conclusión con respecto al valor de . Asimismo, si 2 es la varianza de la distribución de la resistencia a la ruptura (varianza de la población, otro parámetro), el valor de la varianza muestral s2 se utiliza para inferir algo sobre 2 . Cuando se discuten los métodos y conceptos generales de inferencia, es conveniente disponer de un símbolo genérico para el parámetro de interés. Se utilizará la letra griega para este propósito. El objetivo de la estimación puntual es seleccionar un solo número, con base en los datos muestrales, que represente un valor sensible de . Supóngase, por ejem- plo, que el parámetro de interés es , la vida útil promedio verdadera de baterías de un tipo. Una muestra aleatoria de n 3 baterías podría dar las vidas útiles (horas) observadas x1 5.0, x2 6.4, x3 5.9. El valor calculado de la vida útil media muestral es x 5.77 y es razonable considerar 5.77 como un valor muy factible de , la “mejor suposición” del valor de basado en la información muestral disponible. Supóngase que se desea estimar un parámetro de una población (p. ej., o ) con una muestra aleatoria de tamaño n. Recuérdese por el capítulo previo de que antes que los datos estén disponibles, las observaciones muestrales deben ser consideradas como variables alea- torias X1, X2, . . . , Xn. Se deduce que cualquier función de las Xi, es decir, cualquier estadís- tico, tal como la media muestral X o la desviación estándar muestral S también es una variable aleatoria. Lo mismo es cierto si los datos disponibles se componen de más de una muestra. Por ejemplo, se pueden representar las resistencias a la tensión de m especí- menes de tipo 1 y de n especímenes de tipo 2 por X1, . . . , Xm y Y1, . . . , Yn, respectivamen- te. La diferencia entre las dos resistencias medias muestrales es X Y , el estadístico natural para inferir sobre 1 2, la diferencia entre las resistencias medias de la población. DEFINICIÓN Una estimación puntual de un parámetro es un número único que puede ser con- siderado como un valor sensible de . Se obtiene una estimación puntual seleccio- nando un estadístico apropiado y calculando su valor con los datos muestrales dados. El estadístico seleccionado se llama estimador puntual de . En el ejemplo de la batería que se acaba de dar, el estimador utilizado para obtener la estimación puntual de fue X y la estimación puntual de fue 5.77. Si las tres vidas útiles hubieran sido x1 5.6, x2 4.5 y x3 6.1, el uso del estimador X habría dado por resulta- do la estimación x (5.6 4.5 6.1)/3 5.40. El símbolo ˆ (“teta testada”) se utiliza comúnmente para denotar tanto la estimación de como la estimación puntual que resulta de una muestra dada.* Por tanto, ˆ X se lee como “el estimador puntual de es la media * Siguiendo la primera notación, se podría utilizar ˆ (teta mayúscula) para el estimador, pero ésta es difícil de escribir. c6_p227-253.qxd 3/12/08 4:12 AM Page 228
- 247. 6.1 Algunos conceptos generales de estimación puntual 229 Ejemplo 6.1 Ejemplo 6.2 muestral X ”. La proposición “la estimación puntual de es 5.77” se escribe concisamente como ˆ 5.77. Obsérvese que cuando se escribe ˆ 72.5, no hay ninguna indicación de cómo se obtuvo esta estimación puntual (qué estadístico se utilizó). Se recomienda repor- tar tanto el estimador como la estimación resultante. Un fabricante automotriz ha producido un nuevo tipo de defensa, la que se presume absor- be impactos con menos daño que las defensas previas. El fabricante ha utilizado esta defen- sa en una secuencia de 25 choques controlados con un muro, cada uno a 10 mph, utilizando uno de sus modelos de carro compacto. Sea X el número de choques que no provocaron daños visibles al automóvil. El parámetro que tiene que ser estimado es p la proporción de todos los choques que no provocaron daños [alternativamente, p P(ningún daño en un choque)]. Si se observa que X es x 15, el estimador y estimación más razonables son estimador p̂ X n estimación n x 1 2 5 5 0.60 ■ Si por cada parámetro de interés hubiera sólo un estimador puntual razonable, no habría mucho para la estimación puntual. En la mayoría de los problemas, sin embargo, habrá más de un estimador razonable. Reconsidere las 20 observaciones adjuntas de voltaje de ruptura dieléctrica de piezas de resina epóxica introducidas por primera vez en el ejemplo 4.30 (sección 4.6). 24.46 25.61 26.25 26.42 26.66 27.15 27.31 27.54 27.74 27.94 27.98 28.04 28.28 28.49 28.50 28.87 29.11 29.13 29.50 30.88 El patrón en la gráfica de probabilidad normal dado allí es bastante recto, así que ahora se supone que la distribución de voltaje de ruptura es normal con valor medio . Como las dis- tribuciones normales son simétricas, también es la vida útil mediana de la distribución. Se supone entonces que las observaciones dadas son el resultado de una muestra aleatoria X1, X2, . . . , X20 de esta distribución normal. Considere los siguientes estimadores y las estima- ciones resultantes de : a. Estimador X , estimación x xi /n 555.86/20 27.793 b. Estimador , estimación (27.94 27.98)/2 27.960 c. Estimador [mín(Xi) máx(Xi)]/2 el promedio de las dos vidas útiles extremas, esti- mación [mín(xi) máx(xi)]/2 (24.46 30.88)/2 27.670 d. Estimador X tr(10), la media 10% recortada (desechar el 10% más pequeño y más gran- de de la muestra y luego promediar). estimación x tr(10) 27.838 Cada uno de los estimadores a) al d) utiliza una medición diferente del centro de la mues- tra para estimar . ¿Cuál de las estimaciones se acerca más al valor verdadero? No se puede responder esta pregunta sin conocer el valor verdadero. Una pregunta que se puede hacer es: “¿Cuál estimador, cuando se utiliza en otras muestras de Xi, tiende a producir estimaciones cercanas al valor verdadero? En breve se considerará este tipo de pregunta. ■ 555.86 24.46 25.61 29.50 30.88 16 x | X | c6_p227-253.qxd 3/12/08 4:12 AM Page 229
- 248. En el futuro inmediato habrá un creciente interés por desarrollar aleaciones de Mg de bajo costo para varios procesos de fundición. Es por consiguiente importante contar con formas prácticas de determinar varias propiedades mecánicas de esas aleaciones. El artículo “On the Development of a New Approach for the Determination of Yield Strength in Mg-based Alloys” (Light Metal Age, octubre de 1998: 50-53) propuso un método ultrasónico para este propósito. Considere la siguiente muestra de observaciones de módulo elástico (GPa) de especímenes de aleación AZ91D tomados de un proceso de fundición a troquel: 44.2 43.9 44.7 44.2 44.0 43.8 44.6 43.1 Suponga que estas observaciones son el resultado de una muestra aleatoria X1, . . . , X8 toma- da de la distribución de población de módulos elásticos en semejantes circunstancias. Se desea estimar la varianza de la población 2 . Un estimador natural es la varianza muestral: ˆ 2 S2 ( n Xi 1 X )2 La estimación correspondiente es ˆ 2 s2 0.25125 0.251 La estimación de sería entonces ˆ s 0 . 2 5 1 2 5 0.501. Si se utiliza el divisor n en lugar de n 1 se obtendría un estimador alternativo (es decir, la desviación al cuadrado promedio): ˆ 2 estimación 1.75 8 875 0.220 En breve se indicará por qué muchos estadísticos prefieren S2 al estimador con divisor n. ■ En el mejor de todos los mundos posibles, se podría hallar un estimador ˆ con el cual ˆ siempre. Sin embargo, ˆ es una función de las Xi muestrales, así que es una variable aleatoria. Con algunas muestras, ˆ dará un valor más grande que , mientras que con otras muestras ˆ subestimará . Si se escribe ˆ error de estimación entonces un estimador preciso sería uno que produzca errores de estimación pequeños, así que los valores estimados se aproximarán al valor verdadero. Una forma sensible de cuantificar la idea de ˆ cercano a es considerar el error al cuadrado (ˆ )2 . Con algunas muestras, ˆ se acercará bastante a y el error al cuadrado se aproximará a 0. Otras muestras pueden dar valores de ˆ alejados de , correspondientes a errores al cuadrado muy grandes. Una medida general de precisión es el error cuadrático medio ECM E[(ˆ )2 ]. Si un primer estimador tiene una media del error al cuadrado más pequeña que un segundo, es natural decir que el primer estimador es el mejor. Sin embargo, el error cuadrático medio en general dependerá del valor de . Lo que a menudo sucede es que un estimador tendrá una media del error al cuadrado más pequeña con algu- nos valores de y una media del error al cuadrado más grande con otros valores. En gene- ral no es posible determinar un estimador con el error cuadrático medio mínimo. Una forma de librarse de este dilema es limitar la atención sólo en estimadores que tengan una propiedad deseable específica y luego determinar el mejor estimador en este grupo limitado. Una propiedad popular de esta clase en la comunidad estadística es el inses- gamiento. (Xi X )2 n 15533.79 (352.5)2 /8 7 x2 i (xi)2 /8 7 X2 i (Xi)2 /n n 1 230 CAPÍTULO 6 Estimación puntual Ejemplo 6.3 c6_p227-253.qxd 3/12/08 4:12 AM Page 230
- 249. Estimadores insesgados Supóngase que se tienen dos instrumentos de medición: uno ha sido calibrado con precisión, pero el otro sistemáticamente da lecturas más pequeñas que el valor verdadero que se está midiendo. Cuando cada uno de los instrumentos se utiliza repetidamente en el mismo obje- to, debido al error de medición, las mediciones observadas no serán idénticas. Sin embargo, las mediciones producidas por el primer instrumento se distribuirán en torno al valor verdade- ro de tal modo que en promedio este instrumento mide lo que se propone medir, por lo que este instrumento se conoce como instrumento insesgado. El segundo instrumento proporciona observaciones que tienen un componente de error o sesgo sistemático. 6.1 Algunos conceptos generales de estimación puntual 231 Es decir, ˆ es insesgado si su distribución de probabilidad (es decir, muestreo) siempre está “centrada” en el valor verdadero del parámetro. Supóngase que ˆ es un estimador insesgado; entonces si 100, la distribución muestral ˆ está centrada en 100; si 27.5, en ese caso la distribución muestral ˆ está centrada en 27.5, y así sucesivamente. La figura 6.1 ilustra la distribución de varios estimadores sesgados e insesgados. Obsérvese que “centrada” en este caso significa que el valor esperado, no la mediana de la distribución de ˆ es igual a . DEFINICIÓN Se dice que un estimador puntual ˆ es un estimador insesgado de si E(ˆ) con todo valor posible de . Si ˆ no es insesgado, la diferencia E(ˆ) se conoce como el sesgo de ˆ. Parece como si fuera necesario conocer el valor de (en cuyo caso la estimación es innecesaria) para ver si ˆ es insesgado. Éste casi nunca es el caso, puesto que insesgamien- to es una propiedad general del estimador muestral, donde se centra, y generalmente no depende de cualquier valor de parámetro particular. En el ejemplo 6.1, se utilizó la proporción muestral X/n como estimador de p, donde X, el número de éxitos muestrales, tenía una distribución binomial con parámetros n y p. Por lo tanto, E(p̂) E X n 1 n E(X) 1 n (np) p PROPOSICIÓN Cuando X es una variable aleatoria binomial con parámetros n y p, la proporción muestral p̂ X/n es un estimador insesgado de p. ¨ © ª ¨ © ª 1 Sesgo de 1 Sesgo de Función de densidad de probabilidad de2 ^ Función de densidad de probabilidad de1 ^ Función de densidad de probabilidad de2 ^ Función de densidad de probabilidad de1 ^ Figura 6.1 Funciones de densidad de probabilidad de un estimador sesgado ˆ 1 y un estimador in- sesgado ˆ 2 de un parámetro . No importa cuál sea el valor verdadero de p, la distribución del estimador p̂ estará centrada en el valor verdadero. c6_p227-253.qxd 3/12/08 4:12 AM Page 231
- 250. Suponga que X, el tiempo de reacción a un estímulo, tiene una distribución uniforme en el intervalo desde 0 hasta un límite superior desconocido (por tanto la función de densidad de X es rectangular con altura 1/ en el intervalo 0 x ). Se desea estimar con base en una muestra aleatoria X1, X2, . . . , Xn de los tiempos de reacción. Como es el tiempo más grande posible en toda la población de tiempos de reacción, considere como un primer estimador el tiempo de reacción muestral más grande ˆ 1 máx(X1, . . . , Xn). Si n 5 y x1 4.2, x2 1.7, x3 2.4, x4 3.9, x5 1.3, la estimación puntual de es ˆ 1 máx(4.2, 1.7, 2.4, 3.9, 1.3) 4.2. El insesgamiento implica que algunas muestras darán estimaciones que exceden y otras que darán estimaciones más pequeñas que , de lo contrario posiblemente no podría ser el centro (punto de equilibrio) de la distribución de ˆ 1. Sin embargo, el estimador pro- puesto nunca sobrestimará (el valor muestral más grande no puede exceder el valor de la población más grande) y subestimará a menos que el valor muestral más grande sea igual a . Este argumento intuitivo demuestra que ˆ 1 es un estimador sesgado. Más precisamente, se puede demostrar (véase el ejercicio 32) que E(ˆ 1) n n 1 como n n 1 1 n /(n 1) /(n 1) da el sesgo de ˆ 1, el cual tiende a 0 a medida que n se hace grande. Es fácil modificar ˆ 1 para obtener un estimador insesgado de . Considere el estimador ˆ 2 n n 1 máx(X1, . . . , Xn) Utilizando este estimador en los datos se obtiene la estimación (6/5)(4.2) 5.04. El hecho de que (n 1)/n 1 implica que ˆ 2 sobrestimará con algunas muestras y subestimará otras. El valor medio de este estimador es E(ˆ 2) E n n 1 máx(X1, . . . , Xn) n n 1 E[máx(X1, . . . , Xn)] n n 1 n n 1 Si ˆ 2 se utiliza repetidamente en diferentes muestras para estimar , algunas estimaciones serán demasiado grandes y otras demasiado pequeñas, pero a la larga no habrá ninguna ten- dencia simétrica a subestimar o sobreestimar . ■ 232 CAPÍTULO 6 Estimación puntual Ejemplo 6.4 Principio de estimación insesgada Cuando se elige entre varios estimadores diferentes de , se elige uno insesgado. PROPOSICIÓN Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución con media y varian- za 2 . Entonces el estimador ˆ 2 S2 es un estimador insesgado de 2 . (Xi X )2 n 1 De acuerdo con este principio, el estimador insesgado ˆ 2 en el ejemplo 6.4 deberá ser preferido al estimador sesgado ˆ 1. Considérese ahora el problema de estimar 2 . c6_p227-253.qxd 3/12/08 4:12 AM Page 232
- 251. Comprobación Para cualquier variable aleatoria Y, V(Y) E(Y2 ) [E(Y)]2 , por lo tanto E(Y2 ) V(Y) [E(Y)]2 . Aplicando esto a S2 n 1 1 X2 i se obtiene E(S2 ) n 1 1 E(X2 i ) 1 n E[(Xi)2 ] n 1 1 (2 2 ) 1 n {V(Xi) [E(Xi)]2 } n 1 1 n2 n2 1 n n2 1 n (n)2 n 1 1 {n2 2 } 2 (como se desea) ■ El estimador que utiliza el divisor n se expresa como (n 1)S2 /n, por lo tanto E n n 1 E(S2 ) n n 1 2 Este estimador es por consiguiente sesgado. El sesgo es (n 1)2 /n 2 2 /n. Como el sesgo es negativo, el estimador con divisor n tiende a subestimar 2 y por eso muchos estadísticos prefieren el divisor n 1 (aunque cuando n es grande, el sesgo es pequeño y hay poca diferencia entre los dos). Aun cuando S2 es insesgado para 2 , S es un estimador sesgado de (su sesgo es pequeño a menos que n sea bastante pequeño). Sin embargo, existen otras buenas razones para utilizar S como estimador, en especial cuando la distribución de la población es normal. Éstas se volverán más aparentes cuando se discutan los intervalos de confianza y la prueba de hipótesis en los siguientes capítulos. En el ejemplo 6.2, se propusieron varios estimadores diferentes de la media de una distribución normal. Si hubiera un estimador insesgado único para , el problema de esti- mación se resolvería utilizando dicho estimador. Desafortunadamente, éste no es el caso. (n 1)S2 n (Xi)2 n 6.1 Algunos conceptos generales de estimación puntual 233 PROPOSICIÓN Si X1, X2, . . . , Xn es una variable aleatoria tomada de una distribución con media , entonces X es un estimador insesgado de . Si además la distribución es continua y simétrica, entonces y cualquier media recortada también son estimadores insesga- dos de . X | El hecho de que X sea insesgado es simplemente un replanteamiento de una de las reglas de valor esperado: E(X ) con cada valor posible de (para distribuciones discretas y con- tinuas). El insesgamiento de los demás estimadores es más difícil de verificar. El siguiente ejemplo introduce otra situación en la cual existen varios estimadores insesgados para un parámetro particular. En ciertas circunstancias contaminantes, orgánicos se adhieren con facilidad a las superfi- cies de obleas y deterioran los dispositivos de fabricación de semiconductores. El artículo “Ceramic Chemical Filter for Removal of Organic Contaminants” (J. of the Institute of Environmental Sciences and Technology, 2003: 59-65) discutió una alternativa reciente- mente desarrollada de filtros de carbón convencionales para eliminar contaminación molecular transportada por el aire en aplicaciones de cuartos limpios. Un aspecto de la investigación del desempeño de filtros implicó estudiar cómo se relaciona la concentración de contaminantes en aire con la concentración en las superficies de obleas después de una Ejemplo 6.5 c6_p227-253.qxd 3/12/08 4:12 AM Page 233
- 252. exposición prolongada. Considere los siguientes datos representativos de x concentración de DBP en aire y y concentración de DBP en la superficie de obleas luego de 4 horas de exposición (ambas en g/m3 , donde DBP ftalato de dibutilo). Obs. i: 1 2 3 4 5 6 x: 0.8 1.3 1.5 3.0 11.6 26.6 y: 0.6 1.1 4.5 3.5 14.4 29.1 Los autores comentan que la “adhesión de DBP en la superficie de obleas fue aproximada- mente proporcional a la concentración de DBP en aire”. La figura 6.2 muestra una gráfica de y contra x, es decir, de los pares (x, y). 234 CAPÍTULO 6 Estimación puntual Si y fuera exactamente proporcional a x, se tendría y x con algún valor de , la cual expre- sa que los puntos (x, y) en la gráfica quedarían exactamente sobre una línea recta con pendien- de , que pasa por (0, 0). Pero es sólo aproximadamente el caso. Así que a continuación se supone que con cualquier x fija, la concentración de DBP en las obleas es una variable aleato- ria Y con valor medio x. Es decir, se postula que el valor medio de Y está relacionado con x por una línea que pasa por (0, 0) pero que el valor observado de Y en general se desviará de esta línea (esto se conoce en la literatura estadística como “regresión a través del origen”). Ahora se desea estimar el parámetro de la pendiente . Considere los siguientes tres estimadores: #1: ˆ #2: ˆ #3: ˆ Las estimaciones resultantes basadas en los datos dados son 1.3497, 1.1875 y 1.1222, res- pectivamente. Así que de manera definitiva la estimación depende de qué estimador se uti- lice. Si uno de estos tres estimadores fuera insesgado y los otros dos sesgados, habría un buen motivo para utilizar el insesgado. Pero los tres son insesgados; el argumento se apoya en el hecho de que cada uno es una función lineal de las Yi (aquí se supone que las xi son fijas, no aleatorias): E E EYi xi xi E ExiYi xi xi xi 2 ■ 1 xi 2 1 xi 2 1 xi 2 xiYi xi 2 1 xi 1 xi 1 xi Yi xi n n 1 n xi xi 1 n E(Yi) xi 1 n Yi xi 1 n xiYi xi 2 Yi xi Yi xi 1 n Figura 6.2 Gráfica de los datos de ftalato de dibutilo del ejemplo 6.5. 0 5 10 15 20 25 30 30 25 20 15 10 5 0 Ftalato de dibutilo en oblea Ftalato de dibutilo en aire c6_p227-253.qxd 3/12/08 4:12 AM Page 234
- 253. 6.1 Algunos conceptos generales de estimación puntual 235 Tanto en el ejemplo anterior como en la situación que implica estimar una media de pobla- ción normal, el principio de insesgamiento (prefiere un estimador insesgado a uno sesgado) no puede ser invocado para seleccionar un estimador. Lo que ahora se requiere es un crite- rio para elegir entre estimadores insesgados. Estimadores con varianza mínima Supóngase que ˆ 1 y ˆ 2 son dos estimadores de insesgados. Entonces, aunque la distribu- ción de cada estimador esté centrada en el valor verdadero de , las dispersiones de las dis- tribuciones en torno al valor verdadero pueden ser diferentes. La figura 6.3 ilustra las funciones de densidad de probabilidad de los dos estimadores insesgados, donde ˆ1 tiene una varianza más pequeña que ˆ 2. Entonces es más probable que ˆ 1 produzca una estimación próxima al valor verdadero que ˆ 2. El estimador insesgado con varianza mínima es, en cierto sentido, el que tiene más probabilidades entre todos los esti- madores insesgados de producir una estimación cercana al verdadero . En el ejemplo 6.5, supóngase que cada Yi está normalmente distribuida con media xi y va- rianza 2 (la suposición de varianza constante). Entonces se puede demostrar que el tercer estimador ˆ xi Yi /x2 i no sólo tiene una varianza más pequeña que cualquiera de los otros dos estimadores insesgados, sino que de hecho es el estimador insesgado con varian- za mínima, tiene una varianza más pequeña que cualquier otro estimador insesgado de . En el ejemplo 6.4 se argumentó que cuando X1, . . . , Xn es una variable aleatoria tomada de una distribución uniforme en el intervalo [0, ], el estimador ˆ 1 n n 1 máx(X1, . . . , Xn) es insesgado para (previamente este estimador se denotó por ˆ 2 ). Este no es el único esti- mador insesgado de . El valor esperado de una variable aleatoria uniformemente distribuida es simplemente el punto medio del intervalo de densidad positiva, por lo tanto E(Xi) /2. Es- to implica que E(X ) /2, a partir de la cual E(2X ) . Es decir, el estimador 2 2X es in- sesgado para . Si X está uniformemente distribuida en el intervalo A, B, en ese caso V(X) 2 (B A)2 /12. Así pues, en esta situación, V(Xi) 2 /12, V(X ) 2 /n 2 /(12n) y V(ˆ 2) V(2X ) 4V(X ) 2 /(3n). Se pueden utilizar los resultados del ejercicio 32 para Principio de estimación insesgada con varianza mínima Entre todos los estimadores de insesgados, se selecciona el de varianza mínima. El ˆ resultante se llama estimador insesgado con varianza mínima (EIVM) de . Ejemplo 6.6 Función de densidad de probabilidad de 2 ^ Función de densidad de probabilidad de 1 ^ Figura 6.3 Gráficas de las funciones de densidad de probabilidad de dos estimadores insesgados diferentes. c6_p227-253.qxd 3/12/08 4:12 AM Page 235
- 254. 236 CAPÍTULO 6 Estimación puntual demostrar que V(ˆ 1) 2 /[n(n 2)]. El estimador ˆ 1 tiene una varianza más pequeña que ˆ 2 si 3n n(n 2), es decir, si 0 n2 n n(n 1). En tanto n 1, V(ˆ 1) V(ˆ 2), así que ˆ 1 es mejor estimador que ˆ 2. Se pueden utilizar métodos más avanzados para demos- trar que ˆ 1 es el estimador insesgado con varianza mínima de , cualquier otro estimador insesgado de tiene una varianza que excede 2 /[n(n 2)]. ■ Uno de los triunfos de la estadística matemática ha sido el desarrollo de una metodo- logía para identificar el estimador insesgado con varianza mínima en una amplia variedad de situaciones. El resultado más importante de este tipo para nuestros propósitos tiene que ver con la estimación de la media de una distribución normal. Siempre que exista la seguridad de que la población que se está muestreando es normal, el resultado dice que X debería usarse para estimar . Entonces, en el ejemplo 6.2 la estima- ción sería x 27.793. En algunas situaciones, es posible obtener un estimador con sesgo pequeño que se preferiría al mejor estimador insesgado. Esto se ilustra en la figura 6.4. Sin embargo, los estimadores insesgados con varianza mínima a menudo son más fáciles de obtener que el tipo de estimador sesgado cuya distribución se ilustra. TEOREMA Sean X1, . . . , Xn una muestra aleatoria tomada de una distribución normal con pará- metros y . Entonces el estimador ˆ X es el estimador insesgado con varianza mínima para . ^ Función de densidad de probabilidad de 2, el estimador insesgado con varianza mínima Función de densidad de probabilidad de 1, un estimador sesgado ^ Figura 6.4 Un estimador sesgado que es preferible al estimador insesgado con varianza mínima. Algunas complicaciones El último teorema no dice que al estimar la media de una población, se deberá utilizar el estimador X independientemente de la distribución que se está muestreando. Suponga que se desea estimar la conductividad térmica de un material. Con técnicas de medición estándar, se obtendrá una muestra aleatoria X1, . . . , Xn de n mediciones de con- ductividad térmica. Suponga que la distribución de la población es un miembro de una de las siguientes tres familias: f(x) e(x)2 /(2 2 ) ' x ' (6.1) f(x) [1 ( 1 x )2 ] ' x ' (6.2) f(x) {2 1 c c x c (6.3) 0 de lo contrario 1 2 2 Ejemplo 6.7 c6_p227-253.qxd 3/12/08 4:12 AM Page 236
- 255. La función de densidad de probabilidad (6.1) es la distribución normal, (6.2) se llama distri- bución de Cauchy y (6.3) es una distribución uniforme. Las tres distribuciones son simétricas con respecto a y de hecho la distribución de Cauchy tiene forma de campana pero con colas muchos más gruesas (más probabilidad hacia fuera) que la curva normal. La distribu- ción uniforme no tiene colas. Los cuatro estimadores de considerados con anterioridad son X , , X e (el promedio de las dos observaciones extremas) y X rec(10), una media recortada. La muy importante moraleja en este caso es que el mejor estimador de depende cru- cialmente de qué distribución está siendo muestreada. En particular, 1. Si la muestra aleatoria proviene de una distribución normal, en ese caso X es el mejor de los cuatro estimadores, puesto que tiene una varianza mínima entre todos los estima- dores insesgados. 2. Si la muestra aleatoria proviene de una distribución de Cauchy, entonces X y X e son esti- madores terribles de , en tanto que es bastante bueno (el estimador insesgado con varianza mínima no es conocido); X es malo porque es muy sensible a las observacio- nes subyacentes y las colas gruesas de la distribución de Cauchy hacen que sea impro- bable que aparezcan tales observaciones en cualquier muestra. 3. Si la distribución subyacente es uniforme, el mejor estimador es X e; este estimador está influido en gran medida por las observaciones subyacentes, pero la carencia de colas hace que tales observaciones sean imposibles. 4. En ninguna de estas tres situaciones es mejor la media recortada pero funciona razo- nablemente bien en las tres. Es decir, X rec(10) no sufre demasiado en comparación con el mejor procedimiento en cualquiera de las tres situaciones. ■ Investigaciones recientes en estadística han establecido que cuando se estima un punto de simetría de una distribución de probabilidad continua, una media recortada con pro- porción de recorte de 10 o 20% (de cada extremo de la muestra) produce estimaciones razonablemente comportadas dentro de un rango muy amplio de posibles modelos. Por esta razón, se dice que una media recortada con poco porcentaje de recorte es un estima- dor robusto. En algunas situaciones, la selección no es entre dos estimadores diferentes construi- dos con la misma muestra, sino entre estimadores basados en dos experimentos distintos. Suponga que cierto tipo de componente tiene una distribución de vida útil exponencial con parámetro de modo que la vida útil esperada es 1/. Se selecciona una muestra de n de esos componentes y cada uno es puesto en operación. Si el experimento continúa hasta que todas las n vidas útiles, X1, . . . , Xn han sido observadas, en ese caso X es un estimador insesgado de . En algunos experimentos, sin embargo, los componentes se dejan en operación sólo hasta el tiempo de la r-ésima falla, donde r n. Este procedimiento se conoce como cen- sura. Sea Y1 el tiempo de la primera falla (la vida útil mínima entere los n componentes) y Y2 el tiempo en el cual ocurre la segunda falla (la segunda vida útil más pequeña), y así suce- sivamente. Como el experimento termina en el tiempo Yr, la vida útil acumulada al final es Tr r i1 Yi (n r)Yr A continuación se demuestra que ˆ Tr /r es un estimador insesgado de . Para hacerlo, se requieren dos propiedades de variables exponenciales. 1. La propiedad de amnesia (véase la sección 4.4), dice que cualquier punto de tiempo, la vida útil restante tiene la misma distribución exponencial que la vida útil original. 2. Si X1, . . . , Xk son independientes, cada exponencial con parámetro , entonces mín (X1, . . . , Xk) es exponencial con parámetro k y su valor esperado es 1/(k). X | X | 6.1 Algunos conceptos generales de estimación puntual 237 Ejemplo 6.8 c6_p227-253.qxd 3/12/08 4:12 AM Page 237
- 256. Como los n componentes duran hasta Y1, n 1 duran una cantidad de tiempo adicional Y2 Y1 adicional y n 2, duran una cantidad de tiempo Y3 Y2 adicional, y así sucesiva- mente, otra expresión para Tr es Tr nY1 (n 1)(Y2 Y1) (n 2)(Y3 Y2) (n r 1)(Yr Yr1) Pero Y1 es el mínimo de n variables exponenciales, por tanto E(Y1) 1/(n). Asimismo, Y2 Y1 es la más pequeña de las n 1 vidas útiles restantes, cada exponencial con parámetro (según la propiedad de amnesia), así que E(Y2 Y1) 1/[(n 1)]. Continuando, E(Yi1 Yi) 1/[(n i)], así que E(Tr ) nE(Y1) (n 1)E(Y2 Y1) (n r 1)E(Yr Yr 1) n n 1 (n 1) (n 1 1) (n r 1) (n r 1 1) r Por consiguiente, E(Tr /r) (1/r)E(Tr ) (1/r) (r/) 1/ como se dijo. Como un ejemplo, supónganse que se prueban 20 componentes y r 10. Entonces si los primeros diez tiempos de falla son 11, 15, 29, 33, 35, 40, 47, 55, 58 y 72, la estima- ción de es ˆ 111.5 La ventaja del experimento con censura es que termina más rápido que el experimen- to sin censura. Sin embargo, se puede demostrar que V(Tr/r) 1/(2 r), la cual es más gran- de que 1/(2 n), la varianza de X en el experimento sin censura. ■ Reporte de una estimación puntual: el error estándar Además de reportar el valor de una estimación puntual, se debe dar alguna indicación de su precisión. La medición usual de precisión es el error estándar del estimador usado. 11 15 72 (10)(72) 10 238 CAPÍTULO 6 Estimación puntual Ejemplo 6.9 (continuación del ejemplo 6.2) Suponiendo que el voltaje de ruptura está normalmente distribuido, ˆ X es la mejor esti- mación de . Si se sabe que el valor de es 1.5, el error estándar de X es X /n 1.5/2 0 0.335. Si, como casi siempre es el caso, el valor de es desconocido, la esti- mación ˆ s 1.462 se sustituye en X para obtener el error estándar estimado ˆ X sX s/n 1.462/2 0 0.327. ■ El error estándar de p̂ X/n es p̂ V (X /n ) V n (X 2 ) n n p 2 q p n q Como p y q 1 p son desconocidas (¿de otro modo por qué estimar?), se sustituye p̂ x/n y q̂ 1 x/n en p̂ para obtener el error estándar estimado ˆ p̂ p̂ q̂/ n DEFINICIÓN El error estándar de un estimador ˆ es su desviación estándar ˆ V (ˆ ) . Si el error estándar implica parámetros desconocidos cuyos valores pueden ser estimados, la sustitución de estas estimaciones en ˆ da el error estándar estimado (desviación estándar estimada) del estimador. El error estándar estimado puede ser denotado o por ˆ ˆ (el ^ sobre recalca que ˆ está siendo estimada) o por sˆ. Ejemplo 6.10 (continuación del ejemplo 6.1) c6_p227-253.qxd 3/12/08 4:13 AM Page 238
- 257. ( 0 . 6 ) ( 0 . 4 ) / 2 5 0.098. Alternativamente, como el valor más grande de pq se obtiene cuando p q 0.5, un límite superior en el error estándar es 1 /( 4 n ) 0.10. ■ Cuando la distribución del estimador puntual ˆ es normal de modo aproximado, lo que a menudo será el caso cuando n es grande, en tal caso se puede estar confiado de manera razo- nable en que el valor verdadero de queda dentro de aproximadamente dos errores estándar (desviaciones estándar) de ˆ. De este modo si una muestra de n 36 vidas útiles de com- ponentes da ˆ x 28.50 y s 3.60, por consiguiente, s/n 0.60 dentro de dos erro- res estándar estimados de ˆ se transforma en el intervalo 28.50 ! (2)(0.60) (27.30, 29.70). Si ˆ no es necesariamente normal en forma aproximada pero es insesgado, entonces se puede demostrar que la estimación se desviará de hasta por cuatro errores estándar cuando mucho 6% del tiempo. Se esperaría entonces que el valor verdadero quede dentro de cuatro errores estándar de ˆ (y ésta es proposición muy conservadora, puesto que se apli- ca a cualquier ˆ insesgado). Resumiendo, el error estándar indica de forma aproximada a qué distancia de ˆ se puede esperar que quede el valor verdadero de . La forma del estimador de ˆ puede ser suficientemente complicado de modo que la teoría estadística estándar no pueda ser aplicada para obtener una expresión para ˆ. Esto es cierto, por ejemplo, en el caso , ˆ S, la desviación estándar del estadístico S, S, en general no puede ser determinada. No hace mucho, se introdujo un método de computado- ra intensivo llamado bootstrap para abordar este problema. Supóngase que la función de densidad de probabilidad de la población es f(x; ), un miembro de una familia paramétrica particular y que los datos x1, x2, . . . , xn dan ˆ 21.7. Ahora se utiliza la computadora para obtener “muestras bootstrap” tomadas de la función de densidad de probabilidad f(x; 21.7) y por cada muestra se calcula una “estimación bootstrap” ˆ*: Primera muestra “bootstrap”: x* 1, x* 2, . . . , x* n; estimación ˆ* 1 Segunda muestra “bootstrap”: x* 1, x* 2, . . . , x* n; estimación ˆ* 2 B-ésima muestra bootstrap: x* 1, x* 2, . . . , x* n; estimación ˆ* B A menudo se utiliza B 100 o 200. Ahora sea * ˆ* i /B, la media muestral de las esti- maciones “bootstrap”. La estimación bootstrap del error de estándar de las ˆ ahora es sim- plemente la desviación estándar muestral de las ˆ* i : Sˆ B 1 1 (ˆ * i *) 2 (En la literatura de bootstrap, a menudo se utiliza B en lugar de B 1; con valores típicos de B, casi siempre hay poca diferencia entre las estimaciones resultantes.) Un modelo teórico sugiere que X, el tiempo para la ruptura de un fluido aislante entre elec- trodos a un voltaje particular, tiene f(x; ) ex , una distribución exponencial. Una mues- tra aleatoria de n 10 tiempos de ruptura (min) da los datos siguientes: 41.53 18.73 2.99 30.34 12.33 117.52 73.02 223.63 4.00 26.78 Como E(X) 1/, E(X ) 1/, una estimación razonable de es ˆ 1/x 1/55.087 0.018153. Se utilizaría entonces un programa de computadora para obtener B 100 mues- tras bootstrap, cada una de tamaño 10, provenientes de f(x; .018153). La primera muestra fue 41.00, 109.70, 16.78, 6.31, 6.76, 5.62, 60.96, 78.81, 192.25, 27.61, con la cual x* i 545.8 y ˆ * 1 1/54.58 0.01832. El promedio de 100 estimaciones bootstrap es 6.1 Algunos conceptos generales de estimación puntual 239 Ejemplo 6.11 c6_p227-253.qxd 3/12/08 4:13 AM Page 239
- 258. * 0.02153 y la desviación estándar muestral de estas 100 estimaciones es sˆ 0.0091. La estimación bootstrap del error estándar de ˆ . Un histograma de los 100 ˆ * i resultó un tan- to positivamente asimétrico lo que sugiere que la distribución muestral de ˆ también tiene esta propiedad. ■ En ocasiones un investigador desea estimar una característica poblacional sin suponer que la distribución de la población pertenece a una familia paramétrica particular. Una ins- tancia de esto ocurrió en el ejemplo 6.7, cuando una media 10% recortada fue propuesta para estimar el centro de la distribución de la población simétrica. Los datos del ejemplo 6.2 dieron ˆ x rec(10) 27.838 pero ahora no hay ninguna f(x; ) supuesta, por consiguiente ¿cómo se puede obtener una muestra bootstrap? La respuesta es considerar la muestra como que constituye la población (las n 20 observaciones en el ejemplo 6.2) y considerar B muestras diferentes, cada una de tamaño n, con reemplazo de esta población. El libro de Bradley Efron y Robert Tibshirani o el de John Rice incluidos en la bibliografía del capítu- lo proporcionan más información. 240 CAPÍTULO 6 Estimación puntual EJERCICIOS Sección 6.1 (1-19) 1. Los datos adjuntos sobre resistencia a la flexión (MPa) de vigas de concreto de un tipo se introdujeron en el ejemplo 1.2. 5.9 7.2 7.3 6.3 8.1 6.8 7.0 7.6 6.8 6.5 7.0 6.3 7.9 9.0 8.2 8.7 7.8 9.7 7.4 7.7 9.7 7.8 7.7 11.6 11.3 11.8 10.7 a. Calcule una estimación puntual del valor medio de resis- tencia de la población conceptual de todas las vigas fabricadas de esta manera y diga qué estimador utilizó: [Sugerencia: xi 219.8.] b. Calcule una estimación puntual del valor de resistencia que separa el 50% más débil de dichas vigas del 50% más resistente y diga qué estimador se utilizó. c. Calcule e interprete una estimación puntual de la des- viación estándar de la población . ¿Qué estimador uti- lizó? [Sugerencia: x2 i 1860.94.] d. Calcule una estimación puntual de la proporción de las vigas cuya resistencia a la flexión exceda de 10 MPa. [Sugerencia: Considere una observación como “éxito” si excede de 10.] e. Calcule una estimación puntual del coeficiente de varia- ción de la población / y diga qué estimador utilizó. 2. Una muestra de 20 estudiantes que recientemente tomaron un curso de estadística elemental arrojó la siguiente información sobre la marca de calculadora que poseían. (T Texas Instruments, H Hewlett Packard, C Casio, S Sharp): T T H T C T T S C H S S T H C T T T H T a. Estime la proporción verdadera de los estudiantes que poseen una calculadora Texas Instruments. b. De los 10 estudiantes que poseían una calculadora TI, 4 tenían calculadoras con graficación. Estime la propor- ción de estudiantes que no poseen una calculadora con graficación TI. 3. Considere la siguiente muestra de observaciones sobre espesor de recubrimiento de pintura de baja viscosidad (“Achieving a Target Value for a Manufacturing Process: A Case Study”, J. of Quality Technology, 1992: 22-26): 0.83 0.88 0.88 1.04 1.09 1.12 1.29 1.31 1.48 1.49 1.59 1.62 1.65 1.71 1.76 1.83 Suponga que la distribución del espesor de recubrimiento es normal (una gráfica de probabilidad normal soporta fuerte- mente esta suposición). a. Calcule la estimación puntual de la mediana del espesor de recubrimiento y diga qué estimador utilizó. b. Calcule una estimación puntual de la mediana de la dis- tribución del espesor de recubrimiento y diga qué esti- mador utilizó. c. Calcule la estimación puntual del valor que separa el 10% más grande de todos los valores de la distribución del espesor del 90% restante y diga qué estimador utili- zó. [Sugerencia: Exprese lo que está tratando de estimar en función de y .] d. Estime P(X 1.5), es decir, la proporción de todos los valores de espesor menores que 1.5 [Sugerencia: Si conociera los valores de y podría calcular esta pro- babilidad. Estos valores no están disponibles, pero pue- den ser estimados.] e. ¿Cuál es el error estándar estimado del estimador que utilizó en el inciso b)? 4. El artículo del cual se extrajeron los datos en el ejercicio 1 también dio las observaciones de resistencias adjuntas de cilindros: 6.1 5.8 7.8 7.1 7.2 9.2 6.6 8.3 7.0 8.3 7.8 8.1 7.4 8.5 8.9 9.8 9.7 14.1 12.6 11.2 c6_p227-253.qxd 3/12/08 4:13 AM Page 240
- 259. Antes de obtener los datos, denote las resistencias de vigas mediante X1, . . . , Xm y Y1, . . . , Yn las resistencias de cilindros. Suponga que las Xi constituyen una muestra aleatoria de una distribución con media 1 y desviación estándar 1 y que las Yi forman una muestra aleatoria (independiente de las Xi) de otra distribución con media 2 y desviación están- dar 2. a. Use las reglas de valor esperado para demostrar que X Y es un estimador insesgado de 1 2. Calcule la estimación con los datos dados. b. Use las reglas de varianza del capítulo 5 para obtener una expresión para la varianza y desviación estándar (error estándar) del estimador del inciso a) y luego calcule el error estándar estimado. c. Calcule una estimación puntual de la razón 1/2 de las dos desviaciones estándar. d. Suponga que se seleccionan al azar una sola viga y un solo cilindro. Calcule una estimación puntual de la va- rianza de la diferencia X Y entre la resistencia de las vigas y la resistencia de los cilindros. 5. Como ejemplo de una situación en la que varios estadísti- cos diferentes podrían ser razonablemente utilizados para calcular una estimación puntual, considere una población de N facturas. Asociado con cada factura se encuentra su “valor en libros”, la cantidad anotada de dicha factura. Sea T el valor en libros total, una cantidad conocida. Algunos de estos valores en libros son erróneos. Se realizará una audito- ría seleccionando al azar n facturas y determinando el valor auditado (correcto) para cada una. Suponga que la muestra da los siguientes resultados (en dólares). Sea Y valor en libros medio muestral X valor auditado medio muestral D error medio muestral Proponga tres estadísticos diferentes para estimar el valor total (correcto) auditado: uno que implique exactamente N y X , otro que implique T, N y D y el último que implique T y X /Y . Si N 5000 y T 1761300, calcule las tres estima- ciones puntuales correspondientes. (El artículo “Statistical Models and Analysis in Auditing”, Statistical Science, 1989: 2-33, discute propiedades de estos tres estimadores.) 6. Considere las observaciones adjuntas sobre el flujo de una corriente de agua (miles de acres-pies) registradas en una esta- ción en Colorado durante el periodo del 1 de abril al 31 de agosto durante 31 años (tomadas de un artículo que apareció en el volumen 1974 de Water Resources Research). 127.96 210.07 203.24 108.91 178.21 285.37 100.85 89.59 185.36 126.94 200.19 66.24 247.11 299.87 109.64 125.86 114.79 109.11 330.33 85.54 117.64 302.74 280.55 145.11 95.36 204.91 311.13 150.58 262.09 477.08 94.33 Una gráfica de probabilidad apropiada soporta el uso de la distribución lognormal (véase la sección 4.5) como modelo razonable de flujo de corriente de agua. a. Calcule los parámetros de la distribución [Sugerencia: Recuerde que X tiene una distribución lognormal con parámetros y 2 si ln(X) está normalmente distribuida con media y varianza 2 .] b. Use las estimaciones del inciso a) para calcular una esti- mación del valor esperado del flujo de corriente de agua [Sugerencia: ¿Cuál es E(X)?] 7. a. Se selecciona una muestra de 10 casas en un área particu- lar, cada una de las cuales se calienta con gas natural y se determina la cantidad de gas (termias) utilizada por cada casa durante el mes de enero. Las observaciones resultan- tes son 103, 156, 118, 89, 125, 147, 122, 109, 138, 99. Sea el consumo de gas promedio durante enero de todas las casas del área. Calcule una estimación puntual de . b. Suponga que hay 10 000 casas en esta área que utilizan gas natural para calefacción. Sea la cantidad total de gas consumido por todas estas casas durante enero. Calcule con los datos del inciso a). ¿Qué estimador utilizó para calcular su estimación? c. Use los datos del inciso a) para estimar p, la proporción de todas las casas que usaron por lo menos 100 termias. d. Proporcione una estimación puntual de la mediana de la población usada (el valor intermedio en la población de todas las casas) basada en la muestra del inciso a). ¿Qué estimador utilizó? 8. En una muestra aleatoria de 80 componentes de un tipo, se encontraron 12 defectuosos. a. Dé una estimación puntual de la proporción de todos los componentes que no están defectuosos. b. Se tiene que construir un sistema seleccionando al azar dos de estos componentes y conectándolos en serie, como se muestra a continuación. La conexión en serie implica que el sistema funcionará siem- pre y cuando ningún componente esté defectuoso (es decir, ambos componentes funcionan apropiadamente). Estime la proporción de todos los sistemas que funcionan de manera apropiada. [Sugerencia: Si p denota la probabilidad de que el componente funcione apropiadamente, ¿cómo puede ser expresada P(el sistema funciona) en función de p?] 9. Se examina cada uno de 150 artículos recién fabricados y se anota el número de rayones por artículo (se supone que los artículos están libres de rayones) y se obtienen los siguien- tes datos: 6.1 Algunos conceptos generales de estimación puntual 241 Factura 1 2 3 4 5 Valor en libros 300 720 526 200 127 Valor auditado 300 520 526 200 157 Error 0 200 0 0 30 c6_p227-253.qxd 3/12/08 4:13 AM Page 241
- 260. Sea X el número de rayones en un artículo seleccionado al azar y suponga que X tiene una distribución de Poisson con parámetro . a. Determine un estimador insesgado de y calcule la esti- mación de los datos. [Sugerencia: E(X) para una distribución Poisson de X, por lo tanto E(X ) ?] b. ¿Cuál es la desviación estándar (error estándar) de su estimador? Calcule el error estándar estimado. [Sugerencia: 2 X con distribución de Poisson de X.] 10. Con una larga varilla de longitud , va a trazar una curva cuadrada en la cual la longitud de cada lado es . Por con- siguiente el área de la curva será 2 . Sin embargo, no cono- ce el valor de así que decide hacer n mediciones independientes X1, X2, . . . , Xn de la longitud. Suponga que cada Xi tiene una media (mediciones insesgadas) y varianza 2 . a. Demuestre que X 2 no es un estimador insesgado de 2 . [Sugerencia: Con cualquier variable aleatoria Y, E(Y2 ) V(Y) [E(Y)]2 . Aplique ésta con Y X .] b. ¿Con qué valor de k es el estimador X 2 kS2 insesgado para 2 ? [Sugerencia: Calcule E(X 2 kS2 ).] 11. De n1 fumadores seleccionados al azar, X1 fuman cigarrillos con filtro, mientras que de n2 fumadoras seleccionadas al azar, X2 fuman cigarrillos con filtro. Sean p1 y p2 las proba- bilidades de que un varón y una mujer seleccionados al azar, fumen, respectivamente, cigarrillos con filtro. a. Demuestre que (X1/n1) (X2/n2) es un estimador inses- gado de p1 p2. [Sugerencia: E(Xi) ni pi con i 1, 2.] b. ¿Cuál es el error estándar del estimador en el inciso a)? c. ¿Cómo utilizaría los valores observados x1 y x2 para esti- mar el error estándar de su estimador? d. Si n1 n2 200, x1 127 y x2 176, use el estimador del inciso a) para obtener una estimación de p1 p2. e. Use el resultado del inciso c) y los datos del inciso d) para estimar el error estándar del estimador. 12. Suponga que un tipo de fertilizante rinde 1 por acre con varianza 2 , mientras que el rendimiento esperado de un segundo tipo de fertilizante es 2, con la misma varianza 2 . Sean S2 1 y S2 2 las varianzas muestrales de rendimientos basa- das en tamaños muestrales n1 y n2, respectivamente, de los dos fertilizantes. Demuestre que el estimador combinado es ˆ 2 es un estimador insesgado de 2 . 13. Considere una muestra aleatoria de X1, . . . , Xn de la fun- ción de densidad de probabilidad f(x; ) 0.5(1 x) 1 x 1 donde 1 1 (esta distribución se presenta en la física de partículas. Demuestre que ˆ 3X es un estimador inses- gado de . [Sugerencia: Primero determine E(X) E(X ).] 14. Una muestra de n aviones de combate Pandemonium cap- turados tienen los números de serie x1, x2, x3, . . . , xn. La CIA sabe que los aviones fueron numerados consecutivamen- te en la fábrica comenzando con y terminando con , por lo que el número total de aviones fabricados es 1 (p. ej., si 17 y 29, entonces 29 17 1 13 aviones con números de serie 17, 18, 19, . . . , 28, 29 fueron fabricados). Sin embargo, la CIA no conoce los valores de y . Un estadístico de la CIA sugiere utilizar el estimador máx(Xi) mín(Xi) 1 para estimar el número total de aviones fabricados. a. Si n 5, x1 237, x2 375, x3 202, x4 525 y x5 418, ¿cuál es la estimación correspondiente? b. ¿En qué condiciones de la muestra será el valor de la esti- mación exactamente igual al número total verdadero de aviones? ¿Alguna vez será más grande la estimación que el total verdadero? ¿Piensa que el estimador es insesgado para estimar 1? Explique en una o dos oraciones. 15. Si X1, X2, . . . , Xn representan una muestra aleatoria toma- da de una distribución de Rayleigh con función de densidad de probabilidad f(x; ) x e x2/(2 ) x 0 a. Se puede demostrar que E(X2 ) 2 . Use este hecho para construir un estimador insesgado de basado en X2 i (y use reglas de valor esperado para demostrar que es insesgado). b. Calcule a partir de las siguientes n 10 observacio- nes de esfuerzo vibratorio de un aspa de turbina en con- diciones específicas: 16.88 10.23 4.59 6.66 13.68 14.23 19.87 9.40 6.51 10.95 16. Suponga que el crecimiento promedio verdadero de un tipo de planta durante un periodo de un año es idéntico al de un segundo tipo, aunque la varianza del crecimiento del primer tipo es 2 , en tanto que para el segundo tipo, la varianza es 42 . Sean X1, . . . , Xm, m observaciones de crecimiento inde- pendientes del primer tipo [por consiguiente E(Xi) , V(Xi) 2 ] y sean Y1, . . . , Yn, n observaciones de crecimiento independientes del segundo tipo [E(Yi) , V(Yi) 42 ]. a. Demuestre que con cualquier entre 0 y 1, el estimador ˆ X (1 )Y es insesgado para . b. Con m y n fijas, calcule V( ˆ ) y luego determine el valor de que reduzca al mínimo V( ˆ ). [Sugerencia: Derive V( ˆ ) con respecto a .] 17. En el capítulo tres, se definió una variable aleatoria bino- mial negativa como el número de fallas que ocurren antes del r-ésimo éxito en una secuencia de ensayos con éxitos y fallas independientes e idénticos. La función masa de pro- babilidad (fmp) de X es nb(x; r, p) { pr (1 p)x x 0, 1, 2, . . . 0 de lo contrario x r 1 x (n1 1)S2 1 (n2 1)S2 2 n1 n2 2 242 CAPÍTULO 6 Estimación puntual Número de rayones por artículo 0 1 2 3 4 5 6 7 Frecuencia observada 18 37 42 30 13 7 2 1 c6_p227-253.qxd 3/12/08 4:13 AM Page 242
- 261. a. Suponga que r 2. Demuestre que p̂ (r 1)/(X r 1) es un estimador insesgado de p. [Sugerencia: Escriba E(p̂) y elimine x r 1 dentro de la suma.] b. Un reportero desea entrevistar a cinco individuos que apoyan a un candidato y comienza preguntándoles si (S) o no (F) apoyan al candidato. Si la secuencia de res- puestas es SFFSFFFSSS estiman p la proporción ver- dadera que apoya al candidato. 18. Sean X1, X2, . . . , Xn una muestra aleatoria de una función de densidad de probabilidad f(x) simétrica con respecto a , de modo que sea un estimador insesgado de . Si n es grande, se puede demostrar que V( ) 1/(4n[ f()]2 ). a. Compara V( ) con V(X X ) cuando la distribución subya- cente es normal. b. Cuando la función de densidad de probabilidad subya- cente es Cauchy (véase el ejemplo 6.7), V(X ) por lo tanto X es un estimador terrible. ¿Cuál es V( ) en este caso cuando n es grande? 19. Una investigadora desea estimar la proporción de estudian- tes en una universidad que han violado el código de honor. Habiendo obtenido una muestra aleatoria de n estudiantes, se da cuenta que si a cada uno le pregunta “¿Has violado el código de honor?” probablemente recibirá algunas respues- tas faltas de veracidad. Considere el siguiente esquema, conocido de técnica de respuesta aleatorizada. La investi- gadora forma un mazo de 100 cartas de las cuales 50 son de tipo I y 50 de tipo II. Tipo I: ¿Has violado el código de honor (sí o no)? Tipo II: ¿Es el último dígito de su número telefónico un 0, 1 o 2 (sí o no)? A cada estudiante en la muestra aleatoria se le pide que baraje el mazo, que saque una carta y que responda la pre- gunta con sinceridad. A causa de la pregunta irrelevante en las cartas de tipo II, una respuesta sí ya no estigmatiza a quien contesta, así que se supone que éste es sincero. Sea p la proporción de violadores del código de honor (es decir, la probabilidad de que un estudiante seleccionado al azar sea un violador) y sea P(respuesta sí). Entonces y p están relacionados por 0.5p (0.5)(0.3). a. Sea Y el número de respuestas sí, por consiguiente Y Bin(n, ). Por tanto Y/n es un estimador insesgado de . Obtenga un estimador de p basado en Y. Si n 80 y y 20, ¿cuál es su estimación? [Sugerencia: Resuelva 0.5p 1.5 para p y luego sustituya Y/n en lugar de .] b. Use el hecho de que E(Y/n) para demostrar que su estimador p̂ es insesgado. c. Si hubiera 70 cartas de tipo I y 30 de tipo II, ¿cuál sería su estimador para p? X | X | X | X | 6.2 Métodos de estimación puntual 243 La definición de insesgamiento no indica en general cómo se pueden obtener los estimadores insesgados. A continuación se discuten dos métodos “constructivos” para obtener estimado- res puntuales: el método de momentos y el método de máxima verosimilitud. Por constructi- vo se quiere dar a entender que la definición general de cada tipo de estimador sugiere explícitamente cómo obtener el estimador en cualquier problema específico. Aun cuando se prefieren los estimadores de máxima verosimilitud a los de momento debido a ciertas propie- dades de eficiencia, a menudo requieren significativamente más cálculo que los estimadores de momento. En ocasiones es el caso que estos métodos dan estimadores insesgados. El método de momentos La idea básica de este método es poder igualar ciertas características muestrales, tales como la media, a los valores esperados de la población correspondiente. Luego resolviendo estas ecuaciones con valores de parámetros conocidos se obtienen los estimadores. DEFINICIÓN Si X1, . . . , Xn constituyen una muestra aleatoria proveniente de una función masa de probabilidad o de una función de densidad de probabilidad f(x). Con k 1, 2, 3, . . . el k-ésimo momento de la población o el k-ésimo momento de la distribu- ción f(x), es E(Xk ). El k-ésimo momento muestral es (1/n)n i1Xk i. Por consiguiente el primer momento de la población es E(X) y el primer momento muestral es Xi/n X . Los segundos momentos de la población y muestral son E(X2 ) y X2 i/n, respectivamente. Los momentos de la población serán funciones de cualquier pará- metro desconocido 1, 2, . . . 6.2 Métodos de estimación puntual c6_p227-253.qxd 3/12/08 4:13 AM Page 243
- 262. 244 CAPÍTULO 6 Estimación puntual Si, por ejemplo, m 2, E(X) y E(X2 ) serán funciones de 1 y 2. Con E(X) (1/n) Xi ( X ) y E(X2 ) (1/n) X2 i se obtienen dos ecuaciones en 1 y 2. La solución define enton- ces los estimadores. Para estimar una media poblacional, el método da X , por lo tanto el estimador es la media muestral. Si X1, X2, . . . , Xn representan una muestra aleatoria de tiempos de servicio de n clientes en una instalación, donde la distribución subyacente se supone exponencial con el parámetro . Como sólo hay un parámetro que tiene que ser estimado, el estimador se obtiene igua- lando E(X) a X . Como E(X) 1/ con una distribución exponencial, ésta da 1/ X o 1/X . El estimador de momento de es entonces ˆ 1/X . ■ Sean X1, . . . , Xn una muestra aleatoria de una distribución gama con parámetros y . De acuerdo con la sección 4.4, E(X) y E(X2 ) 2 ( 2)/() 2 ( 1). Los esti- madores de momento y se obtienen resolviendo X 1 n X2 i ( 1)2 Como ( 1)2 2 2 2 y la primera ecuación implica 2 2 X 2 , la segunda ecuación se vuelve 1 n X2 i X 2 2 Ahora si se divide cada miembro de esta segunda ecuación entre el miembro correspon- diente de la primera ecuación y se sustituye otra vez se obtienen los estimadores ˆ ˆ Para ilustrar, los datos de tiempo de sobrevivencia mencionados en el ejemplo 4.24 son 152 115 109 94 88 137 152 77 160 165 125 40 128 123 136 101 62 153 83 69 con x 113.5 y (1/20)x2 i 14087.8. Los estimadores son ˆ 10.7 ˆ 10.6 Estas estimaciones de y difieren de los valores sugeridos por Gross y Clark porque ellos utilizaron una técnica de estimación diferente. ■ Sean X1, . . . , Xn una muestra aleatoria de una distribución binomial negativa generalizada con parámetros r y p (sección 3.5). Como E(X) r(1 p)/p y V(X) r(1 p)/p2 , 14 087.8 (113.5)2 113.5 (113.5)2 14 087.8 (113.5)2 (1/n)X2 i X 2 X X 2 (1/n)X2 i X 2 DEFINICIÓN Si X1, X2, . . . , Xn son una muestra aleatoria de una distribución con función masa de probabilidad o función de densidad de probabilidad f(x; 1, . . . , m), donde 1, . . . , m son parámetros cuyos valores son desconocidos. Entonces los estimadores de momen- to ˆ 1, . . . , ˆ m se obtienen igualando los primeros m momentos muestrales con los pri- meros m momentos de la población correspondientes y resolviendo para 1, . . . , m. Ejemplo 6.12 Ejemplo 6.13 Ejemplo 6.14 c6_p227-253.qxd 3/12/08 4:13 AM Page 244
- 263. 6.2 Métodos de estimación puntual 245 E(X2 ) V(X) [E(X)]2 r(1 p)(r rp 1)/p2 . Si se iguala E(X) a X y E(X2 ) a (1/n)X2 i a la larga se obtiene p̂ (1/n)X X 2 i X 2 r̂ Como ilustración, Reep, Pollard y Benjamin (“Skill and Chance in Ball Games”, J. Royal Stat. Soc., 1971: 623-629) consideran la distribución binomial negativa como modelo del número de goles por juego anotados por los equipos de la Liga Nacional de Jockey. Los datos de 1966-1967 son los siguientes (420 juegos): Goles 0 1 2 3 4 5 6 7 8 9 10 Frecuencia 29 71 82 89 65 45 24 7 4 1 3 Entonces, x xi /420 [(0)(29) (1)(71) (10)(3)]/420 2.98 y x2 i /420 [(0)2 (29) (1)2 (71) (10)2 (3)]/420 12.40 Por consiguiente, p̂ 12.40 2 .98 (2.98)2 0.85 r̂ 16.5 Aunque r por definición debe ser positivo, el denominador de r̂ podría ser negativo, lo que indica que la distribución binomial negativa no es apropiada (o que el estimador de momen- to es defectuoso). ■ Estimación de máxima verosimilitud El método de máxima probabilidad lo introdujo por primera vez R. A. Fisher, genetista y estadístico en la década de 1920. La mayoría de los estadísticos recomiendan este método, por lo menos cuando el tamaño de muestra es grande, puesto que los estimadores resultantes tienen ciertas propiedades de eficiencia deseables (véase la proposición en la página 249). Se obtuvo una muestra de diez cascos de ciclista nuevos fabricados por una compañía. Al probarlos, se encontró que el primero, el tercero y el décimo estaban agrietados, en tanto que los demás no. Sea p P(casco agrietado) y defina X1, . . . , X10 como Xi 1 si el i-ésimo casco está agrietado y cero de lo contrario. En ese caso las xi son 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, así que la función masa de probabilidad conjunta de la muestra es f(x1, x2, . . . , x10; p) p(1 p)p p p3 (1 p)7 (6.4) Ahora se hace la pregunta, “¿Con qué valor de p es más probable que la muestra observada haya ocurrido?” Es decir, se desea encontrar el valor de p que incrementa al máximo la fun- ción masa de probabilidad (6.4) o, en forma equivalente, que incrementa al máximo el loga- ritmo natural de (6.4).* Como ln[f(x1, . . . , x10; p)] 3 ln(p) 7 ln(1 p) (6.5) (2.98)2 12.40 (2.98)2 2.98 X 2 (1/n)X2 i X 2 X Ejemplo 6.15 * Como ln[g(x)] es una función monotónica de g(x), determinar x para incrementar al máximo ln[g(x)] equivale a incrementar al máximo g(x). En estadística, si se toma el logaritmo con frecuencia, un producto cambia a una suma, con la cual es más fácil trabajar. c6_p227-253.qxd 3/12/08 4:13 AM Page 245
- 264. la cual es una función derivable de p, igualando la derivada de (6.5) a cero se obtiene el valor maximizante† d d p ln[f(x1, . . . , x10; p)] 3 p 1 7 p 0 ‰ p 1 3 0 n x donde x es el número de éxitos observados (cascos agrietados). La estimación de p ahora es p̂ 1 3 0. Se llama estimación de máxima verosimilitud porque para x1, . . . , x10 estable- cido, es el valor del parámetro que maximiza la probabilidad (función masa de probabili- dad conjunta) de la muestra observada. Obsérvese que si sólo se hubiera dicho que entre los diez cascos había tres agrietados, la ecuación (6.4) sería reemplazada por la función masa de probabilidad binomial (10 3 )p3 (1 p)7 , la cual también se incrementa al máximo con p̂ 1 3 0. ■ La función de verosimilitud dice qué tan probable es que la muestra observada sea una función de los posibles valores de parámetro. Al incrementarse al máximo la probabilidad se obtienen los valores de parámetro con los que la muestra observada es más probable que haya sido generada, es decir, los valores de parámetro que “más concuerdan” con los datos observados. Suponga que X1, X2, . . . , Xn es una muestra aleatoria de una distribución exponencial con parámetro . Debido a la independencia, la función de verosimilitud es un producto de las funciones de densidad de probabilidad individuales: f(x1, . . . , xn; ) (ex1) (exn) n exi El ln(verosimilitud) es ln[f(x1, . . . , xn; )] n ln() xi Si se iguala (d/d)[ln(verosimilitud)] a cero se obtiene n/ xi 0, o n/xi 1/x . Por consiguiente el estimador de máxima verosimilitud es ˆ 1/X ; es idéntico al método de estimador de momentos [pero no es un estimador insesgado, puesto que E(1/X ) 1/E(X )]. ■ † Esta conclusión requiere que se verifique la segunda derivada, pero se omiten los detalles. 246 CAPÍTULO 6 Estimación puntual DEFINICIÓN Que X1, X2, . . . , Xn tengan una función masa de probabilidad o una función de den- sidad de probabilidad f(x1, x2, . . . , xn; 1, . . . , m) (6.6) donde los parámetros 1, . . . , m tienen valores desconocidos. Cuando x1, . . . , xn son los valores muestrales observados y (6.6) se considera como una función de 1, . . . , m, se llama función de verosimilitud. Las estimaciones de máxima verosimilitud (emv) ˆ 1, . . . , ˆ m son aquellos valores de las i que incrementan al máximo la función de pro- babilidad, de modo que f(x1, . . . , xn; ˆ 1, . . . , ˆ m) f(x1, . . . , xn; 1, . . . , m) con todos los 1, . . . , m Cuando se sustituyen las Xi en lugar de las xi, se obtienen los estimadores de máxi- ma verosimilitud. Ejemplo 6.16 c6_p227-253.qxd 3/12/08 4:13 AM Page 246
- 265. Sean X1, . . . , Xn una muestra aleatoria de una distribución normal. La función de probabi- lidad es f(x1, . . . , xn; , 2 ) 2 1 2 e(x1)2/(2 2) 2 1 2 e(xn)2/(2 2) 2 1 2 n/2 e(xi)2/(2 2) por consiguiente ln[ f(x1, . . . , xn; , 2 )] n 2 ln(22 ) 2 1 2 (xi )2 Para determinar los valores maximizantes de y 2 , se deben tomar las derivadas parciales de ln( f) con respecto a y 2 , igualarlas a cero y resolver las dos ecuaciones resultantes. Omitiendo los detalles, los estimadores de máxima probabilidad resultantes son ˆ X ˆ 2 (Xi n X )2 El estimador de máxima verosimilitud de 2 no es el estimador insesgado, por consiguien- te dos principios diferentes de estimación (insesgamiento y máxima verosimilitud) dan dos estimadores diferentes. ■ En el capítulo 3, se analizó el uso de la distribución de Poisson para modelar el número de “eventos” que ocurren en una región bidimensional. Suponga que cuando el área de la región R que se está muestreando es a(R), el número X de eventos que ocurren en R tiene una distribución de Poisson con parámetro a(R) (donde es el número esperado de even- tos por unidad de área) y que las regiones no traslapantes dan X independientes. Suponga que un ecólogo selecciona n regiones no traslapantes R1, . . . , Rn y cuenta el número de plantas de una especie en cada región. La función masa de probabilidad conjun- ta es entonces p(x1, . . . , xn; ) el ln(verosimilitud) es ln[p(x1, . . . , xn; )] xi ln[a(Ri)] ln() xi a(Ri) ln(xi!) Con d/d ln(p) e igualándola a cero da xi a(Ri) 0 por consiguiente a( x R i i) El estimador de máxima verosimilitud es entonces ˆ Xi/a(Ri). Ésta es razonablemen- te intituitiva porque es la densidad verdadera (plantas por unidad de área), mientras que ˆ es la densidad muestral puesto que a(Ri) es tan sólo el área total muestreada. Como E(Xi) a(Ri), el estimador es insesgado. En ocasiones se utiliza un procedimiento de muestreo alternativo. En lugar de fijar las regiones que van a ser muestreadas, el ecólogo seleccionará n puntos en toda la región de [a(R1)]x1 [a(Rn)]xn xi ea(Ri) x1! xn! [ a(Rn)]xnea(Rn) xn! [ a(R1)]x1ea(R1) x1! 6.2 Métodos de estimación puntual 247 Ejemplo 6.17 Ejemplo 6.18 c6_p227-253.qxd 3/12/08 4:13 AM Page 247
- 266. interés y sea yi la distancia del i-ésimo punto a la planta más cercana. La función de dis- tribución acumulativa de Y distancia a la planta más cercana es FY(y) P(Y y) 1 P(Y y) 1 P 1 ey2 0 ( ! y2 )0 1 ey2 Al tomar la derivada de FY (y) con respecto a y proporciona fY(y; ) {2yey2 y 0 0 de lo contrario Si ahora se forma la probabilidad fY(y1; ) fY(yn; ), derive ln(verosimilitud), y así sucesivamente, el estimador de máxima verosimilitud resultante es ˆ n Y2 i la que también es una densidad muestral. Se puede demostrar que un ambiente ralo (peque- ño ), el método de distancia es en cierto sentido mejor, en tanto que en un ambiente den- so, el primer método de muestreo es mejor. ■ Sean X1, . . . , Xn una muestra aleatoria de una función de densidad de probabilidad Weibull f(x; , ) { x1 e(x/) x 0 0 de lo contrario Si se escribe la verosimilitud y el ln(verosimilitud) y luego con (,/,)[ln( f)] 0 y (,/,)[ln(f)] 0 se obtienen las ecuaciones x i x ln i (xi) ln n (xi) 1 n x i 1/ Estas dos ecuaciones no pueden ser resueltas explícitamente para obtener fórmulas generales de los estimadores de máxima verosimilitud ˆ y ˆ . En su lugar, por cada muestra x1, . . . , xn, las ecuaciones deben ser resueltas con un procedimiento numérico iterativo. Incluso los esti- madores de momento de y son un tanto complicados (véase el ejercicio 21). ■ Estimación de funciones de parámetros En el ejemplo 6.17, se obtuvo el estimador de máxima verosimilitud de 2 cuando la distri- bución subyacente es normal. El estimador de máxima verosimilitud de 2 , como el de muchos otros estimadores de máxima verosimilitud, es fácil de derivar con la siguien- te proposición. número de plantas observadas área total muestreada ninguna planta en un círculo de radio y 248 CAPÍTULO 6 Estimación puntual Ejemplo 6.19 PROPOSICIÓN El principio de invarianza Sean ˆ 1, ˆ 2, . . . , ˆ m los estimadores de máxima verosimilitud de los parámetros 1, 2, . . . , m. Entonces el estimador de máxima verosimilitud de cualquier función h( 1, 2, . . . , m) de estos parámetros es la función h(ˆ 1, ˆ 2, . . . , ˆ m) de los estimado- res de máxima verosimilitud. c6_p227-253.qxd 3/12/08 4:13 AM Page 248
- 267. En el caso normal, los estimadores de máxima verosimilitud de y 2 son ˆ X y ˆ 2 (Xi X )2 /n. Para obtener el estimador de máxima verosimilitud de la función h(, 2 ) 2 , sustituya los estimadores de máxima verosimilitud en la función. ˆ ˆ 2 1 n (Xi X )2 1/2 el estimador de máxima verosimilitud de no es la desviación estándar muestral S y se aproximan bastante cuando n es bastante pequeño. ■ El valor medio de una variable aleatoria X que tiene una distribución Weibull es (1 1/) El estimador de máxima verosimilitud de es por consiguiente ˆ ˆ (1 1/ˆ ), donde ˆ y ˆ son los estimadores de máxima verosimilitud de y . En particular X no es el esti- mador de máxima verosimilitud de , aunque es un estimador insesgado. Por lo menos con n grande, ˆ es un mejor estimador que X ■ Comportamiento con muestra grande del estimador de máxima verosimilitud Aunque el principio de la estimación de máxima verosimilitud tiene un considerable atrac- tivo intuitivo, la siguiente proposición proporciona razones adicionales fundamentales para el uso de estimadores de máxima verosimilitud. Debido a este resultado y al hecho de que las técnicas basadas en el cálculo casi siempre pueden ser utilizadas para derivar los estimadores de máxima verosimilitud (aunque a veces se requieren métodos numéricos, tales como el método de Newton), la estimación de máxima verosimilitud es la técnica de estimación más ampliamente utilizada entre los estadísticos. Muchos de los estimadores utilizados en lo que resta del libro son estimadores de máxima verosimilitud. La obtención de un estimador de máxima verosimilitud, sin embargo, requie- re que se especifique la distribución subyacente. Algunas complicaciones En ocasiones no se puede utilizar el cálculo para obtener estimadores de máxima verosimilitud. Suponga que mi tiempo de espera de un autobús está uniformemente distribuido en [0, ] y que se observaron los resultados x1, . . . , xn de una muestra aleatoria tomada de esta distri- bución. Como f(x; ) 1/ con 0 x , y 0 de lo contrario, f(x1, . . . , xn; ) 1 n 0 x1 , . . . , 0 xn 0 de lo contrario En tanto máx(xi) , la verosimilitud es 1/ n , la cual es positiva, pero en cuanto máx(xi), la verosimilitud se reduce a 0. Esto se ilustra en la figura 6.5. El cálculo no fun- ciona porque el máximo de la probabilidad ocurre en un punto de discontinuidad. 6.2 Métodos de estimación puntual 249 Ejemplo 6.22 PROPOSICIÓN En condiciones muy generales en relación con la distribución conjunta de la muestra, cuando el tamaño de la muestra n es grande, el estimador de máxima verosimilitud de cualquier parámetro es aproximadamente insesgado [E(ˆ) ] y su varianza es casi tan pequeña como la que puede ser lograda por cualquier estimador. Expresado de otra manera, el estimador de máxima verosimilitud ˆ es aproximadamente el esti- mador insesgado con varianza mínima de . Ejemplo 6.20 (continuación del ejemplo 6.17) Ejemplo 6.21 (continuación del ejemplo 6.19) c6_p227-253.qxd 3/12/08 4:13 AM Page 249
- 268. pero la figura indica que ˆ máx(Xi). Por consiguiente si mis tiempos de espera son 2.3, 3.7, 1.5, 0.4 y 3.2, entonces el estimador de máxima verosimilitud es ˆ 3.7. ■ Un método que a menudo se utiliza para estimar el tamaño de una población de vida sil- vestre implica realizar un experimento de captura/recaptura. En este experimento, se captu- ra una muestra inicial de M animales, y cada uno se éstos se etiqueta y luego son regresados a la población. Tras de permitir un tiempo suficiente para que los individuos etiquetados se mezclen con la población, se captura otra muestra de tamaño n. Con X el número de animales etiquetados en la segunda muestra, el objetivo es utilizar las x observadas para esti- mar la población de tamaño N. El parámetro de interés es N, el cual asume sólo valores enteros, así que incluso después de determinar la función de verosimilitud (función masa de probabilidad de X en este caso), el uso del cálculo para obtener N presentaría dificultades. Si se considera un éxi- to la recaptura de un animal previamente etiquetado, entonces el muestreo es sin reemplazo de una población que contiene M éxitos y N M fallas, de modo que X es una variable alea- toria hipergeométrica y la función de probabilidad es p(x; N) h(x; n, M, N) La naturaleza de valor entero de N, dificultaría tomar la derivada de p(x; N). Sin embargo, si se considera la razón de p(x; N) a p(x; N 1), se tiene Esta razón es más grande que 1 si y sólo si N Mn/x. El valor de N con el cual p(x; N) se incrementa al máximo es por consiguiente el entero más grande menor que Mn/x. Si se uti- liza la notación matemática estándar [r] para el entero más grande menor que o igual a r, el estimador de máxima probabilidad de N es N̂ [Mn/x]. Como ilustración, si M 200 peces se sacan del lago y etiquetan, posteriormente n 100 son recapturados y entre los 100 hay x 11 etiquetados, en ese caso N̂ [(200)(100)/11] [1818.18] 1818. La estimación es en realidad un tanto intuitiva; x/n es la proporción de la muestra recapturada etiquetada, mientras que M/N es la proporción de toda la población etiquetada. La estimación se obtiene igualando estas dos proporciones (estimando una proporción poblacional mediante una pro- porción muestral). ■ Supóngase que X1, X2, . . . , Xn es una muestra aleatoria de una función de densidad de probabilidad f(x; ) simétrica con respecto a aunque el investigador no está seguro de la forma de la función f. Es entonces deseable utilizar un estimador ˆ robusto, es decir, uno que funcione bien con una amplia variedad de funciones de densidad de probabilidad (N M) (N n) N(N M n x) p(x; N) p(x; N 1) M x N n x M N n 250 CAPÍTULO 6 Estimación puntual máx(xi) Probabilidad Figura 6.5 Función de probabilidad del ejemplo 6.22. Ejemplo 6.23 c6_p227-253.qxd 3/12/08 4:13 AM Page 250
- 269. subyacentes. Un estimador como ése es una media recortada. En años recientes, los esta- dísticos han propuesto otro tipo de estimador, llamado estimador M, basado en una genera- lización de la estimación de máxima verosimilitud. En lugar de incrementar al máximo el logaritmo de la probabilidad ln[ f(x; )] para una f específica, se incrementa al máximo (xi; ). Se selecciona la “función objetivo” para que dé un estimador con buenas pro- piedades de robustez. El libro de David Hoaglin y colaboradores (véase la bibliografía) con- tiene una buena exposición de esta materia. 6.2 Métodos de estimación puntual 251 EJERCICIOS Sección 6.2 (20-30) 20. Se selecciona una muestra aleatoria de n cascos para ciclis- tas fabricados por una compañía. Sea X el número entre los n que están agrietados y sea p P(agrietado). Suponga que sólo se observa X, en lugar de la secuencia de S y F. a. Obtenga el estimador de máxima verosimilitud de p. Si n 20 y x 3, ¿cuál es la estimación? b. ¿Es insesgado el estimador del inciso a)? c. Si n 20 y x 3, ¿cuál es el estimador de máxima verosimilitud de la probabilidad (1 p)5 de que ningu- no de los siguientes cinco cascos esté agrietado? 21. Si X tiene una distribución de Weibull con parámetros y , entonces E(X) (1 1/) V(X) 2 {(1 2/) [(1 1/)]2 } a. Basado en una muestra aleatoria X1, . . . , Xn, escriba ecuaciones para el método de estimadores de momentos y . Demuestre que, una vez que se obtiene la estima- ción de , la estimación de se puede hallar en una tabla de la función gama y que la estimación de es la solución de una ecuación complicada que implica la fun- ción gama. b. Si n 20, x 28.0 y x2 i 16 500, calcule las esti- maciones. [Sugerencia: [(1.2)]2 /(1.4) 0.95.] 22. Sea X la proporción de tiempo destinado que un estudiante seleccionado al azar pasa resolviendo cierta prueba de apti- tud. Suponga que la función de densidad de probabilidad de X es f(x; ) ( 1)x 0 x 1 0 de lo contrario donde 1 . Una muestra aleatoria de diez estudiantes produce los datos x1 0.92, x2 0.79, x3 0.90, x4 0.65, x5 0.86, x6 0.47, x7 0.73, x8 0.97, x9 0.94, x10 0.77. a. Use el método de momentos para obtener un estimador de y luego calcule la estimación con estos datos. b. Obtenga el estimador de máxima verosimilitud de y luego calcule la estimación con los datos dados. 23. Dos sistemas de computadoras diferentes son monitoreados durante un total de n semanas. Sea Xi el número de descom- posturas del primer sistema durante la i-ésima semana y suponga que las Xi son independientes y que se extraen de una distribución de Poisson con parámetro 1. Asimismo, sea Yi el número de descomposturas del segundo sistema du- rante la semana i-ésima y suponga independencia con cada Yi extraída de una distribución de Poisson con parámetro 2. Derive los estimadores de máxima verosimilitud de 1, 2 y 1 2. [Sugerencia: Utilizando independencia, escriba la función masa de probabilidad conjunta de las Xi y Yi juntas.] 24. Remítase al ejercicio 20. En lugar de seleccionar n 20 cascos para examinarlos, suponga que se examinan en suce- sión hasta que se encuentran r 3 agrietados. Si el vigési- mo percentil casco es el tercer agrietado (de modo que el número de cascos examinados que no están agrietados sea x 17), ¿cuál es el estimador de máxima verosimilitud de p? ¿Es ésta la misma estimación del ejercicio 20? ¿Por qué sí o por qué no? ¿Es la misma que la estimación calculada con el estimador insesgado del ejercicio 17? 25. Se determina la resistencia al esfuerzo cortante de soldadu- ras de puntos de prueba y se obtienen los siguientes datos (lb/pulg2 ): 392 376 401 367 389 362 409 415 358 375 a. Suponiendo que la resistencia al esfuerzo cortante está normalmente distribuida, estime la resistencia al esfuer- zo cortante promedio verdadera y la desviación estándar de la resistencia al esfuerzo cortante utilizando el méto- do de máxima verosimilitud. b. De nuevo suponiendo una distribución normal, calcule el valor de resistencia por debajo del cual 95% de todas las soldaduras tendrán sus resistencias. [Sugerencia: ¿Cuál es el percentil 95 en función de y ? Utilice ahora el principio de invarianza.] 26. Remítase al ejercicio 25. Suponga que decide examinar otra soldadura de puntos de prueba. Sea X resistencia al esfuer- zo cortante de la soldadura. Use los datos dados para obtener el estimador de máxima verosimilitud de P(X 400). [Sugerencia: P(X 400) ((400 )/).] 27. Sean X1, . . . , Xn una muestra aleatoria de una distribución gama con parámetros y . a. Derive las ecuaciones cuya solución da los estimadores de máxima verosimilitud de y . ¿Piensa que pueden ser resueltos explícitamente? b. Demuestre que el estimador de máxima verosimilitud de es ˆ X . 28. Si X1, X2, . . . , Xn representan una muestra aleatoria de la distribución Rayleigh con función densidad dada en el ejer- cicio 15. Determine: a. El estimador de máxima verosimilitud de y luego cal- cule la estimación con los datos de esfuerzo de vibración dados en ese ejercicio. ¿Es este estimador el mismo que el estimador insesgado del ejercicio 15? c6_p227-253.qxd 3/12/08 4:13 AM Page 251
- 270. b. El estimador de máxima verosimilitud de la mediana de la distribución del esfuerzo de vibración. [Sugerencia: Exprese primero la mediana en función de .] 29. Considere la muestra aleatoria X1, X2, . . . , Xn de la función de densidad de probabilidad exponencial desplazada f(x; , ) {e(x ) x 0 de lo contrario Con 0 da la función de densidad de probabilidad de la dis- tribución exponencial previamente considerada (con densidad positiva a la derecha de cero). Un ejemplo de la distribución exponencial desplazada apareció en el ejemplo 4.5, en el cual la variable de interés fue el tiempo entre vehículos en el flujo de tráfico y 0.5 fue el tiempo entre vehículos máximo posible. a. Obtenga los estimadores de máxima verosimilitud de y . b. Si n 10 observaciones de tiempo entre vehículos son realizadas y se obtienen los siguientes resultados 3.11, 0.64, 2.55, 2.20, 5.44, 3.42, 10.39, 8.93, 17.82 y 1.30, calcule las estimaciones de y . 30. En los instantes t 0, 20 componentes idénticos son puestos a prueba. La distribución de vida útil de cada uno es expo- nencial con parámetro . El experimentador deja la instala- ción de prueba sin monitorear. A su regreso 24 horas más tarde, el experimentador termina de inmediato la prueba des- pués de notar que y 15 de los 20 componentes aún están en operación (así que 5 han fallado). Derive el estimador de máxima verosimilitud de . [Sugerencia: Sea Y el número que sobreviven 24 horas. En ese caso Y Bin(n, p). ¿Cuál es el estimador de máxima verosimilitud de p? Observe ahora que p P(Xi 24), donde Xi está exponencialmente distri- buida. Esto relaciona con p, de modo que el primero puede ser estimado una vez que lo ha sido el segundo.] 252 CAPÍTULO 6 Estimación puntual EJERCICIOS SUPLEMENTARIOS (31-38) 31. Se dice que un estimador ˆ es consistente si con cualquier 0, P(°ˆ ° ) A 0 a medida que n A . Es decir, ˆ es consistente, si, a medida que el tamaño de muestra se hace más grande, es menos y menos probable que ˆ se ale- je más que del valor verdadero de . Demuestre que X es un estimador consistente de cuando 2 mediante la desigualdad de Chebyshev del ejercicio 44 del capítulo 3. [Sugerencia: La desigualdad puede ser reescrita en la forma P(°Y Y° ) 2 Y / Ahora identifique Y con X .] 32. a. Sean X1, . . . , Xn una muestra aleatoria de una distribu- ción uniforme en [0, ]. Entonces el estimador de máxi- ma verosimilitud de es ˆ Y máx(Xi). Use el hecho de que Y y si y sólo si cada Xi y para obtener la función de distribución acumulativa de Y. Luego demuestre que la función de densidad de probabilidad de Y máx(Xi) es fY(y) { nyn n 1 0 y 0 de lo contrario b. Use el resultado del inciso a) para demostrar que el esti- mador de máxima verosimilitud es sesgado pero que (n 1)máx(Xi)/n es insesgado. 33. En el instante t 0, hay un individuo vivo en una población. Un proceso de nacimientos puro se desarrolla entonces como sigue. El tiempo hasta que ocurre el primer nacimien- to está exponencialmente distribuido con parámetro . Después del primer nacimiento, hay dos individuos vivos. El tiempo hasta que el primero da a luz otra vez es exponencial con parámetro y del mismo modo para el segundo indivi- duo. Por consiguiente, el tiempo hasta el siguiente naci- miento es el mínimo de dos variables () exponenciales, el cual es exponencial con parámetro 2. Asimismo, una vez que el segundo nacimiento ha ocurrido, hay tres individuos vivos, de modo que el tiempo hasta el siguiente nacimiento es una variable aleatoria exponencial con parámetro 3 y así sucesivamente (aquí se está utilizando la propiedad de amnesia de la distribución exponencial). Suponga que se observa el proceso hasta que el sexto nacimiento ha ocurri- do y los tiempos hasta los nacimientos sucesivos son 25.2, 41.7, 51.2, 55.5, 59.5, 61.8 (con los cuales deberá calcular los tiempos entre nacimientos sucesivos). Obtenga el esti- mador de máxima verosimilitud de . [Sugerencia: La vero- similitud es un producto de términos exponenciales.] 34. El error cuadrático medio de un estimador ˆ es ECM(ˆ) E(ˆ )2 . Si ˆ es insesgado, entonces ECM(ˆ) V(ˆ), pero en general ECM(ˆ) V(ˆ) (sesgo)2 . Considere el estima- dor ˆ 2 KS2 , donde S2 varianza muestral. ¿Qué valor de K reduce al mínimo el error cuadrático medio de este estimador cuando la distribución de la población es normal? [Sugerencia: Se puede demostrar que E[(S2 )2 ] (n 1) 4 /(n 1) En general, es difícil determinar ˆ para reducir al mínimo el ECM(ˆ), por lo cual se buscan sólo estimadores insesga- dos y reducir al mínimo V(ˆ).] 35. Sean X1, . . . , Xn una muestra aleatoria de una función de densidad de probabilidad simétrica con respecto a . Un estimador de que se ha visto que funciona bien con una amplia variedad de distribuciones subyacentes es el estima- dor de Hodges-Lehmann. Para definirla, primero calcule para cada i j y cada j 1, 2, . . . , n el promedio por pares X i,j (Xi Xj)/2. Entonces el estimador es la media- na de las X i,j . Calcule el valor de esta estimación con los datos del ejercicio 44 del capítulo 1. [Sugerencia: Construya una tabla con las xi en el margen izquierdo y en la parte superior. Luego calcule los promedios en y sobre la diagonal.] 36. Cuando la distribución de la población es normal, se puede utilizar la mediana estadística {°X1 °, . . . , °Xn °} X | X | c6_p227-253.qxd 3/12/08 4:13 AM Page 252
- 271. /0.6745 para estimar . Este estimador es más resistente a los efectos de los valores apartados (observaciones alejadas del grueso de los datos) que es la desviación estándar muestral. Calcule tanto la estimación puntual correspondiente como s de los datos del ejemplo 6.2. 37. Cuando la desviación estándar muestral S está basada en una muestra aleatoria de una distribución de población nor- mal, se puede demostrar que E(S) 2 /( n 1 ) (n/2)/((n 1)/2) Use ésta para obtener un estimador insesgado de de la forma cS. ¿Cuál es c cuando n 20? 38. Cada uno de n especímenes tiene que ser pesado dos veces en la misma báscula. Sean Xi y Yi los dos pesos observados del i-ésimo espécimen. Suponga que Xi y Yi son independientes uno de otro, cada uno normalmente distribuido con valor me- dio i (el peso verdadero del espécimen i) y varianza 2 . a. Demuestre que el estimador de máxima verosimilitud de 2 es ˆ 2 (Xi Yi)2 /(4n). [Sugerencia: Si z (z1 z2)/2, entonces (zi z )2 (z1 z2)2 /2.] b. ¿Es el estimador de máxima verosimilitud ˆ 2 un estima- dor insesgado de 2 ? Determine una estimador insesga- do de 2 . [Sugerencia: Con cualquier variable aleatoria Z, E(Z2 ) V(Z) [E(Z)]2 . Aplique ésta a Z Xi Yi.] Bibliografía 253 DeGroot, Morris y Mark Schervish, Probability and Statistics (3a. ed.), Addison-Wesley, Boston, MA, 2002. Incluye una excelen- te discusión tanto de propiedades generales como de métodos de estimación puntual; de particular interés son los ejemplos que muestran cómo los principios y métodos generales pueden dar estimadores insatisfactorios en situaciones particulares. Devore, Jay y Kenneth Berk, Modern Mathematical Statistics with Applications. Thomson-Brooks/Cole, Belmont, CA, 2007. La exposición es un poco más completa y compleja que la de este libro. Efron, Bradley y Robert Tibshirani, An Introduction to the Bootstrap, Chapman and Hall, Nueva York, 1993. La Biblia del bootstrap. Hoaglin, David, Frederick Mosteller y John Turkey, Understan- ding Robust and Exploratory Data Analysis, Wiley, Nueva York, 1983. Contiene varios buenos capítulos sobre estimación puntual robusta, incluido uno sobre estimación M. How, Robert y Allen Craig, Introduction to Mathematical Statistics (5a. ed.), Prentice-Hall, Englewood Cliffs, NJ, 1995. Una buena discusión de insesgadez. Rice, John, Mathematical Statistics and Data Analysis (3a. ed.), Thomson-Brooks/Cole, Belmont, CA, 2007. Una agradable mezcla de teoría y datos estadísticos. Bibliografía c6_p227-253.qxd 3/12/08 4:13 AM Page 253
- 272. Intervalos estadísticos basados en una sola muestra 7 254 INTRODUCCIÓN Una estimación puntual, por el hecho de ser un solo número no proporciona infor- mación sobre la precisión y confiabilidad de la estimación. Considérese, por ejemplo, utilizar el estadístico X para calcular una estimación puntual de la resistencia a la rup- tura promedio verdadera (g) de toallas de papel de cierta marca y supóngase que x 9322.7. Debido a la variabilidad del muestreo, virtualmente nunca es el caso de que x . La estimación puntual no dice nada sobre qué tan cerca pudiera estar a . Una alternativa para reportar un solo valor sensible del parámetro que se está es- timando es calcular y reportar un intervalo completo de valores factibles: una estima- ción de intervalo o un intervalo de confianza (IC). Un intervalo de confianza siempre se calcula seleccionando primero un nivel de confianza, el cual mide el grado de con- fiabilidad del intervalo. Un intervalo de confianza con 95% de nivel de confianza de la resistencia a la ruptura promedio verdadera podría tener un límite inferior de 9162.5 y un límite superior de 9482.9. Entonces al nivel de confianza de 95%, cual- quier valor de entre 9162.5 y 9482.5 es factible. Un nivel de confianza de 95% im- plica que 95% de todas las muestras daría un intervalo que incluye , o cualquier otro parámetro que se esté estimando y sólo 5% de las muestras darían un interva- lo erróneo. Los niveles de confianza más frecuentemente utilizados son 95%, 99% y 90%. Mientras más alto es el nivel de confianza, más fuerte es la creencia de que el valor del parámetro que se está estimando queda dentro del intervalo (en breve se dará una interpretación de cualquier nivel de confianza particular). El ancho del intervalo da información sobre la precisión de una estimación de intervalo. Si el nivel de confianza es alto y el intervalo resultante es bastante angos- to, el conocimiento del valor del parámetro es razonablemente preciso. Un muy am- plio intervalo de confianza, sin embargo, transmite el mensaje de que existe gran cantidad de incertidumbre sobre el valor de lo que se está estimando. La figura 7.1 c7_p225-283.qxd 3/12/08 4:15 AM Page 254
- 273. 7.1 Propiedades básicas de los intervalos de confianza 255 Los conceptos y propiedades básicas de los intervalos de confianza son más fáciles de in- troducir si primero se presta atención a un problema simple, aunque un tanto irreal. Supón- gase que el parámetro de interés es una media poblacional y que: 1. La distribución de la población es normal. 2. El valor de la desviación estándar de la población es conocido. Con frecuencia la normalidad de la distribución de la población es una suposición razona- ble. Sin embargo, si el valor de es desconocido, no es factible que el valor de estaría disponible (el conocimiento del centro de una población en general precede a la informa- ción con respecto a la dispersión). En secciones posteriores, se desarrollarán métodos basa- dos en suposiciones menos restrictivas. Ingenieros industriales especialistas en ergonomía se ocupan del diseño de espacios de tra- bajo y dispositivos operados por trabajadores con objeto de alcanzar una alta productividad y comodidad. El artículo “Studies on Ergonomically Designed Alphanumeric Keyboards” (Human Factors, 1985: 175-187) reporta sobre un estudio de altura preferida de un teclado experimental con un gran soporte para el antebrazo y muñeca. Se seleccionó una muestra de n 31 mecanógrafos entrenados y se determinó la altura preferida del teclado de cada me- canógrafo. La altura preferida promedio muestral resultante fue de x 80.0 cm. Suponien- do que la altura preferida está normalmente distribuida con 2.0 cm (un valor sugerido por datos que aparecen en el artículo), obtenga un intervalo de confianza para , la altura pre- ferida promedio verdadera por la población de todos los mecanógrafos experimentados. ■ Se supone que las observaciones muestrales reales x1, x2, . . . , xn son el resultado de una muestra aleatoria X1, . . . , Xn tomada de una distribución normal con valor medio y desviación estándar . Los resultados del capítulo 5 implican entonces que independiente- mente del tamaño de muestra n, la media muestral X está normalmente distribuida con va- lor esperado y desviación estándar /n . Si se estandariza X restando primero su valor esperado y luego dividiendo entre su desviación estándar se obtiene la variable normal es- tándar Z (7.1) X /n 7.1 Propiedades básicas de los intervalos de confianza 255 7.1 Propiedades básicas de los intervalos de confianza Ejemplo 7.1 muestra intervalos de confianza de 95% de resistencias a la ruptura promedio verda- deras de dos marcas diferentes de marcas de toallas de papel. Uno de estos intervalos sugiere un conocimiento preciso de , mientras que el otro sugiere un rango muy am- plio de valores factibles. Marca 1: Marca 2: Resistencia Resistencia ( ) ( ) ( ) ( ) Figura 7.1 Intervalos de confianza que indican información precisa (marca 1) e imprecisa (marca 2) sobre . c7_p225-283.qxd 3/12/08 4:15 AM Page 255
- 274. Como el área bajo la curva normal estándar entre 1.96 y 1.96 es 0.95, P 1.96 1.96 0.95 (7.2) A continuación manipúlense las desigualdades que están adentro del paréntesis en (7.2) de modo que aparezcan en la forma equivalente l u, donde los puntos extremos l y u implican a X y /n . Esto se logra mediante la siguiente secuencia de operaciones y cada una da desigualdades equivalentes a las originales. 1. Multiplíquese por /n : 1.96 X 1.96 2. Réstese X de cada término: X 1.96 X 1.96 3. Multiplíquese por 1 para eliminar el signo menos en frente de (el cual invierte la di- rección de cada desigualdad): X 1.96 X 1.96 es decir, X 1.96 X X 1.96 La equivalencia de cada conjunto de desigualdades con el conjunto original implica que P X 1.96 X 1.96 0.95 (7.3) El evento en el interior del paréntesis en (7.3) tiene una apariencia poco común; previamen- te, la cantidad aleatoria aparecía a la mitad con constantes en ambos extremos, como en a Y b. En (7.3) la cantidad aleatoria aparece en dos extremos, mientras que la constan- te desconocida aparece a la mitad. Para interpretar (7.3), considérese un intervalo aleatorio con el punto extremo izquierdo X 1.96 /n y punto extremo derecho X 1.96 /n . En notación de intervalo, esto se transforma en X 1.96 , X 1.96 (7.4) El intervalo (7.4) es aleatorio porque los dos puntos extremos del intervalo implican una va- riable aleatoria. Está centrada en la media muestral X y se extiende a 1.96/n a cada lado de X . Por consiguiente el ancho del intervalo es 2 (1.96) /n , el cual no es alea- torio; sólo su localización (su punto medio X ) lo es (figura 7.2). Ahora (7.3) puede ser pa- rafraseado como “la probabilidad es 0.95 de que el intervalo aleatorio (7.4) incluya o cubra el valor verdadero de ”. Antes de realizar cualquier experimento y de recolectar cualquier dato, es bastante probable que estará adentro del intervalo (7.4). n n n n n n n n n n n n X /n 256 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra X 1.96 / n 1.96 / n 1.96 / n X 1.96 / n X ⎧ ⎨ ⎩ ⎧ ⎨ ⎩ Figura 7.2 Intervalo aleatorio (7.4) con su centro en X . c7_p225-283.qxd 3/12/08 4:15 AM Page 256
- 275. Las cantidades requeridas para calcular el intervalo de 95% de confianza para la altura pre- ferida promedio verdadera son 2.0, n 31 y x 80.0. El intervalo resultante es x ! 1.96 80.0 ! (1.96) 80.0 ! 0.7 (79.3, 80.7) Es decir, se puede estar totalmente confiado, en el nivel de confianza de 95%, de que 79.3 80.7. Este intervalo es relativamente angosto, lo que indica que ha sido esti- mada con bastante precisión. ■ Interpretación de un intervalo de confianza El nivel de 95% de confianza para el intervalo que se acaba de definir fue heredado de 0.95 de probabilidad para el intervalo aleatorio (7.4). Los intervalos con otros niveles de confian- za serán introducidos en breve. Por ahora, más bien, considérese cómo se puede interpretar el 95% de confianza. Como se inició con un evento cuya probabilidad era de 0.95, de que el intervalo alea- torio (7.4) capturaría el valor verdadero de , y luego se utilizaron los datos del ejemplo 7.1 para calcular el intervalo de confianza (79.3, 80.7), es tentador concluir que está dentro de este intervalo fijo con probabilidad de 0.95. Pero al sustituir x 80.0 en lugar de X , to- da la aleatoriedad desaparece; el intervalo (79.3, 80.7) no es un intervalo aleatorio y es una constante (desafortunadamente desconocida). Es por consiguiente incorrecto escribir la proposición P( queda en (79.3, 80.7)) 0.95. Una interpretación correcta de “95% de confianza” se basa en la interpretación de pro- babilidad de frecuencia relativa a largo plazo. Decir que un evento A tiene una probabilidad de 0.95 es decir que si el experimento en el cual se definió A se realiza una y otra vez, a la larga A ocurrirá el 95% del tiempo. Supóngase que se obtiene otra muestra de alturas pre- feridas por los mecanógrafos y se calcula otro intervalo de 95%. Luego se considera repetir esto con una tercera muestra, una cuarta, una quinta, y así sucesivamente. Sea A el evento en que X 1.96 /n X 1.96 /n . Ya que P(A) 0.95, a la larga el 95% de los intervalos de confianza calculados contendrán . Esto se ilustra en la figura 7.3, donde la línea vertical corta el eje de medición en el valor verdadero (pero desconocido) de . Obsérvese que de los 11 intervalos ilustrados, sólo los intervalos 3 y 11 no contienen . A la larga, sólo 5% de los intervalos construidos así no contendrán . De acuerdo con esta interpretación, el nivel de confianza de 95% no es en sí una pro- posición sobre cualquier intervalo particular tal como (79.3, 80.7). En su lugar pertenece a lo que sucedería si se construyera un número de intervalos como esos por medio de la misma 2.0 3 1 n 7.1 Propiedades básicas de los intervalos de confianza 257 Ejemplo 7.2 (continuación del ejemplo 7.1) DEFINICIÓN Si después de observar X1 x1, X2 x2, . . . , Xn xn, se calcula la media muestral observada x y luego se sustituye x en (7.4) en lugar de X , el intervalo fijo resultante se llama intervalo de 95% de confianza para . Este intervalo de confianza se ex- presa como x 1.96 , x 1.96 es un intervalo de 95% de confianza para o cuando x 1.96 x 1.96 con 95% de confianza Una expresión concisa para el intervalo es x ! 1.96 /n , donde – da el punto ex- tremo izquierdo (límite inferior) y da el punto extremo derecho (límite superior). n n n n c7_p225-283.qxd 3/12/08 4:15 AM Page 257
- 276. fórmula de intervalo de confianza. Aunque esto puede parecer no satisfactorio, el origen de la dificultad yace en la interpretación de probabilidad, es válida para una larga secuencia de réplicas de un experimento en lugar de sólo para una. Existe el método de abordar la cons- trucción e interpretación de intervalos de confianza que utiliza la noción de probabilidad subjetiva y el teorema de probabilidad de Bayes, aunque los detalles técnicos se salen del alcance de este libro; el libro de DeGroot y colaboradores (véase la bibliografía del capítulo 6) es una buena fuente. El intervalo presentado aquí (así como también cada intervalo presenta- do subsecuentemente) se llama intervalo de confianza “clásico” porque su interpretación se apoya en la noción clásica de probabilidad (aunque las ideas principales se desarrollaron tan recientemente como en la década de 1930). Otros niveles de confianza El nivel de confianza de 95% fue heredado de la probabilidad de 0.95 de las desigualdades iniciales que aparecen en (7.2). Si se desea un nivel de confianza de 99%, la probabili- dad inicial de 0.95 debe ser reemplazada por 0.99, lo que implica cambiar el valor crítico z de 1.96 a 2.58. Un intervalo de confianza de 99% resulta entonces de utilizar 2.58 en lugar de 1.96 en la fórmula para el intervalo de confianza de 95 por ciento. Esto sugiere que cualquier nivel de confianza deseado se obtiene reemplazando 1.96 o 2.58 con el valor crítico normal estándar apropiado. Como la figura 7.4 muestra, utilizan- do z/2 en lugar de 1.96 se logra una probabilidad de 1 . 258 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra DEFINICIÓN La siguiente expresión da un intervalo de confianza de 100 (1 )% para la me- dia de una población normal cuando se conoce el valor de x z/2 , x z/2 (7.5) o, de forma equivalente, por x ! z/2 /n . n n Nmero de intervalo (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) Valor verdadero de Figura 7.3 Construcción repetida de intervalos de confianza de 95 por ciento. 0 z /2 z /2 Curva z Área sombreada /2 1 Figura 7.4 P( z/2 Z z/2) 1 . Número de intervalo c7_p225-283.qxd 3/12/08 4:15 AM Page 258
- 277. No hace mucho tiempo que el proceso de producción de una caja de control de un tipo par- ticular para un motor fue modificado. Antes de esta modificación, datos históricos sugirieron que la distribución de diámetros de agujeros para bujes en las cajas era normal con desvia- ción estándar de 0.100 mm. Se cree que la modificación no ha afectado la forma de la distri- bución ni la desviación estándar, pero que el valor del diámetro medio pudo haber cambiado. Se selecciona una muestra de 40 cajas y se determina el diámetro de agujero para cada una y el resultado es un diámetro medio muestral de 5.426 mm. Calcúlese un intervalo de con- fianza para el diámetro de agujero promedio verdadero utilizando un nivel de confianza de 90%. Esto requiere que 100(1 ) 90, de donde 0.10 y z/2 z0.05 1.645 (corres- pondiente a un área de curva z acumulativa de 0.9500). El intervalo deseado es entonces 5.426 ! (1.645) .10 4 0 0 5.426 ! 0.026 (5.400, 5.452) Con un razonablemente alto grado de confianza, se puede decir que 5.400 5.452. Es- te intervalo es algo angosto debido a la pequeña cantidad de variabilidad del diámetro del agujero ( 0.100). ■ Nivel de confianza, precisión y tamaño de muestra ¿Por qué decidirse por un nivel de confianza de 95% cuando un nivel de 99% es alcanza- ble? Porque el precio pagado por el nivel de confianza más alto es un intervalo más ancho. Como el intervalo de 95% se extiende 1.96 /n a cada lado de x , el ancho del intervalo es 2(1.96) /n 3.92 /n . Asimismo, el ancho del intervalo de 99% es 2(2.58) /n 5.16 /n . Es decir, se tiene más confianza en el intervalo de 99% precisamente porque es más ancho. Mientras más alto es el grado de confianza, más ancho es el interva- lo resultante. En realidad, el único intervalo de 100% para es (, ), el cual no es te- rriblemente informativo porque se sabía que este intervalo cubriría incluso antes del muestreo. Si se considera que el ancho del intervalo especifica su precisión o exactitud, enton- ces el nivel de confianza (o confiabilidad) del intervalo está relacionado de manera inversa con su precisión. La estimación de un intervalo altamente confiable puede ser imprecisa por el hecho de que los puntos extremos del intervalo pueden estar muy alejados, mientras que un intervalo preciso puede acarrear una confiabilidad relativamente baja. Por consiguiente no se puede decir de modo inequívoco que se tiene que preferir un intervalo de 99% a uno de 95%; la ganancia de confiabilidad acarrea una pérdida de precisión. Una estrategia atractiva es especificar tanto del nivel de confianza deseado como el ancho del intervalo y luego determinar el tamaño de muestra necesario. Un intensivo monitoreo de un sistema de tiempo compartido de computadoras sugiere que el tiempo de respuesta a un comando de edición particular está normalmente distribuido con desviación estándar de 25 milisegundos. Se instaló un nuevo sistema operativo y se desea estimar el tiempo de respuesta promedio verdadero en el nuevo entorno. Suponiendo que los tiempos de respuesta siguen estando normalmente distribuidos con 25, ¿qué tama- ño de muestra es necesario para asegurarse de que el intervalo de confianza de 95% resul- tante tiene un ancho de (cuando mucho) 10? El tamaño de muestra n debe satisfacer 10 2 (1.96)(25/n ) Reordenando esta ecuación se obtiene n 2 (1.96)(25)/10 9.80 por consiguiente n (9.80)2 96.04 En vista de que n debe ser un entero, se requiere un tamaño de muestra de 97. ■ 7.1 Propiedades básicas de los intervalos de confianza 259 Ejemplo 7.3 Ejemplo 7.4 c7_p225-283.qxd 3/12/08 4:15 AM Page 259
- 278. La fórmula general para el tamaño de muestra n necesario para garantizar un ancho de intervalo w se obtiene a partir de w 2 z/2 /n como Mientras más pequeño es el ancho deseado w, más grande debe ser n. Además, n es una fun- ción creciente de (más variabilidad de la población requiere un tamaño de muestra más grande) y del nivel de confianza 100(1 ) (conforme decrece, z/2 se incrementa). La mitad del ancho 1.96/n del intervalo de confianza de 95% en ocasiones se llama límite en el error de estimación asociado con un nivel de confianza de 95%. Es decir, con 95% de confianza, la estimación puntual x no estará a más de esta distancia de . Antes de obtener datos, es posible que un investigador desee determinar un tamaño de muestra con el cual se logra un valor particular del límite. Por ejemplo, si representa la eficiencia de combustible promedio (mpg) de todos los carros de cierto tipo, el objetivo de una inves- tigación puede ser estimar adentro de 1 mpg con 95% de confianza. Más generalmente, si se desea estimar adentro de una cantidad B (el límite especificado en el error de estima- ción) con confianza de 100(1 )%, el tamaño de muestra necesario se obtiene al reem- plazar 2/w por 1/B en la fórmula adentro del cuadro precedente. Derivación de un intervalo de confianza Sean X1, X2, . . . , Xn la muestra en la cual se tiene que basar el intervalo de confianza para un parámetro . Supóngase que se puede determinar una variable aleatoria que satisface las dos siguientes propiedades: 1. La variable depende funcionalmente tanto de X1, . . . , Xn como de . 2. La distribución de probabilidad de la variable no depende de ni de cualesquiera otros parámetros desconocidos. Sea h(X1, X2, . . . , Xn; ) esta variable aleatoria. Por ejemplo, si la distribución de la población es normal con conocida y la variable h(X1, . . . , Xn; ) (X )/(/n ) satisface ambas propiedades; claramente depende funcionalmente de , no obstante su distribución de probabilidad es normal estándar, la cual no depende de . En ge- neral, la forma de la función h casi siempre se pone de manifiesto al examinar la distribu- ción de un estimador apropiado ˆ. Con cualquier entre 0 y 1, se ve que las constantes a y b satisfacen P(a h(X1, . . . , Xn; ) b) 1 (7.6) A causa de la segunda propiedad, a y b no dependen de . En el ejemplo normal, a z/2 y b z/2. Ahora supóngase que las desigualdades en (7.6) pueden ser manipuladas para ais- lar y así se obtiene la proposición de probabilidad equivalente P(l(X1, X2, . . . , Xn) u(X1, X2, . . . , Xn)) 1 Entonces l(x1, x2, . . . , xn) y u(x1, . . . , xn) son los límites de confianza inferior y superior, respectivamente, para un intervalo de confianza de 100(1 )%. En el ejemplo normal, se vio que l(X1, . . . , Xn) X z/2 /n y u(X1, . . . , Xn) X z/2 /n . Un modelo teórico sugiere que el tiempo hasta la ruptura de un fluido aislante entre electro- dos a un voltaje particular tiene una distribución exponencial con parámetro (véase la sec- ción 4.4). Una muestra aleatoria de n 10 tiempos de ruptura da los siguientes datos 260 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Ejemplo 7.5 n 2z/2 2 w c7_p225-283.qxd 3/12/08 4:15 AM Page 260
- 279. muestrales (en min): x1 41.53, x2 18.73, x3 2.99, x4 30.34, x5 12.33, x6 117.52, x7 73.02, x8 223.63, x9 4.00, x10 26.78. Se desea un intervalo de 95% para y para el tiempo de ruptura promedio verdadero. Sea h(X1, X2, . . . , Xn; ) 2Xi. Se puede demostrar que esta variable aleatoria tiene una distribución de probabilidad llamada distribución ji cuadrada con 2n grados de li- bertad (gl) ( 2n, donde es el parámetro de una distribución ji cuadrada como se men- ciona en la sección 4.4). La tabla A.7 del apéndice ilustra una curva de densidad ji cuadrada típica y tabula valores críticos que capturan áreas de colas específicas. El número pertinen- te de grados de libertad en este caso es 2(10) 20. La fila 20 de la tabla muestra que 34.170 captura un área de cola superior de 0.025 y 9.591 captura un área de cola inferior de 0.025 (área de cola superior de 0.975). Por consiguiente con n 10, P(9.591 2Xi 34.170) 0.95 La división entre 2Xi aísla y se obtiene P(9.591/(2Xi) (34.170/(2Xi)) 0.95 El límite inferior del intervalo de confianza de 95% para es 9.591/(2xi) y el límite supe- rior es 34.170/(2xi). Con los datos dados xi 550.87 da el intervalo (0.00871, 0.03101). El valor esperado de una variable aleatoria exponencial es 1/. Puesto que P(2Xi/34.170 1/ 2Xi/9.591) 0.95 el intervalo de confianza de 95% para el tiempo de ruptura promedio verdadero es (2xi/34.170, 2xi/9.591) (32.24, 114.87). Obviamente este intervalo es bastante ancho, lo que refleja una variabilidad sustancial de los tiempos de ruptura y un pequeño tamaño de muestra. ■ En general, los límites de confianza superior e inferior resultan de reemplazar cada en (7.6) por y resolviendo para . En el ejemplo del fluido aislante que se acaba de con- siderar, 2xi 34.170 da 34.170/(2xi) como límite de confianza superior y el límite inferior se obtiene con la otra ecuación. Obsérvese que los dos límites de intervalo no están equidistantes de la estimación puntual, en vista de que el intervalo no es de la forma ˆ ! c. Intervalos de confianza bootstrap La técnica bootstrap se introdujo en el capítulo 6 como una forma de estimar . También puede ser aplicada para obtener un intervalo de confianza para . Considérese de nuevo la estimación de la media de una distribución normal cuando es conocido. Reemplácese con y úsese ˆ X como estimador puntual. Obsérvese que 1.96/n es el percentil 97.5 de la distribución de ˆ (esto es, P(X 1.96/n ) P(Z 1.96) 0.9750). Del mismo modo 1.96/n es el percentil 2.5, por consiguiente 0.95 P(percentil 2.5 ˆ percentil 97.5) P(ˆ percentil 2.5 ˆ percentil 97.5) Es decir, con l ˆ percentil 97.5 de ˆ u ˆ percentil 2.5 de ˆ (7.7) El intervalo de confianza para es (l, u). En muchos casos, los percentiles en (7.7) no pue- den ser calculados, pero sí pueden serlo con muestras bootstrap. Supóngase que se obtienen B 1000 muestras bootstrap y se calculan ˆ* 1, . . . , ˆ* 1000 y * seguidos por las diferencias ˆ* 1 *, . . . , ˆ* 1000 *. Las 25 más grandes y las 25 más pequeñas de estas diferencias son estimaciones de los percentiles desconocidos en (7.7). Consúltense los libros de Devore y Berk o de Efron citados en el capítulo 6 para más información. 7.1 Propiedades básicas de los intervalos de confianza 261 c7_p225-283.qxd 3/12/08 4:15 AM Page 261
- 280. 262 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra EJERCICIOS Sección 7.1 (1-11) 1. Considere una distribución de población normal con el va- lor de conocido. a. ¿Cuál es el nivel de confianza para el intervalo x ! 2.81/n ? b. ¿Cuál es el nivel de confianza para el intervalo x ! 1.44/n ? c. ¿Qué valor de z/2 en la fórmula de intervalo de confian- za (7.5) da un nivel de confianza de 99.7%? d. Responda la pregunta hecha en el inciso c) para un nivel de confianza de 75%. 2. Cada uno de los siguientes intervalos es un intervalo de confianza para frecuencia de resonancia promedio ver- dadera (Hz) (es decir, media de la población) para todas las raquetas de tenis de un tipo: (114.4, 115.6) (114.1, 115.9) a. ¿Cuál es el valor de la frecuencia de resonancia media muestral? b. Ambos intervalos se calcularon con los mismos datos muestrales. El nivel de confianza para uno de estos inter- valos es de 90% y para el otro es de 99%. ¿Cuál de los intervalos tiene el nivel de confianza de 90% y por qué? 3. Suponga que se selecciona una muestra de 50 botellas de una marca particular de jarabe para la tos y se determina el conte- nido de alcohol. Sea el contenido promedio de alcohol de la población de todas las botellas de la marca estudiada. Supon- ga que el intervalo de confianza de 95% resultante es (7.8, 9.4). a. ¿Habría resultado un intervalo de confianza de 90% calcu- lado con esta muestra más angosto o más ancho que el intervalo dado? Explique su razonamiento. b. Considere la siguiente proposición: Existe 95% de pro- babilidades de que el esté entre 7.8 y 9.4. ¿Es correc- ta esta proposición? ¿Por qué sí o por qué no? c. Considere la siguiente proposición: Se puede estar total- mente confiado de que 95% de todas las botellas de este tipo de jarabe para la tos tienen un contenido de alcohol entre 7.8 y 9.4. ¿Es correcta esta proposición? ¿Por qué sí o por qué no? d. Considere la siguiente proposición: Si el proceso de se- lección de una muestra de tamaño 50 y de cálculo del in- tervalo de 95% correspondiente se repite 100 veces, 95 de los intervalos resultantes incluirán . ¿Es correcta esta proposición? ¿Por qué sí o por qué no? 4. Se desea un intervalo de confianza para la pérdida por car- ga parásita promedio verdadera (watts) de cierto tipo de motor de inducción cuando la corriente a través de la línea se mantiene a 10 amps a una velocidad de 1500 rpm. Su- ponga que la pérdida por carga parásita está normalmente distribuida con 3.0. a. Calcule un intervalo de confianza para de 95% cuando n 25 y x 58.3. b. Calcule un intervalo de confianza para de 95% cuando n 100 y x 58.3. c. Calcule un intervalo de confianza para de 99% cuando n 100 y x 58.3. d. Calcule un intervalo de confianza para de 82% cuando n 100 y x 58.3. e. ¿Qué tan grande debe ser n si el ancho del intervalo de 99% para tiene que ser 1.0? 5. Suponga que la porosidad al helio (en porcentaje) de muestras de carbón tomadas de cualquier costura particular está normal- mente distribuida con desviación estándar verdadera de 0.75. a. Calcule un intervalo de confianza de 95% para la poro- sidad promedio verdadera de una costura si la porosidad promedio en 20 especímenes de la costura fue de 4.85. b. Calcule un intervalo de confianza de 98% para la poro- sidad promedio verdadera de otra costura basada en 16 especímenes con porosidad promedio muestral de 4.56. c. ¿Qué tan grande debe ser un tamaño de muestra si el an- cho del intervalo de 95% tiene que ser de 0.40? d. ¿Qué tan grande debe ser un tamaño de muestra para calcular la porosidad promedio verdadera dentro de 0.2 con confianza de 99%? 6. Con base en pruebas extensas, se sabe que el punto de ceden- cia de un tipo particular de varilla de refuerzo de acero suave está normalmente distribuido con 100. La composición de la varilla se modificó un poco, pero no se cree que la mo- dificación haya afectado o la normalidad o el valor de . a. Suponiendo que éste tiene que ser el caso, si una mues- tra de 25 varillas modificadas dio por resultado un pun- to de cedencia promedio muestral de 8439 lb, calcule un intervalo de confianza de 90% para el punto de cedencia promedio verdadero de la varilla modificada. b. ¿Cómo modificaría el intervalo del inciso a) para obte- ner un nivel de confianza de 92%? 7. ¿En cuánto se debe incrementar el tamaño de muestra n si el ancho del intervalo de confianza (7.5) tiene que ser redu- cido a la mitad? Si el tamaño de muestra n se incrementa por un factor de 25, ¿qué efecto tendrá en el ancho del in- tervalo? Justifique sus aseveraciones. 8. Sea 1 0, 2 0, con 1 2 . Entonces Pz1 z2 1 a. Use esta ecuación para obtener una expresión más gene- ral para un intervalo de confianza de 100(1 )% para del cual el intervalo (7.5) es un caso especial. b. Sea 0.05 y 1 /4, 2 3/4. ¿Da por resultado esto un intervalo más angosto o más ancho que el inter- valo (7.5)? 9. a. En las mismas condiciones que aquellas que conducen al intervalo (7.5), P[(X )/(/n ) 1.645] 0.95. Use esta expresión para obtener un intervalo unilateral para de ancho infinito y que proporcione un límite de confianza inferior para . ¿Cuál es el intervalo para los datos del ejercicio 5(a)? b. Generalice el resultado del inciso a) para obtener un lí- mite inferior con nivel de confianza de 100(1 )%. X /n c7_p225-283.qxd 3/12/08 4:15 AM Page 262
- 281. 7.2 Intervalos de confianza de muestra grande para una media y proporción de población 263 Se supuso en el intervalo de confianza para dado en la sección previa que la distribución de la población es normal con el valor de conocido. A continuación se presenta un inter- valo de confianza de muestra grande cuya validez no requiere estas suposiciones. Después de demostrar cómo conduce el argumento a este intervalo se aplica en forma extensa para producir otros intervalos de muestra grande y habrá que enfocarse en un intervalo para una proporción de población p. Intervalo de muestra grande para Sean X1, X2, . . . , Xn una muestra aleatoria de una población con media y desviación es- tándar . Siempre que n es grande, el teorema del límite central implica que X tiene de ma- nera aproximada una distribución normal cualquiera que sea la naturaleza de la distribución de la población. Se deduce entonces que Z (X )/(/n ) tiene aproximadamente una distribución estándar normal, de modo que P z/2 z/2 1 Un argumento paralelo al dado en la sección 7.1 da x ! z/2 /n como intervalo de confianza de muestra grande para con un nivel de confianza de aproximadamente 100(1 )%. Es decir, cuando n es grande, el intervalo de confianza para dado antes permanece válido cualquiera que sea la distribución de la población, siempre que el califi- cador esté insertado “aproximadamente” enfrente del nivel de confianza. Una dificultad práctica con este desarrollo es que el cálculo del intervalo de confian- za requiere el valor de , el cual rara vez es conocido. Considérese la variable estandariza- da (X )/(S/n ), en la cual la desviación estándar muestral S ha sido reemplazada a . Previamente había aleatoriedad sólo en el numerador de Z gracias a X . En la nueva variable estandarizada, tanto X como S cambian de valor de una muestra a otra. Así que aparente- mente la distribución de la nueva variable deberá estar más dispersa que la curva z para re- flejar la variación extra en el denominador. Esto en realidad es cierto cuando n es pequeño. Sin embargo, con n grande la sustitución de S en lugar de agrega un poco de variabilidad extra, así que esta variable también tiene una distribución normal estándar. La manipulación de la variable en la proposición de probabilidad, como en el caso de conocida, da un in- tervalo de confianza de muestra grande general para . X /n c. ¿Cuál es un intervalo análogo al del inciso b) que pro- porcione un límite superior para ? Calcule este interva- lo de 99% para los datos del ejercicio 4(a). 10. Una muestra aleatoria de n 15 bombas térmicas de cierto ti- po produjo las siguientes observaciones de vida útil (en años): 2.0 1.3 6.0 1.9 5.1 0.4 1.0 5.3 15.7 0.7 4.8 0.9 12.2 5.3 0.6 a. Suponga que la distribución de la vida útil es exponen- cial y use un argumento paralelo al del ejemplo 7.5 para obtener un intervalo de confianza de 95% para la vida útil esperada (promedio verdadero). b. ¿Cómo debería modificarse el intervalo del inciso a) para obtener un nivel de confianza de 99%? c. ¿Cuál es un intervalo de confianza de 95% para la des- viación estándar de la distribución de la vida útil? [Suge- rencia: ¿Cuál es la desviación estándar de una variable aleatoria exponencial?] 11. Considere los siguientes 1000 intervalos de confianza de 95% para que un consultor estadístico obtendrá para va- rios clientes. Suponga que se seleccionan independiente- mente uno de otro los conjuntos de datos en los cuales están basados los intervalos. ¿Cuántos de estos 1000 intervalos espera que capturen el valor correspondiente de ? ¿Cuál es la probabilidad de que entre 940 y 960 de estos intervalos contengan el valor correspondiente de ? [Sugerencia: Sea Y el número entre los 1000 intervalos que contienen . ¿Qué clase de variable aleatoria es Y?] 7.2 Intervalos de confianza de muestra grande para una media y proporción de población c7_p225-283.qxd 3/12/08 4:15 AM Page 263
- 282. 264 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra En general, n 40 será suficiente para justificar el uso de este intervalo. Esto es algo más conservador que la regla empírica del teorema del límite central debido a la variabilidad adi- cional introducida por el uso de S en lugar de . El voltaje de ruptura de corriente alterna (CA) de un líquido aislante indica su resistencia die- léctrica. El artículo “Testing Practices for the AC Breakdown Voltage Testing of Insulation Liquids” (IEEE Electrical Insulation Magazine, 1995: 21-26) dio las observaciones muestra- les adjuntas de voltaje de ruptura (kV) de un circuito particular en ciertas condiciones. 62 50 53 57 41 53 55 61 59 64 50 53 64 62 50 68 54 55 57 50 55 50 56 55 46 55 53 54 52 47 47 55 57 48 63 57 57 55 53 59 53 52 50 55 60 50 56 58 Una gráfica de caja de los datos (figura 7.5) muestra una alta concentración a la mitad de la parte media de los datos (ancho de caja angosto). Hay sólo un valor apartado en el extremo superior, pero éste en realidad está un poco más cerca de la mediana (55) que la observa- ción muestral más pequeña. Las cantidades resumidas incluyen n 48, xi 2626 y xi 2 144 950, a partir de las cuales x 54.7 y s 5.23. El intervalo de confianza de 95% es entonces 54.7 ! 1.96 54.7 ! 1.5 (53.2, 56.2) Es decir, 53.2 56.2 con un nivel de confianza de aproximadamente 95%. El intervalo es angosto de manera ra- zonable, lo que indica que ha sido estimada con precisión. ■ 5.23 4 8 Ejemplo 7.6 PROPOSICIÓN Si n es suficientemente grande, la variable estandarizada Z tiene aproximadamente una distribución normal estándar. Esto implica que x ! z/2 (7.8) es un intervalo de confianza de muestra grande para con nivel de confianza aproximadamente de 100(1 )%. Esta fórmula es válida sin importar la forma de la distribución de la población. s n X S/n 50 40 60 70 Voltaje Figura 7.5 Gráfica de los datos de voltaje de ruptura del ejemplo 7.6. c7_p225-283.qxd 3/12/08 4:15 AM Page 264
- 283. Desafortunadamente, la selección del tamaño de muestra para que dé un ancho de in- tervalo deseado no es simple en este caso como lo fue en el caso de conocida. Por eso el ancho de (7.8) es 2z/2s/n . Como el valor de s no está disponible antes de que los datos hayan sido recopilados, el ancho del intervalo no puede ser determinado tan sólo con la se- lección de n. La única opción de un investigador que desea especificar el ancho deseado es hacer una suposición instruida a qué valor de s podría ser. Siendo conservador y suponien- do un valor más grande de s, se seleccionará un n más grande de lo necesario. El investiga- dor puede ser capaz de especificar un valor razonablemente preciso del rango de población (la diferencia entre los valores más grande y más pequeño). Entonces si la distribución de la población no es demasiado asimétrica, si se divide el rango entre 4 se obtiene un valor aproximado de lo que s podría ser. Remítase al ejemplo 7.6 sobre voltaje de ruptura. Suponga que el investigador cree que vir- tualmente todos los valores en la población se encuentran entre 40 y 70. Entonces (70 – 40)/4 7.5 da un valor razonable para s. El tamaño de muestra apropiado para estimar el voltaje de ruptura promedio verdadero a dentro de 1 kV con nivel de confianza de 95%, es decir, para que el intervalo de confianza de 95% tenga un ancho de 2 kV, es n [(1.96)(7.5)/1]2 217 ■ Un intervalo de confianza de muestra grande general Los intervalos de muestra grande x ! z/2 /n y x ! z/2 s/n son casos especiales de un intervalo de confianza de muestra grande general para un parámetro . Suponga que ˆ es un es- timador que satisface las siguientes propiedades: 1) Tiene aproximadamente una distribución normal; 2) es insesgado (por lo menos aproximadamente); y 3) una expresión para ˆ, la des- viación estándar de ˆ, está disponible. Por ejemplo, en el caso , ˆ X es un estimador insesgado cuya distribución es aproximadamente normal cuando n es grande y ˆ X /n . Estandarizando ˆ se obtiene la variable aleatoria Z (ˆ )/ˆ, la cual tiene aproxima- damente una distribución normal estándar. Esto justifica la proposición de probabilidad Pz/2 z/2 1 (7.9) Suponga, primero, que ˆ parámetros desconocidos (p. ej., conocida en el caso ). Entonces si se reemplaza cada en (7.9) por se obtiene ˆ ! z/2 ˆ, por consiguiente los límites de confianza inferior y superior son ˆ z/2 ˆ y ˆ z/2 ˆ, respectivamente. Suponga ahora que ˆ no implica pero sí implica por lo menos otro parámetro desconoci- do. Sea sˆ la estimación de ˆ obtenido utilizando estimaciones en lugar de los parámetros desconocidos (p. ej., s/n estima /n ). En condiciones generales (esencialmente que sˆ se aproxime a ˆ con la mayoría de las muestras), un intervalo de confianza válido es ˆ ! z/2 sˆ. El intervalo muestral grande x ! z/2 s/n es un ejemplo. Por último, suponga que ˆ no implica el desconocido. Este es el caso, por ejemplo, cuando p, una proporción de población. Entonces (ˆ )/ˆ z/2 puede ser difícil de resolver. Con frecuencia se puede obtener una solución aproximada reemplazando en ˆ por su estimación ˆ. Esto da una desviación estándar estimada sˆ y el intervalo correspon- diente es de nuevo ˆ ! z/2 sˆ. Un intervalo de confianza para una proporción de población Sea p la proporción de “éxitos” en una población, donde éxito identifica a un individuo u objeto que tiene una propiedad específica (p. ej., individuos que se graduaron en una uni- versidad, computadoras que no requieren servicio de garantía, etc.). Una variable aleatoria de n individuos que tiene que ser seleccionada y X es el número de éxitos en la muestra. ˆ ˆ 7.2 Intervalos de confianza de muestra grande para una media y proporción de población 265 Ejemplo 7.7 c7_p225-283.qxd 3/12/08 4:15 AM Page 265
- 284. Siempre que n sea pequeño comparado con el tamaño de la población, X puede ser conside- rada como una variable aleatoria binomial con E(X) np y X n p (1 p ) . Además, si tanto np 10 como nq 10, X tiene aproximadamente una distribución normal. El estimador natural de p es p̂ X/n, la fracción muestral de éxitos. Como p̂ es simplemente X multiplicada por la constante 1/n, p̂ también tiene aproximadamente una distribución normal. Como se muestra en la sección 6.1, E(p̂) p (insesgamiento) y p̂ p (1 p )/ n . La desviación estándar p̂ implica el parámetro desconocido p. Si se es- tandariza p̂ restando p y dividiendo entre p̂ entonces se tiene Pz/2 z/2 1 Procediendo como se sugirió en la subsección “Derivación de un intervalo de confian- za” (sección 7.1), los límites de confianza se obtienen al reemplazar cada por y resol- ver la ecuación cuadrática resultante para p. Esto da las dos raíces p p̂ p p (1 p )/ n Si el tamaño de muestra es bastante grande, z2 /(2n) es insignificante comparado con p̂, z2 /(4n2 ), bajo la raíz cuadrada es insignificante comparado con p̂q̂/n y z2 /n es insignificante comparado con 1. Si se desechan estos términos insignificantes se obtienen los límites de confianza aproximados p̂ ! z/2 p̂q̂/ n (7.11) Esta es la forma general ˆ ! z/2 ˆ ˆ de un intervalo de muestra grande sugerido en la última subsección. Por décadas este último intervalo ha sido recomendado en tanto la aproxima- ción normal para p̂ se justifique. Sin embargo, investigaciones recientes han demostrado que el intervalo un poco más complicado dado en la proposición tiene un nivel de confianza real que tiende a acercarse más al nivel nominal que el intervalo tradicional (Agresti, Alan y Coull, “Approximate Is Better Than ‘Exact’ for Interval Estimation of a Binomial Propor- tion”, The American Statistician, 1998: 119-126). Es decir, si se utiliza z/2 1.96, el nivel de confianza para el “nuevo” intervalo tiende a acercarse más a 95% con casi todos los va- lores de p que en el caso del intervalo tradicional; esto también es cierto con otros niveles de confianza. Además, Agresti y Coull proponen que el intervalo “puede ser recomendado para usarse con casi todos los tamaños de muestra y valores de parámetro” por lo que las condiciones np̂ 10 y nq̂ 10 no tienen que ser verificadas. 266 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra PROPOSICIÓN Un intervalo de confianza para una proporción de población p con nivel de con- fianza aproximadamente de 100(1 )% tiene límite de confianza inferior y (7.10) límite de confianza superior p̂ ! z/2 p̂ n q̂ 1 (z2 /2)/n z 2 /2 4n2 z 2 /2 2n p̂ z/2 p̂ n q̂ 1 (z2 /2)/n z 2 /2 4n2 z 2 /2 2n p̂ z/2 p̂ n q̂ 1 (z2 /2)/n z 2 /2 4n2 z 2 /2 2n c7_p225-283.qxd 3/12/08 4:15 AM Page 266
- 285. El artículo “Repeatability and Reproducibility for Pass/Fail Data” (J. of Testing and Eval., 1997: 151-153) reportó que en n 48 ensayos en un laboratorio particular, 16 dieron por resultado la ignición de un tipo particular de sustrato por un cigarrillo encendido. Sea p la proporción a largo plazo de tales ensayos que producirían ignición. Una estimación puntual de p es p̂ 16/48 0.333. Un intervalo de confianza para p con un nivel de confianza de aproximadamente 95% es 0.373 1 ! .08 0.139 (0.217, 0.474) El intervalo tradicional es 0.333 ! 1.96 (0 .3 3 3 )( 0 .6 6 7 )/ 4 8 0.333 ! 0.133 (0.200, 0.466) Estos dos intervalos concordarían mucho más si el tamaño de muestra fuera sustancialmen- te más grande. ■ Si se iguala al ancho del intervalo de confianza para p al ancho preespecificado w se obtiene una ecuación cuadrática para el tamaño de muestra n necesario para dar un interva- lo con un grado de precisión deseado. Si se suprime el subíndice en z/2, la solución es n (7.12) Omitiendo los términos en el numerador que implican w2 se obtiene n Esta última expresión es lo que resulta de igualar el ancho del intervalo tradicional a w. Estas fórmulas desafortunadamente implican la p̂ desconocida. El método más con- servador es aprovechar el hecho de que p̂q̂ [ p̂(1 p̂)] es un máximo cuando p̂ 0.5. Por consiguiente si se utiliza p̂ q̂ 0.5 en (7.12), el ancho será cuando mucho w hacien- do caso omiso de que el valor de p̂ resulte de la muestra. De manera alternativa, si el inves- tigador cree de manera firme, basado en información previa, que p p0 0.5, en ese caso se utiliza p0 en lugar de p̂. Un comentario similar es válido cuando p p0 0.5. El ancho del intervalo de confianza de 95% en el ejemplo 7.8 es 0.257. El valor de n nece- sario para garantizar un ancho de 0.10 independientemente del valor de p̂ es 4z2 p̂q̂ w2 2z2 p̂q̂ z2 w2 ! 4 z4 p̂q̂ (p̂q̂ w 2 ) w 2 z 4 w2 0.333 (1.96)2 /96 ! 1.96(0 .3 3 3 )( 0 .6 6 7 )/ 4 8 ( 1 .9 6 )2 /9 2 1 6 1 (1.96)2 /48 Por consiguiente se deberá utilizar un tamaño de muestra de 381. La expresión para n basa- da en el intervalo de confianza tradicional da un valor un poco más grande de 385. ■ Intervalos de confianza unilaterales (límites de confianza) Los intervalos de confianza discutidos hasta ahora dan tanto un límite de confianza inferior como uno superior para el parámetro que se está estimando. En algunas circunstancias, es posible que un investigador desee sólo uno de estos dos tipos de límites. Por ejemplo, es po- sible que un psicólogo desee calcular un límite de confianza superior de 95% para el tiempo 7.2 Intervalos de confianza de muestra grande para una media y proporción de población 267 Ejemplo 7.8 Ejemplo 7.9 n 380.3 2(1.96)2 (0.25) (1.96)2 (0.01) ! 4 (1 .9 6 )4 (0 .2 5 )( 0 .2 5 0 .0 1 ) ( 0 .0 1 )( 1 .9 6 )4 0.01 c7_p225-283.qxd 3/12/08 4:15 AM Page 267
- 286. 268 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra de reacción promedio verdadero a un estímulo particular o es posible que un ingeniero de confiabilidad desee sólo un límite de confianza inferior para la vida útil promedio de com- ponentes de un tipo. Como el área acumulativa bajo la curva normal estándar a la izquierda de 1.645 es de 0.95, P 1.645 0.95 Si se manipula la desigualdad entre el paréntesis para aislar en un lado y reemplazan las variables aleatorias con valores calculados se obtiene la desigualdad x 1.645s/n ; la expresión a la derecha es el límite de confianza inferior deseado. Comenzando con P( 1.645 Z) 0.95 y manipulando la desigualdad se obtiene el límite de confianza superior. Un argumento similar da un límite unilateral asociado con cualquier otro nivel de confianza. X S/n La prueba de esfuerzo cortante es el procedimiento más aceptado de evaluar la calidad de una unión entre un material de reparación y su sustrato de concreto. El artículo “Testing the Bond Between Repair Materials and Concrete Substrate” (ACI Materials J., 1996: 553-558) reportó que en una investigación particular, una muestra de 48 observaciones de resistencia al esfuerzo cortante dio una resistencia media muestral de 17.17 N/mm2 y una desviación estándar muestral de 3.28 N/mm2 . Un límite de confianza inferior para la resistencia al es- fuerzo cortante promedio verdadera con nivel de confianza de 95% es 17.17 (1.645) 17.17 0.78 16.39 Es decir, con un nivel de confianza de 95%, el valor de queda en el intervalo (16.39, ). ■ (3.28) 4 8 Ejemplo 7.10 EJERCICIOS Sección 7.2 (12-27) 12. Una muestra aleatoria de 110 relámpagos en cierta región dieron por resultado una duración de eco de radar promedio muestral de 0.81 segundos y una desviación estándar mues- tral de 0.34 segundos (“Lightning Strikes to an Airplane in a Thunderstorm”, J. of Aircraft, 1984: 607-611). Calcule un in- tervalo de confianza de 99% (bilateral) para la duración de eco promedio verdadera e interprete el intervalo resultante. 13. El artículo “Gas Cooking, Kitchen Ventilation, and Expo- sure to Combustion Products” (Indoor Air, 2006: 65-73) reportó que para una muestra de 50 cocinas con estufas de gas monitoreadas durante una semana, el nivel de CO2 me- dio muestral (ppm) fue de 654.16 y la desviación estándar muestral fue de 164.43. a. Calcule e interprete un intervalo de confianza de 95% (bilateral) para un nivel de CO2 promedio verdadero en la población de todas las casas de la cual se seleccionó la muestra. b. Suponga que el investigador había hecho una suposición preliminar de 175 para el valor de la s antes de recopilar los datos. ¿Qué tamaño de muestra sería necesario para obtener un ancho de intervalo de 50 ppm para un nivel de confianza de 95%? PROPOSICIÓN Un límite de confianza superior muestral grande para es x z y un límite de confianza inferior muestral grande para es x z Se obtiene un límite de confianza unilateral para p reemplazando z/2 en lugar de z y ! en lugar de o – en la fórmula para el intervalo de confianza (7.10) para p. En todos los casos, el nivel de confianza es aproximadamente de 100(1 )%. s n s n c7_p225-283.qxd 3/12/08 4:15 AM Page 268
- 287. 7.2 Intervalos de confianza de muestra grande para una media y proporción de población 269 14. El artículo “Evaluating Tunnel Kiln Performance” (Amer. Ceramic Soc. Bull., agosto de 1997: 59-63) reportó la si- guiente información resumida sobre resistencias a la fractu- ra (MPa) de n 169 barras de cerámica horneadas en un horno particular: x 89.10, s 3.73. a. Calcule un intervalo de confianza (bilateral) para la resis- tencia a la fractura promedio verdadera utilizando un nivel de confianza de 95%. ¿Se podría decir que la resistencia a la fractura promedio verdadera fue estimada con precisión? b. Suponga que los investigadores creyeron a priori que la desviación estándar de la población era aproximada- mente de 4 MPa. Basado en esta suposición, ¿qué tan grande tendría que ser una muestra para estimar hasta dentro de 0.5 MPa con 95% de confianza? 15. Determine el nivel de confianza de cada uno de los siguien- tes límites de confianza unilaterales muestrales grandes: a. Límite superior: x 0.84s/n b. Límite inferior: x 2.05s/n c. Límite superior: x 0.67s/n 16. El tiempo desde la carga hasta el vaciado (min) de un ace- ro al carbono en un tipo de horno Siemens-Martin se deter- minó para cada hornada en una muestra de tamaño 46 y el resultado fue un tiempo medio muestral de 382.1 y una des- viación estándar muestral de 31.5. Calcule un límite de con- fianza superior de 95% para el tiempo de carga a vaciado promedio verdadero. 17. El ejercicio 1.13 dio una muestra de observaciones de resis- tencia última a la tensión (klb/pulg2 ). Use los datos de salida estadísticos descriptivos adjuntos de MINITAB para calcular un límite de confianza inferior de 99% para la resistencia a la tensión última promedio verdadera e interprete el resultado. N Media Mediana MediaTrDesvEstand MedianaSE 153 135.39 135.40 135.41 4.59 0.37 Mínimo Máximo Q1 Q3 122.20 147.70 132.95 138.25 18. El artículo “Ultimate Load Capacities of Expansion Anchor Bolts” (J. of Energy Engr., 1993: 139-158) reportó los si- guientes datos resumidos sobre resistencia al esfuerzo cortan- te (klb/pulg2 ) para una muestra de pernos de anclaje de 3/8 pulg: n 78, x 4.25, s 1.30. Calcule un límite de con- fianza inferior utilizando un nivel de confianza de 90% para una resistencia al esfuerzo cortante promedio verdadero. 19. El artículo “Limited Yield Estimation for Visual Defect Sources” (IEEE Trans. on Semiconductor Manuf., 1997: 17-23) reportó que, en un estudio de un proceso de inspec- ción de obleas particular, 356 troqueles fueron examinados por una sonda de inspección y 201 de éstos pasaron la prue- ba. Suponiendo un proceso estable, calcule un intervalo de confianza (bilateral) de 95% para la proporción de todos los troqueles que pasan la prueba. 20. La Prensa Asociada (9 de octubre de 2002) reportó que en una encuesta de 4722 jóvenes estadounidenses de 6 a 19 años de edad, 15% sufría de problemas serios de sobrepeso (un ín- dice de masa corporal de por lo menos 30; este índice mide el peso con respecto a la estatura). Calcule e interprete un in- tervalo de confianza utilizando un nivel de confianza de 99% para la proporción de todos los jóvenes estadounidenses con un problema de sobrepeso serio. 21. Se seleccionó una muestra aleatoria de 539 familias de una ciudad del medio oeste y se determinó que 133 de éstas po- seían por lo menos un arma de fuego (“The Social Determi- nants of Gun Ownership: Self-Protection in an Urban Environment”, Criminology, 1997: 629-640). Utilizando un nivel de confianza de 95%, calcule un límite de confianza inferior para la proporción de todas las familias en esta ciu- dad que poseen por lo menos un arma de fuego. 22. Se seleccionó una muestra aleatoria de 487 mujeres no fuma- doras de peso normal (índice de masa corporal entre 19.8 y 26.0) que había dado a luz en un gran centro médico metro- politano (“The Effects of Cigarette Smoking and Gestatio- nal Weight Change on Birth Outcomes in Obese and Normal Weight Women”, Amer. J. of Public Health, 1997: 591-596). Se determinó que 7.2% de estos nacimientos dieron por resul- tado niños con bajo peso al nacer (menos de 2500 g). Calcule un límite de confianza superior utilizando un nivel de confian- za de 99% para la proporción de todos esos nacimientos que dieron por resultado niños de bajo peso al nacer. 23. El artículo “An Evaluation of Football Helmets Under Im- pact Conditions” (Amer. J. Sports Medicine, 1984: 233- 237) reporta que cuando cada casco de fútbol en una muestra aleatoria de 37 cascos de tipo suspensión se some- tieron a una prueba de impacto, 24 mostraron daños. Sea p la proporción de todos los cascos de este tipo que mostraría daños cuando se someten a prueba de la manera prescrita. a. Calcule un intervalo de confianza de 99% para p. b. ¿Qué tamaño de muestra se requeriría para que el ancho de un intervalo de confianza de 99% sea cuando mucho de 0.10, independientemente dep̂? 24. Una muestra de 56 muestras de algodón produjo un porcen- taje de alargamiento promedio muestral de 8.17 y una des- viación estándar de 1.42 (“An Apparent Relation Between the Spiral Angle , the Percent Elongation E1, and the Di- mensions of the Cotton Fiber”, Textile Research J., 1978: 407-410). Calcule un intervalo de confianza de 95% mues- tral grande para el porcentaje de alargamiento promedio verdadero . ¿Qué suposiciones está haciendo sobre la dis- tribución del porcentaje de alargamiento? 25. Una legisladora estatal desea encuestar a los residentes de su distrito para ver qué proporción del electorado está cons- ciente de su posición sobre la utilización de fondos estatales para solventar abortos. a. ¿Qué tamaño de muestra es necesario si el intervalo de confianza de 95% para p debe tener un ancho de cuando mucho 0.10 independientemente de p? b. Si la legisladora está firmemente convencida de que por lo menos 2 3 del electorado conoce su posición, ¿qué ta- maño de muestra recomendaría? 26. El superintendente de un gran distrito escolar, que una ocasión tomó un curso de probabilidad y estadística, cree que el núme- ro de maestros ausentes en cualquier día dado tiene una distri- bución de Poisson con parámetro . Use los datos adjuntos sobre ausencias durante 50 días para obtener un intervalo de confianza muestral grande para . [Sugerencia: La media y la varianza de una variable de Poisson son iguales a , por con- siguiente Z X /n c7_p225-283.qxd 3/12/08 4:15 AM Page 269
- 288. 270 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra El intervalo de confianza para presentado en la sección 7.2 es válido siempre que n es grande. El intervalo resultante puede ser utilizado cualquiera que sea la naturaleza de la dis- tribución de la población. El teorema del límite central no puede ser invocado, sin embargo, cuando n es pequeña. En este caso, una forma de proceder es hacer una suposición específi- ca sobre la forma de la distribución de la población y luego obtener un intervalo de confian- za adecuado a esa suposición. Por ejemplo, se podría desarrollar un intervalo de confianza para , cuando una distribución gama describe la población, otro para el caso de una pobla- ción Weibull, y así sucesivamente. Estadísticos en realidad han realizado este programa para varias familias distribucionales diferentes. Como la distribución normal es más frecuente- mente apropiada como modelo de una población que cualquier otro tipo de distribución, la atención aquí se concentrará en un intervalo de confianza para esta situación. El resultado clave que sustenta el intervalo de la sección 7.2 fue que con n grande, la variable aleatoria Z (X )/(S/n ) tiene aproximadamente una distribución normal es- tándar. Cuando n es pequeño, no es probable que S se aproxime a , de modo que la varia- bilidad de la distribución de Z surge la aleatoriedad tanto en el numerador como en el denominador. Esto implica que la distribución de probabilidad de (X )/(S/n ) se dis- persará más que la distribución normal estándar. El resultado en el cual están basadas las in- ferencias introduce una nueva familia de distribuciones de probabilidad llamada familia de distribuciones t. Propiedades de distribuciones t Antes de aplicar este teorema, se impone una discusión de propiedades de distribuciones t. Aunque la variable de interés sigue siendo (X )/(S/n ), ahora se denota por T para re- calcar que no tiene una distribución normal estándar cuando n es pequeña. Recuérdese que tiene aproximadamente una distribución normal estándar. Ahora prosiga como en la derivación del intervalo para p haciendo una proposición de probabilidad (con probabili- dad de 1 ) y resolviendo las desigualdades resultantes para (véase el argumento exactamente después de (7.10)).] Número de ausencias 0 1 2 3 4 5 6 7 8 9 10 Frecuencia 1 4 8 10 8 7 5 3 2 1 1 27. Reconsidere el intervalo de confianza (7.10) para p y enfó- quese en un nivel de confianza de 95%. Demuestre que los límites de confianza concuerdan bastante bien con los del intervalo tradicional (7.11) una vez que dos éxitos y dos fallas se anexaron a la muestra [es decir, (7.11) basado en x 2 éxitos (S) en n 4 ensayos]. [Sugerencia: 1.96 2. Nota: Agresti y Coull demostraron que este ajuste del inter- valo tradicional también tiene un nivel de confianza próxi- mo al nivel nominal.] 7.3 Intervalos basados en una distribución de población normal SUPOSICIÓN La población de interés es normal, de modo que X1, . . . , Xn constituyen una muestra aleatoria tomada de una distribución normal con y desconocidas. TEOREMA Cuando X es la media de una muestra aleatoria de tamaño n tomada de una distribu- ción normal con media , la variable aleatoria T (7.13) tiene una distribución de probabilidad llamada distribución t con n – 1 grados de li- bertad (gl). X S/n c7_p225-283.qxd 3/12/08 4:15 AM Page 270
- 289. una distribución normal está regida por dos parámetros, la media y la desviación estándar . Una distribución t está regida por sólo un parámetro, llamado número de grados de li- bertad de la distribución, abreviado como gl. Este parámetro se denota con la letra griega . Posibles valores de son los enteros positivos 1, 2, 3, . . . Cada diferente valor del pará- metro corresponde a una distribución t diferente. Con cualquier valor fijo del parámetro , la función de densidad que especifica la curva t asociada tiene una apariencia incluso más complicada que la función de densidad normal. Afortunadamente, sólo hay que ocuparse de algunas de las más importantes carac- terísticas de estas curvas. 7.3 Intervalos basados en una distribución de población normal 271 La figura 7.6 ilustra varias de estas propiedades con valores seleccionados de . Propiedades de distribuciones t Sea t , la curva de función de densidad para el grado de libertad . 1. Cada curva t tiene forma de campana y con su centro en 0. 2. Cada curva t está más esparcida que la curva (z) normal estándar. 3. Conforme se incrementa, la dispersión de t correspondiente disminuye. 4. A medida que A , la secuencia de curvas t tiende a la curva normal estándar (así que la curva z a menudo se llama curva t con grado de libertad ). Notación Sea t, el número sobre el eje de medición con el cual el área bajo la curva t con grados de libertad a la derecha de t, es ; t, se llama valor crítico t. El número de grados de libertad con T en (7.13) es n 1 porque, aunque S está basa- da en las n desviaciones X1 X , . . . , X n X , (Xi X ) 0 implica que sólo n – 1 de és- tas están “libremente determinadas”. El número de grados de libertad para una variable t es el número de desviaciones libremente determinadas en las cuales está basada la desviación estándar estimada en el denominador de T. Como se desea utilizar T para obtener un intervalo de confianza del mismo modo que Z fue previamente utilizada, es necesario establecer una notación análoga a z para la distri- bución t. 0 Curva z Curva t25 Curva t5 Figura 7.6 Curvas t y z. c7_p225-283.qxd 3/12/08 4:15 AM Page 271
- 290. 272 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Esta notación se ilustra en la figura 7.7. La tabla A.5 del apéndice da t, con valores selec- cionados de y . Esta tabla también aparece en el interior de la tapa posterior. Las colum- nas de la tabla corresponden a diferentes valores de . Para obtener t0.05,15, hay que ir a la columna 0.05, buscar hacia abajo en la fila 15 y leer t0.05,15 1.753. Asimismo, t0.05,22 1.717 (columna 0.05, fila 22) y t0.01,22 2.508. Los valores de t, exhiben un comportamiento regular al recorrer una fila o al descen- der por una columna. Con fijo, t, se incrementa a medida que disminuye, puesto que hay que moverse más a la derecha de cero para capturar el área en la cola. Con fija, a medida que se incrementa (es decir, cuando se recorre hacia abajo cualquier columna par- ticular de la tabla t) el valor de t, disminuye. Esto es porque un valor más grande de im- plica una distribución t con dispersión más pequeña, de modo que no es necesario ir más lejos de cero para capturar el área de cola . Además, t, disminuye más lentamente a me- dida que se incrementa. Por consiguiente, los valores que aparecen en la tabla se muestran en incrementos de 2 entre 30 y 40 grados de libertad y luego saltar a 50, 60, 120 y por último . Como t es la curva normal estándar, los valores z conocidos aparecen en la úl- tima fila de la tabla. La regla empírica sugería con anterioridad que el uso del intervalo de confianza muestral grande (si n 40) proviene de la igualdad aproximada de las distribu- ciones normales estándar y t con 40. Intervalo de confianza t para una muestra La variable estandarizada T tiene una distribución t con n – 1 grados de libertad y el área bajo la curva de densidad t correspondiente entre t/2,n1 y t/2,n1 es 1 (el área /2 que- da en cada cola), por consiguiente P(t/2,n1 T t/2,n1) 1 (7.14) La expresión (7.14) difiere de las expresiones que aparecen en secciones previas en que T y t/2,n1 se utilizan en lugar de Z y z/2, aunque pueden ser manipuladas de la misma manera para obtener un intervalo de confianza para . PROPOSICIÓN Sean x y s la media y la desviación estándar muestrales calculadas con los resultados de una muestra aleatoria tomada de una población normal con media . Entonces un intervalo de confianza de 100(1 )% para es x t/2,n1 , x t/2,n1 (7.15) o, más compactamente, x ! t/2,n1 s/n . Un límite de confianza superior para es x t,n1 y reemplazando por en la última expresión se obtiene un límite de confianza in- ferior para , ambos con nivel de confianza de 100(1 )%. s n s n s n 0 Curva t Área sombreada t , Figura 7.7 Definición pictórica de t, . c7_p225-283.qxd 3/12/08 4:15 AM Page 272
- 291. 7.3 Intervalos basados en una distribución de población normal 273 Como parte de un proyecto más grande para estudiar el comportamiento de paneles de re- vestimiento sometidos a esfuerzo, un componente estructural extensamente utilizado en Es- tados Unidos, el artículo “Time-Dependent Bending Properties of Lumber” (J. of Testing and Eval., 1996: 187-193) reportó sobre varias propiedades mecánicas de especímenes de madera de pino escocés. Considere las siguientes observaciones de módulo de elasticidad (MPa) obtenidas un minuto después de cargar una configuración: 10 490 16 620 17 300 15 480 12 970 17 260 13 400 13 900 13 630 13 260 14 370 11 700 15 470 17 840 14 070 14 760 La figura 7.8 muestra un diagrama de probabilidad normal obtenido con R. La rectitud del diagrama apoya fuertemente la suposición de que la distribución de la población del módu- lo de elasticidad es por lo menos aproximadamente normal. El cálculo manual de la media y la desviación estándar muestrales se simplifica res- tando 10 000 de cada observación: yi xi 10 000. Es fácil verificar que yi 72520 y yi 2 392083800, de donde y 4532.5 y sy 2055.67. Por consiguiente x 14532.5 y sx 2055.67 (el sumar o restar la misma cantidad de cada observación no afecta la variabi- lidad). El tamaño de muestra es 16, así que un intervalo de confianza para el módulo de elas- ticidad medio de la población está basado en 15 grados de libertad. Un nivel de confianza de 95% para un intervalo bilateral requiere el valor crítico t de 2.131. El intervalo resultante es x ! t0.025,15 14 532.5 ! (2.131) 14 532.5 ! 1095.2 (13 437.3, 15 627.7) Este intervalo es bastante ancho tanto debido al tamaño de muestra pequeño como por la gran cantidad de variabilidad de la muestra. Un límite de confianza inferior de 95% se ob- tiene utilizando y 1.753 en lugar de ! y 2.131, respectivamente. ■ Por desgracia, no es fácil seleccionar n para controlar el ancho del intervalo t. Esto es porque el ancho implica la s desconocida (antes de recopilar los datos) y porque n ingresa no sólo a través de 1/n sino también a través de t/2,n1. Por consiguiente, se puede obte- ner una n apropiada sólo mediante ensayo y error. En el capítulo 15, se discutirá un intervalo de confianza de muestra pequeña para que es válido siempre que sólo la distribución de la población sea simétrica, una suposi- ción más débil que la de normalidad. No obstante, cuando la distribución de la población es normal, el intervalo t tiende a acortarse más de lo que lo haría cualquier otro intervalo con el mismo nivel de confianza. 2055.67 1 6 s n Ejemplo 7.11 Figura 7.8 Diagrama de probabilidad normal de los datos de módulo de elasticidad. 18000 16000 14000 12000 10000 Cuartiles teóricos Diagrama Q-Q normal Cuartiles muestrales -2 -1 0 1 2 c7_p225-283.qxd 3/12/08 4:15 AM Page 273
- 292. 274 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Un intervalo de predicción para un solo valor futuro En muchas aplicaciones, un investigador desea predecir un solo valor de una variable que tie- ne que ser observada en un tiempo futuro, en lugar de estimar el valor medio de dicha variable. Considere la siguiente muestra de contenido de grasa (en porcentaje) de n 10 perros ca- lientes seleccionados al azar (“Sensory and Mechanical Assessment of the Quality of Frank- furters”, J. Texture Studies, 1990: 395-409): 25.2 21.3 22.8 17.0 29.8 21.0 25.5 16.0 20.9 19.5 Suponiendo que estas observaciones se seleccionaron de una distribución de población nor- mal, un intervalo de confianza de 95% para (estimación del intervalo de) el contenido de grasa medio de la población es x ! t0.025,9 21.90 ! 2.262 21.90 ! 2.96 (18.94, 24.86) Suponga, sin embargo, que se va a comer un solo perro caliente de este tipo y desea prede- cir el contenido de grasa resultante. Una predicción puntual, análoga a una estimación pun- tual, es simplemente x 21.90. Esta predicción desafortunadamente no da información sobre confiabilidad o precisión. ■ El escenario general es como sigue. Se dispondrá de una muestra aleatoria X1, X2, . . . , Xn tomada de una distribución de población normal y se desea predecir el valor de Xn1, una sola observación futura. Un predictor puntual es X y el error de predicción resultante es X Xn1. El valor esperado del error de predicción es E(X Xn1) E(X ) E(Xn1) 0 Como Xn1, es independiente de X1, . . . , Xn, es independiente de X , así que la varianza del error de predicción es V(X Xn1) V(X ) V(Xn1) 2 2 1 El error de predicción es una combinación lineal de variables aleatorias independientes nor- malmente distribuidas, así que también está normalmente distribuido. Por consiguiente Z tiene una distribución normal estándar. Se puede demostrar que si se reemplaza con la desviación estándar muestral S (de X1, . . . , Xn) se obtiene T distribución t con n 1 grados de libertad Si se manipula esta variable T como se manipuló T (X )/(S/n ) en el desarrollo de un intervalo de confianza se obtiene el siguiente resultado. X Xn1 S 1 1 n X Xn1 2 1 1 n (X Xn1) 0 2 1 1 n 1 n 2 n 4.134 1 0 s n Ejemplo 7.12 PROPOSICIÓN Un intervalo de predicción (IP) para una sola observación que tiene que ser selec- cionado de una distribución de población normal es x ! t/2,n1 s 1 (7.16) El nivel de predicción es 100(1 )%. 1 n c7_p225-283.qxd 3/12/08 4:15 AM Page 274
- 293. La interpretación de un nivel de predicción de 95% es similar a la de un nivel de confianza de 95%; si se calcula el intervalo (7.16) para muestra tras muestra, a la larga 95% de estos intervalos incluirán los valores futuros correspondientes de X. Con n 10, x 21.90, s 4.134 y t0.025,9 2.262, un intervalo de predicción de 95% para el contenido de grasa de un solo perro caliente es 21.90 ! (2.262)(4.134) 1 21.90 ! 9.81 (12.09, 31.71) El intervalo es bastante ancho, lo que indica una incertidumbre sustancial en cuanto al con- tenido de grasa. Obsérvese que el ancho del intervalo de predicción es más de tres veces el del intervalo de confianza. ■ El error de predicción es X Xn1, la diferencia entre dos variables aleatorias, en tan- to que el error de estimación es X , la diferencia entre una variable aleatoria y un valor fijo (aunque desconocido). El intervalo de predicción es más ancho que el intervalo de con- fianza porque hay más variabilidad en el error de predicción (debido a Xn1) que en el error de estimación. De hecho, a medida que n se hace arbitrariamente grande, el intervalo de con- fianza se contrae a un solo valor y el intervalo de predicción tiende a ! z/2 . Existe incertidumbre con respecto a un solo valor X incluso cuando no hay necesidad de estimarlo. Intervalos de tolerancia Considérese una población de automóviles de cierto tipo y supóngase que en condiciones específicas, la eficiencia de combustible (mpg) tiene una distribución normal con 30 y 2. Entonces como el intervalo de 1.645 a 1.645 captura 90% del área bajo la curva z, 90% de todos estos automóviles tendrán valores de eficiencia de combustible entre 1.645 26.71 y 1.645 33.29. Pero ¿qué sucederá si los valores de y no son conocidos? Se puede tomar una muestra de tamaño n, determinar las eficiencias de com- bustible, x y s y formar el intervalo cuyo límite inferior es x x 1.645s y cuyo límite supe- rior es x 1.645s. Sin embargo, debido a la variabilidad de muestreo en las estimaciones de y , existe una buena probabilidad de que el intervalo resultante incluirá menos de 90% de los valores de la población. Intuitivamente, para tener a priori una probabilidad de 95% del intervalo resultante incluido por lo menos 90% de los valores de la población, cuando x y s se utilizan en lugar de y , también se deberá reemplazar 1.645 con un nú- mero más grande. Por ejemplo, cuando n 20, el valor 2.310 es tal que se puede estar 95% confiado en que el intervalo x ! 2.310s incluirá por lo menos 90% de los valores de eficien- cia de combustible en la población. 1 10 7.3 Intervalos basados en una distribución de población normal 275 Ejemplo 7.13 (continuación del ejemplo 7.12) Sea k un número entre 0 y 100. Un intervalo de tolerancia para capturar por lo me- nos el k% de los valores en una distribución de población normal con nivel de con- fianza de 95% tiene la forma x ! (valor crítico de tolerancia) s En la tabla A.6 del apéndice aparecen valores críticos de tolerancia con k 90, 95 y 99 en combinación con varios tamaños de muestra. Esta tabla también incluye valo- res críticos para un nivel de confianza de 99% (estos valores son más grandes que los valores correspondientes al 95%). Si se reemplaza ! con se obtiene un límite de tolerancia superior y si se utiliza en lugar de ! se obtiene un límite de tolerancia inferior. En la tabla A.6 también aparecen valores críticos para obtener estos límites unilaterales. c7_p225-283.qxd 3/12/08 4:15 AM Page 275
- 294. 276 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Regresemos a los datos de módulo de elasticidad discutidos en el ejemplo 7.11, donde n 16, x 14532.5, s 2055.67 y una curva de probabilidad normal de los datos indicaron que la normalidad de la población era bastante factible. Con un nivel de confianza de 95%, un intervalo de tolerancia bilateral para capturar por lo menos 95% de los valores de módu- lo de elasticidad de especímenes de madera en la población muestreada utiliza el valor crí- tico de tolerancia de 2.903. El intervalo resultante es 14532.5 ! (2.903)(2055.67) 14532.5 ! 5967.6 (8564.9, 20500.1) Se puede estar totalmente confiado de que por lo menos 95% de todos los especímenes de madera tienen valores de módulo de elasticidad entre 8564.9 y 20500.1. El intervalo de confianza de 95% para fue (13437.3, 15627.7) y el intervalo de pre- dicción de 95% para el módulo de elasticidad de un solo espécimen de madera es (10017.0, 19048.0). Tanto el intervalo de predicción como el intervalo de tolerancia son sustancial- mente más anchos que el intervalo de confianza. ■ Intervalos basados en distribuciones de población no normales El intervalo de confianza t para una muestra de es robusto en cuanto a alejamientos pe- queños o incluso moderados de la normalidad a menos que n sea bastante pequeño. Con esto se quiere decir que si se utiliza un valor crítico para confianza de 95%, por ejemplo, al calcular el intervalo, el nivel de confianza real se aproximará de manera razonable al nivel nominal de 95%. Sin embargo, si n es pequeño y la distribución de la población es altamente no normal, entonces el nivel de confianza real puede ser diferente en forma considerable del que se utiliza cuando se obtiene un valor crítico particular de la tabla t. Ciertamente ¡sería penoso creer que el nivel de confianza es de más o menos 95% cuando en realidad era como de 88%! Se ha visto que la técnica bootstrap, introducida en la sección 7.1 es bastante exitosa al estimar parámetros en una amplia variedad de situaciones no normales. En contraste con el intervalo de confianza, la validez de los intervalos de predicción y tolerancia descritos en esta sección están estrechamente vinculados a la suposición de norma- lidad. Estos últimos intervalos no deberán ser utilizados sin evidencia apremiante de normali- dad. La excelente referencia Statistical Intervals, citada en la bibliografía al final de este capítulo, discute procedimientos alternativos de esta clase en otras situaciones. Ejemplo 7.14 EJERCICIOS Sección 7.3 (28-41) 28. Determine los valores de las siguientes cantidades: a. t0.1,15 b. t0.05,15 c. t0.05,25 d. t0.05,40 e. t0.005,40 29. Determine el valor crítico t que capturará el área deseada de la curva t en cada uno de los siguientes casos: a. Área central 0.95, gl 10 b. Área central 0.95, gl 20 c. Área central 0.99, gl 20 d. Área central 0.99, gl 50 e. Área de cola superior 0.01, gl 25 f. Área de cola inferior 0.025, gl 5 30. Determine el valor t crítico de un intervalo de confianza bi- lateral en cada una de las siguientes situaciones: a. Nivel de confianza 95%, gl 10 b. Nivel de confianza 95%, gl 15 c. Nivel de confianza 99%, gl 15 d. Nivel de confianza 99%, n 5 e. Nivel de confianza 98%, gl 24 f. Nivel de confianza 99%, n 38 31. Determine el valor t crítico para un límite de confianza in- ferior o superior en cada una de las situaciones descritas en el ejercicio 30. 32. Una muestra aleatoria de n 18 especímenes de prueba de fibra de vidrio E de un tipo dio un esfuerzo de cedencia por esfuerzo cortante interfacial medio muestral de 30.2 y una desviación estándar muestral de 3.1 (“On Interfacial Failu- re in Notched Unidirectional Glass/Epoxy Composites”, J. of Composite Materials, 1985: 276–286). Suponiendo que el esfuerzo de cedencia por esfuerzo cortante interfacial está normalmente distribuido, calcule un intervalo de confian- za de 95% para el esfuerzo promedio verdadero (como lo hicieron los autores del artículo citado). c7_p225-283.qxd 3/12/08 4:15 AM Page 276
- 295. 7.3 Intervalos basados en una distribución de población normal 277 33. El artículo “Measuring and Understanding the Aging of Kraft Insulating Paper in Power Transformers” (IEEE Elec- trical Insul. Mag., 1996: 28-34) contiene las siguientes ob- servaciones de grado de polimerización de especímenes de papel para los cuales la concentración de tiempos de visco- sidad cayeron en un rango medio: 418 421 421 422 425 427 431 434 437 439 446 447 448 453 454 463 465 a. Construya una gráfica de caja de los datos y comente so- bre cualquier característica interesante. b. ¿Es factible que las observaciones muestrales dadas fue- ron seleccionadas de una distribución normal? c. Calcule un intervalo de confianza de 95% bilateral para un grado de polimerización promedio verdadero (como lo hicieron los autores del artículo). ¿Sugiere este inter- valo que 440 es un valor factible del grado de polimeri- zación promedio verdadero? ¿Qué hay en cuanto a 450? 34. Una muestra de 14 especímenes de junta de un tipo particu- lar produjo un esfuerzo límite proporcional medio muestral de 8.48 MPa y una desviación estándar muestral de 0.79 MPa (“Characterization of Bearing Strength Factors in Pegged Timber Connections”, J. of Structural Engr., 1997: 326-332). a. Calcule e interprete un límite de confianza inferior de 95% para el esfuerzo límite proporcional promedio ver- dadero de todas las juntas. ¿Qué suposiciones hizo sobre la distribución del esfuerzo límite proporcional? b. Calcule e interprete un límite de predicción inferior de 95% para el esfuerzo límite proporcional de una sola unión de este tipo. 35. Para corregir deformidades nasales congénitas se utiliza rino- plastia de aumento mediante implante de silicón. El éxito del procedimiento depende de varias propiedades biomecánicas del periostio y fascia nasales humanas. El artículo “Biome- chanics in Augmentation Rhinoplasty” (J. of Med. Engr. and Tech., 2005: 14-17) reportó que para una muestra de 15 adul- tos (recién fallecidos), la deformación de falla media (en por- centaje) fue de 25.0 y la desviación estándar fue de 3.5. a. Suponiendo una distribución normal de la deformación de falla, estime la deformación promedio verdadera en una forma que transmita información acerca de preci- sión y confiabilidad. b. Pronostique la deformación para un solo adulto en una forma que transmita información sobre precisión y con- fiabilidad. ¿Cómo se compara la predicción con la esti- mación calculada en el inciso a)? 36. Las n 26 observaciones de tiempo de escape dadas en el ejercicio 36 del capítulo 1 dan una media y desviación es- tándar muestrales de 370.69 y 24.36, respectivamente. a. Calcule un límite de confianza superior para el tiempo de escape medio de la población utilizando un nivel de confianza de 95 por ciento. b. Calcule un límite de predicción superior para el tiempo de escape de un solo trabajador adicional utilizando un nivel de predicción de 95%. ¿Cómo se compara este lí- mite con el límite de confianza del inciso a)? c. Suponga que se escogerán dos trabajadores más para par- ticipar en el ejercicio de escape simulado. Denote sus tiempos de escape por X27 y X28 y sea X nuevo el promedio de estos dos valores. Modifique la fórmula para un inter- valo de predicción con un solo valor de x para obtener un intervalo de predicción para X nuevo y calcule un intervalo bilateral de 95% basado en los datos de escape dados. 37. Un estudio de la capacidad de individuos de caminar en lí- nea recta (“Can We Really Walk Straight?” Amer. J. of Phy- sical Anthro, 1992: 19-27) reportó los datos adjuntos sobre cadencia (pasos por segundo) con una muestra de n 20 hombres saludables seleccionados al azar. 0.95 0.85 0.92 0.95 0.93 0.86 1.00 0.92 0.85 0.81 0.78 0.93 0.93 1.05 0.93 1.06 1.06 0.96 0.81 0.96 Un diagrama de probabilidad normal apoya de manera sustan- cial la suposición de que la distribución de la población de ca- dencia es aproximadamente normal. A continuación se da un resumen descriptivo de los datos obtenidos con MINITAB: Variable N Media Mediana MediaTR DesvEst MedianaSE Cadencia 20 0.9255 0.9300 0.9261 0.0809 0.0181 Cadencia Mín Máx Q1 Q3 variable 0.7800 1.0600 0.8525 0.9600 a. Calcule e interprete un intervalo de confianza de 95% para la cadencia media de la población. b. Calcule e interprete un intervalo de predicción de 95% para la cadencia de un solo individuo seleccionado al azar de esta población. c. Calcule un intervalo que incluya por lo menos 99% de las cadencias incluidas en la distribución de la población utilizando un nivel de confianza de 95 por ciento. 38. Se seleccionó una muestra de 25 piezas de laminado utili- zado en la fabricación de tarjetas de circuito y se determinó la cantidad de pandeo (pulg) en condiciones particulares con cada pieza y el resultado fue un pandeo medio muestral de 0.0635 y una desviación estándar muestral de 0.0065. a. Calcule una predicción de la cantidad de pandeo de una sola pieza de laminado de una manera que proporcione información sobre precisión y confiabilidad. b. Calcule un intervalo con el cual pueda tener un alto gra- do de confianza de que por lo menos 95% de todas las piezas de laminado produzcan cantidades de pandeo que estén entre los dos límites del intervalo. 39. El ejercicio 72 del capítulo 1 dio las siguientes observacio- nes de afinidad de receptor (volumen de distribución ajus- tado) con una muestra de 13 individuos sanos: 23, 39, 40, 41, 43, 47, 51, 58, 63, 66, 67, 69, 72. a. ¿Es factible que la distribución de la población de la cual se seleccionó esta muestra sea normal? b. Calcule un intervalo con el cual pueda estar 95% con- fiado de que por lo menos 95% de todos los individuos saludables en la población tienen volúmenes de distri- bución ajustados que quedan entre los límites del in- tervalo. c. Pronostique el volumen de distribución ajustado de un solo individuo saludable calculando un intervalo de predicción de 95%. ¿Cómo se compara el ancho de este intervalo con el ancho del intervalo calculado en el in- ciso b)? c7_p225-283.qxd 3/12/08 4:15 AM Page 277
- 296. 278 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Aun cuando las inferencias por lo que se refiere a la varianza 2 o a la desviación estándar de una población en general son de menos interés que aquellas con respecto a una media o proporción, hay ocasiones en que se requieren tales procedimientos. En el caso de una dis- tribución de población normal, las inferencias están basadas en el siguiente resultado por lo que se refiere a la varianza muestral S2 . Como se discutió en las secciones 4.4 y 7.1, la distribución ji cuadrada es una distri- bución de probabilidad continua con un solo parámetro , llamado número de grados de li- bertad, con posibles valores de 1, 2, 3, . . . Las gráficas de varias funciones de distribución de probabilidad 2 se ilustran en la figura 7.9. Cada función de distribución de probabilidad f(x; ) es positiva sólo con x 0 y cada una tiene asimetría positiva (una larga cola supe- rior), aunque la distribución se mueve hacia la derecha y se vuelve más simétrica a medida que se incrementa . Para especificar procedimientos inferenciales que utilizan la distribu- ción ji cuadrada, se requiere una notación análoga a aquella para un valor t crítico t, . 40. El ejercicio 13 del capítulo 1 presentó una muestra de n 153 observaciones de resistencia última a la tensión y el ejercicio 17 de la sección previa dio cantidades resumidas y solicitó un intervalo de confianza muestral grande. Como el tamaño de muestra es grande, no se requieren suposiciones sobre la distribución de la población en cuanto la validez del intervalo de confianza. a. ¿Se requiere alguna suposición sobre la distribución de la resistencia a la tensión antes de calcular un límite de predicción inferior para la resistencia a la tensión del nuevo espécimen seleccionado por medio del método descrito en esta sección? Explique. b. Use un paquete de software estadístico para investigar la probabilidad de una distribución de población normal. c. Calcule un límite de predicción inferior con un nivel de predicción de 95% para la resistencia última a la tensión del siguiente espécimen seleccionado. 41. Una tabla más extensa de valores t críticos que la que apa- rece en este libro muestra que para la distribución t con 20 grados de libertad, las áreas a la derecha de los valores 0.687, 0.860 y 1.064 son 0.25, 0.20 y 0.15, respectivamen- te. ¿Cuál es el nivel de confianza para cada uno de los si- guientes tres intervalos de confianza para la media de una distribución de población normal? ¿Cuál de los tres interva- los recomendaría utilizar y por qué? a. (x 0.687s/2 1 , x 1.725s/2 1 ) b. (x 0.860s/2 1 , x 1.325s/2 1 ) c. (x 1.064s/2 1 , x 1.064s/2 1 ) 7.4 Intervalos de confianza para la varianza y desviación estándar de una población normal TEOREMA Sean X1, X2, . . . , Xn una muestra aleatoria de una distribución normal con parámetros y 2 . Entonces la variable aleatoria tiene una distribución de probabilidad ji cuadrada (2 ) con n 1 grados de libertad. (Xi X )2 2 (n 1)S2 2 Figura 7.9 Gráficas de funciones de densidad ji cuadrada. f(x; ) 8 12 20 x c7_p225-283.qxd 3/12/08 4:15 AM Page 278
- 297. 7.4 Intervalos de confianza para la varianza y desviación estándar de una población normal 279 La simetría de las distribuciones t hizo que fuera necesario tabular sólo valores críti- cos t de cola superior (t, con valores pequeños de ). La distribución ji cuadrada no es si- métrica, por lo que la tabla A.7 del apéndice contiene valores de 2 , tanto para cerca de 0 como cerca de 1, como se ilustra en la figura 7.10b). Por ejemplo, 2 0.025,14 26.119 y 2 0.95,20 (el 5o percentil) 10.851. La variable aleatoria (n 1)S2 /2 satisface los dos parámetros en los cuales está ba- sado el método general de obtener un intervalo de confianza. Es una función del parámetro de interés 2 , no obstante su distribución de probabilidad (ji cuadrada) no depende de este parámetro. El área bajo una curva ji cuadrada con grados de libertad a la derecha de 2 /2, es /2, lo mismo que a la izquierda de 2 1/2, . De este modo el área capturada entre estos dos valores críticos es 1 . Como una consecuencia de esto y el teorema que se acaba de formular, P2 1/2,n1 2 /2,n1 1 (7.17) Las desigualdades en (7.17) equivalen a 2 Sustituyendo el valor calculado s2 en los límites se obtiene un intervalo de confianza para 2 y tomando las raíces cuadradas se obtiene un intervalo para . (n 1)S2 2 1/2,n1 (n 1)S2 2 /2,n1 (n 1)S2 2 Notación Sea 2 , , llamado valor crítico ji cuadrada, el número sobre el eje de medición de modo que del área bajo la curva ji cuadrada con grados de libertad quede a la derecha de 2 , . Un intervalo de confianza de 100(1 )% para la varianza 2 de una población normal tiene un límite inferior (n 1)s2 /2 /2,n1 y límite superior (n 1)s2 /2 1/2,n1 Un intervalo de confianza para tiene límites superior e inferior que son las raíces cuadradas de los límites correspondientes en el intervalo para 2 . Figura 7.10 Notación 2 , ilustrada. 2 función de distribución de probabilidad Área sombreada 2 , 2 a) 0.99, 2 0.01, Cada área sombreada 0.01 b) c7_p225-283.qxd 3/12/08 4:15 AM Page 279
- 298. 280 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Los datos adjuntos sobre voltaje de ruptura de circuitos eléctricamente sobrecargados se to- maron de un diagrama de probabilidad normal que apareció en el artículo “Damage of Fle- xible Printed Wiring Boards Associated with Lightning-Induced Voltage Surges”, (IEEE Transactions on Components, Hybrids, and Manuf. Tech., 1985: 214-220). La linealidad del diagrama apoyó de manera firme la suposición de que el voltaje de ruptura está aproxima- damente distribuido en forma normal. 1470 1510 1690 1740 1900 2000 2030 2100 2190 2200 2290 2380 2390 2480 2500 2580 2700 Sea 2 la varianza de la distribución del voltaje de ruptura. El valor calculado de la varian- za muestral es s2 137 324.3, la estimación puntual de 2 . Con grados de libertad n 1 16, un intervalo de confianza de 95% requiere 2 0.975,16 6.908 y 2 0.025,16 28.845. El intervalo es , (76 172.3, 318 064.4) Tomando la raíz cuadrada de cada punto extremo se obtiene (276.0, 564.0) como el intervalo de confianza de 95% para . Estos intervalos son bastante anchos, lo que refleja la variabilidad sustancial del voltaje de ruptura en combinación con un tamaño de muestra pequeño. ■ Los intervalos de confianza para 2 y cuando la distribución de la población no es normal pueden ser difíciles de obtener, incluso cuando el tamaño de muestra es grande. En esos casos, consulte a un estadístico conocedor. 16(137 324.3) 6.908 16(137 324.3) 28.845 EJERCICIOS Sección 7.4 (42-46) 42. Determine los valores de las siguientes cantidades: a. 2 0.1,15 b. 2 0.1,25 c. 2 0.01,25 d. 2 0.005,25 e. 2 0.99,25 f. 2 0.995,25 43. Determine lo siguiente: a. El 95o percentil de la distribución ji cuadrada con 10. b. El 5o percentil de la distribución ji cuadrada con 10. c. P(10.98 2 36.78), donde 2 es una variable alea- toria ji cuadrada con 22. d. P(2 14.611 o 2 37.652), donde 2 es una variable aleatoria ji cuadrada con 25. 44. Se determinó la cantidad de expansión lateral (mils) con una muestra de n 9 soldaduras de arco de gas metálico de energía pulsante utilizadas en tanques de almacenamiento de buques LNG. La desviación estándar muestral resultan- te fue s 2.81 mils. Suponiendo normalidad, obtenga un intervalo de confianza de 95% para 2 y para . 45. Se hicieron las siguientes observaciones de tenacidad a la fractura de una placa base de acero maraging con 18% de níquel [“Fracture Testing of Weldments”, ASTM Special Publ. No. 381, 1965: 328-356 (en k/pulg — pu — lg., dadas en orden creciente)]: 69.5 71.9 72.6 73.1 73.3 73.5 75.5 75.7 75.8 76.1 76.2 76.2 77.0 77.9 78.1 79.6 79.7 79.9 80.1 82.2 83.7 93.7 Calcule un intervalo de confianza de 99% para la desvia- ción estándar de la distribución de la tenacidad a la fractu- ra. ¿Es válido este intervalo cualquiera que sea la naturaleza de la distribución? Explique. 46. Los resultados de una prueba de turbiedad de Wagner reali- zada con 15 muestras de arena de prueba Ottawa estándar (en microamperes) 26.7 25.8 24.0 24.9 26.4 25.9 24.4 21.7 24.1 25.9 27.3 26.9 27.3 24.8 23.6 a. ¿Es factible que esta muestra fuera seleccionada de una distribución de población normal? b. Calcule un límite de confianza superior con nivel de confianza de 95% para la desviación estándar de turbiedad de la población. Ejemplo 7.15 c7_p225-283.qxd 3/12/08 4:15 AM Page 280
- 299. Ejercicios suplementarios 281 47. El ejemplo 1.10 introdujo las observaciones adjuntas sobre fuerza de adhesión. 11.5 12.1 9.9 9.3 7.8 6.2 6.6 7.0 13.4 17.1 9.3 5.6 5.7 5.4 5.2 5.1 4.9 10.7 15.2 8.5 4.2 4.0 3.9 3.8 3.6 3.4 20.6 25.5 13.8 12.6 13.1 8.9 8.2 10.7 14.2 7.6 5.2 5.5 5.1 5.0 5.2 4.8 4.1 3.8 3.7 3.6 3.6 3.6 a. Calcule la fuerza de adhesión promedio verdadera de una manera que dé información sobre precisión y con- fiabilidad. [Sugerencia: xi 387.8 y x2 i 4247.08.] b. Calcule un intervalo de confianza de 95% para la pro- porción de todas las adhesiones cuyos valores de fuerza excederían de 10. 48. Un triatlón incluye natación, ciclismo y carrera a pie y es uno de los eventos deportivos amateurs más extenuantes. El artículo “Cardiovascular and Thermal Response of Triathlon Performance” (Medicine and Science in Sports and Exercise, 1988: 385-389) reporta sobre un estudio de investigación de nueve triatletas varones. Se registró el rit- mo cardiaco máximo (pulsaciones/min) durante la actua- ción de cada uno de los tres eventos. Para natacion, la media y la desviación estándar muestrales fueron 188.0 y 7.2, respectivamente. Suponiendo que la distribución de ritmo cardiaco es (de manera aproximada) normal, construya un intervalo de confianza de 98% para el ritmo cardiaco medio verdadero de triatletas mientras nadan. 49. Para cada uno de los 18 núcleos de depósitos de carbonato humedecidos con aceite, la cantidad de saturación de gas re- sidual después de la inyección de un solvente se midió en la corriente de agua de salida. Las observaciones, en porcen- taje de volumen de poros, fueron 23.5 31.5 34.0 46.7 45.6 32.5 41.4 37.2 42.5 46.9 51.5 36.4 44.5 35.7 33.5 39.3 22.0 51.2 (Véase “Relative Permeability Studies of Gas-Water Flow Following Solvent Injection in Carbonate Rocks”, Soc. Pe- troleum Engineers J., 1976: 23-30.) a. Construya una gráfica de caja de estos datos y comente sobre cualquier característica interesante. b. ¿Es factible que la muestra fuera seleccionada de una distribución de población normal? c. Calcule un intervalo de confianza de 98% para la canti- dad promedio verdadera de saturación de gas residual. 50. Un artículo publicado en un periódico reporta que se utilizó una muestra de tamaño 5 como base para calcular un inter- valo de confianza de 95% para la frecuencia natural (Hz) promedio verdadera de vigas deslaminadas de cierto tipo. El intervalo resultante fue (229.764, 233.504). Usted decide que un nivel de confianza de 99% es más apropiado que el de 95% utilizado. ¿Cuáles son los límites del intervalo de 99% [Sugerencia: Use el centro del intervalo y su ancho para determinar x y s.] 51. El gerente financiero de una gran cadena de tiendas depar- tamentales seleccionó una muestra aleatoria de 200 de sus clientes que pagan con tarjeta de crédito y encontró que 136 habían incurrido en pago de intereses durante el año previo a causa de saldos vencidos. a. Calcule un intervalo de confianza de 90% para la pro- porción verdadera de clientes de tarjeta de crédito que incurrieron en pago de intereses durante el año previo. b. Si el ancho deseado del intervalo de 90% es de 0.05, ¿qué tamaño de muestra se requiere para garantizar esto? c. ¿Especifica el límite superior del intervalo del inciso a) un límite de confianza superior de 90% para la propor- ción que se está estimando? Explique. 52. La alta concentración del elemento tóxico arsénico es de- masiado común en el agua subterránea. El artículo “Evalua- tion of Treatment Systems for the Removal of Arsenic from Groundwater” (Practice Periodical of Hazardous, Toxic, and Radioactive Waste Magmt., 2005: 152-157) reportó que para una muestra de n 5 especímenes de agua seleccio- nada para tratamiento por coagulación, la concentración de arsénico media muestral fue de 24.3 g/l, y la desviación estándar muestral fue de 4.1. Los autores del artículo citado utilizaron métodos basados en t para analizar sus datos, así que venturosamente tuvieron razón al creer que la distribu- ción de concentración de arsénico era normal. a. Calcule e interprete un intervalo de confianza de 95% para concentración de arsénico verdadera en todos los especímenes de agua. b. Calcule un límite de confianza superior de 90% para la desviación estándar de la distribución de la concentra- ción de arsénico. c. Pronostique la concentración de arsénico de un solo es- pécimen de agua de modo que dé información sobre pre- cisión y confiabilidad. 53. La infestación con pulgones de árboles frutales puede ser controlada rociando un pesticida o mediante la inundación con mariquitas. En un área particular, se seleccionan cuatro diferentes arboledas de árboles frutales para experimenta- ción. Las primeras tres arboledas se rocían con los pestici- das 1, 2 y 3, respectivamente y la cuarta se trata con mariquitas con los siguientes resultados de cosecha: ni x i Número de (Medida de Tratamiento árboles áridos/árbol) si 1 100 10.5 1.5 2 90 10.0 1.3 3 100 10.1 1.8 4 120 10.7 1.6 Sea i la cosecha promedio verdadera (medida de áridos/ árbol) después de recibir el i-ésimo tratamiento. En ese caso 1 3 (1 2 3) 4 mide la diferencia de las cosechas promedio verdaderas entre el tratamiento con pesticidas y el tratamiento con mariquitas. EJERCICIOS SUPLEMENTARIOS (47–62) c7_p225-283.qxd 3/12/08 4:15 AM Page 281
- 300. 282 CAPÍTULO 7 Intervalos estadísticos basados en una sola muestra Cuando n1, n2 y n3 son grandes, el estimador ˆ obtenido al reemplazar cada i con X i es aproximadamente normal. Use esto para obtener un intervalo de confianza muestral grande de 100(1 )% y calcule el intervalo de 95% con los da- tos dados. 54. Es importante que las máscaras utilizadas por bomberos sean capaces de soportar altas temperaturas porque los bomberos comúnmente trabajan en temperaturas de 200- 500°F. En una prueba de un tipo de máscara, a 11 de 55 máscaras se les desprendió la mica a 250°. Construya un in- tervalo de confianza de 90% para la proporción de másca- ras verdadera de este tipo cuya mica se desprendería a 250°. 55. Un fabricante de libros de texto universitarios está interesado en investigar la resistencia de las encuadernaciones produ- cidas por máquina de encuadernar particular. La resistencia puede ser medida registrando la fuerza requerida para arrancar las páginas de la encuadernación. Si esta fuerza se mide en libras, ¿cuántos libros deberán ser probados para calcular la fuerza promedio requerida para romper la encua- dernación dentro de 0.1 lb con 95% de confianza? Suponga que se sabe que es de 0.8. 56. Es bien sabido que la exposición a la fibra de asbesto es un riesgo para la salud. El artículo “The Acute Effects of Chry- sotile Asbestos Exposure on Lung Function” (Environ. Re- search, 1978: 360-372) reporta resultados sobre un estudio basado en una muestra de trabajadores de la construcción que habían estado expuestos a asbesto durante un periodo prolongado. Entre los datos dados en el artículo se encon- traron los siguientes valores (ordenados) de elasticidad pul- monar (cm3 /cm H2O) por cada uno de los 16 sujetos 8 meses después del periodo de exposición (la elasticidad pulmonar mide la elasticidad de los pulmones o cuán efec- tivamente los pulmones son capaces de inhalar y exhalar): 167.9 180.8 184.8 189.8 194.8 200.2 201.9 206.9 207.2 208.4 226.3 227.7 228.5 232.4 239.8 258.6 a. ¿Es factible que la distribución de la población sea normal? b. Calcule un intervalo de confianza de 95% para la elasticidad pulmonar promedio verdadera después de la exposición. c. Calcule un intervalo que, con un nivel de confianza de 95%, incluya por lo menos 95% de los valores de elasti- cidad pulmonar en la distribución de la población. 57. En el ejemplo 6.8, se introdujo el concepto de experimento censurado en el cual n componentes se prueban y el experi- mento termina en cuanto r de los componentes fallan. Su- ponga que las vidas útiles de los componentes son independientes, cada uno con distribución exponencial y parámetro . Sea Y1 el tiempo en el cual ocurre la primera falla, Y2 el tiempo en el cual ocurre la segunda falla, y así sucesivamente, de modo que Tr Y1 Yr (n r) Yr, es la vida útil total acumulada. En ese caso se puede de- mostrar que 2Tr, tiene una distribución ji cuadrada con 2r grados de libertad. Use esto para desarrollar una fórmula para un intervalo de confianza de 100(1 )% para una vi- da útil promedio verdadera 1/. Calcule un intervalo de confianza de 95% con los datos del ejemplo 6.8. 58. Sean X1, X2, . . . , Xn una muestra aleatoria de una distribu- ción de probabilidad continua con mediana ~ (de modo que P(Xi ~ ) P(Xi ~ ) 0.5). a. Demuestre que P(mín(Xi) ~ máx(Xi)) 1 1 2 n1 de modo que (mín(xi), máx(xi)) es un intervalo de confian- za de 100(1 )% para ~ con 1 2n1 . [Sugerencia: El complemento del evento {mín(Xi) ~ máx(Xi)} es {máx(Xi) ~ } {mín(Xi) ~ }. Pero máx(Xi) ~ si y sólo si Xi ~ con todas las i.] b. Para cada uno de seis infantes normales varones, se de- terminó la cantidad de alanina aminoácida (mg/100 ml) mientras que los infantes llevaban un dieta libre de iso- leucina y se obtuvieron los siguientes resultados 2.84 3.54 2.80 1.44 2.94 2.70 Calcule un intervalo de confianza de 97% para cantidad mediana verdadera de alanina para infantes que llevaban esa dieta (“The Essential Amino-Acid Requirements of Infants”, Amer. J. Nutrition, 1964: 322-330). c. Sean x(2) la segunda más pequeña de las xi y x(n1) la se- gunda más grande de las xi. ¿Cuál es el coeficiente de confianza del intervalo (x(2), x(n1)) para ~ ? 59. Sean X1, X2, . . . , Xn una muestra aleatoria de una distribu- ción uniforme en el intervalo [0, ], de modo que f(x) {1 0 x 0 de lo contrario Entonces si Y máx(Xi), se puede demostrar que la varia- ble aleatoria U Y/ tiene una función de densidad fU(u) {nun1 0 u 1 0 de lo contrario a. Use fU(u) para verificar que P(/2)1/n Y (1 /2)1/n 1 y use ésta para derivar un intervalo de confianza de 100(1 )% para . b. Verifique que P(1/n Y/ 1) 1 y obtenga un intervalo de confianza de 100(1 )% para basado en esta proposición de probabilidad. c. ¿Cuál de los dos intervalos derivados previamente es más corto? Si mi tiempo de espera en la mañana de un camión está uniformemente distribuido y los tiempos de espera observados son x1 4.2, x2 3.5, x3 1.7, x4 1.2 y x5 2.4 derive un intervalo de confianza de 95% para utilizando el más corto de los dos intervalos. 60. Sea 0 . Entonces un intervalo de confianza de 100(1 )% para cuando n es grande es x z s n , x z s n La opción de /2 da el intervalo usual derivado en la sección 7.2; si /2, este intervalo no es simétrico con respecto a x . El ancho de este intervalo es w s(z z )/n . Demuestre que w se reduce al mínimo con la op- c7_p225-283.qxd 3/12/08 4:15 AM Page 282
- 301. Bibliografía 283 ción /2, de modo que el intervalo simétrico sea el más corto. [Sugerencia: a) Por definición de z, (z) 1 , de modo que z 1 (1 ); b) la relación entre la deri- vada de una función y f(x) y la función inversa x f 1 (y) es (d/dy) f 1 (y) 1/f (x).] 61. Suponga que x1, x2, . . . , xn son valores observados resultan- tes de una muestra aleatoria tomada de una distribución si- métrica pero posiblemente de cola gruesa. Sean x ~ y fs la mediana muestral y la dispersión de los cuartos, respec- tivamente. El capítulo 11 de Understanding Robust and Exploratory Data Analysis (véase la bibliografía del capítu- lo 6) sugiere el siguiente intervalo de confianza de 95% robusto para la media de la población (punto de simetría): x ~ ! fs n El valor de la cantidad entre paréntesis es 2.10 con n 10, 1.94 con n 20 y 1.91 con n 30. Calcule este intervalo de confianza con los datos del ejercicio 45 y compare con el intervalo de confianza t apropiado para distribución de población normal. 62. a. Use los resultados del ejemplo 7.5 para obtener un lími- te de confianza inferior de 95% para el parámetro de una distribución exponencial y calcule el límite basado en los datos dados en el ejemplo. b. Si la vida útil tiene una distribución exponencial, la pro- babilidad de que la vida útil exceda de t es P(X t) e t . Use el resultado del inciso a) para obtener un lími- te de confianza inferior de 95% para la probabilidad de que el tiempo de ruptura exceda de 100 min. valor crítico t conservador 1.075 DeGroot, Morris y Mark Schervish, Probability and Statistics (3a. ed.), Addison-Wesley, Reading MA, 2002. Una muy bue- na exposición de los principios generales de inferencia esta- dística. Hahn, Gerald y William Meeker, Statistical Intervals, Wiley, Nueva York, 1991. Todo lo que alguna vez quiso saber sobre intervalos estadísticos (de confianza, predicción, tolerancia y otros). Larsen, Richard y Morris Marx, Introduction to Mathematical Statistics: (2a. ed.), Prentice Hall, Englewood, Cliffs, NJ., 1986. Similar a la presentación de DeGroot, pero un poco me- nos matemática. Bibliografía c7_p225-283.qxd 3/12/08 4:15 AM Page 283
- 302. 8 284 INTRODUCCIÓN Un parámetro puede ser estimado a partir de datos muestrales o con un solo núme- ro (una estimación puntual) o un intervalo completo de valores plausibles (un inter- valo de confianza). Con frecuencia, sin embargo, el objetivo de una investigación no es estimar un parámetro sino decidir cuál de dos pretensiones contradictorias sobre el parámetro es la correcta. Los métodos para lograr esto comprenden la parte de la inferencia estadística llamada prueba de hipótesis. En este capítulo, primero se dis- cuten algunos de los conceptos y terminología básicos en la prueba de hipótesis y luego se desarrollan procedimientos para la toma de decisiones para los problemas de realización de pruebas más frecuentemente encontrados con base en una mues- tra tomada de una sola población. Pruebas de hipótesis basadas en una sola muestra c8_p284-324.qxd 3/12/08 4:17 AM Page 284
- 303. Una hipótesis estadística o simplemente hipótesis es una pretensión o aseveración sobre el valor de un solo parámetro (característica de una población o característica de una distri- bución de probabilidad), sobre los valores de varios parámetros o sobre la forma de una distribución de probabilidad completa. Un ejemplo de una hipótesis es la pretensión de que 0.75, donde es el diámetro interno promedio verdadero de un cierto tipo de tubo de PVC. Otro ejemplo es la proposición p 0.10, donde p es la proporción de tarjetas de cir- cuito defectuosas entre todas las tarjetas de circuito producidas por un cierto fabricante. Si 1 y 2 denotan las resistencias a la ruptura promedio verdaderas de dos tipos diferentes de cuerdas, una hipótesis es la aseveración de que 1 2 0 y otra es que 1 2 5. No obstante otro ejemplo de una hipótesis es la aseveración de que la distancia de detención en condiciones particulares tiene una distribución normal. Hipótesis de esta última clase se considerarán en el capítulo 14. En éste y en los siguientes capítulos, la atención se concen- tra en hipótesis en relación con parámetros. En cualquier problema de prueba de hipótesis, existen dos hipótesis contradictorias consideradas. Una podría ser la pretensión de que 0.75 y la otra 0.75 o las dos pro- posiciones contradictorias podrían ser p 0.10 y p 0.10. El objetivo es decidir, con ba- se en información muestral, cuál de las dos hipótesis es la correcta. Existe una analogía conocida de esto en un juicio criminal. Una pretensión es la aseveración de que el individuo acusado es inocente. En el sistema judicial estadounidense, esta es la pretensión que inicial- mente se cree que es cierta. Sólo de cara a una fuerte evidencia que diga lo contrario el ju- rado deberá rechazar esta pretensión a favor de la aseveración alternativa de que el acusado es culpable. En este sentido, la pretensión de inocencia es la hipótesis favorecida o protegi- da y el agobio de comprobación recae en aquellos que creen en la pretensión alternativa. Asimismo, al probar hipótesis estadísticas, el problema se formulará de modo que una de las pretensiones sea inicialmente favorecida. Esta pretensión inicialmente favorecida no será rechazada a favor de la pretensión alternativa a menos que la evidencia muestral la con- tradiga y apoye fuertemente la aseveración alternativa. Una prueba de hipótesis es un método de utilizar datos muestrales para decidir si la hipó- tesis nula debe ser rechazada. Por consiguiente se podría probar H0: 0.75 contra la Ha alternativa: 0.75. Sólo si los datos muestrales sugieren fuertemente que es otra dife- rente de 0.75 deberá ser rechazada la hipótesis nula. Sin semejante evidencia, H0 no deberá ser rechazada, puesto que sigue siendo bastante plausible. En ocasiones un investigador no desea aceptar una aseveración particular a menos y hasta que los datos apoyan fuertemente la aseveración. Como ejemplo, supóngase que una compañía está considerando aplicar un nuevo tipo de recubrimiento en los cojinetes que fa- brica. Se sabe que la vida de desgaste promedio verdadera con el recubrimiento actual es de 8.1 Hipótesis y procedimientos de prueba 285 8.1 Hipótesis y procedimientos de prueba DEFINICIÓN La hipótesis nula denotada por H0, es la pretensión de que inicialmente se supone cierta (la pretensión de “creencia previa”). La hipótesis alternativa denotada por Ha, es la aseveración contradictoria a H0. La hipótesis nula será rechazada en favor de la hipótesis alternativa sólo si la evidencia muestral sugiere que H0 es falsa. Si la muestra no contradice fuertemen- te a H0, se continuará creyendo en la verdad de la hipótesis nula. Las dos posibles conclusiones derivadas de un análisis de prueba de hipótesis son entonces rechazar H0 o no rechazar H0. c8_p284-324.qxd 3/12/08 4:17 AM Page 285
- 304. 1000 horas. Si denota la vida promedio verdadera del nuevo recubrimiento, la compañía no desea cambiar a menos que la evidencia sugiera fuertemente que excede de 1000. Una formulación apropiada del problema implicaría probar H0: 1000 contra Ha: 1000. La conclusión de que se justifica un cambio está identificada con Ha y se requeriría eviden- cia conclusiva para justificar el rechazo de H0 y cambiar al nuevo recubrimiento. La investigación científica a menudo implica tratar de decidir si una teoría actual de- be ser reemplazada por una explicación más plausible y satisfactoria del fenómeno investi- gado. Un método conservador es identificar la teoría actual con H0 y la explicación alternativa del investigador con Ha. El rechazo de la teoría actual ocurrirá entonces sólo cuando la evidencia es mucho más compatible con la nueva teoría. En muchas situaciones, Ha se conoce como “hipótesis del investigador”, puesto que es la pretensión que al investi- gador en realidad le gustaría validar. La palabra nulo significa “sin ningún valor, efecto o consecuencia”, la que sugiere que H0 no deberá ser identificada con la hipótesis de ningún cambio (de la opinión actual), ninguna diferencia, ninguna mejora, y así sucesivamente. Su- póngase, por ejemplo, que 10% de todas las tarjetas de circuito producidas por un cierto fa- bricante durante un periodo reciente estaban defectuosas. Un ingeniero ha sugerido un cambio del proceso de producción en la creencia de que dará por resultado una proporción reducida de tarjetas defectuosas. Sea p la proporción verdadera de tarjetas defectuosas que resultan del proceso cambiado. Entonces la hipótesis de investigación en la cual recae el agobio de comprobación, es la aseveración de que p 0.10. Por consiguiente la hipóte- sis alternativa es Ha: p 0.10. En el tratamiento de la prueba de hipótesis, H0 siempre será formulada como una afir- mación de igualdad. Si denota el parámetro de interés, la hipótesis nula tendrá la forma H0: 0 donde 0 es un número específico llamado valor nulo del parámetro (valor pre- tendido para por la hipótesis nula). Como ejemplo, considérese la situación de la tarjeta de circuito que se acaba de discutir. La hipótesis alternativa sugerida fue Ha: p 0.10, la pretensión de que la modificación del proceso redujo la proporción de tarjetas defectuosas. Una opción natural de H0 en esta situación es la pretensión de que p 0.10 de acuerdo a la cual el nuevo proceso no es mejor o peor que el actualmente utilizado. En su lugar se con- siderará H0: p 0.10 contra Ha: p 0.10. El razonamiento para utilizar esta hipótesis nu- la simplificada es que cualquier procedimiento de decisión razonable para decidir entre H0: p 0.10 y Ha: p 0.10 también será razonable para decidir entre la pretensión de que p 0.10 y Ha. Se prefiere utilizar una H0 simplificada porque tiene ciertos beneficios técnicos, los que en breve serán aparentes. La alternativa de la hipótesis nula H0: 0 se verá como una de las siguientes tres aseveraciones: 1) Ha: 0 (en cuyo caso la hipótesis nula implícita es 0), 2) Ha: 0 (por consiguiente la hipótesis implícita nula establece que 0) o 3) Ha: 0. Por ejemplo, sea la desviación estándar de la distribución de diámetros internos (pulgadas) de un cierto tipo de manguito de metal. Si se decidió utilizar el manguito a menos que la evi- dencia muestral demuestre conclusivamente que 0.001, la hipótesis apropiada sería H0: 0.001 contra Ha: 0.001. El número 0 que aparece tanto en H0 como en Ha (sepa- ra la alternativa de la nula) se llama valor nulo. Procedimientos de prueba Un procedimiento de prueba es una regla, basada en datos muestrales, para decidir si re- chazar H0. Una prueba de H0: p 0.10 contra Ha: p 0.10 en el problema de tarjetas de circuito podría estar basado en examinar una muestra aleatoria de n 200 tarjetas. Sea X el número de tarjetas defectuosas en la muestra, una variable aleatoria binomial; x repre- senta el valor observado de X, Si H0 es verdadera, E(X) np 200(0.10) 20, en tanto que se pueden esperar menos de 20 tarjetas defectuosas si Ha es verdadera. Un valor de x un poco por debajo de 20 no contradice fuertemente a H0, así que es razonable rechazar H0 sólo si x es sustancialmente menor que 20. Un procedimiento de prueba como ése es 286 CAPÍTULO 8 Pruebas de hipótesis basadas en una sola muestra c8_p284-324.qxd 3/12/08 4:17 AM Page 286
- 305. rechazar H0 si x 15 y no rechazarla de lo contrario. Este procedimiento consta de dos constituyentes: 1) un estadístico de prueba o función de los datos muestrales utilizados pa- ra tomar la decisión y 2) una región de rechazo compuesta de aquellos valores x con los cuales H0 será rechazada a favor de Ha. De acuerdo a la regla que se acaba de sugerir, la región de rechazo se compone de x 0, 1, 2, . . . , y 15, H0 no será rechazada si x 16, 17, . . . , 199 o 200. Como otro ejemplo, supóngase que una compañía tabacalera afirma que el contenido de nicotina prometido de los cigarrillos marca B es (cuando mucho) de 1.5 mg. Sería im- prudente rechazar la afirmación del fabricante sin una fuerte evidencia contradictoria, así que una formulación del problema apropiada es probar H0: 1.5 con Ha: 1.5. Con- sidérese una regla de decisión basada en analizar una muestra aleatoria de 32 cigarrillos. Sea X el contenido de nicotina promedio muestral. Si H0 es verdadera E(X ) 1.5, en tanto que si H0 es falsa, se espera que X exceda de 1.5. Una fuerte evidencia contra H0 es propor- cionada por un valor de x que exceda considerablemente de 1.5. Por consiguiente se podría utilizar X como un estadístico de prueba junto con la región de rechazo x 1.6. Tanto en el ejemplo de tarjetas de circuito como en el de contenido de nicotina, la se- lección del estadístico de prueba y la forma de la región de rechazo tienen sentido intuitiva- mente. Sin embargo, la selección del valor de corte utilizado para especificar la región de rechazo es un tanto arbitraria. En lugar de rechazar H0: p 0.10 a favor de Ha: p 0.10 cuando x 15, se podría utilizar la región de rechazo x 14. En esta región, H0 no sería rechazada si se observaran 15 tarjetas defectuosas, mientras que esta ocurrencia conduciría al rechazo de H0 si se emplea la región inicialmente sugerida. Asimismo, se podría utilizar la región de rechazo x 1.55 en el problema de contenido de nicotina en lugar de la región x 1.60. Errores en la prueba de hipótesis La base para elegir una región de rechazo particular radica en la consideración de los erro- res que se podrían presentar al sacar una conclusión. Considérese la región de rechazo x 15 en el problema de tarjetas de circuito. Aun cuando H0: p 0.10 sea verdadera, podría suceder que una muestra inusual dé por resultado x 13, de modo que H0 sea erró- neamente rechazada. Por otra parte, aun cuando Ha: p 0.10 sea verdadera, una muestra inusual podría dar x 20, en cuyo caso H0 no sería rechazada, de nueva cuenta una con- clusión incorrecta. Por lo tanto es posible que H0 pueda ser rechazada cuando sea verda- dera o que H0 no pueda ser rechazada cuando sea falsa. Estos posibles errores no son consecuencia de una región de rechazo tontamente seleccionada. Cualquiera de estos dos errores podría presentarse cuando se emplea la región x 14, o cuando se utiliza cual- quier otra región. 8.1 Hipótesis y procedimientos de prueba 287 Un procedimiento de prueba se especifica como sigue: 1. Un estadístico de prueba, una función de los datos muestrales en los cuales ha de basarse la decisión (rechazar H0 o no rechazar H0) 2. Una región de rechazo, el conjunto de todos los valores estadísticos de prueba por los cuales H0 será rechazada. La hipótesis nula será rechazada entonces si y sólo si el valor estadístico de prueba observado o calculado queda en la región de rechazo. c8_p284-324.qxd 3/12/08 4:17 AM Page 287
- 306. En el problema de contenido de nicotina, un error de tipo I consiste en rechazar la afirma- ción del fabricante de que 1.5 cuando en realidad es cierta. Si se emplea la región de rechazo x 1.6 podría suceder que x 1.63 aun cuando 1.5, con el resultado de un error de tipo I. Alternativamente, puede ser que H0 sea falsa y no obstante x 1.52, lo que conduciría a que H0 no sea rechazada (un error de tipo II). En el mejor de todos los mundos posibles, se podrían desarrollar procedimientos de prueba en los cuales ningún tipo de error es posible. Sin embargo, este ideal puede ser al- canzado sólo si la decisión se basa en el examen de toda la población. La dificultad con la utilización de un procedimiento basado en datos muestrales es que debido a la variabilidad del muestreo, el resultado podría ser una muestra no representativa. Aun cuando E(X ) , el valor observado x puede diferir sustancialmente de (por lo menos si n es pequeño). Por consiguiente cuando 1.5 en la situación de la nicotina, x puede ser mucho más grande que 1.5 y el resultado sería el rechazo erróneo de H0. Alternativamente, puede ser que 1.6 y no obstante que se observe una x mucho más pequeña que este valor, lo que conduce a un error de tipo II. En lugar de demandar procedimientos sin errores, habrá que buscar procedimientos con los cuales sea improbable que ocurra cualquier tipo de error. Es decir, un buen proce- dimiento es uno con el cual la probabilidad de cometer cualquier tipo de error es pequeña. La selección de un valor de corte en una región de rechazo particular fija las probabilidades de errores de tipo I y tipo II. Estas probabilidades de error son tradicionalmente denotadas por y , respectivamente. Como H0, especifica un valor único del parámetro, existe un so- lo valor de . Sin embargo, existe un valor diferente de por cada valor del parámetro com- patible con Ha: Se sabe que un cierto tipo de automóvil no sufre daños visibles el 25% del tiempo en prue- bas de choque a 10 mph. Se ha propuesto un diseño de defensa modificado en un esfuerzo por incrementar este porcentaje. Sea p la proporción de todos los choques a 10 mph con es- ta nueva defensa en los que no producen daños visibles. Las hipótesis a ser tratadas son H0: p 0.25 (ninguna mejora contra Ha: p 0.25. La prueba se basará en un experimento que implica n 20 choques independientes con prototipos del nuevo diseño. Intuitivamente, H0 deberá ser rechazada si un número sustancial de los choques no muestra daños. Considére- se el siguiente procedimiento de prueba: Estadístico de prueba: X número de choques sin daños visibles Región de rechazo: R8 {8, 9, 10, . . . , 19, 20}; es decir, rechazar H0 si x 8, donde x es el valor observado del estadístico de prueba. Esta región de rechazo se llama de cola superior y se compone de sólo grandes valores del estadístico de prueba. Cuando H0 es verdadera, la distribución de probabilidad de X es binomial con n 20 y p 0.25. Entonces P(error de tipo I) P(H0 es rechazada cuando es verdadera) P(X 8 cuando X Bin(20, 0.25)) 1 – B(7; 20, 0.25) 1 0.898 0.102 Es decir, cuando H0 en realidad es verdadera, aproximadamente el 10% de todos los expe- rimentos compuestos de 20 choques darían por resultado que H0 fuera rechazada incorrec- tamente (un error de tipo I). 288 CAPÍTULO 8 Pruebas de hipótesis basadas en una sola muestra DEFINICIÓN Un error de tipo I consiste en rechazar la hipótesis nula cuando es verdadera. Un error de tipo II implica no rechazar H0 cuando H0 es falsa. Ejemplo 8.1 c8_p284-324.qxd 3/12/08 4:17 AM Page 288
- 307. En contraste con , no hay una sola . En su lugar, hay una diferente por cada p di- ferente que exceda de 0.25. Por consiguiente hay un valor de con p 0.3 (en cuyo caso X Bin(20, 0.3), otro valor de con p 0.5 y así sucesivamente. Por ejemplo, (0.3) P(error de tipo II cuando p 0.3) P(H0 no es rechazada cuando es falsa porque p 0.3) P(X 7 cuando X Bin(20, 0.3)) B(7; 20, 0.3) 0.772 Cuando p es en realidad 0.3 y no 0.25 (un “pequeño” alejamiento de H0), ¡aproximadamen- te el 77% de todos los experimentos de este tipo darían por resultado que H0 fuera incorrec- tamente rechazada! La tabla adjunta muestra para valores seleccionados de p (cada uno calculado para la región de rechazo R8). Claramente, disminuye conforme el valor de p se aleja hacia la derecha del valor nulo 0.25. Intuitivamente, mientras más grande es el alejamiento de H0, menos probable es que dicho alejamiento no sea detectado. p 0.3 0.4 0.5 0.6 0.7 0.8 (p) 0.772 0.416 0.132 0.021 0.001 0.000 El procedimiento de prueba propuesto sigue siendo razonable para poner a prueba la hipótesis nula más realista de que p 0.25. En este caso, ya no existe una sola , sino que hay una por cada p que sea cuando mucho de 0.25: (0.25), (0.23), (0.20), (0.15) y así sucesivamente. Es fácil verificar, no obstante, que (p) (0.25) 0.102 si p 0.25. Es decir, el valor más grande de ocurre con el valor límite 0.25 entre H0 y Ha. Por consiguien- te si es pequeña para la hipótesis nula simplificada, también igual o más pequeña para la H0 realista. ■ Se sabe que el tiempo de secado de un cierto tipo de pintura en condiciones de prueba es- pecificadas está normalmente distribuido con valor medio de 75 min y desviación estándar de 9 min. Algunos químicos propusieron un nuevo aditivo para reducir el tiempo de secado. Se cree que los tiempos de secado con este aditivo permanecerán normalmente distribuidos con 9. Debido al gasto asociado con el aditivo, la evidencia deberá sugerir fuertemen- te una mejora en el tiempo de secado promedio antes de que se adopte semejante conclu- sión. Sea el tiempo de secado promedio verdadero cuando se utiliza el aditivo. Las hipótesis apropiadas son H0; 75 contra Ha: 75. Sólo si H0 puede ser rechazada se- rá declarado exitoso y utilizado. Los datos experimentales tienen que estar compuestos de tiempos de secado de n 25 especímenes de prueba. Sean X1, . . . , X25 los 25 tiempos de secado, una muestra aleatoria de tamaño 25 de una distribución normal con valor medio y desviación estándar 9. El tiempo de secado medio muestral X tiene entonces una distribución normal con valor esperado X y desviación estándar X /n 9/2 5 1.80. Cuando H0 es ver- dadera, X 75, así que un valor x un poco menor que 75 no contradeciría fuertemente a H0. Una región razonable de rechazo tiene la forma X c, donde el valor de corte c es ade- cuadamente seleccionado. Considere la opción c 70.8, de modo que el procedimiento de prueba se componga del estadístico de prueba X y una región de rechazo x 70.8. Debido a que la región de rechazo se compone de sólo valores pequeños del estadístico de prueba, se dice que ésta es de cola pequeña. El cálculo de y ahora implica una estandarización de rutina de X seguida por una referencia a las probabilidades normales estándar de la tabla A.3: P(error de tipo I) P(H0 es rechazada cuando es verdadera) P(X 70.8 cuando X normal con X 75, X 1.8) ( 2.33) 0.01 70.8 75 1.8 8.1 Hipótesis y procedimientos de prueba 289 Ejemplo 8.2 c8_p284-324.qxd 3/12/08 4:17 AM Page 289
- 308. (72) P(error de tipo II cuando 72) P(H0 no es rechazada cuando es falsa porque 72) P(X 70.8 cuando X normal con X 72 y X 1.8) 1 1 ( 0.67) 1 0.2514 0.7486 (70) 1 0.3300 (67) 0.0174 Con el procedimiento de prueba especificado, sólo el 1% de todos los experimentos realiza- dos como se describió darán por resultado que H0 sea rechazada cuando en realidad es ver- dadera. No obstante, la probabilidad de un error de tipo II es muy grande cuando 72 (sólo un pequeño alejamiento de H0), un poco menor cuando 70 y bastante pequeño cuando 67 (un alejamiento muy sustancial de H0). Estas probabilidades de error se ilus- tran en la figura 8.1. Obsérvese que se calcula con la distribución de probabilidad del es- tadístico de prueba cuando H0 es verdadera, en tanto que la determinación de requiere conocer la distribución del estadístico cuando H0 es falsa. 70.8 70 1.8 70.8 72 1.8 Como en el ejemplo 8.1, si se considera la hipótesis nula más realista 75, existe una por cada valor de parámetro con el cual H0 es verdadera: (75), (75.8), (76.5), y así sucesivamente. Es fácil verificar que (75) es la más grande de todas estas probabilida- des de error de tipo I. Enfocándose en el valor límite equivale a trabajar explícitamente con el “peor caso”. ■ 290 CAPÍTULO 8 Pruebas de hipótesis basadas en una sola muestra 75 73 70.8 a) Área sombreada 0.01 72 75 70.8 b) 70 75 70.8 c) Área sombreada (70) Área sombreada (72) Figura 8.1 y ilustradas para el ejemplo 8.2: a) la distribución de X cuando 75 (H0 ver- dadera); b) la distribución de X cuando 72 (H0 falsa); c) la distribución de X cuando 70 (H0 falsa). c8_p284-324.qxd 3/12/08 4:17 AM Page 290
- 309. La especificación de un valor de corte para la región de rechazo en los ejemplos que se acaban de considerar fue algo arbitraria. El uso de R8 {8, 9, . . . , 20} en el ejemplo 8.1 dio por resultado 0.102, (0.3) 0.772 y (0.5) 0.132. Muchos pensarán que estas probabilidades de error son intolerablemente grandes. Quizá puedan reducirse si se cambia el valor de corte. Utilice el mismo experimento y el estadístico de prueba X como previamente se descri- bió en el problema de la defensa de automóvil pero ahora considere la región de recha- zo R9 {9, 10, . . . , 20}. Como X sigue teniendo una distribución binomial con parámetros n 20 y p, P(H0 es rechazada cuando p 0.25) P(X 9 cuando X Bin(20, 0.25)) 1 – B(8; 20, 0.25) 0.041 La probabilidad de error de tipo I se redujo con el uso de la nueva región de rechazo. Sin embargo, se pagó un precio por esta reducción: (0.3) P(H0 no es rechazada cuando p 0.3) P(X 8 cuando X Bin(20, 0.3)) B(8; 20, 0.3) 0.887 (0.5) B(8; 20, 0.5) 0.252 Ambas son más grandes que las probabilidades de error correspondientes 0.772 y 0.132 para la región R8. En retrospectiva, no es sorprendente; se calcula sumando las probabili- dades de los valores estadísticos de prueba en la región de rechazo, en tanto que es la pro- babilidad de que X quede en el complemento de la región de rechazo. Al hacerse más pequeña la región de rechazo debe reducirse al mismo tiempo que se incrementa con cualquier valor alternativo fijo del parámetro. ■ El uso del valor de corte c 70.8 en el ejemplo de secado de la pintura dio por resultado un valor de muy pequeño (0.01) pero grande. Considere el mismo experimento y prue- be el estadístico de prueba X con la nueva región de rechazo x 72. Como X sigue siendo normalmente distribuida con valor medio X y X 1.8, P(H0 es rechazada cuando es verdadera) P(X 72 cuando X N(75, 1.82 )) (1.67) 0.0475 0.05 (72) P(H0 no es rechazada cuando 72) P(X 72 cuando X es una variable aleatoria normal con media de 72 y desvia- ción estándar de 1.8) 1 1 (0) 0.5 (70) 1 0.1335 (67) 0.0027 El cambio del valor de corte agrandó la región de rechazo (incluye más valores de x y el re- sultado es una reducción de por cada fija menor que 75. Sin embargo, en esta nueva región se ha incrementado desde el valor previo 0.01 hasta aproximadamente 0.05. Si una probabilidad de error de tipo I así de grande puede ser tolerada, se prefiere la segunda re- gión (c 72) a la primera (c 70.8) debido a las más pequeñas. ■ Los resultados de estos ejemplos pueden ser generalizados de la siguiente manera. 72 70 1.8 72 72 1.8 72 75 1.8 8.1 Hipótesis y procedimientos de prueba 291 Ejemplo 8.3 (continuación del ejemplo 8.1) Ejemplo 8.4 (continuación del ejemplo 8.2) c8_p284-324.qxd 3/12/08 4:17 AM Page 291
- 310. Esta proposición expresa que una vez que el estadístico de prueba y n están fijos, no existe una región de rechazo que haga que al mismo tiempo y sean pequeños. Se debe selec- cionar una región para establecer un compromiso entre y . Debido a las indicaciones sugeridas para especificar H0 y Ha, casi siempre un error de tipo I es más serio que uno de tipo II (esto en general se puede lograr mediante la se- lección apropiada de las hipótesis). El método seguido por la mayoría de los practicantes de la estadística es especificar el valor más grande de que pueda ser tolerado y encontrar una región de rechazo que tenga valor de en lugar de cualquier otro más pequeño. Esto hace a tan pequeño como sea posible sujeto al límite en . El valor resultante de a menudo se conoce como nivel de significación de la prueba. Niveles tradicionales de significación son 0.10, 0.05 y 0.01, aunque el nivel en cualquier problema particular de- penderá de la seriedad de un error de tipo I: mientras más serio es este error, más pequeño deberá ser el nivel de significación. El procedimiento de prueba correspondiente se llama prueba de nivel (p. ej., prueba de nivel 0.05 o prueba de nivel 0.01). Una prueba con ni- vel de significación es una donde la probabilidad de error de tipo I se controla al nivel especificado. Considere la situación previamente mencionada en la cual era el contenido de nicotina promedio verdadero de los cigarrillos marca B. El objetivo es probar H0: 1.5 contra Ha: 1.5 con base en una muestra aleatoria X1, X2, . . . , X32 de contenido de nicotina. Supon- ga que se sabe que la distribución del contenido de nicotina es normal con 0.20. Enton- ces X está normalmente distribuida con valor medio X y desviación estándar X 0.20/ 3 2 0.0354. En lugar de utilizar X como estadístico de prueba, se estandariza X suponiendo que H0 es verdadera. Estadístico de prueba: Z Z expresa la distancia entre X y su valor esperado cuando H0 es verdadera como algún nú- mero de desviaciones estándar. Por ejemplo, z 3 resulta de una x que es 3 desviaciones estándar más grande de lo que se habría esperado si H0 fuera verdadera. Rechazar H0 cuando x excede “considerablemente” de 1.5 equivale a rechazar H0 cuando z excede “considerablemente” de cero. Es decir, la forma de la región de rechazo es z c. Determínese ahora c de modo que 0.05. Cuando H0 es verdadera, Z tiene una distribución estándar normal. Por consiguiente P(error de tipo I) P(rechazar H0 cuando H0 es verdadera) P(Z c cuando Z N(0, 1)) El valor de c debe capturar el área de la cola superior 0.05 bajo la curva z. O de la sección 4.3 o directamente de la tabla A.3, c z0.05 1.645. Obsérvese que z 1.645 equivale a x 1.5 (0.0354)(1.645), es decir, x 1.56. Entonces es la probabilidad de que X 1.56 y puede ser calculada con cualquier ma- yor que 1.5. ■ X 1.5 0.0354 X 1.5 /n 292 CAPÍTULO 8 Pruebas de hipótesis basadas en una sola muestra PROPOSICIÓN Supóngase que un experimento y un tamaño de muestra están fijos y que se seleccio- na un estadístico de prueba. Entonces si se reduce el tamaño de la región de rechazo para obtener un valor más pequeño de se obtiene un valor más grande de con cual- quier valor de parámetro particular compatible con Ha. Ejemplo 8.5 c8_p284-324.qxd 3/12/08 4:17 AM Page 292
- 311. 8.1 Hipótesis y procedimientos de prueba 293 EJERCICIOS Sección 8.1 (1-14) 1. Por cada una de las siguientes aseveraciones, exprese si es una hipótesis estadística legítima y por qué: a. H: 100 b. H: x ~ 45 c. H: s 0.20 d. H: 1/2 1 e. H: X Y 5 f. H: 0.01 donde es el parámetro de una distribución exponencial utilizada para modelar la vida útil de un componente. 2. Para los siguientes pares de aseveraciones, indique cuáles no satisfacen las reglas de establecer hipótesis y por qué (los subíndices 1 y 2 diferencian las cantidades de dos po- blaciones o muestras diferentes). a. H0: 100, Ha: 100 b. H0: 20, Ha: 20 c. H0: p 0.25, Ha: p 0.25 d. H0: 1 2 25, Ha: 1 2 100 e. H0: S2 1 S2 2, Ha: S2 1 S2 2 f. H0: 120, Ha: 150 g. H0: 1/2 1, Ha: 1/2 1 h. H0: p1 p2 0.1, Ha: p1 p2 0.1 3. Para determinar si las soldaduras de las tuberías en una planta de energía nuclear satisfacen las especificaciones, se selecciona una muestra aleatoria de soldaduras y se realizan pruebas en cada una de las soldaduras. La resistencia de la soldadura se mide como la fuerza requerida para romperla. Suponga que las especificaciones indican que la resistencia media de las soldaduras deberá exceder de 100 lb/pulg2 ; el equipo de inspección decide probar H0: 100 contra Ha: 100. Explique por qué podría ser preferible utilizar esta Ha en lugar de 100. 4. Sea el nivel de radioactividad promedio verdadero (pico- curies por litro). Se considera que el valor 5 pCi/L es la lí- nea divisoria entre agua segura e insegura. ¿Recomendaría probar H0: 5 contra Ha: 5 o H0: 5 contra Ha: 5? Explique su razonamiento. [Sugerencia: Piense en las consecuencias de un error de tipo I o de un error de tipo II con cada posibilidad.] 5. Antes de aprobar un gran pedido de fundas de polietileno para un tipo particular de cable de energía submarino relle- no de aceite a alta presión, una compañía desea contar con evidencia conclusiva de la desviación estándar verdadera del espesor de la funda es de menos de 0.05 mm. ¿Qué hi- pótesis deberán ser probadas y por qué? En este contexto, ¿Cuáles son los errores de tipo I y II? 6. Muchas casas viejas cuentan con sistemas eléctricos que uti- lizan fusibles en lugar de cortacircuitos. Un fabricante de fu- sibles de 40 amp desea asegurarse de que el amperaje medio al cual se queman sus fusibles es en realidad de 40. Si el am- peraje medio es menor que 40, los clientes se quejarán porque los fusibles tienen que ser reemplazados con demasiada fre- cuencia. Si el amperaje medio es de más de 40, el fabricante podría ser responsable de los daños que sufra un sistema eléc- trico a causa del funcionamiento defectuoso de los fusibles. Para verificar el amperaje de los fusibles, se selecciona e ins- pecciona una muestra de fusibles. Si tuviera que realizarse una prueba de hipótesis con los datos resultantes, ¿Qué hipó- tesis nula y alternativa sería de interés para el fabricante? Des- criba los errores de tipo I y II en el contexto de este problema. 7. Se toman muestras de agua utilizada para enfriamiento al mo- mento de ser descargada por una planta de energía en un río. Se ha determinado que en tanto la temperatura media del agua descargada sea cuando mucho de 150°F, no habrá efectos ne- gativos en el ecosistema del río. Para investigar si la planta cumple con los reglamentos que prohíben una temperatura media por encima de 150° del agua de descarga, se tomarán al azar 50 muestras de agua y se registrará la temperatura de ca- da muestra. Los datos resultantes se utilizarán para probar la hipótesis H0: 150° contra Ha: 150°. En el contexto de esta situación, describa los errores de tipo I y tipo II. ¿Qué tipo de error consideraría más serio? Explique. 8. Un tipo regular de laminado está siendo utilizado por un fa- bricante de tarjetas de circuito. Un laminado especial ha si- do desarrollado para reducir el alabeo. El laminado regular será utilizado en una muestra de especímenes y el laminado especial en otra muestra y se determinará entonces la canti- dad de alabeo en cada espécimen. El fabricante cambiará entonces al laminado especial sólo si puede demostrar que la cantidad de alabeo promedio verdadera de dicho lamina- do es menor que la del laminado regular. Formule las hipó- tesis pertinentes y describa los errores de tipo I y de tipo II en el contexto de esta situación. 9. Dos compañías diferentes han solicitado proporcionar el servicio de televisión por cable en una cierta región. Sea p la proporción de todos los suscriptores potenciales que favorecen a la primera compañía sobre la segunda. Consi- dere probar H0: p 0.5 contra Ha: p 0.5 basado en una muestra aleatoria de 25 individuos. Sea X el número en la muestra que favorece a la primera compañía y x el valor observado de X. a. ¿Cuál de las siguientes regiones de rechazo es más apro- piada y por qué? R1 {x: x 7 o x 18}, R2 {x: x 8}, R3 {x: x 17} b. En el contexto de este problema, describa cuáles son los errores de tipo I y de tipo II. c. ¿Cuál es la distribución de probabilidad del estadístico de prueba X cuando H0 es verdadera? Úsela para calcu- lar la probabilidad de un error de tipo I. d. Calcule la probabilidad de un error de tipo II en la región seleccionada cuando p 0.3, otra vez cuando p 0.4 y también con p 0.6 y p 0.7. e. Utilizando la región seleccionada, ¿qué concluiría si 6 de los 25 individuos encuestados favorecen a la compañía 1? 10. Una mezcla de cenizas combustibles pulverizadas y cemento Portland utilizada para rellenar con lechada deberá tener una resistencia a la compresión de más de 1300 KN/m2 . La mezcla no será utilizada a menos que la evidencia expe- rimental indique concluyentemente que la especificación de resistencia ha sido satisfecha. Suponga que la resistencia a la compresión de especímenes de esta muestra está normal- mente distribuida con 60. Sea la resistencia a la com- presión promedio verdadera. c8_p284-324.qxd 3/12/08 4:17 AM Page 293
- 312. La discusión general en el capítulo 7 de intervalos de confianza para una media de pobla- ción se enfocó en tres casos diferentes. A continuación se desarrollan procedimientos para estos mismos tres casos. Caso I: Una población normal con conocida Aun cuando la suposición de que el valor de es conocido rara vez se cumple en la prác- tica, este caso proporciona un buen punto de partida debido a la facilidad con que los 294 CAPÍTULO 8 Pruebas de hipótesis basadas en una sola muestra 8.2 Pruebas sobre una media de población a. ¿Cuáles son las hipótesis nula y alternativa apropiadas? b. Sea X la resistencia a la compresión promedio muestral de n 20 especímenes seleccionados al azar. Conside- re el procedimiento de prueba con estadístico de prueba X y región de rechazo x 1331.26. ¿Cuál es la distribu- ción de probabilidad del estadístico cuando H0 es verda- dera? ¿Cuál es la probabilidad de un error de tipo I para el procedimiento de prueba? c. ¿Cuál es la distribución de probabilidad del estadístico de prueba cuando 1350? Utilizando el procedimien- to de prueba de la parte (b), ¿cuál es la probabilidad de que la mezcla será juzgada insatisfactoria cuando en rea- lidad 1350 (un error de tipo II)? d. ¿Cómo cambiaría el procedimiento de prueba de la par- te (b) para obtener una prueba con nivel de significación de 0.05? ¿Qué impacto tendría este cambio en la proba- bilidad de error de la parte (c)? e. Considere el estadístico de prueba estandarizado Z (X 1300)/(/n ) (X 1300)/13.42. ¿Cuáles son los valores de Z correspondientes a la región de rechazo de la parte (b)? 11. La calibración de una báscula tiene que ser verificada pe- sando 25 veces un espécimen de prueba de 10 kg. Suponga que los resultados de diferentes pesadas son independientes entre sí y que el peso en cada ensayo está normalmente dis- tribuido con 0.200 kg. Sea la lectura de peso prome- dio verdadero en la báscula. a. ¿Qué hipótesis deberá poner a prueba? b. Suponga que la báscula tiene que ser recalibrada si o x 10.1032 o x 9.8968. ¿Cuál es la probabilidad de que se realice la recalibración cuando en realidad no es necesaria? c. ¿Cuál es la posibilidad de que la recalibración sea considerada innecesaria cuando en realidad 10.1? ¿Cuándo 9.8? d. Sea z (x 10)/(/n ). ¿Con qué valor de c la región de rechazo de la parte (b) equivale a la región de “dos colas” o z c o z c? e. Si el tamaño de muestra fue de sólo 10 y no de 25, ¿cómo modificaría el procedimiento de la parte (d) de modo que 0.05? f. Utilizando la prueba de la parte (e), ¿qué concluiría ba- sado en los siguientes datos muestrales: 9.981 10.006 9.857 10.107 9.888 9.728 10.439 10.214 10.190 9.793 g. Exprese de nuevo el procedimiento de prueba de la par- te (b) en función del estadístico de prueba estandarizado Z (X 10)/(/n ). 12. Un nuevo diseño del sistema de frenos de un cierto tipo de carro ha sido propuesto. Para el sistema actual, se sabe que la distancia de frenado promedio verdadera a 40 mph en condi- ciones específicas es de 120 pies. Se propone que el nuevo diseño sea implementado sólo si los datos muestrales indi- can fuertemente una reducción de la distancia de frenado promedio verdadera del nuevo diseño. a. Defina el parámetro de interés y formule las hipótesis pertinentes. b. Suponga que la distancia de frenado del nuevo sistema está normalmente distribuido con 10. Sea X la dis- tancia de frenado promedio de una muestra de 36 obser- vaciones. ¿Cuáles de las siguientes regiones de rechazo es apropiada: R1 {x : x 124.80}, R2 {x : x 115.20}, R3 = {x : o x 125.13 o x 114.87}? c. ¿Cuál es el nivel de significación de la región apropiada de la parte (b)? ¿Cómo cambiaría la región para obtener una prueba con 0.001? d. ¿Cuál es la probabilidad de que el nuevo diseño no sea implementado cuando la distancia de frenado promedio verdadera sea en realidad de 115 pies y la región apro- piada de la parte (b) sea utilizada? e. Sea Z (X 120)/(/n ). ¿Cuál es el nivel de signifi- cación de la región de rechazo {z: z 2.33}? ¿Para la región {z: z 2.88}? 13. Sean X1, . . . , Xn una muestra aleatoria de una distribución de población normal con un valor conocido de . a. Para probar las hipótesis H0: 0, contra Ha: 0 (donde 0 es un número fijo), demuestre que la prueba con el estadístico X y región de rechazo x 0 2.33/n tiene un nivel de significación de 0.01. b. Suponga que se utiliza el procedimiento de la parte (a) para probar H0: 0 contra Ha: 0. Si 0 100, n 25 y 5, ¿cuál es la probabilidad de cometer un error de tipo I cuando 99? ¿Cuándo 98? En ge- neral, ¿qué se puede decir sobre la probabilidad de un error de tipo I cuando el valor real de es menor que 0? Verifique su aseveración. 14. Reconsidere la situación del ejercicio 11 y suponga que la región de rechazo es {x : x 10.1004 o x 9.8940} {z: z 2.51 o z 2.65}. a. ¿Cuál es para este procedimiento? b. ¿Cuál es cuando 10.1? ¿Cuándo 9.9? ¿Es ésta deseable? c8_p284-324.qxd 3/12/08 4:17 AM Page 294
- 313. procedimientos generales y sus propiedades pueden ser desarrollados. La hipótesis nula en los tres casos propondrá que tiene un valor numérico particular, el valor nulo, el cual se- rá denotado por 0. Sean X1, . . . , Xn una muestra aleatoria de tamaño n de la población normal. Entonces la media muestral X tiene una distribución normal con valor esperado X y desviación estándar X /n . Cuando H0 es verdadera X 0. Considére- se ahora el estadístico Z obtenido estandarizando X de conformidad con la suposición de que H0 es verdadera: Z Al sustituir la media muestral calculada x se obtiene z, la distancia entre x y 0 expresada en “unidades de desviación estándar”. Por ejemplo, si la hipótesis nula es H0: 100, X /n 10/2 5 2.0 y x 103, entonces el valor estadístico de prueba es z (103 – 100)/2.0 1.5. Es decir, el valor observado de x es 1.5 desviaciones estándar (de X ) más grande de lo que se espera sea cuando H0 es verdadera. El estadístico Z es una medida natural de la distancia X , el estimador de y su valor esperado cuando H0 es verdadera. Si esta distancia es demasiado grande en una dirección consistente con Ha, la hipótesis nula de- berá ser rechazada. Supóngase primero que la hipótesis alternativa tiene la forma Ha: 0. Entonces un valor de x menor que 0 indudablemente no apoya a Ha. Tal x corresponde a un valor ne- gativo de z (puesto que x 0 es negativa y el divisor de /n es positivo). Del mismo modo, un valor de x que exceda de 0 por sólo una pequeña cantidad (correspondiente a z la cual es positiva aunque pequeña) no sugiere que H0 deberá ser rechazada a favor de Ha. El rechazo de H0 es apropiado sólo cuando x excede considerablemente de 0, es decir, cuando el valor de z es positivo y grande. En suma, la región de rechazo apropiada basada en el estadístico de prueba Z en lugar de X tiene la forma z c. Como se discutió en la sección 8.1, el valor de corte c deberá ser elegido para contro- lar la probabilidad de un error de tipo I al nivel deseado. Esto es fácil de lograr porque la distribución del estadístico de prueba Z cuando H0 es verdadera es la distribución normal es- tándar (es por eso que 0 se restó al estandarizar). El valor c de corte requerido es el valor crítico z que captura el área de la cola superior bajo la curva z. Como ejemplo, sea c 1.645, el valor que captura el área de cola 0.05 (z0.05 1.645). Entonces, P(error de tipo I) P(H0 es rechazada cuando H0 es verdadera) P(Z 1.645 cuando Z N(0, 1)) 1 (1.645) 0.05 Más generalmente, la región de rechazo z z tiene un probabilidad de error de tipo I . El procedimiento de prueba es de cola superior porque la región de rechazo se compone de só- lo valores grandes del estadístico de prueba. Un razonamiento análogo para la hipótesis alternativa Ha: 0 sugiere una región de rechazo de la forma z c, donde c es un número negativo adecuadamente seleccionado (x aparece muy debajo de 0 si y sólo si z es bastante negativo). Como Z tiene una distribu- ción normal estándar cuando H0 es verdadera, con c z da P(error de tipo I) . Esta es una prueba de cola inferior. Por ejemplo, z0.10 1.28 implica que la región de rechazo z 1.28 especifica una prueba con nivel de significación de 0.10. Por último, cuando la hipótesis alternativa es Ha: 0, H0 deberá ser rechazada si x está muy lejos a ambos lados de 0. Esto equivale a rechazar H0 si z c o si z c. Su- póngase que se desea 0.05. Entonces, 0.05 P(Z c o Z c cuando Z tiene una distribución normal estándar) (c) 1 (c) 2[1 (c)] Por consiguiente c es tal que 1 (c), el área bajo la curva z a la derecha de c, es 0.025 (¡y no 0.05!). De acuerdo con la sección 4.3 o la tabla A.3, c 1.96 y la región de rechazo X 0 /n 8.2 Pruebas sobre una media de población 295 c8_p284-324.qxd 3/12/08 4:17 AM Page 295
- 314. 296 CAPÍTULO 8 Pruebas de hipótesis basadas en una sola muestra z 1.96 o z 1.96. Con cualquier , la región de rechazo de dos colas z z/2 o z z/2 tiene una probabilidad de error de tipo I (puesto que el área /2 está capturada debajo de cada una de las dos colas de la curva z). De nueva cuenta, la razón clave para uti- lizar el estadístico de prueba estandarizado Z es que como Z tiene una distribución conoci- da cuando H0 es verdadera (estándar normal), es fácil de obtener una región de rechazo con probabilidad de error de tipo I mediante un valor crítico apropiado. El procedimiento de prueba en el caso I se resume en el cuadro adjunto y las regiones de rechazo correspondientes se ilustran en la figura 8.2. Se recomienda utilizar la siguiente secuencia de pasos cuando se prueben hipótesis con res- pecto a un parámetro. 1. Identificar el parámetro de interés y describirlo en el contexto de la situación del pro- blema. 2. Determinar el valor nulo y formular la hipótesis nula. 3. Formular la hipótesis alternativa apropiada. 4. Dar la fórmula para el valor calculado del estadístico de prueba (sustituyendo el valor nulo y los valores conocidos de cualquier otro parámetro, pero no aquellos de cualquier cantidad basada en una muestra). Hipótesis nula: H0: 0 Valor del estadístico de prueba: z Hipótesis alternativa Región de rechazo para la prueba de nivel Ha: 0 z z (prueba de cola superior) Ha: 0 z z (prueba de cola inferior) Ha: 0 o z z/2 o z z/2 (prueba de dos colas) x 0 /n 0 z z Región de rechazo: z z Región de rechazo: z z Área sombreada P(error de tipo I) Área total sombreada P(error de tipo I) 0 0 z /2 z /2 z Región de rechazo: z z /2 o z /2 Área sombreada /2 Área sombreada /2 Curva z (distribución de probabilidad del estadístico de prueba Z cuando H0 es verdadera) a) b) c) Figura 8.2 Regiones de rechazo para pruebas z: a) prueba de cola superior; b) prueba de cola inferior; c) prueba de dos colas. c8_p284-324.qxd 3/12/08 4:17 AM Page 296
- 315. 5. Establecer la región de rechazo para el nivel de significación seleccionado . 6. Calcular cualquier cantidad muestral necesaria, sustituir en la fórmula para el estadísti- co de prueba y calcular dicho valor. 7. Decidir si H0 debe ser rechazada y expresar esta conclusión en el contexto del pro- blema. La formulación de hipótesis (pasos 2 y 3) deberá ser realizada antes de examinar los datos. Un fabricante de sistemas rociadores utilizados como protección contra incendios en edifi- cios de oficinas afirma que la temperatura de activación del sistema promedio verdad