Unidad IV-ProgramaciónDinámica-VersiónFinal.pptx

Universidad Veracruzana
Facultad de Contaduría y Administración
Campus Coatzacoalcos
Programa Educativo:
Administración
Experiencia Educativa:
Métodos Cuantitativos
Presenta: M.C. Eunice Morales Reyes

Unidad IV.
Programación Dinámica

Programación dinámica
La programación dinámica es una técnica desarrollada por el
matemático Richard Bellman en la década de 1950.
La programación dinámica es una técnica para resolver problemas complejos
dividiéndolos en subproblemas más pequeños, resolviendo cada uno una
sola vez, y almacenando sus soluciones para no volver a calcularlas.
Se usa especialmente cuando un problema tiene:
• Subproblemas superpuestos (es decir, los mismos subproblemas se
repiten muchas veces).
• Estructura óptima (la mejor solución global se construye a partir de
soluciones óptimas de los subproblemas).

Principios Básicos
• Richard Bellman, principio de optimidad:
“Una política óptima tiene la propiedad de que
cualquiera que sea el estado inicial y la decisión inicial,
las decisiones restantes deben constituir una política
óptima con respecto al estado resultante de la primera
decisión.” (Véase Bellman, 1957, Cap. III.3.)
A M N O Z
SO St
t=0 t=T

De manera resumida…
Imagina que estás en un laberinto y quieres llegar al tesoro. Para llegar, tienes que
tomar varios caminos.
El mejor camino no solo es el primero que tomas, sino que cada paso que des después
también debe ser el mejor desde donde estés. Aunque cambies de lugar, tienes que
seguir eligiendo los mejores caminos para llegar al tesoro más rápido o sin perderte.
🔁 En pocas palabras: "Si quieres hacer lo mejor desde el principio, también tienes que
hacer lo mejor en cada parte del camino."
Una buena decisión al principio no sirve
de nada si después no seguimos
tomando buenas decisiones.

Principio matemático de la descomposición
Supongamos que para los Instantes to y tn, la información de un
sistema se puede expresar en So como un vector inicial y Sn como
un vector que representa el estado final.
Fn
SO Sn
tO tn
✅ Eso significa:
• En el tiempo t₀, tenemos un punto de partida: el estado inicial del sistema (llamado
S₀).
• En el tiempo tₙ, tenemos el punto de llegada: el estado final (llamado Sₙ).
• Ambos estados se pueden representar con vectores (como una lista de números que
describen al sistema en ese momento).

Principio matemático de la descomposición
f1 f2 fn-1 fn
. . .
Por tanto:
Sn = fn (fn-1 ( ……….. (f2 (f1 (SO ) ……….))
Es decir que el resultado de Sn del sistema no es nada más que
una composición de funciones interrelacionadas y conocidas de
la entrada SO .

Aplicaciones
• Problema de ruta más corta
• Asignación de recursos
• Determinación de políticas de inventarios
• Operación de reservaciones
• Selección de inversiones
• Determinación de políticas de expansión de
capacidad

Problema de Ruta
más corta
Programación Dinámica

Relación recursiva hacia atrás
Es importante definir:
• i = etapas
• Xi = estados de la etapa i (nodos)
• d(xi, xi+1) = distancia o costos del nodo xi al nodo xi+1
• fi (xi ) = distancia más corta o costo más pequeño en la etapa i
Definición de la ecuación recursiva:
fi (xi ) = Minimizar {d(xi, xi+1) +fi+1(xi+1)}
Proceso de retroceder desde el estado actual hacia el estado inicial tomando las decisiones
óptimas en cada etapa y considerando cómo llegar a este estado actual desde el estado anterior
de manera óptima.

Ejemplo 1: El problema de la diligencia (Prof. Harvey M Wagner)
“Un cazafortunas mítico de Missouri que decide ir al oeste a sumergirse en la fiebre del oro que surgió en California a
mediados del siglo XIX. Tiene que hacer el viaje en diligencia a través de territorios sin ley, donde existen serios peligros de ser
atacado por merodeadores. A pesar de que su punto de partida y su destino son fijos, tiene muchas opciones en cuanto a qué
estados – o territorios – debe elegir como puntos intermedios.
Para lograr el viaje se requieren de 4 etapas para ir desde el estado A, a su destino en el estado J, este cazafortunas es un
hombre prudente preocupado por su seguridad. Después de reflexionar un poco ideó una manera bastante ingeniosa para
determinar la ruta más segura. Se ofrecen pólizas de seguros de vida a los pasajeros. Como el costo de la póliza de cualquier
jornada en la diligencia está basado en una evaluación cuidadosa de la seguridad del recorrida, la ruta más segura debe ser
aquella cuya póliza represente el menor costo total”
¿Cuál es la ruta que minimiza el costo total de la póliza ?
7
A
B
C
D
E
F
G
H
I
J
2
4
3
4
6
3 2
4
4
1
5
1
4
6
3
3
3
3
4
Missouri California

Ejemplo 1: El problema de la diligencia
7
B
C
D
E
F
G
H
I
J
4
6
3 2
4
4
1
5
1
4
6
3
3
3
3
4 California
Descomponer el problema en etapas
A
2
4
3
Missouri
B
C
D
H
I
E
F
G
Primera etapa Segunda etapa Tercera etapa Cuarta etapa
𝑋1 𝑋2 𝑋3
𝑋4
𝑋5

J
3
4 California
Solucionar cada etapa:
H
I
La idea general para calcular la ruta más corta es calcular los costos
acumulativos más pequeños a todos los nodos terminales de una
etapa, y luego utilizarlos como dato de entrada a la etapa
subsiguiente.
Para este caso se empleará el desarrollo del problema con un
recorrido hacia atrás. Cuando el cazafortunas tiene una sola etapa
por recorrer (i=4), su ruta de ahí en adelante esta perfectamente
determinada por su estado actual (ya sea H o I) y su destino final, x5
= J.
x5 = J está conectado a H o I(x4 = H o I)
Cuarta etapa
x4
c(x4,x5) Solución óptima
x5= J f4(x4) x5 *
H 3 3 J
I 4 4 J
3
4
𝑋4 𝑋5

H
I
1
4
6
3
3
3
E
F
G
Tercera etapa
3
4
La Etapa 3 tiene dos nodos terminales (H e I).
x4 = H está conectado a E,F,G (x3 = E,F y G)
x4 = I está conectado a E,F,G (x3 = E,F y G)
X3
c(x3,x4) + f4(x4) Solución óptima
x4= H x4= I f3(x3) x4 *
E 1+3=4 4+4=8 4 H
F 6+3=9 3+4=7 7 I
G 3+3=6 3+4=7 6 H
𝑋3 𝑋4

La Etapa 2 tiene tres nodos terminales (E,F y G).
x3 = E está conectado a B,C y D (x2 = B,C y D)
x3 = F está conectado a B,C y D (x2 = B,C y D)
x3 = G está conectado a B,C y D (x2 = B,C y D)
7
B
C
D
E
F
G
4
6
3 2
4
4
1
5
Segunda etapa
4
7
6
X2
x3= E x3= F x3= G f2(x2) x3 *
B 7+4=11 4+7=11 6+6=12 11 E,F
C 3+4=7 2+7=9 4+6=10 7 E
D 4+4=8 1+7=8 5+6=11 8 E,F
𝑋2 𝑋3

A
2
4
3
Missouri
B
C
D
La Etapa 1 tiene tres nodos terminales (B,C y D).
x2 = B está conectado a A (x1 = A)
x2 = C está conectado a A (x1 = A)
x2 = D está conectado a A (x1 = A)
X1
x2= B x2= C x2= D f1(x1) x2 *
A 2+11=13 4+7=11 3+8=11 11 C o D
Primera etapa
11
7
8
SOLUCIÓN
Para gastar 11 dólares como costo total de la póliza se debe tomar el o los
siguiente(s) camino(s):
A
A
C
D
E H J
E H J
F I J
A D
𝑋1 𝑋2

Ejemplo 2: Problema de ruta más corta resuelto mediante
programación dinámica
Suponga que se desea seleccionar la ruta por carretera más corta entre dos
ciudades. La red que se muestra en la figura proporciona las posibles rutas entre la
ciudad de inicio en el nodo A y la ciudad de destino en el nodo G.
¿Cuál es la ruta que minimiza la distancia entre las dos ciudades?
12
A
B
C
D
E
F
G
7
8
5
8
9
7
13
9
6
Inicio
Final
Nota: Distancia en km
𝑋1 𝑋2 𝑋3 𝑋4

programación dinámica: Solución
Descomponer el problema en etapas
Primera etapa Segunda etapa Tercera etapa
E
F
G
9
6
Final
A
B
C
D
7
8
5
Inicio
12
8
9
7
13
E
F
B
C
D
𝑋1 𝑋2
𝑋3 𝑋4

programación dinámica: Solución
La idea general para calcular la ruta más corta es calcular la
distancia acumulativa más corta a todos los nodos terminales de
una etapa, y luego utilizarlos como dato de entrada a la etapa
subsiguiente.
Para este caso se empleará el desarrollo del problema con un
recorrido hacia atrás.
x4 = G está conectado a E o F(x3 = E o F) exactamente con una ruta
cada uno
x3
d(x3 , x4) Solución óptima
x4= G f3(x3) x4 *
E 9 9 G
F 6 6 G
Tercera etapa
E
F
G
9
6
Final
9
6
𝑋3 𝑋4

La Etapa 2 tiene dos nodos terminales (E y F).
x3 = E está conectado a B,C y D (x2 = B,C y D)
x3 = F está conectado a C y D (x2 = C y D)
X2
d(x2,x3) + f2(x2) Solución óptima
x3= E x3= F f2(x2) x3 *
B 12+9=21 ---- 21 E
C 8+9=17 9+6=15 15 F
D 7+9=16 13+6=19 16 E
Segunda etapa
12
8
9
7
13
E
F
B
C
D
9
6
𝑋2
𝑋3

La Etapa 1 tiene tres nodos terminales (B,C y D).
x2 = B está conectado a A (x1 = A)
x2 = C está conectado a A (x1 = A)
x2 = D está conectado a A (x1 = A)
X1
d(x1,x2) + f2(x2) Solución óptima
x2= B x2= C x2= D f1(x1) x2 *
A 7+21=28 8+15=23 5+16=21 21 D
Primera etapa
SOLUCIÓN
Para recorrer una distancia de 21 km se debe tomar el o los
siguiente(s) camino(s):
A D E G
A
B
C
D
7
8
5
Inicio
21
15
16
𝑋1 𝑋2

Ejercicio 1: Ruta más corta – Programación dinámica
Se trata de distribuir un producto de la ciudad A, a la ciudad M pasando por los puntos intermedios
K, T, L,.........,B. Las distancias en kilómetros se muestran en la figura a continuación.
Se trata de minimizar la distancia total, hallando la ruta más corta entre A y M.
12
A
L
K
J
T
R
B
M
15
16
14
16
14
17
14
11
24
17
16
19
Inicio
Final

Ejercicio 2: Ruta más corta– Programación dinámica
Se trata de distribuir los productos de la ciudad A, a la ciudad G, con el objetivo de disminuir los
gastos de transporte de la Empresa “Bimbo S.A. de C.V.” El costo en pesos del traslado entre las
diversas ciudades se definen en la figura a continuación. ¿Cuál es la ruta y el costo mínimo que
permita el traslado de productos de la empresa Bimbo de la ciudad A, a la G?
600
A
B
C
D
E
F
G
400
500
300
400
500
700
700
800
Inicio Final

Problema de
asignación
de recursos
Programación
Dinámica

Ejemplo 1: Modelo de la mochila (Knapsack problem)
• El problema representa un problema de asignación de recursos general
• El objetivo es determinar los artículos más valiosos que se pueden cargar en una
mochila.
• Se busca maximizar el rendimiento total. El problema general se representa como:
Es importante definir:
• W = peso máximo que soporta la mochila
• mi = cantidad de unidades del articulo i
• ri, = ingreso unitario del articulo i
• wi = peso del articulo i
Maximizar Z = r1m1 + r2m2 + … + rnmn
Sujeto a = w1m1 + w2m2 + … + wnmn <= W
m1, m2 , … mn enteros no negativos
Función recursiva:
•La etapa i está representada por el artículo i= 1, 2, … , n
•Las alternativas en la etapa i son la cantidad de unidades del artículo i, mi = 0,1, …,
•El rendimiento para m1 esr1m1
•El estado en la etapa i está representado por xi , el peso total asignado a las etapas (artículos) i , i + 1, … , y n. Esta definición
reconoce que el límite de peso es la única restricción que liga a todas las n etapas.
fi (xi ) = rendimiento máximo para las etapas i , i + 1, … , y n dado el estado xi
fi (xi ) = Max {ri mi + fi+1(xi - wi mi )}, i= 1, 2, … , n

• Un barco de 4 toneladas puede cargarse con uno o más de tres artículos. La
siguiente tabla da el peso unitario en toneladas y el ingreso unitario en miles de
pesos, para el artículo i. El objetivo es determinar la cantidad de unidades de cada
artículo que maximizará el rendimiento total.
Artículo i
Peso unitario wi
(toneladas)
Ingreso unitario ri
(miles de $)
1 2 31
2 3 47
3 1 14

Ejemplo 1: Modelo de la mochila (Knapsack problem) –
Solución
mi fi (xi ) = Max {ri mi + fi+1(xi - wi mi )}
f3 (x3 ) = Max {14 m3} m3 = 0, 1, 2,3,4
m3= = 4
x3
14 m3 Solución Óptima
m3 = 0 m3 = 1 m3 = 2 m3 = 3 m3 = 4 f3 (x3 ) m3
0 0 - - - - 0 0
1 0 14 - - - 14 1
2 0 14 28 - - 28 2
3 0 14 28 42 - 42 3
4 0 14 28 42 56 56 4

Solución
f2 (x2 ) = Max {47 m2} + f3(x2 –w2m2 )}
m2= = 1 m2 = 0, 1
x2
f2 (x2 ) = Max {47 m2} + f3(x2 –3m2 )} Solución Óptima
m2 = 0 m2 = 1 f2 (x2 ) m2
0 {47 m2 + f3(x2 –3m2 )}
47(0) + f3(0 –3(0))
0 + 0 = 0
- 0 0
1 0 + 14 = 14 - 14 0
2 0 + 28 = 28 - 28 0
3 0 + 42 = 42 47 + 0 = 47 47 1
4 0 + 56 = 56 47 + 14 = 61 61 1

Solución
f1 (x1 ) = Max {31 m1 + f2(x1 –w1m1)}
m1= = 2 m1 = 0, 1, 2
x1
f1 (x1 ) = Max {31 m1} + f2(x1 –2m1)} Solución Óptima
m1 = 0 m1 = 1 m1 = 2 f1 (x1 ) m1
0 31 m1 + f2(x1 –2m1)
31(0) + f2(0 –2(0))
0 + 0 = 0
- - 0 0
1 0 + 14 = 14 - - 14 0
2 0 + 28 = 28 31 + 0 = 31 - 31 1
3 0 + 47 = 47 31 + 14 = 45 - 47 0
4 0 + 61 = 61 31 + 28 = 59 62 + 0 = 62 62 2
Por lo tanto, la solución óptima es que el barco cargue dos unidades del artículo 1, y
cero unidades del artículo 2 y 3. El rendimiento asociado es de $ 62,000

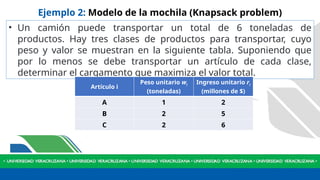
• Un camión puede transportar un total de 6 toneladas de
productos. Hay tres clases de productos para transportar, cuyo
peso y valor se muestran en la siguiente tabla. Suponiendo que
por lo menos se debe transportar un artículo de cada clase,
determinar el cargamento que maximiza el valor total.
Artículo i
Peso unitario wi
(toneladas)
Ingreso unitario ri
(millones de $)
A 1 2
B 2 5
C 2 6

Ejercicio 1: Modelo de la mochila (Knapsack problem)
• Una empresa desea enviar un paquete a un cliente en otra Ciudad.
Hay cuatro artículos que desea enviar, pero entre todos
sobrepasan los 5 kilogramos que considera puede cargar. El peso y
valor de cada artículo se muestran en la siguiente tabla
Artículo i
Peso unitario wi
(Kg)
Valor del articulo
Pesos
A 2 $300
B 3 $400
C 4 $500
D 5 $600
¿Qué artículos tendría que llevar para que el valor del paquete sea
máximo?

Ejercicio 2: Modelo de la mochila (Knapsack problem)
• Un camión puede transportar un total de 10 toneladas de
productos. Hay tres clases de productos para transportar, cuyo
peso y valor se muestran en la siguiente tabla. ¿Qué artículos se
deben poner en la mochila para maximizar el valor total de la
mochila?
Artículo i
Peso unitario wi
(Toneladas)
Valor del articulo
Miles de Pesos
A 3 $4
B 4 $5
C 5 $6

Ejemplo 3: Asignación de recursos humanos
El gerente de ventas de una editorial de libros de texto universitarios tiene seis agentes
de ventas que puede asignar a tres regiones distintas del país. Ha decidido que cada
región debe tener por lo menos un agente y que cada uno de éstos debe quedar
restringido a una de estas regiones, pero ahora quiere determinar cuántos agentes
debe asignar a las respectivas regiones con el fin de maximizar las ventas. La tabla da el
incremento estimado de las ventas en cada región (en las unidades apropiadas) si se le
asignan diferentes cantidades de agentes. Utilice programación dinámica para resolver
este problema, elabore las tablas normales con n=3, n=2 y n=1.
Agente de
Ventas
Región
1 2 3
1 40 24 32
2 54 47 46
3 78 63 70
4 99 78 84

Tabla decisional de Programación Dinámica
Regió
n 1
Regió
n 2
Regió
n 3
d2
d3
d1
R3 R2 R1
n =
3
n =
2
n =
1
S3 = 6 S2 = S3 – d3 S1 = S2 – d2
S0 = S1 – d1
Restricciones >= 1 >= 1 >= 1

Tabla 1: Región 3
n= 1
d1
S1
32 46 70 84
f1* d1*
1 2 3 4
Min 1 32 - - - 32 1
2 32 46 - - 46 2
3 32 46 70 - 70 3
Max 4 32 46 70 84 84 4
Tabla 2: Región 2
n= 2
d2
S2
24 47 63 78
f2* d2*
1 2 3 4
Min 2 56 - - - 56 1
3 70 79 - - 79 2
4 94 93 95 - 95 3
Max 5 108 117 109 11
0
117 2
fk = Rx + f* k-1
Función recursiva = (Retorno o costo) + (Optimo de la etapa anterior)
F(1,1) = 32 + 0 = 32
F(2,1) = 32 + 0 = 32
F(2,2) = 46 + 0 = 46
F(3,1) = 32 + 0 = 32
F(3,2) = 46 + 0 = 46
F(3,3) = 70 + 0 = 70
F(4,1) = 32 + 0 = 32
F(4,2) = 46 + 0 = 46
F(4,3) = 70 + 0 = 70
F(4,4) = 84 + 0 = 84
fk = Rx + f* k-1
F(2,1) = 24 + 32 = 56
F(3,1) = 24 + 46 = 70
F(3,2) = 47 + 32 = 79
F(4,1) = 24 + 70 = 94
F(4,2) = 47 + 46 = 93
F(4,3) = 63 + 32 = 95
F(5,1) = 24 + 84 = 108
F(5,2) = 47 + 70 = 117
F(5,3) = 63 + 46 = 109
F(5,4) = 78 + 32 = 110
Sk-1 = Sk - dk
Sk-1 = 2-1 = 1 E.A.
Sk-1 = 3-1 = 2 E.A.
Sk-1 = 3-2 = 1 E.A.
Sk-1 = 4-1 = 1 E.A.
Sk-1 = 4-2 = 2 E.A.
Sk-1 = 4-3 = 1 E.A.
Sk-1 = 5-1 = 4 E.A.
Sk-1 = 5-2 = 3 E.A.
Sk-1 = 5-3 = 2 E.A.
Sk-1 = 5-4 = 1 E.A.

Tabla 3: Región 1
n= 3
d3
S3
40 54 78 99
f3* d1*
1 2 3 4
6 157 149 157 15
5
157 1,3
Tabla resumen
Etapas Sk dk Sk-1 fk*
3 6 1 5 40
2 5 2 3 47
1 3 3 0 70
157
fk = Rx + f* k-1
F(6,1) = 40 + 117= 157
F(6,2) = 54 + 95 = 149
F(6,3) = 78 + 79 = 157
F(6,4) = 99 + 56 = 155
Sk-1 = 6-1 = 5 E.A.
Sk-1 = 6-2 = 4 E.A.
Sk-1 = 6-3 = 3 E.A.
Sk-1 = 6-4 = 2 E.A.
Decisión:
Región 1: 1 vendedor
Región 2: 2
vendedores
Región 3: 3
vendedores
Sobran 0 Vendedores
Ventas por 157
dólares
Tabla resumen
3 6 3 3 78
2 3 2 1 47
1 1 1 0 32
157
Decisión:
Región 1: 3
vendedores
Región 2: 2
vendedores
Región 1: 1 vendedor
Sobran 0 Vendedores
Ventas por 157
dólares
f3*
f3*

Ejemplo 4: Asignación de cargas a tiendas
El propietario de una cadena de tres supermercados compró cinco cargas de fresas
frescas. La distribución de Probabilidad estimada de las ventas potenciales de las fresas
antes de que se echen a perder difiere entre los tres supermercados. El propietario quiere
saber cómo debe asignar las cinco cargas a las tiendas para maximizar la ganancia
esperada.
Por razones administrativas, no quiere dividir las cargas entre las tiendas. Sin embargo,
está de acuerdo en asignar cero cargas a cualquiera de ellas.
En la siguiente tabla se proporciona la ganancia estimada de cada tienda al asignar
distintas cantidades de cargas. Utilice programación dinámica para determinar cuántas
cargas debe asignarse a cada tienda para maximizar la ganancia total esperada.

Tabla decisional de Programación Dinámica
Tiend
a 3
Tiend
a 2
Tiend
a 1
d2
d3
d1
R3 R2 R1
n =
3
n =
2
n =
1
S3 = 5 S2 = S3 – d3 S1 = S2 – d2
S0 = S1 – d1

Tabla 1: Tienda 1
n= 1
d1
S1
0 5 9 14 17 21
f1*
d1
*
0 1 2 3 4 5
Min 0 0 - - - - - 0 0
1 0 5 - - - - 5 1
2 0 5 9 - - - 9 2
3 0 5 9 14 - - 14 3
4 0 5 9 14 17 - 17 4
Max 5 0 5 9 14 17 21 21 5
Tabla 2: Tienda 2
n= 2
d2
S2
0 6 11 15 19 22
f2* d2*
0 1 2 3 4 5
Min 0 0 - - - - - 0 0
1 5 6 - - - - 6 1
2 9 11 11 - - - 11 1,2
3 14 15 16 15 - - 16 2
4 17 20 20 20 19 - 20 1,2,
3
Max 5 21 23 25 24 24 22 25 2

Tabla 3: Tienda 3
n= 3
Tabla resumen
3 5 0 5 0
2 5 2 3 11
1 3 3 0 14
25
Decisión:
Tienda 3: 0 cargas
Tienda 2: 2 cargas
Tienda 1: 3 cargas
Sobran 0 cargas
Ventas por 25 dólares
Tabla resumen
3 5 2 3 9
2 3 2 1 11
1 1 1 0 5
25
Decisión:
Tienda 3: 2 cargas
Tienda 2: 2 cargas
Tienda 1: 1 carga
Sobran 0 cargas
Ventas por 25 dólares
f3*
f3*
d3
S3
0 4 9 13 18 20
f3* d3*
0 1 2 3 4 5
5 25 24 25 24 24 20 25 0,2

Conclusiones
Frente a una serie de problemas cuyas soluciones pueden ser expresadas
recursivamente en términos matemáticos, posiblemente la manera más
natural de resolverlos es mediante un método recursivo. Sin embargo, el
tiempo de ejecución de una solución, normalmente de orden exponencial,
puede mejorarse mediante la programación dinámica.
Para resolver un problema se pueden hacer muchas divisiones y obtener
subproblemas independientes, de esta manera se puede llegar más fácil a
la solución del problema original, sin embargo no todos los problemas se
pueden resolver de esta forma, ya que cuando los subproblemas
obtenidos no son independientes sino que existe solapamiento entre ellos,
la solución no resulta ser eficiente por la repetición de cálculos que
conlleva. En estos casos es cuando la programación dinámica ofrece una
solución aceptable.

Referencias
• Bronson, R. (1993). Investigación de operaciones, México, Editorial McGraw-Hill. •
• Chediak, F. (2005). Investigación de operaciones, Colombia Ibagué, Editorial El Poira.
• Izar, J.(2012). Investigación de operaciones, México, Editorial Trillas.
• Roscoe, D.(1984). Modelos cuantitativos para administración, México, Editorial
Iberoamérica.
• Lieberman ,G.(2002). Investigación de operaciones. México, Editorial McGraw-Hill.
• Taha, H.(2008). Investigación de operaciones, México, Editorial Alfaomega.
• Winston, W. (2005). Investigación de operaciones, México, Editorial Thomson.

Unidad IV-ProgramaciónDinámica-VersiónFinal.pptx

Más contenido relacionado

Similar a Unidad IV-ProgramaciónDinámica-VersiónFinal.pptx (20)

Último (20)

Unidad IV-ProgramaciónDinámica-VersiónFinal.pptx