Coursmtallurgie 111011084551-phpapp02
- 1. DEPARTEMENT DE GENIE MECANIQUE Unité de Recherche Génie des Matériaux COURS DE METALLURGIE Souad BEN SLIMA Année Universitaire 2010 / 2011
- 2. TABLE DES MATIERES I- INTRODUCTION AUX MATERIAUX:……… …………………………..................................….6 A. LES DIFFERENTS ETATS DES SOLIDES…………...........................................................7 1. L’ETAT AMORPHE 2. L’ETAT MESOMORPHE 3. L’ETAT VIYTREUX 4. L’ETAT CRISTALLIN B.LES LIAISONS DANS LES SOLIDES CRISTALLINS ………………………………….. 9 1. LIAISONS PRIMAIRES 2. LIAISONS SECONDAIRES 3. RECAPITULTION C. LES MATERIAUX CRISTALLINS………………………………………………………...11 1. LES STRUCTURES CRISTALLINES 2. POSITION, DIRECTION ET PLAN ANATOMIQUES 3. LES DEFAUTS CRISTALLINS D. LES DIFFERENTS TYPES DE MATERIAUX ………………………………………..….21 1. QU’EST-CE QU'UN METAL? 2. LES MATERIAUX CERAMIQUES 3. LES POLYMERES 4. LES MATERIAUX COMPOSITES 5. LE CHOIX D'UN MTERIAU II- INTRODUCTION AUX ACIERS ET AUX FONTES …………………………………….........24 A. PROPRIETES DU FER PUR………………………………………………………………….....24 B. LE DIAGRAMME FER-CARBONE …………………………………………………………...25 1. DIAGRAMME Fe-Fe3C (Fer-Cémentite) 2. LES ACIERS 3. LES FONTES ORDINAIRES C. LES DIFFERENTES STRUCTURES DES ACIERS ET DES FONTES …………….. 36 1. LES STRUCTURES D'EQUILIBRE 2. LES STRUCTURES HORS EQUILIBRE
- 3. III- LES ELEMENTS D'ALLIAGE - DIFFERENTES CLASSES D'ACIERS ET FONTES A. CLASSEMENT ET ROLE DES ELEMENTS D'ALLIAGE……………………………………45 1. EFFET DES ELEMENTS D'ALLIAGE 2. ROLE DES DIFFERENTS ELEMENTS D'ALLIAGE B.DESIGNATION DES ACIERS …………………………………………………………………….49 1. ACIERS D'USAGE GENERAL NON ALLIES 2. ACIERS AU CARBONE 3. ACIERS ALLIES C. LES DIFFERENTES CLASSES D'ACIER………………………………………….51 1. Les aciers de construction (non destinés aux traitements thermiques) 2. Les aciers pour traitements thermiques 3. Les aciers à outils 4. Les aciers inoxydables D. LES DIFFÉRENTES FONTES ………………………………………………..57 1.Les fontes non alliées 2.Les fontes alliées IV. AMÉLIORATION DES PROPRIÉTÉS MÉCANIQUES DES MATÉRIAUX PAR INTERVENTION SUR LES DÉFAUTS CRISTALLINS A .DISLOCATIONS: ÉCROUISSAGE (STRAIN HARDENING) ……………….63 B. DÉFAUTS PONCTUELS: DURCISSEMENT PAR SOLUTION SOLIDE …66 V.AMELIORATION DES PROPRIETES MECANIQUE DES MATERIAUX METALLIQUES PAR TRAITEMENTS THERMIQUES DANS LA MASSE A.LES COURBES TTT……………………………………………………………………………70 B.LES COURBES TRC ………………………………………………………………………...…73 C.LES TRAITEMENTS THERMIQUES D'EQUILIBRE ……………………………………..76 1. LE RECUIT (ou RECUIT COMPLET) « FULL ANNEALING » 2. RECUIT D'HOMOGENEISATION « HOMOGENIZING» 3. RECUIT DE NORMALISATION « NORMALIZING » 4. RECUIT DE COALESCENCE OU SPHEROIDISATION « SPHEROIDIZING» 5. RECUIT DE DETENTE « STRESS RELIEVING» 6. RECUIT DE CRISTALLISATION « RECRYSTALLIZATION ANNEALING » D. LES TRAITEMENTS THERMIQUES « HORS D'EQUILIBRE» ………………………...80 1. LA TREMPE 2. LE REVENU E. LES ACCIDENTS DUS AUX TRAITEMENTS THERMIQUES ………………………....95
- 4. VI-COMMENT DURCIR LES MATERIAUX METALLIQUES SANS LES FRAGILISER...98 1. DURCISSEMENT PAR PRECIPITATION OU DURCISSEMENT STRUCTURAL 2. LES TREMPES ETAGEES 3. LES TRAITEMENTS THERMO-MECANIQUES VII-TRAITEMENTS THERMIQUES DES CERAMIQUES………………………………….106 A.LA DEVITRIFICATION DES VERRES-CERAMIQUES ………………………………...106 B.DURCISSEMENT PAR PRECIPITATION ………………………………………………...107 C. TRAITEMENT THERMIQUE DE DENSIFICATION ……………………………………107 D.TREMPES DES VERRES …………………………………………………………………….107 VIII-DURCISSEMENT SUPERFICIEL DES MATERIAUX …………………………………108 A.DURCISSEMENT MECANIQUE ……………………….. ………………………………….....108 1. LE GRENAILLAGE ET LE SABLAGE 2. LE CHOC LASER 3. LE GALETAGE B.TRAITEMENTS THERMIQUES DE SURFACE…………………………………………….…113 1. LA TREMPE SUPERFICIELLE 2. LA TREMPE PAR CONVERSION CHIMIQUE DE LA SURFACE 3. TRAITEMENTS DE REVETEMENT IX. ANNEXE: RAPPEL SUR LES DIAGRAMMES D'ÉQUILIBRE …………………...129 A. HISTORIQUE DES MÉLANGES B. LA NOTION DE SOLUTION SOLIDE ………………………………..… 129 C. INTRODUCTION AUX DIAGRAMMES D'ÉQUILIBRE………………. 134 LEXIQUE DES TERMES DE TRAITEMENTS THERMIQUES …………………………….154 REFERENCES……………………………………………………………………………………..161
- 5. PRÉAMBULE Ce cours de "Matériaux" est dispensé aux étudiants de Génie Mécanique. Les prés requis sont minimes mais nécessitent quand même une bonne base en thermodynamique. Ce cours est lui même un pré requis pour des enseignements tels que la "Technologie de Fabrication" (fonderie, déformation plastique, moulage, ...) et les Méthodes d'assemblage" (soudage, ...). Au deuxième chapitre les aciers et les fontes seront définies en détail à partir du diagramme Fer-carbone, puis répertoriés par classes d'utilisation au chapitre cinq. A partir du chapitre sept et jusqu'au chapitre neuf on répondra à la question comment améliorer les propriétés en service principalement des aciers et fontes qui restent les matériaux les plus utilisés dans l'industrie mécanique. Seront alors détaillés les traitements thermiques à mettre en œuvre pour améliorer des propriétés spécifiques du matériau : Résistance et dureté, ténacité, résistance à l'usure, etc. .... Le lecteur trouvera à la fin de ce fascicule un lexique des termes les plus utilisés en métallurgie, avec leur équivalent en anglais. La seule prétention de ce cours est d'être pour les étudiants une référence qui leur permettra de suivre plus aisément leur cours de matériaux. Les technologies progressent, particulièrement dans le domaine des matériaux : la nécessité d'une mise à jour continue des enseignements apparaît ici clairement. Cours de métallurgie, ENIT-Département de Génie Mécanique 5 Souad BEN SLIMA
- 6. I. INTRODUCTION AUX MATERIAUX Les matériaux ont toujours été d’une importance majeure pour la civilisation humaine. Les différentes époques de I’ humanité ont été marquées à chaque fois que l’homme maîtrisait un matériau : Age de la pierre, âge du cuivre, âge du bronze, âge du fer qui a abouti à notre époque marquée par la révolution industrielle de la fin du 19ème siècle. Il semblerait que le premier contact homme métal a eu lieu il y a à peu près onze mille ans en Anatolie (Turquie). Le premier métal qui fascina l'homme fut l’or, qui attira -et qui attire toujours- de par sa brillance. Cette découverte, comme celle du cuivre, ne nécessitait pas la connaissance de l'action du feu sur les métaux. En effet, ces deux métaux existent dans la nature à l'état natif et sont déformables à froid. L'extraction des métaux de leurs minerais est venue beaucoup plus tard. L'extraction du cuivre de son minerai (cuivre non natif, cette fois) date de 4300 avant J.C. et fut pratiquée pour la première fois par une tribu installée en Mésopotamie. L'âge du bronze fut inauguré au IIIe millénaire en Arménie (semble- t-il), la fusion du cuivre et de l'étain pour la production de cet alliage a été cependant le fruit du hasard. Des découvertes archéologiques récentes attesteraient que l’extraction du fer de son minerai daterait de 3500 avant J.C. par les anciens Egyptiens. L'âge du fer et du bronze se chevaucherait, et le fer ne prendra une place privilégiée qu’au 1er millénaire quand l'homme découvrit que celui ci avait des propriétés plus intéressantes (outils plus tranchants, etc. ...). Toutes ces découvertes faites par l’homme ont été fortuites et les progrès enregistrés purement empiriques. Le pas géant atteint au début de notre siècle a pu être exécuté quand les moyens d'analyse et d'observation ont évolués, et que les processus d1élaboration et de mise en forme ont commencé à être réfléchis et non pas intuitifs. Parmi les 106 éléments chimiques du tableau périodique, à peu près 80 sont métalliques. 70% des éléments constituant la terre sont des métaux. Parmi tous les éléments métalliques, 8 seulement sont produits et utilisés en grande quantité : Fer -----------------> 98% des métaux produits Aluminium ----------------> 0,8% Cuivre------------------------> 0,7% Pb,Zn,Ni,Ti,Mg --------------> 0,5% Ces derniers éléments sont destinés à des utilisations particulières : Le Ni et ses alliages sont utilisés à haute température pour la résistance à la corrosion Le Ti et ses alliages sont utilisés dans l’industrie aérospatiale. Cours de métallurgie, ENIT-Département de Génie Mécanique 6 Souad BEN SLIMA
- 7. A part la construction (mécanique et autres) qui absorbe une grande quantité de matériaux (principalement à base de fer), il existe d'autres domaines d'application qui en consomment en quantité non négligeable selon les propriétés requises : Propriétés électriques : Cu-Al, bonne conductivité électrique Propriétés magnétiques : Fe-Ni pour les matériaux magnétiques Résistance à la corrosion : Zn, Sn Pb Esthétique et grande valeur : Au, Pt D’autres éléments sont constituent des éléments d'addition très recherchés pour l'amélioration des propriétés des alliages courants tels que les aciers : Cr, Co, Nb, Mg, Mo, Ti, W, V, Zr, Sb, Ta, Be, Cd Le choix et l’utilisation d’un matériau dépend d’un certains nombres de propriétés : • Bonne résistance mécanique • Résistance acceptable à la corrosion • Mise en forme facile (usinabilité, mouillabilité, soudabilité) • Possibilité de recyclage • Coût et disponibilité raisonnables Les 3 premières constituent la base de l'étude des matériaux. l- Métallurgie chimique ou extractive 2-Métallurgie physique : La Métallurgie physique relie les manifestations ma- croscopiques (les propriétés en service) au comportement microscopique des mé- taux. Elle permet donc à l'homme de commander les phénomènes microscopiques (microstructure) pour avoir les propriétés macroscopiques désirées. L'accès à la microstructure des métaux est aujourd'hui possible grâce à l'avancement des tech- niques d'observation et d’analyse : microscopie optique, électronique, diffraction des RX, diffraction des électrons, ... Elle permet ainsi de relever les défis qui se posent dans certains domaines "difficiles" tels que l'aérospatiale, l'aéronautique, l'exploitation off shore, l'industrie nucléaire, ... A. LES DIFFÉRENTS ÉTATS DES SOLIDES A l'état solide, les matériaux peuvent avoir différentes structures atomiques qui déterminent leur comportement physique, mécanique, et chimique. Par structure atomique on désigne la répartition des atomes les uns par rapport aux autres et le type de liaisons qui assurent leur cohésion. Les solides peuvent exister sous 3 états différents : 1. L’état amorphe Les atomes ou ions constituant le solide ne présentent aucun ordre les uns par rapport aux autres. On peut assimiler la structure globale à celle d'un liquide figé. 2. L’état mésomorphe Cet état est rencontré dans les matériaux "exotiques" tels que les cristaux liquides où les chaînes d'espèces sont alignées. Cours de métallurgie, ENIT-Département de Génie Mécanique 7 Souad BEN SLIMA
- 8. 3. L’état vitreux C'est l'état rencontré dans les verres et qui est caractérisé par une certaine organisation à courte distance (entre les espèces qui forment une chaîne), mais pas d’ordre à longue distance (chaînes désordonnées les unes par rapport aux autres).La structure des verres doit être considérée sur 3 échelles: 1) l'échelle de 2 à 10 angströms, celle de l'arrangement atomique local, 2) l'échelle de 30 à quelques milliers d'angströms, celle de la sous microstructure, et 3) l'échelle du un au mm et plus, celle de la microstructure et la macrostructure. La température de transition liquide verre (Tt) est moins nette que celle de la V transition liquide-cristal (Tf) et est O caractérisée par une viscosité élevée du L matériau. U La structure du verre dépend de la M manière avec laquelle il a été obtenu. E Ainsi un verre formé à partir de l'état liquide est différent d'un verre formé à partir de la condensation sur un substrat TEMPERATURE froid, ou formé par électrodéposition. a) 4.L'état cristallin Dans un cristal, lors du passage de l'état liquide à l'état solide, les atomes se placent d'une manière ordonnée dans les 3 directions de l'espace, dans des sites bien définis On parle de réseau cristallin. Cet arrangement est périodique suivant les trois directions de l'espace x, y et z et défini par un volume élémentaire qu'on appelle maille et qui représente la structure du cristal. Réseau cristallin Maille élémentaire Figure I-1 : Réseau cristallin Cours de métallurgie, ENIT-Département de Génie Mécanique 8 Souad BEN SLIMA
- 9. Les liaisons qui assurent la cohésion des solides cristallins sont de deux types : primaires et secondaires. Les liaisons primaires assurent les liaisons entre atomes. Les liaisons secondaires entre molécules. B. LES LIAISONS DANS LES SOLIDES CRISTALLINS 1 Liaisons primaires : a) Liaisons ioniques Ce sont des liaisons qui sont assurées par l'attraction d'un ion positif et un ion négatif (Na+,Cl-, K+,CI-, ...). Dans un cristal, chaque ion positif est entouré de plusieurs ions négatifs et vice et versa. Type de force : électrostatique, transfert d'électrons d'un atome à l'autre, non directionnelle Energies de liaison : autour de 600kJ / mol Exemple : NaCI, MgO Conséquences : Matériaux ioniques durs et fragiles, mauvais conducteurs électriques et thermiques b) Liaisons covalentes La liaison qui forme la molécule de H2 est typique des liaisons covalentes. En effet, la formation d'une molécule de H2 correspond au remplissage de la couche 1s2 qui est une configuration plus stable que 1s (un seul atome d'hydrogène). Ce type de liaisons se retrouve dans les composés inorganiques. Dans un cristal, la liaison covalente est similaire à celle de H2, une paire d'électrons est concentrée dans l'espace entres les 2 atomes, chacun contribuant avec un électron. Une structure cristalline du type covalent peut être construite quand il y a répétitivité possible. Ceci se fait grâce à la nature directionnelle de la liaison covalente. Les cristaux covalents se forment par des atomes d'électronégativité similaire et dont la structure électronique est loin de celle des gaz rares (C, Ge, Si, Te, ...) Type de force : covalente, chaque atome participe avec un électron de valence Elle a lieu quand les deux éléments ont une très faible différence d'électronégativité, liaison fortement directionnelle Exemples : • CH4 : 4 électrons de valence, donc peut former 4 liaisons covalentes tétraédriques. Dans CH4, ces liaisons sont utilisées pour former la molécule. Il n'y aura pas d'électrons disponibles pour former une liaison covalente en plus, ainsi une structure cristalline ne peut pas se faire • C (diamant), SiC Energie de liaison : très faible, CH4 E= 8kJ/mol très élevée, Carbone E= 711kJ/mol Propriétés résultantes : dureté élevée, température de fusion élevée, conductivité électrique à basse température c) Liaisons métalliques La caractéristique la plus importante des métaux c'est leur conductivité électrique assurée par la mobilité de certains électrons qu'on appelle électrons de conduction. En première approximation, les métaux peuvent être considérés comme des ions positifs immergés dans un nuage uniforme d'électrons. La mobilité caractéristique des électrons peut être comprise en considérant les changements énergétiques qui ont lieu dans la configuration électronique lorsque des atomes se Cours de métallurgie, ENIT-Département de Génie Mécanique 9 Souad BEN SLIMA
- 10. mettent ensemble pour former un cristal. Les niveaux individuels d'énergie des électrons deviennent très proches et peuvent être considérés comme des bandes continues. Dans les métaux, les niveaux d'énergie permis se chevauchent et sont saturés en électrons. Ceci permet un mouvement relativement libre des électrons d'un atome à l'autre, sans nécessiter d'énergie supplémentaire très élevée comme il est le cas pour les diélectriques où l'énergie des électrons doit augmenter (d'une bande à l'autre) pour que la conduction soit possible. Type de liaison : Nuage d'électrons communs aux deux atomes, électrons de valence délocalisés, liaison non directionnelle Exemples : Les métaux Energies de liaison : Très variables EHg= 68 kJ/mol (Tf=-39°C) Ew= 850 kJ/mol (Tf=3410°C) Conséquences : Bons conducteurs électriques et thermiques 2. Liaisons secondaires a) Liaisons de van der waals Pourquoi une molécule polyéthylénique (polymères,Tf < 120 °C) et le carbone C diamant (Tf >3500 °C) qui présentent tous les deux des liaisons covalentes ont-ils des températures de fusion aussi différentes (donc énergies de liaison) ? La chaîne -(C2H4)n- présente en plus des liaisons covalentes (entre C-C et C-H), des liaisons dites secondaires qui assurent la cohésion de la longue chaîne moléculaire (structure spaghetti). Ces liaisons sont assurées par des dipôles et présentent des énergies très faibles (de l'ordre de 10kJ / mol). Cette faible énergie induit une faible cohésion de la molécule d’où une faible résistance et le point de fusion abaissé, c’est le cas de ce type polymère. Ce type de liaison peut se retrouver dans certaines argiles. Au contraire C diamant ne présente que des liaisons covalentes entre les différents atomes de C d'où la dureté est exceptionnellement importante et la température de fusion est très élevée. b) Liaisons hydrogène C'est un type de liaisons spécial mais assez commun dans les cristaux organiques. Ces liaisons sont dues à l’ion hydrogène qui assure le pont entre anions. La liaison hydrogène est ionique et ne peut se faire qu'avec des anions d'électronégativité élevée (0--, F-). Exemple : Eau, glace Ce type de liaisons est responsable de la polymérisation de HF et de certains acides organiques, ainsi que de la formation d'un certain nombre de polymères inorganiques (pour adhésifs et ciments). 3. Récapitulation Matériau Type de liaison TO de fusion (OC) NaCl Ionique 801 C (diamant) Covalente >3550 -(C2H4) n- Covalente et secondaire <120 Cu Métallique 1083 Ar Secondaire (dipôle induit) -189 H20 Secondaire (dipole permanent) 0 Cours de métallurgie, ENIT-Département de Génie Mécanique 10 Souad BEN SLIMA
- 11. Figure I-2 : Contribution des différents types de liaison pour les 4 catégories de matériaux (Rej: J.F.Shackelford, 1992) C. LES MATÉRIAUX CRISTALLINS Ils sont représentés par un modèle tripériodique caractérisé par des paramètres dits paramètres cristallins (a, b, c. Ce sont les distances entre les atomes les plus proches dans les trois directions de l'espace. On définit aussi α, β et γ les angles que font les 3 axes (respectivement oy.oz, ox.oz et ox.oy) entre eux. a, b, c et α, β, γ définissent un système cristallin (figure 3). Figure I-3 : Définition d'un système cristallin Dans la nature, il existe 7 systèmes cristallins différents à partir desquels sont définis 14 réseaux dits réseaux de Bravais. Systèmes cristallins a, b, c α,β,γ Réseau de Bravais Cubique a=b=c α=β=γ=90 primitif centré faces centrées Hexagonal a=b≠c α=β=90, γ=120 primitif Quadratique a=b≠c α=β=γ=90 primitif centré Orthorhombique a≠b≠c α=β=γ=90 primitif centré bases centrées faces centrées Rhomboédrique a=b=c α=β=y ≠90 primitif Monoclinique a≠b≠c α=β=90≠β primitif bases centrées Cours de métallurgie, ENIT-Département de Génie Mécanique 11 Souad BEN SLIMA
- 12. Triclinique a≠b≠c α≠β≠γ≠90 primitif 1. Les structures cristallines En général, les métaux et céramiques cristallisent dans l'un des systèmes suivants : Système cubique : * cubique centré : a=b=c a = (3 = y = 90° Exemple : Mo, W, Cr, V, Feα * cubique à faces centrées : Exemple : Ni, Cu, Ag, Au, Pt, Al, Feγ • Système hexagonal compact: a = b ≠c α = β = 90°, γ = 120° Exemple: Ti, Zn, Mg, Co. • Système quadratique : a = b ≠c α = β = γ = 90° Exemples : Sn,Mnγ Cours de métallurgie, ENIT-Département de Génie Mécanique 12 Souad BEN SLIMA
- 13. a, b et c sont exprimés en Angstrom : 1 .À = 10-8 cm Exemple : Fe α : a = 2,87 .À - Cu : a = 3,609 .À - Au : a= 4,078 À Remarque : Les dessins des réseaux ne représentent pas réellement le cristal, ces modèles sont éclatés pour bien visualiser la position des atomes. Il faut voir le cristal comme un empilement de billes ou de balles de poing pong. En réalité les atomes ne sont pas empilés de cette façon, mais les sphères peuvent être choisies pour représenter le volume dans lequel l'influence de l'atome s'étend. Le rayon de la sphère représentera donc la plus petite distance à laquelle un atome peut être approché, distance qui varie pour chaque type d'atome et qui est de l'ordre de l'Angstrom (figure contre) : Allotropie : Certains métaux ont plusieurs structures cristallographiques, chaque variété étant stable dans un domaine de températures défini. Exemple : Fer δ Feγ Feα d : CC Fer I __ I ______________ I ____________ I... γ :C.F.C. 1538°C 1394°C 912°C 20°C α: C.C. Ti (CF.C) Ti (H.C.) Titane I _______ ____ I ________ I Tfusion 882°C 20°C 2.Position, direction et plan atomiques a) Position d'un atome : Elle se repère suivant les trois directions de l'espace. Les positions dans un réseau sont exprimées par des fractions (ou multiple) des dimensions de la maille élémentaire Cours de métallurgie, ENIT-Département de Génie Mécanique 13 Souad BEN SLIMA
- 14. Figure I-4 : Position atomiques et directions cristallographiques Exemples : A (1/2, 1/2, 0) B (1/2, 1/2, 1/2) C (0, 1/2, 0) D (1, 2, 1 Toute translation suivant un axe multiplie la position suivant cet axe par le nombre de translation Exemple : C' = 2C C' (0, 1, 0) b)Direction cristallographique : Elle est notée entre crochets et est définie par la position interceptée par la ligne tracée à partir de l'origine. Les directions sont toujours définies par les plus petits nombres entiers. OB, par exemple, n'est pas [1/21/21/2], mais il faut multiplier par 2; c'est donc [111] (qui est équivalent à [222], [333]) Exemples : V1 [111] V2 [121] V3 [110] V4 [11 1] Les directions parallèles qui ne partent pas de la même origine ont les mêmes Indices. Exemple : V1 [111] V'l [11ī ] [111] et [11 ī et [1 ī 1] et [ī 11] appartiennent à la même famille de direction. La famille est désignée par <111> (<uvw>). Une direction est donc définie par : D = ut + vb + wc c) Plan atomique : Il est noté entre parenthèses, Il est défini par le multiple de l'inverse de la position interceptée par le plan suivant les trois directions de l'espace. Pourquoi l’inverse ? Cette convention a été adoptée pour s'affranchir de la notion d'infini. Cours de métallurgie, ENIT-Département de Génie Mécanique 14 Souad BEN SLIMA
- 15. Figure I-5 : Représentation des plans atomiques Les indices qui définissent le plan sont dit indices de Miller et désignés par (hkl) pour (210) : suivant ox : 1/2 suivant oy : 1 suivant oz : ∞ Ainsi le plan sera : (210) ∞ pour (020) : suivant ox : suivant oy : 1/2 suivant oz : ∞ Le plan sera : (020) mais une famille de plan est définie par le plus petit multiple entier des indices de Miller. Ainsi (020) ne peut pas définir une famille car (010) est plus petit. Une famille de plan est désignée entre accolade : {hkI} Remarque: Pour le système hexagonal deux notations peuvent être utilisé pour désigner les plans, la désignation classique déjà vue (indices de .Miller) ou la désignation qui fait intervenir un troisième indice: indices de Bravais-.Miller (hkil) tels que i= - (h+k) Cours de métallurgie, ENIT-Département de Génie Mécanique 15 Souad BEN SLIMA
- 16. Miler : (a1a2c) : (010) Bravais-Miller (a1a2a3c) : (0110) Figure I-6 : Désignation d'un plan atomique dans un système hexagonal d) densités atomiques planaires et linéaires 3. Les défauts cristallins Nous venons de décrire le cristal comme un arrangement continu et parfait des atomes. Cependant la structure réelle d’un cristal n’est pas parfaitement ordonnée suivant toute l’échelle. Elle est perturbée en certains points ou espaces, formant ainsi une discontinuité dans l'arrangement tridimensionnel. Ainsi, le métal réel ne sera plus un seul cristal continu et parfait, mais un ensemble de cristaux. Les défauts de continuité du réseau sont de 3 types : ponctuels, linéaires ou de surface. a)Les défauts ponctuels (1) Lacune : Les lacunes sont des vides à l’échelle atomique qui marquent l’absence d’un atome dans la structure. Elles sont en perpétuel mouvement du fait que chaque atome voisin tente de la combler en laissant sa place vide. (2) Interstitiel : Certains atomes en quittant leur site peuvent se placer entre les atomes régulièrement placés. L'insertion ou la disparition d'un atome crée des distorsions dans le réseau. Les défauts ponctuels sont à la base de la compréhension des phénomènes de diffusion à l'état solide. Ils expliquent la formation de solution solide A- B à partir d’éléments simples A et B selon un schéma d’interdiffusion comme le montre la figure 1-7, ou d'autres phénomènes de diffusion impliquent un déplacement atomique fig.I-8 et 1-9). Cours de métallurgie, ENIT-Département de Génie Mécanique 16 Souad BEN SLIMA
- 17. Figure I-7 : Schéma d’interdiffusion des matériaux A et B, rôle des lacunes Figure I-8 : Migration atomique par un mécanisme lacunaire Exemples : Ni dans Cu, Al203 dans Mg0 migration finale de l'atome interstitiel après n sauts Figure 1-9 : Migration atomique par un mécanisme Interstitiels Exemples : C dans Fe, N dans Fe b) Les défauts linéaires : Les dislocations comment se déforment les cristaux Les dislocations sont des défauts résultant d'un désordre dans l'arrangement des plans d'atomes. Voyons ce qui va se passer si une partie Cours de métallurgie, ENIT-Département de Génie Mécanique 17 Souad BEN SLIMA
- 18. d'un plan d'atomes (plutôt qu’un seul atome) est éliminée (ou ajoutée) : les atomes vont se réarranger au niveau de la partie manquante Dislocation (sur 3 dimensions on aura une ligne de dislocation) Figure I-10 : Effet d’une dislocation Sur 3 dimensions, le défaut va s'étendre comme une ligne perpendiculaire au plan du papier dans la zone indiquée (⊥) : cette ligne est appelée dislocation. Figure I-11 : Dislocation (vue en trois dimensions) Les dislocations existent dans tout cristal réel. La densité de dislocations dans un métal non déformé est de 104 à 108/cm2. La notion de dislocations est à la base de l'explication de la déformation plastique des matériaux : Déformation = mouvement des dislocations En effet, quand un matériau se déforme, ceci se fait par la propagation de la rupture des liaisons interatomiques (2), plutôt que par la rupture simultanée de toutes les liaisons (1) comme illustré en figures 12 et 13. L'énergie E1 nécessaire pour engager le processus (1) est plus élevée que E2, l'énergie de déformation suivant le processus (2). Cours de métallurgie, ENIT-Département de Génie Mécanique 18 Souad BEN SLIMA
- 19. Figure I-12 : Déformation d’un matériau sous contrainte E (1)> E (2) Les difficultés de se mouvoir sans N'est-il pas plus facile de un mécanisme de déplacement des dislocations glisser en se "dislocant" ? Figure I-13 : déformation : mécanisme de glissement des dislocations (Rej : WC. Moss, Ph.D., université de Californie, 1979) Cours de métallurgie, ENIT-Département de Génie Mécanique 19 Souad BEN SLIMA
- 20. Figure I-14 : Le glissement ou déplacement des dislocations est plus facile en (2) Suivant les plans à forte densité atomique (distance de glissement Plus faible) qu'en (1) La déformation d’un matériau correspond à un glissement (ou déplacement) de dislocations. Si les dislocations se déplacent facilement, la déformation du matériau considéré est facile. Les dislocations ne se déplacent pas n'importe comment. Elles vont choisir le chemin le plus court et donc le moins énergétique. Comme le montre la figure 14, les dislocations préfèrent le glissement suivant des plans denses c’est à dire les plans qui contiennent le plus d'atomes. Une augmentation de la densité de dislocations dans un matériau conduit au dur- cissement de celui ci. Ainsi, l'existence des dislocations explique pourquoi les ma- tériaux sont résistants, ductiles ou tenaces, etc. ... Les dislocations sont observables au Microscope Electronique à Transmission (grande résolution) c) Les défauts plan : Les joints de grains Le métal réel est une multitude de petits cristaux parfaits orientés différemment. On dit qu'il est polycristallin. Comme dans un morceau de sucre, les cristaux ne sont pas physiquement séparés. La frontière entre les différents cristaux est des surfaces qu'on appelle joints de grains. Les grains se forment durant la solidification du métal. Les joints de grains peuvent se déformer ou se déplacer sous l'action d'une force mécanique ou de la température. Ce sont des zones plus énergétiques que le grain du fait de l'arrangement spécial des atomes à ce niveau (figure 15). La taille de grain d'un métal a une influence sur les propriétés de ce dernier. Cours de métallurgie, ENIT-Département de Génie Mécanique 20 Souad BEN SLIMA
- 21. Figure I-15 : Arrangement des atomes au niveau du joint de grain Un grain est un volume polyédrique. Quand on observe la section d'un métal au microscope optique, on observe une structure granulaire (figure16). Figure I-16 : Structure granulaire des métaux Quand ces grains (ou cristaux) ont une taille de l'ordre de 0,1 mm chacun, ceci correspond à une dimension considérable à l'échelle atomique (environ un million d'atomes). En fait, cette taille varie entre 10 µm et 10 mm. Dans lcm3 de métal, on peut trouver 10 millions de grains. D. LES DIFFÉRENTS TYPES DE MATÉRIAUX Éléments constituants des céramiques par combinaison avec un métal (+ Si et Ge) Cours de métallurgie, ENIT-Département de Génie Mécanique 21 Souad BEN SLIMA
- 22. Figure 1-17 : Contribution des éléments chimiques dans la constitution des matériaux Les matériaux sont définis à partir de composition d'éléments simples. D'après le tableau de classification des éléments nous pouvons sortir les différentes classes de matériaux. 1. Définition d’un métal Les métaux sont des solides cristallins, ceci ne veut pas dire qu'ils sont transparents comme le verre-cristal, non les métaux ne le sont pas. Dans un cristal, lors du passage de l'état liquide à l'état solide, les atomes se placent d'une manière ordonnée dans les 3 directions de l'espace. On peut donc représenter un cristal par l'arrangement des atomes dans un espace tridimensionnel. Mais ceci est une simplification. Les atomes ne sont pas fixes, ils vibrent autour d'une position moyenne. L'amplitude augmente avec la température mais elle est en général de l'ordre du 1/10ème du diamètre de l'atome (il y a de la vie dans les métaux !). Le métal est défini comme suit : C'est un assemblage d'ions positifs immergés dans un nuage d'électrons, les électrons de ce nuage étant libres. Les cristaux métalliques sont liés entre eux par des forces d'attraction électrostatiques entre ces électrons libres (-) et les ions métalliques (+); ceci est appelé liaison métallique (voir chapitre précédent). Les électrons libres confèrent aux métaux leurs principales propriétés. Les propriétés particulières qui caractérisent l'état métallique sont : • Ce sont de bons conducteurs d'électricité et de chaleur • Ils sont susceptibles d'émettre des électrons sous l'effet de l'échauffement • Ils sont solides à la température ambiante (sauf Hg) • Leur mise en forme est relativement facile (bonne plasticité) • Ils sont opaques (bonnes aptitudes à la réflexion) Les matériaux métalliques sont un mélange chimique de métaux ou de métaux et métalloïdes (où le métal est majoritaire). Nous citerons les plus connus : l'acier et la fonte (Fe+C), le bronze (Cu+Sn), le laiton (Cu+Zn). 2. Les matériaux céramiques Les nouveaux céramiques sont, par opposition avec les céramiques traditionnelles (poterie de Nabeul), des carbures, oxydes et/ ou nitrures de métaux. Les plus typiques sont Si02, Ab03, SiO2. Ce sont des matériaux durs, fragiles, résistants à haute température (réfractaires), isolants de l'électricité et de la chaleur et extrêmement résistants à l'environnement (corrosion). Ils peuvent être cristallin, non cristallin ou un mélange des deux. 3. Les polymères On les appelle communément des plastiques mais il est plus correcte de les appeler polymères ce qui veut dire qu'ils sont constitué de plusieurs (poly) -mères (molécule d'hydrocarbures comme C2H4). C’est donc des composés organiques dont les éléments principaux sont le C et le H. lorsqu'un élément supplémentaire intervient une nouvelle famille naît. C, H exp. polyéthylène C, H, O exp. acryliques, polyesters C, H, N, O exp. nylons C, H, F exp. fluoroplastiques C, H, Si exp. Silicones Cours de métallurgie, ENIT-Département de Génie Mécanique 22 Souad BEN SLIMA
- 23. C, H, CI exp. C, H, CI : PVC Ce sont des matériaux de faible résistance mécanique, de faible densité et d'une grande plasticité. Leur structure est généralement non cristalline. 4. Les matériaux composites Comme leur nom l'indique, ces matériaux sont une composition des matériaux précédemment cités. L'exemple type courant du composite est le béton (Ciment + acier) ou le bois qui est constitué de résine (polymère naturel) et de fibres de cellulose. Plus récemment, on parle assez souvent de« fibres de verre» qui sont en réalité des fibres de verres noyées dans une matrice polymères (céramique+polymère). C'est donc généralement une matrice d'un matériau donné dans lequel seront noyés soit des fibres oit des agrégats d'un autre matériau. Ainsi ces matériaux combinent les propriétés des matériaux qui les constituent. Les fibres de verre noyées dans un polymère donnent un matériau qui a la résistance du verre et la flexibilité du polymère. Cependant ces matériaux auront des propriétés mécaniques fortement anisotropies (dépendent du sens de l'effort appliqué). Cours de métallurgie, ENIT-Département de Génie Mécanique 23 Souad BEN SLIMA
- 24. II. INTRODUCTION AUX ACIERS ET AUX FONTE La métallurgie du fer a été pour l'homme une aventure. L'homme primitif a longtemps travaillé le fer météorique avant d'apprendre à utiliser les minerais ferreux. Il le travaillait avec des outils en pierre (silex). Du fait de la rareté du fer météorite, celui ci était considéré aussi précieux que l'or sinon plus. Il avait aussi une valeur mystique puisqu'il venait du ciel, et pour plusieurs anciennes civilisations, l'étymologie du mot qui désigne le fer veut dire "métal du ciel» : Sumérien "An-Bar" (ciel-feu, métal céleste), Assyrien "Parzillu" (grand métal), Égyptien "Biz-n.pt" (métal du ciel), Grec "Sideros" (Sidus,-eris : étoile). L'âge du fer proprement dit n'a pas débuté avec le fer météorique, mais avec l'exploitation du minerai de fer terrestre. Les historiens fixent vers 1200-1000 avant J.C. les débuts de la métallurgie industrielle, lorsque l'homme a découvert comment faire fondre le minerai pour extraire le métal. Ceci a donné lieu plusieurs siècles plus tard (à la fin du 19ème siècle) à la naissance et la promotion de l'industrie lourde dont le pilier principal était la sidérurgie. Depuis, les matériaux métalliques les plus utilisés en construction mécanique sont les aciers. Ce sont les matériaux de base des pays industrialisés. Ceci est dû à plusieurs facteurs; d'abord l'abondance du fer (élément principal constituant l'acier) sur notre planète, ensuite la diversité des propriétés qu'ils peuvent avoir suivant les éléments d'alliage qu'on y ajoute ou les traitements qu'ils subissent. Cette diversité élargit considérablement l'éventail des utilisations des aciers. C'est pour cette raison qu'en métallurgie, on commence toujours par l'étude des aciers qui sont définis comme étant des alliages à base de fer contenant moins de 2 % en carbone. Leur étude commence donc par la connaissance du diagramme d'équilibre qui leur est associé : Le diagramme Fer Carbone. A. PROPRIÉTÉS DU FER PUR 1- Le fer pur existe sous 2 formes allotropiques : • T < 910 °C et 1394 °C < T< 1538 °C Le fer α une structure cubique centrée et est noté fer α a pour les basses températures et fer δ pour les hautes températures. • 910 °C <T < 1394 °C Le fer α une structure cubique à faces centrées, il sera noté fer y. 2- La température de fusion du fer : Tf = 1538°C 3- Le point Curie : T= 770 °C; à cette température, le fer perd ses propriétés magnétiques. Il passe de l'état ferromagnétique à l'état paramagnétique vers les hautes températures. 4- Densité du fer (20 °C) : d = 7,87 d (Ti) = 4,53 d (AI) =2,69) 5- Propriétés mécaniques du fer pur : Cours de métallurgie, ENIT-Département de Génie Mécanique 24 Souad BEN SLIMA
- 25. • RM (charge à la rupture) : 18 à 30 daN/mm2 • RE (limite d'élasticité) : 10 à 17 daN/mm2 • HB (dureté Brinell) : 45-55 • A % allongement) : 40-50 Le fer n'est que très rarement utilisé à l'état pur, d'abord son obtention coûte très cher, ensuite il a de meilleures propriétés quand il est allié. Le fer est extrait de son minerai pour l'obtention de 2 alliages principaux : • La fonte : % en carbone > 2 • L'acier : % en carbone < 2 Le principal élément d'alliage des fontes et aciers est donc le carbone. Jusqu'en 1771, le rôle du carbone dans le fer était ignoré et tous les progrès étaient purement empiriques. Chez les artisans, ce rôle est encore méconnu. Le professeur Cyril Stanley Smith (Métallurgiste très connu) dans" The discovery of Carbon in Steel" (Technology and culture, vol. V, N°2, 1964) raconte qu'il a demandé un jour de 1962 à un très habile et réputé forgeron d’Iran : " Quelle est la différence entre le fer et l’acier ?" et celui ci lui répond : " Fer et Acier sont 2 espèces aussi différentes que le saule et le chêne" (Encyclopeadia Britannica, Ed.1981) B. LE DIAGRAMME FER-CARBONE Le diagramme Fe-C est une carte qui peut être utilisée pour suivre les séquences de solidification des alliages Fe-C et pour savoir ce qui se passe au cours de certains types de traitements thermiques. Ce diagramme peut être considéré comme un guide, cependant la plupart des aciers contiennent, en plus du carbone, d'autres éléments d'alliage qui modifient la position de certaines courbes. Par ailleurs, le diagramme Fe-C ne peut être utilisé que dans les conditions d'équilibre (refroidissement à vitesse très faible). Or plusieurs traitements thermiques se font dans des conditions hors d'équilibre. Pour les alliages Fe-C, on distingue 2 types de diagramme : le diagramme métastable Fe-Fe3C et le diagramme stable Fe-C graphite (figure II-3). Le graphite est une forme du carbone plus stable que F e3C. F e3C peut se décomposer en graphite. Cependant ce phénomène n'a jamais lieu dans les aciers. Il a, par contre, lieu dans les fontes. C'est pour cette raison que pour les aciers, c'est le diagramme Fe-Fe3C qui est exclusivement utilisé, alors que la technologie des fontes est beaucoup plus basée sur le diagramme Fe- Cgraphite. 1. Diagramme Fe-Fe3C (Fer-Cémentite) Le diagramme comprend 3 paliers caractéristiques qui correspondent à 3 types de transformation : • T = 1495 °C : Transformation péritectique • T = 1148 °C : Transformation eutectique • T = 727 °C : Transformation eutectoïde On distingue aussi 5 phases différentes (5 domaines monophasés) : • La phase liquide vers les hautes températures Cours de métallurgie, ENIT-Département de Génie Mécanique 25 Souad BEN SLIMA
- 26. • La phase solide δ qui est une solution solide du carbone dans le fer Ô, cette phase est appelée ferrite δ . La solubilité maximale du carbone dans cette phase est de 0,1 % et correspond à la température T=1495 °C. Comme le fer la fer δ est cubique centrée • La phase solide γ qui est une solution solide du carbone dans le fer γ, elle est dite Austénite γ. La solubilité maximale du carbone dans cette phase est de 2,11 % à T=1148 °C Comme le fer γ, l'austénite est C.F.C. • La phase solide a qui est une solution solide du carbone dans le fer α, elle est dite ferrite α. La solubilité maximale du carbone dans cette phase est de 0.0218 à T=727 °C Comme le fer αla ferrite α est CC • Le composé défini Fe3C, dit cémentite dont la composition en carbone est de 6,67%. La structure cristallographique de Fe3C est orthorhombique. On note d'une manière particulière certains points de transformation : • AC1 : γ------> α + Fe3C (727 °C) • AC3 : γ ------> α (début de transformation de γ en α au chauffage et AR3 au refroidissement) • ACm :γ ------> Fe3C (début de transformation de y en Fe3C au chauffage et ARm au refroidissement) Nous allons nous intéresser à la partie du diagramme qui correspond aux aciers : % C < 2,11, puis celle des fontes % C > 2,11 2. Les Aciers Les aciers sont des alliages Fer-Carbone qui contiennent moins de 2% en masse de carbone. Deux types de transformation entrent en jeu : la solidification (transformation liquide-solide) et la transformation en phase solide. a) Transformation Liquide- Solide Elle concerne la partie supérieure du diagramme (figure II-1) qui présente un palier péritectique; 3 cas se présentent : Cas 1 : Au cours de la transformation péritectique, c'est le liquide qui disparaît : Liquide + δ------> γ Cas 2 : La fin de la transformation est marquée par la disparition des 2 phases L et δ. Liquide + δ ------>γ Cas 3 : C'est δ qui disparaît à la fin de la transformation péritectique. Liquide + δ ------>γ Cours de métallurgie, ENIT-Département de Génie Mécanique 26 Souad BEN SLIMA
- 27. Figure II-1 : Partie supérieure du diagramme d’équilibre binaire Fer-C Cours de métallurgie, ENIT-Département de Génie Mécanique 27 Souad BEN SLIMA
- 28. ACIERS : TRANSFORMATIONS SOLIDE-SOLIDE b) Transformation Solide-Solide C'est des transformations très importantes à connaître étant donné que tous les traitements effectués sur les pièces métalliques après élaboration se font à l'état Cours de métallurgie, ENIT-Département de Génie Mécanique 28 Souad BEN SLIMA
- 29. solide. La partie du diagramme Fe-Fe3C concernée est la partie inférieure qui présente un palier eutectoïde à 727°C (figure II-2). Figure II-2 : Partie "Aciers" du diagramme Fer-Cémentite Remarque : - SE courbe de limite de solubilité du C dans le ferγ en ce point il y a précipitation du C du fer γ sous forme de Fe3C. - MN courbe de limite de solubilité du C dans le fer α : en ce point il y a précipitation du C du fer a sous forme de Fe3C. Nous distinguerons 2 types d'acier suivant le % en carbone. Ils seront repérés par rapport au point eutectoïde E (0,77%C) : (1) Les aciers hypoeutectoïdes (0/0218 < %C < 0/77) Remarque : Quand %C augmente, AC3 diminue * Processus de transformation d'un acier de composition Xl : en AC3 : début de la transformation γ ------>α pro + y res Cours de métallurgie, ENIT-Département de Génie Mécanique 29 Souad BEN SLIMA
- 30. en AC1 : transformation eutectoïde : γ res------> (α + F e3C) (α + Fe3C) est un composé biphasé nommé perlite, il se présente sous forme de lamelles alternées de α et F e3C. γ res :γ résiduelle α pro : α proeutectoïde (formée avant le palier eutectoïde) * Qualité du produit final : α proeutectoïde + perlite (α + Fe3C) α proeutectoide de α+ Fe3 C = composé eutectoide = perlite * Quantité : α proeutectoïde : à T = 727°C + ε mα _= (0,77 - Xl) m (0,77 - 0,0218) perlite : % γres (à T=727°C+ ε) = % perlite (à T=727°C- ε) = (Xl - 0,0218) (0,77 - 0,0218) = m perlite m Quand Xl augmente, % α diminue et % perlite augmente * Que se passe-t-il au cours du refroidissement ? Quand T diminue, la solubilité du carbone dans γ diminue. Au point AC3, γ se transforme en α moins riche en carbone, α se formera au niveau des joints de grainγs de γ . Cette transformation se poursuit quand la température diminue. γ est alors enrichie en C (courbe AC3-E'). Quand la teneur en carbone atteint 0,77 (E’), la transformation eutectoïde a lieu à température constante (v=0) jusqu'à l'épuisement de. γ (2) Les aciers hypereutectoïdes : 0,77 < %C < 2,11 Remarque : Quand %C augmente, A3 augmente. Cours de métallurgie, ENIT-Département de Génie Mécanique 30 Souad BEN SLIMA
- 31. * Processus de transformation d'un acier de composition X2 : en A3 : début de la transformation γ ------> Fe3CII + γres en AC1 : transformation eutectoïde γres ------> (α + F e3CIII) * Qualité du produit final : F e3CII + (α + Fe3CIII) = perlite * Quantité : Fe3CII (à T = 727°C + ε) mFe3C = (X2 - 0,77) m (6,69 - 0,77) perlite : % γ res (à T=727°C+ε) = % perlite (à T=727°C-ε) mγres = 1- mFe3C m m _ (6,69 - X2) (6,69 - 0,77) = m perlite m Quand X2 augmente, %Fe3CII augmente et % perlite diminue. Remarques : 1- La teneur du constituant proeutectoïde est beaucoup plus importante dans le cas des aciers hypoeutectoïdes que dans celui des aciers hypereutectoïdes, et ceci pour un écart identique du point eutectoïde. I____________ I __ I __ I __ // _____________ I 0' N E’ N' EN==E'N' Acier hypoeutectoïde : α proeutectoïde = Acier hypereutectoïde : ' Fe3Cproeutectoïde= Or E'Q' (6,69-0,77=5,92) est très supérieur à O'E'(O, 77-0,0218=O, 7482) donc apro»Fe3Cpro. Ceci se manifeste au niveau de l'aspect micrographique des structures des aciers; en effet, les aciers hypereutectoïdes sont toujours principalement constitués de perlite. 2- Pour X = 0,77%, la structure est 100% perlitique, il en est de même pour les teneurs très proches de 0,77. Cours de métallurgie, ENIT-Département de Génie Mécanique 31 Souad BEN SLIMA
- 32. α+ Fe 3C =composé eutectoide = perlite 3- Pour X < 0,0218 (ou proche), la phase dominante est la ferrite avec quelques précipités de cémentite aux joints de grains. 3. Les fontes ordinaires Les fontes sont des alliages Fe-C dont le % en C va de 2 à 6. Pratiquement les fontes contiennent de 3 à 4% en C. On désigne par fontes ordinaires des fontes qui n'ont pas subi de traitements particuliers après coulée (mis à part les traitements thermiques ordinaires). Leur solidification est donnée par la partie droite du diagramme d'équilibre. Quand le carbone y existe à l'état libre (graphite) on parle de fontes grises et on se réfère au diagramme Fe- C stable, dans le cas où il apparaît à l'état combiné avec le fer (Fe3C), on parle de fontes blanches et on se réfère au diagramme Fe-Fe3C métastable. La caractéristique de ces fontes par rapport à tous les autres alliages Fe - C c'est leur faible coût. a) Les fontes grises Elles contiennent le carbone sous forme de graphite (figure II-3). Le % en carbone des fontes grises se situe autour de 4,3%, celui de l'eutectique, ceci entraîne une bonne coulabilité et une faible tendance à la retassure (vides dans le lingot dus au phénomène de retrait au passage de l'état liquide à l'état solide). Cours de métallurgie, ENIT-Département de Génie Mécanique 32 Souad BEN SLIMA
- 33. Figure II-3 : Aspect microstructural des fontes grises. (a) Aspect des lamelles de graphite, (b) fonte grise ferrito-perlitique : les lamelles de graphite sont entourées d'auréoles blanches de ferrite, le fond sombre est de la perlite. Le graphite donne aux cassures un aspect gris d'où le nom fontes grises. On distingue les fontes grises hypoeutectiques (%C< 4,3) et les FG hypereutectiques. Figure II-4 : Diagramme Fe-C pour les fontes, en pointillés diagramme métastable et en ligne continue diagramme stable (1)Les fontes hypoeutectiques (2 < %C < 4,3) Processus de transformation depuis l'état liquide : TE <T<To : solidification en cours L------> Cγ T=T E : transformation eutectique L ------> (γ +C graphite) eutectique : Ledéburite (le carbone y est sous forme de lamelles) TE ’ <T<TE : l'austénite va laisser déposer du graphite et son % en carbone va diminuer en suivant la ligne OE'. Dans la pratique, γ est tellement appauvrie en carbone que le dépôt de graphite va donner place à une précipitation de Fe3C avant la température de l'eutectoïde (727°C) et la fonte continuera à refroidir suivant le diagramme Fe-Fe3C. Cours de métallurgie, ENIT-Département de Génie Mécanique 33 Souad BEN SLIMA
- 34. T=TE’ : transformation eutectoïde. Seule γ se transformera à cette température selon la réaction γ ------> α + Fe3C. Trois types de fonte peuvent se former à la suite de ce processus : - fonte hypoeutectique hypereutectoïde : graphite lamellaire + F e3C proeutectoïde + perlite - fonte hypoeutectique eutectoïde : graphite lamellaire + perlite - fonte hypoeutectique hypoeutectoïde : graphite lamellaire + ferrite proeutectoïde + perlite La formation de l'une ou l'autre de ces fontes dépend de la composition en C et Si ainsi que de la vitesse de solidification (déterminée par l'épaisseur du moulage). On peut savoir en fonction du carbone équivalent (C+1/3Si) et de l'épaisseur du moule la structure qu'on obtiendrait et ceci à partir du diagramme de SIPP (figure II-5). Ainsi apparaît la nécessité pour les fontes grises de choisir la nuance en fonction du dessin de la pièce. Figure II-5 : Diagramme de SIPP définissant la microstructure de la matrice d'une fonte grise en fonction de l'épaisseur du moule (2) Les fontes hypereutectiques (%C > 4,3) Processus de transformation depuis l'état liquide : TE <T<T’o : solidification en cours L------> Cgraphite Le reste du processus se fait de la même manière que les fontes hypoeutectiques. (3) Propriétés des fontes grises Les fontes grises eutectoïdes (ou perlitiques) ont la meilleure tenue à l'usure et la meilleure résistance mécanique. C'est pourquoi les FG industrielles sont définies comme ayant un carbone équivalent voisin de 4%. Il est important de noter que les structures souhaitées pour les FG sont obtenues à Cours de métallurgie, ENIT-Département de Génie Mécanique 34 Souad BEN SLIMA
- 35. l'état brut de coulée; en général aucun traitement thermique ultérieur n'est souhaité sauf dans le cas des trempes superficielles. Les FG sont d'une manière générale faciles à usiner (dureté : 170 à 270 HB), mais elles ont une ténacité médiocre à cause du graphite. Par ailleurs ce sont les fontes les plus utilisées pour les bâtis de machine du fait de leur grande capacité d'amortissement des vibrations et leur tenue au frottement (favorisée par la présence de graphite qui est un excellent lubrifiant). De plus, leur charge à la rupture par compression est de 3 À 5 fois plus grande que celle à la traction. Désignation : Ft Rm (daN/mm2), exemple : Pt 10 fonte grise dont Rm=10 daN/mm2. b) Les fontes blanches Le carbone y existe à l'état de Fe3C. Le Fe3C donne à la cassure un aspect blanc et brillant d'où le nom de fontes blanches. La formation de la fonte blanche est favorisée par certains facteurs : - la teneur en carbone, plus elle est élevée (vers l'eutectique), moins la formation est probable - la composition ne doit pas contenir des éléments favorisant la formation de graphite (Si, Al Ti, Ni, Cu). Il faudrait des éléments carburigènes (Mn, Mo, Cr, V) - une vitesse de refroidissement élevée favorise la formation de fonte blanche. Comme pour les fontes grises, il existe des fontes blanches hypo et hypereutectiques. Leur solidification suit exclusivement le diagramme métastable Fe-Fe3C. Il est à signaler que dans le cas de la fonte blanche, le composé eutectique (la ledéburite) garde son aspect malgré la transformation de l'austénite la constituant. (1) Fontes blanches hypoeutectiques Les séquences de transformation de cette fonte à partir de l'état liquide sont : - formation de y proeutectique (jusqu'à 1148°C) - à 1148°C : formation de ledéburite (γ+Fe3C) - formation de cémentite proeutectoïde et appauvrissement de γ en carbone (Jusqu’à 727°C) - à 727°C : l'austénite a un % en C=O, 8; elle se transforme totalement en perlite. Structure à l'ambiante (figure II-6) : Fe3C eutectique et proeutectoïde + perlite (de γ proeutectique) et perlite (de γ eutectique). Cours de métallurgie, ENIT-Département de Génie Mécanique 35 Souad BEN SLIMA
- 36. Figure II-6 : Aspect microstructural d'une fonte blanche hypoeutectique dont le % en C est proche de 2,11. Plages noires : perlite, plages blanches : cémentite. X 200 (2) Fontes blanches hypereutectiques Les séquences de transformation de cette fonte à partir de l'état liquide sont : -Formation de Fe3C primaire (ou proeutectique) (jusqu'à 1148°C) - A 1148°C : formation ledéburite (γ+Fe3C) - Formation de Fe3C secondaire (ou proeutectoïde) (jusqu'à 727°C) - A 727°C : transformation totale de y eutectique en perlite Structure à l'ambiante (figure II-7 b) : matrice de Fe3C (eutectique + proeutectoïde) + plaquette de Fe3C primaire + perlite (de γ eutectique) Figure II-7 : Aspect microstructural de la fonte blanche (a) eutectique (%C=4,3), plages mouchetées : ledéburite, plages noires : perlite. (b) hypereutectique, plaquettes blanches de cémentite + plages mouchetées de ledéburite. (3) Propriétés des fontes blanches Les fontes blanches sont dures et fragiles, elles sont «inusables». Elles Cours de métallurgie, ENIT-Département de Génie Mécanique 36 Souad BEN SLIMA
- 37. sont obtenues pour des vitesses de refroidissement assez élevées et des températures de coulées basses; c'est pourquoi on les appelle parfois fontes trempées. Elles sont très peu utilisées dans l'industrie sauf dans le cas où leur grande résistance à l'usure et à l'abrasion est requise (boulets de broyeurs, mâchoires de concasseurs, plaques d'usure) Désignation : FB (FBO : non alliée, FBA : alliée) C.LES DIFFERENTES STRUCTURES DES ACIERS ET DES FONTES Nous avons défini l’acier et la fonte comme étant des alliages à base de fer. Nous avons aussi vu le processus de solidification de ces alliages suivant leur pourcentages en carbone dans les conditions d’équilibre et ceci à partir du diagramme binaire Fe-C. Les conditions d’équilibre supposent que le refroidissement a lieu à des vitesses faibles pour permettre aux atomes de diffuser et former des différentes phases d’équilibre. Il est évident que les structures qui nous intéressent sont celles qui existent à la température ambiante, aussi allons nous porter notre étude sur les transformations en solution solide uniquement. La transformation solide-solide qui nous concerne aussi bien les aciers que les fontes est celle de l’austénite gamma que nous avons vue lors de l’étude du diagramme binaire Fe-C. Cependant, les refroidissement à des vitesses lentes ne sont pas ceux qui sont fréquemment pratiqués pour 2 raisons, les refroidissements à vitesses élevées sont plus rapides et donc d’un usage plus pratique, mais la raison principale est que celui-ci confère aux aciers des structures qu’on appelle hors d’équilibre qui ont des propriétés mécaniques différentes et diverses. Aussi, allons nous diviser la présentation des structures de l’acier en deux : Les structures d’équilibre et les structures hors d’équilibre. 1. Les structures d’équilibre Ce sont des structures qu’on obtient dans les conditions où la diffusion des atomes est possible. Les transformations qui leur donnent lieu sont dites contrôles par diffusion. Elles ont lieu dans les aciers au carbone et les fontes ordinaires quand le refroidissement de l’austénite γ es relativement lent. a) La ferrite La ferrite a est relativement douce (dureté = 80 HB), sa résistance maximale Rm varie de 25 à 45 daN/mm2 et sa limite d’élasticité Re = 12 daN/mm2. C’est le composé proeutectoïde pour les aciers hypoeutectoïdes. Elle se présente soit sous forme de grains arrondis (ferrite granulaire) ; la ferrite ainsi formée ayant germée et s’étant développé le long des joints de grains de la phase mère austénite (figure II-8 a) soit sous forme allongée (ferrite aciculaire) due à une vitesse de refroidissement légèrement supérieure à celle des conditions d’équilibre, la structure est dite “WIDMANSTATTEN (figure II-8b). Cette ferrite naît aux joints de grains et se développe à l’intérieur du grain. Cours de métallurgie, ENIT-Département de Génie Mécanique 37 Souad BEN SLIMA
- 38. Ferrite granulaire (x250) b- Ferrite aciculaire (xl00) (Structure de Widmanstatten Figure II-8 : Différentes morphologies de la ferrite b)La cémentite C'est le composé proeutectoïde qui se forme dans les aciers hypereutectoïdes; Il se forme aussi dans les fontes blanches. C'est un carbure F e3C, par conséquent sa dureté est très élevée (1000HV), c'est un produit fragile. Dans les aciers, comme la ferrite granulaire, la cémentite se forme aux joints de grains de la phase γ et s'y développe. C'est pour cette raison que la cémentite apparaît toujours comme des liserés blancs qui dessinent les contours des anciens grains de γ (figure II -9a) a - Acier hypoeutectoïde b- Perlite sphéroidisée (Cémentite + perlite) (X 500) (X2000) Figure II-9 : Différentes présentations de la cémentite et la perlite Dans les aciers hypereutectoïdes usuels (% C ne dépassant pas 1,2%), le pourcentage maximal de Fe3C qui peut se former est de 7%. La cémentite ainsi formée peut porter préjudice à certaines propriétés importantes de l'acier, notamment son usinabilité et sa ténacité. Certains traitements sont donc appliqués aux aciers pour éliminer les liserés de cémentite (figure II-9 b) et lui Cours de métallurgie, ENIT-Département de Génie Mécanique 38 Souad BEN SLIMA
- 39. donner un aspect de sphère (sphéroïdisation). c) La perlite Composé biphasé comportant des lamelles alternées de α et Fe3C, c'est le composé eutectoïde. Sa dureté varie entre 180 et 250 HB, sa résistance maximale est autour de 83 daN/mm2. La distance d entre 2 lamelles de Fe3C dépend de la température T à laquelle la perlite s'est formée ou de la vitesse de refroidissement (VR). Quand T diminue, d diminue et quand VR augmente, d augmente. De d dépendra la résistance de la perlite : d=l µm R = 63 daN/mm2 (figure II-l0a) d= 0,5µm R= 75 daN/mm2 (figure II-l0b) d=0,2 µm R= 110 daN/mm2 d < 0,1 µm R= 250 daN/mm2 a- Perlite (d=l µm) b-Perlite (d<0,5µm) (X l000) (X l000) Figure II-10 : Morphologie de la perlite La sphéroïdisation de la cémentite (élimination des lamelles) conduit à des résistances R plus faibles (de 63 à 90 da N/mm2 en fonction du diamètre des sphères), mais réduit la fragilité du produit. d) L'austénite Pour les aciers au carbone et les fontes non alliées, l'austénite est stable seulement aux températures élevées, elle n'existe donc pas à la température ambiante. Cependant, elle influencera beaucoup les propriétés de ces aciers étant donné que aussi Cours de métallurgie, ENIT-Département de Génie Mécanique 39 Souad BEN SLIMA
- 40. bien les phases eutectoïdes que la perlite prennent naissance (germent) au niveau des joints de grains de cette phase qui est la phase mère. Ainsi, si les grains de cette phase sont gros, il y aura peu de joints de grains, donc peu de sites de germination et la transformation de l'austénite γ sera retardée (γ étant stabilisée). De plus, il y aura une relation entre la taille des grains de γ et celles des grains des phases qui se forment : plus γ sera fine plus les produits seront fins et la résistance de l'acier meilleure. La taille du grain de γ dépend de la température et du temps auxquels on maintient l'acier avant refroidissement. Quand T et t augmentent, le diamètre du grain augmente. Dans les aciers et les fontes qui contiennent des éléments d'alliage, l'austénite peut être présente à la température ambiante} et par conséquent stabilisée si les éléments sont gamma gènes (Ni, Co, Mn…) Morphologie : l'austénite se présente sous forme de grains polygonaux (figure II-11). Elle peut avoir des duretés très élevées jusqu'à 800 HB) et des résistances importantes (R=90 daN/mm2) suivant les éléments d'alliage. Sa limite d'élasticité dans ce cas sera très faible. Figure II-11 : Morphologie de l’austénite 2. Les structures hors d'équilibre a) La martensite (du nom d'Adolf Martens, allemand) Lorsque la vitesse de refroidissement d'un acier porté à haute température est très élevée, on n'est plus dans les conditions d'équilibre. Ainsi, les atomes de carbone de l'austénite (haute température) n'auront pas le temps de diffuser lors du refroidissement rapide. Ils resteront emprisonnés dans le réseau de la ferrite alpha (basses températures) qui normalement ne peut pas les contenir (limite de solubilité du carbone dans a à 727°C : 0,025%). Ils déformeront ainsi le réseau qui se transformera alors de cubique à faces centrées (γ) en quadratique centré identifié par les paramètres c et a : C'est la martensite qui est définie comme étant une solution solide Cours de métallurgie, ENIT-Département de Génie Mécanique 40 Souad BEN SLIMA
- 41. sursaturée en carbone. Quand %C augmente, c/a augmente et la tétragonalité du réseau sera plus prononcée (figure II-12). Cette déformation du réseau} qui se fait par cisaillement (la transformation martensitique est dite militaire comparativement aux transformations diffusionnelles dite civiles), entraîne des distorsions et donc le durcissement de l'acier. La martensite sera donc une phase dure (HRC=73). Figure II-12 : Variation des paramètres a et c de la martensite en fonction de la teneur en carbone dans les alliages Fe-C (Ref .1) (1) Cinétique de la transformation La transformation qui engendre la martensite (transformation martensitique) dépend uniquement de la température. Elle ne peut pas se poursuivre si la diminution de la température ne se poursuit pas (dT/dt=0) : elle est athermique. L'équation qui donne la cinétique de cette transformation est la suivante : F = 1- e-(l, 1610-2 ∆T) (Koistiner et Marburger) où f est la fraction volumique de martensite (pour les alliages Fe-C de 0,37 à 1,1 %C) La température de début de transformation de la martensite est plus ou moins basse suivant la composition de l'acier. Elle est notée Ms (Martensite Starting). L'influence des différents éléments d'addition sur Ms ne peut être définie d'une manière univoque et rationnelle. Certaines formules à caractère empirique ont été proposées, elles donnent Cours de métallurgie, ENIT-Département de Génie Mécanique 41 Souad BEN SLIMA
- 42. une idée sur l'évolution de Ms mais ne peuvent être valable dans tous les cas, nous citons ci suit la formule de NEHRENBERG : Ms (°C)= 500-300C-33Mn-22Cr-17Ni-11Si-11Mo Le domaine de transformation de la martensite s'étend de Ms à Mf (Martensite Finishing) qui est une température très souvent inférieure à l'ambiante. Ainsi, lorsque le refroidissement est arrêté à la température ambiante, la transformation austénite (γ------martensite ne sera pas complète et il persistera de l'austénite non transformée (ou austénite résiduelle). La martensite est donc la raison du durcissement des aciers lors d'un refroidissement brusque on dit que c'est le constituant de trempe. Mais sachant qu'une dureté élevée engendre la fragilité du matériau, la martensite sera donc responsable de la fragilité du matériau. Par ailleurs, étant donné que le carbone est responsable de la grande dureté de la martensite (pour les aciers au carbone), la martensite sera d'autant plus dure que le % en carbone est élevé. Il est donc pratiquement impossible d'obtenir de la martensite quadratique centrée pour les aciers ayant despour_cent en carbone inférieurs à 0,2. C'est pourquoi les aciers au carbone sont classifiés de cette manière : Hypoeutectoîdes hypereutectoîdes 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 %C 1---------1--------1-------1-------1------1-----1------1-------1-------1------1--------1-------> Fer/ extra / doux /mi - / mi-dur / dur / extra-dur doux doux A partir de 1,2 %, la dureté de trempe n'augmente plus. Si on dépasse ce pourcentage, pour augmenter la dureté, il faut ajouter des éléments d'alliage qui feront précipiter le carbone en excès sous forme de carbures durcissants. Ms et Mf vont diminuer quand le pourcentage en éléments d'alliage favorisant la phase austénitique augmente. Ces éléments sont dits gammagènes. Ms peut atteindre des valeurs très faibles, c'est la cas des aciers inoxydables 18-10 (18% Cr et 10%Ni) qui même refroidis dans l'eau glacée conservent une structure austénitique (il faut refroidir dans l'azote liquide -200°C pour avoir de la martensite). Cours de métallurgie, ENIT-Département de Génie Mécanique 42 Souad BEN SLIMA
- 43. Figure II-13 : Évolution de la dureté en fonction de la teneur en carbone pour des structures trempées (Ref1) La martensite est facilement caractérisable au microscope, elle se présente sous forme de paquets d’aiguilles allongées et régulières. Elle peut exister sous l’une des deux morphologies suivantes : en lattes ou en plaquettes (figure II-14). Lattes de Martensite Plaquettes de Martensite Figure II-14 : Différentes morphologies de la Martensite, x1000, (Ref3) Les lattes se présentent au microscope sous forme de paquets d'aiguilles courtes et fines. Les plaquettes sont plus grandes et plus larges. La présence de l'une et/ou de l'autre morphologie de la martensite dépend du % en carbone (figure Cours de métallurgie, ENIT-Département de Génie Mécanique 43 Souad BEN SLIMA
- 44. II-15). Quand le %C augmente, la probabilité d'obtenir des plaquettes devient plus grande. Figure II-15 : morphologies de la Martensite en fonction du % en carbone b) La bainite (du nom d'Edgar Bain, Américain) Quand la vitesse de refroidissement n'est pas très élevée, mais intermédiaire, il se forme un composé intermédiaire entre la martensite et la perlite qui groupe certaines propriétés de chacune des deux structures : c'est la bainite. Comme la perlite celle-ci est un composé biphasé contenant de la ferrite + cémentite; comme la martensite elle se présente sous forme d'aiguilles de ferrite dans lesquelles est répartie la cémentite. Ainsi la transformation bainitique est permise par la diffusion partielle des atomes de carbone (transformation perlitique) et par le cisaillement (transformation martensitique). Du fait qu’elle est également assurée par la diffusion, la transformation bainitique peut progresser même dans les conditions isothermes. Bainite supérieur Bainite inférieur Cours de métallurgie, ENIT-Département de Génie Mécanique 44 Souad BEN SLIMA
- 45. Figure II-16 : Morphologies de la bainite, x250 Les aiguilles de bainite seront d'autant plus fines que la vitesse de refroidissement est élevée ou que la température est basse (dans les conditions isothermes) ; on distingue ainsi trois types de bainite : -bainite supérieure : pour les températures relativement hautes, elle est proche de la perlite, la structure se présente sous forme de lamelles de ferrite a entre lesquelles se trouvent les précipités de cémentite Fe3C, -bainite moyenne -bainite inférieure : pour les températures basses, elle est proche de la martensite, les aiguilles sont très fines et ne peuvent pas être résolues au microscope optique. Les carbures de cémentite y sont très petits et parallèles. La bainite est assimilée à des amas de plumes. Lorsque la vitesse de refroidissement augmente la structure devient plus fine, par ailleurs les contraintes internes deviennent plus importantes ce qui engendre une dureté plus élevée. Cours de métallurgie, ENIT-Département de Génie Mécanique 45 Souad BEN SLIMA
- 46. V. AMELIORATION DES PROPRIETES MECANIQUE DES MATERIAUX METALLIQUES PAR TRAITEMENTS THERMIQUES DANS LA MASSE Les traitements thermiques se divisent en deux grandes catégories principales : -les traitements thermiques de base nécessaires pour améliorer l'homogénéisation de la structure et rechercher l'état d'équilibre; il s'agit d'opérations effectuées sur pièces ou lingots bruts de coulée (recuits). - les traitements thermiques orientés vers les applications pour créer des structures le plus souvent hors d'équilibre et qui permettent d'améliorer la résistance à la déformation, au choc, à l'usure, à la corrosion (trempes et revenus). Pour cette deuxième catégorie le traitement peut être général lorsqu'il est appliqué à toute la pièce, local ou partiel lorsqu'il concerne une partie de la pièce, généralement la surface mais ce dernier sera développé au chapitre suivant. Nous avons déjà vu par l'étude du diagramme d'équilibre Fe-C que des transformations en phase solide pouvaient avoir lieu et plus explicitement la transformation de la phase γ (austénite). Mais le diagramme Fe-C reste en ce sens très limité car il ne traduit que les transformations pouvant se faire pour des refroidissements continus à vitesses lentes (recuits). Mais que se passerait-il si on refroidissait rapidement un acier jusqu'à une température T telle que Ms < T < Ac1, et qu'on le maintenait à cette température ? Et si on déviait des conditions d'équilibre en refroidissant un acier d'une manière continue à des vitesses élevées et différentes, quelle serait à chaque fois la microstructure de l'acier et les propriétés mécaniques correspondantes ? A ces questions importantes aussi bien sur le plan fondamental (compréhension des cinétiques de transformation) que celui de l'ingénierie des matériaux (sélection des propriétés désirées par la sélection du traitement thermique approprié), des courbes expérimentales ont été établies : les courbes TIT et TRC A.LES COURBES TTT Nous avons pu d'après le diagramme d'équilibre Fer-Carbone suivre l'évolution de la structure de différents aciers au carbone avec la température, la vitesse de refroidissement étant très lente; la transformation eutectoide (transformation perlitique) est la plus importante. Cette transformation peut avoir lieu dans d'autres conditions notamment par maintien de l'acier à température constante pendant des durées plus ou moins longues. Cette température e sera inférieure à la t température de l'eutectoide (727°C). Le traitement correspondant consistera à rendre l'acier austénitique par un maintien dans le domaine, puis de le porter rapidement dans un bain à température constante. L'acier est alors maintenu pendant des durées différentes à différentes températures, puis observé Cours de métallurgie, ENIT-Département de Génie Mécanique 46 Souad BEN SLIMA
- 47. pour identifier les phases formées ainsi que le taux d'austénite transformée. Tous les résultats sont reportés sur un diagramme température log10t (température de transformation, temps, domaine de chaque phase). Les courbes TTT les plus simples se présentent en général comme représenté figure V-1. Figure V-1 : Courbe TTT pour un acier eutectoide a) Comment lire une courbe TIT : * Les courbes TIT sont lues horizontalement de manière à suivre l'évolution de la transformation en fonction du temps. * Les différentes phases de l'acier sont notées comme suit : A : austénite F : ferrite C : cémentite M : martensite Quand il est noté (FOC), le composé correspondant peut être la perlite ou bainite. La bainite existe pour les basses températures et la perlite pour les températures plus élevées 1) : courbe de début de transformation (2) : transformation de 50% de l'austénite (3) : courbe de fin de transformation * Les courbes TTT sont limitées dans leur partie supérieure par la température de Cours de métallurgie, ENIT-Département de Génie Mécanique 47 Souad BEN SLIMA
- 48. l'eutectoide et dans leur partie inférieure par le point Ms. En dessous de ce point le maintien isotherme, d'aussi longue durée qu'il soit, ne fait pas évoluer la transformation martensitique puisque celle-ci est indépendante du temps et ne peut se poursuivre si dT/dt=0. Exemple de suivie de la courbe TTT (figure V-1), pour la température Tr à ti : la transformation débute par la formation de ferrite + cémentite à partir de l'austénite. Dans ce cas F+C est la perlite à t1/2 : 50% de l'austénite s'est transformée en (F+C) à tf : la totalité de l'austénite s'est transformée en perlite •La verticale limitant à droite le diagramme TTT indique la dureté de la structure finale après un maintien de 24h, les courbes TIT n'étant pas définie - en général- pour des durées de maintien plus élevées. En eutectique donc eutectique = Liqres= c) à T=TE – ε α total = * Mécanisme des transformations isothermes: Aux températures élevées (proche de la température d'austénitisation), la tendance à la transformation A------->F+C est faible puisque le domaine de l'austénite est proche, en effet l'austénite est d'autant plus stable qu'on s'approche de son domaine d'existence. Au fur et à mesure que la température de maintien isotherme diminue, la tendance à la transformation de l'austénite augmente, mais la diffusion devient plus difficile, la structure résultante est donc de moins en moins proche de l'équilibre. Pour une température suffisamment basse (Ms), la transformation se fait dès que le métal atteint Cette température. Il n'y a pas de diffusion, le carbone reste emprisonné dans le réseau : la martensite est formée. * Remarques : 1)Plus la température de maintien est basse et plus la perlite obtenue est fine. 2)Le type de diagramme TIT présenté est le plus simple. On trouve dans certains diagrammes d'acier des domaines d'existence de la ferrite seule, ainsi qu'une différenciation nette entre les domaines de la perlite et de la bainite (figure V-2). Cours de métallurgie, ENIT-Département de Génie Mécanique 48 Souad BEN SLIMA
- 49. Figure V-2 : Diagrammes TTT (a) d'aciers au carbone (b) d'aciers alliés Cours de métallurgie, ENIT-Département de Génie Mécanique 49 Souad BEN SLIMA
- 50. b) Les facteurs influençant la courbe TTT : - La température d’austénitisation : Avant de procéder à la transformation isotherme, on part d'une structure à 100% austénitique; à cet effet l'acier est maintenu à une température supérieure à AC3 (température de début de transformation de l'austénite). Les conditions d'austénitisation seront donc la température et le temps d'austénitisation (Ta et ta)' Ces conditions doivent être spécifiées avant tout traitement isotherme car elles définissent l'état de l'acier avant ces traitements. En effet un temps et une température d'austénitisation plus élevés engendrent une austénite à plus gros grains, donc plus stable; le domaine de l'austénite sera plus étendu et donc la courbe décalée vers la droite. - Les éléments d’alliage : Les éléments gammagènes (Mn, Ni, Cu, N et C) stabilisent l'austénite, leur action est donc de décaler la courbe vers la droite. Les éléments alfa gènes (Cr, Mo, W, V, Ti, Nb) décalent la courbe vers la droite et modifient sa forme car ils ont tendance à former des carbures qui retardent la transformation de l'austénite et favorisent certaines transformations plutôt que d'autres (la transformation bainitique, par exemple). B. LES COURBES TRC : Il est possible de connaître à partir des courbes de transformation isothermes la stabilité d'un acier à l'état austénitique dans les différents domaines de température. Cependant les cycles thermiques que subissent généralement les pièces industrielles ne correspondent pas à des transformations isothermes. En effet, dans la majorité des cas les pièces subissent des traitements à refroidissement continu. C'est les courbes TRC (Transformation à Refroidissement Continu) qu'ils faut alors considérer. Ces courbes permettent de déterminer pour différentes conditions de refroidissement, allant de refroidissement très rapides à des refroidissements très lents, la nature des constituants formés lors de ces refroidissements, les températures de transformation et la dureté de la structure à l'ambiante. Comme pour les transformations isothermes, l'alliage est préalablement austénisé. Les courbes sont tracées suivant une échelle semi-logarithmique. Des courbes de refroidissement correspondant à des lois de refroidissement différentes sont tracées (figure V-3). Le point d'origine de ces courbes sur l'axe des températures est la température d'austénitisation. Figure V-3 : Lois de refroidissement Figure V-4 : Lois de refroidissement correspondant à des milieux différents Correspondant à des différents diamètres de pièces, dans un même milieu de refroidissement On fournit généralement avec la courbe TRC des courbes de refroidissement sur transparents tracées dans le même système de coordonnées que les courbes TRC , et qui Cours de métallurgie, ENIT-Département de Génie Mécanique 50 Souad BEN SLIMA
- 51. correspondent à des milieux de refroidissement précis pour des pièces de diamètres différents (figure V-4). Plus le diamètre de la pièce est grand plus l'échange thermique entre le coeur de la pièce et le milieu est lent et donc la vitesse de refroidissement ressentie faible. Ces courbes sont tracées sur des transparents ou des calques afin de pouvoir les superposer aux courbes TRC. Ces courbes existent pour les milieux de refroidissements les plus usuels : l'air, l'huile et l'eau. Les différentes courbes de refroidissement vont traverser les domaines d'existence des différentes phases, domaines qui auront un aspect et une forme différente suivant la nature de l'acier et les conditions d'austénitisation. Nous représentons ci suit un exemple de courbe TRC. Le domaine intermédiaire (bec de perroquet) est le domaine de la bainite qui n'existe pas pour les aciers au carbone à bas % en carbone. Figure V-5 : Exemple de courbe TRC a) Comment suivre une courbe TRC : Il faut suivre la courbe correspondant à la vitesse de refroidissement adoptée : * vitesse v4 : on prend la courbe correspondante à cette vitesse et on voit à quel moment Elle coupe le diagramme. A T1, on rentre dans le domaine A+F (Transformation de l'austénite en ferrite). A T2, on rentre dans le domaine A+F+C (fin de transformation de l'austénite en ferrite et début de transformation de l'austénite restante en perlite). A T3, fin de transformation de l'austénite. La structure contiendra de la ferrite (K4 %) et de la perlite (K'4 %), avec K4 + K'4 = 100%. D 4 est la dureté de la structure à la suite de ce traitement. * vitesse v3 : on prend la courbe correspondante à cette vitesse et on voit à quel moment elle coupe le diagramme. A T'1 on rentre dans le domaine A+F (transformation de l'austénite en ferrite). A T’2, on rentre dans le domaine A+F+C (fin de transformation de l'austénite en ferrite et début de transformation de l'austénite restante en bainite). A T'3, fin de transformation de l'austénite en bainite. Entre T'’3 et T'’4 aucune transformation n'a lieu, et à T'4 une partie de l'austénite se transforme en martensite. La structure contiendra de la ferrite Cours de métallurgie, ENIT-Département de Génie Mécanique 51 Souad BEN SLIMA
- 52. (K3 %) et de la bainite (K'3 %), de la martensite et de l'austénite résiduelle. D3 est la dureté de la structure à la suite de ce traitement. Remarque : Quand une courbe de refroidissement traverse le domaine de la bainite, on commence à avoir une structure hors d'équilibre. L'austénite n'est dans ce cas jamais transformée à 100%; il reste donc à la fin de la transformation de l'austénite qui est dite résiduelle. * vitesse v2: La courbe de refroidissement coupe le domaine de la bainite à T'1 A cette température débute la transformation bainitique qui s'arrête à T'2 A cette même température, l'austénite qui reste se transforme en partie en martensite, il restera donc de l'austénite à la température ambiante. La structure finale sera : bainite (% :K2) + (martensite + austénite résiduelle) (% = 100-K2). La dureté de cette structure sera D2. * vitesse v1 : La courbe ne coupe pas le domaine de la bainite, la seule transformation qui a lieu est la transformation martensitique qui débute à Ms. La structure finale contiendra : martensite+austénite résiduelle, sa dureté est D3 Si M50 est supérieur à la température ambiante, on aura dans la structure finale plus de 50% de martensite. La quantité de martensite sera d'autant plus importante que VI est grande. b) Vitesses de refroidissement : Pour certaines exploitations, il est nécessaire de déterminer pour une loi de refroidissement la vitesse correspondante. Il est possible dans ce cas de calculer : - soit la vitesse de refroidissement instantanée à 700°C, ce sera la pente de la tangente à la courbe de refroidissement en ce point : - soit la vitesse de refroidissement moyenne entre 700 et 300°C : c) Facteurs influençant la courbe TRC : 1- La température et le temps d’austénitisation : Plus ils sont élevés, plus l'austénite sera stable. La courbe sera décalée vers la droite et on aura à l'ambiante un taux plus élevé d'austénite résiduelle. 2- La composition chimique : Les éléments gammagènes élargissent le domaine de l'austénite ils décalent donc la courbe vers la droite. Les éléments alfa gènes décalent aussi la courbe vers la droite, de plus ils favorisent la transformation bainitique pour laquelle ils font apparaître le domaine distinctement du domaine perlitique. Le seul élément qui décale les courbes TRC à gauche est le cobalt. Cours de métallurgie, ENIT-Département de Génie Mécanique 52 Souad BEN SLIMA
- 53. d) Détermination des vitesses critiques : A partir de la courbe TRC il nous est possible de définir les différents traitements thermiques ainsi que leurs buts. Nous remarquons d'après cette courbe qu'il existe une vitesse limite au delà de laquelle la structure obtenue est uniquement de la martensite (à gauche du diagramme), et une autre vitesse en deçà de laquelle la structure obtenue est une structure d'équilibre (à droite). Ces vitesses sont appelé respectivement vitesse critique de trempe (VCT) et vitesse critique de recuit (V CR) (figure V-6). Figure V-6 : Détermination des vitesses critiques de trempe et de recuit v CR : vitesse critique de recuit v> vCR : on obtient des structures hors d'équilibre v < v CR : ferrite+perlite Lorsque v s'approche de v CR' la structure de la perlite devient de plus en plus fine (les Lamelles se rapprochent, d<O, 2um) v cr : vitesse critique de trempe Si v>v CT : structure martensitique Si v<v CT : structure mixte C. LES TRAITEMENTS THERMIQUES D'ÉQUILIBRE Les traitements traités dans ce paragraphe sont des traitements appliqués pour homogénéiser la structure, améliorer la ductilité, réduire les contraintes internes et/ ou améliorer l'usinabilité des aciers. Ces traitements donnent lieu à des structures d'équilibre et à des distributions différentes de ferrite et cémentite qui conditionneront les propriétés mécaniques. Ces traitements consistent en un chauffage à une certaine Cours de métallurgie, ENIT-Département de Génie Mécanique 53 Souad BEN SLIMA
- 54. température (T), un maintien pendant un certain temps (t) et un refroidissement lent pour lequel on définira la vitesse (VR). Suivant ces 3 paramètres, on définit différents recuits. Un traitement thermique sera défini à priori comme étant un traitement d'équilibre si VR est inférieure à la vitesse critique de recuit V CR précédemment définie (fig.V-6). 1. Le recuit (ou recuit complet) "full annealing" : Il consiste en un chauffage et maintien à une température supérieure à AC3 (température de début de transformation) (AC3+50°C) puis un refroidissement lent au four. Ce traitement effectué, la structure obtenue est celle d'équilibre à basse dureté et excellente ductilité. Ce traitement est généralement effectué sur des pièces à usiner ou à déformer à froid qui ont déjà subi des traitements thermiques ou mécaniques. La température de recuit ne doit pas être trop élevée sous risque de provoquer un grossissement de grains fragilisant. La vitesse de refroidissement est très lente (refroidissement au four) et la structure résultante est en général α + perlite (ou F e3C + perlite) oùα est equiaxe et la perlite constituée de lamelles de distance interlamellaire d assez élevée. Une fois la transformation de γ totale, la vitesse peut augmenter sans danger et ceci pour diminuer le temps de recuit et améliorer ainsi la rentabilité. 2. Recuit d'homogénéisation "nomogenizing» : Ce recuit est effectué sur les aciers bruts de coulée afin d'éliminer tous les phénomènes dus à la ségrégation mineure (au niveau du grain) ou majeure (au niveau du lingot); donc d'hétérogénéité chimique. Ce traitement doit donc favoriser la diffusion des atomes, pour ce faire il sera effectué à des températures très élevées mais toujours dans le domaine de l'austénite (Ac3+200°C, entre 1000 et 1200°C) pour des durées prolongées. 3. Recuit de normalisation "nomogenizing» : C'est un recuit qui est effectué sur les aciers non alliés et qui permet d'obtenir une structure plus fine (grains fins). La température est supérieure à celle du recuit complet (Ac3 + 75°C), ainsi que la vitesse de refroidissement qui se fait à l'air calme, on a ainsi une perlite fine (faible distance interlamellaire). 4. Recuit de coalescence ou sphéroïdisation "spheroidizing" Comme nous l'avons déjà vu, la perlite est un composé constitué de a (phase ductile) et de Fe3C (phase dure). La dureté de ce constituant dépend de l'énergie interfaciale entre a et Fe3C qui sera d'autant plus importante que la surface de contact entre ces 2 phases est grande. Réduire la dureté et par là même la fragilité consistera à réduire cette surface de contact. L'énergie interfaciale minimale correspond à une répartition de sphères de Fe3C Dans une matrice a. D'où la tendance à SPHEROIDISER Fe3C dans les structures d'aciers où la ténacité est une propriété très importante. C'est la structure la moins dure possible dans les aciers. La sphéroïdisation est particulièrement requise pour les aciers chargés en carbone qui doivent subir un usinage important avant leur durcissement. Elle consiste à maintenir l'acier à des températures proches mais plus faibles que ACl, pendant des temps assez longs. Plus la perlite de départ est fine, moins le temps de maintien est long. Cours de métallurgie, ENIT-Département de Génie Mécanique 54 Souad BEN SLIMA
- 55. Figure V-7 : Domaines de températures des différents types de recuit 5. Recuit de détente "stress relieving" : Ce recuit s'effectue à des températures basses, inférieures même à la température de début de transformation (AC1) : 550<T<650°C. Il est exécuté sur les pièces qui ont subies une déformation plastique sévère (mise en forme, usinage, ...). Le soudage aussi, du fait de la contraction de solidification, provoque des contraintes dans les zones adjacentes au cordon de soudure. Ainsi, pour relâcher ces contraintes, le recuit de détente est effectué. Ce type de recuit peut aussi être effectué entre deux opérations d'usinage ou de mise en forme, soit précéder la trempe une fois l'usinage fini. Le chauffage et le refroidissement doivent être très lents pour ne pas introduire d'autres contraintes. Le recuit de détente ne change pas les propriétés mécaniques d'une manière significative; il évite, cependant, une rupture prématurée en service ou pendant le traitement thermique. 6. Recuit de recristallisation " recrystallization annealing» : Pendant la mise en forme par déformation plastique (laminage, forgeage, ...), les grains de la structure vont s'orienter suivant la direction de mise en forme. Ce type de structure n'est généralement pas souhaité (contraintes, anisotropie des propriétés électriques, thermiques et mécaniques, etc...), c'est pourquoi pratique-t-on des traitements de recristallisation à des températures inférieures à AC1 afin de régénérer des grains équiaxes (sans orientations particulières). Ceci se fait d'abord par l'élimination des défauts cristallins produits par la déformation plastique (étape restauration), puis pour des maintiens plus longs, par la germination et croissance de nouveaux grains non Cours de métallurgie, ENIT-Département de Génie Mécanique 55 Souad BEN SLIMA
- 56. déformés (étape recristallisation). Si la première étape se fait pour des températures faibles, l'étape de recristallisation proprement dite se fait à des températures entre 1/3 et 1/2 de la température de fusion du matériau. L'étape de restauration affecte peu ou prou les propriétés mécaniques, l'étape de recristallisation, par contre, provoque une chute spectaculaire de la résistance et la dureté et un accroissement notable de la ductilité (fig. V-8). Figure V-8 : Influence de la température de recuit sur la résistance maximale (tensile strength), et la ductilité d'un laiton (Cu-Zn). La taille des grains (grain size) est schématisée et éventuellement indiquée en fonction de la température. Les différents stades sont indiqués : restauration (recovery), recristallisation (recrystallization), croissance des grains (grain growth). (D’après Ref26, p.171) Cours de métallurgie, ENIT-Département de Génie Mécanique 56 Souad BEN SLIMA
- 57. Figure V-9 : Variation de la température de recristallisation en fonction du taux d'écrouissage (percent cold work) pour le fer. La recristallisation n'a pas lieu en deçà d'un seuil critique D’écrouissage (critical deformation) (d'après Ref26, p.172) Si la température de maintien est supérieure à la température de recristallisation, c'est le grossissement de grains qui prend place. La structure résultante est peu dure et très ductile. Plus le taux d'écrouissage est grand moins la taille des grains régénérés sera importante et plus la température de recristallisation sera basse (fig. V-9) Les différents recuits qu'on vient de citer sont rarement pratiqués individuellement, le recuit pouvant regrouper le but de plusieurs d'entre eux. D. LES TRAITEMENTS THERIQUES "HORS D'ÉQUILIBRE" 1. La trempe On appelle trempe le refroidissement brutal du matériau préalablement porté à haute température. L'état trempé correspond à un état hors d'équilibre. Jusqu'à des temps relativement approchés, les gens pensaient que la trempe des aciers était liée à l'habileté du forgeron et aux secrets des milieux de refroidissement utilisés, que, d'une certaine manière, elle relevait de la sorcellerie. Aujourd'hui, la trempe n'est plus qu'un traitement classique dans lequel on ne voit plus aucun mystère ... ou presque. La trempe peut avoir deux objectifs : -conserver la structure existante à chaud à la température ambiante pour éviter la germination de phases non souhaitées. -obtenir une phase qui améliore les caractéristiques mécaniques de l'alliage sans changer sa composition. La température de trempe varie selon la composition, il faut indiquer qu'elle correspond à la température de maintien à haute température avant refroidissement (température d'austénitisation). Elle doit être telle qu'elle fournit la meilleure dureté au matériau : -Pour les aciers hypoeutectoïdes : T=AC3+50 à 70°C pour éviter la formation de ferrite Qui diminue la dureté. -Pour les aciers hypereutectoïdes : T=AC1 +50 à 70°C pour permettre la formation de Cémentite proeutectoïde qui améliore la dureté. La trempe est un traitement qui, en général, améliore les propriétés de résistance et détériore les propriétés de ductilité. La température de trempe est un facteur très important pour réussir celle ci. Une température trop élevée provoque un grossissement de grain qui diminue la dureté et rend la structure susceptible à la fatigue. Elle peut aussi être la cause d'oxydation et de décarburation superficielle. a) Les milieux de trempe : La vitesse de trempe va dépendre du milieu de refroidissement; de celui ci dépendra la réussite de la trempe. Un milieu de trempe est caractérisé par son aptitude à extraire la chaleur de la pièce à refroidir; cette caractéristique est dite drasticité. La drasticité d'un milieu est fonction de sa viscosité, sa température, son mouvement (agitation) et sa composition. Cours de métallurgie, ENIT-Département de Génie Mécanique 57 Souad BEN SLIMA
- 58. Elle peut être traduite de deux manières : - par la courbe de refroidissement d'une éprouvette définie dans le milieu en question. Cette courbe est utile à tous les points de vue car elle permet de situer les différentes étapes de refroidissement (fig. V-10). - par le facteur de sévérité de trempe H. Il traduit l'efficacité du milieu, c.à.d. la capacité Du milieu de donner pour une barre de diamètre <1>, un volume à 100% trempé. Comme l'efficacité de la trempe dépend de la conductivité thermique du métal (λ) et du coefficient d'échange thermique (h) du milieu (qui dépend lui même de l'agitation du Bain), H est donnée par h/2λ (mm-l). (Pour les aciers, la conductivité thermique λ= 0,2 cal/ cm.s. °C). Plus H est élevé et plus le milieu est efficace. Figure V-10 : Courbe de refroidissement et courbe correspondante de vitesse de refroidissement. Les différentes étapes du refroidissement sont indiquées : évaporation (étape A), ébullition (étape B) et convection (étape C). (D’après Ref23, p.69) a) Cours de métallurgie, ENIT-Département de Génie Mécanique 58 Souad BEN SLIMA
- 59. MILIEU Air Huile Eau Eau salée CIRCULATION Pas de circulation 0,02 0,25 -0,3 0,9-1 2 Circulation modérée 0,35-0,4 1,2-1,3 Bonne circulation 0,4-0,5 1,4-1,5 Forte circulation 0,05 0,5-0,8 1,6-2 Circulation violente 0,8-1,1 4 5 Tableau V-l : Valeur de H en fonction du milieu de trempe (d'après Ref 1, p.143) Il apparaît que pour améliorer l'efficacité d'un milieu, différentes précautions sont à prendre : -La masse du bain de trempe doit être deux fois supérieure à celle de la pièce à tremper pour éviter un échauffement excessif du bain car quand T augmente la drasticité diminue (Fig. V-11a). - Il faut agiter la pièce dans le bain de trempe au cours du refroidissement pour améliorer l'échange thermique. Cependant, ceci n'est pas recommandé pour les pièces de formes irrégulières qui doivent être manipulées avec cure (fig. V- 11b). - Prendre en compte la géométrie de la pièce; en effet, une pièce présentant des épaisseurs différentes ne subira pas un refroidissement homogène, exemple : trempe d'un engrenage (Fig. V-11 c et d) - Les milieux de trempe doivent satisfaire un certain nombre de conditions : bonne conductibilité, viscosité faible, non inflammable, bonne absorption de la chaleur, volatilité basse. Cours de métallurgie, ENIT-Département de Génie Mécanique 59 Souad BEN SLIMA
- 60. Figure V-11 : Influence de quelques paramètres sur l'efficacité de la trempe (a) influence de la température du bain de trempe (b) influence de l'agitation (c) cartographie thermique d'un engrenage à un instant t de son refroidissement, noter que la température varie considérablement d'un point à l'autre en fonction de l'épaisseur (d) influence du diamètre de la pièce trempée (Rej 23) b) La vitesse critique de trempe : Le but de la trempe étant d'obtenir une meilleure dureté, elle sera d'autant plus efficace qu'il est possible d'avoir une structure martensitique. C'est ainsi qu'on définit une vitesse limite au dessus de laquelle la structure sera exclusivement martensitique. Cette vitesse est appelée vitesse critique de trempe qu'il est possible de déterminer à partir des courbes TRC (Fig. V-6). Si v>vCT : structure martensitique Si v<vCT : structure mixte Les aciers dont la vitesse critique de trempe est inférieure à la vitesse de refroidissement à l'air sont dits auto trempant, c'est à dire qu'ils sont martensitiques même refroidi à l'air, leur vitesse critique de trempe est inférieure à la vitesse de refroidissement à l'air (Exple: Z200C12) Les courbes TRC sont des courbes établies à partir d'éprouvettes creuses et de faible épaisseur. Leur utilisation pour des pièces massives donnera des résultats approximatifs puisque le résultat d'une trempe à la surface d'une pièce en acier n'est pas le même qu'au cœur. On a alors établi des essais qui renseigneraient sur l'évolution de la dureté de la surface d'une pièce massive à son cœur. C'est ainsi qu’ont été introduite la notion de trempabilité et l'essai qui lui correspond. c) La trempabilité : La trempabilité d'un acier est son aptitude à former de la martensite dans tout le volume de la pièce trempée; on appelle aussi cette propriété aptitude à la pénétration de trempe. Lorsqu'on trempe une pièce massive, la surface de la pièce va être refroidie plus vite que le cœur, et au fur et à mesure que l'on s'éloigne de la surface la vitesse de refroidissement subie par les différentes parties de la pièce va diminuer. Ainsi, certaines parties vont subir une vitesse de refroidissement supérieure à la vitesse critique de Cours de métallurgie, ENIT-Département de Génie Mécanique 60 Souad BEN SLIMA
- 61. trempe et d’autre une vitesse inférieure. Grossman et Bain (1930-1940) définissent la trempabilité à partir du diamètre critique de trempe. Le diamètre critique est le plus grand diamètre d'une barre trempée dans un milieu donné pour lequel la totalité du volume est trempée. φ<φc : tout le volume est trempée. φ >φc : une partie du coeur est non trempée (V-12). Remarque : On définit comme non trempé, le volume où on produit moins de 50% de martensite. Ainsi quand φ augmente, le diamètre non trempé (φd) augmente aussi. Le diamètre critique de trempe dépend évidement de la sévérité de trempe. Plus H est élevé et plus φc est grand. Figure V-12 : Représentation schématique de l'étendue de la trempe en fonction du diamètre de la pièce Une autre approche a été mise au point pour évaluer la trempabilité d'un acier. Elle consiste en un essai normalisé développé en 1938 par Jominy et Boegehold, il est communément désigné par Essai Jominy. Son avantage par rapport à la méthode de Grossman et Bain est qu'elle permet de caractériser la trempabilité d'un acier à partir d'une seule éprouvette, plutôt que de plusieurs échantillons cylindriques a)Essai Jominy (normalisé AFNOR A 04-303) : L'éprouvette est maintenue à la température de trempe pendant 30 mn, puis elle est soumise à sa base à un jet d'eau bien étudié afin qu'il n'éclabousse pas les surfaces latérales Cours de métallurgie, ENIT-Département de Génie Mécanique 61 Souad BEN SLIMA
- 62. (Durée du jet == 10 mn) (Fig. V-13) Figure V-13 : Schéma du dispositif de l’essai Jominy (NF- A04 -303) L'éprouvette Jominy est cylindrique, meulée suivant 2 génératrices pour la mesure de la dureté. La dureté est relevée en différents points des méplats à partir de la base arrosée. On trace ainsi la courbe représentant la dureté en fonction de la distance à la base (fig. V-14). Figure V-14 : Courbes de trempabilité relatives à différents Types d'acier Cours de métallurgie, ENIT-Département de Génie Mécanique 62 Souad BEN SLIMA
- 63. Figure V-15 : Corrélation entre la trempabilité (hardenability) et la microstructure donnée par la courbe TRC pour un acier au carbone eutectoïde (Ref26, p.330) Les différentes courbes de la figure V-14 expriment 3 comportements différents : (a) la dureté varie très lentement de la surface arrosée au cœur, le matériau a une bonne trempabilité (b) la dureté varie plus rapidement, le matériau a une mauvaise trempabilité (c) la dureté varie considérablement de la surface trempée au cœur. De la surface arrosée jusqu'à l'autre bout de l'éprouvette, la vitesse de refroidissement diminue; donc chaque partie de l'éprouvette aura une structure différente donnée par la courbe TRC (fig. V-15). La courbe déduite de l'essai Jominy permet de connaître la variation de dureté transversale d'une pièce de diamètre quelconque (de la surface au cœur) de la manière suivante : Soit Jx la distance à la surface trempée de l'éprouvette Jominy Cours de métallurgie, ENIT-Département de Génie Mécanique 63 Souad BEN SLIMA
- 64. φ Le diamètre d'une pièce quelconque de l'acier considéré - Connaissant le milieu de trempe (donc H), on choisit ce qu'on appelle la "courbe de sévérité de trempe" correspondante (courbes V-16 a et b) -La courbe de trempabilité de l'acier étudié, déterminée par l'essai Jominy. Exemple : Il est possible de connaître la dureté de la surface au cœur d'une pièce cylindrique de diamètre 100 mm trempée dans l'huile (Figure V-17). Les valeurs prélevées le seront dans l'ordre suivant : Courbe de sévérité de trempe (huile) courbe Jominy o ---------------------------------------- distance de la surface, J x------------------------------Dureté de la pièce La courbe obtenue est appelée courbe en U ou courbe de dureté transversale et représente la dureté en fonction de « la distance à la surface de la pièce d » Figure V-16-a : Courbe de sévérité de trempe (trempe à l'eau, H=2) Cours de métallurgie, ENIT-Département de Génie Mécanique 64 Souad BEN SLIMA
- 65. Figure V-16-b Courbe de sévérité de trempe (trempe à l'huile, H=OA Figure V-17 : Profil de dureté (courbe déterminé à partir à 1a courbe de sévérité de trempe et 1a courbe de trempabilité (Jominy) La courbe Jominy permet aussi avec l'aide du diagramme de Lamont Fig V- 18) d'estimer la dureté au centre, au 1/4 ou au 1/2 du diamètre d'une pièce quand l'acier est trempé dans des milieux de sévérité de trempe (severity of quench) différentes ou de trouver le milieu de trempe adéquat pour obtenir une dureté précise. Cours de métallurgie, ENIT-Département de Génie Mécanique 65 Souad BEN SLIMA
- 66. Figure V-18 : Diagrammes de Lamont (a) pour le centre d'une pièce (b) au 1/4 du diamètre (Distance from water cooled end= Jx) (Ref.23) Cours de métallurgie, ENIT-Département de Génie Mécanique 66 Souad BEN SLIMA
- 67. e) Les éléments améliorant la trempabilité Il ne faut pas confondre trempabilité et capacité de durcissement par trempe. Un acier Al peut avoir après trempe une martensite plus dure qu'un autre acier A2 car il contient plus de carbone. Ceci ne préjuge en aucun cas de sa trempabilité. L'acier A2 peut avoir une meilleure trempabilité s'il contient plus d'éléments d'alliage Un acier qui a une courbe TIT (ou TRC) dont le nez de la perlite (ou domaine de la bainite) est très proche de l'axe des ordonnées a une faible trempabilité car au cours de la trempe il va se former quelque soit la vitesse de trempe, des composés (perlite, bainite) qui amoindrissent la dureté. Plus la vitesse critique de trempe est faible, plus la trempabilité de l'acier est bonne. Tous les éléments d'alliage (à part le cobalt) décalent vers la droite la courbe TIT (ou TRC), ils vont donc améliorer la trempabilité de l'acier, nous en citons : Cr, Mo, W, Ti, V, Nb, etc ... 2. Le revenu La trempe confère aux aciers une structure dure mais particulièrement fragile, une telle structure ne peut être mise en service. Ainsi on procède toujours à un traitement après trempe pour remédier aux effets néfastes de celle ci tout en maintenant à un niveau assez élevé les autres propriétés (dureté, ...). Le revenu est le traitement qu'il faut faire subir au matériau afin d'arriver à un compromis (conditions optimales) entre les propriétés de résistance et celles de ductilité. Il consiste à réchauffer le métal à une température inférieure à la température de début de transformation (AC1 pour les aciers au carbone). Ce réchauffage va éliminer ou atténuer les tensions internes dues à la trempe et causes de fragilité Les caractéristiques de résistance (Re, Rm, et HB) vont diminuer au cours de revenu alors que la résilience augmente; la température idéale de revenu serait celle qui correspond au point d'intersection de ces deux caractéristiques. Notons, cependant, que le revenu peut être un traitement qui conduit à l'amélioration simultanée des propriétés de résistance et de ductilité. Mais ceci n'a lieu que dans certains types d'acier qui subissent ce qu'on appelle un "durcissement secondaire" (voir § durcissement par revenu). a)L'objectif du revenu : a - Soit supprimer les contraintes de trempe (relâchement); on dit que le matériau a subi un adoucissement b - Soit; suivant la composition; former d'autres phases qui ont tendance à améliorer la résistance du matériau, on dit qu'il a subi un durcissement. b) Les paramètres du revenu : Pour réussir un revenu un certain nombre de paramètres est à prendre en considération : (1) Temps de revenu (température fixe) : Lorsque la durée de revenu augmente, la dureté diminue sensiblement pour les temps courts; puis au fur et à mesure que la durée augmente, la dureté ne décroît plus et reste sensiblement constante. La diminution ne se fait donc que pour les premiers temps. Ainsi, on définit une durée limite de revenu au delà de laquelle il n'y a plus de variation Cours de métallurgie, ENIT-Département de Génie Mécanique 67 Souad BEN SLIMA
- 68. sensible de la dureté et donc il sera inutile de chauffer au delà de cette durée. La durée de revenu choisie pratiquement est d'une heure. En général, il y a interchangeabilité entre la durée (t) et la température (T) de revenu. Une même dureté peut être obtenue pour une faible température et une longue durée, ou une température élevée et une durée courte. Cette interchangeabilité est donnée par un paramètre dit paramètre de revenu = T (20 + loge t).10-3. (T : Kelvin, t : heure). Cette formule est à utiliser avec prudence pour les aciers présentant un durcissement secondaire. La durée de revenu généralement adoptée est une heure. (2) Température de revenu (temps fixe) : La température de revenu dépend de la nature de l'acier et du but du revenu. Pour les aciers au carbone ou faiblement alliés, la température de revenu se situe entre 200 et 600°C, cependant il existe des matériaux qui subissent des revenus à la température ambiante (20°C), le temps de revenu qui correspond au durcissement (qu'on appelle aussi vieillissement) est d'environ 4 jours. On dit que l'alliage a subi un revenu de durcissement. En effet, pour certains matériaux, le revenu peut faire précipiter des carbures qui vont durcir la structure (voir §"durcissement par revenu" plus loin). Pour les aciers au carbone et de construction (%C : 0,25-0,6), la conséquence du revenu dépend de la température utilisée. - revenu à basse température (150-200°C) : la ductilité est légèrement améliorée (contraintes résiduelles diminuent), la dureté reste élevée. - revenu à température intermédiaire (350-500°C) : C'est le domaine des compromis où les propriétés de résistance et ceux de ductilité sont correctes. Il existe un domaine "dangereux" de température de revenu (250-350°C) où la ténacité diminue dangereusement (augmentation de la fragilité). Ce domaine de température est dans la pratique toujours évité (voir § « fragilisation de revenu »). - revenu à haute température : C'est les températures où on a les meilleures résilience, par contre la résistance à la traction et la dureté chutent considérablement (adoucissement). La figure V-19 montre l'influence de la température de revenu sur K, Re et Rm, ainsi que sur la dureté et la ductilité (A %, Z%). Lorsque l'utilisation de l'acier nécessite une bonne dureté et que la résilience reste au 2eme plan, la température de revenu sera entre 200 et 400°C; lorsque c'est la résilience qui est sollicitée, les températures de revenu vont de 500 à 680°C. Figure V-19 : Courbes représentant la variation de certaines propriétés mécaniques (Z% : réduction in area, A % Elongation, dureté : hardness, Rm : tensile strengih, Re : yield strengih, Résilience : Izod impact energy) en fonction de la température de revenu d'un acier faiblement allié (Ref23) Cours de métallurgie, ENIT-Département de Génie Mécanique 68 Souad BEN SLIMA
- 69. Pour les aciers à % en carbone élevé (%C>O, 6), les duretés atteintes après trempe sont très élevées et le revenu ne les diminue que légèrement. Il n'est pas possible pour ces aciers d'obtenir par revenu des niveaux de ténacité élevés; le revenu provoque même parfois (pour les températures basses) une légère augmentation de la dureté. Ainsi, ce type d'aciers sont utilisés pour les applications où une grande dureté et une résistance à l'usure élevée sont requises, et où une faible ténacité ne peut pas avoir de conséquences désastreuses Exemple : poinçons pour estampage, matrices, ... (3) Le chauffage de revenu Les températures de revenu étant plus ou moins faibles, il est toujours conseillé d'utiliser des bains d'huile ou de sels afin que le chauffage soit homogène dans toute la pièce, chose difficile dans un four électrique, par exemple. Certains sels utilisés : mélange de nitrate de potassium et de sodium. (4) Le refroidissement après revenu Il est plus prudent de le faire à l'air ambiant pour ne pas provoquer d'éventuelles déformations. La vitesse de refroidissement après revenu n'affecte pas les propriétés de résistance (dureté, Rm, ...) mais peut diminuer la résistance aux chocs (donc la ténacité). C'est le cas de certains aciers au chrome-nickel (aciers faiblement alliés) qui doivent être refroidis après revenu soit à l'eau, soit à l'huile sous risque d'obtenir un produit très fragile (formation de carbures). Il s'agit de la fragilité de revenu qui conduit à une mauvaise résilience et une mauvaise ductilité (à voir plus loin). c) Les courbes de revenu (figure V-20) : Elles donnent l'évolution de la dureté en fonction de la température de revenu pour une durée de revenu fixe. Elles peuvent ainsi fixer l'utilisateur sur la température de revenu à choisir pour obtenir la dureté voulue Figure V-20 : Courbes de revenu de certains aciers, influence des éléments dl alliage sur le comportement au revenu (Ref9) Cours de métallurgie, ENIT-Département de Génie Mécanique 69 Souad BEN SLIMA
- 70. d) Transformations structurales au cours du revenu : Le revenu se fait toujours sur une structure trempée, donc généralement sur une structure martensitique. Rappelons que la martensite est une phase sursaturée en carbone et instable (structure hors d'équilibre); ainsi elle aura tendance sous l'effet de la température à rejoindre l'état d'équilibre par un ré arrangement des atomes. Le revenu va amorcer un tel processus dont la force motrice sera donc la sursaturation en atomes de carbone. Notons que toutes les phases présentes susceptibles de se transformer seront concernées par la transformation au revenu. Ainsi, à côté de la martensite, l’austénite résiduelle se transformera aussi. Les transformations au revenu vont se faire d’une manière graduelle suivant généralement- 3 étapes : Etape 1 : Diffusion du carbone en dehors de la martensite et formation de carbures de transition. Le % en carbone de la martensite diminue en principe de 0,25% : M(X) ------>carbures I + M(X') avec X’<X Etape 2 : L'austénite résiduelle se transforme en ferrite et cémentite : γ res -------> α + F e3C Etape 3 : Transformation des carbures et de la martensite de l'étape 1 en ferrite et cémentite : Carbures I + M ------>α + Fe3C Suivant la température et la durée de revenu mises en œuvre, toutes les étapes ou seulement une partie seront exécutées. Ces transformations expliquent donc l'évolution des propriétés mécaniques au cours du revenu. En effet, la transformation de la martensite (structure hors d1équibre) en ferrite et cémentite (structure d'équilibre) fait passer la structure de dure à moins dure. La première étape fait moins diminuer la dureté dans la mesure où la martensite bien que diminuée en carbone existe toujours. e) Le durcissement par revenu : Le revenu peut être un traitement qui durcit le matériau par un mécanisme que nous allons voir. Pour les aciers, le principe est le même : tout durcissement après revenu est du à la précipitation d'une nouvelle phase (solution solide, composé défini, ...). Ainsi, seront sujets au durcissement par revenu, les aciers qui contiennent des éléments d'alliage favorisant la formation des phases précitées. Cette étape du revenu est dite étape 4. Exemples : 1- Les aciers alliés : Il existe un domaine de température de revenu (entre 450 et 550aC) pour lequel la dureté s'arrête de diminuer, voire augmente. Ce retard à l'adoucissement et/ ou cette augmentation de la dureté sont dus à la formation de carbures (autres que la cémentite) à partir des éléments carburigènes qui existent dans la composition de certains aciers alliés (V, Mo, Ti, W, Cr, ...). Ces éléments étant plus avides de carbone que le fer peuvent -pour ces températures- arracher le carbone de la cémentite provoquant ainsi sa dissolution, et naître. Plus le % en éléments carburigènes est important, plus la quantité de carbures générés est grande. Ces carbures sont en général très fins et dispersés. C'est leur taille, leur répartition et leur densité qui sont responsables du durcissement par revenu (ce Cours de métallurgie, ENIT-Département de Génie Mécanique 70 Souad BEN SLIMA
- 71. qu'on appelle aussi, dans ce cas, durcissement secondaire). En effet, si la température dépasse le domaine défini, ces carbures grossissent et se regroupent (coalescence), et on assiste à une diminution de la dureté (adoucissement). La susceptibilité d'un acier à subir un durcissement secondaire est une propriété très importante dans la mesure où elle peut être mise à profit pour certaines structures qui travaillent à des températures relativement élevées tels que les aciers à outils. En effet, de tels aciers ne risquent pas l'adoucissement en service mais, bien au contraire, un renforcement de leurs propriétés de résistance. 2-Les aciers "Maraging » :(Martensite Aging : vieillissement de la martensite) Ces aciers sont à base de fer, 18 à 20% de Ni, 8 à 18% de Co, avec des addition de Mo et Ti et contenant des % en carbone extrêmement faibles. La présence de cobalt dans ces aciers entraîne la naissance d'une série de phases durcissantes (pas forcément des carbures) et décale le processus d'adoucissement par revenu vers les hautes températures. Le durcissement dans ce type d'acier se fait après trempe par un maintien de 3 à 12 heures à une température entre 450 et 500°C. Ce séjour en température est appelé vieillissement. Dans les aciers maraging, la martensite peut se former pour des vitesses de refroidissement assez lentes (présence d'une quantité importante d'éléments d'alliage), en outre, elle ne sera pas très dure puisque ces aciers contiennent très peu de carbone. Ainsi, le traitement de revenu ou vieillissement qui se fait sur ce type de martensite conduit à des structures à très hautes résistances mécaniques (Re : 1500 à 2500 MPa), combinées à une bonne ductilité et ténacité. f) Fragilité de revenu : Les aciers trempés et revenus sont susceptibles de se fragiliser au cours du revenu. Cette fragilité est traduite par une diminution de la résilience à la température ambiante et une augmentation de la température de transition ductile fragile (figure V-21). Figure V-21 : Courbes de résilience (acier tenace - acier fragile) Il existe 2 types de fragilisation par revenu : fragilisation de la martensite revenue (FMR) et fragilité de revenu (FR). Le premier type de fragilisation (FMR) se fait dans un domaine de température entre 260 et 370°C (durée : 1heure). Cette fragilisation semble être associée à la deuxième étape du revenu c'est à dire à la transformation de l'austénite résiduelle en cémentite. La morphologie de cette cémentite est telle qu'elle fragilise la structure résultante (fines lamelles entre les lattes de martensite). D'ailleurs, la rupture se fait Cours de métallurgie, ENIT-Département de Génie Mécanique 71 Souad BEN SLIMA
- 72. justement au niveau de ces lamelles de cémentite. Contrairement à la fragilisation de la martensite revenue, la fragilité de revenu intervient lorsque les durées de revenu sont très importantes. C'est à dire que si un matériau ne subit pas de FMR, il peut subir une FR. Le domaine de température dans lequel ce type de fragilisation peut avoir lieu est 375-575°C. La FR est due à la présence même discrète (<100ppm) d'impuretés généralement inévitables dans les aciers telles que : P, Zn, As, Sb. Ces éléments ségrégent dans les anciens joints de grains d'austénite causant une rupture fragile à ce niveau. Ce type de fragilisation est important à connaître surtout pour les pièces à sections importantes qui sont généralement revenues à des températures élevées pour assurer un bon compromis entre les propriétés de résistance et de ductilité. Les grands arbres et rotors pour générateurs de puissance, par exemple, sont très susceptibles à la FR car même si le revenu est pratiqué à des températures supérieures à 575°C, du fait de leurs diamètres importants, la vitesse de refroidissement au cœur sera très faible et le séjour dans le domaine de température dangereux est inévitable. Il est possible de remédier à la FR en maintenant le matériau à 575°C pendant quelques minutes. Les phénomènes microstructuraux responsables de la fragilisation et défragilisation par revenu restent encore à éclaircir et approfondir. g) Revenu et éléments d’alliage : Les éléments d'alliage peuvent intervenir au moment du revenu pour retarder l'adoucissement, c. à. d. pousser ce phénomène à avoir lieu vers les plus hautes températures. Les éléments non carburigènes (Ni, Si, Al, Mn) ont un effet très peu sensible sur la dureté après revenu. Les éléments carburigènes (Cr, Mon W, V, Nb, Ti), par contre, durcissent la structure pendant le revenu par la formation de carbures aux hautes températures (voir l'exemple des aciers à outils). h) Technologie du revenu : Le revenu se fait dans différents types de four. Le choix se fera en fonction du type de pièces à traiter et de la finalité du revenu. Ainsi on trouve : - Les fours à convection (circulation d'air chaud) qui œuvrent entre 50 et 750°C. Ils sont adaptés aux grandes pièces mais le contrôle de la température y est difficile. - Les fours à bain de sel œuvrant entre 160 et 750°C. Ils permettent un chauffage uniforme des pièces. Cependant le nettoyage après séjour dans ce type de four étant nécessaire, les pièces à géométries complexes ne peuvent pas y être traitées (nettoyage difficile). - Les huiles chaudes (T≤250°C) : bien adaptées pour les traitements de longue durée. - Les bains de métal fondu (Pb ou eutectique Pb-X, T>390°C) : Ils sont de moins en moins utilisés car ils sont toxiques. Le revenu peut être : - sélectif (ne concerne que quelques parties des pièces), dans ce cas c'est les fours à induction qui sont utilisés. - massif : concerne toute la pièce, c'est le cas le plus courant. - multiple : il consiste en plusieurs étapes qui peuvent avoir des températures et es durées différentes. - double : il est appliqué aux aciers fortement alliés contenant des éléments Cours de métallurgie, ENIT-Département de Génie Mécanique 72 Souad BEN SLIMA
- 73. gamma gènes qui vont stabiliser γ. Celle ci peut se transformer en martensite au cours du refroidissement après revenu. Ainsi un deuxième revenu s'impose pour relâcher les contraintes dues à cette transformation. E.LES ACCIDENTS DUS AUX TRAITEMENTS THERMIQUES : 1. Accidents durant le chauffage : Les accidents pouvant avoir lieu pendant le chauffage peuvent être résumés comme suit : - Chauffage trop rapide qui crée des contraintes dans les zones externes spécialement pour les pièces assez épaisses. Ceci est du à un gradient de température entre la surface et le coeur et une différence de dilatation thermique. - Chauffage non uniforme (surchauffe locale, chauffage d'un seul côté) - Chauffage à trop haute température et/ ou pendant un temps très long. a) Oxydation : Fe + O2 ------> FeO2 C'est un phénomène assez courant et normal dans certaines limites. L'oxydation peut ne pas être considérée comme un accident étant donné qu'en général les traitements ont lieu dans une atmosphère contenant de 1’o2 (air). La couche d’oxyde formée peut s'enlever par décapage ou rectification mécanique. Cependant, si la température et/ou la durée du chauffage sont trop importantes, l'oxydation peut conduire à une rupture. En effet, dans ces conditions, l'oxygène va diffuser vers les joints de γ et les oxydes ainsi formés sont fermement ancrés dans la structure. Ceci provoque au niveau de la surface des défauts qu'on appelle "peau d'orange" ou "peau de crocodile" du fait de leur aspect suggestif. Ces défauts sont des amorces faciles de fissures quand le matériau se déforme (en service ou pour la mise en forme) b) Décarburisation : C + O2 ------> CO2. La décarburisation a très souvent lieu en relation avec l'oxydation puisqu'elle fait aussi intervenir l'action de 1'O2 sur le matériau, mais elle peut aussi faire intervenir dans certains cas l'H2 (hydrogène). La décarburisation par 1'O2 se fait par diffusion du C vers la surface et son dégagement sous forme de gaz. La proportion de C perdu est proportionnelle à la racine carrée du temps de maintien. Le coefficient de diffusion du C dans γ est plus bas que celui du fer α, c'est pourquoi la décarburisation diminue quand on passe du domaine u vers le domaine γ. Cependant, quand l'oxydation intervient avec la décarburation, celle ci ne devient importante que dans le domaine γ (T>800°C). (Quand T augmente, la décarburation est favorisée et l'oxydation défavorisée). La décarburisation superficielle provoque une diminution de la dureté, de la trempabilité et de la résistance à l'usure. Elle diminue aussi considérablement la résistance à la fatigue. Dans les parties décarburées, Ms augmente entraînant ainsi la formation de la martensite plus tôt par rapport aux autres zones, ce qui conduit à la création de contraintes locales. c) Surchauffe/brûlure : Quand Tγ augmente exagérément, des précipités d'oxydes ou de silicates se forment aux joints du grain γ surchauffé. Ces joints se ramperont facilement durant la mise en forme de la pièce. La présence de tels précipités indique qu'une brûlure a eu lieu. Ce type d'accident ne peut être guéri par traitement thermique. La surchauffe est un Cours de métallurgie, ENIT-Département de Génie Mécanique 73 Souad BEN SLIMA
- 74. grossissement exagéré du grain, ce qui diminue considérablement la résistance à la propagation de fissure en fatigue et augmente la sensibilité à la rupture fragile. Cet accident peut être guéri par un recuit de régénération. Ainsi, les températures d'austénitisation doivent être choisies judicieusement pour éviter ce genre d'accident; elles sont très souvent spécifiées (courbes TRC, manuels, ...). d) Non uniformité du chauffage : Elle peut conduire à la création de contraintes responsables de la rupture prématurée des pièces. Ce type de problème est rencontré pour les matériaux à conductivité thermique très faibles tels que les aciers rapides (les aciers alliés ont une conductivité plus faible que celle des aciers au carbone). Leur chauffage doit donc être effectué lentement et d'autant plus lentement que la pièce est grosse. Il ne faut jamais mettre une pièce froide dans un four porté au rouge. Par ailleurs, il faut que le séjour en température se fasse pendant des durées suffisantes pour égaliser la température au cœur et à la surface de la pièce. 2. Accidents durant le refroidissement : Durant le refroidissement rapide d'une pièce, 2 phénomènes interviennent : a) la variation dimensionnelle (contraction), b) la transformation structurale : martensitique. a) La contraction différentielle fait que les différentes parties de la pièce ne refroidissent pas toutes en même temps, ce qui générera des contraintes. La dernière partie du métal qui refroidit sera soumise à une contrainte de traction. La contrainte générée est proportionnelle au gradient de température Cours de métallurgie, ENIT-Département de Génie Mécanique 74 Souad BEN SLIMA
- 75. σthermique = Eα ∆T σ thermique contrainte générée par le gradient thermique ∆T : gradient thermique E: module d'Young α: Coefficient de dilatation thermique b) La transformation γ ------> Martensite est accompagnée d'une variation de volume (Dilatation) telle que Si toutes les parties de la pièce ne se transforment pas en même temps du fait d'un différentiel de température, des contraintes seront générées entre les parties transformées et non transformées. La partie qui se transforme en dernier est en compression. Ce sont ces contraintes qui seront à l'origine des accidents qui ont lieu lors du refroidissement, c'est à dire : a) Les tapures : Ce sont des fissures dues à un gradient de température important à l'intérieur de la pièce qui crée des tensions internes dépassant la limite à la rupture du matériau. La pièce se fend ou éclate. La naissance des gradients de température peut être due à des variations de dimensions dans une seule pièce ou à des angles vifs. Solutions : trempe moins vigoureuse (choix d'un matériau qui trempe bien à l'huile). Pour les pièces à sections différentes, il faut plonger d'abord la partie de φ plus faible. Dans certains cas, il est préférable d'opter pour une trempe étagée. Le choix du milieu ou du processus de trempe dépend beaucoup du dessin de la pièce. Plus celle ci comporte de changements de section, d'angles vifs ou d'évidements, plus la vitesse de trempe doit être faible. L'acier à choisir doit donc être trempable dans le milieu choisi. Certains procédés peuvent éviter ces accidents de trempe comme le bouchage provisoire de trous ou évidements pendant la trempe. b) Les déformations : Ce sont des variations de dimensions et de la forme de la pièce consécutives au traitement thermique. Elles ont lieu lorsque la limite élastique est dépassée. Elles peuvent être dues à un échauffement trop rapide et inégal des pièces de forme irrégulière (exemple : vilebrequin) Solutions : Il faut surdimensionné les pièces de manière à pouvoir effectuer un redressement après traitements et amener la pièce aux côtes désirées. Les déformations peuvent aussi être évitée en choisissant la trempe à l'air plutôt qu'une trempe liquide. Une trempe par étapes (bain de sel +air) peut aussi faire l'affaire et donner des duretés plus élevées qu'une trempe à l'air Cours de métallurgie, ENIT-Département de Génie Mécanique 75 Souad BEN SLIMA
- 76. IX. ANNEXE : RAPPEL SUR LES DIAGRAMMES D’ÉQUILIBRE A.HISTORIQUE DES MÉLANGES L'origine des mélanges des métaux relève d'anciennes traditions métallurgiques, plutôt mystiques. En Afrique noire et dans la Chine ancienne, le mélange des métaux était conçu comme "un mariage" qui devait se faire suivant les rites qui en découlent afin de rendre "la naissance" d'un nouveau matériau possible. Ainsi, les minerais étaient divisés en "mâles" et "femelles" dont le mélange était nécessaire pour assurer "une fusion fructueuse". Les rituels métallurgiques de la Chine ancienne associent en plus à cette fusion un être vivant. Ainsi, un sacrifice s'impose où le mariage mystique entre un être humain et le métaux se fait. D’après la mythologie Chinoise, un couple de forgerons n'a réussi à fondre le minerai pour l'élaboration de deux épées qu'en se jetant tous les deux dans le fourneau. Nous voyons que nous sommes encore loin des règles de miscibilité et de limites de solubilité sur lesquelles s'appuient les méthodes actuelles d'obtention des alliages. Aujourd'hui, pour réussir le mélange et le traitement de 2 ou plusieurs métaux nous n'avons plus besoin de nous jeter dans les hauts fourneaux mais de consulter ce que plusieurs siècles d'expériences et d'études ont donné en abaques et diagrammes. Nous parlerons dans ce chapitre des diagrammes d'équilibre binaires. B.LA NOTION DE SOLUTION SOLIDE Même le plus pur des métaux réels utilisés industriellement contient des atomes étrangers (atomes d'un autre élément). Quand ces éléments sont dissout dans le métal de base, il se forme ce qu'on appelle une solution solide primaire. Dans de tels cas, ces atomes s'arrangent dans le réseau cristallin du métal de base et les caractéristiques cristallographiques de ce dernier ne changent que très peu (réseau cristallin, paramètres cristallins, ...). Suivant la taille de l'élément d'addition, 2 types de solution solide peuvent prendre naissance : Figure IX-1 : Représentation des différents types de Solution solide (substitution, insertion) Cours de métallurgie, ENIT-Département de Génie Mécanique 76 Souad BEN SLIMA
- 77. 1. Solution solide d'insertion (SSI) Les atomes étrangers viennent se loger dans les espaces libres entre atomes; pour cela, ils doivent être de petites tailles. Les atomes susceptibles de former des SSI Elément H O N C B Rayon atomique (Ả) 0 , Ces atomes vont s'insérer dans les lieux vacants de la structure (qui dépendent de la structure). a) Sites d'insertion pour quelques structures : Structure cubique centrée : X : sites d'insertion octaédriques, entourés par 6 atomes du réseau (centre d'un octaèdre) milieu des arêtes : 126 (1/4) = 3 centre des faces : 66 (1/2) = 3 total = 3 + 3 = 6 o : sites d'insertion tétraédriques, entourés par 4 atomes du réseau (centre d'un tétraèdre) : entre 2 sites octaédriques => sur chaque face il y aura 4 atomes : 4666 (1/2) = 12 total = 12 Structure cubique à faces centrées Cours de métallurgie, ENIT-Département de Génie Mécanique 77 Souad BEN SLIMA
- 78. x : sites octaédriques: - centre du cube : 1 6(1) = 1 - milieux des arêtes : 1 2 6 (1/4) = 3 Total = 4 O : site tétraédrique - centre des cubes représentant le 1/8 du cube élémentaire 861=8 Total = 8 2 .Solution solide de substitution (SSS) Les atomes étrangers (B) vont remplacer (substituer) les atomes de base (A) : Atome étranger plus grand Atome étranger plus petit que les atomes de base que les atomes de base Dans les 2 cas il y a distorsion du réseau. Les atomes de B peuvent remplacer ceux de A de 3 manières différentes : - d’une manière ordonnée : SSS ordonnée Cours de métallurgie, ENIT-Département de Génie Mécanique 78 Souad BEN SLIMA
- 79. Chaque type d’atomes occupe des sites bien définis - d'une manière désordonnée : SSS désordonnée Les atomes sont répartis d’une manière aléatoire - d'une manière semi-ordonnée : SSS de rassemblement Les atomes sont rassemblés par groupe 3. Limites de solubilité ou règles de miscibilité Pour les solutions d'insertion, la limite de solubilité dépend de la taille des sites interstitiels qui sont disponibles pour les atomes de l'élément d'addition. Par exemple, les sites dans le fer α (C.C.) sont très petits (sites octaédriques : 0,19 Â), le diamètre des sites que les atomes de carbone peuvent occuper (octaédriques) est seulement le 1/4 du diamètre d'un atome de carbone (Φc =0,77 Â). Ainsi, le fer α ne dissoudra que très peu de carbone : 1 atome de carbone pour 10 millions d'atomes de fer (pour Fe α) et 1 atome de carbone pour 1000 Fe (pour Fe δ, aux températures élevées). Par contre, les sites disponibles dans le fer γ (C.F.C.), bien que moins nombreux, sont plus larges que ceux du fer a (sites octaédriques : 0,52Å). Ainsi, plus de 10 atomes de carbone par 100 atomes de Fer peuvent être dissous Pour les solutions solides de substitution, les facteurs essentiels pour que B (soluté) soit totalement soluble dans A (solvant) sont : * Facteur de taille : il faut que A et B aient des rayons atomiques voisins. D'après la règle de Hume-Rothery, si les rayons atomiques de A et B sont différents de plus de 15% (écart de taille> 15), la solubilité de B dans A est limitée. * Isomorphisme : si les 2 éléments s'arrangent dans le même système cristallin, la Cours de métallurgie, ENIT-Département de Génie Mécanique 79 Souad BEN SLIMA
- 80. miscibilité totale est assurée. * Les 2 éléments doit avoir la même électronégativité (sinon la liaison devient ionique) Exemples : 1- Cu et Ni sont solubles complètement, les 2 sont C.F.C. et leurs rayons atomiques différent de seulement 2%. 2- Cu et Pb ont le même système cristallin (C.F.C.), mais les rayons atomiques différents de 50%, Pb sont insolubles dans Cu. 3- Cu et Zn ont des rayons atomiques qui différent de 4%, mais Cu est C.F.C. et Zn est H.C., la solubilité est limitée. Tout ce qui vient d'être dit à propos de la limite de solubilité s'applique pour les conditions d'équilibre. Cependant, il est possible d'avoir des solutions supersaturées dans des conditions hors d'équilibre (refroidissement à très grande vitesse), l'élément de base contiendra plus d'élément d'addition qu'il ne le peut. Bien sûr, la déformation qui en résulte sera très importante et le produit sera très différent de la solution solide primaire. L'exemple le plus connu - et qu'on traitera plus tard - est celui de la supersaturation du fer a en atomes de carbone, supersaturation qui donne lieu à un autre constituant appelé martensite. Un tel type de solution solide est, cependant, métastable. 4. La notion de phase intermédiaire Que se passe-t-il quand le réseau de l'élément de base A ne peut plus contenir (ou ne peut plus s’accommoder) à d'autres atomes de l'élément d'addition B (limite de solubilité atteinte) ? Les éléments d'addition devront trouver une manière différente pour s'associer avec l'élément de base et ceci en formant une nouvelle phase qui aura une structure cristalline différente des 2 éléments A et B qui la constituent. Cette nouvelle phase, dite intermédiaire, peut être soit une solution solide secondaire ou un composé défini. 5. Composés définis Ils existent pour une composition bien déterminée de B dans A, de manière à pouvoir identifier sa formule stœchiométrique Ax By. 6. solutions secondaires Quand le domaine d'existence d'une seconde phase n'est pas restreint à une composition comme pour le composé défini mais à un domaine de composition, on dit qu'on a une solution solide secondaire. 7. Définition de quelques terminologie (1) Qu'est ce qu'une phase ? Ce mot vient du grec et veut dire "apparence", c.à.d. que pour une même composition chimique on peut avoir plusieurs phases (apparences). Une phase peut être définie comme étant une région du matériau ayant la même composition chimique et la même structure cristalline. Exemple : 1- L'eau (H2O) et la glace (H2O) sont 2 phases de même composition mais d'apparence Cours de métallurgie, ENIT-Département de Génie Mécanique 80 Souad BEN SLIMA
- 81. différente. 2- Le graphite (C) et le diamant (C) sont 2 phases solides du carbone mais de structure différente. 3- L'eau salée : 1 phase, 2 constituants (eau + sel). (2) Qu'est ce qu'un alliage ? C'est le produit solide que l'on obtient en faisant fondre ensemble 2 ou plusieurs métaux, puis en le laissant refroidir jusqu'à la température ambiante. Alliage binaire : 2 éléments Alliage ternaire : 3 éléments C.INTRODUCTION AUX DIAGRAMMES D'ÉQUILIBRE Le premier pas à faire pour obtenir un matériau dans un état qui peut être ultérieurement travaillé, c'est de l'élaborer. L'élaboration consistera à le faire passer de l'état liquide l’état où son extraction du minerai se fera, et/ ou l'addition de différents éléments d'addition est possible) à l'état solide, c'est la solidification; puis de continuer le refroidissement jusqu'à la température ambiante. Les processus qui ont lieu au refroidissement d'un alliage avant, pendant et après sa solidification font intervenir des transformations structurales déterminantes pour la connaissance de la structure du produit solidifié et par conséquent de ses propriétés physiques et mécaniques. Le rôle des diagrammes d'équilibre est de justement décrire ces transformations. Ils permettent ! en outre de connaître pour chaque température la composition et la proportion des phases et / ou constituants en présence dans un alliage donné. Un diagramme d'équilibre binaire décrit les processus ayant lieu dans un alliage binaire (2 éléments) un diagramme ternaire pour un alliage ternaire (3 éléments), etc.… Comme leur nom l'indique, ces diagrammes ne peuvent être utilisés que dans les conditions d'équilibre, c'est à dire dans des conditions de refroidissement ou de chauffage très lents. Un diagramme d'équilibre binaire présente: en abscisse le pourcentage massique ou atomique d'un des 2 éléments de l'alliage (0 à 100%), en ordonnées les températures de 0 ou 20°C à la température de fusion des 2 éléments à l'état pur (voir figure 2). Cours de métallurgie, ENIT-Département de Génie Mécanique 81 Souad BEN SLIMA
- 82. Figure I-2 : Système de coordonnées d'un diagramme d'équilibre binaire Tf A : température de fusion de A Tf B : température fusion de B C= masse de B x100 masse de A +masse de B C = 30% : Alliage A-B contenant 30% en masse de B et 70% de A Pour sortir des informations d'un diagramme d'équilibre binaire, certaines notions sont exigées, notamment la règle des phases. 1. Règles de phases a) La variance La variance v d'un système est définie comme étant le nombre de degrés de liberté du système, c.à.d. le nombre de facteurs pouvant varier librement sans qu'un quelconque changement soit perçu dans l'état du système. Elle s'exprime par la relation de GIBBS (USA) : v=n+2- φ v ≥0 n : nombre de constituants du système φ: nombre de phases 2 désigne le nombre de variables intensives qui varient (la température et la pression) Dans le cas des diagrammes d'équilibre binaires : - n = 2 (2 éléments constituent le système) - On considère qu'on travaille toujours dans les conditions de pression constante et égale à la pression atmosphérique (1Atm) Dansce cas : v=2+1-φ φ v = 3 -φ Les seuls facteurs qui restent et sur lesquels il est possible de jouer sont la température (T) et la composition chimique (C), coordonnées du diagramme binaire. Nous allons examiner les différentes valeurs que peut prendre la variance : α) Si φ= 1 c'est à dire que nous sommes dans un domaine monophasé (1 seule phase). Donc v = 3-1 = 2, T et C varient dans les limites du domaine sans changer la nature de la phase. β) Si φ= 2 c'est à dire que nous sommes dans un domaine biphasé (2 phases). Donc v = 3-2 = 1, si l'une ou l'autre des 2 variables change le système change. Si l'une est fixée, il faut que l'autre évolue pour que le système évolue. γ) Si φ= 3 c'est à dire que nous sommes dans un domaine triphasé (3 phases). Donc v = 3-3 = 0, toutes les variables sont fixées, le système évolue à température et Cours de métallurgie, ENIT-Département de Génie Mécanique 82 Souad BEN SLIMA
- 83. composition constantes, donc sans intervention externe. Dans un système binaire, il ne peut pas exister plus de 3 phases en équilibre car : v=3 - φ≥ 0 => φ ≤ 3 Exercice : Soit un métal pur, sur combien de facteurs peut-on jouer lors du passage du liquide au solide ? Réponse : v=1+1-2=0 (2 : phase liquide+phase solide). La transformation se fait à température constante. 2. les différents types de diagramme binaires Nous allons nous limiter à un nombre restreint de diagrammes d'équilibre, mais qui sont les plus importants dans le cas de mélanges binaires métalliques ou autres. A partir des diagrammes d'équilibre que nous allons étudier, il sera possible d'imaginer tous les cas possibles de solidification des systèmes à 2 composants (binaires). a)Solubilité mutuelle complète (ou miscibilité totale des 2 éléments) Figure IX-3 : Diagramme à fuseau (miscibilité totale de A dans B) Liquidus : ligne au dessus de laquelle il n'y a que du liquide. Solidus : ligne au dessous de laquelle il n'y a que du solide. Nous allons choisir l'un des plus simples diagrammes d'équilibre binaire où les éléments A et B sont miscibles en toutes proportions. Ceci veut dire que, quelque soit la composition en B, à l'état solide il n'y a qu'une seule phase solide quelle que soit la concentration de l'alliage. Les facteurs essentiels pour que B (soluté) soit totalement soluble dans A (solvant) sont : * Facteur de taille : il faut que A et B aient des rayons atomiques voisins. D’après la règle de Hume-Rothery, si les rayons atomiques de A et B sont différents de plus de 15% (écart de taille> 15), la solubilité de B dans A est limitée. * Isomorphisme : si les 2 éléments s'arrangent dans le même système cristallin, la miscibilité totale est assurée. * Les 2 éléments doit avoir la même électronégativité (sinon la liaison devient ionique) Cours de métallurgie, ENIT-Département de Génie Mécanique 83 Souad BEN SLIMA
- 84. Exemples : 1- Cu et Ni sont solubles complètement, les 2 sont C.F.C. et leurs rayons atomiques différent de seulement 2 %. 2- Cu et Pb ont le même système cristallin (C.F.C.), mais les rayons atomiques différents de 50%, Pb est insoluble dans Cu. 3- Cu et Zn ont des rayons atomiques qui différent de 4%, mais Cu est C.F.C. et Zn est H.C., la solubilité est limitée. Ce type de solidification se retrouve pour des éléments qui ont des réseaux cristallins semblable. Soit l'alliage A-B dont la composition en masse en B est noté X. Comment est-il possible de suivre quantitativement et qualitativement la solidification de cet alliage ? b) Règle du bras de levier ou règle des segments inverses : Figure IX-4 : Méthode d'application de la règle des segments inverses Il suffit de suivre la verticale dans le sens de la flèche (figure IX-4). - A Tl, la verticale coupe le liquidus, on rentre dans le domaine biphasé (L+S), il y a apparition du premier germe de solide qui nage dans le reste du liquide, sa composition est Xi. - A Tl, on est dans le domaine biphasé (L +S), nous avons donc en présence un liquide et un solide. Comment est-il possible de déterminer la masse (ou la proportion) de liquide et de solide dans ce cas (connaissant la masse totale m) ? Là, intervient la règle du bras de levier (ou règle des segments inverses) : Loi de conservation de la masse : m= mL + mS Loi de conservation de B : mL Xl + mS.X2=m.X En écrivant : mS = m-mL On a : mLXl + (m-mL).X2 mL (X 2 - X) PN ms =d’où = = = = MP m X2 − X1 MN m MN Cours de métallurgie, ENIT-Département de Génie Mécanique 84 Souad BEN SLIMA
- 85. mL PN = ms MP Cette dernière égalité nous rappelle la règle appliquée en physique pour l'équilibre entre 2 forces (règle des moments) : MPx mL = PN xmS - A T3, on a atteint le solidus, la dernière goutte de liquide de composition X se transforme solide, la transformation liquide solide prend fin. c) Règle de l'horizontale Comment est-il possible de connaître pour une température quelconque T, la composition du liquide et celle du solide ? Il faut tracer l'horizontale à partir de la température considérée (par exemple T2), son intersection avec le liquidus donne la composition du liquide (Xl); celle avec le solidus donne la composition du solide (X2). mB X = X 100 Composition : (% massique en B) B mA + MB Exercice : Connaissant les masses atomiques de A (MA) et de B (MB), comment passer du % massique au % atomique, et vice versa ? Réponse : % massique (XB) -------> % atomique (CB) CB : dans 100 atomes du mélange, il Y a CB atomes de B atome de B pèse MB CB atomes de B pèsera mB = CB. MB De même : CA = 100-CB => mA = (l00-CB).MA Cours de métallurgie, ENIT-Département de Génie Mécanique 85 Souad BEN SLIMA
- 86. De même, on trouve : Remarque : Nous constatons qu'au fur et à mesure que la température diminue, la composition en B du solide formé diminue (de Xi à X). Théoriquement, on aura en fin de solidification un solide de composition X. Or, la réalité est toute autre. Dans la pratique La diffusion en solution solide étant négligeable, le solide formé aura une composition hétérogène du centre à la surface, cette composition allant de Xi à X (figure XI-5) Figure XI-5. Evolution de la composition en B du solide du centre à la surface du grain d) Diagramme présentant un palier du type eutectique : (Exemples : Cu-Zn, Pb-Sn, Al-Si, Fe-C, Cu-Ag) Figure IX-6 : Diagramme présentant un palier eutectique AEB: ligne de début de solidification (liquidus) AMENB : ligne de fin de solidification solidus) Cours de métallurgie, ENIT-Département de Génie Mécanique 86 Souad BEN SLIMA
- 87. α : solution solide primaire de B dans A (riche en A) β: solution solide primaire de A dans B (riche en B) Cαo : concentration maximale de B entrant en solution solide dans A l-Cβo : concentration maximale de A entrant en solution solide dans B Cαo M : limite de solubilité de B dans A en fonction de latempérature Cβo N : limite de solubilité de A dans B en fonction de la température E : Eutectique, coexistence du liquide, α et β. L'alliage correspondant à la composition CE a une température de fusion inférieure aux températures de fusion des 2 éléments qui le constituent. L'éthymologie du mot l'exprime bien : eutexie=qui fond bien. Exemple : Dans les pays froids, lorsque les routes gèlent et qu'elles constituent un danger pour les conducteurs, les autorités parsèment les routes d'un produit qui forme avec le verglas un mélange eutectique qui fond donc à une température assez basse, plus basse que la température ambiante des jours froids. Comment s'effectue la solidification d'un alliage de composition définie dans ce type de diagramme binaire ? 3 cas différents peuvent se présenter (figureIX 6) : Figure IX-7 : Position des 3 types d'alliages A-B (1) Xαo< X < XαE Cours de métallurgie, ENIT-Département de Génie Mécanique 87 Souad BEN SLIMA
- 88. soit l'alliage de composition Xl - à T=To : formation des premiers germes de α à partir du liquide L. Composition du premier cristal de α = Xo. - pour Tf<T<To (v=l) : L------>α + Lrestant La solidification se poursuit jusqu'à T=Tf. A Tf, tout est solide. Durant la solidification, les proportions de liquide et de a pour chaque température est donnée par la règle du bras de levier ! Leurs compositions par la règle de l'horizontale. Pour T'o<T<Tf : on est dans le domaine de la solution solide α (v=2), aucune transformation n'a lieu : refroidissement de α dont la composition dans tout le domaine est X. - à T'o la solution solide α est sursaturée en élément B (v=l). La température ayant baissé, la limite de solubilité est atteinte. L'excès en élément B va provoquer la formation de cristaux de solution solide β de composition X’0. La masse de β va augmenter au fur et à mesure que la température diminue ! suivant la règle du bras de levier ! jusqu'à la température ambiante. (2) XαE<X <XE, soit l'alliage de composition X2 : - TE<T<To (v=l) : Le liquide se transforme en solution solide a au fur et à mesure que la température décroît : L -----> α + Lrestant Les compositions du liquide et du solide sont données respectivement par le liquidus et le solidus d'après la règle de l'horizontale. Les proportions en liquide et en solide pour chaque température sont données par la règle du bras de levier. - T=TE (v=3) : A cette température nous sommes en présence de 3 phases : liquide ! a et β. La transformation du liquide va se faire à température constante Cours de métallurgie, ENIT-Département de Génie Mécanique 88 Souad BEN SLIMA
- 89. (T=TE). Le liquide restant va se transformer totalement suivant la réaction isotherme dite eutectique : Lrestant ----> α + β Le solide (α +β) résultant va avoir une morphologie particulière, c'est le composé eutectique, il se présente généralement sous forme de lamelles alternées de α etβ. Cette réaction eutectique va se poursuivre jusqu'à la transformation totale du liquide. Remarque : Le solide a obtenu pour TE<T<To est dit α proeutectique pour le différencier du α qui constitue l'eutectique. - pour T<TE (v=l) : le liquide ayant disparu, nous n'avons plus que 2 phases en présence α etβ. Au fur et à mesure que T diminue jusqu'à la température ambiante ! la solution solide α s'enrichit en élément A suivant la courbe de limite de solubilité MCαo, et β s'enrichira en B suivant la courbe NCβo). Questions : a) Déterminer l'expression des proportions de a et du liquide restant à T=TE+ ε. b) Déterminer l'expression qui donne la proportion de l'eutectique pour l'alliage de composition X c)Quelles sont les proportions en α et enβ) du même alliage pour T=TE-ε. d)Quelles sont les proportions de α et de β dans l'eutectique (3) X = XE l'alliage est dit eutectique car sa composition correspond à celle de l'eutectique. T>TE (v=2), l'alliage est à l'état liquide. - T=TE (v=0), il y a coexistence de 3 phases : liquide, α etβ. La transformation se fait à température constante : L ------> α + β Le liquide va se transformer totalement en un composé biphasé (α+β) qui est l'eutectique. Les proportions en α et β de l'eutectique sont les mêmes que celles dé- terminées au d) de l'exercice proposé ci-haut. - T<TE (v=l), les proportions et les compositions de α et β évolueront jusqu'à la température ambiante. Cours de métallurgie, ENIT-Département de Génie Mécanique 89 Souad BEN SLIMA
- 90. Figure IX-8 : Présentation schématique des structures d'alliages de compositions différentes Réponses aux questions : a) Liqrestant = b) b) à T=TE Le liquide va se transformer complètement en eutectique donc : d) Proportion de α et β dans l’eutectique : βE = mβ ; mE = mβ total ; e) Digramme présentant un palier du type péritique (Exemples : Ag- Pt, Cu- Sn, Cd- Hg) Cours de métallurgie, ENIT-Département de Génie Mécanique 90 Souad BEN SLIMA
- 91. Figure IX-9 : Diagramme péritectique TfANTfB : Liquidus TfAMPTfB : Solidus α: Solution solide primaire de B dans A β: Solution solide primaire de A dans B MN : Palier péritectique qui correspond à un système invariant dû à la présence simultanée de 3 phases : liquide, α et β. (1) XM <X<Xp - Tp<T<To (v=l) : La solidification commence par l'apparition de cristaux de α dont la composition est donnée par le solidus. La composition du liquide résultant est donnée par le liquidus. L ----> α+ Lrestant A chaque température : mliquide;ma = O'M';O'N' - T=Tp (température du péritectique) : Coexistence des 3 phases : liquide, α et β=> v=0. La transformation va se faire à température constante jusqu'à la disparition d'une des 3 phases; la transformation mise en jeu dans ce cas est la réaction péritectique : L+α ----> β à T=Tp+ε: Cours de métallurgie, ENIT-Département de Génie Mécanique 91 Souad BEN SLIMA
- 92. La fin de la transformation péritectique est marquée par la disparition du liquide. à T =T P-ε (2) X =Xp - Tp<T<To: La solidification commence par la formation des cristaux de a. - T=Tp : La réaction péritectique a lieu L +α ---->β à T=Tp+ε La fin de la transformation péritectique est marquée par la disparition simultanée de α et du liquide. à T=Tp-ε : Il n'y a plus qui une seule phase β qui commencera à se décomposer pour T<Tp en formant des cristaux de α de composition et quantité données par le diagramme. (3) Xp<X<XN -pour Tp<T<T 0 : Apparition de cristaux de α. -pour T=Tp : Transformation péritectique L+α ---->β Cette fois, c'est α qui est en plus petite quantité et qui va disparaître avant le liquide. La transformation péritectique s'arrête avec la disparition de α. -pour Tp<T<Tf : La solidification se poursuit par transformation du liquide enβ. Les proportions en liquide et en β sont données par la règle des segments inverses : Cours de métallurgie, ENIT-Département de Génie Mécanique 92 Souad BEN SLIMA
- 93. -pour T=Tf : fin de la solidification du liquide en B. Si la verticale de composition coupe la ligne de transformation β ---> α + β -pour T<Tf on va avoir coexistence de 2 phases α etβ, sinon on aura une phase unique β.Remarque: Pour ce cas de concentration, nous avons vu que la réaction péritectique se fait d’après : L + α ----> β. Au moment où se déclenche cette réaction, le liquide au contact avec les cristaux α (déjà formés à des températures plus élevées) va donner les cristaux β; seulement ceci se fera uniquement pour les cristaux de α qui se est dite "péritectique" qui veut dire trouvent à la périphérie puisque le cœur "cristallisé autour". n’est pas en contact avec le liquide. Dans la pratique, nous n'aurons donc pas seulement de la phase β en fin de solidification, mais il subsistera de la phase α au cœur des cristaux. C'est d’ailleurs pourquoi cette transformation f)Diagramme présentant un composé défini ou une solution solide secondaire Figure IX-10 : Diagramme présentant une solution solide secondaire stable (Exemple : Cu-Sn, Cu-Zn) Cours de métallurgie, ENIT-Département de Génie Mécanique 93 Souad BEN SLIMA
- 94. Figure IX-ll : Diagramme présentant un composé défini stable (Exemple : Mg-Si Mn-Si) Figure IX-12 : Diagramme présentant une solution solide secondaire instable Si on juxtapose 2 diagrammes eutectiques, péritectiques ou mixtes, il apparaît dans le domaine de juxtaposition une 3ème phase qui peut être une solution Cours de métallurgie, ENIT-Département de Génie Mécanique 94 Souad BEN SLIMA
- 95. solide nouvelle qu'on appellera secondaire (figure9) ou un composé défini (figure9) dans le cas où l'intervalle composition est réduit. Les figures (9) et (10) précédentes correspondent à des solutions solides ou composés définis stables car ils fondent à température constante sans se décomposer (fusion congruente). Les solutions solides ou les composés définis seront instables quand ils se décomposent au cours de la fusion (fusion non congruente) (figure 11). Dans ce cas,γ se décompose à la fusion suivant la réaction péritectique et donne du liquide et une autre phase α: γ -------> Liquide + α Cours de métallurgie, ENIT-Département de Génie Mécanique 95 Souad BEN SLIMA
- 96. g)Diagramme présentant une lacune de miscibilité en phase liquide Figure IX-13 : Diagramme présentant une lacune de miscibilité (exemple : Cu-Pb) Il existe certains cas d'alliages binaires qui ne forment pas une phase unique à l'état fondu. On dit qu'il existe une lacune de miscibilité à l'état liquide. Ceci a lieu quand les 2 éléments ont des masses volumiques très différentes. (Exemple : Cu-Pb). Soit l'alliage de composition X, comment se transforme t-il au refroidissement à partir de l'état liquide jusqu'à la température ambiante ? - pour T> To, il existe une seule phase liquide - pour T=To : Démixtion, c.à.d. apparition de 2 phases liquide distinctes à partir d'une phase liquide homogène : L -------> L1 + L2 - pour Tm <T< To : La démixtion se poursuit. Les compositions en B de L1 et L2 sont définies par les 2 points extrêmes situés sur la courbe en "cloche" (règle de l'horizontale). Les proportions sont données par la règle du bras de levier. - pour T=Tm : Coexistence de 3 phases (L1, L2 et β), v=0. A cette température se déclenche la transformation isotherme : L2 -----> L1 + β Cette transformation isotherme est dite transformation monotectique. - pour TE <T< Tm : Les compositions et proportions de L1 et β) évoluent suivant les courbes LE et NR. - pour T=TE : Coexistence de L1, β et α; v=o : c'est la transformation Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 96 Souad BEN SLIMA
- 97. isotherme eutectique qui a lieu : L1 -----> α + β h) Récapitulation Les diagrammes d'équilibre binaires les plus usuels pour les métaux peuvent présenter 5 types de transformations isothermes en phase liquide et/ ou en phase solide : Transformation Réaction au refroidissement Aspect dans le diagramme de phase Eutectique Liquide α +β Eutectique α β+γ Péritectoide α + Liquide β Péritectoide α + β γ Monotectique L1 α + L1 3. L'analyse thermique a)Principe La méthode la plus facile pour suivre l'évolution d'une transformation est d'enregistrer la température du matériau en fonction du temps : T=f (t). Cette méthode est dite "analyse thermique». L'essai est réalisé en mesurant continuellement la température de l'alliage à étudier au cours du refroidissement (figure 13). Le matériel nécessaire est très réduit : - un four électrique (pour la fusion du matériau) - un thermocouple (pour mesurer la température) - enregistreur (T=f (t)) - creusets Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 97 Souad BEN SLIMA
- 98. Un matériau qui refroidit sans subir de transformation suit la loi de refroidissement normale du type exponentiel (T = A e-αt). Lorsqu'une transformation commence, puisqu’elle est accompagnée par un effet exothermique (dégagement de chaleur), ceci se traduit par un crochet sur la courbe T=f (t). Lorsqu'on atteint le domaine où v=0 (variance), la transformation devient isotherme ceci se traduit par un palier sur la courbe. b)Applications (1) Cas du corps pur : La solidification d'un corps pur se fait à température constante : v =2-φ ∆t est la durée de solidification, elle est d'autant plus grande que la masse de l'alliage à solidifier est grande. (2) Cas de la miscibilité totale Figure IX-14 : Représentation schématique d'un dispositif pour analyse thermique Figure IX-15 : courbe d'analyse thermique correspondant au diagramme à fuseau voisin Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 98 Souad BEN SLIMA
- 99. (2) Cas de l’eutectique : Le palier correspondant à la transformation eutectique est d'autant plus étendu que la quantité d'eutectique est grande (donc, la quantité de liquide résiduel à T=TE + ε) Exemple : Soit l'alliage de composition X, la proportion d'eutectique est donnée par : Par ailleurs, soit : P : puissance évacuée pendant la réaction eutectique tE : durée de la réaction L : chaleur massique à la réaction mE : masse eutectique P.tE = L.mE > P.tE = L.mE d’où : d’où tE = K.OL avec K = Quand OL augmente, tE augmente (la composition se rapproche de l'eutectique) Exercice : Soit un diagramme péritectique, donner la courbe T= f (t) pour 5 alliages de compositions différentes Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 99 Souad BEN SLIMA
- 100. 4 Le diagramme Al2O3-SiO2 Pour l'industrie des céramiques le système A1203-Si02 a presque la même importance que le diagramme Fe-C pour celle des aciers et des fontes. En effet, la plupart des céramiques les plus utilisées sont intégrées dans ce système. Figure IX-16 : Diagramme d'équilibre AI203-Si02 De ce diagramme on ressort les céramiques les plus importantes, notamment : - Les alumines réfractaires qui sont dans ces systèmes celles qui résistent le plus aux hautes températures, la température maximale de service étant celle proche de la fusion de Al203 (2054°C). - Les mullites : Réfractaires œuvrant à des températures allant jusqu'à 1850°C. Leur Composition est celle de la solution solide secondaire à fusion congruente et Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 100 Souad BEN SLIMA
- 101. portant le même nom. Cette composition doit être bien dosée afin de ne pas tomber dans le domaine (M+L). - Les argiles réfractaires : Leurs compositions varient de 55 à 75 % de Si02. La température de mise en service ne doit pas dépasser 1590°C, celle de l'eutectique. - Les briques réfractaires de silices contenant de 0,2 à 1 % d'Al203. Pour ces céramiques aussi il faut veiller à ce que la composition ne soit pas celle de l'eutectique, diminuant ainsi la température maximale d'utilisation. 5. Diagammes d'équilibre ternaires Un diagramme d'équilibre ternaire représente les transformations de phase qui ont lieu pour un mélange de 3 composants. Sa construction se fait généralement sur la base d'un triangle équilatéral. Aux 3 sommets de ce triangle sont représentés chaque composant pur. La figure 16 représente le diagramme ternaire de 3 corps purs A, B et C. En fait cette représentation à deux dimensions donne l'état des mélanges pour une pression (généralement égale à la pression atmosphérique) et une température bien déterminée. C'est une coupe isotherme du diagramme ternaire. Figure IX -17. Représentation d’un digramme de phase ternaire Pour déterminer la composition d'un point O dans le diagramme : - teneur en A, les lignes d'isocomposition en A sont les lignes perpendiculaires à AD : 20% A. - teneur en B, les lignes d'isocomposition en B sont les lignes perpendiculaires à BE : Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 101 Souad BEN SLIMA
- 102. 60% B. - teneur en C, les lignes d'isocomposition en C sont les lignes perpendiculaires à CF : 20% C. Position dans le diagramme d'un alliage ABC de composition 40%A, 20%B, 40%C : C'est le point P Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 102 Souad BEN SLIMA
- 103. TABLE DES MATIERES I.ESSAI DE TRACTION ………………………………………………..5 I-1- PRINCIPE DE L'ESSAI…………………………………………….5 I-2-DISPOSITIF D'AMARRAGES I-3- DIAGRAMME CONVENTIONNEL DE TRACTION …………....6 I-4- MESURES DES CARACTERISTIQUES CLASSIQUES I-5- COURBE RATIONNELLE DE TRACTION………………………8 I-6- LIMITE ELASTIQUE ……………………………………………...10 I-7- EXPRESSIONS DE LA COURBE RATIONNELLE ……………..11 I-8- CONSTRUCTION DE CONSIDERE I-9- MECANISMES DE DEFORMATION …………………………….14 II-ESSAI DE DURETÉ……………………………………………….....30 II-1 INTRODUCTION…………………………………………………..30 II-2 L’ESSAI BRINELL…………………………………………………31 II-3- ESSAI ROCKWELL…………………………………………….....33 II-3- ESSAI DE DURETE VICKERS …………………………………..35 II-4- COMPARAISON DES DIFFERENTES METHODES III-ESSAI DE RESILIENCE ……………………………………………37 III-1 INTRODUCTION …………………………………………………37 III-1- CONDITIONS D'ESSAI ………………………………………….37 III-3- CALCUL DE L'ENERGIE DE RUPTURE……………………….38 III-4-PRATIQUE DE L'ESSAI…………………………………………..39 III-5- MECANISME DE LA RUPTURE………………………………..41 IV -ESSAI DE FLUAGE ………………………………………………..43 IV-1- DESCRIPTION D'UN ESSAI DE FLUAGE …………………….43 IV-2- BUT DE L'ESSAI DE FLUAGE …………………………………44 IV-3- INFLUENCE, DE LA TEMPERATURE D'ESSAIS……………..44 Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 103 Souad BEN SLIMA
- 104. IV-4- EQUATIONS DES COURBES ε = f (t)…………………………..45 V- LA FATIGUE DES MÉTAUX ………………………………………46 V-1- INTRODUCTION ………………………………………………….46 V-2- LES RUPTURES DE FATIGUE …………………………………..46 V-3- MECANISME DE LA FATIGUE ………………………………....47 V-4- LES ESSAIS DE FATIGUE ……………………………………….50 V-6- DIAGRAMME DE GOODMAN - SMITH ………………………..51 V-7- REGLE DE CUMUL DE DOMMAGE …………………………....52 VI LA MÉCANIQUE DE LA RUPTURE LINÉAIRE ……………….....54 VI-1-INTRODUCTION ……………………………………………….....54 VI-2- RUPTURE FRAGILE ET RUPTURE DUCTILE ……………...…56 VI-3- NOTION DE FACTEUR DI INTENSITE DE CONTRAINTE (KI)………………………………………………………58 VI-4- VALIDITE DE LA SOLUTION SINGULIERE ………………….58 VI-5- EXTENSION AUX AUTRES MODES ………………………......59 VI-6- CRITERE DE RUPTURE FRAGILE - MESURE DE LA TENACITE KIC VI-7- EXPRESSION FONDAMENTALE DE LI INTEGRALE J ET PROPRIETE D’INDEPENDANCE VIS A VIS DU CONTOUR D'INTEGRATION …………………………………………………...….64 VI -8- DEFINITION DU MODULE DE DECHIRURE « T »………….68 VII-FROTTEMENT ET ENDOMMAGEMENT DE SURFACE……….70 VII-1-SOLLICITATIONS TRIBOLOGIQUES/ FROTTEMENT...…….71 VII-2-LES DIFFERENTS TYPES DE FROTTEMENT ………………...71 VII-3-LES FACTEURS INFLUENÇANT LE FROTTEMENT…………71 VII-4-ENDOMMAGEMEITT DE SURFACE …………………………..74 BIBLOGRAPHIE…………………………………………………………82 Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 104 Souad BEN SLIMA
- 105. INTRODUCTION Plusieurs matériaux, lorsqu'ils sont en service, sont sujets à des forces (ou charge); c'est le cas d'alliages d'Aluminium utilisés dans les ailes d'avions ou des aciers dans les essieux d'automobiles. Dans de telles situations il est nécessaire de connaître les caractéristiques du matériau et de déterminer les éléments de la structure de façon à ce qu'aucune déformation excessive, ni rupture ne puisse avoir lieu. Le comportement mécanique d'un matériau reflète sa réponse à une charge (ou force) appliquée. Les propriétés mécaniques les plus importantes sont, la résistance, la dureté, la ductilité et la ténacité. Les propriétés mécaniques des matériaux peuvent être approchées par des essais de laboratoires convenablement conçus et qui se rapprochent le maximum des conditions en service. Les paramètres à considérer tiennent compte de la nature de la charge appliquée et de sa durée ainsi qu'une bonne connaissance des conditions opératoires. La charge peut être de trois types: traction, compression ou cisaillement; son intensité peut être constante ou continûment variable en fonction du temps. Le temps d'application peut varier d'une fraction de seconde à plusieurs années. La température de service peut être un facteur déterminant. Le rôle de l'ingénieur affronté à une situation de choix de matériaux est de déterminer convenablement les types de sollicitation de chaque élément de la structure, ensuite fabriquer les matériaux qui répondent aux exigences prévues par les analyses des contraintes. Ceci nécessite impérativement la connaissance de la relation qui existe entre la microstructure et les propriétés mécaniques des matériaux. On s'intéressera dans cet exposé principalement au comportement mécanique des métaux et 'leurs alliages; les polymères et les céramiques sont dans une large mesure mécaniquement différents et seront traités séparément. Nous ferons lorsqu'il est possible des comparaisons entre ces différents matériaux. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 105 Souad BEN SLIMA
- 106. I.ESSAI DE TRACTION I-1- PRINCIPE DE L'ESSAI L’un des essais les plus utilisés est réalisé en traction. L’essai de traction permet d’aboutir à des propriétés mécaniques très importantes pour le design. L'essai de traction consiste à exercer sur une éprouvette des forces croissantes uniaxiales qui vont la déformer progressivement, puis la rompre. La charge est appliquée le long de l’axe de l’éprouvette. La figure I-1 montre une éprouvette de traction normalisée de section circulaire, mais il existe d’autres éprouvettes de traction de section rectangulaire. Durant l’essai, la déformation est confinée dans la région proche du centre (longueur utile) qui possède une section uniforme dans sa longueur. L’éprouvette est montée par ses extrémités dans les mors de serrage de la machine. La machine de traction est conçue de façon à imposer un allongement à vitesse constante, et mesurer instantanément la charge appliquée et l’allongement. L’éprouvette est déformée d’une façon permanente est souvent rompue. Les résultats de l’essai de traction sont enregistrés sur un diagramme charge allongement. Figure I-1 : Eprouvette de traction standard cylindrique I-2-DISPOSITIF D'AMARRAGES On fixe l'éprouvette par deux têtes d'amarrages (mors, coquilles, tiges, filetées, etc.). Celles-ci ont une grande importance, car la force doit être exercée dans le sens de la longueur uniquement, c'est-à-dire sans composante latérale (axialité de l'éprouvette dans les mors). Figure I-2 : Schéma d’une machine de traction. L’éprouvette est allongée par l’effort du au déplacement de la traverse mobile. La cellule et l’éxtensiomètre mesurent respectivement la valeur de la charge appliquée et l’allongement correspondant. I-3- DIAGRAMME CONVENTIONNEL DE TRACTION 1. Les matériaux métalliques La plupart des structures sont conçues de façon à ce qu’il y est seulement Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 106 Souad BEN SLIMA
- 107. des déformations élastiques. Il est souhaitable de connaître le niveau de contrainte pour lequel apparaît la déformation plastique. Si on soumet une éprouvette à un effort de traction, elle se déforme et s'allonge dans le sens de l'effort. Sur un diagramme effort-déformation, on observe les phases suivantes: (figure I- 3). - Pour des déformations faibles, 1 'effort exercé croit proportionnellement à la déformation et si l'on cesse d'exercer l'effort, la déformation s'annule l'éprouvette reprend ses dimensions initiales. C'est la déformation élastique c'est la partie élastique. - Si l'on augmente la déformation, on constate que l'effort n'est plus proportionnel à la déformation, de plus, l'éprouvette ne revient pas à ses dimensions initiales après cessation de l'effort. Il subsiste un allongement permanent. L'allongement de la partie calibrée reste toutefois uniformément réparti sur toute sa longueur: c'est là période des allongements permanents répartis. Si l'on continue la déformation; l’effort passe par un maximum puis se met à décroître : charge maximale qui est appelée charge de rupture. En poursuivant la déformation, l’étranglement s'accentue, 1 'effort continue à diminuer puis l'éprouvette se rompt. Lors du passage de la charge maximale, nous passerons dans la période de striction. Figure I-3 : comportement typique en contrainte – déformation jusqu’au point de rupture F. la résistance maximale σM est indiquée au point M. Les différentes figures représentent la géométrie de l’échantillon déformé en plusieurs points de la courbe. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 107 Souad BEN SLIMA
- 108. I-4- MESURES DES CARACTERISTIQUES CLASSIQUE Figure I-4 : Courbe conventionnelle Chargeelastique Fe Limite d’élasticité Re = = Sectionini tiale So Ch arg e max imale Fm Charge maximale Rm = = Sectionini tiale So Charge de rupture Chargederupture Fr Rr = = Sectionini tiale So L − Lo ∆L Allongement relatif e= = Lo Lo L − Lo Allongement en %, A% = × 100 Lo Avec L : Longueur après rupture Lo: Longueur initiale So − S Coefficient de striction Z% = × 100 So Avec So : Section initiale S : Section finale I-5- COURBE RATIONNELLE DE TRACTION La courbe de traction fait intervenir des grandeurs conventionnelles, puisque l’on rapporte la charge maximale à la section initiale. La contrainte vraie σ correspond à la charge rapportée à la section instantanée. F σ = Soit : S F : charge S : section instantanée Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 108 Souad BEN SLIMA
- 109. De même, l'allongement ordinaire n'est pas additif, on le remplace par la déformation rationnelle. D’où L dl L ε= ∫ = log Lo l Lo ∆L →dl L1 − Lo L2 − L1 L3 − L2 L dL ε= + + + ⋅ ⋅ ⋅ ⋅ ⋅⋅ = ∑ Lo Lo L1 L2 L : Déformation rationnelle logarithmique Donc, on a additionné des εi ε= ε1 + ε2+ ε3+……. εi: déformation successive sur un même axe. Sur un même axe L1 − Lo L2 − Lo L3 − Lo e1 = e2 = e3 = Lo Lo Lo e3 ≠ e1 + e2 En appliquant la loi de conservation de volume, on peut écrire So Lo = S L Donc: Valable pour les déformations homogènes et uniformes D’autre part, on peut établir une relation entre et e ∆L L − Lo e= = = e +1 Lo Lo D’ou ε = Log (e + 1) e: allongement conventionnel Dans une éprouvette, la somme des déformations suivant l’épaisseur, la largeur et la longueur est nulle. ε1 + ε2 + ε3=0 conservation de volume Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 109 Souad BEN SLIMA
- 110. Figure I-5 : Comparaison entre une courbe conventionnelle de traction et une courbe rationnelle. La striction commence au point B Forme de la courbe rationnelle OA : élastique AB' : plastique uniforme BIC’ : striction * Condition d'instabilité On a un maximum de force au point B d’où dF = 0 donc σdS + Sdσ=o D’autre part la loi de conservation de volume dL dS =− SL = cte S dL +L dS = o L S dσ σ = dε dε = dε = pente en B’ La striction apparaît en traction uniaxiale lorsque la pente de la courbe rationnelle est égale à la contrainte vraie en ce point. (Jaoul) Acier extra – doux εp=0,08 (Tricot) Acier inoxydable m de 0,45 à 0,95 γ → α Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 110 Souad BEN SLIMA
- 111. I-6- LIMITE ELASTIQUE Dans la première portion de la courbe, il y a proportionnalité entre contrainte et déformation. C'est la loi de Hooke. σ = E.ε E : désigne le module d’élasticité ou module de Young. Les valeurs du module élastique des alliages métalliques sont plus élevées que celle des métaux ; pour les polymères elles sont plus faibles. Ces différences sont la conséquence directe des différents types de liaisons atomiques. La déformation pour laquelle la contrainte et la déformation sont proportionnelles est dite déformation élastique. La déformation élastique n’est pas permanente, lorsqu’on élimine la contrainte l’éprouvette reprend sa valeur initiale. La limite élastique correspondant, à la contrainte à partir de laquelle le comportement du matériau s’écarte de la loi de Hooke, c'est-à- dire au moment où apparaît la première déformation plastique irréversible. Dans la pratique, on est conduit à distinguer deux types principaux de courbes de traction, suivant la présence ou non d’un crochet à la limite d’élasticité (figure I-6). La courbe avec palier ne présente pas de problèmes pour le calcul de σe, alors que l'autre courbe nécessite la définition des limites conventionnelles. On lève toute ambiguïté en définissant une limite élastique conventionnelle à 0,2% notée σe0,2% FigureI-6 : Courbe de traction définissant la limite élastique à 0,2% Si la contrainte appliquée est uniaxiale (sur z seulement) alors εx=εy. Un paramètre nommé coefficient de Poisson ν est défini comme étant le rapport Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 111 Souad BEN SLIMA
- 112. de la déformation latérale par la déformation axiale : ν = - εx/ εy Le signe (-) est introduit pour que ν soit toujours positif, εx et εy son t de signes opposés. Le coefficient de Poisson pour un matériau isotrope vaut 1/4. Pour beaucoup de métaux et alliages les valeurs de coefficient de Poisson se situent entre 0,25 et 0,35 (Tableau) Métal Limite Résistance Ductilité Module Coeff.de Module de d’élasticité maximale (A%) d’élasticié Poisson cisaillement (MPa) (MPa) (MPa) Or Nul 130 45 Aluminium 28 69 45 6,9 0,33 2,6 Cuivre 69 200 45 11 0,35 4,6 Fer 130 262 45 20,7 0,29 6,8 Nickel 138 480 40 20,7 0,31 7,6 Titane 240 330 30 10,7 0,36 4,5 Molybdène 565 655 35 0,35 12 I-7- EXPRESSIONS DE LA COURBE RATIONNELLE On a vu que l'augmentation du nombre de dislocations dans un cristal que l'on déforme plastiquement fait qu'il devient de plus en plus difficile de déformer. On dit qu’il y a « consolidation du matériau » .On appelle le rapport dσ ( ) Le taux de consolidation. dε La mesure du taux de consolidation d'un matériau nous permet de connaître et d'apprécier sa formalité ou l’augmentation de sa résistance en fonction de la déformation plastique. La méthode le plus souvent utilisée pour déterminer la consolidation d’un matériau est la suivante L'évolution de la contrainte réelle σ en fonction de la déformation réelle est décrite par σ = kε n Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 112 Souad BEN SLIMA
- 113. En coordonnées logarithmiques, la courbe de consolidation est une droite de pente n et K est 1a valeur de σ pour ε=1. La valeur de n est calculée au moment d'apparition de la striction : f (ε ) σs = δε f (ε ) Ici f (ε ) = kε n donc = knε n−1 δε A l’apparition de la striction δσ =σs δε donc kε n = knε n−1 ε =n D’où n représente la déformation du matériau à l'apparition de la striction n mesure donc la limite des allongements répartis. L'ordre de grandeur de n est donc 0,1 à 1. Plus n est grand plus le matériau est ductile. Tableau de valeur n avec σ = kε n Acier extra - doux 0,15 – 0,25 Acier ferritique 17% Cr 0,16 – 0,20 Acier autonomique 0,40 - 0,50 Aluminium 0,07 – 0,27 Aluminium magnésium 0,23 – 0,30 Aluminium Si - Mg 0,23 Al -Cu 0,15 Lation 67Cu – 33Zn 0,55 Cuivre 0,30 – 0,47 Zinc 0,10 Nickel 0,60 Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 113 Souad BEN SLIMA
- 114. I-8- CONSTRUCTION DE CONSIDERE Figure I-7 : Construction de Considère δσ σs = δε Condition d’apparition de la striction δσ δσ δε = × δe δε δe dl dl de = d ε Lo 1 δε = Lo = = l de L 1 + e L − Lo L car e= = −1 Lo Lo δσ 1 Donc l’apparition de la striction : =σs δe 1 + es D’autre part on a : Fs Fs S o S σs = = × = Rm o Ss So Ss Ss Ss : section vraie de l'éprouvette à la striction So : section initiale de l'éprouvette Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 114 Souad BEN SLIMA
- 115. Conversion du volume LoSo = Ls Ss Ls Donc σ s = Rm = Rm(1 + es ) Lo δσ 1 1 δσ =σs = Rm(1 + es ) × R = δe 1 + es 1 + es δε m La pente de la tangente étant Rm, on a dans les triangles semblables: OB CM = = Rm OA CA Donc CM σ CA = = = 1 + es s Rm Rm OA = CA-OC = 1+es-es Et OB = Rm OA = Rm I-9- MECANISMES DE DEFORMATION Les deux principaux mécanismes de déformation plastique sont le glissement et le maclage. I-9-1- LE GLISSEMENT A l’échelle microscopique, la déformation plastique à froid est due essentiellement aux mouvements des dislocations par glissement. La façon dont les dislocations se multiplient et sont freinées ou arrêtées par les divers obstacles (autres dislocations, éléments d1alliages, précipités, joints de grains), détermine l'amplitude à la déformation plastique du métal et l’intensité de l'écrouissage. * Plans et directions de glissement Le glissement correspond à un cisaillement du réseau le long d1un plan cristallographique, l’amplitude du cisaillement étant un vecteur du réseau. Les plans de glissement et les directions de glissement sont bien déterminés dans une structure cristallographique donnée. Ce sont en général les plans et directions denses du réseau (figure I. 8). Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 115 Souad BEN SLIMA
- 116. Figure I-8: Plans et directions de glissement * Lignes et bandes de glissement Dans le domaine de déformation plastique, on peut observer à la surface d'une éprouvette monocristalline (ou à la surface de gros grains) une série de lignes parallèles se terminant par une marche à la surface de l'éprouvette. Ce sont les lignes de glissement (figure I-9). Elles correspondent aux cisaillements du réseau le long des différents plans cristallographiques. En fait, le glissement ne se produit pas sur un seul plan mais il peut se répartir sur plusieurs plans adjacents, en donnant une structure fine à la marche. On parle alors de bandes de glissement. Déformation plastique Dans un cristal, il existe des défauts linéaires appelés dislocations qui peuvent se déplacer sous l'effet d'une contrainte extérieure par glissement. Un type de dislocations très simple à représenter est la dislocation coin, qui est la limite dans le cristal d'un demi-plan d'atome supplémentaire inséré entre deux plans atomiques successifs (figure I-9). On voit sur cette figure, qu'au prix de quelques réarrangements locaux des atomes situés au voisinage de la dislocation; la dislocation peut se déplacer en glissant dans le plan P ; le déplacement étant un vecteur du réseau. Lorsque la dislocation atteint la limite du cristal, tout se passe comme si le demi-plan supplémentaire était venu former une sorte de marche à la surface du cristal qui présente une déformation permanente. On explique ainsi la déformation plastique des métaux. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 116 Souad BEN SLIMA
- 117. La facilité de déformer plastiquement un métal dépend de la facilité avec laquelle les dislocations peuvent glisser. La présence d'obstacles au glissement des dislocations rend le métal plus difficile à déformer. Les obstacles peuvent être de nature très diverses. Des atomes étrangers (impuretés, éléments d'addition), pourront gêner le mouvement des dislocations. Autrement dit, un métal impur sera plus difficile à déformer que le métal pur. On parle de durcissement par solution solide. L'existence de petits précipités peut gêner aussi le mouvement des dislocations. C'est le durcissement par précipitation. Pour qu'un métal puisse se déformer plastiquement, il faut qu'il contienne des dislocations. Au cours de la déformation plastique des dislocations disparaissent à la surface du cristal mais il sien forme de nouvelles, en bien plus grand nombre (mécanismes de Franck Read). Ces nouvelles dislocations, très nombreuses, constituent des obstacles au glissement des dislocations en mouvement. Autrement dit, un métal écroui sera plus difficile à déformer qu’un métal bien recuit. C’est le durcissement par écrouissage. De la même façon, l'augmentation du nombre de dislocations dans un cristal que lion déforme plastiquement fait qui il devient de plus en plus difficile de déformer. On dit qu’il y a "consolidation du métal". On appelle taux de consolidation le rapport : Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 117 Souad BEN SLIMA
- 118. Figure I-9: a)Lignes et bandes de glissement b) Glissement de dislocation I-9-2- MACLAGE Quand les systèmes de glissement autorisés ne peuvent plus jouer, la déformation plastique peut se produire par maclage. L'apparition de ce mode de déformation conduit à des irrégularités sur la courbe de traction s'accompagnant d'un bruit strident indiquant un mécanisme très rapide. La déformation par maclage opère de préférence aux très basses températures ou aux vitesses de déformation élevées pour les métaux cubiques. C’est un mécanisme de déformation courant des métaux hexagonaux. I-10- CAS DE COURBES A PALIER La limite d'élasticité supérieur" dépend de la forme de l éprouvette, de sont état de surface, des conditions d'essai et de la machine d1éssai (alignement de l'éprouvette, vitesse d'essai). - La limite d'élasticité inférieure est moins sensible aux défauts géométriques de l’éprouvette. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 118 Souad BEN SLIMA
- 119. I-10-1- PHENOMENE DE LA LIMITE ELASTIQUE APPARENTE Sur les aciers, il y a glissement au passage de la limite élastique, cela tient à l'influence des atomes présents en solution interstitielle (carbone, 1 azote). Ces atomes se logent au voisinage des dislocations dont ils gênent le déplacement relevant la limite élastique. Mais si tôt qu'un premier glissement a lieu, ils se trouvent « 1achés » par les dislocations et l'en résulte un adoucissement du métal. * Paliers à la limite d’élasticité et lignes de PIOBERT LUDERS Le phénomène du palier correspond à une déformation hétérogène de l’éprouvette c'est à dire à la naissance d'une petite zone déformée locale, en général près des têtes de l'éprouvette, qui se propage ensuite à toute l'éprouvette. L'existence d'un palier après le crochet de traction est observée lorsque la déformation plastique ne démarre pas de façon homogène dans l'éprouvette mais au contraire s'étend progressivement par zones successives. Ces zones successives sont visibles à la surface de l'éprouvette sous forme de bandes sensiblement parallèles (figureI-10 et 11) appelées bandes de Luders. Figure I-10 : Courbe de traction (cas des bandes de Piobert –Lu ders) Figure I-11 : Bandes de Piobert –Lu ders Le palier peut ne pas être observé. Il en est ainsi lorsque l'augmentation du nombre de dislocations avec la déformation est très rapide et que la déformation plastique démarre de façon homogène dans toute l'éprouvette. Dans ce cas, il y a tout de suite durcissement par écrouissage. Les crochets de traction s'observent dans les alliages cubiques faces centrées pour de fortes concentrations, et dans les cristaux semi-conducteurs. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 119 Souad BEN SLIMA
- 120. I-10-2- EFFET PORTEVIN LE CHATELIER Phénomène mis en évidence en 1923 par Portevin et le Chatelier dans les alliages Al-Mg. Il est caractérisé par des discontinuités périodiques sur la courbe de traction, dans le domaine plastique. On distingue : - Effet type A (figure I-12) : la contrainte augmente puis baisse brutalement. L'enveloppe inférieure de la courbe constitue une courbe de consolidation. Figure I-12: Effet Portevin- Le Chatelier - Effet type B (figure I-12) : la contrainte chute brutalement puis rattrape rapidement sa valeur normale. L'enveloppe supérieure de la courbe constitue une courbe de consolidation normale. Cottrell a montré que les atomes d'impuretés en solution dans une matrice de base ont tendance à se rassembler autour des dislocations pour former une sorte de nuage (nuages de Cottre11). La présence de ces impuretés autour des dislocations diminue leur mobilité. La compétition entre la mobilité des dislocations et celle" des atomes d'impuretés peut expliquer, au moins en partie, les discontinuités observées sur lés courbes de traction. Lorsque les dislocations se déplacent dans le cristal, elles peuvent rencontrer des obstacles (autres dis1ocations par exemple) le "s’arrêter" un certain temps, puis repartir. Au cours de ces "arrêts" il peut se-faire que les atomes d'impuretés se trouvant à proximité aient le temps de diffuser et de venir ancrer ces dislocations mobiles. De ce fait, le nombre de dislocations mobiles diminue. La contrainte nécessaire pour poursuivre les déformations plastiques augmente. On trouve les conditions d'apparition du crochet de traction. De nouvelles dislocations sont créées dont Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 120 Souad BEN SLIMA
- 121. beaucoup sont mobiles. La contrainte nécessaire pour poursuivre la déformation plastique chute brutalement. On observe un crochet du type A. Dans le cas précédent, la mobilité des impuretés suffisante pour atteinte des dislocations proches, étaient supposées trop faible cependant, pour suivre la dislocation dans son déplacement, d'où l'effet d1ancrage. Si maintenant la mobilité des impuretés est grande, celles-ci peuvent suivre les dislocations dans leur mouvement en les freinant simplement. Il peut se faire que par moment, des dislocations se libèrent de leur nuage d'impuretés, un temps très court, jusqu’à ce qu’elles retombent dans le nuage des dislocations qui les précèdent. Il en résulte une chute brusque de la contrainte qui reprend rapidement sa valeur normale. On observe une croche de type B. Les crochets du type B apparaît à température plus élevée que les crochets du type A. Les phénomène Portevin le Chatelier a été observé essentiellement dans des solutions de substitution cubiques faces centrées et dans les solutions d'insertion cubiques centrées. I-11-EFFET BAUCHINGER Changement du sens de déformation Figure I-13 Effet Bauchinger - La limite d’élasticité en traction; 1ère déformation A puis M - La limite d'élasticité en compression: 1ère déformation Al puis M' Traction puis compression: OAM M" < M’ irréversibilité. Activation de nouvelles sources avec changement de sens, inégalité des endommagements selon le chemin de déformation (ex. ; tôles, tubes, etc.) I-12- RELATION ENTRE LIMITE D'ELASTICITE ET TAILLE DES GRAINS Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 121 Souad BEN SLIMA
- 122. Si l'on fait varier la taille du grain par des traitements appropriés, on observe une variation de la limite d'élasticité. Figure I-14 : Loi de Petch Loi de Petch σi =σ m + kd −1 / 2 σi : limite inférieure d’élasticité du cristal σm : limite d’élasticité du monocristal d : diamètre des grains, moyen k : une constante I-13- INFLUENCE DE LA TEMPERATURE D'ESSAI De part et d'autre de la température ambiante, on a vers les hautes températures, l'évolution des propriétés à chaud, et vers les basses températures, 1 'évolution des propriétés à froid. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 122 Souad BEN SLIMA
- 123. Figure I-15 : Evolution de la charge maximale et la limite de L'élasticité en fonction de la température Pour les aciers doux aux très basses températures, il y a augmentation très forte de Re et R, avec baisse d'allongement et apparition des phénomènes de fragilité Au dessus de l'ambiante, on observe une baisse de Re et R, en fonction de la température jusque vers 400°C (aciers doux) où les phénomènes de fluage l'emportent. Il n'est plus possible alors de mesurer une limite d'élasticité. Cependant, entre 100°C et 300°C, on observe une augmentation de la résistance et un palier pour la limite élastique. L'azote libre est l'élément principal responsable du vieillissement après écrouissage, or dans une gamme de température comprise entre 100°C et 300°C, la vitesse de diffusion de l'azote est telle que le vieillissement a le temps de se produire pendant la déformation, c’est .ce que l'on désigne par vieillissement dynamique. Cela provoque un durcissement très important du métal déformé, donc une augmentation de la résistance à la rupture. I-14- INFLUENCE DE LA VITESSE DE TRACTION Pour tous les métaux, le comportement au cours d'un essai de traction à l'ambiante, dépend de la vitesse d'application de la charge. On obtient par traction rapide, des résistances plus élevées et des allongements plus faibles. Pratiquement, on fait croître la charge à un taux suffisamment lent pour qu’on puisse considérer les effets dynamiques comme négligeables, et que L’éprouvette puisse être toujours supposée en état d'équilibre. La vitesse de traction est normalisée - domaine élastique : vitesse maximale 30N/mm2/s - domaine plastique : vitesse maximale 15% Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 123 Souad BEN SLIMA
- 124. On constate que l'augmentation de la limite d’élasticité est plus faible à chaud qu'à l'ambiante. 2. Les matériaux polymères Les propriétés mécaniques des polymères sont caractérisées par pratiquement les mêmes paramètres utilisés pour les métaux. Pour plusieurs matériaux polymères! Le simple essai contrainte- déformation est employé pour la caractérisation de certains de ces paramètres mécaniques. Les caractéristiques mécaniques des polymères sont pour la grande part, très sensibles à la vitesse de déformation, la température et la nature (composition) chimique de l'environnement (présence d'eau, d’oxygène, de solvant organique). Quelques modifications des techniques d’essais sont nécessaires avec les polymères, spécialement pour les matériaux fortement élastiques, et les caoutchoucs. On distingue trois types de comportements à la traction (Fig. I-17): Figure I-17:Courbes de traction de polymères (A) fragile, (B) plastique et (C) très élastique La courbe A illustre le comportement des polymères fragiles (la rupture a lieu pendant la déformation élastique). Le comportement du matériau plastique, courbe B, est similaire à celui rencontré avec plusieurs matériaux métalliques; la déformation initiale est élastique. Enfin l’évolution décrite par la courbe C, totalement élastique; ce type de comportement est caractéristique d’une classe de polymères appelée les élastomères. Le module élastique, la résistance à la traction et la ductilité (en pourcentage d'allongement) sont déterminés pour les polymères de la même manière que les métaux, le tableau I-3 donne ces propriétés pour différents matériaux polymères. Les polymères ont dans plusieurs cas des comportements différents des métaux. Par exemple, le module élastique des matériaux polymères fortement élastiques peut être aussi bas que 7 MPa mais peut aussi atteindre 4. 103 MPa. Les modules des métaux sont plus élevés et s’étendent de 48.103 à 410.103. Alors que l’allongement plastique des métaux ne dépasse guère 100%, quelques élastomères peuvent atteindre les 1000%. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 124 Souad BEN SLIMA
- 125. Tableau II-3 : Caractéristique mécaniques à la température ambiante des polymères les plus courants Matériau Module de Résistance Allongement Résistance traction maximale à la rupture aux chocs (MPa (MPa) (%) (ft.1b/in) Polyéthylène (basse 1,7 -2,8 8,3 -31,7 100 -650 Pas de densité) rupture Polyéthylène (haute10, 6 - 22 -31 10 -1200 0,4 -4 densité) 10,9 Chlorure de 24-41 41-52 40-80 0,4-22 polyvinyle Polytétrafluoro 4 -5,5 14 -34 200 - 400 3 éthyléne Polyéthylène 11 - 16 31 - 41 100 - 600 0,4 – 1,2 Polyéthylène 23 -33 36 - 52 1,2 – 2,5 0,35 -0,45 Polyméthyl méthacrylate 22 - 32 48 - 76 2 - 10 0,3 – 0,6 Phénol - 28 – 48 34 – 62 1,5 – 2 0,24 – 4 formaldéhyde Ref: Modern Plastics Encyclopedia 1988, 1987, Mac Graw Hill Inc. En plus, les caractéristiques mécaniques des polymères sont très sensibles aux changements de la température comme le montre la figure I-18; l'augmentation de la température produit: 1/ Une diminution du module élastique 2/ Une réduction de la résistance à la traction 3/ Une augmentation de la ductilité Figure I-18: influence de la température sur les caractéristiques en contrainte- déformation d'un polynzethyl méthacrylate (ref: T.S.Carswell, H.K. Nason, effect of environmental conditions on the mechanical propaties organic plastics, symposium on plastics, ASTMI Pa, 1944 L'influence de la vitesse de déformation sur le comportement mécanique peut être aussi importante. Généralement, une diminution de la vitesse de Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 125 Souad BEN SLIMA
- 126. déformation a le même effet qu'une augmentation de la température; le matériau devient plus douce et ductile. L'analyse des mécanismes de déformation des polymères montre deux modèles Intéressants ; l’un d’eux intéresse les polymères semi – cristallins, l’autre les élastomères a) Déformation des polymères semi –cristallins (1) Mécanisme : Plusieurs polymères semi-cristallins ont une structure sphérulitique. Rappelons que chaque sphérulite en un grand nombre de chaînes pliées ou « lamellaire », les qui se prolongent à partir du centre. Un matériau amorphe sépare ces lamelles ; les lamelles adjacentes sont connectées par des chaînes de liaisons qui passent à travers ces régions amorphes. (Figure I-19). Figure I-19: Structure spherulitique Le mécanisme de déformation p1astique est régit par les interactions entre les lamelles et les régions amorphes sous l'effet de la charge appliquée; ce process a lieu par étapes schématisées par la figure I-20. Deux chaînes lamellaires adjacentes et le matériau amorphe inter lamellaire se déforment en premier (a). Durant l'étape de déformation initiale (b) les rubans lamellaires glissent les uns sur les autres et les chaînes de liaisons des régions amorphes deviennent tendues. La déformation continue dans la deuxième étape par l'inclinaison des lamelles de façon à ce que les chaînes pliées deviennent alignées avec l'axe de traction (c). Par la suite les segments du loc cristallin se séparent des lamelles. Ces segments restent attachées les uns aux autres (d). L'étape finale correspond à l’orientation dans la direction de l'axe de traction des blocs et des chaînes de liaisons. Ainsi, la déformation appréciable des polymères semicristallins produit une structure hautement orientée. Bien évidemment, durant ce processus, les sphérulites changent de configuration (forme). L'une des plus importantes techniques utilisée pour améliorer la résistance mécanique est le pré déformation des polymères, qui deviennent orientées tel que Figure I-20 e. Ce processus fait penser à Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 126 Souad BEN SLIMA
- 127. l’écrouissage des métaux. (2) Déformation macroscopique Quelques aspects de la déformation macroscopique des polymères semicristallins mérite notre attention. Les courbes effort-déformation pour un matériau non orienté initialement (Figure I-21) montre qu'au delà du crochet de traction la courbe prend une forme presque horizontale. Au crochet de traction il se forme une petite entaille dans la section utile de l’éprouvette. Aux abords de cette entaille, les chaînes deviennent orientées, ce qui conduit à une résistance localisée. Par conséquent, il existe une résistance à la continuation de la déformation en ce point, et l'allongement de l'éprouvette a lieu avec propagation de la région entaillée tout le long de la longueur utile; le phénomène de l'orientation de chaîne accompagne l'extension de la striction. Ce comportement en traction peut être approché à celui des métaux ductiles, sauf que dans ce dernier cas la déformation â la striction est localisée. Figure I-20: Étapes de déformation d'un polymère semi-cristallin. (Rej: Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 127 Souad BEN SLIMA
- 128. J.M.Schultz, Sciences des matériaux polymères, 1974, Prentice-Hall Inc. NJ) Figure I-21 Schéma d’une courbe de traction pour polymère semi- cristallin Fig. II-21: Schéma d'une courbe de traction pour un polymère semi-cristallin b) Déformation des élastomères Une des propriétés fascinantes des matériaux élastomères est leur élasticité caoutchouteuse. Ceci étant, ils ont la capacité d'être déformés à de larges valeurs. Ce comportement a été observé probablement en premier avec le caoutchouc naturel; pendant ces dernières années on produit un grand nombre d'élastomères avec de larges variétés de propriétés. Le comportement typique des matériaux élastomères en traction est schématisé à la courbe c de la figure I-17. Leurs modules élastique est très faible et, par ailleurs, varie avec la déformation car l'évolution n'est pas linéaire. Dans un état non chargé, un élastomère est amorphe et composé de chaînes moléculaires très fortement tordues, nouées et enroulées. La déformation élastique lors de l'application d'une charge de tension, réside en un déroulement partiel et un allongement des chaînes dans la direction de la contrainte, (Figure I-22). Lors de l'élimination de la contrainte, les chaînes retournent à leur conformation initiale et la pièce reprend sa forme macroscopique. FigureI-22:Schéma de la chaîne moléculaire d'un élastomère (a) dans un état non contraint (b) pendant la déformation élastique en réponse à une contrainte de traction (2.D. Jastrzebski, The nature and properties of engineering materials, Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 128 Souad BEN SLIMA
- 129. 1987, JohnWiley&sons) 3. Les matériaux céramiques a) Introduction Les matériaux céramiques sont quelque peu limités dans leur application par leurs propriétés mécaniques, qui sont de loin inférieures à celles des métaux. Le principal inconvénient est sa disposition à la rupture catastrophique d'une manière fragile avec très peu d'énergie absorbée. A température ambiante, les céramiques (cristallins et non cristallins) rompent avant le développement d'aucune déformation plastique sous l’effet de l'application d’une charge de traction. Les questions de rupture fragile et de mécanismes de rupture seront discutées ultérieurement. Les céramiques fragiles affichent des résistances plus élevées en compression qu'en traction et sont généralement utilisés lorsque les conditions de charges sont compressives. Dans le cas de contraintes compressives, il n'existe pas de concentration de contrainte au niveau des défauts existants. Le comportement en contrainte-déformation des céramiques fragiles n'est pas assuré par l'essai de traction car il est difficile de préparer des échantillons de géométrie désirée. On réalise plutôt fessai de flexion qui sera décrit ultérieurement. b) Le comportement élastique Le comportement élastique des matériaux céramiques en flexion sont similaires aux résultats obtenus pour les métaux en traction : il existe une relation de proportionnalité entre la contrainte et la déformation. La figure II-23 montre une comparaison on en contrainte -déformation jusqu'à rupture de l'oxyde d'Aluminium et du verre; la pente de la droite représente le module d'élasticité (compris entre 7 et 50. 104 1MPa) légèrement plus élevés que ceux des métaux Figure I-23: Comportement typique en contrainte-déformation jusqu'à la rupture de l’alumine et du verre. c) La déformation plastique Les céramiques cristallines: La déformation plastique a lieu, comme pour les Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 129 Souad BEN SLIMA
- 130. métaux, par le mouvement des dislocations. L'une des raisons de la dureté et la fragilité élevées de ces matériaux est la difficulté de glissement des dislocations. Il existe très peu de systèmes de glissement (plans et directions cristallographiques) le long desquelles les dislocations peuvent se mouvoir. Ceci est la conséquence de la charge électrique des ions. Pour glisser dans une certaine direction, les ions ayant de telles charges sont amenés à se rapprocher des autres ions; à cause de la répulsion électrostatique ce mode de glissement est très limité. Ce problème ne se pose pas dans le cas des métaux dans la mesure ou tous les atomes sont électriquement neutres. Les céramiques non cristallins: La déformation plastique ne peut pas avoir lieu par mouvement de dislocations car il n'y à pas de structure atomique régulière. Par contre ces matériaux se déforment par écoulement visqueux. d) Module élastique et porosité Pour certaines techniques de fabrication des céramiques, le matériau de base est sous forme de poudre. A la suite du compactage (formage) de ces poudres, il existera des pores ou espaces vides entre les particules. Durant le traitement thermique suivant, la majorité de ces pores vont être éliminés; toutefois, cette élimination est souvent incomplète et subsiste une porosité. Une porosité résiduelle aura une influence néfaste sur les propriétés élastiques et les propriétés de résistance. Par exemple, il a été montré que la valeur du module élastique E diminue avec la fraction volumique de porosité P selon l'équation: E = Eo (1-1,9. P + 0,9. P2) Où Eo est le module d’élasticité du matériau non poreux. L'influence de la fraction volumique de porosité sur le module d'élasticité de l'oxyde d'Aluminium est montrée sur la figure I-24. Figure II-24: lnfluence de la porosité sur le module d'élasticité de l'alumine à la température ambiante. (Ref: R.L. Coble, W. D. Kingeny, effect of porosity on physical properties of sintered alumina, J. Am. Ceram. Soc.; 1956) Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 130 Souad BEN SLIMA
- 131. II-ESSAI DE DURETÉ II-1 INTRODUCTION Une autre propriété mécanique importante à considérer est la dureté, qui est une mesure de la résistance d'un métal à la déformation plastique localisée. Les essais de dureté étaient basés sur la capacité qu'a un matériau de rayer un autre, placé après lui sur une échelle. Autre indexage quantitatif mais quelque peu arbitraire est l'échelle de MOHS qui donne la valeur 1 pour le MICA et 10 pour le DIAMANT Les mesures quantitatives de la dureté ont été développés à partir du moment où on a forcé un pénétrateur dans une surface d'un matériau à tester, en contrôlant la charge et la vitesse de son application. On mesure les dimensions de l'empreinte qui seront traduits en nombre de dureté ; plus le matériau est doux, plus l'empreinte est large et profonde, plus la dureté est faible. La mesure de la dureté n'est que relative, l’attention doit être prise lorsqu'on compare des duretés obtenues avec différentes techniques. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 131 Souad BEN SLIMA
- 132. Figure II-1: Comparaison entre plusieurs échelles de dureté (Ref: G.F.Kinney, Engineering properties and applications of plastics, 1957, John Wiley & sons) Il s'agit d'enfoncer un pénétrateur dans le métal à essayer, la charge doit être d'autant plus importante que le métal est plus dur. Il s'agit donc d'une compression, mais par commodité on utilise une charge constante et l'on mesure la dimension de l'empreinte (celle-ci sera d'autant plus petite que le métal sera dur) Dureté (symbole H) F H = S Les différents essais se distinguent par la forme de pénétrateur et sa dimension, la charge appliquée, la dureté d'application, 'la mesure effectuée (surface empreinte ou profondeur), la conversion en dureté grâce à la formule ou non. Les chiffres de dureté sont conventionnel s et sans dimensions (par unité), ils sont donnés par une échelle. Les différents essais sont : L’essai BRINELL → Billes L’essai ROCWELL →Billes ou cônes diamantés L’essai VICKERS → Pyramides de diamant L’essai secondaire → Pénétrateurs variés II-2 L’ESSAI BRINELL II-2-1- PRINCIPE DE L'ESSAI Il découle des lois de Meyer : il consiste à appliquer des charges sur des billes de diamètre convenable. Les machines sont simples et ancienne La charge exercée est fonction du diamètre de la bille : -F = 30 102 pour les aciers, maillechorts, bronze - F = 10 102 pour les laitons, alliages légers spéciaux - F = 5 102 pour le cuivre, duralumin, dural inox - F = 2 102 pour l’étain, le plomb. L’essai le plus courant est : Ou : Eventuellement sauf pour les aciers : Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 132 Souad BEN SLIMA
- 133. Les billes sont en acier dur ou en carbure de tungstène. On mesure l'empreinte avec une réglette ou un oculaire micrométrique. Formule permettant le calcul de la dureté BR INELL : F 2x0,102F (F en Newton) HB = = S ΠD(D − D2 − d 2 F 2xF (F en Kgf) HB= = S ΠD(D− D2 − d 2 1Kgf = 9,81 N D = diamètre de la bille en mm ; d= diamètre de l’empreinte en mm Des tables fournissent, en fonction de F et de D, la valeur de HB en fonction de la mesure de d. En l’absence de table, avec la formule, il est possible (de même que pour l’essai Vickers) de calculer HB II-2-2- PRECAUTIONS OPERATOIRES a- Pour exécuter convenablement un billage il faut avoir une surface propre et éviter les hétérogénéités de surface. Il faut faire plusieurs sondages mais ne pas rapprocher trop les empreintes (3 fois le diamètre de la bille entre chaque centre). Le diamètre de l'empreinte ne doit être ni trop grand ni trop petit (entre le tiers et les deux tiers du diamètre de la bille) b- Prévoir une épaisseur de métal égale au moins au triple du diamètre de l’empreinte, enfin la charge ne doit pas être trop forte ni trop faible (P= 30 02 dans le cas des aciers). c- Dans ces conditions, l’essai Brinell ne se prête pas à la mesure de la dureté des couches superficielles (cimentées par exemple ou de tôles minces). d- Des précautions sont à prendre pour l'application de la charge, 15 secondes pour l'appliquer et 15 secondes pour le maintien. La déformation de la bille limite l'emploi à des duretés inférieures à 400 ou 600 avec la bille en carbure. Il faut se méfier de l'usure des billes (étalonnages fréquents). II-1-3- RELATION ENTRE LA DURETE BRINELL ET LA RESISTANCE A LA TRACTION On constate dans certains cas, celui des aciers en particulier, qu'il existe une relation empirique entre la résistance à la traction R exprimée en Kgf/mm2 et la dureté HB exprimée en Brinell R = C. HB Avec C = 0,362 pour HB < 175 Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 133 Souad BEN SLIMA
- 134. C = 0,344 pour HB > 175 Les essais étant fais avec une bille de 10mm pour une charge de 3000 Kgf. Cette formule qu'on extrapole dans la pratique avec différentes conditions d'essai (bille de 5mm avec charge de 75 Kgf) est seulement approximative. Cependant, si dans la pratique courante, on prend souvent HB = 3R, cette formule s'applique mal aux aciers traités et aux aciers spéciaux, elle est également à déconseiller pour les aciers moulés et ne signifie rien dans le cas des fontes et métaux légers. Pour un type d'acier déterminé, la relation doit être établie expérimentalement à partir de nombreuses mesures. II-3- ESSAI ROCKWELL II-3-1- PRINCIPE DE L'ESSAI L'essai consiste à mesurer l'enfoncement d'un pénétrateur, appuyé sous faible charge sur la surface à essayer, on ne mesure pas le diamètre de 1 ‘empreinte mais sa profondeur, avec un comparateur au micron. La dureté Rockwell s'exprime directement en fonction de la profondeur, le cadran est gradué en conséquence. Il est nécessaire d'appliquer une pré charge pour mettre le comparateur à zéro. On n’a pas besoin de table pour obtenir la dureté, la lecture est directe. FigureII-2 : Principe de l’Essai Rockwell Pénétrateurs employés a- Un cône de diamant (essai C) de section circulaire d'angle au sommet 120°, à pointe sphérique (rayon de 0,2mm). b- Une bille d1acier trempée, polie de diamètre 1,587 mm (1/16 de pouce) (essai B ou F) ou 3,17mm (essai E). La pré charge Fo est dans le cas de 10 Kgf, les surcharges Fl sont de 50, 90 et 140 Kgf, les surcharges d'essai F sont de 60, 100, et 150 Kgf. La combinaison de divers pénétrateurs et de diverses charges, permet d1avoir un assez grand nombre d'échelles Rockwell. Les plus utilisées sont: - Echelle Rockwell C (HRC) cône diamant et charge de 150 Kgf pour les métaux durs ayant une résistance supérieure à 100 Kgf/mm2. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 134 Souad BEN SLIMA
- 135. - Echelle Rockwell B (HRB) bille d1acier de 1,59 mm et charge de 100 Kgf pour les aciers dont la résistance est comprise entre 35-et 100 Kgf/mm2 Les étapes de mesure a- Mise en contact du pénétrateur et de la surface sous la précharge Fo avec une mise au zéro de l'indicateur d’enfoncement. b- Imposition de la surcharge F1 permettant d’atteindre la charge d’essai (Fo + F1 = F). c- Retour à la pré charge et lecture de l’indicateur d'enfoncement. L’indicateur d'enfoncement est un comparateur permettant les mesures au µ m près, de la profondeur de pénétration (e) après suppression de la charge Fl. La dureté est exprimée par les différences à 100 ou 130. Les formules utilisées étant: HR = 100 - 5 x 102e (Rockwell C) HR = 130 - 5 x 102e (Rockwell B, E, F) Avec (e) exprimée en mm La dureté est naturellement d’autant plus grande que le pénétrateur s'enfonce moins. La lecture se fait directement en unités Rockwell. Une unité Rockwell correspond à un enfoncement de 0,002 mm. II-2-2- PRECAUTIONS OPERATOIRES a- Le fini superficiel de la pièce doit être satisfaisant. Si la surface présente des rayures, les empreintes sur le sommet des arrêtes dans les creux donnent des résultats très forts. Un polissage au papier fin est habituellement effectué avant l’essai. b- La pièce doit bien reposer sur son support si non, il se produit un déplacement du métal dans la région où se forme l'empreinte avec erreur. c- Les chocs et vibrations doivent être évités. d- Dans le cas des pièces cylindriques convexes, les normes précisent les corrections à faire et les limites à ne pas dépasser. e- L’épaisseur de la pièce ou de la couche superficielle à essayer ne doit pas être inférieure à 8e. En aucun cas, une déformation doit être observée sur la face opposée à celle de mesure. II-2-3- AUTRES ESSAIS ROCKWELL Essais conventionnels de dureté Rockwell pour produits minces : Ces essais s'effectuent suivant le même principe mais avec des machines permettant d'exercer des efforts plus faibles. Il existe trois variantes: * Essais conventionnels HRB Bille de diamètre 1,59 mm comme HRB, mais les efforts d1enclume interdits par la norme NFA 03-153 sont admis ici. Enclume polie en acier de dureté Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 135 Souad BEN SLIMA
- 136. HV > 250. Cet essai est utilisé pour les produits plats minces, d'épaisseur supérieure ou égale à 0,5mm. * Essais de dureté superficielle HRN et HRT Ces essais s’effectuent comme les essais HRB à bille (N) ou HRC de diamant (T) mais avec une précharge de 3 Kgf et des charges totales 30 ou 45 Kgf. On définit: 3 échelles: N = HR 15N, HR 30N et HR 45N 3échelles: T = HR 15T et HR 30T et HR45T L’unité Rockwell. Correspond ici à un enfoncement de 0,001µ m. La dureté Rockwell est alors égale à 100-e L'enclume polie est en acier trempé de dureté HV > 850 ou en diamant L’essai s’applique soit aux couches minces (cémentation, revêtement, etc.) soit aux produits plats minces (tôles fines, rubans, etc.). II-3- ESSAI DE DURETE VICKERS II- 3- 1 – PRINCIPE DE L’ESSAI Le principe de l'essai est le même que pour l'essai Brinell mais le pénétrateur ici est une pyramide de diamant à base carrée , l’angle entre 2 faces opposées est de 136°, choisi ainsi pour avoir une correspondance avec Brinell. Figure II-3 : Principe de l’essai Vickers L'avantage d'un pénétrateur pyramidal est que la loi de similitude est automatiquement respectée, et quand on fait varier la charge, on obtient des empreintes géométriquement semblables entre elles, donc des valeurs identiques pour la dureté. De plus, l’avantage du diamant réside dans l’absence de déformation du pénétrateur quand on mesure des duretés élevées. Le diamant laisse une empreinte carrée et on mesure la longueur de la diagonale de l'empreinte (ou la moyenne des deux diagonales) à 0,002 mm près grâce à un microscope micrométrique lié à la machine et pouvant venir se placer automatiquement au dessus de l’empreinte. La dureté Vickers HV est le quotient de la charge d’essai F (5, 10, 20, 30, 50,80 ou 100 Kgf) pour l’aire de l’empreinte de diagonale d. c’est à dire Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 136 Souad BEN SLIMA
- 137. 2 FSin(136° / 2) HV = d2 1,8544 F HV = d2 Des tables fournies par les différents constructeurs donnent HV en fonction de F et d. La charge utilisée le plus couramment est 30 Kgf. Cependant, la gamme des charges utilisables (5 à 100 Kgf) permet d'appliquer cette méthode dans toute l'échelle des duretés, et avec toutes les dimensions d'échantillons en choisissant la charge donnant une empreinte telle que la diagonale (d)soit plus grande que 0,4mm, mais inférieure aux 2/3 de l'épaisseur. Dans ces conditions, le symbole HV est suivi de la charge utilisée en Kgf, et du temps de maintien de la charge en secondes (Ex. : HV 30/20). II-3-2- PRECAUTIONS OPERATOIRES a- Les empreintes étant petites, les irrégularités de la surface prennent une importance encore plus grande que dans les essais précédents, particulièrement pour les fortes duretés, et les faibles charges, un polissage aussi parfait que possible est souhaitable (polissage micrographique à l’alumine). b- La distance entre le centre d'une empreinte et le bord de la pièce ou les cotés d'une autre empreinte, ne doit pas être inférieure à 2,5 fois la diagonale. L'épaisseur de la pièce supérieure à 1,5 fois la diagonale de l’empreinte. c- La pièce doit reposer sur le support de façon régulière et uniforme. d- L'état du diamant doit être fréquemment vérifié II-4- COMPARAISON DES DIFFERENTES METHODES - L’essai Brinell sous sa forme habituelle convient spécialement pour les mesures d'atelier. L1état de surface n’a pas besoin d'être particulièrement soigné. - L’essai Rockwell simple et rapide convient pour les pièces les plus petites et les hautes duretés. La dispersion est nettement plus forte qu1en Brinell. Il est en général nécessaire de prendre la moyenne de 2 ou 3 mesures. La pièce doit être bien assise sur son support et l’état de surface doit être correct. Certaines machines possèdent un dispositif de blocage et donnent par conséquent des résultats moins dispersés. - L’essai Vickers convient aussi bien pour les matériaux très durs que pour les matériaux très tendres. En raison de la constante de l’angle de pénétration ; la mesure est indépendante de la charge. Mais le fini superficiel doit être soigné. La lecture au microscope est lente et la pièce ne peut avoir que de faibles dimensions. Ce mode d'essai est plutôt du domaine du laboratoire. II-5- AUTRES ESSAIS En, plus des Rockwell superficiels; on peut citer: Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 137 Souad BEN SLIMA
- 138. - dureté Vickers, sous faible charge et micro dureté - dureté Knopp ; - dureté dynamique. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 138 Souad BEN SLIMA
- 139. III-ESSAI DE RESILIENCE III-1 INTRODUCTION Cet essai est destiné à caractériser la fragilité du métal sous l'action d'un choc, soit par la mesure des propriétés mécaniques du métal à l'ambiance (résilience en long et en travers), soit par la détermination de la température de transition ductile fragile sous contrainte triaxiale (flexion sous entaille).D'exécution très simple, cet essai est très ancien. L'essai permet de mesurer outre l'énergie de rupture et la résistance l'angle de pliage, la contraction latérale, l'étendue de plages cristallines à nerf: enfin à l'aide de dispositifs dynamométriques enregistreurs, la courbe effort-temps (essai Charpy avec enregistrement). III-1- CONDITIONS D'ESSAI L'aptitude d'un matériau à se rompre par fragilité est mesurée par l'énergie absorbée lors de sa rupture. Cet essai fait intervenir les phénomènes d'initiation et de propagation. L'éprouvette est rompue par choc sous l'effet d'une masse pendulaire : FigureIII-1 : Principe de l’essai Dans sa position initiale, l'angle du pendule avec la verticale est α après rupture de l'éprouvette l’angle maximal de remontée est β La différence (α -β) caractérise l'énergie dépensée pour la rupture de l'éprouvette (énergie de rupture). En effet, en l’absence d'éprouvette, le pendule remonterait à une position symétrique de la position de départ avec Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 139 Souad BEN SLIMA
- 140. un angle α. Pour la plupart des moutons pendulaires, la vitesse d'impact est d'environ 5m/s. L'énergie cinétique de la masse oscillante doit être de 30 Kgm (soit environ 295 joules). III-2- DIFFERENTS TYPES D'EPROUVETTES ISO : entaille en V Profondeur : 2mm Angle : 45° r à fond d’entaille : 0,25mm Mesnager : entaille en u Profondeur : 2mm r à fond d’entaille : 1mm ALLEMANDE D. V. M. : entaille en V Profondeur : 3mm r à fond d’entaille : 1mm ISO : entaille en U Profondeur : 5mm r à fond d’entaille : 0,25mm AUTRES TYPES Eprouvette Charpy à entaille en trou de serrure Eprouvette Izod Eprouvette Izod à entaille en trou de serrure Eprouvette suisse VSM Les notations précises pour la résilience sont: - KCV : résilience sur éprouvette ISO entaille en V (J/cm2) -KV : résilience sur éprouvette ISO entaille en V (J) N.B. : KVT sens travers de laminage KVL sens long de laminage On passe de KV à KCV en multipliant la valeur KV par 1,25 (car la section sous entaille S = 0,8cm2) III-3- CALCUL DE L'ENERGIE DE RUPTURE Er = Ei - Ef Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 140 Souad BEN SLIMA
- 141. Ei : énergie initiale Ef : énergie finale Er : énergie de rupture (résilience) FigureIII-2 : Calcul de l’énergie de rupture (résilience) Ei = hi.P hi − ho sin α 1 = ho Hi = ho + ho sin α1 hi = ho (1+ sinα1) Hi = ho + (ho sin α1) ho − hf cos β = ho Ef = hf. P hi = ho + ho cos β hf = ho(1-cosβ) Ef = ho (1- cosβ) P Er = Ei – Ef = ho (1+ sinα1) P - ho (1- cosβ) P Er =hoP (Sinα1+Cosβ) On appelle résilience l'énergie de rupture amenée ou non à la section sous entaille de l'éprouvette. Cette résilience s'exprime en joules j/cm2 ou en joule (on ne ramène alors pas l'énergie à la section sous l'entaille). L'éprouvette la plus utilisée est l’ISO à entaille en V. Elle ne présente pratiquement pas le phénomène de bimodalité de la rupture (éprouvette Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 141 Souad BEN SLIMA
- 142. ductile et fragile en même temps : cas des entailles en V pour une gamme de température pouvant atteindre 60°C). III-4-PRATIQUE DE L'ESSAI L’éprouvette est placée sur deux appuis. Le temps entre le positionnement de l’éprouvette et la rupture est environ 2 secondes. Les éprouvettes sont rompues à différentes températures. Elles sont donc au préalable refroidies dans des bacs réfrigérants. Lorsqu’une éprouvette est à "sa température essai", elle est placée rapidement sur des appuis, l’opération doit être réalisée en 4 ou 5 secondes, du fait de l’inertie thermique, l’éprouvette ne se réchauffe pas. Après avoir effectué les différents essais aux différentes températures trace la courbe dite de résilience de l’acier considéré en fonction de la température. Figure III-3 : Courbe de résilience et cristallinité en fonction de la température Les courbes de résilience sont, en général peu abruptes. Aussi, a-t-on défini des températures de transition (repères) arbitraires, les plus usuelles sont : -TK 3,5 : température pour un niveau de 35 J/cm2 - température à mi-niveau ductile - température correspondant à 50% de cristallinité L’étude des faciès de ruptures permet de constater que le faciès change avec la température de l’essai. Quand la rupture est ductile, on observe une rupture à nerfs et l’on constate qu’il y a eu striction avant rupture. A basse température, on observe une rupture à grains et on ne décèle pas de déformation plastique. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 142 Souad BEN SLIMA
- 143. Surfaceàgrains %Cristallin = ité x100 Surfacetot ale Le pourcentage de cristallinité est défini par : Figure III-4 : Faciès de rupture des éprouvettes de résilience Une rupture ductile correspond à une cristallinité nulle, une rupture fragile à 100% de cristallinité, les ruptures mixtes correspondent à la zone de transition (zone à grains entourée d'une zone à nerfs, la cristallinité est alors comprise entre 0 et 100%). Les deux températures de transition, énergie et faciès ne coïncident pas en général car d'une part macroscopiquement, les zones cristallines apparaissent souvent comme formées à la fois de zones à cupules ductiles et de zone à clivage (d'où l'expression semi-fragile) et que d'autre part, l'énergie de rupture fait intervenir non seulement la propagation de la déchirure mais aussi et surtout son initiation. III-5- MECANISME DE LA RUPTURE Lorsqu'on abaisse la température, la rupture de l'éprouvette se fait selon les mécanismes suivants a- Dans le domaine des températures supérieures à celles de la zone de transition, la rupture demande une énergie élevée, elle présente une cassure à nerfs qui correspond sur les microfractographies, à des cupules. b- Dans le domaine de transition, on constate, pour les températures les plus élevées qu'il y a toujours pliage de l'éprouvette (mais l'angle de pliage diminue avec la température) et amorçage de la déchirure à fond d'entaille. Dans ce domaine il y a toujours amorçage ductile à fond d'entaille, mais il y a transition de propagation entre le mode ductile et le mode fragile qui s'accompagne d'une baisse faible mais régulière de l’énergie de rupture avec l'abaissement de la température. c- A plus basse température, mais toujours dans le domaine de transition, on observe la succession des phénomènes suivants: déformation plastique localisé, accompagnant le pliage de plus en plus limité. Quand la température diminue, amorçage fragile interne et propagation fragile qui traversent toute l'éprouvette. L'énergie totale de rupture qui est faible, continue à diminuer avec l'angle de pliage. Le point d'amorçage se rapproche progressivement de la surface de l'entaille. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 143 Souad BEN SLIMA
- 144. III-6- INFLUENCE DU SENS DE PRELEVEMENT Les aciers ont souvent, au préalable, subi des transformations à chaud (laminage, forgeage). Les propriétés sont donc de ce fait, anisotropes, et particulièrement la résilience. De ce fait, on observe une différence sensible entre les courbes de résiliences, effectuées sur éprouvettes prélevées dans le sens long de laminage, et sur celles prélevées dans le sens travers. La cristallinité par contre, semble peu affectée. Figure III-5 : Influence du sens de prélèvement III-7- PARAMETRES METALLURGIQUES INFLUENCANT LA RESILIENCE A LA RUPTURE FRAGILE Au point de vue structural, un acier trempé et revenu aura une meilleure résistance à la rupture fragile qu’un acier ferrito- perlitique, qui sera d'autant plus fragile que le pourcentage de perlite sera important, et que les grains seront plus gros. Aussi, pour les aciers de construction de structure ferritique, il faut rechercher une dimension minimale des grains, soit en réalisant un laminage contrôlé, soit en ajoutant des éléments de micro- alliage qui donnent des précipités qui affinent le grain austénitique ou qui abaissent la température de transformation γ → α , soit encore une conjonction de ces différentes solutions. D'une façon générale, on peut signaler que les éléments gammagènes Mn ; Ni, Co, abaissent la température de transition, alors que les éléments alphagènes pour des teneurs suffisamment importantes en solution dans la ferrite l’élèvent. Pour les aciers au carbone micro-alliés, il est souvent nécessaire de chercher un compromis. En effet, les fins précipités, s’ils permettent d1affiner les grains, fragilisent la matrice. Cependant, l’addition d1éléments tels que Nb, V ... durcissent suffisamment la matrice pour permettre la diminution de la teneur en carbone, ce qui est favorable au point de vue de la rupture fragile. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 144 Souad BEN SLIMA
- 145. IV -ESSAI DE FLUAGE IV-1- DESCRIPTION D'UN ESSAI DE FLUAGE Au cours d'un essai de fluage, l'éprouvette maintenue à température constante, est soumise à une charge fixe. On mesure alors les déformations qu'elle subit. En général, on réalise l'essai en traction et le résultat obtenu, qui est la courbe du métal dans les conditions adoptées, présente l'aspect schématisé sur la figure suivante: Figure IV-1 : Aspect schématique des courbes de fluage L'examen de cette courbe, montre l1existence de trois domaines: - Un allongement OA instantané lors de la mise en charge. Cet allongement peut être totalement élastique ou partiellement plastique selon la température et la charge. - Un allongement AB à vitesse décroissante. Ce fluage ralenti est appelé fluage primaire ou transitoire, il se produit au cours du 1er stade du fluage. - Un allongement BC à une vitesse sensiblement constante qui est la vitesse minimale de fluage au cours de l'essai considéré. Ce fluage est dit fluage secondaire et correspond au 2ème stade. - Un allongement à vitesse accélérée CD dû au fluage tertiaire qui se produit au 3ème stade et conduit à la rupture de l'éprouvette. L’importance relative des trois stades du fluage peut varier dans des grandes proportions (voir figure) On constate que - A haute température et sous de faibles contraintes, le premier stade peut parfois pratiquement disparaître - Le fluage secondaire diminue et peut même ne présentant alors qu'un point d'inflexion; Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 145 Souad BEN SLIMA
- 146. - Le fluage tertiaire dépend beaucoup de la ductilité à chaud du matériau. C’est ainsi qu1en cas de rupture fragile sans striction, ce 3ème stade peut disparaître presque totalement. IV-2- BUT DE L'ESSAI DE FLUAGE Le but de l'essai de fluage est de chercher la contrainte admissible dans certaines constructions travaillant à haute température. Les caractéristiques de fluage qu'il est alors nécessaire de connaitre, sont les suivants: Contrainte initiale provoquant un allongement déterminé (0,5 à 1%) à température donnée en un temps égal à 10 OOO ou 100000 heures IV-3- INFLUENCE, DE LA TEMPERATURE D'ESSAIS La température d'essai est comparable par rapport à la température de fusion Tf ; on distingue : - Le fluage aux basses températures, lorsque le rapport T/Tf est petit (inférieur à 0,25). On considère qu'aucune restauration, c'est-à-dire aucune élimination ou réduction des effets de la déformation plastique n’est obtenue par action thermique. On admet que dans ces conditions, le fluage est dû aux processus mettant en jeu le glissement des dislocations. La vitesse est alors déterminée par l'efficacité des obstacles qui s'opposent à ce glissement parmi lesquels on classe la friction intrinsèque des monocristaux et la friction due aux défauts cristallins (dislocations, impuretés). Mais, la déformation provoque une augmentation continue de l'écrouissage, la vitesse de fluage diminue constamment au cours du temps de telle sorte que l Ion reste toujours dans le domaine de fluage primaire. - Le fluage aux températures .intermédiaires' lorsque la valeur du rapport T/Tf est compris entre 0,25 et 0,5 environ. Alors la restauration statique et la restauration dynamique interviennent. On parle de fluage-restauration et on admet que peuvent apparaître alors : * des bandes de glissement grossières visibles au microscope optique; * des lignes de glissement fines visibles au microscope électronique. * des macles de déformation aux plus basses températures de l'intervalle considéré; * des bandes de pliage et des bandes de déformation tandis que se forme progressivement une sous structure de polygonisation et que dans les zones les plus déformées, la recristallisation peut débuter. Enfin Des glissements inter granulaires se produit qui engendrent des migrations des joints de grains et une cavitation intergranulaire - Le fluage aux températures élevées, lorsque la valeur du rapport T/Tf est supérieure à 0,5 environ. On admet qu’alors les phénomènes d’auto – diffusion deviennent prépondérantes ils sont responsables de la déformation Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 146 Souad BEN SLIMA
- 147. plastique permettant un transfert d'atomes depuis les joints de grains soumis à un effort de compression jusqu'aux joints de grains soumis à un effort de traction, transfert qui s'accompagnerait d'un déplacement en sens inverse des lacunes produites à haute température IV-4- EQUATIONS DES COURBES ε = f (t) T/ Tf < 0,3 Dans ce domaine de température, la vitesse de fluage semble toujours décroître et l 1 équation qui parait alors représenter au mieux les courbes d’allongement est en tension une forme logarithmique : ε = A Log t +B A et B indépendants de t, varient avec T et σ Cette équation est valable pour de nombreux métaux et alliages quelque soit leur système cristallin, quant la température est basse et la déformation est faible (<2.10-3). Cette équation suppose que la vitesse initiale de fluage déterminée immédiatement après la mise en charge serait infinie. Orl1expérimentation montre qu’il n’en est pas ainsi. Certains autres proposent pour décrire le fluage logarithmique une loi de la forme : ε = εo + Log (1+bt) 0,2 < T/Tf <0,7 Pour le fluage à haute température, nous avons vu que la courbe de fluage pouvait être décomposée en portions correspondantes aux différents stades. En laissant de côté le troisième stade qui correspond à la rupture progressive de l’éprouvette. Il faut donc ici se rendre compte des deux premiers stades. Les observations faites ont montré que le premier stade de fluage est généralement parabolique. ε = εo +atm Ou εo est l'allongement de mise en charge, a et m des paramètres indépendants de t. Il reste donc de compléter cette formule pour se rendre compte du fluage secondaire qui se fait à vitesse constante. ε = εo + atm + bt Où b est la vitesse du fluage dans le 2ème stade. Nous trouvons ici un domaine particulier du fluage à très haute température dit fluage diffusion. Les efforts mis en jeu sont faibles et l'on constate que les courbes de fluage deviennent pratiquement linéaires, le fluage primaire étant inexistant. L'équation de ces courbes est alors de la forme: ε = εo + vt Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 147 Souad BEN SLIMA
- 148. V- LA FATIGUE DES MÉTAUX V-1- INTRODUCTION Depuis longtemps, il a été remarqué que deux pièces mécaniques soumises à des efforts variables, se rompent après avoir subi des sollicitations parfois élevées, avec pratiquement pas de déformations et pour des contraintes inférieures à la limite élastique du matériau. Ce phénomène est appelé fatigue. Il n’existe pratiquement pas d’organes qui ne subissent pas des variations de l’intensité des efforts auxquels ils sont soumis, aussi la connaissance des comportements variables est indispensable pour le calcul de la durée de vie Des organes mécaniques. Cette connaissance permet de mieux utiliser les matériaux. V-2- LES RUPTURES DE FATIGUE Les pièces rompues en fatigue possèdent un faciès caractéristique avec deux zones distinctes (figure V-1) - une zone de rupture par fatigue, d’aspect lisse et soyeux, n’ayant subi aucune déformation plastique apparente ; on y distingue souvent des lignes d’arrêt de la fissure dont la courbure permet de remonter au point d’amorce de la cassure. Ces lignes d’arrêt correspondent le plus souvent à des arrêts de fonctionnement de la pièce. C’est la région de propagation de la fatigue proprement dite. - une zone plus tourmentée qui correspond à la rupture finale. L’examen détaillé de la zone de propagation de la rupture de fatigue permet de localiser, même à l’œil, (la ou) les zones d'amorces qui se situent - soit sur une inclusion en surface ou en sous-couche - soit sur un défaut à la surface de pièce marque quelconque, strie D’usinage. Autour de cette amorce et dans la zone de fatigue, on peut observer dans le cas des pièces qui ont travaillé en régimes variables des lignes parallèles concentriques à l’amorce qui indiquent des positions d’arrêt du front de fissure. Figure V-1 : Rupture de fatigue Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 148 Souad BEN SLIMA
- 149. Des observations à très fort grossissement (microscopie électronique) permettent de voir la progression du front de fissure à chaque cycle de sollicitation. Ces observations permettent de mettre en évidence deux caractéristiques du phénomène de fatigue - le rôle important des défauts de contrainte dans la matière - la rupture se développe pendant une grande partie de la vie de la pièce. V-3- MECANISME DE LA FATIGUE Le processus de rupture par fatigue est caractérisé par trois stades distincts : STADE I : Amorçage Les fissures associées aux ruptures par fatigue sont : En surface amorçage transgranulaire (ligne persistante de glissement) amorçage intergranulaire (suivant un joint de grain) amorçage sur un défaut (porosité, retassure, inclusion) Interne amorçage sur un défaut (porosité, retassure, inclusion) amorçage au joint de grain amorçage sur un joint triple Figure V- 2 : Mécanismes d’amorçage de fissure STADE II : Propagation Une fois formée la fissure se propage à l’intérieur du matériau ; il se produit alors un changement de direction de propagation qui devient perpendiculaire à l’axe de sollicitation. Figure V- 3 : stade 2 propagation de la fissure STADE III : Rupture Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 149 Souad BEN SLIMA
- 150. Le processus se répète jusqu’à ce qu’on atteint la longueur critique de la fissure, la propagation a lieu alors rapidement jusqu’à la rupture, c’est le stade III. Figure V- 4 : Variation de la longueur d’une fissure de fatigue en fonction de N De nombreuses théories du mécanisme de la fatigue ont été proposées sans qu'aucune n’ait permis d'expliquer la totalité des phénomènes observés. Les principales sont: V-3-1- THEORIE DES EFFORTS SECONDAIRES Les ruptures de fatigue partent sur des défauts de continuité dans la matière, aussi la fatigue est attribuée aux surcontraintes provoquées par ces dernières; mais on conçoit facilement l'existence de la fatigue sans ces défauts. V-3-2- THEORIES DE L'HYSTERISIS Ces théories reposent sur le fait que les matériaux ne sont pas parfaitement élastiques et que dans le diagramme déformation contrainte, on décrit le cycle d'hystérésis (figure V-5). Quand le cycle de contrainte est répété un grand nombre de fois, deux phénomènes peuvent se produire suivant les valeurs des contraintes appliquées Figure V-5 : Cycle d’hystérésis dû à une inélasticité du matériau - Le cycle d’hystérésis se couche sur l’axe des déformations quand le nombre de sollicitations croit, le module d'élasticité décroît jusqu'à ce qu’on obtienne la rupture. - Le cycle d’hystérésis se déforme d'abord puis tend vers une courbe limite stable; il y’a eu accommodation du matériau. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 150 Souad BEN SLIMA
- 151. L’existence d’un cycle d’hystérésis apparaît comme une condition nécessaire au phénomène de fatigue mais n'implique pas la fatigue. - Le cycle est observé pour des contraintes inférieures à la limite de fatigue, c'est-à- dire pour des contraintes pour lesquelles il n’y a pas de rupture pour un très grand nombre de sollicitations. - La limite de fatigue n’apparaît pas se confondre avec la limite d’accommodation. L'existence de l'hystérésis est expliquée par - La théorie des glissements moléculaires Il y a formation de bandes de glissement réversibles ou irréversibles suivant l’intensité de la contrainte. - La théorie de l'écrouissage Les bandes de glissement provoquent un écrouissage qui crée des contraintes internes qui s’ajoutent aux contraintes appliquées, la résistance mécanique est dépassée en certains endroits ce qui entraîne la naissance d’une fissure. - La théorie de 1 'amortissement interne Les métaux ne sont capables de dissiper sous forme de chaleur par l'amortissement interne que les quantités limitées d’énergie, au-delà d'une certaine valeur, l’énergie absorbée entraîne une détérioration de la structure qui conduit à la rupture. V-4- LES ESSAIS DE FATIGUE Pour déterminer la capacité des matériaux à résister à des sollicitations variables dans le temps, on les soumet à des essais de fatigue. Les essais les plus simples et les plus couramment employées consistent à faire varier les efforts ou les déformations appliquées suivant des fonctions du temps qui sont le plus souvent sinusoïdales ou s’en rapprochent. Les essais de fatigue sont caractérisés par deux contraintes : une contrainte maximale et la contrainte minimale. Il existe une terminologie particulière pour certaines valeurs de ces contraintes (figureV-6). FigureV-6 : Type de cycles de contrainte Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 151 Souad BEN SLIMA
- 152. - Si la valeur minimale est égale à là contrainte maximale et de signe contraire, les essais sont dits efforts alternés. - Si la valeur minimale est nulle, les essais sont dits sous efforts répétés. - Dans les autres cas, on parle d’efforts ondulés. Les modes de sollicitations sont : - Traction - compression ; - Flexion - Torsion ; - Chocs. Les essais sont réalisés: - soit sur éprouvettes pour études de matériaux - soit directement sur organes. V-4-1- ESSAI DE FATIGUE SUR EPROUVETTES Contrairement aux essais statiques où l'essai de traction est l’essai de référence, en fatigue on utilise surtout l’essai de flexion. Pour les matériaux autres que les matériaux en feuilles, la flexion rotative permet d'avoir un essai de fatigue sous efforts alternés en faisant travailler sur un barreau tournant en flexion. Les tôles sont essayées fatigue plane. Les essais de torsion sur éprouvettes sont peu utilisés, la torsion est utilisée pour les fils à ressorts, car la torsion est le mode de sollicitations des ressorts hélicoïdaux. Il est à noter une différence entre les essais de torsion et les essais de flexion ou traction; dans ces derniers, l'essai est déterminé par des contraintes maximales et minimales (on dit que l’on est à effort imposé) tandis que la construction des machines de torsion impose les déformations maximales (essais à déformation imposée). V-4-2- ESSAIS DE FATIGUE SUR ORGANES Les essais sont faits sur des machines dites universelles comportant une table fixe et une table mobile et permettant de simuler, grâce à un montage adéquat la sollicitation de l’organe en fonctionnement. V-5-PROPRIETES EN FATIGUE DION METAL V-5-1- DUREE DEVIE:N La durée de vie en fatigue d'une éprouvette dans des conditions de charge données est une caractéristique de cette éprouvette. Mais du fait de la dispersion des résultats obtenus pour des éprouvettes macroscopiquement identiques, cette notion ne peut Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 152 Souad BEN SLIMA
- 153. être retenue pour le matériau. On définit la durée de vie en fatigue pour une survie de p pour cent éprouvette, Np, estimée expérimentalement avec d'autant plus de précision que le nombre d'observations est important V-5-2- DIAGRMME DE WOEHLER Ce travail représente la relation observée expérimentalement entre la durée de vie N reportée conventionnellement en abscisses (échelle logarithmique et la contrainte σa ou σmax reportée en ordonnées (échelle linéaire ou logarithmique). Ce diagramme est établi à σm ou R constant (figure V-7) Figure V-7 : Courbe de Whoeler La courbe de Woehler est celle reliant la contrainte à la durée de vie médiane (correspondant à 50% de survie. C'est cette courbe qui est souvent donnée dans les documents techniques ; mais il faut bien observer que la dispersion augmente avec N. V-5-3- LIMITE D’ENDURANCE : σD Pour un type de sollicitations donné et pour σm ou R donnée, la limite d'endurance σD est la valeur limite vers laquelle tend l'amplitude de contrainte lorsque N devient très grand. Pour les aciers, la courbe de Woehler tend vers une asymptote horizontale et la limite d'endurance est réellement approchée de 107 cycles. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 153 Souad BEN SLIMA
- 154. V-6- DIAGRAMME DE GOODMAN - SMITH Pour un même matériau, la limite d'endurance σD varie avec la contrainte moyenne σm superposée à la contrainte variable. Le diagramme de Goodman - Smith donne, pour une durée de vie N (107 pour les aciers), la contrainte maximale, la contrainte minimale admissible en fonction de la contrainte moyenne (figure V-8). Figure V-8: Diagrammede Goodman-Smith V-7- REGLE DE CUMUL DE DOMMAGE Pour évaluer la durée de vie d1un matériau soumis à des séries de sollicitations de fatigue à des niveaux de contraintes différents, on peut admettre en première approximation la règle de cumul linéaire de dommage appelée: Règle de Miner. Soit ni cycles appliqués au niveau de contrainte σi et Ni la durée de vie à ce niveau de contrainte. L'endommagement engendré par cette série de cycles est défini par : ni Ni La rupture du matériau aura lieu lorsque la somme des endommagements engendrés sera égale à 1. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 154 Souad BEN SLIMA
- 155. A la rupture ni ∑ Ni = 1 Figure V-9: Charges variables dans le cas d’application de la règle de Miner Remarque : On utilise la règle de Miner dans le calcul de charge équivalente des roulements soumis à des charges variables lorsqu’on cherche leur durée de vie à la fatigue (figure V-9) V-8 EFFET D’UNE CONTRAINTE NORMALE MOYENNE (TRACTION) Diverses expressions analytiques ont été proposées afin de mieux comprendre les phénomènes de fatigue les plus utilisées sont (Figure V-10) Figure V-10 : Diagramme de Haigh -Le seuil le plus sécuritaire : Soderberg -Le seuil le plus utilisé en général : Goodman - Le seuil le plus utilisé dans l’industrie automobile : Gerber Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 155 Souad BEN SLIMA
- 156. VI LA MÉCANIQUE DE LA RUPTURE LINÉAIRE VI-INTRODUCTION La mécanique de la rupture s’est largement développée, surtout il y a une quinzaine d'années, tant sur le plan théorique que pratique. Les applications industrielles, les considérations économiques et les impératifs de sûreté justifient les efforts consacrés au développement de cette nouvelle science dans de nombreux pays. Le but de cette récente discipline est d'étudier le comportement des pièces contenant des fissures ou défauts, et prédire l’évolution de ces fissures (amorçage, croissance, propagation instable, arrêt). VI-1- DEFINITION MECANIQUE D'UNE FISSURE Modes de sollicitations. Du point de vue cinématique: Une fissure est une surface de discontinuité du champ de déplacement. Deux points situés initialement en vis-à-vis sur les lèvres de la fissure et confondus, lorsque la fissure n'est soumise à aucun chargement, vont subir un déplacement. Dans la rupture, on considère trois modes de sollicitation d'une fissure (figureVI-1). Soit P+ le point situé sur la lèvre supérieure de la fissure et P- le point correspondant situé sur la lèvre inférieure; lorsque la structure est mise en charge, ces deux points ne restent pas confondus mais se séparent. On considère pour simplifier une surface plane de fissure; le front de fissure est la ligne où l'on retrouve la cohésion du matériau et la continuité des déplacements. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 156 Souad BEN SLIMA
- 157. Figure VI-1 : Différents modes de sollicitations d’une fissure Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 157 Souad BEN SLIMA
- 158. MODE I C’est la composante normale au plan de fissure du déplacement qui une discontinuité, à la traversée de la fissure. Dans ce cas : V- = -V+ La fissure s’ouvre et on a séparation effective du matériau à cet endroit. Le chargement responsable d’un tel mode de sollicitation peut se présenter par la contrainte normale σy C’est de loin, le mode le plus dangereux, le plus fréquemment rencontré et par conséquent le plus étudié en mécanique de la rupture. On se bornera, par la suite, à l’étude du mode I MODE II C’est la composante tangentielle au plan de fissure et normale au fond de fissure, qui subit une discontinuité, c’est-à-dire : U- = -U+ Le chargement responsable d’un tel mode peut se présenter par la contrainte de cisaillement σxy = σyx MODE III C’est la composante tangentielle au plan de fissure et parallèle au front de fissure qui est discontinue, c’est-à-dire : W- = -W+ Le chargement provoquant une telle situation peut se présenter par la contrainte de cisaillement. σyz = σzy Les modes II et III se rencontrent fréquemment en mécanique des roches tandis que le mode I est spécifique des appareils soumis à la pression. VI-2- RUPTURE FRAGILE ET RUPTURE DUCTILE (aspect mécanique) VI-2-1- RUPTURE FRAGILE Le point de rupture est situé dans la partie linéaire du diagramme F- (figure VI-2) ; la fissure se propage brutalement, de façon instable et la pièce se rompt sans Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 158 Souad BEN SLIMA
- 159. déformation plastique notable. L'analyse de ce phénomène peut se faire en supposant le comportement du matériau élastique linéaire jusqu'à la rupture. La rupture fragile nécessite une faible énergie pour être produite. Parmi les facteurs favorisant la fragilité des matériaux citons: une limité élastique (σy) élevée, une température basse, l'irradiation par les neutrons, la corrosion chimique (rôle de l'hydrogène), le traitement thermique (cas des soudures). Mais d'autres facteurs liés à la géométrie de la pièce elle-même (forte épaisseur par exemple) et son mode de chargement (choc) peuvent aussi favoriser l'apparition d'une rupture fragile. Figure VI- 2 : Rupture fragile VI-2-2- RUPTURE DUCTILE Le point de rupture se situe dans la partie non linéaire du diagramme F - δ, (figure VI-3) ; la fissure, croît de façon stable à partir du point d'amorçage (point A) ; cette phase de croissance stable peut être très importante et se termine au point d'instabilité (point R). Ce type de rupture s'accompagne de fortes déformations plastiques de la pièce. Le phénomène est beaucoup plus comp1ex que celui de la rupture fragile. Il n’existe malheureusement pas à l'heure actuelle de critères bien étab1isqui permettent de prédire l'amorçage, la croissance stable puis la propagation instable d'une fissure, dans le cas d'une rupture ductile. La rupture ductile est moins dangereuse que la rupture fragile: elle nécessite une forte énergie pour se produire. El1e est associée à une plasticité notable de la structure et s’accompagne d'une période de croissance du défaut, pendant laquelle il faut augmenter le chargement pour faire progresser la fissure. Il existe dans ce cas une marge de sécurité entre l'amorçage du défaut (point A du diagramme) et la ruine de la pièce (point R). Cette marge de sécurité qui peut être plus ou moins importante selon le cas, doit pouvoir être estimée (ce qui nécessite de faire une analyse mécanique assez précise de la croissance stable de la fissure). Notons que le caractère non linéaire F - δ, dans le cas d’une rupture ductile provient de deux facteurs : le comportement élastoplastique du matériau d1une part, et le changement de géométrie de la structure (croissance de la fissure) d'autre part. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 159 Souad BEN SLIMA
- 160. Figure VI- 3 : Rupture ductile VI-3- NOTION DE FACTEUR DI INTENSITE DE CONTRAINTE (KI) On obtient un résultat remarquable au voisinage immédiat de la pointe de fissure, le champ est entièrement caractérisé par un paramètre unique; la constante multiplicative KI que l'on nomme: facteur d'intensité de contrainte, présente deux aspects : un aspect cinématique et un aspect statique. VI-3-1- ASPECT CINEMATIQUE Le facteur d'intensité KI présente un aspect cinématique car il est proportionnel à l'ouverture de la fissure au voisinage de l'origine. En effet, sur la fissure le déplacement vertical subit une discontinuité : [V ] = 2V + = 2(1 + υ ) K I r (k + 1) E 2Π VI-3-2- ASPECT STATIQUE KI présente un aspect statique, car il est proportionnel à l'intensification de la contrainte normale σy devant la pointe de fissure : K σ s = I 2Π r VI-4- VALIDITE DE LA SOLUTION SINGULIERE La validité des expressions du champ singulier, caractérisé par KI est limitée à la fois pour des raisons mécaniques et physiques. Mais il est très difficile de déterminer les limites (R1, R2) (figure VI- 4) de la zone annulaire de validité, appelée "zone singulière". Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 160 Souad BEN SLIMA
- 161. La limite supérieure R2 est due à l'existence des termes supplémentaires du développement en série de la solution: l'importance de ces termes est liée au type de chargement et à la géométrie de la pièce; il n'y a pas de règle générale pour l’évaluer. On peut quand même affirmer que R2 est d1autant plus faible que la pointe de fissure est située dans une région de fort gradient du contrainte Figure VI- 4 : Validation de la solution VI-5- EXTENSION AUX AUTRES MODES Les résultats obtenus précédemment s'étendent sans difficulté au mode II (cisaillement plan) et mode III (cisaillement anti plan). On met en évidence une singularité du champ de contraintes - déformations de même nature, c’est- à-dire en r-1/2, caractérisée par des coefficients d'intensité de contrainte KII et KIII VI-5-1- CAS DU MODE II On obtient, pour le terme singulier de la solution, les expressions : (1+υ) r θ U= KII θ Sin (k + 2 + Cos ) + ⋅ ⋅ ⋅ E 2π 2 (1+υ) r θ V =− KII θ Cos (k − 2 + Cos ) + ⋅⋅⋅ E 2π 2 Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 161 Souad BEN SLIMA
- 162. K= 3 – 4υ en D.P. 3 − υ k = en C.P.G. 1 − υ − K II θ 3θ σx = Sin (2 + CosθCos ) + ⋅ ⋅ ⋅ 2Πr 2 2 KII θ θ σy = θ Sin Cos Cos +⋅⋅⋅ 2Πr 2 2 −K θ 3θ σxy= II Cos (1− Sin Sin ) +⋅⋅⋅ θ 2Πr 2 2 σz = υ(σx + σx) en D.P. σz = 0 en D.P.G VI – 5-2 – CAS DU MODE III Seule la composante non nulle du déplacement est W =W (x,y) ; elle est indépendante de la coordonnée z sur la fissure W- = -W+ On obtient dans ces conditions r w = 4 (1 + υ ) K sin θ + .. 2π III 2 − K III θ σxy = Sin + ⋅⋅⋅ 2Π r 2 − K III θ σyz = COS + ⋅ ⋅ ⋅ 2Π r 2 Le mode III est celui qui conduit aux expressions les plus simples car il ne concerne qu’une composante du déplacement et deux composantes de contrainte. VI-5-3- CAS D’UN MODE MIXTE Pour une fissure sollicitée simultanément en modes I, II et III, la solution est simplement la somme des solutions correspondant à chacun des trois modes (théorème de superposition linéaire) ; la zone singulière est alors caractérisée par trois paramètres: les facteurs d’intensité de contrainte (KI, KII,KIII). Ces quantités ne sont découplées que sous leur aspect cinématique. En effet, on a les trois relations : [V ] = V + −V − = 2(1+ν ) KI r (k +1) E 2π [U] = U + −U − = 2(1+ν ) KII r (k +1) E 2π [W] = W + −W − = 8(1+ν ) KIII r E 2π Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 162 Souad BEN SLIMA
- 163. VI-5-4- NOTION DE FACTEUR DE FORME On pose le cas d’une pièce quelconque, sollicitée en mode I K = FS πa I a : longueur caractéristique de la fissure S : contrainte de référence caractéristique du niveau de chargement F : coefficient sous dimension, appelé « facteur de forme ». Le facteur de forme traduit l'influence de la forme de la pièce fissurée (il ne dépend que des dimensions relatives de la structure fissurée) et type de chargement (traction, flexion) sur le facteur KI VI-6- CRITERE DE RUPTURE FRAGILE - MESURE DE LA TENACITE KIC Le mode I conduit à un champ de contraintes - déformations caractérisé par un seul paramètre: le facteur d'intensité de contrainte KI. Il est donc naturel de fonder sur cette quantité un critère de rupture fragile; la fissure se propagera lorsque KI atteindra une valeur critique KIC caractéristique du matériau et appelée sa ténacité. Le critère de rupture fragile KI = KIC conserve sa validité tant que l'on peut négliger les déformations plastiques de la pièce, c'est-à-dire tant que la zone plastique demeure confinée dans le voisinage immédiat du front de fissure. VI-6-1- PRINCIPE DES MESURES DE TENACITE Mesurer la ténacité KIC c'est réaliser un essai de rupture sur une pièce fissurée de géométrie connue et retenir comme valeur de KI la valeur atteinte par le facteur d'intensité de contrainte KI au moment de la rupture. On utilise des éprouvettes de forme simple: elles sont normalisées et recommandées par A. S. T.M. (American in Society for Testing and Matériels) il s’agit de l'éprouvette C.T (Compact Tension) (figure VI-5). Pour chacune de ces éprouvettes, le facteur de forme est donné par une expression analytique. Pour l'éprouvette C.T., Stanley et Brown proposent la formule KI= Il suffit alors de mesurer la force critique Pc qui provoque l’extension de fissure pour en déduire KIC La validité d'une telle mesure est liée à celle du critère de rupture fragile: elle exige le respect de certaines conditions géométriques dans le but d'obtenir le confinement de la zone plastique en front de fissure ainsi qu’un état de déformation plane dans la majeure partie de l’éprouvette. Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 163 Souad BEN SLIMA
- 164. L’A.S.T.M propose la relation : B, a, b > 2, 5 ( K IC ) 2 y σ B : épaisseur de l'éprouvette a : longueur de fissure A : longueur de fissure b : ligament de l’ éprouvette ; b = W –a Si ces conditions sont respectées, on obtient une valeur de la ténacité KIC caractéristique du matériau et par conséquent, indépendante de la géométrie de l’éprouvette. Figure VI-5 : Eprouvettes utilisées en mécanique de la rupture Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 164 Souad BEN SLIMA
- 165. VI-6-2- RELATIONS ENTRE LA VITESSE EN FATIQUE ET LE FACTEUR D'INTENSITE DE CONTRAINTE Le facteur KI caractérise entièrement le champ de contraintes - déformations à la pointe d'une fissure. Selon les hypothèses de 1 'élasticité linéaire, il peut être utilisé avec profit pour décrire d'autres phénomènes que la rupture fragile, se situant au voisinage immédiat du front de fissure: c’est le cas de la croissance par fatigue. Lorsqu'on soumet une pièce fissurée à un chargement cyclique, on constate que la longueur de la fissure augmente, un chargement variant périodiquement entre zéro et une valeur donnée. Si le chargement maximal n’est pas trop élevé, on peut se limiter à une analyse élastique de la pièce; On obtient un facteur d'intensité de contrainte qui présente une variation périodique d’amplitude ∆K. On considère que l’endommagement progressif du matériau en pointe de fissure et par suite, la vitesse de croissance par cycle, est une fonction de la variation ∆K du facteur d'intensité de contrainte au cours du cycle. C’est pourquoi on cherche à représenter les résultats d'essais de fatigue par des lois empiriques du type : da = f (∆ K ) dN Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 165 Souad BEN SLIMA
- 166. On constate expérimentalement l'existence de trois stades de croissance selon les valeurs de∆K (figure VI- 6). Figure VI-6 : Relation entre la vitesse en fatigue et le facteur d’intensité de contrainte Démarrage de la fissure : Pour de très faibles valeurs de ∆K, on n'observe aucune croissance du défaut. Il semble qu'il existe un seuil de croissance ∆Ks en dessous du quel il n'y a pas de croissance du tout; la mise en évidence expérimentale d'un tel seuil est très difficile. Croissance régulière: La croissance du défaut se fait de façon régulière, on peut décrire la courbe par une loi de la forme : da Loi de Paris = (∆ K ) m dN Le coefficient C et l'exposant m (compris généralement entre 2 et 5), se déterminent graphiquement sur le diagramme à l'issue d'un essai de fatigue. Au cours de ce stade, la croissance d’une fissure par fatigue se traduit par l'existence de stries sur la surface de rupture (on peut les dénombrer par microscopie électronique) perpendiculaires à la direction de propagation. Accélération : La croissance s’accélère parce que ∆K est proche de la ténacité KIC ; il y a pratiquement déchirure à chaque cycle. La situation se complique lorsque la valeur minimale du chargement n’est pas nulle. Deux cas se présentent: - une partie du cycle de chargement est en compression ; dans ce cas, seule la partie positive du cycle est à considérer dans lé loi de croissance : ∆ K = K IMax Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 166 Souad BEN SLIMA
- 167. - la valeur minimale est positive non nulle; dans ce cas, on tient compte dans la loi de croissance du facteur. K R = IMin K IMax Cette loi généralise la loi de Paris et permet de décrire le stade de croissance accélérée. da C (∆ K )m = dN ( 1 − R ) K IC − ∆ K Cette loi généralisé la loi de Paris et permet de décrire le stade de croissance accélérée. VI-7- EXPRESSION FONDAMENTALE DE LI INTEGRALE J ET PROPRIETE D’ INDEPENDANCE VIS A VIS DU CONTOUR Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 167 Souad BEN SLIMA














![Figure I-4 : Position atomiques et directions cristallographiques
Exemples : A (1/2, 1/2, 0) B (1/2, 1/2, 1/2) C (0, 1/2, 0) D (1, 2, 1
Toute translation suivant un axe multiplie la position suivant cet axe par le
nombre de translation
Exemple : C' = 2C C' (0, 1, 0)
b)Direction cristallographique :
Elle est notée entre crochets et est définie par la position interceptée par la ligne tracée
à partir de l'origine. Les directions sont toujours définies par les plus petits nombres
entiers.
OB, par exemple, n'est pas [1/21/21/2], mais il faut multiplier par 2; c'est
donc [111] (qui est équivalent à [222], [333])
Exemples : V1 [111] V2 [121] V3 [110] V4 [11 1]
Les directions parallèles qui ne partent pas de la même origine ont les mêmes
Indices. Exemple : V1 [111] V'l [11ī ]
[111] et [11 ī et [1 ī 1] et [ī 11] appartiennent à la même famille de
direction. La famille est désignée par <111> (<uvw>).
Une direction est donc définie par : D = ut + vb + wc
c) Plan atomique :
Il est noté entre parenthèses, Il est défini par le multiple de l'inverse de la
position interceptée par le plan suivant les trois directions de l'espace.
Pourquoi l’inverse ? Cette convention a été adoptée pour s'affranchir de la
notion d'infini.
Cours de métallurgie, ENIT-Département de Génie Mécanique 14 Souad BEN SLIMA](https://image.slidesharecdn.com/coursmtallurgie-111011084551-phpapp02-120629095722-phpapp01/85/Coursmtallurgie-111011084551-phpapp02-14-320.jpg)
















































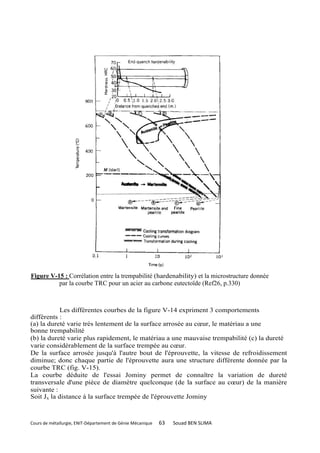
































































































![Figure VI- 3 : Rupture ductile
VI-3- NOTION DE FACTEUR DI INTENSITE DE CONTRAINTE (KI)
On obtient un résultat remarquable au voisinage immédiat de la pointe de fissure, le
champ est entièrement caractérisé par un paramètre unique; la constante
multiplicative KI que l'on nomme: facteur d'intensité de contrainte, présente deux
aspects : un aspect cinématique et un aspect statique.
VI-3-1- ASPECT CINEMATIQUE
Le facteur d'intensité KI présente un aspect cinématique car il est proportionnel à
l'ouverture de la fissure au voisinage de l'origine.
En effet, sur la fissure le déplacement vertical subit une discontinuité :
[V ] = 2V + = 2(1 + υ ) K I r
(k + 1)
E 2Π
VI-3-2- ASPECT STATIQUE
KI présente un aspect statique, car il est proportionnel à l'intensification de la
contrainte normale σy devant la pointe de fissure :
K
σ s = I
2Π r
VI-4- VALIDITE DE LA SOLUTION SINGULIERE
La validité des expressions du champ singulier, caractérisé par KI est limitée à
la fois pour des raisons mécaniques et physiques. Mais il est très difficile de
déterminer les limites (R1, R2) (figure VI- 4) de la zone annulaire de validité,
appelée "zone singulière".
Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 160 Souad BEN SLIMA](https://image.slidesharecdn.com/coursmtallurgie-111011084551-phpapp02-120629095722-phpapp01/85/Coursmtallurgie-111011084551-phpapp02-160-320.jpg)

![K= 3 – 4υ en D.P.
3 − υ
k = en C.P.G.
1 − υ
− K II θ 3θ
σx = Sin (2 + CosθCos ) + ⋅ ⋅ ⋅
2Πr 2 2
KII θ θ
σy = θ
Sin Cos Cos +⋅⋅⋅
2Πr 2 2
−K θ 3θ
σxy= II Cos (1− Sin Sin ) +⋅⋅⋅
θ
2Πr 2 2
σz = υ(σx + σx) en D.P.
σz = 0 en D.P.G
VI – 5-2 – CAS DU MODE III
Seule la composante non nulle du déplacement est W =W (x,y) ; elle est
indépendante de la coordonnée z sur la fissure
W- = -W+ On obtient dans ces conditions
r
w = 4 (1 + υ ) K sin θ + ..
2π
III 2
− K III θ
σxy = Sin + ⋅⋅⋅
2Π r 2
− K III θ
σyz = COS + ⋅ ⋅ ⋅
2Π r 2
Le mode III est celui qui conduit aux expressions les plus simples car il ne
concerne qu’une composante du déplacement et deux composantes de
contrainte.
VI-5-3- CAS D’UN MODE MIXTE
Pour une fissure sollicitée simultanément en modes I, II et III, la solution est
simplement la somme des solutions correspondant à chacun des trois modes
(théorème de superposition linéaire) ; la zone singulière est alors caractérisée
par trois paramètres: les facteurs d’intensité de contrainte (KI, KII,KIII). Ces
quantités ne sont découplées que sous leur aspect cinématique. En effet, on a
les trois relations :
[V ] = V + −V − = 2(1+ν ) KI r
(k +1)
E 2π
[U] = U + −U − = 2(1+ν ) KII r (k +1)
E 2π
[W] = W + −W − = 8(1+ν ) KIII r
E 2π
Cours : Caractérisation des matériaux ENIT-Département de Génie Mécanique 162 Souad BEN SLIMA](https://image.slidesharecdn.com/coursmtallurgie-111011084551-phpapp02-120629095722-phpapp01/85/Coursmtallurgie-111011084551-phpapp02-162-320.jpg)




