Control Systems - Stability
Last Updated :
27 Feb, 2024
Control systems are used to control the behavior of any dynamic system. It provides accurate information about the dynamic system so that it can work well. One of the important aspects of the control system is STABILITY. The stability of the system is important in order to get the desired output from the system. In this article, we will deal with how control system analysis helps in providing stability to the system. We will also study types of stability, applications, and many more.
What is Stability?
The stability of the system means when a controlled input is provided to any dynamic system, it must result in providing the controlled output. In other words, the system must be BIBO stable i.e., bounded input bounded output system. If the system is not in our control i.e., uncontrolled output is obtained on providing the bounded input then the system is said to be unstable.
 Unit Step Signal (Bounded Signal)
Unit Step Signal (Bounded Signal)
The above image shows a Unit Step Signal which is an example of the bounded signal. When the value of time (t) on the x-axis increases, the output value remains 1. This shows that the above signal is stable.
 Ramp Function (Unbounded-Signal)
Ramp Function (Unbounded-Signal)
The above image shows a Unit Ramp Signal which is an example of the un-bounded signal. When the value of time (t) on the x-axis increases, the output value increases continuously. This shows that the above signal is unstable.
Types of Stability
There are 3 types of stability which are as follows:
- Steady State Stability
- Transient Stability
- BIBO Stability
Steady State Stability
Steady-state stability means when a system is subjected to constant input for a long duration of time and the system results in a stable output, it is known as steady-state stability. When a dynamic system provides a stable output during any disturbance in the input, it is said to be a stable system.
Transient Stability
When a system changes its state, it is known as a transition. During the transition period, whether the system is stable or not when subjected to some disturbance is determined by the transient stability.
BIBO Stability
Bounded input and bounded output stability show a system is stable when the system returns the bounded output when the bounded input is given. When the output is controllable, the system is stable else it is unstable.
Types of System Based on Stability
There are 3 types of system based on stability:
- Completely stable system
- Marginally stable system
- Conditionally stable system
- Unstable System
Completely Stable System
As the name suggests, a completely stable system provides a stable output for all ranges of values. One way to identify a completely stable system is to check the poles of the transfer function. If the poles of the open and closed loop system lie in the left half of the s-plane, then the system is completely stable.
The graph given below shows the completely stable system.
 Completely Stable System
Completely Stable SystemMarginally Stable System
A marginally stable system is a system that is stable for the current or present value. Any disturbance in the input can make the output of the system unstable. The marginally stable system can be identified when the poles of the open loop and closed loop system lie on the imaginary axis of the s-plane. The graph given below is the example of marginally stable system.
 Marginally Stable System
Marginally Stable SystemConditionally Stable System
When a system is stable for certain values, then it is known as a conditionally stable system. The system can become unstable during the transient response. In simple terms, a conditionally stable system is stable only when the loop gain of a system is in a particular range. The image given below shows a conditionally stable system.
 Conditionally Stable System
Conditionally Stable SystemUnstable System
A system is said to be unstable when it produces uncontrolled output. The unstable system can be identified when the open and closed loop poles are on the right half of the s-plane. The given graph shows the unstable system.
 Unstable System
Unstable System
Methods to Analyze the Stability
The stability analysis in the control system is done using various methods. Some of the important methods are listed below:
Routh-Hurwitz Stability Criterion
It is a mathematical method that is used to determine the stability of the LTI system. It provides information about the roots in the right half of the s-plane by analyzing the coefficients of the characteristic equation of the system.
According to the Routh Hurwitz Criteria, the polynomial must satisfy the following 3 conditions:
- All coefficients of the polynomial must have same sign.
- All the terms in first column of the Routh's Array must have the same sign.
- All the power of 's' must be present in the characteristic equation.
If the above conditions are satisfied then the system is stable otherwise it is unstable.
Example: Examine the stability of given equation using Routh's method
s^{3}+4s^{2}+s+16=0
Solution:
Creating the Routh's Array:
s3
|
1
|
1
|
|---|
s2
|
4
|
16
|
|---|
s1
| \frac{(4*1)-(16*1)}{4}=-3
|
0
|
|---|
s0
| \frac{-3*16}{-3}=16
|
|
|---|
There are 2 sign change when we do the transition from 4 to -3 and then -3 to 16. As there are 2 sign change, the system is unstable.
Nyquist Stability Criterion
A Nyquist plot is a graphical representation used in control engineering. It is used to analyze the stability and frequency response of a system. This criterion works on the principle of argument. According to the Nyquist Stability Criterion, the number of encirclements of the point (-1, 0) is equal to the P-Z times of the closed loop transfer function. If the number of encirclements is in the anticlockwise direction then the system is stable.
The equation for stability analysis is given below:
N = Z – P
Where,
P = open loop pole of the system on right hand side (RHP)
Z = close loop zero of the system on right hand side (RHP)
N = number of encirclement around (-1,0)
Note: ‘N’ is negative for anticlockwise encirclement around (-1,0) and positive for clockwise encirclement around (-1,0).
Example: Given below is the Nyquist Plot in terms of 'k'. Find the condition of 'k' for which the system is stable.
 Nyquist Plot
Nyquist Plot
Solution
Case 1: If k< 240
The point -1+j0 is not encircled. This means that there are no poles on the right half of the plane. This means the system is stable for k less than 240.
Case 2: k>240
The point -1+j0 is encircled two times in the clockwise direction. This means that Z>P and hence the system is unstable.
Stability condition: 0 < K < 240
Root Locus Method
Root Locus Method plots the graph for the pole's movement. This helps in easy analysis of the dynamic system as it tells how the poles of the system move with the change in the input values. This helps in the identification at which point the system is stable or unstable.
- When the root locus plot is at the right hand side of the plane, the system is unstable.
- When the root locus plot is at the left hand side of the plane, the system is stable.
Example: Given below is the root locus plot for \frac{k}{(s+1)(s+2)(s+3)}
. Comment on the stability of the system.
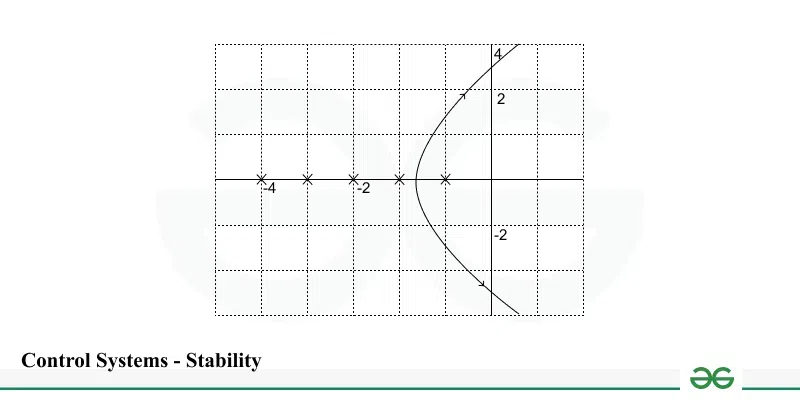 Root Locus Plot
Root Locus PlotSolution:
From the graph, it is clear that for the low values of the gain 'k', the system is stable as the root locus plot is on the left-hand side of the plane. But when we go for a higher value of gain 'k', the plot moves towards the right-hand side of the plane and hence it becomes unstable.
Bode Plot
Bode plots describe linear time-invariant systems’ frequency response (change in magnitude and phase as a function of frequency). It helps in analyzing the stability of the control system. It applies to the minimum phase transfer function i.e. (poles and zeros should be in the left half of the s-plane).
Stability by bode plot:
ωpc > ωgc ->System is stable
ωpc < ωgc ->System is unstable
ωpc = ωgc ->System is marginally stable
Where 'wpc' is gain cross over frequency and 'wpc' is phase crossover frequency.
Gain crossover frequency: It is the frequency at which the magnitude of G(s) H(s) is unity.
|G(jω)H(jω)|ω=ωgc = 1
Phase crossover frequency: It is the frequency where the phase angle of G(s) H(s) is -180 degrees.
∠G(jω)H(jω)∣ω=ωpc= -180∘
Example: Given below is the frequency response of the transfer function. By analyzing the graph, comment on the stability of the system.
 Bode Plot Parameters
Bode Plot Parameters
Solution
The above figure shows the gain and phase plot. The gain cross over frequency (wpc) and phase crossover frequency (wpc) can be calculated using gain plot and phase plot respectively.
Wgc is the value at 0dB whereas Wpc is the value at -180o.
Here ωpc < ωgc. This means the system is unstable
Applications of Control Systems - Stability
- The control system stability is important in the aerospace sector for ensuring the stability of the aircraft, and missiles which helps in maintaining the desired performance with accurate output and stability of the flight.
- In the automobile industry the stability of the control system is important in the stability of the electricity control (ESC), the anti-lock braking, and the high-accuracy active suspension system.
- It find its application in the sector of power system for maintaining the stability of the electric grids and blackout preventions.
Advantages and Disadvantages of Control Systems - Stability
The advantages and disadvantages of the stability are given below :
Advantages
- The open loop control system is very simple in its design which makes it economical.
- Closed-loop systems are more precise and accurate as compared to open-loop due to their complex structure. They can also handle the non-linearity.
- The control systems also remove errors in the signals which leads to a reduction in noise.
- The closed-loop control systems are capable of controlling the external factors which makes them more stable and reliable.
- The closed-loop systems are more resource-efficient.
Disadvantages
- The open loop systems does not have feedback mechanism which makes them highly inaccurate and unreliable for output.
- The open-loop systems are incapable of removing the disturbance which occurs due to external factors.
- The control system requires precise integration and tuning which is a challenging task.
- In the closed loop control system, some oscillations may exist which leads to unstability.
Conclusion
In this article, we have studied stability in the control system. Stability is crucial for any dynamic system for proper functioning. There are various techniques from which we can determine the stability of the system which is discussed in the article. We have also studied its applications, advantages, and disadvantages for a better understanding of the concept. This sows that if the output is controlled then we can say that the system is stable or if in open loop transfer function, any two poles are present on the imaginary axis - then the system is said to be stable.
Similar Reads
Control System Tutorial In this Control System tutorial, we will analyze and understand the concept and applications of a Control System with the help of detailed modules. This tutorial covers each module from the basics to advanced, including features, examples, classifications, applications, advantages, disadvantages, an
9 min read
Introduction to Control Systems
What is Control System? Definition, Types, and ExamplesControl systems are used in a wide range of applications they are the essential parts of many modern devices and systems. In simple terms, Control systems are used to control the behavior of devices or any process. In this article, we will be discussing the topic of Control Systems. We will cover th
9 min read
Types of Control SystemsEvery activity in our daily lives is affected by some form of control system. The concept of a control system also plays an important role in the working of space vehicles, satellites, guided missiles, etc. Such control systems are now an integral part of modern industrialization, industrial process
7 min read
Components of Control SystemsWith the advancement of technology, Human dependency on control system have increased over years and are being used everywhere, playing significant role in our daily lives. Contributing to different applications, they made the work easier by reducing human effort and involvement. They are used to co
8 min read
Classification of Control SystemsIn electronics, control systems are grouped into different types, and each has its unique features and uses. They are Important in electronics engineering for regulating dynamic systems, ensuring stability, accuracy, and top performance in various applications. Understanding their classifications he
15+ min read
Uses of Control SystemControl systems have become a necessary part of our day-to-day lives. There is hardly any field where the control systems are not used. They play a very major role in many sectors by making the process much simpler. They are used in fields like transportation, healthcare, aerospace, etc. In this art
8 min read
Advantages and Disadvantages of Control SystemsControl systems play a significant role in our daily lives, impacting various applications that often go unnoticed by us. They are used to control the behavior of devices and systems to accomplish the desired task. They are made up of many components and the major components are usually sensors, con
8 min read
Classification
Open Loop Control SystemControl systems are of wide use which can be understood in a better way by the following real-life examples which we use every now and then some of the examples are Regulating the speed of a fan with regulator, Oven temperature control, Washing machine cycle selection based on the type of clothes, R
9 min read
Closed-Loop Control SystemIn this article, we're going to discuss about closed loop control system. A closed-loop control system is an electronic device that automatically regulates a system to maintain a desired state or set point without human interaction. The advantages of closed-loop control systems lie in their ability
8 min read
Linear and Non-Linear Control SystemA control system is like a manager for machines. It tells them what to do so they work the way we want. There are different kinds of control systems, like ones that follow a straight line and others that don't. They're all about making sure things work the way we need them to. In this, we will discu
7 min read
Time-Variant and Invariant Control SystemControl systems play an important role in engineering, they help in regulating and controlling a process or a system to obtain controlled output. There are different types of control systems such as Linear and non-linear systems, Causal and Non-causal systems. Time variant and Time invariant control
6 min read
Continuous Time and Discrete Time Control SystemsIn Electronic Engineering, Continuous-time and Discrete-time control systems are essential ideas that are vital to the design and optimization of a wide range of electronic systems and devices. Continuous-time control systems operate on signals that vary continuously over time, where both the input
7 min read
SISO and MIMO Control SystemsIn Electronic Engineering, there are Two Key approaches in the field of control engineering are SISO (Single Input Single Output) and MIMO (Multiple Input Multiple Output) control systems, which are essential to the design and analysis of dynamic systems. SISO systems are designed to control or modi
8 min read
Difference between Feedback and Feed Forward control systemsControl systems play an essential role in regulating processes to ensure stability and productivity, primarily through the use of feedback and feedforward control mechanisms. Feedback control systems respond to output deviations and provide precise corrections but may be slower. Feedforward control
5 min read
Difference between Open-Loop Control System and Closed-Loop Control SystemControl System is a system in which the behavior of the system is determined by a differential equation. It manages the devices and the systems using control loops. There are Open-Loop Control System and Closed-Loop Control System. Open-Loop Control System is used in applications in which no feedbac
3 min read
Feedback
Block Diagram in Control System
Block Diagram AlgebraIn this article, We will discuss about block diagram and its components. We will also discuss about the various rules involved in block diagram algebra along with its equivalent block diagram. In addition to these we will also discuss about the application, advantages and disadvantages. Table of Con
8 min read
Block Diagram Reduction - Control SystemA control system may consist of several components. To show the function performed by each component in control engineering, we commonly use a diagram called the block diagram. A block diagram of a system is a pictorial representation of the functions performed by each component and of the flow of s
8 min read
Block Diagram Reduction RulesAs we know a complex control system is difficult to analyze as various factors are associated with it. In this article, we will see how to easily analyze a control system, and it is only possible by using block diagram reduction rules. This representation of a system involves summing points, functio
7 min read
Basic Elements of Signal Flow GraphSignal Flow Graphs are a crucial component of control systems. Furthermore, the control system is one of the most significant subjects in Electronics. It is primarily covered in the sixth semester of the B.Tech syllabus, though individual universities may alter it based on their syllabus hierarchy.
10 min read
Conversion of Block Diagrams into Signal Flow GraphsIn this article, we will discuss the method of converting the block diagram into a signal flow graph in a control system. We will first discuss about signal flow graph and its terminologies. We also discuss the construction of signal flow graphs from linear equations. We will then discuss about bloc
7 min read
Mason's Gain Formula in Control SystemMason's Gain Formula, also known as Mason's Rule or the Signal Flow Graph Method, is a technique used in control systems and electrical engineering. It provides a systematic way to analyze the transfer function of a linear time-invariant (LTI) system, especially those with multiple feedback loops an
7 min read
Time Response and Time Domain Analysis
Standard Test SignalsThe standard signals are often used in control systems, signal processing, communication and various engineering applications. These are predefined signals with known characteristics. To clarify standard test signals, their uses and application in the control systems. In this article, we will be goi
15+ min read
Unit Step Signal in Control SystemA Control System is a system which manages commands and regulates or directs the behaviour of other devices using control loops. A control system is a device which provides the desired response by controlling the output. A control system can also be defined as a system with a combination of mechanic
9 min read
Unit Ramp SignalThe unit ramp signal is a fundamental and insightful instrument that engineers and researchers both will use in the field of control systems. In order to clarify the meaning, uses, and implications of the unit ramp signal in control system, this article sets out to explore its complexities. The unit
7 min read
Steady State Errors for Unity Feedback SystemsIn this Article, We will be going through Steady State Errors for Unity Feedback Systems in control systems, First, we will start our Article with an introduction to Steady State Errors, then we will through its two types, and then we will see mathematical Expression for calculating the Steady-State
11 min read
Stability Analysis
Frequency Domain Analysis
Compensators in Control System
CompensatorsAll of the topics covered in the Control System Tutorial, including the Introduction to Control Systems, Classification, Transfer Function, Signal Flow Graphs, Mason Gain Formula, Block Diagram, State Space Model, and more, are included in our tutorial. The compensator is an extra part that is intro
10 min read
Lag CompensatorA compensator is a device or component that is used to obtain the desired performance, stability, and behavior of the system. It is the part of the feedback device in a control system and is used to stabilize the system and regulate the other system with its ability of conditioning the input or outp
7 min read
Lead Compensator in control systemCompensators, which have a wide range of functionality and variants, are an essential component of Control Systems. Furthermore, the control system is an important subject in the engineering curriculum, and it incorporates many important electronics components. To understand the Lead Compensator, we
7 min read
Controllers in Control System