Artificial Neural Network (draft)

Artificial Neural Networks
An Introduction

Why study ANNs?
• To understand how the brain actually works
• To understand a type of parallel computation
• IBM’s “The Brain Chip” (1 million neurons and 256 synapses)
• To solve practical problems
• Artificial Neural Networks should be good for things brains are good at
and bad at things brains are bad at
(Vision, speech recognition)
(eg: 32 * 71 = ???)

What neurons look like
Our model will be simplified:
 Synapses -> Weighted Inputs
 Soma -> An activation function
 Axon -> Outputs
Neuron – an electrically excitable cell that
transmits information
 Dendrites receive signals from many
other neurons
 These signals can be either excitatory
or inhibitory
 Soma (cell body) processes this
information
 Above a certain threshold, an
electrical signal is fired down the axon.

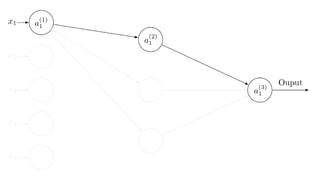
A Feed Forward Neural Net Weighted
connections

What can NNs do?
• Image recognition
 MNIST handwritten digits
 Read reCAPTCHA better than humans do
• Speech recognition and NLP
• Answer the meaning of life

Using recurrent neural net to predict the
next character
• In 2011, Ilya Sutskever used 5 millions strings of 100 characters, taken
from Wikipedia.
• Training took one month on a GPU
• Once trained, the neural net will predict the next character in a
sequence of characters
• He fed it the phrase “The meaning of life is” _______________

A Brief History of ANNs
• 1943 – McCulluogh and Pitts NN models can represent any Boolean
• 1949 – Donald Webb describes how learning might take place: “cells that
fire together, wire together.”
• 1959 – Rosenblatt’s perceptron can learn linearly separable data
• 1969 – Minsky & Papert criticize the perceptron
• 1970-1986 – The dark ages of neural networks (No funding)
• 1986 – Hinton, LeCun et al. describe the backpropagation algorithm for training
neural networks of arbitrary depth ( Paul Werbos, 1974)
• 1997 – A.K. Dewdney – "Although neural nets do solve a few toy problems, their powers of
computation are so limited that I am surprised anyone takes them seriously as a general problem-
solving tool.“
• Other techniques (Random Forests[1995] and Support Vector Machines[1995]) are considered
state of the art ML for classification problems
• 2006 – Second Renaissance of neural networks with new methods for training deep and recurrent
NNs.

1930 1940 1950 1960 1970 1980 1990 2000 2010 2020
Ln(#ofPublications)
ANN Scholarly Publications Per Year
(Ln Normalized)
1986
1969

“the embryo of an electronic computer that [the
Navy] expects will be able to walk, talk, see, write,
reproduce itself and be conscious of its existence."
1958
Frank Rosenblatt’s Perceptron

Weight space
Consider all the different sets of weights that will
output the correct value for a 2-D input vector.
Here, threshold = 0
Input vector with
output value = 1
Good
weight
Bad
weight

NAND example
Input Data
0 0
1 0
0 1
1 1
1
1
1
0
One of many possible solutions:

NAND Decision Boundary
One possible solution:

NAND Decision Boundary
0 0
1 0
0 1
1 1
1
1
1
0
One possible solution:

Training Data
0 0
1 0
0 1
1 1
0
1
1
0
A single perceptron can
only solve linearly
separable problems
XOR Problem

Training Data
0 0
1 0
0 1
1 1
0
1
1
0
Multiple layers of
perceptrons solve the
XOR problem, but
Rosenblatt did not have
an learning algorithm to
set the weights
XOR Problem

Training Data
0 0
1 0
0 1
1 1
0
1
1
0
XOR Problem
1 0
1 1
1 1
0 1
2 weight
planes

Training Data
0 0
1 0
0 1
1 1
0
1
1
0
XOR Problem
1 0
1 1
1 1
0 1
1 weight
plane

Sigmoid (Logistic Function)
• The sigmoid function is similar to the binary threshold function, but it
is continuous
“Squashes” – outputs a value between 0 and 1
• It’s derivative has a nice property – it is computationally inexpensive

Sigmoid Neurons • We can “bake in” the bias by augmenting with
an element, , that we set to a constant value
(say, 1) for every sample.
• now represents the bias value.
• With the bias “baked in,” the model has a simpler
notation and will be more computationally efficient

}
Matrix notation
is easier to
read, and used
in production
code

How to train a feed forward net?
• There are several cost functions (cross entropy, classification error,
squared error).
• To measure the error in this sample we will use the squared error
• Major Difficulty
We know what the output target is, but nobody is telling us directly what the
hidden units should be

How to train a feed forward net?
• Try: randomly perturb one weight and see if it improves performance
• But this is very, very slow

Backpropagation, 1986*
• The “backward propagation of errors” after forward propagation
• Here is the cost for a single training sample
• If we calculate the error derivatives w.r.t. each weight, we can update
the weights with gradient descent.

Backpropagating errors
Step 0. Feed Forward
Network

Step 1. Backpropagate the
error derivative to each
node

Step 1. Backpropagate the
error derivative to each
node
Step 2. Use the node deltas
to compute the incoming
weight derivatives

Backpropagation error derivatives
Feed Forward
Back Propagate
Linear
Output
Neuron

Back Propagation can be used to train a neural net with which of
the following activation functions?
Logistic (sigmoid)
Linear
Binary threshold neurons (Perceptron)
Hyperbolic Tangent ( )


Selecting Hyper-Parameters
Generally, we use trial and error (with cross-validation) to select
hyperparameters
What learning rate?
Momentum?
How many layers?
How many nodes / layer?
Regularization coefficient?
Activation function(s)?

Regularization
• Without some form of regularization, large ANNs are prone to over
fitting
• ANNs can approximate any function; they can fit the noise in the
training data set
• One traditional solution is L2 regularization. We modify our error
function by including for every weight in the matrix.
• L2 regularization drives the weights towards 0
• As the weights approach zero, the sigmoid function becomes more
linear
• Recently, new forms of regularization have improved ANNs learning

New regularizers
• Force neurons to share weights

Learning Curves – Overfitting - regularization

NN libraries
• Theano (python)
• PyLearn2 (python)
• Torch (Lua)
• Deep Learning Toolbox (MATLAB)
• Numenta (python)
• Nnet (R)

Do walk through with ConvnetJS

Google Trends “Neural Network” searches

Google Trends “Random Forests” searches

Google Trends “Deep Learning” searches

Addressing ANN’s weaknesses: Averaging many
models
• Unlike random forests (which average many decision trees),
creating many neural network models has not been feasible
• Averaging models is important because it prevents over fitting
• NN Dropout (2012) provides a way to average many models,
without having to train them separately

Provide motivation for Deep Learning

Artificial Neural Network (draft)

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Artificial Neural Network (draft) (20)

Recently uploaded (20)

Artificial Neural Network (draft)