Ad
Image net classification with Deep Convolutional Neural Networks
- 1. IMAGENet Classification 輪_ with Deep Convolutional Neural Networks 講: NIPS ‘12 2012 / 12 / 20 本位田研究室 M1 堀内 新吾
- 2. 発表論文 『IMAGENet Classification with Deep Convolutional Neural Networks』 会議:NIPS 2012 著者:Alex Krizhevsky, Ilya Sutskever, Geoffrey E Hinton トロント大学のHinton先生と愉快な仲間たち
- 3. Object Recognition 応用例: • カメラの顔認識 • 自動レジ • ロボットの目 • etc… 近年の傾向: • クラス数 • 訓練画像数 • 特徴量の複雑化 Cat? Leopard?
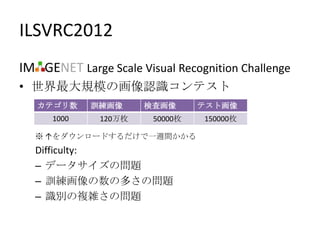
- 4. ILSVRC2012 IM GENET Large Scale Visual Recognition Challenge • 世界最大規模の画像認識コンテスト カテゴリ数 訓練画像 検査画像 テスト画像 1000 120万枚 50000枚 150000枚 ※ ↑をダウンロードするだけで一週間かかる Difficulty: – データサイズの問題 – 訓練画像の数の多さの問題 – 識別の複雑さの問題
- 5. Typical OR Approach 訓練画像 特徴抽出 特徴量 学習 クラスラベル クラス 分類機 テスト画像 特徴量 識別 クラスラベル 特徴抽出 “どんな特徴量を使う か”が最重要、だった
- 6. Proposal Approach 訓練画像 Deep クラスラベル Conventional Neural クラスラベル テスト画像 Networks • 内部で自動で特徴抽出 • 各層の間に荷重付き枝を持つようなNeural Network
- 7. Result of ILSVRC 2012 Error Rate 0.4 34% 0.3 29% 27% 27% 26% 0.2 16% 0.1 0 わけが わからない よ
- 8. Agenda • Overview • ImageNet • Architecture – Deep Learning – Convolutional NNs – Acceleration – Reducing Overfitting • Learning • Result and Evaluation
- 9. Intro.
- 10. Overview why? 実世界におけるクラス分類に耐える識別機を作 る 史上最大規模のNeural Network how? それを動かせるGPU what? Reasonableな時間で圧倒的な性能を出した Reasonableな時間で圧倒的な性能を出した contrib. GPU用のコードを公開した
- 11. IM GENET WordNetの階層に従う画像データベース url: http://www.image-net.org/ • カテゴリ22000 • 画像:1500万枚 1画像1カテゴリでbounding-boxや各種特徴量も配布 ex.)Chain-mailカテゴリの画像
- 12. Architecture
- 13. Deep Learning Output 識別機 教師あり学習 教師なし学習 Input
- 14. Deep Learning Output Traditional Approach Greedy Layer-wise Training[1] • まとめて学習 識別機 • 一層ずつ学習 • 多層autoencoder • 一層のautoencoder × 時間 時間 × 効率 効率 × Vanishing Gradient × Overfitting Problem Input
- 15. Convolutional NNs[2] • NNsの問題 各ユニットが全て繋がっている ↓ • 提案1 • 入力の欠損 • 入力のズレ • ノイズ • 提案2 の影響をNNs全体が学習してしまう • 提案3
- 16. Convolutional NNs[2] • NNsの問題 各ユニットへの入力を制限 • 前の層の一部のユニットの出力だけを受け取る フィルタのようなもの • 提案1 → 入力の誤差を全体に伝搬させない • 入力範囲はオーバーラップするように選ぶ • 提案2 データの欠損に対応するため • 提案3
- 17. Convolutional NNs[2] • NNsの問題 重みを共有 • 入力範囲の同じ入力座標は同じ重みをもつ • 提案1 • 同じフィルタを使って圧縮するイメージ → フィルタに対する入力の傾向を学習 → 入力のズレ,ノイズに対応 • 提案2 問題: 1つのフィルタについてしか学習できない • 提案3
- 18. Convolutional NNs[2] • NNsの問題 フィルタの数を増加 • 多数のフィルタを用意して出力を多次元化 異なる重みをもつ複数のフィルタを学習 • 提案1 • 様々な特徴を学習可能 • 提案2 • 提案3
- 19. Architecture of CNNs 5層のCNNs + 3層のNNs • 入力:150,528次元 • ニューロン:約66万個,GPU2台に配置 253,440 – 186,624 – 64,896 – 64,896 – 43,264 – 4096 – 4096 • 出力:1000次元
- 20. Acceleration ReLU Local Response Overlapping GPU2台の学習 Pooling 非線形変換 正規化
- 21. Acceleration ReLU Local Response Overlapping GPU2台の学習 Pooling 非線形変換 正規化 ニューロンのモデ ル 入力 x : 前の層の出力を各枝ごとに重み付けしたも の 出力 f(x): 入力に非線形な変形を加えたもの ex.) f(x) = tanh(x), (1 + e-x)-1 f(x) 問題点 : 莫大な回数行うとなると遅すぎる -> もっと単純な変形で出力を決定したい ReLU 非線形変換 f(x) = max(0, x) 予備実験において6倍速くネットワークを収束
- 22. Acceleration ReLU Local Response Overlapping GPU2台の学習 Pooling 非線形変換 正規化 GPU間のデータのやり取りを制限 - 2,3層間,5,6層間,6,7層間だけ
- 23. Acceleration ReLU Local Response Overlapping GPU2台の学習 Pooling 非線形変換 正規化 • ReLU非線形変換の入力は全部負だとダメ → 近傍のフィルタの同じ座標の重みで正規 化 予備実験では約2%の性能向上 厚み:N この範囲で正規化す
- 24. Acceleration ReLU Local Response Overlapping GPU2台の学習 Pooling 非線形変換 正規化 • 近傍の出力をまとめる 出力: 平均,最大値,etc… • 一般的には範囲を分ける 図:Poolingのイメージ →Overlapさせることでズレを 吸収 図:3×3, Overlap 1の例 0.3~0.4%の性能向上
- 25. Reducing Overfitting 試験前に必死で勉強 とりあえず丸暗記 問題集は完璧!! 応用問題しか出ない 暗記だけだからヤバい 勉強しない方が良かった
- 26. Reducing Overfitting データの拡張 バリエーションを増やす Dropout ラベルを保存するような変換 1. トリミング+鏡像 訓練時:ランダムに切り取る テスト時:中央+4隅 2. 輝度の変更 主成分分析を利用 ガウス分布から固有値を抽出 固有値と乱数で輝度を変更 約1%の性能向上
- 27. Reducing Overfitting Dropoutなし データの拡張 バリエーションを増やす Dropout[3] ラベルを保存するような変換 • 出力の半分を0にする 1. トリミング+鏡像 CNNsなので重みは共有 訓練時:ランダムに切り取る → 他の部分で学習は可能 テスト時:中央+4隅 Dropoutあり 2. 輝度の変更 • 他ニューロン任せをやめる 主成分分析を利用 ガウス分布から固有値を抽出 NNsは影響度の高いニューロン に 固有値と乱数で輝度を変更 学習をまかせてしまうことがあ 約1%の性能向上 る 図:手書き数字画像から得た特徴
- 28. Learning
- 29. Learning • 学習アルゴリズム:確率的勾配降下法 • 重みの初期化: 平均0のガウス分布からサンプリング • 学習回数:90回 2台のGPUで5,6日かかった
- 31. Result error rate 図:ILSVRCの結果 圧倒的なエラー率の低さ
- 33. Qualitative Evaluation 1層目のレイヤーの出力.上: GPU1,下: GPU2 • 1層目が獲得した特徴 – GPU1:傾き – GPU2:色 • 脳の視覚野にも異なる性質に反応する部位が存 在 ↑GPU間の通信を制限したことによるのではない か?
- 34. Application
- 35. Summary
- 36. Sammary 実世界にも応用可能な識別問題を解くために CNNsとDeep Learningを用いた巨大なネットワーク を GPU2台の上に実装し ImageNetのコンテストに応用したら 常識破りな結果が出ちゃった^^
- 37. Refference [1]Deep Learning: A fast learning algorithm for deep belief nets, GE Hinton, S Osindero, YW Teh - Neural computation, 2006. [2]CNNs: Face recognition: A convolutional neural-network approach, S Lawrence, CL Giles,et al. Neural Networks, IEEE Transactions on 1997 参考http://ceromondo.blogspot.jp/2012/09/convolutional-neural-network.html [3]Dropout: Improving neural networks by preventing co-adaptation of feature detectors, GE Hinton, N Srivastava, A Krizhevsky, et al. 2012













![Deep Learning
Output
Traditional Approach Greedy Layer-wise Training[1]
• まとめて学習 識別機 • 一層ずつ学習
• 多層autoencoder • 一層のautoencoder
× 時間 時間
× 効率 効率
× Vanishing Gradient × Overfitting
Problem
Input](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-14-320.jpg)
![Convolutional NNs[2]
• NNsの問題
各ユニットが全て繋がっている
↓
• 提案1 • 入力の欠損
• 入力のズレ
• ノイズ
• 提案2 の影響をNNs全体が学習してしまう
• 提案3](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-15-320.jpg)
![Convolutional NNs[2]
• NNsの問題
各ユニットへの入力を制限
• 前の層の一部のユニットの出力だけを受け取る
フィルタのようなもの
• 提案1 → 入力の誤差を全体に伝搬させない
• 入力範囲はオーバーラップするように選ぶ
• 提案2 データの欠損に対応するため
• 提案3](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-16-320.jpg)
![Convolutional NNs[2]
• NNsの問題
重みを共有
• 入力範囲の同じ入力座標は同じ重みをもつ
• 提案1 • 同じフィルタを使って圧縮するイメージ
→ フィルタに対する入力の傾向を学習
→ 入力のズレ,ノイズに対応
• 提案2
問題: 1つのフィルタについてしか学習できない
• 提案3](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-17-320.jpg)
![Convolutional NNs[2]
• NNsの問題
フィルタの数を増加
• 多数のフィルタを用意して出力を多次元化
異なる重みをもつ複数のフィルタを学習
• 提案1 • 様々な特徴を学習可能
• 提案2
• 提案3](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-18-320.jpg)








![Reducing Overfitting
Dropoutなし
データの拡張
バリエーションを増やす
Dropout[3]
ラベルを保存するような変換
• 出力の半分を0にする
1. トリミング+鏡像
CNNsなので重みは共有
訓練時:ランダムに切り取る
→ 他の部分で学習は可能
テスト時:中央+4隅
Dropoutあり
2. 輝度の変更
• 他ニューロン任せをやめる
主成分分析を利用
ガウス分布から固有値を抽出
NNsは影響度の高いニューロン
に 固有値と乱数で輝度を変更
学習をまかせてしまうことがあ
約1%の性能向上
る
図:手書き数字画像から得た特徴](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-27-320.jpg)









![Refference
[1]Deep Learning:
A fast learning algorithm for deep belief nets, GE Hinton, S Osindero, YW Teh -
Neural computation, 2006.
[2]CNNs:
Face recognition: A convolutional neural-network approach, S Lawrence, CL
Giles,et al. Neural Networks, IEEE Transactions on 1997
参考http://ceromondo.blogspot.jp/2012/09/convolutional-neural-network.html
[3]Dropout:
Improving neural networks by preventing co-adaptation of feature detectors, GE
Hinton, N Srivastava, A Krizhevsky, et al. 2012](https://image.slidesharecdn.com/imagenetclassification-121220012320-phpapp02/85/Image-net-classification-with-Deep-Convolutional-Neural-Networks-37-320.jpg)

















![[DL輪読会]VoxelPose: Towards Multi-Camera 3D Human Pose Estimation in Wild Envir...](https://cdn.slidesharecdn.com/ss_thumbnails/20201023voxelposekuboshizuma-201023025841-thumbnail.jpg?width=560&fit=bounds)



![[DL輪読会]Swin Transformer: Hierarchical Vision Transformer using Shifted Windows](https://cdn.slidesharecdn.com/ss_thumbnails/swintransformer-210514020542-thumbnail.jpg?width=560&fit=bounds)

![[DL輪読会]Xception: Deep Learning with Depthwise Separable Convolutions](https://cdn.slidesharecdn.com/ss_thumbnails/2017-06-22-170623004409-thumbnail.jpg?width=560&fit=bounds)

















![[論文紹介] Convolutional Neural Network(CNN)による超解像](https://cdn.slidesharecdn.com/ss_thumbnails/cnn-presen-161218113749-thumbnail.jpg?width=560&fit=bounds)











![[DL輪読会]EfficientDet: Scalable and Efficient Object Detection](https://cdn.slidesharecdn.com/ss_thumbnails/191122dlseminar-191122013544-thumbnail.jpg?width=560&fit=bounds)






