![Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil
39
There are various operations of binomial heaps
CreateBHeap—Creates an empty binomial heap, that is, simply
allocates and returns an object H, where head[H] = null
FindMinimumKey—Returns a pointer to the node with the
minimum key in an n-node binomial heap H
UnitingTwoBHeap—Takes the union of the two binomial heaps.
InsertNode—Inserts node into binomial heap H
ExtractMinimumKeyNode—Extracts the node with minimum
key from binomial heap H and returns the pointer to the
extracted node
DecreaseKey—Decreases the key of a node in a binomial heap
H to a new value k
DeleteKey—Deletes the specified key from binomial heap H](https://image.slidesharecdn.com/12heaps-150824112317-lva1-app6891/85/12-Heaps-Data-Structures-using-C-by-Varsha-Patil-39-320.jpg)
![Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil
44
CreateHeap—Creates an empty Fibonacci Heap, that is, simply
allocates and returns an object H, where min[H]=null
FindMinimumKey—Returns a min[H], that is, pointer to the
node with the minimum key in an n-node Fibonacci heap H
UnitingTwoFHeap—Takes the union of the two Fibonacci heaps
InsertNode—Inserts node into Fibonacci heap H
ExtractMinimumKeyNode—Extracts the node with minimum
key from Fibonacci heap H and returns the pointer to the
extracted node
DecreaseKey—Decreases the key of a node in a Fibonacci heap
H to a new value k
DeleteKey—Deletes the specified key from Fibonacci heap H](https://image.slidesharecdn.com/12heaps-150824112317-lva1-app6891/85/12-Heaps-Data-Structures-using-C-by-Varsha-Patil-44-320.jpg)
12. Heaps - Data Structures using C++ by Varsha Patil
- 1. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 1
- 2. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 2 A specialized tree-based data structure known as heaps Usage of heaps efficiently for applications such as priority queues How heaps are implemented using arrays A few more applications such as selection problem and event simulation
- 3. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 3 Definition of heaps: A heap is a binary tree having the following properties: It is a complete binary tree, that is, each level of the tree is completely filled, except at the bottom level At this level, it is filled from left to right It satisfies the heap-order property, that is, the key value of each node is greater than or equal to the key value of its children, or the key value of each node is lesser than or equal to the key value of its children
- 4. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 4 17 50 5 4030913 5065 70 30 5 7 10 Fig 12.1 Heap with height three Fig 12.1 Heap with height two Fig 12.1 Heap with height one Fig 12.1 Fig 12.2 Fig 12.3
- 5. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 5 17 50 4030913 5065 70 30 5 Fig 12.4 Binary Trees with no Heap
- 6. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 6 Min-heap Max-heap
- 7. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 7 Data all >= Data all >= Data Fig 12.5 :Structure of min-heap
- 8. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 8 In min-heap, the key value of each node is lesser than or equal to the key value of its children In addition, every path from root to leaf should be sorted in ascending order 9710 52 1 Fig 12.6 An example of a min heap
- 9. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 9 A max-heap is where the key value of a node is greater than the key values in all of its sub trees In general, whenever the term ‘heap’ is used by itself Data all <= Data all <= Data
- 10. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 10 326 48 9 Fig 12.7 An example of a max-heap
- 11. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 11 326 48 9 Fig 12.7 An example of a max-heap
- 12. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 12 A binary tree is complete if it is of height h and has 2h+1 − 1 nodes. A binary tree of height h is complete if it is empty, or its left sub tree is complete of height h − 1 and its right sub tree is completely full of height h − 2, or its left sub tree is completely full of height h − 1 and its right sub tree is complete of height h − 1. A complete tree is filled from the left when all the leaves are on the same level or two adjacent ones all nodes at the lowest level are as far to the left as possible
- 13. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 13 A binary tree has the heap property if : it is empty or the key in the root is larger than either children and both sub trees have the heap property
- 14. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 14 326 48 9 Fig 12.8 Sample Heap Implementation of Heap
- 15. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 15 In this array, 1. parent of index ith node is at index (i − 1)/2 2. left child of index ith node is at index 2 X i + 1 3. right child of index ith node is at index 2 X i + 2 Data 9 8 4 6 2 3 Index 0 1 2 3 4 5 6 7
- 16. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 16 68 46 22 35 02 13 09 0913235 2246 68 A Heap Tree Representation of heap by using array
- 17. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 17 Declare create() : Heap Insert(Heap,Data) : Heap Deletemaxval(Heap) : Heap ReheapDown(Heap, Child) : Heap ReheapUp(Heap, Root) : Heap End
- 18. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 18 Create—To create an empty heap to which ‘root’ points Insert—To insert an element into the heap Delete—To delete max (or min) element from the heap ReheapUp—To rebuild heap when we use the insert() function ReheapDown—To build heap when we use the delete() function
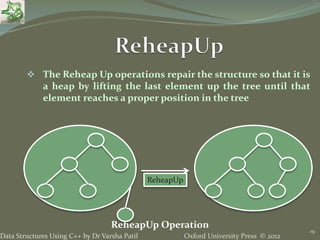
- 19. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 19 The Reheap Up operations repair the structure so that it is a heap by lifting the last element up the tree until that element reaches a proper position in the tree ReheapUp ReheapUp Operation
- 20. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 20 To restore the heap, we need an operation that will sink the root down until the heap ordering property is satisfied and thus the operation ReheapDown comes into action ReheapUDown Operation
- 21. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 21 312327 4332 21 Original Tree, not a Heap Example 41 2624
- 22. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 22 Root 21 moved down (right) 312327 2132 43 41 2624
- 23. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 23 Moved down again yielding a heap 312327 32 43 21 2624 41
- 24. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 24 Insert into heap—A new key can be inserted into a heap. Initially, a new key is inserted by locating the first empty leaf location in an array, and the ReheapUp operation places it in a proper location in the heap Delete into heap—The key can be deleted from heap and it is the root value. After deletion, the heap without root is repaired by ReheapDown operation The last node key is placed at root and then ReheapDown operation places it at proper location
- 25. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 25 Organize the entire collection of data elements as a binary tree stored in an array indexed from 1 to n, where for any node at index i, its two children, if exist, will be stored at index 2 X i + 1 and 2 X i + 2 the top part in which the data elements are in they Divide the binary tree into two parts: r original order and the bottom part in which the data elements are in their heap order, where each node is in higher order than its children, if any Start the bottom part with the half of the array, which contains only leaf nodes. Of course, it is in heap order, because the leaf nodes have no child
- 26. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 26 Move the last node from the top part to the bottom part, compare its order with its children, and swap its location with its highest order child if its order is lower than any child Repeat the comparison and swapping to ensure the bottom part is in heap order again with this new node added Repeat step 4 until the top part is empty. At this time, the bottom part becomes a complete heap tree
- 27. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 27 Heaps are used commonly in the following operations: Selection algorithm Scheduling and prioritizing (priority queue) Sorting
- 28. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 28 For the solution to the problem of determining the kth element, we can create the heap and delete k − 1 elements from it, leaving the desired element at the root. So the selection of the kth element will be very easy as it is the root of the heap For this, we can easily implement the algorithm of the selection problem using heap creation and heap deletion operations This problem can also be solved in O(nlogn) time using priority queues
- 29. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 29 The heap is usually defined so that only the largest element (that is, the root) is removed at a time. This makes the heap useful for scheduling and prioritizing In fact, one of the two main uses of the heap is as a prioriy queue, which helps systems decide what to do next
- 30. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 30 Applications of priority queues where heaps are implemented are as follows: CPU scheduling I/O scheduling Process scheduling.
- 31. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 31 Other than as a priority queue, the heap has one other important usage: heap sort Heap sort is one of the fastest sorting algorithms, achieving speed as that of the quicksort and merge sort algorithms The advantages of heap sort are that it does not use recursion, and it is efficient for any data order There is no worse-case scenario in case of heap sort
- 32. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 32 The steps for building heap sort are as follows: Build the heap tree Start Delete Heap operations, storing each deleted element at the end of the heap array After performing step 2, the order of the elements will be opposite to the order in the heap tree Hence, if we want the elements to be sorted in ascending order, we need to build the heap tree in Descending order—the greatest element will have the highest priority
- 33. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 33 Note that we use only one array, treating its parts differently When building the heap tree, a part of the array will be considered as the heap, and the rest part will be the original array When sorting, a part of the array will be the heap, and the rest part will be the sorted array
- 34. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 34 Binomial tree is an ordered tree defined recursively For the binomial tree Bk, There are 2k nodes The height of the tree is k There are exactly (ki) nodes at depth i for i = 0, 1, …, k The root has degree k, which is greater than that of any other node; moreover, if the children of the root are numbered from left to right by k − 1, k − 2, …, 0, the child i is the root of a subtree
- 35. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 35 A binomial heap H is a set of binomial trees that satisfies the following binomial heap properties Each binomial tree in H follows the min-heap property. We say that each such tree is minheap- ordered For any non-negative integer k, there is utmost one binomial tree in H whose root has degree k
- 36. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 36 The node of a binomial heap can be represented by five tuples as shown in fig 1. Parent—Pointing to parent node 2. Key—Key value, that is, data 3. Degree—Degree of each node, that is, the number of children it has 4. Child—Pointing to any of its child node (mostly pointing to its leftmost child) 5. Siblings—Pointing to sibling node, that is, used to maintain the singly-circular lists of siblings
- 37. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 37 Parent Key Degree Child Sibling
- 38. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 38 Null 11 1 Null Null 2 2 13 1 26 0 Null Null 19 0 Null Null
- 39. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 39 There are various operations of binomial heaps CreateBHeap—Creates an empty binomial heap, that is, simply allocates and returns an object H, where head[H] = null FindMinimumKey—Returns a pointer to the node with the minimum key in an n-node binomial heap H UnitingTwoBHeap—Takes the union of the two binomial heaps. InsertNode—Inserts node into binomial heap H ExtractMinimumKeyNode—Extracts the node with minimum key from binomial heap H and returns the pointer to the extracted node DecreaseKey—Decreases the key of a node in a binomial heap H to a new value k DeleteKey—Deletes the specified key from binomial heap H
- 40. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 40 Like binomial heap, Fibonacci heap is a collection of min- heap-ordered trees The trees in a Fibonacci are not constrained to be binomial trees The roots of all the trees in Fibonacci heap are linked together using left and right pointers into circular doubly- linked list called root list of the Fibonacci heap
- 41. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 41 An example of the Fibonacci heap consisting of 5 min- heap-ordered trees and 15 nodes 9 23 3615 12 30 18 5 2 40 25 33 2124 19
- 42. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 42 Fibonacci heap can be represented using the Fibonacci heap nodes The representation of such a node is shown in Figure Parent Key Degree Mark Left Child Right
- 43. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 43 Parent—Pointing to parent node Key—Key value, that is, data Degree—Degree of each node, that is, the number of children it has Child—Pointing to any of its child node (mostly pointing to its leftmost child) Mark—The Boolean-valued field indicates whether the node has lost a child since the last time the node was made the child of another node. The newly created nodes are,unmarked (i.e., default value is false) Left—Pointing to the left sibling node, that is, used to maintain the doubly circular lists of siblings Right—Pointing to the right sibling node, that is, used to maintain the doubly circular lists of siblings
- 44. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 44 CreateHeap—Creates an empty Fibonacci Heap, that is, simply allocates and returns an object H, where min[H]=null FindMinimumKey—Returns a min[H], that is, pointer to the node with the minimum key in an n-node Fibonacci heap H UnitingTwoFHeap—Takes the union of the two Fibonacci heaps InsertNode—Inserts node into Fibonacci heap H ExtractMinimumKeyNode—Extracts the node with minimum key from Fibonacci heap H and returns the pointer to the extracted node DecreaseKey—Decreases the key of a node in a Fibonacci heap H to a new value k DeleteKey—Deletes the specified key from Fibonacci heap H
- 45. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 45 A complete or nearly complete binary tree where each node is greater or equal to its decedents with each subtree satisfying this property is called as heap The basic operations on heap are as follows: insert, delete, ReheapUp and ReheapDown Heap can be implemented using an array as it is a complete binary tree. It is easy to maintain fixed relationship between a node and its children Among many applications of heap, the key ones are the following priority queue, sorting, and selection
- 46. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 46 Priority queue is implemented using heap by maintaining its relationship of element with other members in a list One of the popular sorting techniques is heap sort that uses heap The popularly heap is used in application where at each stage, the largest element is to be picked up for processing known as selection algorithm
- 47. Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil 47