13. sum and double half-angle formulas-x
- 1. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 2. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 3. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Trig-functions are not additive. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 4. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Trig-functions are not additive. For example, sin(π/2 + π/2) = sin(π) = 0 and sin(π/2 + π/2) ≠ sin(π/2) + sin(π/2) = 1 + 1 = 2. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 5. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Trig-functions are not additive. For example, sin(π/2 + π/2) = sin(π) = 0 and sin(π/2 + π/2) ≠ sin(π/2) + sin(π/2) = 1 + 1 = 2. Hence in general, sin(A ± B) ≠ sin(A) ± sin(B). Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 6. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Trig-functions are not additive. For example, sin(π/2 + π/2) = sin(π) = 0 and sin(π/2 + π/2) ≠ sin(π/2) + sin(π/2) = 1 + 1 = 2. Hence in general, sin(A ± B) ≠ sin(A) ± sin(B). However, we are able to express sin(A ± B) in term of the sine and cosine of A and B. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 7. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Trig-functions are not additive. For example, sin(π/2 + π/2) = sin(π) = 0 and sin(π/2 + π/2) ≠ sin(π/2) + sin(π/2) = 1 + 1 = 2. Hence in general, sin(A ± B) ≠ sin(A) ± sin(B). However, we are able to express sin(A ± B) in term of the sine and cosine of A and B. We list the formulas for sum and difference of angles, for the double-angle, then for the half-angle below. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 8. A function f(x) is said to be additive if f(A ± B) = f(A) ± f(B). Trig-functions are not additive. For example, sin(π/2 + π/2) = sin(π) = 0 and sin(π/2 + π/2) ≠ sin(π/2) + sin(π/2) = 1 + 1 = 2. Hence in general, sin(A ± B) ≠ sin(A) ± sin(B). However, we are able to express sin(A ± B) in term of the sine and cosine of A and B. We list the formulas for sum and difference of angles, for the double-angle, then for the half-angle below. We simplify the notation by notating respectively S(A), C(A) and T(A) for sin(A), cos(A) and tan(A). Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 9. Double-Angle Formulas Sum-Difference of Angles Formulas S(2A) = 2S(A)C(A) C(2A) = C2(A) – S2(A) = 2C2(A) – 1 = 1 – 2S2(A) 1 + C(B) 2 C( ) = Half-Angle Formulas ± 1 – C(B) 2 S( ) = ± B 2 B 2 C(A±B) = C(A)C(B) S(A)S(B)–+ S(A±B) = S(A)C(B) ± S(B)C(A) Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 10. Double-Angle Formulas Sum-Difference of Angles Formulas S(2A) = 2S(A)C(A) C(2A) = C2(A) – S2(A) = 2C2(A) – 1 = 1 – 2S2(A) 1 + C(B) 2 C( ) = Half-Angle Formulas ± 1 – C(B) 2 S( ) = ± B 2 B 2 C(A±B) = C(A)C(B) S(A)S(B)–+ S(A±B) = S(A)C(B) ± S(B)C(A) The cosine difference of angles formula C(A – B) = C(A)C(B) + S(A)S(B) is the basis for all the other formulas listed above. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas
- 11. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B)
- 12. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) A B (1, 0)
- 13. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) A B (1, 0)
- 14. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) A B (1, 0) A(u, v) B(s, t) (1, 0)
- 15. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) A B (1, 0) A(u, v) B(s, t) (1, 0) –B
- 16. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) and A(u, v)→(x, y). A B (1, 0) A(u, v) B(s, t) (1, 0) –B
- 17. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) and A(u, v)→(x, y). A(u, v) B(s, t) (1, 0) (x, y) –B A B –B A–B (1, 0)
- 18. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) and A(u, v)→(x, y). We want to find C(A – B), i.e. x. A(u, v) B(s, t) (1, 0) (x, y) –B A B –B A–B (1, 0)
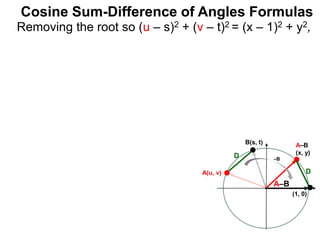
- 19. Cosine Sum-Difference of Angles Formulas Given two angles A and B, then The Cosine Difference-angle Formula C(A – B) = C(A)C(B) + S(A)S(B) Proof: Let A and B be two angles with corresponding coordinates (u, v) and (s, t) on the unit circle as shown. A(u, v) B(s, t) Rotate both angles by –B, so that B(s, t)→(1, 0) and A(u, v)→(x, y). We want to find C(A – B), i.e. x. Equating the distance D which is unchanged under the rotation, we´ve √(u – s)2 + (v – t)2 = √(x – 1)2 + (y – 0)2 . A(u, v) B(s, t) D (1, 0) (x, y) D –B A B –B A–B (1, 0)
- 20. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, Cosine Sum-Difference of Angles Formulas A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B A–B
- 21. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Cosine Sum-Difference of Angles Formulas A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B A–B
- 22. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x Cosine Sum-Difference of Angles Formulas A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B A–B
- 23. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x or x = us+ vt. Cosine Sum-Difference of Angles Formulas A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B A–B
- 24. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x or x = us+ vt. Writing each coordinate as a trig-value, x = C(A – B), u = C(A), s = C(B), v = S(A), t = S(B) we obtain the cosine difference angle formula C(A – B) = C(A)C(B) + S(A)S(B). Cosine Sum-Difference of Angles Formulas A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B A–B
- 25. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x or x = us+ vt. Writing each coordinate as a trig-value, x = C(A – B), u = C(A), s = C(B), v = S(A), t = S(B) we obtain the cosine difference angle formula C(A – B) = C(A)C(B) + S(A)S(B). A–B Writing C(A + B) = C(A – (–B)) Cosine Sum-Difference of Angles Formulas
- 26. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x or x = us+ vt. Writing each coordinate as a trig-value, x = C(A – B), u = C(A), s = C(B), v = S(A), t = S(B) we obtain the cosine difference angle formula C(A – B) = C(A)C(B) + S(A)S(B). A–B Writing C(A + B) = C(A – (–B)) = C(A)C(–B) + S(A)S(–B) Cosine Sum-Difference of Angles Formulas
- 27. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x or x = us+ vt. Writing each coordinate as a trig-value, x = C(A – B), u = C(A), s = C(B), v = S(A), t = S(B) we obtain the cosine difference angle formula C(A – B) = C(A)C(B) + S(A)S(B). A–B Writing C(A + B) = C(A – (–B)) = C(A)C(–B) + S(A)S(–B) = C(A)C(B) – S(A)S(B) since C(–B) = C(B) and that S(–B) = – S(B). Cosine Sum-Difference of Angles Formulas
- 28. Removing the root so (u – s)2 + (v – t)2 = (x – 1)2 + y2, A(u, v) B(s, t) D (1, 0) A–B (x, y) D –B expanding both sides of the equation we obtain: u2 – 2us + s2 + v2 – 2vt + t2 = x2 – 2x + 1 + y2 Setting u2 + v2 = 1, s2 + t2 = 1 and x2 + y2 = 1 we have 2 – 2us – 2vt = 2 – 2x or x = us+ vt. Writing each coordinate as a trig-value, x = C(A – B), u = C(A), s = C(B), v = S(A), t = S(B) we obtain the cosine difference angle formula C(A – B) = C(A)C(B) + S(A)S(B). A–B Writing C(A + B) = C(A – (–B)) = C(A)C(–B) + S(A)S(–B) = C(A)C(B) – S(A)S(B) since C(–B) = C(B) and that S(–B) = – S(B). Hence C(A + B) = C(A)C(B) – S(A)S(B) Cosine Sum-Difference of Angles Formulas
- 29. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) or that C(A B) = C(A)C(B) ± S(A)S(B)–+ In summary: Cosine Sum-Difference of Angles Formulas
- 30. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. or that C(A B) = C(A)C(B) ± S(A)S(B)–+ In summary: Cosine Sum-Difference of Angles Formulas
- 31. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. For examples: 3 π 12 π = – 4 π or that C(A B) = C(A)C(B) ± S(A)S(B)–+ In summary: Cosine Sum-Difference of Angles Formulas
- 32. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. For examples: 12 11π = 12 3π + 12 8π = 4 π + 3 2π 3 π 12 π = – 4 π or that C(A B) = C(A)C(B) ± S(A)S(B)–+ ; In summary: Cosine Sum-Difference of Angles Formulas
- 33. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. For examples: 12 11π = 12 3π + 12 8π = 4 π + 3 2π 3 π 12 π = – 4 π or that C(A B) = C(A)C(B) ± S(A)S(B)–+ ; Example A. Find cos(11π/12) without a calculator. In summary: Cosine Sum-Difference of Angles Formulas
- 34. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. For examples: 12 11π = 12 3π + 12 8π = 4 π + 3 2π 3 π 12 π = – 4 π or that C(A B) = C(A)C(B) ± S(A)S(B)–+ ; Example A. Find cos(11π/12) without a calculator. C ( ) 12 11π = C( ) = C( )C( ) 4 π + 3 2π 4 π – S( ) 4 π 3 2π In summary: Cosine Sum-Difference of Angles Formulas 3 2π S( ) Cosine-Sum Formulas
- 35. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. For examples: 12 11π = 12 3π + 12 8π = 4 π + 3 2π 3 π 12 π = – 4 π or that C(A B) = C(A)C(B) ± S(A)S(B)–+ ; Example A. Find cos(11π/12) without a calculator. C ( ) 12 11π = C( ) = C( )C( ) 4 π + 3 2π 4 π – S( ) 4 π 3 2π Cosine-Sum Formulas = 2 2 (–1) 2 –2 2 3 2 = In summary: Cosine Sum-Difference of Angles Formulas 3 2π S( )
- 36. cos(A – B) = cos(A)cos(B) + sin(A)sin(B) cos(A + B) = cos(A)cos(B) – sin(A)sin(B) All fractions with denominator 12 may be written as sums or differences of fractions with denominators 3, 6 and 4. For examples: 12 11π = 12 3π + 12 8π = 4 π + 3 2π 3 π 12 π = – 4 π or that C(A B) = C(A)C(B) ± S(A)S(B)–+ ; Example A. Find cos(11π/12) without a calculator. C ( ) 12 11π = C( ) = C( )C( ) 4 π + 3 2π 4 π – S( ) 4 π 3 2π Cosine-Sum Formulas = 2 2 (–1) 2 –2 2 3 2 =–2 – 6 4 –0.966 In summary: Cosine Sum-Difference of Angles Formulas 3 2π S( )
- 37. From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) Sine Sum-Difference of Angles Formulas
- 38. From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) = cos((π/2 – A) – B) Sine Sum-Difference of Angles Formulas
- 39. From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) = cos((π/2 – A) – B) = cos(π/2 – A)cos(B)) + sin(π/2 – A)sin(B) Sine Sum-Difference of Angles Formulas the cosine difference of angles law:
- 40. From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) = cos((π/2 – A) – B) = cos(π/2 – A)cos(B)) + sin(π/2 – A)sin(B) = sin(A)cos(B) – cos(A)sin(B) Sine Sum-Difference of Angles Formulas the cosine difference of angles law: the co-relation:
- 41. From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) = cos((π/2 – A) – B) = cos(π/2 – A)cos(B)) + sin(π/2 – A)sin(B) = sin(A)cos(B) – cos(A)sin(B) In summary: sin(A + B) = sin(A)cos(B) + cos(A)sin(B) Sine Sum-Difference of Angles Formulas the cosine difference of angles law: the co-relation:
- 42. From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) = cos((π/2 – A) – B) = cos(π/2 – A)cos(B)) + sin(π/2 – A)sin(B) = sin(A)cos(B) – cos(A)sin(B) In summary: sin(A + B) = sin(A)cos(B) + cos(A)sin(B) By expanding sin(A + (–B)) we have that sin(A – B) = sin(A)cos(B) – cos(A)sin(B) Sine Sum-Difference of Angles Formulas the cosine difference of angles law: the co-relation:
- 43. S(A ± B) = S(A)C(B) ± C(A)S(B) From C(π/2 – A) = S(A) and S(π/2 – A) = C(A), we’ve sin(A + B) = cos(π/2 – (A+B)) = cos((π/2 – A) – B) = cos(π/2 – A)cos(B)) + sin(π/2 – A)sin(B) = sin(A)cos(B) – cos(A)sin(B) In summary: sin(A + B) = sin(A)cos(B) + cos(A)sin(B) By expanding sin(A + (–B)) we have that sin(A – B) = sin(A)cos(B) – cos(A)sin(B) or that UDo. Find sin(–π/12) without a calculator. Sine Sum-Difference of Angles Formulas the cosine difference of angles law: the co-relation:
- 44. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas
- 45. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A)
- 46. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A) cos(2A) = cos2(A) – sin2(A)
- 47. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A) cos(2A) = cos2(A) – sin2(A) (1 – sin2(A)) – sin2(A) so 1 – 2sin2(A) = cos(2A)
- 48. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A) cos(2A) = cos2(A) – sin2(A) (1 – sin2(A)) – sin2(A) cos2(A) – (1 – cos2(A)) so 2cos2(A) – 1 = cos(2A)so 1 – 2sin2(A) = cos(2A)
- 49. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A) cos(2A) = cos2(A) – sin2(A) (1 – sin2(A)) – sin2(A) cos2(A) – (1 – cos2(A)) sin(2A) = sin(A + A) = sin(A)cos(A) + cos(A)sin(A) so 2cos2(A) – 1 = cos(2A)so 1 – 2sin2(A) = cos(2A)
- 50. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A) cos(2A) = cos2(A) – sin2(A) (1 – sin2(A)) – sin2(A) cos2(A) – (1 – cos2(A)) sin(2A) = sin(A + A) = sin(A)cos(A) + cos(A)sin(A) so sin(2A) = 2sin(A)cos(A) so 2cos2(A) – 1 = cos(2A)so 1 – 2sin2(A) = cos(2A)
- 51. From the sum-of-angle formulas, we obtain the double-angle formulas by setting A = B, Double Angle Formulas cos(2A) = cos(A + A) = cos(A)cos(A) – sin(A)sin(A) cos(2A) = cos2(A) – sin2(A) (1 – sin2(A)) – sin2(A) cos2(A) – (1 – cos2(A)) sin(2A) = sin(A + A) = sin(A)cos(A) + cos(A)sin(A) so sin(2A) = 2sin(A)cos(A) cos(2A) = cos2(A) – sin2(A) = 1 – 2sin2(A) = 2cos2(A) – 1 Cosine Double Angle Formulas: Sine Double Angle Formulas: sin(2A) = 2sin(A)cos(A) so 2cos2(A) – 1 = cos(2A)so 1 – 2sin2(A) = cos(2A)
- 52. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Double Angle Formulas
- 53. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 Double Angle Formulas
- 54. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 10/7 = 2cos2(A) 5/7 = cos2(A) ±5/7 = cos(A) Double Angle Formulas
- 55. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 10/7 = 2cos2(A) 5/7 = cos2(A) ±5/7 = cos(A) Since A is in the 2nd quadrant, cosine must be negative, so cos(A) = –5/7 = (–5)/7. Double Angle Formulas –5 Ay 7
- 56. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 10/7 = 2cos2(A) 5/7 = cos2(A) ±5/7 = cos(A) Since A is in the 2nd quadrant, cosine must be negative, so cos(A) = –5/7 = (–5)/7. We may use the right triangle as shown to find tan(A). Double Angle Formulas –5 Ay 7
- 57. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 10/7 = 2cos2(A) 5/7 = cos2(A) ±5/7 = cos(A) Since A is in the 2nd quadrant, cosine must be negative, so cos(A) = –5/7 = (–5)/7. We may use the right triangle as shown to find tan(A). y2 + (–5)2 = (7)2 Double Angle Formulas –5 Ay 7
- 58. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 10/7 = 2cos2(A) 5/7 = cos2(A) ±5/7 = cos(A) Since A is in the 2nd quadrant, cosine must be negative, so cos(A) = –5/7 = (–5)/7. We may use the right triangle as shown to find tan(A). We have that y2 + (–5)2 = (7)2 so y2 = 2 or that y = ±2 y = 2 Double Angle Formulas –5 Ay 7
- 59. Example B. Given the angle A in the 2nd quadrant and that cos(2A) = 3/7, find tan(A). Draw. Using the formula cos(2A) = 2cos2(A) – 1, we get 3/7 = 2cos2(A) – 1 10/7 = 2cos2(A) 5/7 = cos2(A) ±5/7 = cos(A) Since A is in the 2nd quadrant, cosine must be negative, so cos(A) = –5/7 = (–5)/7. We may use the right triangle as shown to find tan(A). We have that y2 + (–5)2 = (7)2 so y2 = 2 or that y = ±2 y = 2 Therefore tan(A) = 2 5 – –0.632 Double Angle Formulas –5 Ay 7
- 60. From cos(2A) = 2cos2(A) – 1, we get 1 + cos(2A) 2 cos2(A) = Half-angle Formulas
- 61. From cos(2A) = 2cos2(A) – 1, we get 1 + cos(2A) 2 cos2(A) = In the square root form, we get Half-angle Formulas 1 + cos(2A) 2 cos(A) =±
- 62. From cos(2A) = 2cos2(A) – 1, we get 1 + cos(2A) 2 cos2(A) = In the square root form, we get Half-angle Formulas 1 + cos(2A) 2 cos(A) =± If we replace A by B/2 so that 2A = B, we have the half-angle formula of cosine: cos( ) =B 2
- 63. From cos(2A) = 2cos2(A) – 1, we get 1 + cos(2A) 2 cos2(A) = In the square root form, we get Half-angle Formulas 1 + cos(2A) 2 cos(A) =± If we replace A by B/2 so that 2A = B, we have the half-angle formula of cosine: 1 + cos(B) 2 cos( ) = ± B 2
- 64. From cos(2A) = 2cos2(A) – 1, we get 1 + cos(2A) 2 cos2(A) = In the square root form, we get Half-angle Formulas 1 + cos(2A) 2 cos(A) =± If we replace A by B/2 so that 2A = B, we have the half-angle formula of cosine: Similarly, we get the half-angle formula of sine: 1 + cos(B) 2 cos( ) = ± B 2 1 – cos(B) 2 sin( ) = ± B 2
- 65. The half-angle formulas have ± choices but the double-angle formulas do not. Half-angle Formulas
- 66. The half-angle formulas have ± choices but the double-angle formulas do not. This is the case because given different angles corresponding to the same position such as π and –π on the unit circle, Half-angle Formulas π –π
- 67. The half-angle formulas have ± choices but the double-angle formulas do not. This is the case because given different angles corresponding to the same position such as π and –π on the unit circle, doubling them to 2π and –2π would result in the same position. Half-angle Formulas π –π 2π –2π
- 68. The half-angle formulas have ± choices but the double-angle formulas do not. This is the case because given different angles corresponding to the same position such as π and –π on the unit circle, doubling them to 2π and –2π would result in the same position. However if we divide them by 2 as π/2 and –π/2, the new angles would result in different positions. Half-angle Formulas π –π 2π –2π π/2 –π/2
- 69. The half-angle formulas have ± choices but the double-angle formulas do not. This is the case because given different angles corresponding to the same position such as π and –π on the unit circle, doubling them to 2π and –2π would result in the same position. However if we divide them by 2 as π/2 and –π/2, the new angles would result in different positions. Hence the half-angle formulas require more information to find the precise answer. Half-angle Formulas π –π 2π –2π π/2 –π/2
- 70. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). Half-angle Formulas
- 71. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). – 7 Half-angle Formulas –3 A Given that tan(A) = 3/7 and A is in the 3rd quadrant, let angle A be as shown.
- 72. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). – 7 Half-angle Formulas –3 A58 Given that tan(A) = 3/7 and A is in the 3rd quadrant, let angle A be as shown. Hence the hypotenuse of the reference triangle is 58.
- 73. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). – 7 Since –π < A < –π /2, so –π/2 < A/2 < –π/4, Half-angle Formulas –3 A58 Given that tan(A) = 3/7 and A is in the 3rd quadrant, let angle A be as shown. Hence the hypotenuse of the reference triangle is 58.
- 74. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). – 7 Since –π < A < –π /2, so –π/2 < A/2 < –π/4, so that A/2 is in the 4th quadrant and cos(A/2) is +. Half-angle Formulas –3 A58 Given that tan(A) = 3/7 and A is in the 3rd quadrant, let angle A be as shown. Hence the hypotenuse of the reference triangle is 58.
- 75. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). – 7 Since –π < A < –π /2, so –π/2 < A/2 < –π/4, so that A/2 is in the 4th quadrant and cos(A/2) is +. 1 + cos(A) 2 cos( ) =A 2 = 1 – 7/58 2 0.201Hence, Half-angle Formulas –3 A58 Given that tan(A) = 3/7 and A is in the 3rd quadrant, let angle A be as shown. Hence the hypotenuse of the reference triangle is 58.
- 76. Example C. Given A where –π < A < –π/2, and tan(A) = 3/7, draw A and find cos(A/2). – 7 Since –π < A < –π /2, so –π/2 < A/2 < –π/4, so that A/2 is in the 4th quadrant and cos(A/2) is +. 1 + cos(A) 2 cos( ) =A 2 = 1 – 7/58 2 0.201Hence, Half-angle Formulas –3 A58 Given that tan(A) = 3/7 and A is in the 3rd quadrant, let angle A be as shown. Hence the hypotenuse of the reference triangle is 58. We list all these formulas and their deduction in the following the flow chart.
- 77. Double-Angle Formulas Sum-Difference of Angles Formulas C(2A) = C2(A) – S2(A) = 2C2(A) – 1 = 1 – 2S2(A) S(2A) = 2S(A)C(A) 1 + C(B) 2 C( ) = Half-Angle Formulas ± 1 – C(B) 2 S( ) = ± B 2 B 2 C(A – B) = C(A)C(B) + S(A)S(B) S(A±B) = S(A)C(B) ± S(B)C(A) Important Trig-relation Formulas 1 + cos(2A) 2 cos(A) = 1 – cos(2A) 2 sin(A) = ± ± C(A + B) = C(A)C(B) – S(A)S(B) C(–B) = C(B) S(–B) = –S(B)
- 78. Exercise. A. Find the exact answers. 1. cos(π/12) Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas 9. sin(7π/12) 11. sin(–7π/12) 7. cos(7π/12) 3. cos(–11π/12) 5. cos(–15o) 13. cos(–5π/12) 2. cos(13π/12) 4. cos(105o) 6. sin(π/12) 8. sin(5π/12) 10. sin(–5π/12) 12. cos(5π/12) 14. sin(–5π/12) 15. cos(π/8) 16. sin(π/8) 17. sin(–3π/8) 18. cos(5π/8) Exercise. B. Find cos(A + B) and cos(A – B). 5. sin(A) = 3/5 and sin(B) = –12/13, A in the 1st quadrant and B in 3rd quad. 3. cos(A) = –1/5 and sin(B) = 3/5, A and B in the 2nd quadrant 1. sin(A) = ½ and cos(B) = ½ , A and B in the 1st quadrant 2. sin(A) = 1/5 and cos(B) = 2/5, A in the 1st quadrant and B in 4th quad. 4. cos(A) = –√3/5 and sin(B) = 2/3, A and B in the 2nd quadrant
- 79. Sum and Difference Angle Formulas Double-Angle and Half-Angle Formulas Exercise. C. Find sin(A + B) 5. sin(A) = 2/3 and sin(B) = –1/3, A in the 2nd quadrant and B in 4th quad. 3. cos(A) = –8/17 and cos(B) = –3/5, A and B in the 2nd quadrant 1. cos(A) = 3/5 and sin(B) = 5/13 , A and B in the 1st quadrant 2. sin(A) = 1/5 and cos(B) = 2/5, A in the 1st quadrant and B in 4th quad. 4. cos(A) = –√3/5 and sin(B) = 2/3, A and B in the 2nd quadrant Exercise. D. Half angle formulas 1. Find cos(A/2) given cos(A) = 1/4 with 0 < A < π. 3. Find sin(A/2) given tan(A) = 2 with 0 < A < π. 2. Find sin(A/2) given cos(A) = 1/3 with –π/2 < A < 0. 4. Find cos(A/2) given cot(A) = 4 with –3π/2 < A < –π.
- 80. Answers A. 2 + 6 4 1. 9. − 2 − 6 4 3. 2 + 6 4 − 2 − 6 4 11.2 − 6 4 7. 5. 2 + 6 4 13. 6 − 2 4 15. 2 + 2 2 − 2 + 2 2 17. B. 16/65 , –56/651. 0, √3/2 3. 5. 4−6 6 25 , 4 + 6 6 25 C. 1. 63/65 3. 5.77/85 4 2 + 5 9 D. 1. 3. 10 4 50 − 10 5 10