18 Basic Graph Algorithms
8 likes2,256 views
This document provides an overview of basic graph algorithms. It begins with examples of graphs in everyday life and a brief history of graph theory starting with Euler. It then covers basic graph terminology and properties like nodes, edges, degrees. Common representations of graphs in computers like adjacency lists and matrices are described. Breadth-first search and depth-first search algorithms for traversing graphs are introduced. Finally, applications of graph algorithms like finding paths, connected components, and topological sorting are mentioned.
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-65-320.jpg)
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-66-320.jpg)
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-67-320.jpg)
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-68-320.jpg)
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-69-320.jpg)
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-70-320.jpg)
![Breadth-First Search Algorithm
Algorithm
BFS(G, s)
1. for each vertex u ∈ G.V − {s}
2. u.color = WHITE
3. u.d = ∞
4. u.π = NIL
5. s.color =GRAY
6. s.d = 0
7. s.π = NIL
8. Q = ∅
9. Enqueue(Q, s)
10. while Q = ∅
11. u =Dequeue(Q)
12. for each v ∈ G.Adj [u]
13. if v.color ==WHITE
14. v.color =GRAY
15. v.d = u.d + 1
16. v.π = u
17. Enqueue(Q, v)
18. u.color = BLACK
33 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-71-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-105-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-106-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-107-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-108-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-109-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-110-320.jpg)
![The Pseudo-code
Code for DFS
DFS(G)
1. for each vertex u ∈ G.V
2. u.color = WHITE
3. u.π = NIL
4. time = 0
5. for each vertex u ∈ G.V
6. if u.color = WHITE
7.
DFS-VISIT(G, u)
DFS-VISIT(G, u)
1. time = time + 1
2. u.d = time
3. u.color = GRAY
4. for each vertex v ∈ G.Adj [u]
5. if v.color == WHITE
6. v.π = u
7. DFS-VISIT(G, v)
8. u.color = BLACK
9. time = time + 1
10. u.f = time
56 / 84](https://image.slidesharecdn.com/18basicgraphalgorithms-151108152237-lva1-app6891/85/18-Basic-Graph-Algorithms-111-320.jpg)
Ad
More Related Content
What's hot (20)
Viewers also liked (20)
Ad
Similar to 18 Basic Graph Algorithms (20)
Ad
More from Andres Mendez-Vazquez (20)
Recently uploaded (20)
18 Basic Graph Algorithms
- 1. Analysis of Algorithms Basic Graph Algorithms Andres Mendez-Vazquez October 28, 2015 1 / 84
- 2. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 2 / 84
- 3. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 3 / 84
- 4. We are full of Graphs Maps 4 / 84
- 5. We are full of Graphs Branch CPU estimators 5 / 84
- 6. We are full of Graphs Social Networks 6 / 84
- 7. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 7 / 84
- 8. History Something Notable Graph theory started with Euler who was asked to find a nice path across the seven Königsberg bridges The Actual City 8 / 84
- 9. History Something Notable Graph theory started with Euler who was asked to find a nice path across the seven Königsberg bridges The Actual City 8 / 84
- 10. No solution for a odd number of Bridges What we want The (Eulerian) path should cross over each of the seven bridges exactly once We cannot do this for the original problem 9 / 84
- 11. No solution for a odd number of Bridges What we want The (Eulerian) path should cross over each of the seven bridges exactly once We cannot do this for the original problem 9 / 84
- 12. Necessary Condition Euler discovered that A necessary condition for the walk of the desired form is that the graph be connected and have exactly zero or two nodes of odd degree. Add an extra bridge 10 / 84
- 13. Necessary Condition Euler discovered that A necessary condition for the walk of the desired form is that the graph be connected and have exactly zero or two nodes of odd degree. Add an extra bridge Add Extra Bridge 10 / 84
- 14. Studying Graphs All the previous examples are telling us Data Structures are required to design structures to hold the information coming from graphs!!! Good Representations They will allow to handle the data structures with ease!!! 11 / 84
- 15. Studying Graphs All the previous examples are telling us Data Structures are required to design structures to hold the information coming from graphs!!! Good Representations They will allow to handle the data structures with ease!!! 11 / 84
- 16. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 12 / 84
- 17. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 18. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 19. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 20. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 21. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 22. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 23. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 24. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 25. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 26. Basic Theory Definition A Graph is composed of the following parts: Nodes and Edges Nodes They can represent multiple things: People Cities States of Being etc Edges They can represent multiple things too: Distance between cities Friendships Matching Strings Etc 13 / 84
- 27. Basic Theory Definition A graph G = (V , E) is composed of a set of vertices (or nodes) V and a set of edges E, each assumed finite i.e. |V | = n and |E| = m. Example 14 / 84
- 28. Basic Theory Definition A graph G = (V , E) is composed of a set of vertices (or nodes) V and a set of edges E, each assumed finite i.e. |V | = n and |E| = m. Example 14 / 84
- 29. Properties Incident An edge ek = (vi, vj) is incident with the vertices vi and vj. A simple graph has no self-loops or multiple edges like below 15 / 84
- 30. Properties Incident An edge ek = (vi, vj) is incident with the vertices vi and vj. A simple graph has no self-loops or multiple edges like below 15 / 84
- 31. Some properties Degree The degree d(v) of a vertex V is its number of incident edges A self loop A self-loop counts for 2 in the degree function. Proposition The sum of the degrees of a graph G = (V , E) equals 2|E| = 2m (trivial). 16 / 84
- 32. Some properties Degree The degree d(v) of a vertex V is its number of incident edges A self loop A self-loop counts for 2 in the degree function. Proposition The sum of the degrees of a graph G = (V , E) equals 2|E| = 2m (trivial). 16 / 84
- 33. Some properties Degree The degree d(v) of a vertex V is its number of incident edges A self loop A self-loop counts for 2 in the degree function. Proposition The sum of the degrees of a graph G = (V , E) equals 2|E| = 2m (trivial). 16 / 84
- 34. Some properties Complete A complete graph Kn is a simple graph with all n(n−1)/2 possible edges, like the graph below for n = 2, 3, 4, 5. Example 17 / 84
- 35. Some properties Complete A complete graph Kn is a simple graph with all n(n−1)/2 possible edges, like the graph below for n = 2, 3, 4, 5. Example 17 / 84
- 36. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 18 / 84
- 37. Clearly We need to represent Nodes Vertices We need to represent Directed edges Undirected edges 19 / 84
- 38. Clearly We need to represent Nodes Vertices We need to represent Directed edges Undirected edges 19 / 84
- 39. We need NICE representations of this definition First One Adjacency Representation Second One Matrix Representation 20 / 84
- 40. We need NICE representations of this definition First One Adjacency Representation Second One Matrix Representation 20 / 84
- 41. Adjacency-list representation Basic Definition It is an array of size |V| with A list for each bucket representing a node telling us which nodes are connected to it by one edge 21 / 84
- 42. Adjacency-list representation Basic Definition It is an array of size |V| with A list for each bucket representing a node telling us which nodes are connected to it by one edge 1 2 3 4 5 6 4 4 6 4 5 1 2 2 3 5 21 / 84
- 43. Properties Space for storage For undirected or directed graphs O (V + E) Search: Successful or Unsuccessful O(1 + degree(v)) In addition Adjacency lists can readily be adapted to represent weighted graphs Weight function w : E → R The weight w(u, v) of the edge (u, v) ∈ E is simply stored with vertex v in u’s adjacency list 22 / 84
- 44. Properties Space for storage For undirected or directed graphs O (V + E) Search: Successful or Unsuccessful O(1 + degree(v)) In addition Adjacency lists can readily be adapted to represent weighted graphs Weight function w : E → R The weight w(u, v) of the edge (u, v) ∈ E is simply stored with vertex v in u’s adjacency list 22 / 84
- 45. Properties Space for storage For undirected or directed graphs O (V + E) Search: Successful or Unsuccessful O(1 + degree(v)) In addition Adjacency lists can readily be adapted to represent weighted graphs Weight function w : E → R The weight w(u, v) of the edge (u, v) ∈ E is simply stored with vertex v in u’s adjacency list 22 / 84
- 46. Properties Space for storage For undirected or directed graphs O (V + E) Search: Successful or Unsuccessful O(1 + degree(v)) In addition Adjacency lists can readily be adapted to represent weighted graphs Weight function w : E → R The weight w(u, v) of the edge (u, v) ∈ E is simply stored with vertex v in u’s adjacency list 22 / 84
- 47. Possible Disadvantage When looking to see if an edge exist There is no quicker way to determine if a given edge (u,v) 23 / 84
- 48. Adjacency Matrix Representation In a natural way the edges can be identified by the nodes For example, the edge between 1 and 4 nodes gets named as (1,4) Then How, we use this to represent the graph through a Matrix or and Array of Arrays??!!! 24 / 84
- 49. Adjacency Matrix Representation In a natural way the edges can be identified by the nodes For example, the edge between 1 and 4 nodes gets named as (1,4) Then How, we use this to represent the graph through a Matrix or and Array of Arrays??!!! 24 / 84
- 50. What about the following? How do we indicate that an edge exist given the following matrix 1 2 3 4 5 6 1 − − − − − − 2 − − − − − − 3 − − − − − − 4 − − − − − − 5 − − − − − − 6 − − − − − − You say it!! Use a 0 for no-edge Use a 1 for edge 25 / 84
- 51. What about the following? How do we indicate that an edge exist given the following matrix 1 2 3 4 5 6 1 − − − − − − 2 − − − − − − 3 − − − − − − 4 − − − − − − 5 − − − − − − 6 − − − − − − You say it!! Use a 0 for no-edge Use a 1 for edge 25 / 84
- 52. We have then... Definition 0/1 N × N matrix with N =Number of nodes or vertices A(i, j) = 1 iff (i, j) is an edge 26 / 84
- 53. We have then... For the previous example 1 2 3 4 5 6 1 0 0 0 1 0 0 2 0 0 0 1 0 0 3 0 0 0 1 0 0 4 1 1 1 0 1 0 5 0 0 0 1 0 1 6 0 0 0 0 1 0 27 / 84
- 54. Properties of the Matrix for Undirected Graphs Property One Diagonal entries are zero. Property Two Adjacency matrix of an undirected graph is symmetric: A (i, j) = A (j, i) for all i and j 28 / 84
- 55. Properties of the Matrix for Undirected Graphs Property One Diagonal entries are zero. Property Two Adjacency matrix of an undirected graph is symmetric: A (i, j) = A (j, i) for all i and j 28 / 84
- 56. Complexity Memory Θ (V 2) (1) Looking for an edge O(1) 29 / 84
- 57. Complexity Memory Θ (V 2) (1) Looking for an edge O(1) 29 / 84
- 58. Traversing the Graph Why do we need to traverse the graph? Do you have any examples? Yes Search for paths satisfying various constraints Shortest Path Visit some sets of vertices Tours Search if two graphs are equivalent Isomorphisms 30 / 84
- 59. Traversing the Graph Why do we need to traverse the graph? Do you have any examples? Yes Search for paths satisfying various constraints Shortest Path Visit some sets of vertices Tours Search if two graphs are equivalent Isomorphisms 30 / 84
- 60. Traversing the Graph Why do we need to traverse the graph? Do you have any examples? Yes Search for paths satisfying various constraints Shortest Path Visit some sets of vertices Tours Search if two graphs are equivalent Isomorphisms 30 / 84
- 61. Traversing the Graph Why do we need to traverse the graph? Do you have any examples? Yes Search for paths satisfying various constraints Shortest Path Visit some sets of vertices Tours Search if two graphs are equivalent Isomorphisms 30 / 84
- 62. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 31 / 84
- 63. Breadth-first search Definition Given a graph G = (V , E) and a source vertex s, breadth-first search systematically explores the edges of Gto “discover” every vertex that is reachable from the vertex s Something Notable A vertex is discovered the first time it is encountered during the search 32 / 84
- 64. Breadth-first search Definition Given a graph G = (V , E) and a source vertex s, breadth-first search systematically explores the edges of Gto “discover” every vertex that is reachable from the vertex s Something Notable A vertex is discovered the first time it is encountered during the search 32 / 84
- 65. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
- 66. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
- 67. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
- 68. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
- 69. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
- 70. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
- 71. Breadth-First Search Algorithm Algorithm BFS(G, s) 1. for each vertex u ∈ G.V − {s} 2. u.color = WHITE 3. u.d = ∞ 4. u.π = NIL 5. s.color =GRAY 6. s.d = 0 7. s.π = NIL 8. Q = ∅ 9. Enqueue(Q, s) 10. while Q = ∅ 11. u =Dequeue(Q) 12. for each v ∈ G.Adj [u] 13. if v.color ==WHITE 14. v.color =GRAY 15. v.d = u.d + 1 16. v.π = u 17. Enqueue(Q, v) 18. u.color = BLACK 33 / 84
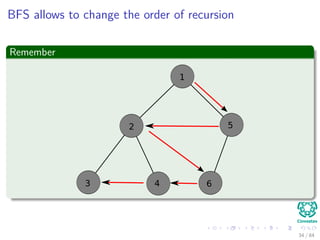
- 72. BFS allows to change the order of recursion Remember 1 2 3 4 5 6 34 / 84
- 73. Loop Invariance The While loop This while loop maintains the following invariant : At the test in line 10, the queue Q consists of the set of gray vertices First iteration Q = sand s.color = GRAY Maintenance The inner loop only pushes gray nodes into the queue. 35 / 84
- 74. Loop Invariance The While loop This while loop maintains the following invariant : At the test in line 10, the queue Q consists of the set of gray vertices First iteration Q = sand s.color = GRAY Maintenance The inner loop only pushes gray nodes into the queue. 35 / 84
- 75. Loop Invariance The While loop This while loop maintains the following invariant : At the test in line 10, the queue Q consists of the set of gray vertices First iteration Q = sand s.color = GRAY Maintenance The inner loop only pushes gray nodes into the queue. 35 / 84
- 76. Loop Invariance Termination When every node that can be visited is painted black 36 / 84
- 77. Example What do you see? 0 0 37 / 84
- 78. Example What do you see? 0 1 1 1 1 38 / 84
- 79. Example What do you see? 0 1 2 1 12 39 / 84
- 80. Example What do you see? 0 2 2 2 1 12 2 2 40 / 84
- 81. Example What do you see? 0 2 2 1 12 2 2 41 / 84
- 82. Example What do you see? 0 2 3 1 12 2 2 3 42 / 84
- 83. Example What do you see? 0 3 3 1 12 2 2 3 3 43 / 84
- 84. Example What do you see? 0 3 1 12 2 2 3 3 44 / 84
- 85. Example What do you see? 01 12 2 2 3 3 45 / 84
- 86. Complexity What about the outer loop? O(V ) Enqueue / Dequeue operations – Each adjacency list is processed only once. What about the inner loop? The sum of the lengths of f all the adjacency lists is Θ(E) so the scanning takes O(E) 46 / 84
- 87. Complexity What about the outer loop? O(V ) Enqueue / Dequeue operations – Each adjacency list is processed only once. What about the inner loop? The sum of the lengths of f all the adjacency lists is Θ(E) so the scanning takes O(E) 46 / 84
- 88. Complexity Overhead of Creation O (V ) Then Total complexity O (V + E) 47 / 84
- 89. Complexity Overhead of Creation O (V ) Then Total complexity O (V + E) 47 / 84
- 90. Properties: Predecessor Graph Something Notable Breadth-first search constructs a breadth-first tree, initially containing only its root, which is the source vertex s Thus We say that u is the predecessor or parent of v in the breadth-first tree. 48 / 84
- 91. Properties: Predecessor Graph Something Notable Breadth-first search constructs a breadth-first tree, initially containing only its root, which is the source vertex s Thus We say that u is the predecessor or parent of v in the breadth-first tree. 48 / 84
- 92. For example From the previous example Predecessor Graph 49 / 84
- 93. For example From the previous example Predecessor Graph s r w v t x yu 49 / 84
- 94. This allow to use the Algorithm for finding The Shortest Path Clearly This is the unweighted version or all weights are equal!!! We have the following function δ (s, v)= shortest path from s to v We claim that Upon termination of BFS, every vertex v ∈ V reachable from s has v.d = δ(s, v) 50 / 84
- 95. This allow to use the Algorithm for finding The Shortest Path Clearly This is the unweighted version or all weights are equal!!! We have the following function δ (s, v)= shortest path from s to v We claim that Upon termination of BFS, every vertex v ∈ V reachable from s has v.d = δ(s, v) 50 / 84
- 96. This allow to use the Algorithm for finding The Shortest Path Clearly This is the unweighted version or all weights are equal!!! We have the following function δ (s, v)= shortest path from s to v We claim that Upon termination of BFS, every vertex v ∈ V reachable from s has v.d = δ(s, v) 50 / 84
- 97. Intuitive Idea of Claim Correctness of breadth-first search Let G = (V , E) be a directed or undirected graph. Suppose that BFS is run on G from a given source vertex s ∈ V . Then Then, during its execution, BFS discovers every vertex v ∈ V that is reachable from the source. 51 / 84
- 98. Intuitive Idea of Claim Correctness of breadth-first search Let G = (V , E) be a directed or undirected graph. Suppose that BFS is run on G from a given source vertex s ∈ V . Then Then, during its execution, BFS discovers every vertex v ∈ V that is reachable from the source. 51 / 84
- 99. Intuitive Idea of Claim Correctness of breadth-first search Let G = (V , E) be a directed or undirected graph. Suppose that BFS is run on G from a given source vertex s ∈ V . Then Then, during its execution, BFS discovers every vertex v ∈ V that is reachable from the source. 51 / 84
- 100. Intuitive Idea of Claim Distance Idea First, once a node u is reached from v, we use the previous shortest distance from s to update the node distance. 52 / 84
- 101. Intuitive Idea of Claim You can use the idea of strong induction Given a branch of the breadth-first search u s, u1, u2, ..., un un.π = un−1.π + 1 = un−1.π + 2 = n + s.π = n (2) Thus, we have that For any vertex v = s that is reachable from s, one of the shortest path from s to v is A shortest path from s to v.π followed by thew edge (v.π, v). 53 / 84
- 102. Intuitive Idea of Claim You can use the idea of strong induction Given a branch of the breadth-first search u s, u1, u2, ..., un un.π = un−1.π + 1 = un−1.π + 2 = n + s.π = n (2) Thus, we have that For any vertex v = s that is reachable from s, one of the shortest path from s to v is A shortest path from s to v.π followed by thew edge (v.π, v). 53 / 84
- 103. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 54 / 84
- 104. Depth-first search Given G Pick an unvisited vertex v, remember the rest. Recurse on vertices adjacent to v 55 / 84
- 105. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 106. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 107. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 108. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 109. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 110. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 111. The Pseudo-code Code for DFS DFS(G) 1. for each vertex u ∈ G.V 2. u.color = WHITE 3. u.π = NIL 4. time = 0 5. for each vertex u ∈ G.V 6. if u.color = WHITE 7. DFS-VISIT(G, u) DFS-VISIT(G, u) 1. time = time + 1 2. u.d = time 3. u.color = GRAY 4. for each vertex v ∈ G.Adj [u] 5. if v.color == WHITE 6. v.π = u 7. DFS-VISIT(G, v) 8. u.color = BLACK 9. time = time + 1 10. u.f = time 56 / 84
- 112. Example What do we do? 57 / 84
- 113. Example What do we do? 58 / 84
- 114. Example What do we do? 59 / 84
- 115. Example What do we do? 60 / 84
- 116. Example What do we do? 61 / 84
- 117. Example What do we do? 62 / 84
- 118. Example What do we do? 63 / 84
- 119. Example What do we do? 64 / 84
- 120. Complexity Analysis 1 The loops on lines 1–3 and lines 5–7 of DFS take Θ (V ). 2 The procedure DFS-VISIT is called exactly once for each vertex v ∈ V . 3 During an execution of DFS-VISIT(G, v) the loop on lines 4–7 executes |Adj (v)| times. 4 But v∈V |Adj (v)| = Θ (E) we have that the cost of executing g lines 4–7 of DFS-VISIT is Θ (E) . Then DFS complexity is Θ (V + E) 65 / 84
- 121. Complexity Analysis 1 The loops on lines 1–3 and lines 5–7 of DFS take Θ (V ). 2 The procedure DFS-VISIT is called exactly once for each vertex v ∈ V . 3 During an execution of DFS-VISIT(G, v) the loop on lines 4–7 executes |Adj (v)| times. 4 But v∈V |Adj (v)| = Θ (E) we have that the cost of executing g lines 4–7 of DFS-VISIT is Θ (E) . Then DFS complexity is Θ (V + E) 65 / 84
- 122. Complexity Analysis 1 The loops on lines 1–3 and lines 5–7 of DFS take Θ (V ). 2 The procedure DFS-VISIT is called exactly once for each vertex v ∈ V . 3 During an execution of DFS-VISIT(G, v) the loop on lines 4–7 executes |Adj (v)| times. 4 But v∈V |Adj (v)| = Θ (E) we have that the cost of executing g lines 4–7 of DFS-VISIT is Θ (E) . Then DFS complexity is Θ (V + E) 65 / 84
- 123. Complexity Analysis 1 The loops on lines 1–3 and lines 5–7 of DFS take Θ (V ). 2 The procedure DFS-VISIT is called exactly once for each vertex v ∈ V . 3 During an execution of DFS-VISIT(G, v) the loop on lines 4–7 executes |Adj (v)| times. 4 But v∈V |Adj (v)| = Θ (E) we have that the cost of executing g lines 4–7 of DFS-VISIT is Θ (E) . Then DFS complexity is Θ (V + E) 65 / 84
- 124. Complexity Analysis 1 The loops on lines 1–3 and lines 5–7 of DFS take Θ (V ). 2 The procedure DFS-VISIT is called exactly once for each vertex v ∈ V . 3 During an execution of DFS-VISIT(G, v) the loop on lines 4–7 executes |Adj (v)| times. 4 But v∈V |Adj (v)| = Θ (E) we have that the cost of executing g lines 4–7 of DFS-VISIT is Θ (E) . Then DFS complexity is Θ (V + E) 65 / 84
- 125. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 126. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 127. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 128. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 129. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 130. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 131. Applications We have several Topological Sort Strongly Connected Components Computer Vision Algorithms Artificial Intelligence Algorithms Importance in Social Network Rank Algorithms for Google Etc. 66 / 84
- 132. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 67 / 84
- 133. Finding a path between nodes We do the following Start a breadth-first search at vertex v. Terminate when vertex u is visited or when Q becomes empty (whichever occurs first). Time Complexity O V 2 when adjacency matrix used. O(V + E) when adjacency lists used. 68 / 84
- 134. Finding a path between nodes We do the following Start a breadth-first search at vertex v. Terminate when vertex u is visited or when Q becomes empty (whichever occurs first). Time Complexity O V 2 when adjacency matrix used. O(V + E) when adjacency lists used. 68 / 84
- 135. Finding a path between nodes We do the following Start a breadth-first search at vertex v. Terminate when vertex u is visited or when Q becomes empty (whichever occurs first). Time Complexity O V 2 when adjacency matrix used. O(V + E) when adjacency lists used. 68 / 84
- 136. Finding a path between nodes We do the following Start a breadth-first search at vertex v. Terminate when vertex u is visited or when Q becomes empty (whichever occurs first). Time Complexity O V 2 when adjacency matrix used. O(V + E) when adjacency lists used. 68 / 84
- 137. This allow to use the Algorithm for finding The Shortest Path Clearly This is the unweighted version or all weights are equal!!! We have the following function δ (s, v)= shortest path from s to v Actually Upon termination of BFS, every vertex v ∈ V reachable from s has distance(v) = δ(s, v) 69 / 84
- 138. This allow to use the Algorithm for finding The Shortest Path Clearly This is the unweighted version or all weights are equal!!! We have the following function δ (s, v)= shortest path from s to v Actually Upon termination of BFS, every vertex v ∈ V reachable from s has distance(v) = δ(s, v) 69 / 84
- 139. This allow to use the Algorithm for finding The Shortest Path Clearly This is the unweighted version or all weights are equal!!! We have the following function δ (s, v)= shortest path from s to v Actually Upon termination of BFS, every vertex v ∈ V reachable from s has distance(v) = δ(s, v) 69 / 84
- 140. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 70 / 84
- 141. Connected Components Definition A connected component (or just component) of an undirected graph is a subgraph in which any two vertices are connected to each other by paths. Example 71 / 84
- 142. Connected Components Definition A connected component (or just component) of an undirected graph is a subgraph in which any two vertices are connected to each other by paths. Example 71 / 84
- 143. Procedure First Start a breadth-first search at any as yet unvisited vertex of the graph. Thus Newly visited vertices (plus edges between them) define a component. Repeat Repeat until all vertices are visited. 72 / 84
- 144. Procedure First Start a breadth-first search at any as yet unvisited vertex of the graph. Thus Newly visited vertices (plus edges between them) define a component. Repeat Repeat until all vertices are visited. 72 / 84
- 145. Procedure First Start a breadth-first search at any as yet unvisited vertex of the graph. Thus Newly visited vertices (plus edges between them) define a component. Repeat Repeat until all vertices are visited. 72 / 84
- 146. Time O (V 2 ) When adjacency matrix used O(V + E) When adjacency lists used (E is number of edges) 73 / 84
- 147. Time O (V 2 ) When adjacency matrix used O(V + E) When adjacency lists used (E is number of edges) 73 / 84
- 148. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 74 / 84
- 149. Spanning Tree with edges with same weight of no weight Definition A spanning tree of a graph G = (V , E) is a acyclic graph where for u, v ∈ V , there is a path between them Example 75 / 84
- 150. Spanning Tree with edges with same weight of no weight Definition A spanning tree of a graph G = (V , E) is a acyclic graph where for u, v ∈ V , there is a path between them Example 2 3 5 1 4 6 7 9 8 75 / 84
- 151. Procedure First Start a breadth-first search at any vertex of the graph. Thus If graph is connected, the n − 1 edges used to get to unvisited vertices define a spanning tree (breadth-first spanning tree). 76 / 84
- 152. Procedure First Start a breadth-first search at any vertex of the graph. Thus If graph is connected, the n − 1 edges used to get to unvisited vertices define a spanning tree (breadth-first spanning tree). 76 / 84
- 153. Time O (V 2 ) When adjacency matrix used O(V + E) When adjacency lists used (E is number of edges) 77 / 84
- 154. Time O (V 2 ) When adjacency matrix used O(V + E) When adjacency lists used (E is number of edges) 77 / 84
- 155. Outline 1 Introduction Graphs Everywhere History Basic Theory Representing Graphs in a Computer 2 Traversing the Graph Breadth-first search Depth-First Search 3 Applications Finding a path between nodes Connected Components Spanning Trees Topological Sorting 78 / 84
- 156. Topological Sorting Definitions A topological sort (sometimes abbreviated topsort or toposort) or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u, v) from vertex u to vertex y, u comes before v in the ordering. From Industrial Engineering The canonical application of topological sorting (topological order) is in scheduling a sequence of jobs or tasks based on their dependencies. Topological sorting algorithms were first studied in the early 1960s in the context of the PERT technique for scheduling in project management (Jarnagin 1960). 79 / 84
- 157. Topological Sorting Definitions A topological sort (sometimes abbreviated topsort or toposort) or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u, v) from vertex u to vertex y, u comes before v in the ordering. From Industrial Engineering The canonical application of topological sorting (topological order) is in scheduling a sequence of jobs or tasks based on their dependencies. Topological sorting algorithms were first studied in the early 1960s in the context of the PERT technique for scheduling in project management (Jarnagin 1960). 79 / 84
- 158. Then We have that The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started. Example When washing clothes, the washing machine must finish before we put the clothes to dry. Then A topological sort gives an order in which to perform the jobs. 80 / 84
- 159. Then We have that The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started. Example When washing clothes, the washing machine must finish before we put the clothes to dry. Then A topological sort gives an order in which to perform the jobs. 80 / 84
- 160. Then We have that The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started. Example When washing clothes, the washing machine must finish before we put the clothes to dry. Then A topological sort gives an order in which to perform the jobs. 80 / 84
- 161. Algorithm Pseudo Code TOPOLOGICAL-SORT 1 Call DFS(G) to compute finishing times v.f for each vertex v. 2 As each vertex is finished, insert it onto the front of a linked list 3 Return the linked list of vertices 81 / 84
- 162. Algorithm Pseudo Code TOPOLOGICAL-SORT 1 Call DFS(G) to compute finishing times v.f for each vertex v. 2 As each vertex is finished, insert it onto the front of a linked list 3 Return the linked list of vertices 81 / 84
- 163. Algorithm Pseudo Code TOPOLOGICAL-SORT 1 Call DFS(G) to compute finishing times v.f for each vertex v. 2 As each vertex is finished, insert it onto the front of a linked list 3 Return the linked list of vertices 81 / 84
- 165. Thus Using the u.f As each vertex is finished, insert it onto the front of a linked list 83 / 84
- 166. Example After Sorting undershortsocks pants beltshirt tie jacketshoes watch 11/16 12/15 6/71/8 2/5 3/417/18 13/14 9/10 84 / 84