A brief introduction to mutual information and its application

A brief introduction to
mutual information and its
application
2015. 2. 4.

Agenda
• Introduction
• Definition of mutual information
• Applications

Why we need?
• We need ‘a good measure’ for somewhat!
Match score?

What is ‘a good measure’?
• Precision
• Significance
• Feasible to various data

What is ‘a good measure’?
• Precision
• Significance
• Feasible to various data
A solution : mutual information!

What is mutual information?
• A measure for two or more random variables
• Entropy based measure
• Non-parametric measure
• Shows good estimation for discrete random
variables

What is entropy?
• A measure in information theory
• Uncertainty, information contents
• Definition of entropy for a random variable 𝑋
• 𝐻 𝑋 = − 𝑥∈𝑋 𝑝 𝑥 log2 𝑝(𝑥)
• Definition of joint entropy for two random variable
𝑋 and 𝑌
• 𝐻 𝑋, 𝑌 = − 𝑥∈𝑋,𝑦∈𝑌 𝑝 𝑥, 𝑦 log2 𝑝(𝑥, 𝑦)

Entropy of a coin flip
• Let 𝑋 = 𝐻, 𝑇
• 𝐻 𝑋 = 1 when 𝑃 𝐻 = 0.5, 𝑃 𝑇 = 0.5
• 𝐻 𝑋 = 0 when 𝑃 𝐻 = 1.0, 𝑃 𝑇 = 0.0

R code for the previous figure
H <- function(p_h, p_t) {
ret <- 0
if( p_h > 0.0 ) ret <- ret - p_h * log2(p_h)
if( p_t > 0.0 ) ret <- ret - p_t * log2(p_t)
return(ret)
}
head <- seq(0,1,0.01)
tail <- 1 - head
entropy <- mapply( H, head, tail)
plot( entropy ~ head, type='n' )
lines( entropy ~ head, lwd=2, col='red' )

Joint entropy
• Venn diagram for definition of entropies
H(X) H(Y)

Joint entropy
• Venn diagram for definition of entropies
H(X,Y)

Example of joint entropy
• 성도 (X) and 성완(Y) tossed coins 10 times at a
time
• 0 : head, 1 : tail
• X : { 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 }
• Y : { 0, 0, 1, 0, 0, 0, 1, 0, 1, 1 }
• H(X,Y) = 1.85
• Note : 𝐻 𝑋, 𝑌 ≤ 𝐻 𝑋 + 𝐻(𝑌)

R code for the calculation
> X <- c(0, 0, 0, 0, 0, 1, 1, 1, 1, 1)
> Y <- c(0, 0, 1, 0, 0, 0, 1, 0, 1, 1)
>
> freq <- table(X,Y)
>
> ret <- 0
> for( i in 1:2 ) {
> for( j in 1:2 ) {
> ret <- freq[i,j]/10.0 * log2(freq[i,j]/10.0)
> }
> }
> ret

‘entropy’ library
> library("entropy")
> x1 = runif(10000)
> hist(x1, xlim=c(0,1), freq=FALSE)
> y1 = discretize(x1, numBins=10, r=c(0,1))
> entropy(y1)
[1] 2.30244
> y1

Mutual information
• Measure for mutual dependence or interaction
• 𝐼 𝑋; 𝑌 = 𝐻 𝑋 + 𝐻 𝑌 − 𝐻 𝑋, 𝑌 ≤ min{𝐻 𝑋 , 𝐻 𝑌 }
I(X;Y)

Mutual information
• Some properties of mutual information
• 𝐼 𝑋; 𝑌 = 𝑥∈𝑋,𝑦∈𝑌 𝑝 𝑥, 𝑦 log
𝑝(𝑥,𝑦)
𝑝 𝑥 𝑝(𝑦)
• 𝐼 𝑋; 𝑌 = 𝐼(𝑌; 𝑋)
• 𝐼 𝑋, 𝑌 ≤ min 𝐻 𝑋 , 𝐻 𝑌
• 𝐼 𝑋, 𝑌 = 𝐻 𝑋 − 𝐻(𝑋|𝑌)

How to measure mutual information
Genotype 𝐴𝐴𝐵𝐵 𝐴𝐴𝐵𝑏 𝐴𝐴𝑏𝑏 𝐴𝑎𝐵𝐵 𝐴𝑎𝐵𝑏 𝐴𝑎𝑏𝑏 𝑎𝑎𝐵𝐵 𝑎𝑎𝐵𝑏 𝑎𝑎𝑏𝑏 sum
Case 39 91 95 92 14 31 63 4 71 500
Control 100 15 55 5 22 150 50 93 10 500
sum 139 106 150 97 36 181 113 97 81 1000
Case 0.039 0.091 0.095 0.092 0.014 0.031 0.063 0.004 0.071 0.500
Control 0.100 0.015 0.055 0.005 0.022 0.150 0.050 0.093 0.010 0.500
sum 0.139 0.106 0.150 0.097 0.036 0.181 0.113 0.097 0.081 1.000
Frequency Table
18

How to measure mutual information
Case 0.183 0.315 0.323 0.317 0.086 0.155 0.251 0.032 0.271 0.500
Control 0.332 0.091 0.230 0.038 0.121 0.411 0.216 0.319 0.066 0.500
sum 0.396 0.343 0.411 0.326 0.173 0.446 0.355 0.326 0.294
Entropy Table
𝐼 𝑔𝑒𝑛𝑜𝑡𝑦𝑝𝑒; 𝑑𝑖𝑠𝑒𝑎𝑠𝑒 = 𝐻 𝑔𝑒𝑛𝑜𝑡𝑦𝑝𝑒 + 𝐻 𝑑𝑖𝑠𝑒𝑎𝑠𝑒 − 𝐻 𝑔𝑒𝑛𝑜𝑡𝑦𝑝𝑒, 𝑑𝑖𝑠𝑒𝑎𝑠𝑒
= 3.07 + 1.00 − 3.76
= 0.31
19

‘entropy’ library
> x1 = runif(10000)
> x2 = runif(10000)
> y2d = discretize2d(x1, x2, numBins1=10, numBins2=10)
> H12 = entropy(y2d)
>
> # mutual information
> mi.empirical(y2d) # approximately zero
> H1 = entropy(rowSums(y2d))
> H2 = entropy(colSums(y2d))
> H1+H2-H12

Association measure between
genomic features and outcome
𝐼 𝑋1, 𝑋2; 𝑌 = 𝐻 𝑋1, 𝑋2 + 𝐻 𝑌 − 𝐻(𝑋1, 𝑋2, 𝑌)
pair of genomic
features
binary outcomes
22

Mutual Information With Clustering
(Leem et al., 2014) (1/2)
: SNPs
: causative SNPs
d1
d2
distance
Score=d1+d2
Centroid 1
Centroid 2
Centroid 3
3 SNPs with the
highest mutual
information value
m candidates
m candidates
m candidates
23

Mutual Information With Clustering
(Leem et al., 2014) (2/2)
• Mutual information
• As distance measure for clustering
• K-means clustering algorithm
• Candidate selection
• Reduce search space dramatically
• Can detect high-order epistatic interaction
• Also, shows better performance (power, execution time)
than previous methods
24

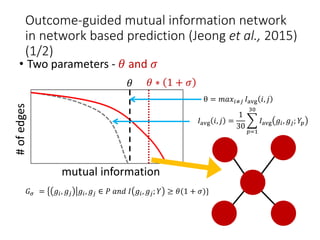
Outcome-guided mutual information network
in network based prediction (Jeong et al., 2015)
(1/2)
• Two parameters - 𝜃 and 𝜎
mutual information
𝜃 𝜃 ∗ 1 + 𝜎
#ofedges
θ = 𝑚𝑎𝑥𝑖≠𝑗 𝐼avg 𝑖, 𝑗
𝐼avg 𝑖, 𝑗 =
1
30
𝑝=1
30
𝐼avg 𝑔𝑖, 𝑔𝑗; 𝑌𝑝
𝐺 𝜎 = 𝑔𝑖, 𝑔𝑗 𝑔𝑖, 𝑔𝑗 ∈ 𝑃 𝑎𝑛𝑑 𝐼 𝑔𝑖, 𝑔𝑗; 𝑌 ≥ 𝜃(1 + 𝜎)}

Outcome-guided mutual information network
in network based prediction (Jeong et al., 2015)
(2/2)
Feature network

Relevance networks for gastritis
(Jeong and Sohn, 2014)

MINA: Mutual Information
Network Analysis framework
https://github.com/hhjeong/MINA

Problems and its solution of
mutual information
• Noises for continuous data
• Alternative discretization technique
• Assessment of significance
• Permutation test
• Also, we should consider for multiple testing problem.
• Mutual information is not a metric!

A brief introduction to mutual information and its application

More Related Content

What's hot (20)

Similar to A brief introduction to mutual information and its application (20)

Recently uploaded (20)

A brief introduction to mutual information and its application

Editor's Notes