A Comparative Study of Histogram Equalization Based Image Enhancement Techniques
- 1. A Comparative Study of Histogram Equalization Based Image Enhancement Techniques Md. Shahbaz Alam Roll: AE-029, Session: 2016-17 27th August, 2017 Institute of Statistical Research and Training University of Dhaka 1
- 2. Outline 1. Introduction 2. Basic definitions and notations 3. Methodology 4. Results and discussion 5. Conclusion 2
- 3. Introduction
- 4. Introducton Digital image processing is the technology of applying a number of algorithms to process digital image. Basically it includes the following three steps: • Importing the image via image acquisition tools. • Analyzing and manipulating the image. • Output (an altered image or image analysis report). 3
- 5. Introduction Image enhancement: A collection of techniques that seek to improve the visual appearance of an image or convert images to a form better suited for analysis by human or machine. In general two major approaches, one is gray level statistics based and the other is spatial frequency content based. The principle objective of image enhancement is to modify attributes of an image to make it more suitable for a given task and a specific observer. 4
- 6. Introduction The existing image enhancement techniques can be classified into two catagories: • Spatial domain enhancement. • Frequency domain enhancement. Spatial domain techniques are performed to the image plane itself and are based on direct manipulation of pixels in an image. Histogram equalization is a well known spatial domain enhancement technique due to its strong performance and easy algorithm in almost all types of images. 5
- 7. Aims and objectives • To describe and implement four popular methods of histogram equalization on images with different levels of contrast. • To compare among these five methods using traditional as well as sophisticated metric. • To illustrate the application of histogram in the field of image processing. 6
- 8. Basic definitions and notations
- 9. Digital image A digital image is a matrix representation of a two-dimensional image. It can be represented by the following matrix: f (x, y) = f (0, 0) f (0, 1) ... f (0, N − 1) f (1, 0) f (1, 1) ... f (1, N − 1) . . ... . . . ... . . . ... . f (M − 1, 0) f (M − 1, 1) ... f (M − 1, N − 1) (1) It is advantageous to use a more traditional matrix notation to denote a digital image and its elements: 7
- 10. Basic definitions A = a0,0 a0,1 ... a0,N−1 a1,0 a1,0 ... a1,N−1 . . ... . . . ... . . . ... . aM−1,0 aM−1,0 ... aM−1,N−1 (2) where, ai,j = f (x = i, y = j) = f (i, j) and thus equations (1) and (2) are identical. 8
- 11. Basic definitions Pixel Each element in the matrix is called an image element, picture element, pixel or pel.Thus a digital image f (x, y) with M rows and N columns contains M × N number of pixels or image elements. In spatial domain technique for image processing, operation is done on this pixel. 9
- 12. Basic definitions Neighbors of a pixel The 4-neighbors of pixel p, N4(p) are the four pixels located at(shaded square) (x + 1, y), (x − 1, y), (x, y + 1), (x, y − 1) (x-1,y-1) (x-1,y) (x-1,y+1) (x, y-1) (x, y) (x, y+1) (x+1,y-1) (x+1,y) (x+1,y+1) Table 1: 8-neighborhood. The four diagonal neighbors of pixel p, ND(p) are the four pixels located at (x + 1, y + 1), (x + 1, y − 1), (x − 1, y + 1), (x − 1, y − 1) and are denoted by ND(p). These points, together with the 4-neighbors, are called the 8-neighbors of p, denoted by N8(p). 10
- 13. Basic definitions Bit-depth It explains the number of possible colors from which a particular value can be selected by a pixel. For example: a binary image is an one bit image which can take any of thee two values: 0 or 1 (black or white). An 8 − bit gray-scale image can assign one of 256( 28) colors to a pixel. The number of b bits required to store a digital image of size M × N with 2k gray level is, b = M × N × k (3) 11
- 14. Figure 1: A bi-tonal image, where pixels can take any of the two values namely 0 and1. 12
- 15. Basic definitions Image histogram Image histogram provides information about brightness and contrast of an image. Discrete function h(rk) showing the number of occurrences nk for the kth gray level rk h(rk) = nk (4) A common practice is to normalize a histogram by dividing each of its values by the total number of pixels, denoted by n. So, p(rk) = nk n , for k = 0, 1, ..., L − 1; and L−1 0 p(rk) = 1 (5) 13
- 16. Basic definitions Image histogram Figure 2: An 8-bit image of Albert Einstein and its histogram 14
- 17. Methodology
- 18. Methodology Four different histogram equalization techniques has been used: 1. Global Histogram Equalization(GHE). 2. Brightness Preserving Bi-Histogram Equalization(BBHE). 3. Equal Area Dualistic Sub Image Histogram Equalization (DSIHE). 4. Recursive Mean Separate Histogram Equalization (RMSHE). 15
- 19. Mathematical formulation of GHE Let, X = {X(i, j)} is a given image composed in L(for 8-bi image L = 256) discrete gray levels denoted as X0, X1, ..., XL−1 • Calculate the probability density function. p(Xk) = nk n , fork = 0, 1, ..., L − 1 (6) • Calculate cumulative distribution function by c(xk) = k j=0 p(Xj ), for k = 0, 1, ..., L − 1 (7) • On the basis of CDF, Define transformation function f (x) as f (Xk) = X0 + (XL−1 − X0)c(xk) (8) • Using the transformation function, calculate new intensity values 16
- 20. Global Histogram Equalization(GHE) Figure 3: Histogram before and after HE or equivalently, RMSHE, r = 0. 17
- 21. An example of GHE Figure 4: Contrast enhancement based on global histogram equalization. 18
- 22. Brightness Preserving Bi-Histogram Equalization(BBHE) • Partitions Histogram in two sub-histograms and equalize them independently. • Proposed to minimize mean intensity change. • Ultimate goal is to preserve brightness and enhance contrast. • Image parameters such as mean gray-scale level used for partitioning. 19
- 23. Equal Area Dualistic Sub Image Histogram Equalization (DSIHE). This method is also known as Dualistic Sub Image Histogram Equalization(DSIHE). • Image parameters such as median grayscale level used for partitioning. • The input image is decomposed into two sub-images, being one dark and one bright. • Then applies Histogram Equalization on two sub-images. 20
- 24. Mathematical Formulation for BBHE and DSIHE • Input image X(i, j) with gray levels 0 to 255. • Image X(i, j) is segmented by a section with gray level of Xm • Xm (mean in case of BBHE and median in case of DSIHE) • The image is decomposed into two sub images XL and XU. • X = XL ∪ XU where XL = {X(i, j)|X(i, j) ≤ Xm, ∀X(i, j) ∈ X} and XU = {X(i, j)|X(i, j) > Xm, ∀X(i, j) ∈ X} 21
- 25. Mathematical Formulation for BBHE and DSIHE • XL is composed by gray level of {l0, l1, ..., lm}, XU is composed by gray level of {lm+1, lm+2, ..., lL−1} • Respective probability density functions of the sub-images are: pL(Xk) = nk L nL , for k = 0, 1, ..., m and pU(Xk) = nk U nU , for k = m + 1, m + 2, ..., L − 1 22
- 26. Mathematical Formulation for BBHE and DSIHE • nk L and nk U are the numbers of Xk • nL = m k=0 nk L , nU = L−1 k=m+1 nk U • The respective cumulative density function for XL and XU are : cL(x) = k j=0 pL(Xj ) and cU(x) = L−1 j=m+1 pU(Xj ) • Transformation function defined for exploiting the cumulative density functions: fL(x) = X0 + (Xm − X0)cL(x) and fU(x) = Xm+1 + (XL−1 − Xm+1)cU(x) 23
- 27. Mathematical Formulation for BBHE and DSIHE • Based on these transform functions, the decomposed sub-image are equalized independently. • The composition of resulting equalized sub-images constitutes the output of BBHE or DSIHE as Y = {Y (i, j)} = fL(XL) ∪ fU(XU) where fL(XL) = {fL(X(i, j)|∀X(i, j) ∈ XL)} and fU(XU) = {fU(X(i, j)|∀X(i, j) ∈ XU)} 24
- 28. Algorithm for BBHE • Obtain the original image. • Get histogram of the original image. • Calculate mean of the histogram. • Divide the histogram on the basis of the mean in two parts. • Equalize each part independently using PDF and CDF. • Combine both sub-images for the processed image 25
- 29. Algorithm for BBHE Figure 5: Histogram before and after BBHE or equivalently, RMSHE, r = 1. 26
- 30. An example of BBHE Figure 6: Contrast enhancement based on brightness preserving bi-histogram equalization. 27
- 31. Algorithm for DSIHE • Obtain the original image. • Get histogram of the original image. • Calculate median of the histogram. • Divide the histogram on the basis of the median in two parts. • Equalize each part independently using PDF and CDF. • Combine both sub-images for the processed image 28
- 32. An example of DSIHE Figure 7: Contrast enhancement based on dualistic sub-image histogram equalization. 29
- 33. Recursive Mean Separate Histogram Equalization (RMSHE) • Generalization of HE and BBHE in term of brightness preservation • Recursively separating the input histogram based on the mean 30
- 34. Recursive Mean Separate Histogram Equalization (RMSHE) Figure 8: Recursive mean separated histogram equalization with recursion level r=2 31
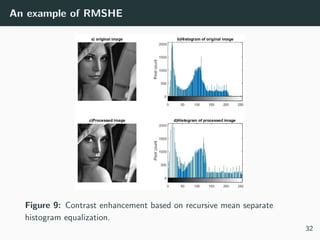
- 35. An example of RMSHE Figure 9: Contrast enhancement based on recursive mean separate histogram equalization. 32
- 37. Results and discussion Quality assessment The following measurement are used to make comparison among the histogram equalization techniques • Mean squared error (MSE) is the average of squared intensity differences distorted and reference image pixels. Lower value of MSE means that the image is of good quality. • Peak signal to noise ratio(PSNR) is the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation. It varies between 25 to 40 dB. Higher value of PSNR is good • Structural similarity index(SSIM) varies between 0 to 1. The value 1 means, the image is of best quality. 33
- 38. Visual Assessment Global histogram equalization Figure 10: Contrast enhancement based on histogram equalization. 34
- 39. Visual Assessment Brightness preserving bi-histogram equalization Figure 11: Contrast enhancement based on brightness preserving bi-histogram equalization. 35
- 40. Visual Assessment Dualistic sub-image histogram equalization Figure 12: Contrast enhancement based on dualistic sub-image histogram equalization. 36
- 41. Visual Assessment Recursive mean separate histogram equalization Figure 13: Contrast enhancement based on recursive mean separate histogram equalization. 37
- 42. Experimental results Simulation results for ’Tungsten-filament’ and ’Barbara’ are presented in table 2 and 3. and Methods Mean SD SSIM MSE PSNR Tungsten filament 128.11 75.31 – – – GHE 127.71 73.5 0.79991 478.83 21.32 BBHE 150.5 69.05 0.80593 843.65 18.86 DSHE 140.43 72.94 0.79856 533.68 20.85 RMSHE 133.99 79.97 0.90909 139.46 26.68 Table 2: Comparison of various histogram equalization methods using objective image quality measures 38
- 43. Methods Mean SD SSIM MSE PSNR Barbara 111.5 48.15 – – – GHE 127.48 73.88 0.875 969.18 18.26 BBHE 118.44 73.77 0.868 782.22 19.19 DSIHE 117.94 73.77 0.867 777.89 19.22 RMSHE 115.93 61.01 0.937 243.36 24.26 Table 3: Comparison of various histogram equalization methods using objective image quality measures 39
- 44. Conclusion
- 45. Conclusion • The experimental results shows that RMSHE processed ’Tungsten-filament’ image has lowest MSE , highest PSNR and highest SSIM among these four techniques. • Similar result shows for ’Barbara’ image. So, recursive mean separate histogram equalization(RMSHE) performs well according to this performance measure as well as visual assessment. 40
- 46. Thank You! 40
- 47. Questions? 40
- 48. Appendix
- 49. Reference i Rafael C Gonzalez and Richard E Woods. Digital image processing prentice hall. Upper Saddle River, NJ , 2002a. Gregory A Baxes. Digital image processing: principles and applications . Yeong-Taeg Kim. Contrast enhancement using brightness preserving bi-histogram equalization. IEEE transactions on Consumer Electronics , 43(1):18, 1997. Yu Wang, Qian Chen, and Baeomin Zhang. Image enhancement based on equal area dualistic sub-image histogram equalization method. IEEE Transactions on Consumer Electronics , 45(1):6875, 1999.
- 50. Reference ii Soong-Der Chen and Abd Rahman Ramli. Contrast enhancement using recursive mean-separate histogram equalization for scalable brightness preservation. IEEE Transactions on consumer Electronics , 49(4):13011309, 2003. Zhou Wang, Alan C Bovik, Hamid R Sheikh, and Eero P Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing , 13(4):600612, 2004.