A presentation for Multiple linear regression.ppt
Download as PPT, PDF0 likes332 views
Multiple linear regression (MLR) is a statistical method used to predict the value of a dependent variable based on the values of two or more independent variables. MLR produces an equation that estimates the best weighted combination of independent variables to predict the dependent variable. MLR can assess the contribution and relative importance of each predictor variable while controlling for the effects of the other predictors. MLR requires that assumptions of independence, normality, homoscedasticity, and linearity are met.
A presentation for Multiple linear regression.ppt
- 1. Multiple Linear Regression Laurens Holmes, Jr. Nemours/A.I.duPont Hospital for Children 1 1 2 2 ' i i y a b x b x b x Nothing explains everythin g
- 2. What is MLR? • Multiple Regression is a statistical method for estimating the relationship between a dependent variable and two or more independent (or predictor) variables.
- 3. Multiple Linear Regression • Simply, MLR is a method for studying the relationship between a dependent variable and two or more independent variables. • Purposes: – Prediction – Explanation – Theory building
- 4. Operation? • Uses the ordinary least squares solution (as does simple linear or bi-variable regression) • Describes a line for which the (sum of squared) differences between the predicted and the actual values of the dependent variable are at a minimum. • Represents the “function” that minimizes the sum of the squared errors. • Ypred = a + b1X1 + B2X2 … + BnXn
- 5. Operation? • MLR produces a model that identifies the best weighted combination of independent variables to predict the dependent (or criterion) variable. • Ypred = a + b1X1 + B2X2 … + BnXn • MLR estimates the relative importance of several hypothesized predictors. • MLR assess the contribution of the combined variables to change the dependent variable.
- 6. Design Requirements • One dependent variable (criterion) • Two or more independent variables (predictor or explanatory variables). • Sample size: >= 50 (at least 10 times as many cases as independent variables)
- 7. Predictable variation by the combination of independent variables Variations Total Variation in Y Unpredictable Variation
- 8. MLR Model: Basic Assumptions • Independence: The data of any particular subject are independent of the data of all other subjects • Normality: in the population, the data on the dependent variable are normally distributed for each of the possible combinations of the level of the X variables; each of the variables is normally distributed • Homoscedasticity: In the population, the variances of the dependent variable for each of the possible combinations of the levels of the X variables are equal. • Linearity: In the population, the relation between the dependent variable and the independent variable is linear when all the other independent variables are held constant.
- 9. Simple vs. Multiple Regression • One dependent variable Y predicted from one independent variable X • One regression coefficient • r2: proportion of variation in dependent variable Y predictable from X • One dependent variable Y predicted from a set of independent variables (X1, X2 ….Xk) • One regression coefficient for each independent variable • R2: proportion of variation in dependent variable Y predictable by set of independent variables (X’s)
- 10. MLR Equation • Ypred = a + b1X1 + B2X2 … + BnXn (pred=predicted, 1 and 2 are underscore) • Ypred = dependent variable or the variable to be • predicted. • X = the independent or predictor variables • a = “raw score equations” include a constant or Y • Intercept ob Y axis, representing the value of Y when X = 0. • b = b weights; or partial regression coefficients. • The bs show the relative contribution of their independent variable on the dependent variable when controlling for the effects of the other predictors
- 11. Variables in the model? • One approach is to perform literature review and examine theories to identify potential predictors , thus building a “theoretical” variate, which may reflect the biologic or clinical relevance of the variable. • This is sometimes referred to as the “standard” (simultaneous) regression method. • A second approach is to examine statistics that show the effects of each variable both within and out of • the equation. • The “statistical variate” is built based on those variables • showing the most effect (significant at 0.25). – These are sometimes called “Forward and Backward Stepwise Regression
- 12. MLR Output • The following notions are essential for the understanding of MLR output: R2, adjusted R2, constant, b coefficient, beta, F-test, t-test • For MLR “R2” (the coefficient of multiple determination) is used rather than “r” (Pearson’s correlation coefficient) to assess the strength of this more complex relationship (as compared to a bivariate correlation)
- 13. Adjusted R square and b coefficient • The adjusted R2 adjusts for the inflation in R2 caused by the number of variables in the equation. As the sample size increases above 20 cases per variable, adjustment is less needed (and vice versa). • b coefficient measures the amount of increase or decrease in the dependent variable for a one- unit difference in the independent variable, controlling for the other independent variable(s) in the equation.
- 14. B coefficient • Ideally, the independent variables are uncorrelated. • Consequently, controlling for one of them will not affect the relationship between the other independent variable and the dependent variable
- 15. Intercorrelation or collinearlity • If the two independent variables are uncorrelated, we can uniquely partition the amount of variance in Y due to X1 and X2 and bias is avoided. • Small intercorrelations between the independent variables will not greatly biased the b coefficients. • However, large intercorrelations will biased the b coefficients and for this reason other mathematical procedures are needed
- 16. MRL Model Building • Each predictor is taken in turn. That is, all other predictors are first placed in the equation and then the predictor of interest is entered. • This allows us to determine the unique (additional) contribution of the predictor variable. • By repeating the procedure for each predictor we can determine the unique contribution of each independent variable.
- 17. Different Ways of Building Regression Models • Simultaneous: all independent variables entered together • Stepwise: independent variables entered according to some order – By size or correlation with dependent variable – In order of significance • Hierarchical: independent variables entered in stages
- 18. Various Significance Tests • Testing R2 – Test R2 through an F test – Test of competing models (difference between R2) through an F test of difference of R2s • Testing b – Test of each partial regression coefficient (b) by t- tests – Comparison of partial regression coefficients with each other - t-test of difference between standardized partial regression coefficients ()
- 19. F and t tests • The F-test is used as a general indicator of the probability that any of the predictor variables contribute to the variance in the dependent variable within the population. • The null hypothesis is that the predictors’ weights are all effectively equal to zero. • Implying that, none of the predictors contribute to the variance in the dependent variable in the population
- 20. F and t tests • t-tests are used to test the significance of each predictor in the equation. • The null hypothesis is that a predictor’s weight is effectively equal to zero when the effects of the other predictors are taken into account. • That is, it does not contribute to the variance in the dependent variable within the population.
- 21. R Square • When comparing the R2 of an original set of variables to the R2 after additional variables have been included, the researcher is able to identify the unique variation explained by the additional set of variables. • Any co-variation between the original set of variables and the new variables will be attributed to the original variables. • R2 (multiple correlation squared) – variation in Y accounted for by the set of predictors • Adjusted R2 – sample variation around R2 can only lead to inflation of the value. • The adjustment takes into account the size of the sample and number of predictors to adjust the value to be a better estimate of the population value. • R2 is similar to η2 value but will be a little smaller because R2 only looks at linear relationship while η2 will account for non-linear relationships.
- 22. Vignette • Suppose we wish to examine the factors that predict the length of hospitalization following spinal surgery in children with CP(dependent continuous variable). • The available variables in the dataset are hematocrit, estimated blood loss, cell saver, operating time, age at surgery, and parked red blood cells. • If the dependent and independent variables are measured on continuous scale, what will be an appropriate test statistic? – Select appropriate variables (theory based and statistical approach), and determine the effect of estimated blood loss while controlling hematocrit and parked red blood cell, age at surgery, cell saver, operating time (duration of surgery).
- 23. SPSS: 1) analyze, 2) regression, 3) linear
- 25. SPSS Screen
- 27. SPSS Output Interpret the r square What does the ANOVA result mean?
- 28. Repeated Measure Analysis of Variance (RM ANOVA) Univariable (Univariate) RM removes variability in baseline prognostic factor – ideal model !!!
- 29. Repeated Measures ANOVA • Between Subjects Design – ANOVA in which each participant participated in one of the three treatment groups for example. • Within Subjects or Repeated Measures Design – Participants participate in one treatment and the outcome of the treatment is measured in different time points for example 3, (before treatment, immediately after, and 6 months after treatment)
- 30. RM ANOVA Vs. Paired T test • Repeated measures ANOVA, also known as within-subjects ANOVA, are an extension of Paired T-Tests. • Like T-Tests, repeated measures ANOVA gives us the statistic tools to determine whether or not changed has occurred over time. • T-Tests compare average scores at two different time periods for a single group of subjects. • Repeated measures ANOVA compared the average score at multiple time periods for a single group of subjects.
- 31. RM ANOVA: Understanding the terms & analysis interpretation • The first step in solving repeated measures ANOVA is to combine the data from the multiple time periods into a single time factor for analysis. • The different time periods are analogous to the categories of the independent variable is a one-way analysis of variance. • The time factor is then tested to see if the mean for the dependent variable is different for some categories of the time factor. • If the time factor is statistically significant in the ANOVA test, then Bonferroni pair wise comparisons are computed to identify specific differences between time periods.
- 32. RM ANOVA: Understanding the terms & analysis interpretation • The dependent variable is measured at three time periods, there are three paired comparisons: • time 1 versus time 2 (preoperative or before treatment measure) • time 2 versus time 3 (immediate after surgery/treatment measure) • time 1 versus time 3 (Follow-up post operative measure)
- 33. Statistical Assumptions of RM ANOVA • Independence • Normality • Homogeneity of within-treatment variances • Sphericity RM is ideal in testing the hypothesis on treatment effectiveness when ethical constraints restricts the use of control subjects
- 34. Homogeneity of Variance • In one-way ANOVA, we expect the variances to be equal – We also expect that the samples are not related to one another (so no covariance or correlation)
- 35. Sphericity and Compound Symmetry • Extension of homogeneity of variance assumption • Compound Symmetry is stricter than Sphericity (but maybe easier to explain) – All variances are equal to each other – All covariance are equal to each other
- 36. Sphericity and Compound Symmetry • If we meet assumption of Compound Symmetry than we meet assumption of Sphericity • Sphericity is less strict and is the only thing we need to meet for RM ANOVA • Sphericity is that the variance of the differences are equal – Variance of difference scores between time 1 and 2 is equal to the variance of difference scores between time 2 and 3.
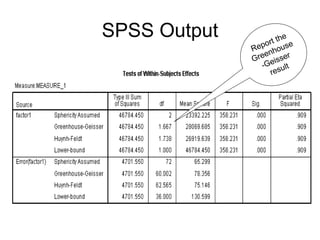
- 37. Spericity Assumption Violations • A more conservative method of evaluating the significance of the obtained F is needed • Greenhouse-Geisser (1958) correction – Gives appropriate critical value for worst situation in which assumptions are maximally violated • Huynh-Feldt correction – The Huynh-Feldt epsilon is an attempt to correct the Greenhouse-Geisser epsilon, which tends to be overly conservative, especially for small sample sizes
- 38. Sample Table for RM ANOVA
- 39. RM ANOVA • All participants participate in all treatment conditions, ex. surgery for spinal deformity correction. • Participant emerges as an independent source of variance. – In RM ANOVA there is no such variability. • The other sources of variance include the repeated measures treatment and the Participant x treatment interaction
- 40. RM ANOVA Equation yi 0i 1i (Time) it 0i 0 1i 1
- 41. Vignette • Suppose a spinal fusion was performed to correct spinal deformities in Adolescent Idiopathic Scoliosis (AIS). If the main cobb angle was measured preoperatively, immediately after surgery (first erect), and during two years of follow-up, was the surgical procedure effective in correcting the curve deformity and maintaining correction after two years of follow-up? • Hint: correction loss > 10 degrees in indicative of a clinically significant loss of correction.
- 42. Sample variables on preoperative, immediate operative and 2 year follow-up Normality assumption of the variables on the three measuring points of the cobb angle.
- 44. SPSS Output From the variables box select accordingly 1, 2, and 3rd measurement points during the study period. Click the option box and select descriptive, and Bon multiple comparison.
- 45. SPSS OUTPUT
- 46. SPSS Output
- 47. SPSS Output
- 48. 48