Algorithm and Programming (Sorting)
8 likes654 views
The document provides an overview of sorting algorithms, specifically bubble sort and selection sort, with detailed definitions and procedures for both ascending and descending orders. It includes step-by-step illustrations of sorting processes and outlines the general algorithms used for each method. Additionally, the document contains contact information for the author, Adam Mukharil Bachtiar.
![General Format for Bubble Sort Ascending
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Procedure BubbleSortAsc(I/O nama_var_array : nama_tipe_array,
Input N : integer)
{I.S. : array[1..N] sudah terdefinisi}
{F.S. : menghasilkan array[1..N] yang tersusun secara ascending}
Kamus:
i, j : integer
temp : tipedata
Algoritma:
for i 1 to N-1 do
for j n downto i+1 do
if(nama_var_array[j] < nama_var_array[j-1])
then
temp nama_var_array[j]
nama_var_array[j] nama_var_array[j-1]
nama_var_array[j-1] temp
endif
endfor
endfor
EndProcedure](https://image.slidesharecdn.com/chapter10-sorting-161018112206/85/Algorithm-and-Programming-Sorting-12-320.jpg)
![General Format for Bubble Sort Descending
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Procedure BubbleSortDesc (I/O nama_var_array : nama_tipe_array,
Input N : integer)
{I.S. : array[1..N] sudah terdefinisi}
{F.S. : menghasilkan array[1..N] yang tersusun secara descending}
Kamus:
i,j : integer
temp : tipedata
Algoritma:
for i 1 to N-1 do
for j 1 to (N - i) do
if(nama_var_array[j] < nama_var_array[j+1])
then
temp nama_var_array[j]
nama_var_array[j] nama_var_array[j+1]
nama_var_array[j+1] temp
endif
endfor
endfor
EndProcedure](https://image.slidesharecdn.com/chapter10-sorting-161018112206/85/Algorithm-and-Programming-Sorting-16-320.jpg)
![General Format for Maximum Sort Ascending
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Procedure MaximumSortAsc(I/O nama_var_array : nama_tipe_array,
Input N : integer)
{I.S. : array [1..N] sudah terdefinisi}
{F.S. : menghasilkan array [1..N] yang tersusun secara ascending}
Kamus:
i, j, max, x : integer
temp : tipedata
Algoritma:
x n
for i 1 to N-1 do
max 1
for j 2 to x do
if(nama_var_array[j] > nama_var_array[max])
then
max j
endif
endfor
temp nama_var_array[max]
nama_var_array[max] nama_var_array[j]
nama_var_array[j] temp
x x - 1
endfor
EndProcedure](https://image.slidesharecdn.com/chapter10-sorting-161018112206/85/Algorithm-and-Programming-Sorting-23-320.jpg)
![General Format for Minimum Sort Ascending
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Procedure MinimumSortAsc(I/O nama_var_array : nama_tipe_array,
Input N : integer)
{I.S. : array[1..n] sudah terdefinisi}
{F.S. : menghasilkan array [1..n] yang tersusun secara ascending}
Kamus:
i, j, min : integer
temp : tipedata
Algoritma:
for i 1 to (N – 1) do
min i
for j i+1 to N do
if(nama_var_array[j] < nama_var_array[min])
then
min j
endif
endfor
temp nama_var_array[min]
nama_var_array[min] nama_var_array[i]
nama_var_array[i] temp
endfor
EndProcedure](https://image.slidesharecdn.com/chapter10-sorting-161018112206/85/Algorithm-and-Programming-Sorting-24-320.jpg)
Algorithm and Programming (Sorting)
- 1. Adam Mukharil Bachtiar English Class Informatics Engineering 2011 Algorithms and Programming Sorting
- 2. Steps of the Day Let’s Start Definition of Sorting Bubble Sort Selection Sort
- 3. Definition of Sorting All About Sorting
- 4. WhatisSorting Process that arranges random data into sorted data. Data can be sorted into ascending or descending.
- 5. AlgorithmsofSorting • Bubble Sort • Selection Sort
- 6. Bubble Sort Definition and Structures of Bubble Sort
- 7. WhatisBubbleSort • Sorting algorithm which was inspired by bubble soap. • Comparing element of array (i) with next element of it (i+1). • If i is bigger than i+1 then swap value of each element.
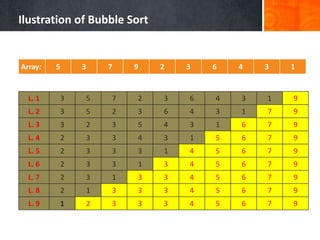
- 8. Ilustration of Bubble Sort Array: 5 3 7 9 2 3 6 4 3 1 L. 1 3 5 7 2 3 6 4 3 1 9 L. 2 3 5 2 3 6 4 3 1 7 9 L. 3 3 2 3 5 4 3 1 6 7 9 L. 4 2 3 3 4 3 1 5 6 7 9 L. 5 2 3 3 3 1 4 5 6 7 9 L. 6 2 3 3 1 3 4 5 6 7 9 L. 7 2 3 1 3 3 4 5 6 7 9 L. 8 2 1 3 3 3 4 5 6 7 9 L. 9 1 2 3 3 3 4 5 6 7 9
- 9. Process of Bubble Sort (Ascending) This is an array that will be sorted in Ascending way: 6 3 9 1 5 Step 1 : 6 3 9 1 5 6 3 9 1 5 6 3 1 9 5 6 1 3 9 5 1 6 3 9 5 j j j j
- 10. Process of Bubble Sort (Ascending) Step 2 : 1 6 3 9 5 1 6 3 5 9 1 6 3 5 9 1 3 6 5 9 j j j
- 11. Process of Bubble Sort (Ascending) Step 3 : 1 3 6 5 9 1 3 6 5 9 1 3 5 6 9 Step 4 : 1 3 5 6 9 1 3 5 6 9 Array after sorted in ascending ways: 1 3 5 6 9 j j j
- 12. General Format for Bubble Sort Ascending 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Procedure BubbleSortAsc(I/O nama_var_array : nama_tipe_array, Input N : integer) {I.S. : array[1..N] sudah terdefinisi} {F.S. : menghasilkan array[1..N] yang tersusun secara ascending} Kamus: i, j : integer temp : tipedata Algoritma: for i 1 to N-1 do for j n downto i+1 do if(nama_var_array[j] < nama_var_array[j-1]) then temp nama_var_array[j] nama_var_array[j] nama_var_array[j-1] nama_var_array[j-1] temp endif endfor endfor EndProcedure
- 13. Process of Bubble Sort (Descending) This is an array that will be sorted in Descending way : 6 3 9 1 5 Step 1 : 6 3 9 1 5 6 3 9 1 5 6 9 3 1 5 6 9 3 1 5 6 9 3 5 1 j j j j
- 14. Process of Bubble Sort (Descending) Step 2 : 6 9 3 5 1 9 6 3 5 1 9 6 3 5 1 9 6 5 3 1 j j j
- 15. Process of Bubble Sort (Descending) Step 3 : 9 6 5 3 1 9 6 5 3 1 9 6 5 3 1 Step 4 : 9 6 5 3 1 9 6 5 3 1 Array after sorted in descending ways: 9 6 5 3 1 j j j
- 16. General Format for Bubble Sort Descending 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Procedure BubbleSortDesc (I/O nama_var_array : nama_tipe_array, Input N : integer) {I.S. : array[1..N] sudah terdefinisi} {F.S. : menghasilkan array[1..N] yang tersusun secara descending} Kamus: i,j : integer temp : tipedata Algoritma: for i 1 to N-1 do for j 1 to (N - i) do if(nama_var_array[j] < nama_var_array[j+1]) then temp nama_var_array[j] nama_var_array[j] nama_var_array[j+1] nama_var_array[j+1] temp endif endfor endfor EndProcedure
- 17. Selection Sort Definition and Structures of Selection Sort
- 18. WhatisSelectionSort Sorting algorithm that arranges random data by selecting the biggest data or the smallest one.
- 19. MethodsinSelectionSort • Maximum Sort • Minimum Sort
- 20. Process of Maximum Sort (Ascending) This is an array that will be sorted in Ascending way : 6 3 9 1 5 Step 1 : 6 3 9 1 5 6 3 9 1 5 6 3 9 1 5 6 3 9 1 5 6 3 9 1 5 6 3 5 1 9 j j j jmax max max max max j
- 21. Process of Maximum Sort (Ascending) Step 2 : 6 3 5 1 9 6 3 5 1 9 6 3 5 1 9 6 3 5 1 9 1 3 5 6 9 j j jmax max max max j
- 22. Process of Maximum Sort (Ascending) Step 3 : 1 3 5 6 9 1 3 5 6 9 1 3 5 6 9 1 3 5 6 9 Step 4 : 1 3 5 6 9 1 3 5 6 9 Array after sorted in descending way: 1 3 5 6 9 j j max max max max j j max
- 23. General Format for Maximum Sort Ascending 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Procedure MaximumSortAsc(I/O nama_var_array : nama_tipe_array, Input N : integer) {I.S. : array [1..N] sudah terdefinisi} {F.S. : menghasilkan array [1..N] yang tersusun secara ascending} Kamus: i, j, max, x : integer temp : tipedata Algoritma: x n for i 1 to N-1 do max 1 for j 2 to x do if(nama_var_array[j] > nama_var_array[max]) then max j endif endfor temp nama_var_array[max] nama_var_array[max] nama_var_array[j] nama_var_array[j] temp x x - 1 endfor EndProcedure
- 24. General Format for Minimum Sort Ascending 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Procedure MinimumSortAsc(I/O nama_var_array : nama_tipe_array, Input N : integer) {I.S. : array[1..n] sudah terdefinisi} {F.S. : menghasilkan array [1..n] yang tersusun secara ascending} Kamus: i, j, min : integer temp : tipedata Algoritma: for i 1 to (N – 1) do min i for j i+1 to N do if(nama_var_array[j] < nama_var_array[min]) then min j endif endfor temp nama_var_array[min] nama_var_array[min] nama_var_array[i] nama_var_array[i] temp endfor EndProcedure
- 25. Contact Person: Adam Mukharil Bachtiar Informatics Engineering UNIKOM Jalan Dipati Ukur Nomor. 112-114 Bandung 40132 Email: [email protected] Blog: http://adfbipotter.wordpress.com Copyright © Adam Mukharil Bachtiar 2011