Ad
Algorithms of graph
- 1. Connected Components, Directed graphs, Topological sort Continuation of Graph 1
- 2. Application 1: Connectivity D E A C F B G K H L N M O R Q P s How do we tell if two vertices are connected? A connected to F? A connected to L? G = 2
- 3. Connectivity • A graph is connected if and only if there exists a path between every pair of distinct vertices. • A graph is connected if and only if there exists a simple path between every pair of distinct vertices (since every non-simple path contains a cycle, which can be bypassed) • How to check for connectivity? • Run BFS or DFS (using an arbitrary vertex as the source) • If all vertices have been visited, the graph is connected. • Running time? O(n + m) 3
- 5. Subgraphs 5
- 6. Connected Components • Formally stated: • A connected component is a maximal connected subgraph of a graph. • The set of connected components is unique for a given graph. 6
- 7. Finding Connected Components For each vertex Call DFS This will find all vertices connected to “v” => one connected component Basic DFS algorithm. If not visited 7
- 8. Time Complexity • Running time for each i connected component • Question: • Can two connected components have the same edge? • Can two connected components have the same vertex? • So: )( ii mnO i i i i i ii mnOmnOmnO )()()( 8
- 9. Trees • Tree arises in many computer science applications • A graph G is a tree if and only if it is connected and acyclic (Acyclic means it does not contain any simple cycles) • The following statements are equivalent • G is a tree • G is acyclic and has exactly n-1 edges • G is connected and has exactly n-1 edges 9
- 10. Tree as a (directed) Graph 15 6 18 3 8 30 16 Is it a graph? Does it contain cycles? (in other words, is it acyclic) How many vertices? How many edges? 10
- 11. Directed Graph • A graph is directed if direction is assigned to each edge. We call the directed edges arcs. • An edge is denoted as an ordered pair (u, v) • Recall: for an undirected graph • An edge is denoted {u,v}, which actually corresponds to two arcs (u,v) and (v,u) 11
- 12. Representations • The adjacency matrix and adjacency list can be used 12
- 13. Directed Acyclic Graph • A directed path is a sequence of vertices (v0, v1, . . . , vk) • Such that (vi, vi+1) is an arc • A directed cycle is a directed path such that the first and last vertices are the same. • A directed graph is acyclic if it does not contain any directed cycles 13
- 14. Indegree and Outdegree • Since the edges are directed • We can’t simply talk about Deg(v) • Instead, we need to consider the arcs coming “in” and going “out” • Thus, we define terms • Indegree(v) • Outdegree(v) 14
- 15. Outdegree • All of the arcs going “out” from v • Simple to compute • Scan through list Adj[v] and count the arcs • What is the total outdegree? (m=#edges) mv v vertex )(outdegree 15
- 16. Indegree • All of the arcs coming “in” to v • Not as simple to compute as outdegree • First, initialize indegree[v]=0 for each vertex v • Scan through adj[v] list for each v • For each vertex w seen, indegree[w]++; • Running time: O(n+m) • What is the total indegree? mv v vertex )(indegree 16
- 17. Indegree + Outdegree • Each arc (u,v) contributes count 1 to the outdegree of u and count 1 to the indegree of v. mvv v )(outdegree)(indegree vertex 17
- 18. Example 0 1 2 3 4 5 6 7 8 9 Indeg(2)? Indeg(8)? Outdeg(0)? Num of Edges? Total OutDeg? Total Indeg? 18
- 19. Directed Graphs Usage • Directed graphs are often used to represent order- dependent tasks • That is we cannot start a task before another task finishes • We can model this task dependent constraint using arcs • An arc (i,j) means task j cannot start until task i is finished • Clearly, for the system not to hang, the graph must be acyclic. i j Task j cannot start until task i is finished 19
- 20. Topological Sort • Topological sort is an algorithm for a directed acyclic graph • It can be thought of as a way to linearly order the vertices so that the linear order respects the ordering relations implied by the arcs 0 1 2 3 4 5 6 7 8 9 For example: 0, 1, 2, 5, 9 0, 4, 5, 9 0, 6, 3, 7 ? 20
- 21. Topological Sort • Idea: • Starting point must have zero indegree! • If it doesn’t exist, the graph would not be acyclic 1. A vertex with zero indegree is a task that can start right away. So we can output it first in the linear order 2. If a vertex i is output, then its outgoing arcs (i, j) are no longer useful, since tasks j does not need to wait for i anymore- so remove all i’s outgoing arcs 3. With vertex i removed, the new graph is still a directed acyclic graph. So, repeat step 1-2 until no vertex is left. 21
- 22. Topological Sort Find all starting points Reduce indegree(w) Place new start vertices on the Q 22
- 23. Example 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 1 2 1 1 2 1 1 2 2 Indegree start Q = { 0 } OUTPUT: 0 23
- 24. Example 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 1 2 1 1 2 1 1 2 2 Indegree Dequeue 0 Q = { } -> remove 0’s arcs – adjust indegrees of neighbors OUTPUT: Decrement 0’s neighbors -1 -1 -1 24
- 25. Example 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 2 1 0 2 0 1 2 2 Indegree Dequeue 0 Q = { 6, 1, 4 } Enqueue all starting points OUTPUT: 0 Enqueue all new start points 25
- 26. Example 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 2 1 0 2 0 1 2 2 Indegree Dequeue 6 Q = { 1, 4 } Remove arcs .. Adjust indegrees of neighbors OUTPUT: 0 6 Adjust neighbors indegree -1 -1 26
- 27. Example 1 2 3 4 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 1 0 0 2 0 1 2 2 Indegree Dequeue 6 Q = { 1, 4, 3 } Enqueue 3 OUTPUT: 0 6 Enqueue new start 27
- 28. Example 1 2 3 4 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 1 0 0 2 0 1 2 2 Indegree Dequeue 1 Q = { 4, 3 } Adjust indegrees of neighbors OUTPUT: 0 6 1 Adjust neighbors of 1 -1 28
- 29. Example 2 3 4 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 2 0 1 2 2 Indegree Dequeue 1 Q = { 4, 3, 2 } Enqueue 2 OUTPUT: 0 6 1 Enqueue new starting points 29
- 30. Example 2 3 4 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 2 0 1 2 2 Indegree Dequeue 4 Q = { 3, 2 } Adjust indegrees of neighbors OUTPUT: 0 6 1 4 Adjust 4’s neighbors -1 30
- 31. Example 2 3 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 1 0 1 2 2 Indegree Dequeue 4 Q = { 3, 2 } No new start points found OUTPUT: 0 6 1 4 NO new start points 31
- 32. Example 2 3 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 1 0 1 2 2 Indegree Dequeue 3 Q = { 2 } Adjust 3’s neighbors OUTPUT: 0 6 1 4 3 -1 32
- 33. Example 2 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 1 0 1 1 2 Indegree Dequeue 3 Q = { 2 } No new start points found OUTPUT: 0 6 1 4 3 33
- 34. Example 2 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 1 0 1 1 2 Indegree Dequeue 2 Q = { } Adjust 2’s neighbors OUTPUT: 0 6 1 4 3 2 -1 -1 34
- 35. Example 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 1 2 Indegree Dequeue 2 Q = { 5, 7 } Enqueue 5, 7 OUTPUT: 0 6 1 4 3 2 35
- 36. Example 5 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 1 2 Indegree Dequeue 5 Q = { 7 } Adjust neighbors OUTPUT: 0 6 1 4 3 2 5 -1 36
- 37. Example 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 1 1 Indegree Dequeue 5 Q = { 7 } No new starts OUTPUT: 0 6 1 4 3 2 5 37
- 38. Example 7 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 1 1 Indegree Dequeue 7 Q = { } Adjust neighbors OUTPUT: 0 6 1 4 3 2 5 7 -1 38
- 39. Example 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 0 1 Indegree Dequeue 7 Q = { 8 } Enqueue 8 OUTPUT: 0 6 1 4 3 2 5 7 39
- 40. Example 8 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 0 1 Indegree Dequeue 8 Q = { } Adjust indegrees of neighbors OUTPUT: 0 6 1 4 3 2 5 7 8 -1 40
- 41. Example 9 0 1 2 3 4 5 6 7 8 9 2 6 1 4 7 5 8 5 3 2 8 9 9 0 1 2 3 4 5 6 7 8 9 0 0 0 0 0 0 0 0 0 0 Indegree Dequeue 8 Q = { 9 } Enqueue 9 Dequeue 9 Q = { } STOP – no neighbors OUTPUT: 0 6 1 4 3 2 5 7 8 9 41
- 42. Example OUTPUT: 0 6 1 4 3 2 5 7 8 9 0 1 2 3 4 5 6 7 8 9 Is output topologically correct? 42
- 43. Topological Sort: Complexity • We never visited a vertex more than one time • For each vertex, we had to examine all outgoing edges • Σ outdegree(v) = m • This is summed over all vertices, not per vertex • So, our running time is exactly • O(n + m) 43
- 44. Graph Algorithms shortest paths, minimum spanning trees, etc. ORD DFW SFO LAX
- 45. 45 Minimum Spanning Trees JFK BOS MIA ORD LAX DFW SFO BWI PVD 867 2704 187 1258 849 144740 1391 184 946 1090 1121 2342 1846 621 802 1464 1235 337
- 46. Outline and Reading • Minimum Spanning Trees • Definitions • A crucial fact • The Prim-Jarnik Algorithm • Kruskal's Algorithm 46
- 47. Reminder: Weighted Graphs • In a weighted graph, each edge has an associated numerical value, called the weight of the edge • Edge weights may represent, distances, costs, etc. • Example: • In a flight route graph, the weight of an edge represents the distance in miles between the endpoint airports 47 ORD PVD MIA DFW SFO LAX LGA HNL
- 48. Spanning Subgraph and Spanning Tree • Spanning subgraph •Subgraph of a graph G containing all the vertices of G • Spanning tree • Spanning subgraph that is itself a (free) tree • So what is minimum spanning Tree ? 48 ORD PIT ATL STL DEN DFW DCA 10 1 9 8 6 3 25 7 4
- 49. Minimum Spanning Tree • A spanning tree of a connected graph is a tree containing all the vertices. • A minimum spanning tree (MST) of a weighted graph is a spanning tree with the smallest weight. • The weight of a spanning tree is the sum of the edge weights. • Graph and its spanning trees: Tree 2 is the minimum spanning tree 49
- 50. MST Origin • Otakar Boruvka (1926). • Electrical Power Company of Western Moravia in Brno. • Most economical construction of electrical power network. • Concrete engineering problem is now a cornerstone problem-solving model in combinatorial optimization. 50
- 51. Applications • MST is fundamental problem with diverse applications. • Network design. • telephone, electrical, hydraulic, TV cable, computer, road • Approximation algorithms for NP-hard problems. traveling salesperson problem, Steiner tree • Transportation networks • Indirect applications. max bottleneck paths LDPC codes for error correction image registration with Renyi entropy learning salient features for real-time face verification reducing data storage in sequencing amino acids in a protein model locality of particle interactions in turbulent fluid flows autoconfig protocol for Ethernet bridging to avoid cycles in a network 51
- 52. 52 Problem: Laying Telephone Wire Central office
- 53. 53 Wiring: Naïve Approach Central office Expensive!
- 54. 54 Wiring: Better Approach Central office Minimize the total length of wire connecting the customers
- 55. MST aka SST • Remark: The minimum spanning tree may not be unique. However, if the weights of all the edges are pairwise distinct, it is indeed unique (we won’t prove this now). Example 55
- 56. Minimum Spanning Tree Problem • MST Problem: Given a connected weighted undirected Graph G, design an algorithm that outputs a minimum spanning tree (MST) of G • Two Greedy algorithms • Prim’s algorithm • Kruskal's Algorithm • What is Greedy algorithm ? An algorithm that always takes the best immediate, or local, solution while finding an answer. Greedy algorithms find the overall, or globally, optimal solution for some optimal problems, but may find less-than-optimal solutions for some instances of other problems. 56
- 57. Greedy Algorithm • Greedy algorithms is a technique for solving problems with the following properties: • The problem is an optimization problem, to find the solution that minimizes or maximizes some value (cost/profit). • The solution can be constructed in a sequence of steps/choices. • For each choice point: • The choice must be feasible. • The choice looks as good or better than alternatives. • The choice cannot be revoked. 57
- 58. Greedy Algorithm cont’d… Example of Making Change • Suppose we want to give change of a certain amount (say 24 cents). • We would like to use fewer coins rather than more. • We can make a solution by repeatedly choosing a coin <= to the current amount, resulting in a new mount. • The greedy solution is to always choose the largest coin value possible (for 24 cents: 10, 10, 1, 1, 1, 1). • If there were an 8-cent coin, the greedy algorithm would not be optimal (but not bad). 58
- 59. Exercise: MST Show an MST of the following graph. 59 ORD PVD MIA DFW SFO LAX LGA HNL
- 60. Cycle Property Cycle Property: • Let T be a minimum spanning tree of a weighted graph G • Let e be an edge of G that is not in T and C let be the cycle formed by e with T • For every edge f of C, weight(f) weight(e) Proof: • By contradiction • If weight(f) > weight(e) we can get a spanning tree of smaller weight by replacing e with f 60 8 4 2 3 6 7 7 9 8 e C f 8 4 2 3 6 7 7 9 8 C e f Replacing f with e yields a better spanning tree
- 61. Partition Property Partition Property: • Consider a partition of the vertices of G into subsets U and V • Let e be an edge of minimum weight across the partition • There is a minimum spanning tree of G containing edge e Proof: • Let T be an MST of G • If T does not contain e, consider the cycle C formed by e with T and let f be an edge of C across the partition • By the cycle property, weight(f) weight(e) • Thus, weight(f) weight(e) • We obtain another MST by replacing f with e 61 U V 7 4 2 8 5 7 3 9 8 e f 7 4 2 8 5 7 3 9 8 e f Replacing f with e yields another MST U V
- 62. Prim-Jarnik’s Algorithm • (Similar to Dijkstra’s algorithm, for a connected graph) • We pick an arbitrary vertex s and we grow the MST as a cloud of vertices, starting from s • Start with any vertex s and greedily grow a tree T from s. At each step, add the cheapest edge to T that has exactly one endpoint in T. • We store with each vertex v a label d(v) = the smallest weight of an edge connecting v to a vertex in the cloud 62 • At each step: • We add to the cloud the vertex u outside the cloud with the smallest distance label • We update the labels of the vertices adjacent to u
- 63. More Detail • Step 0: choose any element r; set S={ r } and A=ø (Take r as the root of our spanning tree) • Step 1: Find a lightest edge such that one endpoint in S and the other is in VS. Add this edge to A and its other endpoint to S. • Step 2: if VS=ø, then stop & output (minimum) spanning tree (S,A). Otherwise go to step 1. • The idea: expand the current tree by adding the lightest (shortest) edge leaving it and its endpoint. 63
- 64. Example 64 B D C A F E 7 4 2 8 5 7 3 9 8 0 7 2 8 B D C A F E 7 4 2 8 5 7 3 9 8 0 7 2 5 7 B D C A F E 7 4 2 8 5 7 3 9 8 0 7 2 5 7 B D C A F E 7 4 2 8 5 7 3 9 8 0 7 2 5 4 7
- 65. Example (contd.) 65 B D C A F E 7 4 2 8 5 7 3 9 8 0 3 2 5 4 7 B D C A F E 7 4 2 8 5 7 3 9 8 0 3 2 5 4 7
- 73. Exercise: Prim’s MST alg • Show how Prim’s MST algorithm works on the following graph, assuming you start with SFO, I.e., s=SFO. • Show how the MST evolves in each iteration (a separate figure for each iteration). 73 ORD PVD MIA DFW SFO LAX LGA HNL
- 74. 74 Kruskal’s Algorithm • priority queue stores the edges outside the cloud • Key: weight • Element: edge • At the end of the algorithm • We are left with one cloud that encompasses the MST • A tree T which is our MST Algorithm KruskalMST(G) for each vertex V in G do define a Cloud(v) of {v} let Q be a priority queue. Insert all edges into Q using their weights as the key T while T has fewer than n-1 edges edge e = T.removeMin() Let u, v be the endpoints of e if Cloud(v) Cloud(u) then Add edge e to T Merge Cloud(v) and Cloud(u) return T Consider edges in ascending order of weight: Add to tree unless it would create a cycle.
- 75. Data Structure for Kruskal Algortihm • The algorithm maintains a forest of trees • An edge is accepted it if connects distinct trees • We need a data structure that maintains a partition, i.e., a collection of disjoint sets, with the operations: • find(u): return the set storing u • union(u,v): replace the sets storing u and v with their union 75
- 76. Representation of a Partition • Each set is stored in a sequence • Each element has a reference back to the set • operation find(u) takes O(1) time, and returns the set of which u is a member. • in operation union(u,v), we move the elements of the smaller set to the sequence of the larger set and update their references • the time for operation union(u,v) is min(nu,nv), where nu and nv are the sizes of the sets storing u and v • Whenever an element is processed, it goes into a set of size at least double, hence each element is processed at most log n times 76
- 77. Partition-Based Implementation • A partition-based version of Kruskal’s Algorithm performs cloud merges as unions and tests as finds. 77 Algorithm Kruskal(G): Input: A weighted graph G. Output: An MST T for G. Let P be a partition of the vertices of G, where each vertex forms a separate set. Let Q be a priority queue storing the edges of G, sorted by their weights Let T be an initially-empty tree while Q is not empty do (u,v) Q.removeMinElement() if P.find(u) != P.find(v) then Add (u,v) to T P.union(u,v) return T Running time: O((n+m) log n)
- 92. Exercise: Kruskal’s MST alg • Show how Kruskal’s MST algorithm works on the following graph. • Show how the MST evolves in each iteration (a separate figure for each iteration). 92 ORD PVD MIA DFW SFO LAX LGA HNL
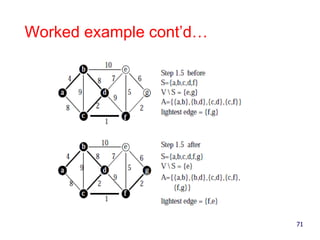
- 94. Example of Kruskal’s Algorithm 94
- 95. Example of Kruskal’s Algorithm, Cont’d.. 95
- 96. Example 96
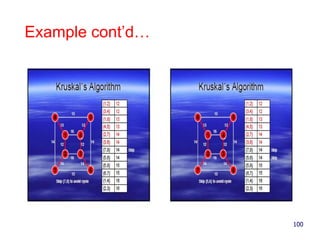
- 100. Example cont’d… 100
- 101. Example cont’d… 101
- 102. Shortest Paths 102 CB A E D F 0 328 5 8 48 7 1 2 5 2 3 9
- 103. Outline and Reading • Weighted graphs • Shortest path problem • Shortest path properties • Dijkstra’s algorithm • Algorithm • Edge relaxation • The Bellman-Ford algorithm • Shortest paths in DAGs • All-pairs shortest paths 103
- 104. Weighted Graphs • In a weighted graph, each edge has an associated numerical value, called the weight of the edge • Edge weights may represent, distances, costs, etc. • Example: • In a flight route graph, the weight of an edge represents the distance in miles between the endpoint airports 104 ORD PVD MIA DFW SFO LAX LGA HNL
- 105. Shortest Path Problem • Given a weighted graph and two vertices u and v, we want to find a path of minimum total weight between u and v. • Length of a path is the sum of the weights of its edges. • Example: • Shortest path between Providence and Honolulu • Applications • Internet packet routing • Flight reservations • Driving directions 105 ORD PVD MIA DFW SFO LAX LGA HNL
- 106. Shortest Path Problem • If there is no path from v to u, we denote the distance between them by d(v, u)=+ • What if there is a negative-weight cycle in the graph? 106 ORD PVD MIA DFW SFO LAX LGA HNL
- 107. Shortest Path Properties Property 1: A subpath of a shortest path is itself a shortest path Property 2: There is a tree of shortest paths from a start vertex to all the other vertices Example: Tree of shortest paths from Providence 107 ORD PVD MIA DFW SFO LAX LGA HNL
- 108. Dijkstra’s Algorithm • The distance of a vertex v from a vertex s is the length of a shortest path between s and v • Dijkstra’s algorithm computes the distances of all the vertices from a given start vertex s (single-source shortest paths) • Assumptions: • the graph is connected • the edge weights are nonnegative • We grow a “cloud” of vertices, beginning with s and eventually covering all the vertices • We store with each vertex v a label D[v] representing the distance of v from s in the subgraph consisting of the cloud and its adjacent vertices • The label D[v] is initialized to positive infinity • At each step • We add to the cloud the vertex u outside the cloud with the smallest distance label, D[v] • We update the labels of the vertices adjacent to u (i.e. edge relaxation) 108
- 109. Single –Source Shortest –Paths Problem • The Problem: Given a Graph with positive edge weights G=(V,E) and a distinguishing source vertex, s € V, determine the distance and a shortest path from the source vertex to every vertex in the graph 109
- 110. The Rough Idea of Djikstra’s Algorithm 110
- 111. Description of Dijkstra’s Algorithm 111
- 112. Example 112 CB A E D F 0 428 48 7 1 2 5 2 3 9 CB A E D F 0 328 5 11 48 7 1 2 5 2 3 9 CB A E D F 0 328 5 8 48 7 1 2 5 2 3 9 CB A E D F 0 327 5 8 48 7 1 2 5 2 3 9 1. Pull in one of the vertices with red labels 2. The relaxation of edges updates the labels of LARGER font size
- 113. Example (cont.) 113 CB A E D F 0 327 5 8 48 7 1 2 5 2 3 9 CB A E D F 0 327 5 8 48 7 1 2 5 2 3 9
- 114. Exercise: Dijkstra’s alg • Show how Dijkstra’s algorithm works on the following graph, assuming you start with SFO, I.e., s=SFO. • Show how the labels are updated in each iteration (a separate figure for each iteration). 114 ORD PVD MIA DFW SFO LAX LGA HNL
- 115. Why Dijkstra’s Algorithm Works • Dijkstra’s algorithm is based on the greedy method. It adds vertices by increasing distance. 115 Suppose it didn’t find all shortest distances. Let F be the first wrong vertex the algorithm processed. When the previous node, D, on the true shortest path was considered, its distance was correct. But the edge (D,F) was relaxed at that time! Thus, so long as D[F]>D[D], F’s distance cannot be wrong. That is, there is no wrong vertex. CB s E D F 0 327 5 8 48 7 1 2 5 2 3 9
- 116. Why It Doesn’t Work for Negative- Weight Edges 116 Dijkstra’s algorithm is based on the greedy method. It adds vertices by increasing distance. If a node with a negative incident edge were to be added late to the cloud, it could mess up distances for vertices already in the cloud. C’s true distance is 1, but it is already in the cloud with D[C]=2! CB A E D F 0 428 48 7 -3 2 5 2 3 9 CB A E D F 0 028 5 11 48 7 -3 2 5 2 3 9
- 117. Analysis of Dijkstra’s Algorithm 117
- 118. Bellman-Ford Algorithm • Works even with negative- weight edges • Must assume directed edges (for otherwise we would have negative-weight cycles) • Iteration i finds all shortest paths that use i edges. • Running time: O(nm). • Can be extended to detect a negative-weight cycle if it exists • How? 118 Algorithm BellmanFord(G, s) for all v G.vertices() if v s setDistance(v, 0) else setDistance(v, ) for i 1 to n-1 do for each e G.edges() { relax edge e } u G.origin(e) z G.opposite(u,e) r getDistance(u) weight(e) if r < getDistance(z) setDistance(z,r)
- 119. Bellman-Ford Example 119 -2 0 48 7 1 -2 5 -2 3 9 0 48 7 1 -2 5 3 9 Nodes are labeled with their d(v) values -2 -28 0 4 48 7 1 -2 5 3 9 8 -2 4 -15 6 1 9 -25 0 1 -1 9 48 7 1 -2 5 -2 3 9 4 First round Second round Third round
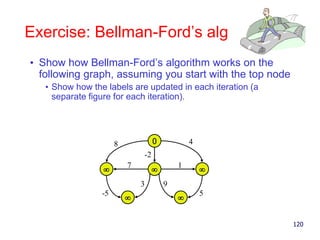
- 120. Exercise: Bellman-Ford’s alg • Show how Bellman-Ford’s algorithm works on the following graph, assuming you start with the top node • Show how the labels are updated in each iteration (a separate figure for each iteration). 120 0 48 7 1 -5 5 -2 3 9
- 121. DAG-based Algorithm • Works even with negative-weight edges • Uses topological order • Is much faster than Dijkstra’s algorithm • Running time: O(n+m). 121 Algorithm DagDistances(G, s) for all v G.vertices() if v s setDistance(v, 0) else setDistance(v, ) Perform a topological sort of the vertices for u 1 to n do {in topological order} for each e G.outEdges(u) { relax edge e } z G.opposite(u,e) r getDistance(u) weight(e) if r < getDistance(z) setDistance(z,r)
- 122. DAG Example 122 -2 0 48 7 1 -5 5 -2 3 9 0 48 7 1 -5 5 3 9 Nodes are labeled with their d(v) values -2 -28 0 4 48 7 1 -5 5 3 9 -2 4 -1 1 7 -25 0 1 -1 7 48 7 1 -5 5 -2 3 9 4 1 2 43 6 5 1 2 43 6 5 8 1 2 43 6 5 1 2 43 6 5 5 0 (two steps)
- 123. Exercize: DAG-based Alg • Show how DAG-based algorithm works on the following graph, assuming you start with the second rightmost node • Show how the labels are updated in each iteration (a separate figure for each iteration). 123 ∞ 0 ∞ ∞∞ ∞ 5 2 7 -1 -2 6 1 3 4 2 1 2 3 4 5
- 124. Summary of Shortest-Path Algs • Breadth-First-Search • Dijkstra’s algorithm • Algorithm • Edge relaxation • The Bellman-Ford algorithm • Shortest paths in DAGs 124
- 125. All-Pairs Shortest Paths • Find the distance between every pair of vertices in a weighted directed graph G. • We can make n calls to Dijkstra’s algorithm (if no negative edges), which takes O(nmlog n) time. • Likewise, n calls to Bellman-Ford would take O(n2m) time. • We can achieve O(n3) time using dynamic programming (similar to the Floyd-Warshall algorithm). 125 Algorithm AllPair(G) {assumes vertices 1,…,n} for all vertex pairs (i,j) if i j D0[i,i] 0 else if (i,j) is an edge in G D0[i,j] weight of edge (i,j) else D0[i,j] + for k 1 to n do for i 1 to n do for j 1 to n do Dk[i,j] min{Dk-1[i,j], Dk-1[i,k]+Dk-1[k,j]} return Dn k j i Uses only vertices numbered 1,…,k-1 Uses only vertices numbered 1,…,k-1 Uses only vertices numbered 1,…,k (compute weight of this edge)














![Outdegree
• All of the arcs going “out” from v
• Simple to compute
• Scan through list Adj[v] and count the arcs
• What is the total outdegree? (m=#edges)
mv
v
vertex
)(outdegree
15](https://image.slidesharecdn.com/algorithmsofgraph-150306065525-conversion-gate01/85/Algorithms-of-graph-15-320.jpg)
![Indegree
• All of the arcs coming “in” to v
• Not as simple to compute as outdegree
• First, initialize indegree[v]=0 for each vertex v
• Scan through adj[v] list for each v
• For each vertex w seen, indegree[w]++;
• Running time: O(n+m)
• What is the total indegree?
mv
v
vertex
)(indegree
16](https://image.slidesharecdn.com/algorithmsofgraph-150306065525-conversion-gate01/85/Algorithms-of-graph-16-320.jpg)

























































































![Dijkstra’s Algorithm
• The distance of a vertex
v from a vertex s is the
length of a shortest path
between s and v
• Dijkstra’s algorithm
computes the distances
of all the vertices from a
given start vertex s
(single-source shortest
paths)
• Assumptions:
• the graph is connected
• the edge weights are
nonnegative
• We grow a “cloud” of vertices,
beginning with s and eventually
covering all the vertices
• We store with each vertex v a
label D[v] representing the
distance of v from s in the
subgraph consisting of the cloud
and its adjacent vertices
• The label D[v] is initialized to
positive infinity
• At each step
• We add to the cloud the vertex u
outside the cloud with the
smallest distance label, D[v]
• We update the labels of the
vertices adjacent to u (i.e. edge
relaxation)
108](https://image.slidesharecdn.com/algorithmsofgraph-150306065525-conversion-gate01/85/Algorithms-of-graph-108-320.jpg)






![Why Dijkstra’s Algorithm Works
• Dijkstra’s algorithm is based on the greedy
method. It adds vertices by increasing distance.
115
Suppose it didn’t find all shortest
distances. Let F be the first wrong
vertex the algorithm processed.
When the previous node, D, on the
true shortest path was considered,
its distance was correct.
But the edge (D,F) was relaxed at
that time!
Thus, so long as D[F]>D[D], F’s
distance cannot be wrong. That is,
there is no wrong vertex.
CB
s
E
D
F
0
327
5
8
48
7 1
2 5
2
3 9](https://image.slidesharecdn.com/algorithmsofgraph-150306065525-conversion-gate01/85/Algorithms-of-graph-115-320.jpg)
![Why It Doesn’t Work for Negative-
Weight Edges
116
Dijkstra’s algorithm is
based on the greedy
method. It adds
vertices by increasing
distance.
If a node with a
negative incident
edge were to be
added late to the
cloud, it could
mess up distances
for vertices already
in the cloud.
C’s true
distance is 1,
but it is already
in the cloud
with D[C]=2!
CB
A
E
D
F
0
428
48
7 -3
2 5
2
3 9
CB
A
E
D
F
0
028
5 11
48
7 -3
2 5
2
3 9](https://image.slidesharecdn.com/algorithmsofgraph-150306065525-conversion-gate01/85/Algorithms-of-graph-116-320.jpg)







![All-Pairs Shortest Paths
• Find the distance between
every pair of vertices in a
weighted directed graph
G.
• We can make n calls to
Dijkstra’s algorithm (if no
negative edges), which
takes O(nmlog n) time.
• Likewise, n calls to
Bellman-Ford would take
O(n2m) time.
• We can achieve O(n3)
time using dynamic
programming (similar to
the Floyd-Warshall
algorithm).
125
Algorithm AllPair(G) {assumes vertices 1,…,n}
for all vertex pairs (i,j)
if i j
D0[i,i] 0
else if (i,j) is an edge in G
D0[i,j] weight of edge (i,j)
else
D0[i,j] +
for k 1 to n do
for i 1 to n do
for j 1 to n do
Dk[i,j] min{Dk-1[i,j], Dk-1[i,k]+Dk-1[k,j]}
return Dn
k
j
i
Uses only vertices
numbered 1,…,k-1 Uses only vertices
numbered 1,…,k-1
Uses only vertices numbered 1,…,k
(compute weight of this edge)](https://image.slidesharecdn.com/algorithmsofgraph-150306065525-conversion-gate01/85/Algorithms-of-graph-125-320.jpg)














































































