![The synchrotron
• Acceleration is performed by RF cavities
• (Piecewise) circular motion is ensured by a guide field FB
• FB : Bending magnets with a homogenous field
• In the arc section:
• RF frequency must stay locked to the revolution frequency of a particle
(later slide)
• Synchrotrons are used for most HEP experiments (LHC, Tevatron, HERA,
LEP, SPS, PS) as well as, as the name tells, in Synchrotron Light Sources
(e.g. ESRF)
]
/
[
]
[
3
.
0
]
[
1
1
F 1
2
B
c
GeV
p
T
B
m
p
qB
v
m
](https://image.slidesharecdn.com/anintroductiontoparticleaccelerators-250802143519-7ef9436f/85/An-Introduction-to-Particle-Accelerators-ppt-19-320.jpg)
![Bending field: dipole magnets
• Dipole magnets provide uniform field in the desired
region
• LHC Dipole magnets: design that allows opposite and
uniform field in both vacuum chambers
• Bonus effect of dipole magnets: geometrical focusing in
the horizontal plane
• 1/: “normalized dipole strength”, strength of the magnet
]
/
[
]
[
3
.
0
]
[
1
1 1
c
GeV
p
T
B
m
p
eB
](https://image.slidesharecdn.com/anintroductiontoparticleaccelerators-250802143519-7ef9436f/85/An-Introduction-to-Particle-Accelerators-ppt-33-320.jpg)
![Focusing field: quadrupoles
• Quadrupole magnets gives linear field in x and y:
Bx = -gy
By = -gx
• However, forces are focusing in one plane and defocusing in the orthogonal
plane:
Fx = -qvgx (focusing)
Fy = qvgy (defocusing)
• Opposite focusing/defocusing is achieved by rotating the quadrupole 90
• Analogy to dipole strength: normalized quadrupole strength:
]
/
[
]
/
[
3
.
0
]
[ 2
c
GeV
p
m
T
g
m
k
p
eg
k
inevitable due to Maxwell](https://image.slidesharecdn.com/anintroductiontoparticleaccelerators-250802143519-7ef9436f/85/An-Introduction-to-Particle-Accelerators-ppt-35-320.jpg)
![References
• Bibliography:
– K. Wille, The Physics of Particle Accelerators, 2000
– ...and the classic: E. D. Courant and H. S. Snyder, "Theory of the Alternating-
Gradient Synchrotron", 1957
– CAS 1992, Fifth General Accelerator Physics Course, Proceedings, 7-18
September 1992
– LHC Design Report [online]
• Other references
– USPAS resource site, A. Chao, USPAS january 2007
– CAS 2005, Proceedings (in-print), J. Le Duff, B, Holzer et al.
– O. Brüning: CERN student summer lectures
– N. Pichoff: Transverse Beam Dynamics in Accelerators, JUAS January 2004
– U. Amaldi, presentation on Hadron therapy at CERN 2006
– Several figures in this presentation have been borrowed from the above
references, thanks to all!](https://image.slidesharecdn.com/anintroductiontoparticleaccelerators-250802143519-7ef9436f/85/An-Introduction-to-Particle-Accelerators-ppt-55-320.jpg)
An Introduction to Particle Accelerators.ppt
- 1. An Introduction to Particle Accelerators Erik Adli, University of Oslo/CERN , University of Oslo/CERN 2009 [email protected] v1.42 - short
- 2. LHC FIRST BEAM 10-sep-2008
- 4. Particle accelerators for HEP •LHC: the world biggest accelerator, both in energy and size (as big as LEP) • Grand start-up and perfect functioning at injection energy in September 2008 •First collisions expected in 2009
- 5. Particle accelerators for HEP The next big thing. After LHC, a Linear Collider of over 30 km length, will probably be needed (why?)
- 6. Medical applications • Therapy – The last decades: electron accelerators (converted to X-ray via a target) are used very successfully for cancer therapy) – Today's research: proton accelerators instead (hadron therapy): energy deposition can be controlled better, but huge technical challenges • Imaging – Isotope production for PET scanners
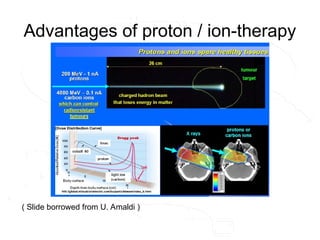
- 7. Advantages of proton / ion-therapy ( Slide borrowed from U. Amaldi )
- 8. Proton therapy accelerator centre ( Slide borrowed from U. Amaldi ) What is all this? Follow the lectures... :) HIBAC in Chiba
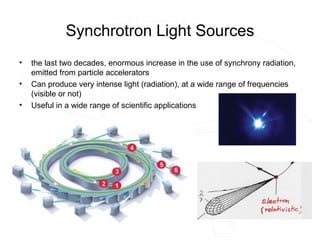
- 9. Synchrotron Light Sources • the last two decades, enormous increase in the use of synchrony radiation, emitted from particle accelerators • Can produce very intense light (radiation), at a wide range of frequencies (visible or not) • Useful in a wide range of scientific applications
- 10. Thorium - Accelerator Driven Systems
- 12. An accelerator • Structures in which the particles will move • Structures to accelerate the particles • Structures to steer the particles • Structures to measure the particles
- 13. Lorentz equation • The two main tasks of an accelerator – Increase the particle energy – Change the particle direction (follow a given trajectory, focusing) • Lorentz equation: • FB v FB does no work on the particle – Only FE can increase the particle energy • FE or FB for deflection? v c Magnetic field of 1 T (feasible) same bending power as en electric field of 3108 V/m (NOT feasible) – FB is by far the most effective in order to change the particle direction B E F F B v q E q B v E q F ) (
- 14. Acceleration techniques: DC field • The simplest acceleration method: DC voltage • Energy kickE=qV • Can accelerate particles over many gaps: electrostatic accelerator • Problem: breakdown voltage at ~10MV • DC field still used at start of injector chain
- 15. Acceleration techniques: RF field • Oscillating RF (radio-frequency) field • “Widerøe accelerator”, after the pioneering work of the Norwegian Rolf Widerøe (brother of the aviator Viggo Widerøe) • Particle must sees the field only when the field is in the accelerating direction – Requires the synchronism condition to hold: Tparticle =½TRF • Problem: high power loss due to radiation vT L ) 2 / 1 (
- 16. Acceleration techniques: RF cavities • Electromagnetic power is stored in a resonant volume instead of being radiated • RF power feed into cavity, originating from RF power generators, like Klystrons • RF power oscillating (from magnetic to electric energy), at the desired frequency • RF cavities requires bunched beams (as opposed to coasting beams) – particles located in bunches separated in space
- 17. From pill-box to real cavities LHC cavity module ILC cavity (from A. Chao)
- 18. Why circular accelerators? • Technological limit on the electrical field in an RF cavity (breakdown) • Gives a limited E per distance Circular accelerators, in order to re-use the same RF cavity • This requires a bending field FB in order to follow a circular trajectory (later slide)
- 19. The synchrotron • Acceleration is performed by RF cavities • (Piecewise) circular motion is ensured by a guide field FB • FB : Bending magnets with a homogenous field • In the arc section: • RF frequency must stay locked to the revolution frequency of a particle (later slide) • Synchrotrons are used for most HEP experiments (LHC, Tevatron, HERA, LEP, SPS, PS) as well as, as the name tells, in Synchrotron Light Sources (e.g. ESRF) ] / [ ] [ 3 . 0 ] [ 1 1 F 1 2 B c GeV p T B m p qB v m
- 20. Digression: other accelerator types • Cyclotron: – constant B field – constant RF field in the gap increases energy – radius increases proportionally to energy – limit: relativistic energy, RF phase out of synch – In some respects simpler than the synchrotron, and often used as medical accelerators • Synchro-cyclotron – Cyclotron with varying RF phase • Betatron – Acceleration induced by time-varying magnetic field • The synchrotron will be the only circular accelerator discussed in this course
- 21. Digression: other accelerator types Linear accelerators for linear colliders - will be covered in lecture about linear colliders at CERN
- 22. Particle motion • We separate the particle motion into: – longitudinal motion: motion tangential to the reference trajectory along the accelerator structure, us – transverse motion: degrees of freedom orthogonal to the reference trajectory, ux, uy • us, ux, uy are unit vector in a moving coordinate system, following the particle
- 23. Longitudinal dynamics for a synchrotron Longitudinal Dynamics: degrees of freedom tangential to the reference trajectory us: tangential to the reference trajectory Part 3
- 24. RF acceleration • We assume a cavity with an oscillating RF-field: • In this section we neglect the transit-transit factor – we assume a field constant in time while the particle passes the cavity • Work done on a particle inside cavity: ) sin( ˆ t E E RF z z ) sin( ˆ ) sin( ˆ t V q dz t E q dz E q Fdz W RF RF z z
- 25. Synchrotron with one cavity • The energy kick of a particle, E, depends on the RF phase seen • We define a “synchronous particle”, s, which always sees the same phase s passing the cavity RF =h rs ( h: “harmonic number” ) • E.g. at constant speed, a synchronous particle circulating in the synchrotron, assuming no losses in accelerator, will always see s=0 sin ˆ ) sin( ˆ V q t V q W E RF
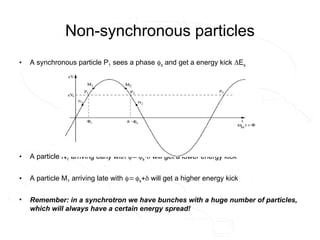
- 26. Non-synchronous particles • A synchronous particle P1 sees a phase s and get a energy kick Es • A particle N1 arriving early with s will get a lower energy kick • A particle M1 arriving late with s will get a higher energy kick • Remember: in a synchrotron we have bunches with a huge number of particles, which will always have a certain energy spread!
- 27. Frequency dependence on energy • In order to see the effect of a too low/high E, we need to study the relation between the change in energy and the change in the revolution frequency : "slip factor") • Two effects: 1. Higher energy higher speed (except ultra-relativistic) 2. Higher energy larger orbit “Momentum compaction” p dp f df r r / / R c fr 2
- 28. Momentum compaction • Increase in energy/mass will lead to a larger orbit • We define the “momentum compaction factor” as: • is a function of the transverse focusing in the accelerator, Dx> / R is a well defined quantity for a given accelerator p dp R dR / /
- 29. Phase stability • >0: velocity increase dominates, fr increases • Synchronous particle stable for 0º<s<90º – A particle N1 arriving early with s will get a lower energy kick, and arrive relatively later next pass – A particle M1 arriving late with s will get a higher energy kick, and arrive relatively earlier next pass • 0: stability for 90º<s<180º • 0 at the transition energy. When the synchrotron reaches this energy, the RF phase needs to be switched rapidly from stos
- 30. Transverse dynamics Transverse dynamics: degrees of freedom orthogonal to the reference trajectory ux: the horizontal plane uy: the vertical plane Part 4
- 31. Bending field • Circular accelerators: deflecting forces are needed • Circular accelerators: piecewise circular orbits with a defined bending radius – Straight sections are needed for e.g. particle detectors – In circular arc sections the magnetic field must provide the desired bending radius: • For a constant particle energy we need a constant B field dipole magnets with homogenous field • In a synchrotron, the bending radius,1/=eB/p, is kept constant during acceleration (last section) B E F F B v E q F ) ( p eB 1
- 32. The reference trajectory • An accelerator is designed around a reference trajectory (also called design orbit in circular accelerators) • This is the trajectory an ideal particle will follow and consist of – a straight line where there is no bending field – arc of circle inside the bending field • We will in the following talk about transverse deviations from this reference trajectory, and especially about how to keep these deviations small Reference trajectory
- 33. Bending field: dipole magnets • Dipole magnets provide uniform field in the desired region • LHC Dipole magnets: design that allows opposite and uniform field in both vacuum chambers • Bonus effect of dipole magnets: geometrical focusing in the horizontal plane • 1/: “normalized dipole strength”, strength of the magnet ] / [ ] [ 3 . 0 ] [ 1 1 1 c GeV p T B m p eB
- 34. Focusing field • reference trajectory: typically centre of the dipole magnets • Problem with geometrical focusing: still large oscillations and NO focusing in the vertical plane the smallest disturbance (like gravity...) may lead to lost particle • Desired: a restoring force of the type Fx,y=-kx,y in order to keep the particles close to the ideal orbit • A linear field in both planes can be derived from the scalar pot. V(x,y) = gxy – Equipotential lines at xy=Vconst – B magnet iron surface Magnet surfaces shaped as hyperbolas gives linear field
- 35. Focusing field: quadrupoles • Quadrupole magnets gives linear field in x and y: Bx = -gy By = -gx • However, forces are focusing in one plane and defocusing in the orthogonal plane: Fx = -qvgx (focusing) Fy = qvgy (defocusing) • Opposite focusing/defocusing is achieved by rotating the quadrupole 90 • Analogy to dipole strength: normalized quadrupole strength: ] / [ ] / [ 3 . 0 ] [ 2 c GeV p m T g m k p eg k inevitable due to Maxwell
- 36. Optics analogy • Physical analogy: quadrupoles optics • Focal length of a quadrupole: 1/f = kl – where l is the length of the quadrupole • Alternating focusing and defocusing lenses will together give total focusing effect in both planes (shown later) – “Alternating Gradient” focusing
- 37. The Lattice • An accelerator is composed of bending magnets, focusing magnets and non-linear magnets (later) • The ensemble of magnets in the accelerator constitutes the “accelerator lattice”
- 39. Transverse beam size RMS beam size: ) ( ) ( s s rms Beam quality Lattice
- 40. Conclusion: transverse dynamics • We have now studied the transverse optics of a circular accelerator and we have had a look at the optics elements, – the dipole for bending – the quadrupole for focusing – the sextupole for chromaticity correction • All optic elements (+ more) are needed in a high performance accelerator, like the LHC
- 42. 1) Synchrotron radiation • Charged particles undergoing acceleration emit electromagnetic radiation • Main limitation for circular electron machines – RF power consumption becomes too high • The main limitation factor for LEP... – ...the main reason for building LHC ! • However, synchrotron radiations is also useful (see later slides)
- 44. Characteristic of SR: power
- 45. Characteristics of SR: distribution • Electron rest-frame: radiation distributed as a "Hertz-dipole" • Relativist electron: Hertz-dipole distribution in the electron rest-frame, but transformed into the laboratory frame the radiation form a very sharply peaked light-cone 2 sin d dPS
- 46. • Broad spectra (due to short pulses as seen by an observer) • But, 50% of power contained within a well defined "critical frequency" Summary: advantages of Synchrotron Radiation 1. Very high intensity 2. Spectrum that cannot be covered easy with other sources 3. Critical frequency easily controlled Characteristics of SR: spectrum
- 47. Typical SR centre Accelerator + Users Some applications of Synchrotron Radiation: •material/molecule analysis (UV, X-ray) •crystallography •archaeology... Example: European Synchrotron Radiation Facility (ESRF), Grenoble, France
- 48. Case: LHC
- 49. LHC
- 50. LHC injector system • LHC is responsible for accelerating protons from 450 GeV up to 7000 GeV • 450 GeV protons injected into LHC from the SPS • PS injects into the SPS • LINACS injects into the PS • The protons are generated by a Duoplasmatron Proton Source
- 51. LHC layout • circumference = 26658.9 m • 8 interaction points, 4 of which contains detectors where the beams intersect • 8 straight sections, containing the IPs, around 530 m long • 8 arcs with a regular lattice structure, containing 23 arc cells • Each arc cell has a FODO structure, 106.9 m long
- 52. LHC beam transverse size m IP 17 * mm typ arc 3 . 0 beta in drift space: (s) = * + (s-s*)2 / rad nm m m typ 5 . 0 , 55 . 0 , 180 *
- 53. LHC cavities • Superconducting RF cavities (standing wave, 400 MHz) • Each beam: one cryostats with 4+4 cavities each • Located at LHC point 4
- 54. LHC main parameters at collision energy Particle type p, Pb Proton energy Ep at collision 7000 GeV Peak luminosity (ATLAS, CMS) 10 x 1034 cm-2 s-1 Circumference C 26 658.9 m Bending radius 2804.0 m RF frequency fRF 400.8 MHz # particles per bunch np 1.15 x 1011 # bunches nb 2808
- 55. References • Bibliography: – K. Wille, The Physics of Particle Accelerators, 2000 – ...and the classic: E. D. Courant and H. S. Snyder, "Theory of the Alternating- Gradient Synchrotron", 1957 – CAS 1992, Fifth General Accelerator Physics Course, Proceedings, 7-18 September 1992 – LHC Design Report [online] • Other references – USPAS resource site, A. Chao, USPAS january 2007 – CAS 2005, Proceedings (in-print), J. Le Duff, B, Holzer et al. – O. Brüning: CERN student summer lectures – N. Pichoff: Transverse Beam Dynamics in Accelerators, JUAS January 2004 – U. Amaldi, presentation on Hadron therapy at CERN 2006 – Several figures in this presentation have been borrowed from the above references, thanks to all!