Applied statistics lecture_4
2 likes365 views
This document provides an introduction to applied statistics and statistical methods, including significance (p-value), correlation coefficients (Pearson's r, Spearman's rho, Kendall's tau-b), and partial correlation. It defines these concepts and provides examples of interpreting correlation results from the SPSS output. Practice examples demonstrate how to conduct and interpret correlation analyses in SPSS to examine relationships between test scores, exam performance and anxiety, and examiner ratings.
Applied statistics lecture_4
- 1. 1 Introduction to applied statistics & applied statistical methods Prof. Dr. Chang Zhu1 objectives • significance p-value • Paired sample t-test • Mann Whitney tests • correlation Pearson’s r Spearman’s rho (rs) Kendall’s tau-b (τ) Partial correlation
- 2. 2 significance – p value value test statistic alternative hypothesis null hypothesis p < .05 significant accepted rejected p > .05 non-significant rejected accepted significance – p value For t-tests • p < .05 the difference is proved to be significant. • Look at the means of the two groups before making decision about the direction of the hypothesis, i.e. which group has a higher/bigger mean?
- 3. 3 correlation • A researcher is interested in the degree to which a person spends time Facebooking (in hours per week) and the amount of time spent socialising with friends (number of social encounters per month). • He comes up with the following data set. (adapted from http://wps.pearsoned.co.uk/ema_uk_he_dancey_statsmath _4/84/21626/5536329.cw/index.html) P_ID Facebook use Social encounters 1 10 1 2 11 2 3 11 3 4 12 3 5 14 4 6 15 9 7 16 10 correlation What can you predict?
- 4. 4 Facebook use (M=12.7) deviance from mean squared deviance s 10 -2.7 7.29 11 -1.7 2.89 11 -1.7 2.89 12 -0.7 0.49 14 1.3 1.69 15 2.3 5.29 16 3.3 10.89 correlation add up all the squared deviances: sum of squared errors affected by sample size divide by the number of participants minus 1: variance Facebook use (M=12.7) Social encounters (M=6.14) 10 1 11 2 11 3 12 3 14 4 15 9 16 10 correlation • variance for Facebook use • covariance: averaged sum of combined deviations • standardized covariance: correlation coefficient
- 5. 5 correlation SPSS output Correlations FB Encounters FB Pearson Correlation 1 .900** Sig. (2-tailed) .006 N 7 7 Encounters Pearson Correlation .900** 1 Sig. (2-tailed) .006 N 7 7 **. Correlation is significant at the 0.01 level (2-tailed). r = .90, p < .01 (significant) Correlation Positive Correlation Negative Correlation Correlation analysis
- 6. 6 correlation The correlation coefficient: measures the relative strength of the linear relationship between two variables • Ranges between –1 and 1 • The closer to –1, the stronger the negative linear relationship • The closer to 1, the stronger the positive linear relationship • The closer to 0, the weaker any positive linear relationship A perfect positive correlation Height Weight Height of A Weight of A Height of B Weight of B A linear relationship
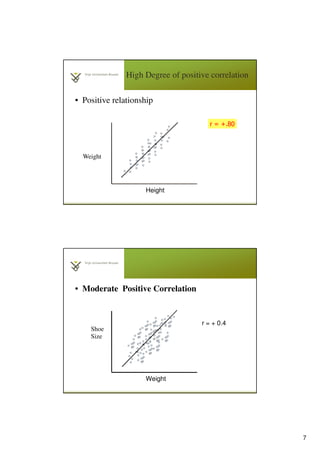
- 7. 7 High Degree of positive correlation • Positive relationship Height Weight r = +.80 • Moderate Positive Correlation Weight Shoe Size r = + 0.4
- 8. 8 • Perfect Negative Correlation Exam score TV watching per week r = -1.0 • Moderate Negative Correlation Exam score TV watching per week r = -.80
- 9. 9 • Weak negative Correlation Weight Shoe Size r = - 0.2 • No Correlation (horizontal line) Height IQ r = 0.0
- 10. 10 Test of Correlations Parametric test: Pearson’s r is the most common correlation coefficient. Non-parametric tests • Spearman’s rho (rs): rank the scores, then use the same equation as above. • Kendall’s tau-b (τ) : taking into account tied ranks. PRACTICE
- 11. 11 Practice 1 Pearson’s correlation •We collect the scores of 200 high school students on various tests, including science, reading, and maths score, and we want to know if there is a correlation between the scores of each pair of the variables. •The data file is named test_score.sav In SPSS, choose Analyse > Correlate > Bivariate practical guidelines page 2 SPSS output Correlations reading score math score science score reading score Pearson Correlation 1 .662** .630** Sig. (2-tailed) .000 .000 N 200 200 200 math score Pearson Correlation .662** 1 .631** Sig. (2-tailed) .000 .000 N 200 200 200 science score Pearson Correlation .630** .631** 1 Sig. (2-tailed) .000 .000 N 200 200 200 **. Correlation is significant at the 0.01 level (2-tailed).
- 12. 12 Practice 1 Conclusion? Reading scores were significantly correlated with math scores, r = .66, p < .01 (one-tailed), and science scores, r = .63, p < .01 (one-tailed); the math scores were also correlated with the science scores, r = .63, p < .01 (one-tailed). (Practical guidelines page 4) Practice 2 Partial correlation • Use the data file Exam Anxiety.sav • Conduct the Pearson’s correlation for the three variables: exam, anxiety, and revise • What is the relationship between the variable anxiety and exam and revise In SPSS, choose Analyse > Correlate > Bivariate
- 13. 13 SPSS output Correlations Time Spent Revising Exam Performance (%) Exam Anxiety Time Spent Revising Pearson Correlation 1 .397** -.709** Sig. (2-tailed) .000 .000 N 103 103 103 Exam Performance (%) Pearson Correlation .397** 1 -.441** Sig. (2-tailed) .000 .000 N 103 103 103 Exam Anxiety Pearson Correlation -.709** -.441** 1 Sig. (2-tailed) .000 .000 N 103 103 103 **. Correlation is significant at the 0.01 level (2-tailed). Practice 2 Partial correlation Observation: • Exam anxiety is negatively correlated with exam performance (r = -.441) • Exam anxiety is also negatively correlated with the time spent revising (revision time) for the exam (r = -.709) • However, exam performance is positively related to the time spent revising (r= .397)
- 14. 14 Practice 2 Partial correlation • The revision time may affect the relationship between exam anxiety and exam performance such that the more one spends time on revision, the less anxiety one perceives, hence better performance. • We are capable of investigating purely the relationship between exam anxiety and exam performance, taking into account the effect of time spent on revising. In SPSS, choose Analyse > Correlate > Partial SPSS output Correlations Control Variables Exam Performance (%) Exam Anxiety Time Spent Revising Exam Performance (%) Correlation 1.000 -.247 Significance (2- tailed) . .012 df 0 100 Exam Anxiety Correlation -.247 1.000 Significance (2- tailed) .012 . df 100 0 not controlling for time spent revising: r = -.441
- 15. 15 Practice 2 Partial correlation Conclusion? Exam anxiety was significantly related to exam performance, r = -.247, p < .05 (two-tailed), controlling for the effect of time spent on revising. (Practical guidelines page 4) Practice 1 •Two examiners rated the presentations of 20 students with 1 being poor and 10 meaning perfect. It is expected that the scores would be similar. •The data file is named presentation_rating.sav. (Practical guidelines page 6) Practice 3 Spearman and Kendall’s tau (nonparametric) In SPSS, choose Analyse > Correlate > Bivariate
- 16. 16 Practice 3 Spearman and Kendall’s tau (nonparametric) Conclusion? •The rating of the two examiners was significantly correlated, rs = .825, p < .01 (one-tailed). Or: •The rating of the two examiners was significantly correlated, τ = .707, p < .01 (one-tailed) (Practical guidelines page 6) Assignment • Conduct paired t-test • Conduct Mann Whitney tests • Conduct correlation analysis