Artificial Neural Networks: Introduction, Neural Network representation, Appropriate problems, Perceptron- Perceptron Training rule, Back propagation algorithm.

MODULE -3
1
ARTIFICIAL NEURAL NETWORKS
By.
Dr. Ravi Kumar B N
Assistant Professor, Dept. of CSE

• Introduction
• Neural Network Representation
• Appropriate Problems for Neural Network Learning
• Perceptrons
• Multilayer Networks and BACKPROPAGATION Algorithms
• Remarks on the BACKPROPAGATIONAlgorithms
2
CONTENT

INTRODUCTION
6
An artificial neural network is an attempt to simulate the network of
neurons that make up a human brain so that the computer will be able
to learn things and make decisions in a humanlike manner.
Artificial neural networks (ANNs) provide a general, practical method
for learning real-valued, discrete-valued, and vector-valued target
functions from examples.

What type of learning is used in ANN?
7
Supervised Learning
This learning process is dependent. During the training of ANN under supervised
learning, the input vector is presented to the network, which will give an output
vector. This output vector is compared with the desired output vector.

Biological Motivation
8
• The study of artificial neural networks (ANNs) has been inspired by the
observation that biological learning systems are built of very complex webs of
interconnected Neurons
• Human information processing system consists of brain neuron: basic building
block cell that communicates information to and from various parts of body
• Simplest model of a neuron: considered as a threshold unit –a processing element
(PE)
• Collects inputs & produces output if the sum of the input exceeds an internal
threshold value

cellbody
synapse
nucleus
axon
9
dendrites

Facts of Human Neurobiology
10
• Number of neurons ~ 1011
• Connection per neuron ~ 10 4 – 5
• Neuron switching time ~ 0.001 second or 10 -3
• Scene recognition time ~ 0.1 second
• 100 inference steps doesn’t seem like enough
• Highly parallel computation based on distributed representation

Properties of Neural Networks
11
• Many neuron-like threshold switching units
• Many weighted interconnections among units
• Highly parallel, distributed process
• Emphasis on tuning weights automatically
• Input is a high-dimensional discrete or real-valued (e.g, sensor input)
What is a threshold unit in neural network?
In neural networks, a threshold is a value that determines
whether the output of a neuron or an activation function is
activated or not. It acts as a decision boundary, where if the
output exceeds the threshold, it is considered as activated or
fired, otherwise it remains inactive.

When to consider Neural Networks ?
12
• Input is a high-dimensional discrete or real-valued (e.g., sensor input)
• Output is discrete or real-valued
• Output is a vector of values
• Possibly noisy data
• Form of target function is unknown
• Human readability of result is unimportant
Examples:
1. Speech phoneme recognition
2. Image classification
3. Financial predition

Different
Activation
Functions
18

NEURAL NETWORK REPRESENTATIONS
19

• A prototypical example of ANN learning is provided by Pomerleau's (1993)
system ALVINN, which uses a learned ANN to steer an autonomous vehicle
driving at normal speeds on public highways.
• The input to the neural network is a 30x32 grid of pixel intensities obtained from
a forward-pointed camera mounted on the vehicle.
• The network output is the direction in which the vehicle is steered.
21

• Figure illustrates the neural network representation.
• The network is shown on the left side of the figure, with the input camera image
depicted below it.
• Each node (i.e., circle) in the network diagram corresponds to the output of a
single network unit, and the lines entering the node from below are its inputs.
• There are four units that receive inputs directly from all of the 30 x 32 pixels in
the image. These are called "hidden" units because their output is available only
within the network and is not available as part of the global network output. Each
of these four hidden units computes a single real-valued output based on a
weighted combination of its 960 inputs
• These hidden unit outputs are then used as inputs to a second layer of 30 "output"
units.
• Each output unit corresponds to a particular steering direction, and the output
values of these units determine which steering direction is recommended most
strongly.
22

• The diagrams on the right side of the figure depict the learned weight values
associated with one of the four hidden units in thisANN.
• The large matrix of black and white boxes on the lower right depicts the weights
from the 30 x 32 pixel inputs into the hidden unit. Here, a white box indicates a
positive weight, a black box a negative weight, and the size of the box indicates
the weight magnitude.
• The smaller rectangular diagram directly above the large matrix shows the
weights from this hidden unit to each of the 30 output units.
23

63
Footage of a Tesla car autonomously driving around along
with the sensing and perception involved.

APPROPRIATE PROBLEMS FOR
NEURAL NETWORK LEARNING
25
ANN is appropriate for problems with the following characteristics :
• Instances are represented by many attribute-value pairs.
• The target function output may be discrete-valued, real-valued, or a vector of
several real- or discrete-valued attributes.
• The training examples may contain errors.
• Long training times are acceptable.
• Fast evaluation of the learned target function may be required
• The ability of humans to understand the learned target function is not important

Architectures of Artificial Neural Networks
26
An artificial neural network can be divided into three parts (layers), which are
known as:
• Input layer: This layer is responsible for receiving information (data), signals,
features, or measurements from the external environment. These inputs are usually
normalized within the limit values produced by activation functions
• Hidden, intermediate, or invisible layers: These layers are composed of neurons
which are responsible for extracting patterns associated with the process or system
being analysed. These layers perform most of the internal processing from a
network.
• Output layer : This layer is also composed of neurons, and thus is responsible for
producing and presenting the final network outputs, which result from the
processing performed by the neurons in the previous layers.

Architectures of Artificial Neural Networks
27
The main architectures of artificial neural networks, considering the neuron
disposition, how they are interconnected and how its layers are composed, can be
divided as follows:
1. Single-layer feedforward network
2. Multi-layer feedforward networks
3. Recurrent or Feedback networks
4. Mesh networks

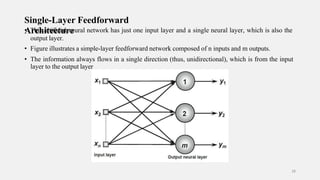
Single-Layer Feedforward
•
AT
rh
cih
s i
at
rt
e
if
c
ic
tiu
alrn
e
eural network has just one input layer and a single neural layer, which is also the
output layer.
• Figure illustrates a simple-layer feedforward network composed of n inputs and m outputs.
• The information always flows in a single direction (thus, unidirectional), which is from the input
layer to the output layer
28

Multi-Layer Feedforward
•
AT
rh
cih
s iatre
tif
c
ic
ti
u
alre
neural feedforward networks with multiple layers are composed of one or more
hidden neural layers.
• Figure shows a feedforward network with multiple layers composed of one input layer with n
sample signals, two hidden neural layers consisting of n1 and n2 neurons respectively, and, finally,
one output neural layer composed of m neurons representing the respective output values of the
problem being analyzed.
29

Recurrent or Feedback
•
AI
r
ncth
heis
teen
c
et
tw
uo
rre
ks, the outputs of the neurons are used as feedback inputs for other neurons.
• Figure illustrates an example of a Perceptron network with feedback, where one of its output
signals is fed back to the middle layer.
30

Mesh Architectures
• The main features of networks with mesh structures reside in considering the spatial arrangement
of neurons for pattern extraction purposes, that is, the spatial localization of the neurons is directly
related to the process of adjusting their synaptic weights and thresholds.
• Figure illustrates an example of the Kohonen network where its neurons are arranged within a two-
dimensional space
31

What is Perceptron?
Perceptron is one of the simplest Artificial neural network architectures. It
was introduced by Frank Rosenblatt in 1957s.
It is the simplest type of feedforward neural network, consisting of a single
layer of input nodes that are fully connected to a layer of output nodes. It
can learn the linearly separable patterns.
it uses slightly different types of artificial neurons known as threshold logic
units (TLU).
32
A perceptron is the simplest type of neural network—
kind of like a tiny brain cell that makes decisions.
•Takes Inputs:
Think of it like getting marks in different subjects:
Math = 90, Science = 80, English = 70
•Multiplies with Weights:
Each input is multiplied by a weight (like giving importance
•Adds a Bias:
A small number added to adjust the output.
•Adds Everything Together:
Total = (Input1 × Weight1) + (Input2 × Weight2) + ... + Bias
•Applies Activation Function:
It decides: “Is the result big enough to say YES (1) or NO (

Types of Perceptron
•Single-Layer Perceptron: This type of perceptron is limited to learning
linearly separable patterns. effective for tasks where the data can be
divided into distinct categories through a straight line.
•Multilayer Perceptron: Multilayer perceptrons possess enhanced
processing capabilities as they consist of two or more layers, adept at
handling more complex patterns and relationships within the data.
Basic Components of Perceptron
A perceptron, the basic unit of a neural network, comprises essential
components that collaborate in information processing.
•Input Features: The perceptron takes multiple input features, each input
feature represents a characteristic or attribute of the input data.
•Weights: Each input feature is associated with a weight, determining the
significance of each input feature in influencing the perceptron’s output.
During training, these weights are adjusted to learn the optimal values.
33

•Summation Function: The perceptron calculates the weighted sum of its inputs using the
summation function. The summation function combines the inputs with their respective
weights to produce a weighted sum.
•Activation Function: The weighted sum is then passed through an activation function.
Perceptron uses Heaviside step function functions. which take the summed values as input
and compare with the threshold and provide the output as 0 or 1.
•Output: The final output of the perceptron, is determined by the activation function’s
result. For example, in binary classification problems, the output might represent a
predicted class (0 or 1).
•Bias: A bias term is often included in the perceptron model. The bias allows the model to
make adjustments that are independent of the input. It is an additional parameter that is
learned during training.
•Learning Algorithm (Weight Update Rule): During training, the perceptron learns by
adjusting its weights and bias based on a learning algorithm or backpropagation. A
common approach is the perceptron learning algorithm, which updates weights based on
the difference between the predicted output and the true output.
34

Bias example?
35
To understand the role of biases, consider a simple example. Imagine a neuron that
processes the brightness of an image pixel . Without a bias, this neuron might only
activate when the pixel's brightness is exactly at a certain threshold.

PERCEPTRONS
• Perceptron is a single layer neural network.
• A perceptron takes a vector of real-valued inputs, calculates a linear combination
of these inputs, then outputs a 1 if the result is greater than some threshold and -1
otherwise
• Given inputs x1 through xn, the output O(x1, . . . , xn) computed by the perceptron
is
• where each wi is a real-valued constant, or weight, that determines the contribution
of input xi to the perceptron output.
• -w0 is a threshold that the weighted combination of inputs w1x1 + . . . + wnxn must
surpass in order for the perceptron to output a 1.
36

Sometimes, the perceptron function is written as,
Learning a perceptron involves choosing values for the weights w0 , . . . , wn .
Therefore, the space H of candidate hypotheses considered in perceptron learning is
the set of all possible real-valued weight vectors
Why do we need Weights and Bias?
Weights shows the strength of the particular node.
A bias value allows you to shift the activation function curve up or down
37

Representational Power of
Perceptrons
*The
viewed
41
perceptron can be
as representing a
hyperplane decision surface
in the n-dimensional space
of instances.
*The perceptron outputs a
1 for instances lying on one
side of the hyperplane and
outputs a -1 for instances
lying on the other side

The Perceptron Training Rule
42
The learning problem is to determine a weight vector that causes the perceptron to
produce the correct + 1 or - 1 output for each of the given training examples.
Tolearn an acceptable weight vector
• Begin with random weights, then iteratively apply the perceptron to each training
example, modifying the perceptron weights whenever it misclassifies an example.
• This process is repeated, iterating through the training examples as many times as
needed until the perceptron classifies all training examples correctly.
• Weights are modified at each step according to the perceptron training rule,
which revises the weight wi associated with input xi according to the rule.

• The role of the learning rate is to moderate the degree to which weights are
changed at each step. It is usually set to some small value (e.g., 0.1) and is
sometimes made to decay as the number of weight-tuning iterations increases
Drawback: The perceptron rule finds a successful weight vector when the training
examples are linearly separable, it can fail to converge if the examples are not
linearly separable.
43

Final perceptron model for AND
49

AND function
Solution 2: If we initialize weights with 0.6 for both W1 and W2 we will get the
solution in single iteration itself. But for better demonstration we should also
show how we change the wights so we considered different weights for W1 and
W2 in solution1
• IfA=0 & B=0 → 0*0.6 + 0*0.6 = 0.
This is not greater than the threshold of 1, so the output = 0.
• IfA=0 & B=1 → 0*0.6 + 1*0.6 = 0.6.
This is not greater than the threshold, so the output = 0.
• IfA=1 & B=0 → 1*0.6 + 0*0.6 = 0.6.
This is not greater than the threshold, so the output = 0.
• IfA=1 & B=1 → 1*0.6 + 1*0.6 = 1.2.
This exceeds the threshold, so the output = 1.
50

Final perceptron model for OR
58

Gradient Descent and the Delta Rule
• If the training examples are not linearly separable, the delta rule converges toward
a best-fit approximation to the target concept.
• The key idea behind the delta rule is to use gradient descent to search the
hypothesis space of possible weight vectors to find the weights that best fit the
training examples.
To understand the delta training rule, consider the task of training an unthresholded
perceptron. That is, a linear unit for which the output O is given by
10
4

To derive a weight learning rule for linear units, specify a
measure for the training error of a hypothesis (weight vector),
relative to the training examples.
Where,
• D is the set of training examples,
• td is the target output for training example d,
• od is the output of the linear unit for training example d
• E [ w ] is simply half the squared difference between the target output td and the linear unit output
od, summed over all training examples.
10
5

MULTILAYER NETWORKS AND THE
BACKPROPAGATION ALGORITHM
12
3
Multilayer networks learned by the BACKPROPACATION algorithm are capable
of expressing a rich variety of nonlinear decision surfaces

• Decision regions of a multilayer feedforward network. The network shown here was trained to recognize 1 of
10 vowel sounds occurring in the context "h_d" (e.g., "had," "hid"). The network input consists of two
parameters, F1 and F2, obtained from a spectral analysis of the sound. The 10 network outputs correspond to
the 10 possible vowel sounds. The network prediction is the output whose value is highest.
• The plot on the right illustrates the highly nonlinear decision surface represented by the learned network.
Points shown on the plot are test examples distinct from the examples used to train the network.
12
4

A Differentiable Threshold Unit
• Sigmoid unit-a unit very much like a perceptron, but based on a smoothed,
differentiable threshold function.
• The sigmoid unit first computes a linear combination of its inputs, then applies a
threshold to the result. In the case of the sigmoid unit, however, the threshold
output is a continuous function of its input.
• More precisely, the sigmoid unit computes its output O as
σ is the sigmoid function
12
5

The BACKPROPAGATION Algorithm
• The BACKPROPAGATION Algorithm learns the weights for a multilayer network, given a
network with a fixed set of units and interconnections. It employs gradient descent to attempt to
minimize the squared error between the network output values and the target values for these
outputs.
• In BACKPROPAGATION algorithm, we consider networks with multiple output units rather than
single units as before, so we redefine E to sum the errors over all of the network output units.
where,
• outputs - is the set of output units in the network
• tkd and Okd - the target and output values associated with the kth output unit
• d - training example
12
7

Stage 1: Forward Pass (Initial)

Final Output After One Update: y=0.6820

Artificial Neural Networks: Introduction, Neural Network representation, Appropriate problems, Perceptron- Perceptron Training rule, Back propagation algorithm.

Recommended

More Related Content

Similar to Artificial Neural Networks: Introduction, Neural Network representation, Appropriate problems, Perceptron- Perceptron Training rule, Back propagation algorithm. (20)

More from BMS Institute of Technology and Management (15)

Recently uploaded (20)

Artificial Neural Networks: Introduction, Neural Network representation, Appropriate problems, Perceptron- Perceptron Training rule, Back propagation algorithm.