Assignment on Numerical Method C Code

Assignment on Numerical Methods Assignment topic: C code using numerical methods Course Code: CSE 234 Fall-2014
Submitted To: Md. Jashim Uddin Assistant Professor Dept. of Natural Sciences Dept. of Computer Science & Engineering Faculty of Science & Information Technology
Submitted by:
Name: Syed Ahmed Zaki
Name: Fatema Khatun
Name: Sumi Basak
Name: Priangka Kirtania
Name: Afruza Zinnurain
ID:131-15-2169
ID:131-15-2372
ID:131-15-2364
ID:131-15-2385
ID:131-15-2345
Sec: B Dept. of CSE,FSIT
Date of submission: 12 , December 2014

Contents:
Root Finding Method Page Bisection Method 2 Newton-Raphson Method 4 Interpolation Newton Forward Interpolation 5 Newton Backward Interpolation 7 Lagrange Method 8
Numerical Integration
Trapezoidal Rule 10 Simpson’s 1/3 Rule 12 Simpson’s 3/8 Rule 13 Weddle’s Rule 14
Ordinary Differential Equations
Euler Method 17 Runge-Kutta 4th order method 18
Linear System Gauss Seidel Method 20
1

Bisection Method: The Bisection Method is a numerical method for estimating the roots of a polynomial f(x). It is one of the simplest and most reliable but it is not the fastest method.
Problem: Here we have to find root for the polynomial x^3+x^2-1
Algorithm:
1. Start
2. Read a1, b1, TOL *Here a1 and b1 are initial guesses TOL is the absolute error or tolerance i.e. the desired degree of accuracy*
3. Compute: f1 = f(a1) and f3 = f(b1)
4. If (f1*f3) > 0, then display initial guesses are wrong and goto step 11 Otherwise continue.
5. root = (a1 + b1)/2
6. If [ (a1 – b1)/root ] < TOL , then display root and goto step 11 * Here [ ] refers to the modulus sign. * or f(root)=0 then display root
7. Else, f2 = f(root)
8. If (f1*f2) < 0, then b1=root
9. Else if (f2*f3)<0 then a1=root
10. else goto step 5 *Now the loop continues with new values.*
11. Stop
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<stdio.h>
#include<math.h>
#define f(y) (pow(x,3)+x*x-1);
int main()
{
double a,b,m=-1,x,y;
int n=0,k,i;
printf("Enter the value of a: ");
scanf("%lf",&a);
printf("Enter the value of b: ");
scanf("%lf",&b);
printf("How many itteration you want: ");
scanf("%d",&k);
printf("n n a b xn=a+b/2 sign of(xn)n");
printf("-------------------------------------------------------------n");
for(i=1;i<=k;i++)
{
x=(a+b)/2;
y=f(x);
2

20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
if(m==x)
{
break;
}
i f(y>=0)
{
printf(" %d %.5lf %.5lf %.5lf +n",i,a,b,x);
b=x;
}
else if(y<0)
{
printf(" %d %.5lf %.5lf %.5lf -n",i,a,b,x);
a=x;
}
m=x;
}
printf("nThe approximation to the root is %.4lf which is upto 4D",b);
return 0;
}
Output:
3

Newton – Raphson Method:
Problem: Here we have to find root for the polynomial x^3-8*x-4 upto 6D(decimal places)
Solution in C:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<stdio.h>
#include<math.h>
#define f(x) pow(a,3)-8*a-4;
#define fd(x) 3*pow(a,2)-8;
int main()
{
double a,b,c,d,h,k,x,y;
int i,j,m,n;
printf("Enter the value of xn: ");
scanf("%lf",&a);
printf("Enter itteration number: ");
scanf("%d",&n);
printf(" xn f(x) f'(x) hn=-f(x)/f'(xn) xn+1=xn+hn");
printf("-----------------------------------------------------------------------------------------n");
for(i=1;i<=n;i++)
{
x=f(a);
y=fd(x);
h=-(x/y);
k=h+a;
printf(" %.7lf %.7lf %.7lf %.7lf %.7lfn",a,x,y,h,k);
a=k;
}
printf("nThe approximation to the root is %.6lf which is upto 6D",k);
return 0;
}
4

Output:
Newton Forward Interpolation: Problem: The population of a town is given below as thousands Year : 1891 1901 1911 1921 1931 Population : 46 66 81 93 101
Find the population of 1895 ?
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
main()
{
float x[20],y[20],f,s,h,d,p;
int j,i,n;
printf("enter the value of n :");
scanf("%d",&n);
printf("enter the elements of x:");
for(i=1;i<=n;i++)
{
scanf("n%f",&x[i]);
}
printf("enter the elements of y:");
for(i=1;i<=n;i++)
{
5

18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
scanf("n%f",&y[i]);
}
h=x[2]-x[1];
printf("Enter the value of f(to findout value):");
scanf("%f",&f);
s=(f-x[1])/h;
p=1;
d=y[1];
for(i=1;i<=(n-1);i++)
{
for(j=1;j<=(n-i);j++)
{
y[j]=y[j+1]-y[j];
}
p=p*(s-i+1)/i;
d=d+p*y[1];
}
printf("For the value of x=%6.5f THe value is %6.5f",f,d);
getch();
}
Output:
6

Newton Backward Interpolation: Problem: The population of a town is given below as thousands Year : 1891 1901 1911 1921 1931 Population : 46 66 81 93 101
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
main()
{
float x[20],y[20],f,s,d,h,p;
int j,i,k,n;
printf("enter the value of the elements :");
scanf("%d",&n);
printf("enter the value of x:n");
for(i=1;i<=n;i++)
{
scanf("%f",&x[i]);
}
printf("enter the value of y:n");
for(i=1;i<=n;i++)
{
scanf("%f",&y[i]);
}
h=x[2]-x[1];
printf("enter the searching point f:");
scanf("%f",&f);
s=(f-x[n])/h;
d=y[n];
p=1;
for(i=n,k=1;i>=1,k<n;i--,k++)
{
for(j=n;j>=1;j--)
{
y[j]=y[j]-y[j-1];
}
p=p*(s+k-1)/k;
d=d+p*y[n];
}
printf("for f=%f ,ans is=%f",f,d);
getch();
}
7

Output:
Lagrange Method: Problem: The population of a town is given below as thousands Year : 1891 1901 1911 1921 1931 Population : 46 66 81 93 101
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<stdio.h>
#include<math.h>
int main()
{
float x[10],y[10],temp=1,f[10],sum,p;
int i,n,j,k=0,c;
printf("nhow many record you will be enter: ");
scanf("%d",&n);
for(i=0; i<n; i++)
{
printf("nnenter the value of x%d: ",i);
scanf("%f",&x[i]);
printf("nnenter the value of f(x%d): ",i);
scanf("%f",&y[i]);
}
printf("nnEnter X for finding f(x): ");
scanf("%f",&p);
for(i=0;i<n;i++)
{
temp = 1;
8

23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
k = i;
for(j=0;j<n;j++)
{
if(k==j)
{
continue;
}
else
{
temp = temp * ((p-x[j])/(x[k]-x[j]));
}
}
f[i]=y[i]*temp;
}
for(i=0;i<n;i++)
{
sum = sum + f[i];
}
printf("nn f(%.1f) = %f ",p,sum);
getch();
}
9

Output:
Trapezoidal Rule: Problem: Here we have to find integration for the (1/1+x*x)dx with lower limit =0 to upper limit = 6
Algorithm:
Step 1: input a,b,number of interval n
Step 2:h=(b-a)/n
Step 3:sum=f(a)+f(b)
Step 4:If n=1,2,3,……i
Then , sum=sum+2*y(a+i*h)
Step 5:Display output=sum *h/2
Code:
10

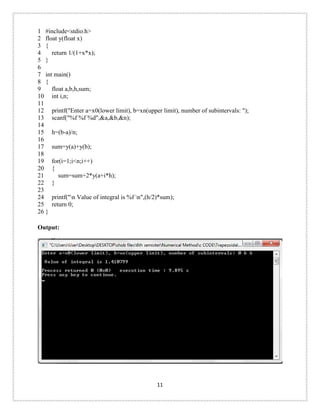
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<stdio.h>
float y(float x)
{
return 1/(1+x*x);
}
int main()
{
float a,b,h,sum;
int i,n;
printf("Enter a=x0(lower limit), b=xn(upper limit), number of subintervals: ");
scanf("%f %f %d",&a,&b,&n);
h=(b-a)/n;
sum=y(a)+y(b);
for(i=1;i<n;i++)
{
sum=sum+2*y(a+i*h);
}
printf("n Value of integral is %f n",(h/2)*sum);
return 0;
}
Output:
11

Simpson’s 1/3 rule:
Problem: Here we have to find integration for the (1/1+x*x)dx with lower limit =0 to upper limit = 6
Algorithm:
Step 2:h=(b-a)/n
Step 3:sum=f(a)+f(b)+4*f(a+h)
Step 4:sum=sum+4*f(a+i*h)+2*f(a+(i-1)*h)
Step 5:Display output=sum * h/3
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<stdio.h>
float y(float x){
return 1/(1+x*x);
}
int main(){
float a,b,h,sum;
int i,n;
scanf("%f%f%d",&a,&b,&n);
h = (b - a)/n;
sum = y(a)+y(b)+4*y(a+h);
for(i = 3; i<=n-1; i=i+2){
sum=sum+4*y(a+i*h) + 2*y(a+(i-1)*h);
}
printf("n Value of integral is %fn",(h/3)*sum);
return 0;
}
12

Output:
Simpson’s 3/8 rule: Problem: Here we have to find integration for the (1/1+x*x)dx with lower limit =0 to upper limit = 6
Algorithm:
Step 2:h=(b-a)/n
Step 3:sum=f(a)+f(b)
Step 4:If n is odd
Then , sum=sum+2*y(a+i*h)
Step 5: else, When n I s even Then, Sum = sum+3*y(a+i*h)
Step 6:Display output=sum *3* h/8
Code:
1
2
3
4
5
#include<stdio.h>
float y(float x){
return 1/(1+x*x); //function of which integration is to be calculated
}
int main(){
13

6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
float a,b,h,sum;
int i,n,j;
sum=0;
h = (b-a)/n;
sum = y(a)+y(b);
for(i=1;i<n;i++)
{
if(i%3==0){
sum=sum+2*y(a+i*h);
}
else{
sum=sum+3*y(a+i*h);
}
}
printf("Value of integral is %fn", (3*h/8)*sum);
}
Output:
Weddle’s Rule: Problem: Here we have to find integration for the (1/1+x*x)dx with lower limit =0 to upper limit = 6
Algorithm:
Step 2:h=(b-a)/n
Step 3:If(n%6==0)
14

Then , sum=sum+((3*h/10)*(y(a)+y(a+2*h)+5*y(a+h)+6*y(a+3*h)+y(a+4*h)+5*y(a+5*h)+y(a+6*h))) ; a=a+6*h and Weddle’s rule is applicable then go to step 6
Step 4: else, Weddle’s rule is not applicable
Step 5:Display output
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<stdio.h>
float y(float x){
return 1/(1+x*x); //function of which integration is to be calculated
}
int main(){
float a,b,h,sum;
int i,n,m;
h = (b-a)/n;
sum=0;
if(n%6==0){
sum=sum+((3*h/10)*(y(a)+y(a+2*h)+5*y(a+h)+6*=a+6*h;
printf("Value of integral is %fn", sum);
}
else{
printf("Sorry ! Weddle rule is not applicable");
}
}
15

Output:
Euler Method: Problem: Here we have to find dy/dx=x+y where y(0)=1 at the point x=0.05 and x=0.10 taking h=0.05
Algorithm:
1. Start
2. Define function
3. Get the values of x0, y0, h and xn *Here x0 and y0 are the initial conditions h is the interval xn is the required value
4. n = (xn – x0)/h + 1
5. Start loop from i=1 to n
6. y = y0 + h*f(x0,y0) x = x + h
7. Print values of y0 and x0
8. Check if x < xn If yes, assign x0 = x and y0 = y If no, goto 9.
9. End loop i
10. Stop
16

Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<stdio.h>
float fun(float x,float y)
{
float f;
f=x+y;
return f;
}
main()
{
float a,b,x,y,h,t,k;
printf("nEnter x0,y0,h,xn: ");
scanf("%f%f%f%f",&a,&b,&h,&t);
x=a;
y=b;
printf("n xt yn");
while(x<=t)
{
k=h*fun(x,y);
y=y+k;
x=x+h;
printf("%0.3ft %0.3fn",x,y);
}
}
Output:
17

Runge-Kutta 4th order method:
Problem: Here we have to find y(0,2) and y(0,4), Given dy/dx=1+y^2 where y=0 when x=0
Algorithm:
Step 1: input x0,y0,h,last point n
Step 2:m1=f(xi,yi)
Step 3:m2=f(xi+h/2,yi+m1h/2)
Step 4:m3=f(xi+h/2,yi+m2h/2)
Step 5:m4=f(xi+h,yi+m3h)
Step 6:yi+1=yi+(m1+2m2+2m3+m4/6)h
Step 5:Display output
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<stdio.h>
#include <math.h>
#include<conio.h>
#define F(x,y) 1 + (y)*(y)
void main()
{
double y0,x0,y1,n,h,f,k1,k2,k3,k4;
system("cls");
printf("nEnter the value of x0: ");
scanf("%lf",&x0);
printf("nEnter the value of y0: ");
scanf("%lf",&y0);
printf("nEnter the value of h: ");
scanf("%lf",&h);
printf("nEnter the value of last point: ");
scanf("%lf",&n);
for(; x0<n; x0=x0+h)
{
f=F(x0,y0);
k1 = h * f;
f = F(x0+h/2,y0+k1/2);
k2 = h * f;
f = F(x0+h/2,y0+k2/2);
k3 = h * f;
f = F(x0+h/2,y0+k2/2);
k4 = h * f;
18

27
28
29
30
31
32
33
34
35
36
y1 = y0 + ( k1 + 2*k2 + 2*k3 + k4)/6;
printf("nn k1 = %.4lf ",k1);
printf("nn y(%.4lf) = %.3lf ",x0+h,y1);
y0=y1;
}
getch();
}
Output:
Gauss Seidel Method
Problem: Solve the following systems using gauss seidel method 5×1-x2-x3-x4=-4 -x1+10×2-x3-x4=12 -x1-x2+5×3-x4=8 -x1-x2-x3+10×4=34
Code:
1
2
3
#include<stdio.h>
#include<conio.h>
#include<math.h>
19

4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#define acc 0.0001
#define X1(x2,x3,x4) ((x2 + x3 + x4 -4)/5)
#define X2(x1,x3,x4) ((x1 + x3 + x4 +12)/10)
#define X3(x1,x2,x4) ((x1 + x2 + x4 +8)/5)
#define X4(x1,x2,x3) ((x1 + x2 + x3 +34)/10)
void main()
{
double x1=0,x2=0,x3=0,x4=0,y1,y2,y3,y4;
int i=0;
system("cls");
printf("n______________________________________________________________n");
printf("n x1tt x2tt x3tt x4n");
printf("n______________________________________________________________n");
printf("n%ft%ft%ft%f",x1,x2,x3,x4);
do
{
y1=X1(x2,x3,x4);
y2=X2(x1,x3,x4);
y3=X3(x1,x2,x4);
y4=X4(x1,x2,x3);
if(fabs(y1-x1)<acc && fabs(y2-x2)<acc && fabs(y3-x3)<acc &&fabs(y4-x4) )
{
printf("n_____________________________________________________________n");
printf("nnx1 = %.3lf",y1);
printf("nnx4= %.3lf",y4);
i = 1;
}
e lse
{
x1 = y1;
x2 = y2;
x3 = y3;
x4 = y4;
printf("n%ft%ft%ft%f",x1,x2,x3,x4);
}
}while(i != 1);
getch();
}
20

Assignment on Numerical Method C Code

More Related Content

What's hot (20)

Viewers also liked (18)

Similar to Assignment on Numerical Method C Code (20)

More from Syed Ahmed Zaki (9)

Recently uploaded (20)

Assignment on Numerical Method C Code