Assignment problems

Assignment Problems
Please note that in this presentation tables with grey background show tables in the previous step for reference

Assignment Problem
•An assignment problem is a special type of transportation problem in which the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximise total profit.
•Resources such as men, machines have varying degree of efficiency for performing different activities such as job

Example A1
•A department has five employees with five jobs to be performed. The time (in hours) each men will take to perform each job is given in the effectiveness matrix.
•How should the jobs be allocated, one per employee so as to minimise total number of manhours required to complete the job
Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
10
5
13
15
16
Job2
3
9
18
13
6
Job3
10
7
2
2
2
Job4
7
11
9
7
12
Job5
7
9
10
4
12

Mathematical model of Assignment Problem
•The assignment problem is a variation of the transportation problem with two characteristics
–The cost matrix is a square matrix
–The optimal solution would always be such that there would be only one assignment in a given row or column of the cost matrix
•If cij is the cost of assignment of resource i to activity j, then assignment problem is to find
  otherwise 0, resource jth toassigned isactivity ith if ,1ijX


 

n
i
n
j
ij ij Z C X
1 1
X i n
n
j
ij 1 1,2,3...,
1
  

X j n
m
i
ij 1 1,2,3...,
1
  

X 0or1 ij 
LPP model for the assignment problem is given as:
Minimize
Subject to

Hungarian Method
•Developed by Hungarian mathematician D Konig
•In this method, opportunity cost is found and allocation is done to the
Steps in Hungarian Method
•Step1 Develop cost table from the given problem (If number of row and columns are not equal, then a dummy row or column must be added. The costs for dummy cells are zero.

•Step 2: Find the opportunity cost table
–Locate smallest element in each row of the given cost table and then subtract that from each element of that row, and
–In the reduced matrix obtained from previous step, locate smallest element in each column and then subtract that from each element of that column. Each row /column now have atleast one zero value.

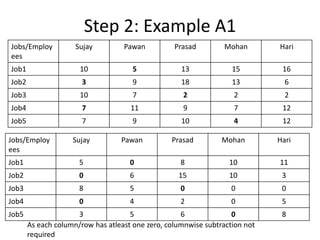
Step 2: Example A1
Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
10
5
13
15
16
Job2
3
9
18
13
6
Job3
10
7
2
2
2
Job4
7
11
9
7
12
Job5
7
9
10
4
12
Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
5
0
8
10
11
Job2
0
6
15
10
3
Job3
8
5
0
0
0
Job4
0
4
2
0
5
Job5
3
5
6
0
8
As each column/row has atleast one zero, columnwise subtraction not required

Step3
•Make assignments in the opportunity cost matrix
–Examine rows until a row with exactly one unmarked zero is obtained. Make an assignment to this single zero by marking a square around it
–For each zero that becomes assigned, strike off other zeroes in the same row/column
–Repeat the above steps for each column with exactly single zero cell
–If a row/column has two or more unmarked zeros and one cannot be chosen by inspection, then choose the assigned zero arbitrarily.
–Continue this process until all zeros in rows are assigned or struck off

Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
5
0
8
10
11
Job2
0
6
15
10
3
Job3
8
5
0
0
0
Job4
0
4
2
0
5
Job5
3
5
6
0
8
Step 3: Example A1

Step 4
•If the number of assigned cells is equal to the number of rows or columns then the solution is optimal. The total cost associated with this solution is obtained by adding original cost figures in occupied cells.
•If zero cell was chosen arbitrarily, then there exists alternative solution
•If optimal solution is not found that proceed to step 5

Step 5
•Revise the opportunity cost table by the following procedure
–For each row in which no assignment is made, mark a tick ( )
–Examine the marked rows. If any zero cell occurs in those rows, mark a ( ) to the respective columns that contain those zeroes.
–Examine marked columns. If any assigned zero occurs in these columns, then tick the respective rows that contain those zeroes
–Repeat this process until no more rows and columns can be marked
–Draw a straight line through each marked column and each unmarked row.
–If the number of lines drawn (or total assignments) is equal to the number of rows or columns then the current solution is optimal, otherwise go to step 6.

Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
5
0
8
10
11
Job2
0
6
15
10
3
Job3
8
5
0
0
0
Job4
0
4
2
0
5
Job5
3
5
6
0
8

Step 6 &7
•Step 6:
–From cells not covered by any line, choose the smallest element. Call this value k.
–Subtract k from every element in the cell not covered by a line.
–Add k to every element in the cell covered by the two lines, i.e intersection of two lines.
–Element in cells covered by one line remains unchanged
•Step 7: Repeat Steps 3 to 6 until an optimal solution is obtained.

Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
5
0
8
10
11
Job2
0
6
15
10
3
Job3
8
5
0
0
0
Job4
0
4
2
0
5
Job5
3
5
6
0
8
K=2
Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
7
0
8
12
11
Job2
0
4
13
10
1
Job3
10
5
0
2
0
Job4
0
2
0
0
3
Job5
3
3
4
0
6

Jobs/Employees
Sujay
Pawan
Prasad
Mohan
Hari
Job1
7
0
8
12
11
Job2
0
4
13
10
1
Job3
10
5
0
2
0
Job4
0
2
0
0
3
Job5
3
3
4
0
6
Job
Job1
Job2
Job3
Job4
Job5
Employee
Pawan
Sujay
Hari
Prasad
Mohan
Time
5
3
2
9
4
Solution of job allocation is as below. Total time: 23 man hours

Example A2 A machine tool company decides to make four subassemblies through four contractors. Each contractor is to receive only one subassembly. The cost of each subassembly is determined by the bids submitted by each contractor and is as shown in the table below (in thousands of rupees). Assign different assemblies to contractors so as to minimize the total cost.
Sub-assemblyContractor
A
B
C
D
1
15
13
14
17
2
11
12
15
13
3
18
12
10
11
4
15
17
14
16

Sub- assemblyContractor
A
B
C
D
1
2
0
1
4
2
0
1
4
2
3
8
2
0
1
4
1
3
0
2
Sub-assemblyContractor
A
B
C
D
1
2
0
1
3
2
0
1
4
1
3
8
2
0
0
4
1
3
0
1
Sub-assembly
Contractor
A
B
C
D
1
15
13
14
17
2
11
12
15
13
3
18
12
10
11
4
15
17
14
16

Example A3: Multiple solution example Five jobs are to be done on five different machines. The cost of producing ith job on the jth machine is given below. Assign the job to different machine so as to minimize the total cost.
JobMachines
A
B
C
D
E
1
9
3
1
13
1
2
1
17
13
20
5
3
0
14
8
11
4
4
19
3
0
5
5
5
12
8
1
6
2

JobMachines
A
B
C
D
E
1
8
2
0
12
0
2
0
16
12
19
4
3
0
14
8
11
4
4
19
3
0
5
5
5
11
7
0
5
1
JobMachines
A
B
C
D
E
1
8
0
0
7
0
2
0
14
12
14
4
3
0
12
8
6
4
4
19
1
0
0
5
5
11
5
0
0
1
Subtracting smallest number from each row, we get the following table (shaded is old table)
JobMachines
A
B
C
D
E
1
9
3
1
13
1
2
1
17
13
20
5
3
0
14
8
11
4
4
19
3
0
5
5
5
12
8
1
6
2
Column B and D does not have any zero, therefore we subtract smallest element from these columns, remaining columns are retained. Assignments are made

JobMachines
A
B
C
D
E
1
8
0
0
7
0
2
0
14
12
14
4
3
0
12
8
6
4
4
19
1
0
0
5
5
11
5
0
0
1
For each row in which no assignment is made, mark a tick ( row 3 ) Examine the marked rows. If any zero cell occurs in those rows, mark to the respective columns that contain those zeroes. (column A) Examine marked columns. If any assigned zero occurs in these columns, then tick the respective rows that contain those zeroes (Row 2) Repeat this process until no more rows and columns can be marked Draw a straight line through each marked column and each unmarked row. (column A, ROW 1,4,5)
The above solution is not optimal as only four lines are there

Among the uncovered elements, 4 is the minimum. Subtract 4 from all the uncovered elements and add the same to elements correspond to intersection of lines. We get the following matrix:
JobMachines
A
B
C
D
E
1
12
0
0
7
0
2
0
10
8
10
0
3
0
8
4
2
0
4
23
1
0
0
5
5
15
5
0
0
1
JobMachines
A
B
C
D
E
1
8
0
0
7
0
2
0
14
12
14
4
3
0
12
8
6
4
4
19
1
0
0
5
5
11
5
0
0
1

:
JobMachines
A
B
C
D
E
1
12
0
0
7
0
2
0
10
8
10
0
3
0
8
4
2
0
4
23
1
0
0
5
5
15
5
0
0
1
JobMachines
A
B
C
D
E
1
12
0
0
7
0
2
0
10
8
10
0
3
0
8
4
2
0
4
23
1
0
0
5
5
15
5
0
0
1
In the table, job 2 and job 3 have zeroes at common locations for employee A and E. Therefore two alternative solutions are possible. Similarly two more alternative solutions are possible with the job 4 and 5. Alternative solutions are shown below
JobMachines
A
B
C
D
E
1
12
0
0
7
0
2
0
10
8
10
0
3
0
8
4
2
0
4
23
1
0
0
5
5
15
5
0
0
1
Alternative 1
Alternative 2

JobMachines
A
B
C
D
E
1
12
0
0
7
0
2
0
10
8
10
0
3
0
8
4
2
0
4
23
1
0
0
5
5
15
5
0
0
1
Alternative 3 and 4 are presented. All the alternative solutions are optimal as number of allocations are equal to 5
JobMachines
A
B
C
D
E
1
12
0
0
7
0
2
0
10
8
10
0
3
0
8
4
2
0
4
23
1
0
0
5
5
15
5
0
0
1
Alternative 3
Alternative 4

Example A4: Unbalanced Assignment Problem A city corporation has decided to carry out road repairs on main four arteries of the city. The government has agreed to make a special grant of Rs. 50 lakh towards the cost with a condition that the repairs be done at the lowest cost and quickest time. If the conditions warrant, a supplementary token grant will also be considered faviurably. The corporation has floated tenders and five contractors have sent in their bids. In order to expedite work only one road will be awarded to only one contractor. Find the best way of assigning repair work to the contractors and the costs. If I is necessary to seek supplementary grants, what should be the amount sought? Which of the five contractors will be unsuccessful in his bid?
R1
R2
R3
R4
C1
9
14
19
15
C2
7
17
20
19
C3
9
18
21
18
C4
10
12
18
19
C5
10
15
21
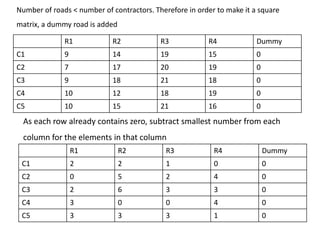
16

Number of roads < number of contractors. Therefore in order to make it a square matrix, a dummy road is added
R1
R2
R3
R4
Dummy
C1
9
14
19
15
0
C2
7
17
20
19
0
C3
9
18
21
18
0
C4
10
12
18
19
0
C5
10
15
21
16
0
R1
R2
R3
R4
Dummy
C1
2
2
1
0
0
C2
0
5
2
4
0
C3
2
6
3
3
0
C4
3
0
0
4
0
C5
3
3
3
1
0
As each row already contains zero, subtract smallest number from each column for the elements in that column

Examine row and do allocation for rows/columns having one zeros. Strike off other zeroes. As there are only four allocations, this solution is not optimal
R1
R2
R3
R4
Dummy
C1
2
2
1
0
0
C2
0
5
2
4
0
C3
2
6
3
3
0
C4
3
0
0
4
0
C5
3
3
3
1
0
R1
R2
R3
R4
Dummy
C1
2
2
1
0
0
C2
0
5
2
4
0
C3
2
6
3
3
0
C4
3
0
0
4
0
C5
3
3
3
1
0

R1
R2
R3
R4
Dummy
C1
2
2
1
0
1
C2
0
5
2
4
1
C3
1
5
2
2
0
C4
3
0
0
4
1
C5
2
2
2
0
0
Among the remaining cells, 1 is the least, Subtract from the cells that are not covered by line (Row c3, c5). Add it to cells in intersection of lines. Other remain same. Reallocation is done. This is not optimal as well
R1
R2
R3
R4
Dummy
C1
2
2
1
0
0
C2
0
5
2
4
0
C3
2
6
3
3
0
C4
3
0
0
4
0
C5
3
3
3
1
0

R1
R2
R3
R4
Dummy
C1
2
2
1
0
1
C2
0
5
2
4
1
C3
1
5
2
2
0
C4
3
0
0
4
1
C5
2
2
2
0
0
Lines are drawn based on the rules. Minimum value is k=1. Subtract 1 from cells that are not covered and add to cells that are at intersection. Resultant table is the second table shown. The allocations are done.
R1
R2
R3
R4
Dummy
C1
1
1
0
0
1
C2
0
5
2
5
2
C3
0
4
1
2
0
C4
3
0
0
5
2
C5
1
1
1
0
0
This solution is optimal as number allocations is 5. Total Cost= 19+7+12+16=54

Find the best way of assigning repair work to the contractors and the costs.
Assignment schedule
If It is necessary to seek supplementary grants, what should be the amount sought?
54-50= 4 lakh rupees
Which of the five contractors will be unsuccessful in his bid?
Contractor 3
Road1
Road2
Road3
Road4
C2
C4
C1
C5

Assignment Problem with maximisation objective
•In the assignment problem,
If the objective is to maximize profit instead minimizing the cost
•Modify the cost matrix by taking maximum of all cost element and
•Replace the all the cost element by the difference between the maximum and the present element.
•Continue with the Hungarian method explained above for the assignment.
•Use the given cost matrix to find the optimal value.

Example A5:
A company has four factories (F1, F2, F3, F4) each of which can produce four products A, B,C,D.
The sales revenue and production cost of the factories differ from one plant to another and is given for the four products (in thousands).
The company wants to determine which product should be manufactured in each factory in order to maximise profit.

Sales Revenue in Factories
Product
F1
F2
F3
F4
A
50
68
49
62
B
60
70
51
74
C
55
67
53
70
D
58
65
54
68
Production cost in Factories
Product
F1
F2
F3
F4
A
49
60
45
61
B
55
63
45
49
C
52
62
49
68
D
55
64
48
66
Profit= Revenue-Cost, Objective:Maximise Profit
Profit in Factories
Product
F1
F2
F3
F4
A
1
8
4
1
B
5
7
6
25
C
3
5
4
2
D
3
1
6
2
The above maximisation problem can be converted into minimisation problem before applying Hungarian method. To convert, identify largest number in the table (25) and subtract every number from 25 to get the new table

Factories
Product
F1
F2
F3
F4
A
24
17
21
24
B
20
18
19
0
C
22
20
21
23
D
22
24
19
23
This converted table is minimisation type and can be solved using usual method.
Factories
Product
F1
F2
F3
F4
A
7
0
4
7
B
20
18
19
0
C
2
0
1
3
D
3
5
0
4
Factories
Product
F1
F2
F3
F4
A
5
0
4
7
B
8
18
19
0
C
0
0
1
3
D
1
5
0
4
Subtract every row with its smallest no.
Subtract every column with its smallest no. Do allocations. The solution obtained is optimal

Solution
The product A- Factory 2
Product B- Factory 4
Product C- Factory 1
Product D- Factory 3
Total Profit = 8+3+6+25 (in thousand)= 42000

Assignment problems

Recommended

More Related Content

What's hot (20)

Similar to Assignment problems (20)

Assignment problems