Basics of Digital Filters

Basics of Digital Filters

Elena Punskaya
www-sigproc.eng.cam.ac.uk/~op205

Some material adapted from courses by
Prof. Simon Godsill, Dr. Arnaud Doucet,
Dr. Malcolm Macleod and Prof. Peter Rayner

1

What is a Digital Filter?

Digital Filter: numerical procedure or algorithm that
transforms a given sequence of numbers
into a second sequence that has some
more desirable properties.

Input sequence Output sequence
xn Digital Filter yn

2

Desired features

Desired features depend on the application, for example

Input Signal Output

generated by sensing having less noise or
device (microphone) interferences

speech with reduced
redundancy for more
efficient transmission

3

Examples of filtering operations

Noise suppression

•  received radio signals

•  signals received by image sensors (TV,
infrared imaging devices)

•  electrical signals measured from human
body (brain heart, neurological signals)

•  signals recorded on analog media such
as analog magnetic tapes
4


Enhancement of selected frequency ranges

•  treble and bass control or graphic equalizers
increase sound level and high and low level frequencies
to compensate for the lower sensitivity of the ear at
those frequencies or for special sound effects

•  enhancement of edges in images

improve recognition of object (by human or computer)

edge – a sharp transition in the image brightness, sharp
transitions in a signal (from Fourier theory) appear as
high-frequency components which can be amplified
5


Bandwidth limiting

•  means of aliasing prevention in
sampling

•  communication
radio or TV signal transmitted over
specific channel has to have a limited
bandwidth to prevent interference with
neighbouring channels

frequency components outside the
permitted band are attenuated below
a specific power level
6


Specific operations

•  differentiation
•  integration
•  Hilbert transform

These operations can be
approximated by digital filters
operating on the sampled input
signal

7

Linear time-invariant (LTI) digital filters.

We limit ourselves to LTI digital filters only.

Time-invariant:
xn LTI yn xn-k LTI yn-k

Linear: defined by the principle of linear superposition

xn1 LTI yn1 xn2 LTI yn2 scaling &
additivity
properties
a1xn1+ a2xn2 LTI a1yn1+ a2yn2

If linear system's parameters are constant
it is Linear Time Invariant 8

Analysis

We analyse DSP algorithms by determining:
•  their time-domain characteristics
–  linear difference equations
–  filter’s unit-sample (impulse) response

•  their frequency-domain characteristics
–  more general, Z-transform domain
•  system transfer function
•  poles and zeros diagram in the z-plane
–  Fourier domain
•  frequency response
•  spectrum of the signal
9

First method in time domain: Linear difference equations

The linear time-invariant digital filter can then be
described by the linear difference equation:

where {ak} and {bk} real

The order of the filter is the larger of M or N

10

Elements of a Digital Filter – Adders and Multipliers

Adders:

x1n + yn=x1n+x2n
x2n
Multipliers:
a
xn yn=axn
x alternative for multiplier

Simple components implemented in the
arithmetic logic unit of the computer
11

Elements of a Digital Filter – Delays

Positive delay (“delay”): stores the current value
for one sample interval

xn Z-1 yn= xn-1
alternative for delay

Negative delay (“advance”): allows to look ahead,
e.g. image processing

xn Z yn= xn+1

Components that allow access to future and
past values in the sequence
12

Example: three-sample averager

Three-sample averager: yn=(xn+1+ xn + xn-1)/3

Z

1/3
xn + yn

Order: Z-1
number of second-order filter
delays &
advances
needed to Nonrecursive filter – output is a
function of only the input sequence
implement
13

Example: first-order recursive filter

First-order recursive filter: yn=ayn-1+ xn

xn + yn
Z-1
a
one delay
Example of feedback first-order
implemented in a
digital filter

Recursive filter – output is also a
function of the previous output
14

Full set of possible linear operations

The operations shown in the slides above are
the full set of possible linear operations:

•  constant delays (by any number of
samples)
•  addition or subtraction of signal paths
•  multiplication (scaling) of signal paths by
constants - (including -1)

Any other operations make the system non-
linear.
15

Linear difference equations and digital filter structure

•  Useful for implementing digital filter
structures

slightly alternative
representation
16

Second method in time domain: unit-sample response

•  Input signal is resolved into a weighted sum of elementary
signal components, i.e. sum of unit samples or impulses
∞
xn= xk δn-k
k=- ∞
•  The response of the system to the unit sample sequence
is determined
δn LTI hn

•  Taking into account properties of the LTI system, the
response of the system to xn is the corresponding sum of
weighted outputs
∞ ∞
xn= xk δn-k LTI yn= xk hn-k
k=- ∞ k=- ∞ 17

Linear convolution

Linear convolution
∞
yn= xk hn-k
k=- ∞

gives the response of the LTI system as a
function of the input signal and the unit
sample (impulse) response

LTI is completely characterized by hn

18

Causal LTI system

Causal system: output at time n depends only on
present and past inputs but not on future

Impulse response:
hn = 0 for n <0

Thus
∞ ∞
Yn = xk hn-k = hk xn-k
k=- ∞ k=0

19

Essentials of the z-transform

For convenience we will use this
For a discrete time signal notation (x(n)) for discrete signal
as well as xn from now on

where is a complex variable

For causal signals is well defined for

20

Essentials of the z-transform - convolution

Convolution

admits a z-transform satisfying
where

Indeed,

21

Transfer function of LTI

Linear difference equation

Now, take z-transforms term by term

Rearranging, transfer function of the filter is

22

FIR and IIR filters

Transfer function of the filter is

Finite Impulse Response (FIR) Filters:
N = 0, no feedback

Infinite Impulse Response (IIR) Filters

23

Poles and Zeros

The roots of the numerator polynomial in H(z) are known as the zeros, and
the roots of the denominator polynomial as poles. In particular, factorize H(z)
top and bottom:

24

Linear Digital Filter in Matlab

Matlab has a filter command for implementation of linear digital filters.

Matlab transfer function:

The format is

y = filter( b, a, x);

where
b = [b0 b1 b2 ... bM ]; a = [ 1 a1 a2 a3 ... aN ];

So to compute the first P+1 samples of the filter’s impulse response,

y = filter( b, a, [1 zeros(1,P)]);

Or step response,
y = filter( b, a, [ones(1,P)]);
25

z-transform and DTFT

DTFT

Similarly, to z-transforms a convolution theorem holds:

26

Frequency Response of LTI

LTI system with impulse response hk
∞
xn LTI yn= hk xn-k
k=0

Fourier Transform convolution

Fourier transform of hk

- frequency response of LTI
27


Indeed, let us excite the system with the complex
exponential

where

The response of the system to complex exponential

Fourier transform of hk

is also in the form of complex exponential but altered by
the multiplicative factor 28

Example

Assume

where for
0 otherwise

Frequency response

2

29


By knowing we can determine the response of the
system to any sinusoidal input signal, hence it specifies
the response of the system in the frequency domain

=

is called magnitude response of a system

is called phase response of a system

30

Frequency response of LTI

Transfer function:

Frequency response:
ω ω ω
ω
ω ω ω

ω
The complex modulus: ω
ω

ω

ω
and argument:

ω ω
ω ω

linear phase term sum of the angles from the zeros/poles to 31 circle
unit

Im(z)
Suppose we have a
system with 2 poles (o)
unit circle and 2 zeros (x)
X
We are going
around the unit
circle with
ω
O O
-1 1

X

32

Im(z)
Transfer function:
unit circle
X
D1

C2
ω
O O
-1 1
C1
D2 Frequency response:

X
C1C2
= D1D2
33

Im(z)

unit circle C1C2
X = D1D2
D1 The magnitude of the frequency
response is given by times
the product of the distances
C2
ω from the zeros to
O O divided by the product of the
-1 1 distances from the poles to
C1
D2

The phase response is given by
X the sum of the angles from the
zeros to minus the
sum of the angles from the
poles to plus a linear
phase term (M-N) ω
34

Im(z)
Thus when 'is
unit circle close to' a pole, the
magnitude of the response
X rises (resonance).
D1
When 'is close
C2 to' a zero, the magnitude
ω falls (a null).
O O
-1 1
C1
D2 The phase response –
more difficult to get
X “intuition”.

35

Frequency response of filter in Matlab
To evaluate the frequency response at n points equally spaced in
the normalised frequency range ω=0 to ω= π, Matlab's function
freqz is used:
freqz(b,a,n);
Peak close to pole frequency
b=[1 -0.1 -0.56];
a=[1 -0.9 0.81];
freqz(b,a)

Troughs at zero frequencies

36 36

Filtering example

Generate a Gaussian random noise sequence:

x=randn(100000,1);
figure(1), plot(x) freqz(b,a);
figure(2), plot(abs(fft(x)))

a = [1 -0.99 0.9801];
b = [1, -0.1, -0.56];

y=filter(b,a,x);
figure(3), plot(y)
Figure(4), plot(abs(fft(y)))

Selective amplification
of one frequency
Use soundsc(x,44100)
and soundsc(y,44100)
and hear the difference! 37 37

Filter specification

Before a filter is designed and implemented we need to
specify its performance requirements.

There are four basic filter types:

•  Low-pass
•  High-pass
•  Band-pass
•  Band-stop

Frequency band where signal is passed is passband
Frequency band where signal is removed is stopband

38

Ideal Low-pass Filter

•  Low-pass: designed to pass low frequencies from zero
to a certain cut-off frequency and to block high
frequencies

Ideal Frequency Response

39

Ideal High-pass Filter

•  High-pass: designed to pass high frequencies from a
certain cut-off frequency to π and to block low
frequencies


40

Ideal Band-pass Filter

•  Band-pass: designed to pass a certain frequency range
which does not include zero and to block other
frequencies


41

Ideal Band-stop Filter

•  Band-stop: designed to block a certain frequency range
which does not include zero and to pass other
frequencies


42

Ideal Filters – Magnitude Response

Ideal Filters are usually such that they admit a gain of 1 in a
given passband (where signal is passed) and 0 in their
stopband (where signal is removed).

43

Ideal Filters – Phase Response

Another important characteristics is related to the phase

Ideal filter: admits a linear phase response

Indeed,

Fourier Transform of

delay
44

Ideal Filters – Linear Phase Response

Important property: all frequencies suffer from
the same delays

In some applications it is critical for this property
to hold (at least approximately)

45

Linear / non-linear phase response

phase distortion
46

Ideal Filters – Linear Phase Response

The derivative of the phase/signal respect with
respect to ω is known as group delay of the
filter - effectively time delay of the frequency

when the phase admits a linear phase response

group delay is constant
47

Designing Ideal Filters is Impossible

48

Ideal Low- pass Filter Example

49

Filter Design

Let’s have a go …

50


Remember? Im(z)
Thus when 'is
unit circle close to' a pole, the
magnitude of the response
X rises (resonance).
D1
When 'is close
C2 to' a zero, the magnitude
ω falls (a null).
O O
-1 1
C1
D2 The phase response –
more difficult to get
X “intuition”.

51

Approximate filter design – rough guidelines

A few rough guidelines to start with:

•  One needs to put the poles within the unit circle to ensure stability

52

Approximate Low-pass filter

Rule 1: The closer to a pole, the higher the magnitude of the response

Rule 2: The closer to a zero, the lower the magnitude of the response

53

Approximate Low-pass filter

one pole

with added zero

54

Approximate High-pass filter

one can simply reflect
We had for Low-pass the poles-zeros
locations of the
lowpass filter about
the imaginary axis

55

Approximate High-pass filter

56

Alternative way: Low-pass to High-pass

in time domain

57

Bandpass and Resonator

a filter which has
its centre of the
passband at ω0

58

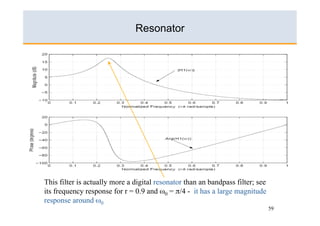
Resonator

This filter is actually more a digital resonator than an bandpass filter; see
its frequency response for r = 0.9 and ω0 = π/4 - it has a large magnitude
response around ω0
59

Band-pass Filter

60

Band-pass Filter

frequency response for r = 0.9 and ω0 = π/4
61

Notch Filter

a filter that
contains one or
several deeps/
notches in
its frequency
response
to eliminate ω0
Frequencies around the desired null are
also seriously attenuated

62

Notch Filter
Frequencies around seriously attenuated

with added pair of poles pair of zeros only

63

All pass Filter

Used as phase
equalizer

64

Inverse Filter

The zeros become
poles and the poles
become zeros

65

Digital Filter Design Considerations

Four steps:

1.  Specification of the filter’s response (very important! -
senior engineers)

3.  Design the transfer function of the filter (main goal:
meet spec with minimum complexity, often = minimum
order)

5.  Verification of the filter’s performance
•  analytic means
•  simulations
•  testing with real data if possible

4. Implementation by hardware / software (or both)
66

Approximate filter design

Given precise specification what
would you do??

67

Basics of Digital Filters

Recommended

More Related Content

What's hot (20)

Similar to Basics of Digital Filters (20)

More from op205 (20)

Basics of Digital Filters