Binary trees1
Download as PPTX, PDF5 likes1,923 views
The document discusses binary trees and binary search trees. It defines key terms like root, child, parent, leaves, height, depth. It explains tree traversal methods like preorder, inorder and postorder. It then describes binary search trees and how they store keys in a way that searching, insertion and deletion can be done efficiently in O(log n) time. It discusses implementation of operations like search, insert, delete on BSTs. It introduces balanced binary search trees like AVL trees that ensure height is O(log n) through rotations during insertions and deletions.
![InsertionFirst, insert the new key as a new leaf just as in ordinary binary search treeThen trace the path from the new leaf towards the root. For each node x encountered, check if heights of left(x) and right(x) differ by at most 1.If yes, proceed to parent(x). If not, restructure by doing either a single rotation or a double rotation [next slide].For insertion, once we perform a rotation at a node x, we won’t need to perform any rotation at any ancestor of x.](https://image.slidesharecdn.com/binarytrees1-110225222634-phpapp02/85/Binary-trees1-37-320.jpg)
Ad
More Related Content
What's hot (20)
Viewers also liked (6)
Ad
Similar to Binary trees1 (20)
Ad
More from Saurabh Mishra (7)
Recently uploaded (20)
Binary trees1
- 1. Binary Trees,Binary Search Trees
- 2. TreesLinear access time of linked lists is prohibitiveDoes there exist any simple data structure for which the running time of most operations (search, insert, delete) is O(log N)?
- 3. TreesA tree is a collection of nodesThe collection can be empty(recursive definition) If not empty, a tree consists of a distinguished node r (the root), and zero or more nonempty subtrees T1, T2, ...., Tk, each of whose roots are connected by a directed edge from r
- 4. Some TerminologiesChild and parentEvery node except the root has one parent A node can have an arbitrary number of childrenLeavesNodes with no children Siblingnodes with same parent
- 5. Some TerminologiesPathLengthnumber of edges on the pathDepthof a nodelength of the unique path from the root to that nodeThe depth of a tree is equal to the depth of the deepest leafHeight of a nodelength of the longest path from that node to a leafall leaves are at height 0The height of a tree is equal to the height of the rootAncestor and descendantProper ancestor and proper descendant
- 7. Binary TreesA tree in which no node can have more than two childrenThe depth of an “average” binary tree is considerably smaller than N, eventhough in the worst case, the depth can be as large as N – 1.
- 8. Example: Expression TreesLeaves are operands (constants or variables)The other nodes (internal nodes) contain operatorsWill not be a binary tree if some operators are not binary
- 9. Tree traversalUsed to print out the data in a tree in a certain orderPre-order traversalPrint the data at the rootRecursively print out all data in the left subtreeRecursively print out all data in the right subtree
- 10. Preorder, Postorder and InorderPreorder traversalnode, left, rightprefix expression++a*bc*+*defg
- 11. Preorder, Postorder and InorderPostorder traversalleft, right, nodepostfix expressionabc*+de*f+g*+Inorder traversalleft, node, right.infix expressiona+b*c+d*e+f*g
- 12. Preorder
- 13. Postorder
- 14. Preorder, Postorder and Inorder
- 15. Binary TreesPossible operations on the Binary Tree ADTparentleft_child, right_childsiblingroot, etcImplementationBecause a binary tree has at most two children, we can keep direct pointers to them
- 16. compare: Implementation of a general tree
- 17. Binary Search TreesStores keys in the nodes in a way so that searching, insertion and deletion can be done efficiently.Binary search tree propertyFor every node X, all the keys in its left subtree are smaller than the key value in X, and all the keys in its right subtree are larger than the key value in X
- 18. Binary Search TreesA binary search treeNot a binary search tree
- 19. Binary search treesAverage depth of a node is O(log N); maximum depth of a node is O(N)Two binary search trees representing the same set:
- 20. Implementation
- 21. Searching BSTIf we are searching for 15, then we are done.If we are searching for a key < 15, then we should search in the left subtree.If we are searching for a key > 15, then we should search in the right subtree.
- 23. Searching (Find)Find X: return a pointer to the node that has key X, or NULL if there is no such nodeTime complexityO(height of the tree)
- 24. Inorder traversal of BSTPrint out all the keys in sorted orderInorder: 2, 3, 4, 6, 7, 9, 13, 15, 17, 18, 20
- 25. findMin/ findMaxReturn the node containing the smallest element in the treeStart at the root and go left as long as there is a left child. The stopping point is the smallest elementSimilarly for findMaxTime complexity = O(height of the tree)
- 26. insertProceed down the tree as you would with a findIf X is found, do nothing (or update something)Otherwise, insert X at the last spot on the path traversedTime complexity = O(height of the tree)
- 27. deleteWhen we delete a node, we need to consider how we take care of the children of the deleted node.This has to be done such that the property of the search tree is maintained.
- 28. deleteThree cases:(1) the node is a leafDelete it immediately(2) the node has one childAdjust a pointer from the parent to bypass that node
- 29. delete(3) the node has 2 childrenreplace the key of that node with the minimum element at the right subtree delete the minimum element Has either no child or only right child because if it has a left child, that left child would be smaller and would have been chosen. So invoke case 1 or 2.Time complexity = O(height of the tree)
- 30. AVL-Trees
- 31. Balanced binary treeThe disadvantage of a binary search tree is that its height can be as large as N-1This means that the time needed to perform insertion and deletion and many other operations can be O(N) in the worst caseWe want a tree with small heightA binary tree with N node has height at least(log N) Thus, our goal is to keep the height of a binary search tree O(log N)Such trees are called balanced binary search trees. Examples are AVL tree, red-black tree.
- 32. AVL treeHeight of a nodeThe height of a leaf is 1. The height of a null pointer is zero.The height of an internal node is the maximum height of its children plus 1Note that this definition of height is different from the one we defined previously (we defined the height of a leaf as zero previously).
- 33. AVL treeAn AVL tree is a binary search tree in whichfor every node in the tree, the height of the left and right subtrees differ by at most 1.AVL property violated here
- 34. AVL treeLet x be the root of an AVL tree of height hLet Nh denote the minimum number of nodes in an AVL tree of height hClearly, Ni≥ Ni-1 by definitionWe haveBy repeated substitution, we obtain the general formThe boundary conditions are: N1=1 and N2 =2. This implies that h = O(log Nh).Thus, many operations (searching, insertion, deletion) on an AVL tree will take O(log N) time.
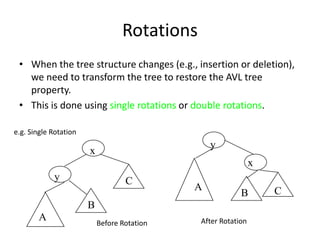
- 35. RotationsWhen the tree structure changes (e.g., insertion or deletion), we need to transform the tree to restore the AVL tree property.This is done using single rotations or double rotations.yxACBe.g. Single RotationxyCBAAfter RotationBefore Rotation
- 36. RotationsSince an insertion/deletion involves adding/deleting a single node, this can only increase/decrease the height of some subtree by 1Thus, if the AVL tree property is violated at a node x, it means that the heights of left(x) ad right(x) differ by exactly 2.Rotations will be applied to x to restore the AVL tree property.
- 37. InsertionFirst, insert the new key as a new leaf just as in ordinary binary search treeThen trace the path from the new leaf towards the root. For each node x encountered, check if heights of left(x) and right(x) differ by at most 1.If yes, proceed to parent(x). If not, restructure by doing either a single rotation or a double rotation [next slide].For insertion, once we perform a rotation at a node x, we won’t need to perform any rotation at any ancestor of x.
- 38. Insertion Let x be the node at which left(x) and right(x) differ by more than 1Assume that the height of x is h+3There are 4 casesHeight of left(x) is h+2 (i.e. height of right(x) is h)Height of left(left(x)) is h+1 single rotate with left childHeight of right(left(x)) is h+1 double rotate with left childHeight of right(x) is h+2 (i.e. height of left(x) is h)Height of right(right(x)) is h+1 single rotate with right childHeight of left(right(x)) is h+1 double rotate with right childNote: Our test conditions for the 4 cases are different from the code shown in the textbook. These conditions allow a uniform treatment between insertion and deletion.
- 39. Single rotationThe new key is inserted in the subtree A. The AVL-property is violated at x height of left(x) is h+2 height of right(x) is h.
- 40. Single rotationThe new key is inserted in the subtree C. The AVL-property is violated at x.Single rotation takes O(1) time.Insertion takes O(log N) time.
- 41. 3144810.83558341x AVL Tree5Cy8BA0.8Insert 0.8After rotation
- 42. Double rotationThe new key is inserted in the subtree B1 or B2. The AVL-property is violated at x.x-y-z forms a zig-zag shapealso called left-right rotate
- 43. Double rotationThe new key is inserted in the subtree B1 or B2. The AVL-property is violated at x.also called right-left rotate
- 44. xCy3Az43.58143.5B55833415 AVL Tree8Insert 3.5After Rotation1
- 45. An Extended Example33222442211133Fig 1335Fig 4Fig 2Fig 31Fig 5Fig 6Insert 3,2,1,4,5,6,7, 16,15,14Single rotationSingle rotation
- 46. 22444Fig 8Fig 755667337311222445566Fig 10Fig 95Fig 1133111Single rotationSingle rotation
- 47. 4447715316316316222Fig 12Fig 131566657Fig 1455111Double rotation
- 48. 4461415161533161422Fig 15Fig 167657511Double rotation