CAD Topology and Geometry Basics

Topology and Geometry Basics
Andrey Dankevich
June 2010

Agenda
 CAGD Topology
 CAGD Geometry
 Parametric curves and surfaces
 Bezier curves, B-Splines, NURBS

Introduction
B-Rep is a method for representing shapes using the limits.

B-Rep models are composed of two parts:
 Topology describes how elements are bounded and connected.
 Geometry describes the shape of each individual element.c

 Topology is a branch of mathematics concerned with spatial
properties preserved under continuous deformation (stretching
without tearing or gluing); these properties are the topological
invariants.
 On its own, topology defines a "rubber" model.

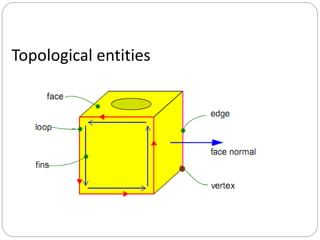
Topological entities
 Topological entities comprise all the entities that are used to
construct the structure or skeleton of a model.

Bodies
 body is the highest level topological entity.
 When we construct models we will create bodies, rather than
stand-alone lower topological entities.
 A body is composed of one or more components, where a
component is a set of connected entities.

Bodies
Type Dim Description

Acorn 0 An isolated vertex.

Wire 1 A set of connected edges.

Sheet 2 A set of connected faces.

Solid 3 A solid region.

0, 1, 2, 3,
A connected set of: regions, faces, edges,
General
vertices
Or mixed

Manifold bodies
 A manifold is a mathematical
term for an object that locally
resembles a line, a plane, or
a space.
 Euler equation:

v – e + f – h = 2(s – p),

v – vertices; h – hole loops;
e – edges; s – shells;
f – faces; p – passages.

Shell
- is a connected collection of oriented faces (each used by the shell
on one or both sides of the face) and edges.

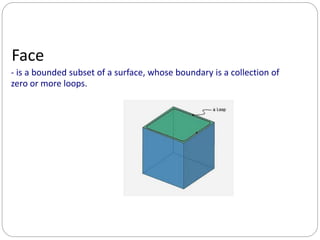
Face
- is a bounded subset of a surface, whose boundary is a collection of
zero or more loops.

Loop
- represents a connected portion of the boundary of a face. It
consists of a chain of coedges (fins).

Fin (coedge)
- represents the oriented use of an edge by a loop.
A fin has logical ‘sense’
indicating whether the fin’s
orientation, and therefore
the orientation of its owning
loop, is the same as its
owning edge.

Edge
- is a bounded piece of a single curve.
 Its boundary is a collection of zero, one or two vertices.
 Each edge contains a record of its sense relative to its underlying
curve.

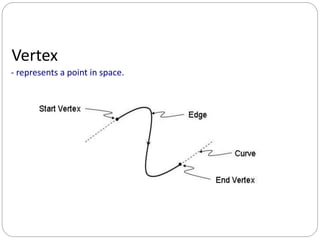
Vertex
- represents a point in space.

Point
 point is a zero-dimensional object that represents a location or
position in a given space.
 A point that resides in a one-dimensional space (that is, it resides
on the real line) is often called a parameter.
 A point that resides in a two-dimensional space defining the
domain of a parametrically defined surface is often termed a
parametric location or a parametric position.
 A point that resides in the three-dimensional object space is often
called a point, a location, or a position.

Curve
 Curves are 1-dimensional, in the sense that for parametric curves
you need a single parameter to obtain a point on the curve;
 The parameter of the curve is u;
 Each curve maps a single parameter value u into a 3-dimensional
point (x,y,z);

Surface
 surface is two-dimensional manifold in a three-dimensional space,
with a single geometrical definition.
 A parametric surface maps a rectangle defined within a 2D real
vector space (called parameter space) into a 3D real vector space
(often called object space)

Natural surface normals
Surface Natural orientation

plane along its plane normal

cylinder away from its axis

cone away from its axis

sphere away from its center

away from the circle described
torus
by its major axis

Continuity
 Continuity is a measure of the smoothness of a curve or surface.
 Parametric continuity, denoted by Cn, describes the maximum
derivative of a parametric equation that is continuous.
 Geometric continuity, denoted by Gn, is a geometric property
describing the smoothness of a that is independent of
parameterization.
 G0 curve or surface is positionally continuous.
 A G1 curve or surface has continuous tangent directions,
although the magnitude of tangent vectors may not be
continuous.
 A G2 curve has a continuous radius of curvature.

A Surface with a Non-G2 Discontinuity

Parametric curves and surfaces

Implicit and parametric forms
 f(x,y) = 0 – implicit curve.
– f(x,y) = x2 + y2 – 1 = 0 – a unit circle at origin.
 C ( u ) = ( x(u), y(u) ), a ≤ u ≤ b.
– C(u) = ( cos(u), sin(u) ), 0 ≤ u ≤ π/2.
 f(x,y,z) = 0 – implicit surface.
– f(x,y) = x2 + y2 + z2 – 1 = 0 – a unit sphere.
 S ( u, v ) = ( x(u, v), y(u, v), z(u, v) ), a ≤ u ≤ b.
– x(u,v) = sin(u)cos(v)
– y(u,v) = sin(u)sin(v)
– z(u,v) = cos(u); 0 ≤ u ≤ π; 0 ≤ v ≤ 2π.

 Coordinate system dependent/independent, the parametric
equations are also vector equations and hence the coord sys
independence
 Given a point determine if its on the curve or surface easy in the
implicit case difficult in the parametric case
 Generating points on the curve or surface easy in the parametric
case, difficult in the implicit case.
 Notion of order in parametric equations, you can generate an
ordered set of points on the curve. The tangent direction is the
direction of increasing parameter values.

Line
 Data:
– P0 – start point,
– P1 – end point.

 Parametrization:
– C ( u ) = ( 1 – u ) * P0 + u * P1.

Arc
 The arc is centered at the origin, and is parameterized by the angle of rotation from the first plane
unit vector in the direction of the second plane vector.
 Data:
– V1[3] - First vector that defines the plane of the arc;
– V2[3] - Second vector that defines the plane of the arc;
– Origin[3] - Origin that defines the plane of the arc;
– start_angle - Angular parameter of the starting point;
– end_angle - Angular parameter of the ending point;
– Radius - Radius of the arc.
– u' (the unnormalised parameter) = (1 - u) * start_angle + u * end_angle;
– C(u) = radius * [cos(u') * V1 + sin(u') * V2] + origin.

Plane
 The plane entity consists of two perpendicular unit vectors (e1 and e2), the normal to the plane
(e3), and the origin of the plane.
 Data:
– E1[3] - Unit vector, in the u direction;
– E2[3] - Unit vector, in the v direction;
– E3[3] - Normal to the plane;
– Origin[3] - Origin of the plane.
– S(u,v) = u * e1 + v * e2 + origin

Cylinder
 The generating curve of a cylinder is a line, parallel to the axis, at a distance R from the axis. The
radial distance of a point is constant, and the height of the point is v.
 Data:
– E1[3] - Unit vector, in the u direction;
– E2[3] - Unit vector, in the v direction;
– E3[3] - Normal to the plane;
– Origin[3] - Origin of the plane.
– Radius - Radius of the cylinder.
– S(u,v) = radius * [cos(u) * e1 + sin(u) * e2] + v * e3 + origin.

Bezier curves, B-Splines, NURBS

Bezier curve
- A special form of a polynominal curve.
Given n+1 points P0, P1, P2, ... and Pn in space, the control points, the
Bézier curve defined by these control points is

the point that corresponds to u on the Bézier curve is the "weighted"
average of all control points, where the weights are the coefficients Bn,i(u).

Examination of cases
- Linear Bézier curves

- Quadratic Bézier curves

- Cubic Bézier curves

Properties of a Bézier curve
 All basis functions are non-negative.
 The sum of the basis functions at a fixed u is 1
 The degree of a curve is number of control points - 1
 Open curves always pass through first and last point.
 Tangent at first point is given by the direction of the first segment
of control polygon.
 the same curve (and properties) exist when starting with the last
control point.
 Convex hull property.
 Variation Diminishing property.
 Affine Invariance.

De Casteljau's Algorithm
 Choose a point C in line segment AB such that C divides the line
segment AB in a ratio of u:1-u.
i.e. C = (1 - u)A + uB

Limitations of Bézier curves
 More complicated shapes require higher order Bezier curves.
 Bézier curves can not be modified “locally”. Movement of any
control point will affect the whole curve.

Basic spline curves
 Instead of considering EVERY control point when evaluating a
point, only consider closest k.

 The B-spline curve is composed of segments, each of degree k-1.

Basic spline equation
 Bézier basis functions are used as weights. B-spline basis functions
will be used the same way; however, they are much more complex

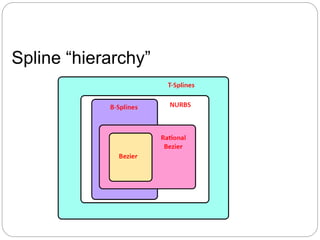
Basic spline data
 Multiple segments:
 Order = k
 Number of control points = n
 Number of knots = n + k
 Knot vector, eg {0, 1, 2, 3, 4, 5, 7, 8}
 Number of segments:
 n-k+2 for open curves
 n-k+1 for closed curves

CAD Topology and Geometry Basics

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to CAD Topology and Geometry Basics (20)

Recently uploaded (20)

CAD Topology and Geometry Basics