Ch 04 Arithmetic Coding (Ppt)

Ch. 4 Arithmetic Coding

1

Motivation – What are Problems w/ Huffman
1. Can be inefficient (i.e., large redundancy)
• This can be “solved” through Block Huffman
• But… # of codewords grows exponentially
See Example 4.2.1: H1(S) = 0.335 bits/symbol
But using Huffman we get avg length = 1.05 bits/symbol
Would need block size of 8 6561-symbol alphabet to get close to H1
2. High-Order Models (Non-IID) Hard to Address
• Can be solved through Block Huffman
• But # of codewords increases exponentially

Underlying difficulty: Huffman requires keeping track of
codewords for all possible blocks

We need a way to assign a codeword to a particular sequence
w/o having to generate codes for all possible sequences
2

Main Idea of Arithmetic Coding
1
Sequence: S1 S2 S3 S4 …. Mapped to… 0.6457351….

Each possible sequence gets mapped 0

to a unique number in [0,1)
• The mapping depends on the prob. of the symbols
• You don’t need to a priori determine all possible mappings
– The Mapping is “built” as each new symbol arrives

Recall CDF of an RV: symbols {a1,a2, a3} RV X w/ values: {1, 2, 3}
Consider P(X=1) = 0.7 P(X=2) = 0.1 P(X=1) = 0.2
FX(x)
1
0.8
0.7

0 1 2 3 x 3

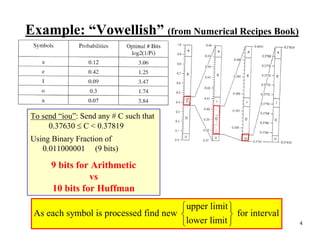
Example: “Vowellish” (from Numerical Recipes Book)

To send “iou”: Send any # C such that
0.37630 ≤ C < 0.37819
Using Binary Fraction of
0.011000001 (9 bits)

9 bits for Arithmetic
vs
10 bits for Huffman
⎧ upper limit ⎫
As each symbol is processed find new ⎨ ⎬ for interval
⎩lower limit ⎭ 4

Math Result Needed to Program
Consider a sequence of RVs X = (x1, x2, x3, … , xn) corresponding
to the sequence of symbols (S1, S2, S3, … , Sn)
Ex. Alphabet = {a1 , a2 , a3 } → RV Values {1, 2, 3}
( S1 S2 S3 S4 ) = ( a2 a3 a3 a1 ) → ( x1 x2 x3 x4 ) = (2 3 31)

Initial Values: l (0) = 0 u (0) = 1

Interval Update: l ( n ) = l ( n −1) + ⎡ u ( n −1) − l ( n −1) ⎤ F ( x − 1)
⎣ ⎦ X n
u ( n ) = l ( n −1) + ⎡u ( n −1) − l ( n −1) ⎤ FX ( xn )
⎣ ⎦

From Prev Interval From Prob Model

5

Checking Some Characteristics of Update
• What is the smallest l(n) can be?
( n −1)
l ( n ) = l ( n −1) + ⎡u ( n −1) − l ( n −1) ⎤ FX ( xn − 1)
⎣ ⎦ l (n)
≥l
>0 ≥0

• What is the largest u(n) can be?

u ( n ) = l ( n −1) + ⎡u ( n −1) − l ( n −1) ⎤ FX ( xn )
⎣ ⎦
( n −1)
≤1
u (n)
≤u
≤l ( n −1)
+ ⎡u
⎣
( n −1)
−l ( n −1)
⎤
⎦

These imply an important requirement for decoding:
New Interval ⊆ Old Interval

6

Example of Applying the Interval Update
Symbols {a1,a2, a3} RV X w/ values: {1, 2, 3}
Consider P(X=1) = 0.7 P(X=2) = 0.1 P(X=1) = 0.2
FX(x)
1
0.8
CDF for this 0.7
alphabet/RV

0 1 2 3 x

Consider the sequence (a1 a3 a2) → (1 3 2)
To process the first symbol “1”
FX(0)

l (1) = l (0) + ⎡u (0) − l (0) ⎤ FX (1 − 1) = 0 + [1 − 0] × 0 = 0
⎣ ⎦
u (1) = l (0) + ⎡u (0) − l (0) ⎤ FX (1)
⎣ ⎦ = 0 + [1 − 0] × 0.7 = 0.7
FX(1) 7

To process the 2nd symbol “3”
FX(2)

l (2) = l (1) + ⎡u (1) − l (1) ⎤ FX (3 − 1) = 0 + [0.7 − 0] × 0.8 = 0.56
⎣ ⎦
u (2) = l (1) + ⎡u (1) − l (1) ⎤ FX (3)
⎣ ⎦ = 0 + [0.7 − 0] × 1 = 0.7
FX(3)

To process the 3rd symbol “2”
FX(1)
1010101000
l (3) = l (2) + ⎡u (2) − l (2) ⎤ FX (2 − 1) = 0.56 + [0.7 − 0.56] × 0.7 = 0.658
⎣ ⎦
u (3) = l (2) + ⎡u (2) − l (2) ⎤ FX (2)
⎣ ⎦ = 0.56 + [0.7 − 0.56] × 0.8 = 0.672
FX(2)

So… send a number in the interval [0.658,0.672) Pick 0.6640625

0.664062510 = 0.10101012 Code = 1 0 1 0 1 0 1
8

Decoding Received Code = 1 0 1 0 1 0 1
⎧0.1111111... = 1 ⎧0.1011111... = 0.75
1→ ⎨ 10 → ⎨
⎩0.1000000... = 0.5 ⎩0.1000000... = 0.5

1 1
a3 a3
0.8 0.8
a2 After 1st bit [0.5 1)… a2
0.7 Can’t Decode 0.7
After 2nd bit [0.5 0.75)…
Can’t Decode… But first
symbol can’t be a3

a1 a1

0 0 9

Decoding Continued: Received Code = 1 0 1 0 1 0 1
⎧0.1011111... = 0.75 ⎧0.1010111... = 0.6875
101 → ⎨ 1010 → ⎨
⎩0.1010000... = 0.625 ⎩0.1010000... = 0.625
1 1
a3 a3
0.8 0.8
a2 [0.625 , 0.75)… a2
0.7 Can’t Decode 0.7 0.7
[0.625 , 0.6875)… a3
Can Decode 1st symbol!!!
a2 0.56
It is a1 0.49

Now slice up [0, 0.7)…
a1 a1 a1
…can decode 2nd symbol

It is a3
0 0 0
10

Decoding Continued: Received Code = 1 0 1 0 1 0 1
⎧0.1010111... = 0.6875 ⎧0.10101011... = 0.671875
10101 → ⎨ 101010 → ⎨
⎩0.1010100... = 0.65625 ⎩0.10101000... = 0.65625

0.7 0.7
[0.65625 , 0.6875)… [0.65625, 0.671875)…
0.672 0.672
Can’t Decode Can’t Decode
0.658 0.658

0.56 0.56

⎧0.1010101111... = 0.671875
1010101 → ⎨
⎩0.1010101000... = 0.6640625

0.7
[0.6640625, 0.671875)
0.672
Can Decode 3rd symbol!!!
0.658

It is a2
0.56
In practice there are ways to handle termination issues! 11

Main Results on Uniqueness & Efficiency
1. A “binary tag” lying between l(n) and u(n) can be found
2. The tag can be truncated to a finite # of bits
3. The truncated tag still lies between l(n) and u(n)
4. The truncated tag is Unique & Decodable
5. For IID sequence of length m: H ( S ) ≤ l < H ( S ) + 2
Arith
m
1
Compared to Huffman: H ( S ) ≤ lHuff < H (S ) +
m

Hey! AC is worse than Huffman??!! So why consider AC???!!!
Remember, this is for coding the entire length of m symbols…
You’d need 2m codewords in Huffman… which is impractical!
But for AC is VERY practical!!!

For Huffman must be kept small but for AC it can be VERY large!
12

How AC Overcomes Huffman’s Problems
1. Efficiency: Huffman can only achieve close to H(S) by using
large block codes… which means you need a pre-designed
codebook of exponentially growing size
– AC enables coding large blocks w/o having to know codewords a priori
– w/ AC you just generate the code for the entire given sequence
• No a priori codebook is needed
2. Higher-Order Models: Huffman can use Cond. Prob.
Models… but you need to build an a priori codebook for each
context… which means a large codebook
– Context coding via conditional probabilities is easy in AC
– For each context you have a prob model for the symbols
• Next “slicing of the interval” is done using prob model for the currently
observed context… no need to generate all the a priori codewords!

13

Ex.: 1st Order Cond. Prob Models for AC
Suppose you have three symbols and you have a 1st order
conditional probability model for the source emitting these
symbols…
For the first symbol in the sequence you have a std Prob Model
For subsequent symbols in the sequence you have 3 context models
P ( a1 ) = 0.2 P ( a1 | a1 ) = 0.1 P ( a1 | a2 ) = 0.95 P ( a1 | a3 ) = 0.45
P ( a2 ) = 0.4 P ( a2 | a1 ) = 0.5 P ( a2 | a2 ) = 0.01 P ( a2 | a3 ) = 0.45
P ( a3 ) = 0.4 P ( a3 | a1 ) = 0.4 P ( a3 | a2 ) = 0.04 P ( a3 | a3 ) = 0.1

∑ P(a ) = 1 ∑ P(a
i
i
i
i | a1 ) = 1 ∑ P(a
i
i | a2 ) = 1 ∑ P(a
i
i | a3 ) = 1

Now let’s see how these are used to code the sequence a2 a1 a3
Note: Decoder needs to know these models
14

P ( a1 ) = 0.2 P ( a1 | a2 ) = 0.95 P ( a1 | a1 ) = 0.1
P ( a2 ) = 0.4 P ( a2 | a2 ) = 0.01 P ( a2 | a1 ) = 0.5
P ( a3 ) = 0.4 P ( a3 | a2 ) = 0.04 P ( a3 | a1 ) = 0.4
1

0.6

a3
a2 a1

0.2

0 15

Ex.: Similar for Adaptive Prob. Models
• Start with some a priori “prototype” prob model (could be cond.)
• Do coding with that for awhile as you observe the actual
frequencies of occurrence of the symbols
– Use these observations to update the probability models to better model the
ACTUAL source you have!!
• Can continue to adapt these models as more symbols are
observed
– Enables tracking probabilities of source with changing probabilities
• Note: Because the decoder starts with the same prototype model
and sees the same symbols the coder uses to adapt… it can
automatically synchronize adaptation of its models to the coder!
– As long as there are no transmission errors!!!

16

Ch 04 Arithmetic Coding (Ppt)

Recommended

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to Ch 04 Arithmetic Coding (Ppt) (20)

More from anithabalaprabhu (20)

Recently uploaded (20)

Ch 04 Arithmetic Coding (Ppt)