![Example 2.7
41
Simplify the Following Expressions
41
𝑒ln(7.2)
𝑙𝑛
sin2 𝑥 tan4 𝑥
𝑥2 + 1 2
𝑙𝑛
4 𝑥2 + 1
𝑥2 − 1
𝑙𝑛𝑒(2 ln 𝑥)
ln[ln 𝑒𝑒 ]
2ln( 𝑒)
𝑒x−ln(𝑥)
𝑒ln(𝑥2+𝑦2)
𝑒 ln 𝑥 −ln 𝑦
𝑒−ln(𝑥2)
ln 𝑒𝑒𝑥
𝑙𝑛
𝑥3 + 1 4sin2 𝑥
3
𝑥
ln(𝑠𝑖𝑛𝜃) − ln
𝑠𝑖𝑛𝜃
5
ln(3𝑥2 − 9𝑥) + ln
1
3𝑥
ln(𝑠𝑒𝑐𝜃) + ln(𝑐𝑜𝑠𝜃)
3𝑙𝑛
3
𝑡2 − 1 − ln(𝑡 + 1)
𝑒5−3𝑥
= 10](https://image.slidesharecdn.com/chapter2-typesofafunction-230228164705-5217142b/85/Chapter-2-Types-of-a-Function-pdf-41-320.jpg)
![ln[ln 𝑒𝑒
]
𝑙𝑛𝑒 = 1
58
Example 2.8](https://image.slidesharecdn.com/chapter2-typesofafunction-230228164705-5217142b/85/Chapter-2-Types-of-a-Function-pdf-58-320.jpg)
Chapter 2 - Types of a Function.pdf
- 1. Types of a Function Chapter 2 This Photo by Unknown Author is licensed under CC BY
- 4. • A polynomial of degree 1 is of the form 𝑓 𝑥 = 𝑚𝑥 + 𝑏 and so it is a linear function. • A polynomial of degree 2 is of the form 𝒇 𝒙 = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 and is called a quadratic function. • The parabola opens upward if 𝑎 > 0 and downward if 𝑎 < 0 . • A polynomial of degree 3 is of the form 𝒇 𝒙 = 𝒂𝒙𝟑 + 𝒃𝒙𝟐 + 𝒄𝒙 + 𝒅 and is called a cubic function. 4 slope Y-intercept
- 6. Example 2.1 6 Sketch 𝑓 𝑥 = 𝑥2 + 6𝑥 + 10 Completing the square, we write the equation of the graph as y = 𝑥2 + 6𝑥 + 10 = 𝑥 + 3 2 + 1 This means we obtain the desired graph by starting with the parabola and shifting 3 units to the left and then 1 unit upward. Base Graph
- 7. Rational Functions Square Root Cubic Root 7
- 8. Sketch the Following Functions in Steps 8 𝑓 𝑥 = 𝑥 − 1 − 2 𝑓 𝑥 = 2 − 1 − 𝑥 𝑓 𝑥 = − −𝑥 Example 2.2
- 9. Example 2.2.a 9 Sketch 𝑓 𝑥 = 𝑥 − 1 − 2
- 10. Example 2.2.b 10 Sketch 𝑓 𝑥 = 2 − 1 − 𝑥
- 11. Example 2.2.c 11 Sketch 𝑓 𝑥 = − −𝑥
- 12. Some Special Radical Functions 12
- 13. Sketch the Following Functions in Steps Example 2.3 𝑓 𝑥 = 1 𝑥 − 1 + 3 𝑓 𝑥 = 1 (𝑥 − 1)2 + 4 𝑓 𝑥 = 1 2(1 − 𝑥)3 + 5
- 14. Example 2.3.a 14 Graph 𝑓 𝑥 = 1 𝑥−1 + 3
- 15. Example 2.3.b 15 Graph 𝑓 𝑥 = 1 (𝑥−1)2 + 4
- 16. Example 2.3.c 16 Graph 𝑓 𝑥 = 1 2(1−𝑥)3 + 5 Challenging Problem
- 17. Absolute Value Functions 17 𝑎 = 𝑎 𝑖𝑓 𝑎 ≥ 0 𝑎 = −𝑎 𝑖𝑓 𝑎 < 0 (Remember that if a is negative, then "a is positive.) 𝑥 = ቊ −𝑥, 𝑥 < 0 𝑥, 𝑥 ≥ 0
- 18. Example 2.4 18 Sketch the Following Functions in Steps 𝑓 𝑥 = 𝑥 − 2 + 1 𝑓 𝑥 = 𝑥2 − 1
- 19. Example 2.4.a 19 Graph 𝑓 𝑥 = 𝑥2 − 1 in steps We first graph the parabola 𝑓 𝑥 = 𝑥2 − 1 by shifting the parabola 𝑦 = 𝑥2 downward 1 unit. We see that the graph lies below the x-axis when − 1 < 𝑥 < 1, so we reflect that part of the graph about the x-axis to obtain the graph of 𝑓 𝑥 = 𝑥2 − 1
- 20. Example 2.4.b 20 Graph 𝑓 𝑥 = 𝑥 − 2 + 1 in steps
- 21. Try to sketch in steps and then find domain & Range 𝑦 = (𝑥 + 1)2 𝑦 = 𝑥2 𝑦 = 𝑥2 + 3 𝑦 = (𝑥 + 1)2 +3 𝑦 = 𝑥2 + 2𝑥 + 1 𝑦 = 𝑥2 − 4𝑥 + 7 𝑦 = 2𝑥2 − 8𝑥 + 14 𝑦 = 2 𝑥 − 3 𝑦 = 2𝑥 − 3 𝑥 − 1 𝑦 = 𝑥 − 1 − 1 𝑦 = 3 𝑥 − 1 − 1 𝑦 = 1 − 𝑥2 𝑦 = 12 − 4𝑥 − 𝑥2 − 2 𝑦 = 2𝑥 − 3 𝑥 − 1 𝑦 = 𝑥 − 1 − 1
- 22. Trigonometric Functions Sine Cosine Tangent 22
- 23. • An important property of the sine and cosine functions is that they are periodic functions and have period 2𝜋. • The period of tangent is 𝜋. • The remaining three trigonometric functions (cosecant, secant, and cotangent) are the reciprocals of the sine, cosine, and tangent functions; therefore, they have the same period. 23 Notice that for both the sine and cosine functions the domain is and the range is the closed interval . Thus, for all values of , we have −1 ≤ 𝑠𝑖𝑛𝑥 ≤ 1 − 1 ≤ 𝑐𝑜𝑠𝑥 ≤ 1 or, in terms of absolute values, 𝑠𝑖𝑛𝑥 ≤ 1 𝑐𝑜𝑠𝑥 ≤ 1
- 24. Example 2.5 Sketch the Following Functions 𝑓(𝑥) = 1 + 4𝑐𝑜𝑠3𝑥 𝑓 𝑥 = 𝑠𝑖𝑛2𝑥 𝑓 𝑥 = 1 − 𝑠𝑖𝑛𝑥 𝑓(𝑥) = 1 4 𝑡𝑎𝑛 𝑥 − 𝜋 4
- 25. Example 2.5.a 25 Sketch the Graph 𝑓 𝑥 = 𝑠𝑖𝑛2𝑥 We obtain the graph of 𝑓 𝑥 from that of 𝑓 𝑥 = 𝑠𝑖𝑛𝑥 by compressing horizontally by a factor of 2. Thus, whereas the period of 𝑓 𝑥 = 𝑠𝑖𝑛𝑥 is 2𝜋, the period of 𝑓 𝑥 = 𝑠𝑖𝑛2𝑥 is 2𝜋 2 = π .
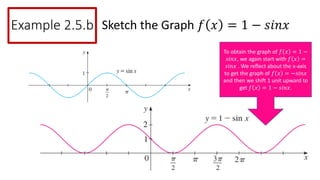
- 26. Example 2.5.b 26 Sketch the Graph 𝑓 𝑥 = 1 − 𝑠𝑖𝑛𝑥 To obtain the graph of 𝑓 𝑥 = 1 − 𝑠𝑖𝑛𝑥, we again start with 𝑓 𝑥 = 𝑠𝑖𝑛𝑥 . We reflect about the x-axis to get the graph of 𝑓 𝑥 = −𝑠𝑖𝑛𝑥 and then we shift 1 unit upward to get 𝑓 𝑥 = 1 − 𝑠𝑖𝑛𝑥.
- 27. Example 2.5.c 27 Sketch The graph 𝑓(𝑥) = 1 4 𝑡𝑎𝑛 𝑥 − 𝜋 4
- 28. Example 2.5.d Sketch The Graph 𝑓(𝑥) = 1 + 4𝑐𝑜𝑠3𝑥
- 29. Trigonometric Functions Cosecant Secant Cotangent 29
- 30. Basic Trigonometric Identities 30 𝑠𝑖𝑛2 𝜃 + 𝑐𝑜𝑠2 𝜃 = 1 𝑡𝑎𝑛2 𝜃 + 1 = 𝑠𝑒𝑐2 𝜃 1 + 𝑐𝑜𝑡2 𝜃 = 𝑐𝑠𝑐2 𝜃 sin −𝜃 = −𝑠𝑖𝑛𝜃 cos −𝜃 = 𝑐𝑜𝑠𝜃 cos 𝐴 + 𝐵 = 𝑐𝑜𝑠𝐴𝑐𝑜𝑠𝐵 − 𝑠𝑖𝑛𝐴𝑠𝑖𝑛𝐵 sin 𝐴 + 𝐵 = 𝑠𝑖𝑛𝐴𝑐𝑜𝑠𝐵 + 𝑐𝑜𝑠𝐴𝑠𝑖𝑛𝐵 𝑐𝑜𝑠2𝜃 = 𝑐𝑜𝑠2 𝜃 − 𝑠𝑖𝑛2 𝜃 = 2𝑐𝑜𝑠2 𝜃 − 1 𝑠𝑖𝑛2𝜃 = 2𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜃 𝑐𝑜𝑠2 𝜃 = 1 + 𝑐𝑜𝑠2𝜃 2 𝑠𝑖𝑛2 𝜃 = 1 − 𝑐𝑜𝑠2𝜃 2
- 31. 31 tan2 𝜃 + 1 = sec2 𝑥 We start with the identity 𝑠𝑖𝑛2 𝜃 + 𝑐𝑜𝑠2 𝜃 = 1 Dividing both sides of this equation by 𝑐𝑜𝑠2 𝜃, we obtain 𝑠𝑖𝑛2𝜃 𝑐𝑜𝑠2𝜃 + 1 = 1 𝑐𝑜𝑠2𝜃 Since 𝑠𝑖𝑛𝜃 𝑐𝑜𝑠𝜃 = 𝑡𝑎𝑛𝜃 and 1 𝑐𝑜𝑠𝜃 = 𝑠𝑒𝑐𝜃, we conclude that tan2 𝜃 + 1 = sec2 𝑥
- 32. Exponential Functions 32 𝑒𝑥+𝑦 = 𝑒𝑥 𝑒𝑦 𝑒𝑥−𝑦 = 𝑒𝑥 𝑒𝑦 (𝑒𝑥 )𝑦 = 𝑒𝑥𝑦 (𝑎𝑏)𝑥 = 𝑎𝑥 𝑏𝑦 𝑒−𝑥 = 1 𝑒𝑥
- 33. Example 2.6 33 𝑓 𝑥 = 𝑒𝑥+1 33 𝑓 𝑥 = 3 − 2𝑥 Sketch the Following Graph in Steps 𝑓 𝑥 = 1 2 𝑒−𝑥 − 1 𝑓 𝑥 = −(3𝑥 + 2) 𝑓 𝑥 = 2𝑥 + 1 𝑓 𝑥 = −3−𝑥
- 34. Example 2.6.a 34 Sketch the Graph 𝑓 𝑥 = 3 − 2𝑥 First, we reflect the graph of 𝑦 = 2𝑥 about the x-axis to get the graph of 𝑦 = − 2𝑥 Base graph Then, we shift the graph of 𝑦 = −2𝑥 upward 3 units to obtain the graph of 𝑦 = 3 − 2𝑥 The Domain is ℝ The Range is (-∞,3)
- 35. Example 2.6.b 35 Sketch the Graph 𝑓 𝑥 = 1 2 𝑒−𝑥 − 1 Base graph First, we reflect the graph of 𝑦 = 𝑒𝑥 about the y-axis to get the graph of 𝑦 = 𝑒−𝑥 . (Notice that the graph crosses the y-axis with a slope of -1) Then, Then we compress the graph vertically by a factor of 2 to obtain the graph of 𝑦 = 1 2 𝑒−𝑥 Finally, we shift the graph downward one unit to get 𝑓 𝑥 = 1 2 𝑒−𝑥 − 1 The Domain is ℝ The Range is (-1, ∞)
- 36. Example 2.6.c 36 Sketch the Graph 𝑓 x = e𝑥+1 36
- 37. Example 2.6.d 37 Sketch the Graph 𝑓 x = −(3𝑥 + 2) 37
- 38. Example 2.6.e 38 Sketch the Graph 𝑓 x = 2𝑥 + 1 38
- 39. Example 2.6.f 39 Sketch the Graph 𝑓 x = −3−𝑥 39
- 40. Logarithmic Functions 40 log𝑎(𝑎𝑥) = 𝑥 𝑥 = ℝ ln 𝑒𝑥 = 𝑥 𝑙𝑛𝑥 = 𝑦 ⇔ 𝑒𝑦 = 𝑥 log𝑎(𝑥𝑟) = rlog𝑎 𝑥 log𝑎(𝑥𝑦) = log𝑎 𝑥 + log𝑎 𝑦 log𝑎 𝑥 𝑦 = log𝑎 𝑥 − log𝑎 𝑦 𝑎log𝑎 𝑥 = 𝑥 𝑥 > 0 log𝑎(𝑥) = 𝑙𝑛𝑥 𝑙𝑛𝑎 for any positive numbers 𝑙𝑛𝑒 = 1 𝑒𝑙𝑛𝑥 = 𝑥 𝑥 > 0
- 41. Example 2.7 41 Simplify the Following Expressions 41 𝑒ln(7.2) 𝑙𝑛 sin2 𝑥 tan4 𝑥 𝑥2 + 1 2 𝑙𝑛 4 𝑥2 + 1 𝑥2 − 1 𝑙𝑛𝑒(2 ln 𝑥) ln[ln 𝑒𝑒 ] 2ln( 𝑒) 𝑒x−ln(𝑥) 𝑒ln(𝑥2+𝑦2) 𝑒 ln 𝑥 −ln 𝑦 𝑒−ln(𝑥2) ln 𝑒𝑒𝑥 𝑙𝑛 𝑥3 + 1 4sin2 𝑥 3 𝑥 ln(𝑠𝑖𝑛𝜃) − ln 𝑠𝑖𝑛𝜃 5 ln(3𝑥2 − 9𝑥) + ln 1 3𝑥 ln(𝑠𝑒𝑐𝜃) + ln(𝑐𝑜𝑠𝜃) 3𝑙𝑛 3 𝑡2 − 1 − ln(𝑡 + 1) 𝑒5−3𝑥 = 10
- 42. Example 2.8 42 Solve the Equation 𝑒5−3𝑥 = 10 42 𝑙𝑛𝑒5−3𝑥 = 𝑙𝑛10 5 − 3𝑥 = 𝑙𝑛10 3𝑥 = 5 − 𝑙𝑛10 𝑥 = 1 3 5 − 𝑙𝑛10 We take natural logarithms of both sides of the equation Apply ln 𝑒𝑥 = 𝑥
- 45. 𝑒 ln 𝑥 −ln 𝑦 𝑒 ln 𝑥 −ln 𝑦 = ൝ 𝑒𝑙𝑛𝑥−𝑙𝑛𝑦 𝑥 ≥ 𝑦 𝑒𝑙𝑛𝑦−𝑙𝑛𝑥 𝑥 < 𝑦 = ቐ ൗ 𝑥 𝑦 𝑥 ≥ 𝑦 ൗ 𝑦 𝑥 𝑥 < 𝑦 45 Example 2.8
- 46. 𝑒ln(𝑥2+𝑦2) 𝑥2 + 𝑦2 46 Example 2.8
- 48. 2ln( 𝑒) 2 ln 𝑒 1 2 = 𝑙𝑛𝑒 = 1 48 Example 2.8
- 50. 𝑙𝑛𝑒(2 ln 𝑥) ln 𝑒𝑙𝑛𝑥2 = 𝑙𝑛𝑥2 = 2𝑙𝑛𝑥 50 Example 2.8
- 51. 𝑙𝑛 4 𝑥2 + 1 𝑥2 − 1 𝑙𝑛 4 𝑥2 + 1 𝑥2 − 1 = 1 4 𝑙𝑛 𝑥2 + 1 𝑥2 − 1 = 1 4 [ln 𝑥2 + 1 − ln(𝑥2 − 1) 51 Example 2.8
- 52. 𝑙𝑛 sin2 𝑥 tan4 𝑥 𝑥2 + 1 2 ln sin2 𝑥 + ln tan4 𝑥 − ln 𝑥2 + 1 2 = 2 ln 𝑠𝑖𝑛𝑥 + 4 ln 𝑡𝑎𝑛𝑥 − 2ln(𝑥2 + 1) 52 Example 2.8
- 53. 𝑙𝑛 𝑥3 + 1 4 sin2 𝑥 3 𝑥 𝑙𝑛 𝑥3 + 1 4 sin2 𝑥 3 𝑥 = 4 ln 𝑥3 + 1 + 2 ln 𝑠𝑖𝑛𝑥 − 𝑙𝑛𝑥 3 53 Example 2.8
- 54. ln(𝑠𝑖𝑛𝜃) − ln 𝑠𝑖𝑛𝜃 5 ln(𝑠𝑖𝑛𝜃) − ln 𝑠𝑖𝑛𝜃 5 = ln 𝑠𝑖𝑛𝜃 − ln 𝑠𝑖𝑛𝜃 − −𝑙𝑛5 = 𝑙𝑛5 54 Example 2.8
- 55. ln(3𝑥2 − 9𝑥) + ln 1 3𝑥 = 𝑙𝑛3𝑥 𝑥 − 3 + 𝑙𝑛 1 3𝑥 = 𝑙𝑛 3𝑥 + 𝑙𝑛 𝑥 − 3 − 𝑙𝑛 3𝑥 = 𝑙𝑛(𝑥 − 3) 55 Example 2.8
- 56. ln(𝑠𝑒𝑐𝜃) + ln(𝑐𝑜𝑠𝜃) ln 𝑐𝑜𝑠𝜃 −1 + ln 𝑐𝑜𝑠𝜃 = 0 56 Example 2.8
- 57. 3𝑙𝑛 3 𝑡2 − 1 − ln(𝑡 + 1) ln 𝑡2 − 1 − ln 𝑡 + 1 = ln 𝑡 − 1 𝑡 + 1 − ln 𝑡 + 1 = ln(𝑡 − 1) 57 Example 2.8
- 58. ln[ln 𝑒𝑒 ] 𝑙𝑛𝑒 = 1 58 Example 2.8
- 59. Example 2.9 59 Sketch the Following Functions 59 𝑦 = ln 𝑥 − 2 − 1 𝑓 𝑥 = ln(𝑥 + 2) 𝑓 𝑥 = 𝑙𝑛𝑥 + 2 𝑓 𝑥 = 1 + ln(−𝑥) 𝑓 𝑥 = 𝑙𝑛 𝑥 𝑓 𝑥 = 2 − log(2 − 𝑥)
- 60. Example 2.9 60 Sketch the Graph 𝑦 = ln 𝑥 − 2 − 1 60 We start with the graph of 𝑦 = 𝑙𝑛𝑥 Using the transformations, we shift it 2 units to the right to get the graph of 𝑦 = ln(𝑥 − 2) Then we shift it 1 unit downward to get the graph of 𝑦 = 𝑥 − 2 − 1
- 61. Example 2.9 61 Sketch the Graph 𝑓 𝑥 = ln(𝑥 + 2) 61
- 62. 62 Sketch the Graph 𝑓 𝑥 = 𝑙𝑛𝑥 + 2 62 Example 2.9
- 63. 63 Sketch the Graph 𝑓 𝑥 = 1 + ln(−𝑥) 63 Example 2.9
- 64. 64 Sketch the Graph 𝑓 𝑥 = 𝑙𝑛 𝑥 64 Example 2.9
- 65. 65 Sketch the Graph 𝑓 𝑥 = 2 − log(2 − 𝑥) 65 Example 2.9
- 66. Hyperbolic Functions Hyperbolic Sine of x 𝑠𝑖𝑛ℎ𝑥 = 𝑒𝑥 − 𝑒−𝑥 2 𝑠𝑖𝑛ℎ0 = 0 Hyperbolic Cosine of x 𝑐𝑜𝑠ℎ𝑥 = 𝑒𝑥 + 𝑒−𝑥 2 𝑐𝑜𝑠ℎ0 = 1 Hyperbolic of Tangent of x 𝑡𝑎𝑛ℎ𝑥 = 𝑠𝑖𝑛ℎ𝑥 𝑐𝑜𝑠ℎ𝑥 = 𝑒𝑥 − 𝑒−𝑥 𝑒𝑥 + 𝑒−𝑥 −1 < 𝑡𝑎𝑛ℎ𝑥 < 1 66
- 67. Exercise 2.10 cosh 2𝑙𝑛𝑥 Simplify the Following Expressions sinh 5𝑙𝑛𝑥 cosh(𝑙𝑛3) sinh(𝑙𝑛2) If 𝑠𝑖𝑛ℎ𝑥 = 3 4 , find the values of the remaining five hyperbolic functions.
- 68. sinh(𝑙𝑛2) Using the definition of sinh function, we write sinh 𝑙𝑛2 = 𝑒𝑙𝑛2 − 𝑒−𝑙𝑛2 2 = 2 − 1 2 2 = 3 4 68
- 69. sinh 5𝑙𝑛𝑥 Using the definition of sinh function, we write sinh 5𝑙𝑛𝑥 = 𝑒5𝑙𝑛𝑥 − 𝑒−5𝑙𝑛𝑥 2 = 𝑒ln 𝑥5 − 𝑒𝑙𝑛𝑥−5 2 = 𝑥5 − 𝑥−5 2 69
- 70. cosh(𝑙𝑛3) Using the definition of cosh function, we write cosh 𝑙𝑛3 = 𝑒ln 3 + 𝑒−𝑙𝑛3 2 = 3 + 1 3 2 = 10 6 = 5 3 70
- 71. If 𝑠𝑖𝑛ℎ𝑥 = 3 4 , find the values of the remaining five hyperbolic functions. Using the identity cosh2 𝑥 − sinh2 𝑥 = 1, we see that cosh2 𝑥 = 1 + 3 4 2 = 25 16 Since 𝑐𝑜𝑠ℎ𝑥 ≥ 1 for all x, we must have cosh 𝑥 = 5 4 . Then, using the definitions for the other hyperbolic functions, we conclude that 𝑡𝑎𝑛ℎ𝑥 = 3 5 , 𝑐𝑠𝑐ℎ𝑥 = 4 3 , 𝑠𝑒𝑐ℎ𝑥 = 4 5 , 𝑐𝑜𝑡ℎ𝑥 = 5 3 . 71
- 72. Hyperbolic Functions Hyperbolic cotangent of x 𝑐𝑜𝑡ℎ𝑥 = 𝑐𝑜𝑠ℎ𝑥 𝑠𝑖𝑛ℎ𝑥 = 𝑒𝑥 + 𝑒−𝑥 𝑒𝑥 − 𝑒−𝑥 Hyperbolic secant of x 𝑠𝑒𝑐ℎ𝑥 = 1 𝑐𝑜𝑠ℎ𝑥 = 2 𝑒𝑥 + 𝑒−𝑥 0 < 𝑠𝑒𝑐ℎ𝑥 ≤ 1 Hyperbolic of cosecant of x cscℎ𝑥 = 1 𝑠𝑖𝑛ℎ𝑥 = 2 𝑒𝑥−𝑒−𝑥 72
- 73. Exercise 2.11 cosh −𝑥 = 𝑐𝑜𝑠ℎ𝑥 Prove the Following Hyperbolic Functions sinh −𝑥 = −𝑠𝑖𝑛ℎ𝑥 𝑐𝑜𝑠ℎ𝑥 + 𝑠𝑖𝑛ℎ𝑥 = 𝑒𝑥 𝑐𝑜𝑠ℎ𝑥 − 𝑠𝑖𝑛ℎ𝑥 = 𝑒−𝑥 coth2 𝑥 − 1 = csch2 𝑥 sinh 𝑥 ± 𝑦 = 𝑠𝑖𝑛ℎ𝑥𝑐𝑜𝑠ℎ𝑦 ± 𝑐𝑜𝑠ℎ𝑥𝑠𝑖𝑛ℎ𝑦 cosh 𝑥 ± 𝑦 = 𝑐𝑜𝑠ℎ𝑥𝑐𝑜𝑠ℎ𝑦 ± 𝑠𝑖𝑛ℎ𝑥𝑠𝑖𝑛ℎ𝑦 tanh 𝑙𝑛𝑥 = 𝑥2 − 1 𝑥2 + 1 1 + 𝑡𝑎𝑛ℎ𝑥 1 − 𝑡𝑎𝑛ℎ𝑥 = 𝑒2𝑥
- 74. Assignment 2.1 2.1.1. 𝑦 = 𝑥2 + 6𝑥 − 8 2.1.2. 𝑦 = 7 + 2𝑥 − 𝑥2 2.1.3. 𝑦 = 2𝑥 + 5 2.1.4. 𝑦 = 2𝑥 + 5 2.1.5. 𝑦 = 2 − 𝑥 + 3 2.1.6. 𝑦 = 3 x+2 2.1.7. 𝑦 = 𝑥−4 2𝑥+3 2.1.8. 𝑦 = −2 − 4𝑥 − 𝑥2 2.1.9. 𝑦 = −𝑠𝑖𝑛2𝑥 2.1.10. 𝑦 = 1 2 1 + 𝑒𝑥 2.1.11. 𝑓 𝑥 = 1 𝑥+2 2.1.12. 𝑓 𝑥 = 5𝑥+1 + 2 2.1.13. 𝑓 𝑥 = 3 + 𝑙𝑛𝑥 2.1.14. 𝑓 𝑥 = ln 𝑥 − 1 2.1.15. 𝑓 𝑥 = 𝑙𝑜𝑔𝑥 − 1 2.1.16. 𝑓 𝑥 = ln −𝑥 2.1.17. 𝑓 𝑥 = 𝑒𝑥 + 2 2.1.18. 𝑓 𝑥 = 𝑒−𝑥 − 1 2.1.19. 𝑓 𝑥 = 4 cos 2𝑥 − 𝜋 2 2.1.20. 𝑓 𝑥 = −3sin(𝜋𝑥 + 2) 74 Graph each of the following functions then from the graph find its the domain and range.