Class3

Non
Deterministic
Automata
This ppt covers 2.2 ~ 2.4.

NFA 1

Nondeterministic FA
 As we know, any w *, then *(q0, w)
corresponds to a unique walk on the
transition graph of a DFA M.

 When we allow FA to act non-
deterministically, it implies *(q0, w) may
not correspond to a unique walk on the
transition graph of such FA anymore.

2

Nondeterministic Finite Accepter
(NFA)
= {a}

q1 a q2
a
q0
a
q3

3

(NFA)
= {a}
More than one choices
q1 a q2
a
q0
a
q3 (q0, a ) = {q1, q3 }

4

(NFA)
= {a} No transition!

q1 a q2
a
q0
a
q3
i.e., (q2, a ) = = (q3, a )
5

(NFA)
Consider input string aa :

q1 a q2
a
q0
a
q3
There are two computations!
6

Example
q1 a q2 q1 a q2
a a
q0 q0
a a
q3 q3

All input is consumed & No transition for (q3, a),
stops at a final state. the automaton hangs, a
dead configuration
aa is “accepted” aa is “rejected”

7

An NFA accepts a string:
when there is one computation of the NFA
that accepts the string

such that

all the input is consumed AND
the automaton is in a final state

Thus aa is “accepted” by the NFA.
8

Therefore, an NFA rejects a string:
when there is NO computation of the NFA
that accepts the string:

• All the input is consumed and the
automaton is in a non final state
OR
• The input cannot be consumed
(dead configuration)
9

Example
a is rejected by the NFA:

“reject”
q1 a q2 q1 a q2
a a
q0 q0
a a
q3 “reject” q3

All possible computations lead to rejection
10

Another Example
aaa is rejected by the NFA:
No transition:
“reject” the automaton hangs
q1 a q2 q1 a q2
a a
q0 q0
a a

“reject”
q3 q3

All possible computations lead to rejection
11

Language accepted: L {aa}

q1 a q2
a
q0
a
q3

12

Another NFA Example

transition is allowed for NFA

q0 a q1 b q2 q3

13

transition is allowed for NFA

It implies that the NFA can move from
state qi to state qj without moving the
read head, i.e. without consuming any
input symbol.

14

Another NFA Example
Consider the input string ab:
q0 a q1 b q2 ab is “accepted”
q0 a q1 b q2 q3 “rejected”
q0 a q1 b q2 q3 q0 “rejected”

q0 a q1 b q2 q3

15

Another String

a b a b

q0 a q1 b q2 q3

16

a b a b

q0 a q1 b q2 q3 q0 a q1 b q2

“accept”

q0 a q1 b q2 q3

17

Language accepted

L ab, abab, ababab, ...
ab

q0 a q1 b q2 q3

18

Another NFA Example

0
q0 q1 0, 1 q2
1

19

Language accepted

L(M ) = {λ, 10, 1010, 101010, ...}
= {10}*
(redundant state,
0 i.e. useless state)
q0 q1 0, 1 q2
1

20

NFAs are interesting because we can
express languages easier than DFAs

Example: design a FA for {a} with ={a}.

Example: design a FA for
{awa: w {a, b}*} with ={a, b}.

21

Formal Definition of NFAs (p.49)
M Q, , , q0 , F

Q : Set of states, Remember:
The is not a symbol,
: Input alphabet, it never appears on the

: Transition function
q0 : Initial state

F : Final states
22

NFA’s Transition Function
:Qx( { }) 2Q

Note that Every DFA is an NFA.

When input is , the original state is always a
member of its transition output, i.e. q (q, )

23

:Qx( { }) 2Q

q0 , 1 q1
0
q0 q1 0, 1 q2
1

24

:Qx( { }) 2Q
(q1,0) {q0 , q2}

0
q0 q1 0, 1 q2
1

25

:Qx( { }) 2Q
(q0 , ) {q0 , q2}

0
q0 q1 0, 1 q2
1

26

:Qx( { }) 2Q
(q2 ,1) . So as (q0, 0) & (q2, 0)

0
q0 q1 0, 1 q2
1

Remark: Every DFA is an NFA.

27

Extended Transition
Function *
Similar as DFA, extended transition function is
defined to work with inputs to be strings.
*
:Qx( { } )* 2Q
*
or simply :Qx * 2Q
When input string is empty ( ), the original state
is always a member of its extended transition, i.e.
q * q,
28

Extended Transition
Function *

* q0 , a q1

q4 q5
a a
q0 a q1 b q2 q3

29

* q0 , aa q4 , q5

q4 q5
a a
q0 a q1 b q2 q3

30

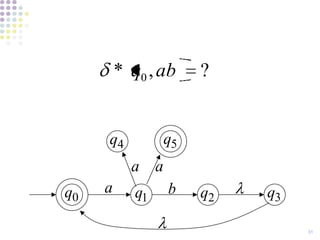
* q0 , ab ?

q4 q5
a a
q0 a q1 b q2 q3

31

* q0 , ab q2 , q3 , q0

q4 q5
a a
q0 a q1 b q2 q3

32

* q0 , b ?

q4 q5
a a
q0 a q1 b q2 q3

33

Consider the transition graph:

a * a
q0 q0

q1 q1

q2 q2

a
q0 q1 q2
34

Formally, for an NFA
There is a walk from qi to q j with label
w 1 2 ... k
qi w qj

if and only if q j * qi , w w 1 2 ... k

qi 1 2 k
qj

Def. 2.5 p.51
For an nfa, the extended transition function is
defined so that qj *( qi , w) iff there is a walk
in the transition graph from qi to qj labeled w.
35

Hw # 20 p.56

 Show that for any nfa

*
(q, wv) 
*
*
( p, v).
p ( q , w)

for all q Q, and all w, v *

36

The Language of an NFA M
aa
F q0 ,q5 q4 q5
a a
q0 a q1 b q2 q3

Consider the aa, or the walk from q0 with label
aa:
* q0 , aa q4 , q5 aa L(M )
F 37

ab
F q0 ,q5 q4 q5
a a
q0 a q1 b q2 q3

* q0 , ab q2 , q3 , q0 ab L M
F 38

abaa
F q0 ,q5 q4 q5
a a
q0 a q1 b q2 q3

* q0 , abaa q4 , q5 abaa L(M )
F 39

F q0 ,q5 q4 q5
a a
q0 a q1 b q2 q3

* q0 , aba q1 aba L M
F 40

q4 q5
a a
q0 a q1 b q2 q3

LM (ab) n aa : n 0

41

Formally
The language accepted by NFA M is:
LM w1, w2 , w3 ,...

where * (q0 , wm ) {qi , q j ,..., qk ,...}

and there is some qk F (final state)
42

w LM * (q0 , w)
qi
w
qk qk F
q0 w
w qj

L( M ) {w *: * ( q0, w) F }
43

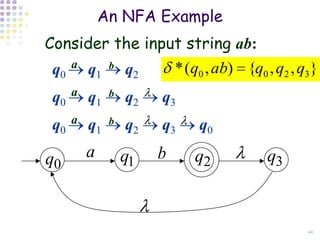
An NFA Example
q0 a q1 b q2 * (q0 , ab) {q0 , q2 , q3}
q0 a q1 b q2 q3
q0 a q1 b q2 q3 q0

q0 a q1 b q2 q3

44

* (q0 , ab) {q0 , q2 , q3}
q0 a q1 b q2 ab is “accepted”
q0 a q1 b q2 q3
q0 a q1 b q2 q3 q0

q0 a q1 b q2 q3

45

Another String

a b a b

q0 a q1 b q2 q3

46

q0 a q1 b q2 q3 q0 a q1 b q2

As long as there is one computation that
consumes all input symbols and stops at a final
state, aabb is accepted.
“accept”

q0 a q1 b q2 q3

47

Language accepted

L ab, abab, ababab, ...
ab

q0 a q1 b q2 q3

48

NFAs are interesting because we can
express languages easier than DFAs

Example: design an FA for {a} with ={a, b}.

Example: design an FA for
{awa: w {a, b}*} with ={a, b}.

49

Consider the transition graph:

a * a
q0 q0

q1 q1

q2 q2

a
q0 q1 q2
50

Hw # 20 p.56

 Show that for any nfa

*
(q, wv) U
*
*
( p, v).
p ( q , w)

for all q Q, and all w, v *

51

Remarks for FA M = {Q, , , q0, F }:
•The symbol never appears on the
input alphabet

•Simple NFA:

M1 M2
q0 q0

L(M1 ) = {} L(M 2 ) = {λ}
52

The language accepted by NFA M is:
L( M ) {w *: * ( q0, w) F }

Is it true that for any NFA M ,

L(M ) {w *: * ( q0, w) F }

Is it true that for any NFA M,
L(M ) {w *: * (q0, w) (Q F ) }
Referring to Hw 2.3 # 5, 6. P.62 53

NFAs accept the
Regular Languages
Hw of 2.2(p.54) 1 – 19 not hand in

NFA 54

Equivalence of Machines

Definition for Automata:

Machine M1 is equivalent to machine M 2
if L M1 L M2

55

Example of equivalent
machines
0
L M1 {10} *
q0 q1
NFA M1 1
0,1
0
L M2 {10}* q1 1 q2
q0
1
DFA M2 0
56

Which is more powerful?

 Every dfa is an nfa.
 Thus, every language accepted by
a dfa is also accepted by an nfa.
 Is nfa more powerful than dfa?

57

We will prove:

Languages
Regular
accepted
Languages
by NFAs
Languages
accepted
by DFAs
NFAs and DFAs have the
same computation power
58

Step 1

Languages
Regular
accepted
Languages
by NFAs

Proof: Every DFA is trivially an NFA

Any language L accepted by a DFA
is also accepted by an NFA
59

Step 2

Languages
Regular
accepted
Languages
by NFAs

Proof: Any NFA can be converted to an
equivalent DFA

Any language L accepted by an NFA
is also accepted by a DFA 60

Convert NFA to DFA
a
NFA M N q0 a q1 q2
b
* a b
q0
q1
q2

An extended transition
function is very helpful
61

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b

Let p0={q0} be the initial state for MD
DFA MD
q0
Back to Procedure NFA to DFA

62

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b

Now, define D(p0,a) for a
DFA MD D(p0,a) = N*({q0},a) ={q1,q2} p1

q0 a
q1, q2

63

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b
D(p0,b) = N*({q0},b) = p2
DFA MD
q0 a
q1, q2
b


64

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b
D(p1,a) = N*({q1,q2},a)= N*({q1},a) N*({q2},a)
= {q1,q2} = {q1,q2} = p1
DFA MD a
q0 a
q1, q2
b

65

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b
D(p1,b)
= N*({q1,q2},b) = N*({q1},b) N*({q2},b)
= {q0} {q0} = {q0} = p0
DFA MD b a
q0 a
q1, q2
b

66

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b
D(p2,a) = N*( ,a) = =p2= D(p2,b)

DFA MD b a

q0 a
q1, q2
b

a, b
67

Convert NFA to DFA
NFA M N a
q0 a q1 q2
b
How about final state? Lastly, check if L(M)
b a
DFA MD
q0 a
q1, q2
b
a, b back
68

NFA to DFA: Remarks

 We are given an NFA MN

 We want to convert it
to an equivalent DFA MD

 With L M N L( M D )
69

 If the NFA has states

q0 , q1, q2 ,...

 the DFA has states in the powerset

, q0 , q1 , q1, q2 , q3 , q4 , q7 ,....

70

Procedure NFA to DFA p.59

1. Initial state of NFA: q0

Initial state of DFA: p0 q0
To Conversion Example

71

Procedure NFA to DFA
2. For every DFA’s state pk {qi , q j ,..., qm }

Compute in the NFA
* qi , a ,
* q j,a , union {qi , q j ,..., qm}
...
Add transition to DFA To Convertion Example

D pk , a D {qi , q j ,..., qm }, a {qi , q j ,..., qm }
72


Repeat Step 2 for all letters in alphabet,
until
no more transitions can be added.
Remark:
In DFA, every vertex must have exactly | | outgoing
edges, each labeled with a different element of .
To Convertion Example

73

3. For any DFA state pk {qi , q j ,..., qm }

If some q j is a final state in the NFA

Then, make p k a final state in the DFA

Remark: If is accepted in the NFA then
p0 q0 should be a final state.
To Convertion Example
74

Theorem
Take NFA MN

Apply procedure to obtain DFA MD

Then MN and MD are equivalent :

L(MN) = L(MD)
75

Proof

L(MN) = L(MD)

L(MN) L(MD
) AND L(MN) L(MD
)

76

First we show: L(MN) L(MD
)

Take arbitrary: w L(MN)

We will prove: w L(MD)

77

w L(MN)

MN q0 w qf

w 1 2 ... k

MN q0 1 2 k
qf

78

We will show that if w L(MN)
w 1 2 ... k

MN q0 1 2 k
qf

1 2 k
MD
{q0} {q f ,...}
w L(MD)
79

More generally, we will show that if in MN :
(arbitrary walk) v a1a2 ... an
a1 a2 an
MN q0 qi qj ql qm

a1 a2 an
MD
{q0} {qi ,...} {q j ,...} {ql ,...} {qm ,...}

80

Proof by induction on |v|

Induction Basis: v a1

a1
MN q0 qi

a1
MD
{q0} {qi ,...}

81

Induction hypothesis: 1 |v| k
v a1a2 ... ak

a1 a2 ak
MN q0 qi qj qc qd

a1 a2 ak
MD
{q0} {qi ,...} {q j ,...} {qc ,...} {qd ,...}

82

Induction Step: |v| k 1
v a1a2 ... ak ak 1 v ak 1
v

a1 a2 ak
MN q0 qi qj qc qd

v
a1 a2 ak
MD
{q0} {qi ,....} {q j ,...} {qc ,...} {qd ,...}

v 83

Induction Step: |v| k 1
v a1a2 ... ak ak 1 v ak 1
v

a1 a2 ak ak 1
MN q0 qi qj qc qd qe

v
a1 a2 ak ak 1
MD
{q0} {qi ,...} {q j ,...} {qc ,...} {qd ,...} {qe ,...}

v 84

Therefore if w L(MN)
w 1 2 ... k

MN q0 1 2 k
qf

1 2 k
MD
{q0} {q f ,...}
w L(MD)
85

We have shown: L(MN) L(MD
)

We also need to show: L(MN) L(MD
)
(proof is similar)

86

Example
a b
NFA
q0 , a, b q1 a, b q2

Convert NFA to DFA Simplified version of DFA
a a

a p1 p1
b a, b a, b
p0 b b
b p2 a, b p3 a p4 p2 a, b p3

Ex. 2.13 Fig. 2.14 (p.59)– in class (you
can eliminate the redundant state first) 87

Minimal DFAs

 A dfa M’ is minimal if M is also a dfa such
that L(M’)=L(M) then |QM | |QM’|

88

Minimal DFAs

 States p and q are called indistinguishable if
* ( p, w) F implies * (q, w) F
and
* ( p, w) F implies * (q, w) F
for all w *

 States p and q are called distinguishable if
w * such that * ( p, w) F and * (q, w) F
89

Minimal DFAs
 To obtain a minimal DFA M’ from a given DFA M:
 Remove all inaccessible states, i.e. not reachable from the
initial state.
 Reduce states until it has no more indistinguishable states.

 Read procedures: mark (p.64) & reduce (p.66), and
theorem 2.3 (p.65) & 2.4 (p.67) for details.
Remove all inaccessible states can be accomplished
by enumerating all simple paths of the graph of the
dfa starting at the initial state, any state not part of
some path is inaccessible. 90

Example: Minimal DFAs

q1 0,1
0 1
0 0
q0 q2 1 q4
0 1
1 0
q3 q5
1

91

Minimal DFAs
Prove or Disprove:
 If M = (Q, , , q0, F) is a minimal DFA for a
regular language L, then M’ = (Q, , , q0, Q-F)
is a minimal DFA for the complement of L.

92

Minimal DFAs
 Prove or Disprove:
 If M = (Q, , , q0, F) is a minimal DFA for a
regular language L, then M’ = (Q, , , q0,
Q-F) is a minimal DFA for the complement of
L.

93

Homework Discussion
 2.3 (p.62) Discuss 7, 8, 11, 14, 15

Homework
2.3 (p.62) 1 ~15 & 2.4 (p.68) 1, 2, 4, 6
Hand in: 3, 5, 6, 9, 12 (p.62) & 2ae (p.68)

94

Class3

Recommended

More Related Content

What's hot (20)

Viewers also liked (9)

Similar to Class3 (20)

More from issbp (20)

Class3