Ad
Cleaned_Lecture 9_Numerical optimization.pdf
- 1. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Lecture 9: Numerical optimization Professor Amany E. Aly Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt. 16 / 12 / 2024 Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 1 / 122
- 2. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Presentation Outline 1 Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Alternatives to lp() Quadratic programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 2 / 122
- 3. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Numerical optimization In many areas of statistics and applied mathematics one has to solve the following problem: given a function f(.), which value of x makes f(x) as large or as small as possible? Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 3 / 122
- 4. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming For example, in financial modeling f(x) might be the expected return from a portfolio, with x being a vector holding the amounts invested in each of a number of possible securities. There might be constraints on x (e.g. the amount to invest must be positive, the total amount invested must be fixed, etc.). Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 4 / 122
- 5. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming In statistical modeling, we may want to find a set of parameters for a model which minimize the expected prediction errors for the model. Here x would be the parameters and f(.) would be a measure of the prediction error. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 5 / 122
- 6. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Knowing how to do minimization is sufficient. If we want to maximize f(x), we simply change the sign and minimize −f(x). We call both operations ”numerical optimization”. Use of derivatives and simple algebra often lead to the solution of such problems, but not nearly always. Because of the wide range of possibilities for functions f(.) and parameters x, this is a rich area of computing. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 6 / 122
- 7. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The golden section search method The golden section search method is a simple way of finding the minimizer of a single-variable function which has a single minimum on the interval [a, b]. Consider minimizing the function f(x) = |x − 3.5| + (x − 2)2 on the interval [0, 5]. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 7 / 122
- 8. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming This function is not differentiable at x = 3.5, so some care must be taken to find the minimizer. We can write an R function to evaluate f(x) as follows: Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 8 / 122
- 9. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming To check that this function has a single minimum in the interval we use the curve() function to plot it: The curve is displayed in the next figure, where we can see that the minimizer is located near x = 2.5. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 9 / 122
- 10. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The function f(x) = |x − 3.5| + (x − 2)2 Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 10 / 122
- 11. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The golden section search method is an iterative method, which may be outlined as follows: 1. Start with the interval [a, b], known to contain the minimizer. 2. Repeatedly shrink it, finding smaller and smaller intervals [a0 , b0 ] which still contain the minimizer. 3. Stop when b0 −a0 is small enough, i.e. when the interval length is less than a pre-set tolerance. When the search stops, the midpoint of the final interval will serve as a good approximation to the true minimizer, with a maximum error of (b0 − a0 )/2. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 11 / 122
- 12. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The shrinkage step 2 begins by evaluating the function at two points x1 < x2 in the interior of the interval [a, b]. How the points are chosen will be described below. Because we have assumed that there is a unique minimum, we know that if f(x1) > f(x2), then the minimum must lie to the right of x1, i.e. in the interval [a0 , b0 ] = [x1, b]. If f(x1) < f(x2), the minimum must lie in [a0 , b0 ] = [a, x2] (see the next figure). Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 12 / 122
- 13. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming One iteration of the golden section search, applied to the test function f(x) = |x − 3.5| + (x − 2)2 Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 13 / 122
- 14. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming What if the values are exactly equal? Convince yourself that we can choose either update. Then new values of x1, f(x1), x2, and f(x2) are computed, and the method is repeated until the tolerance criterion is satisfied. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 14 / 122
- 15. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The choice of the points between a and b makes use of prop- erties of the golden ratio φ = ( √ 5 + 1)/2. The golden ratio has a number of interesting algebraic prop- erties. We make use of the fact that 1/φ = φ−1 and 1/φ2 = 1−1/φ in the following. Some authors call the value Φ = 1/φ the ”silver ratio”, but we’ll stick with φ in our formulas. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 15 / 122
- 16. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We locate the interior points at x1 = b − (b − a)/φ and x2 = a + (b − a)/φ. The reason for this choice is as follows: After one iteration of the search, it is possible that we will throw away a and replace it with a0 = x1. Then the new value to use as x1 will be x 0 1 = b − (b − a0 )/φ = b − (b − x1)/φ = b − (b − a)/φ2 = a + (b − a)/φ = x2, Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 16 / 122
- 17. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming i.e. we can re-use a point we already have, we do not need a new calculation to find it, and we don’t need a new evaluation of f(x 0 1), we can re-use f(x2). Similarly, if we update to b0 = x2, then x 0 2 = x1, and we can re-use that point. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 17 / 122
- 18. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We put this together into the following R function. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 18 / 122
- 19. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We test and see that golden() works, at least on one function: Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 19 / 122
- 20. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Solve exercises from 1 to 3 on pages 224 and 225 . Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 20 / 122
- 21. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Newton-Raphson If the function to be minimized has two continuous derivatives and we know how to evaluate them, we can make use of this information to give a faster algorithm than the golden section search. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 21 / 122
- 22. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We implement this idea as follows, using the Newton-Raphson algorithm to approximate a solution to f0 (x∗ ) = 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 22 / 122
- 23. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Start with an initial guess x0, and compute an improved guess using the solution x1 = x0 − f0 (x0) f00(x0) . This gives a new guess at the minimizer. Then use x1 in place of x0, to obtain a new update x2. Con- tinue with iterations of the form xn+1 = xn − f0 (xn) f00(xn) Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 23 / 122
- 24. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming This iteration stops when f0 (xn) is close enough to 0. Usually, we set a tolerance and stop when |f0 (xn)| . It can be shown that the Newton-Raphson method is guaran- teed to converge to a local minimizer, provided the starting value x0 is close enough to the minimizer and enough contin- uous derivatives exist. As with other numerical optimization techniques, where there are multiple minimizers, Newton-Raphson won’t necessarily find the best one. However, when f00 (xn) 0 everywhere, there will be only one minimizer. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 24 / 122
- 25. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.1 We wish to find the minimizer of f(x) = e−x + x4 . By inspection, we can guess that the minimizer is somewhere to the right of zero, because e−x is a decreasing function, and x4 has a minimum at zero. We start by plotting the function to find an initial guess Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 25 / 122
- 26. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The function f(x) = e−x + x4 Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 26 / 122
- 27. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 27 / 122
- 28. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming From the figure, we can see that the minimizer is somewhere near x0 = 0.5; we will use that as our starting value. Because of the difficulties mentioned above, we will not at- tempt to write a general Newton-Raphson implementation. Instead, we will simply evaluate several updates to see whether it converges or not. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 28 / 122
- 29. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 29 / 122
- 30. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We see that convergence was very rapid, with the derivative numerically equal to zero by the fourth update. The second derivative is positive there, confirming that this is a local minimum. In fact, since f00 (x) = e−x + 12x2 , the second derivative is positive everywhere, and we can be sure that this is a global minimum. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 30 / 122
- 31. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The Nelder-Mead simplex method The Nelder-Mead simplex algorithm is one method for opti- mization of a function of several variables. In p dimensions, it starts with p+1 points x1, ..., xp+1, arranged so that when considered as vertices of a p−dimensional solid (a ”simplex”), they enclose a non-zero volume. For example, in two dimensions the three points would not be allowed to all lie on one line so they would form a triangle, and in three dimensions the four points would form a proper tetrahedron. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 31 / 122
- 32. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The points are labeled in order from smallest to largest values of f(xi), so that f(x1) ⩽ f(x2) ⩽ ... ⩽ f(xp+1). The idea is that to minimize f(x), we would like to drop xp+1 and replace it with a point that gives a smaller value. We do this by calculating several proposed points zi from the existing points. There are four kinds of proposals, illustrated in the next Figure in two dimensions. The first three refer to the midpoint of x1, ..., xp which we calculate as xmid = (x1 + ... + xp)/p. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 32 / 122
- 33. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The four types of proposals of the Nelder-Mead algorithm, illustrated in two dimensions. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 33 / 122
- 34. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming 1. Reflection: reflect xp+1 through xmid to z1. 2. Reflection and expansion: reflect xp+1 through xmid, and dou- ble its distance, giving z2. 3. Contraction 1: contract xp+1 halfway towards xmid to give z3. 4. Contraction 2: contract all points halfway towards x1, giving z4, ..., zp+3. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 34 / 122
- 35. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We consider each of these choices of simplex in order, based on the values of f(zi). It is helpful to consider the line shown in the next Figure as you read through the following pseudocode outline of the decision process for one update of the simplex: f(z1) will fall in region A, B, C, or D in the Nelder-Mead algorithm. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 35 / 122
- 36. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 36 / 122
- 37. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.2 In this example we try to minimize the function Using the Nelder-Mead algorithm. We start by drawing a contour plot of the function, in order to get approximate starting values. After some experimentation, we obtain the plot shown in next Figure using the following code. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 37 / 122
- 38. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 38 / 122
- 39. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Contour plot of f(x, y) = [(x − y)2 + (x − 2)2 + (y − 3)4 ]/10. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 39 / 122
- 40. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We implemented the Nelder-Mead update algorithm in an R function with header neldermead(x, f), where x is our matrix in the pseudocode, and f is the function. The output of neldermead(x, f) is an updated copy of the matrix X. The following log shows the output of nine Nelder-Mead up- dates. Figure 8.7 shows the steps the algorithm took in this demon- stration. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 40 / 122
- 41. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Nine Nelder-Mead updates for f(x, y) = [(x − y)2 + (x − 2)2 + (y − 3)4 ]/10. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 41 / 122
- 42. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 42 / 122
- 43. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming At the end of these nine steps, we see that x should be around 1.9 − 2.6, and y should be around 2.4 − 2.7. A further 50 updates narrows these down to the true minimum at (x, y) = (2.25, 2.5). Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 43 / 122
- 44. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Built-in functions There are several general purpose optimization functions in R. For one-dimensional optimization, the optimize() function performs a variation on the golden section search we described earlier. There are also multi-dimensional optimizers. The first of these is the optim() function. optim() is a general purpose wrapper for several different optimization methods, including Nelder-Mead, variations on Newton-Raphson, and others that we haven’t discussed. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 44 / 122
- 45. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Syntax optim(par, fn, ...) The par parameter to optim() gives starting values for the parameters. Besides telling optim() where to begin, these indicate how many parameters will vary in its calls to fn, the second pa- rameter. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 45 / 122
- 46. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming fn is an R function which evaluates the function to be mini- mized. Its first argument should be a vector of the same length as par; optim() will call it repeatedly, varying the value of this param- eter, in order to find the minimum. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 46 / 122
- 47. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming It should return a scalar value. The optim() function has a number of optional parameters described on its help page. Besides those, the optional parameters in the ... list could include additional parameters to pass to fn. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 47 / 122
- 48. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming There are other functions in R for general function optimiza- tion: nlm() and nlminb(). In most cases optim() is preferred because it offers more flex- ibility, but there may be instances where one of the others performs better. The constrOptim() function is aimed at cases where there are linear inequalities expressing constraints on the parameters. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 48 / 122
- 49. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Solve exercises from 1 to 3 on page 231. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 49 / 122
- 50. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Linear programming We often need to minimize (or maximize) a function subject to constraints. When the function is linear and the constraints can be ex- pressed as linear equations or inequalities, the problem is called a linear programming problem. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 50 / 122
- 51. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The so-called standard form for the minimization problem in linear programming is Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 51 / 122
- 52. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The idea is to find values of the decision variables x1, x2, ..., xn which minimize the objective function C(x), subject to the con- straints and nonnegativity conditions. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 52 / 122
- 53. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.3 A company has developed two procedures for reducing sulfur diox- ide and carbon dioxide emissions from its factory. The first proce- dure reduces equal amounts of each gas at a per unit cost of $5. The second procedure reduces the same amount of sulfur dioxide as the first method, but reduces twice as much carbon dioxide gas; the per unit cost of this method is $8. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 53 / 122
- 54. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The company is required to reduce sulfur dioxide emissions by 2 million units and carbon dioxide emissions by 3 million units. What combination of the two emission procedures will meet this requirement at minimum cost? Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 54 / 122
- 55. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Solution Let x1 denote the amount of the first procedure to be used, and let x2 denote the amount of the second procedure to be used. For convenience, we will let these amounts be expressed in millions of units. Then the cost (in millions of dollars) can be expressed as C = 5 x1 + 8 x2. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 55 / 122
- 56. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Since both methods reduce sulfur dioxide emissions at the same rate, the number of units of sulfur dioxide reduced will then be x1 + x2. There is a requirement to reduce the sulfur dioxide amount by 2 million units, we have the constraint x1 + x2 ⩾ 2. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 56 / 122
- 57. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The carbon dioxide reduction requirement is 3 million units, and the second method reduces carbon dioxide twice as fast as the first method, so we have the second constraint x1 + 2 x2 ⩾ 3. Finally, we note that x1 and x2 must be nonnegative, since we cannot use negative amounts of either procedure. x1, x2 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 57 / 122
- 58. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Thus, we obtain the linear programming problem: min C = 5 x1 + 8 x2 subject to the constraints x1 + x2 ⩾ 2, x1 + 2 x2 ⩾ 3, and x1, x2 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 58 / 122
- 59. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming A graphical interpretation of the pollution emission linear programming example. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 59 / 122
- 60. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The region shaded in grey is the feasible region; this is the set of all possible (x1, x2) combinations which satisfy the con- straints. The unshaded area contains those combinations of values where the constraints are violated. The grey region corresponds to values of x1 and x2 which satisfy all of the constraints. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 60 / 122
- 61. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The dashed grey line corresponds to values of x1 and x2 which give the minimum cost (13); This line intersects the feasible region at exactly one point-the optimal solution to the problem (1,1). The gradient of the function C(x) is (5,8), so this vector gives the direction of most rapid increase for that function. The level sets or contours of this function are perpendicular to this vector. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 61 / 122
- 62. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming One of the level sets is indicated as a dashed line in previous Figure. The solution of the minimization problem lies at the intersec- tion of the first contour which intersects the feasible region. If this happens at a single point, we have a unique minimizer. In this example, this intersection is located at the point (1,1). Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 62 / 122
- 63. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming It can be shown that the only possible minimizers for such lin- ear programming problems must be at the intersections of the constraint boundaries, as in the above example. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 63 / 122
- 64. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The points of intersection of the constraints are called basic solutions. If these intersection points lie in the feasible region, they are called basic feasible solutions. If there is at least one basic feasible solution, then one of them will be an optimal solution. In the above example, the point (1,1) is the optimal solution. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 64 / 122
- 65. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Solving linear programming problems in R There is more than one linear programming function available in R, but we believe the lp() function in the lpSolve package may be the most stable version currently available. It is based on the revised simplex method; this method in- telligently tests a number of extreme points of the feasible region to see whether they are optimal. As usual, we load the package as follows Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 65 / 122
- 66. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The lp() function has a number of parameters; the following are needed to solve minimization problems like the one in the earlier example. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 66 / 122
- 67. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming objective.in−the vector of coefficients of the objective func- tion. const.mat−a matrix containing the coefficients of the decision variables in the left-hand side of the constraints; each row corresponds to a constraint. const.dir−acharacter vector indicating the direction of the constraint inequalities; some of the possible entries are =, == and =. const.rhs−a vector containing the constants given on the right-hand side of the constraints. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 67 / 122
- 68. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.4 To solve the minimization problem set out in Example 8.3, type The output tells us that the minimizer is at x1 = 1, x2 = 1, and the minimum value of the objective function is 13. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 68 / 122
- 69. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Maximization and other kinds of constraints The lp() function can handle maximization problems with the use of the direction = ”max” parameter. The const.dir parameter allows for different types of inequal- ities. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 69 / 122
- 70. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.5 Solve the problem: max C = 5 x1 + 8 x2, subject to the constraints x1 + x2 ⩽ 2, x1 + 2 x2 = 3, and x1, x2 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 70 / 122
- 71. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming In R, this can be coded as The solution is (1,1), giving a maximum value of 13. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 71 / 122
- 72. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Special situations 1. Multiple optima It sometimes happens that there are multiple solutions for a linear programming problem. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 72 / 122
- 73. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.6 A slight modification of the pollution emission Example 8.3 is min C = 4 x1 + 8 x2, subject to the constraints x1 + x2 ⩽ 2, x1 + 2 x2 = 3, and x1, x2 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 73 / 122
- 74. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming This problem has a solution at (1,1) as well as at (3,0). All points on the line joining these two points are solutions as well. Figure 8.9 shows this graphically. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 74 / 122
- 75. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The lp() function does not alert the user to the existence of multiple minima. In fact, the output from this function for the modified pollution emission example is the solution x1 = 3, x2 = 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 75 / 122
- 76. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming A plot of the gradient of the objective function and the constraint boundaries for Example 8.6. The points on the heavy black segment are all optimal for this problem. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 76 / 122
- 77. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming 2. Degeneracy For a problem with m decision variables, degeneracy arises when more than m constraint boundaries intersect at a single point. This situation is quite rare, but it has potential to cause diffi- culties for the simplex method, so it is important to be aware of this condition. In very rare circumstances, degeneracy can prevent the method from converging to the optimal solution; most of the time, however, there is little to worry about. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 77 / 122
- 78. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.7 The following problem has a point of degeneracy which is not at the optimum; however, the lp() function still finds the optimum without difficulty. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 78 / 122
- 79. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming min C = 3 x1 + x2, subject to the constraints x1 + x2 ⩽ 2, x1 + 2 x2 ⩾ 3, x1 + 3 x2 ⩾ 4, 4 x1 + x2 ⩾ 4, and x1, x2 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 79 / 122
- 80. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming A plot of four constraint boundaries, one of which is redundant, leading to degeneracy. The feasible region is shaded. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 80 / 122
- 81. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 81 / 122
- 82. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming 3. Infeasibility Infeasibility is a more common problem. When the constraints cannot simultaneously be satisfied there is no feasible region. Then no feasible solution exists. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 82 / 122
- 83. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.8 In the following example, it is obvious that the constraints cannot simultaneously be satisfied. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 83 / 122
- 84. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming min C = 5 x1 + 8 x2, subject to the constraints x1 + x2 ⩽ 2, x1 + x2 ⩽ 1, and x1, x2 ⩾ 0. Here is the output from the lp() function: Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 84 / 122
- 85. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 85 / 122
- 86. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming 4. Unboundedness In rare instances, the constraints and objective function give rise to an unbounded solution. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 86 / 122
- 87. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.9 A trivial example of unboundedness arises when solving the prob- lem max C = 5 x1 + 8 x2, subject to the constraints x1 + x2 ⩽ 2, x1 + 2 x2 ⩽ 3, and x1, x2 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 87 / 122
- 88. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The feasible region for this problem is the same as for Example 8.3 and is plotted in Figure 8.8. However, instead of trying to minimize the objective function, we are now maximizing, so we follow the direction of increasing the objective function this time. We can make the objective function as large as we wish, by taking x1 and x2 arbitrarily large. Here is what happens when lp() is applied to this problem: Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 88 / 122
- 89. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 89 / 122
- 90. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The condition of unboundedness will most often arise when con- straints and/or the objective function have not been formulated correctly. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 90 / 122
- 91. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming 5. Unrestricted variables Sometimes a decision variable is not restricted to be nonneg- ative. The lp() function is not set up to handle this case directly. However, a simple device gets around this difficulty. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 91 / 122
- 92. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming If x is unrestricted in sign, then x can be written as x1 − x2, where x1 ⩾ 0 and x2 ⩾ 0. This means that every unrestricted variable in a linear pro- gramming problem can be replaced by the difference of two nonnegative variables. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 92 / 122
- 93. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.10 Solve the problem: min C = x1 + 10 x2, subject to the constraints x1 + x2 ⩾ 2, x1 − 2 x2 ⩽ 3, and x1 ⩾ 0. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 93 / 122
- 94. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming x2 is unrestricted in sign, we set x2 = x3 − x4 for nonnegative x3 and x4. Plugging these new variables into the problem gives Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 94 / 122
- 95. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming min C = x1 + 10 x3 − 10 x4, subject to the constraints x1 + x3 − x4 ⩾ 2, x1 − x3 + x4 ⩽ 3, and x1 ⩾ 0, x3 ⩾, x4 ⩾ 0. Converting this to R code, we have Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 95 / 122
- 96. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The solution is given by x1 = 2.5 and x2 = x3 − x4 = −0.5. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 96 / 122
- 97. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Integer programming Decision variables are often restricted to be integers. For example, we might want to minimize the cost of shipping a product by using one, two, or three different trucks. It is not possible to use a fractional number of trucks, so the number of trucks must be integer-valued. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 97 / 122
- 98. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Problems involving integer-valued decision variables are called integer programming problems. Simple rounding of a non-integer solution to the nearest inte- ger is not good practice; the result of such rounding can be a solution which is quite far from the optimal solution. The lp() function has a facility to handle integer-valued vari- ables using a technique called the branch and bound algorithm. The int.vec argument can be used to indicate which variables have integer values. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 98 / 122
- 99. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.11 Find nonnegative x1, x2, x3, and x4 to minimize C(x) = 2 x1 + 3 x2 + 4 x3 − x 4, subject to the constraints x1 + 2 x2 ⩾ 9, 3 x2 + x3 ⩾ 9, and x2 + x4 ⩽ 10. Furthermore, x2 and x4 can only take integer values. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 99 / 122
- 100. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming To set up and solve this problem in R, type Thus, the best solution when x2 and x4 are integer-valued is x1 = 1, x2 = 4, x3 = 0, and x4 = 6. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 100 / 122
- 101. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Here is what happens when the integer variables are ignored: Rounding the solution to the nearest integer will lead to a violation of the first constraint (if x2 is taken to be 4) or to a minimum value of the objective function that is larger than 8 (if x2 = 5). Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 101 / 122
- 102. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Alternatives to lp() The lp() function provides an interface to code written in C. There is another function in the linprog package called solveLP() which is written entirely in R; This latter function solves large problems much more slowly than the lp() function, but it provides more detailed output. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 102 / 122
- 103. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming We note also the function simplex() in the boot package. It should also be noted that, for very large problems, the sim- plex method might not converge quickly enough; other proce- dures, based on interior point methods, often perform better. See the Optimization and Mathematical Programming task view for the latest packages. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 103 / 122
- 104. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Quadratic programming Linear programming problems are a special case of optimiza- tion problems in which a possibly nonlinear function is mini- mized subject to constraints. Such problems are typically more difficult to solve and are be- yond the scope of this text; an exception is the case where the objective function is quadratic and the constraints are linear. This is a problem in quadratic programming. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 104 / 122
- 105. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming A quadratic programming problem with k constraints is often of the form min β 1 2 βT Dβ − dT β, subject to constraints AT β ⩾ b. β is a vector of p unknowns, D is a positive definite p × p matrix, d is vector of length p, A is a p × k matrix, b is a vector of length k. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 105 / 122
- 106. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.12 Consider the following 20 pairs of observations on the variables x and y. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 106 / 122
- 107. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming A scatterplot of the 20 observations with a line of slope 1 and intercept 0.05 overlaid. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 107 / 122
- 108. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Our problem is to pass a line of ”best fit” through these data. We seek a line of the form y = β0 + β1 x, where β0 is the y-intercept and β1 is the slope. However, we have additional background information about these data that indicate that the slope β1 of the required line is at least 1. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 108 / 122
- 109. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The line we want is the one that minimizes the sum of the squared vertical distances between the observed points and the line itself: min β0, β1 20 X i=1 (yi − β0 − β1 xi)2 Our extra information about the slope tells us that this mini- mization is subject to the constraint β1 ⩾ 1. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 109 / 122
- 110. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming This is an example of a restricted least-squares problem and is equivalent to min β βT XT X β − 2Y T X β, subject to AT β ⩾ b, where A = [0 1]T , β = [β0 β1]T , y is a column vector consisting of the 22 y measurements, and X is a matrix consisting of two columns, where the first column contains only 1’s and the second column contains the 22 x observations: Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 110 / 122
- 111. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming X = 1 x1 1 x2 . . . . . . 1 xn = 1 0.45 1 0.08 . . . . . . 1 2.09 . We then have XT X = n Pn i=1 xi Pn i=1 xi Pn i=1 x2 i = 22 0 0 29.0132 , Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 111 / 122
- 112. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming and yT X = Pn i=1 yi Pn i=1 xiyi = 1.1 28.6626 . This is a quadratic programming problem with D = XT X and d = XT y. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 112 / 122
- 113. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Linear programming methods have been adapted to handle quadratic programming problems. The solve.QP() function is in the quadprog package. It solves minimization problems, and the following are param- eters which are required: Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 113 / 122
- 114. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Dmat−a matrix containing the elements of the matrix (D) of the quadratic form in the objective function. dvec−a vector containing the coefficients of the decision vari- ables in the objective function. Amat−a matrix containing the coefficients of the decision variables in the constraints; each row of the matrix corresponds to a constraint. bvec−a vector containing the constants given on the right- hand side of the constraints. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 114 / 122
- 115. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming mvec−a number indicating the number of equality constraints. By default, this is 0. If it is not 0, the equality constraints should be listed ahead of the inequality constraints. The output from this function is a list whose first two elements are the vector that minimizes the function and the minimum value of the function. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 115 / 122
- 116. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.13 For the restricted least squares problem of Example 8.12, we must first set up the matrices D and A as well as the vectors b and d. Here, D = XT X and d = XT y. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 116 / 122
- 117. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 117 / 122
- 118. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming From the output, we see that the required line is b y = 0.05 + x. The rest of the output is indicating that the constraint is ac- tive. If the unconstrained problem had yielded a slope larger than 1, the constraint would have been inactive, and the solution to the unconstrained problem would be the same as the solution to the constrained problem. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 118 / 122
- 119. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming The decision variables in the above example were not restricted in sign. If needed, nonnegativity conditions must be explicitly set when using the solve.QP() function. The inequality constraints are all of the form =. If your problem contains some inequality constraints with =, then the constraints should be multiplied through by -1 to convert them to the required form. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 119 / 122
- 120. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming There are more efficient ways to solve restricted least squares problems in other computing environments. The matrix D in the preceding example is a diagonal matrix, and this special structure can be used to reduce the compu- tational burden. The following example involves a full matrix. This example also places a restriction on the sign of the deci- sion variables. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 120 / 122
- 121. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Example 8.14 Assignment Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 121 / 122
- 122. Lecture 9: Numerical optimization Professor Amany E. Aly Numerical optimization The golden section search method Newton-Raphson The Nelder-Mead simplex method Built-in functions Linear programming Solving linear programming problems in R Maximization and other kinds of constraints Special situations Unrestricted variables Integer programming Solve exercises 1 and 2 on pages 246 and 247. Solve chapter exercises from 1 to 6 on page 247. Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.) Lecture 9: Numerical optimization 16 / 12 / 2024 122 / 122






![Lecture 9:
Numerical
optimization
Professor
Amany E. Aly
Numerical
optimization
The golden
section search
method
Newton-Raphson
The
Nelder-Mead
simplex method
Built-in
functions
Linear
programming
Solving linear
programming
problems in R
Maximization
and other kinds
of constraints
Special
situations
Unrestricted
variables
Integer
programming
The golden section search method
The golden section search method is a simple way of finding
the minimizer of a single-variable function which has a single
minimum on the interval [a, b].
Consider minimizing the function
f(x) = |x − 3.5| + (x − 2)2
on the interval [0, 5].
Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.)
Lecture 9: Numerical optimization 16 / 12 / 2024 7 / 122](https://image.slidesharecdn.com/cleanedlecture9numericaloptimization-250430115014-b516dfea/85/Cleaned_Lecture-9_Numerical-optimization-pdf-7-320.jpg)



![Lecture 9:
Numerical
optimization
Professor
Amany E. Aly
Numerical
optimization
The golden
section search
method
Newton-Raphson
The
Nelder-Mead
simplex method
Built-in
functions
Linear
programming
Solving linear
programming
problems in R
Maximization
and other kinds
of constraints
Special
situations
Unrestricted
variables
Integer
programming
The golden section search method is an iterative method, which
may be outlined as follows:
1. Start with the interval [a, b], known to contain the minimizer.
2. Repeatedly shrink it, finding smaller and smaller intervals [a0
, b0
]
which still contain the minimizer.
3. Stop when b0
−a0
is small enough, i.e. when the interval length
is less than a pre-set tolerance.
When the search stops, the midpoint of the final interval will serve
as a good approximation to the true minimizer, with a maximum
error of (b0
− a0
)/2.
Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.)
Lecture 9: Numerical optimization 16 / 12 / 2024 11 / 122](https://image.slidesharecdn.com/cleanedlecture9numericaloptimization-250430115014-b516dfea/85/Cleaned_Lecture-9_Numerical-optimization-pdf-11-320.jpg)
![Lecture 9:
Numerical
optimization
Professor
Amany E. Aly
Numerical
optimization
The golden
section search
method
Newton-Raphson
The
Nelder-Mead
simplex method
Built-in
functions
Linear
programming
Solving linear
programming
problems in R
Maximization
and other kinds
of constraints
Special
situations
Unrestricted
variables
Integer
programming
The shrinkage step 2 begins by evaluating the function at two
points x1 < x2 in the interior of the interval [a, b].
How the points are chosen will be described below.
Because we have assumed that there is a unique minimum, we
know that if f(x1) > f(x2), then the minimum must lie to
the right of x1,
i.e. in the interval [a0
, b0
] = [x1, b].
If f(x1) < f(x2), the minimum must lie in [a0
, b0
] = [a, x2]
(see the next figure).
Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.)
Lecture 9: Numerical optimization 16 / 12 / 2024 12 / 122](https://image.slidesharecdn.com/cleanedlecture9numericaloptimization-250430115014-b516dfea/85/Cleaned_Lecture-9_Numerical-optimization-pdf-12-320.jpg)

























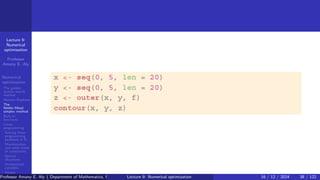
![Lecture 9:
Numerical
optimization
Professor
Amany E. Aly
Numerical
optimization
The golden
section search
method
Newton-Raphson
The
Nelder-Mead
simplex method
Built-in
functions
Linear
programming
Solving linear
programming
problems in R
Maximization
and other kinds
of constraints
Special
situations
Unrestricted
variables
Integer
programming
Contour plot of f(x, y) = [(x − y)2
+ (x − 2)2
+ (y − 3)4
]/10.
Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.)
Lecture 9: Numerical optimization 16 / 12 / 2024 39 / 122](https://image.slidesharecdn.com/cleanedlecture9numericaloptimization-250430115014-b516dfea/85/Cleaned_Lecture-9_Numerical-optimization-pdf-39-320.jpg)

![Lecture 9:
Numerical
optimization
Professor
Amany E. Aly
Numerical
optimization
The golden
section search
method
Newton-Raphson
The
Nelder-Mead
simplex method
Built-in
functions
Linear
programming
Solving linear
programming
problems in R
Maximization
and other kinds
of constraints
Special
situations
Unrestricted
variables
Integer
programming
Nine Nelder-Mead updates for
f(x, y) = [(x − y)2
+ (x − 2)2
+ (y − 3)4
]/10.
Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.)
Lecture 9: Numerical optimization 16 / 12 / 2024 41 / 122](https://image.slidesharecdn.com/cleanedlecture9numericaloptimization-250430115014-b516dfea/85/Cleaned_Lecture-9_Numerical-optimization-pdf-41-320.jpg)




































































![Lecture 9:
Numerical
optimization
Professor
Amany E. Aly
Numerical
optimization
The golden
section search
method
Newton-Raphson
The
Nelder-Mead
simplex method
Built-in
functions
Linear
programming
Solving linear
programming
problems in R
Maximization
and other kinds
of constraints
Special
situations
Unrestricted
variables
Integer
programming
This is an example of a restricted least-squares problem and is
equivalent to
min
β
βT
XT
X β − 2Y T
X β,
subject to AT
β ⩾ b, where A = [0 1]T
, β = [β0 β1]T
, y is a
column vector consisting of the 22 y measurements, and X is a
matrix consisting of two columns, where the first column contains
only 1’s and the second column contains the 22 x observations:
Professor Amany E. Aly ( Department of Mathematics, Faculty of Science, Helwan University, Ain Helwan, Cairo, Egypt.)
Lecture 9: Numerical optimization 16 / 12 / 2024 110 / 122](https://image.slidesharecdn.com/cleanedlecture9numericaloptimization-250430115014-b516dfea/85/Cleaned_Lecture-9_Numerical-optimization-pdf-110-320.jpg)

































































