Computer algorithm(Dynamic Programming).pdf

1
Computer Algorithms
Segment 3
Dynamic Programming

2
Why Dynamic Programming?
• Divide-and-Conquer: a top-down approach. Many smaller
instances are computed more than once.
• Dynamic programming: a bottom-up approach. Solutions for
smaller instances are stored in a table for later use.
• It sometimes happens that the natural way of dividing an
instance suggested by the structure of the problem leads us
to consider several overlapping subinstances.
• If we solve each of these independently, they will in turn
create a large number of identical subinstances.

3
Why Dynamic Programming?....
• If we pay no attention to this duplication, it is likely that
we will end up with an inefficient algorithm.
• If, on the other hand, we take advantage of the
duplication and solve each subinstance only once,
saving the solution for later use, then a more efficient
algorithm will result.
• The underlying idea of dynamic programming is thus
quite simple: avoid calculating the same thing twice,
usually by keeping a table of known results, which we
fill up as subinstances are solved.
• Dynamic programming is a bottom-up technique.

4
What is Dynamic Programming?
• Dynamic Programming is a general algorithm design
technique.
• Invented by American mathematician Richard Bellman in
the 1950s to solve optimization problems.
• “Programming” here means “planning”.
• Main idea:
• solve several smaller (overlapping) subproblems.
• record solutions in a table so that each subproblem
is only solved once.
• final state of the table will be (or contain) solution.

5
What is Dynamic Programming?...
• Dynamic programming solves optimization problems
by combining solutions to subproblems
• “Programming” refers to a tabular method with a series
of choices, not “coding”
• A set of choices must be made to arrive at an optimal
solution
• As choices are made, subproblems of the same form
arise frequently
• The key is to store the solutions of subproblems to be
reused in the future

6
What is Dynamic Programming? ...
• Recall the divide-and-conquer approach
– Partition the problem into independent subproblems
– Solve the subproblems recursively
– Combine solutions of subproblems
• This contrasts with the dynamic programming approach
• Dynamic programming is applicable when subproblems
are not independent
– i.e., subproblems share subsubproblems
– Solve every subsubproblem only once and store the
answer for use when it reappears
• A divide-and-conquer approach will do more work than
necessary

7
Elements of Dynamic Programming?
• Development of a dynamic programming solution to an
optimization problem involves four steps
1. Characterize the structure of an optimal solution
- Optimal substructures, where an optimal solution consists of
sub-solutions that are optimal.
- Overlapping sub-problems where the space of sub-problems is
small in the sense that the algorithm solves the same
sub-problems over and over rather than generating new
sub-problems.
2. Recursively define the value of an optimal solution.
- define the value of an optimal solution based on value of solutions
to sub-problems.
3. Compute the value of an optimal solution in a bottom-up
manner.
- compute in a bottom-up fashion and save the values along the
way
- later steps use the save values of pervious steps
4. Construct an optimal solution from the computed optimal

8
Matrix-chain Multiplication
• Suppose we have a sequence or chain A1
, A2
, …, An
of n matrices to be multiplied
– That is, we want to compute the product
A1
A2
…An
• There are many possible ways (parenthesizations)
to compute the product
• Example: consider the chain A1
, A2
, A3
, A4
of 4
matrices
– Let us compute the product A1
A2
A3
A4
• There are 5 possible ways:
1. (A1
(A2
(A3
A4
))) 2. (A1
((A2
A3
)A4
))
3. ((A1
A2
)(A3
A4
)) 4. ((A1
(A2
A3
))A4
)
5. (((A1
A2
)A3
)A4
)

9
Matrix-chain Multiplication …
• To compute the number of scalar multiplications
necessary, we must know:
- Algorithm to multiply two matrices, matrix dimensions
Input: Matrices Ap×q
and Bq×r
(with dimensions p×q and q×r)
Result: Matrix Cp×r
resulting from the product A·B
MATRIX-MULTIPLY(Ap×q
, Bq×r
)
1. for i ← 1 to p
2. for j ← 1 to r
3. C[i, j] ← 0
4. for k ← 1 to q
5. C[i, j] ← C[i, j] + A[i, k] · B[k, j]
6. return C
Scalar multiplication in line 5 dominates time to compute C
Number of scalar multiplications = pqr

10
• Example: Consider three matrices A10×100
,
B100×5
, and C5×50
• There are 2 ways to parenthesize
– ((AB)C) = D10×5
· C5×50
• AB ⇒ 10·100·5=5,000 scalar multiplications
• DC ⇒ 10·5·50 =2,500 scalar multiplications
– (A(BC)) = A10×100
· E100×50
• BC ⇒ 100·5·50=25,000 scalar multiplications
• AE ⇒ 10·100·50 =50,000 scalar multiplications
Total:
7,500
Total:
75,000

11
• Matrix-chain multiplication problem
– Given a chain A1
, A2
, …, An
of n matrices, where
for i=1, 2, …, n, matrix Ai
has dimension pi-1
×pi
– Parenthesize the product A1
A2
…An
such that the
total number of scalar multiplications is
minimized

12
1. The structure of an optimal solution
– Let us use the notation Ai..j
for the matrix that results from
the product Ai
Ai+1
… Aj
– An optimal parenthesization of the product A1
A2
…An
splits the product between Ak
and Ak+1
for some integer k
where1 ≤ k < n
– First compute matrices A1..k
and Ak+1..n
; then multiply
them to get the final matrix A1..n
– Key observation: parenthesizations of the subchains
A1
A2
…Ak
and Ak+1
Ak+2
…An
must also be optimal if the
parenthesization of the chain A1
A2
…An
is optimal (why?)
– That is, the optimal solution to the problem contains
within it the optimal solution to subproblems

13
2. Recursive definition of the value of an optimal
solution
– Let m[i, j] be the minimum number of scalar
multiplications necessary to compute Ai..j
– Minimum cost to compute A1..n
is m[1, n]
– Suppose the optimal parenthesization of Ai..j
splits
the product between Ak
and Ak+1
for some integer k
where i ≤ k < j

14
– Ai..j
= (Ai
Ai+1
…Ak
)·(Ak+1
Ak+2
…Aj
)= Ai..k
· Ak+1..j
– Cost of computing Ai..j
= cost of computing Ai..k
+
cost of computing Ak+1..j
+ cost of multiplying Ai..k
and Ak+1..j
– Cost of multiplying Ai..k
and Ak+1..j
is pi-1
pk
pj
– m[i, j ] = m[i, k] + m[k+1, j ] + pi-1
pk
pj
for i ≤ k < j
– m[i, i ] = 0 for i=1,2,…,n
– But… optimal parenthesization occurs at one
value of k among all possible i ≤ k < j
– Check all these and select the best one

15
m[i, j ] =
0 if i=j
min {m[i, k] + m[k+1, j ] + pi-1
pk
pj
} if i<j
i ≤ k< j
• To keep track of how to construct an optimal solution,
we use a table s
• s[i, j ] = value of k at which Ai
Ai+1
… Aj
is split for
optimal parenthesization
• Algorithm: next slide
– First computes costs for chains of length l=1
– Then for chains of length l=2,3, … and so on
– Computes the optimal cost bottom-up

16
Input: Array p[0…n] containing matrix dimensions and n
Result: Minimum-cost table m and split table s
MATRIX-CHAIN-ORDER(p[ ], n)
for i ← 1 to n
m[i, i] ← 0
for l ← 2 to n
for i ← 1 to n-l+1
j ← i+l-1
m[i, j] ← ∞
for k ← i to j-1
q ← m[i, k] + m[k+1, j] + p[i-1] p[k] p[j]
if q < m[i, j]
m[i, j] ← q
s[i, j] ← k
return m and s
Takes O(n3
) time
Requires O(n2
) space
3. Computing the optimal costs

17
Print-Optimal-Parens(s, i, j)
1. {
2. if i = j
3. then print “Ai
” :
4. else
5. { print “(”;
6. Print-Optimal-Parens(s, i, s[i, j]);
7. Print-Optimal-Parens(s, s[i, j]+1, j);
8. print “)” ;
9. }
10. }
4. Constructing an optimal solution

18
Matrix-chain Multiplication Example
Matrix Dimension
A1
30×35
A2
35×15
A3
15×5
A4
5×10
A5
10×20
A6
20×25
Assign
p0
=30
p1
=35
p2
=15
p3
=5
p4
=10
p5
=20
p6
=25
m[i,i]
m[1,1]=0
m[2,2]=0
m[3,3]=0
m[4,4]=0
m[5,5]=0
m[6,6]=0

19
Matrix-chain Multiplication Example …
m[1,2]=m[1,1] + m[2,2] + p0
p1
p2
=0+0+30.35.15=15750
m[2,3]=m[2,2] + m[3,3] + p1
p2
p3
=0+0+35.15.5=2625
m[3,4]=m[3,3] + m[4,4] + p2
p3
p4
=0+0+15.5.10=750
m[4,5]=m[4,4] + m[5,5] + p3
p4
p5
=0+0+5.10.20=1000
m[5,6]=m[5,5] + m[6,6] + p4
p5
p6
=0+0+10.20.25=5000
m i
j
1 2 3 4 5 6
6 5000 0
5 1000 0
4 750 0
3 2625 0
2 15750 0
1 0
s i (value of k)
j
1 2 3 4 5
6 5
5 4
4 3
3 2
2 1

20
m[1,3]=min
m[1,1] + m[2,3] + p0
p1
p3
=7875
m i
j
1 2 3 4 5 6
6 3500 5000 0
5 2300 1000 0
4 4375 750 0
3 7875 2625 0
2 15750 0
1 0
s i (value of k)
j
1 2 3 4 5
6 5 5
5 3 4
4 3 3
3 1 2
2 1
m[1,2] + m[3,3] + p0
p2
p3
=18000
m[2,4]=min ? m[3,5]=min ? m[4,6]=min ?

21
m[1,4]=min
m[1,1] + m[2,4] + p0
p1
p4
=?
m i
j
1 2 3 4 5 6
6 5375 3500 5000 0
5 7125 2300 1000 0
4 9375 4375 750 0
3 7875 2625 0
2 15750 0
1 0
s i (value of k)
j
1 2 3 4 5
6 3 5 5
5 3 3 4
4 3 3 3
3 1 2
2 1
m[1,2] + m[3,4] + p0
p2
p4
=?
m[2,5]=min ? m[3,6]=min ?
m[1,3] + m[4,4] + p0
p3
p4
=9375

22
m[1,5]=min
m[1,1] + m[2,5] + p0
p1
p5
=?
m i
j
1 2 3 4 5 6
6 10500 5375 3500 5000 0
5 11875 7125 2300 1000 0
4 9375 4375 750 0
3 7875 2625 0
2 15750 0
1 0
s i (value of k)
j
1 2 3 4 5
6 3 3 5 5
5 3 3 3 4
4 3 3 3
3 1 2
2 1
m[1,2] + m[3,5] + p0
p2
p5
=?
m[2,6]=min
?
m[1,3] + m[4,5] + p0
p3
p5
=11875
m[1,4] + m[5,5] + p0
p4
p5
=?

23
23
m[1,6]=min
m[1,1] + m[2,6] + p0
p1
p6
=?
m i
j
1 2 3 4 5 6
6 15125 10500 5375 3500 5000 0
5 11875 7125 2500 1000 0
4 9375 4375 750 0
3 7875 2625 0
2 15750 0
1 0
s i (value of k)
j
1 2 3 4 5
6 3 3 3 5 5
5 3 3 3 4
4 3 3 3
3 1 2
2 1
m[1,2] + m[3,6] + p0
p2
p6
=?
m[1,3] + m[4,6] + p0
p3
p6
=15125
m[1,4] + m[5,6] + p0
p4
p6
=?
m[1,5] + m[6,6] + p0
p5
p6
=?

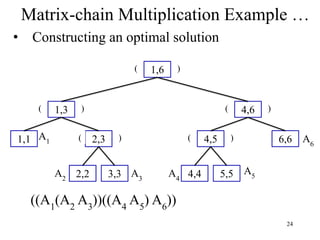
24
• Constructing an optimal solution
1,6
1,3
1,1 2,3
2,2 3,3
4,6
4,5
4,4 5,5
6,6
(
A1
(
( )
A2
A3
) (
( )
)
)
A4
A5
A6
((A1
(A2
A3
))((A4
A5
) A6
))

25
Longest common subsequence (LCS)
The problem we shall consider is the
longest-common-subsequence problem. A subsequence
of a given sequence is just the given sequence with
some elements (possibly none) left out. Formally, given
a sequence X = <x1
, x2
, …, xm
>, another sequence Z =
<z1
, z2
, …, zk
> is a subsequence of X if there exist a
strictly increasing sequence <i1
, i2
, …, ik
> of indices of
X such that for all j = 1, 2, …, k, we have xij
= zj
. For
example, Z = <B, C, D, B> is a subsequence of X = <A,
B, C, B, D, A, B> with corresponding index sequence
<2, 3, 5, 7>

26
LCS…
Given two sequence X and Y, we say that a sequence Z
is a common subsequence of X and Y if Z is a
subsequence of both X and Y. For example, it X = <A,
B, C, B, D, A, B> and Y = <B, D, C, A, B, A>, the
sequence <B, C, A> is a common subsequence of both
X and Y. The sequence <B, C, A> is not a longest
common subsequence (LCS) of X and Y, however,
since it has length 3 and the sequence <B, C, B, A>,
which is also common to both X and Y, has length 4.
The sequence <B, C, B, A> is an LCS of X and Y, as is
the sequence <B, D, A, B>, since there is no common
subsequence of length 5 or greater.

27
In the longest-common-subsequence
problem, we are given two sequence X =
<x1
, x2
, …, xm
> and Y = <y1
, y2
, …, yn
> and
wish to find a maximum-length common
subsequence of X and Y. Now we show that
the LCS problem can be solved efficiently
using dynamic programming.
LCS…

28
Characterizing a LCS
A brute-force approach to solving the LCS problem is to
enumerate all subsequence of X and check each subsequence
to see if it is also a subsequence of Y, keeping track of the
longest subsequence found. Each subsequence of Y
corresponds to a subset of the indices {1, 2, …, m} of X.
There are 2m
subsequences of X, so this approach requires
exponential time, making it impractical for long sequences.
The LCS problem has an optimal-substructure property,
however, the following theorem shows. As we shall see, the
natural class of subproblems correspond to pairs of “prefixes”
of the two input sequences. To be precise, given a sequence X
= <x1
, x2
, …, xm
>, we define the ith
prefix of X, for i = 0, 1,
…, m, as Xi
= <x1
, x2
, … xi
>. For example, if X = <A, B, C, B,
D, A, B>, then X4
= <A, B, C, B> and X0
is the empty
sequence.

29
Characterizing a LCS…
Theorem 1 (Optimal substructure of an LCS)
Let X = <x1
, x2
, …,xm
>, and Y = <y1
, y2
, …, yn
> be sequences, and
let Z = <z1
, z2
, …,zk
> be any LCS of X and Y.
1. If xm
= yn
, then zk
= xm
= yn
and Zk-1
is and LCS of Xm-1
and Yn-1
2. If xm
≠ yn
, then zk
≠ xm
implies that Z is an LCS of Xm-1
and Y.
3. If xm
≠ yn
, then zk
≠ ym
implies that Z is an LCS of X and Yn-1
.
Proof: (case 1: xm
= yn
)
Any sequence Z’ that does not end in xm
= yn
can be made longer by
adding xm
= yn
to the end. Therefore,
(1) longest common subsequence (LCS) Z must end in xm
= yn
.
(2) Zk-1
is a common subsequence of Xm-1
and Yn-1
, and
(3) there is no longer CS of Xm-1
and Yn-1
, or Z would not be an LCS.

30
Characterizing a LCS…
Proof: (case 2: xm
≠ yn
, and zk
≠ xm
)
Since Z does not end in xm
,
(1) Z is a common subsequence of Xm-1
and Y, and
(2) there is no longer CS of Xm-1
and Y, or Z would not be an LCS.
Theorem 1 (Optimal substructure of an LCS)
Let X = <x1
, x2
, …,xm
>, and Y = <y1
, y2
, …, yn
> be sequences, and
let Z = <z1
, z2
, …,zk
> be any LCS of X and Y.
1. If xm
= yn
, then zk
= xm
= yn
and Zk-1
is and LCS of Xm-1
and Yn-1
2. If xm
≠ yn
, then zk
≠ xm
implies that Z is an LCS of Xm-1
and Y.
3. If xm
≠ yn
, then zk
≠ ym
implies that Z is an LCS of X and Yn-1
.
Proof: (case 3: xm
≠ yn
, and zk
≠ ym
)
Symmetric to (case 2)

31
A recursive solution to subproblems
The characterization of Theorem 1 shows that an LCS of two
sequences contains within it an LCS of prefixes of the two
sequences. Thus, the LCS problem has an optimal-substructure
property. A recursive solution also has the
overlapping-subproblems property, as we shall see in a moment.
Theorem 1 implies that there are either on or two subproblems
to examine when finding an LCS of X = <x1
, x2
, …, xm
> and Y
= <y1
, y2
, …,yn
>. If xm
=yn
we must find and LCS of Xm-1
and
Yn-1
. Appending xm
= yn
to this LCS yields an LCS of X and Y.
If xm ≠
yn
, then we must solve two subproblems: finding an LCS
of Xm-1
and Y and finding an LCS of X and Yn-1
. Whichever of
these two LCS’s is longer is an LCS of X and Y.

32
We can readily see the overlapping-subproblems property in
the LCS problem. To find and LCS of X and Y, we may need to
find the LCS’s of X and Yn-1
and of Xm-1
and Y. But each of
these subproblems has the subsubproblem of finding the LCS
of Xm-1
and Yn-1
. Many other subproblems share
subsubproblems.
A recursive solution to subproblems …

33
A recursive solution to subproblems …
Like the matrix-chain multiplication problem, our recursive
solution to the LCS problem involves establishing a recurrence
of the cost of an optimal solution. Let us define c[i,j] to be the
length of an LCS of the sequences Xi
, and Yj
. If either i = 0 or j
= 0, one of the sequences has length 0, so the LCS has length 0.
The optimal substructure of the LCS problem gives the
recursive formula
0 if i = 0 or j = 0
c[i,j] = c[i-1, j-1]+1 if i, j > 0 and xi
= yj
max(c[i,j-1], c[i-1,j]) if i, j > 0 and xi
≠ yj

34
Computing the length of an LCS
Based on recursive equation, we could easily write an
exponential-time recursive algorithm to compute the length of
an LCS of two sequences. Since there are only Θ(mn) distinct
subproblems, however, we can use dynamic programming to
compute the solutions bottom up.
Procedure LCS-LENGTH takes two sequences X = <x1
, x2
,
…, xm
> and Y = <y1
, y2
, …, yn
> as inputs. It stores the c[i,j]
values in a table c[0..m,0..n] whose entries are computed in
row-major order. (That is, the first row of c is filled in form left
to right, then the second row, and so on.) It also maintains the
table b[1.m,1..n] to simplify construction of an optimal solution.
Intuitively, b[i,j] points to the table entry corresponding to the
optimal subproblem solution chosen when computing b[i,j]. The
procedure returns the b and c tables: c[m,n] contains the length
of an LCS of X and Y.

35
LCS-LENGTH (X, Y)
1. m ← length[X]
2. n ← length[Y]
3. for i ← 1 to m
4. do c[i, 0] ← 0
5. for j ← 0 to n
6. do c[0, j ] ← 0
7. for i ← 1 to m
8. do for j ← 1 to n
9. do if xi
= yj
10. then c[i, j ] ← c[i−1, j−1] + 1
11. b[i, j ] ← “ ”
12. else if c[i−1, j ] ≥ c[i, j−1]
13. then c[i, j ] ← c[i− 1, j ]
14. b[i, j ] ← “↑”
15. else c[i, j ] ← c[i, j−1]
16. b[i, j ] ← “←”
17. return c and b
Computing the length of an LCS ….
b[i, j ] points to table
entry whose
subproblem we used in
solving LCS of Xi
and Yj
.
c[m,n] contains the
length of an LCS of X
and Y.

36
Figure 3.1 The c and b tables

37
Figure 3.1 The c and b tables computed by LCS-LENGTH on
the sequence X=<A, B, C, B, D, A, B> and Y=<B, D, C, A, B,
A>. The square in row i and column j contains the value of
c[i,j] and the appropriate arrow for the value of b[i,j]. The
entry 4 in c[7,4]– the lower right-hand corner of the table—is
the length of an LCS <B, C, B, A> of X and Y. For i,j > 0,
entry c[i,j] depends only on whether xi
= yi
and the values in
entries c[i-1,j],c[i,j-1], and c[i-1,j-1], which are computed
before c[i,j]. To reconstruct the elements of an LCS, follow the
b[i,j] arrows from the lower right-hand corner; the path is
shaded. Each “ ” on the path corresponds to an entry
(highlighted) for which xi
= yi
is a member of an LCS

38
Figure 3.1 Shows the tables produced by LCS-LENGTH
on the sequences X = <A, B, C, B, D, A, B> and Y= <B, D, C,
A, B, A>. The running time of the procedure in O(mn), since
each table entry O(1) time to compute.

39
Construction an LCS
The b table returned by LCS-LENGTH can be to quickly
construct an LCS of X = <x1
, x2
, …, xm
> and Y = <y1
, y2
, …,
yn
>. We simply begin at b[m,n] and trace through the table
following the arrows. Whenever we encounter a “ ” in entry
b[i,j], it implies that xi
= yj
is an element of the LCS. The
elements of the LCS are encountered in reverse order by this
method. The following recursive procedure prints out an LCS of
X and Y in the proper, forward order. The initial invocation is
PRINT-LCS(b, X, length[x], lentgh[Y]).

40
Construction an LCS…..
PRINT-LCS (b, X, i, j)
1. if i = 0 or j = 0
2. then return
3. if b[i, j ] = “ ”
4. then PRINT-LCS(b, X, i−1, j−1)
5. print xi
6. elseif b[i, j ] = “↑”
7. then PRINT-LCS(b, X, i−1, j)
8. else PRINT-LCS(b, X, i, j−1)
•Initial call is PRINT-LCS (b, X,m, n).
•When b[i, j ] = , we have extended LCS by one character. So
LCS = entries with in them.
•Time: O(m+n)

42
LCS Example
We’ll see how LCS algorithm works on the
following example:
• X = ABCB
• Y = BDCAB
LCS(X, Y) = BCB
X = A B C B
Y = B D C A B
What is the Longest Common Subsequence
of X and Y?

43
LCS Example (0)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
X = ABCB; m = |X| = 4
Y = BDCAB; n = |Y| = 5
Allocate array c[5,4]
ABCB
BDCAB
j 0 1 2 3 4 5

44
LCS Example (1)
j 0 1 2 3 4 5
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
for i = 1 to m c[i,0] = 0
for j = 1 to n c[0,j] = 0
ABCB
BDCAB

12/25/2022 45
LCS Example (2)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
else c[i,j] = max( c[i-1,j], c[i,j-1] )
0
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 46
LCS Example (3)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
0 0 0
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 47
LCS Example (4)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
0 0 0 1
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 48
LCS Example (5)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
0
0
0 1 1
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 49
LCS Example (6)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
0 0 1
0 1
1
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 50
LCS Example (7)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 1 1
1
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 51
LCS Example (8)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 1 1 1 2
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 52
LCS Example (10)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
2
1 1 1
1
1 1
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 53
LCS Example (11)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 2
1 1
1
1 1 2
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 54
LCS Example (12)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 2
1 1
1 1 2
1
2
2
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 55
LCS Example (13)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 2
1 1
1 1 2
1
2
2
1
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 56
LCS Example (14)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 2
1 1
1 1 2
1
2
2
1 1 2 2
ABCB
BDCAB
j 0 1 2 3 4 5

12/25/2022 57
LCS Example (15)
0
1
2
3
4
i
X
i
A
B
C
B
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
if ( Xi
== Yj
)
c[i,j] = c[i-1,j-1] + 1
1
0
0
0 1
1 2
1 1
1 1 2
1
2
2
1 1 2 2 3
ABCB
BDCAB
j 0 1 2 3 4 5

58
Finding LCS
0
1
2
3
4
i
X
i
A
B
C
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
1
0
0
0 1
1 2
1 1
1 1 2
1
2
2
1 1 2 2 3
B
j 0 1 2 3 4 5

59
Finding LCS (2)
0
1
2
3
4
i
X
i
A
B
C
Y
j
B
B A
C
D
0
0
0
0
0
0
0
0
0
0
1
0
0
0 1
1 2
1 1
1 1 2
1
2
2
1 1 2 2 3
B
B C B
LCS (reversed order):
LCS (straight order): B C B
(this string turned out to be a palindrome)
j 0 1 2 3 4 5

Computer algorithm(Dynamic Programming).pdf

Recommended

More Related Content

Similar to Computer algorithm(Dynamic Programming).pdf (20)

Recently uploaded (20)

Computer algorithm(Dynamic Programming).pdf