Concept Learning - Find S Algorithm,Candidate Elimination Algorithm
- 1. Basics of Learning Theory By : Sharmila Chidaravalli Assistant Professor Global Academy of Technology
- 2. Learning is a process by which one can acquire knowledge and construct new ideas or concepts based on the experiences. Machine learning is an intelligent way of learning general concept from training examples without writing a program. There are many machine learning algorithms through which computers can intelligently learn from past data or experiences, identify patterns, and make predictions when new data is fed.
- 3. What is Concept Learning…? Concept learning can be formulated as a problem of searching through a predefined space of potential hypotheses for the hypothesis that best fits the training examples. “A task of acquiring potential hypothesis (solution) that best fits the given training examples.” Concept learning requires three things: 1. Input 2. Output 3. Test Formally, Concept learning is defined as– "Given a set of hypotheses, the learner searches through the hypothesis space to identify the best hypothesis that matches the target concept".
- 4. Sky AirTemp Humidity Wind Water Forecast EnjoySport Sunny Warm Normal Strong Warm Same Yes Sunny Warm High Strong Warm Same Yes Rainy Cold High Strong Warm Change No Sunny Warm High Strong Cool Change Yes Consider the example task of learning the target concept “days on which John enjoys his favorite water sport.” Below Table describes a set of example days, each represented by a set of attributes. The attribute EnjoySport indicates whether or not John enjoys his favorite water sport on this day. The task is to learn to predict the value of EnjoySport for an arbitrary day, based on the values of its other attributes. Objective is to learn { Sky AirTemp Humidity Wind Water Forecast } → EnjoySport
- 5. Concept Learning Task Notation Input Variables Output < x1 ,x2 ,x3, x4 , x5, x6 > <y> →
- 6. Concept Learning Task Notation Sky AirTemp Humidity Wind Water Forecast EnjoySport Sunny Warm Normal Strong Warm Same Yes Sunny Warm High Strong Warm Same Yes Rainy Cold High Strong Warm Change No Sunny Warm High Strong Cool Change Yes Training Examples (D) Target Concept (C) Training Instances (X) Independent Variables Dependent Variables
- 7. Representation of a Hypothesis A hypothesis ‘h’ approximates a target function ‘f ’ to represent the relationship between the independent attributes and the dependent attribute of the training instances. The hypothesis is the predicted approximate model that best maps the inputs to outputs. Each hypothesis is represented as a conjunction of attribute conditions in the antecedent part. For example, (Tail = Short) ʌ (Color = Black)…. The set of hypothesis in the search space is called as hypotheses. Hypotheses are the plural form of hypothesis. Generally ‘H’ is used to represent the hypotheses and ‘h’ is used to represent a candidate hypothesis.
- 8. What hypothesis representation is provided to the learner? • Let’s consider a simple representation in which each hypothesis consists of a conjunction of constraints on the instance attributes. • Let each hypothesis be a vector of six constraints, specifying the values of the six attributes Sky, AirTemp, Humidity, Wind, Water, and Forecast. Representation of a Hypothesis For each attribute, the hypothesis will either •indicate by a “?’ that any value is acceptable for this attribute, •specify a single required value (e.g., Warm) for the attribute, or •indicate by a “ø” that no value is acceptable.
- 9. Representation of a Hypothesis Most General and Specific Hypothesis The most general hypothesis-that every day is a positive example-is represented by (?, ?, ?, ?, ?, ?) the most specific possible hypothesis-that no day is a positive example-is represented by (ø, ø, ø, ø, ø, ø) If some instance x satisfies all the constraints of hypothesis h, then h classifies x as a positive example (h(x) = 1). To illustrate, the hypothesis that Person enjoys his favorite sport only on cold days with high humidity (independent of the values of the other attributes) is represented by the expression (?, Cold, High, ?, ?, ?)
- 10. • The set of items over which the concept is defined is called the set of instances, which is denoted by X. Example: X is the set of all possible days, each represented by the attributes: Sky, AirTemp, Humidity, Wind, Water, and Forecast • The concept or function to be learned is called the target concept, which is denoted by c. c can be any Boolean valued function defined over the instances X c: X→ {0, 1} Example: The target concept corresponds to the value of the attribute EnjoySport (i.e., c(x) = 1 if EnjoySport = Yes, and c(x) = 0 if EnjoySport = No). Notation
- 11. • Instances for which c(x) = 1 are called positive examples, or members of the target concept. • Instances for which c(x) = 0 are called negative examples, or non-members of the target concept. • The ordered pair (x, c(x)) to describe the training example consisting of the instance x and its target concept value c(x). • D to denote the set of available training examples • The symbol H to denote the set of all possible hypotheses that the learner may consider regarding the identity of the target concept. Each hypothesis h in H represents a Boolean valued function defined over X h: X→{0, 1} The goal of the learner is to find a hypothesis h such that h(x) = c(x) for all x in X. Notation
- 12. • Given: Instances X: Possible days, each described by the attributes • Sky (with possible values Sunny, Cloudy, and Rainy), • AirTemp (with values Warm and Cold), • Humidity (with values Normal and High), • Wind (with values Strong and Weak), • Water (with values Warm and Cool), • Forecast (with values Same and Change). • Hypotheses H: Each hypothesis is described by a conjunction of constraints on the attributes Sky, AirTemp, Humidity, Wind, Water, and Forecast. The constraints may be "?" (any value is acceptable), “Φ” (no value is acceptable), or a specific value. • Target concept c: EnjoySport : X → {0, l} • Training examples D: Positive and negative examples of the target function • Determine: • A hypothesis h in H such that h(x) = c(x) for all x in X.
- 13. A CONCEPT LEARNING TASK Concept learning can be viewed as the task of searching through a large space of hypotheses implicitly defined by the hypothesis representation. The goal of this search is to find the hypothesis that best fits the training examples. It is important to note that by selecting a hypothesis representation, the designer of the learning algorithm implicitly defines the space of all hypotheses that the program can ever represent and therefore can ever learn.
- 14. Instance Space Consider, for example, the instances X and hypotheses H in the EnjoySport learning task. Given that the attribute Sky has three possible values, and that AirTemp, Humidity, Wind, Water, and Forecast each have two possible values, the instance space X contains exactly 3 . 2 . 2 . 2 . 2 . 2 = 96 distinct instances.
- 15. Example: Let’s assume there are two features F1 and F2 with F1 has A and B as possibilities and F2 as X and Y as possibilities. F1 – > A, B F2 – > X, Y Instance Space: (A, X), (A, Y), (B, X), (B, Y) – 4 Examples Hypothesis Space: (A, X), (A, Y), (A, ø), (A, ?), (B, X), (B, Y), (B, ø), (B, ?), (ø, X), (ø, Y), (ø, ø), (ø, ?), (?, X), (?, Y), (?, ø), (?, ?) – 16 Hypothesis Space: (A, X), (A, Y), (A, ?), (B, X), (B, Y), (B, ?), (?, X), (?, Y (?, ?) – 10
- 16. Hypothesis Space Hypothesis space is the set of all possible hypotheses that approximates the target function f. Similarly there are 5 . 4 . 4 . 4 . 4 . 4 = 5120 syntactically distinct hypotheses within H. Notice, however, that every hypothesis containing one or more “ø” symbols represents the empty set of instances; that is, it classifies every instance as negative. Therefore, the number of semantically distinct hypotheses is only 1 + (4 . 3 . 3 . 3 . 3 . 3) = 973. EnjoySport example is a very simple learning task, with a relatively small, finite hypothesis space.
- 17. Find-S Algorithm * Concept Learning * Finds most specific hypothesis * Considers only positive examples General Hypothesis Specific Hypothesis G={ ‘?’ , ’?’ , ‘?’ , ‘?’ , ‘?’ , ‘?’ } S = { ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ } Attributes Find Maximally Specific Hypothesis
- 18. Algorithm : Step 1 : Initialize the hypothesis (h) to most specific hypothesis Step 2 : for each +ve example: for each attribute in the example: if attribute value = hypothesis value : Do Nothing else Replace its hypothesis value with the more general constraint ‘?’
- 19. Dataset 6 attributes (Nominal-valued (symbolic) attributes): Sky (SUNNY, RAİNY, CLOUDY), Temp (WARM,COLD), Humidity (NORMAL, HIGH), Wind (STRONG, WEAK), Water (WARM, COOL), Forecast (SAME, CHANGE) Sky AirTemp Humidity Wind Water Forecast EnjoySport Sunny Warm Normal Strong Warm Same Yes Sunny Warm High Strong Warm Same Yes Rainy Cold High Strong Warm Change No Sunny Warm High Strong Cool Change Yes
- 20. Initially h0 = <Ø, Ø, Ø, Ø, Ø, Ø>
- 21. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = <Sunny, Warm, Normal, Strong, Warm, Same> , +
- 22. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + x2 = <Sunny, Warm, High, Strong, Warm, Same>, +
- 23. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + x2 = <Sunny, Warm, High, Strong, Warm, Same>, + h2 = <Sunny, Warm, ?, Strong, Warm, Same>
- 24. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = < Sunny, Warm, Normal, Strong, Warm, Same> , + x2 = <Sunny, Warm, High, Strong, Warm, Same>, + h2 = <Sunny, Warm, ?, Strong, Warm, Same> x3 = < Rainy, Cold, High, Strong, Warm, Change >, -
- 25. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = < Sunny, Warm, Normal, Strong, Warm, Same> , + x2 = <Sunny, Warm, High, Strong, Warm, Same>, + h2 = <Sunny, Warm, ?, Strong, Warm, Same> x3 = < Rainy, Cold, High, Strong, Warm, Change >, - h3 = < Sunny, Warm, ?, Strong, Warm, Same>
- 26. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = < Sunny, Warm, Normal, Strong, Warm, Same> , + x2 = <Sunny, Warm, High, Strong, Warm, Same>, + h2 = <Sunny, Warm, ?, Strong, Warm, Same> x3 = < Rainy, Cold, High, Strong, Warm, Change >, - h3 = < Sunny, Warm, ?, Strong, Warm, Same> x4 = < Sunny, Warm, High, Strong, Cool, Change >, +
- 27. h0 = <Ø, Ø, Ø, Ø, Ø, Ø> h1 =<Sunny, Warm, Normal, Strong, Warm, Same> x1 = < Sunny, Warm, Normal, Strong, Warm, Same> , + x2 = <Sunny, Warm, High, Strong, Warm, Same>, + h2 = <Sunny, Warm, ?, Strong, Warm, Same> x3 = < Rainy, Cold, High, Strong, Warm, Change >, - h3 = < Sunny, Warm, ?, Strong, Warm, Same> x4 = < Sunny, Warm, High, Strong, Cool, Change >, + h4 = <Sunny, Warm, ?, Strong, ?, ? >
- 29. Problem 2
- 30. Problem 3
- 31. Design of a Learning System A system that is built around a learning algorithm is called a learning system. The design of systems focuses on these steps: 1. Choosing a training experience 2. Choosing a target function 3. Representation of a target function 4. Function approximation Training Experience Let us consider designing of a chess Choosing the Training Experience • The first design choice is to choose the type of training experience from which the system will learn. • The type of training experience available can have a significant impact on success or failure of the learner.
- 32. Determine the Target Function The next step is the determination of a target function. In this step, the type of knowledge that needs to be learnt is determined. In direct experience, a board move is selected and is determined whether it is a good move or not against all other moves. If it is the best move, then it is chosen as: B -> M, where, B and M are legal moves. In indirect experience, all legal moves are accepted and a score is generated for each. The move with largest score is then chosen and executed.
- 33. Determine the Target Function Representation The representation of knowledge may be a table, collection of rules or a neural network. The linear combination of these factors can be coined as: where, x1, x2 and x3 represent different board features and w0, w1, w2 and w3 represent weights.
- 34. Choosing an Approximation Algorithm for the Target Function The focus is to choose weights and fit the given training samples effectively. The aim is to reduce the error given as:
- 35. Problems with Find-S Depending on H, there might be several maximally consistent hypotheses, and there is no way for Find-S to find them. All of them are equally likely. There are several problems with the Find-S algorithm: It cannot determine if it has learnt the concept. There might be several other hypotheses that match as well – has it found the only one? It cannot detect when training data is inconsistent. We would like to detect and be tolerant to errors and noise. Why do we want the most specific hypothesis? Some other hypothesis might be more useful.
- 36. Version Space Definition: A hypothesis h is consistent with a set of training examples D if and only if h(x)=c(x) for each example <x , c ( x )> in D. Version space = the subset of all hypotheses in H consistent with the training examples D. Definition: The version space, denoted VSH,D, with respect to hypothesis space H and training examples D, is the subset of hypotheses from H consistent with the training examples in D.
- 37. Representation of Version Space Option 1: List all of the members in the version space. Works only when the hypothesis space H is finite! Option 2: Store only the set of most general members G and the set of most specific members S. Given these two sets, it is possible to generate any member of the version space as needed.
- 38. List-Eliminate Algorithm 2. For each training example, <x , c ( x )> remove from VSH,D any hypothesis that is inconsistent with the training example h(x) ≠ c(x) 1. VSH,D a list containing every hypothesis in H 3. Output the list of hypotheses in VSH,D Advantage: Guaranteed to output all hypotheses consistent with the training examples. But inefficient! Even in this simple example, there are 1+4·3·3·3·3 = 973 semantically distinct hypotheses.
- 39. Candidate-Elimination Algorithm G maximally general hypothesis in H S maximally specific hypothesis in H For each training example d = <x , c ( x )> modify G and S so that G and S are consistent with d
- 40. Candidate-Elimination Algorithm (detailed) G maximally general hypothesis in H S maximally specific hypothesis in H
- 41. Candidate-Elimination Algorithm (detailed) G maximally general hypothesis in H S maximally specific hypothesis in H For each training example d = <x , c ( x )>
- 42. Candidate-Elimination Algorithm (detailed) G maximally general hypothesis in H S maximally specific hypothesis in H For each training example d = <x , c ( x )> If d is a positive example • Remove from G any hypothesis that is inconsistent with d • For each hypothesis s in S that is not consistent with d • Remove s from S. • Add to S all minimal generalizations h of s such that h consistent with d and Some member of G is more general than h • Remove from S any hypothesis that is more general than another hypothesis in S
- 43. Candidate-Elimination Algorithm (detailed) G maximally general hypothesis in H S maximally specific hypothesis in H For each training example d = <x , c ( x )> If d is a negative example •Remove from S any hypothesis that is inconsistent with d •For each hypothesis g in G that is not consistent with d •Remove g from G. •Add to G all minimal specializations h of g such that h consistent with d and Some member of S is more specific than h •Remove from G any hypothesis that is less general than another hypothesis in G
- 44. Candidate-Elimination Algorithm (detailed) G maximally general hypothesis in H S maximally specific hypothesis in H For each training example d = <x , c ( x )> If d is a negative example •Remove from S any hypothesis that is inconsistent with d •For each hypothesis g in G that is not consistent with d •Remove g from G. •Add to G all minimal specializations h of g such that h consistent with d and Some member of S is more specific than h •Remove from G any hypothesis that is less general than another hypothesis in G If d is a positive example • Remove from G any hypothesis that is inconsistent with d • For each hypothesis s in S that is not consistent with d • Remove s from S. • Add to S all minimal generalizations h of s such that h consistent with d and Some member of G is more general than h • Remove from S any hypothesis that is more general than another hypothesis in S
- 45. Problem 1 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples 6 attributes (Nominal-valued (symbolic) attributes): Sky (SUNNY, RAİNY, CLOUDY), Temp (WARM,COLD), Humidity (NORMAL, HIGH), Wind (STRONG, WEAK), Water (WARM, COOL), Forecast (SAME, CHANGE) Sky AirTemp Humidity Wind Water Forecast EnjoySport Sunny Warm Normal Strong Warm Same Yes Sunny Warm High Strong Warm Same Yes Rainy Cold High Strong Warm Change No Sunny Warm High Strong Cool Change Yes
- 46. Consider Initially General Hypothesis S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > Specific Hypothesis
- 47. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + Consider 1st Instance
- 48. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + Consider 1st Instance S1 = < Sunny, Warm, Normal, Strong, Warm, Same >
- 49. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > Consider 1st Instance G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ >
- 50. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + Consider 2nd Instance
- 51. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same >
- 52. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ >
- 53. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - Consider 3rd Instance
- 54. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same >
- 55. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ?, Normal, ? , ? , ? > , < ?, ? , ? , ? , Cool , ? > , < ?, ? , ? , ? , ? , Same >
- 56. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ?, Normal, ? , ? , ? > , < ?, ? , ? , ? , Cool , ? > , < ?, ? , ? , ? , ? , Same > Sky AirTemp Humidity Wind Water Forecast EnjoySport Sunny Warm Normal Strong Warm Same Yes Sunny Warm High Strong Warm Same Yes Rainy Cold High Strong Warm Change No Sunny Warm High Strong Cool Change Yes
- 57. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? < ?, ? , ? , ? , ? , Same >
- 58. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ? , ? , ? , ? , Same > X4 = < Sunny, Warm, High, Strong, Cool, Change >, + Consider 4th Instance
- 59. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ? , ? , ? , ? , Same > X4 = < Sunny, Warm, High, Strong, Cool, Change >, + S4 = < Sunny, Warm, ?, Strong, ?, ? >
- 60. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ? , ? , ? , ? , Same > X4 = < Sunny, Warm, High, Strong, Cool, Change >, + S4 = < Sunny, Warm, ?, Strong, ?, ? > G4 = < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? > , < ?, ? , ? , ? , ? , Same >
- 61. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ? , ? , ? , ? , Same > X4 = < Sunny, Warm, High, Strong, Cool, Change >, + S4 = < Sunny, Warm, ?, Strong, ?, ? > G4 = < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? > , < ?, ? , ? , ? , ? , Same >
- 62. S0 = < ‘Ø ’ , ’ Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ , ‘Ø ’ > G0= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X1 = <Sunny, Warm, Normal, Strong, Warm, Same> , + S1 = < Sunny, Warm, Normal, Strong, Warm, Same > G1= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X2 = <Sunny, Warm, High, Strong, Warm, Same>, + S2 = < Sunny, Warm, ?, Strong, Warm, Same > G2= < ‘?’ , ’?’, ‘?’ , ‘?’ , ‘?’ , ‘?’ > X3 = < Rainy, Cold, High, Strong, Warm, Change >, - S3 = S2 = < Sunny, Warm, ?, Strong, Warm, Same > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >, < ?, ? , ? , ? , ? , Same > X4 = < Sunny, Warm, High, Strong, Cool, Change >, + S4 = < Sunny, Warm, ?, Strong, ?, ? > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >
- 63. Therefore Most General Hypothesis Most Specific Hypothesis S = < Sunny, Warm, ?, Strong, ?, ? > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? >
- 64. Version Space S = < Sunny, Warm, ?, Strong, ?, ? > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? > < Sunny, Warm , ? , ? , ? ,? > < Sunny, ? , ? , Strong , ? ,? > < Sunny, Warm , ? , ? , ? ,? > < ?, Warm , ? , Strong , ? ,? >
- 65. Version Space S = < Sunny, Warm, ?, Strong, ?, ? > G3= < Sunny, ? , ? , ? , ? ,? > , < ?, Warm , ? , ? , ? , ? > < Sunny, Warm , ? , ? , ? ,? > < Sunny, ? , ? , Strong , ? ,? > < ?, Warm , ? , Strong , ? ,? >
- 66. Problem 2 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples
- 67. Problem 3 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples Sky Air Temp Humidity Wind Water Forecast Enjoy Sport Rainy Cold High Strong Warm Change No Sunny Warm High Strong Warm Same Yes Sunny Warm High Strong Cool Change Yes Sunny Warm Normal Strong Warm Same Yes
- 68. Problem 4 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples Size Color Shape Class/Label Big Red Circle No Small Red Triangle No Small Red Circle Yes Big Blue Circle No Small Blue Circle Yes
- 69. Problem 5 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples Example Citations Size InLibrary Price Editions Buy 1 Some Small No Affordable One No 2 Many Big No Expensive Many Yes 3 Many Medium No Expensive Few Yes 4 Many Small No Affordable Many Yes
- 70. Problem 6 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples
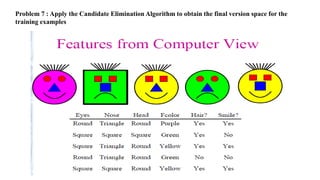
- 71. Problem 7 : Apply the Candidate Elimination Algorithm to obtain the final version space for the training examples