Continuous probability Business Statistics, Management
- 1. A Presentation By, Sourav Snai, Debjit Das, Amrita Nandi, Arpita Acharjya
- 2. Continuous probability distribution is a probability in which a random variable X can be taken on any values (continuous) because there are infinite values that X could assume, the probability of X taking on any one specific values is zero. Therefore we often take ranges of values.
- 3. Any variable can have two types of values. Either the values can be fixed number which is also known as discrete values or a specified range that is known as continuous values
- 4. The probability that a continuous variable will take a specific value is zero. Because of this we can never express continuous probability in tabular form it is always expressed in a equation form or a formula to describe such kind of distribution.
- 5. A continuous random variable say Y is following uniform distribution such that the probability between 4 and 9 is ‘r’. Find the value of r. Solution- In a uniform distribution, the probability is same for all possible values of a given variable between the specified range so if P is the probability of any value between
- 6. Say a and b ten P= 1 -------------- (b – a) Since the sum of all probability is 1 . Here P=r, a=4 and b=9
- 7. So 1 r = _______________ ( 9 – 4 ) 1 = _____ 5
- 8. Uniform probability. Normal probability. Exponential probability.
- 9. the normal probability distribution is the most important distribution for describing a continuous random variable. It is used for finding - height of the people. - scientific measurement. - test scores. - amount of rain fall.
- 10. Normal Probability Density Function μ = mean σ = standard deviation Л = 3.14159 ℮ = 2.71828 2 )( 2 1 2 1 )( x exf
- 12. The highest point on the normal curve is the mean, which is also the median and the mode.
- 13. The mean can be any numerical value: negative or positive. The standard deviation determines the width of the curve. Larger values result in wider, flatter curves. Probability for the normal variable are given by the areas under the curve. The total area under the curve is 1
- 14. .5 to the left of the mean and .5 to the right.
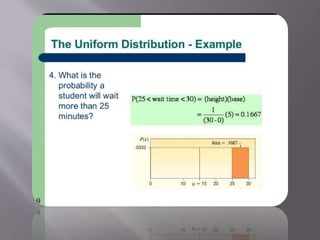
- 15. The uniform probability is perhaps the simplest distribution for a continuous random variable. This is a rectangular in shape and is defined by minimum and maximum values.
- 21. Used to measure the time that elapses between two occurrences of an event (the time between arrivals) Examples: Time between trucks arriving at an unloading dock Time between transactions at an ATM Machine Time between phone calls to the main operator
- 22. The probability that an arrival time is equal to or less than some specified time a is P(0 ≤ x ≤ a) = 1- e^-λa Where 1/λ is the mean time between events. Note that if the number of occurrences per time period is Poisson with mean , then the time between occurrences is exponential with mean time 1/
- 23. Shape the exponential distribution.
- 24. Example: Customers arrive at the claims counter at the rate of 15 per hour. What is the probability that the arrival time between consecutive customers is less than five minutes? Time between arrivals is exponentially distributed with mean time between arrivals of 4 minutes (15 per 60 minutes, on average) 1/ = 4.0, so = .25 P(x < 5) = 1 - e-a = 1 – e-(.25)(5) = .7135
- 25. Scenario analysis. - worst case - best case The worst case would contain some values from the lower end of the probability, likely form the middle and the best case would contain upper end values.
- 26. Risk evaluation. determines the chances of loss or profit earned in the business organization. Sales forecasting. it helps to determine the sales quantity of a product in a particular term(year, quarter, month).
- 27. Probability in manufacturing. it can help to determine the cost benefit ratio or the transfer of a new manufacturing technology process by addressing the likelihood of improved profit.
- 28. From the above we can see that all the three distribution has application in business but the most important of all being normal distribution. It is extensively used in statistical decision making. It can be transformed to the corresponding standard normal distribution which can be used to find probability associated with the origin normal distribution. We could also see how it is used to find the profit and loss chances in a business.
- 29. Even in our day to day life probability is involved i.e. - the probability of attending math class by students on a Monday after a nice holiday of two days. If we think really carefully it is involved in every aspect of our life. Even during birth of a baby the probability of a boy being born is ½ and a girl is ½ since either a boy or girl can be born therefore P = 1. probability is just not a book subject it can be applied in every situation in our life.
- 30. Adamas University References: www.slideshare.com www.google.com/wikipedia/ Nav Kumar Sir’s Notes