![• Consider the infix expression exp = “a+b*c+d”
and the infix expression is scanned using the iterator i, which is
initialized as i = 0.
• 1st Step: Here i = 0 and exp[i] = ‘a’ i.e., an operand. So add this in the
postfix expression. Therefore, postfix = “a”.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-3-320.jpg)
![• 2nd Step: Here i = 1 and exp[i] = ‘+’ i.e., an operator. Push this into the
stack. postfix = “a” and stack = {+}.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-4-320.jpg)
![• 3rd Step: Now i = 2 and exp[i] = ‘b’ i.e., an operand. So add this in the
postfix expression. postfix = “ab” and stack = {+}.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-5-320.jpg)
![• 4th Step: Now i = 3 and exp[i] = ‘*’ i.e., an operator. Push this into the
stack. postfix = “ab” and stack = {+, *}.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-6-320.jpg)
![• 5th Step: Now i = 4 and exp[i] = ‘c’ i.e., an operand. Add this in the
postfix expression. postfix = “abc” and stack = {+, *}.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-7-320.jpg)
![• 6th Step: Now i = 5 and exp[i] = ‘+’ i.e., an operator. The topmost
element of the stack has higher precedence. So pop until the stack
becomes empty or the top element has less precedence. ‘*’ is popped
and added in postfix. So postfix = “abc*” and stack = {+}.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-8-320.jpg)
![• 7th Step: Now i = 6 and exp[i] = ‘d’ i.e., an operand. Add this in the
postfix expression. postfix = “abc*+d”.](https://image.slidesharecdn.com/infixtopostfix-250331092626-3a5af321/85/conversion-of-Infix-to-Postfix-conversion-using-stack-11-320.jpg)
More Related Content
Similar to conversion of Infix to Postfix conversion using stack (20)
More from yashodamb (10)
Recently uploaded (20)
![Leveraging AI to Streamline Operations for Nonprofits [05.20.2025].pdf](https://cdn.slidesharecdn.com/ss_thumbnails/leveragingaitostreamlineoperationsfornonprofits05-250520212021-64a860c5-thumbnail.jpg?width=560&fit=bounds)
conversion of Infix to Postfix conversion using stack
- 1. Infix to Postfix Dr. Yashoda M B
- 2. 1. Scan the infix expression from left to right. 2. If the scanned character is an operand, put it in the postfix expression. 3. Otherwise, do the following • If the precedence of the current scanned operator is higher than the precedence of the operator on top of the stack, or if the stack is empty, or if the stack contains a ‘(‘, then push the current operator onto the stack. • Else, pop all operators from the stack that have precedence higher than or equal to that of the current operator. After that push the current operator onto the stack. 4. If the scanned character is a ‘(‘, push it to the stack. 5. If the scanned character is a ‘)’, pop the stack and output it until a ‘(‘ is encountered, and discard both the parenthesis. 6. Repeat steps 2-5 until the infix expression is scanned. 7. Once the scanning is over, Pop the stack and add the operators in the postfix expression until it is not empty. 8. Finally, print the postfix expression.
- 3. • Consider the infix expression exp = “a+b*c+d” and the infix expression is scanned using the iterator i, which is initialized as i = 0. • 1st Step: Here i = 0 and exp[i] = ‘a’ i.e., an operand. So add this in the postfix expression. Therefore, postfix = “a”.
- 4. • 2nd Step: Here i = 1 and exp[i] = ‘+’ i.e., an operator. Push this into the stack. postfix = “a” and stack = {+}.
- 5. • 3rd Step: Now i = 2 and exp[i] = ‘b’ i.e., an operand. So add this in the postfix expression. postfix = “ab” and stack = {+}.
- 6. • 4th Step: Now i = 3 and exp[i] = ‘*’ i.e., an operator. Push this into the stack. postfix = “ab” and stack = {+, *}.
- 7. • 5th Step: Now i = 4 and exp[i] = ‘c’ i.e., an operand. Add this in the postfix expression. postfix = “abc” and stack = {+, *}.
- 8. • 6th Step: Now i = 5 and exp[i] = ‘+’ i.e., an operator. The topmost element of the stack has higher precedence. So pop until the stack becomes empty or the top element has less precedence. ‘*’ is popped and added in postfix. So postfix = “abc*” and stack = {+}.
- 9. • Now top element is ‘+‘ that also doesn’t have less precedence. Pop it. postfix = “abc*+”.
- 10. • Now stack is empty. So push ‘+’ in the stack. stack = {+}.
- 11. • 7th Step: Now i = 6 and exp[i] = ‘d’ i.e., an operand. Add this in the postfix expression. postfix = “abc*+d”.
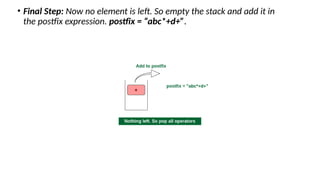
- 12. • Final Step: Now no element is left. So empty the stack and add it in the postfix expression. postfix = “abc*+d+”.