Corelation and regression PowerPoint presentation for basic understanding

Correlation &
Correlation &
Regression
Regression
Md. Fazlul Karim Patwary
IIT
Jahangirnagar University

Correlation
Correlation
Finding the relationship between two
quantitative variables without being
able to infer causal relationships
Correlation is a statistical technique
used to determine the degree to which
two variables are related

• Rectangular coordinate
• Two quantitative variables
• One variable is called independent (X) and
the second is called dependent (Y)
• Points are not joined
• No frequency table
Scatter diagram

Scatter diagram of weight and systolic blood
Scatter diagram of weight and systolic blood
pressure
pressure
80
100
120
140
160
180
200
220
60 70 80 90 100 110 120
wt (kg)
SBP(mmHg)

80
100
120
140
160
180
200
220
60 70 80 90 100 110 120
Wt (kg)
SBP(mmHg)
Scatter diagram of weight and systolic blood pressure

Scatter plots
The pattern of data is indicative of the type of
relationship between your two variables:
 positive relationship
 negative relationship
 no relationship

Positive relationship
Positive relationship

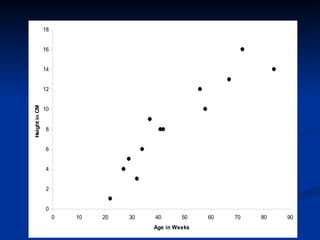
0
2
4
6
8
10
12
14
16
18
0 10 20 30 40 50 60 70 80 90
Age in Weeks
Height
in
CM

Negative relationship
Negative relationship
Reliability
Age of Car

Y
X
Y
X
Y
Y
X
X
Linear relationships Curvilinear relationships
Linear Correlation
Linear Correlation

Slide from: Statistics for Managers Using Microsoft® Excel 4th Edition, 2004 Prentice-Hall

Y
X
Y
X
Y
Y
X
X
Strong relationships Weak relationships
Linear Correlation
Linear Correlation

lide from: Statistics for Managers Using Microsoft® Excel 4th Edition, 2004 Prentice-Hall

Correlation Coefficient
Correlation Coefficient
Statistic showing the degree of relation
between two variables

Simple Correlation coefficient
Simple Correlation coefficient (r)
(r)
 It is also called Pearson's correlation
It is also called Pearson's correlation
or product moment correlation
or product moment correlation
coefficient.
coefficient.
 It measures the
It measures the nature
nature and
and strength
strength
between two variables of
between two variables of
the
the quantitative
quantitative type.
type.

The
The sign
sign of
of r
r denotes the nature of
denotes the nature of
association
association
while the
while the value
value of
of r
r denotes the
denotes the
strength of association.
strength of association.

 If the sign is
If the sign is +ve
+ve this means the relation
this means the relation
is
is direct
direct (an increase in one variable is
(an increase in one variable is
associated with an increase in the
associated with an increase in the
other variable and a decrease in one
other variable and a decrease in one
variable is associated with a
variable is associated with a
decrease in the other variable).
decrease in the other variable).
 While if the sign is
While if the sign is -ve
-ve this means an
this means an
inverse or indirect
inverse or indirect relationship (which
relationship (which
means an increase in one variable is
means an increase in one variable is
associated with a decrease in the other).
associated with a decrease in the other).

 The value of r ranges between ( -1) and ( +1)
The value of r ranges between ( -1) and ( +1)
 The value of r denotes the strength of the
The value of r denotes the strength of the
association as illustrated
association as illustrated
by the following diagram.
by the following diagram.
-
1 1
0
-0.25
-0.75 0.75
0.25
strong strong
intermediate intermediate
weak weak
no relation
perfect
correlation
perfect
correlation
Direct
indirect

If
If r
r = Zero
= Zero this means no association or
this means no association or
correlation between the two variables.
correlation between the two variables.
If
If 0 <
0 < r
r < 0.25
< 0.25 = weak correlation.
= weak correlation.
If
If 0.25 ≤
0.25 ≤ r
r < 0.75
< 0.75 = intermediate correlation.
= intermediate correlation.
If
If 0.75 ≤
0.75 ≤ r
r < 1
< 1 = strong correlation.
= strong correlation.
If
If r
r = l
= l = perfect correlation.
= perfect correlation.





















 
 

 
n
y)
(
y
.
n
x)
(
x
n
y
x
xy
r
2
2
2
2
How to compute the simple correlation
coefficient (r)

Example
Example
:
:
A sample of 6 children was selected, data about their
A sample of 6 children was selected, data about their
age in years and weight in kilograms was recorded as
age in years and weight in kilograms was recorded as
shown in the following table . It is required to find the
shown in the following table . It is required to find the
correlation between age and weight.
correlation between age and weight.
serial
No
Age
(years)
Weight
(Kg)
1
7
12
2
6
8
3
8
12
4
5
10
5
6
11
6
9
13

These 2 variables are of the quantitative type, one
These 2 variables are of the quantitative type, one
variable (Age) is called the independent and
variable (Age) is called the independent and
denoted as (X) variable and the other (weight)
denoted as (X) variable and the other (weight)
is called the dependent and denoted as (Y)
is called the dependent and denoted as (Y)
variables to find the relation between age and
variables to find the relation between age and
weight compute the simple correlation coefficient
weight compute the simple correlation coefficient
using the following formula:
using the following formula:




















 
 

 
n
y)
(
y
.
n
x)
(
x
n
y
x
xy
r
2
2
2
2

Serial
n
.
Age
(years)
(x)
Weight
(Kg)
(y)
xy
X2
Y2
1
7
12
84
49
144
2
6
8
48
36
64
3
8
12
96
64
144
4
5
10
50
25
100
5
6
11
66
36
121
6
9
13
117
81
169
Total
∑
x
=
41
∑
y
=
66
∑
xy=
461
∑
x2
=
291
∑
y2
=
742

r = 0.759
r = 0.759
strong direct correlation
strong direct correlation

















6
(66)
742
.
6
(41)
291
6
66
41
461
r
2
2

EXAMPLE: Relationship between Anxiety and
EXAMPLE: Relationship between Anxiety and
Test Scores
Test Scores
Anxiety
Anxiety
(
(
X
X
)
)
Test
Test
score (Y)
score (Y)
X
X2
2
Y
Y2
2
XY
XY
10
10
2
2
100
100
4
4
20
20
8
8
3
3
64
64
9
9
24
24
2
2
9
9
4
4
81
81
18
18
1
1
7
7
1
1
49
49
7
7
5
5
6
6
25
25
36
36
30
30
6
6
5
5
36
36
25
25
30
30
∑
∑
X = 32
X = 32
∑
∑
Y = 32
Y = 32
∑
∑
X
X2
2
= 230
= 230
∑
∑
Y
Y2
2
= 204
= 204
∑
∑
XY=129
XY=129

Calculating Correlation Coefficient
Calculating Correlation Coefficient
  
94
.
)
200
)(
356
(
1024
774
32
)
204
(
6
32
)
230
(
6
)
32
)(
32
(
)
129
)(
6
(
2
2








r
r = - 0.94
Indirect strong correlation

27
Coefficient of
Coefficient of
Determination
Determination
It is often difficult to interpret r without some familiarity with the expected
values of r
.
A more appropriate measure to use when interest lies in the dependence of
Y on X, is the Coefficient of Determination, R2
.
It measures the proportion of variation in Y that is explained by X, and is
often expressed as a percentage
.

28
Using anova to find R
Using anova to find R2
2
Anova (for 93 rural female headed HHs) of log consumption expenditure versus
number of persons per sleeping room is
:
Source
d.f.
S.S.
M.S.
F
Prob.
Regression
1
4.890
4.890
21.9
0.000
Residual
91
20.342
0.2235
Total
92
25.231
0.2743
R2
= Regre. S.S. / Total S.S.
= 4.89/25.23
=
0.194

29
Interpretation of R
Interpretation of R2
2
From above, we can say that 19.4% of the
variability in the income poverty proxy
measure is accounted for by the number of
persons per sleeping room
.
Clearly there are many other factors that
influence the poverty proxy since over 80%
of the variability is left unexplained
!

30
Relationship of R
Relationship of R2
2
to r
to r
When there is just one explanatory variable
being considered (as in above example),
the squared value of r equals R2
.
In the above example
,
value of r = -  0.194 = - 0.44
The negative value is used when taking the
square root because the graph indicates a
negative relationship (see next slide)
.

31
Plot of poverty proxy measure vs. persons
Plot of poverty proxy measure vs. persons
per sleeping room
per sleeping room

32
Benefits of R
Benefits of R2
2
and r
and r
•
r is useful as an initial exploratory tool when several
variables are being considered. The sign of r gives the
direction of the association
.
•
R2
is useful in regression studies to check how much of
the variability in the key response can be explained
.
•
R2
is most valuable when there is more than one
explanatory variable. High values of R2
are particularly
useful when using the model for predictions
!

33
Limitations of r
Limitations of r
•
Observe that seemingly high values of r, e.g. r=0.70, explain
only about 50% of the variability in the response variable y.
So take care when interpreting correlation coefficients
.
•
a low value for r does not necessarily imply absence of a
relationship – could be a curved relationship! So plotting the
data is crucial
!
•
Tests exist for testing there is no association. But depending
on the sample size, even low values of r, e.g. r=0.20 can
give significant results – not a very useful finding
!

34
Limitations of R
Limitations of R2
2
•
Note that R2
is only a descriptive measure to give a quick
assessment of the model. Other methods exist for
assessing the goodness of fit of the model
.
•
Adding explanatory variables to the model always
increases R2
. Hence in practice, it is more usual to look at
the adjusted R2
•
The adjusted R2
is calculated as
1
( –
Residual M.S./Total M.S
).
As with R2
, the adjusted R2
is often expressed as a
percentage
.

Spearman Rank Correlation Coefficient (r
Spearman Rank Correlation Coefficient (rs
s)
)
It is a non-parametric measure of correlation.
It is a non-parametric measure of correlation.
This procedure makes use of the two sets of
This procedure makes use of the two sets of
ranks that may be assigned to the sample values
ranks that may be assigned to the sample values
of x and Y.
of x and Y.
Spearman Rank correlation coefficient could be
Spearman Rank correlation coefficient could be
computed in the following cases:
computed in the following cases:
Both variables are quantitative.
Both variables are quantitative.
Both variables are qualitative ordinal.
Both variables are qualitative ordinal.
One variable is quantitative and the other is qualitative
One variable is quantitative and the other is qualitative
ordinal.
ordinal.

Procedure
Procedure
:
:
1.
1. Rank the values of X from 1 to n where n
Rank the values of X from 1 to n where n
is the numbers of pairs of values of X and
is the numbers of pairs of values of X and
Y in the sample.
Y in the sample.
2.
2. Rank the values of Y from 1 to n.
Rank the values of Y from 1 to n.
3.
3. Compute the value of di for each pair of
Compute the value of di for each pair of
observation by subtracting the rank of Yi
observation by subtracting the rank of Yi
from the rank of Xi
from the rank of Xi
4.
4. Square each di and compute ∑di2 which
Square each di and compute ∑di2 which
is the sum of the squared values.
is the sum of the squared values.

5.
5. Apply the following formula
Apply the following formula
1)
n(n
(di)
6
1
r 2
2
s




The value of rs denotes the magnitude
and nature of association giving the same
interpretation as simple r.

Example
Example
In a study of the relationship between level
In a study of the relationship between level
education and income the following data was
education and income the following data was
obtained. Find the relationship between them and
obtained. Find the relationship between them and
comment.
comment.
sample
numbers
level education
(X)
Income
(Y)
A
Preparatory.
Preparatory.
25
B
Primary.
Primary.
10
C
University.
University.
8
D
secondary
secondary
10
E
secondary
secondary
15
F
illit
illiterate
erate
50
G
University.
University.
60

Answer:
Answer:
(X)
(Y)
Rank
X
Rank
Y
di
di2
A
Preparatory
25
5
3
2
4
B
Primary.
10
6
5.5
0.5
0.25
C
University.
8
1.5
7
-5.5
30.25
D
secondary
10
3.5
5.5
-2
4
E
secondary
15
3.5
4
-0.5
0.25
F
illiterate
50
7
2
5
25
G
university.
60
1.5
1
0.5
0.25
∑ di2
=64

Comment:
Comment:
There is an indirect weak correlation
There is an indirect weak correlation
between level of education and income.
between level of education and income.
1
.
0
)
48
(
7
64
6
1 




s
r

Regression Analyses
Regression Analyses
Regression: Technique concerned with
predicting some variables by knowing others
The process of predicting variable Y using
variable X

Regression
Regression
 Uses a variable (x) to predict some outcome
Uses a variable (x) to predict some outcome
variable (y)
variable (y)
 Tells you how values in y change as a function
Tells you how values in y change as a function
of changes in values of x
of changes in values of x

Correlation and Regression
Correlation and Regression
 Correlation describes the strength of a
Correlation describes the strength of a linear
relationship between two variables
 Linear means “straight line”
 Regression tells us how to draw the straight line
described by the correlation

Regression
 Calculates the “best-fit” line for a certain set of data
Calculates the “best-fit” line for a certain set of data
The regression line makes the sum of the squares of
The regression line makes the sum of the squares of
the residuals smaller than for any other line
the residuals smaller than for any other line
Regression minimizes residuals
80
100
120
140
160
180
200
220
60 70 80 90 100 110 120
Wt (kg)

By using the least squares method (a procedure
By using the least squares method (a procedure
that minimizes the vertical deviations of plotted
that minimizes the vertical deviations of plotted
points surrounding a straight line) we are
points surrounding a straight line) we are
able to construct a best fitting straight line to the
able to construct a best fitting straight line to the
scatter diagram points and then formulate a
scatter diagram points and then formulate a
regression equation in the form of:
regression equation in the form of:



 



n
x)
(
x
n
y
x
xy
b 2
2
1
x
b
-
y
a  b
bX
a
ŷ 


Regression Equation
 Regression equation
describes the regression
line mathematically
 Intercept
 Slope 80
100
120
140
160
180
200
220
60 70 80 90 100 110 120
Wt (kg)
SBP(mmHg)

Linear Equations
Linear Equations
Y
Y = bX + a
a = Y-intercept
X
Change
in Y
Change in X
b = Slope
bX
a
ŷ 


Hours studying and grades
Hours studying and grades

Regressing grades on hours
grades on hours
Linear Regression
2.00 4.00 6.00 8.00 10.00
Number of hours spent studying
70.00
80.00
90.00












Final grade in course = 59.95 + 3.17 * study
R-Square = 0.88
Predicted final grade in class =
59.95 + 3.17*(number of hours you study per week)

Predict the final grade of
Predict the final grade of
…
…
 Someone who studies for 12 hours
 Final grade = 59.95 + (3.17*12)
 Final grade = 97.99
 Someone who studies for 1 hour:
 Final grade = 59.95 + (3.17*1)
 Final grade = 63.12
Predicted final grade in class = 59.95 + 3.17*(hours of study)

Exercise
Exercise
A sample of 6 persons was selected the
A sample of 6 persons was selected the
value of their age ( x variable) and their
value of their age ( x variable) and their
weight is demonstrated in the following
weight is demonstrated in the following
table. Find the regression equation and
table. Find the regression equation and
what is the predicted weight when age is
what is the predicted weight when age is
8.5 years
8.5 years.
.

Serial no
.
Age (x)
Weight (y)
1
2
3
4
5
6
7
6
8
5
6
9
12
8
12
10
11
13

Answer
Answer
Serial no
.
Age (x)
Weight (y)
xy
X2
Y2
1
2
3
4
5
6
7
6
8
5
6
9
12
8
12
10
11
13
84
48
96
50
66
117
49
36
64
25
36
81
144
64
144
100
121
169
Total
41
66
461
291
742

6.83
6
41
x 
 11
6
66


y
92
.
0
6
)
41
(
291
6
66
41
461
2





b
Regression equation
6.83)
0.9(x
11
ŷ(x) 



0.92x
4.675
ŷ(x) 

12.50Kg
8.5
*
0.92
4.675
ŷ(8.5) 


Kg
58
.
11
7.5
*
0.92
4.675
ŷ(7.5) 



11.4
11.6
11.8
12
12.2
12.4
12.6
7 7.5 8 8.5 9
Age (in years)
Weight
(in
Kg)
we create a regression line by plotting two
estimated values for y against their X component,
then extending the line right and left.

Exercise 2
Exercise 2
The following are the
The following are the
age (in years) and
age (in years) and
systolic blood
systolic blood
pressure of 20
pressure of 20
apparently healthy
apparently healthy
adults.
adults.
Age
(x)
B.P
(y)
Age
(x)
B.P
(y)
20
43
63
26
53
31
58
46
58
70
120
128
141
126
134
128
136
132
140
144
46
53
60
20
63
43
26
19
31
23
128
136
146
124
143
130
124
121
126
123

Find the correlation between age
Find the correlation between age
and blood pressure using simple
and blood pressure using simple
and Spearman's correlation
and Spearman's correlation
coefficients, and comment.
coefficients, and comment.
Find the regression equation?
Find the regression equation?
What is the predicted blood
What is the predicted blood
pressure for a man aging 25 years?
pressure for a man aging 25 years?

Serial
x
y
xy
x2
1
20
120
2400
400
2
43
128
5504
1849
3
63
141
8883
3969
4
26
126
3276
676
5
53
134
7102
2809
6
31
128
3968
961
7
58
136
7888
3364
8
46
132
6072
2116
9
58
140
8120
3364
10
70
144
10080
4900

Serial
x
y
xy
x2
11
46
128
5888
2116
12
53
136
7208
2809
13
60
146
8760
3600
14
20
124
2480
400
15
63
143
9009
3969
16
43
130
5590
1849
17
26
124
3224
676
18
19
121
2299
361
19
31
126
3906
961
20
23
123
2829
529
Total
852
2630
114486
41678




 



n
x)
(
x
n
y
x
xy
b 2
2
1 4547
.
0
20
852
41678
20
2630
852
114486
2




=
=112.13 + 0.4547 x
for age 25
B.P = 112.13 + 0.4547 * 25=123.49 = 123.5 mm hg
ŷ

Multiple Regression
Multiple regression analysis is a
straightforward extension of simple
regression analysis which allows more
than one independent variable.

Corelation and regression PowerPoint presentation for basic understanding

Corelation and regression PowerPoint presentation for basic understanding

Recommended

More Related Content

Similar to Corelation and regression PowerPoint presentation for basic understanding (20)

Recently uploaded (20)

Corelation and regression PowerPoint presentation for basic understanding