More Related Content
What's hot (20)
Viewers also liked (20)
Similar to Csc1401 lecture03 - computer arithmetic - arithmetic and logic unit (alu) (20)
More from IIUM (20)
Recently uploaded (20)
Csc1401 lecture03 - computer arithmetic - arithmetic and logic unit (alu)
- 1. Madam Raini Hassan Office: C5 - 23, Level 5, KICT Building Department: Computer Science Emails: [email protected], [email protected] 1Semester II 2014/2015
- 2. Du’a for Study Semester II 2014/2015 2
- 3. LECTURE 03 Computer Arithmetic: Arithmetic and Logic Unit (ALU) (Chapter 10)
- 4. Arithmetic & Logic Unit (ALU) • Part of the computer that actually performs arithmetic and logical operations on data • All of the other elements of the computer system are there mainly to bring data into the ALU for it to process and then to take the results back out • Based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations
- 5. ALU Inputs and Outputs
- 6. Integer Representations • In the binary number system arbitrary numbers can be represented with: – The digits zero and one – The minus sign (for negative numbers) – The period, or radix point (for numbers with a fractional component) – For purposes of computer storage and processing we do not have the benefit of special symbols for the minus sign and radix point – Only binary digits (0,1) may be used to represent numbers
- 7. Integer Representations • There are 4 commonly known (1 not common) integer representations. • All have been used at various times for various reasons. 1. Unsigned 2. Sign Magnitude 3. One’s Complement 4. Two’s Complement 5. Biased (not commonly known)
- 8. 1. Unsigned • The standard binary encoding already given. • Only positive value. • Range: 0 to ((2 to the power of N bits) – 1) • Example: 4 bits; (2ˆ4)-1 = 16-1 = values 0 to 15 Semester II 2014/2015 8
- 9. 1. Unsigned (Cont’d.) Semester II 2014/2015 9
- 10. 2. Sign-Magnitude There are several alternative conventions used to represent negative as well as positive integers Sign-magnitude representation is the simplest form that employs a sign bit Drawbacks: Because of these drawbacks, sign- magnitude representation is rarely used in implementing the integer portion of the ALU • All of these alternatives involve treating the most significant (leftmost) bit in the word as a sign bit • If the sign bit is 0 the number is positive • If the sign bit is 1 the number is negative • Addition and subtraction require a consideration of both the signs of the numbers and their relative magnitudes to carry out the required operation • There are two representations of 0
- 11. 2. Sign-Magnitude (Cont’d.) • It is a human readable way of getting both positive and negative integers. • The hardware that does arithmetic on sign magnitude integers. • Not fast. 2-11
- 12. 2. Sign-Magnitude (Cont’d.) • Left most bit is sign bit • 0 means positive • 1 means negative • +18 = 00010010 • -18 = 10010010 2-12
- 13. 3. One’s Complement • Used to get two’s complement integers. • Nowadays, it is not being applied to any of the machines. • Stated in this slide for historical purpose. Semester II 2014/2015 13
- 14. 4. Two’s Complement • Uses the most significant bit as a sign bit • Differs from sign-magnitude representation in the way that the other bits are interpreted Table 10.1 Characteristics of Twos Complement Representation and Arithmetic
- 15. 5. Biased • an integer representation that skews the bit patterns so as to look just like unsigned but actually represent negative numbers. Semester II 2014/2015 15
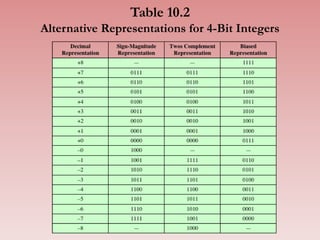
- 16. Table 10.2 Alternative Representations for 4-Bit Integers
- 17. Range Extension – Range of numbers that can be expressed is extended by increasing the bit length – In sign-magnitude notation this is accomplished by moving the sign bit to the new leftmost position and fill in with zeros – This procedure will not work for twos complement negative integers – Rule is to move the sign bit to the new leftmost position and fill in with copies of the sign bit – For positive numbers, fill in with zeros, and for negative numbers, fill in with ones – This is called sign extension
- 18. Range of Numbers • 8 bit 2s complement – +127 = 01111111 = 27 -1 – -128 = 10000000 = -27 • 16 bit 2s complement – +32767 = 011111111 11111111 = 215 - 1 – -32768 = 100000000 00000000 = -215 2-18
- 19. Negation • Twos complement operation – Take the Boolean complement of each bit of the integer (including the sign bit) – Treating the result as an unsigned binary integer, add 1 – The negative of the negative of that number is itself: +18 = 00010010 (twos complement) bitwise complement = 11101101 + 1 11101110 = -18 -18 = 11101110 (twos complement) bitwise complement = 00010001 + 1 00010010 = +18
- 20. Negation Special Case 1 0 = 00000000 (twos complement) Bitwise complement = 11111111 Add 1 to LSB + 1 Result 100000000 Overflow is ignored, so: - 0 = 0
- 21. Negation Special Case 2 -128 = 10000000 (twos complement) Bitwise complement = 01111111 Add 1 to LSB + 1 Result 10000000 So: -(-128) = -128 X Monitor MSB (sign bit) It should change during negation
- 22. OVERFLOW RULE: If two numbers are added, and they are both positive or both negative, then overflow occurs if and only if the result has the opposite sign.
- 23. Addition
- 24. SUBTRACTION RULE: To subtract one number (subtrahend) from another (minuend), take the twos complement (negation) of the subtrahend and add it to the minuend.
- 25. Subtraction
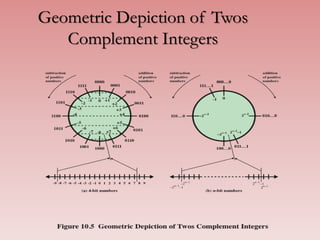
- 26. Geometric Depiction of Twos Complement Integers
- 27. Hardware for Addition and Subtraction
- 28. Multiplication
- 32. Comparison
- 34. Division
- 36. Example of Restoring Twos Complement Division
- 37. + Floating-Point Representation • With a fixed-point notation it is possible to represent a range of positive and negative integers centered on or near 0 • By assuming a fixed binary or radix point, this format allows the representation of numbers with a fractional component as well • Limitations: – Very large numbers cannot be represented nor can very small fractions – The fractional part of the quotient in a division of two large numbers could be lost Principles
- 38. Typical 32-Bit Floating-Point Format
- 39. + Floating-Point • The final portion of the word • Any floating-point number can be expressed in many ways • Normal number – The most significant digit of the significand is nonzero Significand The following are equivalent, where the significand is expressed in binary form: 0.110 * 25 110 * 22 0.0110 * 26
- 40. IEEE Standard 754 Most important floating-point representation is defined Standard was developed to facilitate the portability of programs from one processor to another and to encourage the development of sophisticated, numerically oriented programs Standard has been widely adopted and is used on virtually all contemporary processors and arithmetic coprocessors IEEE 754-2008 covers both binary and decimal floating- point representations
- 41. IEEE 754 Formats
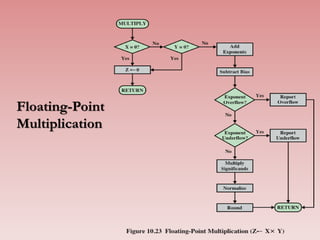
- 42. Floating-Point Addition and Subtraction