Data collection & Organization (Organizing Data: Frequency Distribution and Graphical Presentations).pptx

DATA COLLECTION &
ORGANIZATION
(Organizing Data: Frequency Distribution
and Graphical Presentations)

FREQUENCY DISTRIBUTION
In most cases, the data collected from
the different sources through various
methods of data collection are generally
raw, unorganized and haphazard. (Broto,
2nd
Edition)

One method for simplifying and
organizing data is to construct a
frequency distribution.

Frequency –how many times
it appears

It is the tabulation of data of measures grouped
with class interval.
 A frequency distribution is an organized tabulation
showing exactly how many individuals are located
in each category on the scale of measurement.
 A frequency distribution presents an organized
picture of the entire set of scores, and it shows
where each individual is located relative to others
in the distribution.

The frequency f of a class is the number of data
entries in the class. Each class will have a “lower
class limit” and an “upper class limit” which are
the lowest and highest numbers in each class.The
“class width” is the distance between the lower
limits of consecutive classes.The range is the
difference between the maximum and minimum
data entries.
When the data has a wide range, we can
group it. (Grouped Frequency Distribution)

Table 2
Frequency Distribution of the
Examination Results of Thirty
Seven Students in Mathematics
Table 3
Frequency Distribution of the Thirty
Seven Students Grouped According to
their Respective Courses
Table 4
Frequency Distribution of Thirty Seven
Students Grouped According to Sex

GRAPHICAL PRESENTATION
It is a method of presenting statistical results and can
present clear picture of data.
The data can be presented graphically according to their
scales or levels of measurement.The most common graphic
presentations are the pie chart or circle graph, histogram
or bar graph and frequency polygon or line graph.

Consider this table of enrollment
by sex in the College of Arts and
Communication.
Table 1
Frequency Distribution of Enrollment by
Sex
PIE CHART NOMINAL DATA
The pie chart or circle graph can provide an easy presentation of
nominal data or any categorical data. The whole circular graph
equals 100%. Likewise, one complete revolution equals 360º . So in
making the graph, multiply the 360º by the percentage in every
category.
Solutions:
25% of 360º =90º
75% of 360º =270º
Using a protractor, measure the 90º and the 270º that will represent
the graph for male and female enrollment.
Male
25%
Female
75%
Fig.1 Distribution of Enrollment by Sex in the College of Arts
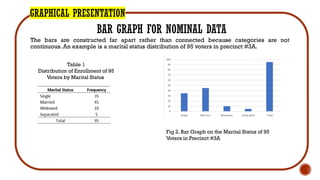
and Communication

BAR GRAPH FOR NOMINAL DATA
The bars are constructed far apart rather than connected because categories are not
continuous. An example is a marital status distribution of 95 voters in precinct #3A.
Table 1
Distribution of Enrollment of 95
Voters by Marital Status
Fig 2. Bar Graph on the Marital Status of 95
Voters in Precinct #3A

BAR GRAPH FOR ORDINAL DATA
The rectangular bar should be connected to show the degree of difference. For example 100
individuals in the community are classified according to their social classes.
Table 1
Frequency Distribution of 100
Individuals Classified According to
their Social Classes
Fig 3 Bar Graph of the Social Class of 100
Individuals
Using bars, the social classes are plotted in ascending order from the left to the right on the x-
axis; the frequency on the y-ordinate.

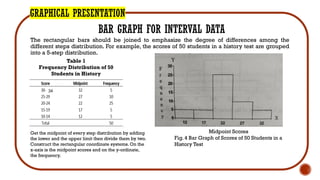
BAR GRAPH FOR INTERVAL DATA
The rectangular bars should be joined to emphasize the degree of differences among the
different steps distribution. For example, the scores of 50 students in a history test are grouped
into a 5-step distribution.
Table 1
Students in History
Midpoint Scores
Fig. 4 Bar Graph of Scores of 50 Students in a
History Test
Get the midpoint of every step distribution by adding
the lower and the upper limit then divide them by two.
Construct the rectangular coordinate systems. On the
x-axis is the midpoint scores and on the y-ordinate,
the frequency.
34

FREQUENCY POLYGON OR LINE
GRAPH
 The frequency polygon is prepared by making a histogram, plotting the points using the frequency and the midpoints,
and connecting the points by straight lines. This kind of presentation can also be applied to ordinal or interval data
because it stresses continuity along a scale. For example, the scores of 50 students in a history test are grouped into a 5-
step distribution.
 The midpoint of every step distribution is taken by adding the lower and the upper limit and dividing them by two. The
x-axis is then constructed for the midpoint score and the y-ordinate for the frequency
Table 1
Students in History
Midpoint Scores
Fig. 5 Scores of 50 Students in History
34

“Frequency distribution is a vital technique for organizing
data in research. By grouping data into intervals, researchers
can make sense of large data set, identify trends and
anomalies, and present their findings in an easily
interpretable format. Whether you use tables, histograms,
bar graphs, or pie chats, frequency distribution offers a
powerful way to make complex data more accessible and
meaningful”
https://journalism.university/communication-research-methods/organizing-data-frequency-distribution/

Thank You
So Much
Thank You
So Much

Data collection & Organization (Organizing Data: Frequency Distribution and Graphical Presentations).pptx

More Related Content

Similar to Data collection & Organization (Organizing Data: Frequency Distribution and Graphical Presentations).pptx (20)

Recently uploaded (20)

Data collection & Organization (Organizing Data: Frequency Distribution and Graphical Presentations).pptx

Editor's Notes