Data structure using c++

SECOND PUC
Prof. K. Adisesha
COMPUTER SCIENCE (41)
SYLLABUS

Learning Outcomes
 UNIT A 31 Marks
 Backdrop of Computers 35 hrs
 UNIT B 39 Marks
 Computing in C++ 45hrs
 UNIT C 18 Marks
 Large Data, Database and Queries 20hrs
 UNIT D 17 Marks
 Advanced Concepts in Communication Technology
20hrs
2

UNIT A
Typical configuration of Computer system
 Review of Block diagram of CPU 4 Marks
 Mother board
 Types of Motherboards
 Components of Motherboard
 Processor and clock speed
 BIOS, CMOS
 Memory and Expansion slots
 Disk Controllers
 I/O Ports and Interfaces, BUS
 Power supply SMPS and UPS
3

UNIT A
BOOLEAN ALGEBRA 13 Marks
 Development of Boolean Algebra (History)
 Logical operators
 Logic gates
 Basic gates
 Derived Gates
 Design of gates
 NAND to NAND design
 NOR to NOR design
 Basic postulates of Boolean Algebra
 Minimization of Boolean expressions 4

UNIT A
Data structures 14 Marks
 Introduction to Data Structures
 Types of Data structures -Linear and non linear
 Arrays
 Types of arrays
 Basic operations
 Stacks and Queues
 Data representation
 Applications
 Linked lists 5

UNIT B
Object Oriented Programming in C++
 Review of C++ covered in First PUC 03 Marks
 Basic concepts of OOPS 04 Marks
 Classes and objects 06 Marks
 Declaration & definition of class and objects
 Access specifies
 Members of the class
 Array within class
 array of objects
 Functions returning objects
6

UNIT B
 Inheritance(Extending classes) 08 Marks
 Concepts of Inheritance
 Visibility modes
 Levels of inheritance
 Relationship between classes
 Pointers 07 Marks
 Declaration & initialization of pointers
 Address operator
 Pointer operator(indirection operator)
 Pointer arithmetic
 Pointer and functions 7

UNIT B
 Data file handling 06 Marks
 Header files(fstream.h)
 Types of data files
 Opening & closing files
 File modes
 Detecting end of file
 File pointers
 Operation on files
8

UNIT C
LARGE DATA, DATABASE AND QUERIES
 Database Concepts 18 Marks
 Need for Databases
 Data Models
 Keys/ Constraints
 Relational Algebra
 Structured Query Language
 SQL Commands
 SQL Functions
9

UNIT D
Advanced concepts in communication technology
 Networking Concepts 09 Marks
 Evolution of Networking and Protocols
 Terminologies used in Network
 Switching techniques
 Type of Networking
 Transmission Media
 Network Topologies
 Network Devices
 Network Security
10

UNIT D
Advanced concepts in communication technology
 Internet and Open source concepts 04 Marks
 Definition and Applications
 Internetworking terms and concepts
 Open source
 E-commerce
 Web Designing 04 Marks
 HTML, -text,layout,images,table,forms,settings
 XML
 DYNAMIC HTML
 Web HOSTING
11

Data Structures
using C++
by
Prof. K. Adisesha

Data structures
14 Marks
13
 Introduction to Data Structures
 Types of Data structures -Linear and non linear
 Arrays
 Types of arrays
 Stacks and Queues
 Data representation
 Applications
 Linked lists

Definition
14
Data structures
 Data: Collection of raw facts.
 Data structure is representation of the logical
relationship existing between individual
elements of data.
 Data structure is a specialized format for
organizing and storing data in memory that
considers not only the elements stored but also
their relationship to each other.

Definition
15
Data structures
 Data structure affects the design of both structural
& functional aspects of a program.
 A algorithm is a step by step procedure to solve a
particular function.
 Program=algorithm + Data Structure

Classification of Data Structure
16
Data structures
 Data structure are normally divided into two
broad categories:
 Primitive Data Structure
 Non-Primitive Data Structure

Classification of Data Structure
17
Data structures

Primitive Data Structure
18
Data structures
 There are basic structures and directly operated
upon by the machine instructions.
 Data structures that are directly operated
upon the machine-level instructions are
known as primitive data structures.
 Integer, Floating-point number, Character
constants, string constants, pointers etc, fall in
this category.

Primitive Data Structure
19
Data structures
 The most commonly used operation on data
structure are broadly categorized into
following types:
 Create
 Selection
 Updating
 Destroy or Delete

Non-Primitive Data Structure
20
Data structures
 There are more sophisticated data structures.
 The Data structures that are derived from the
primitive data structures are called Non-primitive
data structure.
 Linear Data structures
 Non-Linear Data structures
 The non-primitive data structures emphasize
on structuring of a group of homogeneous
(same type) or heterogeneous (different type)
data items.

21
Data structures
Linear Data structures:
 Linear Data structures are kind of data structure that has
homogeneous elements.
 The data structure in which elements are in a sequence
and form a liner series.
 Linear data structures are very easy to implement, since
the memory of the computer is also organized in a linear
fashion.
 Some commonly used linear data structures are Stack,
Queue and Linked Lists.

22
Data structures
Non-Linear Data structures:
 A Non-Linear Data structures is a data structure in which
data item is connected to several other data items.
 Non-Linear data structure may exhibit either a hierarchical
relationship or parent child relationship.
 The data elements are not arranged in a sequential
structure.
 The different non-linear data structures are trees and
graphs.

23
Data structures
 The most commonly used operation on data
structure are broadly categorized into
following types:
 Traversal
 Insertion
 Selection
 Searching
 Sorting
 Merging
 Destroy or Delete

Differences between Data Structure
24
Data structures
 A primitive data structure is generally a
basic structure that is usually built into the
language, such as an integer, a float.
 A non-primitive data structure is built out of
primitive data structures linked together in
meaningful ways, such as a or a linked-list,
binary search tree, AVL Tree, graph etc.

Arrays
25
Data structures
 An array is defined as a set of finite number of
homogeneous elements or same data items.
 It means an array can contain one type of data
only, either all integer, all float-point number
or all character.

Arrays
26
Data structures
 Declaration of array is as follows:
Syntax: Datatype Array_Name [Size];
Example: int arr[10]
 Where int specifies the data type or type of
elements arrays stores.
 “arr” is the name of array & the number specified
inside the square brackets is the number of
elements an array can store, this is also called sized
or length of array.

Represent a Linear Array in memory
27
Data structures
 The elements of linear array are stored in
consecutive memory locations.
 It is shown below:
int A[5]={10, 100, 20, 500, 600}

Calculating the length of the array
28
Data structures
 The elements of array will always be stored in the consecutive
(continues) memory location.
 The number of elements that can be stored in an array, that is
the size of array or its length is given by the following
equation:
 A[n] is the array size or length of n elements.
 The length of the array can be calculated by:
L = UB – LB + 1
 To Calculate the address of any element in array:
Loc(A[P])=Base(A)+W(P-LB)
 Here, UB is the largest Index and LB is the smallest index
 Example: If an array A has values 10, 20, 30, 40, 50, stored in location
0,1, 2, 3, 4 the UB = 4 and LB=0
 Size of the array L = 4 – 0 + 1 = 5

Types of Arrays
29
Data structures
 Single Dimension Array
 Array with one subscript
 Ex: int A[i];
 Two Dimension Array
 Array with two subscripts (Rows and Column)
 Ex: int A[i][j];
 Multi Dimension Array
 Array with Multiple subscripts
 Ex: int A[i][j]..[n];

Basic operations of Arrays
30
Data structures
 Some common operation performed on array
are:
 Traversing
 Searching
 Insertion
 Deletion
 Sorting
 Merging

Traversing Arrays
31
Data structures
Traversing: It is used to access each data item exactly once so that it
can be processed.
We have linear array A as below:
1 2 3 4 5
10 20 30 40 50
Here we will start from beginning and will go till last element and during this
process we will access value of each element exactly once as below:
A [1] = 10
A [2] = 20
A [3] = 30
A [4] = 40
A [5] = 50

Program:To find the frequency of presence element in the given array.
32
Data structures

Insertion into Array
33
Data structures
 Insertion: It is used to add a new data item in the
given collection of data items.
 E.g. We have linear array A as below:
1 2 3 4 5
10 20 50 30 15
 New element to be inserted is 100 and location for insertion is
3. So shift the elements from 5th location to 3rd location
downwards by 1 place. And then insert 100 at 3rd location.
 It is shown below

Insertion into Array
34
Data structures
 It is shown below:

Insertion into Array: Add a new data item in the given array of data
35
Data structures
 Program: to add a new data item in the given array of data.

Deletion from Array
36
Data structures
 Deletion: It is used to delete an existing data item
from the given collection of data items.

Program to delete an existing data item from the array.
37
Data structures

Searching in Arrays
38
Data structures
 Searching: It is used to find out the location of the data item if
it exists in the given collection of data items.
E.g. We have linear array A as below:
1 2 3 4 5
15 50 35 20 25
 Suppose item to be searched is 35. We will start from beginning
and will compare 35 with each element.
 This process will continue until element is found or array is
finished.
 Types of searching Algorithms:
 Linear searching
 Binary Searching

Linear searching
39
Data structures
 Linear Searching: Also called Sequential Searching.
 It is used to find out the location of the data item if it exists in
the given collection of data items.
 Example Searching element 33 from the array of elements:

Linear searching
40
Data structures
 Linear Searching: Also called Sequential Searching.

Binary Searching
41
Data structures
 The binary search algorithm can
be used with only sorted list of
elements.
 Binary Search first divides a
large array into two smaller
sub-arrays and then recursively
operate the sub-arrays.
 Binary Search basically reduces
the search space to half at each
step

Binary Searching
42
Data structures
 The binary search algorithm can be used with only sorted list of
elements.
 Example: Searching the element 5 from the array of elements

Binary Searching
43
Data structures

Binary Searching
44
Data structures

Difference in Searching
45
Data structures

Difference in Searching
46
Data structures

Sorting in Arrays
47
Data structures
 A Sorting Algorithm is used to rearrange a given array or list
elements according to a comparison operator on the elements.
 The comparison operator is used to decide the new order of
element in the respective data structure.
 Types of Sorting Algorithms are:
 Bubble Sort
 Insertion Sort
 Selection Sort
 Merge Sort
 Quick Sort
 Heap Sort
 Radix Sort
 Bucket Sort
 Shell Sort

Bubble Sort
48
Data structures
 Bubble Sort is the simplest sorting algorithm that works by
repeatedly swapping the adjacent elements if they are in wrong
order.

Insertion Sorting
49
Data structures
 Insertion sort is a simple sorting algorithm that builds the final
sorted array (or list) one item at a time.
 This is an in-place comparison-based sorting algorithm. Here,
a sub-list is maintained which is always sorted.

Insertion Sorting
50
Data structures
 This is an in-place comparison-based sorting algorithm. Here, a
sub-list is maintained which is always sorted.

Insertion Sorting
51
Data structures
 ALGORITHM: Insertion Sort (A, N) A is an array with N unsorted
elements.
 Step 1: for I=1 to N-1
 Step 2: J = I
While(J >= 1)
if ( A[J] < A[J-1] ) then
Temp = A[J];
A[J] = A[J-1];
A[J-1] = Temp;
[End if]
J = J-1
[End of While loop]
[End of For loop]
 Step 3: Exit

Selection Sort
52
Data structures

Selection Sort
53
Data structures

Merging from Array
54
Data structures
 Merging: It is used to combine the data items of two sorted files into
single file in the sorted form
We have sorted linear array A as below:
1 2 3 4 5 6
10 40 50 80 95 100
And sorted linear array B as below:
1 2 3 4
20 35 45 90
After merging merged array C is as below:
1 2 3 4 5 6 7 8 9 10
10 20 35 40 45 50 80 90 95 100

Two dimensional array
55
Data structures
 A two dimensional array is a collection of elements and each element is
identified by a pair of subscripts. ( A[3] [3] )
 The elements are stored in continuous memory locations.
 The elements of two-dimensional array as rows and columns.
 The number of rows and columns in a matrix is called as the
order of the matrix and denoted as MxN.
 The number of elements can be obtained by multiplying number
of rows and number of columns.
A[0] A[1] A[2]
A[0] 10 20 30
A[1] 40 50 60
A[2] 70 80 90

Representation of Two Dimensional Array
56
Data structures
 A two dimensional array is a collection of elements
and each element is identified by a pair of subscripts.
( A[m] [n] )
 A is the array of order m x n. To store m*n number of
elements, we need m*n memory locations.
 The elements should be in contiguous memory locations.
 There are two methods:
o Row-major method
o Column-major method

Representation of Two Dimensional Array
57
Data structures
 Row-Major Method: All the first-row elements are stored in
sequential memory locations and then all the second-row
elements are stored and so on. Ex: A[Row][Col]
 Column-Major Method: All the first column elements are
stored in sequential memory locations and then all the second-
column elements are stored and so on. Ex: A [Col][Row]
1000 10 A[0][0]
1002 20 A[0][1]
1004 30 A[0][2]
1006 40 A[1][0]
1008 50 A[1][1]
1010 60 A[1][2]
1012 70 A[2][0]
1014 80 A[2][1]
1016 90 A[2][2]
Row-Major Method
1000 10 A[0][0]
1002 40 A[1][0]
1004 70 A[2][0]
1006 20 A[0][1]
1008 50 A[1][1]
1010 80 A[2][1]
1012 30 A[0][2]
1014 60 A[1][2]
1016 90 A[2][2]
Col-Major Method

Calculating the length of the 2d-Array
58
Data structures
 The elements of array will always be stored in the consecutive
(continues) memory location.
 The size of array or its length is given by the following
equation:
 A[i][j] is the array size or length of m*n elements.
 To Calculate the address of i*j th element in array:
 Row-Major Method:
Loc(A[i][j])=Base(A)+W[n(i-LB)+(j-LB)]
 Col-Major Method:
Loc(A[i][j])=Base(A)+W[(i-LB)+m(j-LB)]
 Here, W is the number of words per memory location and LB is the
smallest index

Advantages of Array
59
Data structures
 It is used to represent multiple data items of same
type by using single name.
 It can be used to implement other data structures like
linked lists, stacks, queues, tree, graphs etc.
 Two-dimensional arrays are used to represent
matrices.
 Many databases include one-dimensional arrays
whose elements are records.

Disadvantages of Array
60
Data structures
 We must know in advance the how many elements
are to be stored in array.
 Array is static structure. It means that array is of
fixed size. The memory which is allocated to array
cannot be increased or decreased.
 Array is fixed size; if we allocate more memory than
requirement then the memory space will be wasted.
 The elements of array are stored in consecutive
memory locations. So insertion and deletion are very
difficult and time consuming.

Stack
61
Data structures
 Stack is a linear data structure which follows a particular order
in which the operations are performed.
 Insertion of element into stack is called PUSH and deletion of
element from stack is called POP.
 The order may be LIFO(Last In First Out) or FILO(First In
Last Out).

Memory Representation of Stack
62
Data structures
 The stack can be implemented into two ways:
 Using arrays (Static implementation)
 Using pointer (Dynamic

Operation on Stacks
63
Data structures
 Stack( ): It creates a new stack that is empty. It needs
no parameter and returns an empty stack.
 push(item): It adds a new item to the top of the
stack.
 pop( ): It removes the top item from the stack.
 peek( ): It returns the top item from the stack but
does not remove it.
 isEmpty( ): It tests whether the stack is empty.
 size( ): It returns the number of items on the stack.

Stack Conditions
64
Data structures

PUSH Operation
65
Data structures
 The process of adding one element or item to the
stack is represented by an operation called as the
PUSH operation.

PUSH Operation
66
Data structures
 The new element is added at the topmost position of the stack.
ALGORITHM:
PUSH (STACK, TOP, SIZE, ITEM)
STACK is the array with N elements. TOP is the pointer to the top of the
element of the array. ITEM to be inserted.
Step 1: if TOP = N then [Check Overflow]
PRINT “ STACK is Full or Overflow”
Exit
[End if]
Step 2: TOP = TOP + 1 [Increment the TOP]
Step 3: STACK[TOP] = ITEM [Insert the ITEM]
Step 4: Return

POP Operation
67
Data structures
 The process of deleting one element or item from the stack is
represented by an operation called as the POP operation.
 When elements are removed continuously from a stack, it
shrinks at same end i.e., top

POP Operation
68
Data structures
The process of deleting one element or item from the stack is
represented by an operation called as the POP operation.
ALGORITHM: POP (STACK, TOP, ITEM)
STACK is the array with N elements. TOP is the pointer to the top of the
element of the array. ITEM to be DELETED..
Step 1: if TOP = 0 then [Check Underflow]
PRINT “ STACK is Empty or Underflow”
Exit
[End if]
Step 2: ITEM = STACK[TOP] [copy the TOP Element]
Step 3: TOP = TOP - 1 [Decrement the TOP]
Step 4: Return

PEEK Operation
69
Data structures
The process of returning the top item from the stack
but does not remove it called as the PEEK operation.
ALGORITHM: PEEK (STACK, TOP)
STACK is the array with N elements. TOP is the pointer to the
top of the element of the array.
Step 1: if TOP = NULL then [Check Underflow]
PRINT “ STACK is Empty or Underflow”
Exit
[End if]
Step 2: Return (STACK[TOP] [Return the top
element of the stack]
Step 3:Exit

Application of Stacks
70
Data structures
 It is used to reverse a word. You push a given word to stack –
letter by letter and then pop letter from the stack.
 “Undo” mechanism in text editor.
 Backtracking: This is a process when you need to access the most
recent data element in a series of elements. Once you reach a dead
end, you must backtrack.
 Language Processing: Compiler’ syntax check for matching
braces in implemented by using stack.
 Data Conversion of decimal number to binary.
 To solve tower of Hanoi.
 Conversion of infix expression into prefix and postfix.
 Quick sort
 Runtime memory management.

Arithmetic Expression
71
Data structures
 An expression is a combination of operands and operators that
after evaluation results in a single value.
 Operand consists of constants and variables.
 Operators consists of {, +, -, *, /, ), ] etc.
 Expression can be
Infix Expression: If an operator is in between two operands, it is called infix
expression.
 Example: a + b, where a and b are operands and + is an operator.
Postfix Expression: If an operator follows the two operands, it is called
postfix expression.
 Example: ab +
Prefix Expression: an operator precedes the two operands, it is called prefix
expression.
 Example: +ab

Arithmetic Expression
72
Data structures

Queue
73
Data structures
A queue is an ordered collection of items where an item is
inserted at one end called the “rear” and an existing item
is removed at the other end, called the “front”.
 Queue is also called as FIFO list i.e. First-In First-Out.
 In the queue only two operations are allowed enqueue
and dequeue.
 Enqueue means to insert an item into back of the queue.
 Dequeue means removing the front item.The people
standing in a railway reservation row are an example of
queue.

Memory Representation of Queue
74
Data structures
The queue can be implemented into two ways:
 Using arrays (Static implementation)
 Using pointer (Dynamic

Memory Representation of a queue using array
75
Data structures
 Queue is represented in memory using linear array.
 Let QUEUE is a array, two pointer variables called
FRONT and REAR are maintained.
 The pointer variable FRONT contains the location of the
element to be removed or deleted.
 The pointer variable REAR contains location of the last
element inserted.
 The condition FRONT = NULL indicates that queue is
empty.
 The condition REAR = N-1 indicates that queue is full.

Types of Queues
76
Data structures
 Queue can be of four types:
o Simple Queue
o Circular Queue
o Priority Queue
o De-queue ( Double Ended Queue)

Simple Queue
77
Data structures
 Simple Queue: In simple queue insertion
occurs at the rear end of the list and deletion
occurs at the front end of the list.

Circular Queue
78
Data structures
 Circular Queue: A circular queue is a queue in
which all nodes are treated as circular such that
the last node follows the first node.

Priority Queue
79
Data structures
 A priority queue is a queue that contains items that
have some present priority. An element can be
inserted or removed from any position depending
upon some priority.

Dequeue Queue
80
Data structures
 Dequeue: It is a queue in which insertion and
deletion takes place at the both ends.

Operation on Queues
81
Data structures
 Queue( ): It creates a new queue that is empty.
 enqueue(item): It adds a new item to the rear of the
queue.
 dequeue( ): It removes the front item from the
queue.
 isEmpty( ): It tests to see whether the queue is
empty.
 size( ): It returns the number of items in the queue.

Queue Insertion Operation (ENQUEUE)
82
Data structures
 ALGORITHM: ENQUEUE (QUEUE, REAR, FRONT, ITEM)
QUEUE is the array with N elements. FRONT is the pointer that contains the
location of the element to be deleted and REAR contains the location of the
inserted element. ITEM is the element to be inserted.
Step 1: if REAR = N-1 then [Check Overflow] Front Rear
PRINT “QUEUE is Full or Overflow”
Exit
[End if]
Step 2: if FRONT = NULL then [Check Whether Queue is empty]
FRONT = -1
REAR = -1
else
REAR = REAR + 1 [Increment REAR Pointer]
Step 3: QUEUE[REAR] = ITEM [Copy ITEM to REAR position]
Step 4: Return

Queue Deletion Operation (DEQUEUE)
83
Data structures
ALGORITHM: DEQUEUE (QUEUE, REAR, FRONT, ITEM)
QUEUE is the array with N elements. FRONT is the pointer that contains the
location of the element to be deleted and REAR contains the location of the inserted
element. ITEM is the element to be inserted.
Step 1: if FRONT = NULL then [Check Whether Queue is empty]
PRINT “QUEUE is Empty or Underflow”
Exit
[End if]
Step 2: ITEM = QUEUE[FRONT]
Step 3: if FRONT = REAR then [if QUEUE has only one element]
FRONT = NULL
REAR = NULL
else
FRONT = FRONT + 1 [Increment FRONT pointer]
Step 4: Return

Application of Queue
84
Data structures
 Simulation
 Various features of Operating system
 Multi-programming platform systems.
 Different types of scheduling algorithms
 Round robin technique algorithms
 Printer server routines
 Various application software’s is also based
on queue data structure.

Lists
85
Data structures
 A lists (Linear linked list) can be defined as a collection of
variable number of data items called nodes.
 Lists are the most commonly used non-primitive data
structures.
 Each nodes is divided into two parts:
 The first part contains the information of the element.
 The second part contains the memory address of the
next node in the list. Also called Link part.

Types of linked lists
86
Data structures
 Single linked list
 Doubly linked list
 Single circular linked list
 Doubly circular linked list

Single linked list
87
Data structures
A singly linked list contains two fields in each node - an
information field and the linked field.
 The information field contains the data of that node.
 The link field contains the memory address of the next node.
There is only one link field in each node, the linked list is called
singly linked list.

Single circular linked list
88
Data structures
The link field of the last node contains the memory address of the
first node, such a linked list is called circular linked list.
 In a circular linked list every node is accessible from a given
node.

Doubly linked list
89
Data structures
It is a linked list in which each node is points both to the next node
and also to the previous node.
 In doubly linked list each node contains three parts:
 FORW : It is a pointer field that contains the address of the next node
 BACK: It is a pointer field that contains the address of the previous node.
 INFO: It contains the actual data.
 In the first node, if BACK contains NULL, it indicated that it is the first node
in the list.
 The node in which FORW contains, NULL indicates that the node is the last
node.

Doubly circular linked list
90
Data structures
It is a linked list in which each node is points both to the next
node and also to the previous node.
 In doubly linked list each node contains three parts:
 FORW : It is a pointer field that contains the address of the next node
 BACK: It is a pointer field that contains the address of the previous
node.
 INFO: It contains the actual data.

Operation on Linked List
91
Data structures
 The operation that are performed on linked
lists are:
 Creating a linked list
 Traversing a linked list
 Inserting an item into a linked list.
 Deleting an item from the linked list.
 Searching an item in the linked list
 Merging two or more linked lists.

Creating a linked list
92
Data structures
 The nodes of a linked list can be created by the
following structure declaration.
struct Node
{
int info;
struct Node *link;
}*node1, *node2;
 Here info is the information field and link is the link field.
 The link field contains a pointer variable that refers the same
node structure. Such a reference is called as Self addressing
pointer.

Operator new and delete
93
Data structures
 Operators new allocate memory space.
 Operators new [ ] allocates memory space for
array.
 Operators delete deallocate memory space.
 Operators delete [ ] deallocate memory space for
array.

Traversing a linked list
94
Data structures
 Traversing is the process of accessing each node of the linked
list exactly once to perform some operation.
 ALGORITHM: TRAVERS (START, P) START contains
the address of the first node. Another pointer p is temporarily
used to visit all the nodes from the beginning to the end of the
linked list.
Step 1: P = START
Step 2: while P != NULL
Step 3: PROCESS data (P) [Fetch the data]
Step 4: P = link(P) [Advance P to next node]
Step 5: End of while
Step 6: Return

Inserting a node into the linked list
95
Data structures
 Inserting a node at the beginning of the linked
list
 Inserting a node at the given position.
 Inserting a node at the end of the linked list.

Inserting node at Front
96
Data structures
Inserting a node at the beginning of the linked list
1. Create a node.
2. Fill data into the data field of the new node.
3. Mark its pointer field as NULL
4. Attach this newly created node to START
5. Make the new node as the START node.

Inserting node at Front
97
Data structures
 ALGORITHM: INS_BEG (START, P)
START contains the address of the first node.
Step 1: P new Node;
Step 2: data(P) num;
Step 3: link(P) START
Step 4: START P
Step 5: Return

Inserting node at End
98
Data structures

Inserting node at End
99
Data structures
 ALGORITHM: INS_END (START, P)
 START contains the address of the first node.
Step 1: START
Step 2: P START [identify the last node]
while P!= null
P next (P)
End while
Step 3: N new Node;
Step 4: data(N) item;
Step 5: link(N) null
Step 6: link(P) N
Step 7: Return

Inserting node at a given Position
100
Data structures
ALGORITHM: INS_POS (START, P1, P2)
START contains the address of the first node. P2 is new node
Step 1: START
Step 2: P1 START [Initialize node]
Count 0
Step 3: while P!= null
count count+1
P1 next (P1)
End while
Step 4: if (POS=1)
Call function INS_BEG( )
else if (POS=Count +1)
Call function INS_END( )
else if (POS<=Count)
P1 Start
For(i=1; i<=pos; i++)
P1 next(P1);
end for
[create] P2 new node
data(P2) item;
link(P2) link(P1)
link(P1) P2
else
PRINT “Invalid position”
Step 5: Return

Deleting an node
101
Data structures
 Deleting an item from the linked list:
 Deletion of the first node
 Deletion of the last node
 Deletion of the node at the give position

Deletion of the first node
102
Data structures
This algorithm first copies data in the first node to a
variable and delete the first node of the linked list.
ALGORITHM: DEL_BEG(P, START) This used pointers P
Step 1: START
Step 2: P START;
Step 3: PRINT data(P)
Step 4: START Link(P)
Step 5: Free(P)
Step 6: STOP

Deleting node from end
103
Data structures

Deleting node from end
104
Data structures
ALGORITHM: DEL_END (P1, P2, START) This used two
pointers P1 and P2. Pointer P2 is used to traverse the linked list
and pointer P1 keeps the location of the previous node of P2.
Step 1: START
Step 2: P2 START;
Step 3: while ( link(P2) ! = NULL)
P1 P2
P2 link(P2)
While end
Step 4: PRINT data(p2)
Step 5: link(P1) NULL
Free(P2)
Step 6: STOP

Non-Linear Data structures
105
Data structures
A Non-Linear Data structures is a data structure in
which data item is connected to several other data
items.
 The data items in non-linear data structure represent
hierarchical relationship.
 Each data item is called node.
 The different non-linear data structures are
 Trees
 Graphs.

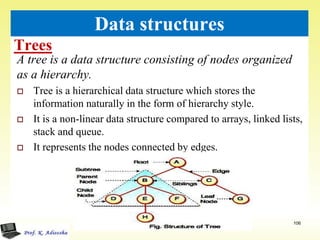
Trees
106
Data structures
A tree is a data structure consisting of nodes organized
as a hierarchy.
 Tree is a hierarchical data structure which stores the
information naturally in the form of hierarchy style.
 It is a non-linear data structure compared to arrays, linked lists,
stack and queue.
 It represents the nodes connected by edges.

Terminology of a Tree
107
Data structures

Binary Tree
108
Data structures
 A binary tree is an ordered tree in which each internal node
can have maximum of two child nodes connected to it.
 A binary tree consists of:
 A node ( called the root node)
 Left and right sub trees.
 A Complete binary tree is a binary tree in which each leaf is at the same
 distance from the root i.e. all the nodes have maximum two subtrees.
Binary tree using array represents a node which
is numbered sequentially level by level from left
to right. Even empty nodes are numbered.

Graph
109
Data structures
 Graph is a mathematical non-linear data structure
capable of representing many kind of physical
structures.
 A graph is a set of vertices and edges which
connect them.
 A graph is a collection of nodes called vertices and
the connection between them called edges.
 Definition: A graph G(V,E) is a set of vertices V and
a set of edges E.

Graph
110
Data structures
 Example of graph:
v2
v1
v
4
v5
v3
10
15
8
6
11
9
v4
v1
v2
v4
v3
[a] Directed &
Weighted Graph
[b] Undirected Graph

Graph
111
Data structures
 An edge connects a pair of vertices and many
have weight such as length, cost and another
measuring instrument for according the graph.
 Vertices on the graph are shown as point or
circles and edges are drawn as arcs or line
segment

Graph
112
Data structures
 Types of Graphs:
 Directed graph
 Undirected graph
 Simple graph
 Weighted graph
 Connected graph
 Non-connected graph

Data structure using c++

More Related Content

What's hot (20)

Similar to Data structure using c++ (20)

More from Prof. Dr. K. Adisesha (20)

Recently uploaded (20)

Data structure using c++