Data Structures - Lecture 10 [Graphs]
Download as pptx, pdf11 likes6,635 views
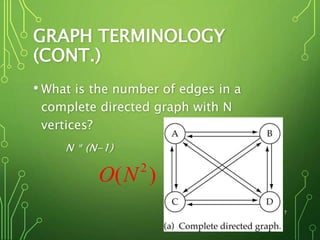
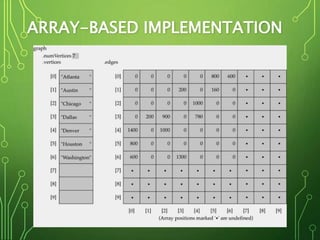
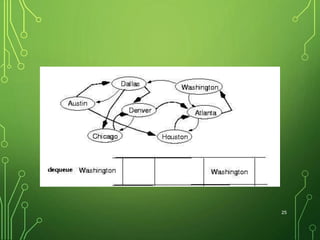
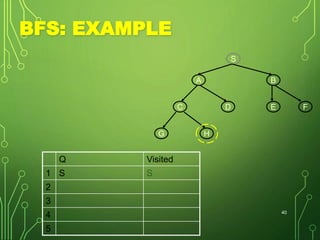
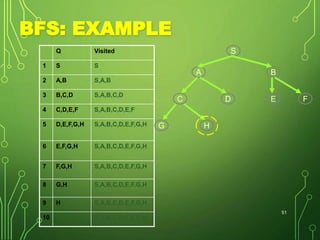
Graphs are data structures consisting of nodes and edges connecting nodes. They can be directed or undirected. Trees are special types of graphs. Common graph algorithms include depth-first search (DFS) and breadth-first search (BFS). DFS prioritizes exploring nodes along each branch as deeply as possible before backtracking, using a stack. BFS explores all nodes at the current depth before moving to the next depth, using a queue.
1 of 52
Downloaded 568 times















































Ad
Recommended
Data structure - Graph
Data structure - GraphMadhu Bala The document defines and describes various graph concepts and data structures used to represent graphs. It defines a graph as a collection of nodes and edges, and distinguishes between directed and undirected graphs. It then describes common graph terminology like adjacent/incident nodes, subgraphs, paths, cycles, connected/strongly connected components, trees, and degrees. Finally, it discusses two common ways to represent graphs - the adjacency matrix and adjacency list representations, noting their storage requirements and ability to add/remove nodes.
THREADED BINARY TREE AND BINARY SEARCH TREE
THREADED BINARY TREE AND BINARY SEARCH TREESiddhi Shrivas The document discusses threaded binary trees. It begins by defining a regular binary tree. It then explains that in a threaded binary tree, null pointers are replaced by threads (pointers) to other nodes. Threading rules specify that a null left/right pointer is replaced by a pointer to the inorder predecessor/successor. Boolean fields distinguish threads from links. Non-recursive traversals are possible by following threads. Insertion and deletion of nodes may require updating threads. Threaded binary trees allow efficient non-recursive traversals without a stack.
Graph representation
Graph representationTech_MX A graph consists of vertices and edges, where vertices represent entities and edges represent relationships between vertices. Graphs can be represented sequentially using matrices like adjacency and incidence matrices, or linked using data structures like adjacency lists. Adjacency matrices allow fast addition/removal of edges but use more memory, while adjacency lists use less memory but are slower to modify. The best representation depends on whether the graph is dense or sparse.
Trees (data structure)
Trees (data structure)Trupti Agrawal This document discusses trees as a data structure. It defines trees as structures containing nodes where each node can have zero or more children and at most one parent. Binary trees are defined as trees where each node has at most two children. The document discusses tree terminology like root, leaf, and height. It also covers binary search trees and their properties for storing and searching data, as well as algorithms for inserting and deleting nodes. Finally, it briefly discusses other types of trees like balanced search trees and parse trees.
Skip list vinay khimsuriya_200430723005
Skip list vinay khimsuriya_200430723005vinaykhimsuriya1 A skip list is a probabilistic data structure that allows for efficient search, insertion, and removal of elements. It consists of a hierarchy of linked lists that connect nodes in a sorted manner. The lowest level is a standard sorted linked list, while higher levels contain nodes that skip over nodes on the level below, acting as an "express lane" for searches. Operations like search have O(log n) time complexity on average due to this hierarchy. Nodes contain links to nodes before and after on their level as well as links to nodes below, allowing efficient traversal. Skip lists provide an alternative to balanced binary search trees.
Data Structure and Algorithms Binary Search Tree
Data Structure and Algorithms Binary Search TreeManishPrajapati78 Binary search trees (BSTs) are data structures that allow for efficient searching, insertion, and deletion. Nodes in a BST are organized so that all left descendants of a node are less than the node's value and all right descendants are greater. This property allows values to be found, inserted, or deleted in O(log n) time on average. Searching involves recursively checking if the target value is less than or greater than the current node's value. Insertion follows the search process and adds the new node in the appropriate place. Deletion handles three cases: removing a leaf, node with one child, or node with two children.
Graph data structure and algorithms
Graph data structure and algorithmsAnandhasilambarasan D This document discusses graph data structures and algorithms. A graph consists of nodes and edges, where nodes represent entities and edges represent relationships between nodes. There are different types of graphs including undirected, directed, weighted, and cyclic graphs. Graphs can be represented using an adjacency matrix or adjacency list. Graphs are used to model real-world networks and solve problems in areas like social networks, maps, robot path planning, and neural networks.
DFS and BFS
DFS and BFSsatya parsana This document discusses and provides examples of depth-first search (DFS) and breadth-first search (BFS) algorithms for traversing graphs. It explains that DFS involves recursively exploring all branches of the graph as deep as possible before backtracking, while BFS involves searching the neighbors of the starting node first before moving to the next level. Examples are given showing the step-by-step process of applying DFS and BFS to traverse graphs and mark visited vertices.
Tree Traversal
Tree TraversalMd. Israil Fakir The document discusses tree traversal in the context of discrete mathematics, detailing its definition and types: pre-order, in-order, and post-order traversal. It provides the sequence of node visits for each traversal type and includes algorithms for implementation. Examples are given for each traversal method to illustrate the concepts.
Dijkstra's Algorithm
Dijkstra's AlgorithmArijitDhali Dijkstra's algorithm allows finding the shortest path between any two vertices in a graph. It works by overestimating the distance of each vertex from the starting point and then visiting neighbors to find shorter paths. The algorithm uses a greedy approach, finding the next best solution at each step. It maintains path distances in an array and maps each vertex to its predecessor in the shortest path. A priority queue is used to efficiently retrieve the closest vertex. The time complexity is O(E Log V) and space is O(V). Applications include social networks, maps, and telephone networks.
Bellman Ford's Algorithm
Bellman Ford's AlgorithmTanmay Baranwal The document covers the Bellman-Ford algorithm for finding shortest paths in graphs, including its ability to detect negative-weight cycles. It includes specific algorithmic steps, examples, and discusses its applications in linear programming and VLSI layout compaction. Additionally, it emphasizes the algorithm's efficiency and correctness under certain conditions, along with methodologies for solving systems of difference constraints.
Depth-First Search
Depth-First SearchDakshitha Dissanayaka Depth-first search (DFS) is an algorithm for traversing tree and graph data structures. It starts at the root node and explores as far as possible along each branch before backtracking. It continues visiting neighbors in a recursive pattern, recursively visiting all unvisited neighbors of each visited vertex before backtracking. The DFS algorithm works by starting with any vertex on a stack, visiting and removing it from the stack while adding its unvisited neighbors to the top of the stack, repeating until the stack is empty.
Graph in data structure
Graph in data structureAbrish06 This document defines and provides examples of graphs and their representations. It discusses:
- Graphs are data structures consisting of nodes and edges connecting nodes.
- Examples of directed and undirected graphs are given.
- Graphs can be represented using adjacency matrices or adjacency lists. Adjacency matrices store connections in a grid and adjacency lists store connections as linked lists.
- Key graph terms are defined such as vertices, edges, paths, and degrees. Properties like connectivity and completeness are also discussed.
Binary Tree in Data Structure
Binary Tree in Data StructureMeghaj Mallick Binary trees are a data structure where each node has at most two children. A binary tree node contains data and pointers to its left and right child nodes. Binary search trees are a type of binary tree where nodes are organized in a manner that allows for efficient searches, insertions, and deletions of nodes. The key operations on binary search trees are searching for a node, inserting a new node, and deleting an existing node through various algorithms that traverse the tree. Common traversals of binary trees include preorder, inorder, and postorder traversals.
SINGLE-SOURCE SHORTEST PATHS
SINGLE-SOURCE SHORTEST PATHS Md. Shafiuzzaman Hira The document discusses different single-source shortest path algorithms. It begins by defining shortest path and different variants of shortest path problems. It then describes Dijkstra's algorithm and Bellman-Ford algorithm for solving the single-source shortest paths problem, even in graphs with negative edge weights. Dijkstra's algorithm uses relaxation and a priority queue to efficiently solve the problem in graphs with non-negative edge weights. Bellman-Ford can handle graphs with negative edge weights but requires multiple relaxation passes to converge. Pseudocode and examples are provided to illustrate the algorithms.
Binary search tree(bst)
Binary search tree(bst)Hossain Md Shakhawat The document provides an in-depth overview of binary trees and binary search trees (BST), detailing their properties, structures, and algorithms for insertion, searching, and deletion. It emphasizes the efficiency of BSTs for search operations compared to linear data structures, with performance being largely determined by the tree's height. Additionally, various pseudocode examples clarify the algorithms for these operations within the context of binary trees.
Singly linked list
Singly linked listAmar Jukuntla This document discusses different operations on linked lists such as insertion, deletion, and traversal. It begins with an introduction to linked lists explaining that each node contains a data field and pointer to the next node. It then covers implementing a basic node structure and various functions like creating a new node, adding a node to the beginning or end of the list, and deleting a node from the beginning, end, or a given position. Traversal and keeping track of previous nodes is important for operations like deletion from within the list. The document provides pseudocode to demonstrate common linked list operations.
sparse matrix in data structure
sparse matrix in data structureMAHALAKSHMI P This document discusses sparse matrices. It defines a sparse matrix as a matrix with more zero values than non-zero values. Sparse matrices can save space by only storing the non-zero elements and their indices rather than allocating space for all elements. Two common representations for sparse matrices are the triplet representation, which stores the non-zero values and their row and column indices, and the linked representation, which connects the non-zero elements. Applications of sparse matrices include solving large systems of equations.
Insertion Sort Algorithm
Insertion Sort AlgorithmGail Carmichael The document describes the insertion sort algorithm sorting the array [15, 9, 9, 10, 12, 1, 11, 3, 9]. It works by taking each element from the unsorted part of the array and inserting it into the correct position in the sorted part. It iterates through the array, swapping elements if the current element is less than the element preceding it, until the subarray is sorted.
Functional dependencies and normalization
Functional dependencies and normalizationdaxesh chauhan Functional dependencies play a key role in database design and normalization. A functional dependency (FD) is a constraint that one attribute determines another. FDs have various definitions but generally mean that given the value of one attribute (left side), the value of another attribute (right side) is determined. Armstrong's axioms are used to derive implied FDs from a set of FDs. The closure of an attribute set or set of FDs finds all attributes/FDs logically implied. Normalization aims to eliminate anomalies and is assessed using normal forms like 1NF, 2NF, 3NF, BCNF which impose additional constraints on table designs.
Hashing Technique In Data Structures
Hashing Technique In Data StructuresSHAKOOR AB This document discusses different searching methods like sequential, binary, and hashing. It defines searching as finding an element within a list. Sequential search searches lists sequentially until the element is found or the end is reached, with efficiency of O(n) in worst case. Binary search works on sorted arrays by eliminating half of remaining elements at each step, with efficiency of O(log n). Hashing maps keys to table positions using a hash function, allowing searches, inserts and deletes in O(1) time on average. Good hash functions uniformly distribute keys and generate different hashes for similar keys.
Depth first search [dfs]
Depth first search [dfs]DEEPIKA T Depth-first search (DFS) is an algorithm that explores all the vertices reachable from a starting vertex by traversing edges in a depth-first manner. DFS uses a stack data structure to keep track of vertices to visit. It colors vertices white, gray, and black to indicate their status. DFS runs in O(V+E) time and can be used for applications like topological sorting and finding strongly connected components. The edges discovered during DFS can be classified as tree, back, forward, or cross edges based on the order in which vertices are discovered.
Insertion sort
Insertion sortalmaqboli Insertion sort works by iterating through an array, inserting each element into its sorted position by shifting other elements over. It finds the location where each element should be inserted into the sorted portion using a linear search, moving larger elements out of the way to make room. This sorting algorithm is most effective for small data sets and can be implemented recursively or iteratively through comparisons and shifts.
Tree in data structure
Tree in data structureghhgj jhgh 1) Trees are hierarchical data structures that store data in nodes connected by edges. They are useful for representing hierarchical relationships.
2) Binary search trees allow quick search, insertion, and deletion of nodes due to the organizational property that the value of each node is greater than all nodes in its left subtree and less than all nodes in its right subtree.
3) Common tree traversal algorithms include preorder, inorder, and postorder traversals, which visit nodes in different orders depending on whether the left/right children or root is visited first.
Insertion sort
Insertion sort Monalisa Patel This document discusses insertion sort, including its mechanism, algorithm, runtime analysis, advantages, and disadvantages. Insertion sort works by iterating through an unsorted array and inserting each element into its sorted position by shifting other elements over. Its worst case runtime is O(n^2) when the array is reverse sorted, but it performs well on small, nearly sorted lists. While simple to implement, insertion sort is inefficient for large datasets compared to other algorithms.
Ppt on Linked list,stack,queue
Ppt on Linked list,stack,queueSrajan Shukla This document discusses different types of linked lists, including singly linked lists, circular linked lists, and doubly linked lists. It provides examples of circular linked lists and explains that in a circular linked list, the last node contains the address of the first node so that the list can be traversed repeatedly. The document also discusses common linked list operations like insertion and deletion of nodes. Finally, it covers stacks and queues, defining them as LIFO and FIFO data structures, respectively, and providing examples of their implementation and different types.
Linked lists
Linked listsSARITHA REDDY This document discusses different types of linked lists including single linked lists, double linked lists, circular linked lists, and circular double linked lists. It describes the basic operations that can be performed on linked lists such as creation, insertion, deletion, traversal, searching, concatenation, and display. It provides examples of how to insert and delete nodes from both single and double linked lists. The document also discusses recursive operations and advantages and disadvantages of using linked lists.
Threaded Binary Tree.pptx
Threaded Binary Tree.pptxpavankumarjakkepalli A threaded binary tree is a variant of a binary tree that stores in-order predecessor and successor pointers instead of null pointers to facilitate faster traversal without recursion or an auxiliary stack. There are two types: single-threaded stores successor pointers only, and double-threaded stores both predecessor and successor pointers. This decreases wasted space from null pointers but makes insertion and deletion more complex. Advantages include optimal memory usage and faster traversal, while disadvantages include more complex insertion/deletion and slightly more memory usage for thread indicators.
Graphs In Data Structure
Graphs In Data StructureAnuj Modi A graph G is composed of vertices V connected by edges E. It can be represented using an adjacency matrix or adjacency lists. Graph search algorithms like depth-first search (DFS) and breadth-first search (BFS) are used to traverse the graph and find paths between vertices. DFS recursively explores edges until reaching the end of a branch before backtracking, while BFS explores all neighbors at each level before moving to the next.
Lecture8 data structure(graph)
Lecture8 data structure(graph)Taibah University, College of Computer Science & Engineering This document outlines the fundamentals of graph data structures, including definitions, types (directed and undirected), and their relationships. It explains concepts such as vertices, edges, loops, paths, and the significance of weighted graphs, along with traversal algorithms for processing graphs. Additionally, it covers operations related to graphs, including essential actions for nodes and edges, and discusses implementations such as adjacency lists.
More Related Content
What's hot (20)
Tree Traversal
Tree TraversalMd. Israil Fakir The document discusses tree traversal in the context of discrete mathematics, detailing its definition and types: pre-order, in-order, and post-order traversal. It provides the sequence of node visits for each traversal type and includes algorithms for implementation. Examples are given for each traversal method to illustrate the concepts.
Dijkstra's Algorithm
Dijkstra's AlgorithmArijitDhali Dijkstra's algorithm allows finding the shortest path between any two vertices in a graph. It works by overestimating the distance of each vertex from the starting point and then visiting neighbors to find shorter paths. The algorithm uses a greedy approach, finding the next best solution at each step. It maintains path distances in an array and maps each vertex to its predecessor in the shortest path. A priority queue is used to efficiently retrieve the closest vertex. The time complexity is O(E Log V) and space is O(V). Applications include social networks, maps, and telephone networks.
Bellman Ford's Algorithm
Bellman Ford's AlgorithmTanmay Baranwal The document covers the Bellman-Ford algorithm for finding shortest paths in graphs, including its ability to detect negative-weight cycles. It includes specific algorithmic steps, examples, and discusses its applications in linear programming and VLSI layout compaction. Additionally, it emphasizes the algorithm's efficiency and correctness under certain conditions, along with methodologies for solving systems of difference constraints.
Depth-First Search
Depth-First SearchDakshitha Dissanayaka Depth-first search (DFS) is an algorithm for traversing tree and graph data structures. It starts at the root node and explores as far as possible along each branch before backtracking. It continues visiting neighbors in a recursive pattern, recursively visiting all unvisited neighbors of each visited vertex before backtracking. The DFS algorithm works by starting with any vertex on a stack, visiting and removing it from the stack while adding its unvisited neighbors to the top of the stack, repeating until the stack is empty.
Graph in data structure
Graph in data structureAbrish06 This document defines and provides examples of graphs and their representations. It discusses:
- Graphs are data structures consisting of nodes and edges connecting nodes.
- Examples of directed and undirected graphs are given.
- Graphs can be represented using adjacency matrices or adjacency lists. Adjacency matrices store connections in a grid and adjacency lists store connections as linked lists.
- Key graph terms are defined such as vertices, edges, paths, and degrees. Properties like connectivity and completeness are also discussed.
Binary Tree in Data Structure
Binary Tree in Data StructureMeghaj Mallick Binary trees are a data structure where each node has at most two children. A binary tree node contains data and pointers to its left and right child nodes. Binary search trees are a type of binary tree where nodes are organized in a manner that allows for efficient searches, insertions, and deletions of nodes. The key operations on binary search trees are searching for a node, inserting a new node, and deleting an existing node through various algorithms that traverse the tree. Common traversals of binary trees include preorder, inorder, and postorder traversals.
SINGLE-SOURCE SHORTEST PATHS
SINGLE-SOURCE SHORTEST PATHS Md. Shafiuzzaman Hira The document discusses different single-source shortest path algorithms. It begins by defining shortest path and different variants of shortest path problems. It then describes Dijkstra's algorithm and Bellman-Ford algorithm for solving the single-source shortest paths problem, even in graphs with negative edge weights. Dijkstra's algorithm uses relaxation and a priority queue to efficiently solve the problem in graphs with non-negative edge weights. Bellman-Ford can handle graphs with negative edge weights but requires multiple relaxation passes to converge. Pseudocode and examples are provided to illustrate the algorithms.
Binary search tree(bst)
Binary search tree(bst)Hossain Md Shakhawat The document provides an in-depth overview of binary trees and binary search trees (BST), detailing their properties, structures, and algorithms for insertion, searching, and deletion. It emphasizes the efficiency of BSTs for search operations compared to linear data structures, with performance being largely determined by the tree's height. Additionally, various pseudocode examples clarify the algorithms for these operations within the context of binary trees.
Singly linked list
Singly linked listAmar Jukuntla This document discusses different operations on linked lists such as insertion, deletion, and traversal. It begins with an introduction to linked lists explaining that each node contains a data field and pointer to the next node. It then covers implementing a basic node structure and various functions like creating a new node, adding a node to the beginning or end of the list, and deleting a node from the beginning, end, or a given position. Traversal and keeping track of previous nodes is important for operations like deletion from within the list. The document provides pseudocode to demonstrate common linked list operations.
sparse matrix in data structure
sparse matrix in data structureMAHALAKSHMI P This document discusses sparse matrices. It defines a sparse matrix as a matrix with more zero values than non-zero values. Sparse matrices can save space by only storing the non-zero elements and their indices rather than allocating space for all elements. Two common representations for sparse matrices are the triplet representation, which stores the non-zero values and their row and column indices, and the linked representation, which connects the non-zero elements. Applications of sparse matrices include solving large systems of equations.
Insertion Sort Algorithm
Insertion Sort AlgorithmGail Carmichael The document describes the insertion sort algorithm sorting the array [15, 9, 9, 10, 12, 1, 11, 3, 9]. It works by taking each element from the unsorted part of the array and inserting it into the correct position in the sorted part. It iterates through the array, swapping elements if the current element is less than the element preceding it, until the subarray is sorted.
Functional dependencies and normalization
Functional dependencies and normalizationdaxesh chauhan Functional dependencies play a key role in database design and normalization. A functional dependency (FD) is a constraint that one attribute determines another. FDs have various definitions but generally mean that given the value of one attribute (left side), the value of another attribute (right side) is determined. Armstrong's axioms are used to derive implied FDs from a set of FDs. The closure of an attribute set or set of FDs finds all attributes/FDs logically implied. Normalization aims to eliminate anomalies and is assessed using normal forms like 1NF, 2NF, 3NF, BCNF which impose additional constraints on table designs.
Hashing Technique In Data Structures
Hashing Technique In Data StructuresSHAKOOR AB This document discusses different searching methods like sequential, binary, and hashing. It defines searching as finding an element within a list. Sequential search searches lists sequentially until the element is found or the end is reached, with efficiency of O(n) in worst case. Binary search works on sorted arrays by eliminating half of remaining elements at each step, with efficiency of O(log n). Hashing maps keys to table positions using a hash function, allowing searches, inserts and deletes in O(1) time on average. Good hash functions uniformly distribute keys and generate different hashes for similar keys.
Depth first search [dfs]
Depth first search [dfs]DEEPIKA T Depth-first search (DFS) is an algorithm that explores all the vertices reachable from a starting vertex by traversing edges in a depth-first manner. DFS uses a stack data structure to keep track of vertices to visit. It colors vertices white, gray, and black to indicate their status. DFS runs in O(V+E) time and can be used for applications like topological sorting and finding strongly connected components. The edges discovered during DFS can be classified as tree, back, forward, or cross edges based on the order in which vertices are discovered.
Insertion sort
Insertion sortalmaqboli Insertion sort works by iterating through an array, inserting each element into its sorted position by shifting other elements over. It finds the location where each element should be inserted into the sorted portion using a linear search, moving larger elements out of the way to make room. This sorting algorithm is most effective for small data sets and can be implemented recursively or iteratively through comparisons and shifts.
Tree in data structure
Tree in data structureghhgj jhgh 1) Trees are hierarchical data structures that store data in nodes connected by edges. They are useful for representing hierarchical relationships.
2) Binary search trees allow quick search, insertion, and deletion of nodes due to the organizational property that the value of each node is greater than all nodes in its left subtree and less than all nodes in its right subtree.
3) Common tree traversal algorithms include preorder, inorder, and postorder traversals, which visit nodes in different orders depending on whether the left/right children or root is visited first.
Insertion sort
Insertion sort Monalisa Patel This document discusses insertion sort, including its mechanism, algorithm, runtime analysis, advantages, and disadvantages. Insertion sort works by iterating through an unsorted array and inserting each element into its sorted position by shifting other elements over. Its worst case runtime is O(n^2) when the array is reverse sorted, but it performs well on small, nearly sorted lists. While simple to implement, insertion sort is inefficient for large datasets compared to other algorithms.
Ppt on Linked list,stack,queue
Ppt on Linked list,stack,queueSrajan Shukla This document discusses different types of linked lists, including singly linked lists, circular linked lists, and doubly linked lists. It provides examples of circular linked lists and explains that in a circular linked list, the last node contains the address of the first node so that the list can be traversed repeatedly. The document also discusses common linked list operations like insertion and deletion of nodes. Finally, it covers stacks and queues, defining them as LIFO and FIFO data structures, respectively, and providing examples of their implementation and different types.
Linked lists
Linked listsSARITHA REDDY This document discusses different types of linked lists including single linked lists, double linked lists, circular linked lists, and circular double linked lists. It describes the basic operations that can be performed on linked lists such as creation, insertion, deletion, traversal, searching, concatenation, and display. It provides examples of how to insert and delete nodes from both single and double linked lists. The document also discusses recursive operations and advantages and disadvantages of using linked lists.
Threaded Binary Tree.pptx
Threaded Binary Tree.pptxpavankumarjakkepalli A threaded binary tree is a variant of a binary tree that stores in-order predecessor and successor pointers instead of null pointers to facilitate faster traversal without recursion or an auxiliary stack. There are two types: single-threaded stores successor pointers only, and double-threaded stores both predecessor and successor pointers. This decreases wasted space from null pointers but makes insertion and deletion more complex. Advantages include optimal memory usage and faster traversal, while disadvantages include more complex insertion/deletion and slightly more memory usage for thread indicators.
Viewers also liked (20)
Graphs In Data Structure
Graphs In Data StructureAnuj Modi A graph G is composed of vertices V connected by edges E. It can be represented using an adjacency matrix or adjacency lists. Graph search algorithms like depth-first search (DFS) and breadth-first search (BFS) are used to traverse the graph and find paths between vertices. DFS recursively explores edges until reaching the end of a branch before backtracking, while BFS explores all neighbors at each level before moving to the next.
Lecture8 data structure(graph)
Lecture8 data structure(graph)Taibah University, College of Computer Science & Engineering This document outlines the fundamentals of graph data structures, including definitions, types (directed and undirected), and their relationships. It explains concepts such as vertices, edges, loops, paths, and the significance of weighted graphs, along with traversal algorithms for processing graphs. Additionally, it covers operations related to graphs, including essential actions for nodes and edges, and discusses implementations such as adjacency lists.
Data structure computer graphs
Data structure computer graphsKumar A graph is a data structure consisting of vertices and edges connecting the vertices. Graphs can be directed or undirected. Depth-first search (DFS) and breadth-first search (BFS) are algorithms for traversing graphs by exploring neighboring vertices. DFS uses a stack and explores as far as possible along each branch before backtracking, while BFS uses a queue and explores all neighbors at each depth level first before moving to the next level.
Graph data structure
Graph data structureTech_MX The document discusses various topics related to graphs:
- It defines directed and undirected graphs, paths, connected graphs, trees, degree, isomorphic graphs, cut sets, and labeled graphs.
- Key aspects include paths being sequences of vertices with edges connecting them, connected graphs having paths between all vertex pairs, trees being connected and acyclic graphs, and isomorphic graphs having the same structure.
- It also covers graph concepts such as degrees measuring incident edges, cut sets separating graphs, and labeling providing additional data to graphs' vertices or edges.
Matrix Representation Of Graph
Matrix Representation Of GraphAbhishek Pachisia The document discusses different matrix representations of graphs:
1) Incidence matrix shows which edges are incident to each vertex with 1s and 0s.
2) Adjacency matrix shows which vertices are adjacent to each other with 1s and 0s.
3) Cut-set matrix shows which edges are part of given cut sets that disconnect the graph with 1s and 0s.
Graphs in data structure
Graphs in data structurehamza javed Graphs are a data structure composed of nodes connected by edges. There are two main types: directed graphs where edges show a flow between nodes, and undirected graphs where edges simply show a relationship between nodes. Key terminology includes adjacent nodes, paths, cyclic vs acyclic paths, and representations like adjacency matrices and lists. Graphs can model many real-world applications such as social networks, computer networks, road maps, and more.
17. Trees and Graphs
17. Trees and GraphsIntro C# Book The document provides an overview of tree-like data structures, including definitions, types (such as binary trees and balanced trees), and terminology associated with trees. It discusses tree implementations, traversal algorithms such as depth-first search (DFS) and breadth-first search (BFS), as well as balanced search trees (e.g., AVL and B-trees) and their applications in .NET. Examples illustrate the construction of trees, their operations, and the complexity of searching and balancing these structures.
DATA STRUCTURES
DATA STRUCTURESbca2010 This document provides information about Dream Valley College for Girls Centre for Educational Excellence. It includes an index and presentation on data structures covering topics like arrays, linked lists, queues, trees, and graphs. The presentation was presented by Harish Sir and includes definitions, examples, and diagrams to explain each data structure concept.
Graphs in Data Structure
Graphs in Data Structurehafsa komal The document discusses graphs and their applications. It defines graphs as consisting of vertices and edges. Graphs can be undirected or directed. It also defines concepts like paths, cycles, and connectivity in graphs. Common applications of graphs mentioned are maps, computer networks, and CAD designs. The document then discusses different ways to represent graphs using adjacency matrices and adjacency lists. It also discusses using graphs to model and solve problems like traffic light timing by coloring the vertices.
Graphs data Structure
Graphs data StructureMahmoud Alfarra This document discusses graphs and their representation in Java. It begins with basic graph terminology like vertices, edges, directed/undirected graphs. It then discusses modeling graphs in Java using interfaces and data structures like arrays and lists to store vertices and edges. Specific implementations are shown to represent sample graphs. The document is intended to introduce basic graph concepts and their modeling in Java.
Data structure & its types
Data structure & its typesRameesha Sadaqat This document defines and describes different types of data structures. It first defines a data structure as a logical way to store and retrieve data. It then describes common data structure operations like traversing, searching, insertion and deletion. The main types discussed are linear data structures like arrays, linked lists, stacks and queues, as well as non-linear structures like trees and graphs. Specific linear structures are defined and their representations and operations are outlined. Non-linear structures like trees and graphs are also introduced along with common operations.
Graph Basic In Data structure
Graph Basic In Data structureIkhlas Rahman The document provides an overview of graph concepts including definitions of a graph as a pair of vertices and edges, different types of graphs such as directed/undirected graphs and cyclic/acyclic graphs. It also discusses graph coloring, adjacency matrices/lists for representing graphs, and algorithms for traversing graphs including depth-first search and breadth-first search. Examples are given for each concept to illustrate key differences and properties.
Data structure and its types
Data structure and its typesNavtar Sidhu Brar Data structures allow for the organization and storage of data. There are linear and non-linear data structures. Linear structures include arrays, stacks, queues, and linked lists. Arrays store elements in contiguous memory locations. Stacks and queues follow first-in last-out and first-in first-out rules respectively. Linked lists connect nodes using pointers. Non-linear structures include trees and graphs which emulate hierarchical and network-like connections. Common operations on data structures include traversing, searching, insertion, and deletion.
Trees data structure
Trees data structureSumit Gupta This document defines and describes trees and graphs as non-linear data structures. It explains that a tree is similar to a linked list but allows nodes to have multiple children rather than just one. The document defines key tree terms like height, ancestors, size, and different types of binary trees including strict, full, and complete. It provides properties of binary trees such as the number of nodes in full and complete binary trees based on height.
Depth First Search and Breadth First Search
Depth First Search and Breadth First SearchBenjamin Sach The document discusses data structures and algorithms related to graphs, focusing on undirected and unweighted graphs. It introduces graph notation, various graph representations (like adjacency matrices and lists), and basic operations performed on these graphs. Depth-first search and breadth-first search algorithms are also mentioned as methods for exploring graphs.
Preparation Data Structures 11 graphs
Preparation Data Structures 11 graphsAndres Mendez-Vazquez The document provides an overview of graphs, including their history, basic theory, representations, and traversal methods. It discusses various applications of graphs, such as pathfinding and component analysis, and introduces both matrix and adjacency list representations. Additionally, it highlights time complexity and storage considerations in graph data structures.
Data Structures, Graphs
Data Structures, GraphsJibrael Jos The document discusses graphs and graph algorithms. It describes graph operations like adding and deleting vertices and edges. It also describes data structures for representing graphs like adjacency lists. It then covers algorithms for finding minimum spanning trees and shortest paths in graphs, like Prim's and Dijkstra's algorithms. Pseudocode and examples are provided for building an adjacency list and walking through the minimum spanning tree and shortest path algorithms.
Graphss
Graphssfika sweety The document details the structure and properties of graphs, which represent relationships among objects through vertices and edges. It explains directed and undirected graphs, their weighted versions, paths, cycles, connectivity, and various applications including trees and directed acyclic graphs (DAGs). Additionally, it covers graph representation techniques and introduces the concept of topological sorting.
Data structure introduction
Data structure introductionramyasanthosh This document provides an overview of key concepts related to data structures. It defines data as values or sets of values, and distinguishes data from information which results from processing data. Different data types are discussed including numeric, string, array, and date values. A data structure is defined as a logical organization of data that can be processed as a single unit. Key components of a data structure are also defined including the domain, functions that can be applied, and axioms that govern operations. Common linear and non-linear data structures are listed including arrays, linked lists, stacks, queues, trees and graphs.
Graphs in data structures
Graphs in data structuresSavit Chandra A graph G is composed of a set of vertices V connected by edges E. It can be represented using an adjacency matrix, with a 1 or 0 in position (i,j) indicating whether vertices i and j are connected, or an adjacency list storing the neighbors of each vertex. Graph search algorithms like depth-first search (DFS) and breadth-first search (BFS) are used to traverse the graph and find paths between vertices, with DFS prioritizing depth and BFS prioritizing breadth of exploration. DFS uses recursion to implicitly store paths while BFS uses queues and must store paths separately.
Ad
Similar to Data Structures - Lecture 10 [Graphs] (20)
Unit 9 graph
Unit 9 graphDabbal Singh Mahara This document provides information about graphs and graph algorithms. It discusses different graph representations including adjacency matrices and adjacency lists. It also describes common graph traversal algorithms like depth-first search and breadth-first search. Finally, it covers minimum spanning trees and algorithms to find them, specifically mentioning Kruskal's algorithm.
LEC 12-DSALGO-GRAPHS(final12).pdf
LEC 12-DSALGO-GRAPHS(final12).pdfMuhammadUmerIhtisham This document discusses graphs and graph data structures. It defines a graph as a pictorial representation of a set of objects connected by links, with the objects represented as vertices and the links as edges. It provides definitions and examples of basic graph terminology like vertices, edges, adjacency, and different types of graphs like directed vs undirected graphs. It also covers graph implementations using adjacency matrices and adjacency lists, as well as common graph algorithms like depth-first search and breadth-first search. Finally, it lists some applications of graphs like social networks, maps, and computer networks.
Unit ix graph
Unit ix graph Tribhuvan University This document provides an overview of graphs and graph algorithms. It begins with an introduction to graphs, including definitions of vertices, edges, directed/undirected graphs, and graph representations using adjacency matrices and lists. It then covers graph traversal algorithms like depth-first search and breadth-first search. Minimum spanning trees and algorithms for finding them like Kruskal's algorithm are also discussed. The document provides examples and pseudocode for the algorithms. It analyzes the time complexity of the graph algorithms. Overall, the document provides a comprehensive introduction to fundamental graph concepts and algorithms.
22-graphs1-dfs-bfs.ppt odiehehei7hoh97ho7bi6vi6go7gp
22-graphs1-dfs-bfs.ppt odiehehei7hoh97ho7bi6vi6go7gpchandrashekarr799 This document discusses graphs and graph algorithms. It defines what a graph is - a set of vertices connected by edges. It covers different types of graphs like directed/undirected graphs and weighted graphs. It then explains two common graph search algorithms - depth-first search (DFS) and breadth-first search (BFS). DFS explores each path as deep as possible before backtracking while BFS explores all neighbors of a node before moving deeper. Both algorithms run in O(V+E) time where V is vertices and E is edges. BFS always finds the shortest path while DFS is not guaranteed to.
22-graphs1-dfs-bfs.ppt
22-graphs1-dfs-bfs.pptKarunaBiswas3 This document discusses graphs and graph algorithms. It defines what a graph is - a data structure containing vertices and edges. It provides examples of graphs like social networks and road maps. It explains concepts like paths, connectedness, and cycles. It then covers two graph search algorithms - depth-first search (DFS) and breadth-first search (BFS). DFS explores each path as deeply as possible before backtracking, while BFS explores all neighbors of a vertex before moving deeper. Both algorithms run in O(V+E) time where V is vertices and E is edges. BFS always finds the shortest path.
U1 L5 DAA.pdf
U1 L5 DAA.pdfLakshyaBaliyan2 This document provides an overview of graphs and graph algorithms. It begins with definitions and data structures for representing graphs. It then covers graph traversal algorithms, including depth-first search (DFS) and breadth-first search (BFS). Topological sorting of directed acyclic graphs is also discussed. Exercises are provided to implement DFS, BFS, and topological sorting.
Graph Data Structure
Graph Data StructureAfaq Mansoor Khan The document provides an overview of graph data structures, including definitions, types (directed and undirected), and terminology such as nodes, edges, and paths. It covers various implementations (array-based and linked-list) and graph traversal methods (depth-first search and breadth-first search), as well as algorithms for finding the shortest path. Additionally, it includes a summary of key concepts and links to further resources.
Breadth first search
Breadth first searchSazzad Hossain The document provides an overview of graphs, their components (vertices and edges), and various representations like adjacency matrices and lists. It discusses applications of graphs such as modeling an air flight system, and explains traversal algorithms, particularly breadth-first search (BFS) for finding shortest paths. Key concepts include types of graphs, graph variations, and performance considerations for different graph data structures.
Unit-6 Graph.ppsx ppt
Unit-6 Graph.ppsx pptDhruvilSTATUS This document provides an overview of the topics covered in Unit 5, which include graphs, hashing, and collision resolution techniques. It defines graphs and their components such as vertices, edges, directed and undirected graphs. It also discusses different graph representations like adjacency matrix and adjacency list. Elementary graph operations like breadth-first search and depth-first search are explained along with examples. Hashing functions and collision resolution are also introduced.
Data Structures-Non Linear DataStructures-Graphs
Data Structures-Non Linear DataStructures-Graphssailaja156145 Graphs Trminology,Traversal,Spaaning Tree,MST
lecture 17
lecture 17sajinsc The document discusses interval trees and breadth-first search (BFS) algorithms. Interval trees are used to maintain a set of intervals and efficiently find overlapping intervals given a query. BFS is a graph search algorithm that explores all neighboring vertices of a starting node before moving to neighbors of neighbors. BFS builds a breadth-first tree and calculates the shortest path distances from the source node in O(V+E) time and space.
Graphs
GraphsDwight Sabio Graphs can be represented abstractly as a set of vertices and edges connecting pairs of vertices. They are used to model various real-world relationships and can be represented using adjacency lists or matrices. Breadth-first search (BFS) and depth-first search (DFS) are common graph traversal algorithms that systematically explore the edges of a graph to discover reachable vertices. BFS produces a breadth-first tree and finds the shortest paths from the source, while DFS explores edges deeper first before backtracking.
Graphs
GraphsLavanyaJ28 This document defines and explains various graph concepts:
- A graph consists of vertices and edges connecting the vertices. Graphs can be directed or undirected.
- Common graph terminology includes adjacent vertices, paths, complete graphs, weighted graphs, and representations using adjacency matrices and lists.
- Graph searching algorithms like depth-first search (DFS) and breadth-first search (BFS) are used to find paths between vertices.
- Graphs have applications in areas like maps, networks, and computational systems. Other graph topics covered include topological sorting, biconnectivity, cut vertices, Euler circuits, and minimum spanning trees.
graphin-c1.pnggraphin-c1.txt1 22 3 83 44 5.docx
graphin-c1.pnggraphin-c1.txt1 22 3 83 44 5.docxwhittemorelucilla The document outlines the requirements for a programming assignment involving depth-first search (DFS) to determine if a directed graph is acyclic and to generate a topological sort if it is. It details input/output specifications, algorithmic expectations, and grading criteria, emphasizing accurate implementation and efficiency. Additionally, the document includes educational content on DFS, edge classifications, and potential applications in graph theory.
Graphical reprsentation dsa (DATA STRUCTURE ALGORITHM)
Graphical reprsentation dsa (DATA STRUCTURE ALGORITHM)abdulrafaychaudhry The document explains the concept of a graph as a collection of vertices and edges, illustrating how they relate through pairs of connected objects. It covers key terms such as vertices, edges, adjacency, and paths, and introduces graph traversal algorithms like Depth First Search (DFS) and Breadth First Search (BFS). Both traversal methods are detailed with examples of their respective open and closed lists during search operations.
Unit 2: All
Unit 2: AllHector Zenil Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph consists of vertices and edges connecting pairs of vertices. There are many types of graphs including trees, which are connected acyclic graphs. Spanning trees are subgraphs of a graph that connect all vertices using the minimum number of edges. Key concepts in graph theory include paths, connectedness, cycles, and isomorphism between graphs.
Unit II_Graph.pptxkgjrekjgiojtoiejhgnltegjte
Unit II_Graph.pptxkgjrekjgiojtoiejhgnltegjtepournima055 The document discusses graphs and graph algorithms. It covers basic graph concepts like vertices, edges, paths, cycles. It describes different ways to represent graphs like adjacency matrix, adjacency list and their pros and cons. It also discusses operations on graphs like inserting and deleting vertices and edges. The document explains traversal algorithms like depth-first search and breadth-first search. It covers minimum spanning tree algorithms like Prim's and Kruskal's. It also briefly discusses shortest path algorithms like Dijkstra's and topological sorting.
Ad
More from Muhammad Hammad Waseem (20)
[ITP - Lecture 17] Strings in C/C++
[ITP - Lecture 17] Strings in C/C++Muhammad Hammad Waseem This document discusses strings in C programming. It defines strings as arrays of characters that end with a null terminator (\0). It explains how to initialize and print strings. Common string functions like strlen(), strcpy(), strcat(), and strcmp() are described. The document contrasts strings and character pointers, noting strings cannot be reassigned while pointers can. Finally, it lists and briefly explains other standard string library functions.
[ITP - Lecture 16] Structures in C/C++
[ITP - Lecture 16] Structures in C/C++Muhammad Hammad Waseem The document explains the concept of structures in programming, highlighting their utility in handling collections of dissimilar data types, such as storing various attributes of a book. It describes how to declare and initialize structures and illustrates accessing their elements with examples. Additionally, it discusses the use of arrays of structures for convenience and outlines various applications and benefits of using structures in programming.
[ITP - Lecture 15] Arrays & its Types
[ITP - Lecture 15] Arrays & its TypesMuhammad Hammad Waseem The document introduces arrays in programming, explaining their purpose as a collection of similar variables that allow the storage of multiple values, such as student marks, more efficiently than using individual variables. It covers array declaration, initialization, and accessing elements using subscripts, along with examples to illustrate how to read from and write to arrays. Additionally, the document touches on multidimensional arrays and how to pass arrays to functions, highlighting their significance in programming logic.
[ITP - Lecture 14] Recursion
[ITP - Lecture 14] RecursionMuhammad Hammad Waseem Recursion is a process where a function calls itself. In C, functions can call themselves recursively. As an example, calculating the factorial of a number recursively is described. Factorial of a number n is defined as n * (n-1) * (n-2) ... * 1. The recursive factorial function calls itself with decreasing arguments until it reaches 1, at which point it returns 1. It then multiplies the returned values together up the call stack to calculate the final factorial value. Visualizing the recursive calls is difficult, but it is drawn out step-by-step in the document as an example for calculating 3!. Though recursion may seem complex, it can often be the most direct way to code certain algorithms
[ITP - Lecture 13] Introduction to Pointers
[ITP - Lecture 13] Introduction to PointersMuhammad Hammad Waseem Pointers allow a variable to hold the memory address of another variable. A pointer variable contains the address of the variable it points to. Pointers can be used to pass arguments to functions by reference instead of by value, allowing the function to modify the original variables. Pointers also allow a function to return multiple values by having the function modify pointer variables passed to it by the calling function. Understanding pointers involves grasping that a pointer variable contains an address rather than a value, and that pointers enable indirect access to the value at a specific memory address.
[ITP - Lecture 12] Functions in C/C++
[ITP - Lecture 12] Functions in C/C++Muhammad Hammad Waseem Functions allow programmers to structure code into modular, reusable units. A function contains a block of code that is executed when the function is called. Functions take parameters as input and can return a value. The example function "addition" takes two integer parameters, adds them together, and returns the result. The main function calls addition, passing it the values 5 and 3, and stores the returned value 8 in the variable z. Functions help avoid duplicating code and make programs easier to design, understand, and maintain.
[ITP - Lecture 11] Loops in C/C++
[ITP - Lecture 11] Loops in C/C++Muhammad Hammad Waseem This document discusses different types of loops in programming - for loops, while loops, and do-while loops. It provides examples of each loop type and explains their syntax and usage. The key points are:
- For loops allow specifying an initialization, condition, and increment in one line and are best for known iterations.
- While loops repeat until a condition is false and are useful when the number of iterations is unknown.
- Do-while loops are similar but check the condition after running the block once, guaranteeing it runs at least once.
- Loops can be nested, with inner loops running fully each time the outer loop increments.
[ITP - Lecture 10] Switch Statement, Break and Continue Statement in C/C++
[ITP - Lecture 10] Switch Statement, Break and Continue Statement in C/C++Muhammad Hammad Waseem The document discusses the switch, break, and continue statements in C programming. It explains that a switch statement allows a program to evaluate different code blocks based on the result of an expression. It will execute the matched case and any subsequent cases until reaching a break statement. The break statement exits the current block like a loop. The continue statement skips the rest of the current block and continues to the next iteration of the loop.
[ITP - Lecture 09] Conditional Operator in C/C++
[ITP - Lecture 09] Conditional Operator in C/C++Muhammad Hammad Waseem The conditional operators ? and : are sometimes called ternary operators since they take three arguments. They provide a shorthand way to write if-then-else statements in one line. The general form is expression 1 ? expression 2 : expression 3, which will return expression 2 if expression 1 is true, and expression 3 if expression 1 is false. Examples show how conditional operators can be used to assign values based on boolean expressions or character ranges. Nested conditional operators and limitations where only one statement is allowed after ? or : are also discussed.
[ITP - Lecture 08] Decision Control Structures (If Statement)
[ITP - Lecture 08] Decision Control Structures (If Statement)Muhammad Hammad Waseem The document discusses different types of if statements in C programming. It describes the basic if statement syntax which executes a statement if a condition is true. It also covers the if-else statement which executes one block of code if the condition is true and another block if false. Else-if clauses allow checking multiple conditions. Logical operators like &&, || and ! can be used to combine conditions. Nested if statements allow if-else blocks within other if/else blocks. Examples are provided to demonstrate calculating discounts, employee bonuses, student grades and more using if and if-else statements.
[ITP - Lecture 07] Comments in C/C++
[ITP - Lecture 07] Comments in C/C++Muhammad Hammad Waseem Comments help explain a program's purpose and operation to readers. There are two styles of comments in C/C++: single-line comments that begin with // and multi-line comments enclosed in /* and */. Comments should provide context around code at a high level and be used liberally to aid future understanding of the program.
[ITP - Lecture 06] Operators, Arithmetic Expression and Order of Precedence
[ITP - Lecture 06] Operators, Arithmetic Expression and Order of PrecedenceMuhammad Hammad Waseem The document discusses arithmetic operators and order of precedence in C++. It defines the basic arithmetic operators (+, -, *, /, %) and their usage. It also explains the rules for integer and float conversions during arithmetic operations. Finally, it describes the order of precedence followed in C++, with multiplication and division having higher precedence than addition and subtraction, and operations in parentheses being evaluated first. Examples are provided to demonstrate how expressions are evaluated based on these rules.
[ITP - Lecture 05] Datatypes
[ITP - Lecture 05] DatatypesMuhammad Hammad Waseem There are three primary data types in C - char, int, and float. Programmers can derive many other data types from these. For integers, C offers short and long types which occupy 2 and 4 bytes respectively and have different value ranges. Integers can also be declared as signed or unsigned, changing whether negative values are allowed. Char values can also be signed or unsigned, affecting their range from -128 to 127 or 0 to 255. Floating point types include float, double, and long double with increasing range and memory usage.
[ITP - Lecture 04] Variables and Constants in C/C++
[ITP - Lecture 04] Variables and Constants in C/C++Muhammad Hammad Waseem The document introduces constants and variables in programming, particularly in C, explaining that constants do not change while variables can hold varying values. It outlines the rules for constructing primary constants (integer, real, and character) and the guidelines for naming variables, which must be meaningful and follow specific structural rules. The text further clarifies the different forms and structures of real constants and the types of variables supported by the C language.
[ITP - Lecture 03] Introduction to C/C++
[ITP - Lecture 03] Introduction to C/C++Muhammad Hammad Waseem C++ is an object-oriented programming language that is an enhanced version of C. A C++ program consists of three main parts: preprocessor directives, the main function, and C++ statements. Preprocessor directives provide instructions to the compiler, such as including header files. The main function indicates the beginning of the program and contains the main body of code. C++ statements are the individual lines of code written within the main function and end with semicolons.
[ITP - Lecture 02] Steps to Create Program & Approaches of Programming
[ITP - Lecture 02] Steps to Create Program & Approaches of ProgrammingMuhammad Hammad Waseem 1. To write a C program, the programmer opens an edit window in an IDE to write code. They must then save the file, which the editor assigns a default name by default or the programmer can specify a name and location.
2. The programmer then compiles the code, which converts it into an object file. If there are no errors, it is successfully compiled. Otherwise, errors are reported.
3. The object file is then linked with library files by a linker, which produces an executable file.
4. Finally, the programmer executes the program by running the executable file, which loads it into memory.
[ITP - Lecture 01] Introduction to Programming & Different Programming Languages
[ITP - Lecture 01] Introduction to Programming & Different Programming LanguagesMuhammad Hammad Waseem This document provides an introduction to programming languages. It defines programming as a sequence of steps to solve a problem and explains why learning to program is important for developing problem solving skills. It then describes the main types of programming languages - low-level languages like machine language and assembly language that are close to hardware, and high-level languages that are more abstract and English-like. It also discusses the concepts of source code, object code, and language translators like assemblers, interpreters, and compilers that convert source code into executable object code.
[OOP - Lec 20,21] Inheritance
[OOP - Lec 20,21] InheritanceMuhammad Hammad Waseem Inheritance allows one class to inherit properties from another parent class. This creates a hierarchy where child classes inherit behavior from the parent class and can add or override behavior. There are three types of access specifiers that determine whether inherited members are public, private, or protected. Virtual functions allow runtime polymorphism by overriding functions in derived classes. Pure virtual functions define an interface that derived classes must implement.
[OOP - Lec 19] Static Member Functions
[OOP - Lec 19] Static Member FunctionsMuhammad Hammad Waseem Static member functions can be accessed without creating an object of the class. They are used to access static data members, which are shared by all objects of a class rather than each object having its own copy. The examples show declaring a static data member n and static member function show() that prints n. show() is called through the class name without an object. Each object creation in the constructor increments n, and show() prints the updated count.
[OOP - Lec 18] Static Data Member
[OOP - Lec 18] Static Data MemberMuhammad Hammad Waseem The document discusses static data members in C++. It explains that a static data member is shared among all objects of a class and is defined with the static keyword. Only one variable is created in memory even if there are multiple objects. It is visible only within the class and persists for the lifetime of the program. The document provides examples of declaring and defining static data members separately, and using them to assign unique roll numbers to student objects.
[ITP - Lecture 01] Introduction to Programming & Different Programming Languages
[ITP - Lecture 01] Introduction to Programming & Different Programming LanguagesMuhammad Hammad Waseem
Recently uploaded (20)
IIT KGP Quiz Week 2024 Sports Quiz (Prelims + Finals)
IIT KGP Quiz Week 2024 Sports Quiz (Prelims + Finals)IIT Kharagpur Quiz Club The document outlines the format for the Sports Quiz at Quiz Week 2024, covering various sports & games and requiring participants to Answer without external sources. It includes specific details about question types, scoring, and examples of quiz questions. The document emphasizes fair play and enjoyment of the quiz experience.
VCE Literature Section A Exam Response Guide
VCE Literature Section A Exam Response Guidejpinnuck This practical guide shows students of Unit 3&4 VCE Literature how to write responses to Section A of the exam. Including a range of examples writing about different types of texts, this guide:
*Breaks down and explains what Q1 and Q2 tasks involve and expect
*Breaks down example responses for each question
*Explains and scaffolds students to write responses for each question
*Includes a comprehensive range of sentence starters and vocabulary for responding to each question
*Includes critical theory vocabulary lists to support Q2 responses
Plate Tectonic Boundaries and Continental Drift Theory
Plate Tectonic Boundaries and Continental Drift TheoryMarie This 28 slide presentation covers the basics of plate tectonics and continental drift theory. It is an effective introduction into a full plate tectonics unit study, but does not cover faults, stress, seismic waves, or seafloor spreading.
To download PDF, visit The Homeschool Daily. We will be uploading more slideshows to follow this one. Blessings, Marie
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptx
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptxYale School of Public Health - The Virtual Medical Operations Center (VMOC) BLUF:
The Texas outbreak has slowed down, but sporadic cases continue to emerge in Kansas, Oklahoma, and New Mexico.
Elsewhere in the US, we continue to see signs of acceleration due to outbreaks outside the Southwest (North Dakota, Montana, and Colorado) and travel-related cases. Measles exposures due to travel are expected to pose a significant challenge throughout the summer.
The U.S. is on track to exceed its 30-year high for measles cases (1,274) within the next two weeks.
Here is the latest update:
CURRENT CASE COUNT: 919
•Texas: 744 (+2) (55% of cases are in Gaines County).
•New Mexico: 81 (83% of cases are from Lea County).
•Oklahoma: 20 (+2)
•Kansas: 74 (+5) (38.89% of the cases are from Gray County).
HOSPITALIZATIONS: 104
• Texas: 96 (+2) – This accounts for 13% of all cases in Texas.
• New Mexico: 7 – This accounts for 9.47% of all cases in New Mexico.
• Kansas: 3 – This accounts for 5.08% of all cases in the state of Kansas.
DEATHS: 3
•Texas: 2 – This is 0.27% of all cases in Texas.
•New Mexico: 1 – This is 1.23% of all cases in New Mexico.
US NATIONAL CASE COUNT: 1,197
INTERNATIONAL SPREAD
•Mexico: 2337 (+257), 5 fatalities
‒Chihuahua, Mexico: 2,179 (+239) cases, 4 fatalities, 7 currently hospitalized.
•Canada: 3,207 (+208), 1 fatality
‒Ontario Outbreak, Canada: 2,115 (+74) cases, 158 hospitalizations, 1 fatality.
‒Alberta, Canada: 879(+118) cases, 5 currently hospitalized.
Romanticism in Love and Sacrifice An Analysis of Oscar Wilde’s The Nightingal...
Romanticism in Love and Sacrifice An Analysis of Oscar Wilde’s The Nightingal...KaryanaTantri21 The story revolves around a college student who despairs not having a red rose as a condition for dancing with the girl he loves. The nightingale hears his complaint and offers to create the red rose at the cost of his life. He sang a love song all night with his chest stuck to the thorns of the rose tree. Finally, the red rose grew, but his sacrifice was in vain. The girl rejected the flower because it didn’t match her outfit and preferred a jewellery gift. The student threw the flower on the street and returned to studying philosophy
Aprendendo Arquitetura Framework Salesforce - Dia 02
Aprendendo Arquitetura Framework Salesforce - Dia 02Mauricio Alexandre Silva Aprendendo Arquitetura Framework Salesforce - Dia 02
Vitamin and Nutritional Deficiencies.pptx
Vitamin and Nutritional Deficiencies.pptxVishal Chanalia Vitamin and nutritional deficiency occurs when the body does not receive enough essential nutrients, such as vitamins and minerals, needed for proper functioning. This can lead to various health problems, including weakened immunity, stunted growth, fatigue, poor wound healing, cognitive issues, and increased susceptibility to infections and diseases. Long-term deficiencies can cause serious and sometimes irreversible health complications.
List View Components in Odoo 18 - Odoo Slides
List View Components in Odoo 18 - Odoo SlidesCeline George In Odoo, there are many types of views possible like List view, Kanban view, Calendar view, Pivot view, Search view, etc.
The major change that introduced in the Odoo 18 technical part in creating views is the tag <tree> got replaced with the <list> for creating list views.
Paper 107 | From Watchdog to Lapdog: Ishiguro’s Fiction and the Rise of “Godi...
Paper 107 | From Watchdog to Lapdog: Ishiguro’s Fiction and the Rise of “Godi...Rajdeep Bavaliya Dive into a captivating analysis where Kazuo Ishiguro’s nuanced fiction meets the stark realities of post‑2014 Indian journalism. Uncover how “Godi Media” turned from watchdog to lapdog, echoing the moral compromises of Ishiguro’s protagonists. We’ll draw parallels between restrained narrative silences and sensationalist headlines—are our media heroes or traitors? Don’t forget to follow for more deep dives!
M.A. Sem - 2 | Presentation
Presentation Season - 2
Paper - 107: The Twentieth Century Literature: From World War II to the End of the Century
Submitted Date: April 4, 2025
Paper Name: The Twentieth Century Literature: From World War II to the End of the Century
Topic: From Watchdog to Lapdog: Ishiguro’s Fiction and the Rise of “Godi Media” in Post-2014 Indian Journalism
[Please copy the link and paste it into any web browser to access the content.]
Video Link: https://youtu.be/kIEqwzhHJ54
For a more in-depth discussion of this presentation, please visit the full blog post at the following link: https://rajdeepbavaliya2.blogspot.com/2025/04/from-watchdog-to-lapdog-ishiguro-s-fiction-and-the-rise-of-godi-media-in-post-2014-indian-journalism.html
Please visit this blog to explore additional presentations from this season:
Hashtags:
#GodiMedia #Ishiguro #MediaEthics #WatchdogVsLapdog #IndianJournalism #PressFreedom #LiteraryCritique #AnArtistOfTheFloatingWorld #MediaCapture #KazuoIshiguro
Keyword Tags:
Godi Media, Ishiguro fiction, post-2014 Indian journalism, media capture, Kazuo Ishiguro analysis, watchdog to lapdog, press freedom India, media ethics, literature and media, An Artist of the Floating World
SCHIZOPHRENIA OTHER PSYCHOTIC DISORDER LIKE Persistent delusion/Capgras syndr...
SCHIZOPHRENIA OTHER PSYCHOTIC DISORDER LIKE Persistent delusion/Capgras syndr...parmarjuli1412 SCHIZOPHRENIA INCLUDED TOPIC IS INTRODUCTION, DEFINITION OF GENERAL TERM IN PSYCHIATRIC, THEN DIFINITION OF SCHIZOPHRENIA, EPIDERMIOLOGY, ETIOLOGICAL FACTORS, CLINICAL FEATURE(SIGN AND SYMPTOMS OF SCHIZOPHRENIA), CLINICAL TYPES OF SCHIZOPHRENIA, DIAGNOSIS, INVESTIGATION, TREATMENT MODALITIES(PHARMACOLOGICAL MANAGEMENT, PSYCHOTHERAPY, ECT, PSYCHO-SOCIO-REHABILITATION), NURSING MANAGEMENT(ASSESSMENT,DIAGNOSIS,NURSING INTERVENTION,AND EVALUATION), OTHER PSYCHOTIC DISORDER LIKE Persistent delusion/Capgras syndrome(The Delusion of Doubles)/Acute and Transient Psychotic Disorders/Induced Delusional Disorders/Schizoaffective Disorder /CAPGRAS SYNDROME(DELUSION OF DOUBLE), GERIATRIC CONSIDERATION, FOLLOW UP, HOMECARE AND REHABILITATION OF THE PATIENT,
Peer Teaching Observations During School Internship
Peer Teaching Observations During School InternshipAjayaMohanty7 FOR B.ED,M.ED,M.A.EDUCATION AND ANY STUDENT OF TEACHER EDUCATION
Tanja Vujicic - PISA for Schools contact Info
Tanja Vujicic - PISA for Schools contact InfoEduSkills OECD Tanja Vujicic, Senior Analyst and PISA for School’s Project Manager at the OECD spoke at the OECD webinar 'Turning insights into impact: What do early case studies reveal about the power of PISA for Schools?' on 20 June 2025
PISA for Schools is an OECD assessment that evaluates 15-year-old performance on reading, mathematics, and science. It also gathers insights into students’ learning environment, engagement and well-being, offering schools valuable data that help them benchmark performance internationally and improve education outcomes. A central ambition, and ongoing challenge, has been translating these insights into meaningful actions that drives lasting school improvement.
2025 June Year 9 Presentation: Subject selection.pptx
2025 June Year 9 Presentation: Subject selection.pptxmansk2 2025 June Year 9 Presentation: Subject selection
How to use search fetch method in Odoo 18
How to use search fetch method in Odoo 18Celine George The search_fetch is a powerful ORM method used in Odoo for some specific addons to combine the functionality of search and read for more efficient data fetching. It might be used to search for records and fetch specific fields in a single call. It stores the result in the cache memory.
A Visual Introduction to the Prophet Jeremiah
A Visual Introduction to the Prophet JeremiahSteve Thomason These images will give you a visual guide to both the context and the flow of the story of the prophet Jeremiah. Feel free to use these in your study, preaching, and teaching.
Photo chemistry Power Point Presentation
Photo chemistry Power Point Presentationmprpgcwa2024 Photochemistry is the branch of chemistry that deals with the study of chemical reactions and processes initiated by light.
Photochemistry involves the interaction of light with molecules, leading to electronic excitation. Energy from light is transferred to molecules, initiating chemical reactions.
Photochemistry is used in solar cells to convert light into electrical energy.
It is used Light-driven chemical reactions for environmental remediation and synthesis. Photocatalysis helps in pollution abatement and environmental cleanup. Photodynamic therapy offers a targeted approach to treating diseases It is used in Light-activated treatment for cancer and other diseases.
Photochemistry is used to synthesize complex organic molecules.
Photochemistry contributes to the development of sustainable energy solutions.
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...Ultimatewinner0342 🧠 Lazy Sunday Quiz | General Knowledge Trivia by SMC Quiz Club – Silchar Medical College
Presenting the Lazy Sunday Quiz, a fun and thought-provoking general knowledge quiz created by the SMC Quiz Club of Silchar Medical College & Hospital (SMCH). This quiz is designed for casual learners, quiz enthusiasts, and competitive teams looking for a diverse, engaging set of questions with clean visuals and smart clues.
🎯 What is the Lazy Sunday Quiz?
The Lazy Sunday Quiz is a light-hearted yet intellectually rewarding quiz session held under the SMC Quiz Club banner. It’s a general quiz covering a mix of current affairs, pop culture, history, India, sports, medicine, science, and more.
Whether you’re hosting a quiz event, preparing a session for students, or just looking for quality trivia to enjoy with friends, this PowerPoint deck is perfect for you.
📋 Quiz Format & Structure
Total Questions: ~50
Types: MCQs, one-liners, image-based, visual connects, lateral thinking
Rounds: Warm-up, Main Quiz, Visual Round, Connects (optional bonus)
Design: Simple, clear slides with answer explanations included
Tools Needed: Just a projector or screen – ready to use!
🧠 Who Is It For?
College quiz clubs
School or medical students
Teachers or faculty for classroom engagement
Event organizers needing quiz content
Quizzers preparing for competitions
Freelancers building quiz portfolios
💡 Why Use This Quiz?
Ready-made, high-quality content
Curated with lateral thinking and storytelling in mind
Covers both academic and pop culture topics
Designed by a quizzer with real event experience
Usable in inter-college fests, informal quizzes, or Sunday brain workouts
📚 About the Creators
This quiz has been created by Rana Mayank Pratap, an MBBS student and quizmaster at SMC Quiz Club, Silchar Medical College. The club aims to promote a culture of curiosity and smart thinking through weekly and monthly quiz events.
🔍 SEO Tags:
quiz, general knowledge quiz, trivia quiz, SlideShare quiz, college quiz, fun quiz, medical college quiz, India quiz, pop culture quiz, visual quiz, MCQ quiz, connect quiz, science quiz, current affairs quiz, SMC Quiz Club, Silchar Medical College
📣 Reuse & Credit
You’re free to use or adapt this quiz for your own events or sessions with credit to:
SMC Quiz Club – Silchar Medical College & Hospital
Curated by: Rana Mayank Pratap
Filipino 9 Maikling Kwento Ang Ama Panitikang Asiyano
Filipino 9 Maikling Kwento Ang Ama Panitikang Asiyanosumadsadjelly121997 Filipino 9 Maikling Kwento Ang Ama Panitikang Asiyano
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptx
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptxYale School of Public Health - The Virtual Medical Operations Center (VMOC)
Data Structures - Lecture 10 [Graphs]
- 1. GRAPHS DATA STRUCTURES MUHAMMAD HAMMAD WASEEM 1
- 2. WHAT IS A GRAPH? • A data structure that consists of a set of nodes (vertices) and a set of edges that relate the nodes to each other • The set of edges describes relationships among the vertices 2
- 3. FORMAL DEFINITION OF GRAPHS • A graph G is defined as follows: G=(V,E) V(G): a finite, nonempty set of vertices E(G): a set of edges (pairs of vertices) 3
- 4. DIRECTED VS. UNDIRECTED GRAPHS • When the edges in a graph have no direction, the graph is called undirected. • When the edges in a graph have a direction, the graph is called directed (or digraph) 4 E(Graph2) = {(1,3) (3,1) (5,9) (9,11)
- 5. TREES VS. GRAPHS • Trees are special cases of graphs!! 5
- 6. GRAPH TERMINOLOGY • Adjacent nodes: two nodes are adjacent if they are connected by an edge • Path: a sequence of vertices that connect two nodes in a graph • Complete graph: a graph in which every vertex is directly connected to every other vertex • Degree of a vertex: The degree of a vertex in a graph is the number of edges that touch it. • The Size of a Graph: The size of a graph is the number of vertices that it has. 6 5 is adjacent to 7 7 is adjacent from 5
- 7. GRAPH TERMINOLOGY (CONT.) • What is the number of edges in a complete directed graph with N vertices? N * (N-1) 7 2 ( )O N
- 8. GRAPH TERMINOLOGY (CONT.) • What is the number of edges in a complete undirected graph with N vertices? N * (N-1) / 2 8 2 ( )O N
- 9. GRAPH TERMINOLOGY (CONT.) • Weighted graph: a graph in which each edge carries a value 9
- 10. GRAPH IMPLEMENTATION • Array-based implementation • A 1D array is used to represent the vertices • A 2D array (adjacency matrix) is used to represent the edges 10
- 12. GRAPH IMPLEMENTATION (CONT.) • Linked-list implementation • A 1D array is used to represent the vertices • A list is used for each vertex v which contains the vertices which are adjacent from v (adjacency list) 12
- 14. ADJACENCY MATRIX VS. ADJACENCY LIST REPRESENTATION • Adjacency matrix • Good for dense graphs --|E|~O(|V|2) • Memory requirements: O(|V| + |E| ) = O(|V|2 ) • Connectivity between two vertices can be tested quickly • Adjacency list • Good for sparse graphs -- |E|~O(|V|) • Memory requirements: O(|V| + |E|)=O(|V|) • Vertices adjacent to another vertex can be found quickly 14
- 15. GRAPH SEARCHING • Problem: find a path between two nodes of the graph (e.g., Austin and Washington) • Methods: Depth-First-Search (DFS) or Breadth- First-Search (BFS) 15
- 16. DEPTH-FIRST-SEARCH (DFS) • What is the idea behind DFS? • Travel as far as you can down a path • Back up as little as possible when you reach a "dead end" (i.e., next vertex has been "marked" or there is no next vertex) • DFS can be implemented efficiently using a stack 16
- 17. DEPTH-FIRST-SEARCH (DFS) (CONT.)Set found to false stack.Push(startVertex) DO stack.Pop(vertex) IF vertex == endVertex Set found to true ELSE Push all adjacent vertices onto stack WHILE !stack.IsEmpty() AND !found IF(!found) Write "Path does not exist" 17
- 19. 19
- 20. 20
- 21. BREADTH-FIRST-SEARCHING (BFS) • What is the idea behind BFS? • Look at all possible paths at the same depth before you go at a deeper level • Back up as far as possible when you reach a "dead end" (i.e., next vertex has been "marked" or there is no next vertex) 21
- 22. BREADTH-FIRST-SEARCHING (BFS) (CONT.) • BFS can be implemented efficiently using a queue Set found to false queue.Enqueue(startVertex) DO queue.Dequeue(vertex) IF vertex == endVertex Set found to true ELSE Enqueue all adjacent vertices onto queue WHILE !queue.IsEmpty() AND !found • Should we mark a vertex when it is enqueued or when it is dequeued ? 22 IF(!found) Write "Path does not exist"
- 24. next: 24
- 25. 25
- 26. SINGLE-SOURCE SHORTEST- PATH PROBLEM • There are multiple paths from a source vertex to a destination vertex • Shortest path: the path whose total weight (i.e., sum of edge weights) is minimum • Examples: • Austin->Houston->Atlanta->Washington: 1560 miles • Austin->Dallas->Denver->Atlanta->Washington: 2980 miles 26
- 27. SINGLE-SOURCE SHORTEST- PATH PROBLEM (CONT.) • Common algorithms: Dijkstra's algorithm, Bellman-Ford algorithm • BFS can be used to solve the shortest graph problem when the graph is weightless or all the weights are the same (mark vertices before Enqueue) 27
- 28. SIMPLE SEARCH ALGORITHM Let S be the start state 1. Initialize Q with the start node Q=(S) as only entry; set Visited = (S) 2. If Q is empty, fail. Else pick node X from Q 3. If X is a goal, return X, we’ve reached the goal 4. (Otherwise) Remove X from Q 5. Find all the children of node X not in Visited 6. Add these to Q; Add Children of X to Visited 7. Go to Step 2 28
- 29. DEPTH FIRST SEARCH(DFS) • Expand deepest unexpanded node • Implementation: • fringe = LIFO queue, i.e., put successors at front • Properties of DFS • Complete: No, fails in infinite-depth spaces, spaces with loops • Modify to avoid repeated states along path • Complete in finite spaces • Time: O(bm): terrible if m is much larger than d • but if solutions are dense, may be much faster than breadth-first • Space: O(bm), i.e., linear space! 29
- 30. DFS: EXAMPLE Q Visited 1 2 3 4 5 30 S BA E FDC G H
- 31. DFS: EXAMPLE Q Visited 1 S S 2 3 4 5 31 S BA E FDC G H
- 32. DFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 4 5 32 S BA E FDC G H
- 33. DFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 C,D,B S,A,B,C,D 4 5 33 S BA E FDC G H
- 34. DFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 C,D,B S,A,B,C,D 4 G,H,D,B S,A,B,C,D,G,H 5 34 S BA E FDC G H
- 35. DFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 C,D,B S,A,B,C,D 4 G,H,D,B S,A,B,C,D,G,H 5 H,D,B S,A,B,C,D,G,H 35 S BA E FDC G H
- 36. DFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 C,D,B S,A,B,C,D 4 G,H,D,B S,A,B,C,D,G,H 5 H,D,B S,A,B,C,D,G,H 6 D,B S,A,B,C,D,G,H 36 S BA E FDC G H
- 37. DFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 C,D,B S,A,B,C,D 4 G,H,D,B S,A,B,C,D,G,H 5 H,D,B S,A,B,C,D,G,H 6 D,B S,A,B,C,D,G,H 37 S BA E FDC G H
- 38. BREADTH FIRST SEARCH(BFS) • Expand shallowest unexpanded node • Implementation: • fringe = FIFO queue, i.e., New successors go at end • Properties of DFS • Complete: Yes(if b is finite) • Time: 1+b+b2+b3+… +bd + b(bd-1) = O(bd+1) • Space: O(bd+1) (keeps every node in memory) • Imagine searching a tree with branching factor 8 and depth 10. Assume a node requires just 8 bytes of storage. The breadth first search might require up to: = (8)10 nodes = (23)10 X 23 = 233 bytes = 8,000 Mbytes = 8 Gbytes • Optimal: Yes (if cost = 1 per step) 38
- 39. BFS: EXAMPLE Q Visited 1 2 3 4 5 39 S BA E FDC G H
- 40. BFS: EXAMPLE Q Visited 1 S S 2 3 4 5 40 S BA E FDC G H
- 41. BFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 4 5 41 S BA E FDC G H
- 42. BFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 B,C,D S,A,B,C,D 4 5 42 S BA E FDC G H
- 43. BFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 B,C,D S,A,B,C,D 4 5 43 S BA E FDC G H
- 44. BFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 B,C,D S,A,B,C,D 4 C,D,E,F S,A,B,C,D,E,F 5 44 S BA E FDC G H
- 45. BFS: EXAMPLE Q Visited 2 A,B S,A,B 3 B,C,D S,A,B,C,D 4 C,D,E,F S,A,B,C,D,E,F 5 D,E,F,G,H S,A,B,C,D,E,F,G,H 6 45 S BA E FDC G H
- 46. BFS: EXAMPLE Q Visited 3 B,C,D S,A,B,C,D 4 C,D,E,F S,A,B,C,D,E,F 5 D,E,F,G,H S,A,B,C,D,E,F,G,H 6 E,F,G,H S,A,B,C,D,E,F,G,H 7 46 S BA E FDC G H
- 47. BFS: EXAMPLE Q Visited 4 C,D,E,F S,A,B,C,D,E,F 5 D,E,F,G,H S,A,B,C,D,E,F,G,H 6 E,F,G,H S,A,B,C,D,E,F,G,H 7 F,G,H S,A,B,C,D,E,F,G,H 8 47 S BA E FDC G H
- 48. BFS: EXAMPLE Q Visited 5 D,E,F,G,H S,A,B,C,D,E,F,G,H 6 E,F,G,H S,A,B,C,D,E,F,G,H 7 F,G,H S,A,B,C,D,E,F,G,H 8 G,H S,A,B,C,D,E,F,G,H 9 48 S BA E FDC G H
- 49. BFS: EXAMPLE Q Visited 6 E,F,G,H S,A,B,C,D,E,F,G,H 7 F,G,H S,A,B,C,D,E,F,G,H 8 G,H S,A,B,C,D,E,F,G,H 9 H S,A,B,C,D,E,F,G,H 10 49 S BA E FDC G H
- 50. BFS: EXAMPLE Q Visited 6 E,F,G,H S,A,B,C,D,E,F,G,H 7 F,G,H S,A,B,C,D,E,F,G,H 8 G,H S,A,B,C,D,E,F,G,H 9 S,A,B,C,D,E,F,G,H 10 S,A,B,C,D,E,F,G,H 50 S BA E FDC G H
- 51. BFS: EXAMPLE Q Visited 1 S S 2 A,B S,A,B 3 B,C,D S,A,B,C,D 4 C,D,E,F S,A,B,C,D,E,F 5 D,E,F,G,H S,A,B,C,D,E,F,G,H 6 E,F,G,H S,A,B,C,D,E,F,G,H 7 F,G,H S,A,B,C,D,E,F,G,H 8 G,H S,A,B,C,D,E,F,G,H 9 H S,A,B,C,D,E,F,G,H 10 S,A,B,C,D,E,F,G,H 51 S BA E FDC G H
- 52. THANKS • Implement DFS and BFS in lab and submit softcopy at [email protected] 52
