Datastructure tree
Download as PPTX, PDF3 likes861 views
The document discusses binary index trees (also called Fenwick trees) and segment trees, which are data structures that allow efficient querying of array prefixes and intervals. Binary index trees support adding values to array elements and retrieving prefix sums in O(log n) time. Segment trees similarly support adding values and finding maximum/minimum values in intervals in O(log n) time. Both achieve faster query times than naive solutions by representing the array as a tree structure.
1 of 63
Downloaded 44 times

![Binary Index Tree
Problem:
Give an array A[1], A[2] , … , A[n] and m
queries as follows (n, m ~ 10^6)
type 1: add x to A[k] (1 <= k <= n)
type 2: calculate sum of interval [l , r] of array](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-2-320.jpg)


![Binary Index Tree
Support two operations in O(log(n))
[1] Add value x to an element A[k]
A[k] → A[k] + x
[2] Return sum of prefix k
prefix[k] = A[1] + A[2] + ... + A[k]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-5-320.jpg)
![Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-6-320.jpg)
![Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[1]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-7-320.jpg)
![Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[3]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-8-320.jpg)
![Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
get prefix[3]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-9-320.jpg)
![Binary Index Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
get prefix[7]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-10-320.jpg)

![Binary Index Tree
[1] Add value to element at position index
void add(int index, int value) {
for (int i = index; i <= size; i += i & -i) {
bit[index] += value;
}
} → O(log(n))](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-12-320.jpg)
![Binary Index Tree
[1] Get sum of elements from postion 1 -> index
int get(int index) {
int ans = 0;
for (int i = index; i > 0; i -= i & -i) {
ans += bit[i];
}
return ans;
} → O(log(n))](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-13-320.jpg)

![Count Inverse Pair
Give an array A[1], A[2], ..., A[n], n ~ 10^6
Count number of pair (A[i], A[j]) such that
i < j and A[i] > A[j]
Naive solution: scan all pairs (A[i], A[j]) , i < j
→ time complexity O(n^2) → impossible](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-15-320.jpg)
![Another solution
• Using technique of merge sort
Divide and conquer (A[1], ... ,A[n])
→ (A[1], ... ,A[n/2]) ∨ (A[n/2+1], ..., A[n])
solve(A[1], ... ,A[n/2])
solve(A[n/2+1], ..., A[n])
merge(A[1], ... ,A[n/2] ∨A[n/2+1], ..., A[n])
Time complexity O(nlog(n))](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-16-320.jpg)
![Using BIT
Suppose 1 <= A[1], A[2], ..., A[n] <= n and are
integer.
If not, we can make a mapping by sort because
we only consider about magnitude correlation
ex: (1.2, -9.8, 5.0, 3.4) → (2, 1, 4, 3)](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-17-320.jpg)
![Using BIT
int ans = 0;
void solve() {
for (int i = 1; i <= n; ++i) {
ans += i - 1 - get(a[i]);
add(a[i], 1);
}
}](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-18-320.jpg)
![D-Query
Problem:
Given an array n number A[1], A[2], ..., A[n]
and m queries as follows (n ~ 3x10^4, m ~
2x10^5, 1 <= A[i] <= 10^6)
query : (l, r) return number of distinct
elements in subarray A[l], A[l+1], ..., A[r]
→ Cann’t solve with naive solution](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-19-320.jpg)
![D-Query
Solution with BIT
[1] Sort queries based on right value
(l1,r1), (l2,r2), ..., (lm, rm)
→ r1 <= r2 <= ... <= rm
[2] Go through array from left to right, using
index[] to save last position each value
→ index[x] is last position of x in current array](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-20-320.jpg)
![D-Query
Solution with BIT
[3] Current value a[i]
*if index[a[i]] != i then update index[a[i]] = i
*if there is some r[j] = i then calculate
answer and go to next queries
*else go to next postion
[4] Print answers](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-21-320.jpg)

![D-Query
for (int j = 0, i = 1; j < num_queries;) {
if (index[a[i]] != i) {
bit.add(index[a[i]], -1);
index[a[i]] = i;
bit.add(i, 1);
}
if (queries[j].r == i) {
ans[queries[j].id] += bit.get(i) – bit.get(queries[j].l – 1);
j++;
}
else i++;
}](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-23-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
index[1] = -1
index[2] = -1
index[3] = -1
3 queries
[2, 4]
[1, 5]
[3, 5]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-24-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 1
→ bit.add(-1, -1) , bit.add(1, 1)
index[2] = -1
index[3] = -1](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-25-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 2
→ bit.add(1, -1) , bit.add(2, 1)
index[2] = -1
index[3] = -1](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-26-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 2
index[2] = 3
→ bit.add(-1, -1) , bit.add(3, 1)
index[3] = -1](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-27-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 4
→ bit.add(2, -1) , bit.add(4, 1)
→ ans[2] = bit.get(4) – bit.get(1)
index[2] = 3
index[3] = -1](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-28-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 4
index[2] = 3
index[3] = 5
→ bit.add(-1, -1) , bit.add(5, 1)
→ ans[1] = bit.get(5) – bit.get(0)](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-29-320.jpg)
![D-Query
1 1 2 1 3
3 queries
[1, 5]
[2, 4]
[3, 5]
3 queries
[2, 4]
[1, 5]
[3, 5]
index[1] = 4
index[2] = 3
index[3] = 5
→ ans[3] = bit.get(5) – bit.get(2)](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-30-320.jpg)
![Segment Tree
Problem:
Give an array A[1], A[2], ..., A[n] and m queries
as follows (n, m ~ 10^6)
type 1: add x to A[k]
type 2: calculate max, min on interval [l, r]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-31-320.jpg)


![Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-34-320.jpg)
![Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[2]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-35-320.jpg)
![Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
add to A[6]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-36-320.jpg)
![Segment Tree
A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8]
A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8]
A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
get max on [3,8]](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-37-320.jpg)
![Segment Tree
• Each node of tree is an interval [l, r]
• If l < r, it has two children [l, m] and [m+1, r]
with m = (l + r)/2
• Length of array is n → total node of tree is
1 + 2 + 4 + ... + 2^k = 2^(k+1) – 1
k is smallest number such that 2^k >= n
→ total node <= 4n, memory O(n)](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-38-320.jpg)

![Segment Tree
*Initialize: build(1, 1, n)
void build(int node, int l, int r) {
if (l == r) {sg[node] = A[l]; return;}
int m = (l + r)/2;
build(node * 2, l, m);
build(node * 2 + 1, m + 1, r);
sg[node] = max(sg[node * 2], sg[node * 2 + 1]);
} → O(n)](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-40-320.jpg)
![Segment Tree
*Add x to A[k]: update(1, 1, n, k, x)
void update(int node, int l, int r, int k, int x) {
if (l == r) {sg[node] = A[k] + x; return;}
int m = (l + r)/2;
if (m >= k) update(node * 2, l, m, k, x);
else update(node * 2 + 1, m + 1, r, k, x);
sg[node] = max(sg[node * 2], sg[node * 2 + 1]);
} → O(log(n))](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-41-320.jpg)
![Segment Tree
*Get max on interval [l,r]: query(1, 1, n, l, r)
int query(int node, int i, int j, int l, int r) {
if (l<=i && j <= r) {return sg[node];}
int m = (i + j)/2;
if (m >= r) return query(node * 2, i, m, l, r);
else if (m < l) return query(node * 2 + 1, m + 1, j, l, r);
else return max(query(node * 2, i, m, l, r),
query(node * 2 + 1, m + 1, j, l, r));
} → O(log(n))](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-42-320.jpg)



![Treap
typedef struct node {
int val, pri, cnt, sum;
struct node * child[2];
node(int v, int p) : val(v), pri(p), cnt(1), sum(v) {
child[0] = child[1] = NULL;
}
} * node_t;](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-46-320.jpg)
![Treap
int count(node_t t) {
return t ? t->cnt : 0;
}
int sum(node_t t) {
return t ? t->sum : 0;
}
node_t update(node_t t) {
t->cnt = count(t->child[0]) + count(t->child[1]) + 1;
t->sum = sum(t->child[0]) + sum(t->child[1]) + t->val;
return t;
}](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-47-320.jpg)


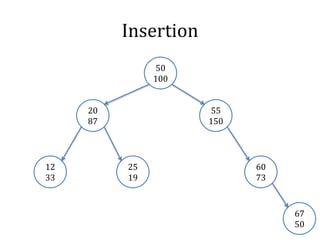

![Rotation
node_t rotate(node_t t, int b) {
node_t s = t->child[b];
t->child[1-b] = s->child[b];
s->child[b] = t;
update(t);
update(s);
return s;
}](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-52-320.jpg)



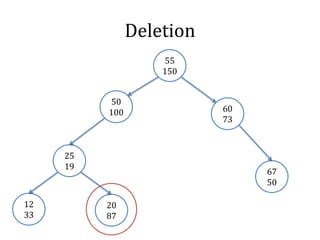





![Merge
node_t merge(node_t l, node_t r) {
if (!l || !r) return !l ? r : l;
if (l->pri > r->pri) {
l->child[1] = merge(l->child[1], r);
return update(l);
}
else {
r->child[0] = merge(l, r->child[0]);
return update(r);
}
}](https://image.slidesharecdn.com/datastructure-tree-141114225212-conversion-gate02/85/Datastructure-tree-62-320.jpg)

Ad
Recommended
Lowest common ancestor



Lowest common ancestorShakil Ahmed The document discusses the lowest common ancestor (LCA) concept in graph theory and computer science. The LCA of two nodes v and w in a rooted tree T is the lowest node that has both v and w as descendants. The document also provides sample code for finding the LCA of two nodes in a tree and calculating the minimum weight path between them.
Gwt presen alsip-20111201



Gwt presen alsip-20111201Yasuo Tabei The document describes using a wavelet tree data structure to enable fast similarity searches of massive graph databases. A Weisfeiler-Lehman procedure is used to represent graphs as bags-of-words. The wavelet tree indexes these bags-of-words and allows semi-conjunctive queries to find graphs sharing a minimum number of words with a query graph in sublinear time. Experiments on 25 million molecular graphs showed the approach significantly outperformed inverted indexes in search time and memory usage.
Gwt sdm public



Gwt sdm publicYasuo Tabei (1) The document describes a method for efficient similarity search in massive graph databases using wavelet trees. (2) It converts graphs into bags-of-words representations using the Weisfeiler-Lehman procedure and indexes the words with a wavelet tree to enable fast semi-conjunctive queries. (3) Experiments on 25 million chemical compounds showed the method was significantly faster than alternative approaches while using less memory.
LeetCode Solutions In Java .pdf



LeetCode Solutions In Java .pdfzupsezekno This document contains summaries of solutions to various LeetCode problems in Java. It begins with a 3-sentence summary of the Rotate Array problem and its solutions, followed by shorter 1-sentence summaries of other problems and their solutions, including Evaluate Reverse Polish Notation, Longest Palindromic Substring, Word Break, and more. Dynamic programming and recursion are discussed as approaches for some of the problems.
Positive and negative solutions of a boundary value problem for a fractional ...



Positive and negative solutions of a boundary value problem for a fractional ...journal ijrtem : In this work, we study a boundary value problem for a fractional
q, -difference equation. By
using the monotone iterative technique and lower-upper solution method, we get the existence of positive or
negative solutions under the nonlinear term is local continuity and local monotonicity. The results show that we
can construct two iterative sequences for approximating the solutions
2-D array



2-D arraySwarup Kumar Boro The document discusses 2D arrays including their definition, implementation, and how to calculate the address of elements. It covers storing arrays in row-major and column-major order and includes formulas to calculate addresses based on the lower and upper bounds. Operations on 2D arrays like addition, subtraction, and multiplication are also explained. Some example problems are provided at the end to demonstrate calculating addresses of elements in 2D arrays stored in both row-major and column-major order.
On the Zeros of Complex Polynomials



On the Zeros of Complex PolynomialsInternational Journal of Engineering Inventions www.ijeijournal.com The peer-reviewed International Journal of Engineering Inventions (IJEI) is started with a mission to encourage contribution to research in Science and Technology. Encourage and motivate researchers in challenging areas of Sciences and Technology.
The International Journal of Engineering and Science (IJES)



The International Journal of Engineering and Science (IJES)theijes The International Journal of Engineering & Science is aimed at providing a platform for researchers, engineers, scientists, or educators to publish their original research results, to exchange new ideas, to disseminate information in innovative designs, engineering experiences and technological skills. It is also the Journal's objective to promote engineering and technology education. All papers submitted to the Journal will be blind peer-reviewed. Only original articles will be published.
DISCRETE LOGARITHM PROBLEM



DISCRETE LOGARITHM PROBLEMMANISH KUMAR The document discusses public key cryptography based on the discrete logarithm problem (DLP). It defines the DLP and describes some common algorithms for solving it, including the ElGamal cryptosystem, Diffie-Hellman key exchange, baby-step giant-step algorithm, Pohlig-Hellman algorithm, and Pollard's rho algorithm. It also explains how the difficulty of solving the DLP can provide the basis for secure cryptographic systems.
04 quadratic equations



04 quadratic equationsprofashfaq This document contains 26 multiple choice questions about quadratic equations. The questions cover a range of topics including finding the roots of quadratic equations, determining the nature of the roots based on coefficients, and other properties of quadratic equations. Sample answers are provided but no full solutions are shown.
Aaex2 group2



Aaex2 group2Shiang-Yun Yang This document contains solutions to 10 algorithm problems. It begins by providing efficient O(n) time algorithms to: 1) Remove digits from an integer to maximize its value. 2) Find a subsequence of integers that sums to a given value k. It then provides linear time algorithms to: 3) Find the largest square submatrix of 1s in a binary matrix. 4) Find a maximum independent set on trees. It also provides efficient algorithms to: 5) Find the maximum/minimum product substrings. 6) Find the maximum sum substring of length <=L. 7) Find a weight maximizing increasing value subsequence. Finally, it provides two algorithms to solve Problem 10154 on finding maximum weight within a strength limit.
redes neuronais



redes neuronaisRoland Silvestre This document provides resolutions to exercises related to artificial neural networks. It includes derivatives of activation functions, recursive definitions of B-spline functions, correlation matrices for input patterns, and explanations of linear separability and implementing logic functions like AND, OR, and XOR using perceptrons.
Ee693 sept2014midsem



Ee693 sept2014midsemGopi Saiteja This document contains a 30 question mid-semester exam for a data structures and algorithms course. The exam covers topics like asymptotic analysis, sorting algorithms, hashing, binary search trees, and recursion. It provides multiple choice questions to test understanding of algorithm time complexities, worst-case inputs, and recursive functions. Students are instructed to attempt all questions in the 2 hour time limit and notify the proctor if any electronic devices other than calculators are used.
Skiena algorithm 2007 lecture15 backtracing



Skiena algorithm 2007 lecture15 backtracingzukun This document discusses backtracking algorithms and provides examples for solving problems using backtracking, including:
1) Generating all subsets and permutations of a set using backtracking.
2) The eight queens problem, which can be solved using a backtracking algorithm that places queens on a chessboard one by one while checking for threats.
3) Key components of backtracking algorithms including candidate construction, checking for solutions, and pruning search spaces for efficiency.
Definite Integrals 8/ Integration by Parts



Definite Integrals 8/ Integration by PartsLakshmikanta Satapathy JEE Mathematics/ Lakshmikanta Satapathy/ Definite integrals part 8/ JEE question on definite integral involving integration by parts solved with complete explanation
CppConcurrencyInAction - Chapter07



CppConcurrencyInAction - Chapter07DooSeon Choi This document discusses the implementation of a lock-free queue in C++. It begins with an overview of blocking vs non-blocking behavior and synchronization primitives like mutexes. It then presents the implementation of a single-producer, single-consumer lock-free queue using atomic operations. It shows how push and pop operations are performed concurrently without locking by atomically updating shared queue pointers. It also discusses techniques like helping other threads complete operations to ensure lock-free progress.
Lec8



Lec8Anjneya Varshney The document discusses ordered dictionaries and binary search trees (BSTs). It describes how to implement ordered dictionaries using BSTs to support operations like minimum, maximum, predecessor, and successor in logarithmic time. The key aspects are:
1) BSTs allow searching, minimum, maximum, predecessor, and successor operations in O(h) time where h is the height of the tree.
2) Insertion and deletion in a BST takes O(h) time in the worst case, as repeatedly inserting keys in ascending or descending order yields a skewed tree of height n for n nodes.
3) Search works by comparing the search key to the root node's key, and recursively searching the left or right
Pert 05 aplikasi clustering



Pert 05 aplikasi clusteringaiiniR This document provides an overview of clustering techniques including k-means clustering, expectation maximization algorithms, and spectral clustering. It discusses how k-means clustering works by initializing random cluster centers, assigning data points to the closest centers, and adjusting the centers iteratively. Expectation maximization is presented as a way to learn the parameters of a Gaussian mixture model to cluster data. Finally, applications of clustering like document clustering using mixture models are briefly described.
5.3 dynamic programming



5.3 dynamic programmingKrish_ver2 Dynamic programming is a technique for solving problems with overlapping subproblems and optimal substructure. It works by breaking problems down into smaller subproblems and storing the results in a table to avoid recomputing them. Examples where it can be applied include the knapsack problem, longest common subsequence, and computing Fibonacci numbers efficiently through bottom-up iteration rather than top-down recursion. The technique involves setting up recurrences relating larger instances to smaller ones, solving the smallest instances, and building up the full solution using the stored results.
On Nets and Meshes



On Nets and MeshesDon Sheehy What is the difference between a mesh and a net?
What is the difference between a metric space epsilon-net and a range space epsilon-net?
What is the difference between geometric divide-and-conquer and combinatorial divide-and-conquer?
In this talk, I will answer these questions and discuss how these different ideas come together to finally settle the question of how to compute conforming point set meshes in optimal time. The meshing problem is to discretize space into as few pieces as possible and yet still capture the underlying density of the input points. Meshes are fundamental in scientific computing, graphics, and more recently, topological data analysis.
This is joint work with Gary Miller and Todd Phillips
Presentation OCIP2014



Presentation OCIP2014Fabian Froehlich Dynamical models are widely used to describe chemical, physical and biochemical processes. The main challenge for this class of problems is the identification of kinetic parameters from given measurement data, the so called parameter estimation. However, parameters of such models are never exactly determined, due to measurement noise and the limited amount of data, but remain uncertain. This uncertainty can be captured by a probability density over the parameter space. Unfortunately, studying this probability density is often computationally demanding as this requires the repeated simulation of the underlying model. In this talk we will present a novel method for analysis of such probability densities using networks of radial basis functions.
A particular characteristic of radial basis function approximation schemes is meshless nature, which allows for the free choice of sampling nodes. We will show that root lattices have optimality properties and propose a novel algorithm for the generation of lattices restricted to superlevel-sets. Furthermore we introduce an adaptive method for the generation of nodes based on interacting particles.
Numerical examples show that our method can yield an expected L2 approximation error that is several orders of magnitude lower compared to classical approximations. This allows a drastic reduction of sampling points, which in turn facilitates the analysis of uncertainty for problems with high computational complexity.
Further mathematics notes zimsec cambridge zimbabwe



Further mathematics notes zimsec cambridge zimbabweAlpro Further mathematics notes zimsec cambridge zimbabwe advanced level A level
Zimbabwe
Zimsec
cambridge Alpro
[1062BPY12001] Data analysis with R / week 2![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
[1062BPY12001] Data analysis with R / week 2Kevin Chun-Hsien Hsu R is a programming language for data analysis and statistics. It allows users to enter commands at the prompt ">" to perform calculations and manipulate numeric and other objects like vectors and matrices. Basic objects in R include numeric, integer, character, complex, and logical values. Vectors are the most basic data structure and can contain elements of the same type. Matrices are two-dimensional vectors that store values in rows and columns. Functions like c(), seq(), and rep() can be used to create, combine and replicate vectors and sequences of values.
Thesis Defence for Doctor of Information Science



Thesis Defence for Doctor of Information ScienceYuma Inoue This document summarizes Yuma Inoue's doctoral thesis defense presentation on permutation set manipulation based on decision diagrams. The presentation covered topics including reversible circuit debugging, cycle-type partitioning of permutations, enumeration of topological orders using rotation-based πDDs, and other applications of permutation decision diagrams (πDDs) and related data structures. It provided examples and outlined Inoue's contributions to algorithms for manipulating and analyzing permutation sets in an efficient manner using decision diagrams.
Nbvtalkatbzaonencryptionpuzzles



NbvtalkatbzaonencryptionpuzzlesNagasuri Bala Venkateswarlu This presentation contains my view on how to use puzzles while teaching Encryption, Security, Forensics to the students
A Generic Algebraic Model for the Analysis of Cryptographic Key Assignment Sc...



A Generic Algebraic Model for the Analysis of Cryptographic Key Assignment Sc...dhruvgairola This document presents an algebraic model for analyzing cryptographic key assignment schemes. It proposes representing keys as elements of a semiring structure and schemes as models with a key structure, security classes partially ordered by a key derivation relation, and an assignment function. Existing schemes like Akl-Taylor are generalized in this framework. Properties like security and key derivation can be formally verified using the theories of the algebraic structure.
Sub1567



Sub1567International Journal of Science and Research (IJSR) This document presents the solution to quadruple Fourier series equations involving heat polynomials. Quadruple series equations are useful for solving four-part boundary value problems in fields like electrostatics and elasticity. The document considers two sets of quadruple series equations, the first kind and second kind, involving heat polynomials of the first and second kind. The solutions are obtained by reducing the problems to simultaneous Fredholm integral equations of the second kind. The specific equations considered and the steps to solve them using operator theory are presented.
Psimd open64 workshop_2012-new



Psimd open64 workshop_2012-newdibyendu_das0708 The document describes experience with partial SIMDization in the Open64 compiler using dynamic programming. It discusses applying partial SIMDization to pack isomorphic instructions into SIMD instructions without fully vectorizing loops. It outlines applying a dynamic programming approach based on the Barik-Zhao-Sarkar algorithm to choose optimal SIMD tile combinations. Initial results show applying this to a hot loop in GROMACS was able to SIMDize over 88% of operations, demonstrating the potential of the technique.
Binary tree



Binary treeRajendran This document discusses binary trees. It defines a binary tree as a structure containing nodes with two self-referenced fields - a left reference and a right reference. Each node can have at most two child nodes. It provides examples of common binary tree terminology like root, internal nodes, leaves, siblings, depth, and height. It also describes different ways to represent binary trees using arrays or links and their tradeoffs. Complete binary trees are discussed as an optimal structure with height proportional to log of number of nodes.
Introduction to Data structure & Algorithms - Sethuonline.com | Sathyabama Un...



Introduction to Data structure & Algorithms - Sethuonline.com | Sathyabama Un...sethuraman R The document discusses data structures and algorithms. It provides an overview of binary trees, binary search trees, and their traversals. It then discusses graphs and poses questions related to binary trees, binary search tree traversals, and graphs.
Ad
More Related Content
What's hot (20)
DISCRETE LOGARITHM PROBLEM



DISCRETE LOGARITHM PROBLEMMANISH KUMAR The document discusses public key cryptography based on the discrete logarithm problem (DLP). It defines the DLP and describes some common algorithms for solving it, including the ElGamal cryptosystem, Diffie-Hellman key exchange, baby-step giant-step algorithm, Pohlig-Hellman algorithm, and Pollard's rho algorithm. It also explains how the difficulty of solving the DLP can provide the basis for secure cryptographic systems.
04 quadratic equations



04 quadratic equationsprofashfaq This document contains 26 multiple choice questions about quadratic equations. The questions cover a range of topics including finding the roots of quadratic equations, determining the nature of the roots based on coefficients, and other properties of quadratic equations. Sample answers are provided but no full solutions are shown.
Aaex2 group2



Aaex2 group2Shiang-Yun Yang This document contains solutions to 10 algorithm problems. It begins by providing efficient O(n) time algorithms to: 1) Remove digits from an integer to maximize its value. 2) Find a subsequence of integers that sums to a given value k. It then provides linear time algorithms to: 3) Find the largest square submatrix of 1s in a binary matrix. 4) Find a maximum independent set on trees. It also provides efficient algorithms to: 5) Find the maximum/minimum product substrings. 6) Find the maximum sum substring of length <=L. 7) Find a weight maximizing increasing value subsequence. Finally, it provides two algorithms to solve Problem 10154 on finding maximum weight within a strength limit.
redes neuronais



redes neuronaisRoland Silvestre This document provides resolutions to exercises related to artificial neural networks. It includes derivatives of activation functions, recursive definitions of B-spline functions, correlation matrices for input patterns, and explanations of linear separability and implementing logic functions like AND, OR, and XOR using perceptrons.
Ee693 sept2014midsem



Ee693 sept2014midsemGopi Saiteja This document contains a 30 question mid-semester exam for a data structures and algorithms course. The exam covers topics like asymptotic analysis, sorting algorithms, hashing, binary search trees, and recursion. It provides multiple choice questions to test understanding of algorithm time complexities, worst-case inputs, and recursive functions. Students are instructed to attempt all questions in the 2 hour time limit and notify the proctor if any electronic devices other than calculators are used.
Skiena algorithm 2007 lecture15 backtracing



Skiena algorithm 2007 lecture15 backtracingzukun This document discusses backtracking algorithms and provides examples for solving problems using backtracking, including:
1) Generating all subsets and permutations of a set using backtracking.
2) The eight queens problem, which can be solved using a backtracking algorithm that places queens on a chessboard one by one while checking for threats.
3) Key components of backtracking algorithms including candidate construction, checking for solutions, and pruning search spaces for efficiency.
Definite Integrals 8/ Integration by Parts



Definite Integrals 8/ Integration by PartsLakshmikanta Satapathy JEE Mathematics/ Lakshmikanta Satapathy/ Definite integrals part 8/ JEE question on definite integral involving integration by parts solved with complete explanation
CppConcurrencyInAction - Chapter07



CppConcurrencyInAction - Chapter07DooSeon Choi This document discusses the implementation of a lock-free queue in C++. It begins with an overview of blocking vs non-blocking behavior and synchronization primitives like mutexes. It then presents the implementation of a single-producer, single-consumer lock-free queue using atomic operations. It shows how push and pop operations are performed concurrently without locking by atomically updating shared queue pointers. It also discusses techniques like helping other threads complete operations to ensure lock-free progress.
Lec8



Lec8Anjneya Varshney The document discusses ordered dictionaries and binary search trees (BSTs). It describes how to implement ordered dictionaries using BSTs to support operations like minimum, maximum, predecessor, and successor in logarithmic time. The key aspects are:
1) BSTs allow searching, minimum, maximum, predecessor, and successor operations in O(h) time where h is the height of the tree.
2) Insertion and deletion in a BST takes O(h) time in the worst case, as repeatedly inserting keys in ascending or descending order yields a skewed tree of height n for n nodes.
3) Search works by comparing the search key to the root node's key, and recursively searching the left or right
Pert 05 aplikasi clustering



Pert 05 aplikasi clusteringaiiniR This document provides an overview of clustering techniques including k-means clustering, expectation maximization algorithms, and spectral clustering. It discusses how k-means clustering works by initializing random cluster centers, assigning data points to the closest centers, and adjusting the centers iteratively. Expectation maximization is presented as a way to learn the parameters of a Gaussian mixture model to cluster data. Finally, applications of clustering like document clustering using mixture models are briefly described.
5.3 dynamic programming



5.3 dynamic programmingKrish_ver2 Dynamic programming is a technique for solving problems with overlapping subproblems and optimal substructure. It works by breaking problems down into smaller subproblems and storing the results in a table to avoid recomputing them. Examples where it can be applied include the knapsack problem, longest common subsequence, and computing Fibonacci numbers efficiently through bottom-up iteration rather than top-down recursion. The technique involves setting up recurrences relating larger instances to smaller ones, solving the smallest instances, and building up the full solution using the stored results.
On Nets and Meshes



On Nets and MeshesDon Sheehy What is the difference between a mesh and a net?
What is the difference between a metric space epsilon-net and a range space epsilon-net?
What is the difference between geometric divide-and-conquer and combinatorial divide-and-conquer?
In this talk, I will answer these questions and discuss how these different ideas come together to finally settle the question of how to compute conforming point set meshes in optimal time. The meshing problem is to discretize space into as few pieces as possible and yet still capture the underlying density of the input points. Meshes are fundamental in scientific computing, graphics, and more recently, topological data analysis.
This is joint work with Gary Miller and Todd Phillips
Presentation OCIP2014



Presentation OCIP2014Fabian Froehlich Dynamical models are widely used to describe chemical, physical and biochemical processes. The main challenge for this class of problems is the identification of kinetic parameters from given measurement data, the so called parameter estimation. However, parameters of such models are never exactly determined, due to measurement noise and the limited amount of data, but remain uncertain. This uncertainty can be captured by a probability density over the parameter space. Unfortunately, studying this probability density is often computationally demanding as this requires the repeated simulation of the underlying model. In this talk we will present a novel method for analysis of such probability densities using networks of radial basis functions.
A particular characteristic of radial basis function approximation schemes is meshless nature, which allows for the free choice of sampling nodes. We will show that root lattices have optimality properties and propose a novel algorithm for the generation of lattices restricted to superlevel-sets. Furthermore we introduce an adaptive method for the generation of nodes based on interacting particles.
Numerical examples show that our method can yield an expected L2 approximation error that is several orders of magnitude lower compared to classical approximations. This allows a drastic reduction of sampling points, which in turn facilitates the analysis of uncertainty for problems with high computational complexity.
Further mathematics notes zimsec cambridge zimbabwe



Further mathematics notes zimsec cambridge zimbabweAlpro Further mathematics notes zimsec cambridge zimbabwe advanced level A level
Zimbabwe
Zimsec
cambridge Alpro
[1062BPY12001] Data analysis with R / week 2![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
![[1062BPY12001] Data analysis with R / week 2](https://cdn.slidesharecdn.com/ss_thumbnails/dataanalyzer01-180307063046-thumbnail.jpg?width=560&fit=bounds)
[1062BPY12001] Data analysis with R / week 2Kevin Chun-Hsien Hsu R is a programming language for data analysis and statistics. It allows users to enter commands at the prompt ">" to perform calculations and manipulate numeric and other objects like vectors and matrices. Basic objects in R include numeric, integer, character, complex, and logical values. Vectors are the most basic data structure and can contain elements of the same type. Matrices are two-dimensional vectors that store values in rows and columns. Functions like c(), seq(), and rep() can be used to create, combine and replicate vectors and sequences of values.
Thesis Defence for Doctor of Information Science



Thesis Defence for Doctor of Information ScienceYuma Inoue This document summarizes Yuma Inoue's doctoral thesis defense presentation on permutation set manipulation based on decision diagrams. The presentation covered topics including reversible circuit debugging, cycle-type partitioning of permutations, enumeration of topological orders using rotation-based πDDs, and other applications of permutation decision diagrams (πDDs) and related data structures. It provided examples and outlined Inoue's contributions to algorithms for manipulating and analyzing permutation sets in an efficient manner using decision diagrams.
Nbvtalkatbzaonencryptionpuzzles



NbvtalkatbzaonencryptionpuzzlesNagasuri Bala Venkateswarlu This presentation contains my view on how to use puzzles while teaching Encryption, Security, Forensics to the students
A Generic Algebraic Model for the Analysis of Cryptographic Key Assignment Sc...



A Generic Algebraic Model for the Analysis of Cryptographic Key Assignment Sc...dhruvgairola This document presents an algebraic model for analyzing cryptographic key assignment schemes. It proposes representing keys as elements of a semiring structure and schemes as models with a key structure, security classes partially ordered by a key derivation relation, and an assignment function. Existing schemes like Akl-Taylor are generalized in this framework. Properties like security and key derivation can be formally verified using the theories of the algebraic structure.
Sub1567



Sub1567International Journal of Science and Research (IJSR) This document presents the solution to quadruple Fourier series equations involving heat polynomials. Quadruple series equations are useful for solving four-part boundary value problems in fields like electrostatics and elasticity. The document considers two sets of quadruple series equations, the first kind and second kind, involving heat polynomials of the first and second kind. The solutions are obtained by reducing the problems to simultaneous Fredholm integral equations of the second kind. The specific equations considered and the steps to solve them using operator theory are presented.
Psimd open64 workshop_2012-new



Psimd open64 workshop_2012-newdibyendu_das0708 The document describes experience with partial SIMDization in the Open64 compiler using dynamic programming. It discusses applying partial SIMDization to pack isomorphic instructions into SIMD instructions without fully vectorizing loops. It outlines applying a dynamic programming approach based on the Barik-Zhao-Sarkar algorithm to choose optimal SIMD tile combinations. Initial results show applying this to a hot loop in GROMACS was able to SIMDize over 88% of operations, demonstrating the potential of the technique.
Viewers also liked (20)
Binary tree



Binary treeRajendran This document discusses binary trees. It defines a binary tree as a structure containing nodes with two self-referenced fields - a left reference and a right reference. Each node can have at most two child nodes. It provides examples of common binary tree terminology like root, internal nodes, leaves, siblings, depth, and height. It also describes different ways to represent binary trees using arrays or links and their tradeoffs. Complete binary trees are discussed as an optimal structure with height proportional to log of number of nodes.
Introduction to Data structure & Algorithms - Sethuonline.com | Sathyabama Un...



Introduction to Data structure & Algorithms - Sethuonline.com | Sathyabama Un...sethuraman R The document discusses data structures and algorithms. It provides an overview of binary trees, binary search trees, and their traversals. It then discusses graphs and poses questions related to binary trees, binary search tree traversals, and graphs.
Binary tree



Binary treeVanitha Chandru This document discusses binary trees and various tree traversal algorithms. It defines what a binary tree is, including nodes, roots, leaves, and siblings. It explains different types of binary tree traversals including preorder, inorder, postorder, and level order. Pseudocode is provided for algorithms to perform inorder, preorder, and postorder traversals on a binary tree. Advantages of using trees are also listed.
Data structures



Data structuresIIUI Here are pseudocodes for the 3 important binary tree operations:
Insertion:
Function Insert(root, key):
If root is null:
Create new node with key
Return new node
If key < root's key:
root.left = Insert(root.left, key)
Else If key > root's key:
root.right = Insert(root.right, key)
Return root
Deletion:
Function Delete(root, key):
If root is null: return null
If key < root's key:
root.left = Delete(root.left, key)
Else If key > root's key:
root.right = Delete(root.right
Hash table



Hash tableRajendran This document discusses hashing techniques for implementing symbol tables. It begins by reviewing the motivation for symbol tables in compilers and describing the basic operations of search, insertion and deletion that a hash table aims to support efficiently. It then discusses direct addressing and its limitations when key ranges are large. The concept of a hash function is introduced to map keys to a smaller range to enable direct addressing. Collision resolution techniques of chaining and open addressing are covered. Analysis of expected costs for different operations on chaining hash tables is provided. Various hash functions are described including division and multiplication methods, and the importance of choosing a hash function to distribute keys uniformly is discussed. The document concludes by mentioning universal hashing as a technique to randomize the hash function
C++ Pointers



C++ PointersChaand Sheikh This document discusses pointers in C++. It defines pointers as variables that store memory addresses and uses the address of (&) and indirection/dereference (*) operators. It provides several examples demonstrating how to declare pointer variables, assign the addresses of non-pointer variables to pointers, and use pointers to access and modify variable values indirectly through memory addresses. Key points covered include declaring pointer data types, assigning addresses to pointers using &, accessing values at addresses using *, and chaining pointers by assigning the address of one pointer to another pointer.
Problem tree



Problem treeJenny Catherine Late return of feedback from lecturers was demoralizing students and causing frustration, poor NSS results, and some students considering dropping out. The causes included lecturers' busy schedules, the issue not being raised by course reps, academics not seeing it as a priority, and no monitoring of timescales. Potential solutions included setting targets for admin staff and course reps raising the issue to get academics more supported in meeting deadlines, informing students of any delays, and monitoring progress with university departments. This could lead to higher marks for students as they learn from feedback and improve motivation, retention, and NSS scores.
Chapter04 -- network protocols



Chapter04 -- network protocolsRaja Waseem Akhtar The document summarizes key network protocols including TCP/IP, IPX/SPX, NetBIOS, and AppleTalk. It describes the layers of the TCP/IP protocol suite and how they correspond to the OSI model. It also discusses important TCP/IP protocols like TCP, IP, UDP, ICMP, and ARP as well as addressing schemes, dynamic host configuration protocol (DHCP), and port numbers.
Unit 6 pointers



Unit 6 pointersGeorge Erfesoglou This document provides an overview of pointers and dynamic arrays in C++. It discusses pointer variables, memory management, pointer arithmetic, array variables as pointers, functions for manipulating strings like strcpy and strcmp, and advanced pointer notation for multi-dimensional arrays. Code examples are provided to demonstrate concepts like passing pointers to functions, dereferencing pointers, pointer arithmetic on arrays, and using string functions. The overall objective is to introduce pointers and how they enable dynamic memory allocation and manipulation of data structures in C++.
Stack Applications



Stack ApplicationsKulachi Hansraj Model School Ashok Vihar Stack applications: Conversion of Infix To Postfix Expression algorithm and evaluation of postfix expression
Applications of stack



Applications of stackeShikshak The document discusses applications of stacks, including reversing strings and lists, Polish notation for mathematical expressions, converting between infix, prefix and postfix notations, evaluating postfix and prefix expressions, recursion, and the Tower of Hanoi problem. Recursion involves defining a function in terms of itself, with a stopping condition. Stacks can be used to remove recursion by saving local variables at each step.
Binary Search Tree in Data Structure



Binary Search Tree in Data StructureDharita Chokshi Content of slide
Tree
Binary tree Implementation
Binary Search Tree
BST Operations
Traversal
Insertion
Deletion
Types of BST
Complexity in BST
Applications of BST
Tree and binary tree



Tree and binary treeZaid Shabbir The document discusses tree data structures and binary search trees. It defines key tree terminology like root, internal and leaf nodes. It explains tree traversal algorithms like preorder, inorder and postorder traversal using recursion and iteration. It also describes operations on binary search trees like searching, inserting and deleting nodes. The complexity of these BST operations is provided. Algorithms to find the inorder predecessor and successor of a node in a BST are presented.
Developing a problem tree



Developing a problem treeNational Centre for Sustainability, Swinburne University of Technology An overview of how to undertake a problem tree analysis as part of the formative evaluation of a project's design. This is taken from the Evaluation Toolbox www.evaluationtoolbox.net.au
Network topology



Network topologylekshmik This document discusses different network topologies including bus, star, ring, and mesh. It describes the key characteristics of each topology such as their physical layout, how data is transmitted, advantages and disadvantages. Hybrid topologies that combine two or more standard topologies are also discussed. The document emphasizes understanding network topologies is essential for designing efficient computer networks and choosing the best option for different network requirements.
Chapter 2 - Operating System Structures



Chapter 2 - Operating System StructuresWayne Jones Jnr The document summarizes key aspects of operating system structures including:
1) Operating systems provide services to users like user interfaces, program execution, I/O, file manipulation and resource allocation. They also ensure efficient system operation through accounting and protection.
2) System calls are the programming interface to OS services, accessed via APIs. Common APIs include Win32, POSIX, and Java.
3) Operating systems can have different structures like layered, modular, microkernel and virtual machine approaches. They are implemented through system programs, boot processes, and configuration for specific hardware.
Operating System 2



Operating System 2tech2click The document discusses operating system structures and design. It covers topics such as system calls, system programs, operating system services, and different operating system designs including monolithic, layered, and microkernel structures. Specifically, it describes how early systems like MS-DOS and UNIX had monolithic structures with limited separation of components, while later designs focused more on modularity, separation of mechanisms and policies, and other principles.
Network topology.ppt



Network topology.pptSiddique Ibrahim The document discusses different network topologies including mesh, star, bus, ring, tree, and hybrid topologies. For each topology, it describes the logical layout, advantages, disadvantages, and examples of applications. Mesh topology has every device connected to every other device but requires a large amount of cabling. Star topology has each device connected to a central hub, requiring less cabling than mesh. Bus topology uses a single backbone that devices connect to via taps. Ring topology passes signals in one direction between devices connected in a closed loop. Tree topology connects multiple star networks. A hybrid uses elements of different topologies under a single backbone. Factors like cost, cable needs, growth and cable type should be considered when choosing a topology
DATA STRUCTURES



DATA STRUCTURESbca2010 This document provides information about Dream Valley College for Girls Centre for Educational Excellence. It includes an index and presentation on data structures covering topics like arrays, linked lists, queues, trees, and graphs. The presentation was presented by Harish Sir and includes definitions, examples, and diagrams to explain each data structure concept.
Hype vs. Reality: The AI Explainer



Hype vs. Reality: The AI ExplainerLuminary Labs Artificial intelligence (AI) is everywhere, promising self-driving cars, medical breakthroughs, and new ways of working. But how do you separate hype from reality? How can your company apply AI to solve real business problems?
Here’s what AI learnings your business should keep in mind for 2017.
Ad
Similar to Datastructure tree (20)
Advanced data structure



Advanced data structureShakil Ahmed A data structure is needed to represent a country with cities connected by bidirectional roads. The data structure will allow finding the longest road between any two cities in the country based on query inputs of two cities. A graph data structure using adjacency lists can model the country, with cities as nodes and roads as edges between nodes labeled with their costs. Queries can then find the longest cost path between two cities using graph traversal algorithms.
19. algorithms and-complexity



19. algorithms and-complexityshowkat27 The document discusses algorithms complexity and data structures efficiency, explaining that algorithm complexity can be measured using asymptotic notation like O(n) or O(n^2) to represent operations scaling linearly or quadratically with input size, and different data structures have varying time efficiency for operations like add, find, and delete.
11 1. multi-dimensional array eng



11 1. multi-dimensional array eng웅식 전 The document discusses multidimensional arrays in C, including two-dimensional and three-dimensional arrays. It explains the syntax for declaring multidimensional arrays and how they are logically and physically stored in memory as one-dimensional arrays. The document also covers passing multidimensional arrays to functions, including type conversions, and initializing multidimensional arrays.
Thinking Functionally In Ruby



Thinking Functionally In RubyRoss Lawley The document discusses functional programming concepts in Ruby. It begins by stating that functional programming and Enumerable methods can be useful in Ruby. It then provides examples of various Enumerable methods like zip, select, partition, map, and inject. It encourages thinking functionally by avoiding side effects, mutating values, and using functional parts of the standard library. The document concludes by suggesting learning a true functional language to further improve functional programming skills.
Programming meeting #8



Programming meeting #8Hideyuki Tabata The document summarizes the key steps in performing a least squares regression analysis on data to calculate the slope and y-intercept of the linear regression line. It discusses defining arrays to store the x and y coordinate data, functions to calculate summations and the sum of x times y for the data, and the formulas to calculate the slope using these summations and the number of data points. It also covers calculating the y-intercept from the slope and summations. The document concludes by asking for any questions and thanking attendees for the meeting.
Clojure for Data Science



Clojure for Data ScienceMike Anderson This document provides an overview of using Clojure for data science. It discusses why Clojure is suitable for data science due to its functional programming capabilities, performance on the JVM, and rich library ecosystem. It introduces core.matrix, a Clojure library that provides multi-dimensional array programming functionality through Clojure protocols. The document covers core.matrix concepts like array creation and manipulation, element-wise operations, broadcasting, and optional support for mutability. It also discusses core.matrix implementation details like the performance benefits of using Clojure protocols.
R



Rexsuns R is a programming language and software environment for statistical analysis and graphics. It allows users to analyze data, create visualizations, and perform statistical tests. Common R commands include functions to get and set the working directory, list objects in the workspace, remove objects, view and set options, save and load the command history, and save and load the entire workspace. R supports various data structures like vectors, arrays, matrices, data frames, and lists to store and manipulate different types of data. Data can be input into R from files, databases, and Excel spreadsheets. Graphs and visualizations created in R can be exported to file formats like PNG, JPEG, PDF and others.
pradeepbishtLecture13 div conq



pradeepbishtLecture13 div conqPradeep Bisht (1) The document discusses algorithms analysis using the divide and conquer paradigm and the master theorem. It analyzes the running times of binary search, merge sort, and quicksort using the master theorem.
(2) For quicksort, it shows that picking a random pivot element leads to an expected running time of O(n log n) since it balances the problem sizes on both sides of the pivot in each recursive call.
(3) It ultimately derives that the expected running time of quicksort is O(n log n).
Elementary Linear Algebra 5th Edition Larson Solutions Manual



Elementary Linear Algebra 5th Edition Larson Solutions Manualzuxigytix Full download : https://goo.gl/p9St6K
Elementary Linear Algebra 5th Edition Larson Solutions Manual
Basic operations by novi reandy sasmita



Basic operations by novi reandy sasmitabeasiswa - R can be used as a calculator to perform basic math operations like addition, subtraction, multiplication, division, exponents, logarithms, and trigonometric functions. It handles complex numbers and vectors.
- Matrices can be created using cbind() and rbind() functions. Elements are extracted using row and column indices. Common operations include addition, subtraction, scalar and element-wise multiplication on matrices.
- Eigenvalues and eigenvectors of a matrix can be computed using the eigen() function. The uniroot() function finds the root of a univariate function by calling a user-defined function.
Python Puzzlers



Python PuzzlersTendayi Mawushe Following a game show format made popular by Joshua Bloch and Neal Gafter's Java Puzzlers this presentation intends to both entertain and inform. Snippets of Python code the whose behaviour is not entirely obvious are shown, the audience will then be asked to pick from a number of options what the behaviour of the program is. The correct and sometimes non-intuitive answer will then be given along with a brief explanation of the idea the puzzle exposes. Only a modest working knowledge of the Python language is required to understand the puzzles, but the puzzles may also entertain the more experienced Python programmer.
Data Structure Lecture Array and Recursion.pdf



Data Structure Lecture Array and Recursion.pdfokokji4201 Data Structure in java -Array and Recursion
Big datacourse



Big datacourseMassimiliano Ruocco The document outlines an introduction to analyzing and visualizing geo-data in R. It discusses exploring the structure of spatially distributed point data through point process statistics like the Complete Spatial Randomness test and Ripley's K-function. It also covers visualizing maps and point patterns with packages like maps, ggmap, rworldmap, and ggplot2. The document provides examples of mapping different regions, geocoding location data, and plotting point patterns on maps in R.
Segment tree



Segment treeShakil Ahmed A segment tree is a data structure that allows for efficient query and update operations on array intervals in logarithmic time. It represents intervals as nodes in a tree structure, where each node corresponds to an interval. Segment trees allow querying the minimum value in a range in O(log n) time and updating values in O(log n) time. The document provides pseudocode for initializing, updating, and querying a segment tree to solve problems involving finding minimum values over ranges.
Numpy tutorial(final) 20160303



Numpy tutorial(final) 20160303Namgee Lee https://docs.scipy.org/doc/numpy-dev/user/quickstart.html
에 내용 중 Shape Manipulation과 Copies And Views 부분에 대한 발표자료.
array2d.ppt



array2d.pptDeveshDewangan5 Two dimensional arrays allow the storage of tables of values arranged in rows and columns. They are declared with the general form type array_name[row_size][column_size]. Elements are accessed using two indices, the first for the row and second for the column. Elements are stored in memory in row-major order, with contiguous blocks for each row. Dynamic allocation of 2D arrays involves allocating an array of pointers, with each pointer storing the address of a dynamically allocated 1D array for that row.
Algebra and function



Algebra and functionAzlan Ahmad This document contains sample algebra and function questions with answers:
1) It finds the sum of f+g and fg, where f(x)=1/x^2 and g(x)=sqrt(x).
2) It solves an inequality involving rational functions and determines the solution range.
3) It finds the inverse of a 3x3 matrix using the ERO method.
4) It provides answers to additional questions about domains, ranges, function composition, sequences, systems of equations, and classifying number sets.
Algorithms - "Chapter 2 getting started"



Algorithms - "Chapter 2 getting started"Ra'Fat Al-Msie'deen The document discusses insertion sort and its analysis. It begins by providing an overview of insertion sort, describing how it works to sort a sequence by iteratively inserting elements into their sorted position. It then gives pseudocode for insertion sort and works through an example. Next, it analyzes insertion sort's runtime, showing it is O(n^2) in the worst case and O(n) in the best case. The document concludes by introducing the divide and conquer approach for sorting, which will be covered in the next section on merge sort.
Haskellで学ぶ関数型言語



Haskellで学ぶ関数型言語ikdysfm The document describes a Haskell program that translates characters in one string to characters in another string. It defines a translate function that maps characters from the first string (set1) to the corresponding characters in the second string (set2). A translateString function applies the translate function to a given string, and the main function gets the set1 and set2 strings from arguments, reads stdin, applies translateString, and writes the result to stdout, catching any errors.
Ad
Recently uploaded (20)
SCI BIZ TECH QUIZ (OPEN) PRELIMS XTASY 2025.pptx



SCI BIZ TECH QUIZ (OPEN) PRELIMS XTASY 2025.pptxRonisha Das SCI BIZ TECH QUIZ (OPEN) PRELIMS - XTASY 2025
YSPH VMOC Special Report - Measles Outbreak Southwest US 5-3-2025.pptx



YSPH VMOC Special Report - Measles Outbreak Southwest US 5-3-2025.pptxYale School of Public Health - The Virtual Medical Operations Center (VMOC) A measles outbreak originating in West Texas has been linked to confirmed cases in New Mexico, with additional cases reported in Oklahoma and Kansas. The current case count is 817 from Texas, New Mexico, Oklahoma, and Kansas. 97 individuals have required hospitalization, and 3 deaths, 2 children in Texas and one adult in New Mexico. These fatalities mark the first measles-related deaths in the United States since 2015 and the first pediatric measles death since 2003.
The YSPH Virtual Medical Operations Center Briefs (VMOC) were created as a service-learning project by faculty and graduate students at the Yale School of Public Health in response to the 2010 Haiti Earthquake. Each year, the VMOC Briefs are produced by students enrolled in Environmental Health Science Course 581 - Public Health Emergencies: Disaster Planning and Response. These briefs compile diverse information sources – including status reports, maps, news articles, and web content– into a single, easily digestible document that can be widely shared and used interactively. Key features of this report include:
- Comprehensive Overview: Provides situation updates, maps, relevant news, and web resources.
- Accessibility: Designed for easy reading, wide distribution, and interactive use.
- Collaboration: The “unlocked" format enables other responders to share, copy, and adapt seamlessly. The students learn by doing, quickly discovering how and where to find critical information and presenting it in an easily understood manner.
CURRENT CASE COUNT: 817 (As of 05/3/2025)
• Texas: 688 (+20)(62% of these cases are in Gaines County).
• New Mexico: 67 (+1 )(92.4% of the cases are from Eddy County)
• Oklahoma: 16 (+1)
• Kansas: 46 (32% of the cases are from Gray County)
HOSPITALIZATIONS: 97 (+2)
• Texas: 89 (+2) - This is 13.02% of all TX cases.
• New Mexico: 7 - This is 10.6% of all NM cases.
• Kansas: 1 - This is 2.7% of all KS cases.
DEATHS: 3
• Texas: 2 – This is 0.31% of all cases
• New Mexico: 1 – This is 1.54% of all cases
US NATIONAL CASE COUNT: 967 (Confirmed and suspected):
INTERNATIONAL SPREAD (As of 4/2/2025)
• Mexico – 865 (+58)
‒Chihuahua, Mexico: 844 (+58) cases, 3 hospitalizations, 1 fatality
• Canada: 1531 (+270) (This reflects Ontario's Outbreak, which began 11/24)
‒Ontario, Canada – 1243 (+223) cases, 84 hospitalizations.
• Europe: 6,814
Multi-currency in odoo accounting and Update exchange rates automatically in ...



Multi-currency in odoo accounting and Update exchange rates automatically in ...Celine George Most business transactions use the currencies of several countries for financial operations. For global transactions, multi-currency management is essential for enabling international trade.
To study the nervous system of insect.pptx



To study the nervous system of insect.pptxArshad Shaikh The *nervous system of insects* is a complex network of nerve cells (neurons) and supporting cells that process and transmit information. Here's an overview:
Structure
1. *Brain*: The insect brain is a complex structure that processes sensory information, controls behavior, and integrates information.
2. *Ventral nerve cord*: A chain of ganglia (nerve clusters) that runs along the insect's body, controlling movement and sensory processing.
3. *Peripheral nervous system*: Nerves that connect the central nervous system to sensory organs and muscles.
Functions
1. *Sensory processing*: Insects can detect and respond to various stimuli, such as light, sound, touch, taste, and smell.
2. *Motor control*: The nervous system controls movement, including walking, flying, and feeding.
3. *Behavioral responThe *nervous system of insects* is a complex network of nerve cells (neurons) and supporting cells that process and transmit information. Here's an overview:
Structure
1. *Brain*: The insect brain is a complex structure that processes sensory information, controls behavior, and integrates information.
2. *Ventral nerve cord*: A chain of ganglia (nerve clusters) that runs along the insect's body, controlling movement and sensory processing.
3. *Peripheral nervous system*: Nerves that connect the central nervous system to sensory organs and muscles.
Functions
1. *Sensory processing*: Insects can detect and respond to various stimuli, such as light, sound, touch, taste, and smell.
2. *Motor control*: The nervous system controls movement, including walking, flying, and feeding.
3. *Behavioral responses*: Insects can exhibit complex behaviors, such as mating, foraging, and social interactions.
Characteristics
1. *Decentralized*: Insect nervous systems have some autonomy in different body parts.
2. *Specialized*: Different parts of the nervous system are specialized for specific functions.
3. *Efficient*: Insect nervous systems are highly efficient, allowing for rapid processing and response to stimuli.
The insect nervous system is a remarkable example of evolutionary adaptation, enabling insects to thrive in diverse environments.
The insect nervous system is a remarkable example of evolutionary adaptation, enabling insects to thrive
Exploring-Substances-Acidic-Basic-and-Neutral.pdf



Exploring-Substances-Acidic-Basic-and-Neutral.pdfSandeep Swamy Exploring Substances:
Acidic, Basic, and
Neutral
Welcome to the fascinating world of acids and bases! Join siblings Ashwin and
Keerthi as they explore the colorful world of substances at their school's
National Science Day fair. Their adventure begins with a mysterious white paper
that reveals hidden messages when sprayed with a special liquid.
In this presentation, we'll discover how different substances can be classified as
acidic, basic, or neutral. We'll explore natural indicators like litmus, red rose
extract, and turmeric that help us identify these substances through color
changes. We'll also learn about neutralization reactions and their applications in
our daily lives.
by sandeep swamy
How to Set warnings for invoicing specific customers in odoo



How to Set warnings for invoicing specific customers in odooCeline George Odoo 16 offers a powerful platform for managing sales documents and invoicing efficiently. One of its standout features is the ability to set warnings and block messages for specific customers during the invoicing process.
UNIT 3 NATIONAL HEALTH PROGRAMMEE. SOCIAL AND PREVENTIVE PHARMACY



UNIT 3 NATIONAL HEALTH PROGRAMMEE. SOCIAL AND PREVENTIVE PHARMACYDR.PRISCILLA MARY J NATIONAL HEALTH PROGRAMMEE
Metamorphosis: Life's Transformative Journey



Metamorphosis: Life's Transformative JourneyArshad Shaikh *Metamorphosis* is a biological process where an animal undergoes a dramatic transformation from a juvenile or larval stage to a adult stage, often involving significant changes in form and structure. This process is commonly seen in insects, amphibians, and some other animals.
Social Problem-Unemployment .pptx notes for Physiotherapy Students



Social Problem-Unemployment .pptx notes for Physiotherapy StudentsDrNidhiAgarwal Unemployment is a major social problem, by which not only rural population have suffered but also urban population are suffered while they are literate having good qualification.The evil consequences like poverty, frustration, revolution
result in crimes and social disorganization. Therefore, it is
necessary that all efforts be made to have maximum.
employment facilities. The Government of India has already
announced that the question of payment of unemployment
allowance cannot be considered in India
Niamh Lucey, Mary Dunne. Health Sciences Libraries Group (LAI). Lighting the ...



Niamh Lucey, Mary Dunne. Health Sciences Libraries Group (LAI). Lighting the ...Library Association of Ireland
The ever evoilving world of science /7th class science curiosity /samyans aca...



The ever evoilving world of science /7th class science curiosity /samyans aca...Sandeep Swamy The Ever-Evolving World of
Science
Welcome to Grade 7 Science4not just a textbook with facts, but an invitation to
question, experiment, and explore the beautiful world we live in. From tiny cells
inside a leaf to the movement of celestial bodies, from household materials to
underground water flows, this journey will challenge your thinking and expand
your knowledge.
Notice something special about this book? The page numbers follow the playful
flight of a butterfly and a soaring paper plane! Just as these objects take flight,
learning soars when curiosity leads the way. Simple observations, like paper
planes, have inspired scientific explorations throughout history.
Presentation of the MIPLM subject matter expert Erdem Kaya



Presentation of the MIPLM subject matter expert Erdem KayaMIPLM Presentation of the MIPLM subject matter expert Erdem Kaya
pulse ppt.pptx Types of pulse , characteristics of pulse , Alteration of pulse



pulse ppt.pptx Types of pulse , characteristics of pulse , Alteration of pulsesushreesangita003 what is pulse ?
Purpose
physiology and Regulation of pulse
Characteristics of pulse
factors affecting pulse
Sites of pulse
Alteration of pulse
for BSC Nursing 1st semester
for Gnm Nursing 1st year
Students .
vitalsign
Unit 6_Introduction_Phishing_Password Cracking.pdf



Unit 6_Introduction_Phishing_Password Cracking.pdfKanchanPatil34 Initial stages of attacks, Phishing, Password Cracking, guidelines to prevent password attacks, Strong password, weak password,
Odoo Inventory Rules and Routes v17 - Odoo Slides



Odoo Inventory Rules and Routes v17 - Odoo SlidesCeline George Odoo's inventory management system is highly flexible and powerful, allowing businesses to efficiently manage their stock operations through the use of Rules and Routes.
Quality Contril Analysis of Containers.pdf



Quality Contril Analysis of Containers.pdfDr. Bindiya Chauhan Quality control test for containers, rubber closures and secondary packing materials.
Ultimate VMware 2V0-11.25 Exam Dumps for Exam Success



Ultimate VMware 2V0-11.25 Exam Dumps for Exam SuccessMark Soia Boost your chances of passing the 2V0-11.25 exam with CertsExpert reliable exam dumps. Prepare effectively and ace the VMware certification on your first try
Quality dumps. Trusted results. — Visit CertsExpert Now: https://www.certsexpert.com/2V0-11.25-pdf-questions.html
LDMMIA Reiki Master Spring 2025 Mini Updates



LDMMIA Reiki Master Spring 2025 Mini UpdatesLDM Mia eStudios As of Mid to April Ending, I am building a new Reiki-Yoga Series. No worries, they are free workshops. So far, I have 3 presentations so its a gradual process. If interested visit: https://www.slideshare.net/YogaPrincess
https://ldmchapels.weebly.com
Blessings and Happy Spring. We are hitting Mid Season.
How to Manage Opening & Closing Controls in Odoo 17 POS



How to Manage Opening & Closing Controls in Odoo 17 POSCeline George In Odoo 17 Point of Sale, the opening and closing controls are key for cash management. At the start of a shift, cashiers log in and enter the starting cash amount, marking the beginning of financial tracking. Throughout the shift, every transaction is recorded, creating an audit trail.
YSPH VMOC Special Report - Measles Outbreak Southwest US 5-3-2025.pptx



YSPH VMOC Special Report - Measles Outbreak Southwest US 5-3-2025.pptxYale School of Public Health - The Virtual Medical Operations Center (VMOC)
Niamh Lucey, Mary Dunne. Health Sciences Libraries Group (LAI). Lighting the ...



Niamh Lucey, Mary Dunne. Health Sciences Libraries Group (LAI). Lighting the ...Library Association of Ireland
Datastructure tree
- 1. Data Structure - Tree
- 2. Binary Index Tree Problem: Give an array A[1], A[2] , … , A[n] and m queries as follows (n, m ~ 10^6) type 1: add x to A[k] (1 <= k <= n) type 2: calculate sum of interval [l , r] of array
- 3. Binary Index Tree Naive solution type 1: O(1) type 2: O(n) → time complexity O(mn) m, n ~ 10^6 → impossible
- 4. Binary Index Tree • Fenwick Tree (also called BIT) • Peter M. Fenwick, "A New Data Structure for Cumulative Frequency Tables" (1994) • Support fast operations on array
- 5. Binary Index Tree Support two operations in O(log(n)) [1] Add value x to an element A[k] A[k] → A[k] + x [2] Return sum of prefix k prefix[k] = A[1] + A[2] + ... + A[k]
- 6. Binary Index Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
- 7. Binary Index Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] add to A[1]
- 8. Binary Index Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] add to A[3]
- 9. Binary Index Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] get prefix[3]
- 10. Binary Index Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] get prefix[7]
- 11. Binary Index Tree • Observation Express k as binary number 1→1 2→10 3→11 4→100 5→101 6→110 7→111 8→1000 Pay attention to number of ‘0’ at the end add operation : k → k + (last bit 1 of k) get operation: k → k – (last bit 1 of k)
- 12. Binary Index Tree [1] Add value to element at position index void add(int index, int value) { for (int i = index; i <= size; i += i & -i) { bit[index] += value; } } → O(log(n))
- 13. Binary Index Tree [1] Get sum of elements from postion 1 -> index int get(int index) { int ans = 0; for (int i = index; i > 0; i -= i & -i) { ans += bit[i]; } return ans; } → O(log(n))
- 14. Binary Index Tree • Total time complexity for m queries Naive: O(mn) → BIT: O(mlog(n)) Amazing 🎉 Bravo 👏 Let see some practical uses of BIT
- 15. Count Inverse Pair Give an array A[1], A[2], ..., A[n], n ~ 10^6 Count number of pair (A[i], A[j]) such that i < j and A[i] > A[j] Naive solution: scan all pairs (A[i], A[j]) , i < j → time complexity O(n^2) → impossible
- 16. Another solution • Using technique of merge sort Divide and conquer (A[1], ... ,A[n]) → (A[1], ... ,A[n/2]) ∨ (A[n/2+1], ..., A[n]) solve(A[1], ... ,A[n/2]) solve(A[n/2+1], ..., A[n]) merge(A[1], ... ,A[n/2] ∨A[n/2+1], ..., A[n]) Time complexity O(nlog(n))
- 17. Using BIT Suppose 1 <= A[1], A[2], ..., A[n] <= n and are integer. If not, we can make a mapping by sort because we only consider about magnitude correlation ex: (1.2, -9.8, 5.0, 3.4) → (2, 1, 4, 3)
- 18. Using BIT int ans = 0; void solve() { for (int i = 1; i <= n; ++i) { ans += i - 1 - get(a[i]); add(a[i], 1); } }
- 19. D-Query Problem: Given an array n number A[1], A[2], ..., A[n] and m queries as follows (n ~ 3x10^4, m ~ 2x10^5, 1 <= A[i] <= 10^6) query : (l, r) return number of distinct elements in subarray A[l], A[l+1], ..., A[r] → Cann’t solve with naive solution
- 20. D-Query Solution with BIT [1] Sort queries based on right value (l1,r1), (l2,r2), ..., (lm, rm) → r1 <= r2 <= ... <= rm [2] Go through array from left to right, using index[] to save last position each value → index[x] is last position of x in current array
- 21. D-Query Solution with BIT [3] Current value a[i] *if index[a[i]] != i then update index[a[i]] = i *if there is some r[j] = i then calculate answer and go to next queries *else go to next postion [4] Print answers
- 22. D-Query struct queries { int l, r, id; }; bool comp(queries x, queries y) { return x.r < y.r; } sort(queries.begin(), queries.end(), comp);
- 23. D-Query for (int j = 0, i = 1; j < num_queries;) { if (index[a[i]] != i) { bit.add(index[a[i]], -1); index[a[i]] = i; bit.add(i, 1); } if (queries[j].r == i) { ans[queries[j].id] += bit.get(i) – bit.get(queries[j].l – 1); j++; } else i++; }
- 24. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] index[1] = -1 index[2] = -1 index[3] = -1 3 queries [2, 4] [1, 5] [3, 5]
- 25. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] 3 queries [2, 4] [1, 5] [3, 5] index[1] = 1 → bit.add(-1, -1) , bit.add(1, 1) index[2] = -1 index[3] = -1
- 26. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] 3 queries [2, 4] [1, 5] [3, 5] index[1] = 2 → bit.add(1, -1) , bit.add(2, 1) index[2] = -1 index[3] = -1
- 27. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] 3 queries [2, 4] [1, 5] [3, 5] index[1] = 2 index[2] = 3 → bit.add(-1, -1) , bit.add(3, 1) index[3] = -1
- 28. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] 3 queries [2, 4] [1, 5] [3, 5] index[1] = 4 → bit.add(2, -1) , bit.add(4, 1) → ans[2] = bit.get(4) – bit.get(1) index[2] = 3 index[3] = -1
- 29. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] 3 queries [2, 4] [1, 5] [3, 5] index[1] = 4 index[2] = 3 index[3] = 5 → bit.add(-1, -1) , bit.add(5, 1) → ans[1] = bit.get(5) – bit.get(0)
- 30. D-Query 1 1 2 1 3 3 queries [1, 5] [2, 4] [3, 5] 3 queries [2, 4] [1, 5] [3, 5] index[1] = 4 index[2] = 3 index[3] = 5 → ans[3] = bit.get(5) – bit.get(2)
- 31. Segment Tree Problem: Give an array A[1], A[2], ..., A[n] and m queries as follows (n, m ~ 10^6) type 1: add x to A[k] type 2: calculate max, min on interval [l, r]
- 32. Segment Tree Naive solution Same as previous one type 1: O(1) type 2: O(n) → time complexity O(mn) → impossible when n, m ~ 10^6
- 33. Segment Tree • Discoverd by Bentley in 1977 in “Solution to Klee’s rectangle problems” • Support fast operations on interval
- 34. Segment Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
- 35. Segment Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] add to A[2]
- 36. Segment Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] add to A[6]
- 37. Segment Tree A[1] + A[2] + A[3] + A[4] A[5] + A[6] + A[7] + A[8] A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] A[1] + A[2] A[3] + A[4] A[5] + A[6] A[7] + A[8] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8] get max on [3,8]
- 38. Segment Tree • Each node of tree is an interval [l, r] • If l < r, it has two children [l, m] and [m+1, r] with m = (l + r)/2 • Length of array is n → total node of tree is 1 + 2 + 4 + ... + 2^k = 2^(k+1) – 1 k is smallest number such that 2^k >= n → total node <= 4n, memory O(n)
- 39. Segment Tree (1 , 4) (5 , 8) (1 , 8) (1 , 2) (3 , 4) (5 , 6) (7 , 8) (1 , 1) (2 , 2) (3 , 3) (4 , 4) (5 , 5) (6 , 6) (7 , 7) (8 , 8) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
- 40. Segment Tree *Initialize: build(1, 1, n) void build(int node, int l, int r) { if (l == r) {sg[node] = A[l]; return;} int m = (l + r)/2; build(node * 2, l, m); build(node * 2 + 1, m + 1, r); sg[node] = max(sg[node * 2], sg[node * 2 + 1]); } → O(n)
- 41. Segment Tree *Add x to A[k]: update(1, 1, n, k, x) void update(int node, int l, int r, int k, int x) { if (l == r) {sg[node] = A[k] + x; return;} int m = (l + r)/2; if (m >= k) update(node * 2, l, m, k, x); else update(node * 2 + 1, m + 1, r, k, x); sg[node] = max(sg[node * 2], sg[node * 2 + 1]); } → O(log(n))
- 42. Segment Tree *Get max on interval [l,r]: query(1, 1, n, l, r) int query(int node, int i, int j, int l, int r) { if (l<=i && j <= r) {return sg[node];} int m = (i + j)/2; if (m >= r) return query(node * 2, i, m, l, r); else if (m < l) return query(node * 2 + 1, m + 1, j, l, r); else return max(query(node * 2, i, m, l, r), query(node * 2 + 1, m + 1, j, l, r)); } → O(log(n))
- 43. Treap • What is treap? • Combination of tree and heap → treap • Height of tree is proportional to log(n) with high probability (n is number of keys in tree) • Each node has two attributes: key and priority number • Key is binary-tree ordered, priority number is heap ordered
- 44. Treap • Support search, insertion, deletion, merge and split • When insert a key, priority number is randomed → time complexity of all operations are expected O(log(n))
- 46. Treap typedef struct node { int val, pri, cnt, sum; struct node * child[2]; node(int v, int p) : val(v), pri(p), cnt(1), sum(v) { child[0] = child[1] = NULL; } } * node_t;
- 47. Treap int count(node_t t) { return t ? t->cnt : 0; } int sum(node_t t) { return t ? t->sum : 0; } node_t update(node_t t) { t->cnt = count(t->child[0]) + count(t->child[1]) + 1; t->sum = sum(t->child[0]) + sum(t->child[1]) + t->val; return t; }
- 48. Insertion • Randomize a priority number • Insert node to tree as binary search tree • Rotate tree until priority number is heap- ordered • Expected time complexity: O(log(n))
- 52. Rotation node_t rotate(node_t t, int b) { node_t s = t->child[b]; t->child[1-b] = s->child[b]; s->child[b] = t; update(t); update(s); return s; }
- 54. Deletion • Find node as binary search tree • Bring node to leaf and delete • Rotate tree until priority number is heap- ordered • Expected time complexity: O(log(n))
- 59. Merge-Split • Merge two treaps into one • Split treap into two treaps • Implement indirectly by insertion and deletion • Implement directly • Expected time complexity: O(log(n))
- 60. Merge A B C D a b
- 62. Merge node_t merge(node_t l, node_t r) { if (!l || !r) return !l ? r : l; if (l->pri > r->pri) { l->child[1] = merge(l->child[1], r); return update(l); } else { r->child[0] = merge(l, r->child[0]); return update(r); } }
- 63. Merge → Insert T val pri merge(treap T, node x)

