![TESTING
Method
Generate a random data set of n elements
with values ranging between 0 and 50.
Then trim values between 25 and
25+epsilon on the x and y axis. This
should give us at least 4 clusters.
Run the each algorithm 100 times on each
data set and record the average running
time for each algorithm and the average
accuracy of Randomized DBSCAN.
Repeat for 1000, 2000, 3000, 4000 initial
points (before trim)
Repeat for eps = [1:10]
0
5
10
15
20
25
30
0 1,000 2,000 3,000 4,000 5,000
RunTime(s)
Number of Elements (N)
Complexity Analysis
DBSCAN t
eps=1
eps=2
eps=3
eps=4
eps=5
eps=6
eps=7
eps=8
eps=9
eps=10
Poly. (DBSCAN t)
Poly. (eps=2)
Linear (eps=10)](https://image.slidesharecdn.com/0531c85b-92a8-4a8d-8d2e-5097617e7402-150613174508-lva1-app6891/85/DBSCAN-2014_11_25-06_21_12-UTC-16-320.jpg)
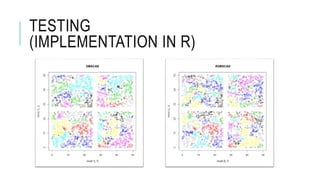
DBSCAN (2014_11_25 06_21_12 UTC)
- 1. DBSCAN Density-based spatial clustering of applications with noise By: Cory Cook
- 2. CLUSTER ANALYSIS The goal of cluster analysis is to associate data elements with each other based on some relevant element distance analysis. Each ‘cluster’ will represent elements that are part of a disjoint set in the superset. IMAGE REFERENCE: HTTP://CA- SCIENCE7.WIKISPACES.COM/FILE/VIEW/CLUSTER_ANALYSIS.GIF/343040618/CLUSTER_ANALYSIS.GIF
- 3. DBSCAN Originally proposed by Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu in 1996 Allows the user to perform data cluster analysis without specifying the number of clusters before hand Can find clusters of arbitrary shape and size (albeit uniform density) Is noise and outlier resistant Requires only a number of minimum points and neighborhood distance as input parameters.
- 4. DBSCAN ALGORITHMDBSCAN(D, eps, MinPts) C = 0 for each unvisited point P in dataset D mark P as visited NeighborPts = regionQuery(P, eps) if sizeof(NeighborPts) < MinPts mark P as NOISE else C = next cluster expandCluster(P, NeighborPts, C, eps, MinPts) expandCluster(P, NeighborPts, C, eps, MinPts) add P to cluster C for each point P' in NeighborPts if P' is not visited mark P' as visited NeighborPts' = regionQuery(P', eps) if sizeof(NeighborPts') >= MinPts NeighborPts = NeighborPts joined with NeighborPts' if P' is not yet member of any cluster add P' to cluster C regionQuery(P, eps) return all points within P's eps-neighborhood (including P) IMAGE REFERENCE: HTTP://UPLOAD.WIKIMEDIA.ORG/WIKIPEDIA/COMMONS/A/AF/DBSCAN-ILLUSTRATION.SVG
- 5. DBSCAN COMPLEXITY Complexity is in 𝑂(𝑛) for the main algorithm and additional complexity for the region query. Resulting in 𝑂(𝑛2 ) for the entire algorithm. The algorithm “visits” each point and determines the neighbors for that point. Determining neighbors depends on the algorithm used for region query; however, it is most likely in 𝑂(𝑛) as the distance will need to be queried between each point and the point in question.
- 6. DBSCAN IMPROVEMENTS It is possible to improve the time complexity of the algorithm by utilizing an indexing structure to query neighborhoods in 𝑂 log 𝑛 ; however, the structure would require 𝑂 𝑛2 space to store the indices. A majority of attempts to improve DBSCAN involve overcoming the statistical limitations, such as varying density in the data set.
- 8. RANDOMIZED DBSCAN • Instead of analyzing every single point in the neighborhood we can select a random subset of points to analyze. • Randomizing ensures that the selection will roughly represent the entire distribution. • Selecting on an order fewer points to analyze will result in an improvement in the overall complexity of the algorithm. • Effectiveness of this approach is largely determined by the data density relative to the epsilon distance. Edge cases will not be analyzed by DBSCAN as they do not meet the minimum points requirement. Any of the points in the epsilon-neighborhood will share many of the same points. IMAGE REFERENCE: HTTP://I.STACK.IMGUR.COM/SU734.JPG
- 9. ALGORITHM expandCluster(P, NeighborPts, C, eps, MinPts, k) add P to cluster C for each point P' in NeighborPts if P' is not visited mark P' as visited NeighborPts' = regionQuery(P', eps) if sizeof(NeighborPts') >= MinPts NeighborPts’ = maximumCoercion(NeighbotPts’, k) NeighborPts = NeighborPts joined with NeighborPts' if P' is not yet member of any cluster add P' to cluster C maximumCoercion(Pts, k) visited <- number of visited points in Pts points <- select max(sizeof(Pts) – k – visited, 0) elements from Pts for each point P’ in points mark P’ as visited return Pts The algorithm is the same as DBSCAN with a slight modification. We force a maximum number of points to continue analysis. If there are more points in the neighborhood than the maximum then we mark them as visited. Marking points as visited allows us to “skip” them by not performing a region query for those points. This effectively reduces the overall complexity.
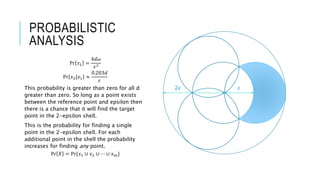
- 10. PROBABILISTIC ANALYSIS For now, assume uniform distribution and two dimensions. The probability of selecting a point 𝑥1 distance d from the reference point is defined as Pr 𝑥1 = 𝑑−𝜔 𝑑+𝜔 2𝜋𝑟 𝑑𝑟 𝜋𝜖2 ; 0 ≤ 𝑑 ≤ 𝜖 Pr 𝑥1 = 𝜋 𝑑 + 𝜔 2 − 𝑑 − 𝜔 2 𝜋𝜖2 Pr 𝑥1 = 4𝑑𝜔 𝜖2 The probability increases as d increases. 𝜖2𝜖
- 11. PROBABILISTIC ANALYSIS The probability of finding a point in the 2- epsilon shell given a k-point at distance d is defined as Pr 𝑥2|𝑥1 = 2𝜖2 arctan 𝑑 4𝜖2 − 𝑑2 + 𝑑 2 4𝜖2 − 𝑑2 3𝜋𝜖2 This is from a modified lens equation 𝐴 = a2 𝜋 − 2𝑎2 arctan 𝑑 4𝑎2 − 𝑑2 − 𝑑 2 4𝑎2 − 𝑑2 Divided by the area of the 2-epsilon shell 𝜋 2𝜖 2 − 𝜋𝜖2 = 3𝜋𝜖2 This can be approximated (from Vesica Piscis) as Pr 𝑥2|𝑥1 ≈ 0.203𝑑 𝜖 ; 0 ≤ 𝑑 ≤ 𝜖 𝜖2𝜖
- 12. PROBABILISTIC ANALYSIS Pr 𝑥1 = 4𝑑𝜔 𝜖2 Pr 𝑥2|𝑥1 ≈ 0.203𝑑 𝜖 This probability is greater than zero for all d greater than zero. So long as a point exists between the reference point and epsilon then there is a chance that it will find the target point in the 2-epsilon shell. This is the probability for finding a single point in the 2-epsilon shell. For each additional point in the shell the probability increases for finding any point. Pr 𝑋 = Pr{𝑥1 ∪ 𝑥2 ∪ ⋯ ∪ 𝑥 𝑚} 𝜖2𝜖
- 13. COMPLEXITY The affect of a point in a neighborhood is independent of the size of the problem and the epsilon chosen. Choose k points as the maximum number of neighbors to propagate. Assume m (size of the neighborhood) is constant: 𝑖=1 𝑛/𝑚 𝑘 = 𝑘 𝑚 𝑛 = 𝑂 𝑛 Assume m = n/p where p is constant. Meaning that the neighborhood size is a fraction of the total size: 𝑖=1 𝑛 𝑛/𝑝 𝑘 = 𝑝𝑘 = 𝑂(1) Assume 𝑚 = 𝑛 𝑖=1 𝑛/ 𝑛 𝑘 = 𝑘 𝑛 = 𝑂 𝑛 Therefore, it is possible choose epsilon and minimum points to maximize the efficiency of the algorithm.
- 14. COMPLEXITY Choosing epsilon and minimum points such that the average number of points in a neighborhood is the square root of the number of points in the universe allows us to reduce the time complexity of the problem from 𝑂 𝑛2 to 𝑂(𝑛 𝑛).
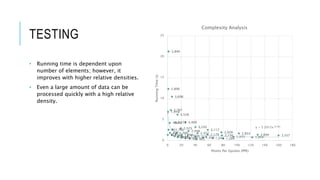
- 16. TESTING Method Generate a random data set of n elements with values ranging between 0 and 50. Then trim values between 25 and 25+epsilon on the x and y axis. This should give us at least 4 clusters. Run the each algorithm 100 times on each data set and record the average running time for each algorithm and the average accuracy of Randomized DBSCAN. Repeat for 1000, 2000, 3000, 4000 initial points (before trim) Repeat for eps = [1:10] 0 5 10 15 20 25 30 0 1,000 2,000 3,000 4,000 5,000 RunTime(s) Number of Elements (N) Complexity Analysis DBSCAN t eps=1 eps=2 eps=3 eps=4 eps=5 eps=6 eps=7 eps=8 eps=9 eps=10 Poly. (DBSCAN t) Poly. (eps=2) Linear (eps=10)
- 17. TESTING • Randomized DBSCAN improves as the epsilon increases (increasing the number of points per epsilon and the relative density). • DBSCAN will perform in 𝑂(𝑛2 ) regardless of epsilon and relative density. • Randomized DBSCAN always performs as well as DBSCAN regardless of the relative density and chosen epsilon. 0 5 10 15 20 25 30 0 1,000 2,000 3,000 4,000 5,000 RunTime(s) Number of Elements (N) Complexity Analysis DBSCAN t eps=1 eps=2 eps=3 eps=4 eps=5 eps=6 eps=7 eps=8 eps=9 eps=10 Poly. (DBSCAN t) Poly. (eps=2) Linear (eps=10)
- 18. TESTING • Running time is dependent upon number of elements; however, it improves with higher relative densities. • Even a large amount of data can be processed quickly with a high relative density. 957 921 877 835835785764711662 665 1,918 1,845 1,766 1,709 1,6481,5501,5181,416 1,344 1,284 2,890 2,797 2,672 2,525 2,448 2,322 2,179 2,156 1,973 1,954 3,840 3,696 3,528 3,409 3,250 3,117 2,928 2,833 2,694 2,557 y = 5.2012x-0.364 0 5 10 15 20 25 0 20 40 60 80 100 120 140 160 180 RunningTime(s) Points Per Epsilon (PPE) Complexity Analysis
- 19. TESTING • For any relative density above the minimum points threshold the Randomized DBSCAN algorithm returns the exact same result as the DBSCAN algorithm. • We would expect the Randomized DBSCAN to be more accurate at higher densities (higher probability for each point in epsilon range); however, it doesn’t seem to matter above a very small threshold. 0 10 20 30 40 50 60 70 0 20 40 60 80 100 120 140 160 180 Error(%) Points Per Epsilon (PPE) Accuracy Analysis
- 20. FUTURE WORK • Probabilistic analysis to determine accuracy of the algorithm in n dimensions. Does the k-accuracy relationship scale linearly or (more likely) exponentially with the number of dimensions. • Determine performance and accuracy implications for classification and discreet attributes. • Combine the randomized DBSCAN with an indexed region query to reduce the time complexity of the clustering algorithm from 𝑂 𝑛2 to 𝑂 𝑛 log 𝑛 . • Rerun tests with balanced data sets to highlight (and better represent) improvement. • Determining optimal epsilon for performance and accuracy of a particular data set.
- 21. DBRS A Density-based Spatial Clustering Method with Random Sampling Initially proposed by Xin Wang and Howard J. Hamilton in 2003 Randomly selects points and assigns clusters Merges clusters that should be together Advantages Handles varying densities Disadvantages Same time and space complexity limitations as DBSCAN Requires an additional parameter and accompanying concept: purity
- 22. REFERENCES I. Ester, Martin; Kriegel, Hans-Peter; Sander, Jörg; Xu, Xiaowei (1996). "A density-based algorithm for discovering clusters in large spatial databases with noise". In Simoudis, Evangelos; Han, Jiawei; Fayyad, Usama M. "Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96)". AAAI Press. pp. 226– 231. ISBN 1-57735-004-9. CiteSeerX: 10.1.1.71.1980. II. Wang, Xin; Hamilton, Howard J. (2003) “DBRS: A Desity-Based Spatial Clustering Method with Random Sampling.” III. Gareth James, Daniela Witten, Trevor Hastie and Robert Tibshirani, An Introduction to Statistical Learning: with Applications in R, Springer, 1st ed, 2013, ISBN: 978-1461471370 IV. Michael Mitzenmacher and Eli Upfal, Probability and Computing: Randomized Algorithms and Probabilistic Analysis, Cambridge University Press, 1st ed, 2005, ISBN: 978-0521835404 V. Weisstein, Eric W. "Lens." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Lens.html