Decision Tree Algorithm Implementation Using Educational Data

International Journal of Computer-Aided technologies (IJCAx) Vol.1,No.1,April 2014
31
Decision Tree Algorithm Implementation
Using Educational Data
Priyanka Saini1
,Sweta Rai2
and Ajit Kumar Jain3
1,2
M.Tech Student, Banasthali University, Tonk, Rajasthan
3
Assistant Professor , Department of Computer Science, Banasthali University
ABSTRACT
There is different decision tree based algorithms in data mining tools. These algorithms are used for
classification of data objects and used for decision making purpose. This study determines the decision tree
based ID3 algorithm and its implementation with student data example.
Keywords
Decision tree, ID3 algorithm, Entropy and Information Gain
1.Introduction
Decision Tree is a tree structure like a flow-chart, in which the rectangular boxes are called the
node. Each node represents a set of records from the original data set. Internal node is a node that
has a child and leaf (terminal) node is nodes that don’t have children. Root node is a topmost
node. The decision tree is used for finding the best way to distinguish a class from another class.
There are five mostly & commonly used algorithms for decision tree: - ID3, CART, CHAID,
C4.5 algorithm and J48.
Age
Has Job Own House Credit rating
Young Middle Old
False
True
Yes No
False
True
Yes No
Excellent
Fair
Yes Yes
Good
No
Figure1: Decision Tree example for the loan problem

32
Decision tree example is shown in above figure. In Figure1, “Age” attribute is a decision node
and the “Has Job” attribute, “Credit rating attribute “and “Own house” attribute are the leaf node.
These leaf nodes have homogenous records (not further classification required).The ID3
algorithm builds similar decision trees until its leaf nodes have homogenous records.
ID3 Algorithm:-
ID3 algorithm is a precursor of C4.5 algorithm and it was developed by a data mining computer
science researcher Ross Quinlan in 1983.It is used to construct a decision tree by testing each
node’s attribute of tree in top-down manner. ID algorithm performs attribute selection mechanism
using Entropy and Information Gain concept.
1.1.1 Attribute selection
Entropy and Information Gain terms are used for selecting attributes in ID3 algorithm and these
selected attributes become node of decision tree.
1.1.1.1 Entropy Calculation
Entropy is a kind of uncertainty measurement. In decision tree it determine informative node.
Entropy(S) = ∑n=1-p(I)log2p(I) Where:
S is set,Entropy(S) is information entropy of S
p(I)= proportion of S belonging to class I
1.1.1.2 Information Gain G(S,A)
Information gain is used to select a particular attribute to become a decision node of a decision
tree in ID3 algorithm. For splitting the tree node, a optimal attribute is selected (attribute with
entropy reduction is selected).Information gain is defined as the most expected reduction in
entropy of a attribute at the time of splitting a node.
Gain(S, A) = Entropy(S) - ∑( ( |Sv|/|S| ) x Entropy(Sv) )
Where:
S is records collection.
A :- attribute
Gain(S,A) is the gain of S after split on A
v is all the possible values of the attribute A.
Sv is the number of elements for each v.
∑ is the summation of ( ( |Sv|/|S| ) x Entropy(Sv) ) for all the items from the set of v
2. Related Work
In 1986 J.R Quinlan summarizes an approach and describes ID3 and this was the first research
work on ID3 algorithm [1].

33
Anand Bahety implemented the ID3 algorithm on the “Play Tennis” database and classified
whether the weather is suitable for playing tennis or not?.Their results concluded that ID3 doesn’t
works well in continuous attributes but gives good results for missing values [2].
Mary Slocum gives the implementation of the ID3 in the medical area. She transforms the data
into information to make a decision and performed the task of collecting and cleaning the data.
Entropy and Information Gain concepts are used in this study [3].
Kumar Ashok (et.al) performed the id3 algorithm classification on the “census 2011 of India”
data to improving or implementing a policy for right people. The concept of information theory is
used here. In the decision tree a property on the basis of calculation is selected as the root of the
tree and this process’s steps are repeated [4].
Sonika Tiwari used the ID3 algorithm for detecting Network Anomalies with horizontal
portioning based decision tree and applies different clustering algorithms. She checks the network
anomalies from the decision tree then she discovers the comparative analysis of different
clustering algorithms and existing id3 decision tree [5].
3. The ID3 algorithm procedure
With an example, Id3 algorithm is best described. Firstly, a student table is shown in table1.
Table1: MCA Student Table
S.N
.
Mathematics Grade in
XII XII Grade UG Stream
UG
Grade
PG
Grade
1 F C BSC(IT) B D
2 A B BSC(Math) C A
3 A B BSC(CS) B B
4 A B BSC(Math) C A
5 A A BSC(CS) C B
6 F A BCA B C
7 F D BCA C C
8 B B BSC(Math) B A
9 C C BCA B A
10 B B BCA B A
11 F C BSC(IT) B D
12 C D BSC C C
13 B B BCA B C
14 B B BCA A C
15 B B BCA B A
16 F C BSC(IT) B D
17 B B BCA C B
18 B B BSC(CS) B B
19 B B BSC C C
20 B B BCA B B
21 F C BCA B C
22 B C BSC(CS) C D
STEP 1: Data sample is taken.

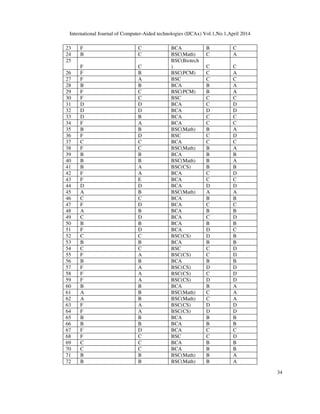
34
23 F C BCA B C
24 B C BSC(Math) C A
25
F C
BSC(Biotech
) C C
26 F B BSC(PCM) C A
27 F A BSC C C
28 B B BCA B A
29 F C BSC(PCM) B A
30 F C BSC C C
31 D D BCA C D
32 D D BCA D D
33 D B BCA C C
34 F A BCA C C
35 B B BSC(Math) B A
36 F D BSC C D
37 C C BCA C C
38 F C BSC(Math) B A
39 B B BCA B B
41 B A BSC(CS) B B
42 F A BCA C D
43 F E BCA C C
44 D D BCA D D
45 A B BSC(Math) A A
46 C C BCA B B
47 F D BCA C C
48 A B BCA B B
49 C D BCA C D
50 B B BCA B B
51 F D BCA D C
52 C C BSC(CS) D B
53 B B BCA B B
54 C C BSC C D
55 F A BSC(CS) C D
56 B B BCA B B
57 F A BSC(CS) D D
58 F A BSC(CS) C D
59 F A BSC(CS) D D
60 B B BCA B A
61 A B BSC(Math) C A
63 F A BSC(CS) D D
64 F A BSC(CS) D D
65 B B BCA B B
66 B B BCA B B
67 F D BCA C C
68 F C BSC C D
69 C C BCA B B
70 C C BCA B B

35
74 A B BSC(CS) B B
76 A A BSC(CS) C B
77 F A BSC(CS) C D
78 B B BCA B B
79 F A BSC(CS) D D
80 F A BSC(CS) C D
81 F A BSC(CS) D D
82 B B BCA B A
84 C C BSC C D
85 C C BSC C D
93 B B BCA B A
94 B B BCA B A
95 F C BSC(PCM) B A
96 F C BSC(PCM) B A
98 A B BSC(CS) B B
99 A B BSC(CS) B B
100 A B BSC(CS) B B
STEP 2: In this table PG Grade attribute is a decision column and refer as Class(C) or Classifier.
Because based on other attributes student performance in post graduation (PG) is predicted. All the
records in the student table refer as Collection (S).To calculate the entropy value, table 1 is used.
Since Entropy Formula:Entropy(S) = ∑n=1-p(I)log2p(I)
p(I)= proportion of S belonging to class I. In the table PG attribute have four class {A, B, C, D}
and S=99.
=) Entropy(S) = -p(A/S)log2p(A/S) + -p(B/S)log2p(B/S) + -p(C/S)log2p(C/S) + -p(D/S)log2p(D/S)
=) Entropy (S) = -(34/99) Log2 (34/99) – (23/99) Log2 (23/99) -(19/99) Log2 (19/99) – (23/99)
Log2 (23/99) = 1.965031 So the Entropy of S is 1.965031
STEP 3: Information gain value is calculated for each columns (attributes).
a) Starts with XII Grade attribute
Attribute XII Grade value are A, B, C, D and E and calculate entropy of each pg grades “A”,
“B”, “C”, “D” for XII Grade/A, XII Grade/B, XII Grade/C, XII Grade/D, XII Grade/E.

36
XII
Grade
Occurrences
A 17-(3 of the examples are ”B”, 3 &11of the examples are “C”,“D”
respectively)
B 48-( 28-A, 16-B, 4-C)
C 23-(6-A, 4-B, 6-C, 7-D)
D 10-(5-C,5-D)
E 1-(1-C)
Entropy(SXA)= -(3/17)xlog2(3/17) – (3/17)xlog2(3/17) –(11/17)xlog2(11/17) =1.289609
Entropy(SXB)= -(28/48)xlog2(28/48) – (16/48)xlog2(16/48) –(4/48)xlog2(4/48) =1.280672
Entropy(SXC)= -(6/23)xlog2(6/23) – (4/23)xlog2(4/23) –(6/23)xlog2(6/23) –(7/23)xlog2(7/23)=
1.972647
Entropy (SXD) = - (5/10) xlog2 (5/10) – (5/10)xlog2(5/10) =1
Entropy (SXE) = - (1/1) xlog2 (1/1) = 0
Gain (S, XII Grade) = Entropy (S) – (17/99) x Entropy (SXA) - (48/99) x Entropy (SXB) -
(23/99) x Entropy (SXC)-(10/99) x Entropy (SXD) - (1/99) x Entropy (SXE)
Gain(S,XII Grade)= 1.965031-(17/99) x 1.289609- (48/99) x 1.280672- (23/99) x 1.972647 -
(10/99) x 1- (1/99) x 0=0.563349283
STEP 4: Information Gain of MCA student attribute
Entropy(S) 1.965031
Gain (S, XII Grade) 0.563349283
Gain(S, Mathematics Grade in XII) 0.557822111
Gain (S,UG Stream) 0.925492111
Gain (S,UG Grade) 0.35823184
STEP 5: Find which attribute is the root node
After calculating the information Gain for each attribute, it is determined that UG Stream has the
highest gain as largest value(0.925492111), so UG Stream will be the root node with seven
possible values as shown in Figure 2.
Figure 2: Decision tree with UG Stream root node
STEP 6: Find which attribute is next decision node.
Now, the next set of children need to be determined using this same process and each UG Stream
subsets is looked.
UG
Stream
BSC(
IT)
BSC(
BSC(
CS)
BC
A
BSC(B
io)
BSC(PC
M)
BS
C

37
Since Entropy of Stream BSC in Mathematics, IT and Biotech are zero so no classification
required.
Since Entropy (SBSC (CS)) = 0.998364
For UG Stream= BSC (CS)
1. For finding the next node in branch of BSC (CS), calculate the gain value of BSC(CS) with
other nodes such as XII Grade, Mathematics Grade in XII and UG Grade
a) Gain(SBSC(CS)),XII Grade) = ?
UG Stream BSC(CS) with XII Grade Occurrences
A 13-(0-A,3-B, 0-C, 10-D)
B 6- (0-A, 6-B)
C 2(1-D,1-B)
D 0
Entropy (SBSC(CS)XA)= -(3/13)xlog2(3/13) –(10/13)xlog2(10/13)= 0.77934984
Entropy (SBSC(CS)XB)= -(6/6)xlog2(6/6)=0
Entropy (SBSC(CS)XC)= -(1/2)xlog2(1/2) –(1/2)xlog2(1/2)= 1
Gain(SBSC(CS)),XIIGrade) =Entropy(SBSC(CS))-(13/21)*Entropy(SBSC(CS)XA)-(6/21)*
Entropy (SBSC(CS)XB)-(2/21)* Entropy (SBSC(CS)XC)
Gain(SBSC(CS)),XIIGrade)= 0.998364 –(13/21)* 0.779349-(6/21)*0-(2/21)* 1=0.42067176
b) Gain (SBSC (CS)), Mathematics Grade in XII) = ?
UG Stream BSC(CS) with Mathematics Grade in XII Occurrences
A 7-(7-B)
B 3-(2-B,1-D)
C 1-(1-B)
F 10-(10-D)
Entropy (SBSC(CS)MA)= -(7/7)xlog2(7/7) =0
Entropy (SBSC(CS)MB)= -(2/3)xlog2(2/3)-(1/3)xlog2(1/3) =0.918296
Entropy (SBSC(CS)MC)= -(1/1)xlog2(1/1) =0
Entropy (SBSC(CS)MF)= -(10/10)xlog2(10/10) =0
Gain(SBSC(CS)),Mathematics Grade in XII) =Entropy(SBSC(CS))-
(7/21)*Entropy(SBSC(CS)MA)-(3/21)* Entropy (SBSC(CS)MB)-(1/21)* Entropy
(SBSC(CS)MC)-(10/21)*Entropy(SBSC(CS)MF)
Gain(SBSC(CS)),Mathematics Grade in XII) =0.998364-(7/21)*0-(3/21)* 0.918296-(1/21)*0-
(10/21)*0=0.867179
c) Gain (SBSC (CS), UG Grade) = ?

38
UG Stream BSC(CS) with UG Grade Occurrences
A 0
B 7(7-B)
C 7 (2-B,5-D)
D 7(1-B,6-D)
Entropy (SBSC(CS)UA),Entropy (SBSC(CS)UB)= 0
Entropy (SBSC(CS)UC)= -(2/7)xlog2(2/7)-(5/7)xlog2(5/7)= 0.863120569
Entropy (SBSC(CS)UD)= -(1/7)xlog2(1/7)-(6/7)xlog2(6/7)= 0.591672779
Gain(SBSC(CS),UG Grade) =Entropy(SBSC(CS))-(7/21)*Entropy(SBSC(CS)UB)-(7/21)*
Entropy (SBSC(CS)UC)-(7/21)* Entropy (SBSC(CS)UD)
Gain(SBSC(CS),UGGrade)=0.998364-(7/21)*0-(7/21)*0.863120569-(7/21)*
0.591672779=0.513432884
Gain(SBSC(CS),Mathematics Grade in XII) is higher than other attributes, so Mathematics Grade
in XII is the next node in BSC(CS) branch.
STEP 7: This classification process goes on until all MCA students’ data is classified. The
generated decision tree is shown here.
Id3
UG Stream = BSC(IT): D
UG Stream = BSC(Math): A
UG Stream = BSC(CS)
| Mathematics Grade in XII = F: D
| Mathematics Grade in XII = A: B
| Mathematics Grade in XII = B
| | XII Grade = C: D
| | XII Grade = B: B
| | XII Grade = A: B
| | XII Grade = D: null
| | XII Grade = E: null
| Mathematics Grade in XII = C: B
| Mathematics Grade in XII = D: null
UG Stream = BCA
| Mathematics Grade in XII = F
| | XII Grade = C: C
| | XII Grade = B: null
| | XII Grade = A
| | | UG Grade = B: C
| | | UG Grade = C: D
| | | UG Grade = A: null
| | | UG Grade = D: null
| | XII Grade = D: C
| | XII Grade = E: C
| Mathematics Grade in XII = A: B
| Mathematics Grade in XII = B

40
4. Conclusion
The ID3 decision tree can be used to make a decision by traversing as a breadth-first.ID3
algorithm generates a smallest decision tree. The ID3 algorithm is improved using C4.5
algorithm. Related to this study, this implementation on educational data concluded that the
decision tree ID3 algorithm is a perfect algorithm for classification. Using the decision tree (in
Figure 3) it can be determined that what is the final grade of a student? The final rules are:
Rules Predicted
class
IF UG Stream=BSC(IT) Class=D
IF UG Stream=BSC(Math) Class=A
IF UG Stream=BSC(CS), Mathematics Grade in XII=A Class=B
IF UG Stream=BSC(CS), Mathematics Grade in XII=C Class=B
IF UG Stream=BSC(CS), Mathematics Grade in XII=F Class=D
IF UG Stream=BSC(CS), Mathematics Grade in XII=B,XII Grade=A Class=B
IF UG Stream=BSC(CS), Mathematics Grade in XII=B,XII Grade=B Class=B
IF UG Stream=BSC(CS), Mathematics Grade in XII=B,XII Grade=C Class=D
IF UG Stream=BCA, Mathematics Grade in XII=A Class=B
IF UG Stream=BCA, Mathematics Grade in XII=B,UG Grade=B Class=B
IF UG Stream=BCA, Mathematics Grade in XII=B,UG Grade=C Class=B
IF UG Stream=BCA, Mathematics Grade in XII=B,UG Grade=A Class=C
IF UG Stream=BCA, Mathematics Grade in XII=C,UG Grade=B Class=B
IF UG Stream=BCA, Mathematics Grade in XII=C,UG Grade=C,XII Class=C
IF UG Stream=BCA, Mathematics Grade in XII=C,UG Grade=C,XII Class=D
IF UG Stream=BCA, Mathematics Grade in XII=D,XII Grade=B Class=C
IF UG Stream=BCA, Mathematics Grade in XII=D,XII Grade=D Class=D
IF UG Stream=BCA, Mathematics Grade in XII=F,XII Grade=C Class=C
IF UG Stream=BCA, Mathematics Grade in XII=F,XII Grade=A,UG
Grade=B
Class=C
IF UG Stream=BCA, Mathematics Grade in XII=F,XII Grade=A,UG
Grade=C
Class=D
IF UG Stream=BCA, Mathematics Grade in XII=F,XII Grade=E Class=C
IF UG Stream=BCA, Mathematics Grade in XII=F,XII Grade=D Class=C
IF UG Stream=BSC,XII Grade=A Class=C
IF UG Stream=BSC,XII Grade=B Class=C
IF UG Stream=BSC,XII Grade=C, Mathematics Grade in XII=C Class=D
IF UG Stream=BSC,XII Grade=C, Mathematics Grade in XII=F Class=C
IF UG Stream=BSC(Biotech) Class=C
IF UG Stream=BSC(PCM) Class=A

41
5. References
[1] Quinlan, J.R. 1986, Induction of Decision trees, Machine Learning.
[2] Anand Bahety,’ Extension and Evaluation of ID3 – Decision Tree Algorithm’. University of
Maryland, College Park.
[3] Mary Slocum,‟,Decision making using ID3,RIVIER ACADEMIC JOURNAL, VOLUME 8,
NUMBER 2, FALL 2012.
[4] Kumar Ashok, Taneja H C, Chitkara Ashok K and Kumar Vikas,’ Classification of Census Using
Information Theoretic Measure Based ID3 Algorithm’ . Int. Journal of Math. Analysis, Vol. 6, 2012,
no. 51, 2511 – 2518.
[5] Sonika Tiwari and Prof. Roopali Soni,’ Horizontal partitioning ID3 algorithm A new approach of
detecting network anomalies using decision tree’, International Journal of Engineering Research &
Technology (IJERT)Vol. 1 Issue 7, eptember – 2012.

Decision Tree Algorithm Implementation Using Educational Data

More Related Content

What's hot (16)

Similar to Decision Tree Algorithm Implementation Using Educational Data (20)

More from ijcax (20)

Recently uploaded (20)

Decision Tree Algorithm Implementation Using Educational Data