Deep Feed Forward Neural Networks and Regularization
1 like3,051 views
Deep feedforward networks use regularization techniques like L2/L1 regularization, dropout, batch normalization, and early stopping to reduce overfitting. They employ techniques like data augmentation to increase the size and variability of training datasets. Backpropagation allows information about the loss to flow backward through the network to efficiently compute gradients and update weights with gradient descent.
![LOSS FUNCTION
• A loss function (cost function) tells us how good our current model is, or
how far away our model to the real answer.
𝐿(𝑤) =
1
𝑁
𝑖
𝑁
𝑙𝑜𝑠𝑠 (𝑓(𝑥 𝑖 ; 𝑤), 𝑦 𝑖 )
• Hinge loss
• Softmax loss
• Mean Squared Error (L2 loss) Regression 𝐿(𝑤) =
1
𝑁
∑𝑖
𝑁
𝑓 𝑥 𝑖
; 𝑤 − 𝑦 𝑖 2
• Cross entropy Loss Classification 𝐿 𝑤 =
1
𝑁
∑𝑖
𝑁
[ 𝑦 𝑖
𝑙𝑜𝑔 𝑓 𝑥 𝑖
; 𝑤 + 1 − 𝑦 𝑖
log 1 − 𝑓 𝑥 𝑖
; 𝑤 ]
• …
N = # examples
predicted actual](https://image.slidesharecdn.com/2018-03-17meetup-180319032650/85/Deep-Feed-Forward-Neural-Networks-and-Regularization-15-320.jpg)
Deep Feed Forward Neural Networks and Regularization
- 1. DEEP FEEDFORWARD NETWORKS AND REGULARIZATION LICHENG ZHANG
- 2. OVERVIEW • Regularization • L2/L1/elastic • Dropout • Batch normalization • Data augmentation • Early stopping • Neural network • Perceptron • Activation functions • Back-propagation
- 3. FEEDFORWARD NETWORK “3-layer neural net” or “2-hidden-layers neural net”
- 6. PERCEPTRON FORWARD PASS 2 3 -1 1 Inputs weights sum activation function ∑ f bias 0.1 0.5 2.5 3.0 output (2*0.1)+ (3*0.5)+ (-1*2.5)+ (1*3.0) Output = f( )
- 7. PERCEPTRON FORWARD PASS 2 3 -1 1 Inputs weights sum activation function ∑ f bias 0.1 0.5 2.5 3.0 output Output = f(2.2) =𝜎(2.2) = 1 1+𝑒−2.2 = 0.90
- 8. MULTI-OUTPUT PERCEPTRON 𝑥0 𝑜0 𝑥1 𝑥2 Input layer Output layer
- 9. MULTI-OUTPUT PERCEPTRON 𝑥0 𝑜1 𝑥1 𝑥2 Input layer Output layer 𝑜0
- 10. MULTI-LAYER PERCEPTRON (MLP) 𝑥0 ℎ2 𝑥1 𝑥2 Input layer Hidden layer ℎ1 𝑜1 Output layer 𝑜0 ℎ0 ℎ3
- 11. DEEP NEURAL NETWORK 𝑥0 ℎ2 𝑥1 𝑥2 Input layer Hidden layer ℎ1 𝑜1 Output layer 𝑜0 ℎ0 ℎ3 ℎ2 ℎ1 ℎ0 ℎ3 ……
- 13. UNIVERSAL APPROXIMATION THEOREM “A feedforward network with a linear output layer and at least one hidden layer with any ‘squashing’ activation function (such as the logistic sigmoid) can approximate any Borel measurable function from one finite-dimensional space to another with any desired nonzero amount of error, provided that the network is given enough hidden units.” • ----- Hornik et al., Cybenko, 1989
- 14. COMPUTATIONAL GRAPHS Z=x*y 𝑦 = 𝜎(𝑤𝑥 + 𝑏) H = 𝑟𝑒𝑙𝑢(𝑊𝑋 + 𝑏) = max(0, 𝑊𝑋 + 𝑏) 𝑦 = 𝑤𝑥 𝑢(3) = 𝜆∑ 𝑤
- 15. LOSS FUNCTION • A loss function (cost function) tells us how good our current model is, or how far away our model to the real answer. 𝐿(𝑤) = 1 𝑁 𝑖 𝑁 𝑙𝑜𝑠𝑠 (𝑓(𝑥 𝑖 ; 𝑤), 𝑦 𝑖 ) • Hinge loss • Softmax loss • Mean Squared Error (L2 loss) Regression 𝐿(𝑤) = 1 𝑁 ∑𝑖 𝑁 𝑓 𝑥 𝑖 ; 𝑤 − 𝑦 𝑖 2 • Cross entropy Loss Classification 𝐿 𝑤 = 1 𝑁 ∑𝑖 𝑁 [ 𝑦 𝑖 𝑙𝑜𝑔 𝑓 𝑥 𝑖 ; 𝑤 + 1 − 𝑦 𝑖 log 1 − 𝑓 𝑥 𝑖 ; 𝑤 ] • … N = # examples predicted actual
- 16. GRADIENT DESCENT • Designing and training a neural network is not much different from training any other machine learning model with gradient descent: use Calculus to get derivatives of the loss function respect to each parameter. 𝑤𝑗 = 𝑤𝑗 − α 𝜕𝐿(𝑤) 𝜕𝑤𝑗 𝛼 is learning rate https://developers.google.com/machine-learning/crash-course/fitter/graph
- 17. GRADIENT DESCENT • In practice, instead of using all data points, we do • Stochastic gradient descent (using 1 sample at each iteration) • Mini-Batch gradient descent (using n samples at each iteration) Problems with SGD: • If loss changes quickly in one direction and slowly in another jitter along steep direction • If loss function has a local minima or saddle point zero gradient, SGD gets stuck Solutions: • SGD + momentum, etc
- 18. BACK-PROPAGATION • It allows the information from the loss to flow backward through the network in order to compute the gradient. 𝑥0 ℎ0 𝑂0 𝐿(𝑤) 𝑊1 𝑊2 𝜕𝐿 𝑤 𝜕𝑤2 =
- 19. BACK-PROPAGATION • It allows the information from the loss to flow backward through the network in order to compute the gradient. 𝑥0 ℎ0 𝑂0 𝐿(𝑤) 𝑊1 𝑊2 𝜕𝐿 𝑤 𝜕𝑤2 = 𝜕𝐿 𝑤 𝜕𝑂0 ∗
- 20. BACK-PROPAGATION • It allows the information from the loss to flow backward through the network in order to compute the gradient. 𝑥0 ℎ0 𝑂0 𝐿(𝑤) 𝑊1 𝑊2 𝜕𝐿 𝑤 𝜕𝑤2 = 𝜕𝐿 𝑤 𝜕𝑂0 ∗ 𝜕𝑂0 𝜕𝑤2 Chain rule
- 21. BACK-PROPAGATION • It allows the information from the loss to flow backward through the network in order to compute the gradient. 𝑥0 ℎ0 𝑂0 𝐿(𝑤) 𝑊1 𝑊2 𝜕𝐿 𝑤 𝜕𝑤1 =
- 22. BACK-PROPAGATION • It allows the information from the loss to flow backward through the network in order to compute the gradient. 𝑥0 ℎ0 𝑂0 𝐿(𝑤) 𝑊1 𝑊2 𝜕𝐿 𝑤 𝜕𝑤1 = 𝜕𝐿 𝑤 𝜕𝑂0 ∗ 𝜕𝑂0 𝜕ℎ0 ∗ Chain rule
- 23. BACK-PROPAGATION • It allows the information from the loss to flow backward through the network in order to compute the gradient. 𝑥0 ℎ0 𝑂0 𝐿(𝑤) 𝑊1 𝑊2 𝜕𝐿 𝑤 𝜕𝑤1 = 𝜕𝐿 𝑤 𝜕𝑂0 ∗ 𝜕𝑂0 𝜕ℎ0 ∗ 𝜕ℎ0 𝜕𝑤1 Chain rule
- 24. BACK-PROPAGATION: SIMPLE EXAMPLE 𝑓 𝑥, 𝑦, 𝑧 = 𝑥 + 𝑦 𝑧 e.g. x = -2, y = 5, z=-4 𝑞 = 𝑥 + 𝑦 𝜕𝑞 𝜕𝑥 = 1, 𝜕𝑞 𝜕𝑦 = 1 f = qz 𝜕𝑓 𝜕𝑞 = 𝑧, 𝜕𝑓 𝜕𝑧 = 𝑞 + * x y z -2 5 -4 3 -12f q Want: 𝜕𝑓 𝜕𝑥 , 𝜕𝑓 𝜕𝑦 , 𝜕𝑓 𝜕𝑧 𝜕𝑓 𝜕𝑓 1 𝜕𝑓 𝜕𝑧 3 𝜕𝑓 𝜕𝑞 -4 𝜕𝑓 𝜕𝑦 -4 Chain Rule: 𝜕𝑓 𝜕𝑦 = 𝜕𝑓 𝜕𝑞 𝜕𝑞 𝜕𝑦 𝜕𝑓 𝜕𝑥 -4 Chain Rule: 𝜕𝑓 𝜕𝑥 = 𝜕𝑓 𝜕𝑞 𝜕𝑞 𝜕𝑥
- 25. ACTIVATION FUNCTIONS 𝒇 Importance of activation functions is to introduce non-linearity into the network.
- 26. ACTIVATION FUNCTIONS For output layer: • Sigmoid • Softmax • Tanh For hidden layer: • ReLU • LeakyReLU • ELU
- 28. ACTIVATION FUNCTIONS 3 problems: 1. Saturated neurons “kill” the gradients
- 29. • What happens when x= -10? • What happens when x = 0? • What happens when x = 10 Sigmoid gate 𝜎 𝑥 = 1 1 + 𝑒−𝑥 𝜕𝜎 𝜕𝑥 x 𝜕𝐿 𝜕𝜎 𝜕𝐿 𝜕𝜎 = 𝜕𝜎 𝜕𝑥 𝜕𝐿 𝜕𝜎
- 30. ACTIVATION FUNCTIONS 3 problems: 1. Saturated neurons “kill” the gradients 2. Sigmoid outputs are not zero-centered
- 31. Consider what happens when the input to a neuron is always positive… 𝑓( 𝑖 𝑤𝑖 𝑥𝑖 + 𝑏 ) What can we say about the gradients on w? Always all positive or all negative (this is also why you want zero-mean data!) 𝜕𝐿 𝜕𝑤𝑖 = 𝜕𝐿 𝜕𝑓 𝜕𝑓 𝜕𝑤𝑖 = 𝜕𝐿 𝜕𝑓 ∗ 𝑥𝑖 Inefficient!
- 32. ACTIVATION FUNCTIONS 3 problems: 1. Saturated neurons “kill” the gradients 2. Sigmoid outputs are not zero-centered 3. Exp() is a bit compute expensive
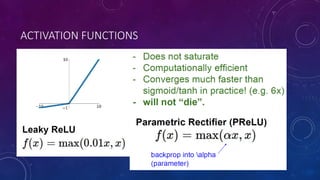
- 35. ACTIVATION FUNCTIONS • Not zero-centered output • An annoyance when x < 0 People like to initialize ReLU neurons with slightly positive biases (e.g. 0.01)
- 37. ACTIVATION FUNCTIONS Clevert et al., 2015
- 38. MAXOUT “NEURON”
- 39. IN PRACTICE (GOOD RULE OF THUMB) • For hidden layers: • Use ReLU. Be careful with your learning rates • Try out Leaky ReLU / Maxout / ELU • Try out tanh but don’t expect too much • Don’t use Sigmoid
- 40. REGULARIZATION • Regularization is “any modification we make to the learning algorithm that is intended to reduce the generalization error, but not its training error”.
- 41. REGULARIZATION 𝐿 𝑊 = 1 𝑁 𝑖 𝑁 𝐿𝑖 𝑓 𝑥 𝑖 ; 𝑊 , 𝑦 𝑖 Data loss: model predictions should match training data
- 42. REGULARIZATION 𝐿(𝑊) = 1 𝑁 𝑖 𝑁 𝐿𝑖 𝑓 𝑥 𝑖 ; 𝑊 , 𝑦 𝑖 + 𝜆𝑅(𝑊) Data loss: model predictions should match training data Regularization: Model Should be “simple”, so it works on test data Occam’s Razor: “Among competing hypotheses, The simplest is the best” William of Ockham, 1285-1347
- 43. REGULARIZATION • In common use: • L2 regularization • L1 regularization • Elastic net (L1 + L2) • Dropout • Batch normalization • Data Augmentation • Early Stopping 𝑅 𝑤 = ∑𝑤𝑗 2 𝑅 𝑤 = ∑|𝑤𝑗| 𝑅 𝑤 = ∑(𝛽𝑤𝑗 2 + wj ) Regularization is a technique designed to counter neural network over-fitting. 𝐿(𝑊) = 1 𝑁 𝑖 𝑁 𝐿𝑖 𝑓 𝑥 𝑖 ; 𝑊 , 𝑦 𝑖 + 𝜆𝑅(𝑊)
- 44. L2 REGULARIZATION • penalizes the square value of the weight (which explains also the “2” from the name). • tends to drive all the weights to smaller values. 𝐿(𝑊) = 1 𝑁 𝑖 𝑁 𝐿𝑖 𝑓 𝑥 𝑖 ; 𝑊 , 𝑦 𝑖 + 𝜆∑𝑤𝑗 2 No regularization L2 regularization Weights distribution
- 45. L1 REGULARIZATION • penalizes the absolute value of the weight (v- shape function) • tends to drive some weights to exactly zero (introducing sparsity in the model), while allowing some weights to be big 𝐿(𝑊) = 1 𝑁 𝑖 𝑁 𝐿𝑖 𝑓 𝑥 𝑖 ; 𝑊 , 𝑦 𝑖 + 𝜆|𝑤𝑗| No regularization L1 regularization Weights distribution
- 46. DROPOUT In each forward pass, randomly set some neurons to zero. Probability of dropping is a hyperparameter; 0.5 is common. You can imagine that if neurons are randomly dropped out of the network during training, that other neurons will have to step in and handle the representation required to make predictions for the missing neurons. This is believed to result in multiple independent internal representations being learned by the network.
- 47. DROPOUT Another interpretation: • Dropout is training a large ensemble of models (that share parameters) • Each binary mask is one model An fully connected layer with 4096 units has 24096 ~101233 possible masks! Only ~1082 atoms in the universe…
- 49. BATCH NORMALIZATION “you want unit Gaussian activations? Just make them so.”
- 50. BATCH NORMALIZATION Usually inserted after fully connected or convolutional layers, and before nonlinearity. • Improves gradient flow through the network • Allows higher learning rates • Reduces the strong dependence on initialization • Acts as a form of regularization in a funny way, and slightly reduces the need for dropout, maybe Note: at test time BatchNorm layer functions differently: The mean/std are not computed based on the batch. Instead, a single fixed empirical mean of activations during training is used. (e.g. can be estimated during training with running averages)
- 51. DATA AUGMENTATION The best way to make a machine learning model generalize better is to train it on more data.
- 52. DATA AUGMENTATION The best way to make a machine learning model generalize better is to train it on more data.
- 53. DATA AUGMENTATION Horizontal flips Random crops and scales Color Jitter • Simple: Randomize contrast and brightness Get creative for your problem! Translation Rotation Stretching Shearing Lens distortions (go crazy)
- 54. EARLY STOPPING It is probably the most commonly used form of regularization in deep learning to prevent overfitting: • Effective • Simple Think of this as a hyperparameter selection algorithm. The number of training steps is another hyperparameter.
- 55. REFERENCE • Deep Learning book ------ http://www.deeplearningbook.org/ • Stanford CNN course ----- http://cs231n.stanford.edu/index.html • Regularization in deep learning ----- https://chatbotslife.com/regularization-in-deep-learning-f649a45d6e0 • So much more to learn, go explore!
- 56. • THANK YOU