DS-MLR: Scaling Multinomial Logistic Regression via Hybrid Parallelism

Scaling Multinomial Logistic Regression via
Hybrid Parallelism
Parameswaran Raman
University of California Santa Cruz
KDD 2019
Aug 4-8
Joint work with:
Sriram Srinivasan, Shin Matsushima, Xinhua Zhang, Hyokun Yun,
S.V.N. Vishwanathan
1 / 54

Multinomial Logistic Regression (MLR)
Given:
Training data (xi , yi )i=1,...,N,
xi ∈ RD
Labels yi ∈ {1, 2, . . . , K}
N
D
X
Data
y
2 / 54

Given:
xi ∈ RD
Labels yi ∈ {1, 2, . . . , K}
N
D
X
Data
y
Goal:
Learn a model W
Predict labels for the test
data points using W
D
K
W
Model
2 / 54

Given:
xi ∈ RD
Labels yi ∈ {1, 2, . . . , K}
N
D
X
Data
y
Goal:
Learn a model W
Predict labels for the test
data points using W
D
K
W
Model
Assume: N, D and K are large (N >>> D >> K)
2 / 54

Motivation for Hybrid Parallelism
Popular ways to distribute MLR:
Data parallel (partition data,
duplicate parameters)
N
D
X
Data
D
K
W
Model
Storage Complexity:
O(ND
P ) data, O(KD) model
e.g. L-BFGS
3 / 54

Popular ways to distribute MLR:
Data parallel (partition data,
duplicate parameters)
N
D
X
Data
D
K
W
Model
Storage Complexity:
O(ND
P ) data, O(KD) model
e.g. L-BFGS
Model parallel (partition
parameters, duplicate data)
N
D
X
Data
D
K
W
Model
Storage Complexity:
O(ND) data, O(KD
P ) model
e.g. LC [Gopal et al 2013]
3 / 54

Can we get the best of both worlds?
4 / 54

Yes! Hybrid Parallelism
N
D
X
Data
D
K
W
Model
Storage Complexity:
O(ND
P ) data, O(KD
P ) model
We propose a Hybrid Parallel method DS-MLR
5 / 54

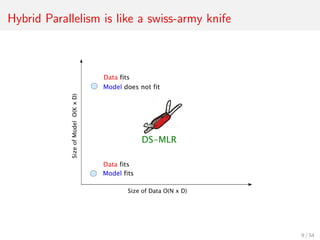
Hybrid Parallelism is like a swiss-army knife
6 / 54

7 / 54

8 / 54

9 / 54

10 / 54

11 / 54

Empirical Study - Multi Machine
0 2 4 6
·105
10
10.2
10.4
time (secs)
objective
Reddit-Full dataset (Data Size: 228 GB, Model Size: 358 GB)
DS-MLR
Figure: Data does not ﬁt, Model does not ﬁt
211 million examples - O(N)
44 billion parameters - O(K × D)
12 / 54

How do we achieve Hybrid Parallelism in machine learning models?
13 / 54

Double-Separability
Hybrid Parallelism
14 / 54

Double-Separability
Deﬁnition
Let {Si }m
i=1 and {Sj }m
j=1 be two families of sets of parameters. A function
f : m
i=1 Si × m
j=1 Sj → R is doubly separable if ∃ fij : Si × Sj → R for
each i = 1, 2, . . . , m and j = 1, 2, . . . , m such that:
f (θ1, θ2, . . . , θm, θ1, θ2, . . . , θm ) =
m
i=1
m
j=1
fij (θi , θj )
15 / 54

Double-Separability
f (θ1, θ2, . . . , θm, θ1, θ2, . . . , θm ) =
m
i=1
m
j=1
fij (θi , θj )
Each sub-function fij can be
computed independently
and in parallel
16 / 54

Are all machine learning models doubly-separable?
17 / 54

Sometimes . . .
e.g. Matrix Factorization
L(w1, w2, . . . , wN, h1, h2, . . . , hM) =
N
i=1
M
j=1
f (wi , hj )
Objective function is trivially doubly-separable!
18 / 54

Others need algorithmic reformulations . . .
- Binary Classiﬁcation (”DSO: Distributed Stochastic Optimization for the
Regularized Risk”, Matsushima et al 2014)
- Ranking (”RoBiRank: Ranking via Robust Binary Classiﬁcation”, Yun et al
2014)
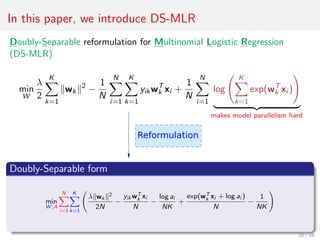
19 / 54

In this paper, we introduce DS-MLR
Doubly-Separable reformulation for Multinomial Logistic Regression
(DS-MLR)
min
W
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yikwT
k xi +
1
N
N
i=1
log
K
k=1
exp(wT
k xi )
makes model parallelism hard
Doubly-Separable form
min
W ,A
N
i=1
K
k=1
λ wk
2
2N
−
yik wT
k xi
N
−
log ai
NK
+
exp(wT
k xi + log ai )
N
−
1
NK
20 / 54

DS-MLR CV
Fully de-centralized distributed algorithm (data and model fully
partitioned across workers)
Asynchronous (communicate model in the background while
computing parameter updates)
Avoids expensive Bulk Synchronization steps
22 / 54

Delving deeper
Reformulation
Parallelization
Empirical Study
24 / 54

Given
Training data (xi , yi )i=1,...,N where xi ∈ RD
corresp. labels yi ∈ {1, 2, . . . , K}
N, D and K are large (N >>> D >> K)
Goal
The probability that xi belongs to class k is given by:
p(yi = k|xi , W ) =
exp(wk
T xi )
K
j=1 exp(wj
T xi )
where W = {w1, w2, . . . , wK } denotes the parameter for the model.
25 / 54

The corresponding l2 regularized negative log-likelihood loss:
min
W
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yikwk
T
xi +
1
N
N
i=1
log
K
k=1
exp(wk
T
xi )
where λ is the regularization hyper-parameter.
26 / 54

The corresponding l2 regularized negative log-likelihood loss:
min
W
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yikwk
T
xi +
1
N
N
i=1
log
K
k=1
exp(wk
T
xi )
makes model parallelism hard
where λ is the regularization hyper-parameter.
27 / 54

Reformulation into Doubly-Separable form
Step 1: Introduce redundant constraints (new parameters A) into the
original MLR problem
min
W ,A
L1(W , A) =
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yik wk
T
xi −
1
N
N
i=1
log ai
s.t. ai =
1
K
k=1 exp(wk
T xi )
28 / 54

Step 2: Turn the problem to unconstrained min-max problem by
introducing Lagrange multipliers βi , ∀i = 1, . . . , N
min
W ,A
max
β
L2(W , A, β) =
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yik wk
T
xi −
1
N
N
i=1
log ai
+
1
N
N
i=1
K
k=1
βi ai exp(wk
T
xi ) −
1
N
N
i=1
βi
Primal Updates for W , A and Dual Update for β (similar in spirit to
dual-decomp. methods).
29 / 54

Step 3: Stare at the updates long-enough
When at+1
i is solved to optimality, it admits an exact closed-form
solution given by a∗
i = 1
βi
K
k=1 exp(wk
T xi )
.
Dual-ascent update for βi is no longer needed, since the penalty is
always zero if βi is set to a constant equal to 1.
min
W ,A
L3(W , A) =
λ
2
K
k=1
wk
2
−
1
N
N
i=1
K
k=1
yik wk
T
xi −
1
N
N
i=1
log ai
+
1
N
N
i=1
K
k=1
ai exp(wk
T
xi ) −
1
N
30 / 54

Step 4: Simple re-write
min
W ,A
N
i=1
K
k=1
λ wk
2
2N
−
yik wk
T
xi
N
−
log ai
NK
+
exp(wk
T
xi + log ai )
N
−
1
NK
31 / 54

min
W ,A
N
i=1
K
k=1
λ wk
2
2N
−
yik wk
T
xi
N
−
log ai
NK
+
exp(wk
T
xi + log ai )
N
−
1
NK
Each worker samples a pair (wk, ai ).
Update wk using stochastic gradient
Update ai using its exact closed-form solution ai = 1
K
k=1 exp(wk
T xi )
32 / 54

Delving deeper
Reformulation
Parallelization
Empirical Study
33 / 54

Parallelization - Asynchronous NOMAD [Yun et al 2014]
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
(a) Initial Assignment of W and A
34 / 54

x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
(b) worker 1 updates w2 and
communicates it to worker 4
34 / 54

x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
(c) worker 4 can now update w2
34 / 54

x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
A
W
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
(c) worker 4 can now update w2
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
xx
x
x
x
x
x
x
x
x
xx
x
x
xx
(d) As algorithm proceeds, ownership of
wk changes continuously.
34 / 54

Delving deeper
Reformulation
Parallelization
Empirical Study
35 / 54

LSHTC1-small
LSHTC1-large
ODP
Youtube8M-Video
Reddit-Full
101
102
103
104
105
106
max memory of commodity machine
SizeinMB(log-scale)
data size (MB)
parameters size (MB)
Reddit-Full dataset: Data 228 GB and Model: 358 GB
36 / 54

Empirical Study - Single Machine
100 101 102 103
1.45
1.5
1.55
1.6
1.65
time (secs)
objective
NEWS20 dataset
DS-MLR
L-BFGS
LC
10−1 100 101 102 103 104 105
1
2
3
4
time (secs)
objective
CLEF dataset
DS-MLR
L-BFGS
LC
101 102 103 104
0
0.2
0.4
0.6
0.8
1
time (secs)
objective
LSHTC1-small dataset
DS-MLR
L-BFGS
LC
Figure: Data ﬁts, Model ﬁts
38 / 54

103 104
0.5
0.6
0.7
0.8
time (secs)
objective
LSHTC1-large dataset (Model Size: 34 GB)
DS-MLR
LC
0 1 2 3 4 5 6
·105
9.4
9.6
9.8
10
10.2
10.4
time (secs)objective
ODP dataset (Model Size: 355 GB)
DS-MLR
Figure: Data ﬁts, Model does not ﬁt
39 / 54

0 1 2 3
·105
0
20
40
60
time (secs)
objective
Youtube-Video dataset (Data Size: 76 GB)
DS-MLR
Figure: Data does not ﬁt, Model ﬁts
40 / 54

0 2 4 6
·105
10
10.2
10.4
time (secs)
objective
Reddit-Full dataset (Data Size: 228 GB, Model Size: 358 GB)
DS-MLR
Figure: Data does not ﬁt, Model does not ﬁt
211 million examples - O(N)
44 billion parameters - O(K × D)
41 / 54

Conclusion
We proposed DS-MLR
Hybrid Parallel reformulation for MLR → O(Data)
P and O(Parameters)
P
Fully De-centralized and Asynchronous algorithm
Avoids Bulk-synchronization
Empirical results suggest wide applicability and good predictive
performance
42 / 54

Future Extensions
Design Doubly-Separable losses for other machine learning models:
Extreme multi-label classiﬁcation
Log-linear parameterization for undirected graphical models
Deep Learning
Thank You!
43 / 54

More details
Please check out our paper / poster
Code: https://bitbucket.org/params/dsmlr
44 / 54

Acknowledgements
Thanks to all my collaborators!
45 / 54

DS-MLR: Scaling Multinomial Logistic Regression via Hybrid Parallelism

Recommended

More Related Content

What's hot (20)

Similar to DS-MLR: Scaling Multinomial Logistic Regression via Hybrid Parallelism (20)

Recently uploaded (20)

DS-MLR: Scaling Multinomial Logistic Regression via Hybrid Parallelism