Filtering: a method for solving graph problems in map reduce
- 1. Filtering: A Method for Solving Graph Problems in MapReduce Benjamin Moseley Silvio Lattanzi Siddharth Suri Sergei Vassilvitski UIUC Google Yahoo! Yahoo! Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 2. Overview • Introduction to MapReduce model • Our settings • Our results • Open questions Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 3. Introduction to the MapReduce model Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 4. XXL Data • Huge amount of data • Main problem is to analyze information quickly Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 5. XXL Data • Huge amount of data • Main problem is to analyze information quickly • New tools • Suitable efficient algorithms Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
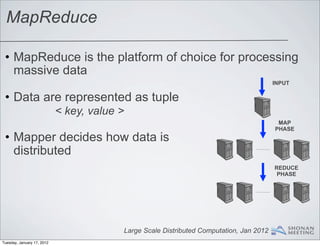
- 6. MapReduce • MapReduce is the platform of choice for processing massive data INPUT MAP PHASE REDUCE PHASE Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 7. MapReduce • MapReduce is the platform of choice for processing massive data INPUT • Data are represented as tuple < key, value > MAP PHASE REDUCE PHASE Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
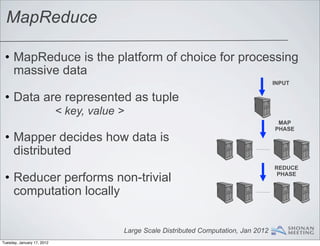
- 8. MapReduce • MapReduce is the platform of choice for processing massive data INPUT • Data are represented as tuple < key, value > MAP PHASE • Mapper decides how data is distributed REDUCE PHASE Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 9. MapReduce • MapReduce is the platform of choice for processing massive data INPUT • Data are represented as tuple < key, value > MAP PHASE • Mapper decides how data is distributed REDUCE • Reducer performs non-trivial PHASE computation locally Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 10. How can we model MapReduce? PRAM •No limit on the number of processors •Memory is uniformly accessible from any processor •No limit on the memory available Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 11. How can we model MapReduce? STREAMING •Just one processor •There is a limited amount of memory •No parallelization Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 12. MapReduce model [Karloff, Suri and Vassilvitskii] • N is the input size and 0 is some fixed constant Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 13. MapReduce model [Karloff, Suri and Vassilvitskii] • N is the input size and 0 is some fixed constant 1− •Less than N machines Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 14. MapReduce model [Karloff, Suri and Vassilvitskii] • N is the input size and 0 is some fixed constant 1− •Less than N machines 1− •Less than N memory on each machine Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 15. MapReduce model [Karloff, Suri and Vassilvitskii] • N is the input size and 0 is some fixed constant 1− •Less than N machines 1− •Less than N memory on each machine i i MRC : problem that can be solved in O(log N ) rounds Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 16. Combining map and reduce phase •Mapper and Reducer work only on a subgraph Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 17. Combining map and reduce phase •Mapper and Reducer work only on a subgraph •Keep time in each round polynomial Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 18. Combining map and reduce phase •Mapper and Reducer work only on a subgraph •Keep time in each round polynomial •Time is constrained by the number of rounds Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 19. Algorithmic challenges •No machine can see the entire input Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 20. Algorithmic challenges •No machine can see the entire input •No communication between machines during each phase Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 21. Algorithmic challenges •No machine can see the entire input •No communication between machines during each phase 2−2 •Total memory is N Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 22. MapReduce vs MUD algorithms •In MUD framework each reducer operates on a stream of data. •In MUD, each reducer is restricted to only using polylogarithmic space. Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 23. Our settings Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 24. Our settings •We study the Karloff, Suri and Vassilvitskii model Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 25. Our settings •We study the Karloff, Suri and Vassilvitskii model 0 •We focus on class MRC Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 26. Our settings •We assume to work with dense graph m = n, 1+c for some constant c 0 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 27. Our settings •We assume to work with dense graph m = n, 1+c for some constant c 0 •Empirical evidences that social networks are dense graphs [Leskovec, Kleinberg and Faloutsos] Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 28. Dense graph motivation [Leskovec, Kleinberg and Faloutsos] •They study 9 different social networks Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 29. Dense graph motivation [Leskovec, Kleinberg and Faloutsos] •They study 9 different social networks •They show that several graphs from different 1+c domains have n edges Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 30. Dense graph motivation [Leskovec, Kleinberg and Faloutsos] •They study 9 different social networks •They show that several graphs from different 1+c domains have n edges •Lowest value of c founded .08 and four graphs have c .5 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 31. Our results Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 32. Results Constant rounds algorithms for •Maximal matching •Minimum cut •8-approx for maximum weighted matching •2-approx for vertex cover •3/2-approx for edge cover Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 33. Notation • G = (V, E) : Input graph • n: number of nodes • m : number of edges • η : memory available on each machine • N : input size Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 34. Filtering •Part of the input is dropped or filtered on the first stage in parallel Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 35. Filtering •Part of the input is dropped or filtered on the first stage in parallel •Next some computation is performed on the filtered input Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 36. Filtering •Part of the input is dropped or filtered on the first stage in parallel •Next some computation is performed on the filtered input •Finally some patchwork is done to ensure a proper solution Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 37. Filtering Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 38. Filtering FILTER Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 39. Filtering FILTER COMPUTE SOLUTION Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 40. Filtering FILTER COMPUTE SOLUTION PATCHWORK ON REST OF THE GRAPH Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 41. Filtering FILTER COMPUTE SOLUTION PATCHWORK ON REST OF THE GRAPH Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
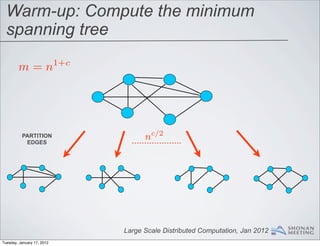
- 42. Warm-up: Compute the minimum spanning tree m=n 1+c Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 43. Warm-up: Compute the minimum spanning tree m=n 1+c PARTITION EDGES nc/2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 44. Warm-up: Compute the minimum spanning tree m=n 1+c PARTITION EDGES nc/2 n1+c/2 edges Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 45. Warm-up: Compute the minimum spanning tree n1+c/2 edges Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 46. Warm-up: Compute the minimum spanning tree n1+c/2 edges COMPUTE MST nc/2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 47. Warm-up: Compute the minimum spanning tree n1+c/2 edges COMPUTE MST nc/2 SECOND ROUND nc/2 n1+c/2 edges Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 48. Show that the algorithm is in MRC0 •The algorithm is correct Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 49. Show that the algorithm is in MRC0 •The algorithm is correct •No edge in the final solution is discarded in partial solution Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 50. Show that the algorithm is in MRC0 •The algorithm is correct •No edge in the final solution is discarded in partial solution •The algorithm runs in two rounds Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 51. Show that the algorithm is in MRC0 •The algorithm is correct •No edge in the final solution is discarded in partial solution •The algorithm runs in two rounds c •No more than O n 2 machines are used Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 52. Show that the algorithm is in MRC0 •The algorithm is correct •No edge in the final solution is discarded in partial solution •The algorithm runs in two rounds c •No more than O n 2 machines are used •No machine uses memory greater than O(n 1+c/2 ) Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 53. Maximal matching •Algorithmic difficulty is that each machine can only see edges assigned to the machine Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 54. Maximal matching •Algorithmic difficulty is that each machine can only see edges assigned to the machine •Is a partitioning based algorithm feasible? Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 55. Partitioning algorithm Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 56. Partitioning algorithm PARTITIONING Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 57. Partitioning algorithm PARTITIONING COMBINE MATCHINGS Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 58. Partitioning algorithm PARTITIONING COMBINE MATCHINGS It is impossible to build a maximal matching using only red edges!! Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 59. Algorithmic insight •Consider any subset of the edges E Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 60. Algorithmic insight •Consider any subset of the edges E •Let M be a maximal matching on G[E ] Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 61. Algorithmic insight •Consider any subset of the edges E •Let M be a maximal matching on G[E ] •The unmatched vertices form a independent set Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 62. Algorithmic insight •We pick each edge with probability p Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 63. Algorithmic insight •We pick each edge with probability p •Find a matching on a sample and then find a matching on unmatched vertices Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 64. Algorithmic insight •We pick each edge with probability p •Find a matching on a sample and then find a matching on unmatched vertices •For dense portions of the graph, many edges should be sampled Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 65. Algorithmic insight •We pick each edge with probability p •Find a matching on a sample and then find a matching on unmatched vertices •For dense portions of the graph, many edges should be sampled •Sparse portions of the graph are small and can be placed on a single machine Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 66. Algorithm •Sample each edge independently with probability 10 log n p= nc/2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 67. Algorithm •Sample each edge independently with probability 10 log n p= nc/2 •Find a matching on the sample Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 68. Algorithm •Sample each edge independently with probability 10 log n p= nc/2 •Find a matching on the sample •Consider the induced subgraph on unmatched vertices Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 69. Algorithm •Sample each edge independently with probability 10 log n p= nc/2 •Find a matching on the sample •Consider the induced subgraph on unmatched vertices •Find a matching on this graph and output the union Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
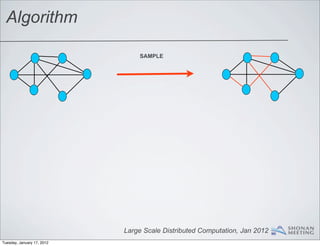
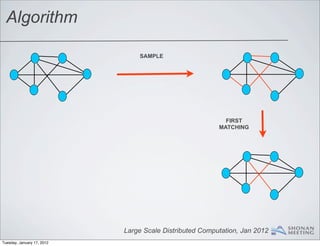
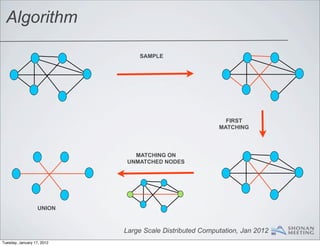
- 70. Algorithm Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 71. Algorithm SAMPLE Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 72. Algorithm SAMPLE FIRST MATCHING Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 73. Algorithm SAMPLE FIRST MATCHING MATCHING ON UNMATCHED NODES Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 74. Algorithm SAMPLE FIRST MATCHING MATCHING ON UNMATCHED NODES UNION Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 75. Correctness •Consider the last step of the algorithm Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 76. Correctness •Consider the last step of the algorithm •All unmatched vertices are placed on a machine Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 77. Correctness •Consider the last step of the algorithm •All unmatched vertices are placed on a machine •All unmatched vertices or are matched at the last step or have only matched neighbors Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 78. Bounding the rounds Three rounds: •Sampling the edges Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 79. Bounding the rounds Three rounds: •Sampling the edges •Find a matching on a single machine for the sampled edges Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 80. Bounding the rounds Three rounds: •Sampling the edges •Find a matching on a single machine for the sampled edges •Find a matching for the unmatched vertices Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 81. Bounding the memory 10 log n •Each edge was sampled with probability p = nc/2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 82. Bounding the memory 10 log n •Each edge was sampled with probability p = nc/2 ˜ 1+c/2 ) •Using Chernoff the sampled graph has size O(n with high probability Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 83. Bounding the memory 10 log n •Each edge was sampled with probability p = nc/2 ˜ 1+c/2 ) •Using Chernoff the sampled graph has size O(n with high probability •Can we bound the size of the induced subgraph on the unmatched vertices? Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 84. Bounding the memory 1+c/2 •For a fixed induced subgraph with at least n edges the probability an edge is not sampled is: n1+c/2 10 log n 1− ≤ exp(−10n log n) nc/2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 85. Bounding the memory 1+c/2 •For a fixed induced subgraph with at least n edges the probability an edge is not sampled is: n1+c/2 10 log n 1− ≤ exp(−10n log n) nc/2 •Union bounding over all 2 induced subgraphs shows n that at least one edge is sampled from every dense subgraph with probability 1 1 − exp(−10 log n) ≥ 1 − 10 n Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 86. Using less memory ˜ 1+c/2 ) •Can we run the algorithm with less then O(n memory? Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 87. Using less memory ˜ 1+c/2 ) •Can we run the algorithm with less then O(n memory? •We can amplify our sampling technique! Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 88. Using less memory •Sample as many edges as possible that fits in memory Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 89. Using less memory •Sample as many edges as possible that fits in memory •Find a matching Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 90. Using less memory •Sample as many edges as possible that fits in memory •Find a matching •If the edges between unmatched vertices fit onto a single machine, find a matching on those vertices Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 91. Using less memory •Sample as many edges as possible that fits in memory •Find a matching •If the edges between unmatched vertices fit onto a single machine, find a matching on those vertices •Otherwise, recurse on the unmatched nodes Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 92. Using less memory •Sample as many edges as possible that fits in memory •Find a matching •If the edges between unmatched vertices fit onto a single machine, find a matching on those vertices •Otherwise, recurse on the unmatched nodes 1+ •With n memory each iteration a factor of n edges are removed resulting in O(c/) rounds Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 93. Parallel computation power •Maximal matching algorithm does not use parallelization Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 94. Parallel computation power •Maximal matching algorithm does not use parallelization •We use a single machine in every step Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 95. Parallel computation power •Maximal matching algorithm does not use parallelization •We use a single machine in every step •When parallelization is used? Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
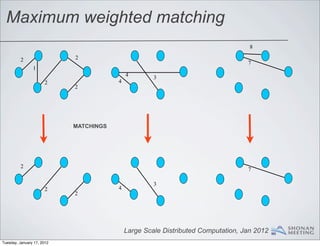
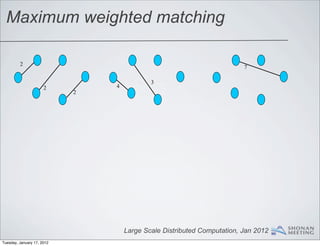
- 96. Maximum weighted matching 8 2 2 7 1 4 3 4 2 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 97. Maximum weighted matching 8 2 2 7 1 4 3 4 2 2 SPLIT THE GRAPH 8 2 2 7 1 4 3 2 4 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 98. Maximum weighted matching 8 2 2 7 1 4 3 2 4 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 99. Maximum weighted matching 8 2 2 7 1 4 3 2 4 2 MATCHINGS 2 7 3 2 4 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 100. Maximum weighted matching 2 7 3 2 4 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 101. Maximum weighted matching 2 7 3 2 4 2 SCAN THE EDGE SEQUENTIALLY 2 7 3 4 2 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 102. Bounding the rounds and memory Four rounds: •Splitting the graph and running the maximal matching: ˜ 1+c/2 ) memory 3 rounds and O(n •Compute the final solution: 1 round and O(n log n) memory Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 103. Approximation guarantee (sketch) •An edge in the solution can block at most 2 edges in each subgraph of smaller weight 8 2 7 3 2 4 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 104. Approximation guarantee (sketch) •An edge in the solution can block at most 2 edges in each subgraph of smaller weight 8 2 7 3 2 4 2 •We loose a factor or 2 because we do not consider the weight Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 105. Other algorithms Based on the same intuition: •2-approx for vertex cover •3/2-approx for edge cover Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 106. Minimum cut •Partition does not work, because we loose structural informations Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 107. Minimum cut •Partition does not work, because we loose structural informations •Sampling does not seem to work either Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 108. Minimum cut •Partition does not work, because we loose structural informations •Sampling does not seem to work either •We can use the first steps of Karger algorithm as a filtering technique Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 109. Minimum cut •Partition does not work, because we loose structural informations •Sampling does not seem to work either •We can use the first steps of Karger algorithm as a filtering technique •The random choices made in the early rounds succeed with high probability, whereas the later rounds have a much lower probability of success Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 110. Minimum cut 1 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 111. Minimum cut RANDOM WEIGHT n δ1 3 1 5 1 2 3 2 2 3 1 1 3 4 4 4 3 4 4 3 1 3 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 112. Minimum cut RANDOM WEIGHT n δ1 3 1 5 1 2 3 2 2 3 1 1 3 4 4 4 3 4 4 3 1 3 2 COMPRESS EDGES WITH SMALL WEIGTH 2 2 2 2 2 2 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 113. Minimum cut RANDOM WEIGHT n δ1 3 1 5 1 2 3 2 2 3 1 1 3 4 4 4 3 4 4 3 1 3 2 COMPRESS EDGES WITH SMALL WEIGTH 2 2 2 2 2 2 2 From Karger at least one graph will contain a min cut w.h.p. Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
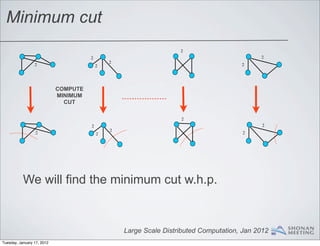
- 114. Minimum cut 2 2 2 2 2 2 2 Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 115. Minimum cut 2 2 2 2 2 2 2 COMPUTE MINIMUM CUT 2 2 2 2 2 2 2 We will find the minimum cut w.h.p. Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 116. Empirical result (matching) %#! '()(**+*,*-.)/012 30)+(2/4- %!! !#$%'(%)#*+,' $#! $!! #! ! !!!$ !!!# !!$ !!% !!# !$ $ -.%/0'1234.4)0)*5'(/,' Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 117. Open problems Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 118. Open problems 1 •Maximum matching •Shortest path •Dynamic programming Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 119. Open problems 2 •Algorithms for sparse graph •Does connected components require more than 2 rounds? •Lower bounds Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012
- 120. Thank you! Large Scale Distributed Computation, Jan 2012 Tuesday, January 17, 2012









![MapReduce model
[Karloff, Suri and Vassilvitskii]
• N is the input size and 0 is some fixed
constant
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-12-320.jpg)
![MapReduce model
[Karloff, Suri and Vassilvitskii]
• N is the input size and 0 is some fixed
constant
1−
•Less than N machines
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-13-320.jpg)
![MapReduce model
[Karloff, Suri and Vassilvitskii]
• N is the input size and 0 is some fixed
constant
1−
•Less than N machines
1−
•Less than N memory on each machine
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-14-320.jpg)
![MapReduce model
[Karloff, Suri and Vassilvitskii]
• N is the input size and 0 is some fixed
constant
1−
•Less than N machines
1−
•Less than N memory on each machine
i i
MRC : problem that can be solved in O(log N )
rounds
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-15-320.jpg)











![Our settings
•We assume to work with dense graph m = n, 1+c
for some constant c 0
•Empirical evidences that social networks are dense
graphs
[Leskovec, Kleinberg and Faloutsos]
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-27-320.jpg)
![Dense graph motivation
[Leskovec, Kleinberg and Faloutsos]
•They study 9 different social networks
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-28-320.jpg)
![Dense graph motivation
[Leskovec, Kleinberg and Faloutsos]
•They study 9 different social networks
•They show that several graphs from different
1+c
domains have n edges
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-29-320.jpg)
![Dense graph motivation
[Leskovec, Kleinberg and Faloutsos]
•They study 9 different social networks
•They show that several graphs from different
1+c
domains have n edges
•Lowest value of c founded .08 and four graphs
have c .5
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-30-320.jpg)



























![Algorithmic insight
•Consider any subset of the edges E
•Let M be a maximal matching on
G[E ]
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-60-320.jpg)
![Algorithmic insight
•Consider any subset of the edges E
•Let M be a maximal matching on
G[E ]
•The unmatched vertices form a
independent set
Large Scale Distributed Computation, Jan 2012
Tuesday, January 17, 2012](https://image.slidesharecdn.com/slidesfilteringamethodforsolvinggraphproblemsinmapreduce-120703014253-phpapp01/85/Filtering-a-method-for-solving-graph-problems-in-map-reduce-61-320.jpg)