Functional data structures

Functional data structures
Ralf Lämmel
Software Languages Team
University of Koblenz-Landau
Important comment on sources: Most code, text, and illustrations
(modulo rephrasing or refactoring) have been extracted from the „Handbook
of Data Structures and Applications“, Chapter 40 „Functional Data Structures“
by Chris Okasaki. At the time of writing (these slides), the handbook is freely
available online: http://www.e-reading-lib.org/bookreader.php/138822/Mehta_-
_Handbook_of_Data_Structures_and_Applications.pdf
!
Further sources are cited on individual slides.

http://101companies.org/wiki/
Data_structure

A functional data structure is a data structure that is suitable for
implementation in a functional programming language, or for coding in
an ordinary language like C or Java using a functional style. Functional
data structures are closely related to persistent data structures and
immutable data structures.
Source: Chapter 40: Functional Data Structures by C. Okasaki. In: Handbook of Data Structures and Applications. Chapman & Hall/CRC.

Stacks

A functional data structure
for stacks in Haskell
data Stack = Empty | Push Int Stack
empty = Empty
push x s = Push x s
top (Push x s) = x
pop (Push x s) = s

The „functional“ push operationl Data Structures
s′
= push(4, s)
(Before)
123
s
(After)
1234
ss′

The „functional“ pop operationFIGURE 40.3: The push operation.
s′′
= pop(s′
)
(Before)
1234
ss′
(After)
1234
ss′
s′′

for stacks in Java
public class Stack {
private int elem;
private Stack next;
public static final Stack empty = null;
public static Stack push(int x,Stack s) {
return new Stack(x,s);
}
public static int top(Stack s) { return s.elem; }
public static Stack pop(Stack s) { return s.next; }
private Stack(int elem, Stack next) {
this.elem = elem;
this.next = next;
}
}

A non-functional data structure
for stacks in Java
public class Stack {
private class Node {
private int elem;
private Node next;
}
private Node first;
public Stack() {} // "empty"
public void push(int x) {
Node n = new Node();
n.elem = x;
n.next = first;
first = n;
}
public int top() { return first.elem; }
public void pop() { first = first.next; }
}

persistent immutable
functional

• The term persistent data structures refers to the general
class of data structures in which an update does not destroy
the previous version of the data structure, but rather creates
a new version that co-exists with the previous version. See
the handbook (Chapter 31) for more details about persistent
data structures.
• The term immutable data structures emphasizes a
particular implementation technique for achieving
persistence, in which memory devoted to a particular version
of the data structure, once initialized, is never altered.
• The term functional data structures emphasizes the
language or coding style in which persistent data structures
are implemented. Functional data structures are always
immutable, except in a technical sense discussed (related to
laziness and memoization).

Functional programming speciﬁcs
related to data structures
• Immutability as opposed to imperative variables
• Recursion as opposed to control ﬂow with loops
• Garbage collection as opposed to malloc/dealloc
• Pattern matching

Perceived advantages of
functional data structures
• Fewer bugs as data cannot change suddenly
• Increased sharing as defensive cloning is not needed
• Decreased synchronization as a consequence

Sets
data Set e s = Set {
empty :: s e,
insert :: e -> s e -> s e,
search :: e -> s e -> Bool
}
Let’s look at different
implementations of this signature!

A naive, equality- and list-based
implementation of sets in Haskell
set :: Eq e => Set e []
set = Set {
empty = [],
insert = e s ->
case s of
[] -> [e]
s'@(e':s'') ->
if e==e'
then s'
else e':insert set e s'',
search = e s ->
case s of
[] -> False
(e':s') -> e==e' || search set e s'
}
The time complexity is
embarrassing: insertion and
search takes time proportional
to the size of the set.

Sets based on binary search trees
in Haskell
data BST e = Empty | Node (BST e) e (BST e)
set :: Ord e => Set e BST
set = Set {
empty = Empty,
insert = ...,
search = ...
}
That is, we go for
another implementation
with, hopefully, better
time complexity.

in Haskell
search = e s ->
case s of
Empty -> False
(Node s1 e' s2) ->
if e<e'
then search set e s1
else if e>e'
then search set e s2
else True
The running time of search is proportional
to the length of the search path — just like
in a non-persistent implementation.

in Haskell
insert = e s ->
case s of
Empty -> Node Empty e Empty
(Node s1 e' s2) ->
if e<e'
then Node (insert set e s1) e' s2
else if e>e'
then Node s1 e' (insert set e s2)
else Node s1 e' s2,
The running time of insert is
also proportional to the
length of the search path.

Operations of functional data structures involve
path copying8 Handbook of Data Structures a
t′
= insert(8, t)
(Before)
4
2 6
1 3 5 7
t
(After)
t t′
Handbook of Data Structures and Applications
t′
= insert(8, t)
(Before)
4
2 6
1 3 5 7
t
(After)
t ′
4
2 6
1 3 5 7
t
(After)
4
2 6
1 3 5 7
t
4
6
7
8
t′
For example:

Benchmark results
benchmarking NaiveSet/insert
mean: 5.673453 ms, lb 5.610866 ms, ub 5.836548 ms, ci 0.950
std dev: 480.9444 us, lb 228.4352 us, ub 986.8636 us, ci 0.950
found 16 outliers among 100 samples (16.0%)
4 (4.0%) high mild
12 (12.0%) high severe
variance introduced by outliers: 72.809%
variance is severely inflated by outliers
benchmarking BinarySearchTree/insert
mean: 241.3734 us, lb 240.6849 us, ub 242.4783 us, ci 0.950
15 (15.0%) low severe
5 (5.0%) low mild
2 (2.0%) high mild
variance is moderately inflated by outliers
Insert is (much)
faster with binary
search trees.
https://github.com/101companies/101repo/tree/master/concepts/Functional_data_structure/Set

Benchmark results
benchmarking NaiveSet/search
10 (10.0%) high mild
benchmarking BinarySearchTree/search
std dev: 172.8071 ns, lb 139.6882 ns, ub 203.6180 ns, ci 0.950
Search is (much)
faster with binary
search trees.
https://github.com/101companies/101repo/tree/master/concepts/Functional_data_structure/Set

Discussion of binary search trees
• „Of course“, a balanced variation would be needed:
• AVL trees
• Red-black trees
• 2-3 trees
• Weight-balanced trees
• Path copying still applies
• Time complexity Ok
• Space complexity Ok because of garbage collection

Priority queues — a tougher example

Priority queues
Path copying is suﬃcient for implementing many tree-based data structures besides bina
40.4 Skew Heaps: Amortization and Lazy Evaluation
• empty: a constant representing the empty heap.
• insert(x,h): insert the element x into the heap h and return the new heap.
• findMin(h): return the minimum element of h.
• deleteMin(h): delete the minimum element of h and return the new heap.
• merge(h1,h2): combine the heaps h1 and h2 into a single heap and return the
new heap.
2005 by Chapman & Hall/CRC
earch trees, including binomial queues [7, 15] (Chapter 7), leftist heaps [18, 24] (Chapter
Next, we turn to priority queues, or heaps, supporting the following primitives:
Patricia tries [26] (Chapter 28), and many others.

Heaps:
an efﬁcient implementation of priority queues
• A tree structure with keys at the nodes.
• Max-heap: maximum key value always at the root.
• Min-heap: minimum key value always at the root.
• Note:
• No particular order on the children.
• Heaps are essentially partially ordered trees.

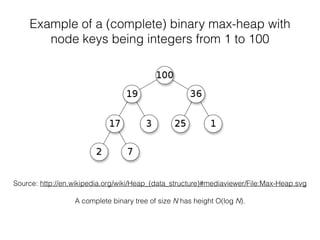
Example of a (complete) binary max-heap with
node keys being integers from 1 to 100
Source: http://en.wikipedia.org/wiki/Heap_(data_structure)#mediaviewer/File:Max-Heap.svg
!
A complete binary tree of size N has height O(log N).

Signature of heaps
data Heap e t = Heap {
empty :: t e,
insert :: e -> t e -> t e,
findMin :: t e -> Maybe e,
deleteMin :: t e -> Maybe (t e),
merge :: t e -> t e -> t e
}

A tree-based representation type
for heaps
data Tree e
= Empty
| Node e (Tree e) (Tree e)
deriving (Eq, Show)
leaf e = Node e Empty Empty

heap = Heap {
empty = Empty,
insert = x t -> merge' (Node x Empty Empty) t,
findMin = t -> case t of
Empty -> Nothing
(Node x _ _) -> Just x,
deleteMin = t -> case t of
Empty -> Nothing
(Node _ l r) -> Just (merge' l r),
merge = l r -> case (l, r) of
(Empty, t) -> t
(t, Empty) -> t
(t1@(Node x1 l1 r1), t2@(Node x2 l2 r2)) ->
if x1 <= x2
then Node x1 (merge' l1 r1) t2
else Node x2 t1 (merge' l2 r2)
}
where merge' = merge heap
This is not yet „optimal“.

heap = Heap {
empty = Empty,
insert = x t -> merge' (Node x Empty Empty) t,
findMin = t -> case t of
Empty -> Nothing
(Node x _ _) -> Just x,
deleteMin = t -> case t of
Empty -> Nothing
(Node _ l r) -> Just (merge' r l),
merge = l r -> case (l, r) of
(Empty, t) -> t
(t, Empty) -> t
(t1@(Node x1 l1 r1), t2@(Node x2 l2 r2)) ->
if x1 <= x2
then Node x1 (merge' t2 r1) l1
else Node x2 (merge' t1 r2) l2
}
where merge' = merge heap
Let’s make our heaps self-adjusting.!
We swap arguments of merge.!
These are so-called skew heaps.

Merging two skew heaps
Merge interleaves the rightmost
paths of the two trees in sorted order
(on the left path), swapping the
children of nodes along the way.

Without swapping, the rightmost
path would get „too“ long.

public class Skew {
public static final Skew empty = null;
public static Skew insert(int x,Skew s) { return merge(new Skew(x,null,null),s); }
public static int findMin(Skew s) { return s.elem; }
public static Skew deleteMin(Skew s) { return merge(s.left,s.right); }
public static Skew merge(Skew s,Skew t) {
if (t == null) return s;
else if (s == null) return t;
else if (s.elem < t.elem)
return new Skew(s.elem,merge(t,s.right),s.left);
else
return new Skew(t.elem,merge(s,t.right),t.left);
}
private int elem;
private Skew left,right;
private Skew(int elem, Skew left, Skew right) {
this.elem = elem; this.left = left; this.right = right;
}
}
for skew heaps in Java
We will need to revise this
implementation.

this.left = left;
this.right = right;
}
}
FIGURE 40.10: First attempt at skew heaps in
1
6 2
6 3
6 4
6 5
6
FIGURE 40.11: An unbalanced skew heap
[5, 6, 4, 6, 3, 6, 2, 6, 1, 6]
The shown tree is an
unbalanced skew heap
generated by inserting the
listed numbers.
Skew heaps are not
balanced, and individual
operations can take linear
time in the worst case.

Complexity of operation sequences
ght;
URE 40.10: First attempt at skew heaps in Java
1
6 2
6 3
6 4
6 5
6
FIGURE 40.11: An unbalanced skew heap.
Inserting a new element such as 7 into this
unbalanced skew heap would take linear time.
However, in spite of the fact that any one
operation can be inefﬁcient, the way that
children are regularly swapped keeps the
operations efﬁcient „in average“. Insert,
deleteMin, and merge run in logarithmic
(amortized) time.

Amortization
Available online: https://www.cs.cmu.edu/~sleator/papers/adjusting-heaps.pdf
SIAM J. COMPUT.
Vol. 15, No. 1, February 1986
@ 1986 Society for Industrial and Applied Mathematics
004
SELF-ADJUSTING HEAPS*
DANIEL DOMINIC SLEATORt AND ROBERT ENDRE TARJANt
Abstract. In this paper we explore two themes in data structure design: amortized computational
complexity and self-adjustment. We are motivated by the following observations. In most applications of
data structures, we wish to perform not just a single operation but a sequence of operations, possibly having
correlated behavior. By averaging the running time per operation over a worst-case sequence of operations,
we can sometimes obtain an overall time bound much smaller than the worst-case time per operation
multiplied by the number of operations. We call this kind of averaging amortization.
Standard kinds of data structures, such as the many varieties of balanced trees, are specifically designed
so that the worst-case time per operation is small. Such efficiency is achieved by imposing an explicit
structural constraint that must be maintained during updates, at a cost of both running time and storage
space. However, if amortized running time is the complexity measure of interest, we can guarantee efficiency
without maintaining a structural constraint. Instead, during each access or update operation we adjust the
data structure in a simple, uniform way. We call such a data structure self-adjusting.
In this paper we develop the skew heap, a self-adjusting form of heap related to the leftist heaps of
Crane and Knuth. (What we mean by a heap has also been called a “priority queue” or a “mergeable
heap”.) Skew heaps use less space than leftist heaps and similar worst-case-efficient data structures and are
…

Persistence may break amortized bounds.
ght;
1
6 2
6 3
6 4
6 5
6
However, naively incorporating path
copying causes the logarithmic
amortized bounds to degrade to the
linear worst-case bounds.

!
To see this, consider repeated insertion
of large elements into a tree. Each
insertion could be applied to the
original tree. Thus, each insertion
would have linear costs resulting also
in average linear costs.

Impact of laziness
ght;
1
6 2
6 3
6 4
6 5
6
If we benchmark the Haskell
implementation, we do not observe linear
behavior though! Instead, the operations
appear to retain their logarithmic
amortized bounds, even under persistent
usage. This pleasant result is a
consequence of a fortuitous interaction
between path copying and lazy
evaluation.

Pending merge
ﬁndMin
Under lazy evaluation, operations such as merge are not actually executed until their
results are needed. Instead, a new kind of node that we might call a pending merge
(see the diamonds) is automatically created. The pending merge lays dormant until
some other operation such as ﬁndMin needs to know the result. Then and only then is
the pending merge executed. The node representing the pending merge is overwritten
with the result so that it cannot be executed twice. (This is benign mutation.)

(a) insert 2,3,1,6,4,5,7 (b) findMin (returns 1)
7
5
4
6
1
3 2
1
7
4 2
3
5 6
(c) deleteMin (d) findMin (returns 2)
7
4 2
3
5 6
2
5
6
4 7 3
A sequence of
operations
Pending merges do not affect the end
results of those steps. After all the
pending merges have been executed, the
ﬁnal tree is identical to the one
produced by skew heaps without lazy
evaluation. (Printing the tree would
execute all pending nodes!) Some
functional languages allow this kind of
mutation, known as memoization,
because it is invisible to the user, except
in terms of efﬁciency.

public class Skew {
private int elem;
private Skew left,right;
private boolean pendingMerge;
public static final Skew empty = null;
public static Skew insert(int x,Skew s) {
return merge(new Skew(x,null,null),s);
}
public static int findMin(Skew s) {
executePendingMerge(s);
return s.elem;
}
public static Skew deleteMin(Skew s) {
executePendingMerge(s);
return merge(s.left,s.right);
}
public static Skew merge(Skew s,Skew t) {
if (t == null) return s;
else if (s == null) return t;
else return new Skew(s,t); // create a pending merge
}
private Skew(int elem, Skew left, Skew right) { ... }
private Skew(Skew left,Skew right) { ... } // create a pending merge
private static void executePendingMerge(Skew s) { ... }
}
A
Java
im
plem
entation
with
pending
m
erges

private Skew(int elem, Skew left, Skew right) {
this.elem = elem;
this.left = left;
this.right = right;
pendingMerge = false;
}
private Skew(Skew left,Skew right) { // create a pending merge
this.left = left;
this.right = right;
pendingMerge = true;
}
private static void executePendingMerge(Skew s) {
if (s != null && s.pendingMerge) {
Skew s1 = s.left, s2 = s.right;
executePendingMerge(s1);
executePendingMerge(s2);
if (s2.elem < s1.elem) {
Skew tmp = s1;
s1 = s2; s2 = tmp;
} s.elem = s1.elem;
s.left = merge(s2,s1.right);
s.right = s1.left;
s.pendingMerge = false;
}
}
A
Java
im
plem
entation
with
pending
m
erges

Summary
• Functional DS are persistent and in „functional style“.
• We looked at stacks, sets, and heaps.
• Functional and „non“-f. DS can be equally efﬁcient.
• Lazy evaluation includes memoization.
• Have a look at methods of amortized analysis!

Functional data structures

Recommended

More Related Content

What's hot (20)

Similar to Functional data structures (20)

More from Ralf Laemmel (15)

Recently uploaded (20)

Functional data structures