Game theory for neural networks
- 1. Game theory for Neural Networks David Balduzzi VUW C3 Research Camp
- 2. Goals “a justification is objective if, in principle, it can be tested and understood by anybody” — Karl Popper
- 3. Objective knowledge • How is knowledge created? • How is knowledge shared? Goals
- 4. • Deductive reasoning (a priori knowledge) • foundation of mathematics • formal: mathematical logic • operational: Turing machines, lambda calculus Background
- 5. Tiny Turing Machine Alvy Ray Smith, based on [Yurii Rogozhin 1996]
- 6. Tiny Turing Machine Alvy Ray Smith, based on [Yurii Rogozhin 1996]
- 7. • Deductive reasoning (a priori knowledge) • foundation of mathematics • formal: mathematical logic • operational: Turing machines, lambda calculus • Inductive reasoning (empirical knowledge) • foundation of science • formal: learning theory • operational: SVMs, neural networks, etc. Background
- 8. • What’s missing? • To be objective, knowledge must be shared • How can agents share knowledge? • A theory of distributed reasoning • induction builds on deduction • distribution should build on both
- 9. Neural Networks • Superhuman performance on object recognition (ImageNet) • Outperformed humans at recognising street-signs (Google streetview). • Superhuman performance on Atari games (Google). • Real-time translation: English voice to Chinese voice (Microsoft).
- 10. 30 years of trial-and-error • Architecture • Weight-tying (convolutions) • Max-pooling • Nonlinearity • Rectilinear units (Jarrett 2009) • Credit assignment • Backpropagation • Optimization • Stochastic Gradient Descent • Nesterov momentum, BFGS, AdaGrad, etc. • RMSProp (Riedmiller 1993, Hinton & Tieleman 200x) • Regularization • Dropout (Srivastava 2014) or • Batch-Normalization (Szegedy & Ioffe 2015)
- 11. • Concrete problem: • Why does gradient descent work on neural nets? • Not just gradient descent; many methods designed for convex problems work surprisingly well on neural nets. • Big picture: • Neural networks are populations of learners • that distribute knowledge extremely effectively. We should study them as such. This tutorial
- 12. • Deduction • Induction • Gradients • Games • Neural networks Outline
- 13. Deductive reasoning “we are regarding the function of the mathematician as simply to determine the truth or falsity of propositions”
- 14. All men are mortal Socrates is a man Deductive reasoning Socrates is mortal
- 15. All men are mortal Socrates is a man Deductive reasoning Socrates is mortal Idea: Intelligence is deductive reasoning!
- 16. Articles
- 17. Trenchard More, John McCarthy, Marvin Minsky, Oliver Selfridge, Ray Solomonoff 50 years later
- 18. “To understand the real world, we must have a different set of primitives from the relatively simple line trackers suitable and sufficient for the blocks world” — Patrick Winston (1975) Director of MIT’s AI lab from 1972-1997 A bump in the road
- 20. Reductio ad absurdum “Intelligence is 10 million rules” — Doug Lenat
- 21. Deductive reasoning • Structure: • axioms; • logical laws; • production system • Derive complicated (empirical) truths from simple (self- evident) truths • Deductive reasoning provides no guidance about which axiom(s) to eliminate when “derived truths” contradict experience • In general, deductive reasoning has nothing to say about mistakes except “avoid them” • In retrospect, it’s hard to understand why anyone thought deduction would yield artificial intelligence.
- 22. Inductive reasoning “this book is composed […] upon one very simple theme […] that we can learn from our mistakes”
- 23. Inductive reasoning Socrates is mortal Plato is mortal [ … more examples …] All men are mortal
- 24. Inductive reasoning All observed As are Bs a is an A a is a B
- 25. The problem of induction All observed As are Bs a is an A a is a B This is clearly false. The conclusion does not follow from the premises.
- 26. “If a machine is […] infallible, it cannot also be intelligent. There are […] theorems which say almost exactly that. But these theorems say nothing about how much intelligence may be displayed if a machine makes no pretence at infallibility.” [ it’s ok to make mistakes ]
- 27. Let’s look at some examples
- 28. Sequential prediction Scenario: At time t, Forecaster predicts 0 or 1. Nature then reveals the truth. Forecaster has access to N experts. One of them is always correct. Goal: Predict as accurately as possible.
- 29. Halving Algorithm While t>0: Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. t ← t+1Step 3. Set t = 1.
- 30. While t>0: Question: Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. t ← t+1Step 3. How long to find correct expert? Set t = 1. Halving Algorithm
- 31. While t>0: BAD!!! Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. t ← t+1Step 3. How long to find correct expert? Set t = 1. Halving Algorithm
- 32. While t>0: Question: Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. t ← t+1Step 3. How many errors? Set t = 1. Halving Algorithm
- 33. Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. How many errors? Halving Algorithm
- 34. Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. How many errors? When algorithm makes a mistake, it removes ≥ half of experts Halving Algorithm
- 35. ≤ log N Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. How many errors? When algorithm makes a mistake, it removes ≥ half of experts Halving Algorithm
- 36. What’s going on? Didn’t we just use deductive reasoning!?!
- 37. What’s going on? Didn’t we just use deductive reasoning!?! Yes… but No!
- 38. What’s going on? Algorithm: makes educated guesses about Nature Analysis: proves theorem about number of errors (inductive) (deductive)
- 39. What’s going on? Algorithm: makes educated guesses about Nature Analysis: proves theorem about number of errors (inductive) (deductive) The algorithm learns — but it does not deduce!
- 40. Adversarial prediction Scenario: At time t, Forecaster predicts 0 or 1. Nature then reveals the truth. Forecaster has access to N experts. One of them is always correct. Nature is adversarial. Goal: Predict as accurately as possible.
- 41. At time t, Forecaster predicts 0 or 1. Nature then reveals the truth. Forecaster has access to N experts. One of them is always correct. Nature is adversarial. Goal: Predict as accurately as possible. Seriously?!?!
- 42. Regret Let m* be the best expert in hindsight. regret := # mistakes(Forecaster) - # mistakes(m*) Goal: Predict as accurately as possible. Minimize regret.
- 43. While t>0: Question: Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. t ← t+1Step 3. What is the regret? Set t = 1. Halving Algorithm ADVERSARIAL SETTING
- 44. While t>0: Question: Predict by majority vote.Step 1. Remove experts that are wrong.Step 2. t ← t+1Step 3. What is the regret? Set t = 1. Halving Algorithm ADVERSARIAL SETTING BAD!
- 45. While t ≤ T: Question: Predict by weighted majority vote.Step 1. Multiply incorrect experts by β.Step 2. t ← t+1Step 3. What is the regret? Set t = 1. Weighted Majority Alg Pick β in (0,1). Assign 1 to experts.
- 46. While t ≤ T: Predict by weighted majority vote.Step 1. Multiply incorrect experts by β.Step 2. t ← t+1Step 3. Set t = 1. What is the regret? [ choose β carefully ] r T · log N 2 Pick β in (0,1). Assign 1 to experts. Weighted Majority Alg
- 47. Loss functions `(y, y0 ) = 1 2 ⇣ y y0 ⌘2 `(p, i) = ( log(1 p) if i = 0 log(p) else `(y, y0 ) = ( 0 if y = y0 1 else • 0/1 loss • Mean square error • Logistic loss
- 48. Loss functions `(y, y0 ) = 1 2 ⇣ y y0 ⌘2 `(p, i) = ( log(1 p) if i = 0 log(p) else `(y, y0 ) = ( 0 if y = y0 1 else • 0/1 loss • Mean square error • Logistic loss not convex convex
- 49. Exp. Weights Alg. While t ≤ T: Predict the weighted sum.Step 1. Multiply expert i byStep 2. t ← t+1Step 3. Set t = 1. What is the regret? [ choose β carefully ] Pick β > 0. Assign 1 to experts. e ·`(ft i ,yt ) log N + p 2T log N
- 50. Inductive reasoning • Structure: • game played over a series of rounds • on each round, experts make predictions • Forecaster takes weighted average of predictions • Nature reveals the truth and a loss is incurred • Forecaster adjusts weights • correct experts —> increase weights; • incorrect —> decrease • Goal: • average loss per round converges to best-in- hindsight
- 51. Inductive reasoning • How it works • Forecaster adjusts strategy according to prior experience • Current strategy encodes previous mistakes • No guarantee on any particular example • Performance is optimal on average • Still to come • How can Forecaster communicate its knowledge with others, in a way that is useful to them?
- 52. Gradient descent “the great watershed in optimisation isn’t between linearity and nonlinearity, but convexity and nonconvexity” — Tyrrell Rockafellar
- 53. Gradient descent • Everyone knows (?) gradient descent • Take a fresh look: • gradient descent is a no-regret algorithm • —> game theory • —> neural networks
- 54. Online Convex Opt. Scenario: Convex set K; differentiable loss L(a,b) that is convex function of a At time t, Forecaster picks at in K Nature responds with bt in K [ Nature is adversarial ] Forecaster’s loss is L(a,b) Goal: Minimize regret. � �� �� �� � � � � � � �� �
- 55. Follow the Leader Idea: Predict the at that would have worked best on { b1, … ,bt-1 }
- 56. While t ≤ T: Step 1. Step 2. Set t = 1. Follow the Leader Idea: t ← t+1 Pick a1 at random. at := argmin a2K "t 1X i=1 L(a, bi) # Predict the at that would have worked best on { b1, … ,bt-1 }
- 57. While t ≤ T: Step 1. Step 2. Set t = 1. Follow the Leader BAD! Problem: Nature pulls Forecaster back-and-forth No memory! t ← t+1 Pick a1 at random. at := argmin a2K "t 1X i=1 L(a, bi) #
- 58. While t ≤ T: Step 1. Step 2. Set t = 1. t ← t+1 FTRL Pick a1 at random. regularize at := argmin a2K "t 1X i=1 L(a, bi) + 2 · kak2 2 #
- 59. While t ≤ T: Step 1. Step 2. Set t = 1. FTRL t ← t+1 Pick a1 at random. gradient descent at at 1 · @ @a L(at 1, bt 1)
- 60. While t ≤ T: Step 1. Step 2. Set t = 1. FTRL Intuition: β controls memory t ← t+1 Pick a1 at random. at at 1 · @ @a L(at 1, bt 1)
- 61. While t ≤ T: Step 1. Step 2. Set t = 1. FTRL What is the regret? [ choose β carefully ] diam(K) · Lipschitz(L) · p T t ← t+1 Pick a1 at random. at at 1 · @ @a L(at 1, bt 1)
- 62. Logarithmic regret regret [ choose β carefully ] Convergence at rate is actually quite slow • For many common loss functions • (e.g. mean-square error, logistic loss) • it is possible to do much better p T T log T T
- 63. Information theory Two connections • Entropic regularization <—> • Exponential Weights Algorithm • Analogy between gradients and Fano information • “the information represented by y about x” log P(x|y) P(x)
- 64. Gradient descent • Gradient descent is fast, cheap, and guaranteed to converge — even against adversaries • “a hammer that smashes convex nails” � �� �� �� � � � � � � �� � • GD is well-understood in convex settings • Convergence rate depends on the structure of the loss, size of search space, etc.
- 65. Convex optimization Convex methods • Stochastic gradient descent • Nesterov momentum • BFGS (Broyden-Fletcher-Goldfarb-Shanno) • Conjugate gradient methods • AdaGrad
- 66. Online Convex Opt. (deep learning) Apply Gradient Descent to nonconvex optimization (neural networks). • Theorems don’t work (not convex) • tons of engineering (decades of tweaking) Amazing performance. Figure 3 | From image to text. Captions generated by a recurrent neural network (RNN) taking, as extra input, the representation extracted by a deep with permission from ref. 102. When the RNN is given the ability to focus attention on a different location in the input image (middle and bottom; th Deep CNN Generating RNN A group of people shopping at an outdoor market. There are many vegetables at the fruit stand. A woman is throwing a frisbee in a park. A little girl sitting on a bed with a teddy bear. A group of people sitting on a boat in the water. A giraffe standing in a forest with trees in the background. A dog is standing on a hardwood floor. A stop sign is on a road with a mountain in the background
- 67. Deep Learning • Superhuman performance on object recognition (ImageNet) • Outperformed humans at recognising street-signs (Google streetview). • Superhuman performance on Atari games (Google). • Real-time translation: English voice to Chinese voice (Microsoft).
- 68. Game theory “An equilibrium is not always an optimum; it might not even be good. This may be the most important discovery of game theory.” — Ivar Ekeland
- 69. Game theory • So far • Seen how Forecaster can learn to use “expert” advice. • Forecaster modifies the weights of experts such that it converges to optimal-in-hindsight predictions. • Who are these experts? • We will model them as Forecasters in their own right • First, let’s develop tools for modeling populations.
- 70. Setup • Players A, B with actions {a1, a2, … am} and {b1, b2, … bn} • Two payoff matrices, describing the losses/gains of the players for every combination of moves • Goal of players is to maximise-gain / minimise-loss • Neither player knows what the other will do
- 71. Setup • Players A, B with actions {a1, a2, … am} and {b1, b2, … bn} • Two payoff matrices, describing the losses/gains of the players for every combination of moves A B R P R P 0 Rock-paper -scissors (zero-sum game) S S 0 0 -1 1 1 -1 -1 1 A B R P R P 0 S S 0 0 1 -1 -1 1 1 -1
- 72. Minimax theorem inf a2K sup b2K L(a, b) = sup b2K inf a2K L(a, b)
- 73. Minimax theorem Forecaster picks a, Nature responds b inf a2K sup b2K L(a, b) = sup b2K inf a2K L(a, b)
- 74. Minimax theorem Forecaster picks a, Nature responds b Nature picks b, Forecaster responds a inf a2K sup b2K L(a, b) = sup b2K inf a2K L(a, b)
- 75. Minimax theorem Forecaster picks a, Nature responds b Nature picks b, Forecaster responds a inf a2K sup b2K L(a, b) = sup b2K inf a2K L(a, b) A B R P R P 0 S S 0 0 -1 1 1 -1 -1 1 A B R P R P 0 S S 0 0 1 -1 -1 1 1 -1
- 76. Minimax theorem Forecaster picks a, Nature responds b Nature picks b, Forecaster responds a inf a2K sup b2K L(a, b) = sup b2K inf a2K L(a, b) inf a2K sup b2K L(a, b) sup b2K inf a2K L(a, b) going first hurts Forecaster, so
- 77. Minimax theorem Proof idea: No-regret algorithm → → → Forecaster can asymptotically match hindsight Order of players doesn’t matter asymptotically Convert series of moves into average via online-to-batch. Let m* be the best move in hindsight. regret := loss(Forecaster) - loss(m*) inf a2K sup b2K L(a, b) sup b2K inf a2K L(a, b)
- 78. Minimax theorem Proof idea: No-regret algorithm → → → Forecaster can asymptotically match hindsight Order of players doesn’t matter asymptotically Convert series of moves into average via online-to-batch. Let m* be the best move in hindsight. regret := loss(Forecaster) - loss(m*) inf a2K sup b2K L(a, b) sup b2K inf a2K L(a, b)
- 79. Minimax theorem Proof idea: No-regret algorithm → → → Forecaster can asymptotically match hindsight Order of players doesn’t matter asymptotically Convert series of moves into average via online-to-batch. Let m* be the best move in hindsight. regret := loss(Forecaster) - loss(m*) inf a2K sup b2K L(a, b) sup b2K inf a2K L(a, b)
- 80. Minimax theorem Proof idea: No-regret algorithm → → → Forecaster can asymptotically match hindsight Order of players doesn’t matter asymptotically Convert series of moves into average via online-to-batch. Let m* be the best move in hindsight. regret := loss(Forecaster) - loss(m*) ¯a = 1 T TX t=1 at inf a2K sup b2K L(a, b) sup b2K inf a2K L(a, b)
- 81. Nash equilibrium Nash equilibrium <—> no player benefits by deviating
- 82. Nash equilibrium Nash equilibrium <—> no player benefits by deviating A B Deny Confess Deny Confess -2/-2 -6/0 0/-6 -6/-6 Prisoner’s dilemma:
- 83. Nash equilibrium Problems: • Computationally hard (PPAD-complete, Daskalakis 2008) • Some outcomes are very bad
- 84. Nash equilibrium A B Stop Go Stop Go 0/0 10/0 0/10 -∞/-∞ Blind-intersection dilemma:
- 85. Nash equilibrium A B Stop Go Stop Go 0/0 10/0 0/10 -∞/-∞ Blind-intersection dilemma: Equilibrium: both drivers STOP; no-one uses intersection
- 86. Correlated equilibrium A B Stop Go Stop Go 0/0 10/0 0/10 -∞/-∞ Traffic light: P(x, y) = 8 >< >: 1 2 if x = S and y = G 1 2 if x = G and y = S 0 else Blind-intersection dilemma:
- 87. Correlated equilibrium A B Stop Go Stop Go 0/0 10/0 0/10 -∞/-∞ Blind-intersection dilemma: • Better outcomes for players: Correlated equilibria can be much better than Nash equilibria (depending on the signal)
- 88. Convex games • Players with convex action sets • Loss functions where and each loss is separately convex in each argument • Players aim to minimize their losses • Player do not know what other players will do `i(w1, . . . , wN) {Pi}N i=1 {Ki}N i=1 wi 2 Ki
- 89. Sketch of proof: Since player j applies a no-regret algorithm, it follows that after T rounds, its sequence of moves {wt j} has a loss within of the optimal, wj *. Interpreting the historical sequence of plays as a signal obtains The result follows by letting —> 0. No-regret —> Corr. eqm 1 T X `i(wt j , wt j) `i(w⇤ j , wt j) ✏ 8w⇤ j ✏ ✏ E h `(w) i E h `(w⇤ j , w j) i + ✏
- 90. Nash —> Aumann From Nash equilibrium to correlated equilibrium: • Computationally tractable: No-regret algorithms converge on coarse correlated equilibria • Better outcomes: Signal is the past actions of players, chosen according to an optimal strategy
- 91. • Every game has a Nash equilibrium • Economists typically assume that economy is in Nash equilibrium • But Nash equilibria are hard to find and are often unpleasant • Correlated equilibria are easier to compute and can be better for the players • A signal is required to coordinate players: • set signally externally • e.g. traffic light • in repeated games, construct signal as the average of historical behavior • e.g. no-regret learning Game theory
- 92. • Correlated equilibrium • Players converge on mutually agreeable outcomes by adapting to each other’s behavior over repeated rounds • The signal provides a “strong hint” about where to find equilibria. • Nash equilibrium • It’s hard to guess what others will do when playing de novo (intractability); and • You haven’t established a track record to build on (undesirability) Game theory
- 93. Gradients and Games Gradient descent is a no-regret algorithm • Insert players using gradient descent into any convex game, and they will converge on a correlated equilibrium • Global convergence to correlated equilibrium is controlled by convergence of players to their best-in-hindsight local optimum Next: • Gradient descent + chain rule = backprop
- 94. Neural networks “Anything a human can do in a fraction of a second, a deep network can do too” — Ilya Sutskever
- 95. • Origins • Backpropagation (Werbos 1974, Rumelhart 1986) • Convolutional nets (Fukushima 1980, LeCun 1990) • Mid-1990s — Mid-2000s • back to convex methods; neural networks ignored • Unsupervised pre-training • restricted Boltzmann machines (Hinton 2006) • autoencoders (Bengio 2007) • Convolutional nets • sharp improvement on ImageNET challenge (Krizhevsky 2012) • back to fully-supervised training History
- 96. • Convolutional nets • sharp improvement on ImageNET challenge (Krizhevsky 2012) • back to fully-supervised training History
- 97. 30 years of trial-and-error • Architecture • Weight-tying (convolutions) • Max-pooling • Nonlinearity • Rectilinear units (Jarrett 2009) • Credit assignment • Backpropagation • Optimization • Stochastic Gradient Descent • Nesterov momentum, BFGS, AdaGrad, etc. • RMSProp (Riedmiller 1993, Hinton & Tieleman 200x) • Regularization • Dropout (Srivastava et al 2014) or • Batch-Normalization (Szegedy & Ioffe 2015)
- 98. Why (these) NNs? • Why neural networks? • GPUs • Good local minima (no-one knows why) • “Mirrors the world’s compositional structure” • Why ReLUs, Why Max-Pooling, Why convex methods? • “locally” convex optimization (this talk)
- 99. Neural networks Input Layer1 W1 Matrix mult Layer2 W2 Matrix mult Output W3 Matrix mult Nonlinearity Nonlinearity fW(x)
- 100. Neural networks Input Layer1 W1 Matrix mult Layer2 W2 Matrix mult Output W3 Matrix mult Nonlinearity Nonlinearity `(fW(x), y) label loss
- 101. Univ Function Approx Theorem (Leshno 1993): A two-layer neural network with infinite width and nonpolynomial nonlinearity is dense in the space of continuous functions. � ��� �� � � �� ���� ���� ��� ��� ��� � � ��� �� � � �� ���� ���� ��� ��� ��� � Sigmoid Tanh (x) = 1 1 + e x ⌧(x) = ex e x ex + e x � ��� �� � � �� ���� ���� ��� ��� ��� � ReLU ⇢(x) = max(0, x)
- 102. � ��� �� � � �� ���� ���� ��� ��� ��� � � ��� �� � � �� ���� ���� ��� ��� ��� � � ��� �� � � �� ���� ���� ��� ��� ��� � d⇢ dx d dx d⌧ dx � ��� �� � � �� ���� ���� ��� ��� ��� � � ��� �� � � �� ���� ���� ��� ��� ��� � � ��� �� � � �� ���� ���� ��� ��� ��� � ⌧⇢
- 103. The chain rule h g f df dx = df dg · dg dh · dh dx f g h(x) = f(g(h(x)))
- 106. Input W1 W2 W3 Weight updates j Gradient descent Wt+1 ij Wt ij ⌘ · @` @Wij
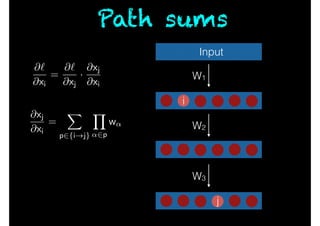
- 107. Input W1 W2 W3 Weight updates j Gradient descent Wt+1 ij Wt ij ⌘ · @` @Wij by the chain rule @` @Wij = @` @xj · @xj @Wij
- 108. Input W1 W2 W3 Weight updates j Gradient descent Wt+1 ij Wt ij ⌘ · @` @Wij by the chain rule since @xj @Wij = xi @` @Wij = @` @xj · xi
- 109. Input W1 W2 W3 Weight updates j Gradient descent Wt+1 ij Wt ij ⌘ · @` @Wij by the chain rule also, define j := @` @xj @` @Wij = j · xi
- 110. Input W1 W2 W3 Weight updates j Gradient descent Wt+1 ij Wt ij ⌘ · @` @Wij by the chain rule How to compute? j := @` @xj @` @Wij = j · xi
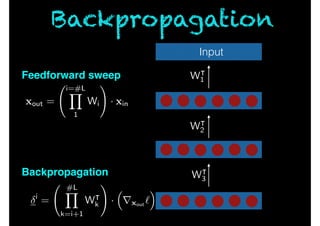
- 111. Input i = #LY k=i+1 W| k ! · ⇣ rxout ` ⌘ xout = i=#LY 1 Wi ! · xin W| 1 W| 2 W| 3 Feedforward sweep Backpropagation Backpropagation
- 112. Max-pooling Pick element with max output in each block; zero out the rest
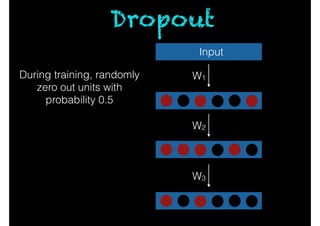
- 113. Dropout Input W1 W2 W3 During training, randomly zero out units with probability 0.5
- 114. ReLU networks Input W1 W2 W3 � ��� �� � � �� ���� ���� ��� ��� ��� � ReLU ⇢(x) = max(0, x)
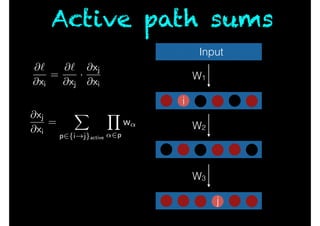
- 117. Active path sums Input W1 W2 W3 i j @` @xi = @` @xj · @xj @xi @xj @xi = X p2{i!j}active Y ↵2p w↵
- 118. Knowledge distribution • Units in NN <—> Players in a game • All units have the same loss • Loss is convex function of units’ weights when unit is active • Units in output layer compute error-gradients • Other units distribute signals of the form (error-gradients) x (path-sums)
- 119. Circadian games • Units have convex losses when active • Neural networks are circadian games • i.e. game that is convex for active (awake) players Main Theorem. Convergence of neural network to correlated equilibrium is upper-bounded by convergence rates of individual units. Corollary. Units perform convex optimization when active. Convex methods and guarantees (on convergence rates) apply to neural networks. —> Explains why ReLUs work so well.
- 120. Philosophical Corollary • Neural networks are games Units are no-regret learners • Unlike many games (e.g. in micro-economic theory), the equilibria in NNs are extremely desirable • Error-backpropagation distributes gradient- information across units • Claim: There is a theory of distributed reasoning implicit in gradient descent and the chain rule.
- 121. The End. Questions?





![Tiny Turing Machine
Alvy Ray Smith, based on [Yurii Rogozhin 1996]](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-5-320.jpg)
![Tiny Turing Machine
Alvy Ray Smith, based on [Yurii Rogozhin 1996]](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-6-320.jpg)















![Inductive reasoning
“this book is composed […] upon one very simple theme
[…] that we can learn from our mistakes”](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-22-320.jpg)
![Inductive reasoning
Socrates is mortal
Plato is mortal
[ … more examples …]
All men are mortal](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-23-320.jpg)


![“If a machine is […] infallible, it cannot also be intelligent.
There are […] theorems which say almost exactly that. But
these theorems say nothing about how much intelligence may
be displayed if a machine makes no pretence at infallibility.”
[ it’s ok to make mistakes ]](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-26-320.jpg)



















![While t ≤ T:
Predict by weighted majority vote.Step 1.
Multiply incorrect experts by β.Step 2.
t ← t+1Step 3.
Set t = 1.
What is the regret? [ choose β carefully ]
r
T · log N
2
Pick β in (0,1). Assign 1 to experts.
Weighted Majority Alg](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-46-320.jpg)


![Exp. Weights Alg.
While t ≤ T:
Predict the weighted sum.Step 1.
Multiply expert i byStep 2.
t ← t+1Step 3.
Set t = 1.
What is the regret?
[ choose β carefully ]
Pick β > 0. Assign 1 to experts.
e ·`(ft
i ,yt
)
log N +
p
2T log N](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-49-320.jpg)




![Online Convex Opt.
Scenario: Convex set K;
differentiable loss L(a,b)
that is convex function of a
At time t,
Forecaster picks at in K
Nature responds with bt in K
[ Nature is adversarial ]
Forecaster’s loss is L(a,b)
Goal: Minimize regret.
�
�� �� �� � � � �
�
�
��
�](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-54-320.jpg)






![While t ≤ T:
Step 1.
Step 2.
Set t = 1.
FTRL
What is the regret?
[ choose β carefully ]
diam(K) · Lipschitz(L) ·
p
T
t ← t+1
Pick a1 at random.
at at 1 ·
@
@a
L(at 1, bt 1)](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-61-320.jpg)
![Logarithmic regret
regret
[ choose β carefully ]
Convergence at rate is actually quite slow
• For many common loss functions
• (e.g. mean-square error, logistic loss)
• it is possible to do much better
p
T
T
log T
T](https://image.slidesharecdn.com/gtnn-160126192355/85/Game-theory-for-neural-networks-62-320.jpg)