Greedy algorithm activity selection fractional
- 1. Greedy Algorithms Dr. AMIT KUMAR @JUET
- 2. Greedy algorithms • A greedy algorithm always makes the choice that looks best at the moment – My everyday examples: • Driving • Playing cards • Invest on stocks • Choose a university – The hope: a locally optimal choice will lead to a globally optimal solution – For some problems, it works • greedy algorithms tend to be easier to code Dr. AMIT KUMAR @JUET
- 3. An Activity Selection Problem (Conference Scheduling Problem) • Input: A set of activities S = {a1,…, an} • Each activity has start time and a finish time – ai=(si, fi) • Two activities are compatible if and only if their interval does not overlap • Output: a maximum-size subset of mutually compatible activities Dr. AMIT KUMAR @JUET
- 4. The Activity Selection Problem • Here are a set of start and finish times • What is the maximum number of activities that can be completed? • {a3, a9, a11} can be completed • But so can {a1, a4, a8’ a11} which is a larger set • But it is not unique, consider {a2, a4, a9’ a11} Dr. AMIT KUMAR @JUET
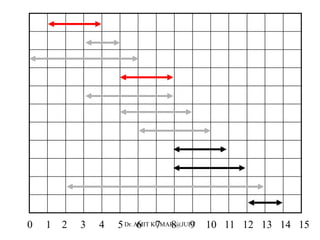
- 5. Interval Representation Dr. AMIT KUMAR @JUET
- 6. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 7. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 8. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 9. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 10. Early Finish Greedy • Select the activity with the earliest finish • Eliminate the activities that could not be scheduled • Repeat! Dr. AMIT KUMAR @JUET
- 11. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 12. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 13. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 14. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 15. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 16. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 17. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET
- 18. Example: The solution set = {1, 4, 8, 11} Algorithm: Step 1: Sort fi into nondecreasing order. After sorting, f1 f2 f3 … fn. Step 2: Add the next activity i to the solution set if i is compatible with each in the solution set. Step 3: Stop if all activities are examined. Otherwise, go to step 2. Time complexity: O(nlogn) i 1 2 3 4 5 6 7 8 9 10 11 si 1 3 0 5 3 5 6 8 8 2 12 fi 4 5 6 7 8 9 10 11 12 13 14 Dr. AMIT KUMAR @JUET
- 19. Solution of the example: Solution = {1, 4, 8, 11} i si fi accept 1 1 4 Yes 2 3 5 No 3 0 6 No 4 5 7 Yes 5 3 8 No 7 6 10 No 8 8 11 Yes 9 8 12 No 10 2 13 No 11 12 14 Yes Dr. AMIT KUMAR @JUET
- 20. Assuming activities are sorted by finish time Dr. AMIT KUMAR @JUET
- 21. Why it is Greedy? • Greedy in the sense that it leaves as much opportunity as possible for the remaining activities to be scheduled • The greedy choice is the one that maximizes the amount of unscheduled time remaining Dr. AMIT KUMAR @JUET
- 22. Why this Algorithm is Optimal? • We will show that this algorithm uses the following properties • The problem has the optimal substructure property • The algorithm satisfies the greedy-choice property • Thus, it is Optimal Dr. AMIT KUMAR @JUET
- 23. Elements of Greedy Strategy • An greedy algorithm makes a sequence of choices, each of the choices that seems best at the moment is chosen – NOT always produce an optimal solution • Two ingredients that are exhibited by most problems that lend themselves to a greedy strategy – Greedy-choice property – Optimal substructure Dr. AMIT KUMAR @JUET
- 24. Greedy-Choice Property • A globally optimal solution can be arrived at by making a locally optimal (greedy) choice – Make whatever choice seems best at the moment and then solve the sub-problem arising after the choice is made – The choice made by a greedy algorithm may depend on choices so far, but it cannot depend on any future choices or on the solutions to sub-problems • Of course, we must prove that a greedy choice at each step yields a globally optimal solution Dr. AMIT KUMAR @JUET
- 25. Optimal Substructures • A problem exhibits optimal substructure if an optimal solution to the problem contains within it optimal solutions to sub-problems – If an optimal solution A to S begins with activity 1, then A’ = A – {1} is optimal to S’={i S: si f1} Dr. AMIT KUMAR @JUET
- 26. Knapsack Problem • One wants to pack n items in a luggage – The ith item is worth vi dollars and weighs wi pounds – Maximize the value but cannot exceed W pounds – vi , wi, W are integers • 0-1 knapsack each item is taken or not taken • Fractional knapsack fractions of items can be taken • Both exhibit the optimal-substructure property – 0-1: If item j is removed from an optimal packing, the remaining packing is an optimal packing with weight at most W-wj – Fractional: If w pounds of item j is removed from an optimal packing, the remaining packing is an optimal packing with weight at most W-w that can be taken from other n-1 items plus wj – w of item j Dr. AMIT KUMAR @JUET
- 27. Greedy Algorithm for Fractional Knapsack problem • Fractional knapsack can be solvable by the greedy strategy – Compute the value per pound vi/wi for each item – Obeying a greedy strategy, take as much as possible of the item with the greatest value per pound. – If the supply of that item is exhausted and there is still more room, take as much as possible of the item with the next value per pound, and so forth until there is no more room – O(n lg n) (we need to sort the items by value per pound) – Greedy Algorithm? – Correctness? Dr. AMIT KUMAR @JUET
- 28. The Fractional knapsack problem • n objects, each with a weight wi > 0 a profit pi > 0 capacity of knapsack: M Maximize Subject to 0 xi 1, 1 i n p xi i i n1 w x Mi i i n1 Dr. AMIT KUMAR @JUET
- 29. • The greedy algorithm: Step 1: Sort pi/wi into nonincreasing order. Step 2: Put the objects into the knapsack according to the sorted sequence as possible as we can. • e. g. n = 3, M = 20, (p1, p2, p3) = (25, 24, 15) (w1, w2, w3) = (18, 15, 10) Sol: p1/w1 = 25/18 = 1.39 p2/w2 = 24/15 = 1.6 p3/w3 = 15/10 = 1.5 Optimal solution: x1 = 0, x2 = 1, x3 = 1/2 total profit = 24 + 7.5 = 31.5 The Fractional knapsack problem Dr. AMIT KUMAR @JUET
- 30. Optimal substructures • Define the following subset of activities which are activities that can start after ai finishes and finish before aj starts • Sort the activities according to finish time • We now define the the maximal set of activities from i to j as • Let c[i,j] be the maximal number of activities • We can solve this using dynamic programming, but a simpler approach exists • Our recurrence relation for finding c[i, j] becomes Dr. AMIT KUMAR @JUET





























![Optimal substructures
• Define the following subset of activities which are activities that
can start after ai finishes and finish before aj starts
• Sort the activities according to finish time
• We now define the the maximal set of activities from i to j as
• Let c[i,j] be the maximal number of activities
• We can solve this using dynamic programming, but a simpler
approach exists
• Our recurrence relation for finding c[i, j] becomes
Dr. AMIT KUMAR @JUET](https://image.slidesharecdn.com/greedyalgorithmactivityselectionfractional-180514053110/85/Greedy-algorithm-activity-selection-fractional-30-320.jpg)