Integer programming branch and bound

C-1
C
IntegerProgramming:
TheBranchand
BoundMethod

C-2 Module C Integer Programming: The Branch and Bound Method
TheBranchandBoundMethod
The branch and bound method is not a solution technique specifically limited to integer
programming problems. It is a solution approach that can be applied to a number of differ-
ent types of problems. The branch and bound approach is based on the principle that the
total set of feasible solutions can be partitioned into smaller subsets of solutions. These
smaller subsets can then be evaluated systematically until the best solution is found. When
the branch and bound approach is applied to an integer programming problem, it is used
in conjunction with the normal noninteger solution approach. We will demonstrate the
branch and bound method using the following example.
The owner of a machine shop is planning to expand by purchasing some new
machines—presses and lathes. The owner has estimated that each press purchased will
increase profit by $100 per day and each lathe will increase profit by $150 daily. The num-
ber of machines the owner can purchase is limited by the cost of the machines and the
available floor space in the shop. The machine purchase prices and space requirements are
as follows.
Required
Machine Floor Space (ft2) Purchase Price
Press 15 $8,000
Lathe 30 4,000
The owner has a budget of $40,000 for purchasing machines and 200 square feet of
available floor space. The owner wants to know how many of each type of machine to pur-
chase to maximize the daily increase in profit.
The linear programming model for an integer programming problem is formulated in
exactly the same way as the linear programming examples in chapters 2 and 4 of the text.
The only difference is that in this problem, the decision variables are restricted to integer
values because the owner cannot purchase a fraction, or portion, of a machine. The linear
programming model follows.
maximize Z ϭ $100x1 ϩ 150x2
subject to
8,000x1 ϩ 4,000x2 Յ $40,000
15x1 ϩ 30x2 Յ 200 ft2
x1, x2 Ն 0 and integer
The branch and bound method is
a solution approach that parti-
tions the feasible solution space
into smaller subsets of solutions.

where
x1 ϭ number of presses
x2 ϭ number of lathes
The decision variables in this model are restricted to whole machines. The fact that both
decision variables, x1 and x2, can assume any integer value greater than or equal to zero is
what gives this model its designation as a total integer model.
We begin the branch and bound method by first solving the problem as a regular linear
programming model without integer restrictions (i.e., the integer restrictions are relaxed).
The linear programming model for the problem and the optimal relaxed solution is
subject to
8,000x1 ϩ 4,000x2 Յ $40,000
15x1 ϩ 30x2 Յ 200 ft2
x1, x2 Ն 0
and
x1 ϭ 2.22, x2 ϭ 5.56, and Z ϭ 1,055.56
The branch and bound method employs a diagram consisting of nodes and branches as
a framework for the solution process. The first node of the branch and bound diagram,
shown in Figure C-1 contains the relaxed linear programming solution shown earlier and
the rounded-down solution.
The Branch and Bound Method C-3
A linear programming model solu-
tion with no integer restrictions is
called a relaxed solution.
The branch and bound method
uses a tree diagram of nodes and
branches to organize the solution
partitioning.
Figure C-1
The initial node in the branch
and bound diagram
1
1,055.56
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
Notice that this node has two designated bounds: an upper bound (UB) of $1,055.56 and
a lower bound (LB) of $950. The lower bound is the Z value for the rounded-down solu-
tion, x1 ϭ 2 and x2 ϭ 5; the upper bound is the Z value for the relaxed solution, x1 ϭ 2.22
and x2 ϭ 5.56. The optimal integer solution will be between these two bounds.
Rounding down might result in a suboptimal solution. In other words, we are hoping
that a Z value greater than $950 might be possible. We are not concerned that a value lower
than $950 might be available. Thus, $950 represents a lower bound for our solution.
Alternatively, since Z ϭ $1,055.56 reflects an optimal solution point on the solution space
boundary, a greater Z value cannot possibly be attained. Hence, Z ϭ $1,055.56 is the upper
bound of our solution.
Now that the possible feasible solutions have been narrowed to values between the
upper and lower bounds, we must test the solutions within these bounds to determine the
best one. The first step in the branch and bound method is to create two solution subsets
from the present relaxed solution. This is accomplished by observing the relaxed solution
value for each variable,
x1 ϭ 2.22
x2 ϭ 5.56
The optimal integer solution will
always be between the upper
bound of the relaxed solution and
a lower bound of the rounded-
down integer solution.
Branch on the variable with the
solution value with the greatest
fractional part.

Figure C-2
Solution subsets x2
1
1,055.56
2 3
x2 5Յ x2 6Ն
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
and seeing which one is the farthest from the rounded-down integer value (i.e., which vari-
able has the greatest fractional part). The .56 portion of 5.56 is the greatest fractional part;
thus, x2 will be the variable that we will “branch” on.
Because x2 must be an integer value in the optimal solution, the following constraints
can be developed.
x2 Յ 5
x2 Ն 6
In other words, x2 can be 0, 1, 2, 3, 4, 5, or 6, 7, 8, etc., but it cannot be a value between
5 and 6, such as 5.56. These two new constraints represent the two solution subsets for our
solution approach. Each of these constraints will be added to our linear programming
model, which will then be solved normally to determine a relaxed solution. This sequence
of events is shown on the branch and bound diagram in Figure C-2. The solutions at nodes
2 and 3 will be the relaxed solutions obtained by solving our example model with the
appropriate constraints added.
Create two constraints (or subsets)
to eliminate the fractional part of
the solution value
First, the solution at node 2 is found by solving the following model with the constraint
x2 Յ 5 added.
subject to
The optimal solution for this model with integer restrictions relaxed (solved using the
computer) is x1 ϭ 2.5, x2 ϭ 5, and Z ϭ 1,000.
Next, the solution at node 3 is found by solving the model with x2 Ն 6 added.
subject to
8,000x1 ϩ 4,000x2 Յ 40,000
15x1 ϩ 30x2 Յ 200
x2 Ն 6
x1, x2 Ն 0
The optimal solution for this model with integer restrictions relaxed is x1 ϭ 1.33,
x2 ϭ 6, and Z ϭ 1,033.33.
x1, x2 Ն 0
x2 Յ 5
15x1 ϩ 30x2 Յ 200
8,000x1 ϩ 4,000x2 Յ 40,000

These solutions with x2 Յ 5 and x2 Ն 6 reflect the partitioning of the original relaxed
model into two subsets formed by the addition of the two constraints. The resulting solu-
tion sets are shown in the graphs in Figure C-3.
Figure C-3
Feasible solution spaces for
nodes 2 and 3
2
6
10
14
18
2 6 10 14 18 x1
x2
x1 = 2.5
x2 = 5
Feasible solution space
x2 = 5
Z = $1,000
Node 2
2
6
10
14
18
2 6 10 14 18 x1
x2
x1 = 1.33
x2 = 6
Feasible solution space
x2 = 6
Z = $1,033
Node 3
Figure C-4
Branch and bound diagram
with upper and lower bounds at
nodes 2 and 3 1
1,055.56
3
1,033
2
1,000
x2 5Յ x2 6Ն
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,033 (x1 = 1.33, x2 = 6)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,000 (x1 = 2.5, x2 = 5)
LB = 950 (x1 = 2, x2 = 5)
Notice that in the node 2 graph in Figure C-3, the solution point x1 ϭ 2.5, x2 ϭ 5
results in a maximum Z value of $1,000, which is the upper bound for this node. Next, notice
that in the node 3 graph,the solution point x1 ϭ 1.33,x2 ϭ 6 results in a maximum Z value of
$1,033. Thus, $1,033 is the upper bound for node 3. The lower bound at each of these
nodes is the maximum integer solution. Since neither of these relaxed solutions is totally
integer, the lower bound remains $950, the integer solution value already obtained at node
1 for the rounded-down integer solution. The diagram in Figure C-4 reflects the addition
of the upper and lower bounds at each node.
Since we do not have an optimal and feasible integer solution yet, we must continue to
branch (i.e., partition) the model, from either node 2 or node 3. A look at Figure C-4
reveals that if we branch from node 2, the maximum value that can possibly be achieved is
$1,000 (the upper bound). However, if we branch from node 3, a higher maximum value
of $1,033 is possible. Thus, we will branch from node 3. In general, always branch from the
node with the maximum upper bound.
Now the steps for branching previously followed at node 1 are repeated at node 3. First,
the variable that has the value with the greatest fractional part is selected. Because x2 has an
integer value, x1, with a fractional part of .33, is the only variable we can select. Thus, two
new constraints are developed from x1,

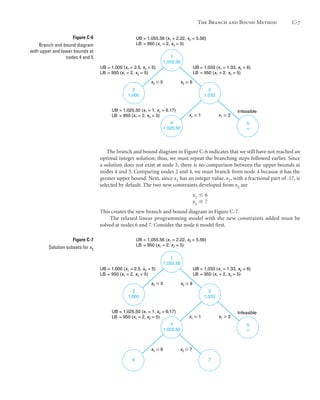
Figure C-5
Solution subsets for x1
1
1,055.56
3
1,033
2
1,000
54
x2 5Յ x2 6Ն
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,033 (x1 = 1.33, x2 = 6)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,000 (x1 = 2.5, x2 = 5)
LB = 950 (x1 = 2, x2 = 5)
x1 1Յ x1 2Ն
x1 Յ 1
x1 Ն 2
This process creates the new branch and bound diagram shown in Figure C-5.
Next, the relaxed linear programming model with the new constraints added must be
solved at nodes 4 and 5. (However, do not forget that the model is not the original, but the
original with the constraint previously added, x2 Ն 6.) Consider the node 4 model first.
maximum Z ϭ 100x1 ϩ 150x2
subject to
8,000x1 ϩ 4,000x2 Յ 40,000
15x1 ϩ 30x2 Յ 200
x2 Ն 6
x1 Յ 1
x1, x2 Ն 0
The optimal solution for this model with integer restrictions relaxed is x1 ϭ 1, x2 ϭ
6.17, and Z ϭ 1,025.
Next, consider the node 5 model.
maximize Z ϭ 100x1 ϩ 150x2
subject to
8,000x1 ϩ 4,000x2 Յ 40,000
15x1 ϩ 30x2 Յ 200
x2 Ն 6
x1 Ն 2
x1, x2 Ն 0
However, there is no feasible solution for this model. Therefore, no solution exists at
node 5, and we have only to evaluate the solution at node 4. The branch and bound dia-
gram reflecting these results is shown in Figure C-6.

Figure C-6
Branch and bound diagram
with upper and lower bounds at
nodes 4 and 5 1
1,055.56
3
1,033
2
1,000
5
∞
4
1,025.50
x2 5Յ x2 6Ն
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,033 (x1 = 1.33, x2 = 6)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,000 (x1 = 2.5, x2 = 5)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,025.50 (x1 = 1, x2 = 6.17)
LB = 950 (x1 = 2, x2 = 5)
Infeasible
x1 1Յ x1 2Ն
Figure C-7
Solution subsets for x2
1
1,055.56
3
1,033
2
1,000
5
∞
4
1,025.50
76
x2 5Յ x2 6Ն
x2 6Յ x2 7Ն
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,033 (x1 = 1.33, x2 = 6)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,000 (x1 = 2.5, x2 = 5)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,025.50 (x1 = 1, x2 = 6.17)
LB = 950 (x1 = 2, x2 = 5)
Infeasible
x1 1Յ x1 2Ն
The branch and bound diagram in Figure C-6 indicates that we still have not reached an
optimal integer solution; thus, we must repeat the branching steps followed earlier. Since
a solution does not exist at node 5, there is no comparison between the upper bounds at
nodes 4 and 5. Comparing nodes 2 and 4, we must branch from node 4 because it has the
greater upper bound. Next, since x1 has an integer value, x2, with a fractional part of .17, is
selected by default. The two new constraints developed from x2 are
x2 Յ 6
x2 Ն 7
This creates the new branch and bound diagram in Figure C-7.
The relaxed linear programming model with the new constraints added must be
solved at nodes 6 and 7. Consider the node 6 model first.

Figure C-8
The branch and bound
diagram with optimal solution
at node 6 1
1,055.56
3
1,033
2
1,000
5
∞
4
1,025.50
7
∞
6
1,000
x2 5Յ x2 6Ն
x2 6Յ x2 7Ն
UB = 1,055.56 (x1 = 2.22, x2 = 5.56)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,033 (x1 = 1.33, x2 = 6)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,000 (x1 = 2.5, x2 = 5)
LB = 950 (x1 = 2, x2 = 5)
UB = 1,025.50 (x1 = 1, x2 = 6.17)
LB = 950 (x1 = 2, x2 = 5)
Infeasible
UB = 1,000 (x1 = 1, x2 = 6)
LB = 1,000 (x1 = 1, x2 = 6)
Infeasible
x1 1Յ x1 2Ն
An optimal integer solution is
reached when a feasible integer
solution is achieved at a node that
has an upper bound greater than
or equal to the upper bound at any
other ending node.
subject to
8,000x1 ϩ 4,000x2 Յ 40,000
15x1 ϩ 30x2 Յ 200
x2 Ն 6
x1 Յ 1
x2 Յ 6
x1, x2 Ն 0
The optimal solution for this relaxed linear programming model is x1 ϭ 1, x2 ϭ 6, and
Z ϭ 1,000.
Next, consider the node 7 model.
subject to
8,000x1 ϩ 4,000x2 Յ 40,000
15x1 ϩ 30x2 Յ 200
x2 Ն 6
x1 Յ 1
x2 Ն 7
x1, x2 Ն 0
However, the solution to this model is infeasible and no solution exists at node 7. The
branch and bound diagram reflecting these results is shown in Figure C-8. This version of
the branch and bound diagram indicates that the optimal integer solution, x1 ϭ 1, x2 ϭ 6,
has been reached at node 6. The value of 1,000 at node 6 is the maximum, or upper bound,
integer value that can be obtained. It is also the recomputed lower bound because it is the
maximum integer solution achieved to this point. Thus, it is not possible to achieve any
higher value by further branching from node 6. A comparison of the node 6 solution with

those at nodes 2, 5, and 7 shows that a better solution is not possible. The upper bound at
node 2 is 1,000, which is the same as that obtained at node 6; thus, node 2 can result in no
improvement. The solutions at nodes 5 and 7 are infeasible (and thus further branching
will result in only infeasible solutions). By the process of elimination, the integer solution at
node 6 is optimal.
In general, the optimal integer solution is reached when a feasible integer solution is
generated at a node and the upper bound at that node is greater than or equal to the upper
bound at any other ending node (i.e., a node at the end of a branch).
In the context of the original example, this solution indicates that if the machine shop
owner purchases one press and six lathes, a daily increase in profit of $1,000 will result.
The steps of the branch and bound method for determining an optimal integer solution
for a maximization model (with Յ constraints) can be summarized as follows.
1. Find the optimal solution to the linear programming model with the integer restric-
tions relaxed.
2. At node 1 let the relaxed solution be the upper bound and the rounded-down integer
solution be the lower bound.
3. Select the variable with the greatest fractional part for branching. Create two new
constraints for this variable reflecting the partitioned integer values. The result will
be a new Յ constraint and a new Ն constraint.
4. Create two new nodes, one for the Ն constraint and one for the Յ constraint.
5. Solve the relaxed linear programming model with the new constraint added at each
of these nodes.
6. The relaxed solution is the upper bound at each node, and the existing maximum
integer solution (at any node) is the lower bound.
7. If the process produces a feasible integer solution with the greatest upper bound
value of any ending node, the optimal integer solution has been reached. If a feasible
integer solution does not emerge, branch from the node with the greatest upper
bound.
8. Return to step 3.
For a minimization model, relaxed solutions are rounded up, and upper and lower
bounds are reversed.
Mixed integer linear programming problems can also be solved using the branch and
bound method. The same basic steps that were applied to the total integer model in the
previous section are used for a mixed integer model with only a few differences.
First, at node 1 only those variables with integer restrictions are rounded down to
achieve the lower bound. Second, in determining which variable to branch from, we select
the greatest fractional part from among only those variables that must be integer. All other
steps remain the same. The optimal solution is reached when a feasible solution is gener-
ated at a node that has integer values for those variables requiring integers and that has
reached the maximum upper bound of all ending nodes.
The 0–1 integer model can also be solved using the branch and bound method. First, the
0–1 restrictions for variables must be reflected as model constraints, xj Յ 1. As an example,
consider the following 0–1 integer model for selecting recreational facilities following from
chapter 5 in the text.
A community council must decide which recreation facilities to construct in its com-
munity. Four new recreation facilities have been proposed—a swimming pool, a tennis
The steps of the branch and bound
method.
can be used for mixed integer
problems, except only variables
with integer restrictions are
rounded down to achieve the ini-
tial lower bound and only integer
variables are branched on.
Solution of the Mixed
Integer Model
Solution of the 0–1
Integer Model

center, an athletic field, and a gymnasium. The council wants to construct facilities that will
maximize the expected daily usage by the residents of the community subject to land and
cost limitations. The expected daily usage and cost and land requirements for each facility
follow.
Expected Usage Land Requirements
Recreation Facility (people/day) Cost ($) (acres)
Swimming pool 300 35,000 4
Tennis center 90 10,000 2
Athletic field 400 25,000 7
Gymnasium 150 90,000 3
The community has a $120,000 construction budget and 12 acres of land. Because the
swimming pool and tennis center must be built on the same part of the land parcel, how-
ever, only one of these two facilities can be constructed. The council wants to know which
of the recreation facilities to construct in order to maximize the expected daily usage. The
model for this problem is formulated as follows.
maximize Z ϭ 300x1 ϩ 90x2 ϩ 400x3 ϩ 150x4
subject to
$35,000x1 ϩ 10,000x2 ϩ 25,000x3 ϩ 90,000x4 Յ $120,000 (capital budget)
4x1 ϩ 2x2 ϩ 7x3 ϩ 3x4 Յ 12 acres (space available)
x1 ϩ x2 Յ 1 facility
x1, x2, x3, x4 ϭ 0 or 1
where
Z ϭ expected daily usage (people per day)
x1 ϭ construction of a swimming pool
x2 ϭ construction of a tennis center
x3 ϭ construction of an athletic field
x4 ϭ construction of a gymnasium
In this model, the decision variables can have a solution value of either zero or one. If a
facility is not selected for construction, the decision variable representing it will have a value
of zero. If a facility is selected, its decision variable will have a value of one.
The last constraint, x1 ϩ x2 Յ 1, reflects the contingency that either the swimming pool
(x1) or the tennis center (x2) can be constructed, but not both. In order for the sum of x1
and x2 to be less than or equal to one, either of the variables can have a value of one, or both
variables can equal zero. This is also referred to as a mutually exclusive constraint.
To apply the branch and bound method, the following four constraints have to be added
to the model in place of the single restriction x1, x2, x3, x4 ϭ 0 or 1.
x1 Յ 1
x2 Յ 1
x3 Յ 1
x4 Յ 1
The only other change in the normal branch and bound method is at step 3. Once the
variable xj with the greatest fractional part has been determined, the two new constraints
can be used for 0–1 integer prob-
lems by adding “ Յ 1” constraints
for each variable.

Problems C-11
Problems
developed from this variable are xj ϭ 0 and xj ϭ 1. These two new constraints will form
the two branches at each node.
Another method for solving 0–1 integer problems is implicit enumeration. In implicit
enumeration, obviously infeasible solutions are eliminated and the remaining solutions are
evaluated (i.e., enumerated) to see which is the best. This approach will be demonstrated
using our original 0–1 example model for selecting a recreational facility (i.e., without the
xj Յ 1 constraints).
The complete enumeration (i.e., the list of all possible solution sets) for this model is as
follows.
1. Consider the following linear programming model
In implicit enumeration all fea-
sible solutions are evaluated to see
which is best.
Solution x1 x2 x3 x4 Feasibility Z Value
1 0 0 0 0 Feasible 0
2 1 0 0 0 Feasible 300
3 0 1 0 0 Feasible 90
4 0 0 1 0 Feasible 400
5 0 0 0 1 Feasible 150
6 1 1 0 0 Infeasible ϱ
7 1 0 1 0 Feasible 700
9 0 1 1 0 Feasible 490
10 0 1 0 1 Feasible 240
11 0 0 1 1 Feasible 550
Solutions 6, 12, 14, and 16 can be immediately eliminated because they violate the third
constraint, x1 ϩ x2 Յ 1. Solutions 8, 13, and 15 can also be eliminated because they violate
the other two constraints. This leaves eight possible solution sets (assuming that solution
1—i.e., choosing none of the recreational facilities—can be eliminated) for consideration.
After evaluating the objective function value of these eight solutions, we find the best solu-
tion to be 7, with x1 ϭ 1, x2 ϭ 0, x3 ϭ 1, x4 ϭ 0. Within the context of the example, this
solution indicates that a swimming pool (x1) and an athletic field (x3) should be con-
structed and that these facilities will generate an expected usage of 700 people per day.
The process of eliminating infeasible solutions and then evaluating the feasible solu-
tions to see which is best is the basic principle behind implicit enumeration. However,
implicit enumeration is usually done more systematically, by evaluating solutions with
branching diagrams like those used in the branch and bound method, rather than by sort-
ing through a complete enumeration as in this previous example.

subject to
3x1 ϩ 4x2 Յ 10
a. Solve this model using the branch and bound method.
b. Demonstrate the solution partitioning graphically.
2. Solve the following linear programming model using the branch and bound method.
minimize Z ϭ 3x1 ϩ 6x2
subject to
7x1 ϩ 3x2 Ն 40
3. A tailor makes wool tweed sport coats and wool slacks. He is able to get a shipment of 150 square
yards of wool cloth from Scotland each month to make coats and slacks, and he has 200 hours of
his own labor to make them each month. A coat requires 3 square yards of wool and 10 hours to
make, and a pair of pants requires 5 square yards of wool and 4 hours to make. He earns $50 in
profit from each coat he makes and $40 from each pair of slacks. He wants to know how many coats
and slacks to produce to maximize profit.
a. Formulate an integer linear programming model for this problem.
b. Determine the integer solution to this problem using the branch and bound method. Compare
this solution with the solution without integer restrictions and indicate if the rounded-down
solution would have been optimal.
4. A jeweler and her apprentice make silver pins and necklaces by hand. Each week they have 80 hours
of labor and 36 ounces of silver available. It requires 8 hours of labor and 2 ounces of silver to make a
pin, and 10 hours of labor and 6 ounces of silver to make a necklace. Each pin also contains a small
gem of some kind. The demand for pins is no more than six per week. A pin earns the jeweler $400
in profit, and a necklace earns $100. The jeweler wants to know how many of each item to make
each week in order to maximize profit.
a. Formulate an integer programming model for this problem.
b. Solve this model using the branch and bound method. Compare this solution with the solu-
tion without integer restrictions and indicate if the rounded-down solution would have been
optimal.
5. A glassblower makes glass decanters and glass trays on a weekly basis. Each item requires 1 pound
of glass, and the glassblower has 15 pounds of glass available every week. A glass decanter requires
4 hours of labor, a glass tray requires only 1 hour of labor, and the glassblower works 25 hours
a week. The profit from a decanter is $50, and the profit from a tray is $10. The glassblower wants
to determine the total number of decanters (x1) and trays (x2) that he needs to produce in order to
maximize his profit.
b. Solve this model using the branch and bound method.
c. Demonstrate the solution partitioning graphically.
6. The Livewright Medical Supplies Company has a total of 12 salespeople it wants to assign to
three regions—the South, the East, and the Midwest. A salesperson in the South earns $600 in
profit per month for the company, a salesperson in the East earns $540, and a salesperson in the
Midwest earns $375. The southern region can have a maximum assignment of 5 salespeople.
The company has a total of $750 per day available for expenses for all 12 salespeople. A sales-

Problems C-13
person in the South has average expenses of $80 per day, a salesperson in the East has average
expenses of $70 per day, and a salesperson in the Midwest has average daily expenses of $50. The
company wants to determine the number of salespeople to assign to each region to maximize
profit.
7. Helen Holmes makes pottery by hand in her basement. She has 20 hours available each week to
make bowls and vases. A bowl requires 3 hours of labor, and a vase requires 2 hours of labor. It
requires 2 pounds of special clay to make a bowl and 5 pounds to produce a vase; she is able to
acquire 35 pounds of clay per week. She sells her bowls for $50 and her vases for $40. She wants to
know how many of each item to make each week in order to maximize her revenue.
b. Solve this model using the branch and bound method. Compare this solution with the solu-
tion with integer restrictions and indicate if the rounded-down solution would have been
optimal.
8. Lauren Moore has sold her business for $500,000 and wants to invest in condominium units
(which she intends to rent) and land (which she will lease to a farmer). She estimates that she will
receive an annual return of $8,000 for each condominium and $6,000 for each acre of land. A con-
dominium unit costs $70,000, and land is $30,000 per acre. A condominium will cost her $1,000
per unit and an acre of land $2,000 for maintenance and upkeep. Lauren wants to know how much
to invest in condominiums and land in order to maximize her annual return.
a. Formulate a mixed integer programming model for this problem.
9. The owner of the Consolidated Machine Shop has $10,000 available to purchase a lathe, a press,
a grinder, or some combination thereof. The following 0–1 integer linear programming model has
been developed for determining which of the three machines (lathe, x1; press, x2; grinder, x3)
should be purchased in order to maximize the annual profit.
maximize Z ϭ 1,000x1 ϩ 700x2 ϩ 800x3 (profit, $)
subject to
5,000x1 ϩ 6,000x2 ϩ 4,000x3 Յ 10,000 (cost, $)
x1, x2, x3 ϭ 0 or 1
Solve this model using the branch and bound method.
10. Solve the following mixed integer linear programming model using the branch and bound method.
maximize Z ϭ 5x1 ϩ 6x2 ϩ 4x3
subject to
5x1 ϩ 3x2 ϩ 6x3 Յ 20
x1 ϩ 3x2 Յ 12
x1, x3 Ն 0
x2 Ն 0 and integer
11. Solve problem 9 using the implicit enumeration method.
12. Consider the following linear programming model.
maximize Z ϭ 20x1 ϩ 30x2 ϩ 10x3 ϩ 40x4

subject to
2x1 ϩ 4x2 ϩ 3x3 ϩ 7x4 Յ 10
10x1 ϩ 7x2 ϩ 20x3 ϩ 15x4 Յ 40
x1 ϩ 10x2 ϩ x3 Յ 10
x1, x2, x3, x4 = 0 or 1
a. Solve this problem using the implicit enumeration method.
b. What difficulties would be encountered with the implicit enumeration method if this problem
were expanded to contain five or more variables and more constraints?

Integer programming branch and bound

Recommended

More Related Content

What's hot (20)

Similar to Integer programming branch and bound (20)

Recently uploaded (20)

Integer programming branch and bound