Introduction to Algorithm Design and Analysis.pdf

Introduction to Algorithms
Dr. Kiran K
Associate Professor
Department of CSE
UVCE
Bengaluru, India.

What is an Algorithm ?
• A sequence of Unambiguous Instructions for Solving a Problem, i.e., for Obtaining
a required Output for any Legitimate Input in a Finite Amount of Time.
• A Finite Set of Instructions that, if followed, Accomplishes a particular Task.
• In addition, all algorithms must satisfy the following criteria:
1. Input :
2. Output :
3. Definiteness :
4. Finiteness :
5. Effectiveness :
• Abu Ja’far Mohammed Ibn Musa al Khowarizmi – Persian Mathematician (825 A.D)
Zero or More.
At Least One.
Clear and Unambiguous.
Terminates after a finite number of steps.
Every Instruction must be very Basic.

Why Study Algorithms ?
• Practical Standpoint:
 It is necessary to Know a Standard Set of Important Algorithms from Different
Areas of Computing.
 Design New Algorithms and Analyze their Efficiency.
• Theoretical Standpoint:
 Algorithmics (Study of Algorithms)
 Recognized as the Cornerstone of Computer Science.
 Relevant to Science, Business, and Technology, etc.
 Develops Analytical Skills.

Examples Illustrating the Notion of Algorithm
Greatest Common Divisor (GCD) of Two Integers m and n
• Three Methods to solve illustrating the following important points:
 Non-Ambiguity.
 Range of Inputs.
 Representing the same algorithm in Several Different Ways.
 Several Algorithms for solving the Same Problem.
 Algorithms for the same problem can be based on Very Different Ideas and can
solve the problem with Dramatically Different Speeds.

Examples Illustrating the Notion of Algorithm…
1. Middle-School Procedure
Step 1: Find the Prime Factors of the First number, m.
Step 2: Find the Prime Factors of the Second number, n.
Step 3: Identify all the Common Factors in the two prime expansions found in
Step 1 and Step 2.
Step 4: Compute the Product of All the Common Factors and return it as the GCD.
GCD (60, 24):
Prime Factors of 60
Prime Factors of 24
Common Factors
Product of Common Factors
= 2 . 2 . 3 . 5
= 2 . 2 . 2 . 3
= 2, 2 and 3
= 2 * 2 * 3 → GCD (60, 24)
= 12

2. Euclid’s Algorithm – Euclid of Alexandria (3rd Century B.C)
GCD (60, 24):
GCD (60, 24)
GCD (24, 12)
n = 0
Euclid’s Algorithm for Computing GCD of m and n
Step 1: If n = 0, return the value of m as the GCD and stop;
otherwise, proceed to Step 2.
Step 2: Divide m by n and assign the value of the Remainder to r.
Step 3: Assign the value of n to m and the value of r to n.
Go to Step 1.
Algorithm Euclid(m, n)
while (n ≠ 0) do
r ← m mod n
m ← n
n ← r
Return m
= GCD (24, 60 mod 24)
= GCD (12, 24 mod 12)
→ GCD = 12
= GCD (24, 12)
= GCD (12, 0)
- GCD (m, n) = GCD (n, m mod n)

3. Consecutive Integer Checking Algorithm
Common Divisor cannot be Greater than the Smaller of the Two Numbers.
Consecutive Integer Checking Algorithm for Computing GCD of m and n
Step 1: Assign the value of min{m, n} to t
Step 2: Divide m by t. If the Remainder of this division is 0, go to Step 3;
otherwise, go to Step 4.
Step 3: Divide n by t. If the Remainder of this division is 0, return the
value of t as the GCD and stop; otherwise, proceed to Step 4.
Step 4: Decrease the value of t by 1. Go to Step 2.
Algorithm Euclid(m, n)
1 t ← min (m, n)
2 if (m % t = 0)
goto 3
else
goto 4
3 if (n % t = 0)
return t
else
goto 4
4 t ← t - 1
5 goto 2

GCD (60, 24):
Min (60, 24) = 24
60 % 24 ≠ 0
60 % 23 ≠ 0
60 % 22 ≠ 0
60 % 21 ≠ 0
60 % 20 = 0
60 % 19 ≠ 0
60 % 18 ≠ 0
60 % 17 ≠ 0
60 % 16 ≠ 0
60 % 15 = 0
60 % 14 ≠ 0
60 % 13 ≠ 0
60 % 12 = 0
24 % 20 ≠ 0
24 % 15 ≠ 0
24 % 12 = 0 → GCD = 12

Comparison:
Range of Inputs Ambiguity Speed
> = 1
> = 0
> = 1 -
-
Steps 1, 2 and 3 Moderate
Fast
Slow
Middle-School Procedure
Euclid’s Algorithm
Consecutive Integer Checking Algorithm

Sieve of Eratosthenes
• Invented in Ancient Greece (200 B.C)
• Generates Consecutive Prime Numbers not exceeding Integer n > 1.
Sieve of Eratosthenes for Generating Prime Numbers up to n
Step 1: Initialize a list of Prime Candidates with consecutive
integers from 2 to n.
Step 2: Eliminate all Multiples of 2.
Step 3: Eliminate all Multiples of the Next Integer Remaining in
the list.
Step 4: Continue in this fashion until no more numbers can be
Eliminated.
Step 5: The Remaining Integers are the Primes needed.
Algorithm Seive (n)
For (p ← 2 to n) do A[p] ← p
For (p ←2 to 𝑛 ) do
If (A[p] ≠ 0)
j ← p ∗ p
While ( j ≤ n) do
A[j ] ← 0
j ← j + p
i ← 0
For (p ← 2 to n) do
If (A[p] ≠ 0)
L[i] ← A[p]
i ← i + 1
Return L
Note:
If p is a number whose multiples are being eliminated, then the First
Multiple existing is p * p because all smaller multiples. 2p, . . , (p − 1) p
have been eliminated on earlier passes through the list.
→ p * p Not Greater than n → p < 𝑛

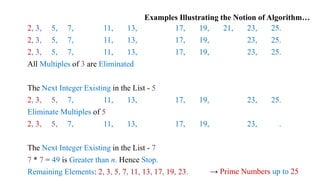
Generate Prime Numbers up to 25
Initialize List with Integers from 2 to 25
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
Consider the First Integer in the List - 2
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
Eliminate Multiples of 2
2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 11, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 11, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25.

2, 3, 5, 7, 9, 11, 13, 15, 17, 18, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 20, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 22, 23, 24, 25.
2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 24, 25.
2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25.
All Multiples of 2 are Eliminated
The Next Integer Existing in the List - 3
2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25.
2, 3, 5, 7, 11, 13, 15, 17, 19, 21, 23, 25.
2, 3, 5, 7, 11, 13, 15, 17, 19, 21, 23, 25.
2, 3, 5, 7, 11, 13, 17, 19, 21, 23, 25.

2, 3, 5, 7, 11, 13, 17, 19, 21, 23, 25.
2, 3, 5, 7, 11, 13, 17, 19, 23, 25.
2, 3, 5, 7, 11, 13, 17, 19, 23, 25.
All Multiples of 3 are Eliminated
2, 3, 5, 7, 11, 13, 17, 19, 23, 25.
2, 3, 5, 7, 11, 13, 17, 19, 23, .
7 * 7 = 49 is Greater than n. Hence Stop.
Remaining Elements: 2, 3, 5, 7, 11, 13, 17, 19, 23. → Prime Numbers up to 25

Fundamentals of Algorithmic Problem Solving
Algorithm Design and Analysis Process

Fundamentals of Algorithmic Problem Solving…
Understanding the Problem:
• Read the Problem’s Description carefully and Ask Questions in case of any Doubts.
• Do a Few Small Examples by Hand.
• Think about Special Cases, and Ask Questions again if needed.
• If the Problem is one of the Type that Arises in computing applications quite often:
 Use a known Algorithm to solve it. it helps to understand how such an algorithm works
and to know its strengths and weaknesses.
 If a algorithm is Not Readily Available, Design a New Algorithm.
• Specify exactly the Set of Instances the algorithm needs to handle.
 Instance – An Input the algorithm solves.
 If Not Specified Correctly, the algorithm may Crash on some Boundary Value.
Note:
A Correct Algorithm is not one that works most of the time, but
one that Works Correctly for All Legitimate Inputs.

Ascertaining the Capabilities of the Computational Device:
• Random-Access Machines – John Von Neumann
 Instructions are Executed one after another, One Operation at a Time.
 Design Sequential Algorithms.
• Parallel Machines
 Can Execute Operations Concurrently, i.e., in Parallel.
 Design Parallel Algorithms.
• Memory and Speed:
 Scientific Purposes:
 No Need to worry
Algorithms are studied in terms Independent of specification parameters for a Particular Computer.
 Practical Purposes:
 Depends on the Problem
o In many situations need not worry.
o If Problems are Very Complex, or have to Process Huge Volumes of Data, or deal with applications
where the Time is Critical, Memory and Speed availability are Crucial.

Choosing between Exact and Approximate Problem Solving:
• Solve a Problem Exactly – Exact Algorithm
• Solve a Problem Approximately – Approximation Algorithm
 Reasons for Developing Approximation Algorithm:
 Problems Cannot be Solved Exactly. Eg.: Extracting Square Roots, Solving Nonlinear
Equations, Evaluating Definite Integrals, etc.
 Available algorithms for solving a problem exactly can be Unacceptably Slow because
of the problem’s intrinsic complexity.
 An Approximation algorithm can be a Part of a More Sophisticated Algorithm that
solves a problem exactly.

Algorithm Design Techniques:
• A General Approach to solving problems algorithmically.
• They provide Guidance for designing algorithms for New Problems.
• Make it possible to Classify Algorithms according to an Underlying Design Idea; therefore,
they can serve as a natural way to both Categorize and Study algorithms.
Designing an Algorithm and Data Structures:
• Designing an Algorithm – Challenging Task.
 Some Design Techniques can be Inapplicable to the problem in question.
 Several Techniques may be Combined - Hard to pinpoint algorithms as applications of
known design techniques.
 Particular Design Technique is Applicable - Requires a Nontrivial Ingenuity.
 Choosing among the general techniques and Applying them gets Easier With Practice.

• Data Structures – Challenging Task.
 Choose data structures Appropriate for the Operations Performed by the algorithm.
Eg.: Sieve of Eratosthenes runs longer if linked list is used instead of an array.
 Some algorithm design techniques depend intimately on Structuring or Restructuring data
specifying a problem’s instance.
 Data structures remain crucially Important for both Design and Analysis of algorithms.
 Algorithms + Data Structures = Programs.
Methods of Specifying an Algorithm:
1. Natural Language:
 Important Skill one should develop.
 Inherent Ambiguity makes a succinct and clear description surprisingly Difficult.

2. Pseudocode:
 Mixture of a Natural Language and Programming Language like constructs.
 More Precise than natural language.
 Usage often yields More Succinct algorithm descriptions.
 No Single Form leaving authors with a need to design their Own Dialects.
3. Flowchart:
 Collection of Connected Geometric Shapes containing descriptions of the algorithm’s steps.
 Dominant in the earlier days of computing.
 Inconvenient except for very simple algorithms.
4. Program:
 Written in a particular Computer Language.
 Considered as the Algorithm’s Implementation.

Proving an Algorithm’s Correctness:
• Prove that the algorithm yields a Required Result for Every Legitimate Input in a finite
amount of time.
• For some algorithms, a proof of correctness is quite easy; for others, it can be quite complex.
• Common Technique – Mathematical Induction.
• For an Approximation Algorithm, show that the error produced by the algorithm does not
Exceed a Predefined Limit.
Note:
• Although Tracing the algorithm’s performance for a few specific inputs can be a very
worthwhile activity, it Cannot Prove the Algorithm’s Correctness Conclusively.
• In order to show that an algorithm is Incorrect, just One Instance of its input for which the
Algorithm Fails is Sufficient.

Analyzing an Algorithm:
• Qualities an algorithm must possess:
1. Correctness
2. Efficiency
 Time Efficiency – How Fast the algorithm runs.
 Space Efficiency – How much Extra Memory an algorithm uses.
3. Simplicity
 Simpler algorithms are Easier to Understand and easier to Program.
 Resulting programs usually contain Fewer Bugs.
 Has Aesthetic appeal.
 Sometimes simpler algorithms are More Efficient than more complicated alternatives.
 Cannot be precisely Defined and Investigated with mathematical rigor.

4. Generality
a) Generality of the Problem the algorithm Solves
 Sometimes it is Easier to design an algorithm for a problem posed in more general
terms.
Eg.: Determine whether two integers are Relatively Prime:
 Design an algorithm for a more general problem of computing the GCD of
two integers.
 Solve the former problem by checking whether the GCD is 1 or not.
 Sometimes designing a more general algorithm is Unnecessary or Difficult or even
Impossible
Eg.: Find the roots of a Quadratic Equation
 Cannot be generalized to handle Polynomials of Arbitrary Degrees.

b) Generality of the Set of Inputs an algorithm Accepts.
 Design an algorithm that can handle a Set of Inputs that is Natural for the
problem at hand.
Eg.: (a) Finding GCD
 Excluding 1 as input is Unnatural.
(b) Find the roots of a Quadratic Equation
 Not implemented for Complex Coefficients unless this capability is
explicitly required.
Coding an Algorithm:
 Presents both a Peril and an Opportunity.
 Peril - Possibility of making the Transition from an algorithm to a program either
Incorrectly or very Inefficiently.
Modern compilers can be used in code optimization mode to avoid Inefficient implementation.

 Unless the Correctness is proven with full Mathematical Rigor, the program cannot be
considered Correct.
 Practically the validity of programs is established by Testing.
 Provide Verification to check whether Inputs belong to the Specified Sets.
 Use Standard Tricks as computing a loop’s invariant outside the loop, collecting
common subexpressions, replacing expensive operations by cheap ones, and so on.

Important Problem Types
1. Sorting
2. Searching
3. String processing
4. Graph problems
5. Combinatorial problems
6. Geometric problems
7. Numerical problems

Important Problem Types…
1. Sorting
• Rearrange the items of a given list in Order.
Eg.: Numbers, Character Strings, Records, etc.
• Nature of the list items must Allow such an Ordering.
Eg.: Number – Value, Character Strings – Alphabet Order.
• Key - a piece of information used to Guide Sorting.
Eg.: Numbers – Number itself, Records – Student No., Name, etc.
• Sorting makes many Questions about the list Easier to answer. Eg:. Searching.
• Sorting is used as an Auxiliary Step in several important algorithms. Eg.: Geometric
algorithms and Data Compression.
• There are a few good sorting algorithms that sort an arbitrary array of size n using
about n log2 n comparisons.
• No algorithm that sorts by key comparisons can do better than n log2 n comparisons.

• Properties of Sorting Algorithms:
1. Stable
 Preserves the Relative Order of any two Equal Elements in its input.
 If an Input List contains Two Equal Elements in Positions i and j where i < j, then
in the Sorted List they have to be in positions i‘ and j’ respectively, such that i’ < j’.
Eg.: Sort a list of students alphabetically and sort it according to student GPA:
A stable algorithm will yield a list in which students with the same GPA will
still be sorted alphabetically.
 Algorithms that can Exchange Keys located far apart are Not Stable, but they
usually work faster.
2. In-Place
 Does not require Extra Memory, except, possibly, for a few memory units.

2. Searching
• Finding a given value, called a search Key, in a given set.
• Range from the Straightforward Sequential Search to a spectacularly Efficient but
limited Binary Search and algorithms based on representing the underlying set in a
different form.
3. String Processing
• String - A Sequence of Characters from an alphabet.
Eg.: Text Strings – Letters, Numbers and Special Characters.
Bit Stings – Zeros and Ones.
Gene Sequences
• String Matching - Searching for a given Word in a Text.

4. Graph Problems
• Graph – Collection of Points called Vertices, some of which are connected by Line
Segments called Edges.
 Graphs Applications - Transportation, Communication, Social and Economic
Networks, Project Scheduling, and Games.
• Graph Algorithms - Graph-Traversal, Shortest-Path, Topological Sorting, etc.
• Some graph problems are computationally very hard. Eg.: Graph-Coloring Problem,
Travelling Salesman Problem, etc.
5. Combinatorial Problems
• Require to find a combinatorial object such as a Permutation, Combination or Subset
that satisfies certain constraints.
• May also be required to have some Additional Property such as a maximum value or a
minimum cost.

• Most Difficult problems in computing, from both a theoretical and practical standpoint
because:
 The Number typically Grows Extremely Fast with a problem’s size, reaching
unimaginable magnitudes even for moderate-sized instances.
 There are No Known Algorithms for solving most such problems exactly in an
acceptable amount of time
6. Geometric Problems
• Geometric algorithms deal with geometric objects such as Points, Lines, and
Polygons.
• Geometric algorithms applications – Computer Graphics, Robotics, and Tomography.
7. Numerical Problems
• Involve mathematical objects of Continuous Nature. Eg.: Solving equations and
systems of equations, computing definite integrals, evaluating functions, etc.

7. Numerical Problems
• Involve mathematical objects of Continuous Nature. Eg.: Solving equations and
systems of equations, computing definite integrals, evaluating functions, etc.
• Play a critical role in many Scientific and Engineering applications.
• Majority of such mathematical problems can be solved only Approximately.
• Typically require manipulating Real Numbers, which can be represented in a
computer only approximately.
• A large number of arithmetic operations performed on approximately represented
numbers can lead to an Accumulation of the Round-off Error to a point where it can
drastically distort an output.

References:
• Anany Levitin, Introduction to the Design and Analysis of Algorithms, 3rd Edition,
2012, Pearson Education.
• Ellis Horowitz, Sartaj Sahni, and Sanguthevar Rajasekaran, Computer Algorithms,
1997, Computer Science Press.

Introduction to Algorithm Design and Analysis.pdf

Recommended

More Related Content

What's hot (20)

Similar to Introduction to Algorithm Design and Analysis.pdf (20)

More from Kiran K (8)

Recently uploaded (20)

Introduction to Algorithm Design and Analysis.pdf